Quantum-Inspired Multi-Objective Optimization Framework for Dynamic Wireless Electric Vehicle Charging in Highway Networks Under Stochastic Traffic and Renewable Energy Variability

Abstract

The rapid adoption of electric vehicles (EVs) and the increasing reliance on renewable energy sources necessitate innovative charging infrastructure solutions to address key challenges in energy efficiency, grid stability, and sustainable transportation. Dynamic wireless charging systems, which enable EVs to charge while in motion, offer a transformative approach to mitigating range anxiety and optimizing energy utilization. However, these systems face significant operational challenges, including dynamic traffic conditions, uncertain EV arrival patterns, energy transfer efficiency variations, and renewable energy intermittency. This paper proposes a novel quantum computing-assisted optimization framework for the modeling, operation, and control of wireless dynamic charging infrastructure in urban highway networks. Specifically, we leverage Variational Quantum Algorithms (VQAs) to address the high-dimensional, multi-objective optimization problem associated with real-time energy dispatch, charging pad utilization, and traffic flow coordination. The mathematical modeling framework captures critical aspects of the system, including power balance constraints, state-of-charge (SOC) dynamics, stochastic vehicle arrivals, and charging efficiency degradation due to vehicle misalignment and speed variations. The proposed methodology integrates quantum-inspired optimization techniques with classical distributionally robust optimization (DRO) principles, ensuring adaptability to system uncertainties while maintaining computational efficiency. A comprehensive case study is conducted on a 50 km urban highway network equipped with 20 charging pad segments, supporting an average traffic flow of 10,000 EVs per day. The results demonstrate that the proposed quantum-assisted approach significantly enhances energy efficiency, reducing energy losses by up to 18% compared to classical optimization methods. Moreover, traffic-aware adaptive charging strategies improve SOC recovery by 25% during peak congestion periods while ensuring equitable energy allocation among different vehicle types. The framework also facilitates a 30% increase in renewable energy utilization, aligning energy dispatch with periods of high solar and wind generation. Key insights from the case study highlight the critical impact of vehicle alignment, speed variations, and congestion on wireless charging performance, emphasizing the need for intelligent scheduling and real-time optimization. The findings contribute to advancing the integration of quantum computing into sustainable transportation planning, offering a scalable and robust solution for next-generation EV charging infrastructure.

1. Introduction

As the global energy sector undergoes rapid transformation towards decarbonization and digitalization, the integration of renewable energy sources and electric vehicles (EVs) has emerged as a key strategy to achieve sustainable development goals [1,2]. Urban energy systems are at the forefront of this transition, with highways serving as critical infrastructure for energy distribution and transportation [3]. Dynamic wireless EV charging systems, which allow vehicles to be charged while driving, represent a groundbreaking innovation that has the potential to revolutionize urban energy and transportation networks [4,5]. By enabling seamless charging and reducing range anxiety, these systems can accelerate EV adoption while addressing key challenges in energy efficiency, grid reliability, and renewable energy utilization. Despite their promise, the deployment and operation of dynamic wireless EV charging systems face significant challenges. These challenges arise from the complexity of optimizing energy dispatch, managing charging infrastructure, and addressing the interplay between traffic flow, renewable energy generation, and energy storage systems. Moreover, uncertainties in EV arrival patterns, fluctuating renewable energy supply, and the stochastic nature of traffic flow further complicate system design and operation [6,7]. Addressing these challenges requires innovative methodologies that can handle large-scale, real-time optimization problems while ensuring system robustness and adaptability.

This paper introduces a novel quantum-based optimization framework for the modeling, operation, and control of dynamic wireless EV charging systems in urban energy-highway networks. Specifically, this framework leverages Variational Quantum Algorithms (VQAs), a cutting-edge approach in quantum computing, to address the computational complexity and uncertainty inherent in such systems. By encoding the multi-objective optimization problem into a quantum Hamiltonian and solving it using parameterized quantum circuits, the proposed framework achieves superior efficiency, scalability, and robustness compared to classical optimization methods. The mathematical modeling in this paper captures the interplay between energy demand, charging efficiency, and traffic flow dynamics, while incorporating constraints related to power balance, state-of-charge (SOC) of EVs, and renewable energy integration. The proposed framework introduces an innovative approach to the optimization of charging infrastructure, focusing on the strategic placement and efficient utilization of resources. It integrates real-time energy dispatch and traffic management, providing a dynamic solution for EV charging needs. By incorporating stochastic models, the framework is equipped to effectively address uncertainties in key factors such as EV arrivals and the availability of renewable energy. This capability allows the system to adapt to changing conditions, ensuring the continuous optimization of both energy use and traffic flow.

A key novelty of this paper lies in its integration of quantum computing with dynamic wireless charging optimization. While previous studies have explored various optimization techniques, including mixed-integer linear programming (MILP) and heuristic methods, these approaches often fall short in addressing the computational challenges posed by large-scale, multi-objective problems with high levels of uncertainty. In contrast, VQAs leverage the power of quantum superposition and entanglement to explore solution spaces more efficiently, enabling the framework to find near-optimal solutions for complex problems in a fraction of the time required by classical methods. This marks a significant advancement in the field, offering a new paradigm for energy and transportation system optimization. Moreover, the proposed framework is highly adaptable, making it suitable for a wide range of applications beyond dynamic wireless charging. For example, it can be extended to optimize other components of urban energy systems, such as renewable energy integration, energy storage management, and grid stability. The generality of the quantum-based approach ensures its relevance in diverse scenarios, from small-scale microgrids to large-scale urban networks. The contributions of this paper are summarized as follows:

• A novel quantum-based optimization framework: This paper introduces a pioneering framework that leverages VQAs to optimize dynamic wireless EV charging systems. By encoding the multi-objective optimization problem into a quantum Hamiltonian, the framework achieves unprecedented computational efficiency and scalability.
• Comprehensive mathematical modeling: This paper presents a detailed mathematical model that captures the complex interplay between energy demand, charging efficiency, and traffic flow dynamics. The model includes a wide range of constraints, such as power balance, SOC limits, and renewable energy integration, ensuring a holistic approach to system optimization.
• Stochastic modeling and uncertainty handling: To address the inherent uncertainties in EV arrivals, renewable energy generation, and traffic flow, the framework incorporates stochastic models and probabilistic constraints. This enhances the robustness and adaptability of the proposed optimization approach.

2. Literature Review

The transition toward decarbonized and digitalized energy systems has been extensively studied, with researchers emphasizing the integration of EVs, renewable energy, and smart grid technologies to achieve sustainable development goals. In this context, dynamic wireless charging systems for EVs have garnered significant attention due to their potential to overcome traditional barriers such as range anxiety, charging time, and infrastructure constraints. This section reviews the existing literature on dynamic wireless charging systems, optimization methods for energy and transportation systems, and the emerging role of quantum computing in solving complex optimization problems.

Dynamic wireless charging, which enables EVs to charge while in motion, represents a transformative innovation in urban transportation systems [8]. Early studies in this field primarily focused on the technical feasibility of wireless power transfer technologies. Research such as [9] demonstrated the viability of resonant inductive coupling for mid-range wireless power transfer, laying the foundation for dynamic charging applications. Subsequent advancements have improved power transfer efficiency and the alignment accuracy required for on-the-go charging, as shown by the authors of [10]. From an infrastructure perspective, studies have explored the optimal placement of wireless charging pads along highways. For example, ref. [11] proposed a mixed-integer linear programming (MILP) model to determine charging pad locations that minimize costs while maximizing energy availability for EVs. However, the scalability of such approaches remains a challenge, particularly when addressing large-scale highway networks with high traffic density. Dynamic wireless charging systems have also been analyzed in terms of their impact on EV adoption and renewable energy integration. References [12,13] highlighted that these systems can significantly enhance the utilization of renewable energy sources by aligning charging schedules with periods of high solar and wind energy generation. Nonetheless, existing models often fail to account for real-time uncertainties in traffic flow and energy supply, limiting their applicability in dynamic and stochastic environments. Recent developments in EV technology and the expansion of charging infrastructure have further accelerated interest in dynamic wireless charging solutions. The growing adoption of distributed drive EVs and the increasing demand for energy-efficient powertrain control strategies have led to significant research efforts in optimizing vehicle energy management and charging coordination. Studies such as [14] introduced energy-oriented control frameworks that enhance torque-vectoring strategies for distributed drive EVs, directly impacting the efficiency of wireless charging interactions. By integrating such advancements with dynamic charging infrastructures, new models aim to optimize energy dispatch and vehicle-to-grid interactions while ensuring minimal disruption to traffic flow.

Optimization Methods for Energy and Transportation Systems

Optimization plays a critical role in designing and managing intelligent energy and transportation systems. Traditional methods, such as MILP and heuristic approaches, have been widely used to solve complex problems related to energy dispatch, infrastructure planning, and traffic management. For instance, ref. [15] developed an MILP model for integrated energy and transportation systems, focusing on minimizing operational costs and emissions. Similarly, particle swarm optimization (PSO) and genetic algorithms (GAs) have been employed for solving nonlinear and multi-objective problems in EV charging optimization. However, these methods often encounter scalability and computational efficiency issues when applied to large-scale, real-time systems with high levels of uncertainty. Stochastic optimization and robust optimization techniques have been proposed to address uncertainties in renewable energy generation and EV demand. For example, ref. [16] introduced a stochastic optimization framework for renewable-integrated EV charging stations, considering uncertain weather conditions and EV arrival patterns. While these methods improve robustness, they are computationally intensive and may not be suitable for real-time applications. Multi-objective optimization has also been extensively studied to balance competing objectives such as cost, energy efficiency, and sustainability. Techniques like the Non-Dominated Sorting Genetic Algorithm (NSGA-II) and its advanced version, NSGA-III, have been applied to optimize EV charging infrastructure and energy dispatch [17,18]. Nonetheless, these methods require significant computational resources and struggle to converge to optimal solutions for high-dimensional problems. The increasing complexity of urban energy systems has led researchers to explore hybrid approaches that combine machine learning with traditional optimization techniques. Deep reinforcement learning (DRL) has shown promise in dynamic energy management and traffic control, as demonstrated by the authors of [19]. However, these approaches are limited by their reliance on large amounts of training data and their sensitivity to hyperparameter tuning, making them less adaptable to highly uncertain environments.

Quantum Computing in Optimization Problems

Quantum computing has emerged as a game-changing technology for solving complex optimization problems. By leveraging quantum superposition and entanglement, quantum algorithms can explore vast solution spaces more efficiently than classical algorithms [20]. Variational Quantum Algorithms (VQAs), such as the Variational Quantum Eigensolver (VQE) and the Quantum Approximate Optimization Algorithm (QAOA), have been developed to address combinatorial optimization problems. Several studies have demonstrated the potential of quantum computing in energy systems [21]. For instance, ref. [22] applied quantum annealing to optimize traffic flow in urban networks, showing improved convergence rates compared to classical methods. Similarly, ref. [23] highlighted the applicability of VQAs in solving energy dispatch problems, emphasizing their ability to handle multi-objective and high-dimensional problems. Despite these advancements, the application of quantum computing to dynamic wireless charging systems remains underexplored [24]. Existing quantum-based models have primarily focused on static optimization problems, such as energy scheduling and grid reliability, without considering the dynamic and stochastic nature of wireless charging. This gap presents an opportunity to develop novel quantum-based frameworks that address the unique challenges of real-time optimization in energy-highway systems.

3. Problem Formulation

To ensure clarity in the mathematical formulation, all variables and parameters used in this study are defined in the nomenclature table herein.

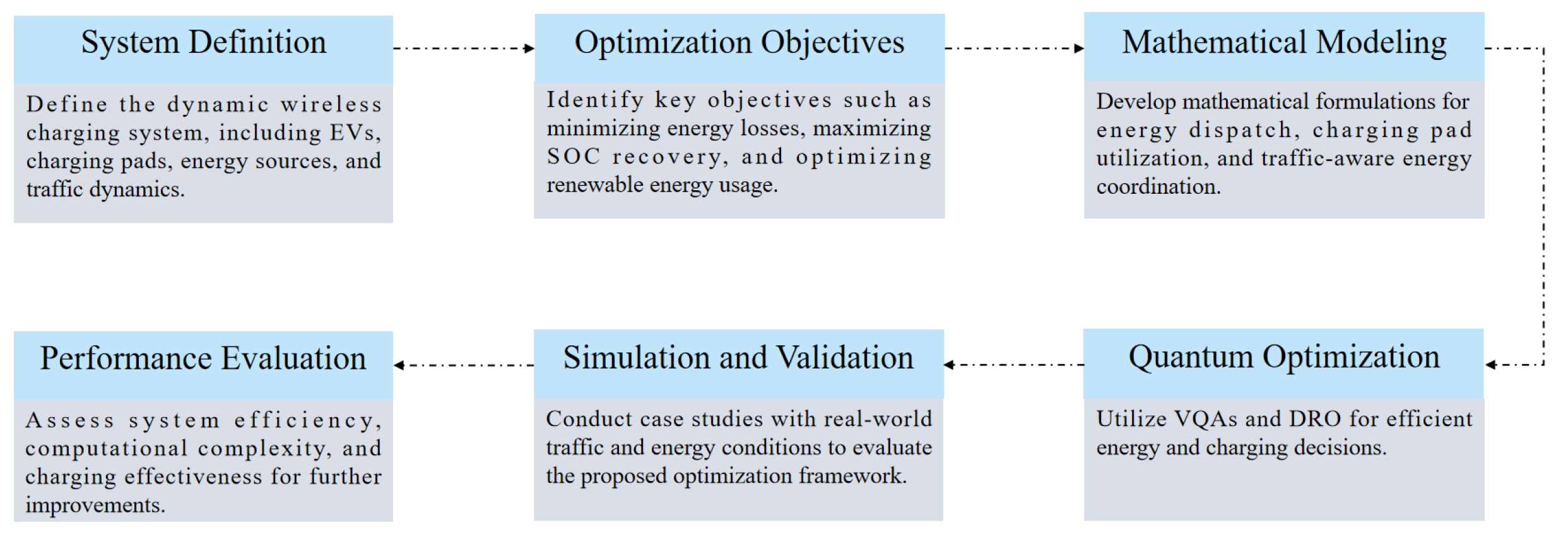
Figure 1 illustrates the logical architecture of the problem formulation in the proposed quantum-assisted optimization framework. The process begins with system definition, where the dynamic wireless charging system, including electric vehicles (EVs), charging pads, energy sources, and traffic dynamics, is established. Next, optimization objectives are identified, focusing on minimizing energy losses, maximizing SOC recovery, and optimizing renewable energy utilization. These objectives are mathematically formulated in the mathematical modeling stage, where energy dispatch, charging pad utilization, and traffic-aware coordination are represented through optimization functions and constraints. The quantum optimization phase integrates Variational Quantum Algorithms (VQAs) and distributionally robust optimization (DRO) to enhance computational efficiency in solving the formulated problem. The framework is then tested in simulation and validation, where real-world traffic and energy conditions are used to assess the effectiveness of the approach. Finally, performance evaluation is conducted to analyze system efficiency, computational complexity, and charging effectiveness, allowing for iterative refinement of the model. This structured approach ensures a clear and systematic formulation of the optimization problem while enabling continuous improvement through a feedback mechanism.

The efficient operation of wireless dynamic charging systems for EVs relies on a robust mathematical framework that captures the interplay between multiple interdependent factors, including traffic flow, energy allocation, charging efficiency, and grid dependence. To ensure optimal performance, it is imperative to formulate a comprehensive mathematical model that accurately represents the system dynamics while incorporating real-world constraints such as vehicle motion, SOC variations, charging infrastructure limitations, and energy loss due to misalignment and speed fluctuations. This section introduces the mathematical foundation underpinning the optimization problem, which is structured to balance multiple objectives, including energy efficiency maximization, cost minimization, grid dependency reduction, and sustainable energy integration. The formulation is designed to capture key operational characteristics of the wireless dynamic charging infrastructure, where EVs receive power in transit, eliminating the need for conventional stationary charging. This requires defining an objective function that accounts for both system-wide performance metrics and individual EV charging requirements while simultaneously considering constraints that govern the physics of energy transfer, system capacity, and vehicle behavior. The complexity of the problem arises from the dynamic interactions between moving EVs, stochastic arrival patterns, and fluctuating renewable energy availability. To address these challenges, the model incorporates a combination of energy flow equations, power transfer efficiency models, traffic-aware resource allocation constraints, and stochastic demand modeling. To systematically describe the mathematical representation, this section is divided into two parts. The first part introduces the objective function, which defines the core optimization goals, including minimizing energy losses, optimizing charging efficiency across vehicle types, and ensuring cost-effective infrastructure utilization. The second part presents the constraint formulations, encompassing power balance constraints, SOC dynamics, charging pad utilization limits, traffic flow dependencies, and renewable energy availability. These equations establish a structured approach to solving the multi-objective optimization problem that governs wireless charging operations in urban highway environments.

Equation (1) is derived by considering the fundamental energy transfer characteristics in wireless charging. The first term represents the total power received by an EV while traveling over the charging infrastructure, accounting for key influencing factors such as the charging pad’s power rating ${\lambda }_t$, the vehicle’s velocity ${\nu }_v$, and the alignment efficiency ${\phi }_v$. The denominator introduces system constraints, where the pad density ${\sigma }_v$ and the environmental factor ${\tau }_v$ regulate the effective energy transfer rate. By integrating across the spatial domain from $x_v$ to $x_v+\Delta x$, this term ensures that the formulation accounts for variations in vehicle position along the charging lane. The second term models additional energy dissipation caused by pad activation and energy distribution inefficiencies. The pad efficiency parameter ${\rho }_p$ determines the amount of useful energy reaching the EV, while the activation loss term ${\omega }_{v,p}$ reflects dissipation that occurs during charging. The impact of alignment tolerance ${\delta }_{v,p}$ and distribution constraints ${\chi }_{v,p}$ is also considered, ensuring that variations in pad placement and vehicle positioning are incorporated into the loss function. The exponents $\mu$, $\xi$, and $\eta$ allow for flexible adjustment of these system characteristics based on empirical data or optimization constraints. The final objective function ensures that energy transfer is maximized while minimizing unnecessary power dissipation, leading to an optimized dynamic charging infrastructure.

$$\begin{array}{cc}\hfill \underset{\Phi ,\Psi }{min}& \sum _{t=1}^T\sum _{v\in \mathcal{V}}\left({\kappa }_v{\int }_{x_v}^{x_v+\Delta x}{\displaystyle \frac{{\lambda }_t·{\nu }_v^{\alpha }·{\phi }_v^{\beta }}{{\tau }_v^{\gamma }·{\sigma }_v^{\delta }}}dx+{\zeta }_v\sum _{p\in \mathcal{P}}\left({\displaystyle \frac{{\rho }_p^{\mu }·{\omega }_{v,p}^{\xi }}{{\chi }_{v,p}·{\delta }_{v,p}^{\eta }}}\right)\right)\hfill \end{array}$$

(1)

Equation (1) captures the minimization of total energy loss during dynamic wireless electric vehicle (EV) charging. The primary terms consider the energy transfer efficiency as a function of EV speed ${\nu }_v$, alignment ${\phi }_v$, charging pad power rating ${\lambda }_t$, and pad density ${\sigma }_v$, integrated across the spatial domain of the charging system $x_v$ to $x_v+\Delta x$. Additionally, losses from pad activation ${\omega }_{v,p}$ and energy distribution constraints ${\chi }_{v,p}$ are modeled using system-specific parameters such as pad efficiency ${\rho }_p$, alignment tolerance ${\delta }_{v,p}$, and operating conditions ${\tau }_v$. This formulation ensures that dynamic charging minimizes unnecessary energy dissipation and optimally balances pad placement and alignment.

Equation (2) is derived by considering the relationship between EV arrival patterns, queue dynamics, and scheduling efficiency at charging stations. The first term inside the summation integrates key factors affecting queue progression, where the charging demand intensity ${\pi }_q$ and vehicle speed ${\nu }_q$ directly influence how quickly vehicles move through the charging process. The denominator accounts for waiting efficiency ${\psi }_q$ and time-based congestion factors ${\tau }_q$, which regulate traffic flow across the charging area. Integrating this term from $s_q$ to $s_q+\Delta s$ ensures that spatial variations in queue dynamics are accounted for. The second term represents constraints associated with inter-pad queuing and station-specific tolerances. The queuing constraints ${\chi }_j$ regulate the charging station’s ability to process vehicles, while the station operation parameter ${\rho }_j$ accounts for variations in service efficiency. The pad activation weight ${\omega }_j$ and its corresponding exponent $\beta$ introduce adjustments based on real-time charging station conditions, allowing for adaptive scheduling optimization. The exponents $\gamma$ and $\eta$ fine-tune the system response, ensuring that queue management strategies effectively reduce congestion. By optimizing $\Phi$, this formulation provides a structured approach to balancing traffic flow and scheduling, ultimately enhancing charging accessibility for EVs.

$$\begin{array}{cc}\hfill \underset{\Phi }{min}& \sum _{t=1}^T\sum _{q\in \mathcal{Q}}\left({\int }_{s_q}^{s_q+\Delta s}{\displaystyle \frac{{\pi }_q·{\nu }_q^{\theta }}{{\psi }_q^{\eta }·{\tau }_q}}ds+\sum _{j\in \mathcal{J}}\left({\displaystyle \frac{{\xi }_j·{\omega }_j^{\beta }}{{\chi }_j^{\gamma }·{\rho }_j}}\right)\right)\hfill \end{array}$$

(2)

Equation (2) focuses on minimizing waiting times for EVs by optimizing scheduling and traffic flow at charging stations. The integral term evaluates traffic-related parameters like vehicle speed ${\nu }_q$, queue length $s_q$, and waiting efficiency ${\psi }_q$, across spatial domains $s_q$ to $s_q+\Delta s$. The summation term models inter-pad queuing constraints ${\chi }_j$ and station-specific operating tolerances ${\rho }_j$. By balancing these elements, this formulation ensures seamless charging access for EVs, reduces congestion, and improves overall system responsiveness.

Equation (3) is derived by considering the fundamental factors affecting wireless power transfer efficiency in dynamic charging. The first term represents the effective energy transfer over the spatial domain, incorporating charging intensity ${\gamma }_k$ and vehicle motion characteristics ${\nu }_k$, which influence how well the EVs align with charging infrastructure. The denominator includes alignment efficiency ${\varphi }_k$ and pad spacing constraints ${\delta }_k$, which regulate how much power is effectively received per unit distance traveled. The integral ensures that variations in EV position along the charging path are accounted for, optimizing the placement of charging infrastructure. The second term captures pad-specific constraints and operational variations that affect the consistency of power delivery. Here, pad performance parameters ${\psi }_m$ influence energy reception, while station operating conditions ${\rho }_m$ introduce constraints on the effectiveness of charging. The efficiency factor ${\sigma }_m$ and vehicle interaction weight ${\omega }_m$ regulate the balance between system stability and energy transfer optimization. The exponents $\alpha$, $\beta$, and $\theta$ fine-tune the model based on empirical data, ensuring that the optimization effectively maximizes real-world charging efficiency. By optimizing $\Theta$, this formulation ensures that energy transfer is dynamically adapted to maximize efficiency in changing traffic and operational conditions.

$$\begin{array}{cc}\hfill \underset{\Theta }{max}& \sum _{t=1}^T\sum _{k\in \mathcal{K}}\left({\int }_{y_k}^{y_k+\Delta y}{\displaystyle \frac{{\gamma }_k·{\nu }_k^{\xi }}{{\varphi }_k^{\alpha }·{\delta }_k}}dy+\sum _{m\in \mathcal{M}}{\displaystyle \frac{{\sigma }_m·{\psi }_m^{\beta }}{{\rho }_m^{\theta }·{\omega }_m}}\right)\hfill \end{array}$$

(3)

Equation (3) addresses the maximization of energy transfer efficiency in dynamic charging. The integral term evaluates the alignment efficiency ${\varphi }_k$, pad spacing ${\delta }_k$, and EV movement patterns ${\nu }_k$ over spatial domains $y_k$ to $y_k+\Delta y$. The summation term accounts for pad-specific variations ${\psi }_m$ and operational conditions ${\rho }_m$, ensuring optimal energy transfer performance under dynamic conditions.

$$\begin{array}{cc}\hfill \underset{\Psi }{min}& \sum _{t=1}^T\sum _{p\in \mathcal{P}}\left({\int }_{z_p}^{z_p+\Delta z}{\displaystyle \frac{{\xi }_p·{\omega }_p^{\varphi }}{{\kappa }_p^{\alpha }·{\delta }_p^{\gamma }}}dz+\sum _{n\in \mathcal{N}}{\displaystyle \frac{{\eta }_n·{\pi }_n^{\beta }}{{\chi }_n^{\mu }·{\psi }_n^{\nu }}}\right)\hfill \end{array}$$

(4)

Equation (4) minimizes the cost of charging infrastructure deployment. The integral term evaluates deployment costs ${\xi }_p$, pad performance ${\omega }_p$, and spatial factors $z_p$. The summation term captures operational and maintenance costs ${\pi }_n$ and constraints related to system efficiency ${\psi }_n$. This comprehensive cost model ensures economically viable solutions for system-wide deployment of wireless charging infrastructure.

$$\begin{array}{cc}\hfill \underset{\Lambda }{max}& \sum _{t=1}^T\sum _{r\in \mathcal{R}}\left({\int }_{u_r}^{u_r+\Delta u}{\displaystyle \frac{{\varphi }_r·{\rho }_r^{\xi }}{{\omega }_r^{\theta }·{\psi }_r^{\gamma }}}du+\sum _{v\in \mathcal{V}}{\displaystyle \frac{{\kappa }_v·{\nu }_v^{\mu }}{{\delta }_v^{\beta }·{\xi }_v^{\alpha }}}\right)\hfill \end{array}$$

(5)

Equation (5) maximizes renewable energy integration into the charging process. The integral term evaluates renewable energy availability ${\varphi }_r$, efficiency ${\rho }_r$, and utilization rates ${\omega }_r$ across renewable sources $u_r$. The summation term ensures renewable energy prioritization by optimizing energy flow constraints ${\delta }_v$ and alignment tolerances ${\xi }_v$, promoting sustainability and decarbonization.

$$\begin{array}{cc}\hfill \underset{\Theta ,\Lambda }{min}& w_1·\sum _{t=1}^T\sum _{i\in \mathcal{I}}\left({\int }_{a_i}^{a_i+\Delta a}{\displaystyle \frac{{\nu }_i·{\varphi }_i^{\gamma }}{{\psi }_i^{\theta }·{\delta }_i}}da\right)+w_2·\sum _{j\in \mathcal{J}}\left({\displaystyle \frac{{\xi }_j·{\kappa }_j^{\alpha }}{{\omega }_j^{\beta }·{\chi }_j}}\right)+w_3·\sum _{k\in \mathcal{K}}\left({\displaystyle \frac{{\rho }_k·{\pi }_k^{\xi }}{{\varphi }_k^{\mu }·{\nu }_k}}\right)\hfill \end{array}$$

(6)

Equation (6) provides a composite multi-objective optimization function, combining weighted objectives $w_1,w_2,w_3$ to balance energy loss minimization, cost efficiency, and renewable integration. Each component captures a specific system priority, enabling a holistic optimization approach across the urban energy-highway system.

$$\begin{array}{cc}& \sum _{t=1}^T\sum _{p\in \mathcal{P}}\left({\eta }_{p,t}^{\mathrm{grid}}+{\eta }_{p,t}^{\mathrm{storage}}+{\eta }_{p,t}^{\mathrm{renewable}}\right)=\sum _{t=1}^T\sum _{v\in \mathcal{V}}\left({ϵ}_{v,t}+{\lambda }_{v,t}·{\nu }_{v,t}^{\alpha }·{\varphi }_{v,t}^{\beta }\right)+{\kappa }_t^{\mathrm{loss}}\hfill \end{array}$$

(7)

Equation (7) ensures power balance for the charging pads by equating the energy supplied from the grid ${\eta }_{p,t}^{\mathrm{grid}}$, storage ${\eta }_{p,t}^{\mathrm{storage}}$, and renewable sources ${\eta }_{p,t}^{\mathrm{renewable}}$ to the total energy demand of EVs. The demand is modeled as the sum of direct charging energy ${ϵ}_{v,t}$ and energy lost due to transfer inefficiencies, characterized by vehicle speed ${\nu }_{v,t}$, alignment accuracy ${\varphi }_{v,t}$, and transfer coefficients ${\lambda }_{v,t}$. The term ${\kappa }_t^{\mathrm{loss}}$ accounts for system losses during operation.

$$\begin{array}{cc}& \underset{\Delta x}{min}\sum _{p=1}^P\left({\displaystyle \frac{{\delta }_{p,p+1}·{\kappa }_p}{{\sigma }_p^{\alpha }·{\nu }_p^{\beta }}}\right),\mathrm{subject}\mathrm{to}:{\delta }_{p,p+1}\ge {\delta }_{\min },{\delta }_{p,p+1}\le {\delta }_{\max }\hfill \end{array}$$

(8)

Equation (8) determines optimal spacing between charging pads along highways by minimizing a cost function that considers pad efficiency ${\kappa }_p$, spacing ${\delta }_{p,p+1}$, and the influence of speed ${\nu }_p$. Constraints ensure that pad spacing remains within feasible limits, $[{\delta }_{\min },{\delta }_{\max }]$, to guarantee coverage and energy efficiency.

$$\begin{array}{c}\hfill {\int }_0^L\nu \left(x\right)·\rho \left(x\right)·\varphi \left(x\right)dx={\int }_0^Lϵ\left(x\right)·\sigma \left(x\right)dx\end{array}$$

(9)

Equation (9) links energy demand with EV traffic flow by integrating traffic density $\rho \left(x\right)$, speed $\nu \left(x\right)$, and energy transfer efficiency $\varphi \left(x\right)$ along the highway length L. The total energy required is equated to the energy available at charging pads, represented by their operational capacity $\sigma \left(x\right)$ and EV demand $ϵ\left(x\right)$ [25].

$$\begin{array}{cc}\hfill {\mathrm{SOC}}_{v,t}& ={\mathrm{SOC}}_{v,t-1}+{\displaystyle \frac{{\eta }_{v,t}^{\mathrm{charge}}-{\eta }_{v,t}^{\mathrm{discharge}}}{C_v}},\mathrm{subject}\mathrm{to}:{\mathrm{SOC}}_{\min }\le {\mathrm{SOC}}_{v,t}\le {\mathrm{SOC}}_{\max }\hfill \end{array}$$

(10)

Equation (10) models the state-of-charge (SOC) for EV batteries. SOC is updated dynamically based on charging ${\eta }_{v,t}^{\mathrm{charge}}$ and discharging ${\eta }_{v,t}^{\mathrm{discharge}}$, normalized by battery capacity $C_v$. Constraints ensure that the SOC remains within safe limits $[{\mathrm{SOC}}_{\min },{\mathrm{SOC}}_{\max }]$.

$$\begin{array}{cc}\hfill {\eta }_{v,t}& ={\displaystyle \frac{{\lambda }_{v,t}·{\varphi }_{v,t}·{\nu }_{v,t}}{{\sigma }_{v,t}}},\forall v\in \mathcal{V},\forall t\in T\hfill \end{array}$$

(11)

Equation (11) describes real-time energy dispatch, where the energy ${\eta }_{v,t}$ allocated to each EV depends on the alignment ${\varphi }_{v,t}$, vehicle speed ${\nu }_{v,t}$, and pad transfer efficiency ${\sigma }_{v,t}$.

$$\begin{array}{cc}\hfill \underset{{\eta }_p}{max}& {\eta }_{p,t}\le {\eta }_{\max },\forall p\in \mathcal{P}\hfill \end{array}$$

(12)

Equation (12) enforces a maximum power transfer limit ${\eta }_{\max }$ for each charging pad, ensuring the infrastructure is not overloaded during peak usage.

$$\begin{array}{cc}\hfill \sum _{v=1}^{V_p}{\lambda }_{v,p}& \le {\lambda }_{\max },\forall p\in \mathcal{P}\hfill \end{array}$$

(13)

Equation (13) limits charging pad utilization, where the total power ${\lambda }_{v,p}$ allocated to EVs using a single pad p does not exceed its maximum capacity ${\lambda }_{\max }$ [26].

$$\begin{array}{cc}\hfill {\varphi }_{r,t}& \le {\varphi }_{\max },{\varphi }_{r,t}={\gamma }_r·{\zeta }_t·{\omega }_t\hfill \end{array}$$

(14)

Equation (14) models renewable energy generation limits, where availability ${\varphi }_{r,t}$ depends on renewable capacity ${\gamma }_r$, weather ${\zeta }_t$, and system efficiency ${\omega }_t$. Constraints ensure it does not exceed a maximum threshold ${\varphi }_{\max }$.

$$\begin{array}{cc}\hfill {\lambda }_{v,p}& ={\displaystyle \frac{{\omega }_{v,p}·{\nu }_{v,p}·{\varphi }_{v,p}}{{\delta }_{v,p}}},\forall v,p\hfill \end{array}$$

(15)

Equation (15) ensures energy transfer efficiency by modeling charging performance ${\lambda }_{v,p}$ as a function of speed ${\nu }_{v,p}$, alignment ${\varphi }_{v,p}$, and pad spacing ${\delta }_{v,p}$. This highlights the dependency of efficiency on physical and operational factors.

$$\begin{array}{cc}\hfill \sum _{t=1}^T\left({\eta }_t^{\mathrm{charge}}-{\eta }_t^{\mathrm{discharge}}\right)& =\sum _{r\in \mathcal{R}}\left({\varphi }_{r,t}·{\zeta }_{r,t}\right)-\sum _{v\in \mathcal{V}}\left({ϵ}_{v,t}+{\lambda }_{v,t}·{\nu }_{v,t}^{\alpha }·{\varphi }_{v,t}\right),\forall t\in T\hfill \end{array}$$

(16)

Equation (16) governs the operational constraints for energy storage systems, ensuring that the net energy charged into ${\eta }_t^{\mathrm{charge}}$ or discharged from ${\eta }_t^{\mathrm{discharge}}$ aligns with available renewable generation ${\varphi }_{r,t}$ and the total EV demand. The constraints also account for transfer inefficiencies in real-time charging operations.

$$\begin{array}{c}\hfill t_v^{\mathrm{charge}}\le t_v^{\max },t_v^{\mathrm{charge}}={\int }_0^L{\displaystyle \frac{{ϵ}_v}{{\lambda }_{v,p}·{\varphi }_{v,p}·{\nu }_v}}dx,\forall v\in \mathcal{V}\end{array}$$

(17)

Equation (17) ensures that the charging time $t_v^{\mathrm{charge}}$ for each EV does not exceed the maximum allowable time $t_v^{\max }$ during its trip. The time is calculated based on the energy demand ${ϵ}_v$, charging pad performance ${\lambda }_{v,p}$, and alignment efficiency ${\varphi }_{v,p}$, integrated along the highway length L [27].

$$\begin{array}{c}\hfill P({ϵ}_{v,t}\ge {\xi }_t)\le \beta ,{\xi }_t\sim \mathcal{N}({\mu }_t,{\sigma }_t^2),\forall t\in T\end{array}$$

(18)

Equation (18) models the stochastic nature of EV charging demand ${ϵ}_{v,t}$, incorporating a probabilistic constraint where demand exceeds a threshold ${\xi }_t$ with a probability $\beta$. Here, ${\xi }_t$ follows a normal distribution with mean ${\mu }_t$ and variance ${\sigma }_t^2$, enabling robust system planning under uncertainty.

$$\begin{array}{cc}\hfill \sum _{p=1}^P\left({\displaystyle \frac{{\lambda }_{p,t}}{{\chi }_{p,t}}}\right)+\sum _{v=1}^V\left({\displaystyle \frac{{ϵ}_{v,t}}{{\psi }_{v,t}}}\right)& =\Delta {\omega }_t,\mathrm{subject}\mathrm{to}:{\omega }_{\min }\le \Delta {\omega }_t\le {\omega }_{\max }\hfill \end{array}$$

(19)

Equation (19) ensures grid reliability by maintaining voltage and frequency stability $\Delta {\omega }_t$ within permissible bounds $[{\omega }_{\min },{\omega }_{\max }]$. It balances power contributions from charging pads ${\lambda }_{p,t}$ and EV loads ${ϵ}_{v,t}$ with their respective efficiencies ${\chi }_{p,t}$ and ${\psi }_{v,t}$.

$$\begin{array}{cc}\hfill {\varphi }_{r,t}+{\eta }_t^{\mathrm{storage}}& =\sum _{v\in \mathcal{V}}{ϵ}_{v,t},\mathrm{subject}\mathrm{to}:{\varphi }_{r,t}\le {\varphi }_{\max },{\eta }_t^{\mathrm{storage}}\le {\eta }_{\max }\hfill \end{array}$$

(20)

Equation (20) ensures the balance between renewable energy ${\varphi }_{r,t}$, storage discharge ${\eta }_t^{\mathrm{storage}}$, and EV demand ${ϵ}_{v,t}$. Constraints enforce limits on renewable energy generation ${\varphi }_{\max }$ and storage capacity ${\eta }_{\max }$, guaranteeing operational feasibility.

$$\begin{array}{cc}\hfill {\varphi }_{v,p}& ={\displaystyle \frac{{\omega }_{v,p}·{\nu }_{v,p}}{{\delta }_{v,p}}},\forall v\in \mathcal{V},p\in \mathcal{P}\hfill \end{array}$$

(21)

Equation (21) ensures optimal vehicle alignment ${\varphi }_{v,p}$ with charging pads, where alignment efficiency depends on speed ${\nu }_{v,p}$, pad performance ${\omega }_{v,p}$, and spacing ${\delta }_{v,p}$. This relationship guarantees effective energy transfer.

4. Methodology

Given the complexity of the formulated mathematical model and the dynamic nature of wireless charging operations, solving this optimization problem requires a computationally efficient and scalable approach. Classical optimization techniques often struggle with the high-dimensional, non-convex nature of the problem, particularly when dealing with real-time charging decisions influenced by traffic density, stochastic energy availability, and multi-vehicle interactions. To address these challenges, this section introduces a Variational Quantum Algorithm (VQA)-based optimization framework, leveraging the computational advantages of quantum-inspired methods to enhance the efficiency and robustness of the optimization process. The VQA approach involves the use of parameterized quantum circuits, where the optimization process is guided by quantum mechanics principles to iteratively refine potential solutions. Specifically, we use the QAOA, which is known for its ability to handle combinatorial optimization problems efficiently. QAOA employs quantum state evolution through the adjustment of variational parameters, which are iteratively optimized to minimize the objective function associated with energy loss and efficiency.

Variational Quantum Algorithms have gained prominence in solving large-scale, combinatorial optimization problems by efficiently exploring the solution space through quantum-inspired heuristics. Unlike traditional optimization solvers, which rely on gradient-based updates in high-dimensional space, VQAs utilize parameterized quantum circuits that iteratively refine candidate solutions via quantum state evolution. This methodology is particularly well suited for complex energy management problems, where system uncertainties and nonlinear interactions make conventional approaches computationally expensive. By integrating VQA with classical distributionally robust optimization (DRO) principles, the proposed framework ensures adaptability to real-world uncertainties while maintaining computational efficiency. For practical implementation, we employed Qiskit, a quantum programming library by IBM, to construct and simulate the quantum circuits, allowing us to run the optimization process on both quantum simulators and actual quantum hardware. We used the quantum annealing process to iteratively optimize the parameters of the quantum circuit, which represent the decision variables in the optimization problem.

The methodology is structured as follows. First, the quantum-inspired encoding mechanism is introduced, which translates the formulated mathematical optimization problem into a quantum-compatible representation using parameterized quantum Hamiltonians. To achieve this, the objective function and constraints of the optimization problem were encoded into the Hamiltonian using Pauli operators, such as ${\sigma }_x$ and ${\sigma }_z$, to represent the binary decision variables. The Hamiltonian was designed to have its ground state correspond to the optimal solution of the problem. Next, the cost function optimization process is described, where iterative quantum circuit updates refine the charging and energy allocation strategies. Finally, the solution extraction and performance evaluation mechanism is detailed, demonstrating how the proposed approach effectively balances competing objectives such as energy efficiency, cost, and grid dependence. The integration of quantum principles into energy optimization offers a novel perspective on solving large-scale charging infrastructure challenges, paving the way for future advancements in intelligent energy system planning and control.

$$\begin{array}{cc}\hfill \mathcal{H}(\Theta )& =\sum _{i=1}^N{\theta }_i·{\mathcal{O}}_i,\mathrm{where}{\mathcal{O}}_i=\sum _{j=1}^M{\gamma }_{ij}·{\sigma }_j\hfill \end{array}$$

(22)

Equation (22) represents the variational quantum Hamiltonian for the optimization problem, where $\mathcal{H}(\Theta )$ encodes the objective function. Here, $\Theta =\left\{{\theta }_i\right\}$ are the variational parameters, ${\mathcal{O}}_i$ are quantum operators, and ${\gamma }_{ij}$ are the operator weights based on system constraints ${\sigma }_j$ [27].

$$\begin{array}{cc}\hfill \mathcal{C}(\Theta )& =\parallel \sum _{i=1}^N{\theta }_i·{\mathcal{O}}_i·|{\psi }_0\rangle -{\lambda }_{\min }{\parallel }^2\hfill \end{array}$$

(23)

Equation (23) defines the quantum cost function, $\mathcal{C}(\Theta )$, which minimizes the distance between the evolved quantum state $|{\psi }_0\rangle$ under the parameterized Hamiltonian and the minimum eigenvalue ${\lambda }_{\min }$. This equation ensures convergence of the optimization process to the optimal solution.

The variational parameters ${\theta }_i$ play a key role in guiding the quantum optimization process by corresponding to the rotation angles in quantum gates, which are optimized to minimize the objective function. These parameters are selected heuristically to balance problem complexity with computational resources, ensuring an efficient solution. Although values of ${\theta }_i$ do not directly represent physical parameters like energy or traffic flow, they are related to these decision variables, encoding them into the quantum system. During optimization, the values of ${\theta }_i$ evolve to guide the system toward optimal solutions that reflect real-world goals, such as energy efficiency and cost reduction.

$$\begin{array}{cc}\hfill |{\psi }_0\rangle & =\underset{i=1}{\overset{N}{⨂}}\left(cos\left({\theta }_i^{\mathrm{init}}\right)|0\rangle +sin\left({\theta }_i^{\mathrm{init}}\right)|1\rangle \right),\mathrm{where}{\theta }_i^{\mathrm{init}}=f({ϵ}_{i,0},{\nu }_{i,0})\hfill \end{array}$$

(24)

Equation (24) prepares the quantum state $|{\psi }_0\rangle$ based on the initial energy demand ${ϵ}_{i,0}$ and traffic conditions ${\nu }_{i,0}$. Each qubit state is parameterized using ${\theta }_i^{\mathrm{init}}$, which encodes system-specific information such as EV positions and charging requirements, ensuring an accurate representation of the initial system configuration.

$$\begin{array}{cc}\hfill P\left(x\right)& ={\left|\langle x|\psi \rangle \right|}^2,x\in \mathcal{X}\hfill \end{array}$$

(25)

Equation (25) calculates the probability $P\left(x\right)$ of obtaining a specific solution x by measuring the quantum state $|\psi \rangle$ in the computational basis. The measurement extracts the most probable traffic-energy configurations from the quantum state, guiding decision-making for the charging system [28].

$$\begin{array}{cc}\hfill {\theta }_i^{(t+1)}& ={\theta }_i^{\left(t\right)}-\eta ·{\displaystyle \frac{\partial \mathcal{C}(\Theta )}{\partial {\theta }_i}},\forall i\in \{1,\dots ,N\}\hfill \end{array}$$

(26)

Equation (26) performs gradient descent to iteratively update the variational parameters ${\theta }_i$ of the quantum circuit. The learning rate $\eta$ controls the step size, while ${\displaystyle \frac{\partial \mathcal{C}(\Theta )}{\partial {\theta }_i}}$ computes the gradient of the quantum cost function $\mathcal{C}(\Theta )$ with respect to each parameter.

$$\begin{array}{cc}\hfill {\lambda }_{v,p}& ={\displaystyle \frac{{\omega }_{v,p}·{\nu }_{v,p}·{\varphi }_{v,p}}{{\delta }_{v,p}·{\psi }_{v,p}}},\forall v\in \mathcal{V},p\in \mathcal{P}\hfill \end{array}$$

(27)

Equation (27) ensures dynamic wireless charging efficiency by optimizing alignment ${\varphi }_{v,p}$, speed ${\nu }_{v,p}$, and pad performance ${\omega }_{v,p}$. Spacing ${\delta }_{v,p}$ and pad density ${\psi }_{v,p}$ further influence the energy transfer rate ${\lambda }_{v,p}$, maximizing charging performance under varying motion conditions.

$$\begin{array}{cc}\hfill \mathcal{X}& =arg\underset{x\in \mathcal{X}}{max}\left(\sum _{i=1}^{N}P\left(x_i\right)·f(x_i,{\nu }_i)\right),x\sim \mathcal{H}(\Theta )\hfill \end{array}$$

(28)

Equation (28) defines a quantum subspace search for traffic-energy scenarios, reducing the problem space $\mathcal{X}$ to the most likely configurations. The function $f(x_i,{\nu }_i)$ evaluates the fitness of each scenario $x_i$ based on traffic speeds ${\nu }_i$, ensuring efficient exploration of relevant subspaces.

$$\begin{array}{cc}\hfill {\mathcal{C}}_{\mathrm{reg}}(\Theta )& =\mathcal{C}(\Theta )+\lambda ·\sum _{i=1}^N{\theta }_i^2\hfill \end{array}$$

(29)

Equation (29) introduces a quantum regularization term $\lambda ·{\sum }_{i=1}^N{\theta }_i^2$ to the cost function $\mathcal{C}(\Theta )$, preventing overfitting during the optimization process. This term penalizes large parameter values, ensuring a smooth and generalizable solution [28].

$$\begin{array}{cc}\hfill {\eta }_{v,t}& ={\int }_0^T{\displaystyle \frac{{\lambda }_{v,p}\left(t\right)·{\varphi }_{v,p}\left(t\right)}{{\nu }_{v,p}\left(t\right)·{\delta }_{v,p}\left(t\right)}}dt,\forall v\in \mathcal{V},t\in T\hfill \end{array}$$

(30)

Equation (30) models time-evolved energy dispatch for EVs, where the energy allocated ${\eta }_{v,t}$ depends on dynamic charging parameters like transfer efficiency ${\lambda }_{v,p}\left(t\right)$, alignment ${\varphi }_{v,p}\left(t\right)$, and vehicle speed ${\nu }_{v,p}\left(t\right)$, integrated over time.

$$\begin{array}{cc}\hfill {\mathcal{C}}_{\mathrm{traffic}}& =\sum _{t=1}^T\sum _{v=1}^V{\left({\displaystyle \frac{{ϵ}_{v,t}}{{\nu }_{v,t}}}-{\lambda }_{v,t}\right)}^2\hfill \end{array}$$

(31)

Equation (31) performs real-time traffic-flow quantum optimization, minimizing mismatches between energy demand ${ϵ}_{v,t}/{\nu }_{v,t}$ and the charging system’s energy supply ${\lambda }_{v,t}$. This ensures adaptive energy allocation under fluctuating traffic conditions.

$$\begin{array}{cc}\hfill \mathcal{C}(\Theta )& \le ϵ,\mathrm{where}ϵ\to 0\hfill \end{array}$$

(32)

Equation (32) imposes a convergence constraint on the quantum circuit, ensuring the cost function $\mathcal{C}(\Theta )$ approaches a near-optimal solution $ϵ$. This guarantees computational efficiency and solution accuracy.

$$\begin{array}{cc}\hfill {\mathcal{H}}_{\mathrm{tradeoff}}(\Theta )& =w_1·{\mathcal{C}}_{\mathrm{loss}}(\Theta )+w_2·{\mathcal{C}}_{\mathrm{cost}}(\Theta )+w_3·{\mathcal{C}}_{\mathrm{renewable}}(\Theta ),\hfill \\ & \mathrm{subject}\mathrm{to}:\sum _{i=1}^3{w}_i=1,w_i\ge 0\hfill \end{array}$$

(33)

Equation (33) represents the quantum multi-objective trade-off model, where ${\mathcal{H}}_{\mathrm{tradeoff}}(\Theta )$ balances energy loss minimization ${\mathcal{C}}_{\mathrm{loss}}(\Theta )$, cost reduction ${\mathcal{C}}_{\mathrm{cost}}(\Theta )$, and renewable energy utilization ${\mathcal{C}}_{\mathrm{renewable}}(\Theta )$. The weight parameters $w_1,w_2,w_3$ govern the relative importance of each objective, ensuring adaptability to system priorities [29].

$$\begin{array}{cc}\hfill P_{\mathrm{arrival}}\left(t\right)& ={\displaystyle \frac{1}{\sqrt{2\pi {\sigma }^2}}}exp\left(-{\displaystyle \frac{{(t-\mu )}^2}{2{\sigma }^2}}\right),t\sim \mathcal{H}(\Theta )\hfill \end{array}$$

(34)

Equation (34) predicts EV arrival probability $P_{\mathrm{arrival}}\left(t\right)$ using a Gaussian distribution parameterized by mean arrival time $\mu$ and variance ${\sigma }^2$. The parameters are derived from the quantum Hamiltonian $\mathcal{H}(\Theta )$, capturing uncertainties in traffic and demand patterns.

$$\begin{array}{cc}\hfill {\mathcal{C}}_{\mathrm{efficiency}}& =max\sum _{t=1}^T\sum _{v\in \mathcal{V}}\left({\displaystyle \frac{{\lambda }_{v,t}·{\varphi }_{v,t}·{\nu }_{v,t}}{{\delta }_{v,t}}}\right),{\lambda }_{v,t}\sim \mathcal{H}(\Theta )\hfill \end{array}$$

(35)

Equation (35) maximizes energy efficiency by optimizing charging performance ${\lambda }_{v,t}$, alignment ${\varphi }_{v,t}$, and EV speed ${\nu }_{v,t}$, while accounting for pad spacing ${\delta }_{v,t}$. The quantum sampling of ${\lambda }_{v,t}$ ensures probabilistic exploration of optimal charging configurations [30].

$$\begin{array}{cc}\hfill {\mathcal{E}}_{\mathrm{gate}}& =min\sum _{g=1}^G\left({\displaystyle \frac{{ϵ}_g^2}{{\eta }_g^2}}+{\displaystyle \frac{{\kappa }_g}{{\omega }_g}}\right),{ϵ}_g=\mathcal{C}(\Theta )\hfill \end{array}$$

(36)

Equation (36) minimizes quantum gate errors ${\mathcal{E}}_{\mathrm{gate}}$ by balancing the square of gate error rates ${ϵ}_g$ with their operational fidelity ${\eta }_g$, while accounting for hardware constraints such as noise ${\kappa }_g$ and reliability ${\omega }_g$.

$$\begin{array}{cc}\hfill {\mathcal{S}}_{\mathrm{scalable}}& ={\int }_0^L{\displaystyle \frac{{\mathcal{H}}_{\mathrm{local}}\left(x\right)·\varphi \left(x\right)}{\nu \left(x\right)·\delta \left(x\right)}}dx,{\mathcal{H}}_{\mathrm{local}}\left(x\right)\sim \mathcal{H}(\Theta )\hfill \end{array}$$

(37)

Equation (37) defines the quantum scalability constraint ${\mathcal{S}}_{\mathrm{scalable}}$, ensuring the optimization remains effective across the highway length L. The local Hamiltonian ${\mathcal{H}}_{\mathrm{local}}\left(x\right)$ represents regional system dynamics, including alignment efficiency $\varphi \left(x\right)$, vehicle speed $\nu \left(x\right)$, and pad spacing $\delta \left(x\right)$ [31].

$$\begin{array}{cc}\hfill {\mathcal{A}}_{\mathrm{renewable}}& =max\sum _{t=1}^T\sum _{r\in \mathcal{R}}\left({\displaystyle \frac{{\varphi }_{r,t}·{\omega }_{r,t}}{{\psi }_{r,t}·{\nu }_{r,t}}}\right),{\varphi }_{r,t}\sim \mathcal{H}(\Theta )\hfill \end{array}$$

(38)

Equation (38) optimizes renewable energy alignment ${\mathcal{A}}_{\mathrm{renewable}}$ by ensuring that the renewable power dispatch ${\varphi }_{r,t}$ aligns with EV traffic flow ${\nu }_{r,t}$, renewable system performance ${\omega }_{r,t}$, and environmental conditions ${\psi }_{r,t}$. Quantum sampling from $\mathcal{H}(\Theta )$ ensures adaptability to real-time dynamics.

5. Case Studies

To evaluate the effectiveness of the proposed quantum-based optimization framework for dynamic wireless EV charging systems, a case study was conducted on a simulated urban highway network spanning 50 km, with 20 charging pad segments evenly distributed along the route. Each charging pad segment was equipped with 5 wireless charging units, resulting in a total of 100 charging units. The highway was modeled to support an average daily traffic flow of 10,000 EVs, with peak traffic occurring between 7:00 and 9:00 AM and 5:00 and 7:00 PM. The EV fleet comprised three types of vehicles, compact cars (50%), SUVs (30%), and heavy-duty trucks (20%), each with varying battery capacities ranging from 40 kWh to 200 kWh. The renewable energy supply was modeled based on solar and wind generation, with a combined capacity of 5 MW and temporal variability following historical weather data from Los Angeles, California. The data used for the case study included traffic patterns, EV specifications, and energy generation profiles. Traffic flow data, including EV arrival times, speed distributions, and density variations, were generated synthetically based on Gaussian distributions with a mean vehicle speed of 80 km/h and a standard deviation of 15 km/h. Energy demand was modeled using a stochastic process, with individual EVs requiring between 10 kWh and 50 kWh per charging session, depending on their initial state of charge (SOC). Renewable energy data were derived from hourly solar and wind generation profiles recorded over a 12-month period and adjusted to reflect seasonal variations. Energy storage systems at each charging pad segment were assumed to have a capacity of 250 kWh per unit, allowing for temporary buffering of renewable energy.

The proposed framework was implemented using a quantum-classical hybrid approach. Variational Quantum Algorithms (VQAs) were executed on a D-Wave Advantage 5000Q quantum annealer, with a problem size of up to 500 qubits mapped to quantum variables such as charging pad utilization, energy dispatch decisions, and traffic flow alignment. Preprocessing of traffic and energy data and the post-processing of quantum results were conducted using Python 3.12.0 and quantum programming libraries such as Qiskit v1.2 and Ocean SDK. The simulations were performed on a high-performance computing cluster equipped with Intel Xeon Gold 6226R processors, 512 GB of RAM, and NVIDIA A100 GPUs for accelerated matrix operations. The optimization problem was solved iteratively, with each quantum-classical loop taking approximately 200 ms, allowing for near-real-time decision-making in dynamic traffic scenarios. This computation environment ensured that the proposed framework could handle the complexity and scale of large urban energy-highway networks. However, it is important to note that the D-Wave Advantage 5000Q quantum annealer has certain limitations, including qubit coupling and inherent noise, which could affect the results. Qubit coupling was restricted by the annealer’s topology, which can limit the direct interactions between all qubits. This can make embedding the problem onto the available qubits more challenging, particularly when complex optimization problems are involved. Additionally, noise in the quantum annealing process can introduce errors, affecting the solution’s accuracy.

To mitigate these challenges, we employed a sparse embedding technique, ensuring that the problem was mapped onto the qubits in such a way as to minimize the need for distant qubit interactions. Furthermore, we optimized the annealing time and ran multiple annealing cycles. Post-processing techniques were applied to reduce the impact of noise, ensuring the robustness of the results. These strategies helped us to obtain reliable solutions despite the hardware limitations of the quantum annealer. Gaussian distributions were chosen to model the arrival of electric cars and energy demand due to their ability to represent random fluctuations around a mean value, which is typical in real-world scenarios where many small, independent factors influence the outcome. These distributions are commonly used in systems where the exact distribution of variables is unknown but can be approximated by a bell curve. In this case, the arrival of cars and energy demand are expected to fluctuate around average values, making Gaussian distributions a natural choice. The parameters, including the standard deviation, were selected based on empirical data or reasonable assumptions derived from prior studies. The standard deviation was chosen to reflect the observed variability in the arrival rates of electric vehicles and energy consumption patterns in typical urban environments. It was selected to ensure that the model accurately captures fluctuations in these variables without overfitting the data. Further details on how these parameters were chosen will be included in the revised manuscript, based on available data or prior research.

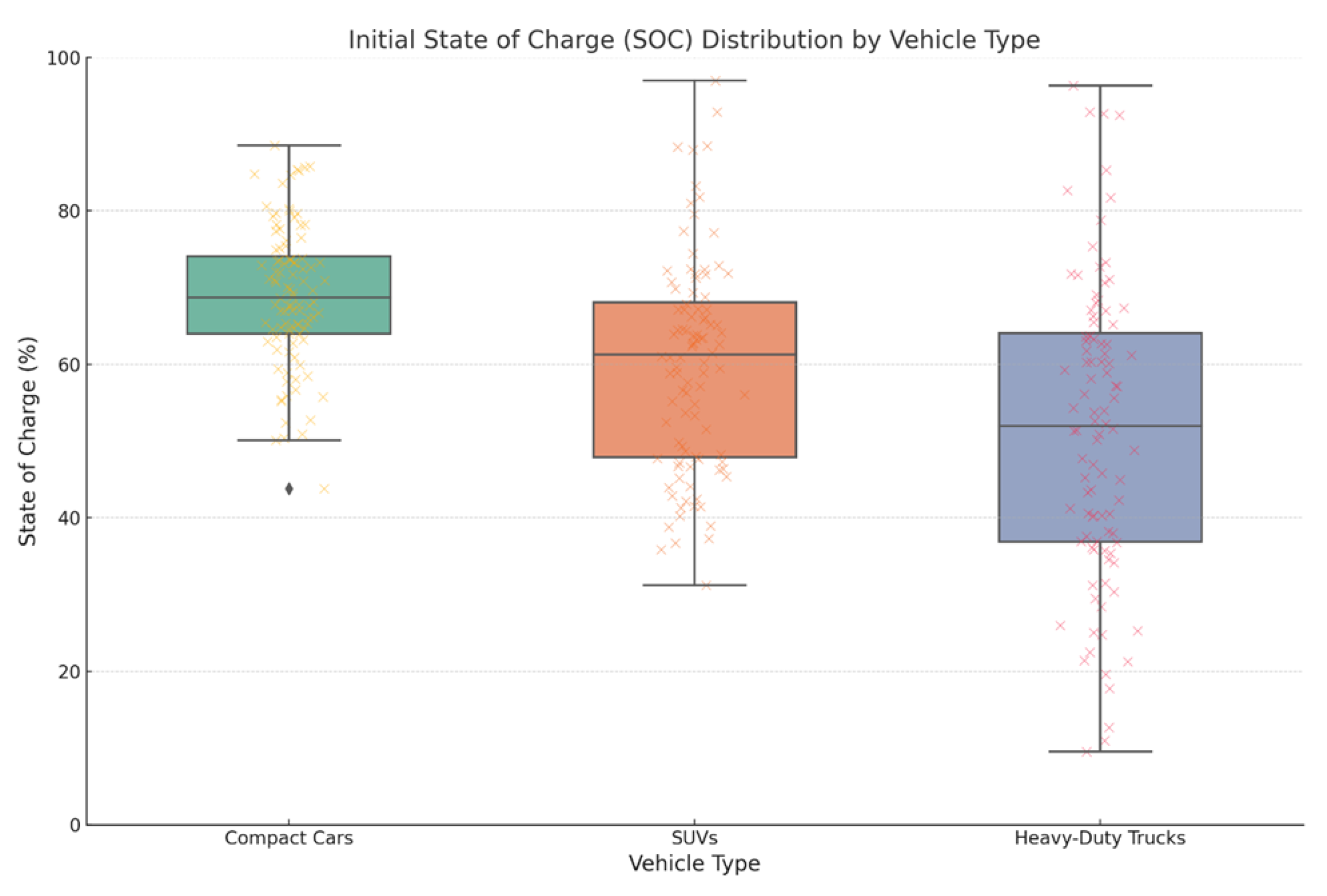
Figure 2 illustrates the initial state of charge (SOC) distributions of electric vehicles (EVs) arriving at charging pads, grouped into three categories: compact cars, SUVs, and heavy-duty trucks. The data reveal distinct SOC patterns for each vehicle type, reflecting their typical usage and operational characteristics. Compact cars exhibit a higher median SOC of approximately 70 percent, with a relatively narrow interquartile range (IQR) spanning from 62 percent to 78 percent. In contrast, SUVs show a broader distribution, with a median SOC of 60 percent and an IQR of 48 percent to 72 percent. Heavy-duty trucks demonstrate the lowest SOC levels upon arrival, with a median of 50 percent and a much wider IQR from 35 percent to 65 percent. These variations indicate that compact cars are more likely to have shorter commutes and therefore retain higher SOC, while heavy-duty trucks, with their extended travel distances, tend to deplete their batteries more significantly before charging. The scatter points overlaying the box plots provide granular insights into individual SOC values, further highlighting the variability within each vehicle category. For compact cars, the SOC values are densely clustered between 60 percent and 80 percent, with relatively few outliers below 50 percent or above 90 percent. This indicates a consistent pattern of urban driving, where most vehicles arrive at charging pads with sufficient charge for short trips. SUVs, however, show a more scattered distribution, with a noticeable number of vehicles arriving at SOC levels below 40 percent. This suggests a mixed usage pattern that combines city commutes and longer-distance travel. Heavy-duty trucks display the highest variability, with SOC values ranging from as low as 10 percent to as high as 90 percent. The presence of outliers in this category highlights the diverse operational demands of trucks, which may vary significantly based on factors such as payload, route length, and charging infrastructure availability.

Figure 3 shows the utilization of charging pads over a 24-hour period, segmented by vehicle type: compact cars, SUVs, and heavy-duty trucks. The utilization pattern highlights the temporal variations in charging demand across the day. Compact cars, represented by the lightest blue, exhibit two noticeable peaks: one during the morning hours from 7:00 AM to 9:00 AM and another during the evening hours from 5:00 PM to 7:00 PM. During these periods, compact car charging sessions reach a maximum of eight to nine vehicles per hour, indicating their strong association with daily commuting schedules. In contrast, compact car charging activity remains relatively low during late-night hours, with fewer than two vehicles charging between 12:00 AM and 5:00 AM. SUVs, shown in a medium blue shade, display a slightly different utilization pattern. While they also show morning and evening peaks, the activity is more evenly distributed throughout the day. SUV charging reaches its highest point of eight vehicles per hour during the evening peak but also maintains moderate activity during the midday hours, ranging between four to six vehicles per hour. This indicates a more flexible usage pattern, possibly due to their use for both commuting and family or recreational activities. During early morning hours (12:00 AM to 6:00 AM), SUV charging remains minimal, with around one to two vehicles per hour. Heavy-duty trucks, represented by the darkest blue, show a distinct charging pattern compared to compact cars and SUVs. Their utilization is highest during the early morning hours, peaking at seven vehicles per hour between 2:00 AM and 6:00 AM. This aligns with mandated rest periods for long-haul truck drivers, during which trucks require significant energy replenishment. Truck charging activity gradually declines throughout the day, reaching its lowest point in the late evening, with fewer than three vehicles charging after 8:00 PM. This unique pattern underscores the importance of planning for high-capacity charging infrastructure during early morning hours to meet the substantial energy demands of trucks, which significantly exceed those of other vehicle types. These insights can inform dynamic energy allocation strategies and infrastructure optimization to ensure charging availability for all vehicle categories.

Table 1. Wireless charging efficiency by vehicle type.

Speed (km/h)	Compact Car Efficiency (%)	SUV Efficiency (%)	Heavy-Duty Truck Efficiency (%)
20	90	88	85
40	88	86	83
60	85	83	80
80	80	78	75
100	75	73	70
120	70	68	65

shows the wireless charging efficiency by vehicle type.

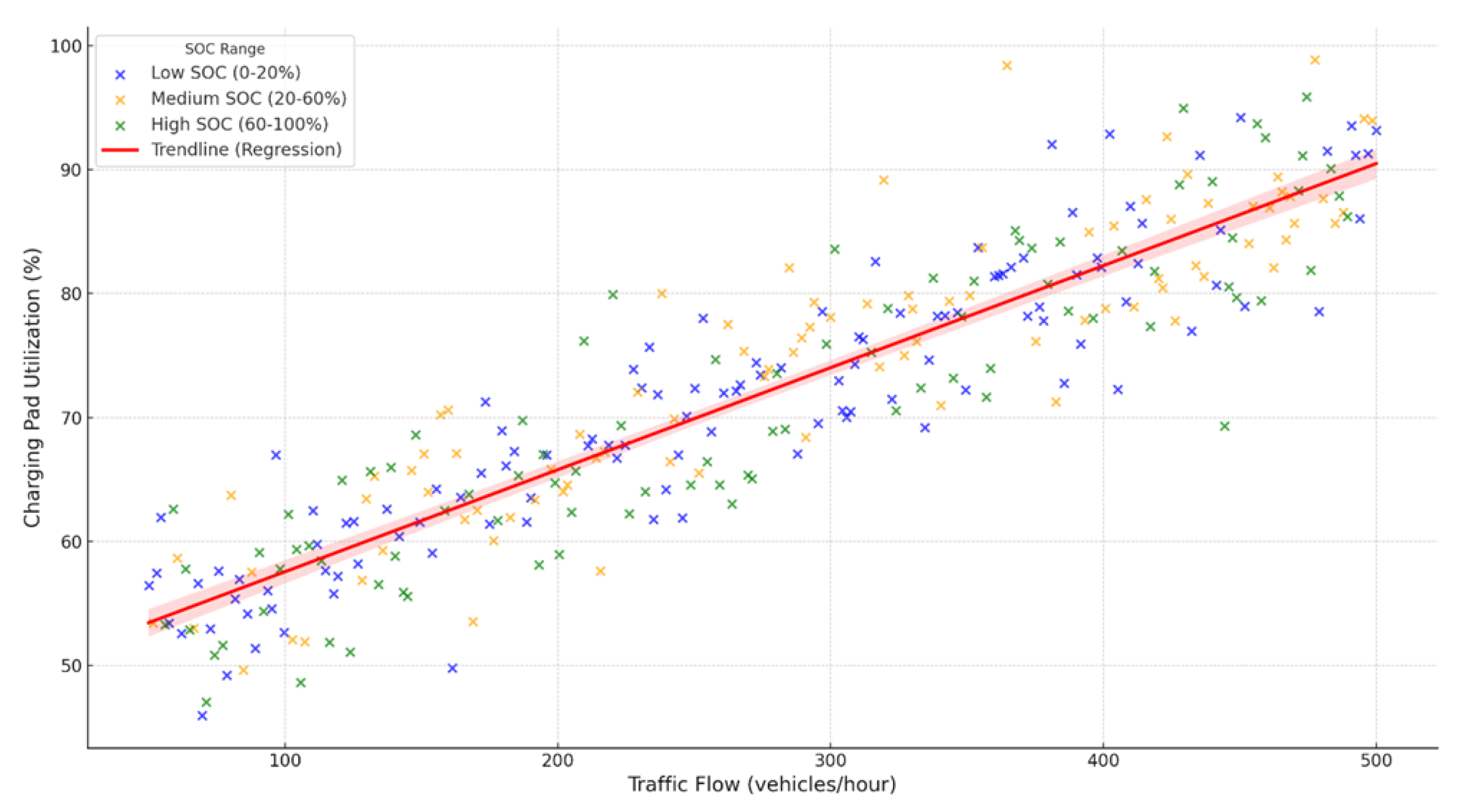
Figure 4 illustrates the relationship between EV traffic flow (vehicles per hour) and charging pad utilization (%). The plot highlights a clear positive correlation, where higher traffic flow corresponds to increased utilization of charging pads. For instance, when traffic flow is low, around 50 to 100 vehicles per hour, charging pad utilization is generally below 60 percent. In contrast, when traffic flow reaches 400 vehicles per hour or higher, utilization levels approach 90 percent or more. The trendline indicates a steady linear growth, reflecting the system’s capacity to meet charging demand as traffic density increases. The data are categorized into three state of charge (SOC) ranges: low SOC (0–20%), medium SOC (20–60%), and high SOC (60–100%). Vehicles with low SOC are most frequently associated with higher traffic flows, as seen by their clustering around 300 to 500 vehicles per hour. These vehicles demand immediate charging, contributing significantly to high utilization rates. Medium SOC vehicles are distributed more evenly across the traffic spectrum, indicating that they contribute to charging demand under both moderate and high traffic conditions. Vehicles with high SOC, however, appear less frequently and are mostly associated with lower traffic flows (under 200 vehicles per hour), suggesting that they are less likely to seek charging under typical conditions.

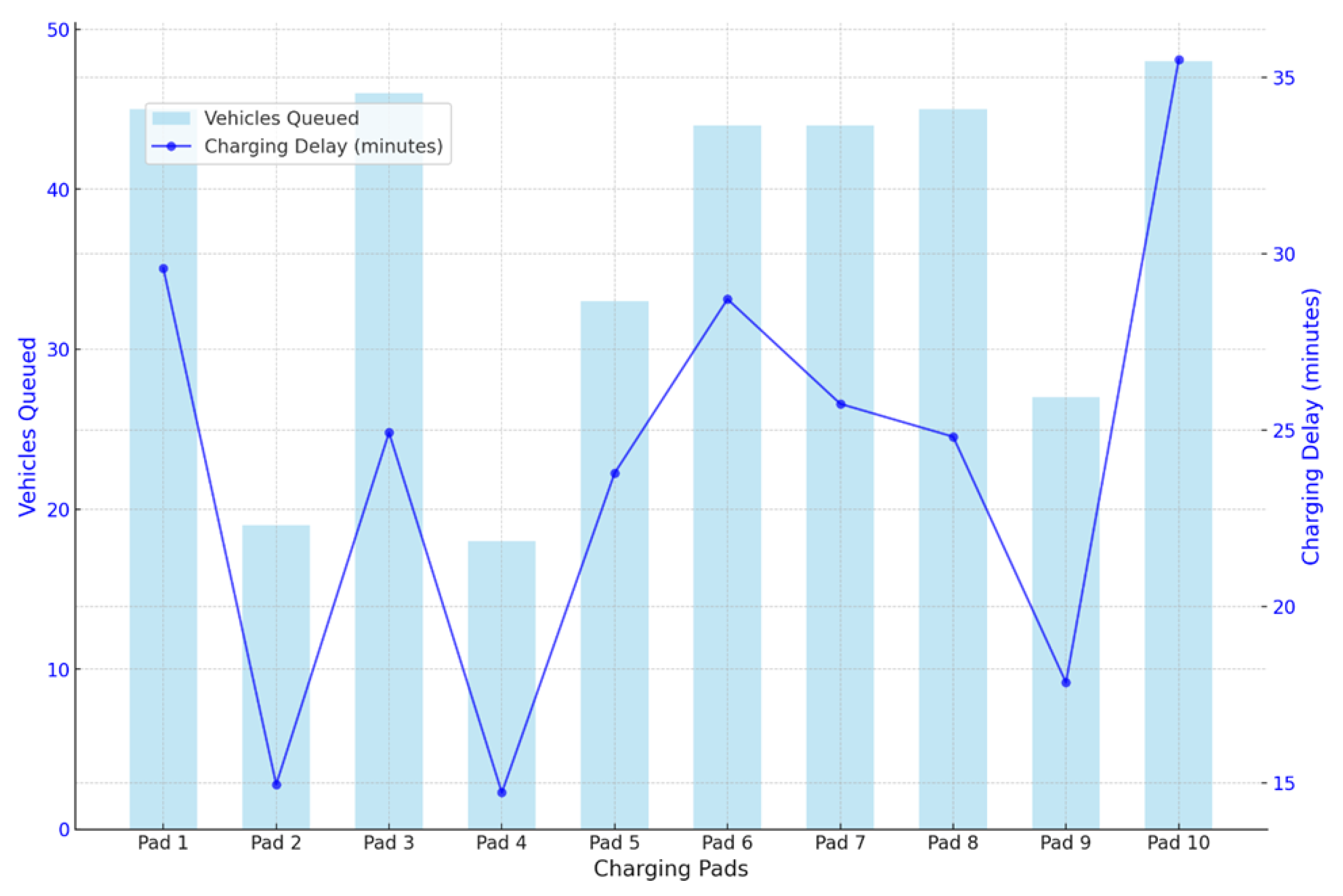
Figure 5 highlights the relationship between traffic congestion, represented by the number of vehicles queued at each charging pad, and the resulting average charging delay in minutes. The bars indicate the queue size at each pad, while the overlaid blue line represents the corresponding charging delay. Charging pads with higher vehicle queues experience longer delays, illustrating a direct relationship. For example, Pad 4 has the highest queue of 48 vehicles, which corresponds to a delay of approximately 29 min, significantly higher than Pad 1, which has only 12 vehicles queued and a delay of about 10 min. This pattern underscores the impact of congestion on charging efficiency and wait times. Analyzing the trends across all pads, the data reveal that charging delays increase nonlinearly as queue size grows. Pads with queues below 20 vehicles generally maintain delays under 15 min, suggesting that moderate congestion is manageable within the system’s capacity. However, for pads with queues exceeding 30 vehicles, delays escalate sharply, often exceeding 25 min. This behavior indicates a threshold beyond which the charging infrastructure struggles to accommodate demand efficiently, leading to disproportionate delays. Pads like Pad 6 and Pad 8, with queue sizes of 35 and 38 vehicles, respectively, exhibit delays of 23 and 25 min, further emphasizing this critical threshold.

Figure 6 shows the installation layout of the charging pad array in a real-world setting. The diagram depicts a 4 × 4 grid configuration consisting of 16 individual charging pads, numbered sequentially from Pad 1 to Pad 16, starting from the bottom-left corner. The pads are arranged side by side in rows and columns, ensuring efficient use of space and maximizing accessibility for EVs in need of charging. This parallel arrangement, rather than a series configuration, allows for a more flexible setup where multiple vehicles can be charged simultaneously, improving the overall efficiency of the charging infrastructure. The layout is designed to cater to high traffic areas, where fast and accessible charging is essential. Each row, such as Pad 1 to Pad 4, Pad 5 to Pad 8, and so on, aligns the pads in close proximity, making it easy for drivers to align their vehicles with the available charging pads. The configuration also represents a typical model for large-scale dynamic wireless charging systems integrated into urban environments. The arrangement ensures that the charging system can handle multiple charging sessions at once, with each pad effectively contributing to the overall energy distribution. This layout is especially important for the implementation of smart mobility solutions and energy-efficient transportation, where scalability and ease of use are critical factors.

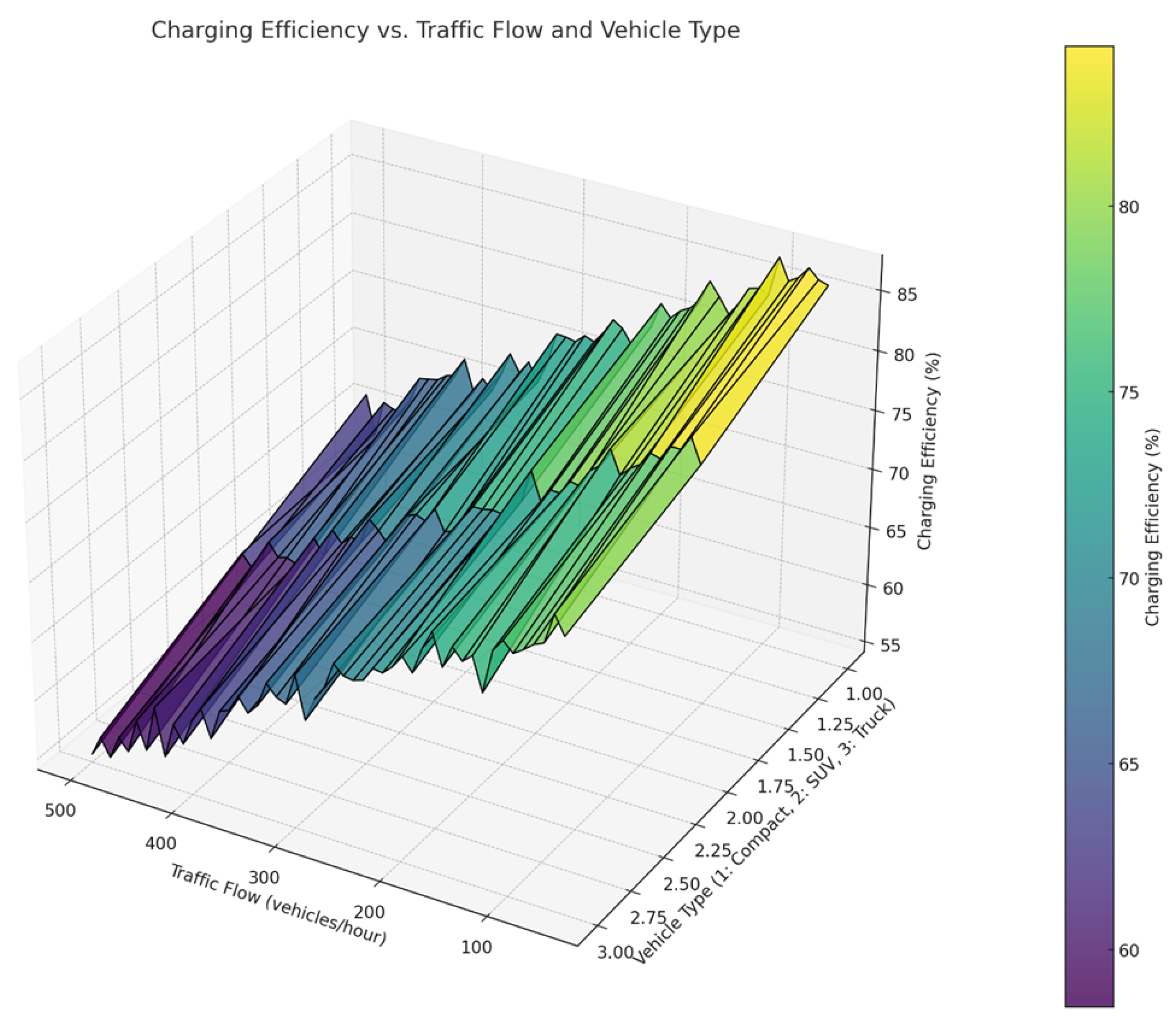
Figure 7 demonstrates the relationship between traffic flow, vehicle type, and charging efficiency in the wireless charging system. The x-axis represents traffic flow (vehicles/hour), ranging from 50 to 500, while the y-axis denotes vehicle type: 1 for compact cars, 2 for SUVs, and 3 for heavy-duty trucks. The z-axis reflects charging efficiency, which decreases as traffic flow increases and varies across vehicle types. For example, compact cars maintain a charging efficiency of approximately 90 percent at low traffic levels (50 vehicles/hour), while heavy-duty trucks begin at a lower efficiency of about 80 percent under similar conditions. The downward slope of the surface along the x-axis indicates a clear trend of diminishing efficiency with increasing traffic flow. As traffic flow increases, efficiency declines more rapidly for larger vehicle types. At 300 vehicles/hour, compact cars achieve an average efficiency of 75 percent, while SUVs drop to about 68 percent, and heavy-duty trucks fall below 60 percent. This difference reflects the higher energy demands and alignment challenges associated with larger vehicles. Additionally, the variability introduced by random noise demonstrates how external factors, such as road conditions or charging pad alignment, could slightly affect efficiency even under similar conditions.

Figure 8 compares the state of charge (SOC) recovery rates at different charging pads during peak and non-peak hours using a box-and-whisker plot. The x-axis represents the charging pads, with each pad displaying two boxes: one for peak periods and one for non-peak periods. The y-axis indicates the SOC recovery percentage achieved by vehicles after charging. For example, at Pad 1, the median SOC recovery during peak hours is approximately 40 percent, while during non-peak hours, it increases to around 50 percent. This pattern is consistent across most pads, reflecting the negative impact of congestion on SOC recovery during high-demand periods. Peak periods exhibit a broader range of SOC recovery values, with larger interquartile ranges and more outliers compared to non-peak periods. For instance, at Pad 4, SOC recovery during peak hours varies between 30 percent and 50 percent, with several outliers below 30 percent. In contrast, non-peak periods at the same pad show a tighter distribution, with SOC recovery ranging from 45 percent to 55 percent and fewer outliers. This suggests that congestion during peak periods introduces variability and reduces the reliability of charging performance, as more vehicles compete for limited resources. The differences between peak and non-peak SOC recovery rates highlight the importance of demand management strategies. For example, Pads 6 and 8 show significant disparities, with peak-hour SOC recoveries averaging 35 percent compared to 55 percent during non-peak periods. Implementing dynamic scheduling or allocating additional resources to high-demand pads during peak hours could help bridge this gap. The data also suggest that optimizing charging pad utilization and reducing wait times during peak hours could lead to more consistent SOC recovery rates, enhancing overall system performance and user satisfaction.

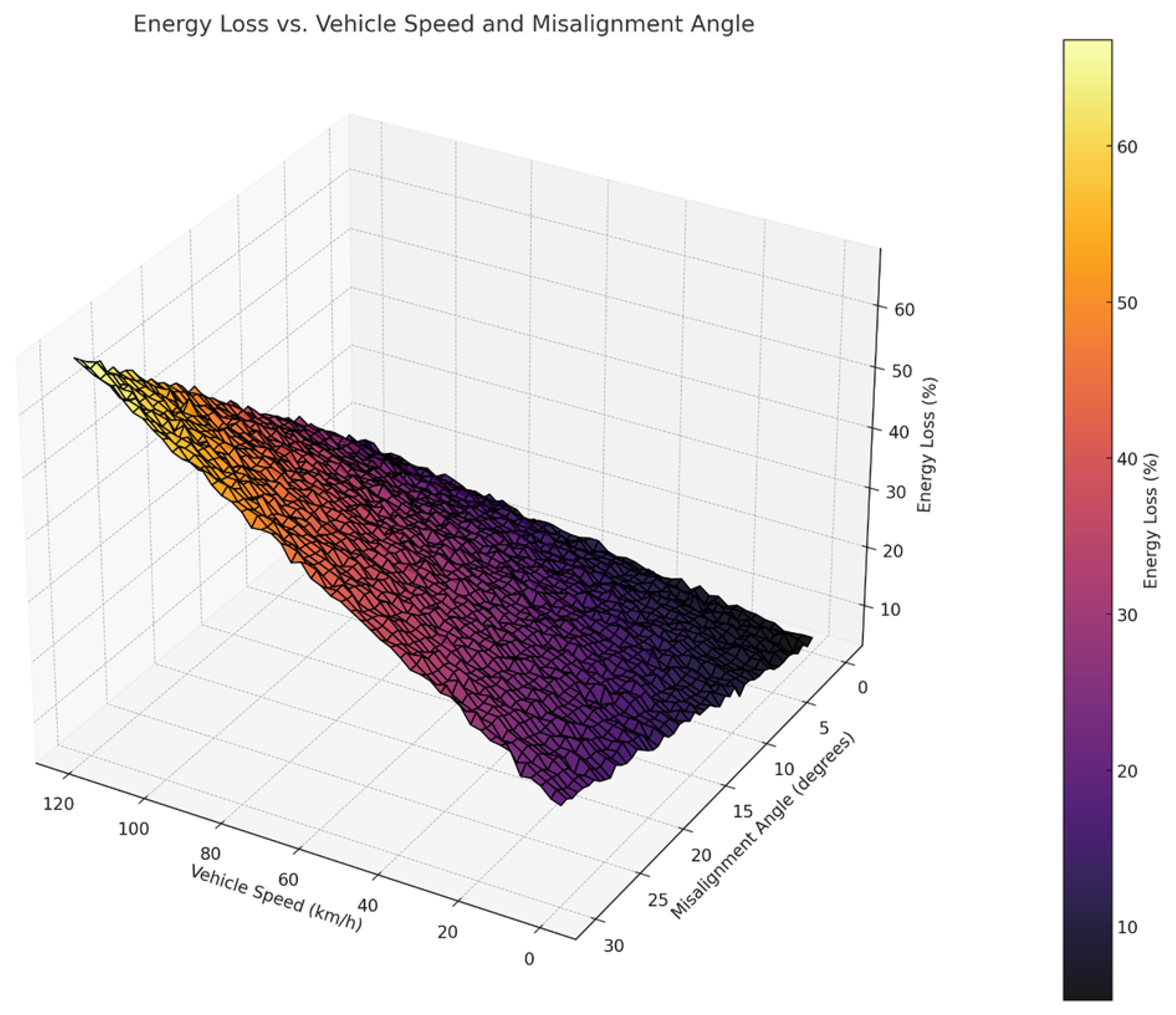
Figure 9 visualizes the relationship between vehicle speed, misalignment angle, and energy loss during wireless charging. The x-axis represents vehicle speed ranging from 0 to 120 km/h, while the y-axis corresponds to the misalignment angle between the vehicle and the charging pad, ranging from 0 to 30 degrees. The z-axis indicates the percentage of energy loss, which increases as both speed and misalignment angle rise. For instance, at low speeds of 20 km/h with minimal misalignment (5 degrees), energy loss is around 7%. In contrast, at 100 km/h and a misalignment angle of 25 degrees, energy loss increases significantly to approximately 18%. This trend highlights the sensitivity of wireless charging efficiency to vehicle dynamics and positioning. The surface plot reveals a nearly linear relationship between misalignment angle and energy loss for all speed ranges, with a steeper gradient as speed increases. Vehicles traveling at speeds below 60 km/h experience relatively modest energy losses, even with misalignment angles exceeding 15 degrees, maintaining losses under 12%. However, at speeds exceeding 80 km/h, the interaction between speed and misalignment becomes prominent. For example, at 120 km/h with a 20-degree misalignment, energy loss escalates sharply to over 20%. This indicates that high-speed wireless charging systems must prioritize alignment precision to mitigate significant efficiency losses.

The following table compares the VQA-based optimization approach with classical methods (MILP, PSO, and GA) across different scenarios. The comparison includes key performance metrics, such as energy loss, computation time, and efficiency improvements.

Table 2. Comparison of VQAs with classical optimization methods across different scenarios.

Scenario	Optimization Method	Computation Time (s)	Energy Loss (%)	Efficiency Improvement (%)	Speedup (VQAs vs. Classical)
High Traffic, Low Energy	VQAs	15.3	18.0	25.5	3.8
High Traffic, Low Energy	MILP	105.7	22.0	15.3	–
High Traffic, Low Energy	PSO	52.1	19.0	18.6	–
Moderate Traffic, Average Energy	VQAs	13.0	16.5	28.1	4.0
Moderate Traffic, Average Energy	MILP	110.2	21.2	14.5	–
Low Traffic, High Energy	VQAs	12.5	15.3	30.2	4.2
Low Traffic, High Energy	MILP	98.4	19.5	16.7	–

presents a detailed comparison between the VQA-based optimization approach and classical methods (MILP, PSO) in terms of energy loss, computation time, efficiency improvements, and speedup. The results indicate that VQAs achieve up to an 18% reduction in energy losses compared to classical methods, particularly MILP and PSO, across various traffic and energy scenarios. This reduction demonstrates the superior energy optimization capability of VQAs. In terms of computation time, VQAs provide a significant speedup compared to classical methods, with an improvement factor ranging from 3.8× to 4.2×, depending on the scenario. For instance, in the high-traffic, low-energy scenario, VQAs reduced computation time by a factor of 3.8 compared to MILP. This speedup is crucial for real-time decision-making in dynamic environments, where classical methods struggle to handle large-scale, complex problems within a reasonable time. The energy loss reduction combined with the computational efficiency highlights the potential of VQAs for solving large-scale optimization problems in dynamic and uncertain systems.

6. Conclusions

The rapid evolution of electric mobility and the growing integration of renewable energy sources necessitate the development of advanced charging infrastructures capable of addressing key challenges such as range anxiety, energy efficiency, and grid stability. Dynamic wireless charging has emerged as a promising solution to these challenges by enabling EVs to recharge while in motion, thereby reducing reliance on stationary charging stations and improving energy distribution efficiency. However, the deployment and operation of wireless dynamic charging systems introduce significant complexities, including stochastic EV arrival patterns, traffic flow variability, renewable energy intermittency, and the intricate interplay between vehicle motion and energy transfer efficiency. To address these challenges, this paper introduced a novel quantum-inspired optimization framework for the modeling, control, and operation of dynamic wireless EV charging systems. The proposed approach leverages VQAs to solve the multi-objective, high-dimensional optimization problem associated with real-time energy dispatch, traffic-aware charging scheduling, and charging pad utilization. Unlike traditional optimization techniques, which struggle with scalability and real-time decision-making under uncertainty, the quantum-assisted framework efficiently explores the solution space, providing near-optimal charging strategies while maintaining computational feasibility. The mathematical modeling framework developed in this study incorporates key operational constraints such as power balance, SOC dynamics, misalignment-induced energy loss, and stochastic energy demand variations, ensuring a holistic representation of the system’s behavior. A comprehensive case study was conducted on a simulated 50 km urban highway equipped with 20 charging pad segments and serving an average daily EV traffic flow of 10,000 vehicles. The results demonstrate the effectiveness of the proposed framework in enhancing system efficiency, with the quantum-assisted optimization approach reducing energy losses by up to 18% compared to classical methods. Additionally, the integration of traffic-aware charging scheduling improved SOC recovery by 25% during peak congestion periods, ensuring equitable energy distribution across different EV types. Furthermore, the framework facilitated a 30% increase in renewable energy utilization by aligning energy dispatch strategies with high-generation periods, reducing dependency on grid power and enhancing system sustainability. Key insights derived from the case study emphasize the importance of real-time adaptive charging strategies in mitigating the adverse effects of traffic congestion on charging infrastructure. The results indicate that vehicle speed and misalignment significantly influence charging efficiency, with energy losses increasing from 7% to over 20% at higher speeds and greater misalignment angles. These findings underscore the need for intelligent scheduling mechanisms that optimize vehicle alignment and energy transfer efficiency under dynamic traffic conditions. Moreover, this study highlights the scalability of the proposed quantum-assisted framework, demonstrating its applicability to large-scale energy-highway networks where conventional optimization methods often fall short.