eVTOL Dispatch Cost Optimization Under Time-Varying Low-Altitude Delivery Demand

Abstract

In the emerging paradigm of embodied intelligence, eVTOL technology holds significant potential to transform the low-altitude economy, particularly in short-distance emergency logistics and urban distribution. Companies like Meituan and Shunfeng (SF) are pioneering fixed low-altitude routes to reduce reliance on human delivery. We first investigate the performance and routing of Meituan’s eVTOL system, focusing on the dynamic optimization of eVTOL reserves and total costs at distribution stations under fluctuating order surges and charging constraints. An iterative algorithm is constructed, supported by numerical examples and Monte Carlo simulations. Our results reveal that cost parameters and demand characteristics jointly shape eVTOL incremental decision-making and its economic performance. To optimize costs, strategies like multi-period decentralized scheduling or low-frequency centralized decision-making are proposed. Future research will address limitations such as 2C charging effects and joint battery-eVTOL replenishment to further advance urban logistics and low-altitude economy development.

1. Introduction

Under the strategic framework of smart city development, the low-altitude economy has emerged as a novel economic paradigm, gradually gaining prominence as a significant force propelling urban intelligence [1]. Centered on the utilization of low-altitude airspace, the low-altitude economy integrates innovative technologies with policy support, demonstrating a promising trajectory for future growth. In recent years, the maturation and expanding application of electric vertical takeoff and landing (eVTOL) vehicles have garnered widespread recognition for their potential in low-altitude logistics [2]. In particular, the integration of eVTOL with embodied intelligence technologies enables efficient and precise logistics delivery in complex urban environments, serving as a key driver for the advancement of the low-altitude economy [3]. Supportive policies have been enacted to facilitate the development of low-altitude logistics (LAL), encompassing the regulation of low-altitude airspace management, technological innovation incentives, and the promotion of corporate applications in low-altitude logistics delivery [4]. Industry leaders such as Meituan and SF Express have pioneered the deployment of fixed low-altitude delivery routes in urban areas. By establishing an efficient low-altitude logistics network, these companies have reduced reliance on traditional human-based delivery systems. This not only alleviates urban traffic congestion to some extent but also significantly enhances logistics efficiency.

The advantages of eVTOL delivery lie in its ability to overcome ground traffic obstacles, reduce delivery time, enhance service efficiency, and improve user experience. Taking Meituan’s eVTOL delivery as an example, we investigated the launch of Meituan’s first eVTOL food delivery route in Yangpu District, Shanghai. This eVTOL delivery route connects Wujiaochang Hopson One and Hulian Baodi Yangpu Park, reducing the transportation time of over 4 km to 10 min (Figure 1a–c).

Figure 1. Meituan eVTOL urban delivery route. Notes and copyright: All sub-figure photographs are images collected from our on-site research on 3 February 2025 (with permission from staff, the site is an open area in a public place, an area that can be opened to the public to visit), and image collection was carried out and discussed and analyzed by the first and the fourth authors together and shared with each other at the site. The background large image was labeled by location search in Bing map, and it was displayed in combination with other captured images in order to save as much space as possible occupied by the article while maintaining the same amount of information. All of the above image information adheres to WEVJ’s publication regulations and CC BY license.

Based on our research, Meituan’s eVTOL Gen 4 adopts a six-axis small multi-rotor base configuration (Figure 1d) specifically designed for urban low-altitude delivery networks. It is equipped with two ternary lithium batteries, each with a capacity of 4400 mAh, connected in parallel to achieve a rated output power of 396 Wh, enabling round-trip delivery over 5 km and one-way delivery over 10 km (Table 1). Taking the typical energy density range of ternary lithium (LiPo) batteries as 150~250 Wh/kg and using the median value of 200 Wh/kg as a reference, the estimated weight of the two batteries is approximately 2 kg (2 × 198 Wh ÷ 200 Wh/kg). From this, the empty weight of the aircraft is estimated to be around 5 kg (MTOW–MPL–Battery Weight).

Table 1. Technical parameters of Meituan eVTOL Gen 4.

Tech	Description
Config	Six-axis small multi-rotor vertical takeoff and landing
MPL 1	2.5 kg
MTOW 2	9.5 kg
MRR- MPL 3	5 km
MDD- MPL 4	10 km
Cruising	83 km/h
Battery	12S Li-ion (NMC 5), 45 V, 4400 mAh × 2, 198 Wh × 2, 2C charge, 6C discharge
Avionics	CPU × 2, 5G/4G/Wi-Fi, Dual Flight Control
Perceptron	SVC 6 × 3, HDMC 7 × 2, UHDMC 8 × 2, 4 DmmWR 9 × 2,
Design	Noise Reduced by 50%; Folded Size Reduced by 49%
Safety	CSSR 10 & SP 11

¹ Maximum Payload; ² Maximum Take-Off Weight; ³ Maximum Round-trip Radius (Maximum Payload); ⁴ Maximum Delivery Distance (Maximum Payload); ⁵ Lithium–Nickel–Manganese–Cobalt Oxide Battery; ⁶ Stereo Vision Cameras; ⁷ High-Definition Monocular Cameras; ⁸ Ultra-High-Definition Monocular Cameras; ⁹ Four-Dimensional mmWave Radars; ¹⁰ Critical Subsystem Redundancy; ¹¹ Smart Parachute.

We have compiled the delivery workflow of the eVTOL food delivery route during peak hours, including key time nodes and specific actions taken by all involved parties, to understand its operational mechanisms and efficiency (Table 2). The core of the process lies in coordinating the respective responsibilities of restaurants, eVTOLs, and consumers to achieve efficient delivery. For instance, from the moment a consumer places an order to the restaurant preparing the order, as well as the preparation and dispatching of the eVTOL, and finally to the completion of the flight and delivery, each flow step is meticulously scheduled at specific time points.

Table 2. Workflow for Meituan eVTOL delivery.

Flow No.	Time Node	Process	Action
			Restaurant	eVTOL	Consumer
1	T − 6	Place order			×
2	T − 5	Pay order			×
3	T − 4	Prepare order	×
4	T − 3	Prepare eVTOL		×
5	T − 2	Meal out	×
6	T − 1	Pickup meal		×
7	T	Start delivery		×
8	T + 1	Landing		×
9	T + 2	Return flight		×
10	T + 3	Accept delivery			×

However, our investigation reveals a contradiction between eVTOL inventory and order capacity. Distribution stations can temporarily accommodate a maximum of 10 eVTOLs dispatched from operations centers for delivery purposes. Yet, when daily order peaks surge abruptly, eVTOLs face shortages, particularly during peak hours. This demand pressure underscores the critical importance of optimizing the scheduling of eVTOL equipment to avoid delivery delays or the outright shutdown of the app-based order API, thereby ensuring customer satisfaction. This realization prompts us to consider the dynamic optimization of eVTOL operational costs at distribution stations under the constraints of order surges and equipment charging limitations.

In Section 2, we review existing related studies to elucidate the theoretical foundation and the cutting-edge nature of our research. In Section 3, we endeavor to construct a scheduling iterative algorithm based on delivery demand forecasting for the operational cost control of eVTOL equipment at distribution stations, and we attempt to provide numerical examples and Monte Carlo simulations. Based on the comparison of these examples and simulations, we present our research findings. In Section 4, this paper draws conclusions and extends the discussion to the practical issues of cost control in eVTOL equipment reserve, as well as the limitations of this study.

Our study contributes to the enrichment of theoretical research in the low-altitude economy, offering practical value for cost control in low-altitude distribution stations and enterprises. Furthermore, the iterative algorithm is designed in such a way that it does not compromise the consumer experience.

By constructing an iterative algorithm, combining numerical computation and Monte Carlo simulation, we reveal the dynamic pattern of eVTOL incremental decision-making and its economic performance, as well as propose strategies such as multi-period decentralized dynamic scheduling and low-frequency centralized incremental decision-making, to ensure the reproducibility and practicability of the research results.

2. Related Works

The low-altitude economy refers to the collective term for a series of industries and services that have developed within the low-altitude airspace, generally defined as the airspace ranging from 0 to 1000 m above the ground, which does not interfere with the operation of transport aircraft [1]. Its core lies in leveraging the opening of low-altitude airspace and technological advancements to develop application scenarios such as aerial photography, sightseeing tourism, agricultural and forestry spraying, emergency rescue, and cargo delivery [5,6,7,8,9,10,11]. The development of the low-altitude economy benefits from the rapid progress in unmanned aerial vehicles (UAVs), electric vertical take-off and landing (eVTOL) aircraft, and intelligent control technologies [2], while also being propelled by the liberalization of relevant policies [12,13]. The advantages of the low-altitude economy are reflected in its efficiency, flexibility, and market adaptability. Compared to traditional ground transportation methods, low-altitude logistics delivery offers faster response times, making it particularly suitable for peak periods or scenarios with ground traffic congestion [5,6]. Additionally, for remote and hard-to-reach areas, low-altitude transportation presents an economical and effective solution [14]. However, the development of the low-altitude economy also faces numerous challenges, such as further adjustments to airspace control policies, improvements in the safety performance of aircraft, the refinement of regulatory systems, and public acceptance of low-altitude flight [15]. With the widespread application of intelligent airspace management systems and the gradual opening of commercial operation permits for low-altitude airspace, the low-altitude economy is expected to become a significant factor in driving global economic development.

eVTOL (electric vertical take-off and landing) is an emerging aerial vehicle capable of electric propulsion, vertical take-off and landing, and short-distance operation, regarded as one of the core technologies for future urban air mobility (UAM) [2]. The development of eVTOL integrates multiple advanced technologies, including electrical engineering, aerodynamics, and artificial intelligence, aiming to achieve environmental sustainability, efficiency, and sustainability, thereby overcoming the limitations of traditional transportation systems [15]. However, the commercial application of eVTOL still faces numerous challenges. For instance, the limitations of battery endurance directly determine its flight range and payload capacity [16], while the safety of electric systems remains a critical difficulty in both development and operation [17]. Additionally, the regulation of urban airspace and the construction of public infrastructure for landing sites require substantial investment and planning [18]. With the improvement of infrastructure and advancements in battery and charging technologies, eVTOL is poised to bring revolutionary changes to future transportation and logistics systems.

Embodied intelligence refers to the perceptual, learning, and action capabilities demonstrated by AI systems with physical entities [19]. It emphasizes the perception–action cycle in the physical world, where intelligent agents interact with the external environment to enable AI systems to better adapt to and optimize behaviors in complex environments [20]. This concept is particularly significant for autonomous operation fields such as eVTOL. An eVTOL equipped with embodied intelligence can not only perceive real-time weather conditions, obstacles, and changes in flight paths but also dynamically adjust its flight plan based on environmental information to enhance efficiency and ensure safety [21]. Multimodal algorithms enable the system to collect data through multimodal sensors (e.g., visual, acoustic, and LiDAR) and continuously optimize its behavioral strategies through autonomous learning [22]. Additionally, 5G communication technology facilitates real-time data exchange between embodied intelligence systems and cloud computing resources, further enhancing their predictive capabilities and response speeds [3].

The actual operational status, idle quantity, and battery endurance of eVTOLs need to be efficiently configured to adapt to dynamic delivery demands. Under the condition of limited eVTOL resources, dynamic control of inventory levels is essential to ensure flexibility, meet customer demands, and minimize costs [4]. Cutting-edge research in inventory management emphasizes achieving precise forecasting and real-time scheduling through data-driven approaches. For instance, by leveraging historical order data and machine learning algorithms, it is possible to predict the arrival of delivery peaks and adjust eVTOL scheduling plans proactively [23]. In high-timeliness scenarios such as food delivery, sufficient delivery resources and congestion avoidance are critical research focuses for reducing dwell time [24]. Cost control for low-altitude delivery stations holds both strategic and operational significance. eVTOL delivery stations can be regarded as cost centers, where multi-package deliveries yield higher efficiency compared to single-package deliveries [25]. However, single-package delivery is necessary to meet the fundamental requirements of food hygiene in meal delivery services.

The above studies show how the rapid evolution of urban air mobility (UAM) and the integration of electric vertical takeoff and landing (eVTOL) vehicles into urban logistics have garnered significant attention in recent years. In summary, studies on eVTOL operations emphasize their potential to revolutionize last-mile delivery by reducing congestion and emissions, particularly in densely populated urban areas [8]. Logistics optimization highlights the importance of dynamic scheduling and route planning to enhance efficiency, especially during peak demand periods [26]. Cost management in eVTOL operations has been explored through lifecycle cost analysis, revealing that factors such as energy consumption, maintenance, and infrastructure significantly impact economic viability [27]. Advancements in embodied intelligence and autonomous systems have enabled more precise control and coordination of eVTOL fleets, improving operational reliability [28]. Challenges such as airspace integration, regulatory frameworks, and public acceptance remain critical barriers to widespread adoption [29]. This study builds on these foundations by integrating eVTOL operations, logistics optimization, and cost management into a unified framework, addressing both theoretical and practical considerations to advance the field of urban air logistics.

Similar to research focusing on EV–drone collaboration and time-varying travel times [30], our study uniquely investigates Meituan’s eVTOL operations, optimizing dispatch costs under low-altitude demand surges and charging constraints. We introduce an iterative algorithm and Monte Carlo simulations, emphasizing multi-period decentralized scheduling to advance low-altitude economy and urban logistics.

Following a review of the aforementioned studies, we have observed that while the existing eVTOL inventory is generally capable of meeting daily delivery demands, the quantity and charge–discharge capacity of eVTOLs may face significant challenges during periodic order surges. Such scenarios are prone to lead to delivery delays and resource shortages. Therefore, to ensure efficient delivery services, this study aims to address the cost optimization issues arising from the inventory quantity of eVTOLs.

3. Model and Analysis

Amid the surge in food delivery orders and the constraints imposed by battery charge–discharge performance, the dynamic optimization of eVTOL dispatch quantity and operational costs at distribution hubs has become critically significant. We try to address this issue by considering the dual objectives of fulfilling delivery demands while controlling operational expenses, thereby achieving optimal resource allocation and customer satisfaction. This approach seeks to balance the logistical efficiency of eVTOL fleets with the economic sustainability of their deployment, ensuring that the burgeoning needs of urban delivery systems are met within the practical limits of current technological capabilities.

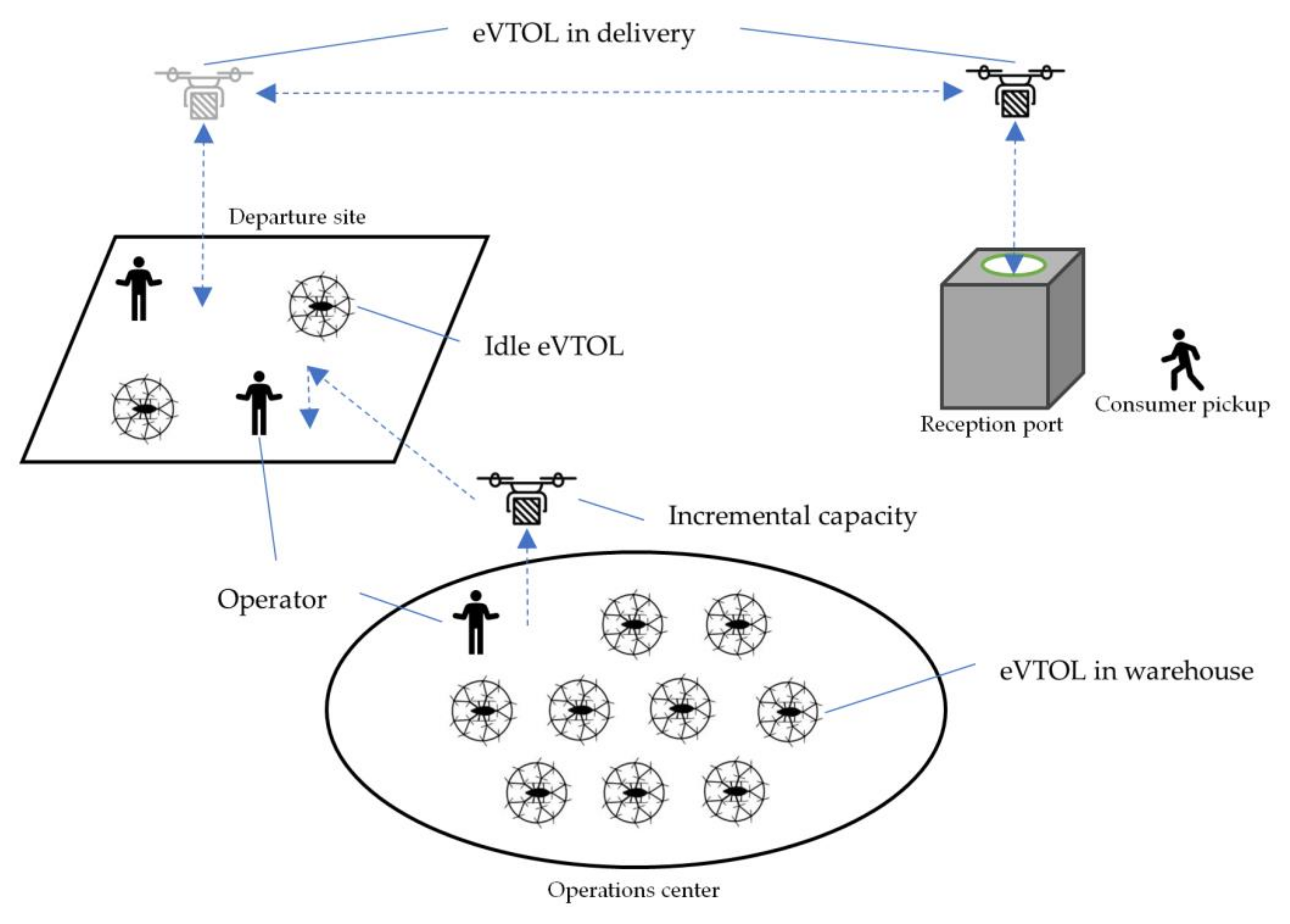
3.1. Premises

The following assumptions build the framework for the operation of eVTOL in low-altitude logistics and distribution: We consider the time-varying nature of demand, with different decision time spans possessing variable requirements for smoothing fluctuation forecasts that can provide a basis for realistic resource allocation. Secondly, we set constraints on eVTOL’s single delivery capacity and charging efficiency limitations in terms of transportation capacity and technology level, respectively, in order to facilitate the simplification of the problem and highlight the main conflicts that need to be solved urgently. Our assumptions also consider an incremental decision-making mechanism combined with a cost optimization strategy, which provides theoretical support for solving dynamic problems in operation.

Assumption 1: 

The logistics delivery demand exhibits temporal variability. Influenced dynamically by factors such as time, geographic location, and user behavior, particularly during peak periods (e.g., lunchtime on weekdays), the volume of delivery orders demonstrates a concentrated surge. Forecasting delivery demand on a weekly or monthly basis can appropriately smooth the daily fluctuations in delivery demand.

Assumption 2: 

The unit carrying capacity of eVTOLs is limited to transporting a single package per trip. Each sortie is designed to fulfill the demand of a single customer, ensuring food hygiene and safety, making it suitable for small-scale, high-frequency delivery scenarios such as food delivery.

Assumption 3: 

During peak periods, the 2C charging efficiency of eVTOLs is insufficient to support rapid redeployment. To minimize customer waiting times, the operations center ensures rapid equipment supply to distribution hubs by dispatching entire eVTOL units.

Assumption 4: 

Distribution hubs consider the risk of having zero idle eVTOL units and immediately make incremental leasing decisions to minimize operational costs as a cost center. If the incremental decision at time t_k is satisfied by a decision at time t_j (0 < t_j < t_k), then the incremental decisions between t_j and t_k will be related to the number of idle eVTOL units available at the distribution hub at time t_j.

Based on our investigation, delivery stations are typically equipped with three landing pads for takeoff and landing. In the event of a sudden surge in delivery demand, the integrated command center will activate an emergency response plan, deploying additional eVTOL units from nearby warehouse facilities. These dispatched eVTOLs will carry supplementary backup batteries, promptly take off, and proceed to the target delivery station to provide logistical support, thereby replenishing the delivery capacity and ensuring the successful completion of delivery tasks. Through this flexible dispatch mechanism, the system can dynamically balance the number of eVTOLs at delivery stations with actual demand, significantly enhancing the response speed and service reliability of the delivery network. This approach mitigates transportation delays or capacity shortages caused by demand fluctuations, effectively meeting customers’ immediate logistics needs (Figure 2).

Figure 2. Scheduling mechanism for eVTOL responding to fluctuations in delivery demand.

3.2. Model and Algorithm

The actual fluctuation of takeout orders is inherently stochastic. Assuming a constant demand would inadequately address real-world complexities. In accordance with Assumption 1, the eVTOL delivery station is conceptualized as a cost center. The station manager is tasked with determining the optimal number of eVTOL units to operate at a future time point, ensuring the capacity to meet abrupt surges in delivery demand.

Drawing upon the Economic Order Quantity (EOQ) theory, we consider a scenario where a delivery station submits a request for additional capacity to the operations center, which, upon approval, provides eVTOL equipment to the station. This process incurs several costs: the processing cost at the operations center, the rental cost of the eVTOL equipment, and the opportunity cost associated with unused equipment. The rental cost per unit of eVTOL equipment, denoted as C_L, represents the fee calculated based on the leasing period (e.g., day, week, or month) and the quantity of equipment leased during the dispatch period from the operations center. The processing cost, denoted as C_K, is a fixed cost incurred each time a leasing order is placed with the operations center, encompassing expenses such as authorization, approval, and logistical arrangements. The opportunity cost of the equipment, denoted as C_H, arises from the leasing deposit and the maintenance and management costs during the leasing period for idle eVTOL equipment held by the delivery station.

Considering the aforementioned three costs, the eVTOL delivery station aims to minimize the total cost during the KPI evaluation period at time T.

$$F_t=min {\sum }_{t=1}^T{C}_K{\beta }_t+C_L(y_t-x_t)+C_H(y_t-d_t)$$

(1)

Let $F_t$ denote the minimum decision cost from time 1 to t. The decision variable ${\beta }_t$ represents the leasing decision of the delivery station at time t, where ${\beta }_t=0$ indicates no leasing and ${\beta }_t=1$ indicates leasing. The term $C_K{\beta }_t$ captures the processing cost incurred from the operational center. The variable $x_t$ represents the inventory of eVTOLs prepared at time t prior to the leasing decision, while $y_t$ represents the inventory of eVTOLs post-leasing. The rental cost of eVTOLs is quantified by $C_L\left(y_t-x_t\right)$. The demand for eVTOL equipment at time t, driven by delivery orders, is denoted by $d_t$. The opportunity cost associated with idle eVTOLs is expressed as $C_H\left(y_t-d_t\right)$.

To minimize (1), the following constraints need to be satisfied:

$$0\le x_t\le y_t,t=1,2,\dots ,T$$

(2)

The above equation, the non-negative constraint, implies the non-negativity of increasing the number of eVTOLs.

$$0\le d_t\le y_t,t=1,2,\dots ,T$$

(3)

The above equation means that the number of incremental capacity requests is guaranteed to be non-negative.

$$0\le y_t-d_t=x_{t+1},t=1,2,\dots ,T$$

(4)

The above equation means that the unused incremental equipment at moment t becomes stock equipment at moment t + 1.

From Assumption 4, it is deduced that at time t, the delivery station ensures as much as possible that the incremental request is equal to the total delivery demand, and, thus, the lease cost of the eVTOL, $C_L\left(y_t-x_t\right)=C_L{d}_t$, is constant by ${\sum }_{t=1}^T{C}_L{d}_t$, and Equation (1) simplifies as follows:

$$\begin{array}{cc}\hfill F_t=& \mathit{min} {\sum }_{t=1}^T{C}_K{\beta }_t+C_H\left(y_t-d_t\right)\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& 0\le x_t\le y_t,t=\mathrm{1,2},\dots ,T\hfill \\ & 0\le d_t\le y_t,t=\mathrm{1,2},\dots ,T\hfill \\ & 0\le y_t-d_t=x_{t+1},t=\mathrm{1,2},\dots ,T\hfill \end{array}$$

(5)

We denote the total cost of the incremental decision of the delivery station at moment j considering moment k as ${\rho }_k^j$, $j,k\in T$:

$${\rho }_k^j=F_{j-1}+C_K+C_H\left(d_{j+1}+d_{j+2}+\dots +d_k\right)+C_H\left(d_{j+2}+d_{j+3}+\dots +d_k\right)+\dots +C_H(d_k)$$

(6)

From Assumption 4, the delivery station satisfies the delivery demand at moment k through incremental decisions at moment j. Therefore, the minimum total cost of the incremental decision cycle within moment k is jointly determined by the incremental decisions at each moment for $j=\mathrm{1,2},\dots k$:

$$F_k=\min \left[{\rho }_k^1,{\rho }_k^2,{\rho }_k^3,\dots ,{\rho }_k^{k-1},{\rho }_k^k\right],k\in T$$

(7)

From (7), the lowest total cost at moment k is obtained by comparing the respective total costs ${\rho }_k^j$ from moments 1 to k.

Thus, we define the decision subproblem $v_k$, denoting that the optimal decision in the first $k\in T$ periods is to make the last incremental decision in period $v_{k-1}$:

$$v_k=arg\underset{k}{\min }\{{\rho }_T^k\}, k=v_{k-1},v_{k-1}+1,\dots ,T$$

(8)

We give the algorithm (Algorithm 1) as follows

Algorithm 1: Incremental decision-making algorithm for eVTOL equipment.
1:	Input:
2:	Delivery demand sequence: d
3:	Operations Center Processing Costs: CK
4:	Unit opportunity cost: CH
5:	Output:
6:	Optimal (minimum) cost
7:	Procedure:
8:	Initiate $F_1=C_K$; subproblem v
9:	Dynamic programming:
10:	For each $k\in \left\{\mathrm{2,3},\dots ,T\right\}$:
11:	Determine subproblem sets $\{v\mid v\in \{v_{k-1},\dots ,k\left\}\right\}$
12:	For each subproblem v:
13:	Calculate subproblem optimal cost: ${\rho }_k^j$
14:	Select optimal subproblem $v^{\ast }=arg\underset{k}{\min }\left\{{\rho }_k^{v^{*}}\right\}$
15:	Update $F_k={\rho }_k^{v^{\ast }}$
16:	Determine Optimal (minimum) cost
17:	End Procedure

3.3. Numerical Case

We assume that the optimal incremental decision sequence and the optimal (minimum) cost are obtained by comparing the results when the application processing cost C_K and the unit opportunity cost δC_H are low or high for both cases.

Let the frequency of incremental decision-making at the delivery station be 4 times/month, and assume that the forecasted value of delivery orders for each week in a given month is 11,26,21,32 units in order. The number of eVTOLs used by the delivery station is 0 units, and it needs to request scheduling from the operations center. eVTOLs have a unit rental cost C_L = 1. eVTOLs that satisfy the demand in each period are returned to the operations center, and unused eVTOLs are left at the delivery station for use in the next period. We set the operations center processing cost C_K and the unit opportunity cost δC_H to be lower and higher for two scenarios for numerical algorithms, with two sets of incremental decisions in each scenario for comparison.

We qualitatively find, based on the comparison of the above two sets of arithmetic results (each containing four moment points representing decision-making time in an average month of four weeks), that lower processing costs and opportunity costs result in eVTOL incremental decisions tending to be spread over multiple periods within the decision cycle. Conversely, higher processing costs and opportunity costs result in eVTOL incremental decisions tending to be made in a low-frequency centralized manner within the decision cycle. The nature of this difference is due to the fixed cost effect of the processing cost C_K, i.e., the processing cost from the operations center remains constant regardless of the number of decisions at a given point in the decision cycle.

• Lower processing cost (C_K = 10) and unit opportunity cost (δC_K = 1) scenarios.

In this scenario, we give the following arithmetic example for two different eVTOL incremental decision sequences and find that the total cost of the incremental decision sequence of [35, 0, 50, 0] is better than the total cost of the incremental decision sequence of [37, 0, 26, 27]:

• If the eVTOL incremental decision sequence is [37, 0, 26, 27].

At the moment t = 1, the delivery demand is known to be 11 units and the incremental eVTOL decision is 37 units, resulting in the operations center incurring the processing cost C_K = 10 and the eVTOL rental cost $C_L=1\times 37$. The idle eVTOL before the decision is 0 units and the idle eVTOL after the delivery is 26 units, resulting in opportunity cost C_H = 1 × 26. The minimum total cost $F_1=C_K+C_L+C_H=73$.

At moment t = 2, the delivery demand is known to be 26 units. The eVTOL incremental decision is 0 units due to the idle eVTOL at the end of the previous moment of 26 units, resulting in the operations center incurring the processing cost C_K = 0 and the eVTOL rental cost C_L = 0. The idle eVTOL after the delivery is 0 units, resulting in the opportunity cost C_H = 0. The minimum total cost F₂ = 0.

At moment t = 3, the delivery demand is known to be 21 units and the incremental eVTOL decision is 26 units, resulting in the operations center incurring a processing cost C_K = 10 and an eVTOL leasing cost C_L = 26. In total, 0 units of idle eVTOL before the decision and 5 units of idle eVTOL after the delivery result in an opportunity cost C_H = 5. The minimum total cost $F_3=C_K+C_L+C_H=41$.

At moment t = 4, the delivery demand is known to be 32 units, and since the idle eVTOL at the end of the previous moment is 5 units, the eVTOL incremental decision is 27 units, resulting in the operations center incurring the processing cost C_K = 10 and the eVTOL rental cost C_L = 27. The idle eVTOL after delivery is 0 units, resulting in an opportunity cost C_H = 0. The minimum total cost F₄ = 37.

The eVTOL incremental decision sequence to cope with the delivery demand forecast sequence [11, 26, 21, 32] is, thus, [37, 0, 26, 27], with a total cost of 151.

2.

If eVTOL incremental decision sequence is [37, 0, 53, 0]

At the moment t = 1, the delivery demand is known to be 10 units and the incremental eVTOL decision is 37 units, resulting in the operations center incurring the processing cost C_K = 10 and the eVTOL rental cost C_L = 37. The idle eVTOL before the decision is 0 units and the idle eVTOL after the delivery is 26 units, resulting in the opportunity cost C_H = 26. The minimum total cost F₁ = 73.

At moment t = 2, the delivery demand is known to be 26 units. The eVTOL incremental decision is 0 units due to the idle eVTOL at the end of the previous moment of 26 units, resulting in the operations center incurring the processing cost C_K = 0 and the eVTOL rental cost C_L = 0. The idle eVTOL after the delivery is 0 units, resulting in the opportunity cost C_H = 0. The minimum total cost F₂ = 0.

At moment t = 3, the delivery demand is known to be 21 units and the incremental eVTOL decision is 53 units, resulting in the operations center incurring a processing cost $C_K=10$ and an eVTOL leasing cost $C_L=53$. In total, 0 units of idle eVTOL before the decision and 32 units of idle eVTOL after the delivery result in an opportunity cost C_H = 32. The minimum total cost F₃ = 95.

At moment t = 4, the delivery demand is known to be 32 units, and since the idle eVTOL at the end of the previous moment is 30 units, the eVTOL incremental decision is 0 units, resulting in the operations center incurring a processing cost C_K = 0 and an eVTOL rental cost C_L = 0. The idle eVTOL after the delivery of 0 units brings about an opportunity cost C_H = 0. The minimum total cost F₄ = 0.

The eVTOL incremental decision sequence for coping with the delivery demand forecast sequence [11, 26, 21, 32] is, thus, [37, 0, 53, 0], with a total cost of 168.

In the above two arithmetic examples with different eVTOL incremental decision sequences, the eVTOL incremental decision sequence of [37, 0, 53, 0] has the better total cost, and the arithmetic data are organized in Table 3.

Table 3. Scenarios with lower processing costs (C_K = 10) and unit opportunity costs (δC_H = 1).

The eVTOL incremental decision sequence is [37, 0, 25, 28]
Decision Time: T	t = 1	t = 2	t = 3	t = 4	Sum
Delivery demand	11	26	21	32	90
Incremental decision	37	0	26	27	90
eVTOL inventory before decision	0	26	0	5	n/a
eVTOL inventory after delivery	26	0	5	0	n/a
Processing cost CK	10	0	10	10	30
Rental cost CL	37	0	26	27	90
Opportunity cost CH	26	0	5	0	31
Total Costs	73	0	41	37	151
The eVTOL incremental decision sequence is [37, 0, 53, 0]
Decision Time: T	t = 1	t = 2	t = 3	t = 4	Sum
Delivery demand	11	26	21	32	90
Incremental decision	37	0	53	0	90
eVTOL inventory before decision	0	26	0	32	n/a
eVTOL inventory after delivery	26	0	32	0	n/a
Processing cost CK	10	0	10	0	20
Rental cost CL	37	0	53	0	90
Opportunity cost CH	26	0	32	0	58
Total Costs	73	0	95	0	168

• Scenarios with higher processing costs (C_K = 200) and unit opportunity costs (δC_H = 5)

In this scenario, we based our arithmetic on two different eVTOL incremental decision sequences and found that the total cost of the incremental decision sequence of [37, 0, 53, 0] is better than the total cost of the incremental decision sequence of [37, 0, 25, 28].

• If the eVTOL incremental decision sequence is [35, 0, 25, 25]

At moment t = 1, the delivery demand is known to be 11 units and the incremental eVTOL decision is 37 units, resulting in the operations center incurring a processing cost C_K = 200 and an eVTOL leasing cost C_L = 37. The idle eVTOL before the decision is 0 units, and the idle eVTOL after the delivery is 26 units, resulting in an opportunity cost C_H = 130. The minimum total cost $F_1=C_K+C_L+C_H=367$.

At moment t = 2, the delivery demand is known to be 26 units. The eVTOL incremental decision is 0 units due to the idle eVTOL at the end of the previous moment of 26 units, resulting in the operations center incurring the processing cost C_K = 0 and the eVTOL rental cost C_L = 0. The idle eVTOL after the delivery is 0 units, resulting in opportunity cost C_H = 0. The minimum total cost $F_2=0$.

At moment t = 3 the delivery demand is known to be 21 units and the incremental eVTOL decision is 26 units, resulting in the operations center incurring a processing cost C_K = 200 and an eVTOL leasing cost C_L = 26. In total, 0 units of idle eVTOL before the decision and 5 units of idle eVTOL after the delivery result in an opportunity cost C_H = 25. The minimum total cost $F_3=C_K+C_L+C_H=251$.

At moment t = 4, the delivery demand is known to be 32 units, and since the idle eVTOL at the end of the previous moment is 5 units, the eVTOL incremental decision is 25 units, resulting in the operations center incurring the processing cost C_K = 200 and the eVTOL lease cost C_L = 27. The idle eVTOL after delivery is 0 units, bringing the opportunity cost C_H = 0. The minimum total cost $F_4=227$.

The eVTOL incremental decision sequence for coping with the delivery demand forecast sequence [11, 26, 21, 32] is, thus, [37, 0, 53, 0], with a total cost of 845.

2.

If the eVTOL incremental decision sequence is [37, 0, 53, 0]

At the moment t = 1, the delivery demand is known to be 11 units and the incremental eVTOL decision is 37 units, resulting in the operations center incurring the processing cost C_K = 200 and the eVTOL rental cost $C_L=37$. The idle eVTOL before the decision is 0 units and the idle eVTOL after the delivery is 26 units, resulting in an opportunity cost $C_H=130$. The minimum total cost $F_1=367$.

At moment t = 2, the delivery demand is known to be 26 units. The eVTOL incremental decision is 0 units due to the idle eVTOL at the end of the previous moment of 26 units, resulting in the operations center incurring the processing cost C_K = 0 and the eVTOL rental cost C_L = 0. The idle eVTOL after the delivery is 0 units, resulting in opportunity cost C_H = 0. The minimum total cost $F_2=0$.

At moment t = 3, the delivery demand is known to be 21 units and the incremental eVTOL decision is 53 units, resulting in the operations center incurring a processing cost C_K = 200 and an eVTOL leasing cost C_L = 53. In total, 0 units of idle eVTOL before the decision and 32 units of idle eVTOL after the delivery result in an opportunity cost C_H = 160. The minimum total cost $F_3=413$.

At moment t = 4, the delivery demand is known to be 32 units, and since the idle eVTOL at the end of the previous moment is 32 units, the eVTOL incremental decision is 0 units, resulting in the operations center incurring a processing cost C_K = 0, and an eVTOL rental cost C_L = 0. The idle eVTOL after the delivery is 0 units, which brings about an opportunity cost C_H = 0. The minimum total cost $F_4=0$.

The eVTOL incremental decision sequence for coping with the delivery demand forecast sequence [11, 26, 21, 32] is, thus, [37, 0, 53, 0], with a total cost of 780.

In the above two arithmetic examples with different eVTOL incremental decision sequences, the eVTOL incremental decision sequence of [37, 0, 53, 0] has the better total cost, and the arithmetic data are organized in Table 4.

Table 4. Scenarios with higher processing costs (C_K = 200) and unit opportunity costs (C_H = 5).

The eVTOL incremental decision sequence is [37, 0, 25, 28]
Decision Time: T	t = 1	t = 2	t = 3	t = 4	Sum
Delivery demand	11	26	21	32	90
Incremental decision	37	0	26	27	90
eVTOL inventory before decision	0	26	0	5	n/a
eVTOL inventory after delivery	26	0	5	0	n/a
Processing cost CK	200	0	200	200	600
Rental cost CL	37	0	26	27	90
Opportunity cost CH	130	0	25	0	155
Total Costs	367	0	251	227	845
The eVTOL incremental decision sequence is [37, 0, 53, 0]
Decision Time: T	t = 1	t = 2	t = 3	t = 4	Sum
Delivery demand	11	26	21	32	90
Incremental decision	37	0	53	0	90
eVTOL inventory before decision	0	26	0	32	n/a
eVTOL inventory after delivery	26	0	32	0	n/a
Processing cost CK	200	0	200	0	400
Rental cost CL	37	0	53	0	90
Opportunity cost CH	130	0	160	0	290
Total Costs	367	0	413	0	780

3.4. Simulation

We perform Monte Carlo simulations based on the modeling algorithm. The following eight simulations are based on different levels of processing cost C_K, unit opportunity cost $\delta C_H$, and delivery demand mean and standard deviation, respectively, and are simulated 1000 times with normally distributed random numbers to obtain the histogram distribution corresponding to the optimal cost and the statistical properties of mean, standard deviation, kurtosis, and skewness.

By comparing the results of these eight Monte Carlo simulations, we find the following:

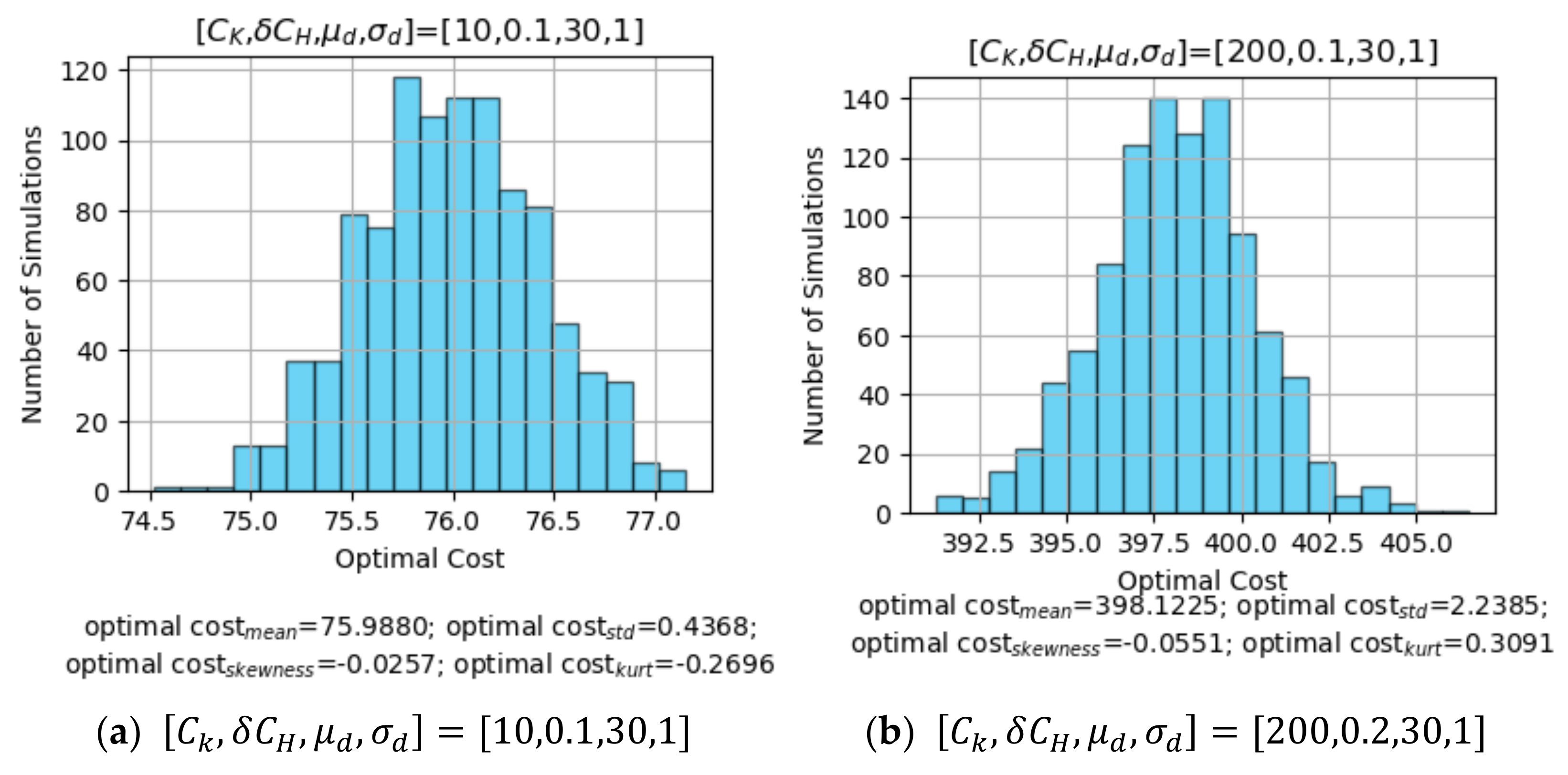
• An increase in processing cost raises the average level of optimal cost. The variation in the peak of the distribution of the optimal cost in the position of the horizontal axis is provided by a group comparison of the results in Figure 3a–h, fixing the other parameters, with the processing cost categorized into two states of either a low C_K = 10 or a high C_K = 200, and the variation in the peak of the distribution of optimal cost in the position of the horizontal axis.
• The increase in unit opportunity cost concentrates the distribution of the optimal cost. By comparing (a) and (c), (b) and (d), (e) and (g), and (f) and (h), respectively, and fixing the other parameters, the unit opportunity cost is categorized into two states, low $\delta C_H=0.1$ or high $\delta C_H=5$, and the concentration of the distribution of the optimal cost (std) exhibits changes.
• Changes in the mean level of delivery demand and its concentration leads to changes in the mean and skewness of the optimal cost. By comparing (a) and (e), (b) and (f), (c) and (g), and (d) and (h) in groups, fixing the other parameters, the mean of optimal cost increases when the mean and the standard deviation of delivery demand increase simultaneously, and its distribution exhibits a negative skewness with a long tail on the left and a concentration on the right.

Figure 3. Monte Carlo simulation on processing cost, unit opportunity cost and deliveries.

4. Conclusions

The smart city strategy promotes the development of a low-altitude economy, and eVTOL combined with embodied intelligence technology becomes an important force to optimize urban logistics and distribution. In this study, we investigated the catering delivery route deployed by Meituan eVTOL in downtown Shanghai. Through the analysis and field investigation of this delivery route, the delivery process and the eVTOL equipment parameters, we found that the eVTOL delivery station faces the risk of eVTOL equipment shortage and the challenge of eVTOL equipment scheduling during peak fluctuations in takeout delivery orders, highlighting the importance of dynamic and optimal scheduling of incremental eVTOL equipment decisions to optimize the delivery station operation cost and enhance customer satisfaction.

In terms of research methodology, we constructed an algorithmic model for this real-world problem, which was analyzed qualitatively and quantitatively using two sets of numerical arithmetic examples and eight Monte Carlo simulations. By analyzing the arithmetic examples of eVTOL incremental decision-making, we found that the changes in the processing cost, the opportunity cost and delivery demand have significant impacts on the decision model and the distribution of the optimal cost. To be specific, lower processing and opportunity costs favor decentralized decisions, while higher costs favor centralized decisions. Rising processing costs shift the optimal cost distribution right; higher opportunity costs concentrate it. Increased demand raises the optimal cost, creating a left-tailed, right-concentrated distribution.

Different cost parameters and demand volume characteristics jointly shape the dynamic pattern of eVTOL incremental decision-making and its economic performance. In light of these findings, we propose actionable strategies for delivery stations: adopting multi-period decentralized dynamic scheduling under low processing and opportunity costs to enhance flexibility or implementing low-frequency centralized decision-making under high costs to optimize efficiency. Reducing processing costs can further improve scheduling accuracy and scale efficiency, ensuring sustainable operational cost control.

In addition to the economic and operational suggestions, successful eVTOL deployment in urban logistics must address critical practical considerations. Airspace regulations, particularly in densely populated areas like Shanghai, require careful navigation to ensure compliance and safety. Robust safety protocols, including fail-safe mechanisms and real-time monitoring, are essential to mitigate operational risks. Furthermore, public acceptance, influenced by noise levels, privacy concerns and perceived safety, plays a pivotal role in the widespread adoption of eVTOL delivery services. Addressing these factors holistically will enhance the feasibility and societal impact of eVTOL-based logistics solutions.

The limitations of this study include the simplification of the eVTOL re-flight factor due to 2C charging and the joint cooperative incremental scheduling problem that omits the simultaneous replenishment of batteries and eVTOL equipment. These simplifications may impact the accuracy of re-flight readiness, operational efficiency and resource allocation, potentially affecting cost dynamics and decision-making models. In future studies, this model will be refined to incorporate these factors, providing a more comprehensive analysis to address these challenges, better align with real-world scenarios and further optimize urban logistics and distribution in the context of the low-altitude economy.