Systemic Optimization of Electric Vehicles Power System

Abstract

This paper presents a comparative study between two permanent magnet motor structures, one with trapezoidal waveforms and the other with sinusoidal waveforms, from the perspective of production cost, dynamic characteristic performance, and energy economy. The novel element of the research is also in using an electromagnetic converter to reduce the vehicle’s overall energy consumption and to push the multiple disadvantages of using the insolated bipolar transistors. This study is based on the sizing of the electromagnetic converter and the two motor structures using the method of combined analytical finite elements. The program for sizing is coupled with two control laws relating to the motor types in order to choose the top performers according to good dynamic characteristics and energy saving. The simulation results show, on the one hand, the equivalence of these structures from a dynamic characteristic point of view and, on the other hand, that the trapezoidal waveform motor structure is more economical. The design of an excitation system optimizing the consumed energy equipped by a hybrid excitation motor is also developed.

1. Introduction

Three-phase synchronous motors with permanent magnets fall into two categories: brushless DC motor with trapezoidal currents and back electromotive forces and AC motor with sinusoidal currents and back electromotive forces. In the literature, there are several studies that are concerned with these categories of motors [1,2,3,4,5]. In [1], an optimal design and control tool of permanent magnet motors improving electric vehicle power chain efficiency is presented. This study shows the importance of energy losses in the static converter caused by conduction and switching losses of power transistors. In addition, this study evokes the problem of the converter arm’s floating potential, causing the control circuit to become complicated. The works in [2,3,4,5] illustrate the design results precision advantage by using the combined analytical finite elements method for electric vehicle power chain design. In [6,7,8,9,10], interactions between the analytical design programs of permanent-magnet motors and control lows are presented.

Indeed, the motor design is performed using the analytical method, considering how the control models and design interact to increase power chain efficiency. An analytical dimensioning program of permanent motor structures compatible with stochastic optimization software on a large scale using the finite element approach for validation is developed. In this case, the research discussed in this paper focuses on using an electromagnetic switch in conjunction with a converter to push the multiple disadvantages of using power transistors. The combined analytical finite elements approach is used to design the power chain, drawing from research that has been presented in [5,6,7,8,9,10].

In addition, this paper presents two control approaches compatible with the sizing program of the electric vehicle power chain. The first is an improved scalar command by adding three current control loops compared to the conventional scalar control, which generally uses a single velocity control loop. This command generates trapezoidal phase currents compatible with permanent magnet synchronous motors with trapezoidal electromotive forces called brushless DC motors. The second control approach is a sinusoidal scalar control also enhanced by three current control loops. This second control is adapted to brushless DC motors with shortened magnets in order to have sinusoidal back electromotive forces. These control approaches are compatible with sizing and modeling programs of the two types of motors; for example, the DC bus voltage is determined with the objective of achieving the vehicle’s maximal speed. Maximum current is held in account for dimensioning the slot and has an influence on the inductances and the phase resistances, as well as on the mass of the motor. As a result, the control laws make it possible to consider all the systemic relationships that exist between the elements of the power chain.

A not insignificant point presented in this paper is the alternate use of batteries and a super-capacity, on the one hand, to increase the life of the batteries and, on the other hand, to boost the energy accumulator’s storage capacity. The following are the main components of this work: selection criteria for the control laws that are offered, the model’s implementation in the Matlab environment display of the simulation’s findings, and energy control. For a power chain using a hybrid excitation motor, the excitation system optimizes the energy used while also optimizing autonomy.

2. Electric Motor and Converter Chosen

The study line’s benefit includes the usage of electromagnetic switches, permanent magnet motor structure optimization, and control law improvement for electric vehicles saving energy. Really, insulated gate bipolar transistors (IGBTs) are widely used in DC-AC electrical energy conversion, and they have the following advantages: operation at high switching frequency, zero control energy (absence of gate current), and adaptability to high-power applications. In contrast, this transistor type has many disadvantages, like significant switching losses at opening and closing, mainly due to the high switching frequency. In addition, conduction losses are not negligible, and a floating potential problem for DC–AC conversion applications of electrical energy makes the control circuit complex. The static and dynamic latch-up problem for insulated bipolar transistors is incontrollable [1,2,3,4,5,6,7,8,9,10].

In view of these multiple drawbacks, it was considered to replace the IGBTs with electromagnetic switches controlled for opening and closing by electromagnets operating at low switching frequencies, having a modular structure. The switching frequency is optimized by adding electromagnet modules to increase the closing and opening frequency, which can reach 100 Hz under these conditions. A gearbox is added for adaptation of the low frequency of the DC–AC converter to the vehicle speed. The advantages of electromagnetic switches are as follows:

• They are adaptable to very-high-power applications.
• No switching losses when opening and closing and zero conduction losses.
• No floating potential problem for DC–AC conversion applications of electrical energy, making the control circuit simple.
• No static and dynamic latch-up problem.

For the selection of a motorization structure, there are several studied configurations, such as permanent magnet motors with trapezoidal or sinusoidal waveforms, coiled rotor motors with trapezoidal or sinusoidal waveforms, and hybrid excitation motors with trapezoidal or sinusoidal waveforms [1,2,3,4]. These motor configurations are either radial or axial. Actually, axial structures have several advantages, such as straight and open slots that facilitate easy production, the possibility to install more modules on the motor axis to increase power, and a greater ratio of mass to power ratio compared to radial flux motors [4]. Compared to radial flux motors, axial architectures are more compact and take up less space, and the end coil is smaller, resulting in lower copper losses [6,7,8,9,10,11,12,13,14,15].

The relation between the sinusoidal and trapezoidal extracted electromagnetic power is as follows [1,2,3,4,5,6,7,8,9,10]:

$${\mathrm{P}}_{\mathrm{emT}}={\displaystyle \frac{4}{3}}\times {\mathrm{P}}_{\mathrm{emS}}$$

(1)

Equation (1) shows that for the same magnitude of the electromotive forces that are induced and the same magnitude of the stator currents, the structures of trapezoidal waveform motors make it possible to extract a much greater electromagnetic power compared to the structures with sinusoidal waveforms.

2.1. Selection Criteria for the Power Chain Control Law

The fundamental criteria for choosing a control law dedicated to the speed variation in motors in general and, in particular, for the motorization application of electric vehicles, can be summarized firstly by real-time integration on electronic cards and energy saving and good profitability. Secondly, good dynamic characteristics reducing the causes of breakdowns. Finally, the command is without sensors. A strong ripple of electromagnetic torque accompanies direct torque control (DTC), and it has a high execution time and requires a large memory space for electronic integration. Vector control requires electronic integration of the motor model conversion matrices from the abc axis to the dq axis. These matrices are called park transformation matrices.

On the other hand, the improved scalar command developed requires the shortest execution time compared to the two direct torque control and vector control laws. It offers the best dynamic characteristics and waveforms of voltages and currents. It is chosen for these reasons to solve the problem of driving electric vehicles with variable speed.

2.2. Setting the Two Motor Structures in Equivalency

Due to their axial design, straight and open slots, and concentrated winding, both permanent magnet motor structures have lower production costs [5]. Switching from a trapezoidal waveform structure to a sinusoidal waveform structure is sufficient to shorten the magnets by a factor equal to 2/3. The stators of the two structures differ only in slot height, since the dimensioning current is different for both structures. To have an equivalence of the two structures, the outer and inner diameters of the two structures are the same as the number of turns per phase. The combined analytical finite elements method dimensioned the two structures for the results to be as precise as possible. The dimensional program is coupled with a genetic algorithm to optimize the performance of both engines.

2.3. Enhanced Scalar Control Principle

The principle of enhanced scalar control is based on imposing currents of either trapezoidal or sinusoidal waveforms in phase with the electromotive forces to maintain a constant electromagnetic torque at a constant speed and to reduce consumption, since the power factor in this way will be equal to unity. Indeed, four adjustment loops are required: a speed control loop for generating the reference currents amplitude and three current control loops for imposing currents in phase with the electromotive forces and possessing a form that is either trapezoidal or sinusoidal according to the applied control law to reduce the energy consumed by extraction of maximum power.

3. Power Chain Model

From the fundamental relationship of dynamics, the vehicle motion equation is obtained by [1,2,3,4,5,6,7]:

$${\mathrm{M}}_{\mathrm{v}}\times {\mathrm{R}}_{\mathrm{roue}}\times {\displaystyle \frac{\mathrm{dv}}{\mathrm{dt}}}={\mathrm{r}}_{\mathrm{d}}\times \left({\mathrm{T}}_{\mathrm{em}}-{\mathrm{T}}_{\mathrm{f}}-{\mathrm{T}}_{\mathrm{mec}}\right)-\left({\mathrm{F}}_{\mathrm{r}}+{\mathrm{F}}_{\mathrm{a}}+{\mathrm{F}}_{\mathrm{c}}\right)\times {\mathrm{R}}_{\mathrm{roue}}$$

(2)

where M_v is the vehicle mass, R_roue is the wheel radius, V is the speed of vehicle, r_d is the gear ratio, T_em is the electromagnetic torque, T_f is the torque due to iron losses, T_mec is the torque due to mechanical losses, F_r is the rolling resistance, F_a is the aerodynamic resistance, and F_c is the climbing resistance.

The maximal current frequency is expressed by Equation (3) [8,9,10].

$${\mathrm{f}}_{\max }=\left({\displaystyle \frac{{\mathrm{V}}_{\max }\times 1000}{3600}}\times {\displaystyle \frac{{\mathrm{r}}_{\mathrm{d}}}{{\mathrm{R}}_{\mathrm{roue}}}}\times \mathrm{p}\right)\times {\displaystyle \frac{1}{2\times \pi }}$$

(3)

where V_max is the maximal speed of the vehicle in Km/h and p is the motor pole pair’s number. According to Equation (1), for V_max = 80 Km/h, R_roue = 0.26 m, p = 4 and r_d = 0.12, the stator frequency is f_max = 6.53 Hz.

First, the speed regulator provides the reference current’s amplitude. The response speed is contrasted with the reference speed. A proportional/integral regulator type (PI) is driven by the comparator output to supply the reference current’s amplitude while reducing the speed error. The following equation gives the transfer function connecting the amplitude of the reference currents and the speed error [1,2,3,4,5,6,7,8,9].

$${\displaystyle \frac{{\mathrm{I}}_{\mathrm{ref}}\left(\mathrm{s}\right)}{\mathrm{error}\left(\mathrm{s}\right)}}=\left({\mathrm{K}}_{\mathrm{pv}}+{\displaystyle \frac{{\mathrm{K}}_{\mathrm{iv}}}{\mathrm{s}}}\right)\times {\mathrm{K}}_{\mathrm{s}}$$

(4)

where I_ref is the reference current magnitude, error(s) is the difference between the reference speed and the response speed, s is the Laplace operator, K_pv is the speed regulator proportional constant, K_pv is the speed regulator proportional constant, and K_s is a serial constant.

Second, the current regulator permits the generation of the reference current magnitude for vehicle speed regulation. An integral–proportional regulator is employed. The transfer functions that connect comparator errors and the following equations provide the reference voltages [1,2,3,4,5,6,7,8,9,10]:

$${\displaystyle \frac{{\mathrm{I}}_{\mathrm{ref}1}\left(\mathrm{s}\right)}{\mathrm{ec}1\left(\mathrm{s}\right)}}={\mathrm{K}}_{\mathrm{ic}}+{\displaystyle \frac{{\mathrm{K}}_{\mathrm{pc}}}{\mathrm{s}}}$$

(5)

$${\displaystyle \frac{{\mathrm{I}}_{\mathrm{ref}2}\left(\mathrm{s}\right)}{\mathrm{ec}2\left(\mathrm{s}\right)}}={\mathrm{K}}_{\mathrm{ic}}+{\displaystyle \frac{{\mathrm{k}}_{\mathrm{pc}}}{\mathrm{s}}}$$

(6)

$${\displaystyle \frac{{\mathrm{I}}_{\mathrm{ref}3}\left(\mathrm{s}\right)}{\mathrm{ec}3\left(\mathrm{s}\right)}}={\mathrm{K}}_{\mathrm{ic}}+{\displaystyle \frac{{\mathrm{k}}_{\mathrm{pc}}}{\mathrm{s}}}$$

(7)

where e_cn and I_refn for n = 1 to 3 are, respectively, the error between the reference current and the measured current of the phase n, K_ic is the proportional constant of the phase currents regulator, and K_pc is the integral constant of the phase currents regulator.

Thirdly, the control signal generator permits the generation of the six control signals of the electromagnetic switch converter. Indeed, the three reference voltages from the current regulator are modulated by a triangular signal and converted into control signals through three hysteresis pulsing between ‘0’ and ‘1’ logic. The two control signals of one arm are complementary and shorten in relation to one another to prevent the issue of an arm short circuit [5,6,7,8,9,10,11,12]. The back electromotive forces are given by these equations [1,2,3,4,5,6,7,8,9,10]:

$${\mathrm{e}}_1={\displaystyle \frac{2}{3}}\times {\mathrm{k}}_{\mathrm{e}}\times \mathsf{\Omega }\times \cos \left(\mathrm{p}\times \mathsf{\Omega }\times \mathrm{t}+{\displaystyle \frac{\pi }{2}}\right)$$

(8)

$${\mathrm{e}}_2={\displaystyle \frac{2}{3}} \times {\mathrm{k}}_{\mathrm{e}} \times \mathsf{\Omega } \times \cos \left(\mathrm{p}\times \mathsf{\Omega } \times -{\displaystyle \frac{2\times \pi }{3}}+{\displaystyle \frac{\pi }{2}}\right)$$

(9)

$${\mathrm{e}}_3={\displaystyle \frac{2}{3}}\times {\mathrm{k}}_{\mathrm{e}}\times \mathsf{\Omega }\times \cos \left(\mathrm{p}\times \mathsf{\Omega }\times \mathrm{t}-{\displaystyle \frac{4\times \pi }{3}}+{\displaystyle \frac{\pi }{2}}\right)$$

(10)

where e_i is the back electromotive force of the phase i, k_e is the back electromotive forces constant, Ω is the motor angular speed, and p the pole pair’s number.

The flux constants are given by the following three equations:

$${\mathrm{K}}_1={\displaystyle \frac{2}{3}}\times {\mathrm{k}}_{\mathrm{e}}\times \cos \left(\mathrm{p}\times \mathsf{\Omega }\times \mathrm{t}+{\displaystyle \frac{\pi }{2}}\right)$$

(11)

$${\mathrm{K}}_2={\displaystyle \frac{2}{3}}\times {\mathrm{k}}_{\mathrm{e}}\times \cos \left(\mathrm{p}\times \mathsf{\Omega }\times \mathrm{t}-{\displaystyle \frac{2\times \pi }{3}}+{\displaystyle \frac{\pi }{2}}\right)$$

(12)

$${\mathrm{K}}_3={\displaystyle \frac{2}{3}}\times {\mathrm{k}}_{\mathrm{e}}\times \cos \left(\mathrm{p}\times \mathsf{\Omega }\times \mathrm{t}-{\displaystyle \frac{4\times \pi }{3}}+{\displaystyle \frac{\pi }{2}}\right)$$

(13)

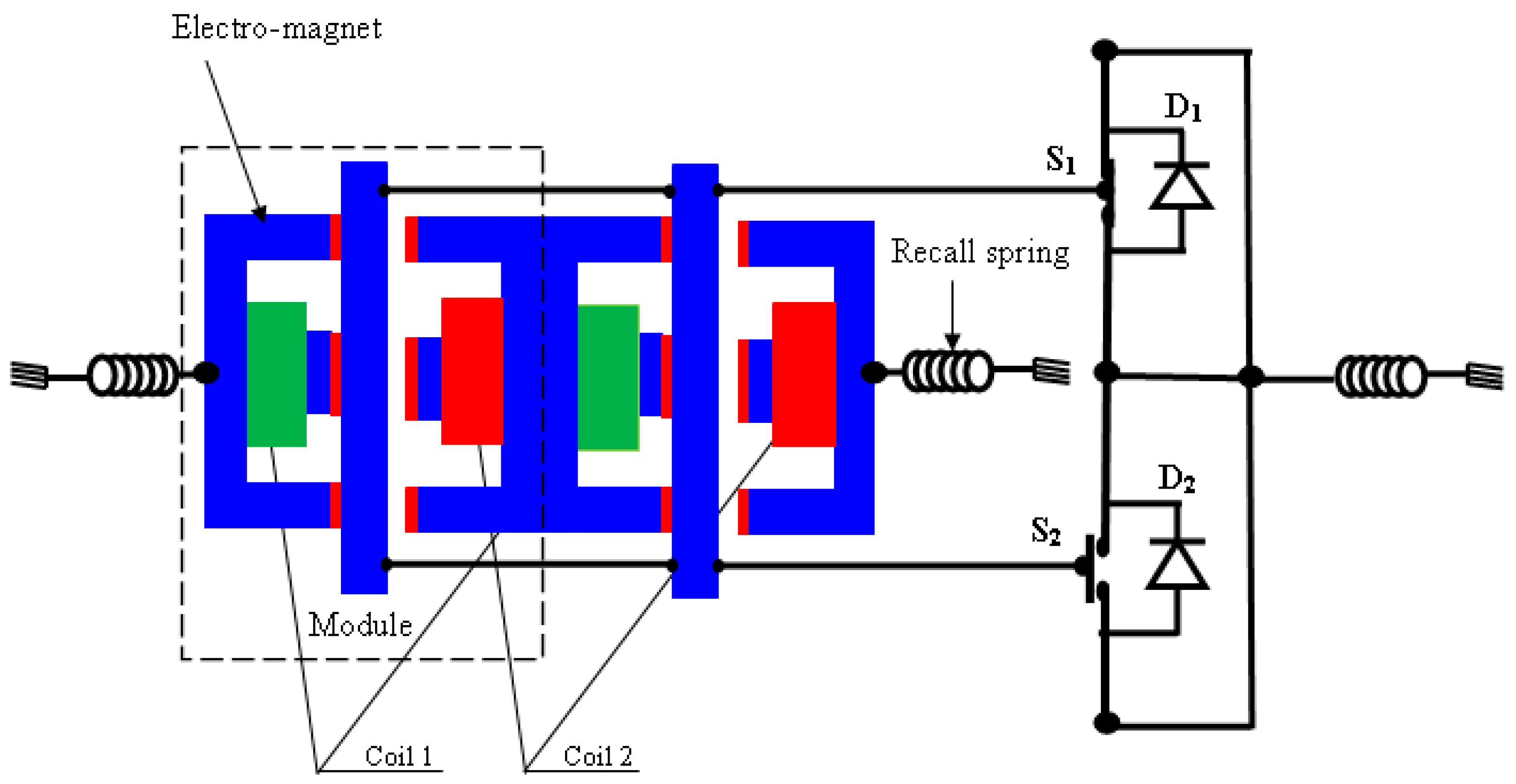
Fourth, the all-batteries-motor-converter model can use the association of the electromagnet and the two switches of the converter arm; it is illustrated by Figure 1 [4].

Two modules of electromagnets in both directions are used to increase the driving force. The two red colored coils connected in series are powered by a midpoint chopper, which creates a positive force for displacement in direction 1.

The two green colored coils connected in series are powered by another identical chopper, which creates a negative force for displacement in direction 2. To prevent the moving rods’ dry assault, three springs are used for damping. The control circuit uses approximately thirty watts [8,9,10]. The control circuit model of the electromagnet’s arm is based on the comparison of the reference voltage delivered from the speed and current regulator of the electric vehicle’s power chain. The comparator output drives a hysteresis varying between 0 and 1 to reproduce the waveform of the control signal 1. The output of the hysteresis is converted into a voltage varying between the values +Vcc when the signal is at 1 and −Vcc when the signal is at zero. This signal is related to the voltage supplying the coils of the electromagnet 1 (V1). The design parameters of the electromagnet are shown in Figure 2 [5].

The two electromagnets inductances are expressed by the following equations:

$${\mathrm{L}}_1={\mathrm{m}}_{\mathrm{uv}}\times {\mathrm{N}}_{\mathrm{sp}}^2\times \left({\displaystyle \frac{\frac{{\mathrm{S}}_{\mathrm{d}}}{2}}{2\times \left({\mathrm{E}}_{\mathrm{cu}}+{\mathrm{D}}_{\mathrm{co}}-{\mathrm{x}}_{\mathrm{t}}\right)}}\right)+{\displaystyle \frac{{\mathrm{H}}_{\mathrm{cu}}\times {\mathrm{E}}_{\mathrm{b}}}{{\mathrm{E}}_{\mathrm{lc}}+{\mathrm{L}}_{\mathrm{dc}}}}$$

(14)

$${\mathrm{L}}_2={\mathrm{m}}_{\mathrm{uv}}\times {\mathrm{N}}_{\mathrm{sp}}^2\times \left({\displaystyle \frac{\frac{{\mathrm{S}}_{\mathrm{d}}}{2}}{2\times \left({\mathrm{E}}_{\mathrm{cu}}+{\mathrm{x}}_{\mathrm{t}}\right)}}\right)+{\displaystyle \frac{{\mathrm{H}}_{\mathrm{cu}}\times {\mathrm{E}}_{\mathrm{b}}}{{\mathrm{E}}_{\mathrm{lc}}+{\mathrm{L}}_{\mathrm{dc}}}}$$

(15)

where N_sp is the coil spire number, S_d is the main tooth section, m_uv is the air permeability, E_b is the length of the main tooth, H_cu is the height of the coil, L_dc is the distance between the coil and the right tooth, D_co is the maximum opening of the mobile armature, xt is the displacement of the mobile armature, E_lc is the coil copper thickness, E_cu is the thickness of the copper layer, and L_dc is the distance between the coil and the right tooth. The coil phase voltages are expressed by the following equations:

$${\mathrm{v}}_1=\mathrm{R}\times {\mathrm{i}}_1+{\displaystyle \frac{\mathrm{d}\left({\mathrm{L}}_1\times {\mathrm{i}}_1\right)}{\mathrm{d}\mathrm{t}}}$$

(16)

$${\mathrm{v}}_2=\mathrm{R}\times {\mathrm{i}}_2+{\displaystyle \frac{\mathrm{d}\left({\mathrm{L}}_2\times {\mathrm{i}}_2\right)}{\mathrm{d}\mathrm{t}}}$$

(17)

where R is the coil resistance, L₁ and L₂ are, respectively, the inductance of the coil 1 and 2, and i₁ and i₂ are, respectively, the current of the coil 1 and 2.

The strength developed by the two electromagnets is expressed by the following equation:

$${\mathrm{F}}_{\mathrm{em}}={\displaystyle \frac{1}{{\mathrm{v}}_{\mathrm{t}}}}\times {\displaystyle \frac{\mathrm{d}\left(\frac{1}{2}\times \left({\mathrm{L}}_1\times {\mathrm{i}}_1^2+{\mathrm{L}}_2\times {\mathrm{i}}_2^2\right)\right)}{\mathrm{dt}}}$$

(18)

The mobile armature motion equation is derived from the fundamental relation of dynamic [8,9,10].

$${\mathrm{m}}_{\mathrm{t}} \times {\displaystyle \frac{\mathrm{d}{\mathrm{v}}_{\mathrm{t}}}{\mathrm{dt}}}={\mathrm{F}}_{\mathrm{em}}-\left(\mathrm{s}+{\mathrm{n}}_{\mathrm{u}}\times \mathrm{abs}\left({\mathrm{v}}_{\mathrm{t}}\right)+{\mathrm{x}}_{\mathrm{si}}\times {\mathrm{v}}_{\mathrm{t}}^2\right)-{\mathrm{F}}_{\mathrm{R}}\left({\mathrm{x}}_{\mathrm{t}}\right)$$

(19)

$${\mathrm{v}}_{\mathrm{t}}={\displaystyle \frac{\mathrm{d}{\mathrm{x}}_{\mathrm{t}}}{\mathrm{dt}}}$$

(20)

$$\left\{\begin{array}{c}\mathrm{i}\mathrm{f} {\mathrm{x}}_{\mathrm{t}}\ge {\mathrm{D}}_{\mathrm{c}\mathrm{o}}, {\mathrm{F}}_{\mathrm{R}}\left({\mathrm{x}}_{\mathrm{t}}\right)=\mathrm{k}\times \left({\mathrm{x}}_{\mathrm{t}}-{\mathrm{D}}_{\mathrm{c}\mathrm{o}}\right)\\ \mathrm{i}\mathrm{f} {\mathrm{x}}_{\mathrm{t}}\le 0, {\mathrm{F}}_{\mathrm{R}}\left({\mathrm{x}}_{\mathrm{t}}\right)=-\mathrm{k}\times \left|{\mathrm{x}}_{\mathrm{t}}\right|\end{array}\right.$$

(21)

where m_t is the mobile shaft mass, x_t and V_t are, respectively, the mobile armature position and speed, D_co is the power contacts opening, s is the dry friction coefficient, n_u is the viscous friction coefficient, x_si is the fluid friction coefficient, F_R is the total resistance strength, k is stiffness of the spring, and, finally, F_em is the mobile armature strength.

Increasing the supply current of the electromagnetic converter coils, reducing the maximal displacement of the moving rod, and increasing the number of electromagnet modules allows for reaching a ratio close to fifteen between the switching frequency and the frequency of the motor currents, which makes it possible to control the motor by a two-level voltage inverter with an electromagnetic switch.

A two-level voltage inverter powers the motor. Ideal electromagnetic switches to reduce losses and avoid the multiple disadvantages of insulated gate bipolar transistor (IGBT) replace IGBTs. A resistor connected in series with an inductance and a back electromotive force is similar to each motor phase. The motor–converter assembly model is implanted under the Simulink environment. The equations below describe the three-phase model [1,2,3,4,5,6,7]:

$${\mathrm{v}}_1=\mathrm{R}\times {\mathrm{i}}_1+\left(\mathrm{L}-\mathrm{M}\right)\times {\displaystyle \frac{{\mathrm{di}}_1}{\mathrm{dt}}}+{\mathrm{e}}_1$$

(22)

$${\mathrm{v}}_2=\mathrm{R}\times {\mathrm{i}}_2+\left(\mathrm{L}-\mathrm{M}\right)\times {\displaystyle \frac{{\mathrm{di}}_2}{\mathrm{dt}}}+{\mathrm{e}}_2$$

(23)

$${\mathrm{v}}_3=\mathrm{R}\times {\mathrm{i}}_3+\left(\mathrm{L}-\mathrm{M}\right)\times {\displaystyle \frac{{\mathrm{di}}_3}{\mathrm{dt}}}+{\mathrm{e}}_3$$

(24)

The following equation provides the electromagnetic torque:

$${\mathrm{T}}_{\mathrm{em}}={\displaystyle \frac{1}{\mathsf{\Omega }}}\left({\mathrm{e}}_1\times {\mathrm{i}}_1+{\mathrm{e}}_2\times {\mathrm{i}}_2+{\mathrm{e}}_3\times {\mathrm{i}}_3\right)$$

(25)

where R, L, and M are, respectively, the resistance, the inductance, the mutual inductance, and the electric constant of the motor, and i_i and u_i are, respectively, the current and the voltage of the phase i.

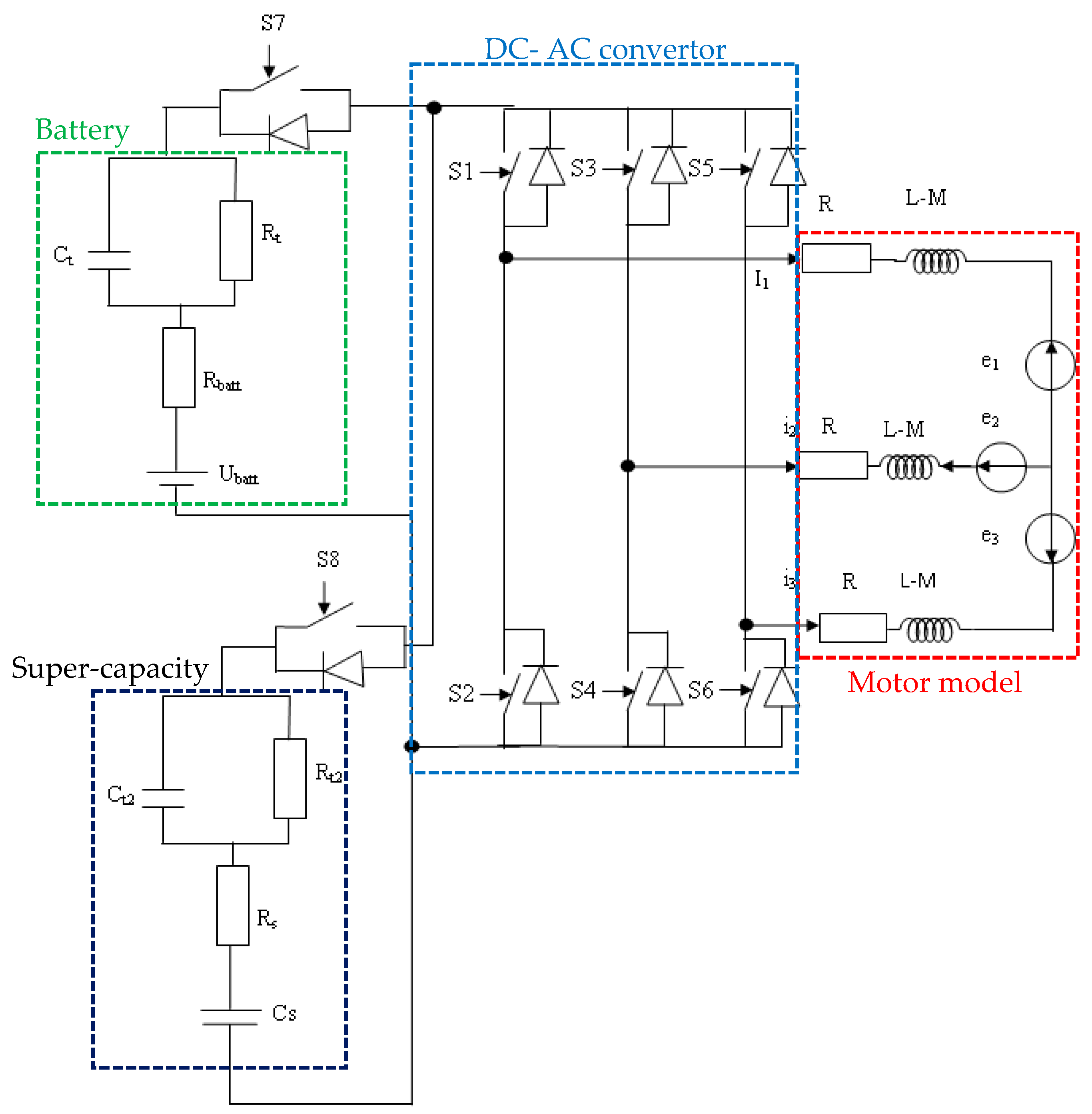
Lastly, the global model in Figure 3 is implanted under the Matlab/Simulink environment results from the connecting of the powertrain components of different models.

In this model, the power converter drives the motor with electromagnetic switches according to a trapezoidal or sinus control strategy, keeping the motor’s phase current in phase with the electromotive force, resulting in a reduction in energy consumption and recovery energy during the phases of strong decelerations. The passage of a law from one control law to another is realized by changing the model of the back electromotive forces and the generator’s control signals.

4. Simulation Results

The parameters taken from the sizing program shown in

Table 1. Simulation parameters.

Parameters	Values	Units
External diameter of the motor (De)	350	mm
Internal diameter of the motor (Di)	150	mm
Air-gap thickness (e)	5	mm
Magnets thickness (Ha)	71.504	mm
Magnet width for trapezoidal case (Lat)	98.175	mm
Magnet width for sinusoidal case (Las)	65.45	mm
Magnets mass on trapezoidal case (Mat)	8.077	Kg
Stator yoke thickness (Hcr)	52.86	mm
Rotor yoke mass (Mcr)	32.6	Kg
Magnets mass on sinusoidal case (Mas)	5.385	Kg
Stator yoke thickness (Hcs)	52.875	mm
Stator teeth high (Hd)	71.5	mm
Stator teeth (Mds)	36.37	Kg
Stator yoke mass (Mcs)	32.6	Kg
Back electromotive force constant (ke)	0.76	Volt/(rad/s)
Air-gap’s flux density (Be)	0.75	Tesla
Number of turns per phase (Nsph)	20	/
Resistance phase (R)	0.003	Ohm
Mutual inductance (M)	0.08648975361	mh
Inductance (L)	0.40039909640	mH
DC bus voltage (Udc)	150	Volt
Switching frequency (fsw)	100	Hz

are used to run the simulations.

Figure 4 illustrates the mobile armature speed, position, and coil control signals.

The design parameters of the electromagnetic converter can be optimized in order to maximize the switching frequency. The vehicle’s response speed progression in relation to the reference speed is depicted in Figure 5. The vehicle’s good dynamic characteristics for the sinusoidal and trapezoidal control technologies are depicted in this image. It is accurate to say that the reference speed and response speed nearly correspond.

The phase currents for the trapezoidal control scenario are shown in Figure 6. It demonstrates the effectiveness of the established control mechanism by demonstrating that the currents’ shapes are extremely similar to a trapezoidal form. The efficiency of the method for determining the settings of the speed and current regulators is demonstrated, which also show that these currents are decreased throughout the startup phases.

The phase currents for the sinusoidal instance are shown in Figure 7. The near-sinusoidal shape of the currents in this figure demonstrates the effectiveness of the established control mechanism.

Figure 8 illustrates the use of pulse width modulation technique performances for control of the phase current to a sinusoidal form at low frequency.

Compared to the same power chain modeled using an IGBT, the developed model using electromagnetic switch leads to a net reduction in the magnitude of the phase currents [16]. This reduction results from the compensation of the voltage drop in the IGBTs, which leads to a reduction in energy losses in the studied power chain.

The effectiveness of the method for determining the parameters of the speed and current regulators is demonstrated by the following figure, which also demonstrates that these currents are decreased to the start-up phases. The electromagnetic torque produced by the electric motor in the two scenarios is shown in Figure 9. It illustrates the similarity of these torques. The success of the control strategy established and the method for determining the speed and current regulator parameters is demonstrated by the torque’s decreased fluctuation during the constant speed operating phases. Since the vehicle recovers energy during these operation phases, this figure also demonstrates that the torque is negative during deceleration phases.

With the travels depicted in Figure 5, the evolution of the batteries’ state of charge is shown in Figure 10, with an energy storage capacity of 800 kWh. The battery discharges faster in the sinusoidal case than in the trapezoidal instance, as seen in this figure. This is because the phase currents make a big difference on the energy losses across the power chain. In fact, the phase currents in the sinusoidal case have a larger amplitude than in the trapezoidal example.

In conclusion, the simulation results indicate that both control laws are competitive, with the exception that the trapezoidal control law is the most cost-effective based on the features that depict the batteries’ state of charge. Additionally, the power chain-sizing program is fully validated by the simulation findings. However, because the magnets are shortened for the sinusoidal case by a factor of two-thirds compared to the trapezoidal case, the permanent magnet motor costs more for the trapezoidal case than for the sinusoidal case.

5. Energy Management System

The system of energy management (Figure 11) makes it possible to connect the batteries to the electromagnetic converter during the operating phases at both constant speed and deceleration; complementarily, the super-capacitance powers the converter due to the fact that when operating at high accelerations, the energy accumulator’s current delivery is high. This technique makes it possible to avoid the stress of running with high current for the batteries, which makes it possible to increase their lifetime. When the acceleration is positive and greater than a threshold α, the signal s8 is active (s8 = ‘1’ and s7 = ‘0’), and, in this case, the supercapacitor is connected to the converter. Otherwise, the s7 signal is active (s8 = ‘0’ and s7 = ‘1’); in this case, the converter is attached to the battery [11,12,13,14,15,16,17,18,19,20,21,22,23].

According to the earlier study, the most effective way to save energy is to use a power chain that has a permanent magnet motor connected to an enhanced sinusoidal control law. For the upcoming study, this power chain is chosen, and a comparable hybrid excitation motor is used in place of the permanent magnet motor. One benefit of this structure is that it has an extra degree of freedom—the excitation current. The stator currents are strong when the acceleration is high. An overflow technique that involves raising the excitation current is employed to overcome this issue. Using this method, energy consumption can be decreased based on stator copper losses [13,14,15,16,17,18,19,20].

The vehicle has energy excess during the deceleration phases because kinetic energy is significant. Because of this, the current of excitation is decreased to offset the torque that the electric motor’s surplus provides. This defluxion method permits an energy gain as well. Equation (17) demonstrates this property [1,2,3,4,5]:

$${\mathrm{M}}_{\mathrm{v} }\times {\mathrm{R}}_{\mathrm{r}\mathrm{oue}}\times {\displaystyle \frac{\mathrm{dV}}{\mathrm{dt}}}={\mathrm{r}}_{\mathrm{d}}\times {\mathrm{T}}_{\mathrm{em}}-{\mathrm{T}}_{\mathrm{R}}\left(\mathrm{V}\right)$$

(26)

where T_R is the resistance torque.

In the sinusoidal regime:

$${\mathrm{T}}_{\mathrm{em}}={\mathrm{K}}_{\mathrm{e}}\times \mathrm{I}$$

(27)

From Equations (17) and (18), we can deduce the following relation:

$$\mathrm{I}={\displaystyle \frac{{\mathrm{M}}_{\mathrm{v} }\times {\mathrm{R}}_{\mathrm{r}\mathrm{oue}}\times \frac{\mathrm{dV}}{\mathrm{dt}}+{\mathrm{T}}_{\mathrm{R}}\left(\mathrm{V}\right)}{{\mathrm{r}}_{\mathrm{d}}\times {\mathrm{K}}_{\mathrm{e}}}}$$

(28)

$$\mathrm{a}={\displaystyle \frac{\mathrm{dV}}{\mathrm{dt}}}$$

(29)

where a is the vehicle acceleration.

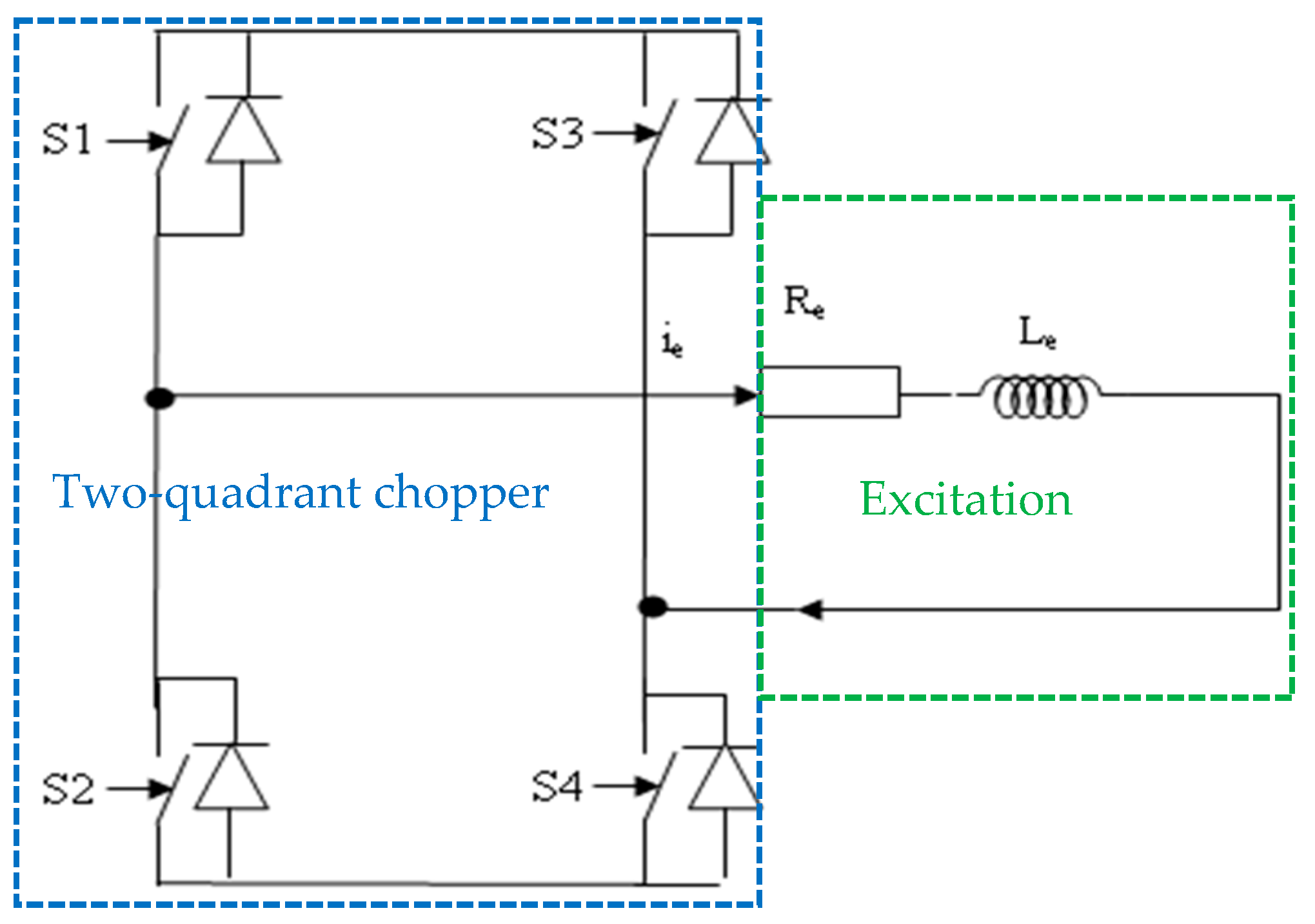
According to Equations (19) and (20), the motor’s current amplitudes depend essentially on the vehicle acceleration (a) and the electric motor constant (Ke). Indeed, the used optimization technology consist of the augmentation of the electric constant by augmentation of the excitation current (Ie) for high acceleration to reduce the stator currents amplitude I, causing a reduction in the motor’s copper losses, and thereafter a reduction in power chain consumed energy. For low acceleration and to compensate for the reduction in the motor’s current amplitudes, it is necessary to reduce the electric motor constant and thereafter the excitation current. This technology permits users to reduce the excitation winding copper losses. In this case, the consumed energy is also reduced. The low and high excitation current values are optimized by several simulations in the goal of the maximization of the consumed energy. To carry out these steps, a system for optimizing the excitation current is designed (Figure 12) [15,16,17,18,19,20,21,22,23]. This system enables the excitation current to be regulated between two higher and lower values according to the operating speed of the vehicle, that is to say in acceleration or deceleration. Indeed, a chopper with two quadrants powers the excitation winding of the rotor, and the reference excitation current is selected according to the operating speed of the vehicle. The excitation system makes it possible to calculate the acceleration by derivation of the speed to test the operating regime. A proportional–integral-type excitation current regulator according to the operating regime is used to produce the excitation winding’s reference voltage. This reference is converted into the two control signals necessary to control the chopper, making use of a triangle signal and a hysteresis that fluctuates between “0” and “1” logic [11,12,13,14,15,16,17,18,19,20].

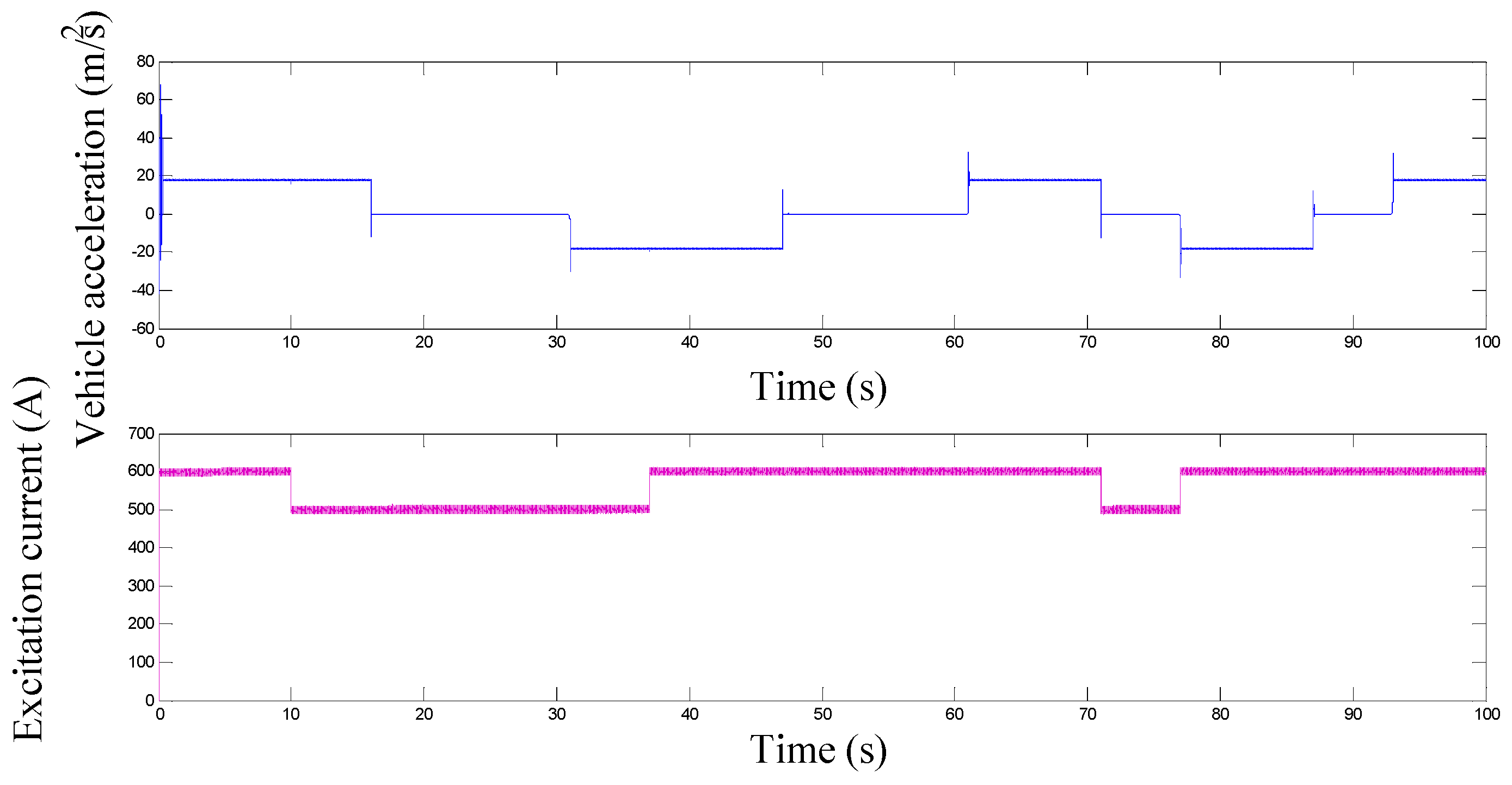
Figure 13 shows how the excitation current changes in response to vehicle acceleration and how the excitation current varies in response to variations in acceleration.

Figure 14 illustrates the consumed energy with and without the optimization system. With the excitation system improving the vehicle consumption, it shows that the power chain uses less energy.

6. Conclusions

Two control laws—an enhanced trapezoidal scalar control law and an enhanced sinusoidal scalar control law—that are tailored to the power chain’s size program are provided in this study. The interactions between all components in the power chain are taken into consideration by these two control laws. The values taken from the sizing program are used to implement these control laws in the Simulink environment. The performance of the electromagnetic converter, which was substituted for the IGBTs converter, is shown in this study. Simulation results demonstrate that both control laws are competitive, with the exception that the trapezoidal control law is the most cost-effective based on the features that depict the batteries’ state of charge. Additionally, the power chain-sizing program is fully validated by the simulation findings.

However, the cost of the permanent magnet motor is higher in the trapezoidal case than in the sinusoidal case because the magnets are shorter in the sinusoidal case by a factor of two-thirds, and the cost of the magnets mostly determines the motor’s total cost. The simulation results thoroughly validate the power chain’s dimensioning and control algorithms, which are at a good scientific level. This work is accomplished by designing an excitation system that maximizes energy consumption for a power chain with a hybrid excitation motor and using genetic algorithms to optimize autonomy. Finally, comparing the robustness of the developed control laws with those of other control laws will be an interesting prospect.

As for principal future works, it will be interesting to use the studied power chain to design a hybrid and especially parallel vehicle in order to increase the performance of future vehicles, establish a comparative study between the production and maintenance cost between the DC–AC converters with IGBT and with electromagnetic switches, and industrialize the global system.