Stochastic Optimal Scheduling of Flexible Traction Power Supply System for Heavy Haul Railway Considering the Online Degradation of Energy Storage
Abstract
1. Introduction
- (1)
- An HFTPSS integrated with ESS and PFC is developed to enhance the economic operation of the system. The PFC facilitates power interactions between various traction substations to improve the entire system’s energy efficiency, while the ESS achieves peak shaving by flexibly regulating RBE, thereby reducing the electricity costs of HFTPSS.
- (2)
- Considering the volatility of traction power in heavy-haul railways, a classical scenario generation method combining LSTM, LHS, and FCM is proposed to generate classical scenarios that reflect actual situations, accurately accounting for power uncertainty and thereby reducing its impact on system scheduling.
- (3)
- Taking into account the impact of traction power uncertainty and the state of ESS capacity on energy dispatch, a stochastic optimal scheduling model for HFTPSS is proposed. This model considers the online degradation of ESS and aims to improve RBE utilization, enhance energy efficiency, and reduce electricity costs by optimizing the operational strategy of flexible devices.
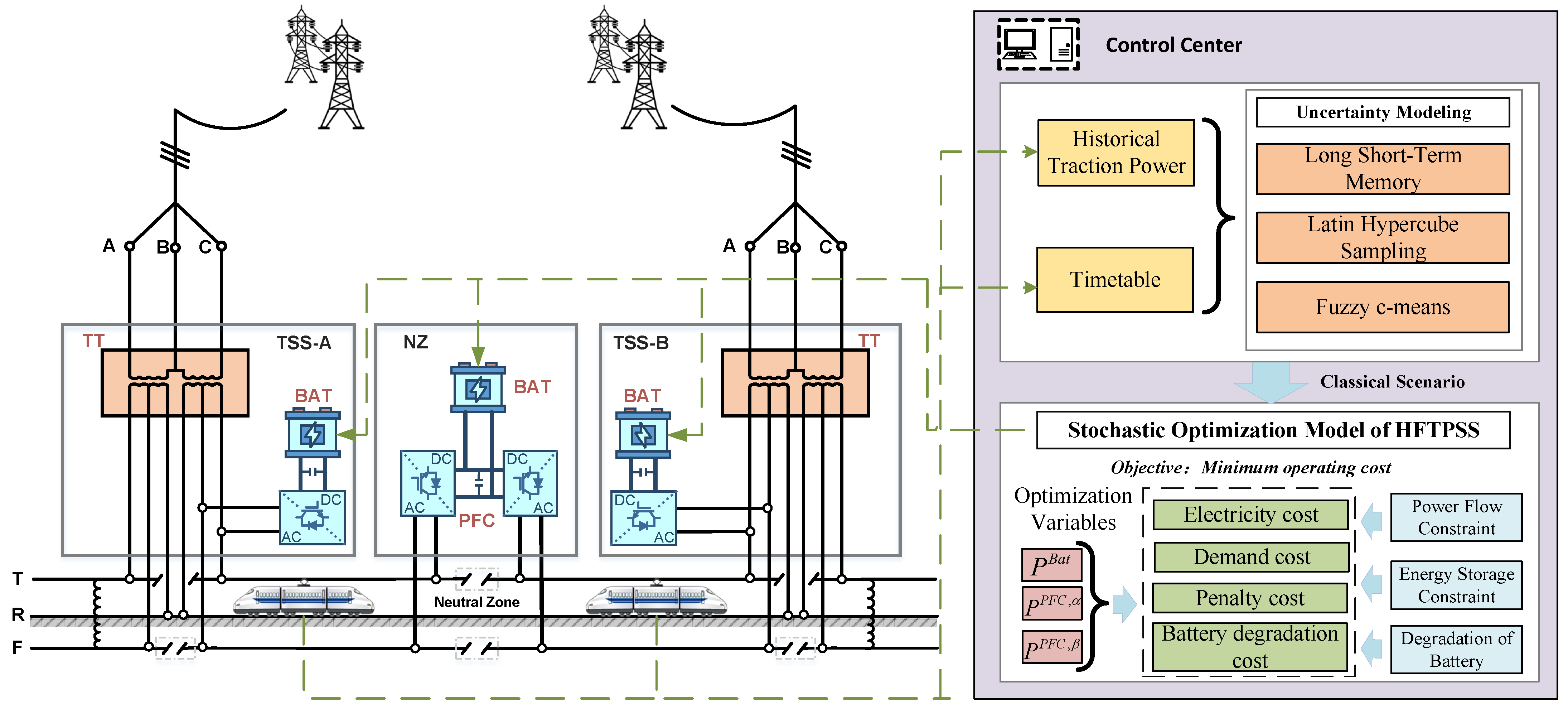
2. System Description
3. Uncertainty Modeling of Traction Power
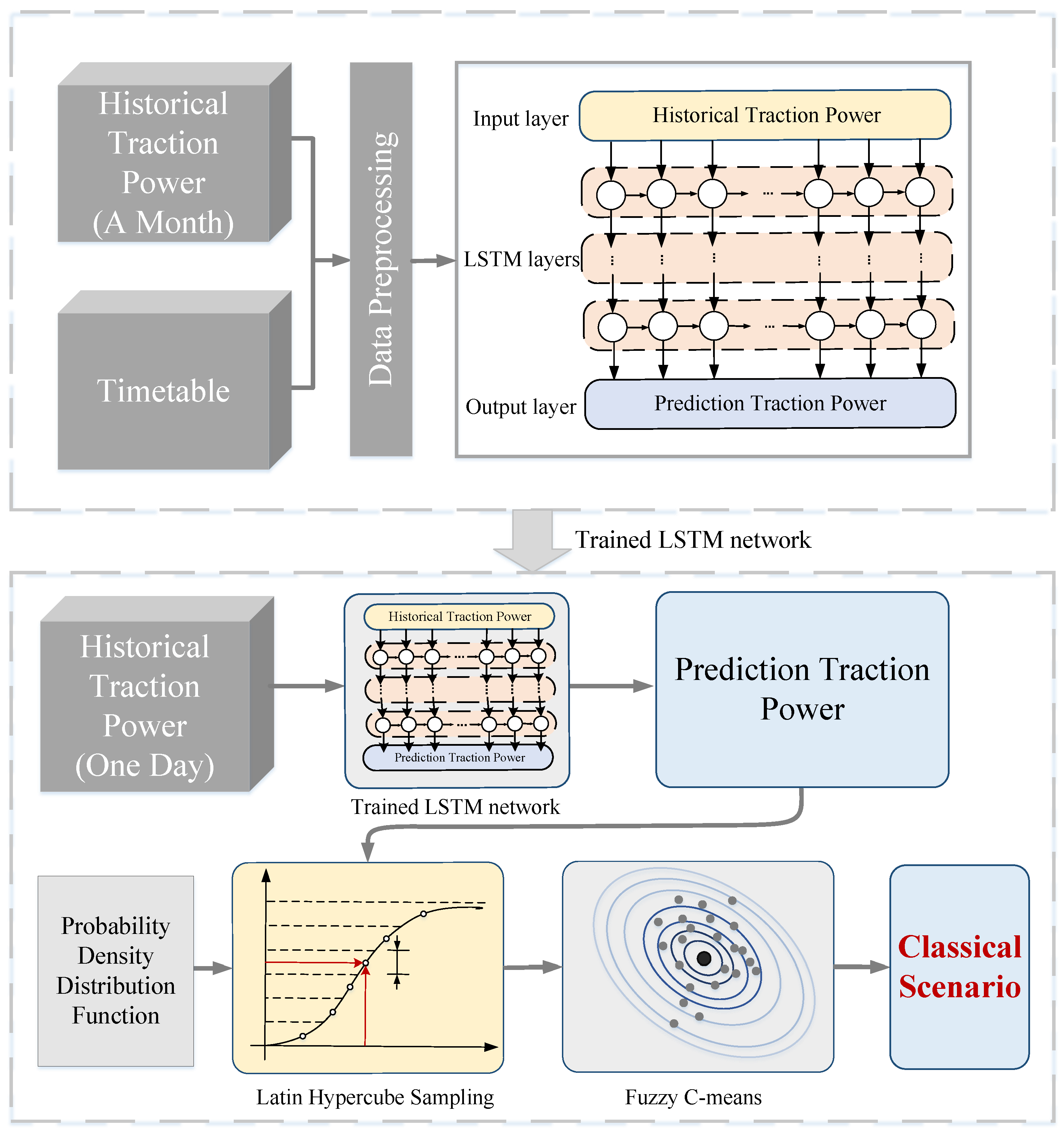
3.1. Framework of Uncertainty Modeling
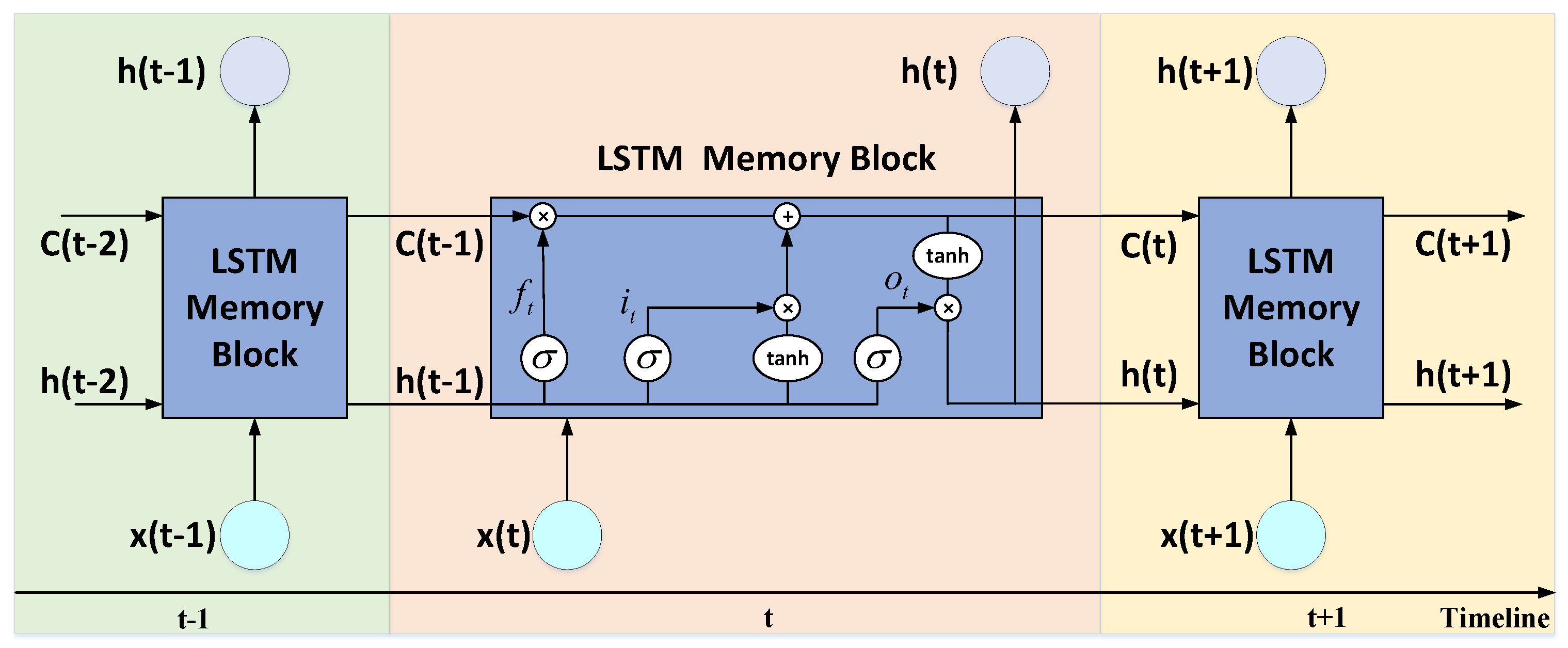
3.2. Prediction Model of Traction Power
3.3. Scenario Generation and Reduction
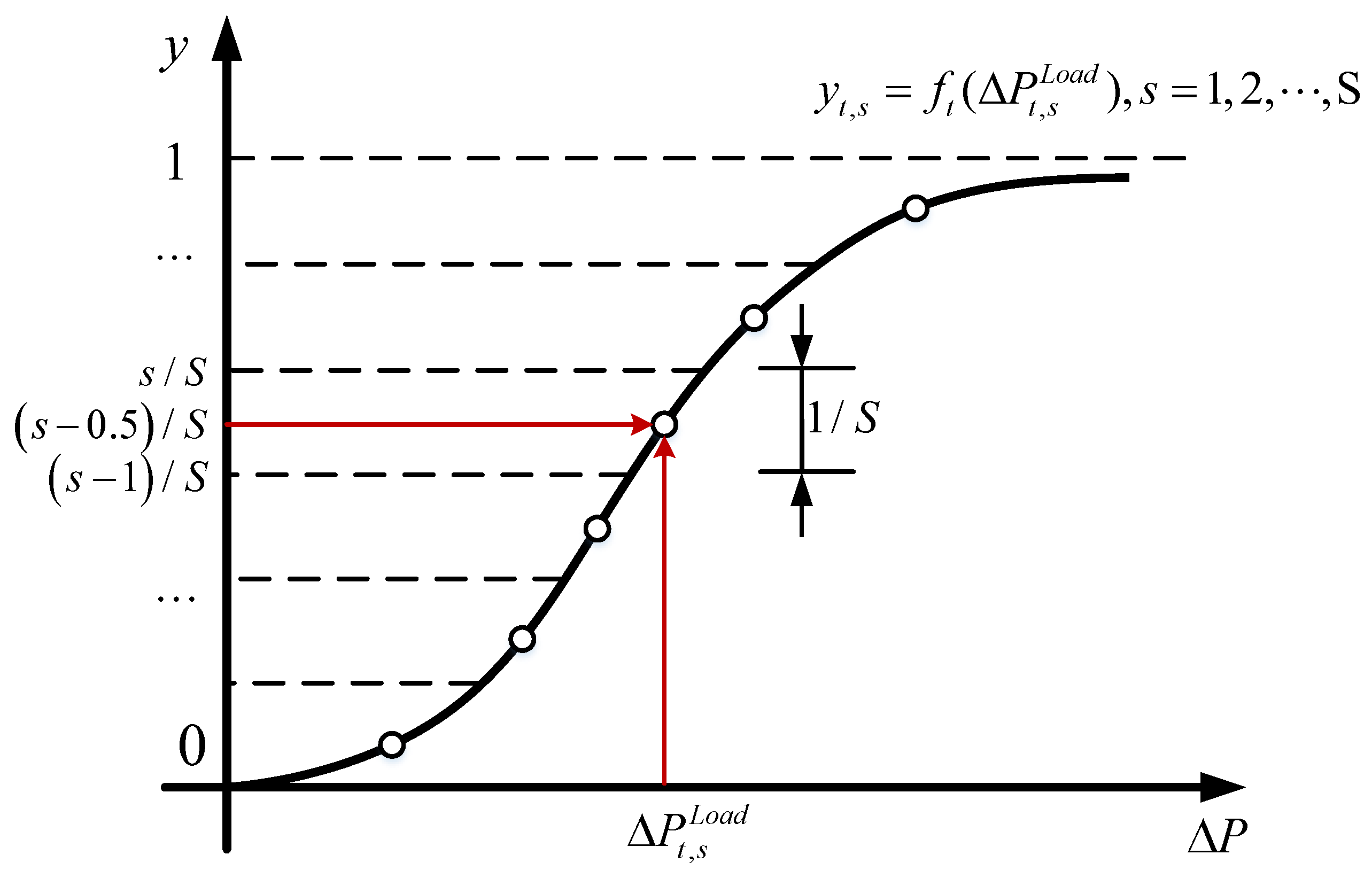
3.3.1. Latin Hypercube Sampling
3.3.2. Fuzzy C-Means
4. Stochastic Optimization Model for HFTPSS
4.1. Objective Function
4.2. Constraints
4.2.1. Power Flow Constraints
4.2.2. Energy Storage Constraints
4.3. Online Degradation of Battery
4.3.1. Calendar Aging of Battery
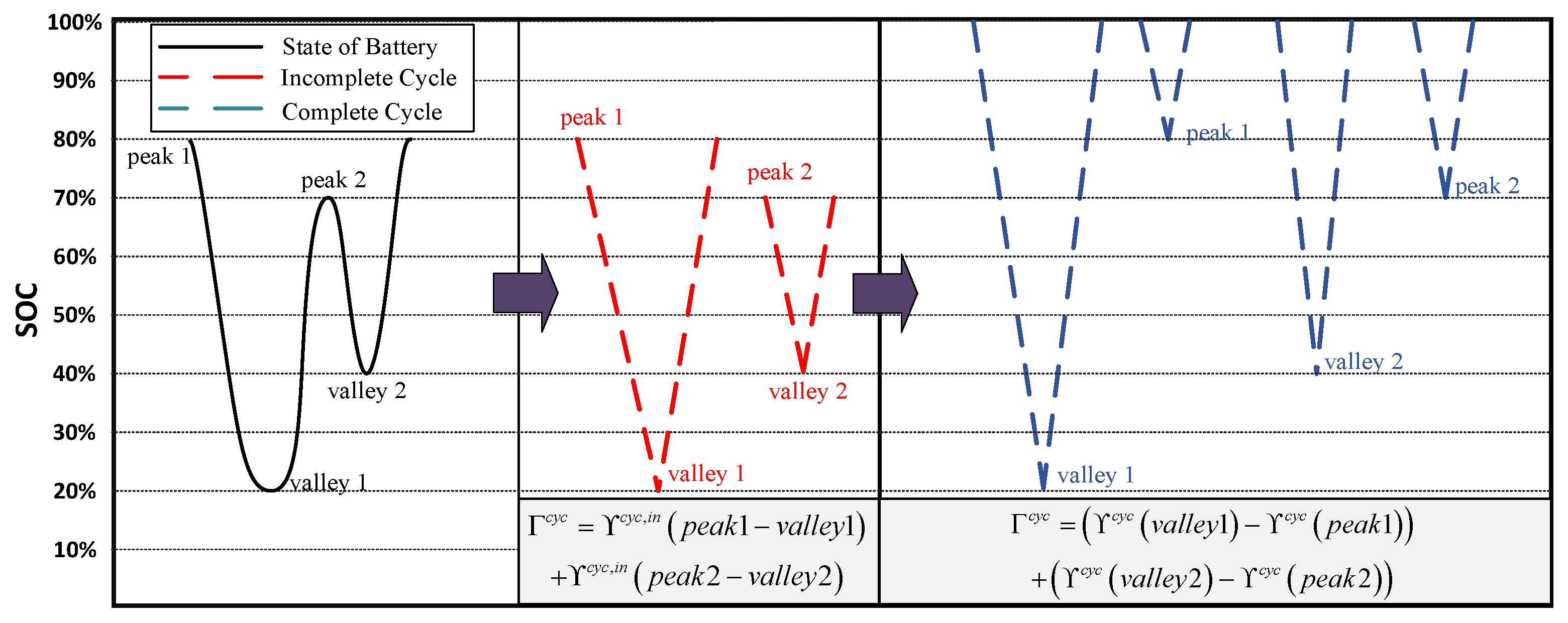
4.3.2. Cycle Aging of Battery
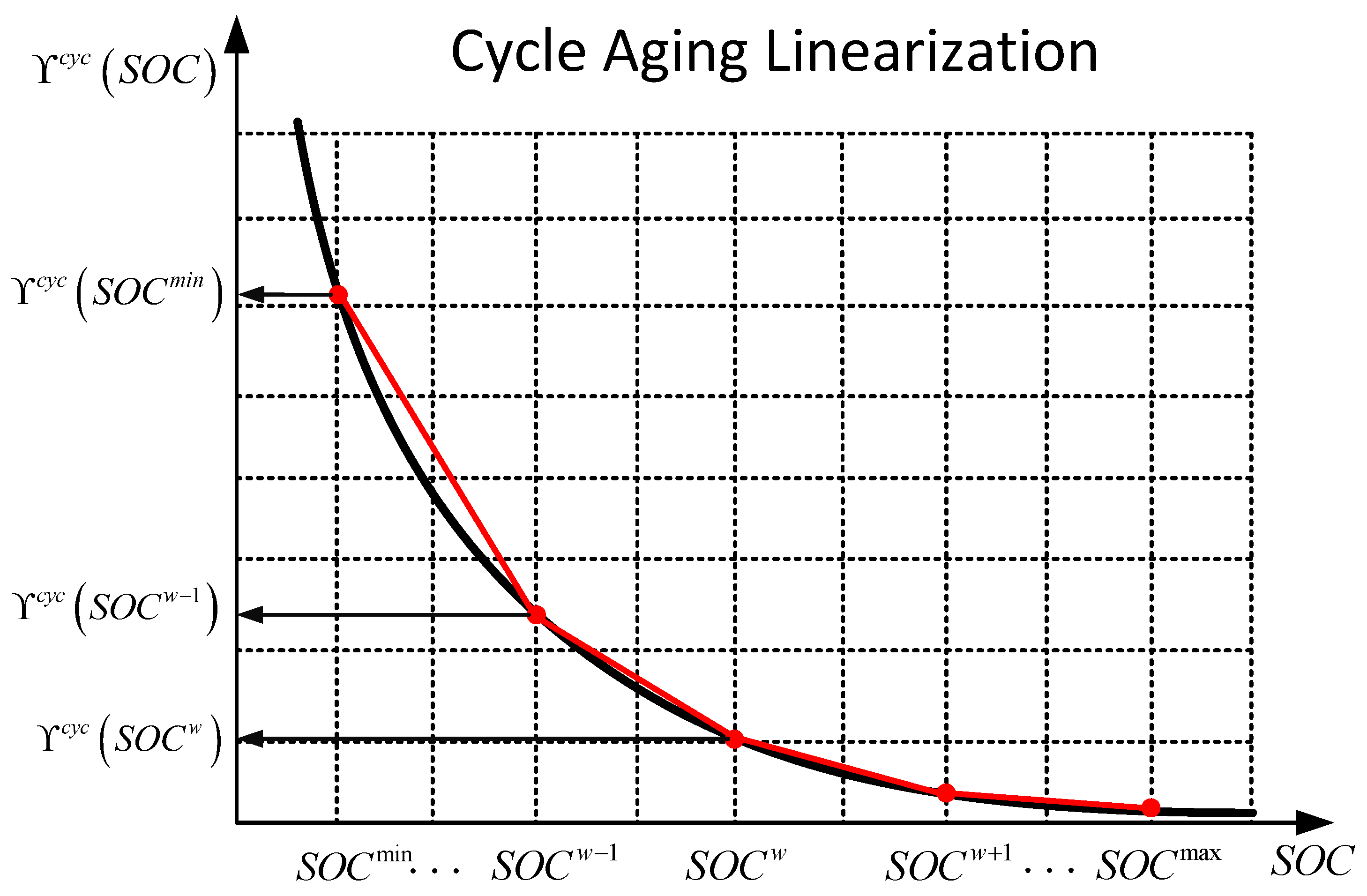
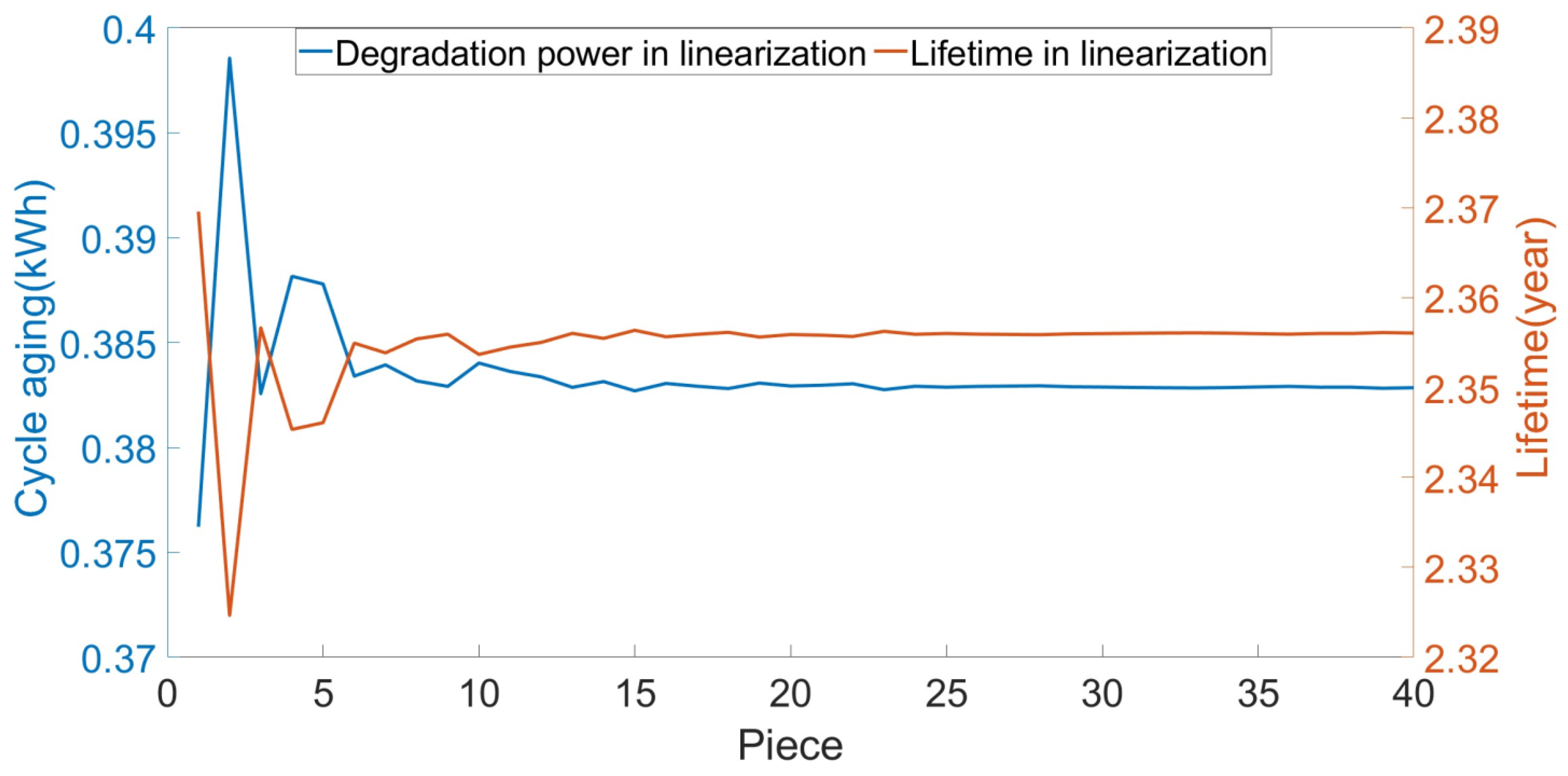
4.4. Linearization of Battery Degradation
5. Case Study
5.1. System Parameter Setting
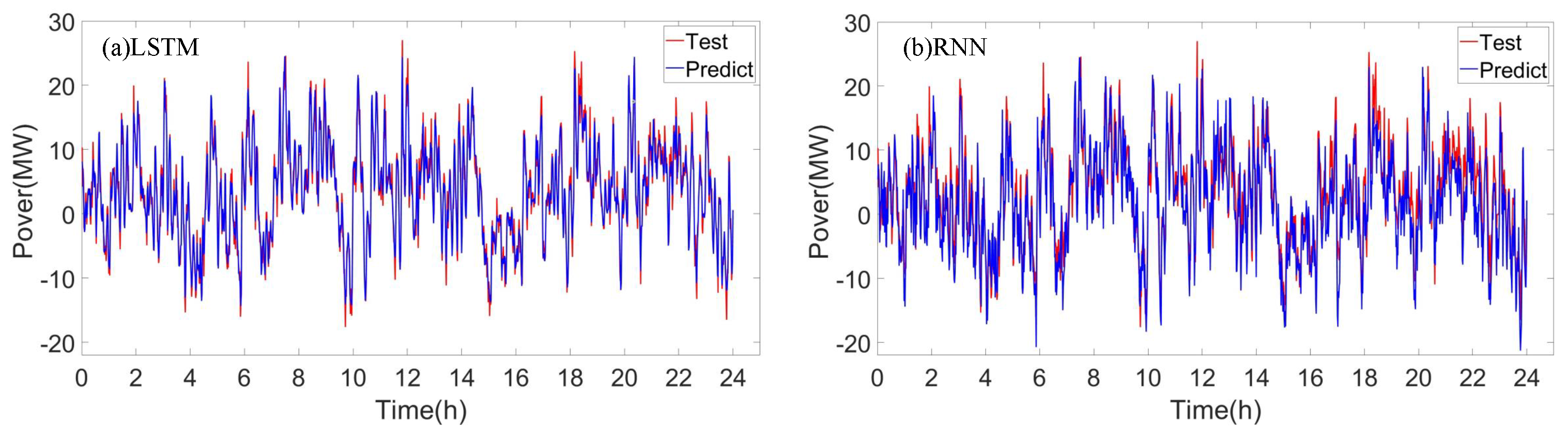
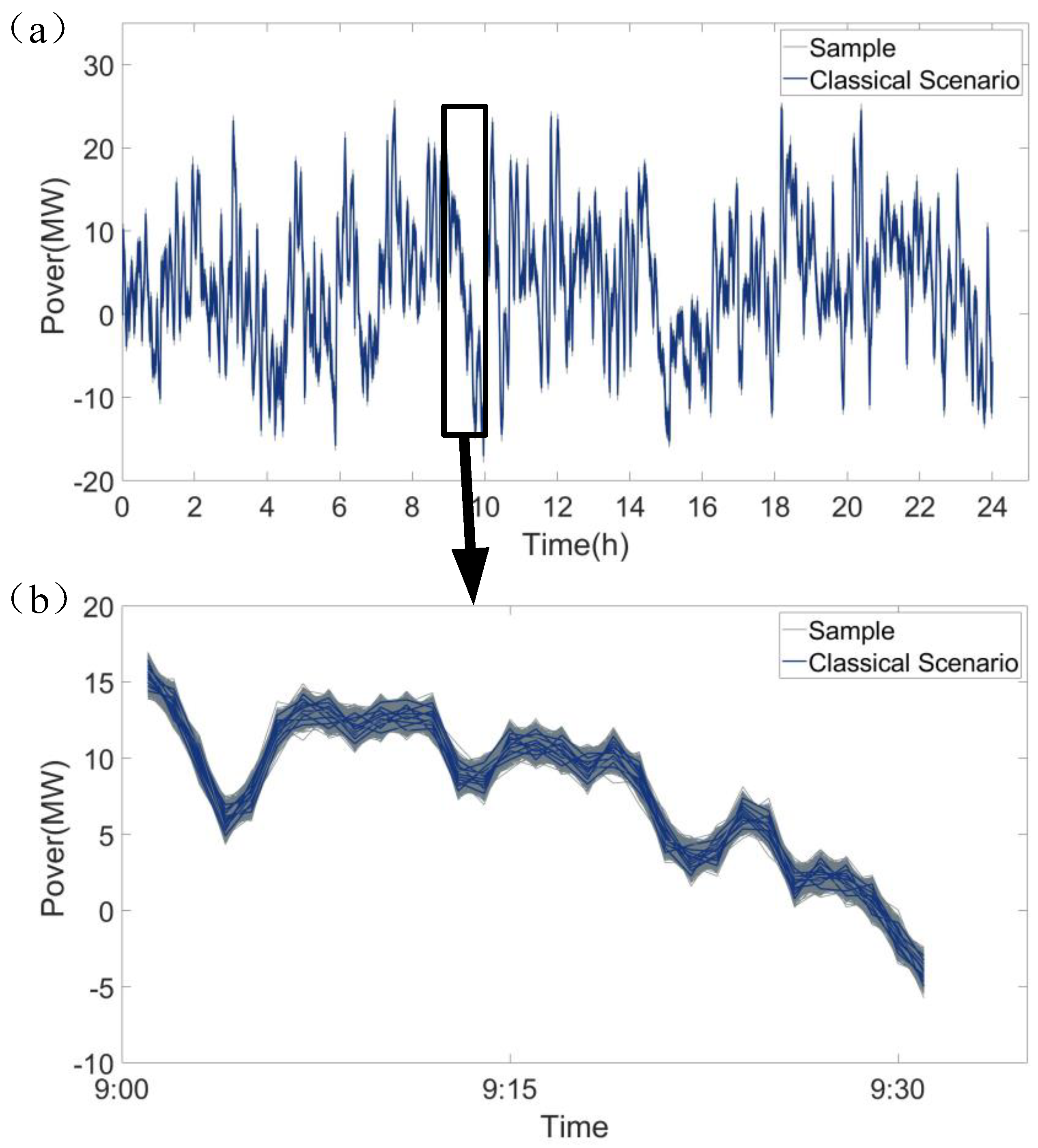
5.2. Performance of Uncertainty Modeling
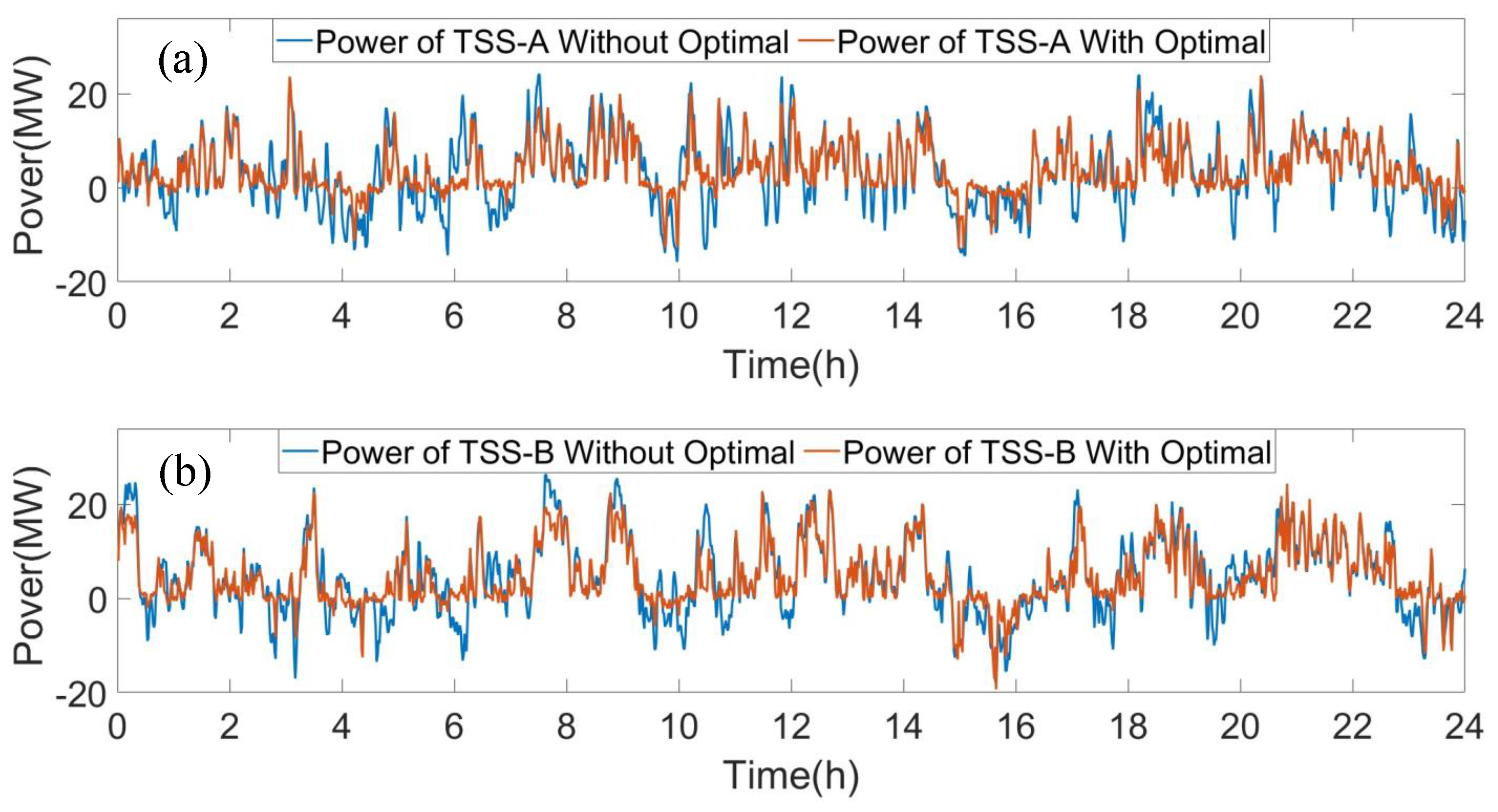
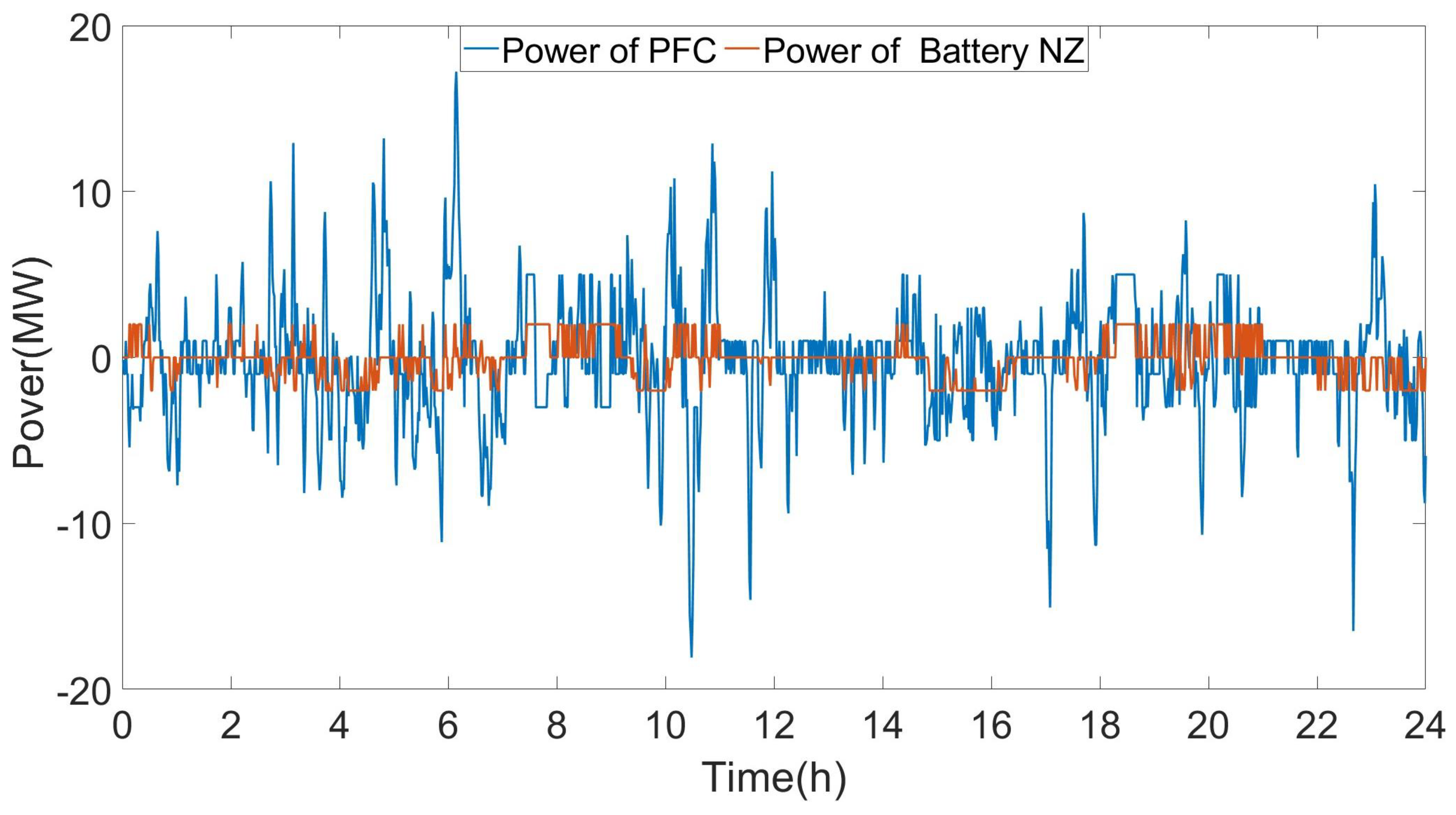
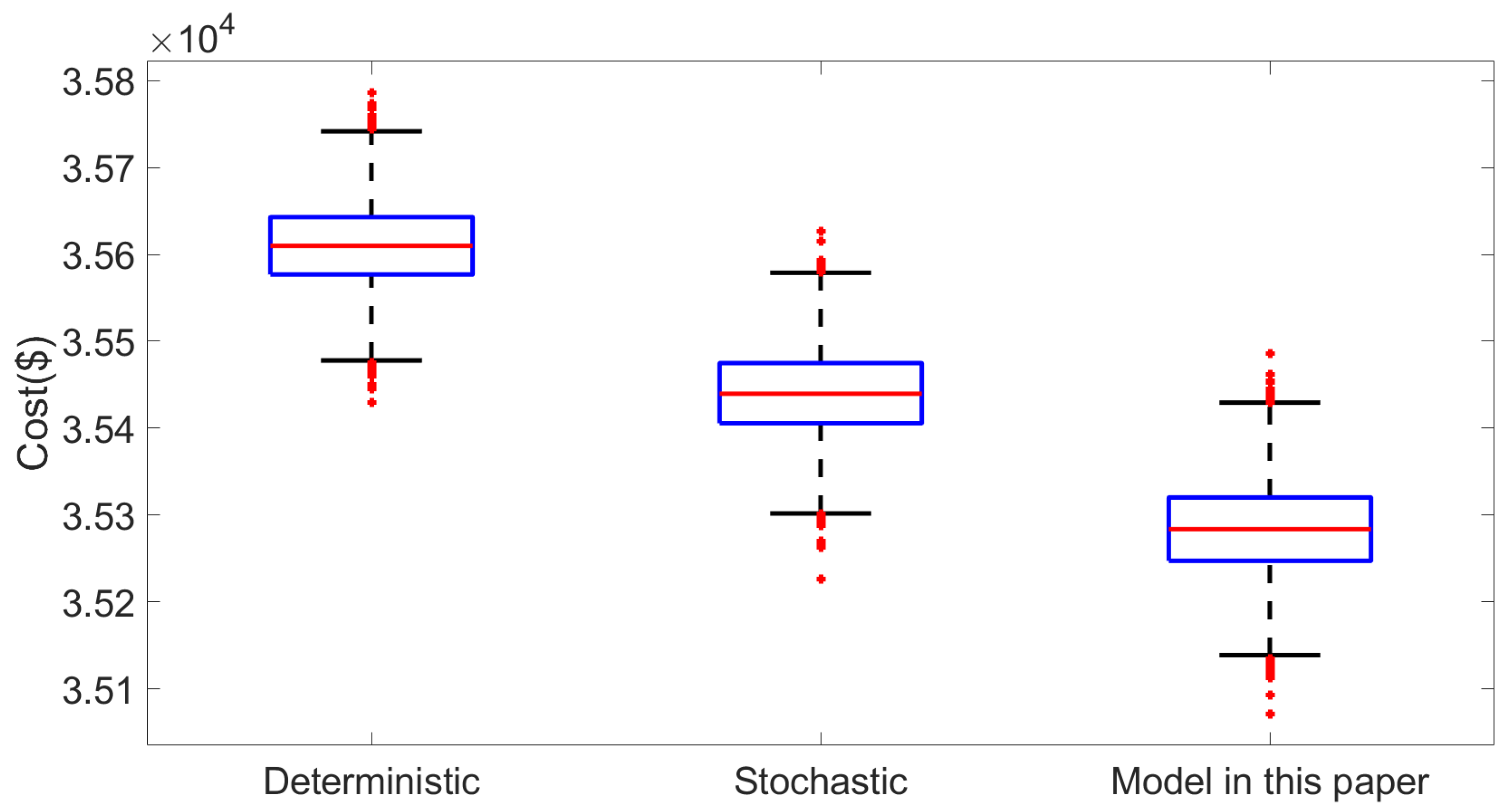
5.3. Performance of Stochastic Optimization Model
5.4. Sensitivity Analysis
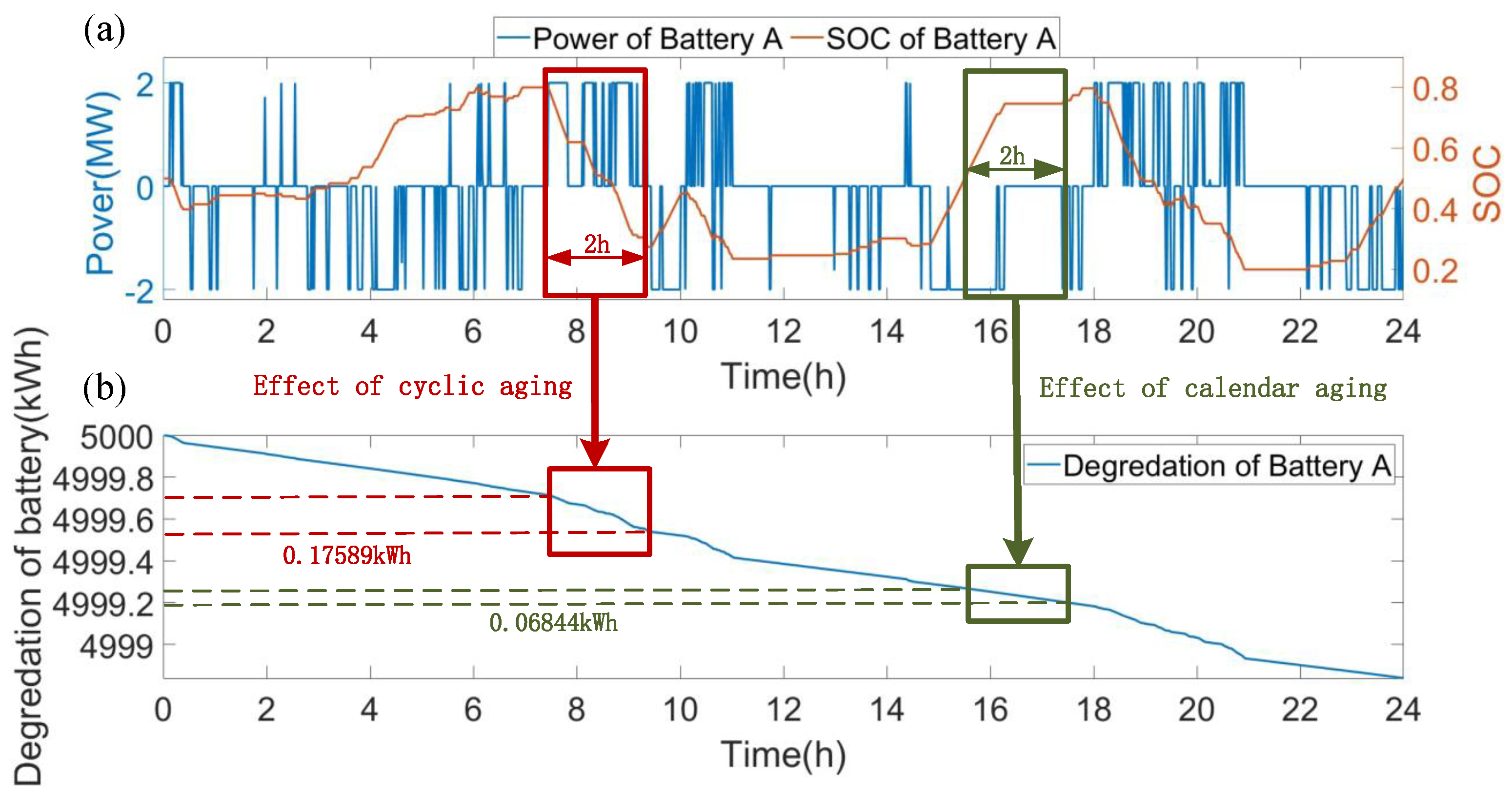
5.4.1. Battery Degradation Analysis
5.4.2. Economy and Robustness Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- International Energy Agency. The Future of Rail; OECD: Paris, France, 2019; p. 175. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, P.; Wei, M.; Wang, Q.; Feng, X. Trajectory Optimization for Heavy Haul Train with Pneumatic Braking via QCMIP. IEEE Trans. Intell. Veh. 2024, 9, 2419–2428. [Google Scholar]
- Shunkai, L. Research and Application of Regenerative Braking Energy Utilization Scheme for Heavy Haul Railway. China Railw. 2022, 11, 45–54. [Google Scholar]
- Zhao, S.; Li, K.; Yu, J.; Xing, C. Scheduling of futuristic railway microgrids—A FRA-pruned twins-actor DDPG approach. Energy 2024, 313, 134089. [Google Scholar] [CrossRef]
- Milićević, S.; Blagojević, I.; Milojević, S.; Bukvić, M.; Stojanović, B. Numerical Analysis of Optimal Hybridization in Parallel Hybrid Electric Powertrains for Tracked Vehicles. Energies 2024, 17, 3531. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, M.; Xu, L.; Liang, Z. Chance-Constrained Optimization of Storage and PFC Capacity for Railway Electrical Smart Grids Considering Uncertain Traction Load. IEEE Trans. Smart Grid 2024, 15, 286–298. [Google Scholar] [CrossRef]
- Han, Y.; Li, Q.; Wang, T.; Chen, W.; Ma, L. Multisource Coordination Energy Management Strategy Based on SOC Consensus for a PEMFC–Battery–Supercapacitor Hybrid Tramway. IEEE Trans. Veh. Technol. 2018, 67, 296–305. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, M.; Lu, W.; Egea-Àlvarez, A.; Xu, L. Improving energy efficiency for suburban railways: A two-stage scheduling optimization in a rail-EV smart hub. eTransportation 2024, 22, 100366. [Google Scholar] [CrossRef]
- Pilo, E.; Mazumder, S.K.; González-Franco, I. Smart Electrical Infrastructure for AC-Fed Railways with Neutral Zones. IEEE Trans. Intell. Transp. Syst. 2015, 16, 642–652. [Google Scholar] [CrossRef]
- Aguado, J.A.; Sánchez Racero, A.J.; de la Torre, S. Optimal Operation of Electric Railways with Renewable Energy and Electric Storage Systems. IEEE Trans. Smart Grid 2018, 9, 993–1001. [Google Scholar] [CrossRef]
- Novak, H.; Lešić, V.; Vašak, M. Hierarchical Model Predictive Control for Coordinated Electric Railway Traction System Energy Management. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2715–2727. [Google Scholar] [CrossRef]
- Chen, M.; Cheng, Z.; Liu, Y.; Cheng, Y.; Tian, Z. Multitime-Scale Optimal Dispatch of Railway FTPSS Based on Model Predictive Control. IEEE Trans. Transp. Electrif. 2020, 6, 808–820. [Google Scholar] [CrossRef]
- Chen, M.; Lv, Y.; Lu, W.; Zhang, D.; Chen, Y. Train-Network-HESS Integrated Optimization for Long-Distance AC Urban Rail Transit to Minimize the Comprehensive Cost. IEEE Trans. Intell. Transp. Syst. 2023, 24, 54–67. [Google Scholar] [CrossRef]
- EN 50388; Railway Applications. Power Supply and Rolling Stock. Technical Criteria for the Coordination Between Power Supply (Substation) and Rolling Stock to Achieve Interoperability. BSI-Standards: London, UK, 2010; pp. 1–44.
- Kummerow, A.; Klaiber, S.; Nicolai, S.; Bretschneider, P.; System, A. Recursive analysis and forecast of superimposed generation and load time series. In Proceedings of the International ETG Congress 2015; Die Energiewende-Blueprints for the New Energy Age, Bonn, Germany, 17–18 November 2015; pp. 1–6. [Google Scholar]
- Christiaanse, W.R. Short-Term Load Forecasting Using General Exponential Smoothing. IEEE Trans. Power Appar. Syst. 1971, PAS-90, 900–911. [Google Scholar] [CrossRef]
- Kalra, S.; Beniwal, R.; Singh, V.; Beniwal, N.S. Innovative Approaches in Residential Solar Electricity: Forecasting and Fault Detection Using Machine Learning. Electricity 2024, 5, 585–605. [Google Scholar] [CrossRef]
- Liu, L.; Guo, K.; Chen, J.; Guo, L.; Ke, C.; Liang, J.; He, D. A Photovoltaic Power Prediction Approach Based on Data Decomposition and Stacked Deep Learning Model. Electronics 2023, 12, 2764. [Google Scholar] [CrossRef]
- Song, K.B.; Baek, Y.S.; Hong, D.H.; Jang, G. Short-term load forecasting for the holidays using fuzzy linear regression method. IEEE Trans. Power Syst. 2005, 20, 96–101. [Google Scholar] [CrossRef]
- Aneiros, G.; Vilar, J.; Raña, P. Short-term forecast of daily curves of electricity demand and price. Int. J. Electr. Power Energy Syst. 2016, 80, 96–108. [Google Scholar] [CrossRef]
- Ma, Q.; Peng, Y.; Luo, P.; Li, Q.; Sun, J.; Wang, H. Electrified Railway Traction Load Prediction Based on Deep Learning. In Proceedings of the IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 4679–4684. [Google Scholar]
- Yu, F.; Xu, X. A short-term load forecasting model of natural gas based on optimized genetic algorithm and improved BP neural network. Appl. Energy 2014, 134, 102–113. [Google Scholar] [CrossRef]
- Wang, W.; He, Y.; Xiong, X.; Chen, H. Robust Survivability-Oriented Scheduling of Separable Mobile Energy Storage and Demand Response for Isolated Distribution Systems. IEEE Trans. Power Deliv. 2022, 37, 3521–3535. [Google Scholar] [CrossRef]
- Li, J.; Du, Z.; Yuan, L.; Huang, Y.; Liu, J. A Two-Stage Distributionally Robust Optimization Model for Managing Electricity Consumption of Energy-Intensive Enterprises Considering Multiple Uncertainties. Electronics 2024, 13, 5058. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, M.; Cheng, Z.; Chen, Y.; Li, Q. Robust Energy Management of High-Speed Railway Co-Phase Traction Substation with Uncertain PV Generation and Traction Load. IEEE Trans. Intell. Transp. Syst. 2022, 23, 5079–5091. [Google Scholar] [CrossRef]
- Ebadi, R.; Sadeghi Yazdankhah, A.; Kazemzadeh, R.; Mohammadi-Ivatloo, B. Techno-economic evaluation of transportable battery energy storage in robust day-ahead scheduling of integrated power and railway transportation networks. Int. J. Electr. Power Energy Syst. 2021, 126, 106606. [Google Scholar] [CrossRef]
- Mirzaei, M.A.; Hemmati, M.; Zare, K.; Mohammadi-Ivatloo, B.; Abapour, M.; Marzband, M.; Farzamnia, A. Two-Stage Robust-Stochastic Electricity Market Clearing Considering Mobile Energy Storage in Rail Transportation. IEEE Access 2020, 8, 121780–121794. [Google Scholar]
- Zhao, S.; Li, K.; Yang, Z.; Xu, X.; Zhang, N. A new power system active rescheduling method considering the dispatchable plug-in electric vehicles and intermittent renewable energies. Appl. Energy 2022, 314, 118715. [Google Scholar] [CrossRef]
- Lin, S.; Liu, C.; Shen, Y.; Li, F.; Li, D.; Fu, Y. Stochastic Planning of Integrated Energy System via Frank-Copula Function and Scenario Reduction. IEEE Trans. Smart Grid 2022, 13, 202–212. [Google Scholar] [CrossRef]
- Ehteshami, H.; Hashemi-Dezaki, H.; Javadi, S. Optimal stochastic energy management of electrical railway systems considering renewable energy resources’ uncertainties and interactions with utility grid. Energy Sci. Eng. 2022, 10, 578–599. [Google Scholar]
- Yang, S.; Song, K.; Zhu, G. Stochastic Process and Simulation of Traction Load for High Speed Railways. IEEE Access 2019, 7, 76049–76060. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Sun, M.; Zhang, N. Two-Stage Bootstrap Sampling for Probabilistic Load Forecasting. IEEE Trans. Eng. Manag. 2022, 69, 720–728. [Google Scholar] [CrossRef]
- Mei, F.; Gu, J.; Lu, J.; Lu, J.; Zhang, J.; Jiang, Y.; Shi, T.; Zheng, J. Day-Ahead Nonparametric Probabilistic Forecasting of Photovoltaic Power Generation Based on the LSTM-QRA Ensemble Model. IEEE Access 2020, 8, 166138–166149. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef]
- Huang, K.; Wei, K.; Li, F.; Yang, C.; Gui, W. LSTM-MPC: A Deep Learning Based Predictive Control Method for Multimode Process Control. IEEE Trans. Ind. Electron. 2023, 70, 11544–11554. [Google Scholar] [CrossRef]
- Yu, H.; Chung, C.Y.; Wong, K.P.; Lee, H.W.; Zhang, J.H. Probabilistic Load Flow Evaluation with Hybrid Latin Hypercube Sampling and Cholesky Decomposition. IEEE Trans. Power Syst. 2009, 24, 661–667. [Google Scholar] [CrossRef]
- Xu, Q.; Yang, Y.; Liu, Y.; Wang, X. An Improved Latin Hypercube Sampling Method to Enhance Numerical Stability Considering the Correlation of Input Variables. IEEE Access 2017, 5, 15197–15205. [Google Scholar] [CrossRef]
- Sun, H.; Yi, J.; Xu, Y.; Wang, Y.; Qing, X. Crack Monitoring for Hot-Spot Areas Under Time-Varying Load Condition Based on FCM Clustering Algorithm. IEEE Access 2019, 7, 118850–118856. [Google Scholar] [CrossRef]
- Amini, M.; Nazari, M.H.; Hosseinian, S.H. Optimal Scheduling and Cost-Benefit Analysis of Lithium-Ion Batteries Based on Battery State of Health. IEEE Access 2023, 11, 1359–1371. [Google Scholar] [CrossRef]
- Ju, C.; Wang, P.; Goel, L.; Xu, Y. A Two-Layer Energy Management System for Microgrids with Hybrid Energy Storage Considering Degradation Costs. IEEE Trans. Smart Grid 2018, 9, 6047–6057. [Google Scholar] [CrossRef]
- Chen, M.; Liang, Z.; Cheng, Z.; Zhao, J.; Tian, Z. Optimal Scheduling of FTPSS with PV and HESS Considering the Online Degradation of Battery Capacity. IEEE Trans. Transp. Electrif. 2022, 8, 936–947. [Google Scholar] [CrossRef]
- Minh, N.Q.; Linh, N.D.; Khiem, N.T. A mixed-integer linear programming model for microgrid optimal scheduling considering BESS degradation and RES uncertainty. J. Energy Storage 2024, 104, 114663. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, M.; Lu, S.; Chen, Y.; Li, Q. Optimized sizing and scheduling of hybrid energy storage systems for high-speed railway traction substations. Energies 2018, 11, 2199. [Google Scholar] [CrossRef]
- Yang, J.; Gao, H.; Ye, S.; Lv, L.; Liu, J. Applying multiple types of demand response to optimal day-ahead stochastic scheduling in the distribution network. IET Gener. Transm. Distrib. 2020, 14, 4509–4519. [Google Scholar] [CrossRef]
| Time Pired | 0:00–6:00 22:00–0:00 | 8:00–11:00 18:00–21:00 | Others |
|---|---|---|---|
| Energy ($/kWh) | 0.051 | 0.172 | 0.108 |
| Demand ($/kWh/mon) | 5.785 | 5.785 | 5.785 |
| Parameters | Initial SOC | Efficiency | SOC Range | Self Discharge Rate (/mon ) |
|---|---|---|---|---|
| Battery | 0.5 | 0.85/0.85 | 0.2/0.8 | 0.05 |
| MODEL | MAPE | RMSE | PCC | |
|---|---|---|---|---|
| LSTM | 1.2592 | 1.6243 | 0.9551 | 0.9774 |
| RNN | 3.0225 | 3.7794 | 0.7563 | 0.9040 |
| Cost ($) | ECC | DC | PC | BC | Total Cost | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| TSS-A | TSS-B | TSS-A | TSS-B | TSS-A | TSS-B | Bat-A | Bat-B | Bat-NZ | ||
| Without Optimal | 12,750 | 15,136 | 3030 | 4195 | 2068 | 2064 | - | - | - | 39,243 |
| With Optimal | 11,461 | 13,588 | 2299 | 3163 | 820 | 935 | 1026 | 1036 | 1023 | 35,351 |
| Model | Capacity Degradation (kWh) | Cost of Degradation ($) | Total Cost ($) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Canlder Aging | Cycle Aging | Canlder Aging | Cycle Aging | ||||||
| A | B | NZ | A | B | NZ | ||||
| Model in this paper | 0.778 | 0.773 | 0.778 | 0.383 | 0.399 | 0.376 | 2062 | 1023 | 35,351 |
| Model in [41] | 0.774 | 0.775 | 0.776 | 0.448 | 0.448 | 0.45 | 2058 | 1191 | 35,416 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; He, Y.; Peng, G.; Yin, J. Stochastic Optimal Scheduling of Flexible Traction Power Supply System for Heavy Haul Railway Considering the Online Degradation of Energy Storage. World Electr. Veh. J. 2025, 16, 206. https://doi.org/10.3390/wevj16040206
Li Z, He Y, Peng G, Yin J. Stochastic Optimal Scheduling of Flexible Traction Power Supply System for Heavy Haul Railway Considering the Online Degradation of Energy Storage. World Electric Vehicle Journal. 2025; 16(4):206. https://doi.org/10.3390/wevj16040206
Chicago/Turabian StyleLi, Zhe, Yanlin He, Gaoqiang Peng, and Jie Yin. 2025. "Stochastic Optimal Scheduling of Flexible Traction Power Supply System for Heavy Haul Railway Considering the Online Degradation of Energy Storage" World Electric Vehicle Journal 16, no. 4: 206. https://doi.org/10.3390/wevj16040206
APA StyleLi, Z., He, Y., Peng, G., & Yin, J. (2025). Stochastic Optimal Scheduling of Flexible Traction Power Supply System for Heavy Haul Railway Considering the Online Degradation of Energy Storage. World Electric Vehicle Journal, 16(4), 206. https://doi.org/10.3390/wevj16040206





