Research on Efficient Prediction and Suppression of Electromagnetic Interference in Electric Drive Systems
Abstract
1. Introduction
2. Impact of Modules on EMI in Multi-in-One EDS
2.1. An Integrated Electrified Power Train Conducted Emission Simulation Model
2.2. Impact of Three-Phase AC Module
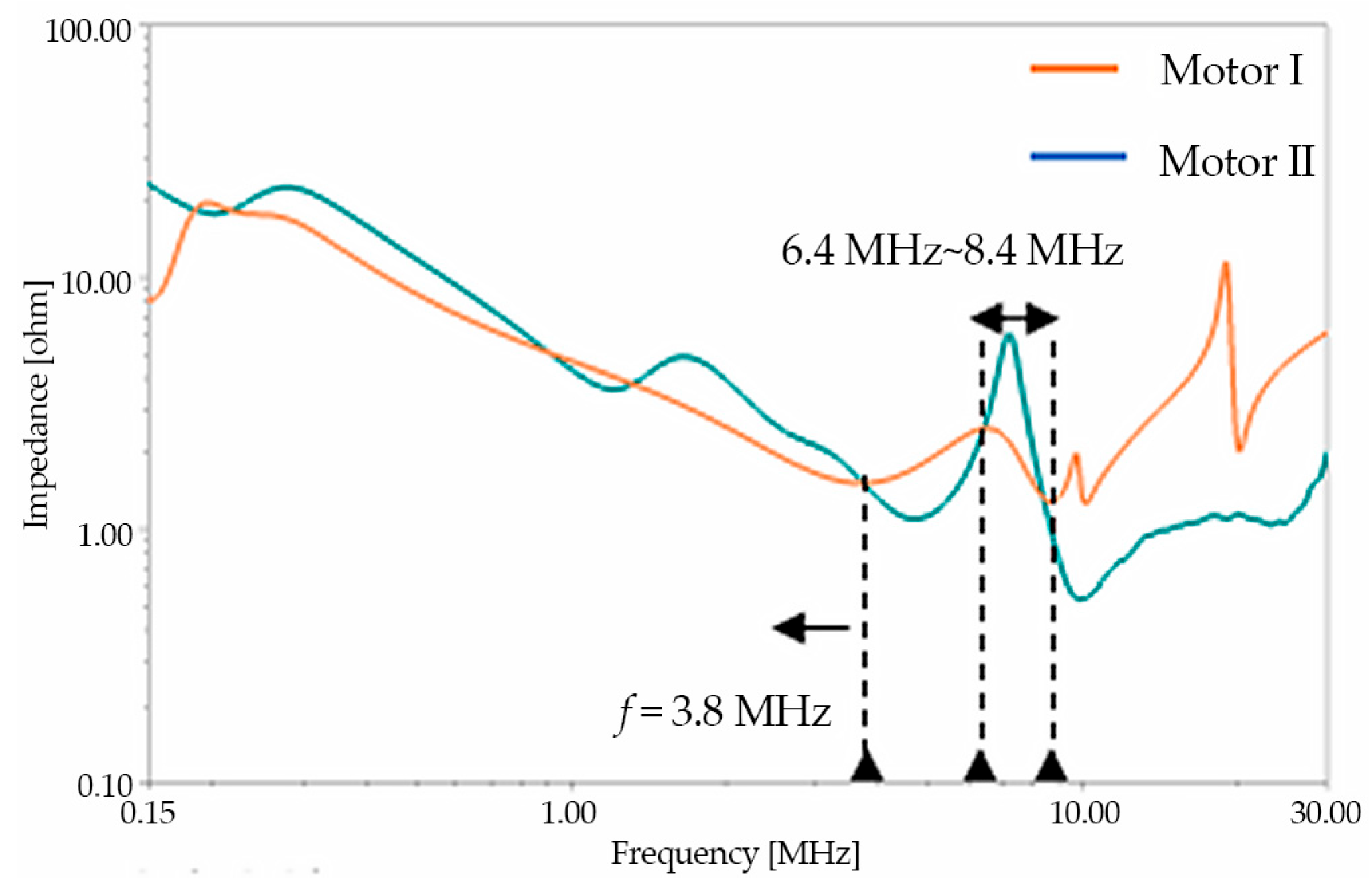
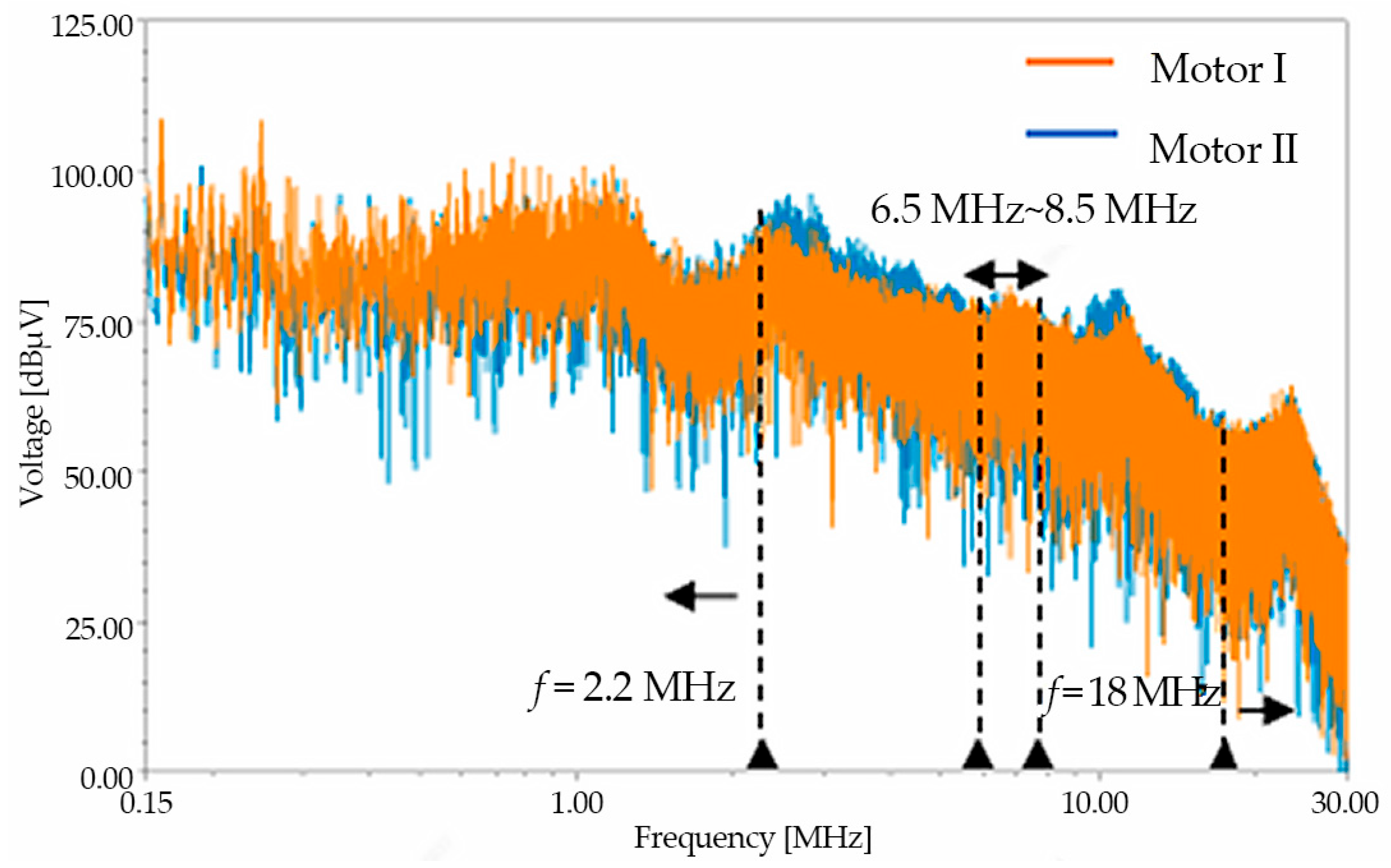
2.3. Impact of Motor Impedance on EMI in EDS
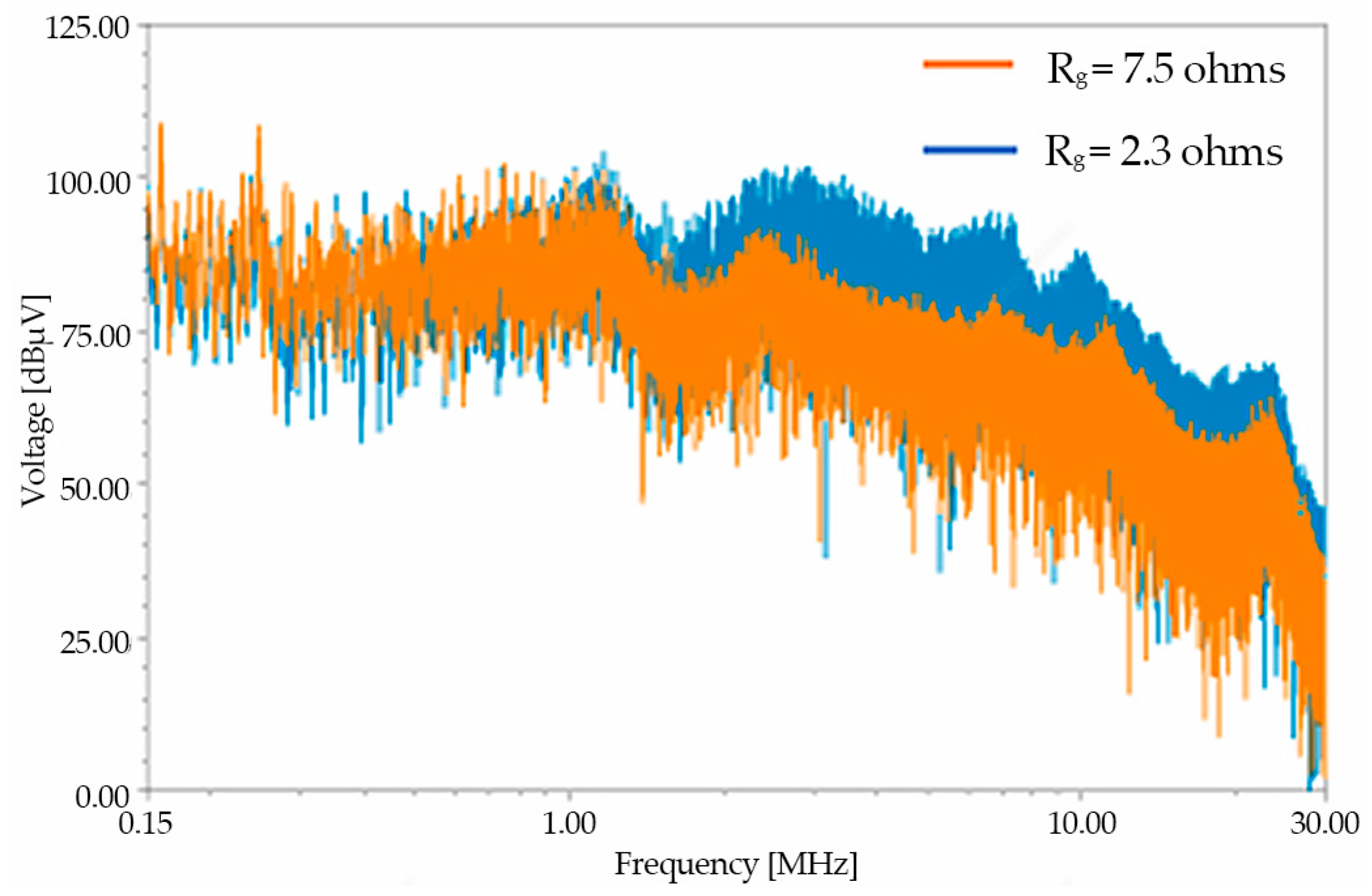
2.4. Analysis of the Impact of IGBT Drive Resistance
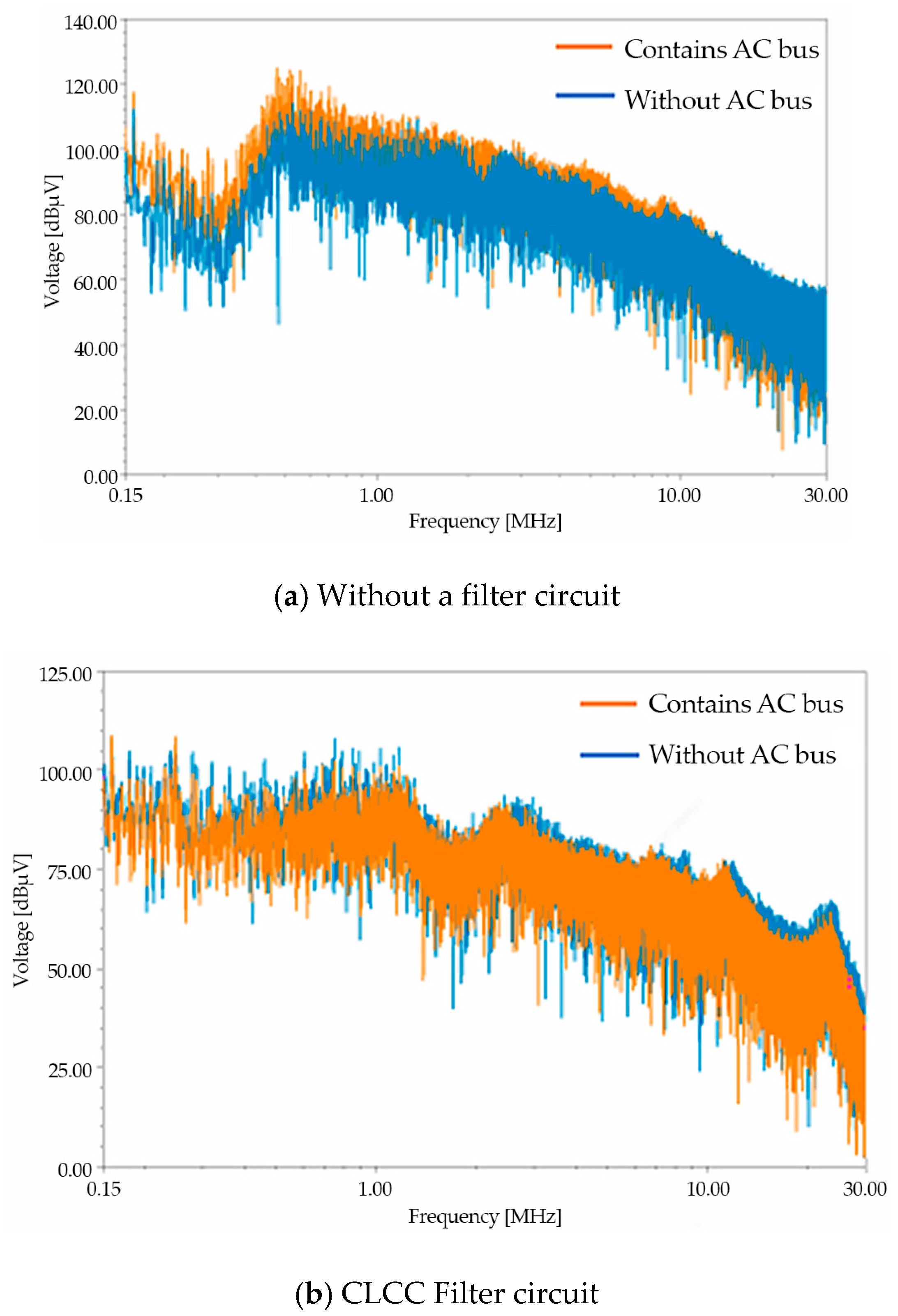
3. Impact of Filters on EMI in EDS
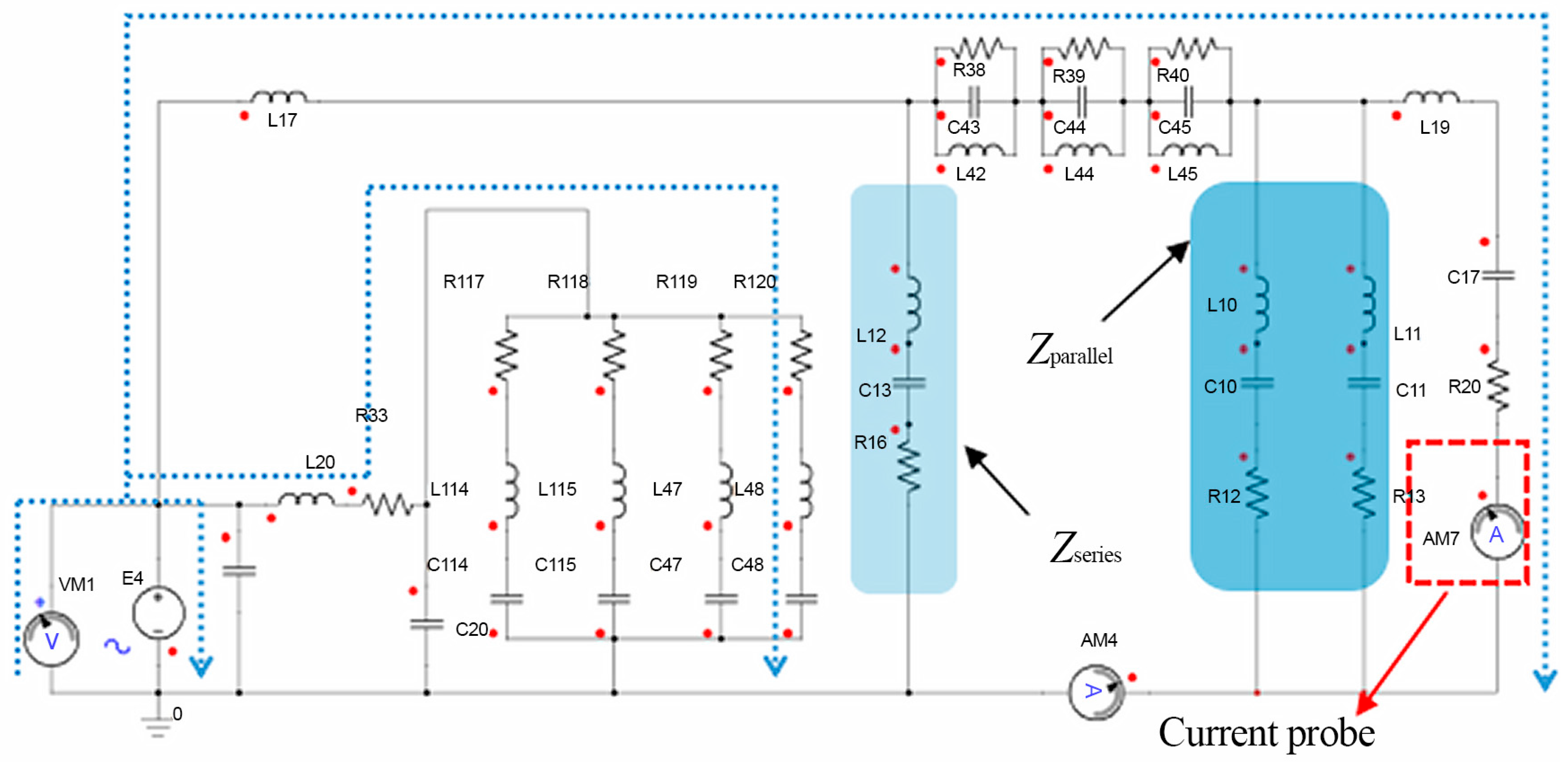
3.1. Simulation Analysis of Filter Impedance Characteristics in EDS Based on Critical Paths
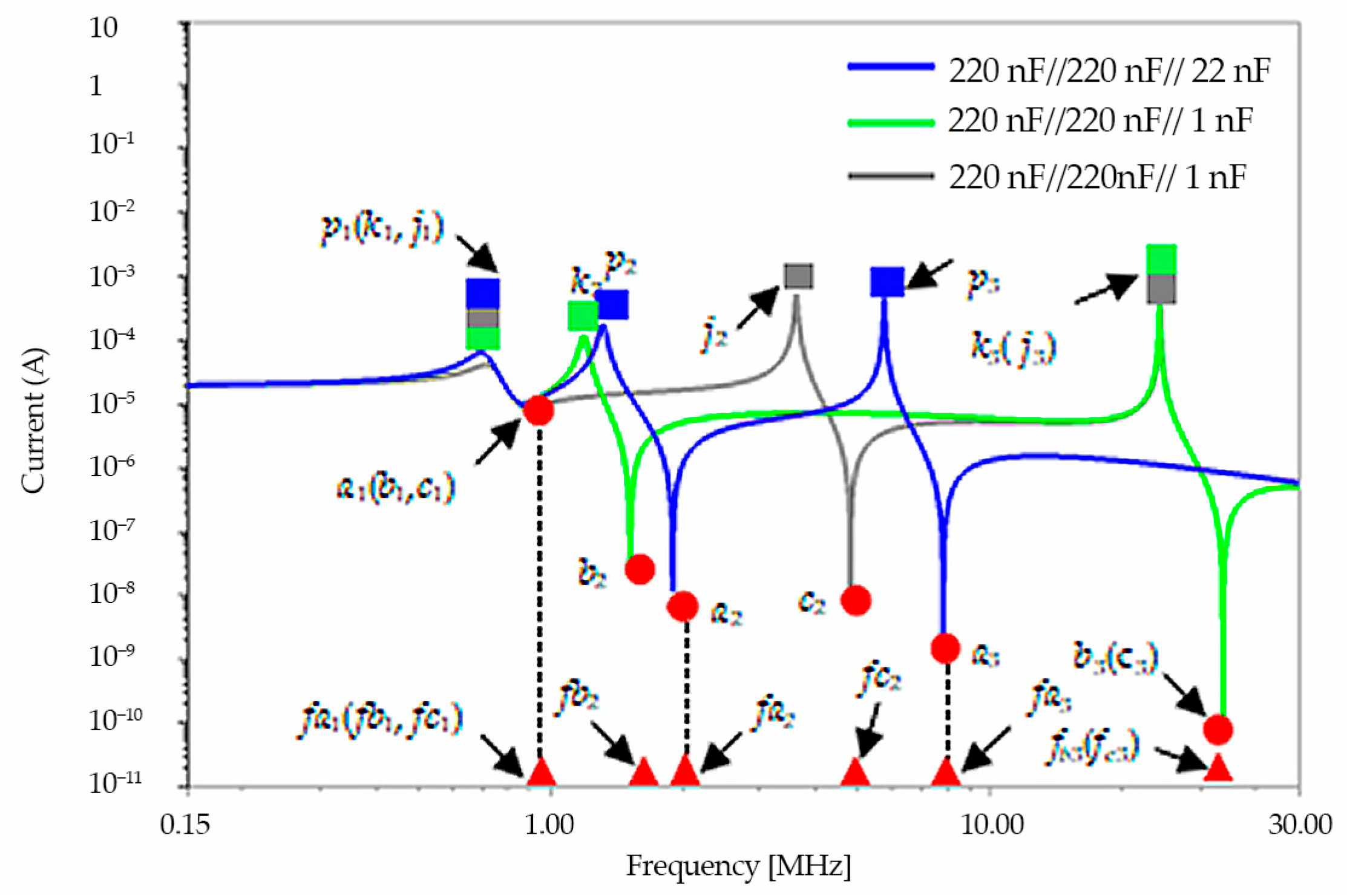
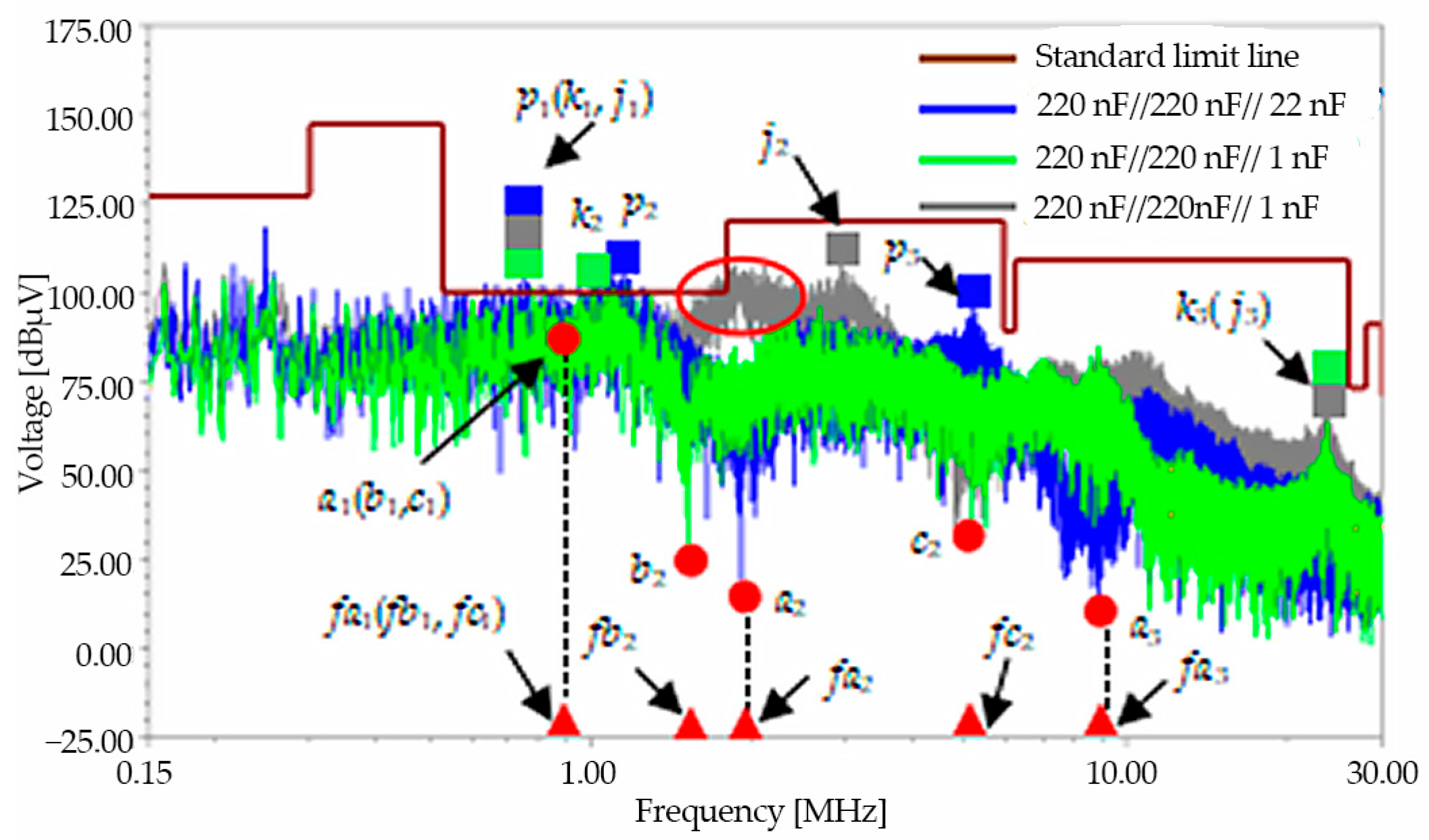
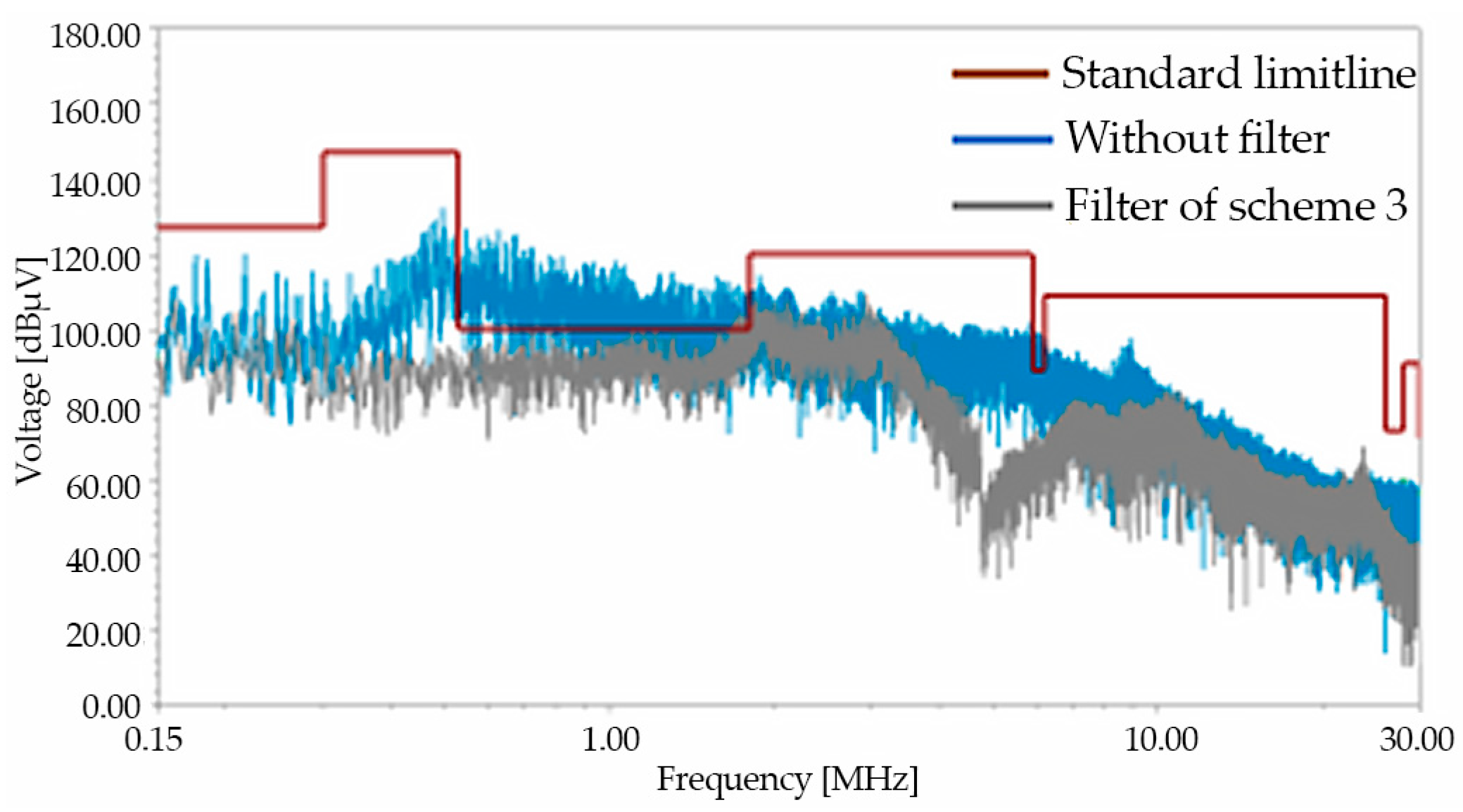
3.2. Filter Parameter Optimization Based on Electric Drive System Model
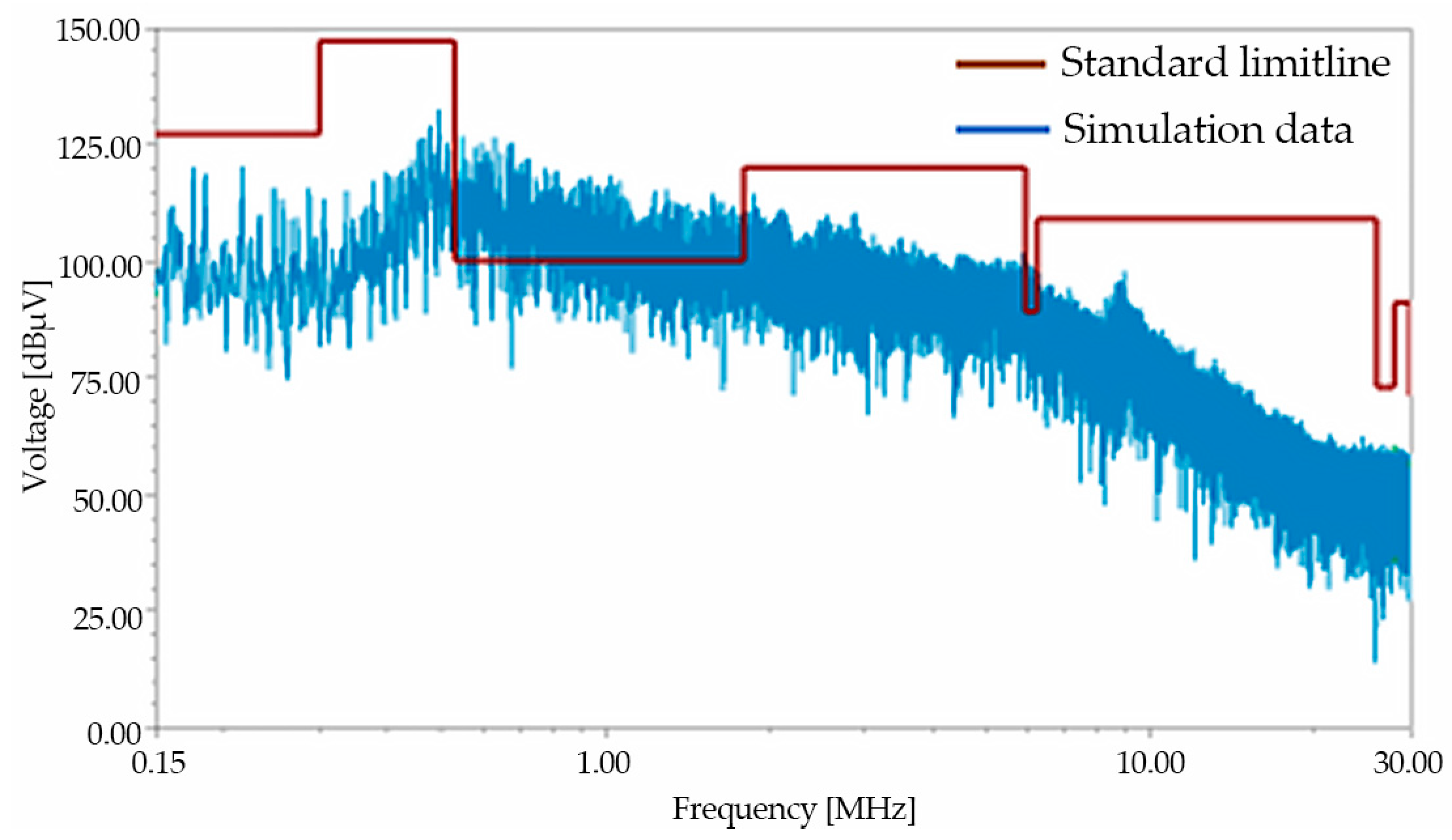
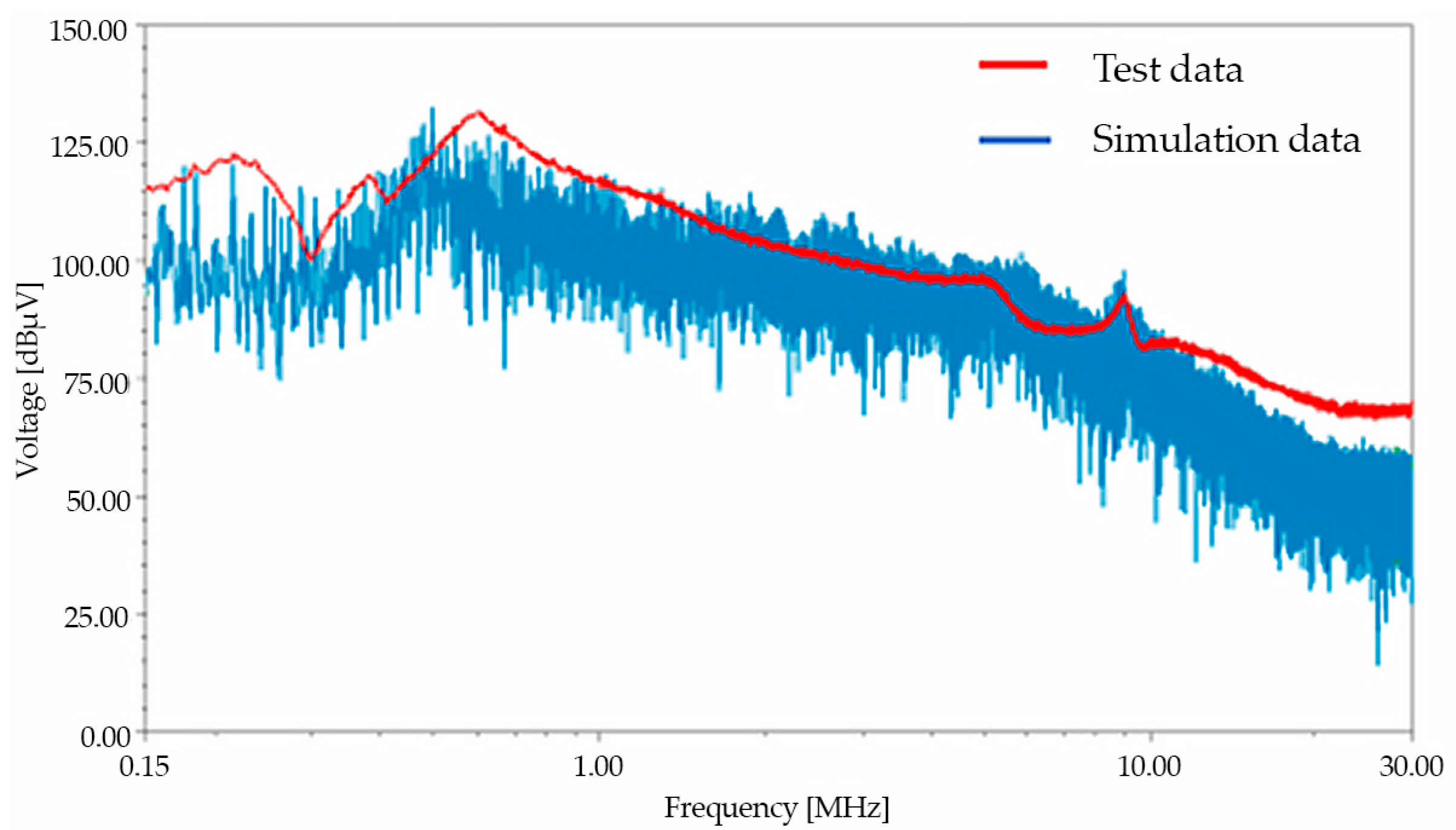
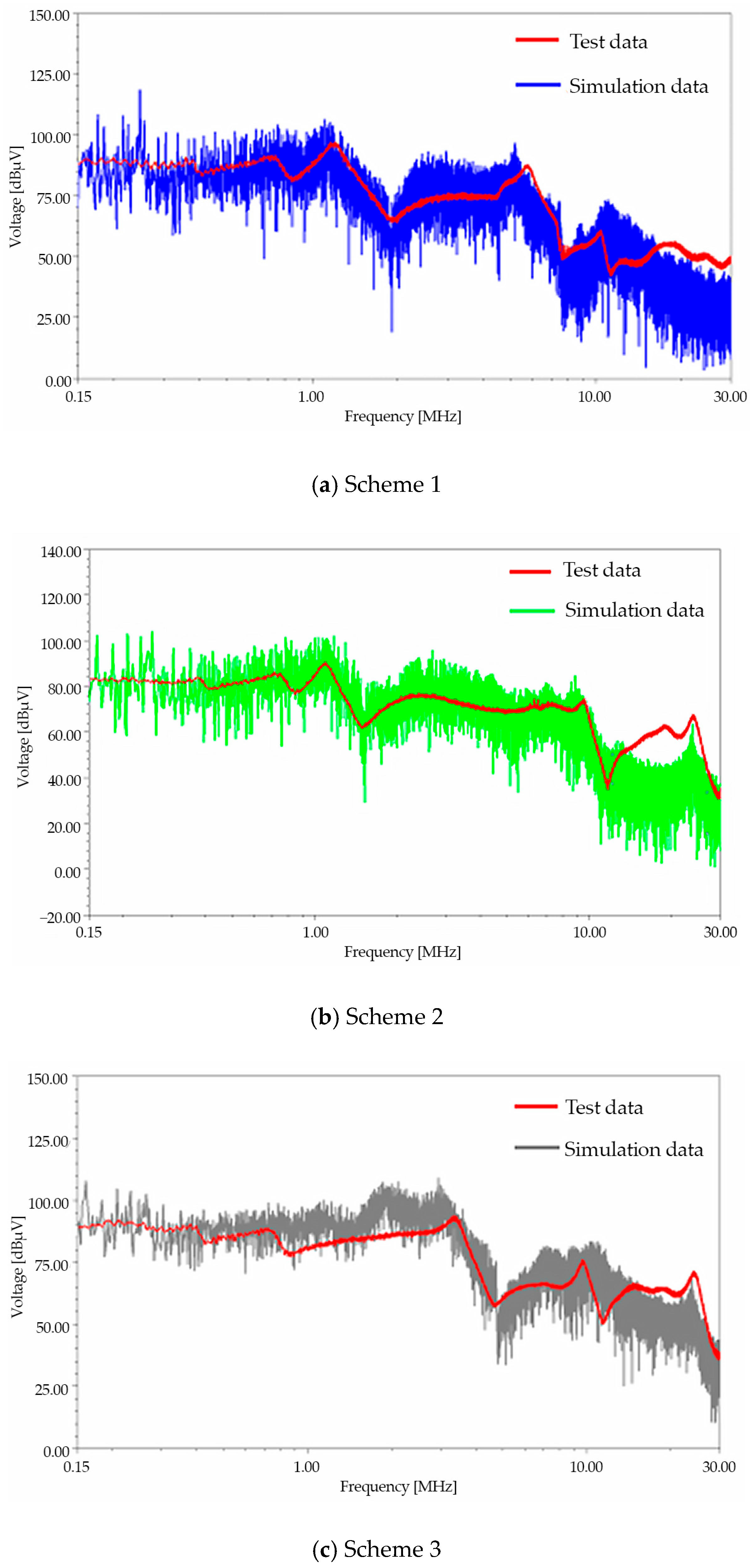
4. Comparison Between Simulation and Measurement
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Definition |
| AC | Alternating Current |
| IGBT | Insulated Gate Bipolar Transistor |
| EMI | Electromagnetic Interference |
| EDS | Electric Drive System |
| SiC | Silicon Carbide |
| CLCC | Capacitor-Inductance-Capacitor-Capacitor |
| L | Inductance |
| or di/dt | Current Change Rate |
| or dv/dt | Voltage Change Rate |
| LISN | Line-Impedance Stabilization Network |
| DC | Direct Current |
| Rg | Gate Drive Resistances |
| EMC | Electromagnetic Compatibility |
References
- Global EV Outlook 2023: Catching Up with Climate Ambitions; International Energy Agency: Paris, France, 2023.
- Li, Z.; Shuangjie, Y.; Guixing, H.; Shuliang, W. Modeling on Conducted Electromagnetic Interference for Motor Drive System of Electric Vehicle. Trans. Beijing Inst. Technol. 2022, 42, 824–833. [Google Scholar] [CrossRef]
- Yongda, R.; Qiang, X.; Hongxing, X.; Jiahai, Z.; Hongmin, L. Modeling and Simulation Research of Electromagnetic Interference Source in Vehicle Electric Drive System. Electron. Sci. Technol. 2023, 36, 81–86. [Google Scholar] [CrossRef]
- Liu, S.L.; Yang, T.F.; Zhi, Y.J.; Min, J.J. Modeling and prediction of conducted interference in electric vehicle motor drive systems. Electr. Drives 2021, 51, 50–58. [Google Scholar]
- Duan, Z.; Wen, X. A new analytical conducted EMI prediction method for SiC motor drive systems. eTransportation 2020, 3, 100047. [Google Scholar] [CrossRef]
- Wang, K.; Lu, H.; Li, X. High-Frequency Modeling of the High-Voltage Electric Drive System for Conducted EMI Simulation in Electric Vehicles. IEEE Trans. Transp. Electrif. 2022, 9, 2808–2819. [Google Scholar] [CrossRef]
- Jia, X.; Hu, C.; Dong, B.; He, F.; Wang, H.; Xu, D. Influence of System Layout on CM EMI Noise of SiC Electric Vehicle Powertrains. CPSS Trans. Power Electron. Appl. 2021, 6, 298–309. [Google Scholar] [CrossRef]
- Wang, K.; Lu, H.; Chen, C.; Xiong, Y. Modeling of System-Level Conducted EMI of the High-Voltage Electric Drive System in Electric Vehicles. IEEE Trans. Electromagn. Compat. 2022, 64, 741–749. [Google Scholar] [CrossRef]
- Tan, R.; Ye, S.; Deng, C.; Yu, C.; Zhou, A.; Du, C. Research on Prediction Modeling of EMI in Multi-in-one Electric Drive System. In Proceedings of the 4th International Conference on Energy, Chongqing, China, 23–25 April 2021; pp. 621–626. [Google Scholar] [CrossRef]
- Tan, R.; Ye, S.; Yu, C.; Deng, C.; Zhou, A. Research on Electromagnetic-Radiated Emission of Multi-in-One Electric Drive System. World Electr. Veh. J. 2021, 12, 127. [Google Scholar] [CrossRef]
- Qiu, Y. Study on Electromagnetic Interference Caused by Parasitic Parameters in EV Drive System. Master’s Thesis, Tianjin University of Technology, Tianjin, China, 2015. [Google Scholar]
- Ouhammam, A.; Mahmoudi, H.; El Hachimi, Y.; Daghouri, A. Simulation and optimization of EMI filter of conducted emission for high voltage gain DC–DC converter. Int. J. Power Electron. Drive Syst. (IJPEDS) 2024, 15, 902–912. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, L.; Liao, C. Analysis of IGBT and Inverter for Electric Vehicles. High Volt. Technol. 2014, 40, 1732–1737. (In Chinese) [Google Scholar] [CrossRef]
- Fu, R.; Grekov, A.; Peng, K.; Santi, E. Parasitic modeling for accurate inductive switching simulation of converters using SIC devices. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 1259–1265. [Google Scholar] [CrossRef]
- Vehicles, Boats and Internal Combustion Engines–Radio Disturbance Characteristics–Limits and Methods of Measurement for the Protection of on-Board Receivers; CISPR 25-201; American National Standards Institute: Washington, DC, USA, 2006.
- Wang, J.; Chung, H.S.-H.; Li, R.T.-H. Characterization and Experimental Assessment of the Effects of Parasitic Elements on the MOSFET Switching Performance. IEEE Trans. Power Electron. 2012, 28, 573–590. [Google Scholar] [CrossRef]
- Runcen, W. Modeling of Switching Devices and Research on Its Application in EMI Prediction. Master’s Thesis, Tongji University, Shanghai, China, 2014. [Google Scholar]
- Ramakrishnan, J.; Ravi, C.N. Optimization of passive filter components through active filtering of current ripple reduction in an inverter. Int. J. Power Electron. Drive Syst. (IJPEDS) 2022, 13, 298–308. [Google Scholar] [CrossRef]
- Khelladi, S.; Saci, K.; Hadjadj, A.; Ales, A. A Hybrid Common Mode Choke Optimization Method for Input Line EMI Filter Design. Adv. Electromagn. 2021, 10, 1677. [Google Scholar] [CrossRef]
- Dey, S.; Mallik, A.; Mishra, S. A Mathematical Design Approach to Volumetric Optimization of EMI Filter and Modeling of CM Noise Sources in a Three-Phase PFC. IEEE Trans. Power Electron. 2021, 37, 5678–5687. [Google Scholar] [CrossRef]
- Ouhammam, A.; Mahmoudi, H.; Ouadi, H. Design and control of high voltage gain DC–DC converter for CubeSat propulsion. CEAS Space J. 2023, 15, 345–360. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, R.; Ye, S.; Peng, Q.; Du, C.; Zhou, Z. Research on Efficient Prediction and Suppression of Electromagnetic Interference in Electric Drive Systems. World Electr. Veh. J. 2025, 16, 201. https://doi.org/10.3390/wevj16040201
Tan R, Ye S, Peng Q, Du C, Zhou Z. Research on Efficient Prediction and Suppression of Electromagnetic Interference in Electric Drive Systems. World Electric Vehicle Journal. 2025; 16(4):201. https://doi.org/10.3390/wevj16040201
Chicago/Turabian StyleTan, Ruoxi, Shangbin Ye, Qianlei Peng, Changhong Du, and Zeyan Zhou. 2025. "Research on Efficient Prediction and Suppression of Electromagnetic Interference in Electric Drive Systems" World Electric Vehicle Journal 16, no. 4: 201. https://doi.org/10.3390/wevj16040201
APA StyleTan, R., Ye, S., Peng, Q., Du, C., & Zhou, Z. (2025). Research on Efficient Prediction and Suppression of Electromagnetic Interference in Electric Drive Systems. World Electric Vehicle Journal, 16(4), 201. https://doi.org/10.3390/wevj16040201






