Design of Adaptive Trajectory-Tracking Controller for Obstacle Avoidance and Re-Planning
Abstract
1. Introduction
2. Materials and Methods
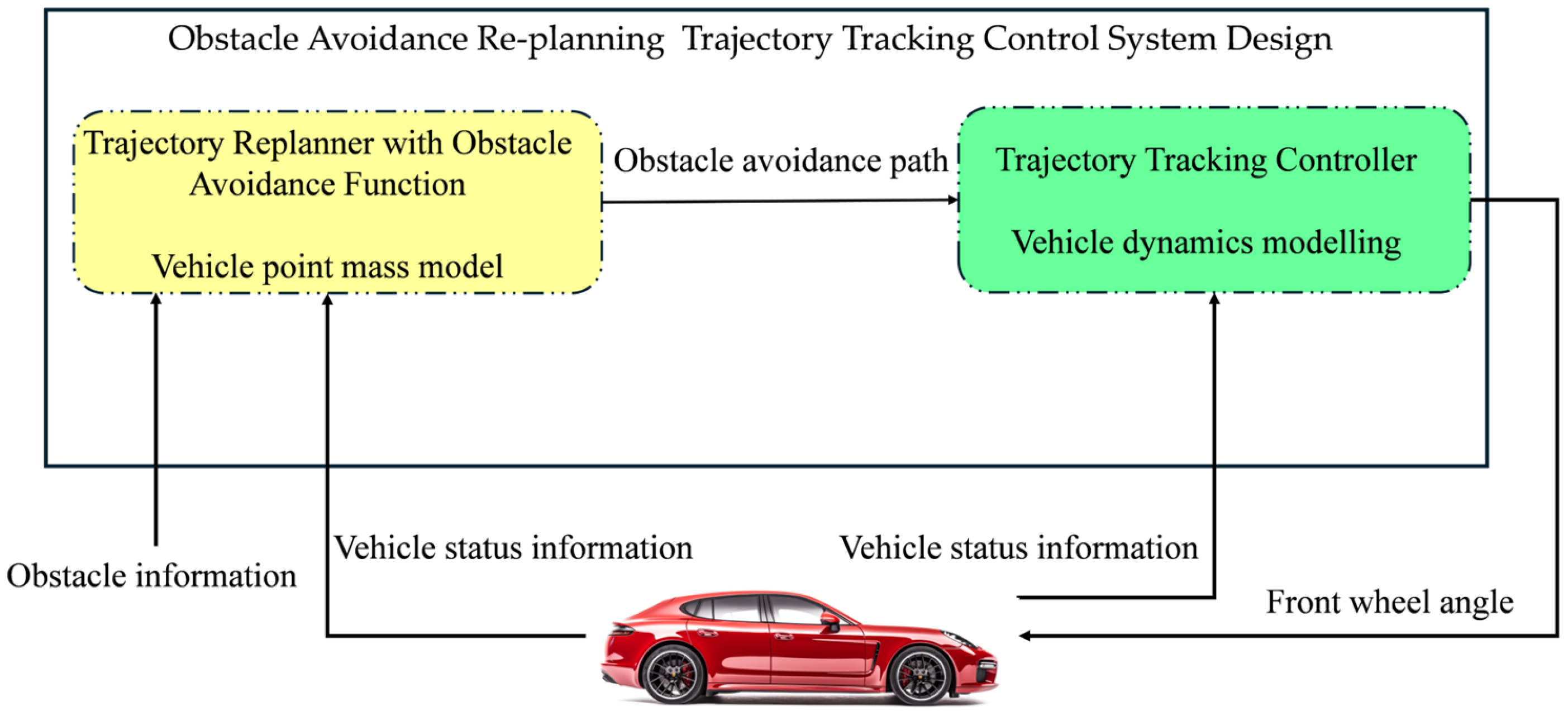
2.1. Obstacle Avoidance Re-Planning Trajectory-Tracking Control System Design
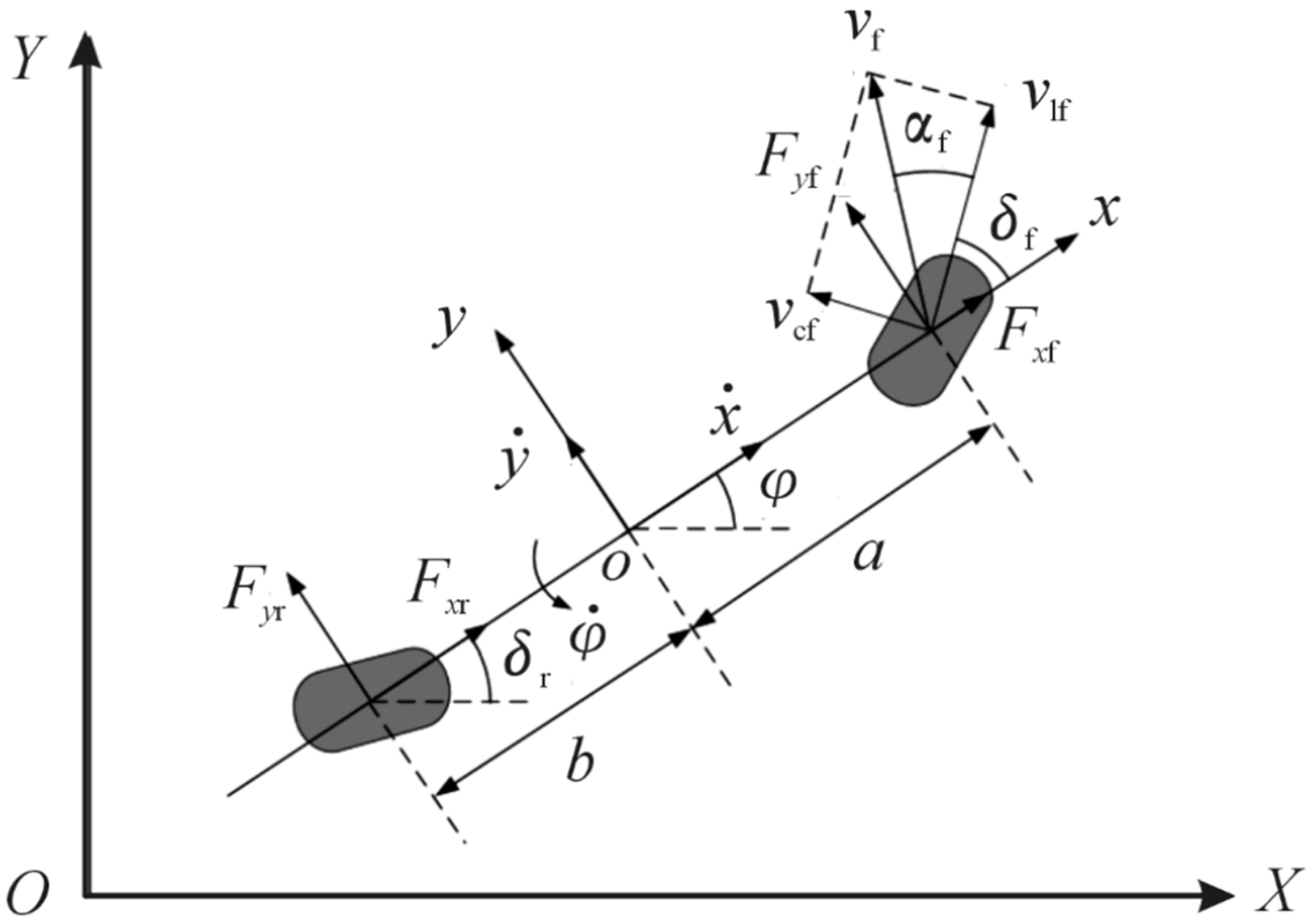
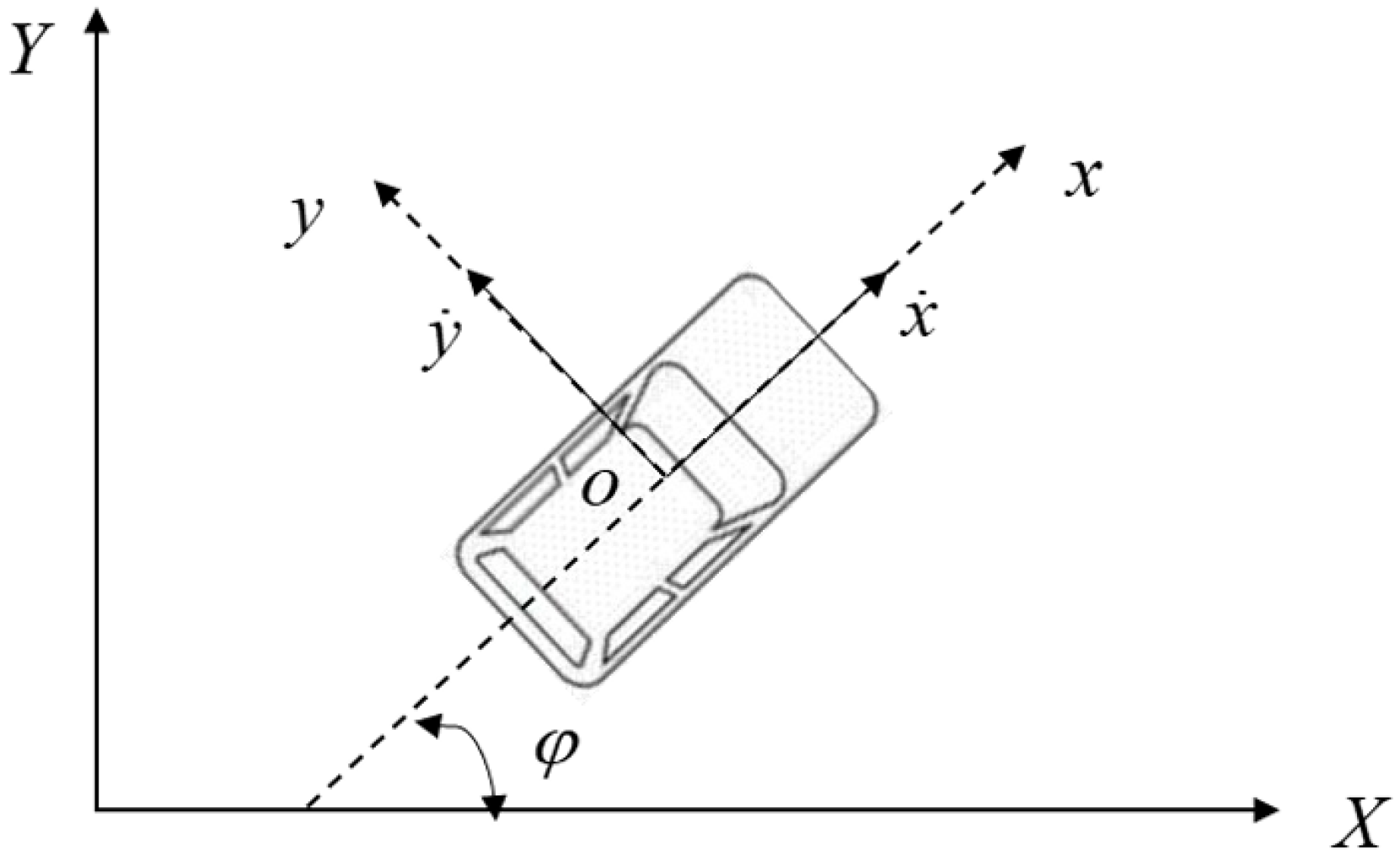
2.2. Modelling of Vehicle Dynamics
2.3. Obstacle Avoidance Trajectory Re-Planning Controller Design
2.3.1. Predictive Model
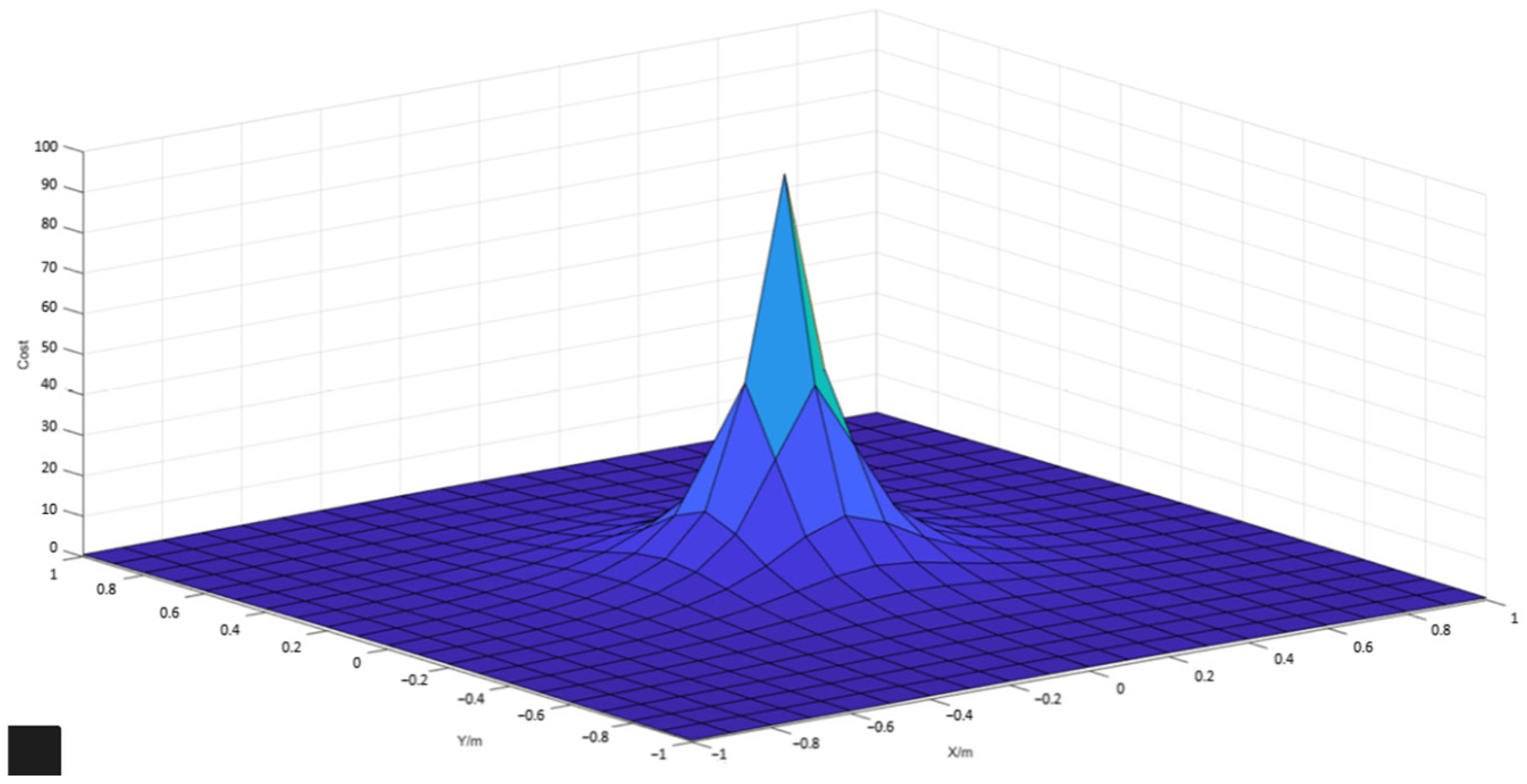
2.3.2. Obstacle Avoidance Function and Objective Function Design
2.3.3. Fifth-Degree Polynomial Fitting of Obstacle Avoidance Trajectories
2.4. Adaptive Predictive Time Domain Trajectory Tracker Design
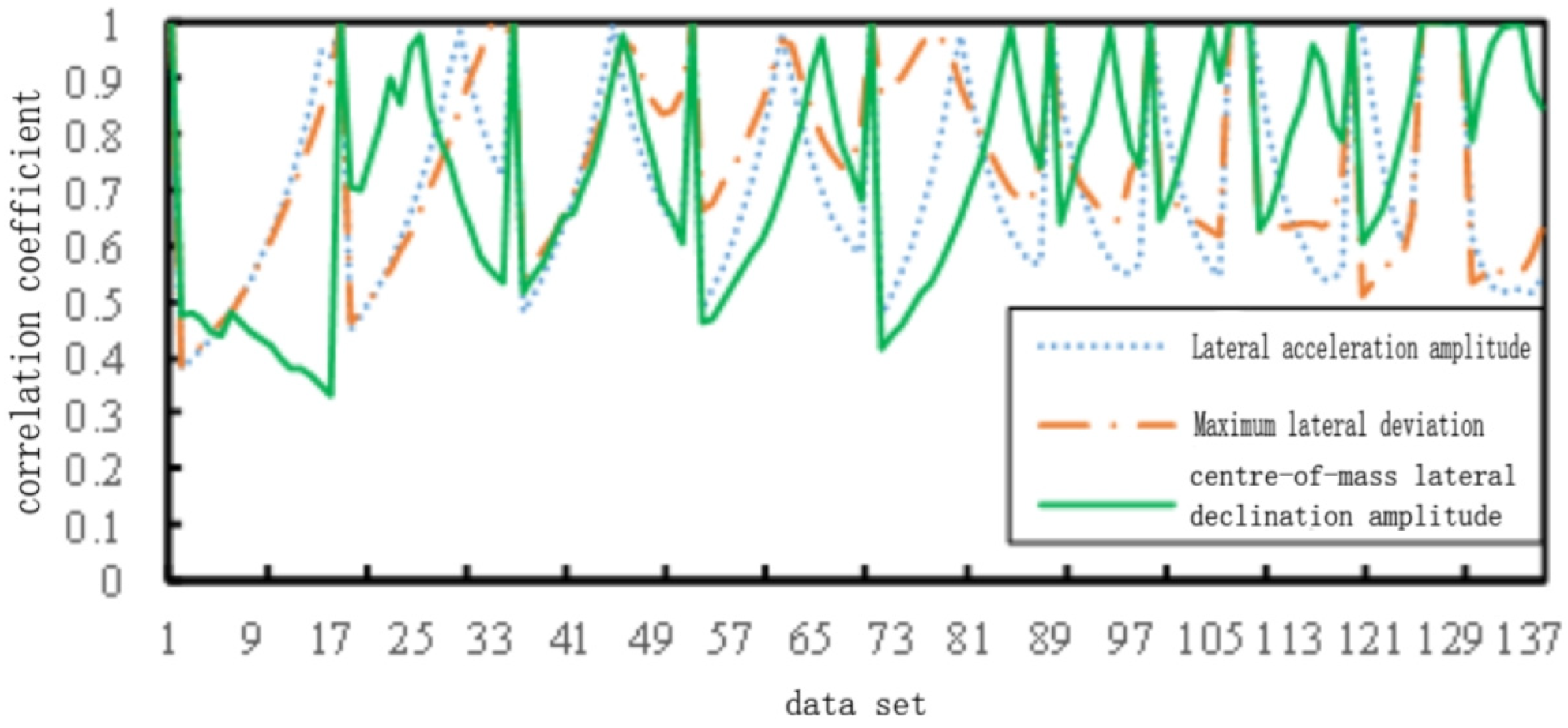
2.4.1. Gray Correlation Analysis
- Determining the analytical series;
- 2.
- Dimensionlessness of variables;
- 3.
- Calculate the grey correlation coefficient between the parent sequence and the subsequence.
- 4.
- Calculating correlation;
- 5.
- Order by relevance;
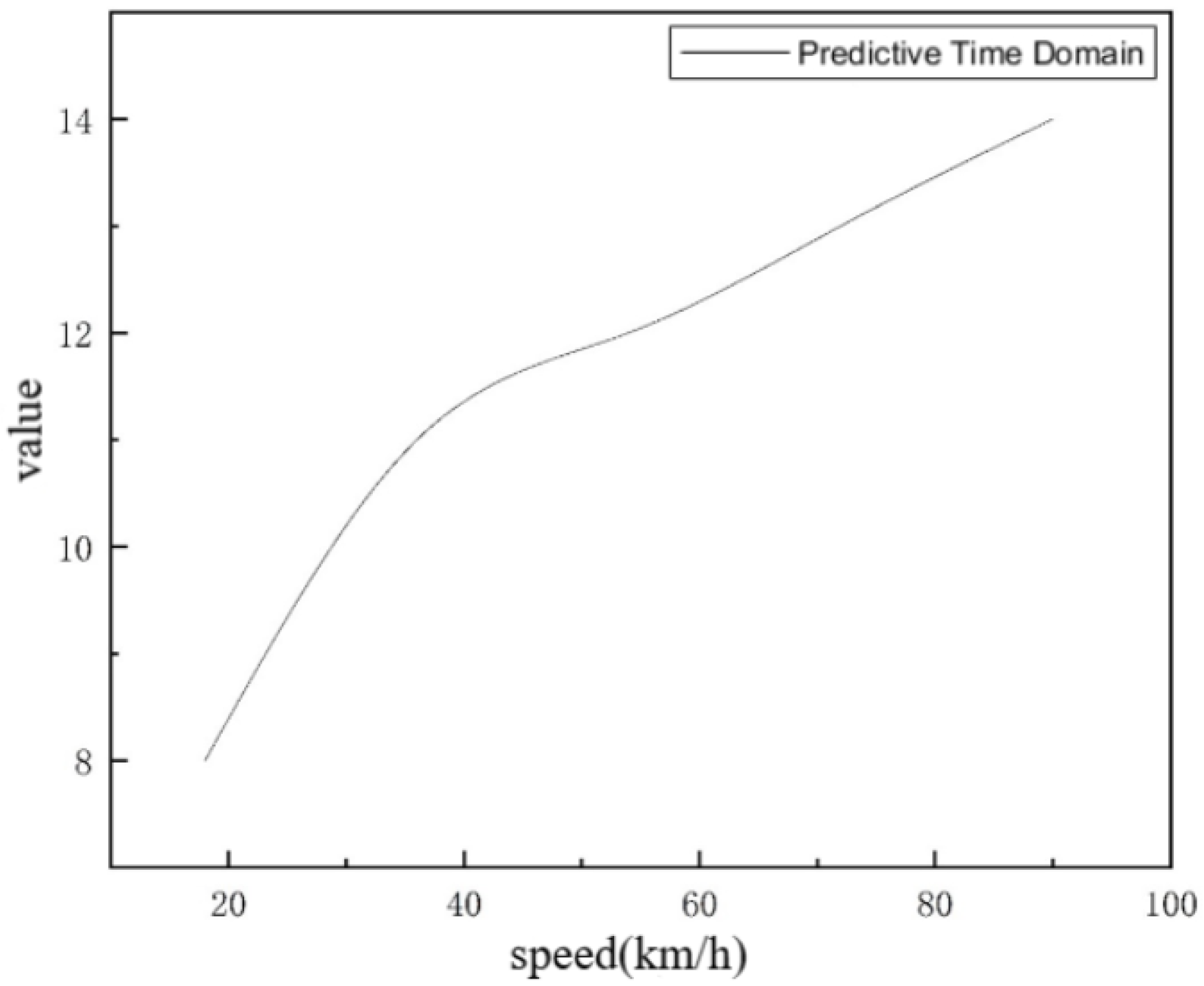
2.4.2. Determination of Optimal Time-Domain Parameters
- The selected time-domain parameters should enable the trajectory re-planning process to smoothly avoid obstacles;
- The selected time-domain parameters should result in a new trajectory, obtained after re-planning by the controller, having the smallest deviation from the original reference trajectory;
- The selected time-domain parameters should enable the vehicle to re-track the original reference trajectory after obstacle avoidance actions;
- The selected time-domain parameters should not cause overshooting during the tracking test;
- The selected time-domain parameters should not cause yaw angle oscillation during the tracking test.
2.4.3. Trajectory-Tracking Controller Function Design
3. Local Obstacle Avoidance Path Planning and Trajectory Tracking Verification
3.1. Comparative Experimental Analysis of Fixed Prediction Time Domain Simulation
3.2. Simulation Comparison Experiment of AP-MPC
3.3. Comparative Test of AP-MPC Simulation Under Multiple Obstacle Conditions
- Test results at a longitudinal speed of 36 km/h:
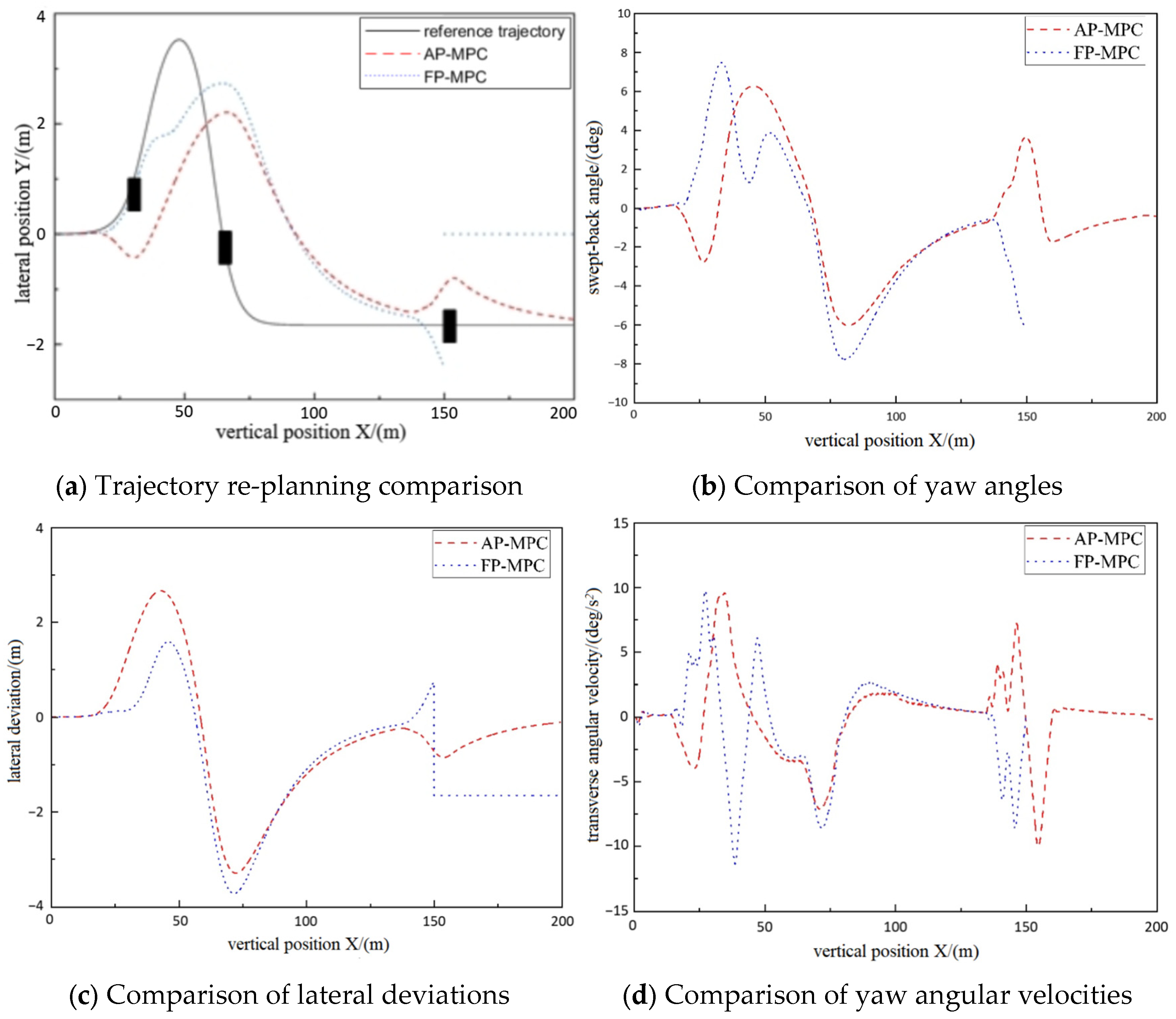
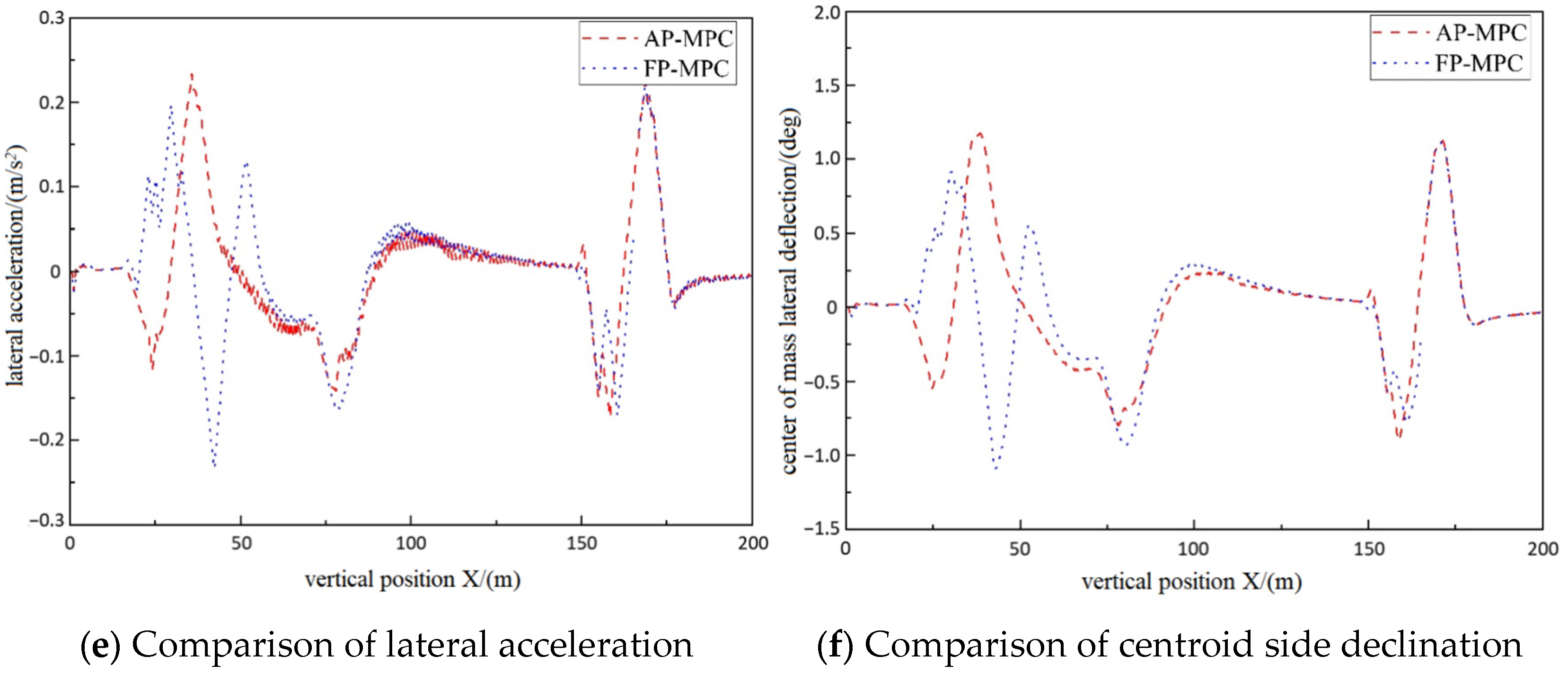
- 2.
- Test results at a longitudinal speed of 72 km/h:
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, H.Y.; Chen, S.P.; Gong, J.W. A Review on the Research of Lateral Control for Intelligent Vehicles. Acta Armamentarii 2017, 38, 1203–1214. [Google Scholar]
- Zeng, F.Z.; Gao, X.J.; Yuan, Z.Q.; You, S.H.; Zhang, B.C.; Huang, W.Y.; Han, Y. Design of Fuzzy PID Longitudinal Automatic Control Algorithm Based on Vehicle Parameter Adjustment. China Meas. Test 2023, 1–10. Available online: https://www.google.com/url?sa=t&source=web&rct=j&opi=89978449&url=https://scholar.google.co.in/scholar%3Fq%3DDesign%2Bof%2Bfuzzy%2BPID%2Blongitudinal%2Bautomatic%2Bcontrol%2Balgorithm%2Bbased%2Bon%2Bvehicle%2Bparameter%2Badjustment%26hl%3Den%26as_sdt%3D0%26as_vis%3D1%26oi%3Dscholart&ved=2ahUKEwjmxsvq1aGMAxW7jGMGHbjbCQoQgQN6BAgIEAE&usg=AOvVaw3PzBUSpCQNDszNidL929Yn (accessed on 21 February 2025).
- Chen, L.B.; Tang, L.; Tan, P.Y. Research on collaborative control of intelligent vehicle path tracking in lane changing. China Meas. Test 2022, 48, 108–115. [Google Scholar]
- Mei, S.Y.; Tao, W.G.; Hou, H. Research on fuzzy control and feedforward compensation for permanent magnet synchronous motor. China Meas. Test 2023, 1–6. [Google Scholar]
- Hen, G.; Yao, J.; Hu, H.; Gao, Z.; He, L.; Zheng, X. Design and experimental evaluation of an efficient MPC based lateral motion controller considering path preview for autonomous vehicles. Control. Eng. Pract. 2022, 123, 105164. [Google Scholar]
- Khan, M.; Tahiyat, M.; Imtiaz, S.; Choudhury, M.S.; Khan, F. Experimental evaluation of control performance of mpc as a regulatory controller. ISA Trans. 2017, 70, 512–520. [Google Scholar] [PubMed]
- Mackinnon, L.; Ramesh, P.S.; Mhaskar, P.; Swartz, C.L. Dynamic real-time optimization for nonlinear systems with Lyapunov stabilizing MPC. J. Process Control 2022, 114, 1–15. [Google Scholar]
- Francesco, B.; Paolo, F. MPC-based approach to active steering for autonomous vehicle systems. Int. J. Veh. Auton. Syst. 2005, 3, 265–291. [Google Scholar]
- You, Z.H. Research on Model Predictive Control-Based Trajectory Tracking for Unmanned Vehicles; Jilin University: Changchun, China, 2018. [Google Scholar]
- Ji, J.; Khajepour, A.; Melek, W.W.; Huang, Y. Path planning and tracking for vehicle collision avoidance based on model predictive control with multiconstraints. IEEE Trans. Veh. Technol. 2017, 66, 952–964. [Google Scholar]
- Xu, X.; Tang, Z.; Wang, F.; Chen, L. Varied Weight Coefficients Based Trajectory Tracking of Distributed Drive Self-driving Vehicle. China J. Highw. Transp. 2019, 32, 36–45. [Google Scholar]
- Wang, J.N.; Teng, F.; Li, J.; Zang, L.; Fan, T.; Zhang, J.; Wang, X. Intelligent vehicle lane change trajectory control algorithm based on weight coefficient adaptive adjustment. Adv. Mech. Eng. 2021, 13, 168781402110033. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, Y.; Chen, L.; Wang, H.; He, Y.; Li, J. Design of Intelligent and Connected Vehicle Path Tracking Controller Based on Model Predictive Control. J. Mech. Eng. 2019, 55, 136–144,153. [Google Scholar] [CrossRef]
- Yuan, X.F.; Huang, G.M.; Shi, K. Improved adaptive path following control system for autonomous vehicle in different velocities. IEEE Trans. Intell. Transp. Syst. 2020, 21, 3247–3256. [Google Scholar] [CrossRef]
- Deng, W.; Guo, H.; Zhang, K.; Lin, M.; Zhang, X.; Yu, F. Obstacle-avoidance algorithm design for autonomous vehicles considering driver subjective feelings. Proc. Inst. Mech. Eng. 2021, 235, 945–960. [Google Scholar]
- Hu, C.; Zhao, L.; Cao, L.; Tjan, P.; Wang, N. Steering control based on model predictive control for obstacle avoidance of unmanned ground vehicle. Meas. Control 2020, 53, 501–518. [Google Scholar] [CrossRef]
- Liu, K.; Gong, J.; Chen, S.; Zhang, Y.; Chen, H. Dynamic Modeling Analysis of Optimal Motion Planning and Control for High-speed Self-driving Vehicles. J. Mech. Eng. 2018, 54, 141–151. [Google Scholar] [CrossRef]
- Gong, J.; Jiang, Y.; Xu, W. Model Predictive Control for Unmanned Vehicles; Beijing Institute of Technology Press: Beijing, China, 2020. [Google Scholar]
- Wang, K. Intelligent Vehicle Trajectory Planning and Motion Control Based on Vehicle Information Interaction; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2018. [Google Scholar]
- Ma, Y.; Li, Y.; Sun, W. Application of comprehensive evaluation system based on gray correlation analysis and TOPSIS theory. Electron. Technol. Softw. Eng. 2018, 184–187. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, G.; Zhang, Y.; Wang, N.; Meng, H. Fourier series-based interpolation estimation method for zero-tuning cells. Electron. Qual. 2022, 7, 11–14. [Google Scholar]
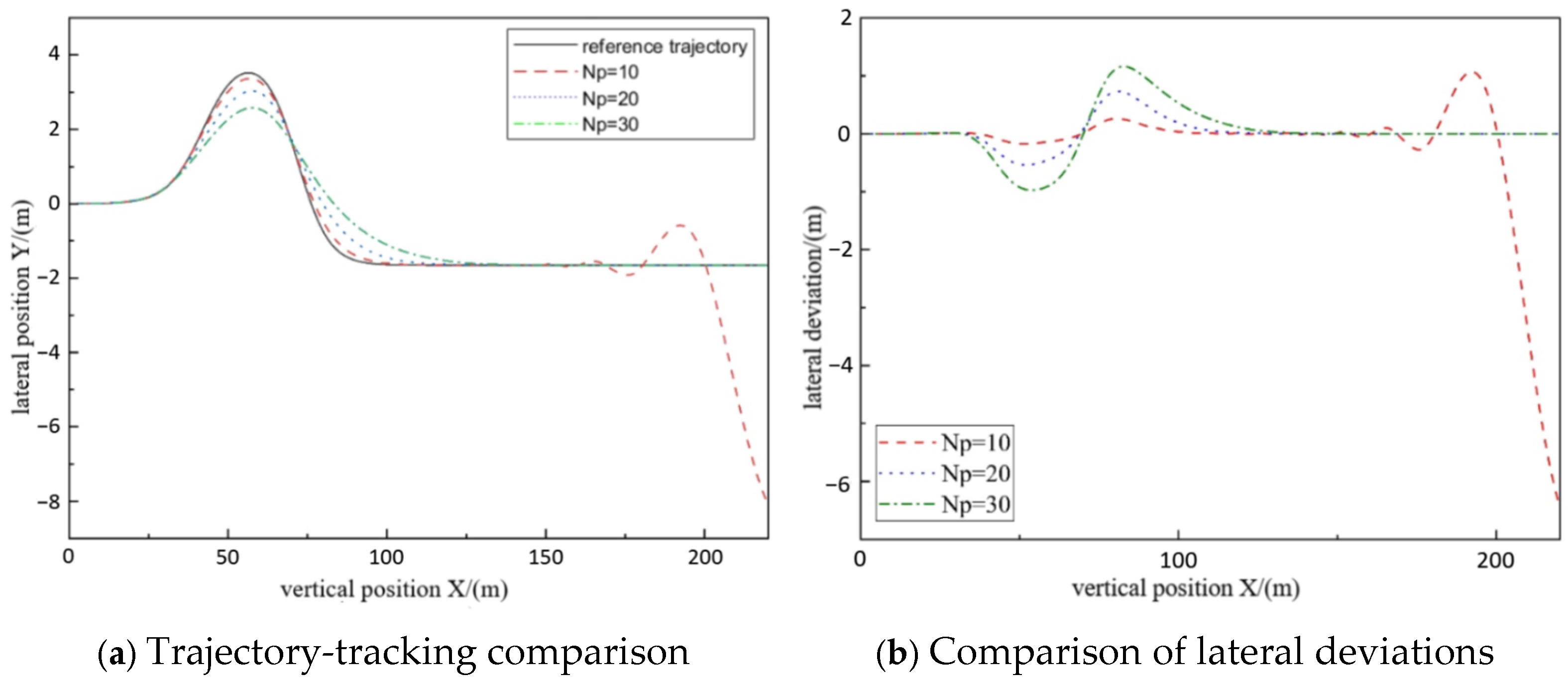
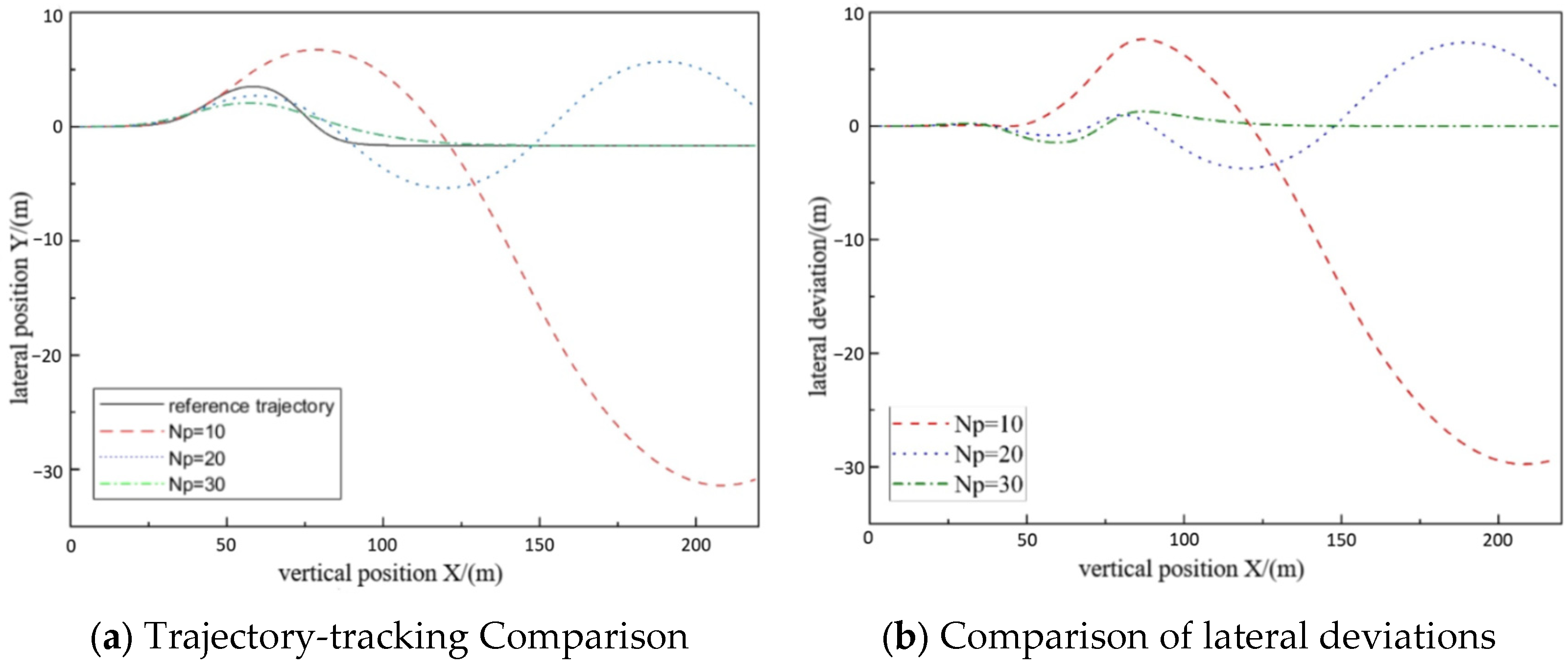
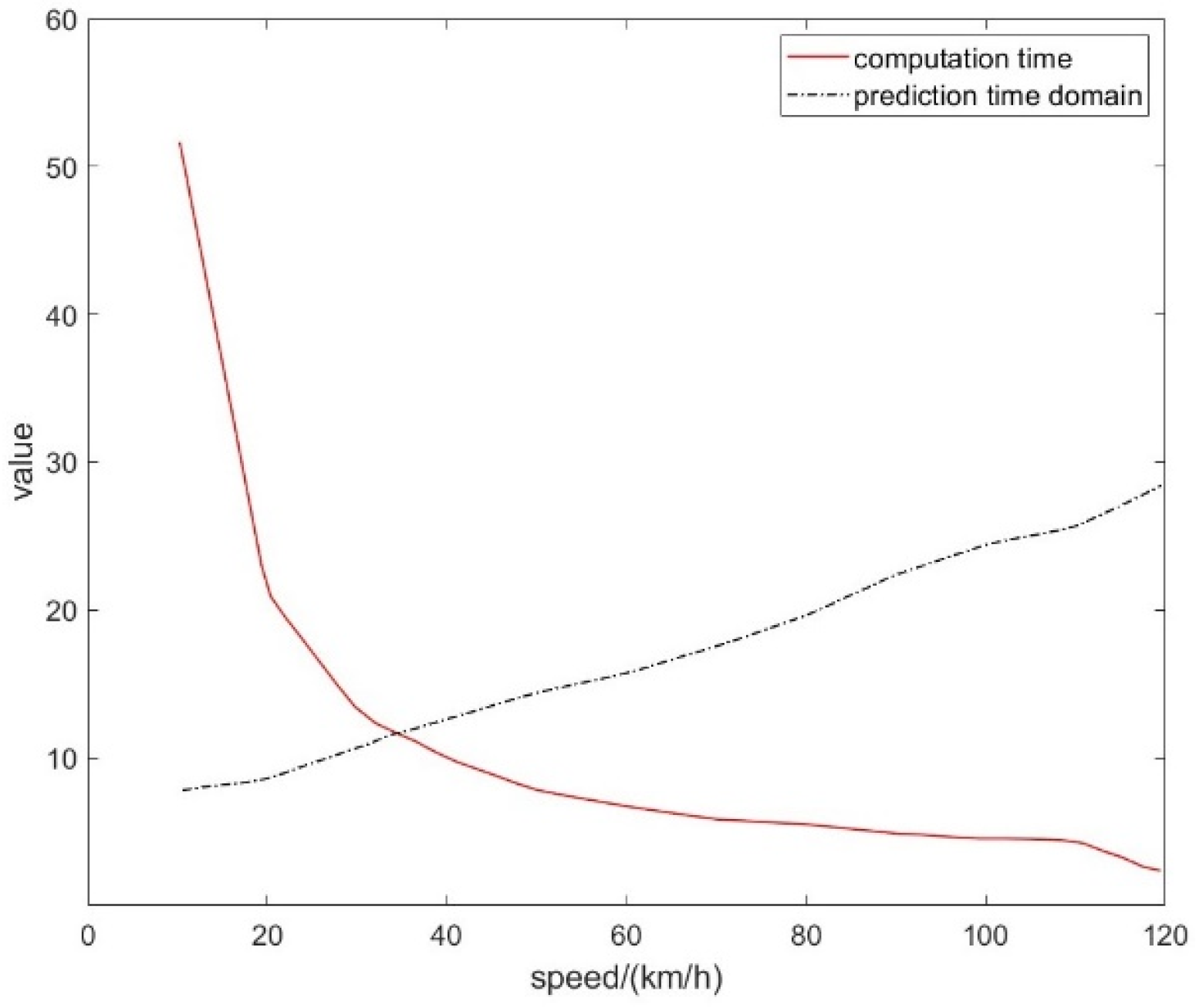
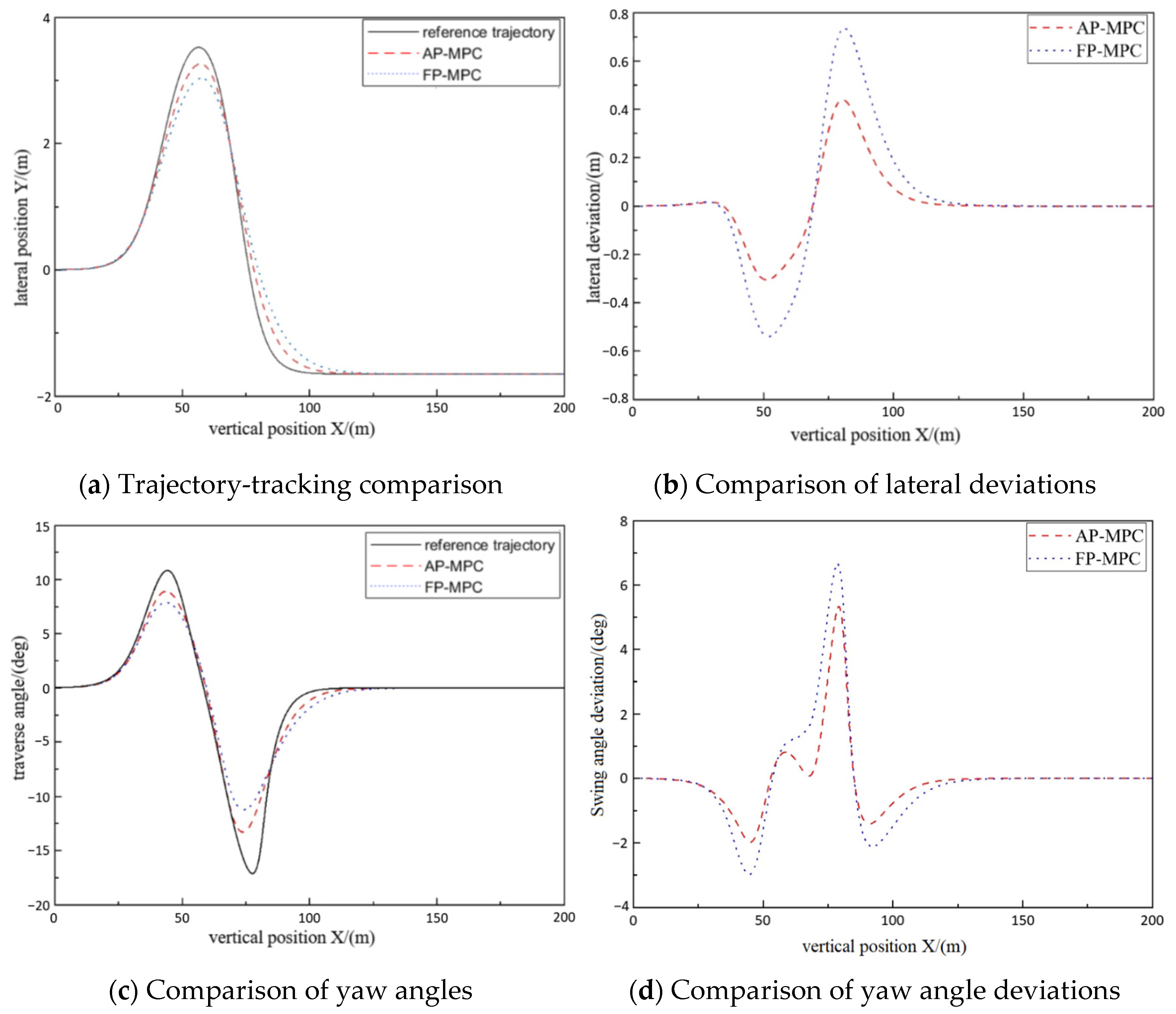
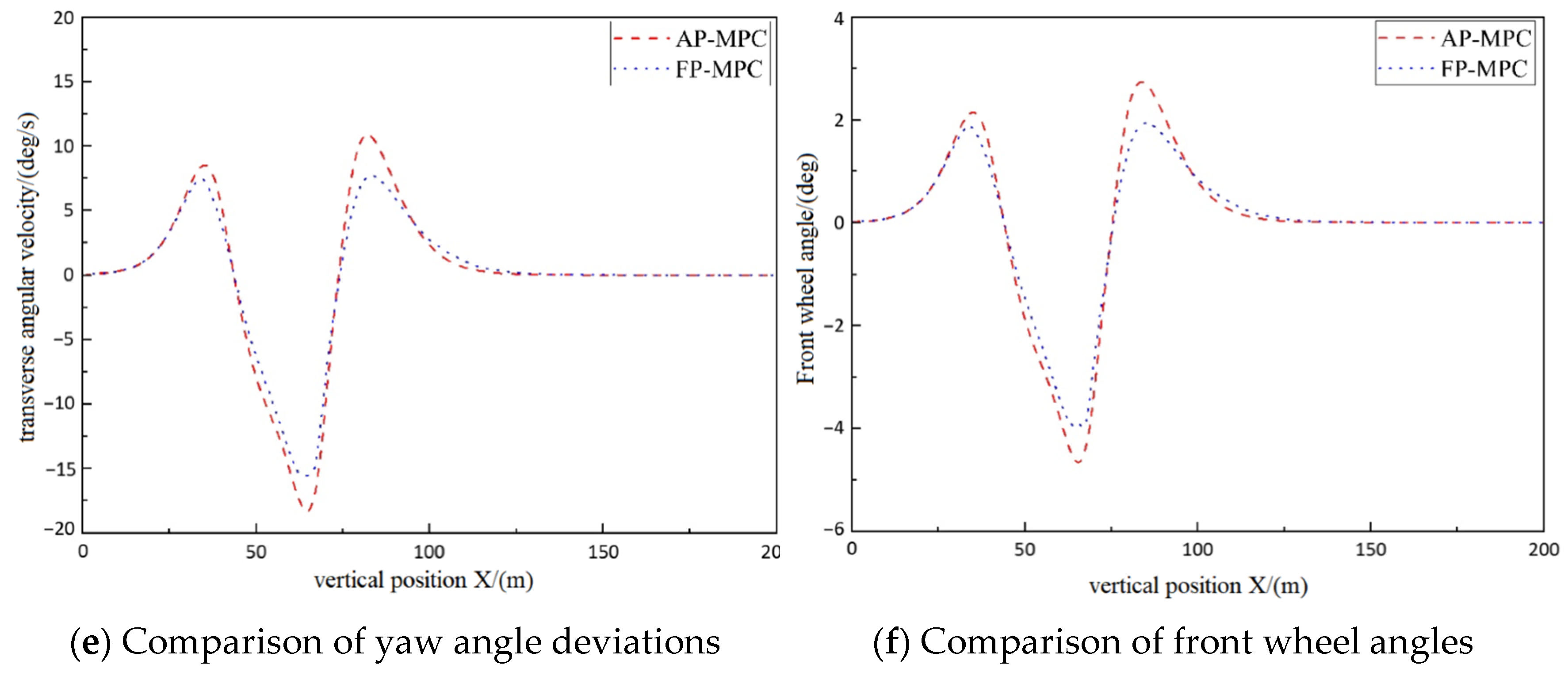
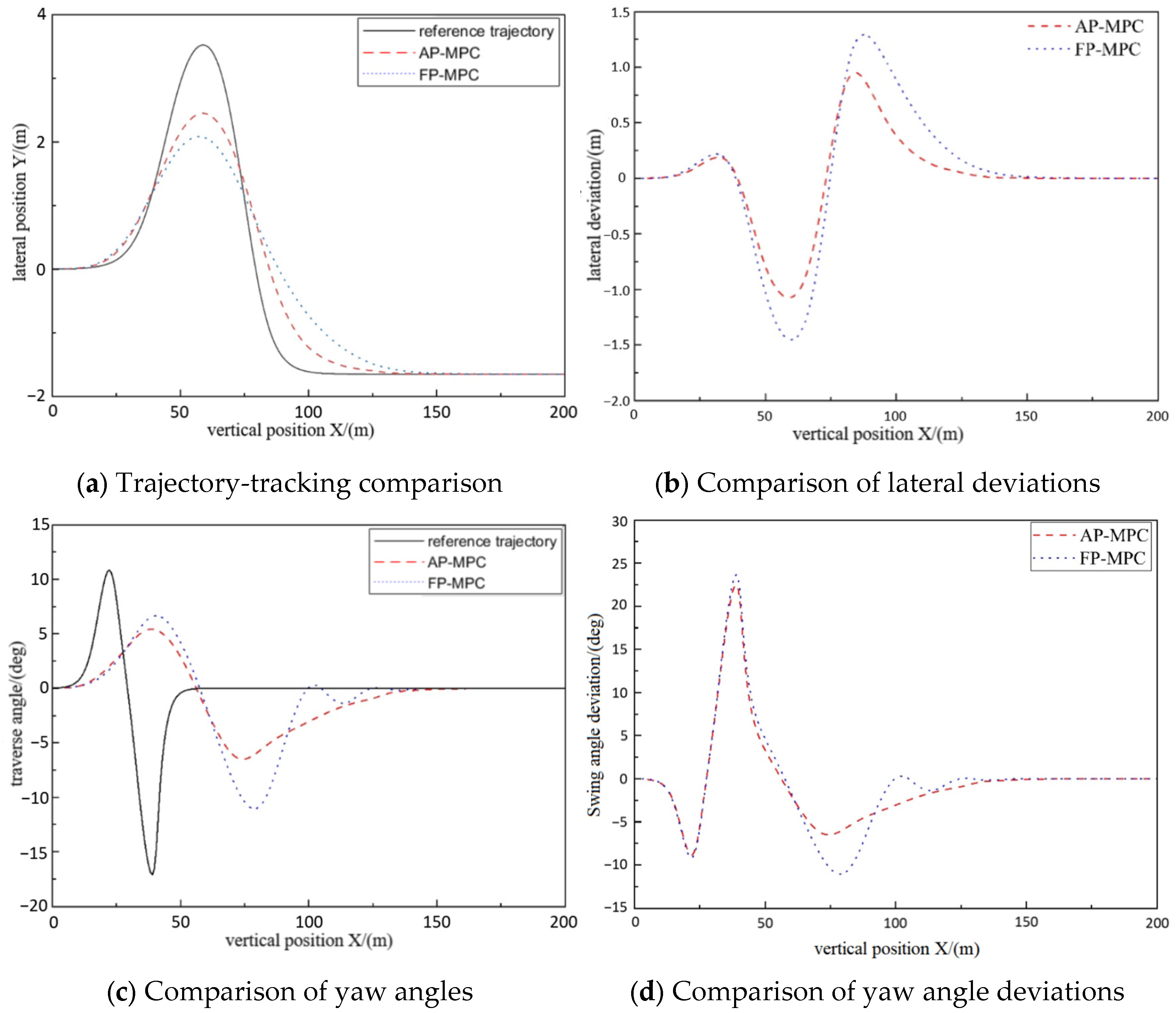
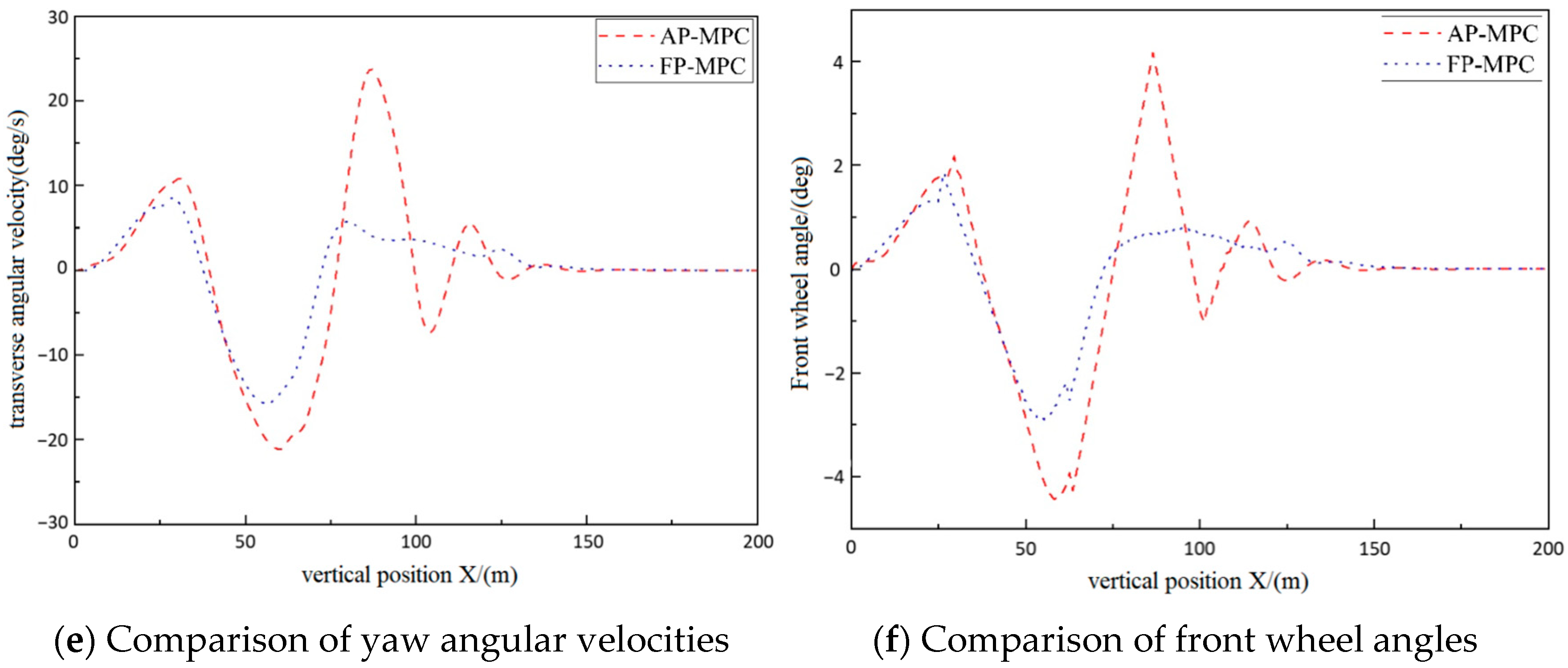
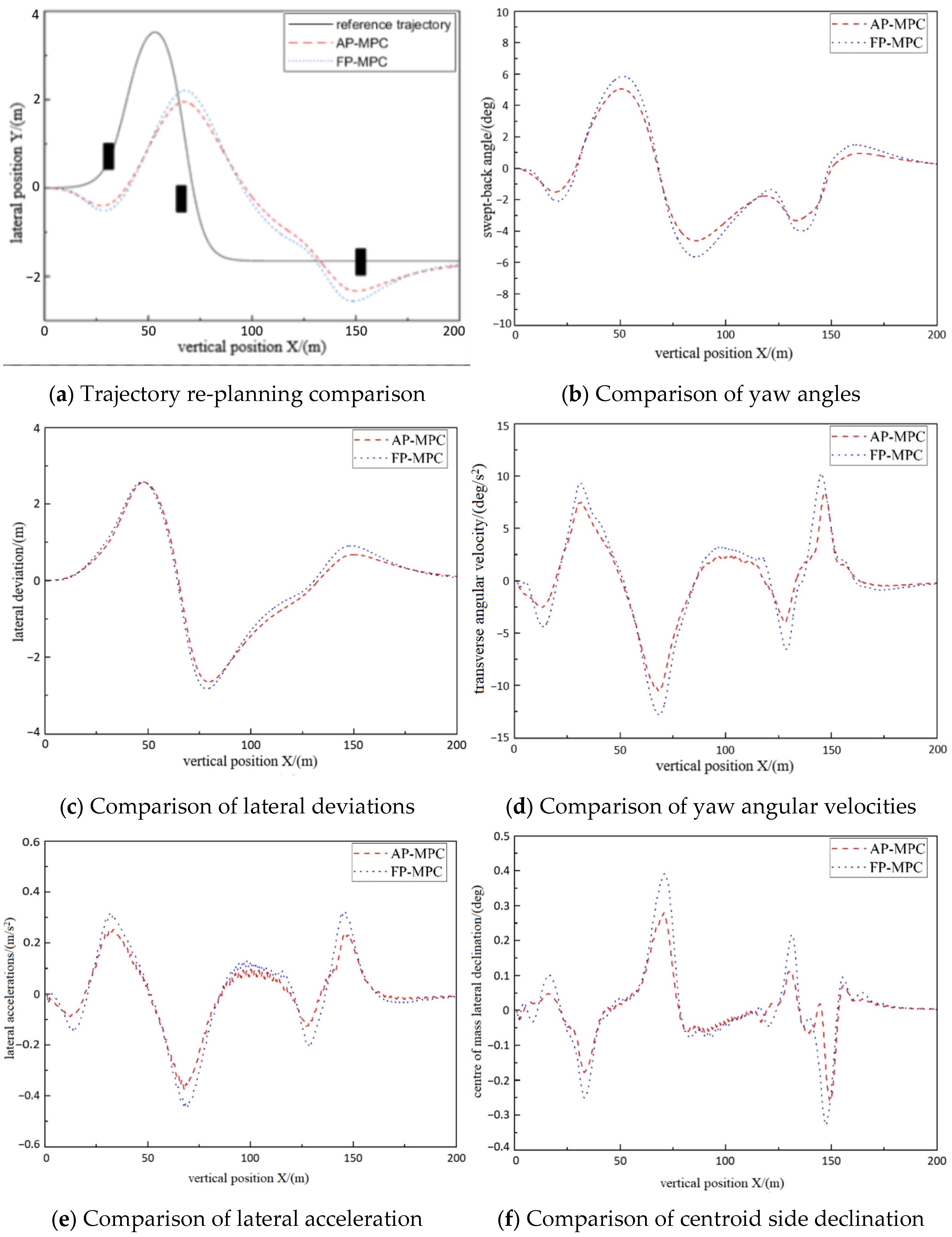
| Evaluation Item | Main Sequence | Relevance | Rank |
|---|---|---|---|
| Maximum Lateral Deviation | 0.776 | 1 | |
| Lateral Acceleration Amplitude | 0.714 | 2 | |
| Centroid Lateral Deviation Amplitude | 0.679 | 3 |
| Parameter | Value |
|---|---|
| Vehicle mass, m/kg | 1650 |
| Distance from rear axle to vehicle centre of mass, b/m | 1.65 |
| Moment of inertia around Z-axis, | 3234 |
| Effective rolling radius of tire, | 0.32 |
| Centre of mass height, | 0.53 |
| Front and rear wheel slip ratio, | 0.2 |
| Parameter | Value |
|---|---|
| Prediction Time Domain | 10, 20, 30 |
| Control Time Domain | 3 |
| Sampling Period, t/s | 0.03 |
| Front Wheel Angle Restraint | −10~10° |
| Front Wheel Angle Increment | |
| Control Parameter | Trajectory Planning Layer | Trajectory-Tracking Layer |
|---|---|---|
| Predictive time domain | 15 | / |
| Control time domain | 2 | 2 |
| Sampling period T | 0.1 s | 0.05 s |
| Front Wheel Angle Restraint | / | |
| Front wheel angle increment | / | 0.85° |
| Weighting matrix Q | ||
| Weighting coefficients of the Obstacle avoidance function | / | |
| Weighting matrix R | ||
| Weighting factor | / | 1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, Z.; Wu, C. Design of Adaptive Trajectory-Tracking Controller for Obstacle Avoidance and Re-Planning. World Electr. Veh. J. 2025, 16, 191. https://doi.org/10.3390/wevj16040191
Kang Z, Wu C. Design of Adaptive Trajectory-Tracking Controller for Obstacle Avoidance and Re-Planning. World Electric Vehicle Journal. 2025; 16(4):191. https://doi.org/10.3390/wevj16040191
Chicago/Turabian StyleKang, Zihao, and Changshui Wu. 2025. "Design of Adaptive Trajectory-Tracking Controller for Obstacle Avoidance and Re-Planning" World Electric Vehicle Journal 16, no. 4: 191. https://doi.org/10.3390/wevj16040191
APA StyleKang, Z., & Wu, C. (2025). Design of Adaptive Trajectory-Tracking Controller for Obstacle Avoidance and Re-Planning. World Electric Vehicle Journal, 16(4), 191. https://doi.org/10.3390/wevj16040191





