Energy Consumption Prediction for Electric Buses Based on Traction Modeling and LightGBM
Abstract
1. Introduction
- While EBs’ motor systems are generally more efficient from battery to wheels compared to combustion engines, their complex energy transmission systems, including non-linear motor efficiency curves [51] and variable regenerative braking recovery rates [52], make accurate energy consumption evaluation challenging. This becomes even more critical as power system efficiency decreases over time [53,54].
- Passenger load significantly impacts energy consumption per trip [55], but gathering passenger data poses difficulties. Data from electronic payment systems and vehicle operations are often separately managed and hard to integrate. Additionally, collecting data from non-electronic payment passengers or onboard devices (infrared or cameras) is complicated by low device adoption rates and privacy concerns.
- While macro-level models have modest computational requirements, real-time energy consumption models are more complex, challenging onboard hardware capabilities. Therefore, models must balance complexity with computational efficiency for practical vehicle deployment.
2. Data Acquisition and Preprocessing
2.1. Data Acquisition
2.2. Data Preprocessing
- Mild outliers: data points that moderately deviate from the central values and occur with relatively high frequency.
- Extreme outliers: isolated points that show substantial deviations from central values.
2.3. Trip Segmentation
- The vehicle location was closest to a station;
- Both vehicle speed and motor speed were zero, indicating a complete stop.
3. Methodology
3.1. Driving Patterns Analysis
- Idle State ();
- High-voltage system active;
- .
- Constant Speed State ();
- ;
- .
- Acceleration State ();
- ;
- .
- Deceleration State ().
- ;
- .
- Idle Time Ratio;
- 2.
- Acceleration Time Ratio;
- 3.
- Deceleration Time Ratio;
- 4.
- Constant Speed Time Ratio;
- 5.
- Average Speed;
- 6.
- Average Travel Speed;
- 7.
- Maximum Speed;
- 8.
- Speed Standard Deviation;
- 9.
- Acceleration-Related Parameters;
- Maximum Acceleration:
- Maximum Deceleration:
- Average Acceleration:
- Average Deceleration:
- Acceleration–Deceleration Standard Deviation:
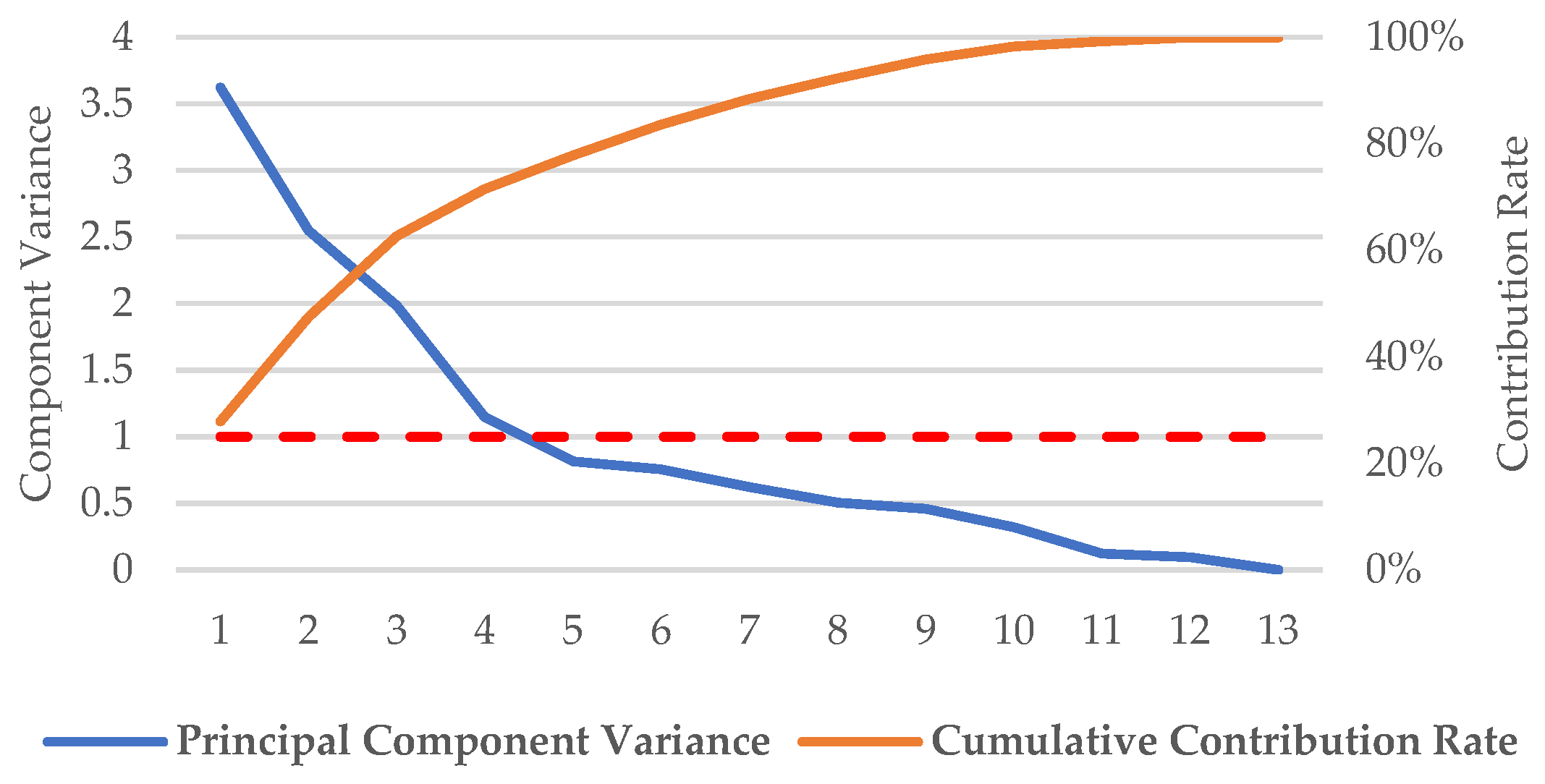
- First Principal Component (PC1): primarily describes the balance between acceleration and deceleration, with significant contributions from the Deceleration Time Ratio and Acceleration–Deceleration Standard Deviation;
- Second Principal Component (PC2): mainly characterizes variations in speed-related features, particularly the Idle Time Ratio and Average Speed;
- Third Principal Component (PC3): focuses on speed metrics and their deviations, as indicated by contributions from the Average Travel Speed and Maximum Speed;
- Fourth Principal Component (PC4): reflects the interplay of speed and acceleration, especially through contributions from Average Deceleration and Maximum Speed;
- Fifth Principal Component (PC5): primarily associated with the variability in deceleration, dominated by the Maximum Deceleration.
3.2. Energy Consumption Evaluation
3.2.1. Battery Output Power
- represents the net energy consumption [kWh];
- is the battery voltage at time step [V];
- represents the battery current at time step [A], positive for discharge and negative for charging;
- is the sampling time interval [s];
- is the total number of sampling points.
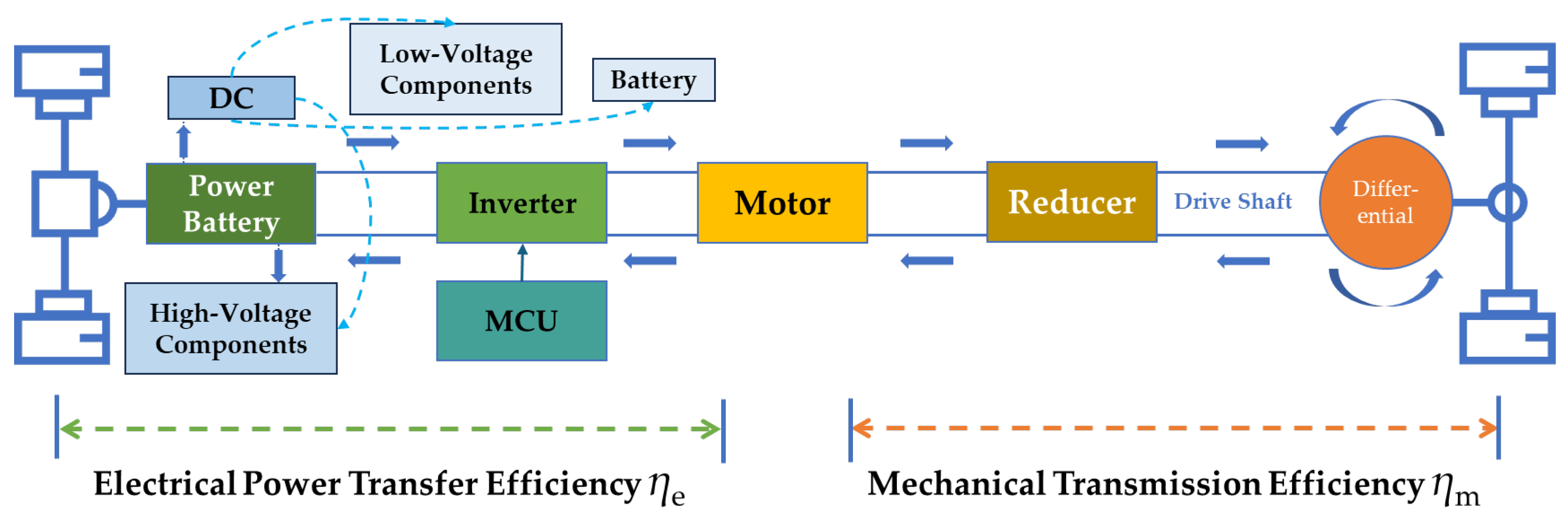
3.2.2. Traction Modeling
- 1.
- Electrical Power Transfer Efficiency ();
- Traction Motor Output Power [73] ():
- Electrical Input Power ():
- 2.
- Mechanical Transmission Efficiency ();
- ●
- •
- (rolling resistance coefficient);
- •
- (vehicle mass);
- •
- (gravitational acceleration);
- ●
- Aerodynamic Drag Force [77] ():
- •
- (aerodynamic drag coefficient for buses);
- •
- (frontal area);
- •
- vehicle velocity [].
- ●
- Mechanical Input Power at Constant Speed ():
- 3.
- System-Level Energy Transfer Efficiency ();
3.3. LightGBM Algorithm Description
- Discretizing continuous floating-point features into discrete bins and creating histograms of a fixed width.
- Iterating through the training data to accumulate statistics for each discrete bin in the histogram.
- Determining the optimal split point by iterating over the histogram bins during feature selection.
3.4. Trip-Level Energy Consumption Prediction Model Construction
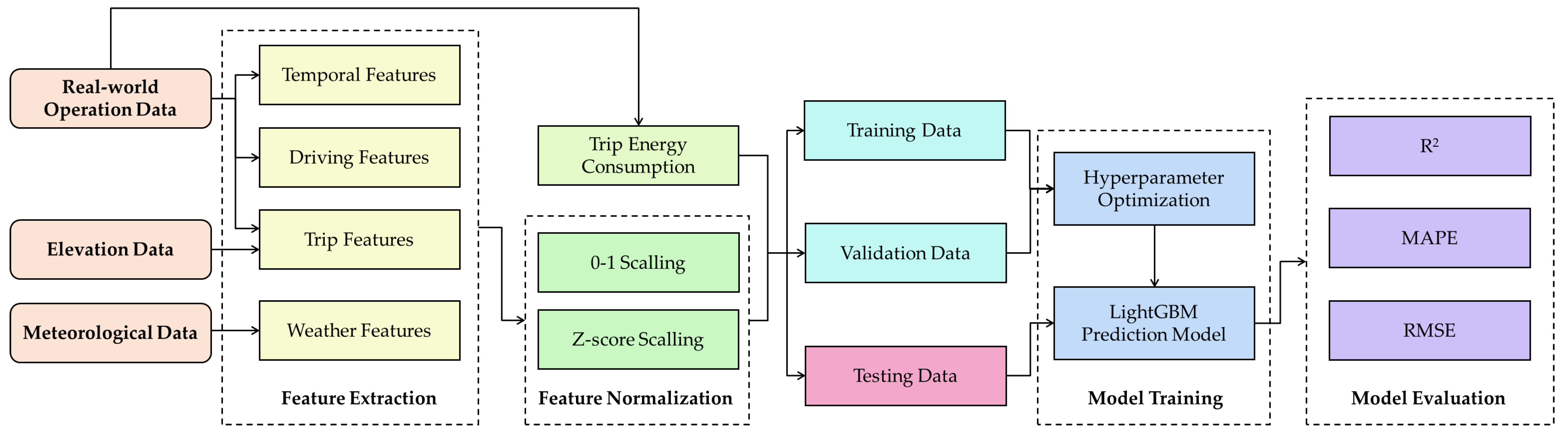
3.4.1. Feature Extraction
- Temporal Features;
- 2.
- Driving Features;
- 3.
- Trip Features;
- is the dynamically estimated total mass (including passenger load);
- represents motor torque;
- is vehicle acceleration;
- is the wheel radius.
- Sum of product of load and stop distances.
- Sum of product of load and elevation difference
- Assumption of linear additivity: energy consumption across segments is roughly additive, adhering to the common practice of piecewise linearization in engineering.
- Data availability: with available stop distances, elevation differences, and dynamic mass estimates (), the results can be directly calculated, making practical implementation feasible.
- Feature interpretability: The design of these features intuitively reflects the physical sources of energy consumption, aiding in identifying key influencing factors during model analysis. By summing the products of mass-distance and mass-elevation differences, we effectively capture the core physical mechanisms of vehicle energy consumption.
- Strong model interpretability: Feature design adheres to the law of conservation of energy, facilitating causal analysis in real-world scenarios.
- 4.
- Weather Features;
- A positive wind_x value indicates an eastward wind, while a negative value indicates a westward wind.
- A positive wind_y value indicates a northward wind, while a negative value indicates a southward wind.
3.4.2. Feature Normalization
- Step 1: Linear Normalization
- Step 2: Z-Score Standardization
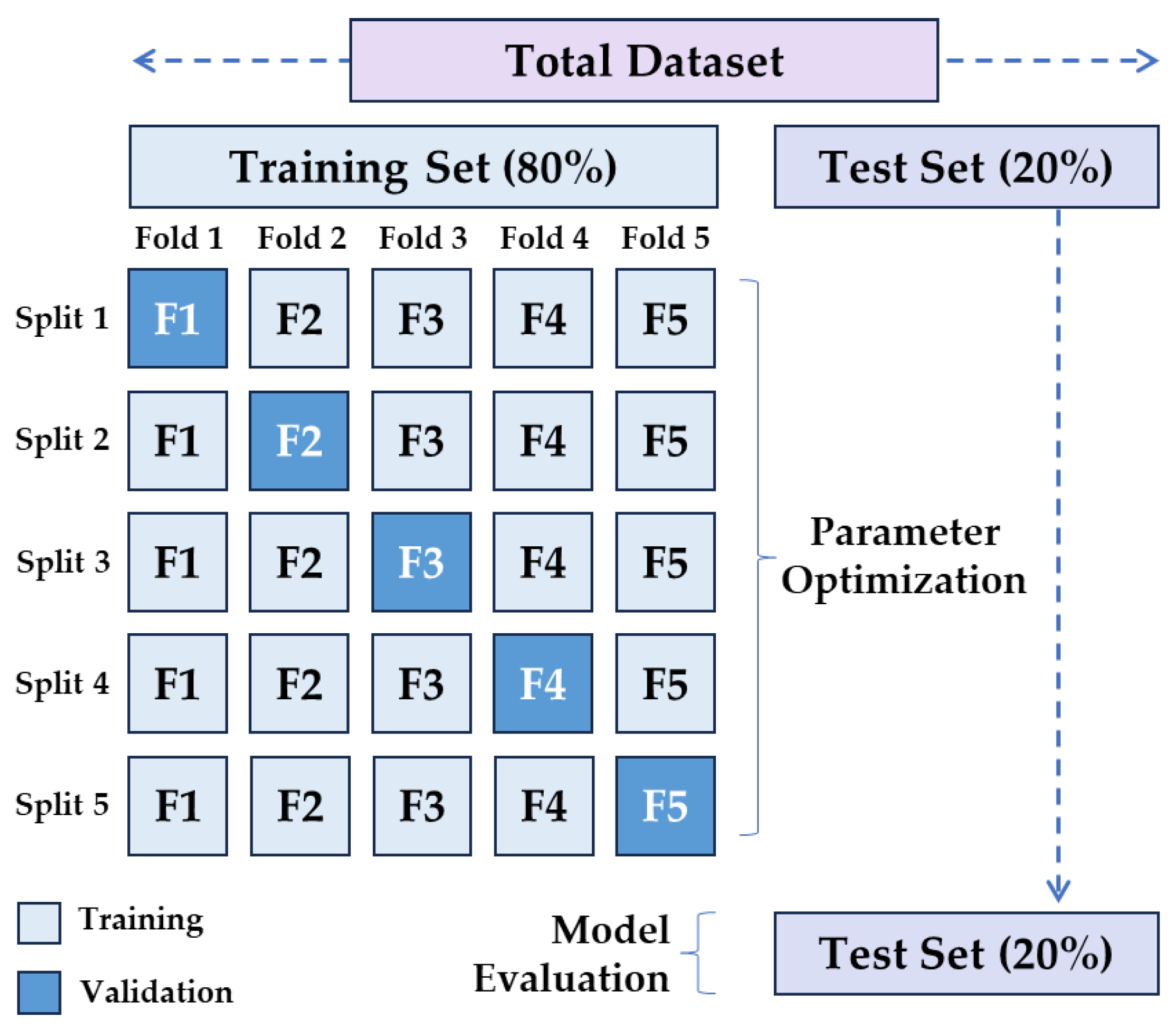
3.4.3. Model Training
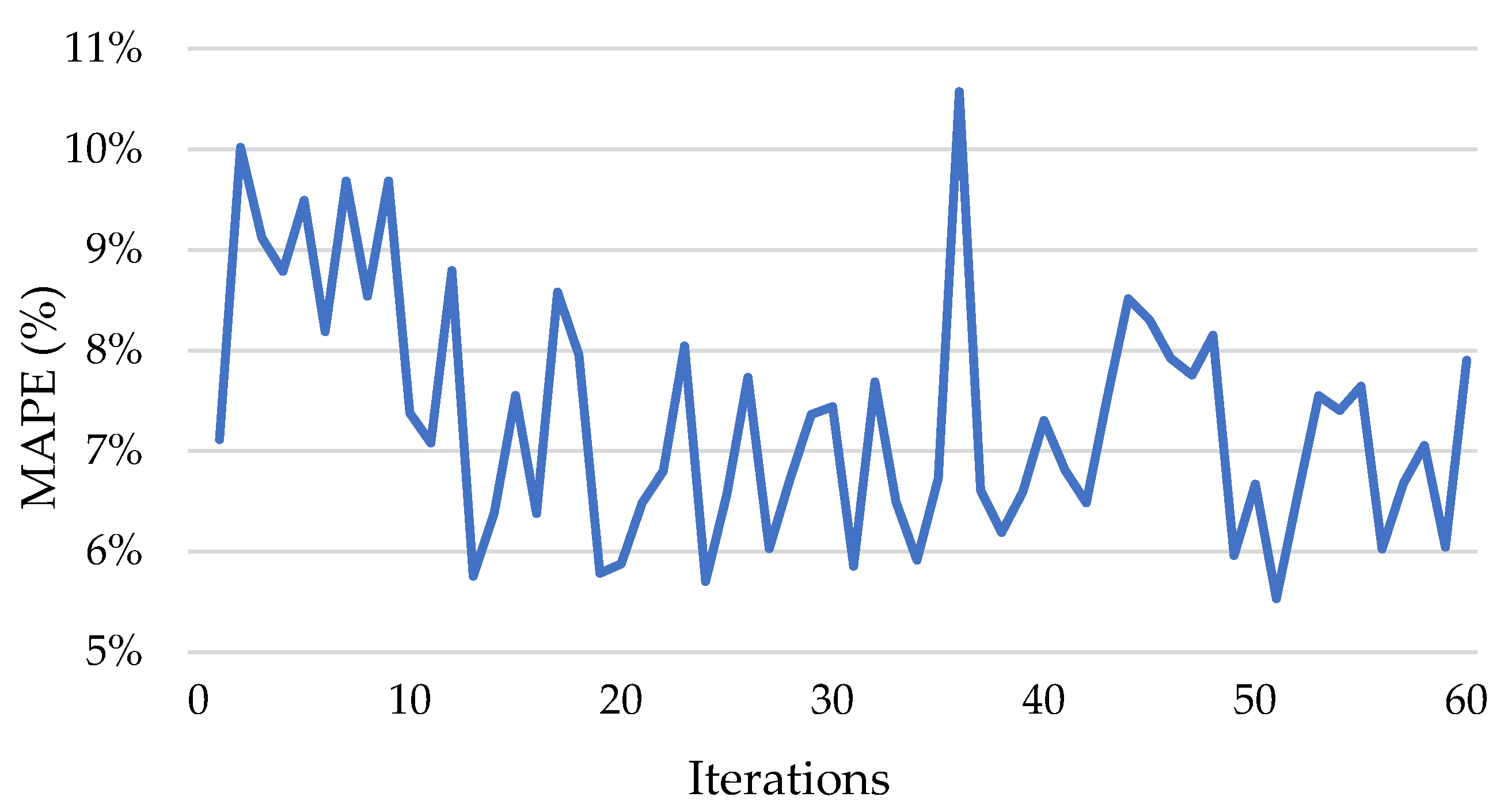
3.4.4. Model Evaluation
4. Results and Discussion
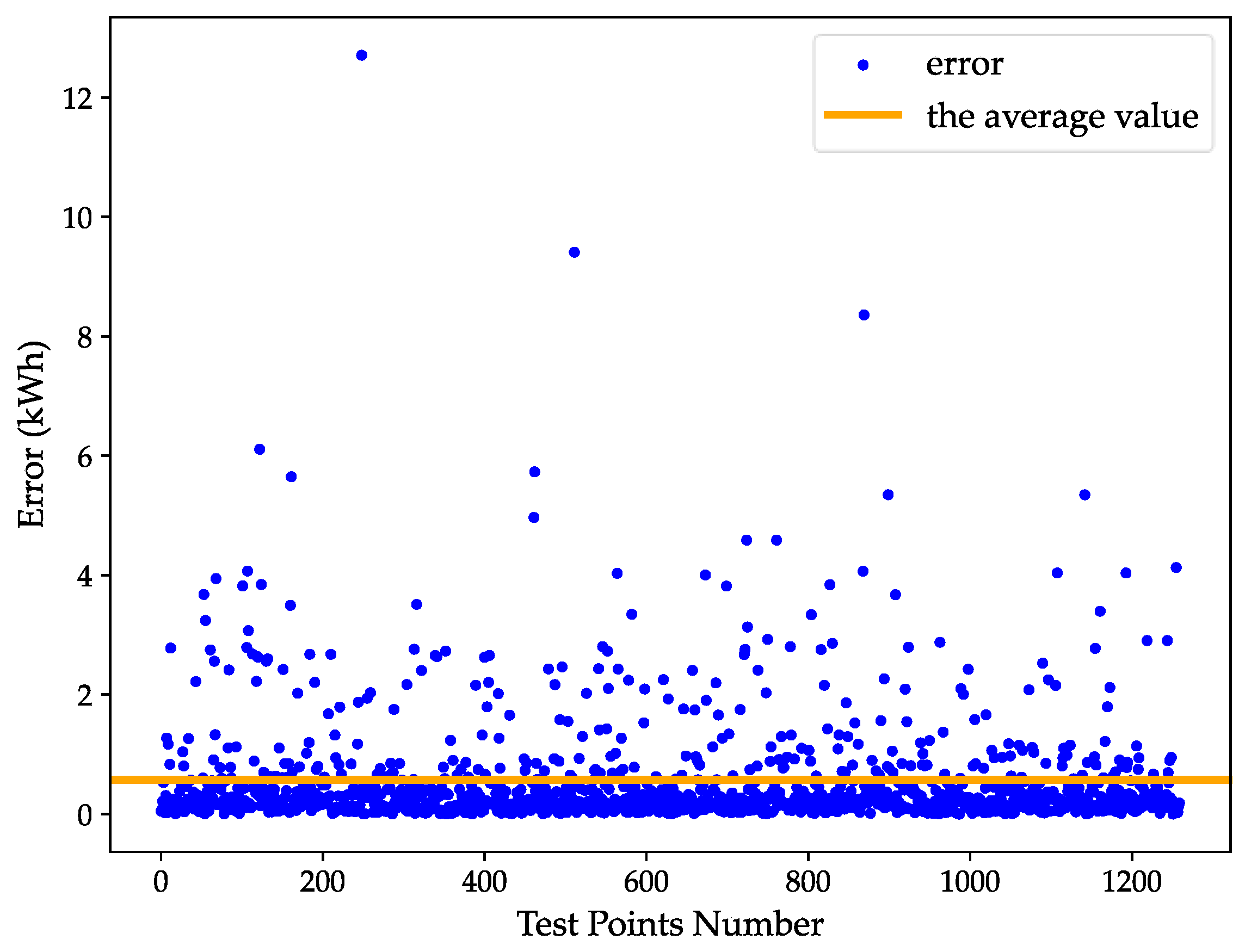
4.1. Model Validation
- Data Accessibility: Input features (datetime, weather, trip dynamics, and driving patterns) can be directly obtained or calculated from real-time operation data or public APIs.
- Computational Efficiency: Model requires only 1.0337 s and 177.91 MB of memory on personal computer, meeting real-time operational requirements.
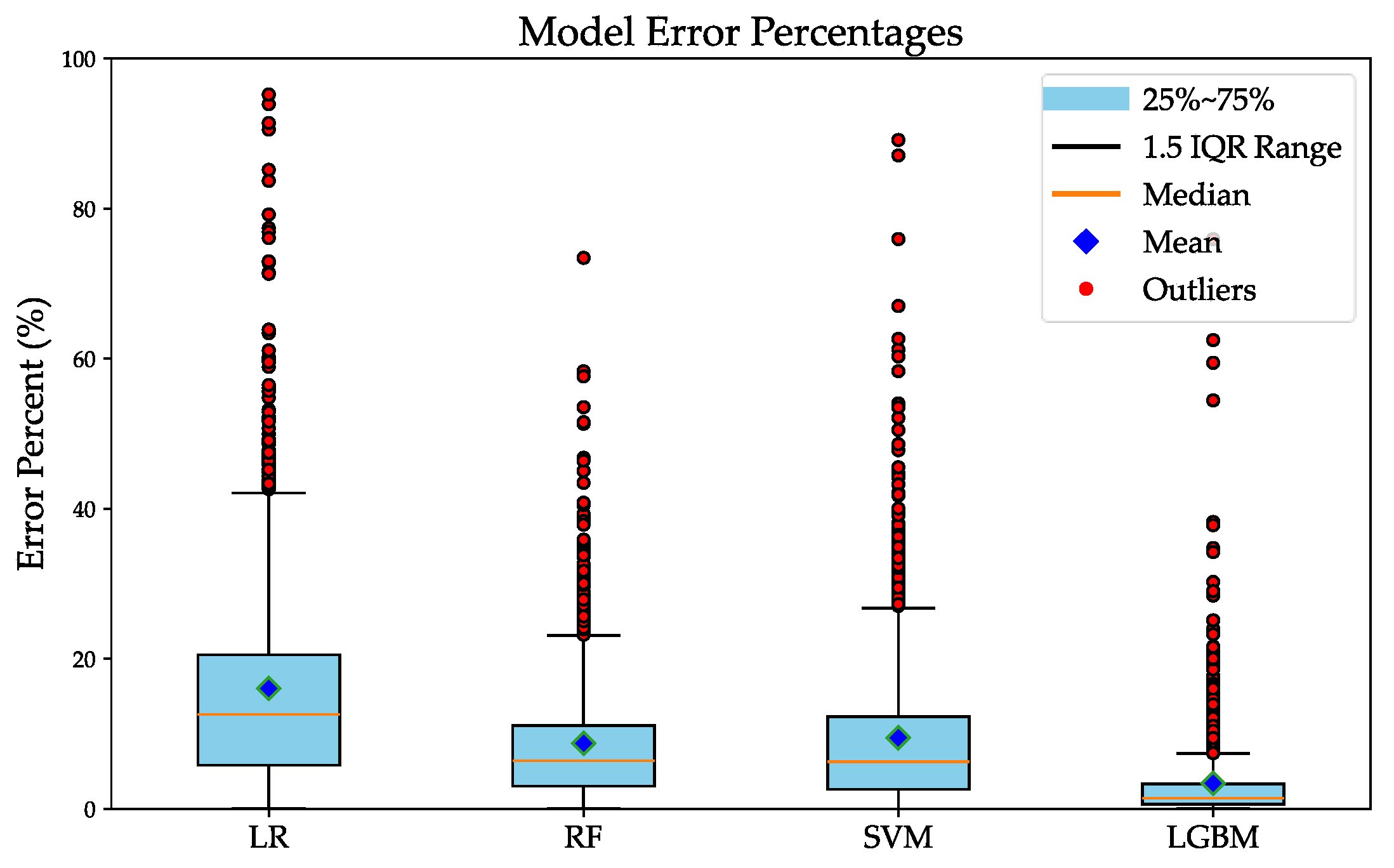
4.2. Different Algorithms’ Comparation
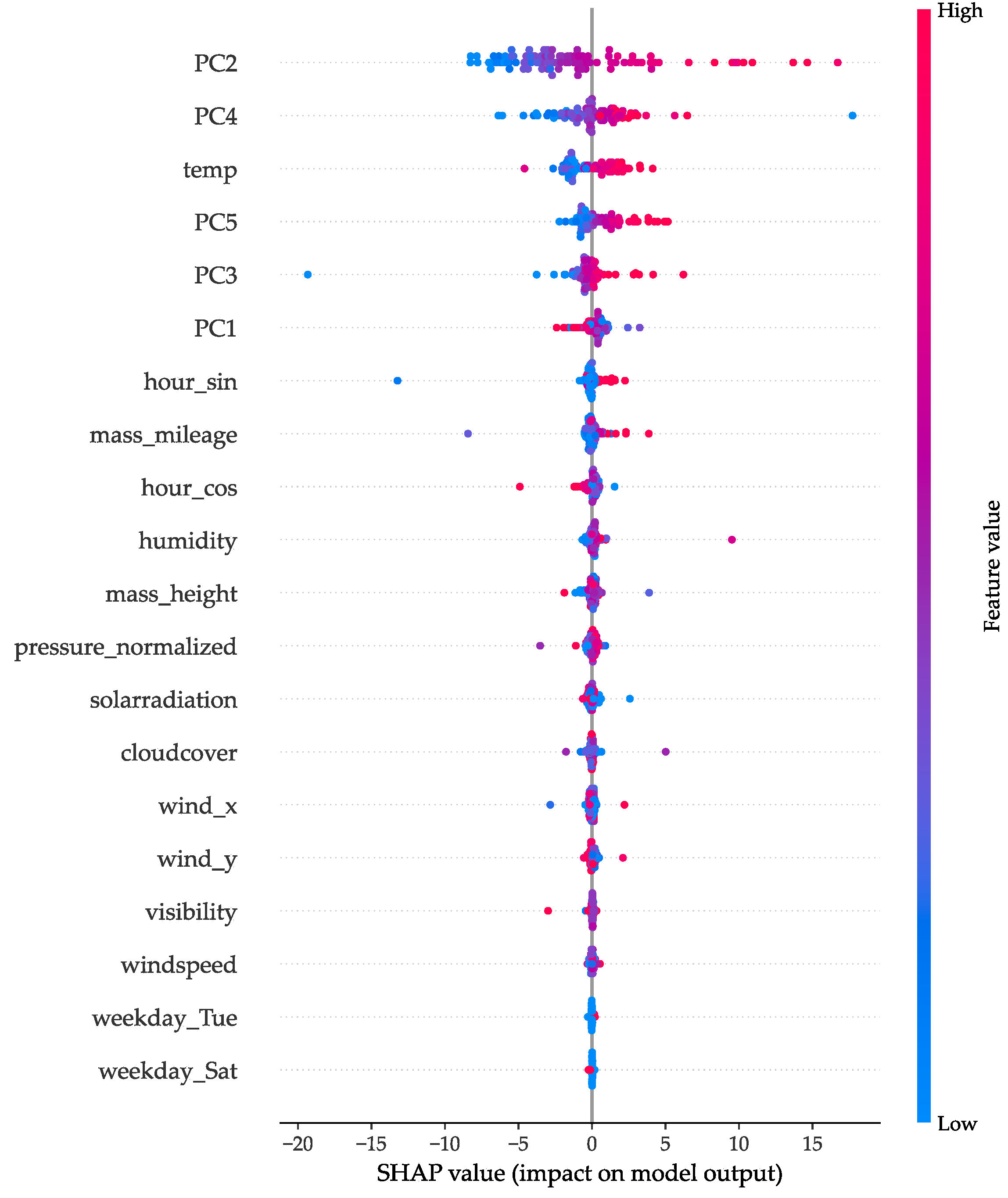
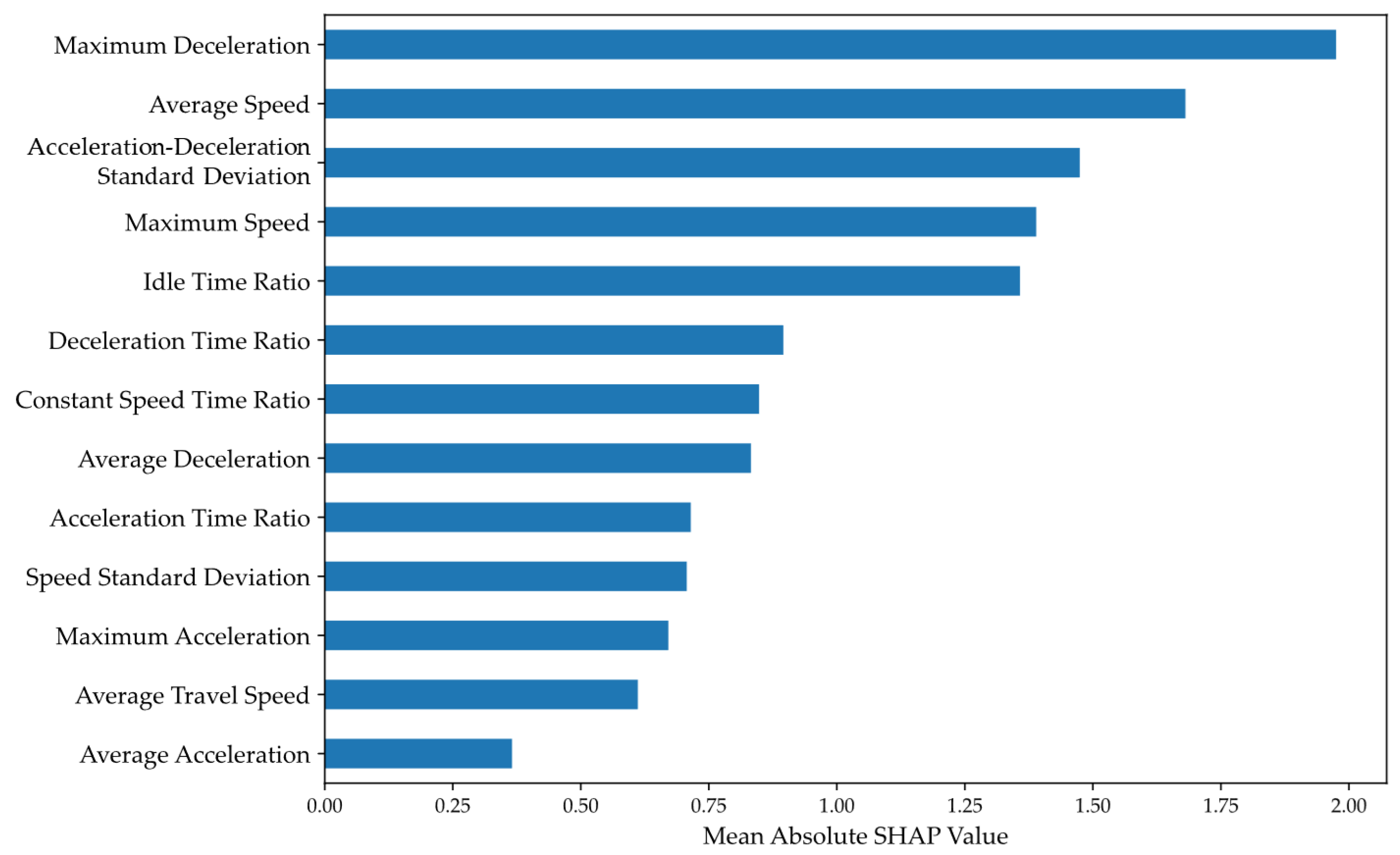
4.3. SHAP Analysis
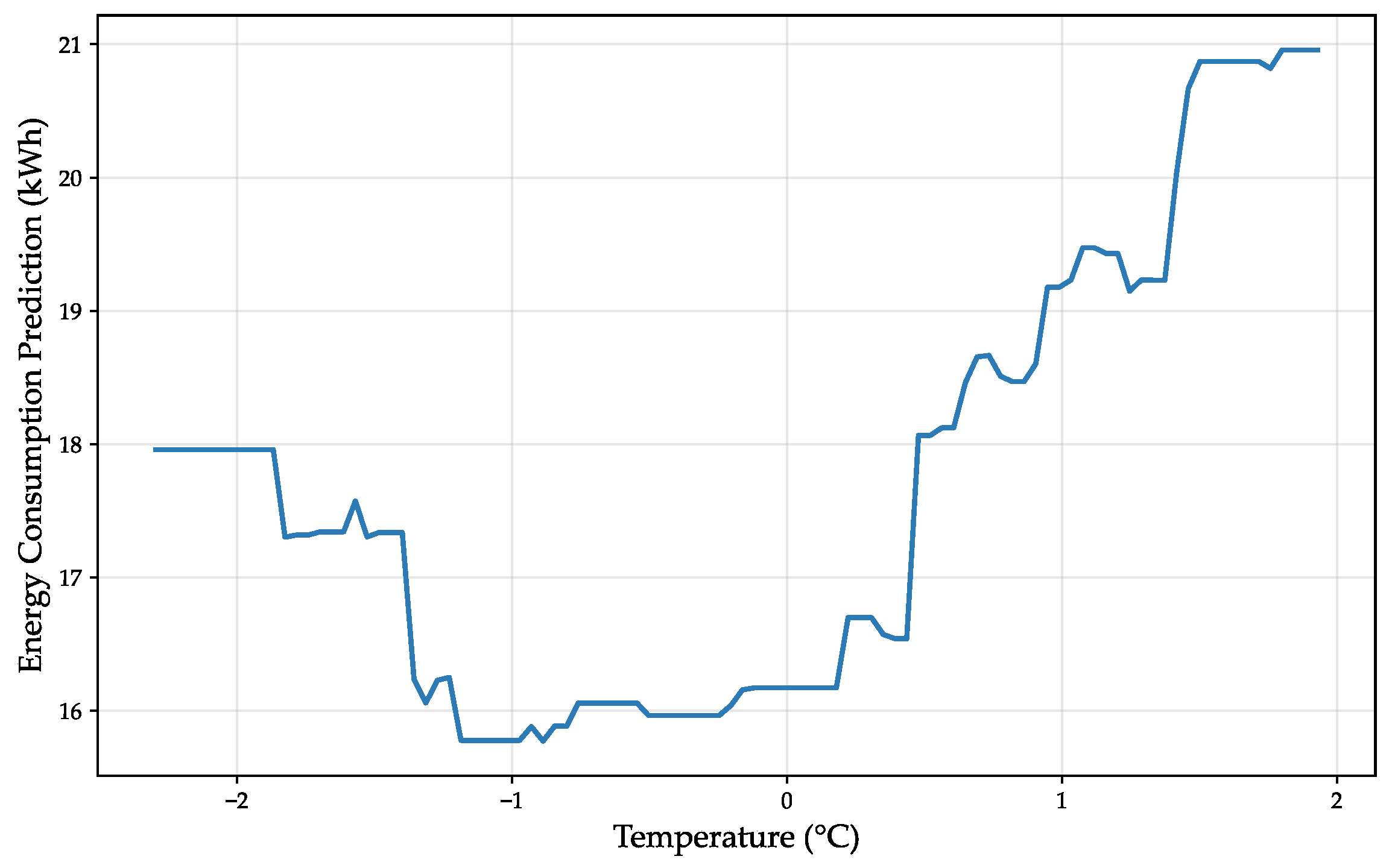
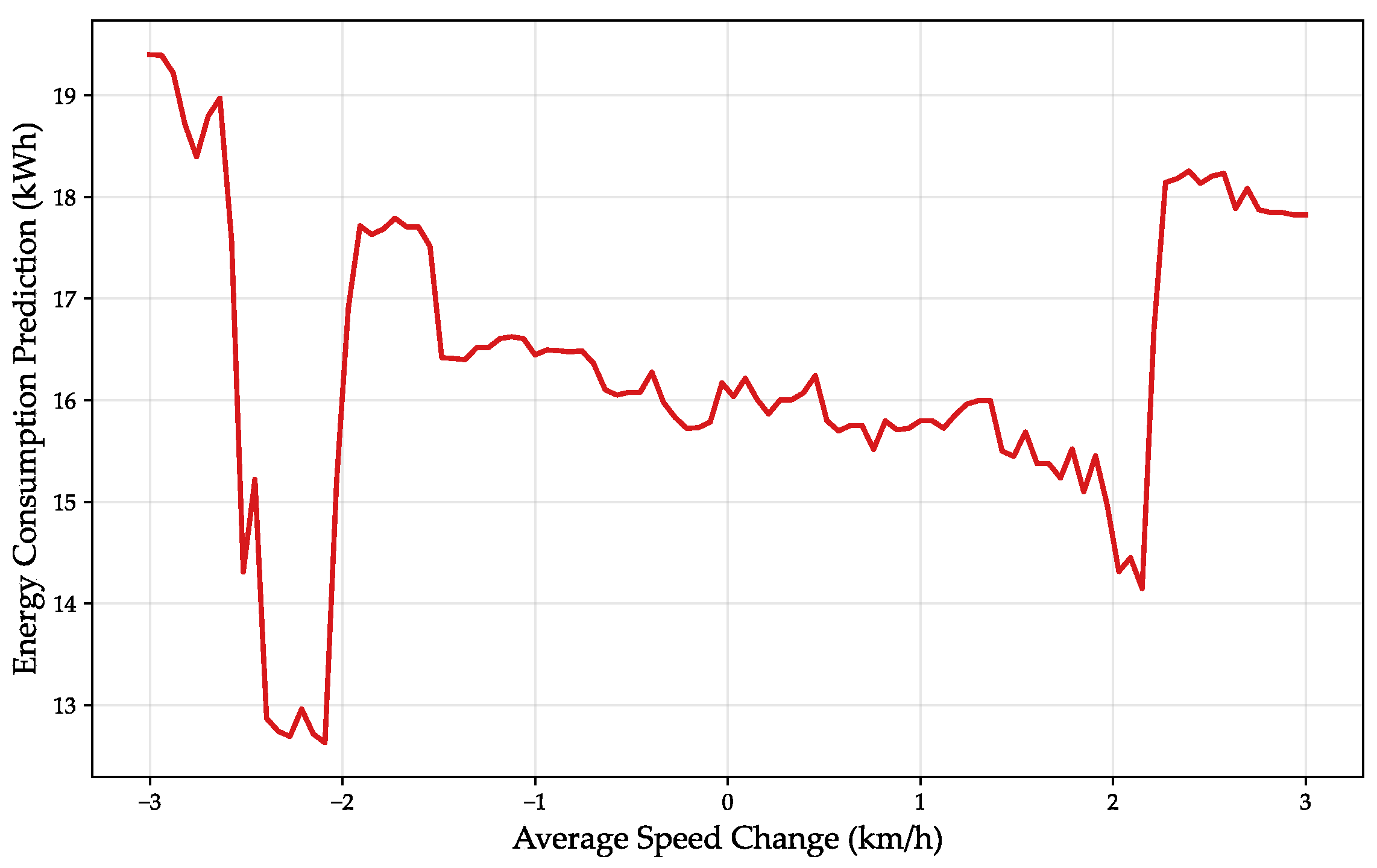
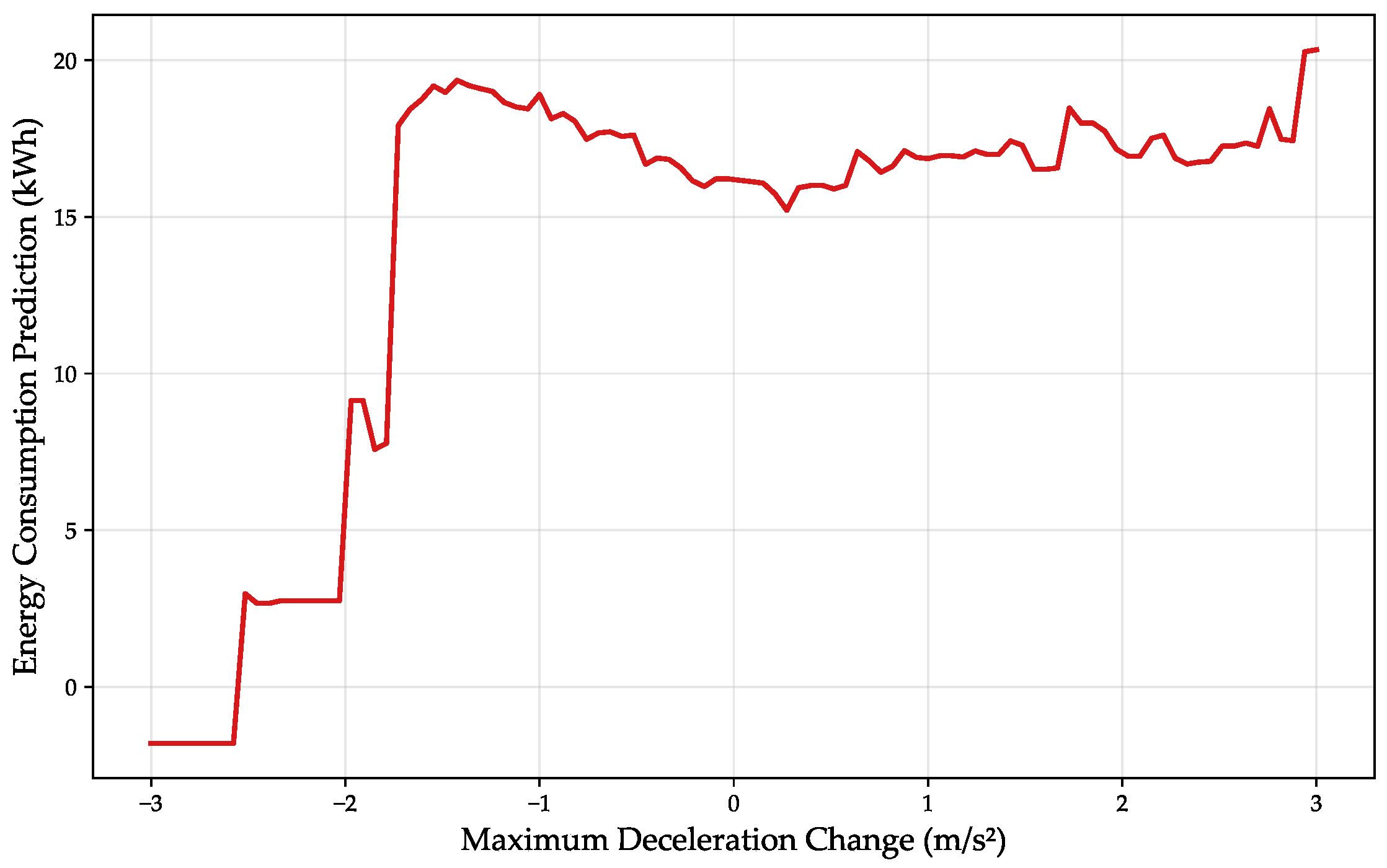
4.4. Sensitivity Analysis
- Impact of Average Speed;
- 2.
- Impact of Maximum Deceleration;
5. Conclusions
- Firstly, the traction modeling component lacks validation through actual experiments, which could further refine its accuracy.
- Secondly, the absence of detailed terrain data, such as slopes and curves, limits the model’s ability to fully capture the complexities of real-world routes, as it primarily focuses on relatively flat road segments.
- Thirdly, given that the studied vehicles were of similar condition and efficiency, the research may not have fully demonstrated the value of incorporating efficiency considerations under more diverse operational scenarios.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Manzolli, J.A.; Trovão, J.P.; Antunes, C.H. A review of electric bus vehicles research topics—Methods and trends. Renew. Sustain. Energy Rev. 2022, 159, 112211. [Google Scholar] [CrossRef]
- Gao, H.; Liu, K.; Yao, E. Formation and scheduling optimization of electric modular buses with station-based demand-responsive model. China J. Highw. Transp. 2024, 37, 24–36. [Google Scholar] [CrossRef]
- Gao, H.; Liu, K.; Wang, J.; Guo, F. Modular bus unit scheduling for an autonomous transit system under range and charging constraints. Appl. Sci. 2023, 13, 7661. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y.; Xing, X.; Zhan, Y.; Chan, W.K.V.; Tiwari, S. A data-driven system for cooperative-bus route planning based on generative adversarial network and metric learning. Ann. Oper. Res. 2024, 339, 427–453. [Google Scholar] [CrossRef]
- IEA. Global EV Outlook 2024; IEA: Paris, France, 2024. [Google Scholar]
- Wang, X.; Liu, W.; Zhang, L.; Zhang, M. CO2 emission reduction effect of electric bus based on energy chain in life cycle. J. Transp. Syst. Eng. Inf. Technol. 2019, 19, 19–25. [Google Scholar]
- He, J.; Yan, N.; Zhang, J.; Wang, T.; Chen, Y.Y.; Tang, T.Q. Battery electricity bus charging schedule considering bus journey’s energy consumption estimation. Transp. Res. Part D Transp. Environ. 2023, 115, 103587. [Google Scholar] [CrossRef]
- Berk Saner, C.; Trivedi, A.; Srinivasan, D. A multi-module modeling and optimization framework for integrated planning and operation of electric bus shuttle fleets. IEEE Trans. Intell. Transp. Syst. 2024, 25, 16910–16924. [Google Scholar] [CrossRef]
- Liu, X.; Qu, X.; Ma, X. Optimizing electric bus charging infrastructure considering power matching and seasonality. Transp. Res. Part D Transp. Environ. 2021, 100, 103057. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, W.; Bao, Y.; Gao, D.W.; Fan, S. Game theory-based peer-to-peer energy storage sharing for multiple bus charging stations: A real-time distributed cooperative framework. J. Energy Storage 2025, 109, 115148. [Google Scholar] [CrossRef]
- Liu, Z.; Ma, X.; Zhuo, S.; Liu, X. Optimizing shared charging services at sustainable bus charging hubs: A queue theory integration approach. Renew. Energy 2024, 237, 121860. [Google Scholar] [CrossRef]
- Liu, K.; Wang, J.; Yamamoto, T.; Morikawa, T. Exploring the interactive effects of ambient temperature and vehicle auxiliary loads on electric vehicle energy consumption. Appl. Energy 2018, 227, 324–331. [Google Scholar] [CrossRef]
- Gao, Y.; Guo, S.; Ren, J.; Zhao, Z.; Ehsan, A.; Zheng, Y. An electric bus power consumption model and optimization of charging scheduling concerning multi-external factors. Energies 2018, 11, 2060. [Google Scholar] [CrossRef]
- Liu, K.; Gao, H.; Liang, Z.; Zhao, M.; Li, C. Optimal charging strategy for large-scale electric buses considering resource constraints. Transp. Res. Part D Transp. Environ. 2021, 99, 103009. [Google Scholar] [CrossRef]
- Liu, K.; Gao, H.; Wang, Y.; Feng, T.; Li, C. Robust charging strategies for electric bus fleets under energy consumption uncertainty. Transp. Res. Part D Transp. Environ. 2022, 104, 103215. [Google Scholar] [CrossRef]
- Chikishev, E. Impact of natural and climatic conditions on electric energy consumption by an electric city bus. Transp. Res. Procedia 2021, 57, 113–121. [Google Scholar] [CrossRef]
- Li, M.; Yan, M.; He, H.; Peng, J. Data-driven predictive energy management and emission optimization for hybrid electric buses considering speed and passengers prediction. J. Clean. Prod. 2021, 304, 127139. [Google Scholar] [CrossRef]
- Liu, K.; Wang, J.; Yamamoto, T.; Morikawa, T. Modelling the multilevel structure and mixed effects of the factors influencing the energy consumption of electric vehicles. Appl. Energy 2016, 183, 1351–1360. [Google Scholar] [CrossRef]
- Galvin, R. Energy consumption effects of speed and acceleration in electric vehicles: Laboratory case studies and implications for drivers and policymakers. Transp. Res. Part D Transp. Environ. 2017, 53, 234–248. [Google Scholar] [CrossRef]
- Hjelkrem, O.A.; Lervåg, K.Y.; Babri, S.; Lu, C.; Södersten, C.J. A battery electric bus energy consumption model for strategic purposes: Validation of a proposed model structure with data from bus fleets in China and Norway. Transp. Res. Part D Transp. Environ. 2021, 94, 102804. [Google Scholar] [CrossRef]
- Ji, J.; Wang, L.; Bie, Y. Determination of GPS sampling interval for trip energy consumption estimation of electric buses: Analysis of real-world data. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 09544070241239384. [Google Scholar] [CrossRef]
- Czapla, Z.; Sierpiński, G. Driving and energy profiles of urban bus routes predicted for operation with battery electric buses. Energies 2023, 16, 5706. [Google Scholar] [CrossRef]
- Szilassy, P.Á.; Földes, D. Consumption estimation method for battery-electric buses using general line characteristics and temperature. Energy 2022, 261, 125080. [Google Scholar] [CrossRef]
- Saadon Al-Ogaili, A.; Ramasamy, A.; Juhana Tengku Hashim, T.; Al-Masri, A.N.; Hoon, Y.; Neamah Jebur, M.; Verayiah, R.; Marsadek, M. Estimation of the energy consumption of battery driven electric buses by integrating digital elevation and longitudinal dynamic models: Malaysia as a case study. Appl. Energy 2020, 280, 115873. [Google Scholar] [CrossRef]
- Li, X.; Wang, T.; Li, J.; Tian, Y.; Tian, J. Energy consumption estimation for electric buses based on a physical and data-driven fusion model. Energies 2022, 15, 4160. [Google Scholar] [CrossRef]
- Zhou, X.; An, K.; Ma, W. Data-driven approach for estimating energy consumption of electric buses under on-road operation conditions. J. Transp. Eng. Part A Syst. 2023, 149, 04023089. [Google Scholar] [CrossRef]
- Zhu, G.; Shi, M.; He, J. energy consumption prediction model for electric buses considering actual quantifiable features. J. Adv. Transp. 2024, 2024, 3058575. [Google Scholar] [CrossRef]
- Sennefelder, R.M.; Martín-Clemente, R.; González-Carvajal, R. Energy consumption prediction of electric city buses using multiple linear regression. Energies 2023, 16, 4365. [Google Scholar] [CrossRef]
- Blades, L.A.W.; Matthews, T.; McGrath, T.E.; Early, J.; Cunningham, G.; Harris, A. Predicting energy consumption of zero emission buses using route feature selection methods. Transp. Res. Part D Transp. Environ. 2024, 130, 104158. [Google Scholar] [CrossRef]
- Qin, W.; Wang, L.; Liu, Y.; Xu, C. Energy consumption estimation of the electric bus based on grey wolf optimization algorithm and support vector machine regression. Sustainability 2021, 13, 4689. [Google Scholar] [CrossRef]
- Hu, Z.; Zeng, X.; Feng, C.; Diao, H. optimizing charging and discharging at bus battery swap stations under varying environmental temperatures. Processes 2025, 13, 81. [Google Scholar] [CrossRef]
- Zeng, Z.; Wang, T.; Qu, X. En-route charge scheduling for an electric bus network: Stochasticity and real-world practice. Transp. Res. Part E Logist. Transp. Rev. 2024, 185, 103498. [Google Scholar] [CrossRef]
- Pan, Y.; Xi, Y.; Fang, W.; Liu, Y.; Zhang, Y.; Zhang, W. An eco-driving strategy for electric buses at signalized intersection with a bus stop based on energy consumption prediction. Energy 2025, 317, 134672. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, S.; Ye, B.; Ma, Y. A feature prediction-based method for energy consumption prediction of electric buses. Energy 2025, 314, 134345. [Google Scholar] [CrossRef]
- Xing, Y.; Li, Y.; Liu, W.; Li, W.; Meng, L. Operation energy consumption estimation method of electric bus based on CNN time series prediction. Math. Probl. Eng. 2022, 2022, 6904387. [Google Scholar] [CrossRef]
- Pamuła, T.; Pamuła, D. Prediction of electric buses energy consumption from trip parameters using deep learning. Energies 2022, 15, 1747. [Google Scholar] [CrossRef]
- Lin, M.; Chen, S.; Meng, J.; Wang, W.; Wu, J. Instantaneous energy consumption estimation for electric buses with a multi-model fusion method. IEEE Trans. Intell. Transp. Syst. 2025, 26, 371–381. [Google Scholar] [CrossRef]
- Dong, C.; Xiong, Z.; Li, N.; Yu, X.; Liang, M.; Zhang, C.; Li, Y.; Wang, H. A real-time prediction framework for energy consumption of electric buses using integrated machine learning algorithms. Transp. Res. Part E Logist. Transp. Rev. 2025, 194, 103884. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, J.; Lund, P.D.; Zhang, Y. Analysis of energy consumption for electric buses based on low-frequency real-world data. Transp. Res. Part D Transp. Environ. 2023, 122, 103857. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Y.; Sun, R. Data-driven estimation of energy consumption for electric bus under real-world driving conditions. Transp. Res. Part D Transp. Environ. 2021, 98, 102969. [Google Scholar] [CrossRef]
- Liu, Y.; Liang, H. A data-driven approach for electric bus energy consumption estimation. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17027–17038. [Google Scholar] [CrossRef]
- Smieszek, M.; Mateichyk, V.; Mosciszewski, J. The Influence of stops on the selected route of the city its on the energy efficiency of the public bus. Energies 2024, 17, 4179. [Google Scholar] [CrossRef]
- Yi, F.; Guo, W.; Gong, H.; Shen, Y.; Zhou, J.; Yu, W.; Lu, D.; Jia, C.; Zhang, C.; Gong, F. Research on speed planning and energy management strategy for fuel cell hybrid bus in green wave scenarios at traffic light intersections based on deep reinforcement learning. Sustainability 2024, 16, 11156. [Google Scholar] [CrossRef]
- Alarrouqi, R.A.; Ahmad, F.; Bayhan, S.; Al-Fagih, L. Electric buses in hot climates: Challenges, technologies, and the road ahead. IEEE Access 2024, 12, 55531–55550. [Google Scholar] [CrossRef]
- Alarrouqi, R.A.; Bayhan, S.; Al-Fagih, L. An assessment of the energy performance of battery-electric buses in hot environments. Sustain. Energy Grids Netw. 2024, 38, 101352. [Google Scholar] [CrossRef]
- Li, P.; Zhang, Y.; Zhang, Y.; Zhang, K.; Jiang, M. The effects of dynamic traffic conditions, route characteristics and environmental conditions on trip-based electricity consumption prediction of electric bus. Energy 2021, 218, 119437. [Google Scholar] [CrossRef]
- Abdelaty, H.; Mohamed, M. A Prediction model for battery electric bus energy consumption in transit. Energies 2021, 14, 2824. [Google Scholar] [CrossRef]
- Viana-Fons, J.D.; Payá, J. HVAC system operation, consumption and compressor size optimization in urban buses of Mediterranean cities. Energy 2024, 296, 131151. [Google Scholar] [CrossRef]
- Zhao, L.; Li, Y.; Li, S.; Ke, H. A frequency item mining based embedded feature selection algorithm and its application in energy consumption prediction of electric bus. Energy 2023, 271, 126999. [Google Scholar] [CrossRef]
- Li, P.; Zhang, Y.; Zhang, Y.; Zhang, Y.; Zhang, K. Prediction of electric bus energy consumption with stochastic speed profile generation modelling and data driven method based on real-world big data. Appl. Energy 2021, 298, 117204. [Google Scholar] [CrossRef]
- Corbet, S.; Larkin, C.; McCluskey, J. The influence of inclement weather on electric bus efficiency: Evidence from a developed European network. Case Stud. Transp. Policy 2023, 12, 100971. [Google Scholar] [CrossRef]
- Feng, N.; Yong, J.; Zhan, Z. A direct multiple shooting method to improve vehicle handling and stability for four hub-wheel-drive electric vehicle during regenerative braking. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 1047–1056. [Google Scholar] [CrossRef]
- Takeno, M.; Ogasawara, S.; Chiba, A.; Takemoto, M.; Hoshi, N. Power and efficiency measurements and design improvement of a 50 kW switched reluctance motor for hybrid electric vehicles. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 1495–1501. [Google Scholar]
- Roshandel, E.; Mahmoudi, A.; Kahourzade, S.; Yazdani, A.; Shafiullah, G.M. Losses in efficiency maps of electric vehicles: An overview. Energies 2021, 14, 7805. [Google Scholar] [CrossRef]
- Zhang, Z.; Ye, B.; Wang, S.; Ma, Y. Analysis and estimation of energy consumption of electric buses using real-world data. Transp. Res. Part D Transp. Environ. 2024, 126, 104017. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, S.; Lin, N.; Wang, Z.; Liu, P. State of health estimation of lithium-ion batteries in electric vehicles based on regional capacity and LGBM. Sustainability 2023, 15, 2052. [Google Scholar] [CrossRef]
- She, C.; Zhang, Z.; Liu, P.; Sun, F. Overview of the application of big data analysis technology in new energy vehicle industry: Based on operating big data of new energy vehicle. J. Mech. Eng. 2019, 55, 3–16. [Google Scholar]
- Li, F.; Min, Y.; Zhang, Y. Review of key technology research on the reliability of power lithium batteries based on big data. Energy Storage Sci. Technol. 2023, 12, 1981–1994. [Google Scholar]
- Li, S.; He, H.; Zhao, P.; Cheng, S. Data cleaning and restoring method for vehicle battery big data platform. Appl. Energy 2022, 320, 119292. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, Z.; Chen, Y.; Liu, P.; Wang, S.; Zhang, Z.; Dorrell, D.G. Modified relative entropy-based lithium-ion battery pack online short-circuit detection for electric vehicle. IEEE Trans. Transp. Electrif. 2022, 8, 1710–1723. [Google Scholar] [CrossRef]
- Hou, Y.; Zhang, Z.; Liu, P.; Song, C.; Wang, Z. Research on a novel data-driven aging estimation method for battery systems in real-world electric vehicles. Adv. Mech. Eng. 2021, 13, 16878140211027735. [Google Scholar] [CrossRef]
- Huo, Q.; Ma, Z.; Zhao, X.; Zhang, T.; Zhang, Y. Bayesian network based state-of-health estimation for battery on electric vehicle application and its validation through real-world data. IEEE Access 2021, 9, 11328–11341. [Google Scholar] [CrossRef]
- Li, S.; He, H.; Li, J. Big data driven lithium-ion battery modeling method based on SDAE-ELM algorithm and data pre-processing technology. Appl. Energy 2019, 242, 1259–1273. [Google Scholar] [CrossRef]
- Wang, T.; Jing, Z.; Zhang, S.; Qiu, C. Utilizing principal component analysis and hierarchical clustering to develop driving cycles: A case study in Zhenjiang. Sustainability 2023, 15, 4845. [Google Scholar] [CrossRef]
- Yu, H.; Liu, Y.; Zhang, H.; Li, J.; Liu, H. Impact of driving and driver’s operating characteristics on high fuel consumption set based on real-road driving data. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 238, 1455–1466. [Google Scholar] [CrossRef]
- Wang, W.; Gao, G.; Wang, Z.; Liang, Y. A Method for Constructing Automobile Operation Condition. J. Highw. Transp. Res. Dev. 2020, 37, 128–138. [Google Scholar] [CrossRef]
- Cao, Q.; Li, J.; Qu, D. Construction of Typical Driving Cycle for Passenger Cars in the City of Dalian. J. Shanghai Jiaotong Univ. 2018, 52, 1537–1542. [Google Scholar]
- Rahimi-Eichi, H.; Ojha, U.; Baronti, F.; Chow, M.-Y. Battery Management System: An Overview of Its Application in the Smart Grid and Electric Vehicles. IEEE Ind. Electron. Mag. 2013, 7, 4–16. [Google Scholar] [CrossRef]
- Zheng, F.; Jiang, J.; Sun, B.; Zhang, W.; Pecht, M. Temperature Dependent Power Capability Estimation of Lithium-Ion Batteries for Hybrid Electric Vehicles. Energy 2016, 113, 64–75. [Google Scholar] [CrossRef]
- Bianchi, E.L.; Polinder, H.; Bandyopadhyay, S. Energy consumption of electric powertrain architectures: A comparative study. In Proceedings of the 2017 19th European Conference on Power Electronics and Applications (EPE’17 ECCE Europe), Warsaw, Poland, 11–14 September 2017; pp. P.1–P.10. [Google Scholar]
- Lajunen, A.; Kalttonen, A. Investigation of thermal energy losses in the powertrain of an electric city bus. In Proceedings of the 2015 IEEE Transportation Electrification Conference and Expo (ITEC), Chennai, India, 27–29 August 2015; pp. 1–6. [Google Scholar]
- Moein Jahromi, M.; Heidary, H. Chapter 14—Automotive applications of PEM technology. In PEM Fuel Cells; Kaur, G., Ed.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 347–405. ISBN 978-0-12-823708-3. [Google Scholar]
- Meißner, M.; Massalski, L. Modeling the electrical power and energy consumption of automated guided vehicles to improve the energy efficiency of production systems. Int. J. Adv. Manuf. Technol. 2020, 110, 481–498. [Google Scholar] [CrossRef]
- Ji, J.; Bie, Y.; Zeng, Z.; Wang, L. Trip energy consumption estimation for electric buses. Commun. Transp. Res. 2022, 2, 100069. [Google Scholar] [CrossRef]
- Kamran, M. Chapter 10—Electric vehicles and smart grids. In Fundamentals of Smart Grid Systems; Kamran, M., Ed.; Academic Press: Cambridge, MA, USA, 2023; pp. 431–460. ISBN 978-0-323-99560-3. [Google Scholar]
- Yang, Y.; Gao, K.; Cui, S.; Xue, Y.; Najafi, A.; Andric, J. Data-driven rolling eco-speed optimization for autonomous vehicles. Front. Eng. Manag. 2024, 11, 620–632. [Google Scholar] [CrossRef]
- Ni, D. Chapter 20—Vehicle Modeling. In Traffic Flow Theory; Ni, D., Ed.; Butterworth-Heinemann: Oxford, UK, 2016; pp. 279–285. ISBN 978-0-12-804134-5. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A highly efficient gradient boosting decision tree. In Proceedings of the Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Newry, Ireland, 2017; Volume 30. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Hochachka, W.M.; Caruana, R.; Fink, D.; Munson, A.; Riedewald, M.; Sorokina, D.; Kelling, S. Data-mining discovery of pattern and process in ecological systems. J. Wildl. Manag. 2007, 71, 2427–2437. [Google Scholar] [CrossRef]
- Zhou, B.; Xu, J.; Han, F.; Yan, F.; Peng, S.; Li, Q.; Jiao, F. Pressure of different gases injected into large-scale coal matrix: Analysis of time–space dependence and prediction using light gradient boosting machine. Fuel 2020, 279, 118448. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, Y.; Han, Z.; Yang, Z. Ship target detection based on LightGBM algorithm. In Proceedings of the 2020 International Conference on Computer Information and Big Data Applications (CIBDA), Guiyang, China, 17–19 April 2020; pp. 425–429. [Google Scholar]
- Yin, L.; Ma, P.; Deng, Z. JLGBMLoc—A novel high-precision indoor localization method based on LightGBM. Sensors 2021, 21, 2722. [Google Scholar] [CrossRef]
- Liang, W.; Luo, S.; Zhao, G.; Wu, H. Predicting hard rock pillar stability using GBDT, XGBoost, and LightGBM algorithms. Mathematics 2020, 8, 765. [Google Scholar] [CrossRef]
- Massaoudi, M.; Refaat, S.S.; Chihi, I.; Trabelsi, M.; Oueslati, F.S.; Abu-Rub, H. A novel stacked generalization ensemble-based hybrid lgbm-xgb-mlp model for short-term load forecasting. Energy 2021, 214, 118874. [Google Scholar] [CrossRef]
- Gan, M.; Pan, S.; Chen, Y.; Cheng, C.; Pan, H.; Zhu, X. Application of the machine learning LightGBM model to the prediction of the water levels of the lower Columbia river. J. Mar. Sci. Eng. 2021, 9, 496. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, T. Application of improved LightGBM model in blood glucose prediction. Appl. Sci. 2020, 10, 3227. [Google Scholar] [CrossRef]
- Jabeur, S.B.; Gharib, C.; Mefteh-Wali, S.; Arfi, W.B. CatBoost model and artificial intelligence techniques for corporate failure prediction. Technol. Forecast. Soc. Change 2021, 166, 120658. [Google Scholar] [CrossRef]
- Fu, X.Y.; Mao, X.L.; Wu, H.W.; Lin, J.Y.; Ma, Z.Q.; Liu, Z.C.; Cai, Y.; Yan, L.L.; Sun, Y.; Ye, L.P.; et al. Development and validation of LightGBM algorithm for optimizing of helicobacter pylori antibody during the minimum living guarantee crowd based gastric cancer screening program in Taizhou, China. Prev. Med. 2023, 174, 107605. [Google Scholar] [CrossRef]
- Jiao, S.; Zou, Q. Identification of plant vacuole proteins by exploiting deep representation learning features. Comput. Struct. Biotechnol. J. 2022, 20, 2921–2927. [Google Scholar] [CrossRef] [PubMed]
- Svetnik, V.; Liaw, A.; Tong, C.; Wang, T. Application of breiman’s random forest to modeling structure-activity relationships of pharmaceutical molecules. In Proceedings of the Multiple Classifier Systems, Cagliari, Italy, 9–11 June 2004; Roli, F., Kittler, J., Windeatt, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 334–343. [Google Scholar]
- Frazier, P.I. A Tutorial on bayesian optimization. arXiv 2018, arXiv:1807.02811. [Google Scholar] [CrossRef]
- Morita, Y.; Rezaeiravesh, S.; Tabatabaei, N.; Vinuesa, R.; Fukagata, K.; Schlatter, P. Applying bayesian optimization with gaussian process regression to computational fluid dynamics problems. J. Comput. Phys. 2022, 449, 110788. [Google Scholar] [CrossRef]
- Microsoft Corporation Parameters Tuning. Available online: https://lightgbm.readthedocs.io/en/latest/Parameters-Tuning.html (accessed on 16 February 2025).
- Van Hoof, J.; Vanschoren, J. Hyperboost: Hyperparameter Optimization by Gradient Boosting surrogate models. arXiv 2021, arXiv:2101.02289. [Google Scholar] [CrossRef]
- Lundberg, S.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. arXiv 2017, arXiv:1705.07874. [Google Scholar] [CrossRef]
- Takeishi, N. Shapley values of reconstruction errors of pca for explaining anomaly detection. In Proceedings of the 2019 International Conference on Data Mining Workshops (ICDMW), Beijing, China, 8–9 November 2019; pp. 793–798. [Google Scholar]
- Zhong, L.; Zeng, Z.; Huang, Z.; Shi, X.; Bie, Y. Joint optimization of electric bus charging and energy storage system scheduling. Front. Eng. Manag. 2024, 11, 676–696. [Google Scholar] [CrossRef]
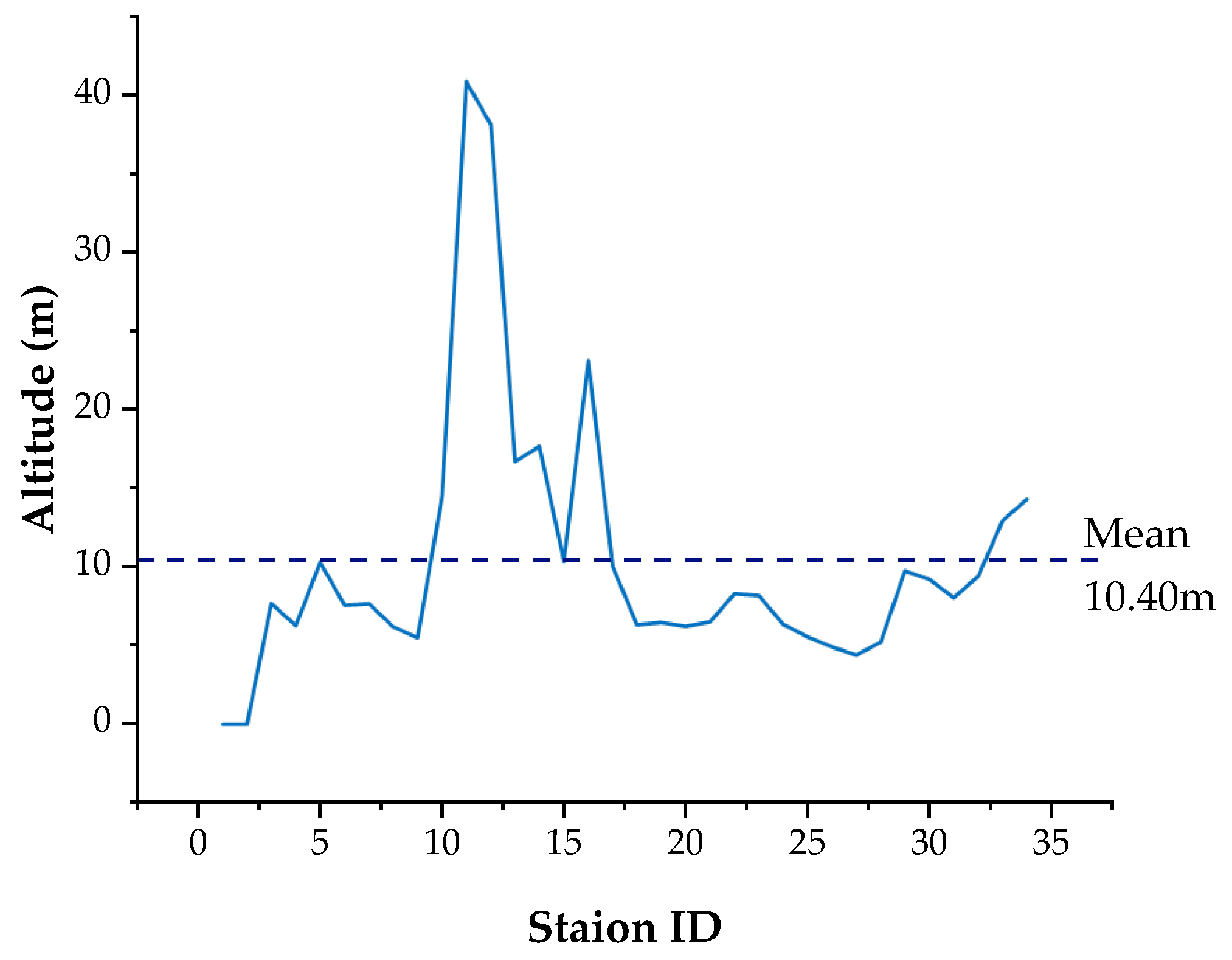
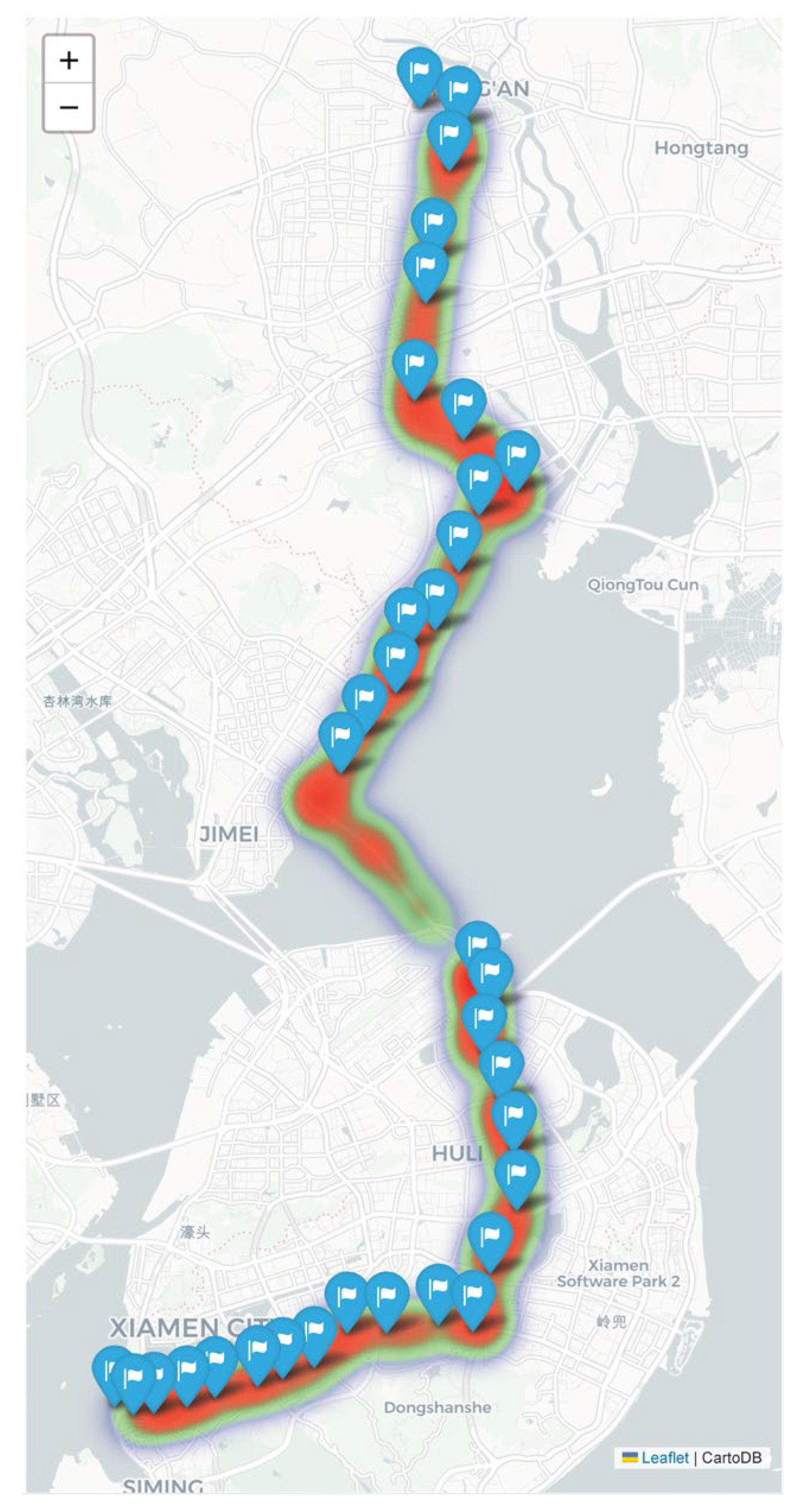
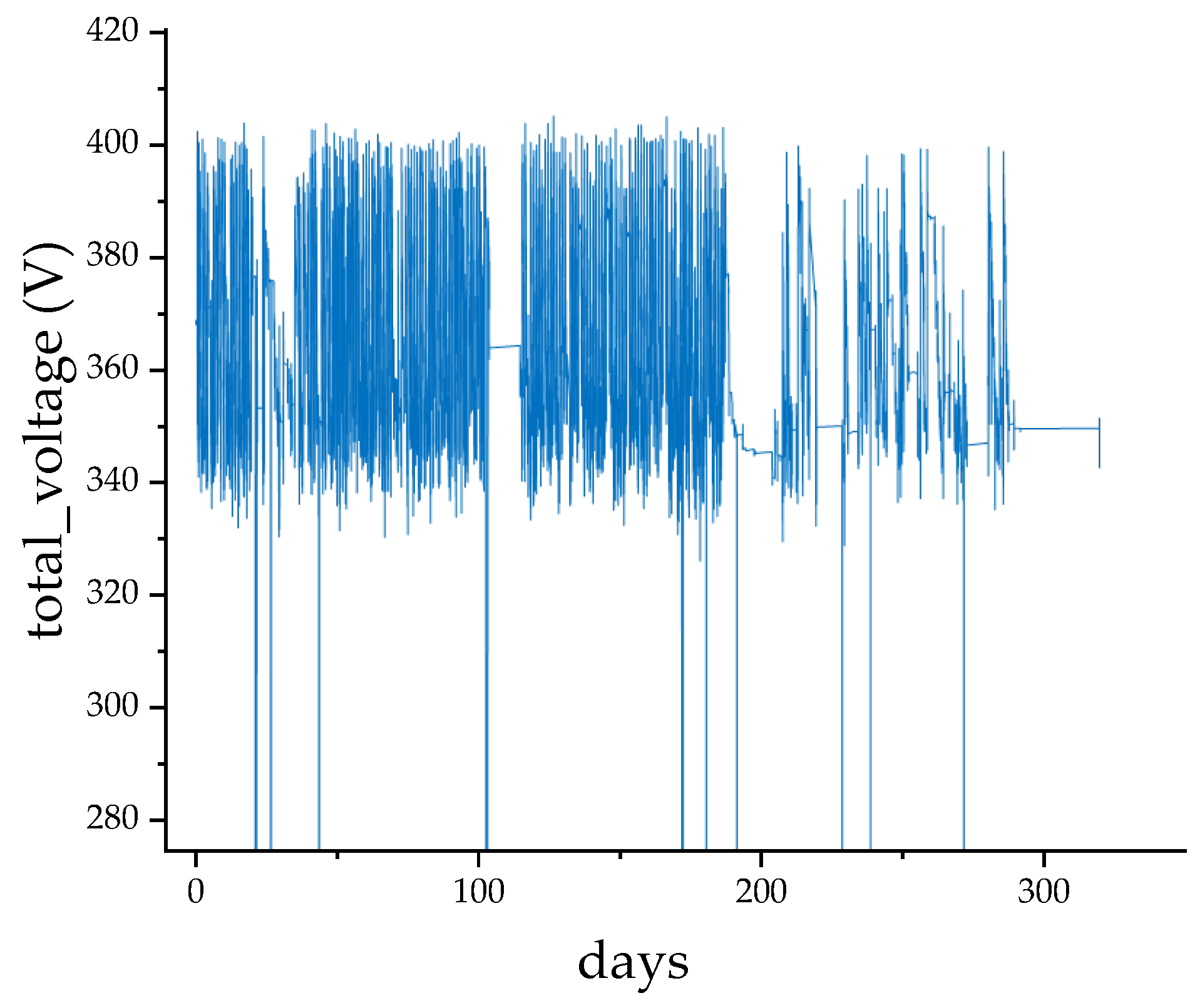
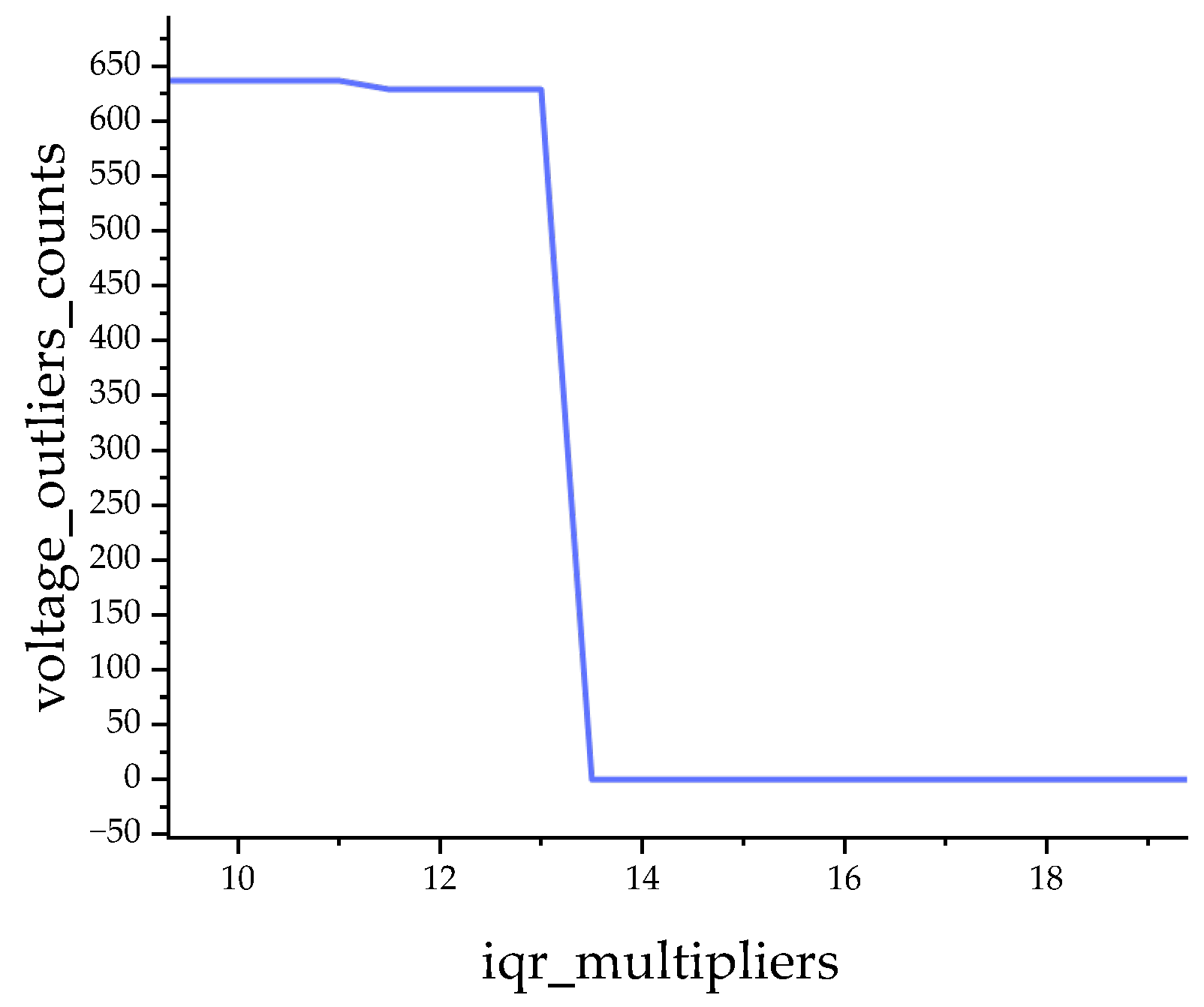




| Parameters | Value |
|---|---|
| Curb weight | 11,800 kg |
| Rim size | 22.5 inch |
| Maximum speed | 69 km/h |
| Vehicle dimensions | 10.5 × 2.5 × 3.07 m (L × W × H) |
| Battery chemistry | LiFePO4 (Lithium Iron Phosphate) |
| Battery system mass | 1728 kg |
| Battery system capacity | 250 kWh |
| Features | Description |
|---|---|
| vin | ID of bus |
| datetime | Time stamps in seconds |
| vehicle_status | Vehicle operating status (0/1) |
| charge_status | Charging status (0/1) |
| speed | Real-time speed (km/h) |
| mileage | Total accumulated mileage (km) |
| soc | State of charge (%) |
| total_voltage | Total battery system voltage (V) |
| total_current | Total battery system current (A) |
| motor_status | Motor operating status (0/1) |
| motor_speed | Motor speed (r/min) |
| motor_torque | Motor torque (Nm) |
| longitude | Geographic longitude (°) |
| latitude | Geographic latitude (°) |
| Characteristic | Symbol | Unit |
|---|---|---|
| Idle Time Ratio | % | |
| Acceleration Time Ratio | % | |
| Deceleration Time Ratio | % | |
| Constant Speed Time Ratio | % | |
| Average Speed | km/h | |
| Average Travel Speed | km/h | |
| Maximum Speed | km/h | |
| Speed Standard Deviation | km/h | |
| Maximum Acceleration | ||
| Maximum Deceleration | ||
| Average Acceleration | ||
| Average Deceleration | ||
| Acceleration-Deceleration Standard Deviation |
| Characteristic | PC1 | PC2 | PC3 | PC4 | PC5 |
|---|---|---|---|---|---|
| Idle Time Ratio | −0.079 | −0.418 | 0.438 | 0.045 | −0.361 |
| Acceleration Time Ratio | −0.234 | −0.061 | 0.051 | 0.258 | 0.280 |
| Deceleration Time Ratio | 0.538 | −0.052 | 0.021 | −0.547 | −0.119 |
| Constant Speed Time Ratio | 0.189 | −0.234 | −0.096 | 0.113 | −0.212 |
| Average Speed | 0.402 | −0.424 | −0.007 | −0.025 | 0.154 |
| Average Travel Speed | 0.252 | 0.154 | −0.407 | −0.013 | −0.001 |
| Maximum Speed | −0.066 | 0.274 | 0.373 | −0.555 | 0.206 |
| Speed Standard Deviation | −0.164 | 0.213 | −0.033 | 0.008 | 0.156 |
| Maximum Acceleration | −0.212 | 0.093 | 0.349 | −0.206 | 0.012 |
| Maximum Deceleration | −0.125 | 0.373 | −0.168 | −0.052 | −0.758 |
| Average Acceleration | −0.022 | 0.085 | 0.061 | −0.117 | 0.036 |
| Average Deceleration | −0.103 | −0.254 | 0.305 | 0.048 | −0.257 |
| Acceleration-Deceleration Standard Deviation | 0.535 | 0.470 | 0.494 | 0.500 | 0.000 |
| Parameter | Description | Unit |
|---|---|---|
| temp | Ambient temperature | °C |
| humidity | Relative humidity | % |
| precip | Precipitation (rain/snow) | mm |
| windspeed | Wind speed | m/s |
| winddir | Wind direction (raw 0–360° azimuth) | degrees |
| cloudcover | Cloud coverage | % |
| visibility | Horizontal visibility | km |
| solarradiation | Incident solar radiation | W/m2 |
| solarenergy | Cumulative solar energy | MJ/m2 |
| uvindex | Ultraviolet radiation intensity | Index (0–11+) |
| sealevelpressure | Sea-level atmospheric pressure | hPa |
| Method | Execution Time (s) | Test Set MAPE (%) |
|---|---|---|
| Default Params | N/A * | 9.37 |
| Grid Search | 29,376.28 | 4.72 |
| BO Search | 708.10 | 3.92 |
| Parameter | Value |
|---|---|
| learning_rate | 0.298 |
| max_depth | 13 |
| n_estimators | 633 |
| reg_alpha | 0.167 |
| subsample | 0.824 |
| Metric | Model | Test Set Performance |
|---|---|---|
| R2 | Linear Regression | 0.145 |
| Random Forest | 0.830 | |
| Support Vector Machine | 0.061 | |
| LightGBM | 0.995 | |
| MAPE (%) | Linear Regression | 16.07% |
| Random Forest | 8.74% | |
| Support Vector Machine | 9.46% | |
| LightGBM | 3.92% | |
| RMSE (kWh) | Linear Regression | 17.495 |
| Random Forest | 7.789 | |
| Support Vector Machine | 18.332 | |
| LightGBM | 1.398 |
| Parameter | Value |
|---|---|
| Temperature | 24.76 °C |
| Average Speed | 57.42 km/h |
| Maximum Deceleration | −1.38 m/s2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; He, J.; Wang, J.; Liu, K. Energy Consumption Prediction for Electric Buses Based on Traction Modeling and LightGBM. World Electr. Veh. J. 2025, 16, 159. https://doi.org/10.3390/wevj16030159
Zhao J, He J, Wang J, Liu K. Energy Consumption Prediction for Electric Buses Based on Traction Modeling and LightGBM. World Electric Vehicle Journal. 2025; 16(3):159. https://doi.org/10.3390/wevj16030159
Chicago/Turabian StyleZhao, Jian, Jin He, Jiangbo Wang, and Kai Liu. 2025. "Energy Consumption Prediction for Electric Buses Based on Traction Modeling and LightGBM" World Electric Vehicle Journal 16, no. 3: 159. https://doi.org/10.3390/wevj16030159
APA StyleZhao, J., He, J., Wang, J., & Liu, K. (2025). Energy Consumption Prediction for Electric Buses Based on Traction Modeling and LightGBM. World Electric Vehicle Journal, 16(3), 159. https://doi.org/10.3390/wevj16030159









