Generating Realistic Vehicle Trajectories Based on Vehicle–Vehicle and Vehicle–Map Interaction Pattern Learning
Abstract
1. Introduction
- The multihead self-attention module effectively captures intricate intervehicle dependencies by computing the influence each vehicle has on others. This allows the model to understand how each participant’s behavior is shaped by the surrounding vehicles. By modeling dynamic relationships such as mutual avoidance, following, and cooperation, this module significantly enhances the accuracy and reliability of trajectory generation.
- The multihead cross-attention module integrates map information with vehicle trajectories, addressing the challenge of incorporating static environmental constraints like road structures, landmark positions, and traffic rules. This module captures the geometric characteristics of the road, the impact of landmarks, and the influence of traffic rules, thereby improving the model’s adaptability in complex environments.
2. Related Work
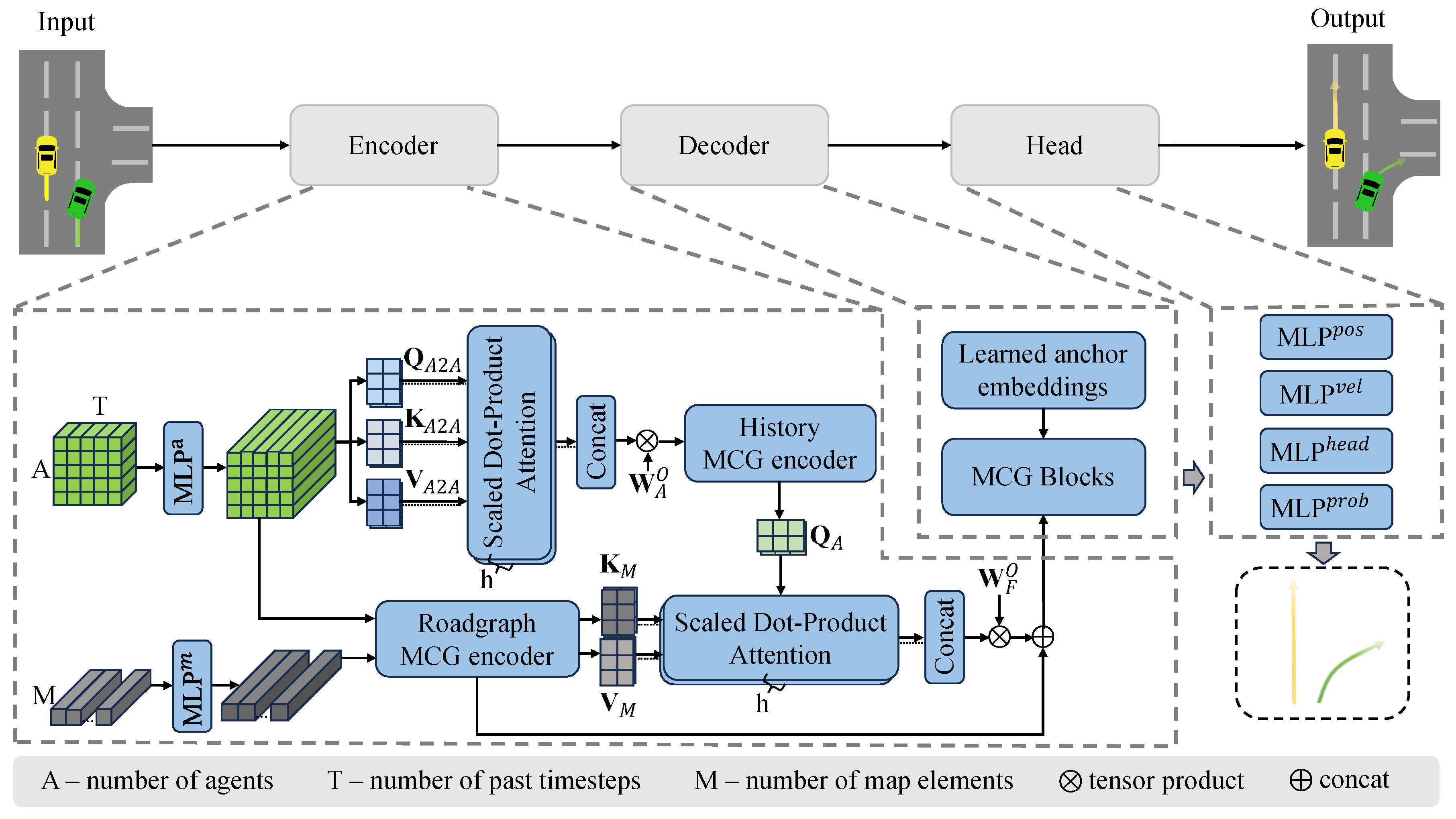
3. Our Method
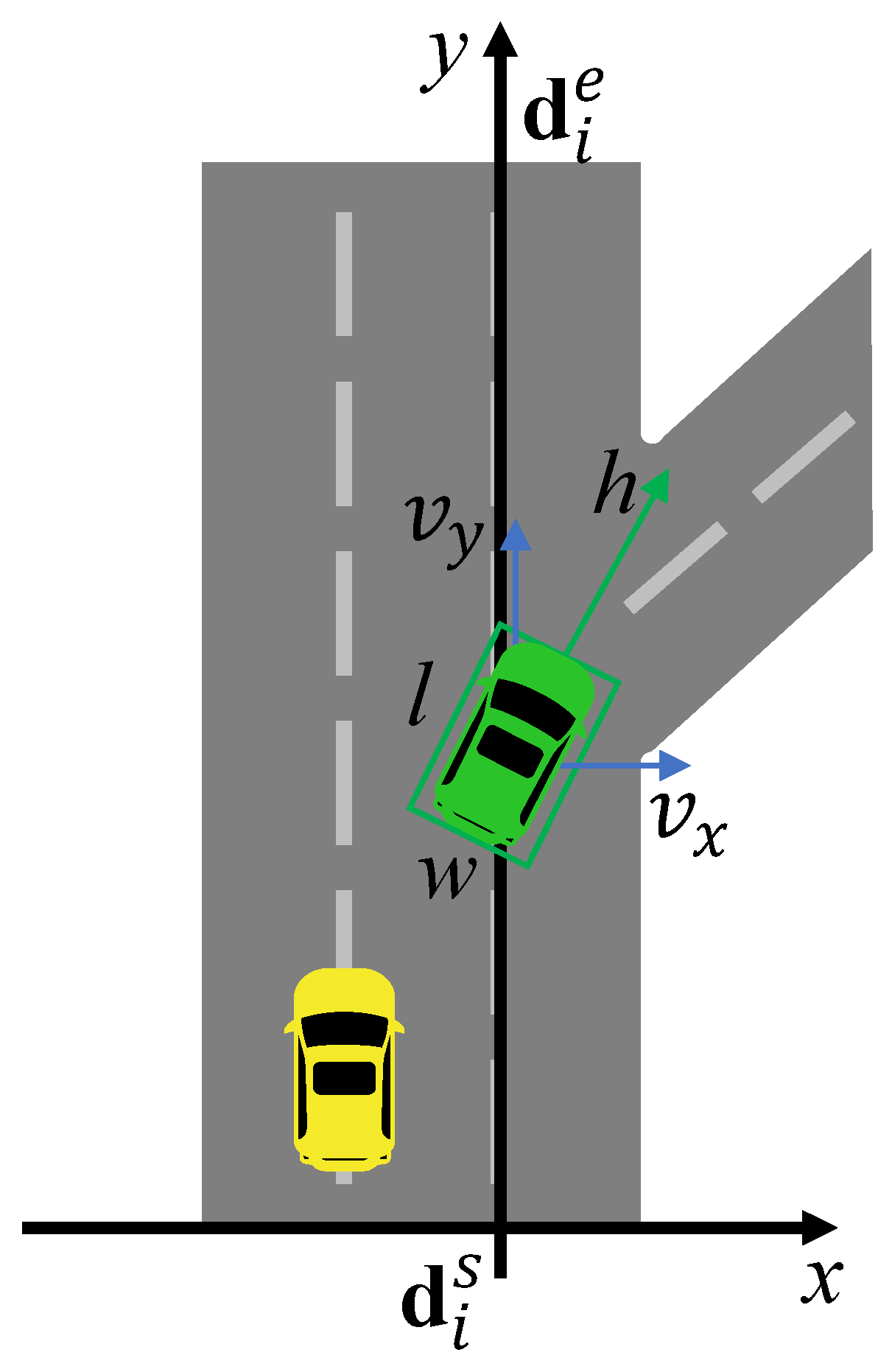
3.1. Multidimensional Vehicle Initial State Sampling
3.2. Encoder Module
3.3. Decoder Module
3.4. Head
3.5. Loss Function
4. Experiment
4.1. Datasets and Experimental Setting
4.2. Evaluation Metrics
- Average Displacement Error (ADE): The average Euclidean distance (in meters) between the predicted trajectory and the ground-truth trajectory across all time points.
- Final Displacement Error (FDE): The Euclidean distance (in meters) between the predicted trajectory’s final time point and the ground-truth trajectory’s final time point.
- Minimum Average Displacement Error (minADE): The average L2 distance (in meters) between the best forecasted trajectory and the ground truth. The best here refers to the trajectory that has the minimum endpoint error.
- Minimum Final Displacement Error (minFDE): The L2 distance (in meters) between the endpoint of the best forecasted trajectory and the ground truth. The best here refers to the trajectory that has the minimum endpoint error.
- Miss Rate (MR): The number of scenarios where none of the forecasted trajectories are within 2.0 m of the ground truth according to endpoint error.
4.3. Results and Discussion
4.3.1. Hyperparameter Adjustment
4.3.2. Quantitative Analysis of Trajectory Generation
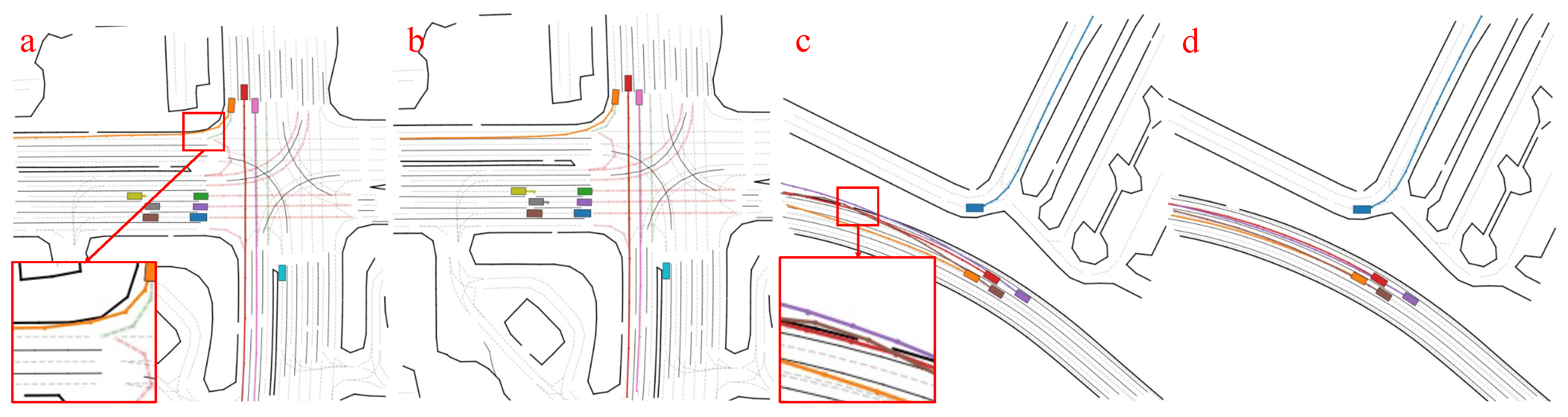
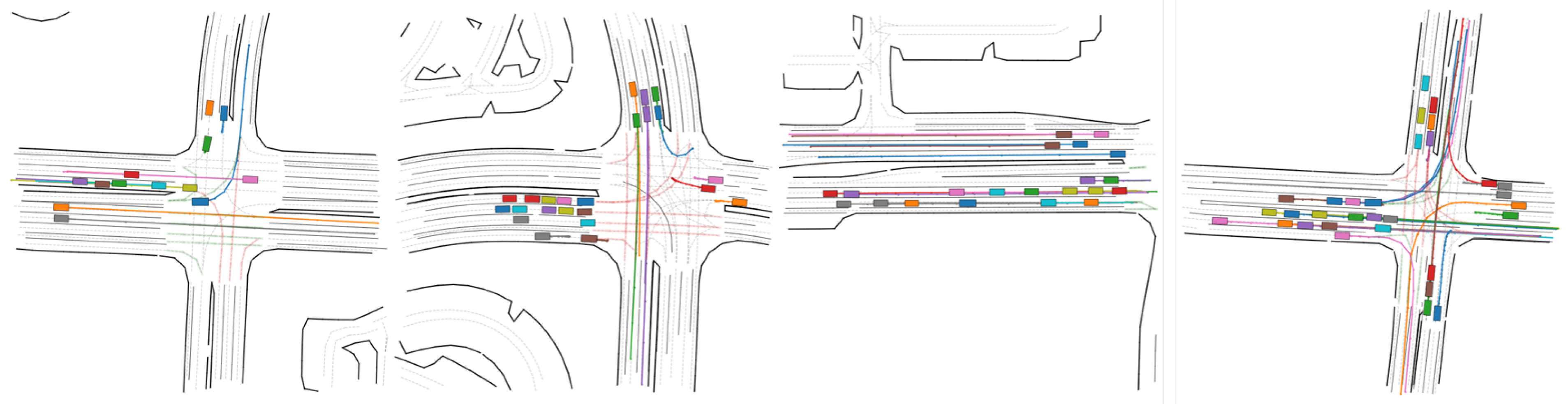
4.3.3. Qualitative Analysis of Trajectory Generation
4.3.4. Trajectory Prediction Analysis
4.3.5. Ablation Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dosovitskiy, A.; Ros, G.; Codevilla, F.; Lopez, A.; Koltun, V. CARLA: An open urban driving simulator. In Proceedings of the Conference on Robot Learning, PMLR, Mountain View, CA, USA, 13–15 November 2017; pp. 1–16. [Google Scholar]
- Ming, Z.; Jun, L. Smarts: Scalable multi-agent reinforcement learning training school for autonomous driving. arXiv 2020, arXiv:2010.09776. [Google Scholar]
- Lopez, P.A.; Behrisch, M.; Bieker-Walz, L.; Erdmann, J.; Flötteröd, Y.P.; Hilbrich, R.; Lücken, L.; Rummel, J.; Wagner, P.; Wießner, E. Microscopic traffic simulation using sumo. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), IEEE, Maui, HI, USA, 4–7 November 2018; pp. 2575–2582. [Google Scholar] [CrossRef]
- Waymo LLC. Waymo Open Dataset: An Autonomous Driving Dataset. Available online: https://waymo.com/open (accessed on 26 February 2025).
- Feng, L.; Li, Q.; Peng, Z.; Tan, S.; Zhou, B. Trafficgen: Learning to generate diverse and realistic traffic scenarios. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), IEEE, London, UK, 29 May–2 June 2023; pp. 3567–3575. [Google Scholar] [CrossRef]
- Chao, Q.; Bi, H.; Li, W.; Mao, T.; Wang, Z.; Lin, M.C.; Deng, Z. A Survey on Visual Traffic Simulation: Models, Evaluations, and Applications in Autonomous Driving. Comput. Graph. Forum 2020, 39, 287–308. [Google Scholar] [CrossRef]
- Bergamini, L.; Ye, Y.; Scheel, O.; Chen, L.; Hu, C.; Del Pero, L.; Osiński, B.; Grimmett, H.; Ondruska, P. Simnet: Learning reactive self-driving simulations from real-world observations. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), IEEE, Xi’an, China, 30 May–5 June 2021; pp. 5119–5125. [Google Scholar] [CrossRef]
- Chang, M.F.; Lambert, J.; Sangkloy, P.; Singh, J.; Bak, S.; Hartnett, A.; Wang, D.; Carr, P.; Lucey, S.; Ramanan, D.; et al. Argoverse: 3d tracking and forecasting with rich maps. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8748–8757. [Google Scholar]
- Pérez, J.; Godoy, J.; Villagrá, J.; Onieva, E. Trajectory generator for autonomous vehicles in urban environments. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, IEEE, Karlsruhe, Germany, 6–10 May 2013; pp. 409–414. [Google Scholar] [CrossRef]
- Uhrmacher, A.M.; Weyns, D. Multi-Agent Systems: Simulation and Applications; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Gao, Y.; Cao, P.; Yang, A. Realistic Trajectory Generation Using Dynamic Deduction for Stochastic Microscopic Traffic Flow Model; SAE Technical Paper 2024-01-7045; SAE International: Warrendale, PA, USA, 2024. [Google Scholar] [CrossRef]
- Mullakkal-Babu, F.A.; Wang, M.; van Arem, B.; Shyrokau, B.; Happee, R. A hybrid submicroscopic-microscopic traffic flow simulation framework. IEEE Trans. Intell. Transp. Syst. 2020, 22, 3430–3443. [Google Scholar] [CrossRef]
- Dobrilko, O.; Bublil, A. Leveraging SUMO for Real-World Traffic Optimization: A Comprehensive Approach. SUMO Conf. Proc. 2024, 5, 179–194. [Google Scholar] [CrossRef]
- Wheeler, T.A.; Kochenderfer, M.J.; Robbel, P. Initial scene configurations for highway traffic propagation. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems, IEEE, Gran Canaria, Spain, 15–18 September 2015; pp. 279–284. [Google Scholar]
- Wheeler, T.A.; Kochenderfer, M.J. Factor graph scene distributions for automotive safety analysis. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), IEEE, Rio de Janeiro, Brazil, 1–4 November 2016; pp. 1035–1040. [Google Scholar]
- Jesenski, S.; Stellet, J.E.; Schiegg, F.; Zöllner, J.M. Generation of scenes in intersections for the validation of highly automated driving functions. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV), IEEE, Paris, France, 9–12 June 2019; pp. 502–509. [Google Scholar]
- Fang, J.; Zhou, D.; Yan, F.; Zhao, T.; Zhang, F.; Ma, Y.; Wang, L.; Yang, R. Augmented LiDAR simulator for autonomous driving. IEEE Robot. Autom. Lett. 2020, 5, 1931–1938. [Google Scholar] [CrossRef]
- Caesar, H.; Bankiti, V.; Lang, A.H.; Vora, S.; Liong, V.E.; Xu, Q.; Krishnan, A.; Pan, Y.; Baldan, G.; Beijbom, O. Nuscenes: A multimodal dataset for autonomous driving. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11621–11631. [Google Scholar]
- Gao, J.; Sun, C.; Zhao, H.; Shen, Y.; Anguelov, D.; Li, C.; Schmid, C. Vectornet: Encoding hd maps and agent dynamics from vectorized representation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11525–11533. [Google Scholar]
- Suo, S.; Regalado, S.; Casas, S.; Urtasun, R. Trafficsim: Learning to simulate realistic multi-agent behaviors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 10400–10409. [Google Scholar]
- Ngiam, J.; Caine, B.; Vasudevan, V.; Zhang, Z.; Chiang, H.T.L.; Ling, J.; Roelofs, R.; Bewley, A.; Liu, C.; Venugopal, A.; et al. Scene transformer: A unified architecture for predicting multiple agent trajectories. arXiv 2021, arXiv:2106.08417. [Google Scholar]
- Rempe, D.; Philion, J.; Guibas, L.J.; Fidler, S.; Litany, O. Generating useful accident-prone driving scenarios via a learned traffic prior. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 17305–17315. [Google Scholar]
- Igl, M.; Kim, D.; Kuefler, A.; Mougin, P.; Shah, P.; Shiarlis, K.; Anguelov, D.; Palatucci, M.; White, B.; Whiteson, S. Symphony: Learning realistic and diverse agents for autonomous driving simulation. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), IEEE, Philadelphia, PA, USA, 23–27 May 2022; pp. 2445–2451. [Google Scholar]
- Zhong, Z.; Rempe, D.; Xu, D.; Chen, Y.; Veer, S.; Che, T.; Ray, B.; Pavone, M. Guided conditional diffusion for controllable traffic simulation. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), IEEE, London, UK, 29 May–2 June 2023; pp. 3560–3566. [Google Scholar]
- Jiang, C.; Cornman, A.; Park, C.; Sapp, B.; Zhou, Y.; Anguelov, D. Motiondiffuser: Controllable multi-agent motion prediction using diffusion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 9644–9653. [Google Scholar]
- Philion, J.; Peng, X.B.; Fidler, S. Trajeglish: Traffic Modeling as Next-Token Prediction. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Varadarajan, B.; Hefny, A.; Srivastava, A.; Refaat, K.S.; Nayakanti, N.; Cornman, A.; Chen, K.; Douillard, B.; Lam, C.P.; Anguelov, D.; et al. Multipath++: Efficient information fusion and trajectory aggregation for behavior prediction. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), IEEE, Philadelphia, PA, USA, 23–27 May 2022; pp. 7814–7821. [Google Scholar]
- Liang, M.; Yang, B.; Hu, R.; Chen, Y.; Liao, R.; Feng, S.; Urtasun, R. Learning lane graph representations for motion forecasting. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part II 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 541–556. [Google Scholar]
- Wang, M.; Zhu, X.; Yu, C.; Li, W.; Ma, Y.; Jin, R.; Ren, X.; Ren, D.; Wang, M.; Yang, W. Ganet: Goal area network for motion forecasting. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), IEEE, London, UK, 29 May–2 June 2023; pp. 1609–1615. [Google Scholar]
- Gao, X.; Jia, X.; Li, Y.; Xiong, H. Dynamic scenario representation learning for motion forecasting with heterogeneous graph convolutional recurrent networks. IEEE Robot. Autom. Lett. 2023, 8, 2946–2953. [Google Scholar] [CrossRef]
| Number of Self-Attention Heads | Number of Cross-Attention Heads | ADE↓ | FDE↓ |
|---|---|---|---|
| 4 | 32 | 1.186 | 3.800 |
| 4 | 64 | 1.126 | 3.628 |
| 8 | 32 | 1.319 | 4.212 |
| 8 | 64 | 1.202 | 3.896 |
| Trafficgen | The Proposed | Improvement | |
|---|---|---|---|
| ADE↓ | 1.55 | 1.14 | 26% |
| FDE↓ | 4.62 | 3.67 | 20% |
| Metric | Trafficgen | The Proposed | ||||
|---|---|---|---|---|---|---|
| 2 | 4 | 10 | 2 | 4 | 10 | |
| ADE↓ | 1.515 | 1.458 | 1.594 | 1.186 | 1.324 | 1.336 |
| FDE↓ | 4.782 | 4.489 | 5.056 | 3.800 | 4.291 | 4.305 |
| minADE↓ | 0.998 | 0.982 | 1.014 | 0.869 | 0.904 | 0.915 |
| minFDE↓ | 2.109 | 2.056 | 2.141 | 1.846 | 1.907 | 1.932 |
| MR↓ | 0.879 | 0.884 | 0.870 | 0.870 | 0.872 | 0.869 |
| Model | minADE↓ | minFDE↓ | MR↓ |
|---|---|---|---|
| LaneGCN[28] | 0.87 | 1.36 | 0.16 |
| Multipath++ [27] | 0.79 | 1.21 | 0.13 |
| GANet[29] | 0.81 | 1.16 | 0.12 |
| HeteroGCN[30] | 0.79 | 1.16 | 0.12 |
| The proposed | 0.75 | 1.19 | 0.11 |
| Model | ADE↓ | FDE↓ |
|---|---|---|
| Baseline (Trafficgen) | 1.55 | 4.62 |
| Baseline with self-attention | 1.50 | 4.54 |
| Baseline with cross-attention | 1.42 | 4.58 |
| Baseline with both | 1.14 | 3.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; Yu, B.; Wang, J.; Zhu, X.; Zhang, H.; Yu, C.; Hua, C. Generating Realistic Vehicle Trajectories Based on Vehicle–Vehicle and Vehicle–Map Interaction Pattern Learning. World Electr. Veh. J. 2025, 16, 145. https://doi.org/10.3390/wevj16030145
Li P, Yu B, Wang J, Zhu X, Zhang H, Yu C, Hua C. Generating Realistic Vehicle Trajectories Based on Vehicle–Vehicle and Vehicle–Map Interaction Pattern Learning. World Electric Vehicle Journal. 2025; 16(3):145. https://doi.org/10.3390/wevj16030145
Chicago/Turabian StyleLi, Peng, Biao Yu, Jun Wang, Xiaojun Zhu, Hui Zhang, Chennian Yu, and Chen Hua. 2025. "Generating Realistic Vehicle Trajectories Based on Vehicle–Vehicle and Vehicle–Map Interaction Pattern Learning" World Electric Vehicle Journal 16, no. 3: 145. https://doi.org/10.3390/wevj16030145
APA StyleLi, P., Yu, B., Wang, J., Zhu, X., Zhang, H., Yu, C., & Hua, C. (2025). Generating Realistic Vehicle Trajectories Based on Vehicle–Vehicle and Vehicle–Map Interaction Pattern Learning. World Electric Vehicle Journal, 16(3), 145. https://doi.org/10.3390/wevj16030145








