A Communication Scheme with Privacy Protection in V2V Power Transaction Based on Linkable Ring Signature
Abstract
1. Introduction
1.1. Related Work
1.2. Contributions
1.3. Roadmap
2. Preliminaries
2.1. Linkable Ring Signature
2.2. Consortium Blockchain
2.3. Stealth Address
2.4. Related Difficult Problems
3. Scheme Design
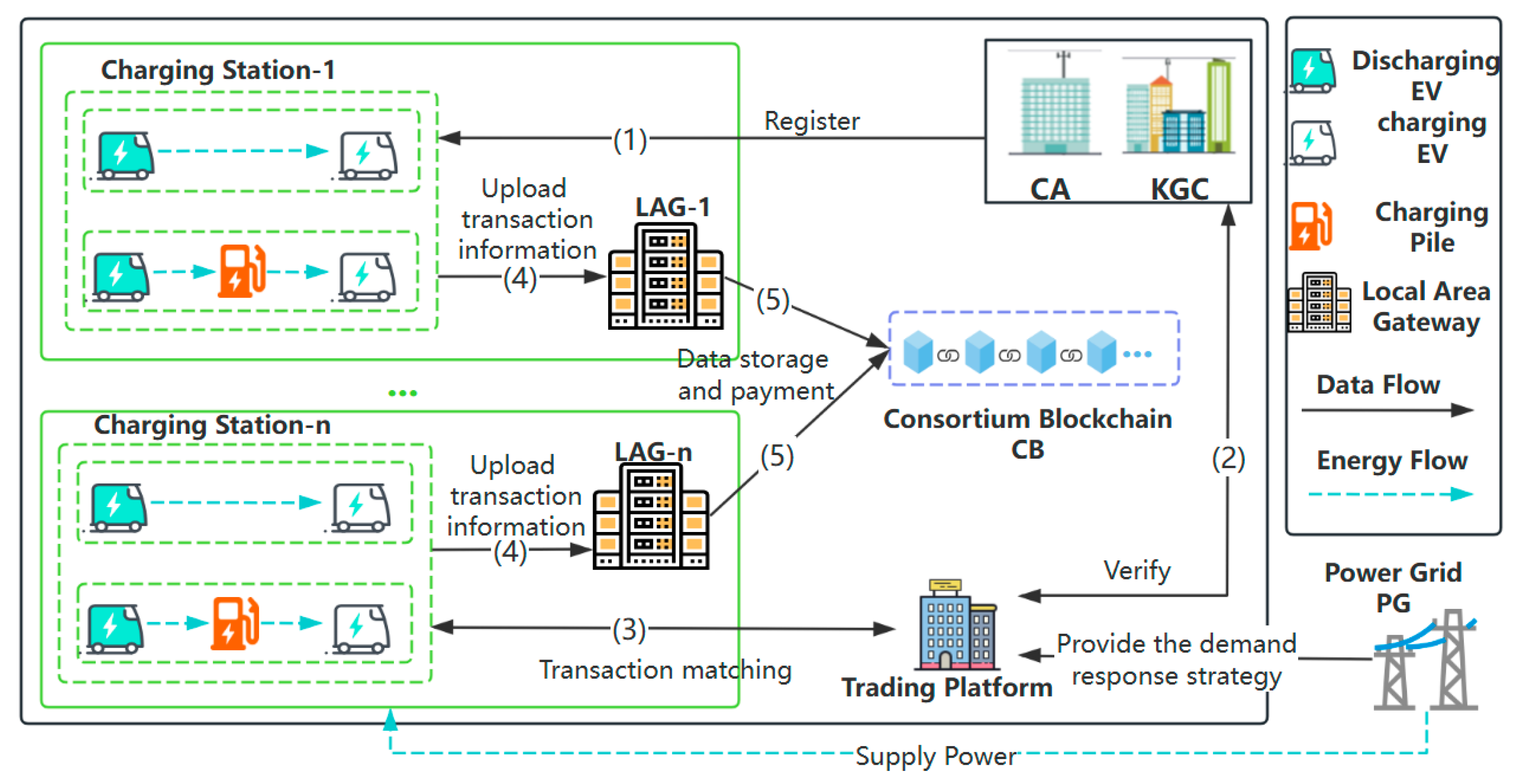
3.1. Scheme Design Ideas
- The EV user key in the system is jointly calculated by the KGC and the EV users themselves, avoiding the key leakage problem caused by the key generated entirely by the KGC, which exists in the scheme based on public key infrastructure.
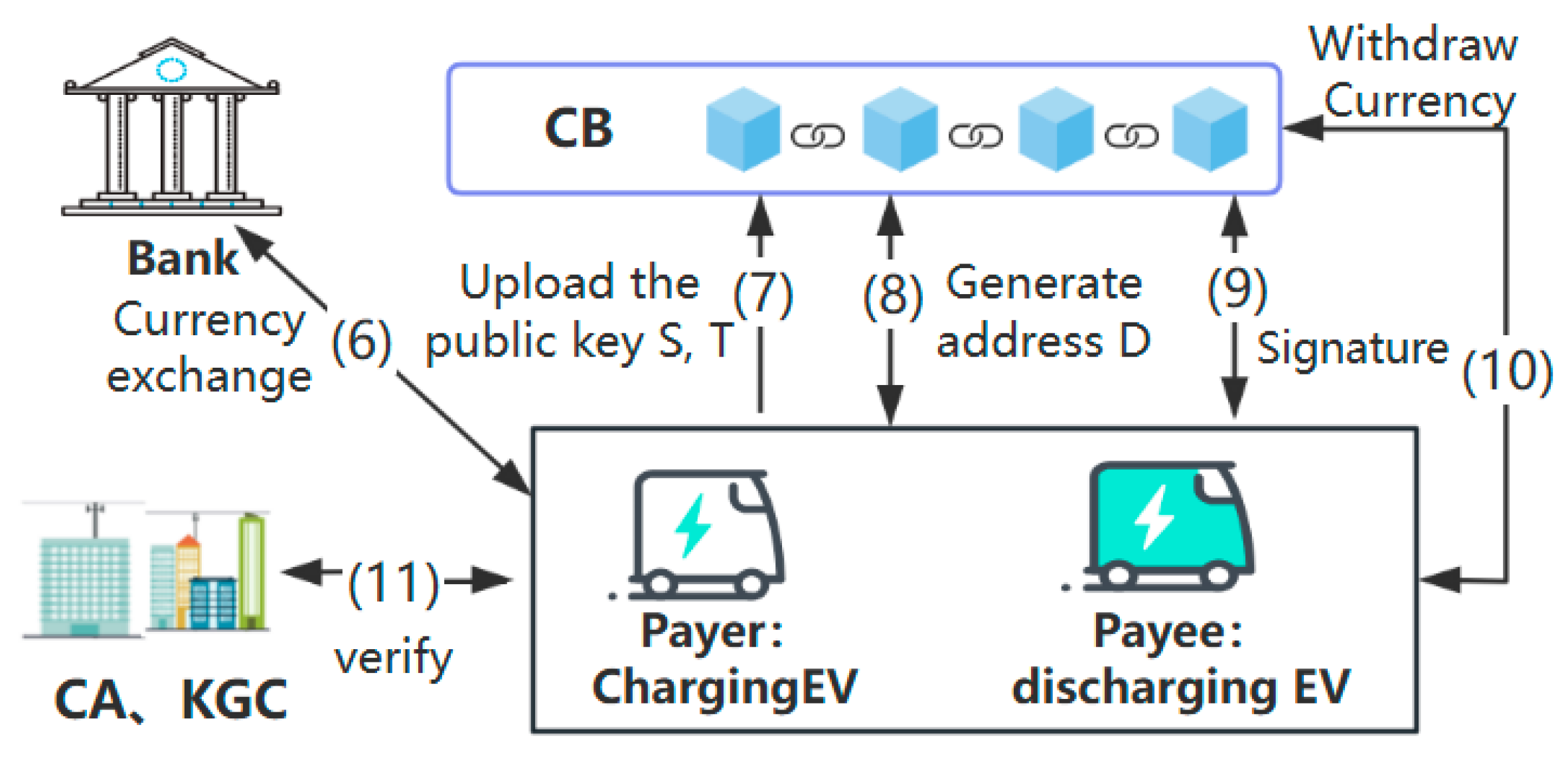
- When the power transmission of the transaction is over, the charging EV needs to pay the corresponding currency for the purchased power, which is protected by the individual private key because the currency is stored on the address in the blockchain. The charging EV will generate an exclusive stealth address for the discharging EV using a random number and the public key of the discharging EV and transfer the corresponding amount of currency. The discharging EV can use its private key to extract the currency on the address without revealing its real identity, ensuring both parties’ anonymity in the transaction.
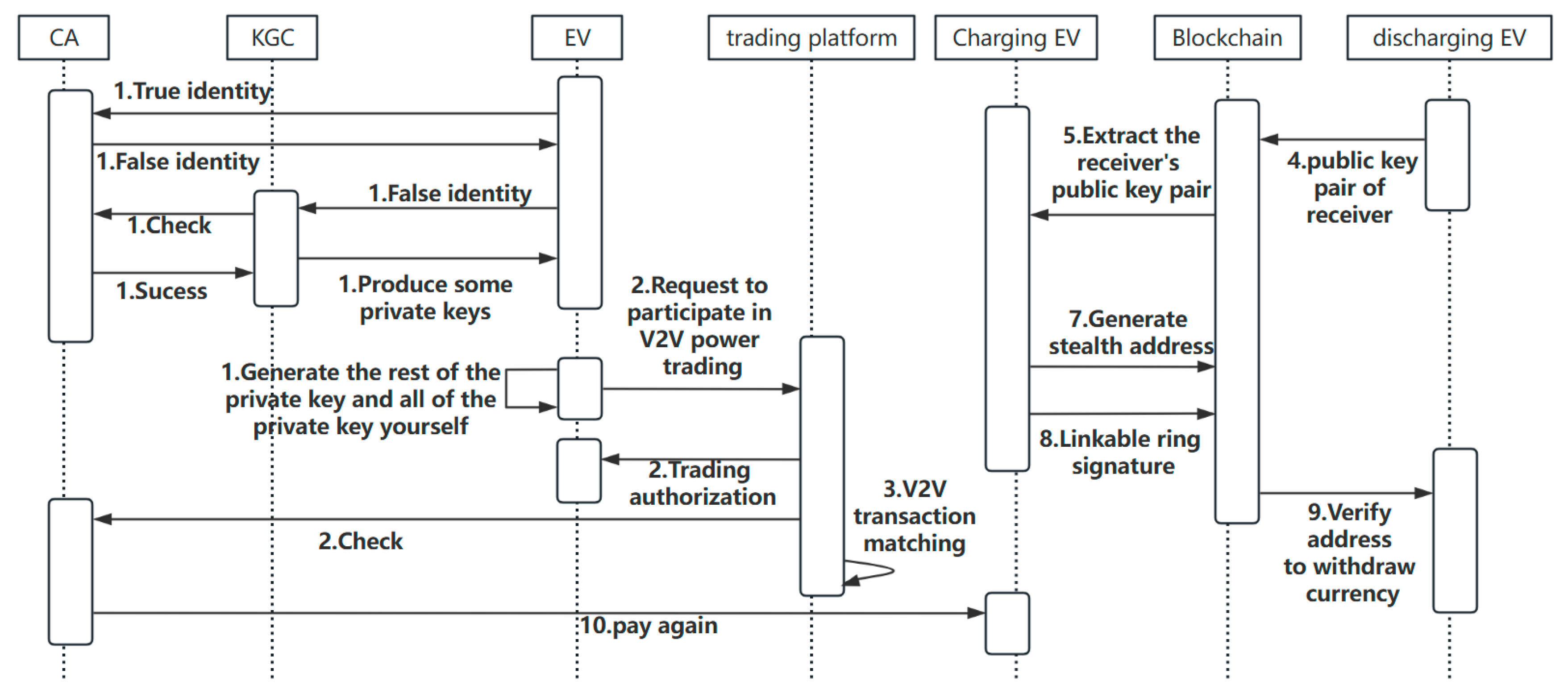
- The charging EV signs the power transaction information and the stealth address with its private key and the system public key set using the linkable ring signature algorithm. Suppose a malicious EV tries to generate multiple signatures. In that case, the linkability of the signature will be triggered to determine that the signature is invalid, and the CA will intervene promptly to punish the malicious EV and ensure the uniqueness of the transaction.
3.2. Scheme Models and Implementation Process
4. Scheme Implementation
5. Scheme Analysis
5.1. Correctness Analysis
5.2. Security Analysis
5.2.1. Unforgeable
5.2.2. Anonymity
5.2.3. Linkability
5.2.4. Indefensible
5.2.5. Resist All Types of Attacks
5.3. Performance Analysis
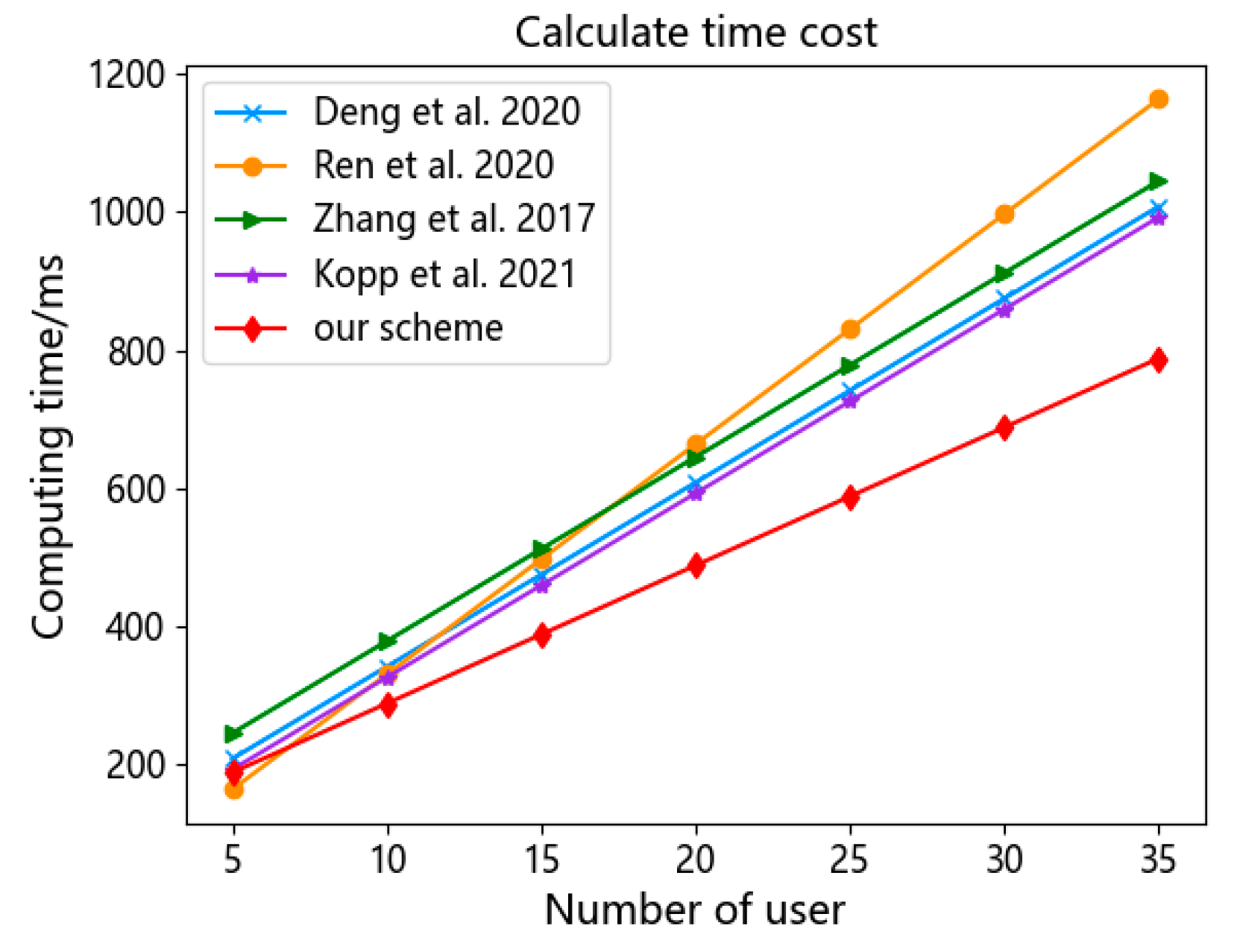
5.3.1. Computational Overhead of Linkable Ring Signatures
5.3.2. Time Overhead of Stealth Address Generation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, J.; Liang, M.; Cheng, W.; Wang, S. Life Cycle Cost of Conventional, Battery Electric, and Fuel Cell Electric Vehicles Considering Traffic and Environmental Policies in China. Int. J. Hydrogen Energy 2021, 46, 9553–9566. [Google Scholar] [CrossRef]
- Available online: https://www.gov.cn/lianbo/bumen/202401/content_6925362.html (accessed on 6 May 2024).
- Available online: https://auto.huanqiu.com/article/4KzwkQWCUdy (accessed on 10 January 2025).
- Huda, A.; Hadi, O.; Rabeb, M.; Shakti, S. A V2V Charging Allocation Protocol for Electric Vehicles in VANET. Veh. Commun. 2021, 33, 100427. [Google Scholar]
- Xu, Y.; Wang, S.; Long, C. A Vehicle-to-vehicle Energy Trading Platform Using Double Auction with High Flexibility. In Proceedings of the 2021 IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Espoo, Finland, 18–21 October 2021. [Google Scholar]
- Yuvaraj, T.; Devabalaji, K.R.; Kumar, J.A.; Thanikanti, S.B.; Nwulu, N.I. A Comprehensive Review and Analysis of the Allocation of Electric Vehicle Charging Stations in Distribution Networks. IEEE Access 2024, 12, 5404–5461. [Google Scholar] [CrossRef]
- Wang, M.; Ismail, M.; Zhang, R.; Shen, X.S.; Serpedin, E.; Qaraqe, K. A Semi-Distributed V2V Fast Charging Strategy Based on Price Control. In Proceedings of the Global Communications Conference, Austin, TX, USA, 8–12 December 2014. [Google Scholar]
- Available online: https://xueqiu.com/9331049986/258887932 (accessed on 7 May 2024).
- Ghani, R.; Farjah, E.; Oboudi, M.R. A Mathematical Model for the Development of Distributed Energy Storage Devices in the V2V Charging Process Systems Based on Fuzzy Graph Theory. J. Energy Storage 2025, 110, 115269. [Google Scholar] [CrossRef]
- Li, Z.; Shang, Y.; Lei, X.; Shao, Z.; Jia, Y.; Jian, L. An Accessible Close-Loop V2V Charging Mechanism under Charging Station with Non-Cooperative Game. Energy Rep. 2022, 8, 1038–1044. [Google Scholar] [CrossRef]
- Kim, O.T.T.; Tran, N.H.; Nguyen, V.; Kang, S.M.; Hong, C.S. Cooperative Between V2C and V2V Charging: Less Range Anxiety and More Charged EVs. In Proceedings of the International Conference on Information Networking, Chiang Mai, Thailand, 10–12 January 2018; pp. 679–683. [Google Scholar]
- Hussain, A.; Bui, V.H.; Musilek, P. Local Demand Management of Charging Stations Using Vehicle-to-vehicle Service: A Welfare Maximization-Based Soft Actor-Critic Model. Etransportation 2023, 18, 100280. [Google Scholar] [CrossRef]
- Shurrab, M.; Singh, S.; Otrok, H.; Mizouni, R.; Khadkikar, V.; Zeineldin, H. An Efficient Vehicle-to-Vehicle (V2V) Energy Sharing Framework. IEEE Internet Things J. 2021, 9, 5315–5328. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, Y.; Li, D.; Han, L. An Optimal Scheduling Algorithm for Hybrid EV Charging Scenario Using Consortium Blockchains. Future Gener. Comput. Syst. 2018, 91, 555–562. [Google Scholar] [CrossRef]
- Luo, L.; Feng, J.; Yu, H.; Sun, G. Blockchain-Enabled Two-Way Auction Mechanism for Electricity Trading in Internet of Electric Vehicles. IEEE Internet Things J. 2022, 9, 8105–8118. [Google Scholar] [CrossRef]
- Baza, M.; Sherif, A.; Mahmoud, M.M.; Bakiras, S.; Alasmary, W.; Abdallah, M.; Lin, X. Privacy-Preserving Blockchain-Based Energy Trading Schemes for Electric Vehicles. IEEE Trans. Veh. Technol. 2021, 70, 9369–9384. [Google Scholar] [CrossRef]
- Kim, M.; Lee, J.; Oh, J.; Park, K.; Park, Y.; Park, K. Blockchain Based Energy Trading Scheme for Vehicle-to-vehicle Using Decentralized Identifiers. Appl. Energy 2022, 322, 119445. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, W.; Chen, C.; Li, N.; Bao, Z.; Luo, M. Toward Privacy-Preserving Blockchain-Based Electricity Auction for V2G Networks in the Smart Grid. Secur. Commun. Netw. 2022, 2022, 6911463. [Google Scholar] [CrossRef]
- Lin, C.; He, D.; Huang, X.; Khan, M.K.; Choo, K.K.R. DCAP: A Secure and Efficient Decentralized Conditional Anonymous Payment System Based on Blockchain. IEEE Trans. Inf. Forensics Secur. 2020, 15, 2440–2452. [Google Scholar] [CrossRef]
- Erdin, E.; Cebe, M.; Akkaya, K.; Solak, S.; Bulut, E.; Uluagac, S. Building a Private Bitcoin-Based Payment Network among Electric Vehicles and Charging Stations. In Proceedings of the 2018 IEEE International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData), Halifax, NS, Canada, 30 July–3 August 2018. [Google Scholar]
- Deng, L.; Shi, H.; Gao, Y. Certificateless Linkable Ring Signature Scheme. IEEE Access 2020, 8, 54641–54651. [Google Scholar] [CrossRef]
- Deng, L.; Jiang, Y.; Ning, B. Identity-Based Linkable Ring Signature Scheme. IEEE Access 2019, 7, 153969–153976. [Google Scholar] [CrossRef]
- Ren, Y.; Zhao, Q.; Guan, H.; Lin, Z. On Design of Single-Layer and Multilayer Code-Based Linkable Ring Signatures. IEEE Access 2020, 8, 17854–17862. [Google Scholar] [CrossRef]
- Zhang, Y.; Zeng, J.; Li, W.; Zhu, H. A Certificateless Ring Signature Scheme with High Efficiency in the Random Oracle Model. Math. Probl. Eng. 2017, 2017, 7696858. [Google Scholar] [CrossRef]
- Liu, Z.; Nguyen, K.; Yang, G.; Wang, H.; Wong, D.S. A Lattice-Based Linkable Ring Signature Supporting Stealth Addresses. In Computer Security–ESORICS 2019; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2019; pp. 726–746. [Google Scholar]
- Kopp, H.; Mödinger, D.; Hauck, F.J.; Kargl, F. Cryptographic Design of PriCloud, a Privacy-preserving Decentralized Storage with Remuneration. IEEE Trans. Dependable Secur. Comput. 2021, 18, 1908–1919. [Google Scholar] [CrossRef]
- Esmat, A.; de Vos, M.; Ghiassi-Farrokhfal, Y.; Palensky, P.; Epema, D. A Novel Decentralized Platform for Peer-to-peer Energy Trading Market with Blockchain Technology. Appl. Energy 2020, 282, 116123. [Google Scholar] [CrossRef]
- Wang, Q.; Li, X.; Yu, Y. Anonymity for Bitcoin from Secure Escrow Address. IEEE Access 2018, 6, 12336–12341. [Google Scholar] [CrossRef]
- Feng, C.; Tan, L.; Xiao, H.; Yu, K.; Qi, X.; Wen, Z.; Jiang, Y. PDKSAP: Perfected Double-Key Stealth Address Protocol Without Temporary Key Leakage in Blockchain. In Proceedings of the 2020 IEEE/CIC International Conference on Communications in China (ICCC Workshops), Chongqing, China, 9–11 August 2020; pp. 151–155. [Google Scholar]
- Gai, K.; Wu, Y.; Zhu, L.; Qiu, M.; Shen, M. Privacy-Preserving Energy Trading Using Consortium Blockchain in Smart Grid. IEEE Trans. Ind. Inform. 2019, 15, 3548–3558. [Google Scholar] [CrossRef]
- Qing, F.; Debiao, H.; Min, L.; Xinyi, H.; Dawei, L. Ring Signature Schemes Based on SM2 Digital Signature Algorithm. J. Cryptolog. Res. 2021, 8, 710–723. [Google Scholar]
| Scheme | Architecture | V2V or V2G | Privacy | Authentication | Anonymity | Traceability |
|---|---|---|---|---|---|---|
| Ref. [10] | Center | √ | × | × | × | × |
| Ref. [11] | Center | √ | × | × | × | × |
| Ref. [12] | Center | √ | × | × | × | × |
| Ref. [15] | Blockchain | √ | √ | × | × | × |
| Ref. [16] | Blockchain | √ | √ | × | √ | √ |
| Ref. [17] | Blockchain | √ | √ | √ | × | × |
| our scheme | Blockchain | √ | √ | √ | √ | √ |
| Symbols | Meaning |
|---|---|
| Finite field of prime numbers | |
| An elliptic curve on | |
| Large prime number | |
| Additive cyclic group | |
| A set of positive integer prime order groups less than | |
| The q-th order generating element of , with as the base point | |
| CA’s public and private keys | |
| KGC’s public and private keys | |
| Hash function | |
| User set | |
| Public key set | |
| Stealth address | |
| Amount of transaction | |
| Electricity trading message () | |
| A linkable ring signature | |
| Linkable ring signature tag | |
| V2V power trading list description |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Xiao, T.; Wang, B. A Communication Scheme with Privacy Protection in V2V Power Transaction Based on Linkable Ring Signature. World Electr. Veh. J. 2025, 16, 141. https://doi.org/10.3390/wevj16030141
Zhang S, Xiao T, Wang B. A Communication Scheme with Privacy Protection in V2V Power Transaction Based on Linkable Ring Signature. World Electric Vehicle Journal. 2025; 16(3):141. https://doi.org/10.3390/wevj16030141
Chicago/Turabian StyleZhang, Shaomin, Tao Xiao, and Baoyi Wang. 2025. "A Communication Scheme with Privacy Protection in V2V Power Transaction Based on Linkable Ring Signature" World Electric Vehicle Journal 16, no. 3: 141. https://doi.org/10.3390/wevj16030141
APA StyleZhang, S., Xiao, T., & Wang, B. (2025). A Communication Scheme with Privacy Protection in V2V Power Transaction Based on Linkable Ring Signature. World Electric Vehicle Journal, 16(3), 141. https://doi.org/10.3390/wevj16030141