Multi Objective Optimization of Electric Vehicle Charging Strategy Considering User Selectivity

Abstract

Electric vehicles (EVs) are increasing in number every year, and large-scale uncontrolled EV charging can impose significant load pressure on the power grid (PG), affecting its stability and economy. This paper proposes an EV charging strategy that considers user selectivity. The user’s selection strategy includes options for fast and slow charging types, as well as the choice of whether to comply with grid-controlled charging. Charging types are selected based on the ability to reach the desired state of charge (SOC), while compliance with grid-controlled charging is determined by comparing the unit charging cost (CC). An objective function is established to minimize the peak valley load difference (PVLD) rate of PGs and users’ CC. To achieve this, an improved non-dominated sorting whale optimization algorithm (INSWOA) is proposed which initializes the population through logistic mapping, introduces nonlinear convergence factors for position updates, and uses adaptive inertia weights to improve population diversity, enhance global optimization ability, reduce premature convergence, and improve solution accuracy. Finally, simulating distribution networks in a certain region, the results obtained from the INSWOA were compared with those from the non-dominated sorting whale optimization algorithm (NSWOA) and other algorithms. The comparisons demonstrated that the INSWOA significantly reduced the PVLD rate of the PG load and users’ CCs, highlighting its high practical value.

1. Introduction

With the acceleration of global energy transition and the proposal of green and low-carbon development goals, electric vehicles (EVs) have become an important research direction in modern transportation and energy fields due to their significant environmental friendliness and economic advantages [1,2]. However, EVs’ charging behavior is highly coupled with power grid (PG) operations. The rapid growth of their charging loads (CLs) has brought unprecedented difficulties to PGs, including intensified load peaks, decreased power system stability, and limited the efficiency of renewable energy consumption [3,4]. In this context, the issue of how to reduce the load pressure on the PG and improve the stability of the PG for EV charging has received attention [5].

Numerous EVs being connected to the PG has an impact on load balancing, operating costs, and other aspects. Therefore, researchers have proposed various optimization strategies to reconcile the contradiction between user demand and grid operation. Adjusting charging prices can affect users’ charging periods. Reference [6] developed a pricing strategy to lower service interruptions in charging stations; methods were introduced to optimize EVs’ charging processes, propose an optimal pricing approach to guide and coordinate the charging processes of EVs in the charging station, the results show the performance of the proposed charging scheduling scheme and show the efficiency of the proposed pricing scheme. Reference [7] proposed an ordered charging strategy involving tiered carbon pricing, adaptive time-of-use electricity pricing. The strategy was solved using optimization algorithms with an elite strategy, which not only significantly reduced the charging cost (CC) but also effectively balanced carbon emissions and power loads. Reference [8] proposed a new dynamic optimization method for electricity prices which can update the electricity prices of EVs based on their load information when connected to the PG, reducing the load difference between peak and valley load in the grid. Reference [9] proposed an optimization strategy for EV charging guided by a regional dynamic electricity pricing mechanism, which establishes different dynamic electricity prices based on the load characteristics in different regions to optimize the charging of EVs in corresponding regions. Reference [10] proposed a pricing incentive based on an EV charging navigation strategy. It considers both the charging request and spatiotemporal location of EVs. It analyzes the origin-destination data to determine the spatiotemporal distribution of charging demand. Reference [11] proposed an optimization scheduling strategy which includes not only two types of electricity prices but also a two-stage implementation, and it also reduces system operating costs and the peak valley load difference (PVLD) rate.

In terms of research on the strategy of connecting EVs to PGs, most of the literature focuses on price incentives for EV pricing, the optimization of time-sharing EV charging strategies considering time, and research on hierarchical and gradient EV charging strategies. However, there is relatively little research on EV charging strategy planning that considers user selectivity. Considering the user’s selective charging strategy can not only help people understand how to adjust grid loads during charging but also respect the user’s autonomous choice, allowing users to charge according to their choices. While alleviating load on the PG, it can effectively reduce user CCs, which is more in line with actual needs.

The research on heuristic algorithms in engineering applications is receiving increasing attention. Faced with the problem of controlled charging strategies for EVs, many scholars have studied the problem by formulating effective charging strategies and utilizing heuristic algorithms. Common algorithms include particle swarm optimization, the genetic algorithm, gray wolf algorithm, whale algorithm, and so on. Reference [12] proposed an improved whale optimization algorithm incorporating teaching strategies and compared it with standard whale and particle swarm optimization algorithms to optimize controlled charging for EVs. Reference [13] proposed a decentralized whale optimization algorithm to optimize EVs’ discharge strategy. Reference [14] compared six algorithms, including the whale algorithm, genetic algorithm, and particle swarm optimization from three categories to provide the most suitable optimization techniques for solving microgrid optimization problems. Reference [15] proposed a hierarchical optimization-based orderly charging strategy for EVs. It establishes a bi-level charging optimization model for EVs and optimizes the starting charging time using an improved particle swarm optimization algorithm. The effectiveness of the optimization is demonstrated by analyzing the responsiveness of different users. Reference [16] proposed a multi-agent dynamic time-sharing optimization model based on cooperative game theory which uses a particle swarm optimization algorithm to solve the dynamic time-of-use transaction electricity price between agents and EV users. The model demonstrates the coordination potential between economy and fairness, avoiding the new peak of load while improving the benefits of agents and users. Reference [17] proposed the application of an improved whale algorithm to optimize the fuzzy control strategy for EV regeneration and improve the adaptive weights to enhance energy recovery and braking performance after optimization. Reference [18] established a charging guidance and coordination compensation model for EVs under different emergency charging needs and solved the model through a genetic algorithm to prove the effectiveness of the compensation strategy. Reference [19] proposed an improved whale optimization algorithm by introducing nonlinear time-varying adaptive weights, which optimizes the control parameters of the power generation controller in the power system to obtain effective strategies. Reference [20] proposed a battery replacement plan strategy for EV battery swapping stations and compared it with a binary bat algorithm, whale optimization algorithm, and gray wolf optimization algorithm to obtain the optimal strategy solution.

This paper proposes an EV charging strategy that considers user selectivity. User selectivity refers to the ability of users to choose whether to comply with grid-controlled charging and select the type of charging according to their own preferences. Current research on EV charging strategies primarily focuses on adjusting electricity pricing to improve charging strategies, with little attention being given to charging strategies that consider the selectivity of individual EV users. This paper proposes a user-selective charging strategy that not only accommodates users’ charging preferences but also aligns with PG scheduling. The specific steps are as follows. First, the system determines whether the user’s charging requirements and the state of charge (SOC) of an EV upon arrival at a charging station meet the criteria for participation in charging optimization. Then, among users who satisfy requirements for charging, the system analyzes and compares the costs of uncontrolled charging when users comply with or deviate from the grid-controlled charging schedule. Based on an analysis of user CCs, the system evaluates whether users should comply with grid-controlled charging arrangements. Complying with grid-controlled charging arrangements refers to users not charging at the station immediately but arranging charging through a PG according to the PG load situation. The grid then develops an optimal charging strategy aimed at minimizing grid load variance and CCs based on users’ choices. An improved non-dominated sorting whale optimization algorithm (INSWOA) is proposed to solve the strategy using the actual load of a specific region as the base load, validating the practicality of the proposed optimization scheme.

In Section 2, this paper employs the Monte Carlo algorithm (MCA) to model the charging load of EVs. Section 3 introduces the details of the user-selective strategy, including the optimization objectives and constraints of the model. It also presents the non-dominated sorting whale optimization algorithm (NSWOA) and proposes an INSWOA based on it. Section 4 provides the simulation results of the established model. Section 5 discusses the innovations of the proposed strategy, and Section 6 concludes the results of this paper.

2. Mathematical Model for EV Charging

2.1. Modeling of CL for EVs

The driving situation of EVs plays a crucial role in daily travel, influencing both charging and discharging times. There are many types of EVs, among which private EVs have the characteristics of large quantities, relatively difficult scheduling, and high randomness. According to a survey conducted by the US Department of Transportation in 2009 on household vehicle travel in the United States [21], the private car travel data were fitted, and the CL model of EVs is obtained as follows:

The final return home time of an EV can be seen as a normal distribution obeying $N({\mu }_S,{{\sigma }_S}^2)$, and can be expressed as [22]

$$f_s=\left\{\begin{array}{c}{\displaystyle \frac{1}{{\sigma }_s\sqrt{2\pi }}}\exp [-{\displaystyle \frac{{(x_1-{\mu }_s)}^2}{2{\sigma }_s^2}}],{\mu }_s-12<x_1<24\hfill \\ {\displaystyle \frac{1}{{\sigma }_s\sqrt{2\pi }}}\exp [-{\displaystyle \frac{{(x_1+24-{\mu }_s)}^2}{2{\sigma }_s^2}}],0<x_1<{\mu }_s-12\hfill \end{array}\right.$$

(1)

where x₁ is the return home time; σ_s is the standard deviation, usually taken as 3.4 km; and μ_S is the expectation, taken as 17.6 km.

The daily mileage of EVs can be seen as a normal distribution following $N({\mu }_S,{{\sigma }_S}^2)$ and can be expressed as

$$f_D(L)={\displaystyle \frac{1}{L{\sigma }_D\sqrt{2\pi }}}\exp \left[-{\displaystyle \frac{{(InL-{\mu }_D)}^2}{2{\sigma }_D^2}}\right]$$

(2)

where L is the daily driving distance; σ_D is the standard deviation, usually taken as 3.2 km; and μ_D is the expectation, taken as 0.88 km.

The travel time of EVs can be seen as a normal distribution obeying $N({\mu }_S,{{\sigma }_S}^2)$ and can be expressed as [23]

$$f_c=\left\{\begin{array}{l}{\displaystyle \frac{1}{\sigma \sqrt{2\pi }}}\exp \left[-{\displaystyle \frac{{(x_2-{\mu }_c)}^2}{2{\sigma }_c^2}}\right],0<x_2<{\mu }_c+12\\ {\displaystyle \frac{1}{\sigma \sqrt{2\pi }}}\exp \left[-{\displaystyle \frac{{(x_2-24-{\mu }_c)}^2}{2{\sigma }_c^2}}\right],{\mu }_c+12<x_2<24\end{array}\right.$$

(3)

where x₂ is the travel time; σ_c is the standard deviation, with a value of 3.24 km; and μ_c is the expectation, taken as 8.92 km.

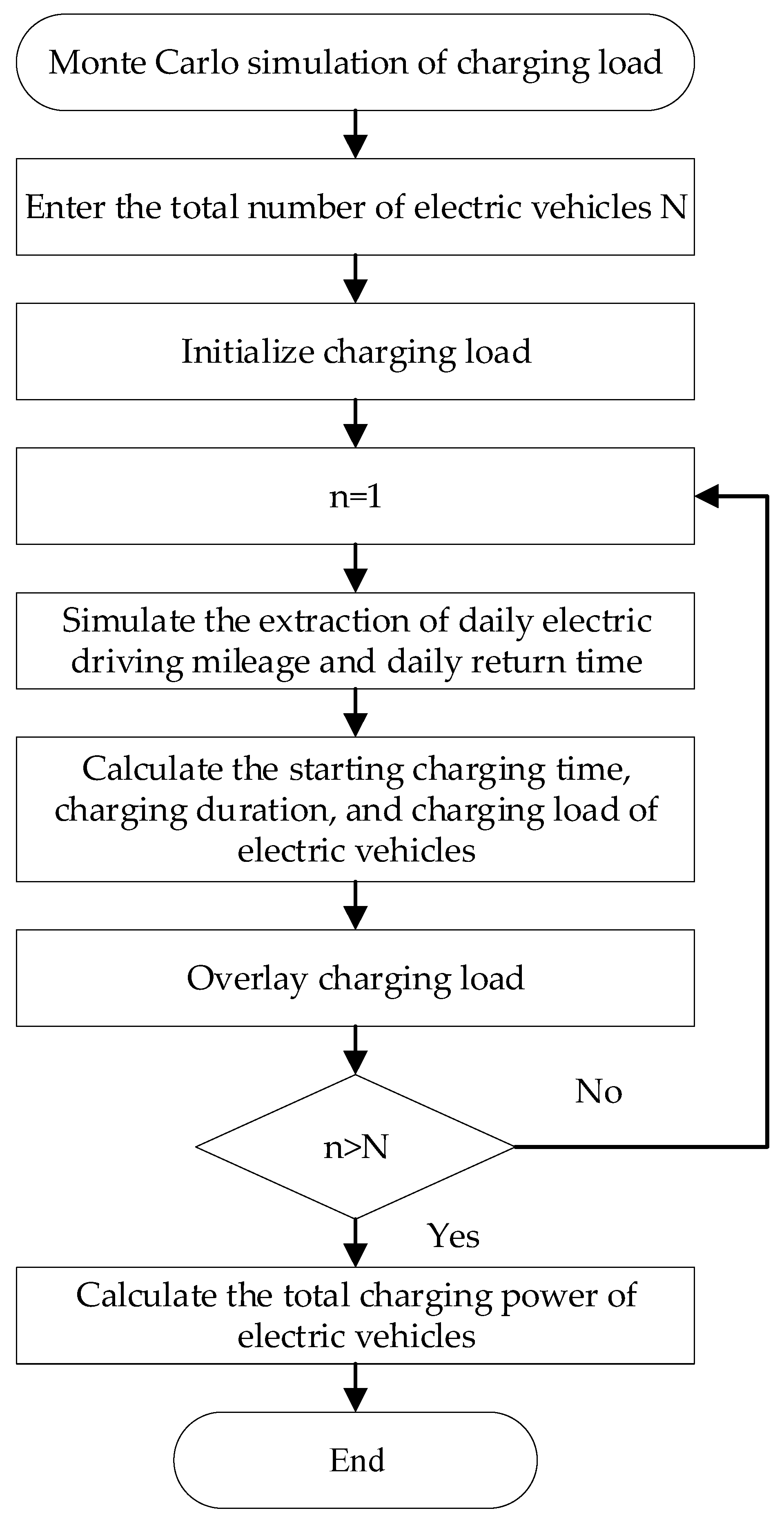
2.2. EV Load Sampling Based on Monte Carlo Algorithm

The MCA is a numerical calculation method based on random sampling and statistical principles that is widely used to solve complex problems, especially in situations where analytical solutions are difficult to obtain or traditional algorithms are inefficient. The core idea is to use a large number of random experiments to approximate the true solution of the problem by utilizing the statistical properties of the samples. The advantage of MCA lies in its universality and ease of implementation, but its accuracy depends on the number of samples and usually requires a large amount of computing resources to achieve high accuracy. The charging of EVs invoves randomness, and it is impossible to grasp the charging analysis formula of each EV. Moreover, the research problem is about the large number of EVs existing in a certain region. As a high-dimensional problem, using the MCA to simulate the CL of EVs is more suitable.

We can extract the final return time and daily mileage data from the obtained EVs’ travel patterns using the MCA, and we assume that users expect to fully charge before going out every time. After obtaining the daily driving history of EVs, the SOC of EVs at charging stations can be calculated [24] as follows:

$$SO{C}_s=(1-{\displaystyle \frac{L}{L_{\max }}})\times 100\%$$

(4)

where SOC_s is the SOC when arriving at the charging station; L_max is the maximum driving range of EVs; and L is the distance traveled before reaching a charging station. Charging completion time of EVs can be obtained as [25]

$$T_{\mathrm{C}}={\displaystyle \frac{(SO{C}_{ec}-SO{C}_s)\times W}{\eta p}}$$

(5)

where SOC_ec is the expected amount of electricity that EVs can achieve and the users’ expected amount of electricity is fully charged; W is the battery capacity; η is EVs’ charging efficiency; p is EVs’ charging power.

Based on the starting charging time (assuming the last return time of EVs is the starting charging time) and charging duration, the CLs of EVs can be calculated through the following equation:

$$P_{\mathrm{charge}}={\displaystyle \sum _{z=1}^N{P}_{z,j}}$$

(6)

where P_charge is all EVs’ total CL; N is EVs’ number in the PG; and P_z,j is the charging power of the z-th EV during time period j. Dividing a day into 24 time periods by the hour, denoted as j = 1, 2, 3 … 24, and adding the CL of EVs to the original base load, the following can be obtained [26]:

$$P_{\mathrm{total}}=P_{\mathrm{charge}}+P_t$$

(7)

where P_total is the total load of the PG at the moment; P_t is the basic load of the PG at the moment.

Figure 1 shows a flowchart of the MC simulation of the CL for EVs. (1) First, we input the total number of EVs in the regional PG and initialize the CL. (2) We then use the MCA to extract EVs’ return time and daily mileage. (3) We calculate the remaining SOC of EVs before charging based on daily mileage, consider the return time as the charging start time, and calculate the charging time required to reach the desired charge. (4) We then calculate the CL of each EV based on its starting power and charging duration and add up all the CLs of the EVs to obtain the total CL of the EVs. (5) Finally, we add the total CL to the original base load to obtain the current total PG load.

3. Multi Objective Optimization Model and Solving Algorithm for EV Charging

3.1. Selective Strategy for EV Users

According to the Charging Station Charging Regulations of Jiangsu Province, a time-based pricing strategy is adopted for peak, flat, and valley periods. Electricity prices are in unequal stages according to time. Considering EV user perspectives, although users’ willingness to charge may be affected by high or low electricity prices, from the perspective of battery life and user convenience, once users charge, they will not choose to continuously interrupt and start charging due to fluctuations in electricity prices [27]. Therefore, it is believed that users’ charging behaviors are continuous and the entire process only starts and ends once, with when it ends depending on whether the amount of charging meets the next trip.

Taking a single EV as the research object, users can choose whether to choose grid-arranged charging as well as choose fast charging or conventional slow charging when charging. The selection methods are as follows:

$$F=\left\{\begin{array}{ll}\lambda \times H_1+(1-\lambda )\times H_0& SO{C}_S<SO{C}_e\\ L_0& SO{C}_S=SO{C}_e\\ \beta \times L_1+(1-\beta )\times L_0& SO{C}_S>SO{C}_e\end{array}\right.$$

(8)

where H₁ is a fast-charging system that complies with the arrangements of the PG; H₀ refers to fast charging that does not comply with the arrangement of the PG; λ and β can take values of 0 or 1, with 1 indicating compliance with grid arrangements and 0 indicating non-compliance with grid arrangements; L₁ represents slow charging that complies with the grid arrangement, while L₀ represents slow charging that does not comply with the grid arrangement. SOC_S is the SOC when arriving at the charging station; SOC_e is the minimum initial SOC for slow charging to the desired charge throughout the entire charging cycle.

Considering the battery wear caused by charging, this study assumes that users prioritize slow charging [28]. Users who do not comply with the grid’s schedule begin charging immediately upon arrival at the station. Analyzing Equation (8), when the initial SOC of an EV is less than the minimum initial SOC required for slow charging to reach the desired SOC, fast charging must be used to meet the user’s travel needs. When the initial SOC is just sufficient for charging to the desired minimum SOC, users choose slow charging without following the grid’s schedule; when both charging types are available and the EV battery can be fully charged, it is preferred to choose slow charging to minimize battery loss. When the initial SOC exceeds the desired minimum SOC, users are free to decide whether to comply with the grid-controlled charging schedule and may opt for slow charging. For simplicity in model development, it is assumed that the decision to comply with the grid-controlled charging schedule is based on a comparison of the unit CC of the two methods, as expressed in the following equation:

$$C_{M_1}={\displaystyle {\sum }_{s=1}^{s=l-m-1}\frac{f(\mathrm{s})}{(l-m+1)\times E}}$$

(9)

$$C_{M_0}={\displaystyle \frac{f(M_0)}{E}}$$

(10)

$$\beta =\left\{\begin{array}{ll}1& {\mathrm{C}}_{M_1}\le C_{M_0}\\ 0& {\mathrm{C}}_{M_1}>C_{M_0}\end{array}\right.$$

(11)

where $C_{M_1}$ is the unit cost of complying with the grid arrangement for charging, $C_{M_0}$ is the unit cost of not complying with the grid arrangement, and s is the number of charging schemes that comply with the grid-controlled charging arrangement. The process of charging EVs from arrival to departure from the charging station is divided into l time periods, including m time periods for the continuous charging of EVs. When following the arrangement of the PG, in order to ensure that EVs meet the expected SOC during travel, there are l − m + 1 options available for EVs to start charging during l time periods. $f(\mathrm{s})$ is the cost of the option to start charging at one of the time periods, E is the EV charging amount, and $f(M_0)$ is the cost of charging that does not comply with the grid-controlled charging arrangement. In situations where the electricity load on the PG is high but the electricity price is low, users who do not comply with the grid-controlled charging arrangements will save more costs. When the unit cost of complying with the grid arrangement for charging is greater than the unit cost of not complying with the grid arrangement for charging, users start charging when they reach the charging station and stop charging when the expected charging amount is reached. When the unit cost of complying with the grid arrangement for charging is less than the unit cost of not complying with the grid arrangement for charging, users choose to comply with the grid-controlled charging arrangement and participate in grid scheduling while meeting the expected charging capacity of EVs, maximizing the interests of the grid and users.

Under real conditions, user-selective strategies can be applied to household charging stations, which can provide users with suitable charging solutions while reasonably meeting their charging needs, enabling them to participate in PG scheduling while saving costs.

3.2. Objective Function

This paper establishes an optimization model from the perspectives of the PG and users for minimizing the peak valley difference (PVLD) and CCs of the PG.

3.2.1. The Minimum PVLD Rate of the PG

$$\min F_1={\displaystyle \frac{\max (L_t)-\min (L_t)}{\max (L_t)}}$$

(12)

$$L_t=L_t^{load}+L_t^c$$

(13)

where F₁ represents the PVLD of the PG; L_t represents the total PG load; $L_t^{load}$ is the initial load of PG; and $L_t^c$ is the CL of EVs. Reducing the PVLD of the PG can make it more stable and smoothen the load, which is helpful for keeping the PG safe.

3.2.2. The Minimum CC for Users

$$\min F_2={\displaystyle {\sum }_{j=1}^N{\displaystyle {\sum }_{h=1}^M(P\times C_t\times \Delta }}t)$$

(14)

where p represents EVs’ charging power, including two types of power (fast charging and slow charging); C_t is the charging price; $\Delta t$ is the charging time interval; N is the EV charging count; and M is the divided time periods count.

3.3. Constraints

All users must reach the expected battery level when leaving the charging station, [29]:

$${\displaystyle {\sum }_{h=1}^{M}P\times \eta \times \Delta t=E\times (SO{C}_E-SO{C}_S)}$$

(15)

where η is the charging efficiency and SOC_E is the expected charging capacity. Battery levels should not exceed a certain range during the charging process [30]:

$$SO{C}_{\min }\le SOC\le SO{C}_{\max }$$

(16)

where SOC_min is the lower limit of the EV charging capacity and SOC_max is the upper limit of the EV charging capacity.

3.4. Improving Non-Dominated Sorting Whale Optimization Algorithm

3.4.1. Multi Objective Whale Optimization Algorithm (WOA)

The WOA is an emerging optimization algorithm that is easy to implement and has strong global search capability. However, the original WOA cannot directly handle multi-objective optimization problems, so it needs to be improved by combining non-dominated sorting mechanisms. A NSWOA was developed based on the WOA framework. The NSWOA has good global convergence and high generality, and is commonly used in multi-objective optimization problems [31].

The core of the NSWOA lies in using three strategies of whale hunting behavior (trapping prey, bubble net hunting, tracking prey) to update solutions while introducing a non-dominated sorting mechanism to screen high-quality solutions, ensuring the diversity and superiority of the solutions. Catching prey is when other whales move around the prey after it has found its location. The location update equation is [32]

$$W(n+1)=W*(n)-B\times \left|D\times W*(n)-W(n)\right|$$

(17)

$$\left\{\begin{array}{l}B=2a\times r_1-a\\ D=2r_2\end{array}\right.$$

(18)

where $n$ is iteration number; $W(n+1)$ is current solution position vector in the next iteration; $W*(n)$ is the current optimal solution position; $W(n)$ is the current solution position; B is the adjustment vector that controls the direction and magnitude of solution updates; D is the adjustment vector that controls the direction and magnitude of solution updates; r₁ and r₂ are random number vectors; and a is the weight coefficient.

Bubble net predation is a simulation of a whale’s spiral upward bubble net predation behavior around prey, with the equation being

$$W(n+1)=\left|W*(n)-W(n)\right|\times e^{bl}\times \cos \left(2\pi l\right)+W*(n)$$

(19)

where $e^{bl}$ is an exponential function that simulates the rise of a spiral bubble and $\cos \left(2\pi l\right)$ is the cosine function that simulates the shape of a spiral.

Searching for prey can randomly select a target for search, enhancing the algorithm’s global exploration ability. The equation is

$$W(n+1)=W_{rand}-B\times \left|D\times W_{rand}-W(n)\right|$$

(20)

where W_rand is a randomly selected solution value.

However, as the iteration count increases, the NSWOA may suffer from local convergence and insufficient search efficiency when solving multi-objective optimization problems. Therefore, this paper proposes an improved non-dominated sorting whale optimization algorithm (INSWOA) by combining multiple improvement strategies to enhance its global exploration capability and optimization accuracy.

3.4.2. Improvement Methods

(1)

Logistic chaotic mapping (LCM)

To address the issue of low randomness in the initial population, LCM is used for initialization with the following equation [33]:

$$x_{n+1}=\mu \times x_n\times (1-x_n)$$

(21)

where x_n is the current value; x_n+1 is the next value, which is the value generated by the chaotic mapping; and μ is the control parameter. The selected value for this paper is 3.9. According to the LCM, it is integrated into the algorithm in this paper, and the equation is as follows:

$$f(g,v)=\min (v)+(\max (v)-\min (v))\times \mathrm{mod}(\left|value\right|,1)$$

(22)

where $f(g,v)$ is the initial population matrix; $\max (v)$ and $\min (v)$ are the upper and lower bounds for decision variable v; and value is the value generated by LCM, limited to the range of [0, 1) by taking the absolute value and modulo 1.

(2)

Nonlinear convergence factor

In the standard NSWOA, the weight coefficient linearly decreases from 2 to 0, which can lead to incomplete search and slow convergence speeds. This paper proposes a nonlinear convergence factor that combines the cosine convergence factor and logarithmic convergence factor with the equation

$$a=a_{\max }-(a_{\max }-a_{\min })\times ({\displaystyle \frac{\ln (1+iteration)}{\ln (1+Max\_iteration)}}\times {\displaystyle \frac{1+\cos (\pi \times \frac{iteration}{Max\_iteration})}{2}})$$

(23)

where a_max and a_min are the initial and final values for the convergence factor, iteration is the current iteration count, and Max_iteration is the maximum number of iterations.

By combining the cosine convergence factor and logarithmic convergence factor, the logarithmic factor changes rapidly in the initial stage. Combining the cosine factor can more effectively cover the solution space and improve global search capability, and, in the later stages of iteration, the stability of the logarithmic factor and the decay of the cosine factor result in a stable convergence factor which is beneficial for local development.

(3)

Adaptive inertia weight

In the spiral encirclement and random search stages, an adaptive inertia weight based on population diversity was used, and this improvement was introduced in Equations (19) and (20). The improved equations are shown in (24) and (25) [34]

$$W(n+1)=(1-\omega )\times \left|W*(n)-W(n)\right|\times e^{bl}\times \cos \left(2\pi l\right)+\omega \times W*(n)$$

(24)

$$W(n+1)=\omega W_{rand}-(1-\omega )\times (B\times \left|D\times W_{rand}-W(n)\right|)$$

(25)

where ω is the inertia weight, dynamically adjusted based on population diversity, with following equation:

$$\omega ={\omega }_{\min }+{\displaystyle \frac{{\omega }_{\max }-{\omega }_{\min }}{1-e^{-k(d_1-d_0)}}}$$

(26)

where ω_max and ω_min are the initial and final values for inertia weight; d₁ is the mean Euclidean distance between individuals in the population; d₀ is the diversity of the initial population, obtained by calculating the root mean square Euclidean distance between individuals in the initial population; and k is the parameter that controls the rate of weight change, with a typical value of 5.

In the early stages of the search, when the population diversity is high, the algorithm needs to explore the solution space broadly to avoid becoming stuck in local optima. A larger inertia weight helps maintain a higher degree of movement among the individuals, facilitating broader exploration. At this stage, the larger inertia weight encourages random exploration of potential solutions and prevents the particles from converging too early. As the search progresses and the population diversity decreases, the algorithm begins to converge toward an optimal region. In practice, d₀ is often calculated based on the initial population generated at the beginning of the algorithm. It is automatically determined from the problem’s initial conditions, as it depends on the distance between individuals in the first generation. However, it is important to ensure that the initial population has sufficient diversity to allow for effective exploration of the solution space. The value of k is typically chosen based on experimental tuning or domain knowledge. A higher k results in a faster reduction in inertia weight, leading to quicker convergence during the exploitation phase. A smaller k leads to a more gradual reduction. A smaller inertia weight at this stage helps the algorithm reduce the search space, focusing on fine-tuning the best solutions found and speeding up convergence. As the inertia weight decreases, the algorithm’s exploration capacity diminishes, allowing for more focused exploitation around the promising regions, resulting in faster convergence. d₀ and k allow the algorithm to adjust its search behavior dynamically based on the population’s diversity, enhancing the balance between exploration and exploitation. d₀ ensures that the inertia weight starts at an appropriate level based on the initial diversity of the population, promoting exploration early on. k controls the rate at which inertia weight decreases, preventing premature convergence and allowing for more controlled and efficient search progression.

Introducing adaptive inertia weights, dynamic weights can be adjusted in real time based on the population state to avoid becoming stuck in local optima. We can enhance the exploration ability of the population in the initial stage and enhance the development capabilities in the later stages while improving the accuracy of solutions.

3.5. The INSWOA Process

The INSWOA uses LCM for population initialization, improving the algorithm’s global optimization ability. Introducing a nonlinear convergence factor during the position update phase is beneficial for exploring better solutions around the current optimal solution in a targeted manner; introducing adaptive inertia weights based on population diversity during the stages of bubble net hunting and trapping can effectively improve the quality of solutions, population diversity, and the convergence efficiency of algorithms, achieving a dynamic balance between local exploitation and global search. Because there are two optimization objective functions in this paper, it is not possible to minimize both optimization objectives through optimization. Therefore, a compromise solution needs to be found to achieve the best combination of the two optimization objectives. The specific steps of the INSWOA are as follows: (1) Set various algorithm parameters, input initialization data based on the EV charging model data. (2) Initialize the population through logistic mapping, generate an initial population, and perform non-dominated sorting. Calculate the fitness for each individual and find an optimal position to preserve. (3) Update $a$ and then update B and D according to Equation (4). If the probability p is below 50%, go to step (5). Otherwise, update the position using Equation (24). (5) Check whether the absolute value of the coefficient vector B is less than 1. If it is, use Equation (17). If not, perform a global random search for prey and update the position based on a randomly selected individual. (6) Once a maximum iteration count is reached, output a Pareto solution set that satisfies the constraint conditions. Otherwise, return to step (3) and repeat until the output conditions are fulfilled.

The algorithm flow is shown in Figure 2.

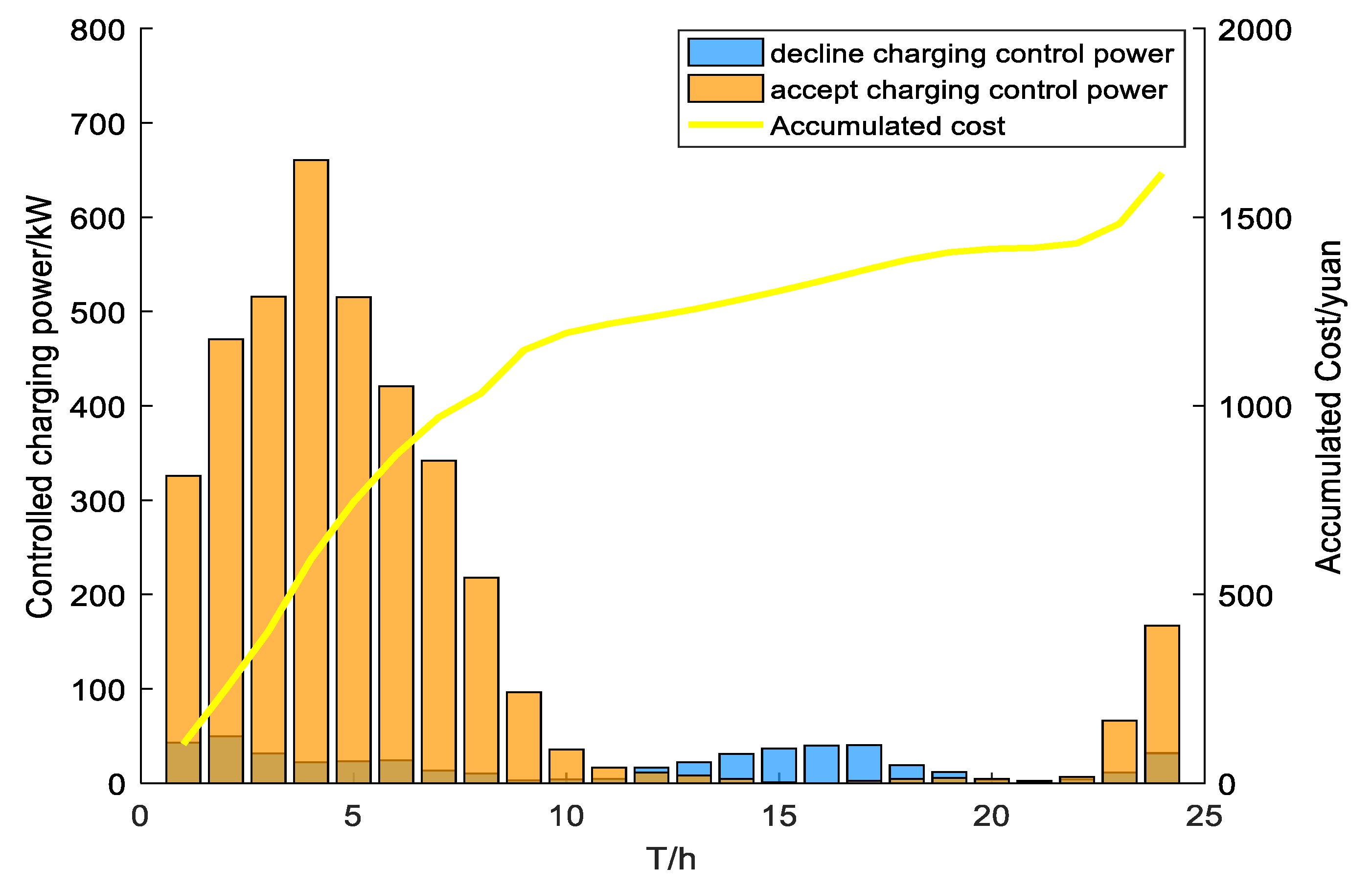
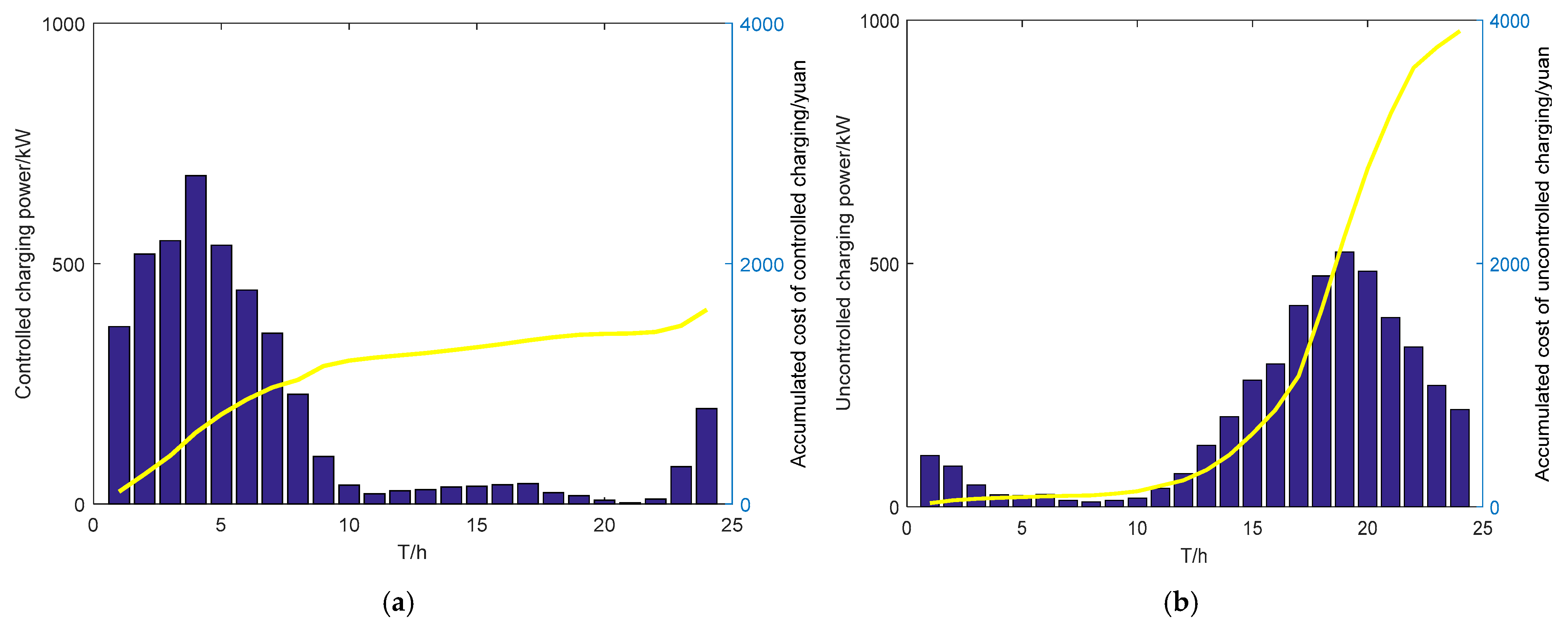
4. Simulation Examples and Result Analysis

This paper uses an INSWOA to solve the charging model. Using actual load in a certain region, it is assumed that there are 1000 EVs connected to the PG; the farthest travel distance of EVs is 320 km, and the charging power and battery capacity of EVs will change over time, but the short-term changes can be ignored. The simulation model used in this paper is for daily charging strategy planning, so fixed values can be selected for charging power and battery capacity when selecting values. The battery capacity is 40 kWh, the charging efficiency is 0.9, the slow charging power is 5 kW, and the fast charging power is 20 kW. The expected battery charge is 1. The initial population has 50 individuals and 100 generations of evolution. Individuals are represented as the starting charging time of the EVs. Through continuous iteration of the population, the starting charging time is optimized to minimize the PVLD of the PG and the CCs for users.

According to “28 Measures for Refining and Improving the Electricity Price Policy for EV Charging and Swapping Facilities” issued by the Jiangsu Provincial, which will be implemented from 1 December 2023, the time-based electricity pricing and peak, flat, valley period division are shown in

Table 1. EV charging price.

Time Division	Time-Based Electricity Pricing (CNY/kWh)
Peak time 8:00–11:00, 17:00–22:00	1.1526
Flat time 11:00–17:00, 22:00–24:00	0.6703
Valley time 0:00–8:00	0.2805

, as follows:

Substituting the above charging price into the EV charging model, the simulation results are as follows:

Figure 3 shows the non-dominated Pareto optimal solution set obtained after algorithm optimization. The specific values of the generated Pareto solution set are as follows:

In order to determine final charging strategy, we must make a selection based on the optimal solution set generated in

Table 2. Optimal solution set.

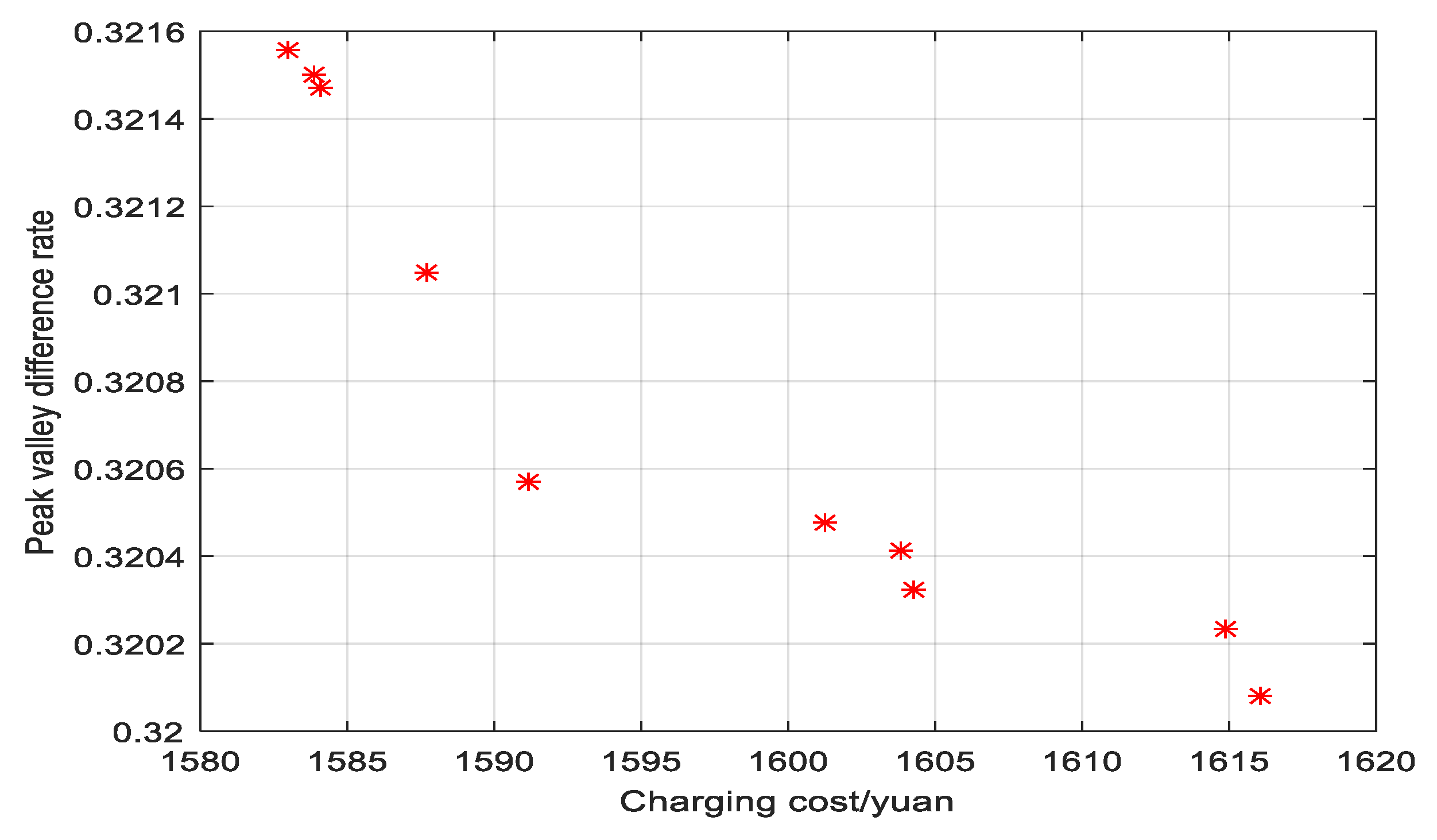
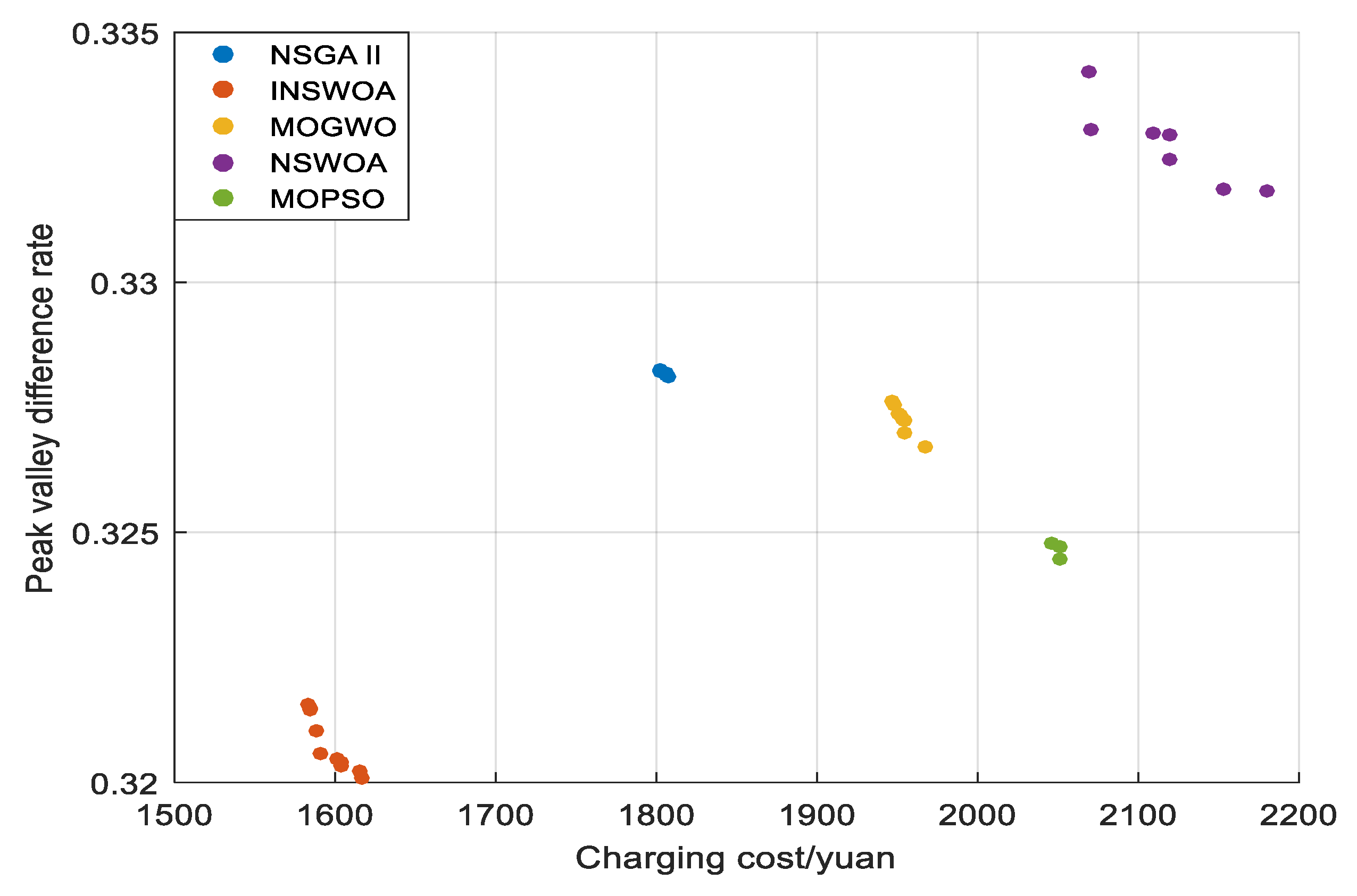
PVLD	CC
0.3216	1582.952
0.3201	1616.057
0.3204	1603.865
0.3215	1584.116
0.3206	1591.188
0.3210	1587.734
0.3215	1583.843
0.3205	1601.284
0.3203	1604.304
0.3202	1614.886

. The selection can be based on the importance of comparing the two optimization objectives. As the premise for users to obtain better economic efficiency is that the PG can operate safely and reliably, the optimal solution should be prioritized. Considering the minimum PVLD of the PG load, the scheme with a PVLD rate of 32.01% and a CC of CNY 1616.057 is chosen as the charging strategy scheme.

According to the selected data, Figure 4 can be obtained as follows:

Figure 4 shows the decline and accept charging control power, reflecting the proportion and charging time of users who comply with the grid arrangement for charging and those who do not. The number of users who comply with the grid arrangement for charging in the figure is 878, and the number of users who do not comply with the grid arrangement for charging is 122. Users who do not comply with the grid arrangement for charging will start charging as soon as they arrive at the station. From the figure, it can be clearly seen that the decline charging control power is higher from 13 o’clock to 18 o’clock and from 24 o’clock to 6 o’clock. Most of these periods are during periods of low electricity prices, and the cost of starting charging is relatively low. Compared to simply following the grid arrangement, it can better compensate for the interests of users.

Under this charging strategy, the controlled and uncontrolled charging power and CC are shown in Figure 5a,b:

In unregulated charging, the CL of EVs reached its highest at 523.5 kW at 19 o’clock, and the total CC for all users was CNY 3910.054. Based on the charging optimization strategy proposed in this paper, the maximum CL for EVs reaches 682.6 kW at 4 o’clock, and the total CC for all users is CNY 1616.057. Through comparative analysis, it can be concluded that users participating in grid dispatching mainly concentrate on charging during valley periods, and, due to the low electricity prices during this period, the CC is significantly lower than that of unregulated charging, while the start time of charging is later than that of uncontrolled charging users. At midnight and early morning next day, the CL of uncontrolled charging is mainly concentrated between 15 and 22 o’clock, and it is directly charged after returning home, as shown in Figure 6. During this period, not only is the electricity price high, but the grid load is also at its peak, which can lead to high CCs for users and is not conducive to stable operation in the PG.

According to

Table 3. The PVLD rate under various charging modes.

Charge Mode	Peak Load/kW	Valley Load/kW	PVLD Rate
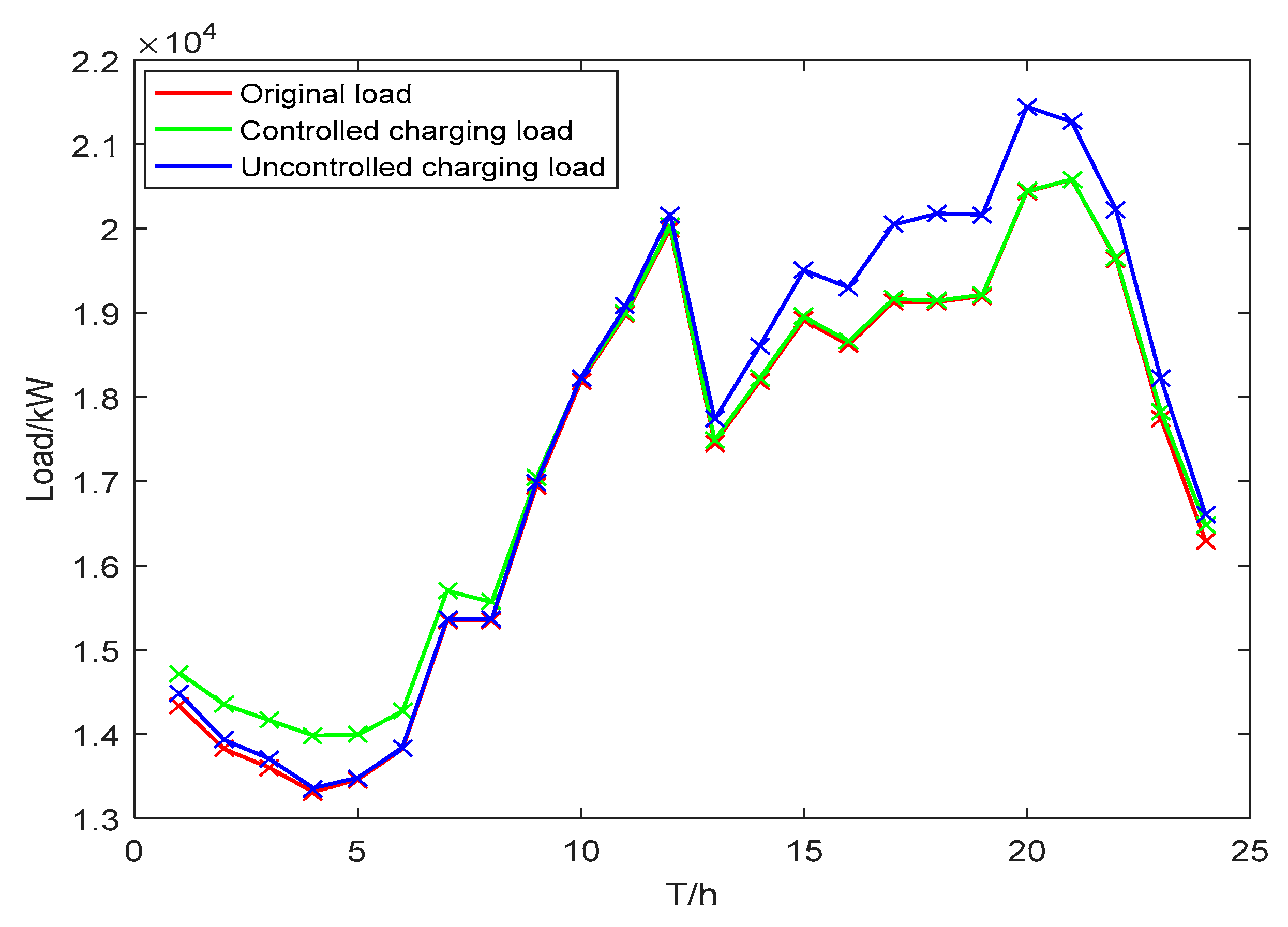
Original load	20,583.000	13,314.000	35.32%
uncontrolled charging	21,449.036	13,357.356	37.73%
controlled charging	20,585.268	13,995.924	32.01%

, the PVLD rate of the original PG load is 35.32%. When charging randomly, the low load characteristic of the PG during valley periods is not utilized well, and the charging power of EVs is also high when the PG load is high, resulting in an increase in the PVLD rate to 37.73%, which wastes energy resources. The controlled charging strategy proposed in this paper schedules the start time of most users’ charging to valley period, reducing the load PVLD rate by 3.31% compared to the original load, improving load utilization, and achieving the goal of smoothing the load curve.

In order to fairly compare the optimization capabilities of the INSWOA used in this paper with other algorithms, a maximum iteration count of 100 and a population size of 50 were unanimously selected. The NSGA-II algorithm, multi-objective particle swarm optimization (MOPSO), multi-objective gray wolf optimizer (MOGWO), NSWOA, and INSWOA used in this paper were chosen to verify the performance and Pareto of the INSWOA [35,36,37]. The solution set is as follows:

From Figure 7, it can be seen that, under the same parameter settings, the INSWOA has significant advantages over both the WOA and other algorithms, achieving better optimization results. Compared to the NSWOA, through three improvement methods, it has jumped out of the local optimal solution of the population, enhanced its global search ability, and made it have stronger exploration and development capabilities. The INSWOA greatly outperforms other algorithms in optimizing dual objectives, demonstrating the superiority of the algorithm.

5. Discussion

There has been extensive research on EV charging strategies, with most researchers focusing on adjusting electricity pricing strategies to encourage charging or the designing of multi-tiered charging schemes. However, there has been limited research on charging strategies that take into account the selectivity of EV users. In practice, electricity prices in a region are typically determined by government regulations, making it less practical to influence EV users’ charging behavior solely through price adjustments. EV users exhibit subjective selectivity in their charging behavior. This paper considers the selectivity of EV users, allowing them to choose their preferred charging type and decide whether to comply with grid-controlled charging. By respecting users’ choices while simultaneously involving them in grid scheduling, this approach ensures user satisfaction while enhancing grid stability. In the field of EV charging strategy optimization, many researchers have utilized the NSWOA. Building on this foundation, this paper proposes an INSWOA. Enhancements have been made at various stages of the algorithm, including population initialization, convergence factors, catching prey, bubble net predation, and searching for prey. Compared to the standard NSWOA and other algorithms, the improved algorithm demonstrates significant advantages, achieving better optimization results.

6. Conclusions

This paper takes reducing the impact of EV CL on the PG as the starting point and proposes an optimization strategy for EV charging that considers user selectivity. Users can choose whether to comply with the PG arrangement for charging based on the CC, the model is established to optimize the PVLD in the PG and the users’ CCs. The simulation results show that, under uncontrolled charging without any intervention, the charging power of EVs peaks at 19 o’clock, with a total CC of CNY 3910.054 and a PVLD rate of 37.73%. Under the EV charging strategy proposed in this paper, the charging power peaks at 4 o’clock, with a total CC of CNY 1616.057 and a PVLD rate of 32.01%. Compared to uncontrolled charging without any intervention, the charging strategy considering user selectivity considered in this paper can effectively reduce the peak load of the PG, reduce users’ costs, and play a role in load transfer, peak shaving, and valley filling. At the same time, an INSWOA was proposed which uses logistic mapping for population initialization, introduces nonlinear convergence factors, and combines adaptive inertia weights to improve population diversity, enhance global optimization ability, reduce premature convergence, and improve solution accuracy. The results show the following: (1) Compared with other optimization algorithms, the improved INSWOA has significant optimization effects and achieves good optimization results for both optimization objectives. (2) The algorithm proposed in this paper can significantly reduce users’ CCs and grid PVLDs, demonstrating its superiority and practicality. Under real conditions, it can be used in home charging station systems to provide users with selectable solutions by detecting their charging information. This allows users to reduce CCs and participate in grid scheduling while meeting their charging needs. It can bring better economic benefits and effectively alleviate the impact of CLs on the grid, providing a good reference for EV charging scheduling problems.