Thermal Performance Assessment of Lithium-Ion Battery Packs Under Air-Cooling Conditions

Abstract

Electric vehicles (EVs) have garnered significant attention in recent years due to their near-zero carbon dioxide emissions and compatibility with sustainable transportation systems. However, the lack of high-performance batteries remains a major barrier to widespread EV adoption. This study examines the variations in heat transfer coefficient and surface temperature of prismatic lithium iron phosphate (LiFePO₄) battery packs during discharge operations. Experiments were conducted using both forced air convection and natural convection. A wind tunnel was constructed to maintain an ambient temperature of 25 °C. The air flow rates were set at 0, 40, 80, and 120 g/s, while the battery pack spacings were 5, 10, and 15 mm. Discharge rates of 0.50, 0.75, and 1.00 C-rate were also examined. The results reveal that increasing the discharge rate led to a significant and uniform rise in surface temperature across the battery pack. Additionally, the voltage decreased gradually until an approximately 90% depth of discharge, after which it declined rapidly until the battery pack was depleted. Under forced convection, the voltage drop occurred slightly faster than that under natural convection. Greater spacing between battery packs enhanced cooling efficiency. Higher air flow rates increased the convection coefficient, whereas an increased discharge rate elevated the heat generation but reduced the heat convection coefficient. The highest heat dissipation was observed at a battery pack spacing of 15 mm, a discharge rate of 1.00 C, and an air flow rate of 120 g/s. The highest convection coefficient was achieved under the same spacing and air flow rate, but with a discharge rate of 0.50 C-rate.

1. Introduction

Excessive consumption of fossil fuels in internal combustion engines causes severe global warming through the release of large amounts of greenhouse gases. Carbon dioxide (CO₂) is the main greenhouse gas, which is released from driving cars and transportation. As a result, electric vehicles (EVs) have attracted a lot of attention. They considered technologies that emit almost zero carbon dioxide and are friendly to the environment [1234]. Numerous nations are encouraging wider adoption of electric cars, and some have already transitioned parts of their public transportation systems to electric vehicles. However, we lack high-performance batteries in the present, which are the most important parts for electric cars. This is considered a serious obstacle to consumer purchasing decisions and the expansion of the electric vehicle industry. For this reason, the Thai government has outlined initiatives to strengthen research capabilities and advance the development of systems associated with electric vehicle technologies, with particular emphasis on battery innovation [5].

Lithium-ion batteries are widely used in electric vehicles because they have the advantages of high specific energy and working voltage and long life [6,7,8,9]. But the thermal safety problems cannot be ignored. The main considerations influencing the transition to electric vehicles include the duration required for battery charging, safety issues arising from heat generated within the battery pack, and the maximum distance achievable per charging cycle [10,11,12]. The charging duration is determined by the charging rate, and increasing the charge or discharge rate (C-rate) can greatly shorten the required time. However, a higher C-rate also causes a substantial rise in the internal battery temperature [13]. When the temperature increases, the available driving range can drop dramatically—from the full rated distance to nearly forty percent. This is why battery pack cooling plays a critical role, as the ideal operating temperature range for the cells is between 15 and 40 °C [14,15,16]. If the temperature exceeds this range, excess heat can trigger reactions in the cathode and electrolyte, releasing gases that may ignite. This can lead to a self-accelerating sequence of heat generation and combustion, known as the “thermal runaway phenomenon,” which directly contributes to faster battery degradation [1,17].

Battery-pack thermal management plays a vital role in maintaining the overall performance of electric vehicle systems. By limiting excessive heat and ensuring that the cells operate within an appropriate temperature range, an effective cooling strategy helps slow down battery aging and prolongs the usable lifetime of the pack. In general, the cooling characteristics for battery packs can be classified into two systems. A passive cooling system does not require energy, relying on natural heating convection. However, the cooling efficiency of this system may also depend on the surface area of the battery; therefore, this method may be suitable for applications where the compression or discharge rate is not very high. Another approach is the active cooling system, which relies on external energy to function. In this configuration, additional components are needed to circulate the working fluid, such as air, water, or refrigerants, so that heat can be removed through forced convection. This technique is well-suited for applications involving relatively high charge or discharge rates; however, part of the battery’s stored energy must be allocated to operate the cooling equipment. Moreover, incorporating extra hardware reduces the available internal space, thereby lowering the pack’s usable capacity [5]. Although air cooling generally provides lower heat-removal capability than that of liquid- or refrigerant-based systems, it offers advantages in simplicity, reduced cost, and minimal power consumption due to air’s inherently low thermal conductivity [18,19,20]. Enhancing the air flow rate is an effective way to improve its thermal performance, allowing it to approach the cooling efficiency of liquid-based systems.

Previous research has studied the characteristics of battery packs such as via changing the distance between electric vehicle batteries studied at distances of 1–8 mm using a mathematical model. It was found that increasing the distance between battery packs can lower the battery pack surface temperature because reducing the air flow resistance increases the cooling efficiency of the battery packs [21]. The heat distribution on the surface of a battery pack was studied under the battery pack discharge rate condition of 2.00 C-rate by studying the changes in ambient temperature at 28, 35, and 42 °C, respectively [22]. The experimental results showed that the temperature of the atmosphere caused the voltage to decrease faster as the atmospheric temperature decreased. This characteristic was the result of an electrochemical reaction that varied with the battery pack temperature. It was also found that the surface temperature of the battery pack was the highest at a depth of discharge equal to 100%.

Although recent studies are informative, they still reveal important gaps in the understanding of air-cooled lithium-ion battery thermal management. For instance, a comparative simulation of phase change materials and fin-equipped air-cooling systems [23] focused solely on numerical modeling and did not consider battery spacing or variable airflow rate, both of which strongly influence convective heat transfer in multi-cell modules. Similarly, an optimized air-cooled structure proposed through simulation [24] lacks experimental validation and statistical assessment, limiting its applicability under real operating conditions where airflow maldistribution and environmental fluctuations are common. Another numerical work addressing air-cooling–based thermal safety [25] also omits voltage analysis and statistical correlations, despite voltage behavior being a critical indicator of electrochemical performance. Collectively, these gaps demonstrate the need for experimentally supported investigations that integrate temperature behavior, voltage response, and statistical evaluation to produce reliable and practically applicable results for electric vehicle battery systems.

To address these gaps, this study experimentally examines the heat convection coefficient and surface temperature characteristics of rectangular lithium-ion battery packs under controlled air-cooling conditions. A custom wind tunnel was constructed to regulate airflow rate (40, 80, and 120 g/s), ambient temperature (25 °C), battery cell spacing (5, 10, and 15 mm), and discharge rate (0.50, 0.75, and 1.00 C-rate). Beyond thermal measurements, the study evaluates temperature–voltage relationships during discharge, offering deeper insights into electrochemical behavior under varying cooling conditions. Statistical analysis using one-way ANOVA was applied to determine the significance of air flow, spacing, and discharge rate on both temperature and voltage responses. This integrated experimental approach provides more reliable evidence to support the design of efficient and thermally stable battery packs for electric vehicle applications.

2. Numerical Simulation

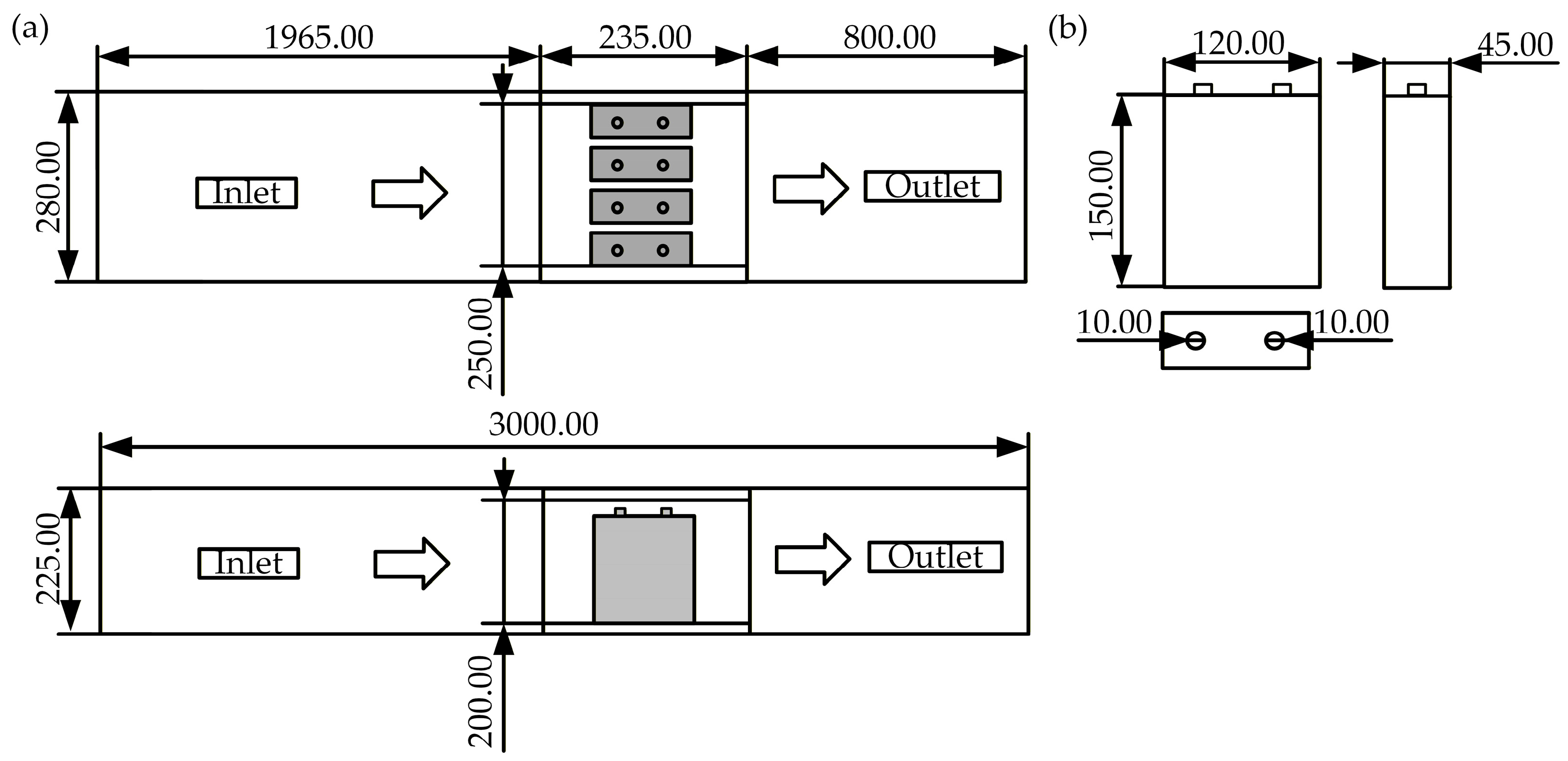
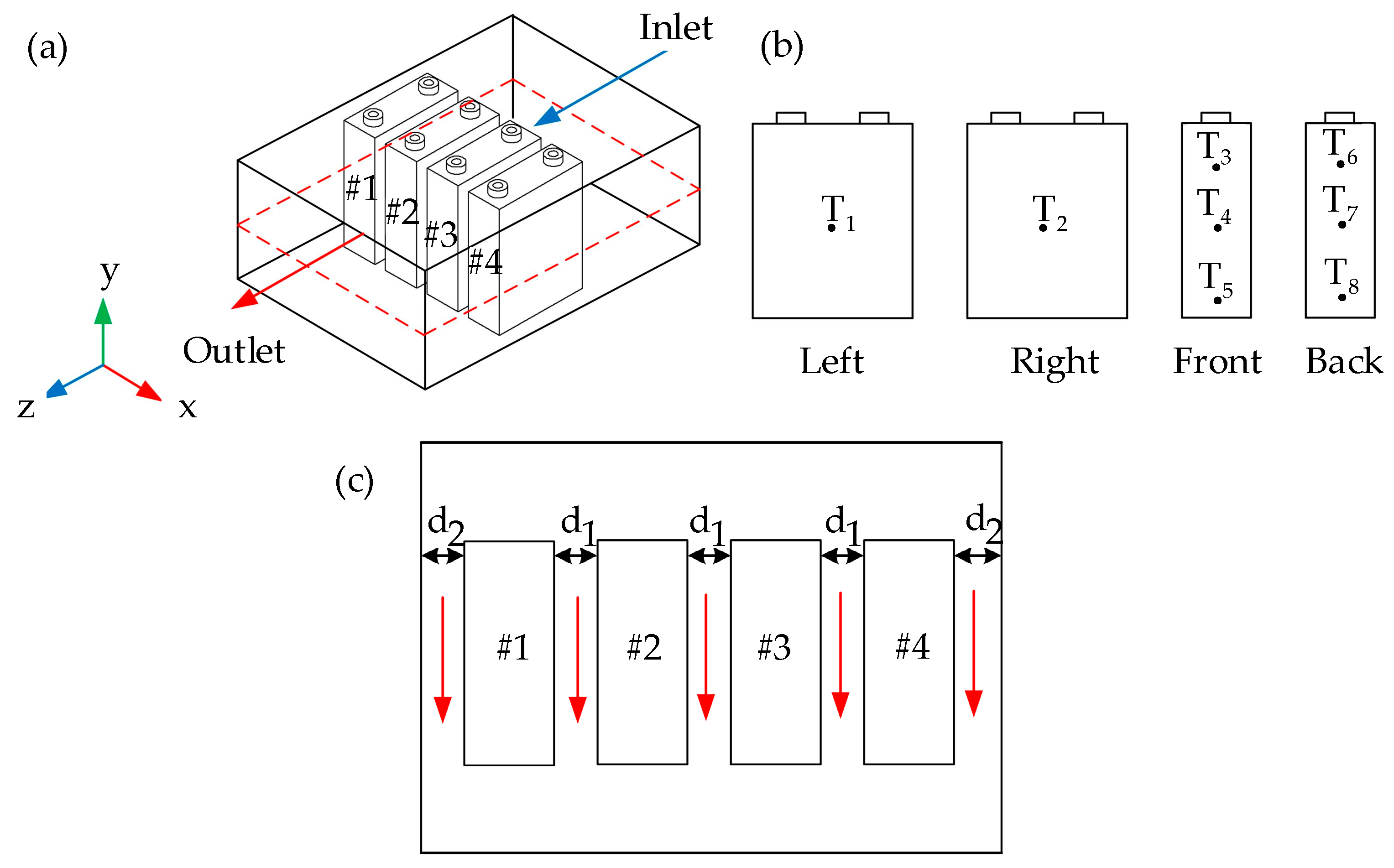
2.1. Geometry Model

The rectangular wind tunnel, illustrated in Figure 1a, is used in the geometric model to represent an air-cooling configuration for the battery pack. The tunnel features an inlet and an outlet [26], with airflow directed along its longitudinal axis. The separation between the inlet and outlet is approximately 3000 mm. The duct measures 200 mm in width and 250 mm in height and has a wall thickness of 12.7 mm. The battery pack contains four lithium-ion phosphate battery (LiFePO₄) prismatic cells arranged in a single row. Each cell has dimensions of 45 mm × 120 mm × 150 mm, as shown in Figure 1b, and the pack provides a capacity of 50 Ah at 3.3 V with a maximum discharge rate of 3.00 C-rate. Air enters the tunnel, moves through the battery cell arrangement, and finally exits.

2.2. Equations and Methods

In this study, numerical modeling and simulation techniques were applied to analyze the cooling behavior of the battery pack, with particular attention given to the temperature distribution on the cell surfaces and the temperature of the outlet airflow [27]. Finite Element Analysis was conducted using the SolidWorks Flow Simulation platform (version 2021 SP03.7). The simulation setup followed fundamental fluid dynamics principles, incorporating four governing equations: the mass-continuity equation, the momentum equation, the energy equation, and the heat-transfer equation [28].

The mass continuity equation is shown as follows:

$${\displaystyle \frac{\partial \rho }{\partial t}}+\nabla \left(\rho \cdot \overline{\nu }\right)=0$$

(1)

The momentum equation is shown as follows:

$${\displaystyle \frac{\partial \left(\rho \cdot \overline{\nu }\right)}{\partial t}}+\nabla \left(\rho \cdot \overline{\nu }\cdot \overline{\nu }\right)+\nabla P=\nabla \left(\mu \cdot \Delta \overline{\nu }\right)$$

(2)

The energy equation is shown as follows:

$${\displaystyle \frac{\partial \left(\rho \cdot \overline{\nu }\right)}{\partial t}}+\nabla \left(\rho \cdot c\cdot \overline{\nu }\cdot T\right)=\nabla \left(K\cdot {\nabla }^{2}T\right)$$

(3)

where $\rho$ is the density (kg/m³), $t$ is the time (s), $\overline{\nu }$ is the velocity vector (m/s), $P$ is the pressure (N/m²), $\mu$ is the dynamic viscosity (Pa·s), $T$ is the temperature (°C), $c$ is the specific heat capacity (J/kg·°C), and $K$ is the thermal conductivity (W/m·°C).

In the present work, modeling turbulence was neglected by the turbulent model selection in the simulation. In addition, the heat transfer equations were calculated to investigate the convection as follows:

$$Q=\dot{m}\cdot C_p\cdot \Delta T$$

(4)

$$Q=h\cdot A_s\cdot \left(T_s-T_{\propto }\right)$$

(5)

where $Q$ is heat transfer (W), $\dot{m}$ is the air flow rate (g/s), $C_p$ is the specific heat capacity at constant pressure (J/kg·°C), $h$ is the convection coefficient (W/m²·°C), $A_s$ is the surface area for heat convection (m²), $\Delta T$ is the air temperature difference between the inlet and outlet (°C), $T_s$ is the surface temperature of the battery (°C), and $T_{\propto }$ is the ambient temperature (°C).

The mesh used for the air-cooling analysis was generated through SolidWorks Flow Simulation [29,30]. A mesh density of level 6 (on a scale where 7 is the finest) was selected for the model. High-resolution rectangular elements were employed to better match the geometry of the wind tunnel and the prismatic battery cells. Simulation parameters were defined using the Wizard tool, with air specified as the working fluid for the battery pack thermal management environment. The total computation time for each simulation run was configured to be 60 min. The volume source heating was selected to determine the surface heating value of the battery pack. The boundary conditions used in the simulation are indicated as follows: the material was made of 1060 alloy, the inlet temperature was 25 °C, the relative humidity was about 50%, and the atmospheric pressure was considered 101,325 Pa. The air flow rate was determined as various values of 40, 80, and 120 g/s. The different discharge rates were considered 0.50, 0.75, and 1.00 C-rate.

2.3. The Simulation Results

The simulation results indicate that increasing the spacing between battery cells leads to a slight reduction in the battery pack’s surface temperature [31]. When the installation angle of the battery pack increases, the resulting uneven cooling generates wake vortex turbulence. Under conditions of an increased discharge rate, the battery pack exhibits the lowest surface temperature at a discharge rate of 0.50 C-rate and an air flow rate of 120 g/s. Therefore, a comparison between natural convection and forced convection was conducted to investigate the effects of inlet temperature and airflow rate on battery surface temperature. For this analysis, the largest cell spacing of 15 mm was selected, with the discharge rate and air flow rate fixed at 1.00 C-rate and 40 g/s, respectively. The inlet temperatures of the wind tunnel were set to 25, 30, and 40 °C.

At the same inlet temperature, the battery surface temperature (ST) under the forced convection (FC) model at 40 g/s is lower than that under the natural convection (NC) model, as shown in Figure 2. A similar trend is observed in the outlet temperature (OT), where forced convection consistently produces lower outlet temperatures than natural convection for all inlet temperature conditions.

Furthermore, increasing the inlet temperature results in only minor changes in both the battery surface temperature and the outlet temperature. At a depth of discharge ratio of 1.00, the outlet temperature differences are approximately 7.69, 7.67, and 7.73 °C, respectively. Increasing the airflow rate reduces the variation in battery surface temperature, and at a depth of discharge ratio of 1.00, the outlet temperature decreases by approximately 4.99, 5.02, and 5.09 °C, respectively.

The comparison between forced convection and natural convection demonstrates the substantial advantages of active cooling for battery thermal management. Forced convection consistently produces lower surface and outlet temperatures, confirming its superior ability to dissipate heat generated during battery operation. This behavior highlights the necessity of incorporating active air flow to maintain thermal safety, prevent overheating during high discharge rates, and promote longer battery cycle life. The findings clearly indicate that forced air flow is a critical component of effective thermal management systems, particularly when the battery pack operates under high-load conditions.

The comparative analyses also clarify the broader influence of different cooling mechanisms and operating conditions on the thermal behavior of the battery pack. The minimal impact of inlet temperature variations demonstrates that the cooling system maintains stable performance across a range of ambient conditions. Additionally, the reduction in temperature variation with increased air flow rate emphasizes the role of sufficient forced air flow in preventing localized thermal accumulation. Collectively, these results provide valuable guidance for optimizing battery thermal management strategies and support the development of more reliable and thermally robust battery systems.

3. Experimental Procedure

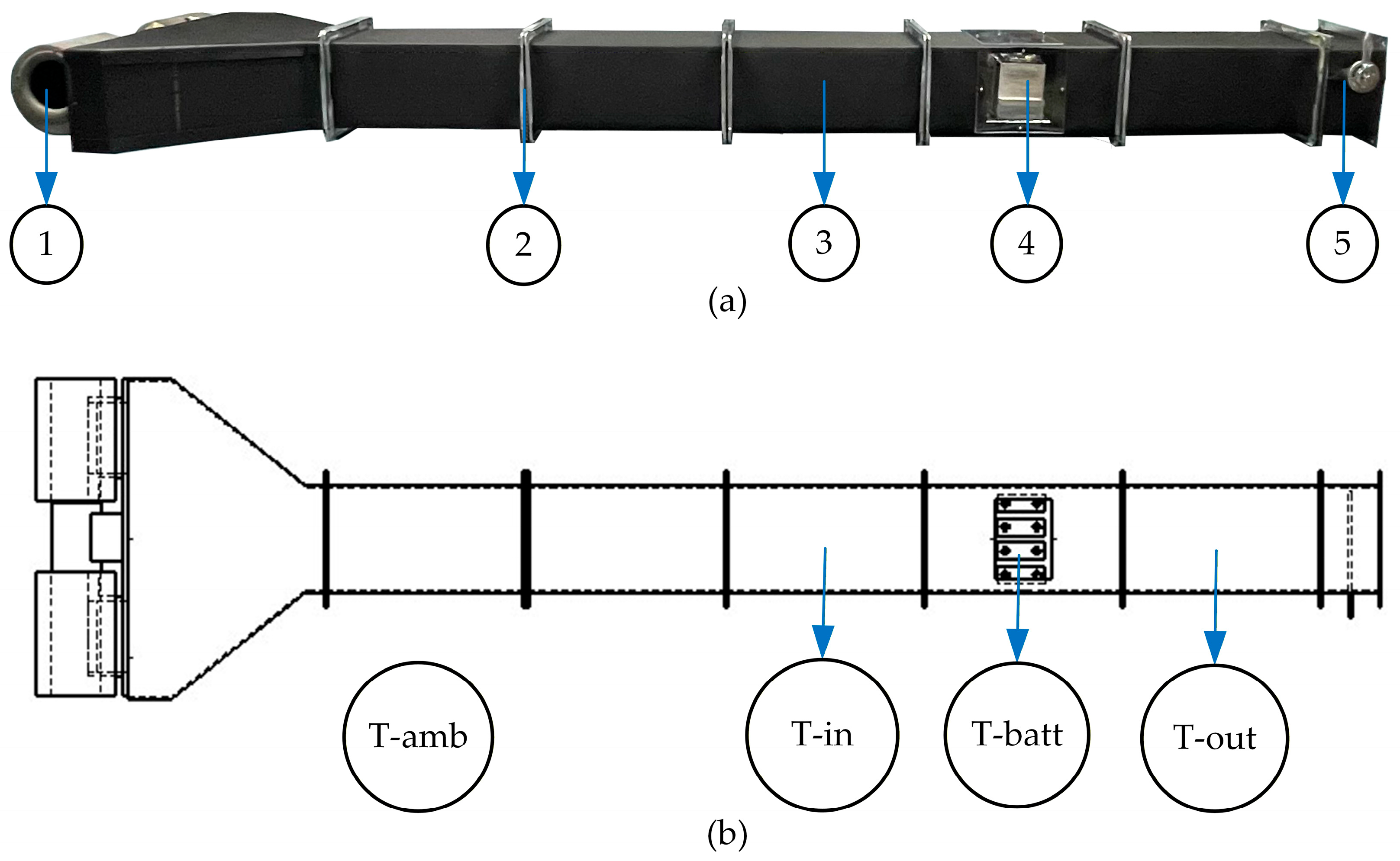
3.1. Experimental Preparation

The wind tunnel system in the experiment had two-way an inlet and an outlet. It was constructed of Stainless-Steel plates (Grade 304) and covered by synthetic insulation (Aero flex, EPDM) with a thickness of 12.70 mm to protect against potential temperature effects during the experiment. The wind tunnel had dimensions of 255 mm × 3000 mm × 200 mm. Figure 3a shows the components of the wind tunnel used in the experiment, detailed as follows:

(1)

A centrifugal blower with a power rating of 141 W was used to create a pressure difference inside the wind tunnel and was equipped with a speed control system (variable speed drive).

(2)

A grille increased air distribution evenly throughout the cross-section.

(3)

The air flow rate inside the wind tunnel was controlled at values of 0.50, 0.75, and 1.00 g/s. The average air flow rate across the cross-section was derived from 25 measurements using an Air Velocity and IAQ instrument (Testo 440 dp) connected to a 16 mm vane probe (range: 0.6–50 m/s; accuracy: ±0.2 m/s). The measurement locations were defined according to the Log-Tchebycheff rule, as recommended by ASHRAE Standard 111:2008.

(4)

Location of four prismatic-shaped battery cells: The four battery packs used in the experiment were LiFePO₄ prismatic-shaped lithium-ion batteries (Brand: NBCELL) with dimensions of 135.3 × 29.3 × 185.3 mm³. The battery had a capacity of 50 Ah, a nominal voltage of 3.2 volts, and a continuous maximum discharge rate of 3 C-rate. These batteries are commonly used in electric golf carts. In addition, the experimental discharge rate control device was an Electric Load Battery Tester (Brand: Chin) with a power rating of 180 W. It can control a maximum discharge rate of 20 A with a current measurement range of 0.0–20 A, with an accuracy of ± 0.01 A, and a voltage measurement range of 0.0–200 V, with an accuracy of ±0.01 V.

(5)

The damper was used to control the mass flow rate.

The location of temperature measurement and airflow rate measurement is shown in Figure 3b. The K-type thermocouple set was used to measure the temperature by starting from the ambient temperature (T-amb) and progressing to the inlet of the wind tunnel (T-in), the battery surface (T-batt) in various positions, and the outlet of the wind tunnel (T-out) [32]. The recording device of the battery pack surface temperature was a midi Logger (Brand: GRAPHTECH Model GL840), which consists of up to 20 measurement channels and has a temperature measurement range of −200 °C to −1260 °C with an accuracy ±0.05% and a reading value ±1 °C. It was connected to a set of thermocouple cables (type K). The parameters were controlled in the experiment, such as the ambient temperature of 25 ± 1 °C, the mass flow rate, and the battery distance.

3.2. Battery Pack and Controlling Device

The battery pack under investigation consists of four prismatic lithium iron phosphate (LiFePO₄) cells, each measuring 45 mm × 120 mm × 150 mm [33]. The assembled pack provides a capacity of 50 Ah at a nominal voltage of 3.3 V, and it is capable of operating at a maximum discharge rate of 3.00 C-rate. The size of the battery pack used for Electric golf carts is shown in Figure 4a. The Electric Load Battery Tester was the electrical equipment used in controlling the discharge rate in the research, as shown in Figure 4b. It has an electric power of about 180 W with an accuracy of ±0.01 A and the ability to draw a maximum charge of 20 A.

3.3. Experimental Procedures

The experiment preparation was focused on the three main conditions: the different depths of discharge, the different airflow rates, and the different battery cell distances. Characteristics of the battery within the wind tunnel used in the experiment for studying the conditions are shown in Figure 5. In the first step, the battery pack was placed in a direction parallel to the length of the wind tunnel, as shown in Figure 5a. Eight thermocouples were attached to a battery cell for temperature measurement in eight positions: a thermocouple at the left surface position, a thermocouple at the right surface position, three thermocouples at the front surface position, and three thermocouples behind the surface position, as shown in Figure 5b.

In the second step, each battery cell was placed at different distances of 5, 10, and 15 mm for studying these conditions in the experiments, as shown in Figure 5c. Meanwhile, the other conditions were set to single values, and the values did not change throughout operation. The data was recorded. In the third step, after the end of studying the battery cell distance, the above experimental process was repeated for studying the next condition and results were recorded. The battery was studied by adjusting the air flow rate from 0.00 (natural convection) to 40, 80, and 120 g/s and comparing the depth of discharge at 0.50, 0.75, and 1.00 C-rate, respectively. In the final step, the total experimental data under different working conditions could be analyzed using one-way ANOVA at a statistical significance value of less than 5% (p < 0.05). The results are expressed in the next section.

4. Results and Discussion

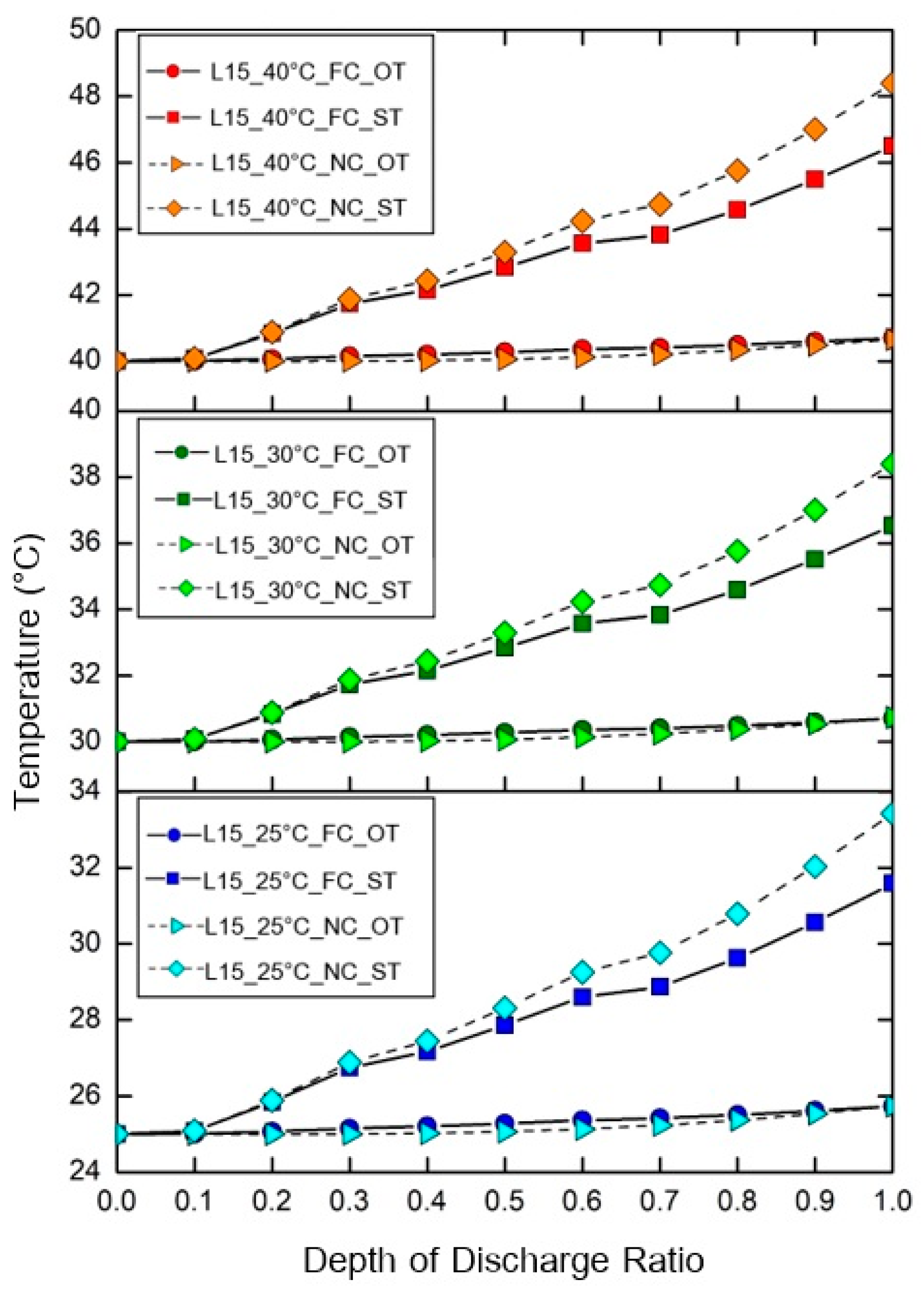
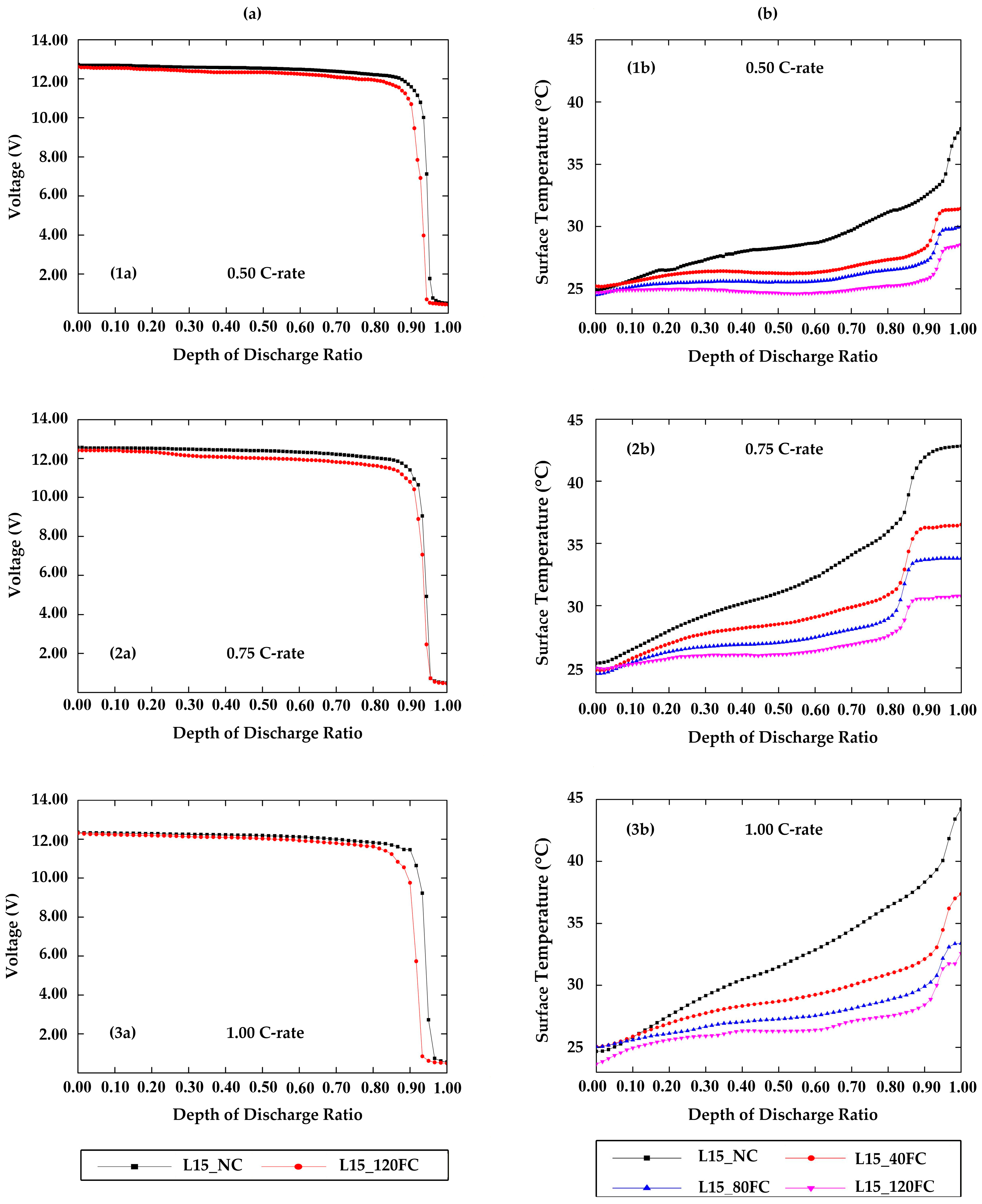
4.1. The Effect of Depth of Discharge (DOD)

We analyzed the effect of the battery surface temperature changing while the depth of discharge ratio changed from 0 to 100% for four battery packs by the natural convection heat exchange method using the statistical analysis principle. We used analysis of variance (one-way ANOVA) with Duncan’s multiple-range test using the SPSS program (SPSS, Version 25, Inc., Chicago, IL, USA) at the 95% confidence level (p < 0.05). The results of the battery surface temperature analysis are shown as the depth of discharge ratio increases. The results are the average values of the battery surface temperature, along with their standard deviations. In addition, the exponents indicate significant differences in the data in the same column.

Table 1. The results of battery surface temperature analysis at various depths of discharge and with natural convection.

Battery Pack Number	Depth of Discharge (DOD) Ratio
	0.00	0.25	0.50	0.75	1.00
1	24.71 ± 0.07 a	28.21 ± 0.08 b	31.12 ± 0.06 c	34.97 ± 0.09 c	45.62 ± 0.09 c
2	24.64 ± 0.16 a	27.67 ± 0.16 a	30.08 ± 0.15 a	33.53 ± 0.15 a	42.92 ± 0.54 b
3	24.63 ± 0.16 a	27.78 ± 0.27 a	30.40 ± 0.27 b	34.05 ± 0.23 b	41.51 ± 0.15 a
4	24.60 ± 0.07 a	29.66 ± 0.19 c	34.02 ± 0.27 d	38.82 ± 0.21 d	46.67 ± 0.25 d

Values in the same column with different superscripts mean that the average values are significantly different (p < 0.05).

presents the variation in battery surface temperature at different depth of discharge (DOD) ratios under both natural convection and forced convection conditions, with an air flow rate of 120 g/s. During the early stages of discharge (DOD = 0.00–0.25), there was no statistically significant difference between the two cooling conditions (p > 0.05). This indicates that at low DOD levels, the rate of heat generation within the battery pack remained relatively low, and therefore, airflow had minimal influence on heat dissipation. However, as the DOD increased beyond 0.50, a significant rise in surface temperature was observed for both conditions (p < 0.05). This temperature increase corresponded to higher internal resistance and increased electrochemical activity during the discharge process.

Notably, the natural convection condition consistently exhibited higher surface temperatures than forced convection did at 120 g/s, particularly at DOD values of 0.75 and 1.00. This trend indicates that natural convection was insufficient to remove the accumulated heat from the battery cell surface, whereas forced convection enhanced heat transfer by providing more effective air movement across the battery surface. As a result, the forced convection system maintained a comparatively lower temperature profile at higher DOD levels. This confirms that air flow rate plays a crucial role in mitigating thermal stress during high-discharge operations.

To further evaluate the influence of convection,

Table 2. The results of battery surface temperature analysis at various depths of discharge and with forced convection at an air flow rate of 120 g/s.

Battery Pack Number	Depth of Discharge (DOD) Ratio
	0.00	0.25	0.50	0.75	1.00
1	24.81 ± 0.11 c	26.91 ± 0.13 c	27.35 ± 0.13 b	28.34 ± 0.14 a	35.14 ± 0.36 d
2	24.10 ± 0.15 a	26.01 ± 0.12 a	26.74 ± 0.15 a	27.79 ± 0.23 a	32.44 ± 0.67 b
3	24.76 ± 0.21 c	26.39 ± 0.27 b	26.71 ± 0.30 a	27.75 ± 0.29 a	30.82 ± 0.29 a
4	24.58 ± 0.18 b	27.25 ± 0.23 d	27.88 ± 0.28 a	29.13 ± 0.24 d	32.11 ± 0.24 b

Values in the same column with different superscripts mean that the average values are significantly different (p < 0.05).

presents the results of battery surface temperature analysis exclusively under forced convection with an air flow rate of 120 g/s. The data confirms that the increase in DOD resulted in a proportional and statistically significant rise in average battery temperature across all battery packs. Compared to the natural convection data in Table 1, the reduction in temperature under forced convection became increasingly evident as DOD progressed from 0.50 to 1.00. Battery packs 1 and 3 showed greater sensitivity to DOD variation, suggesting nonuniform heat distribution within the pack structures. This may be attributed to variations in airflow exposure or differences in internal cell arrangement.

Additionally, under the condition of 1.00 C-rate, the temperature distribution became more uniform across the battery cross-section, as observed in Table 2. Based on this temperature behavior, thermocouple installation at positions 2 and 4 (as shown in Figure 5b) was selected to minimize interference with air flow and provide reliable readings. These positions were determined to offer an optimal balance between measurement accuracy and practical feasibility for the experimental setup.

4.2. The Effect of Battery Voltage

The analysis of battery voltage and surface temperature as a function of the depth of discharge (DOD) ratio under different cooling conditions provides critical insights into the coupled thermo-electrochemical behavior of the battery cells. In this study, the battery cells were spaced 15 mm apart, and the effects of natural convection (NC) and forced convection (FC) with air flow rates of 40, 80, and 120 g/s were examined. Figure 6a demonstrates that the battery voltage remained relatively stable from the beginning of discharge up to an approximately 0.85 DOD. A slight voltage decline occurs near a 0.90 DOD, followed by a steep drop as full discharge was approached. This characteristic voltage behavior represents typical electrochemical kinetics in lithium-ion batteries, where stable voltage at lower DODs corresponds to efficient charge transfer and ion transport, while a rapid decline at high DODs indicates lithium-ion depletion and increased internal resistance caused by concentration polarization and changes at the electrode interface.

Interestingly, a comparison between natural convection and forced convection at an air flow rate of 120 g/s and a battery cell spacing of 15 mm indicates that the voltage under natural convection (L15_NC) dropped slightly slower than that under forced convection of 120 g/s (L15_120FC). This phenomenon can be explained by the temperature difference between the cooling conditions. Under natural convection, insufficient heat dissipation results in higher temperature accumulation within a battery. The elevated temperature promotes faster electrochemical reactions, consistent with Arrhenius’ law, leading to improved internal reaction kinetics and lower internal resistance (RI). Conversely, under forced convection of 120 g/s, the lower temperature accumulation suppresses electrochemical reaction rates and leads to increased internal resistance, thus accelerating the voltage decline [34]. Although higher temperatures may offer short-term benefits in terms of reduced RI and reaction enhancement, they also increase the risk of accelerated degradation and thermal instability, highlighting a trade-off between electrochemical efficiency and thermal safety.

Figure 6b further elucidates the relationship between DOD and surface temperature, revealing a progressive temperature increase as discharge increased. This temperature rise was primarily caused by internal heat generation mechanisms, including ohmic heating due to current flow through internal resistance, entropic heat from electrochemical reactions, and heat from side reactions within the electrolyte. As the DOD increased, the cumulative effect of these processes resulted in significant heat accumulation within the battery cells. This finding is consistent with the research of Yongqi Xie [22], which demonstrates that an increase in the depth of discharge leads to a rise in battery pack surface temperature. The pronounced temperature escalation observed between 0.80 and 0.90 DOD aligned temporally with the onset of the voltage drop, underscoring the strong coupling between thermal effects and electrochemical performance degradation. This coupling suggests that elevated temperatures exacerbated internal resistance and reaction inefficiencies, thereby accelerating voltage decline.

Moreover, the data highlights the critical role of forced convection in mitigating thermal accumulation. Increasing the air flow rate led to a marked reduction in battery surface temperature, demonstrating the enhanced convective heat transfer capability of forced airflow in removing internally generated heat. This thermal regulation is essential to prevent localized hotspots and thermal runaway risks, which can severely compromise battery safety and cycle life. The results confirm that effective thermal management, through optimizing airflow rates and cooling strategies, is indispensable for maintaining battery performance, especially under high-load and high-discharge scenarios where heat generation is most significant.

In summary, the observed voltage and temperature behaviors reflect the intrinsic electrochemical–thermal interactions within the battery cells. The stability of voltage at low DOD and its rapid drop at high DOD correspond to the dynamic balance of ion transport, reaction kinetics, and heat generation. Forced convection significantly enhances thermal management, preserving battery integrity and performance by controlling temperature rise, thereby delaying voltage degradation. These findings provide valuable guidance for designing thermal management systems that ensure safe and reliable operation of lithium-ion batteries under varying discharge rates and environmental conditions.

4.3. The Effect of Battery Cell Spacing

In this experiment, a discharge rate of 1.00 C-rate was used for the analysis of the effects of battery cell spacing of 5 mm (L05), 10 mm (L10), and 15 mm (L15), respectively. Figure 7 shows the relationship between the changed battery surface temperature and the effect of the depth of discharge. The results tend to show that the surface temperature of the battery pack varied with the depth of discharge in the cases of different battery spacings. The graph shows that the surface temperature of the battery pack increased when the depth of discharge increased. In addition, it was found that increasing the air flow rate resulted in better air flow through the battery, which led to better heat convection from the battery surface as well. It can be seen that the forced convection was the direct cause that promoted the trend of battery surface temperature decreasing significantly and greatly improved the cooling efficiency of the battery pack. This is consistent with previous research [20]. In addition, increasing the battery pack spacing also helped reduce the battery pack surface temperature. The reason is that the airflow resistance decreased as the battery pack spacing increased, resulting in a decrease in battery surface heating.

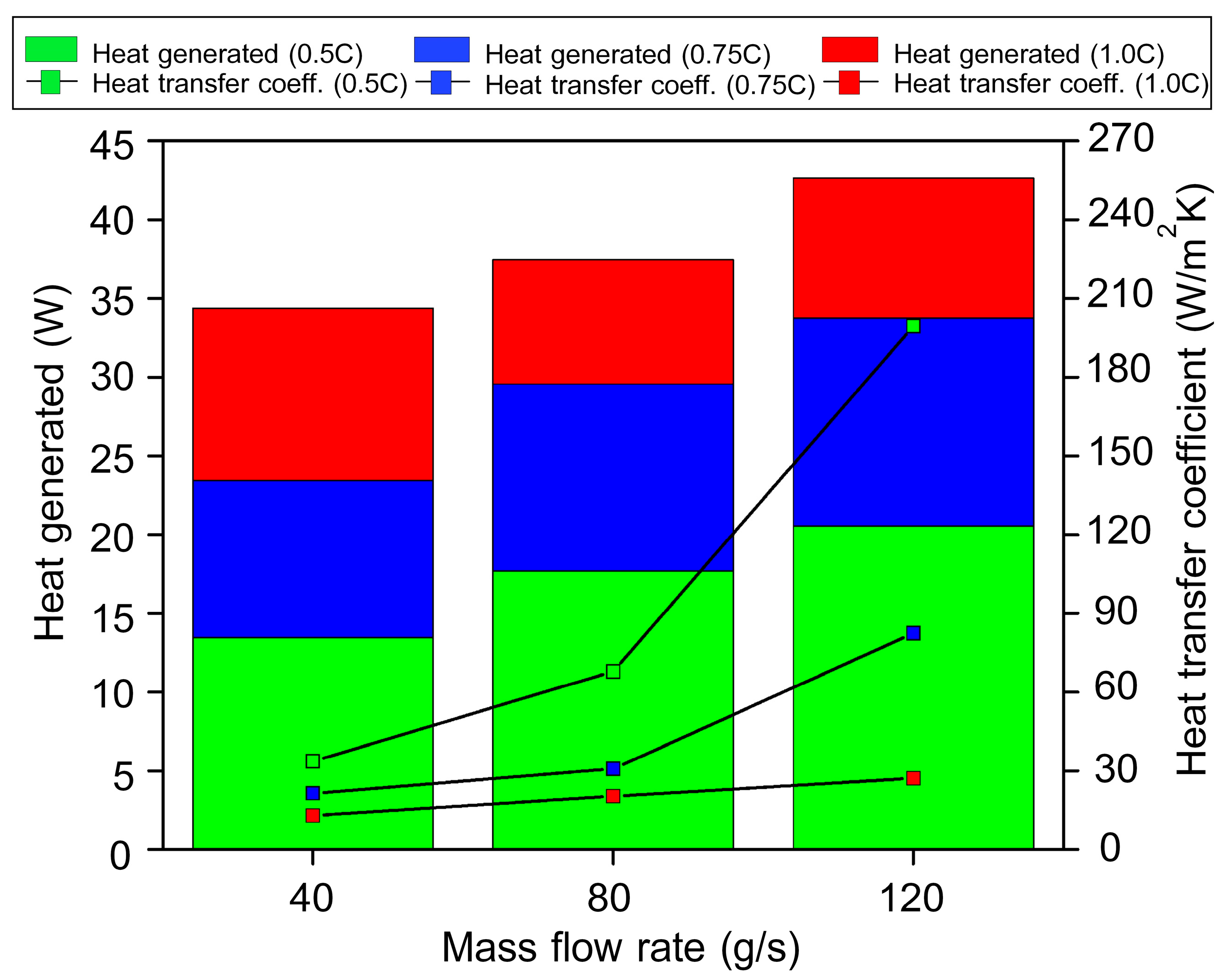
4.4. The Effect of Air Flow Rate

A detailed analysis of the relationship between the air flow rate, the discharge rate, and the thermal behavior of the battery pack reveals several important trends. As demonstrated in Figure 8, both the heat generated at the surface of the battery pack and the corresponding heat transfer coefficient increased with higher air flow rates. This observation aligns with previous studies [16,20], which have established that enhanced air flow is an effective strategy for improving the cooling efficiency of battery systems.

The increase in heat generation at higher air flow rates can be attributed to the improved convective heat transfer environment around the battery cells. When the air flow rate was elevated, the convective heat transfer coefficient at the battery surface rose due to the greater velocity gradient and enhanced turbulence of the cooling air. This promoted more effective removal of thermal energy from the battery surface, resulting in a larger temperature difference between the battery and the cooling medium. Consequently, the battery can dissipate the internally generated heat more rapidly, which is particularly advantageous during periods of high-power demand or elevated discharge rates. Moreover, the increased air flow rate can help maintain a more uniform temperature distribution within the battery pack, thereby minimizing the risk of local hot spots that could otherwise accelerate cell degradation or compromise safety.

Furthermore, when examining conditions at a constant air flow rate, it is evident that an increase in the discharge rate led to a higher amount of heat generated by the battery pack. However, this was accompanied by a decrease in the heat transfer coefficient. This phenomenon can be attributed to the reduced discharge time associated with higher discharge rates, which in turn shortened the period available for heat exchange between the battery pack and the cooling medium. The diminished heat exchange duration reduced the temperature gradient, ultimately resulting in a lower heat transfer coefficient for the battery pack under these circumstances.

The experimental data further indicate that the maximum heat transfer occurred under the condition of 15 mm battery cell spacing with a discharge depth ratio of 1.00 C-rate and at a forced convection rate of 120 g/s (L15_1C_120FC). Conversely, the highest heat convection coefficient was observed for the same battery cell spacing (15 mm) but with a lower discharge depth ratio of 0.50, also at a forced convection rate of 120 g/s (L15_0.5C_120FC). These findings underscore the significant influence of both cooling air flow rate and operational parameters on the thermal management performance of battery packs.

5. Conclusions

This research studied the heat convection coefficient and change in surface temperature of box-shaped electric vehicle battery packs by air cooling using wind tunnel construction to determine experimental parameters that affect the heat convection coefficient, as follows: the highest surface temperature location, the change in voltage, the changes in battery pack surface temperature, and battery cell distance. The following conclusions were obtained:

(1)

The battery surface temperature tended to increase, and the average surface temperature of the battery pack was not significantly different when the discharge rate increased.

(2)

The voltage difference in the electric vehicle battery pack under conditions of natural convection and forced convection at 120 g/s was only slight until the depth of discharge ratio was in the range of 0.90; the voltage dropped rapidly to the point that there was almost no voltage remaining in the battery. This may have been caused by a reaction of the solution in the battery.

(3)

Increasing the battery pack spacing resulted in a downward trend in the surface temperature of the battery pack.

(4)

The increased air flow rates resulted in higher heat transfer rates and heat convection coefficients. When the discharge rate increased, the heat value of the battery increased as well, but the heat convection coefficient decreased. The highest heat transfer value was obtained with a battery cell spacing of 15 mm and a discharge depth ratio of 1.00 at forced convection of 120 g/s, and the highest heat convection coefficient was obtained under the condition of a battery cell spacing of 15 mm with a discharge depth ratio of 0.50 and forced convection of 120 g/s.