FPGA Implementation of Battery State-of-Charge Estimation Using Extended Kalman Filter and Dynamic Sampling
Abstract
1. Introduction
2. Materials and Methods
2.1. First-Order Equivalent Circuit
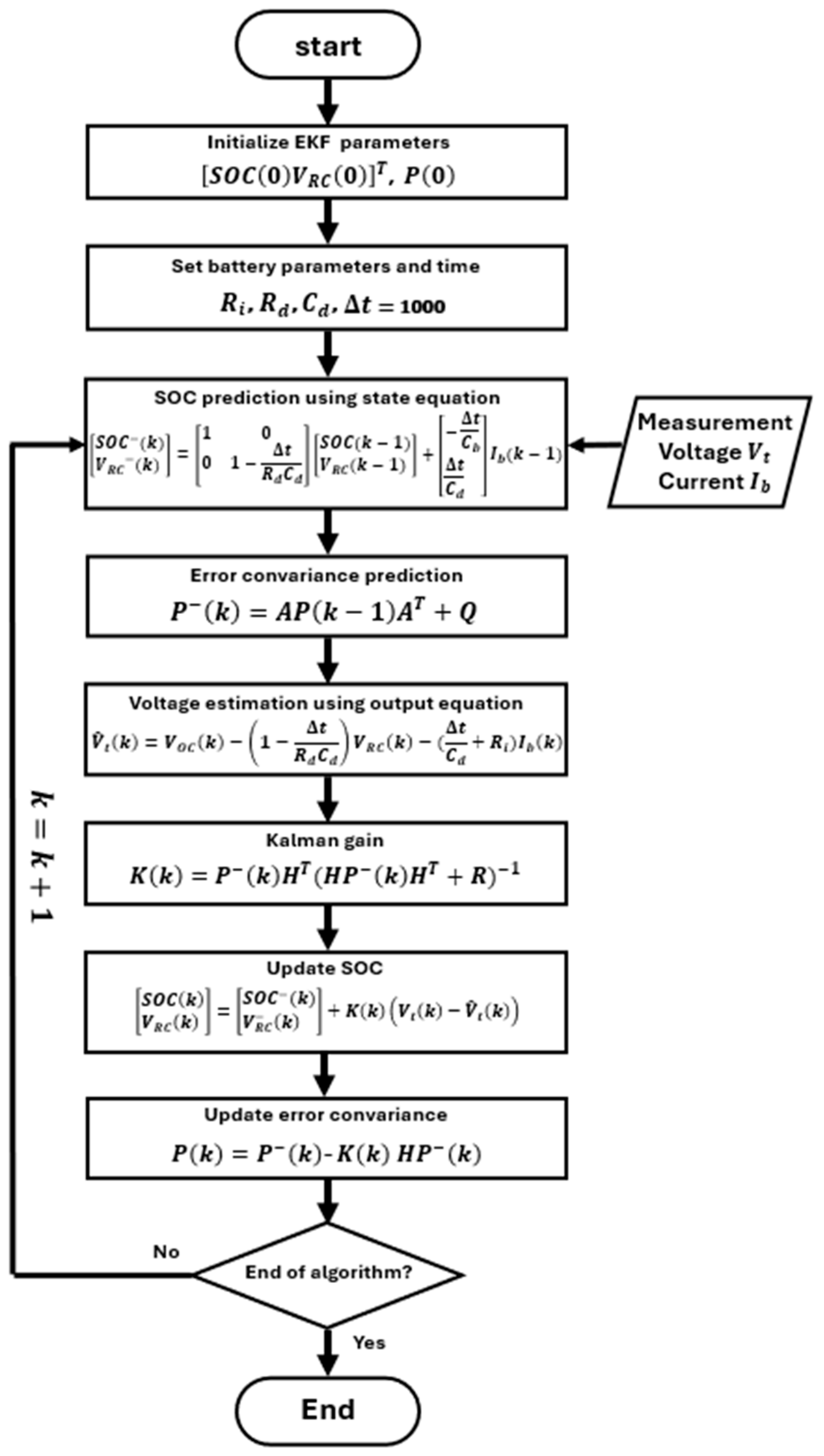
2.2. EKF Algorithm
2.3. Proposed SOC Estimation Using Dynamic Sampling
2.4. Hardware Design
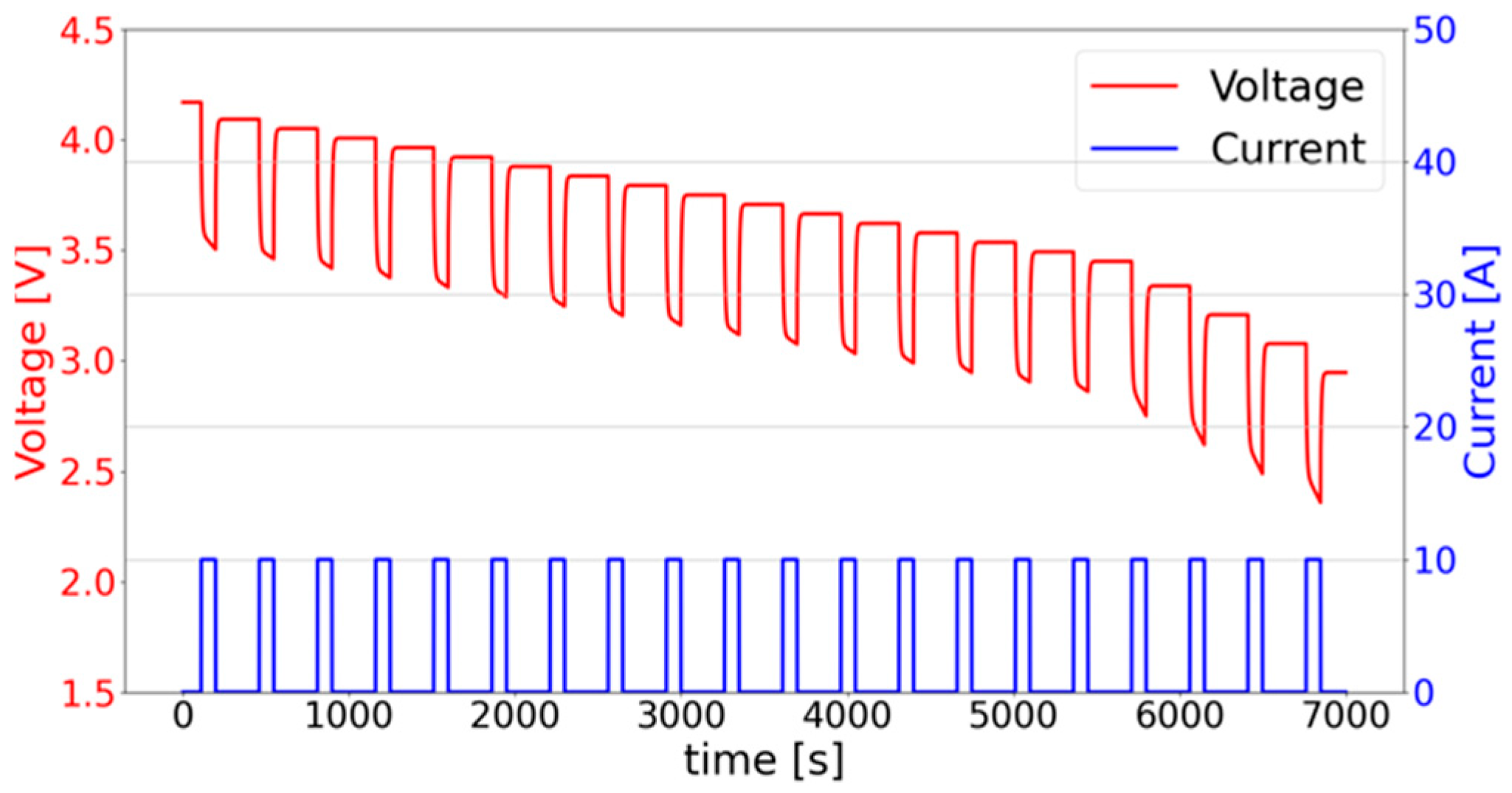
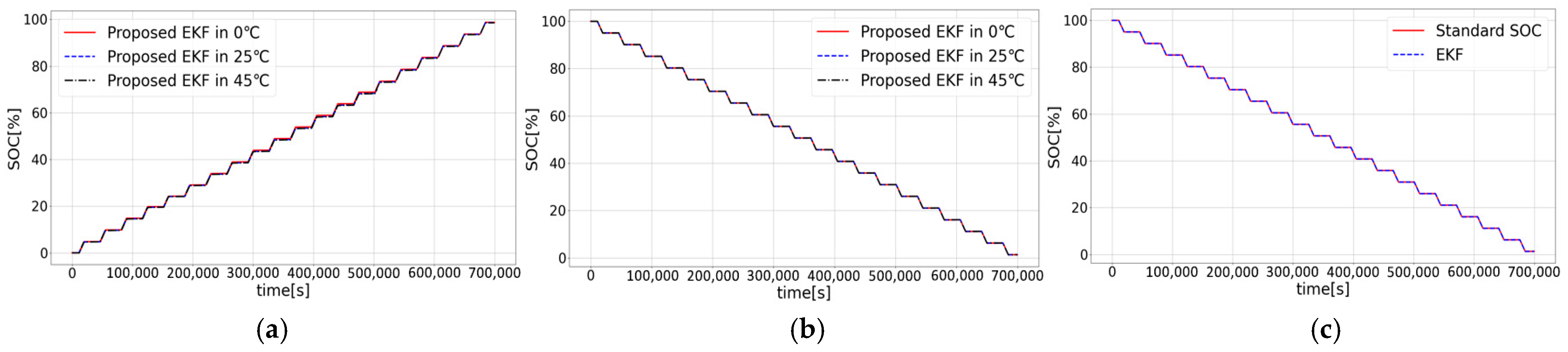
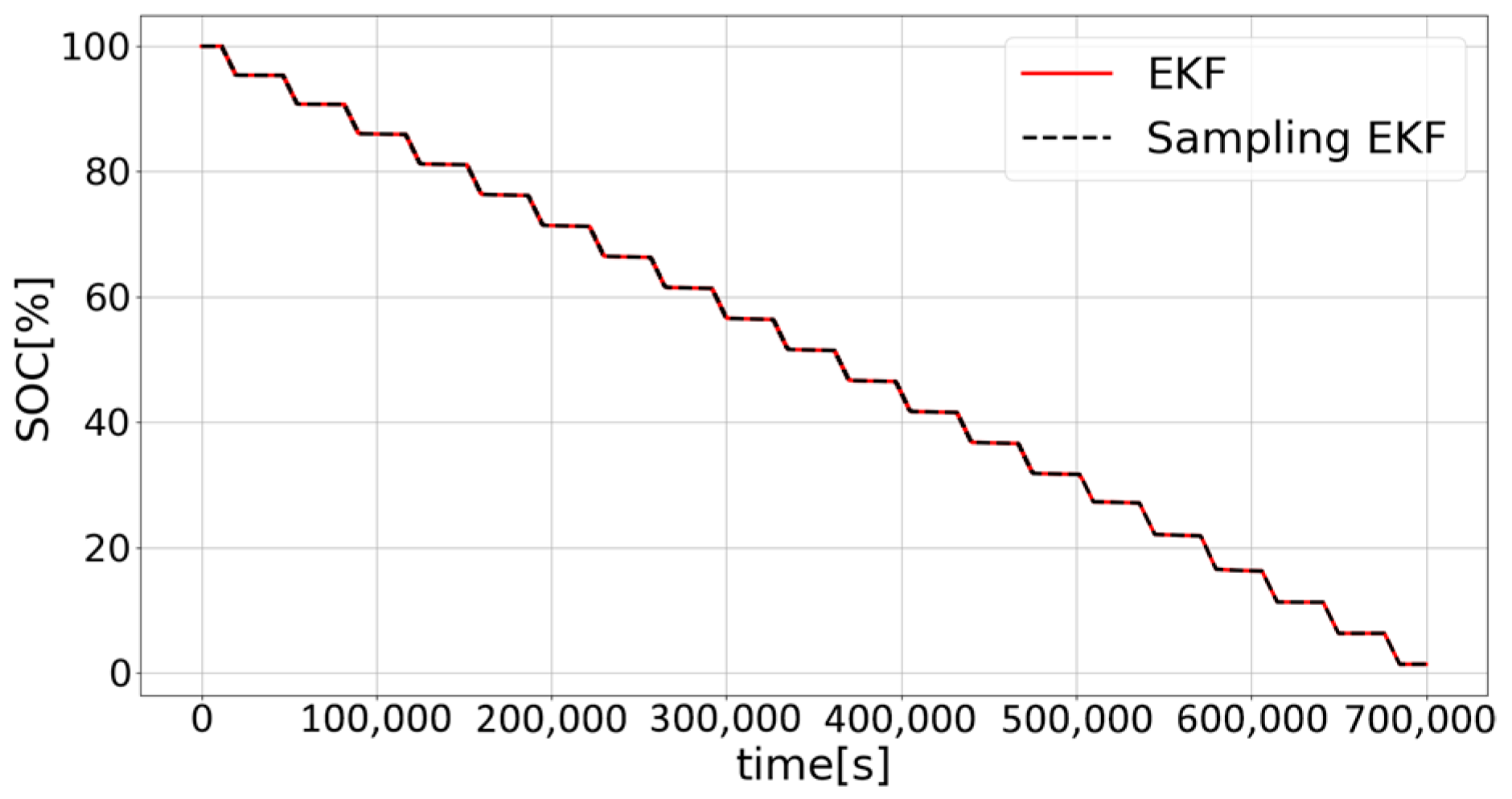
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EV | Electric Vehicle |
| BMS | Battery Management System |
| SOC | State of Charge |
| OCV | Open-Circuit Voltage |
| EKF | Extended Kalman Filter |
| ECM | Equivalent Circuit Model |
| FEM | Finite Element Model |
| RMSE | Root Mean Square Error |
References
- Lee, S.J.; Son, S.E.; Park, M.H. A study on the Prediction and Effect Analysis of EV Motorization in the Republic of Korea. Innov. Stud. 2017, 12, 117–133. [Google Scholar] [CrossRef]
- Yun, J.; Choi, Y.; Lee, J.; Choi, S.; Shin, C. State-of-charge estimation method for lithium-ion batteries using extended Kalman filter with adaptive battery parameters. IEEE Access 2023, 11, 90901–90915. [Google Scholar] [CrossRef]
- Gabbar, H.A.; Othman, A.M.; Abdussami, M.R. Review of battery management systems (BMS) development and industrial standards. Technologies 2021, 9, 28. [Google Scholar] [CrossRef]
- Pattipati, B.; Pattipati, K.; Christopherson, J.; Namburu, A.; Prokhorov, D.; Qiao, L. Automotive Battery Management Systems. In Proceedings of the IEEE Autotestcon, Salt Lake City, UT, USA, 8–11 September 2008. [Google Scholar] [CrossRef]
- Ouyang, Q.; Chen, J.; Zheng, J. State-of-Charge Observer Design for Batteries with Online Model Parameter Identification: A Robust Approach. IEEE Trans. Power Electron. 2020, 35, 5820–5831. [Google Scholar] [CrossRef]
- Yoo, S.-H. A Nonlinear Observer Design for Estimating State-of-Charge of Lithium Polymer Battery. J. Korea Inst. Inf. Commun. Eng. 2012, 16, 2187–2193. [Google Scholar] [CrossRef]
- Kai, W.; Xiao, F.; Jinbo, P.; Jun, R.; Chongxiong, D.; Liwei, L. State of Charge (SOC) Estimation of Lithium-ion Battery Based on Adaptive Square Root Unscented Kalman Filter. Int. J. Electrochem. Sci. 2020, 15, 9499–9516. [Google Scholar] [CrossRef]
- Meng, J.; Ricco, M.; Luo, G.; Swierczynski, M.; Stroe, D.-I.; Store, A.-I. An Overview and Comparison of Online Implementable SOC Estimation Methods for Lithium-Ion Battery. IEEE Trans. Ind. Appl. 2018, 54, 1583–1591. [Google Scholar] [CrossRef]
- Jo, S.; Jung, S.-K.; Kim, H.-T. Development of battery monitoring system using the extended Kalman Filter. J. Korea Converg. Soc. 2020, 11, 7–14. [Google Scholar] [CrossRef]
- Rivera-Barrera, J.P.; Muñoz-Galeano, N.; Sarmiento-Maldonado, H.O. SoC Estimation for Lithium-ion Batteries: Review and Future Challenges. Electronics 2017, 6, 102. [Google Scholar] [CrossRef]
- Zhao, F.; Guo, Y.; Chen, B. A Review of Lithium-Ion Battery State of Charge Estimation Methods Based on Machine Learning. World Electr. Veh. J. 2024, 15, 131. [Google Scholar] [CrossRef]
- Liu, K.; Li, K.; Peng, Q.; Zhang, C. A Brief Review on Key Technologies in the Battery Management System of Electric Vehicles. Front. Energy Res. 2019, 14, 669856. [Google Scholar] [CrossRef]
- Ryu, K.-S.; Kim, B.; Jang, M.-S. A State-of-charge estimation using extended Kalman filter for battery of electric vehicle. J. Korea Acad.-Ind. Coop. Soc. 2017, 18, 15–23. [Google Scholar] [CrossRef]
- Dai, H.; Xu, T.; Zhu, L.; Wei, X.; Sun, Z. Adaptive model parameter identification for large capacity Li-ion batteries on separated time scales. Appl. Energy 2016, 184, 119–131. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 1. Background. J. Power Sources 2004, 134, 252–261. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H.; Sun, F. Robustness analysis of State-of-Charge estimation methods for two types of Li-ion batteries. J. Power Sources 2012, 217, 209–219. [Google Scholar] [CrossRef]
- Peng, S.; Chen, C.; Shi, H.; Yao, Z. State of Charge Estimation of Battery Energy Storage Systems Based on Adaptive Unscented Kalman Filter with a Noise Statistics Estimator. IEEE Access 2017, 5, 13202–13212. [Google Scholar] [CrossRef]
- Nijhawan, G.; Annapurna, T. Advanced battery management systems: An in-depth comparative study. In Proceedings of the MATEC Web of Conferences, Telangana, India, 23–25 February 2024. [Google Scholar] [CrossRef]
- Krishna, T.N.V.; Kumar, S.V.S.V.P.D.; Srinivasa Rao, S.; Chang, L. Powering the Future: Advanced Battery Management Systems (BMS) for Electric Vehicles. Energies 2024, 17, 3360. [Google Scholar] [CrossRef]
- Ahn, J.H. The Present and Future of BMS Research for Safe Energy Society. Korean Inst. Electr. Eng. 2023, 72, 21–27. [Google Scholar]
- Yang, S.; Zhou, S.; Hua, Y.; Zhou, X.; Liu, X.; Pan, Y.; Ling, H.; Wu, B. A parameter adaptive method for state of charge estimation of lithium-ion batteries with an improved extended Kalman filter. Sci. Rep. 2021, 11, 5805. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.; Lee, J.; Cho, B.H. State-of-charge and capacity estimation of lithium-ion battery using a new open-circuit voltage versus state-of-charge. J. Power Sources 2008, 185, 1367–1373. [Google Scholar] [CrossRef]
- Johnson, V.H. Battery performance models in ADVISOR. J. Power Sources 2002, 110, 321–329. [Google Scholar] [CrossRef]
- Battery Test Manual For Plug-In Hybrid Electric Vehicles. Idaho National Laboratory. 2010. Available online: https://inldigitallibrary.inl.gov/sites/sti/sti/4655291.pdf (accessed on 18 October 2025).
- Newman, J.; Thomas, K.E.; Hafezi, H.; Wheeler, D.R. Modeling of lithium-ion batteries. J. Power Sources 2003, 119, 838–843. [Google Scholar] [CrossRef]
- Jang, K.-W.; Kim, H.-J.; Chung, G.-B. Comparison of Battery Modelings and SOC Estimation Methods. In Proceedings of the KIPE Conference, Pyeongchang, Republic of Korea, 6 July 2010. [Google Scholar]
- Park, H.-W.; Lee, J.-H.; Choi, Y.-H.; Son, S.-J.; Yun, J.-J. Analysis of Change in Battery Parameters according to Ambient Temperature and C-rate. J. Korean Inst. Illum. Electr. Install. Eng. 2022, 36, 24–32. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Fan, J. Evaluation of Lithium-Ion Battery Equivalent Circuit Models for State of Charge Estimation by an Experimental Approach. Energies 2011, 4, 582–598. [Google Scholar] [CrossRef]
- Meng, J.; Luo, G.; Ricco, M.; Swierczynski, M.; Stroe, D.-I.; Teodorescu, R. Overview of Lithium-Ion Battery Modeling Methods for State-of-Charge Estimation in Electrical Vehicles. Appl. Sci. 2018, 8, 659. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Zhang, X.; Sun, F.; Fan, J. State-of-Charge Estimation of the Lithium-Ion Battery Using an Adaptive Extended Kalman Filter Based on an Improved Thevenin Model. IEEE Trans. Veh. Technol. 2011, 60, 1461–1469. [Google Scholar] [CrossRef]
- Cui, Z.; Hu, W.; Zhang, G.; Zhang, Z.; Chen, Z. An extended Kalman filter based SOC estimation method for Li-ion battery. Energy Rep. 2022, 8, 81–87. [Google Scholar] [CrossRef]
- Jugović, D.; Uskoković, D. A review of recent developments in the synthesis procedures of lithium iron phosphate powders. J. Power Sources 2009, 190, 538–544. [Google Scholar] [CrossRef]
- Jwo, D.; Chuang, F.; Weng, T. Adaptive Kalman Filter for Navigation Sensor Fusion. In Sensor Fusion and its Applications; Thomas, C., Ed.; InTech China: Sanghai, China, 2010; pp. 65–90. [Google Scholar]
- Klein, R.; Chaturvedi, N.A.; Christensen, J.; Ahmed, J.; Findeisen, R.; Kojic, A. Electrochemical Model Based Observer Design for a Lithium-Ion Battery. IEEE Trans. Control Syst. Technol. 2013, 21, 289–301. [Google Scholar] [CrossRef]
- Jemmali, S.; Manaï, B.; Hamouda, M. Pure hardware design and implementation on FPGA of an EKF based accelerated SoC estimator for a lithium-ion battery in electric vehicles. IET Power Electron. 2022, 15, 1004–1015. [Google Scholar] [CrossRef]
- He, Z.; Yang, Z.; Cui, X.; Li, E. A Method of State-of-Charge Estimation for EV Power Lithium-Ion Battery Using a Novel Adaptive Extended Kalman Filter. IEEE Trans. Veh. Technol. 2020, 69, 14618–14630. [Google Scholar] [CrossRef]
- Schacht-Rodriguez, R.; Ortiz-Torres, G.; García-Beltrán, C.D.; Astorga-Zaragoza, C.M.; Ponsart, J.C.; Theilliol, D. SoC estimation using an Extended Kalman filter for UAV applications. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 27 July 2017. [Google Scholar] [CrossRef]
- Jiao, S.; Zhang, G.; Zhou, M.; Li, G. A Comprehensive Review of Research Hotspots on Battery Management Systems for UAVs. IEEE Access 2023, 11, 84636–84650. [Google Scholar] [CrossRef]
- Verstraten, T.; Hosen, M.S.; Berecibar, M.; Vanderborght, B. Selecting Suitable Battery Technologies for Untethered Robot. Energies 2023, 16, 4904. [Google Scholar] [CrossRef]
- Omariba, Z.B.; Zhang, L.; Sun, A.D. Review of Battery Cell Balancing Methodologies for Optimizing Battery Pack Performance in Electric Vehicles. IEEE Access 2019, 7, 129335–129352. [Google Scholar] [CrossRef]
- Kim, G.-Y.; Lee, H.-J.; Kim, J.-G.; Heo, H.-I. Development Trends of Battery Technologies and Electrical-driven System for Aerospace Missions (PART 1: Development Trends of Lithium based Batteries and Electrified Aircraft Propulsion System). J. Korean Soc. Aeronaut. Space Sci. 2023, 51, 693–708. [Google Scholar] [CrossRef]


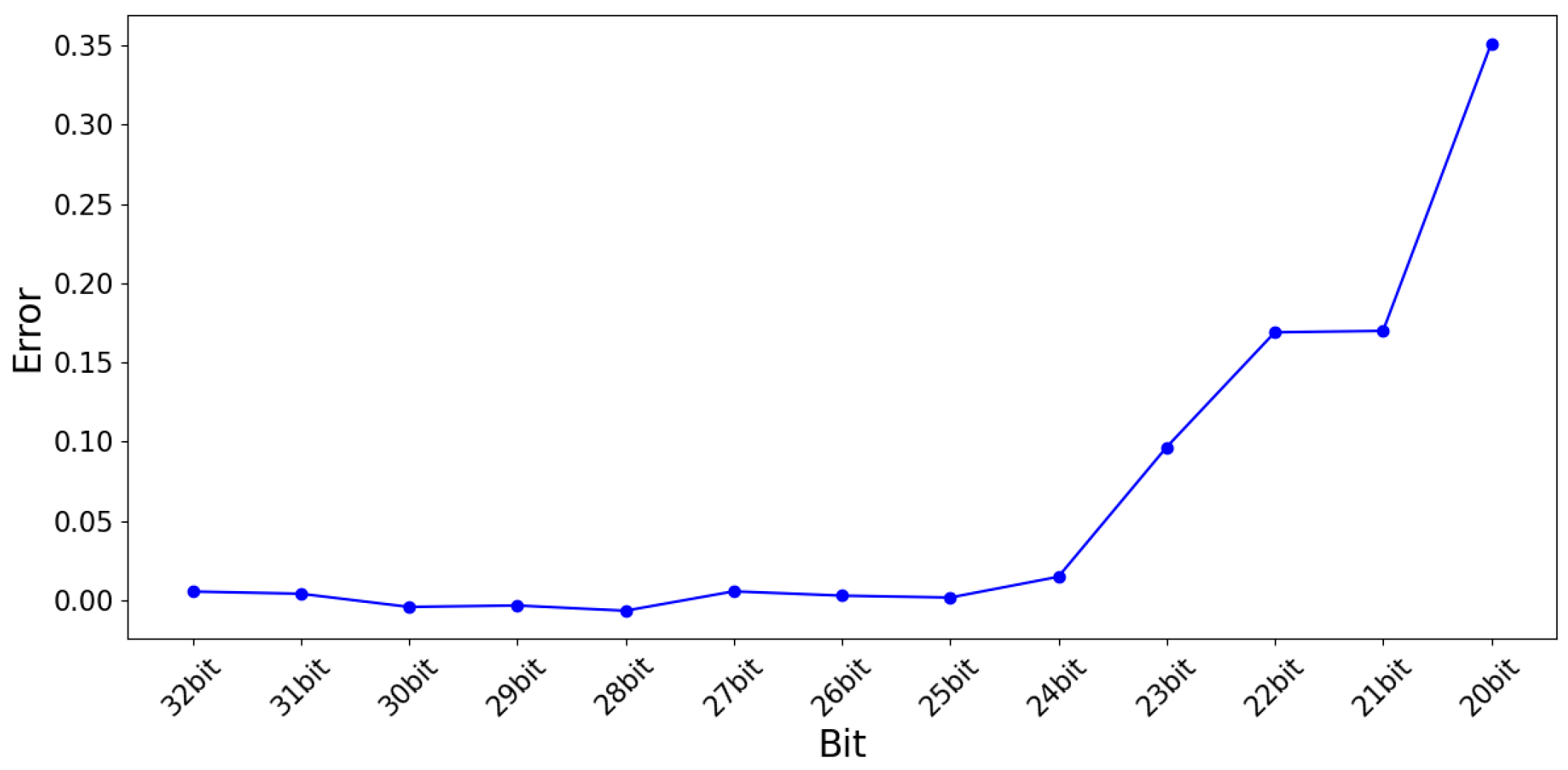
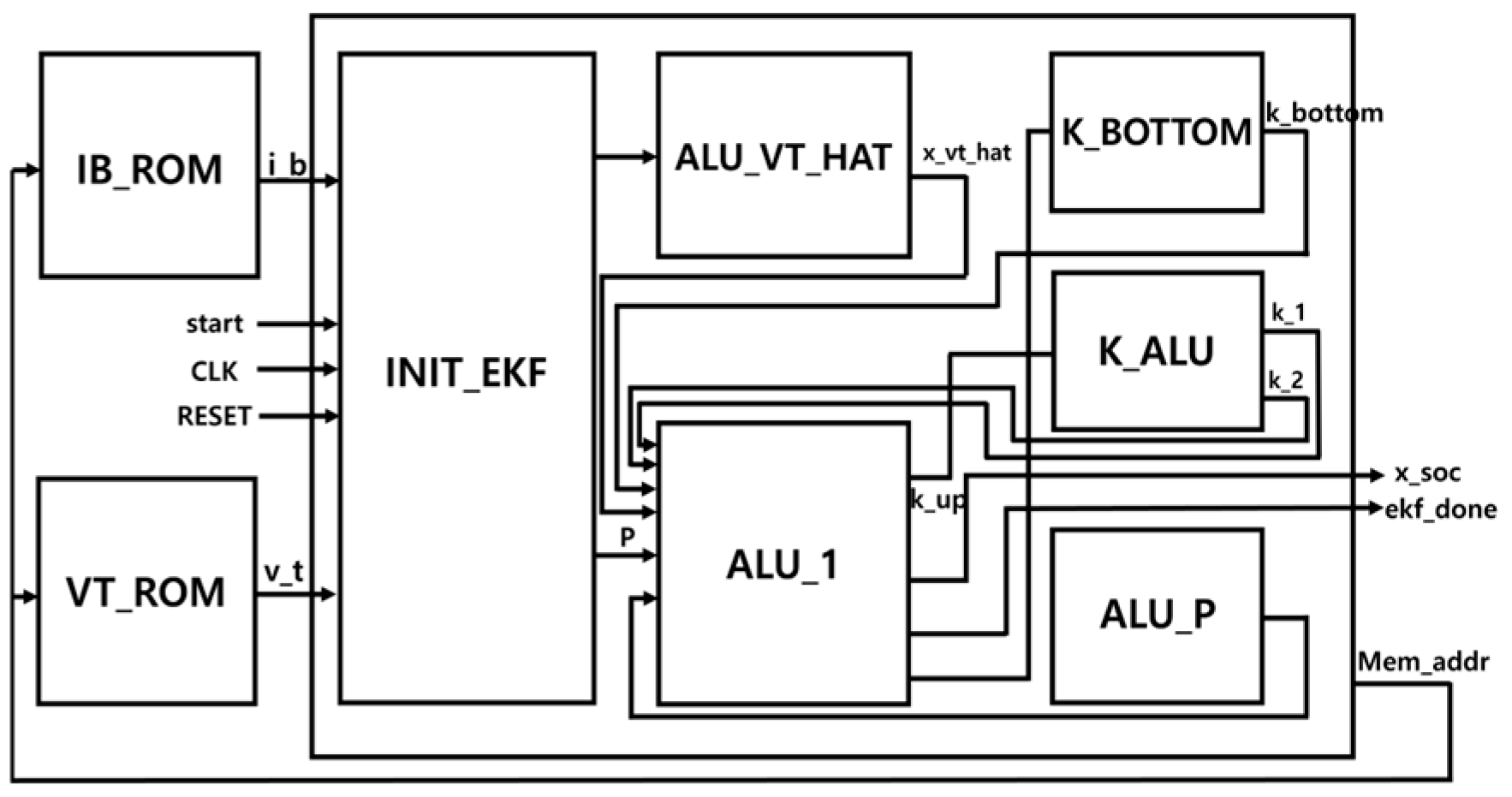
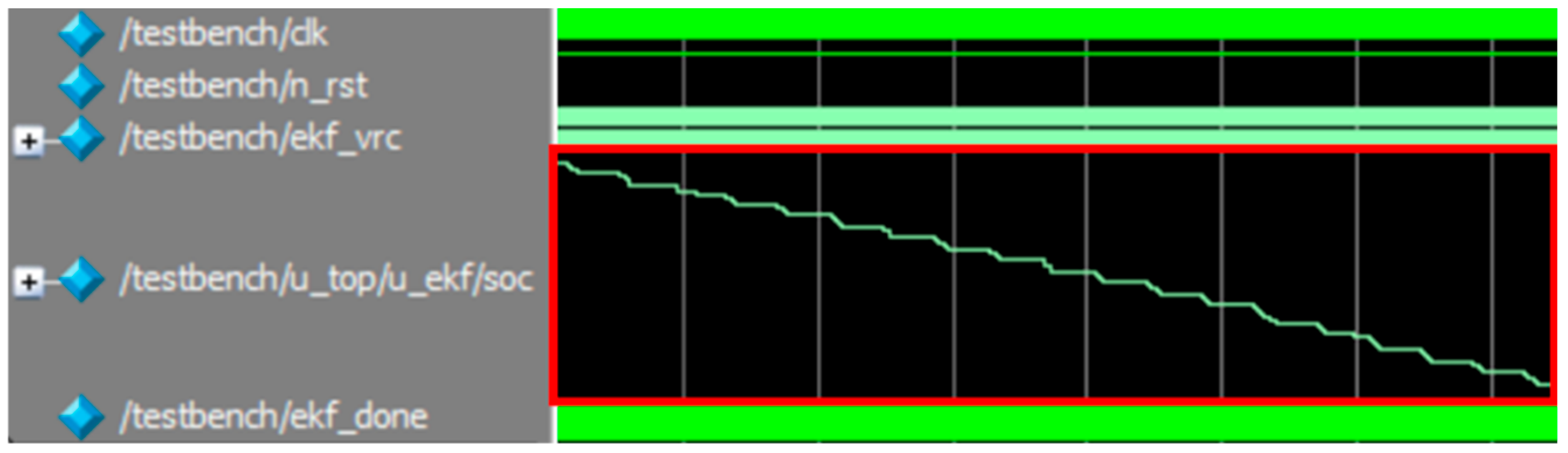


| Parameter | Value |
|---|---|
| Nominal capacity | 4900 mAh |
| Charging cutoff voltage | 4.2 V |
| Nominal voltage | 3.7 V |
| Discharging cutoff voltage | 2.5 V |
| 0 °C | 25 °C | 45 °C | |
|---|---|---|---|
| 0.038 | 0.025 | 0.024 | |
| 0.062 | 0.034 | 0.031 | |
| 7782 | 17,890 | 23,525 |
| Resource | Errors [%] |
|---|---|
| Standard SOC & EKF | 0.0166 |
| EKF & Proposed EKF | 0.7465 |
| Errors [%] | |
|---|---|
| Compare H/W and S/W | 0.001 |
| Non-Optimized H/W | Proposed H/W | |
|---|---|---|
| Adder | 32 | 31 |
| Subtractor | 7 | 13 |
| Multiplier | 63 | 13 |
| Divider | 3 | 2 |
| Clock cycles required for one SOC estimation | 18 | 6 |
| Resource | [35] (Zynq-7000 SoC ZC702) | Proposed (CycloneIII EP4CE115) |
|---|---|---|
| LE | 12,192 | 5770 |
| FF | 5520 | 1919 |
| DSP | 220 (DSP48E1s) | 148 (9-bit Multiplier) |
| Max Frequency | 100 MHz | 38.12 MHz |
| Time of one iteration | 1.025 μs | 0.157 μs |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yun, S.; Jeon, J.; Lee, E.; Jeong, T.; Kim, S. FPGA Implementation of Battery State-of-Charge Estimation Using Extended Kalman Filter and Dynamic Sampling. World Electr. Veh. J. 2025, 16, 587. https://doi.org/10.3390/wevj16100587
Yun S, Jeon J, Lee E, Jeong T, Kim S. FPGA Implementation of Battery State-of-Charge Estimation Using Extended Kalman Filter and Dynamic Sampling. World Electric Vehicle Journal. 2025; 16(10):587. https://doi.org/10.3390/wevj16100587
Chicago/Turabian StyleYun, Seungjae, Jeongju Jeon, Eunseong Lee, Taeyeon Jeong, and Sunhee Kim. 2025. "FPGA Implementation of Battery State-of-Charge Estimation Using Extended Kalman Filter and Dynamic Sampling" World Electric Vehicle Journal 16, no. 10: 587. https://doi.org/10.3390/wevj16100587
APA StyleYun, S., Jeon, J., Lee, E., Jeong, T., & Kim, S. (2025). FPGA Implementation of Battery State-of-Charge Estimation Using Extended Kalman Filter and Dynamic Sampling. World Electric Vehicle Journal, 16(10), 587. https://doi.org/10.3390/wevj16100587





