Analysis and Improvement of the Dynamic Characteristics of an Electro-Hydrostatic Actuator Based on a Vehicle’s Active Suspension
Abstract
1. Introduction
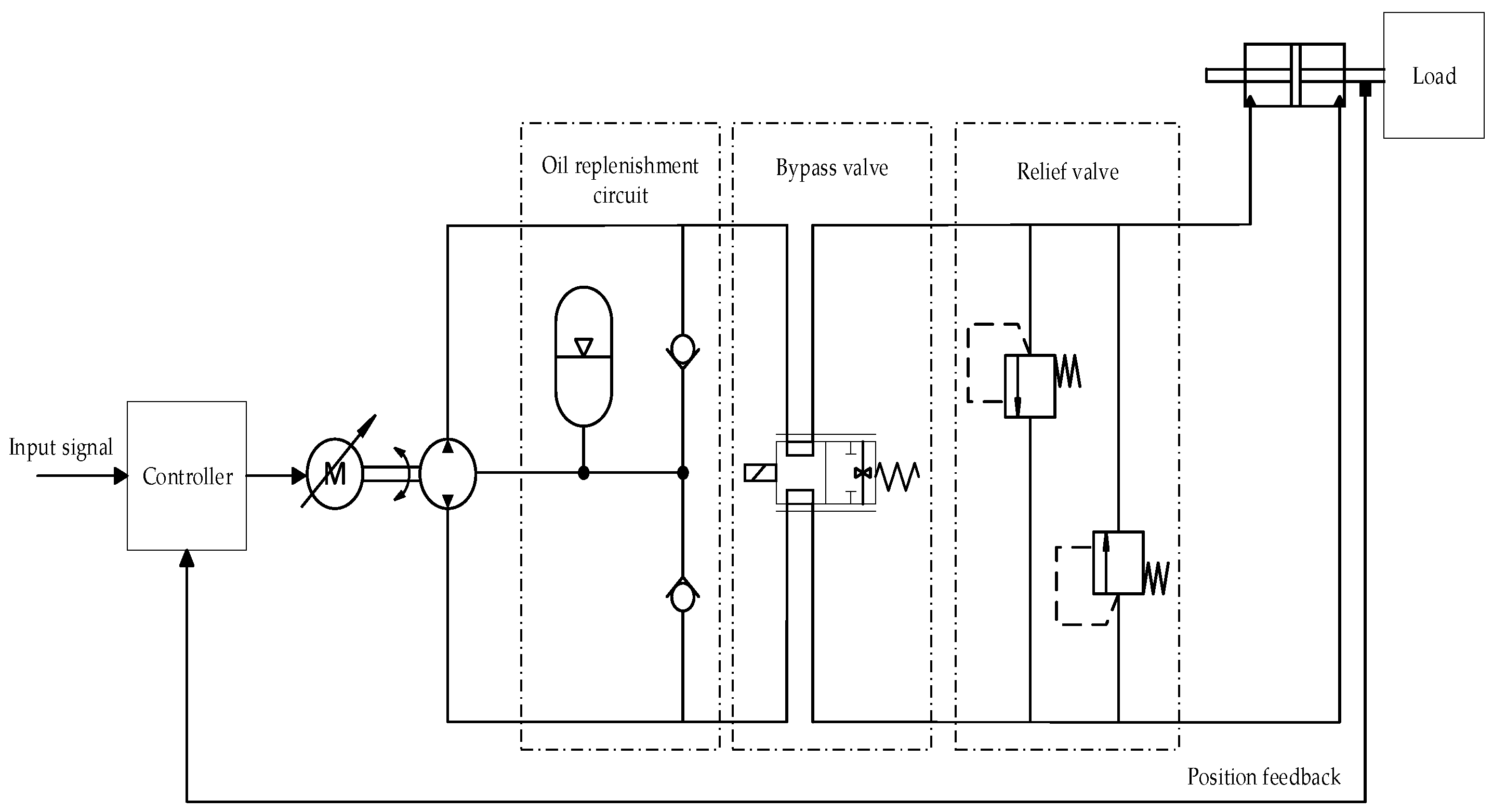
2. Dynamic Characteristic Analysis of EHA Subsystem
2.1. Hydraulic Subsystem Dynamic Performance
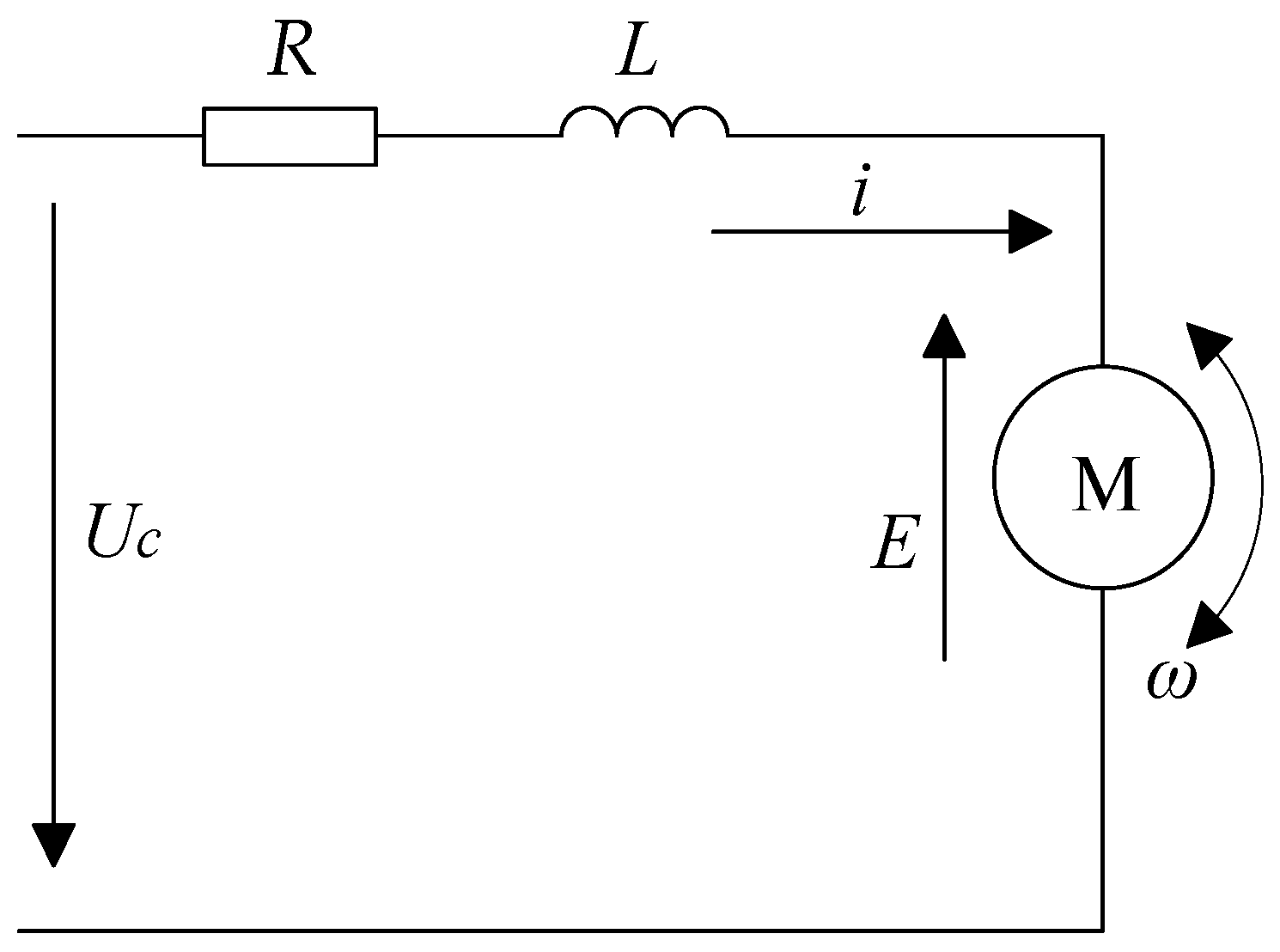
2.2. Motor-Pump Subsystem Dynamic Performance
3. Subsystem Load Characteristic Analysis
3.1. Load Characterization Demands in Hydraulic Systems
3.2. Load Characterization Demands in Electromechanical Systems
4. Dynamic Characteristic Enhancement Methods
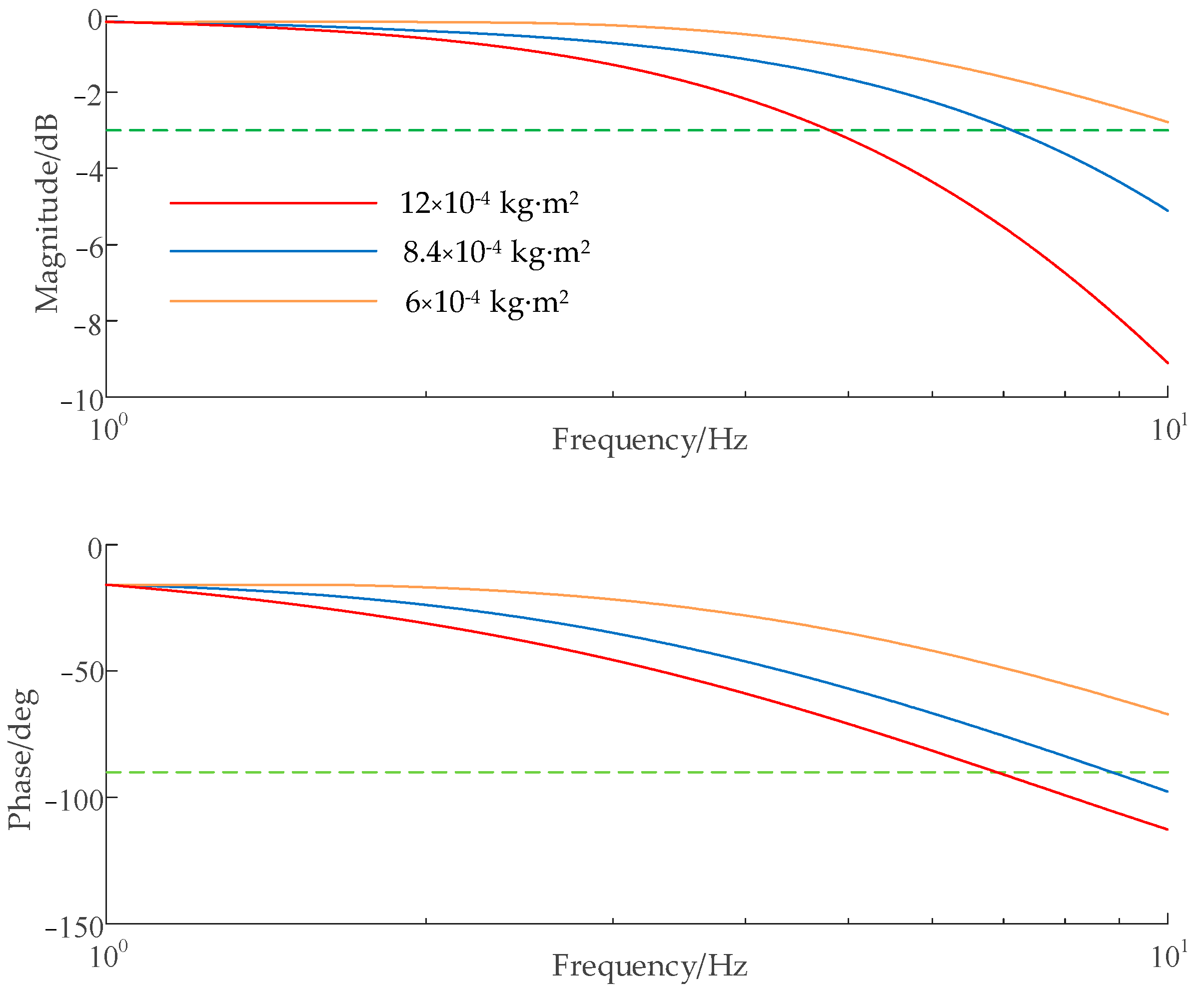
4.1. Reducing Rotational Inertia of Motor-Pump
4.2. Increasing Motor Output Torque
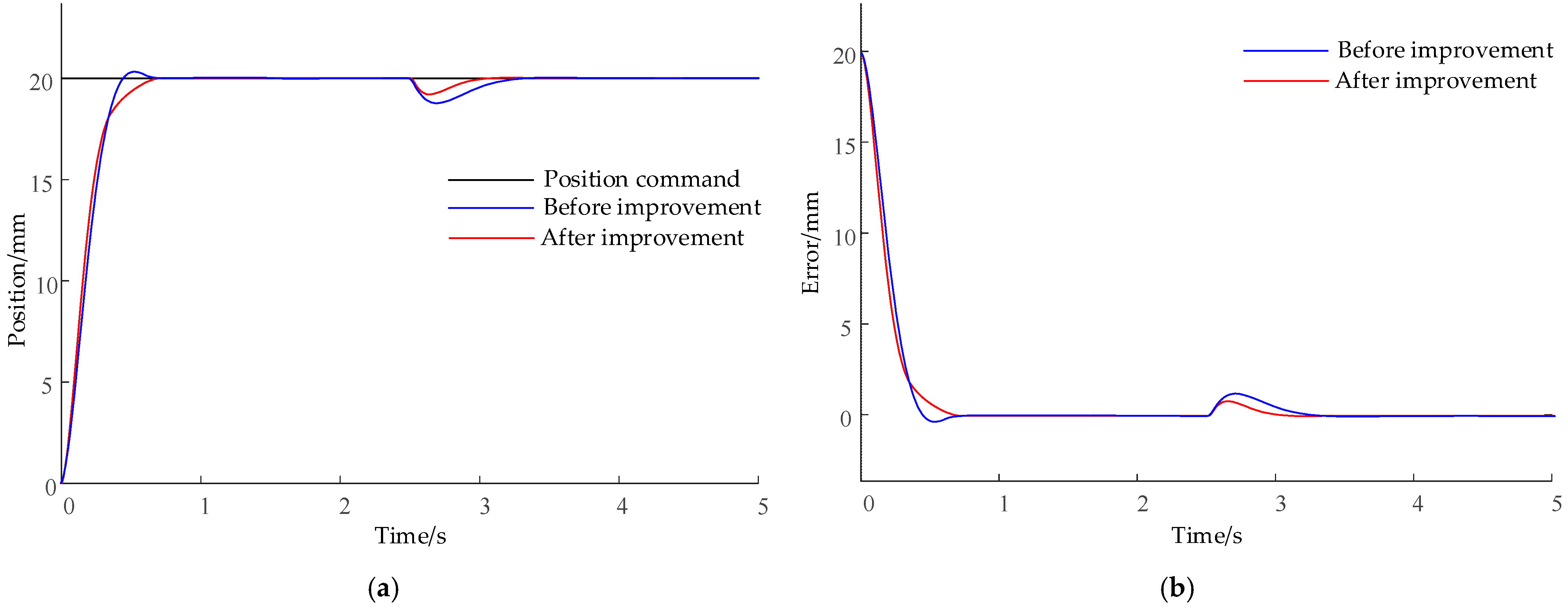
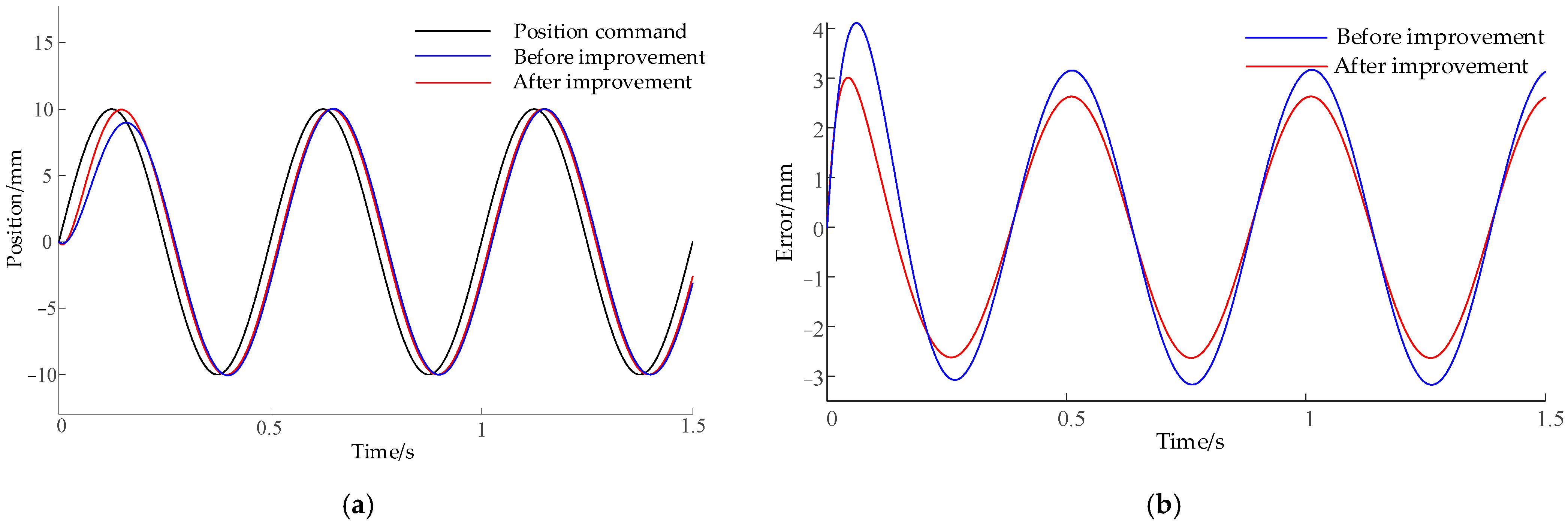
5. EHA Simulation Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kumar, M. A survey on electro hydrostatic actuator: Architecture and way ahead. Mater. Today Proc. 2021, 45, 6057–6063. [Google Scholar] [CrossRef]
- Van Den Bossche, D. The A380 flight control electro-hydrostatic actuators, achievements and lessons learnt. In Proceedings of the ICAC 2006: 25th International Congress of the Aeronautical Sciences, Hamburg, Germany, 3–8 September 2006; pp. 1–8. [Google Scholar]
- Moog Inc. Electro Hydrostatic Actuators; Moog Inc.: Elma, NY, USA, 2014. [Google Scholar]
- Parker Inc. Control Systems and Actuation Technologies; Parker Inc.: Cleveland, OH, USA, 2014. [Google Scholar]
- Li, K.; Wang, S.P. Multidisciplinary modeling method and simulation for electro-hydrostatic actuator. In Proceedings of the ICIEA 2010: 5th IEEE Conference on Industrial Electronics and Applications, Taichung, Taiwan, 15–17 June 2010; pp. 544–548. [Google Scholar]
- Huang, X.Y.; Gerada, C.; Goodman, A.; Bradley, K.; Zhang, H.; Fang, Y.T. A Brushless DC motor design for an aircraft electro-hydraulic actuation system. In Proceedings of the IEMDC 2011: 2011 IEEE International Electric machines and Drives Conference, Niagara Falls, ON, Canada, 15–18 May 2011; pp. 1153–1158. [Google Scholar]
- Martin, G.; Louis, D. Multidomain high-detailed modeling of an electro-hydrostatic actuator and advanced position control. In Proceedings of the IECON 2012: 38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 5463–5470. [Google Scholar]
- Wang, J.L.; Zeng, S.K.; Ma, J.M.; Wu, W.W. Research on an integrated methodology of the dynamic performance and reliability evaluation. In Proceedings of the ICRMS’2011 9th International Conference on Reliability, Maintainability and Safety: Safety First, Reliability Primary, Guiyang, China, 12–15 June 2011; pp. 122–128. [Google Scholar]
- Hu, X.; Mao, Z.J.; Jiao, Z.X.; Wu, S.; Yu, X.; Li, F.Y. Analysis of the characteristics by modeling and simulation of actuator in flight control system. In Proceedings of the CGNCC 2014, 6th IEEE Chinese Guidance, Navigation and Control Conference, Yantai, China, 8–10 August 2014; pp. 2618–2623. [Google Scholar]
- Hu, W.N.; Zhou, L.; Tian, Y.S.; Jiao, Z.X.; Shang, Y.X.; Song, Z.N.; Yan, L. Analysis for the power loss of electro hydrostatic actuator and hydraulic actuator. In Proceedings of the 2015 IEEE International Conference on Advanced Intelligent Mechatronics, Busan, Republic of Korea, 7–11 July 2015; pp. 613–616. [Google Scholar]
- Janne, K.; Jouni, M. Stable and high performance energy-efficient motion control of electric load sensing controlled hydraulic manipulators. In Proceedings of the FPMC 2013: Proceedings of the ASME/BATH 2013 Symposium on Fluid Power & Motion Control, Sarasota, FL, USA, 6–9 October 2013; p. V001T01A024. [Google Scholar]
- Yasuo, S. Calculation of dynamic overall efficiency of a load sensing hydraulic system by bondgraphs. In Proceedings of the IECON 2000: 26th Annual Conference of the IEEE Electronics Society, Nagoya, Japan, 22–28 October 2000; pp. 1568–1573. [Google Scholar]
- Wang, M.K.; Fu, Y.L.; Zhao, J.A.; Yang, R. Novel Variable-Damping Cascade Sliding Mode Control for Electro-Hydrostatic Actuators. J. Beijing Univ. Aeronaut. Astronaut. 2021, 47, 1612–1618. [Google Scholar] [CrossRef]
- Ren, G.; Costa, G.K.; Sepehri, N. Position control of an electro-hydrostatic asymmetric actuator operating in all quadrants. Mechatronics 2020, 67, 102344. [Google Scholar] [CrossRef]
- Song, B.; Lee, D.; Park, S.Y.; Baek, Y.S. Design and Performa nce of Nonlinear Control for an Electro-Hydraulic Actuator Considering a Wearabl e Robot. Processes 2019, 7, 389. [Google Scholar] [CrossRef]
- Johan, J.K.; Kjeld, E.M.; Rygaard, H.M. Novel Conce pt for Electro-Hydrostatic Actuators for Motion Control of Hydraulic Manipulators. Energies 2021, 14, 6566. [Google Scholar] [CrossRef]
- Agostini, T.; De Negri, V.; Minav, T.; Pietola, M. Effect of Energy Rec overy on Efficiency in Electro-Hydrostatic Closed System for Differential Actuator. Actuators 2020, 9, 12. [Google Scholar] [CrossRef]
- Gao, B.; Shi, L. The nonlinearity simulation study on electrical hydrostatic actuator. In Proceedings of the 2012 2nd International Conference on Consumer Electronics, Communications and Networks (CECNet), Yichang, China, 21–23 April 2012. [Google Scholar]
- Fu, Y.; Li, Y.; Wang, M.; Lin, Z.; Zhu, D. Adaptive Variable-Damping Sliding Mode Control for Electro-Hydrostatic Actuators. J. Beijing Inst. Technol. 2021, 41, 1171–1178. [Google Scholar]
- Gao, Q.; Jin, Y.; Wang, L.; Hou, Y.; Ji, L. Modeling Study of Pump-Controlled Cylinder Electro-Hydraulic Position Servo System. Acta Armamentarii 2011, 32, 950–956. [Google Scholar]
- Wang, Y.P.; Guo, C.; Chen, Y.; Xie, W. Simulation of Genetic Optimization Control for EHA in Aircraft Hydraulic Servo Systems. Comput. Simul. 2016, 33, 53–57+62. [Google Scholar] [CrossRef]
- Sun, L.; Zheng, C.S. Research on Global Sliding Mode Control for Hydraulic Actuators. Manuf. Autom. 2014, 36, 19–22. [Google Scholar]
- Liu, L.T.; Jiao, H.B. Research on Position Tracking of Electro-Hydrostatic Actuators Using Sliding Mode Control. Chin. J. Constr. Mach. 2020, 18, 430–435. [Google Scholar]
- Kou, F.; Du, J.; Wang, Z.; Li, D.; Xu, J. Nonlinear Modeling and Coordinate Optimization of a Semi-Active Energy Regenerative Suspension with an Electro-Hydraulic Actuator. Algorithms 2018, 11, 12. [Google Scholar] [CrossRef]
- Guo, Q.; Zhao, D.; Zhao, X.; Li, Z.; Wu, L.; Shi, X. Research on Position Control of Active Suspension Electro-Hydraulic Servo Actuator Based on Internal Model Control. Trans. Chin. Soc. Agric. Mach. 2020, 51, 394–404. [Google Scholar]
- Kou, F.; Zhang, H.; Xu, J.; Tian, H.; Peng, X. Adaptive Smith feedback time-delay control for electro-hydrostatic hydraulic active suspension. J. Vib. Meas. Diagn. 2022, 42, 864–870+1030. [Google Scholar]
- Ni, T.; Lv, B.; Zhang, P.H.; Zhao, Z.; Sun, X.; Zhang, H. Research on Control Strategy of Electro-Hydraulic Servo Actuator Based on Strict Feedback Model. China Mech. Eng. 2024, 35, 928–937+949. [Google Scholar]
- Kalyoncu, M.; Haydim, M. Mathematical modelling and fuzzy logic based position control of an electrohydraulic servosystem with internal leakage. J. Mechatron. 2009, 19, 847–858. [Google Scholar] [CrossRef]
- Loan, U.; Adrian, T.; Andrei, H.; Silvia, B. New stabilization and tracking control laws for electrohydraulic servomechanisms. Eur. J. Control 2013, 19, 65–70. [Google Scholar]
- Zhang, Q.; Li, B.Q. Feedback linearization PID control for electrohydrostatic actuator. In Proceedings of the AIMSEC 2011: 2nd International Conference on Artificial Intelligence, Management Science and Electronic Commerce, Dengfeng, China, 8–10 August 2011; pp. 358–361. [Google Scholar]
- Ji, H. Hydraulic and Pneumatic Transmission and Control Edited; Huazhong University of Science: Wuhan, China, 2014. [Google Scholar]




| Parameter | Value | Unit |
|---|---|---|
| Actuator cylinder stroke | ±50 | mm |
| Maximum output force | 100 | kN |
| Hydraulic pump displacement | 1.5 | mL/r |
| Effective area of the piston | 71 | cm2 |
| Total leakage coefficient | 1.58 | m3/(s·Pa) |
| Hydraulic cylinder initial volume | 0.45 | L |
| Bulk modulus of the hydraulic oil | 650 | MPa |
| Load equivalent mass | 2000 | kg |
| Piston damping coefficient | 150 | N/(m·s−1) |
| Parameter | Value | Unit |
|---|---|---|
| Stator winding resistance | 1.5 | Ω |
| Stator inductance | 2.3 × 10−3 | H |
| Back electromotive coefficient | 0.2 | V/(rad·s−1) |
| Motor torque coefficient | 0.2 | Nm/A |
| Moment of inertia | 1.2 × 10−3 | kg·m2 |
| Motor damping coefficient | 4.2 × 10−4 | N·m/(rad·s−1) |
| System | Rise Time (s) | Overshoot | Settling Time (s) |
|---|---|---|---|
| Before improvement | 0.46 | 2.3% | 0.82 |
| After improvement | 0.47 | 0 | 0.58 |
| System | Rise Time (s) | Overshoot | Settling Time (s) |
|---|---|---|---|
| Before improvement | 0.48 | 2.1% | 0.85 |
| After improvement | 0.51 | 0 | 0.61 |
| System | Phase Lag (°) | Maximum Tracking Error (mm) |
|---|---|---|
| Before improvement | 18.24 | 3.1 |
| After improvement | 15.12 | 2.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, P.; Chen, X. Analysis and Improvement of the Dynamic Characteristics of an Electro-Hydrostatic Actuator Based on a Vehicle’s Active Suspension. World Electr. Veh. J. 2025, 16, 586. https://doi.org/10.3390/wevj16100586
Chen P, Chen X. Analysis and Improvement of the Dynamic Characteristics of an Electro-Hydrostatic Actuator Based on a Vehicle’s Active Suspension. World Electric Vehicle Journal. 2025; 16(10):586. https://doi.org/10.3390/wevj16100586
Chicago/Turabian StyleChen, Peng, and Xing Chen. 2025. "Analysis and Improvement of the Dynamic Characteristics of an Electro-Hydrostatic Actuator Based on a Vehicle’s Active Suspension" World Electric Vehicle Journal 16, no. 10: 586. https://doi.org/10.3390/wevj16100586
APA StyleChen, P., & Chen, X. (2025). Analysis and Improvement of the Dynamic Characteristics of an Electro-Hydrostatic Actuator Based on a Vehicle’s Active Suspension. World Electric Vehicle Journal, 16(10), 586. https://doi.org/10.3390/wevj16100586





