Research on Deep Adaptive Clustering Method Based on Stacked Sparse Autoencoders for Concrete Truck Mixers Driving Conditions
Abstract
1. Introduction
- (1)
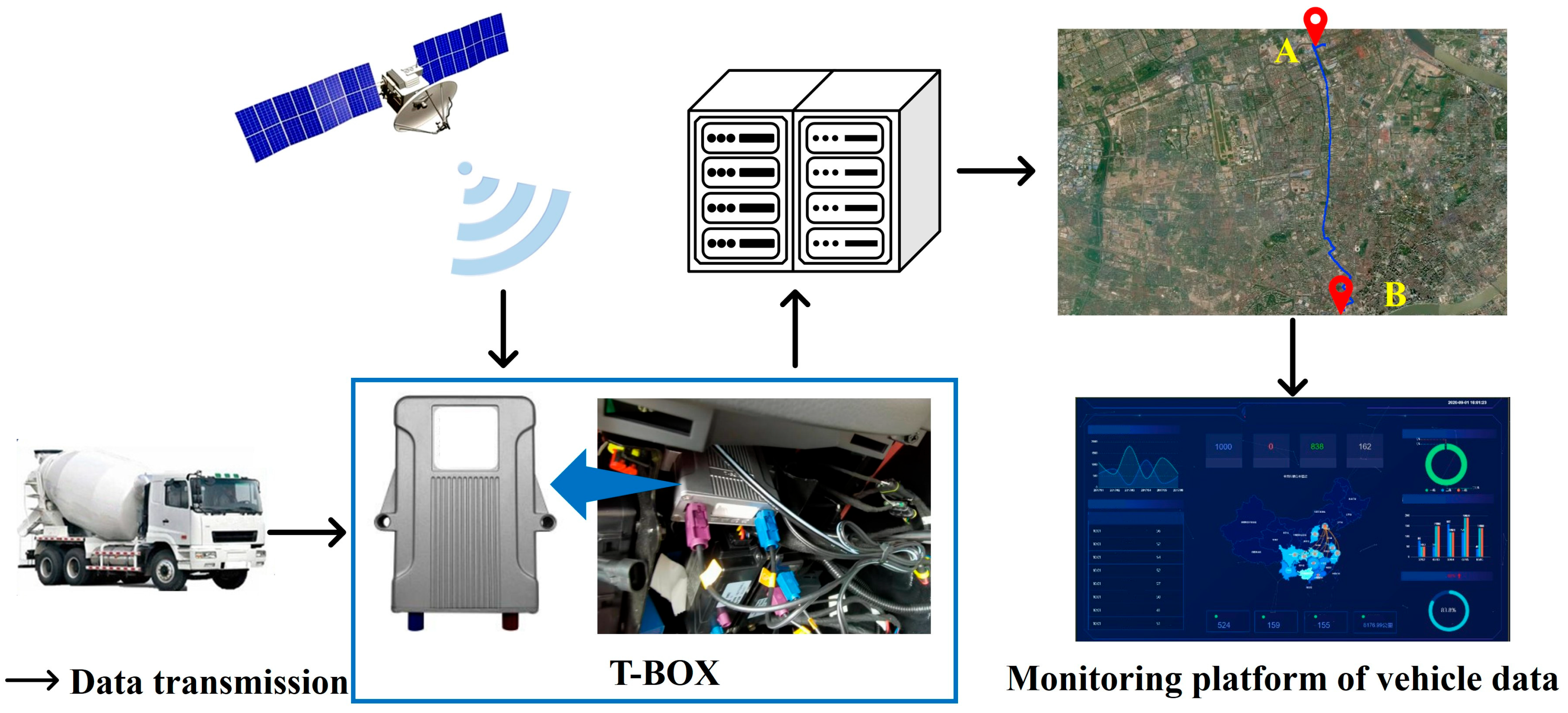
- The vehicle real data experiment considering the vehicle monitoring platform is designed to collect the driving data, including speed profiles, vehicle mass and operation mode sequences.
- (2)
- A deep adaptive clustering method based on the SSAE algorithm is utilized for the precise extraction of complex driving condition features and the achievement of optimal cluster partitioning.
2. SSAE-Based Feature Extraction
2.1. Data Collection Experiment
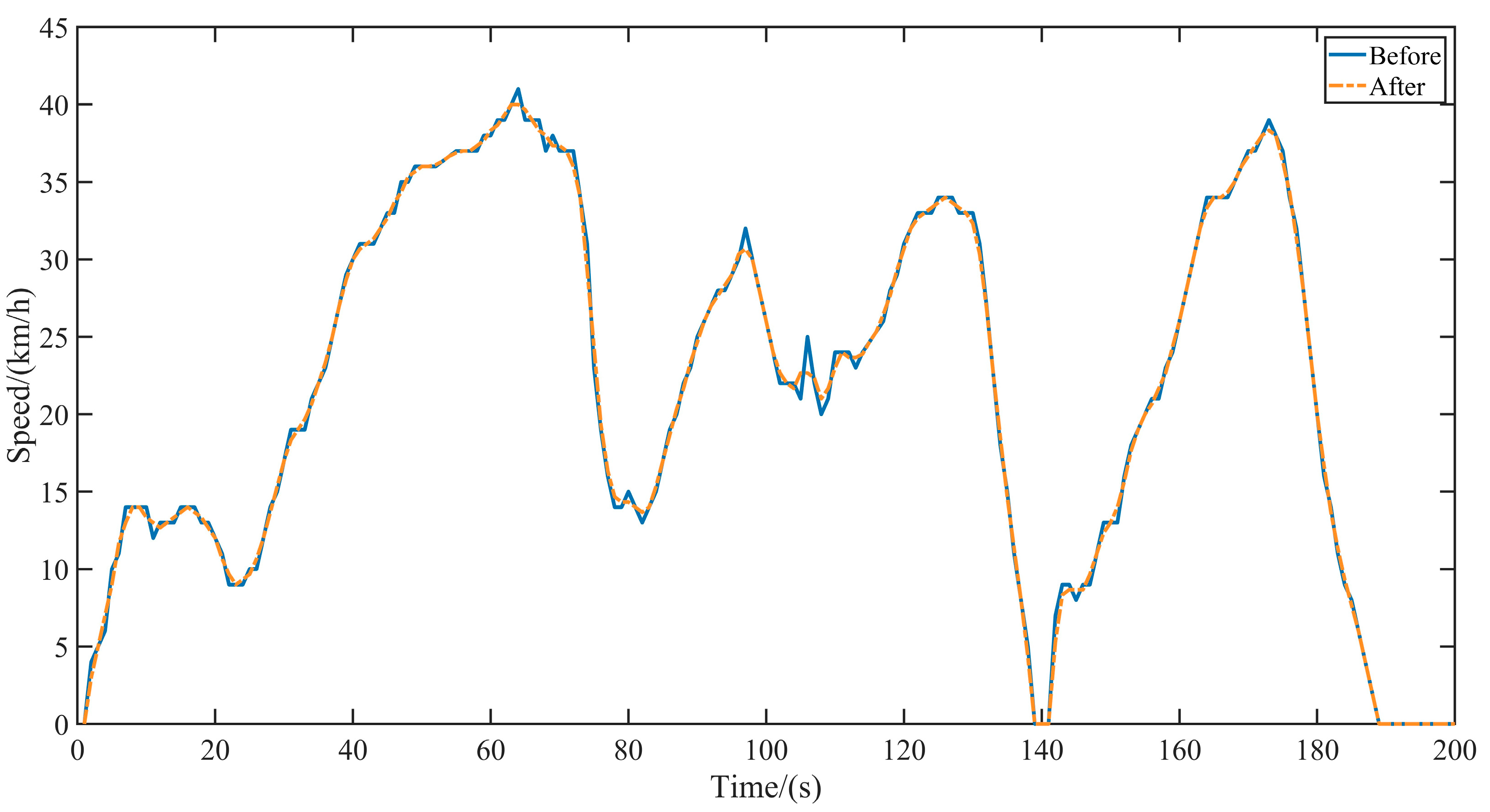
2.2. Data Preprocessing
- (1)
- Since timestamps and corresponding trajectory points in the data file are in Greenwich Mean Time (GMT), they should be converted to Beijing time (GMT + 8);
- (2)
- The hexadecimal format of the ‘time’ keyword in the data file should be converted to a decimal time series and cross-day indexing appropriately processed.
- (1)
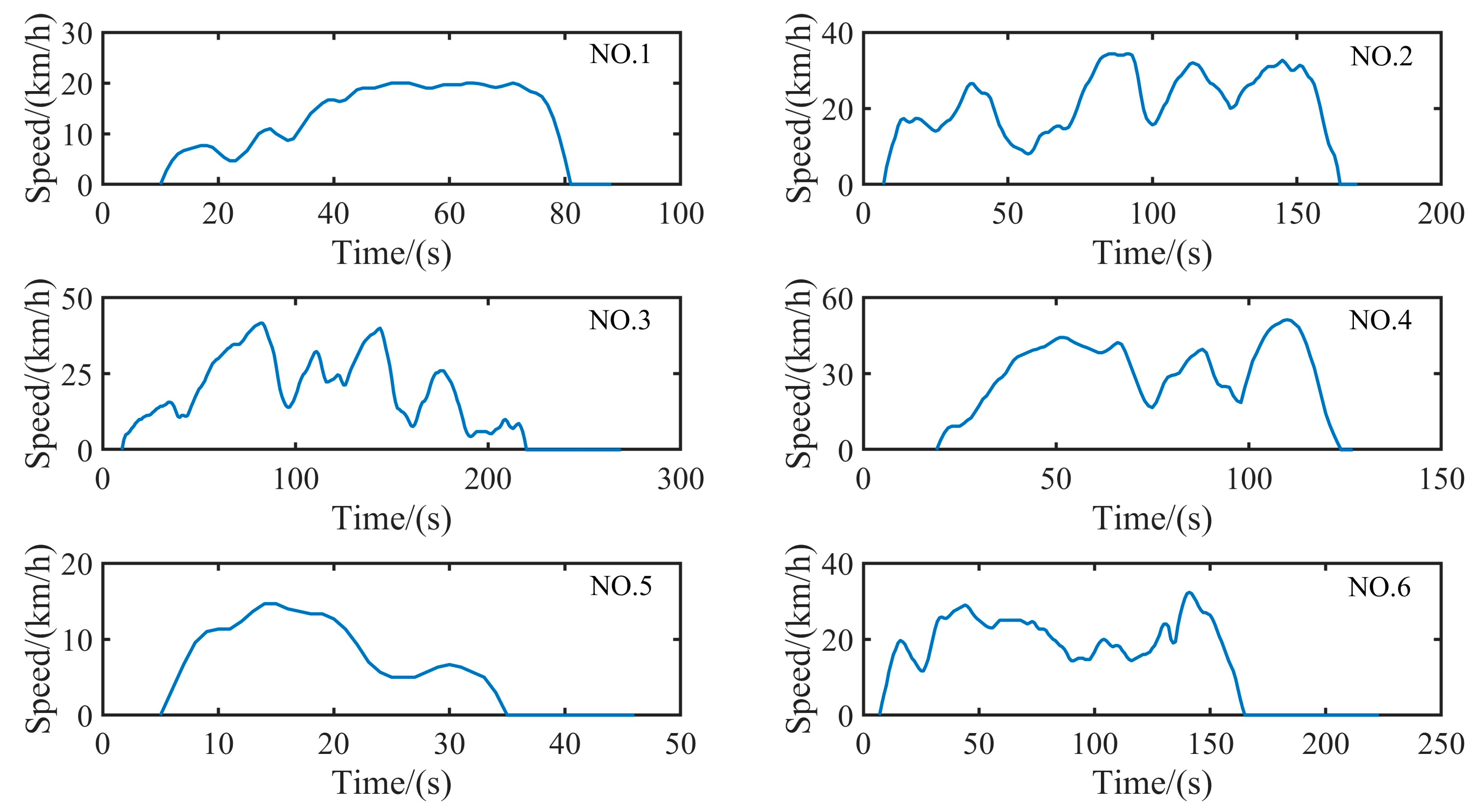
- Using the micro-trip partitioning method, the collected driving data of the CTM is divided into multiple micro-trips. After being chosen by criteria, a total of micro-trips are obtained. The following criteria are involved.
- (a)
- Due to equipment failures, abnormal driver operations, or weak GPS signals, some micro-trips have missing or discontinuous data. If a micro-trip has more than 10 consecutive missing sample points, it is discarded; otherwise, interpolation is used to supplement it.
- (b)
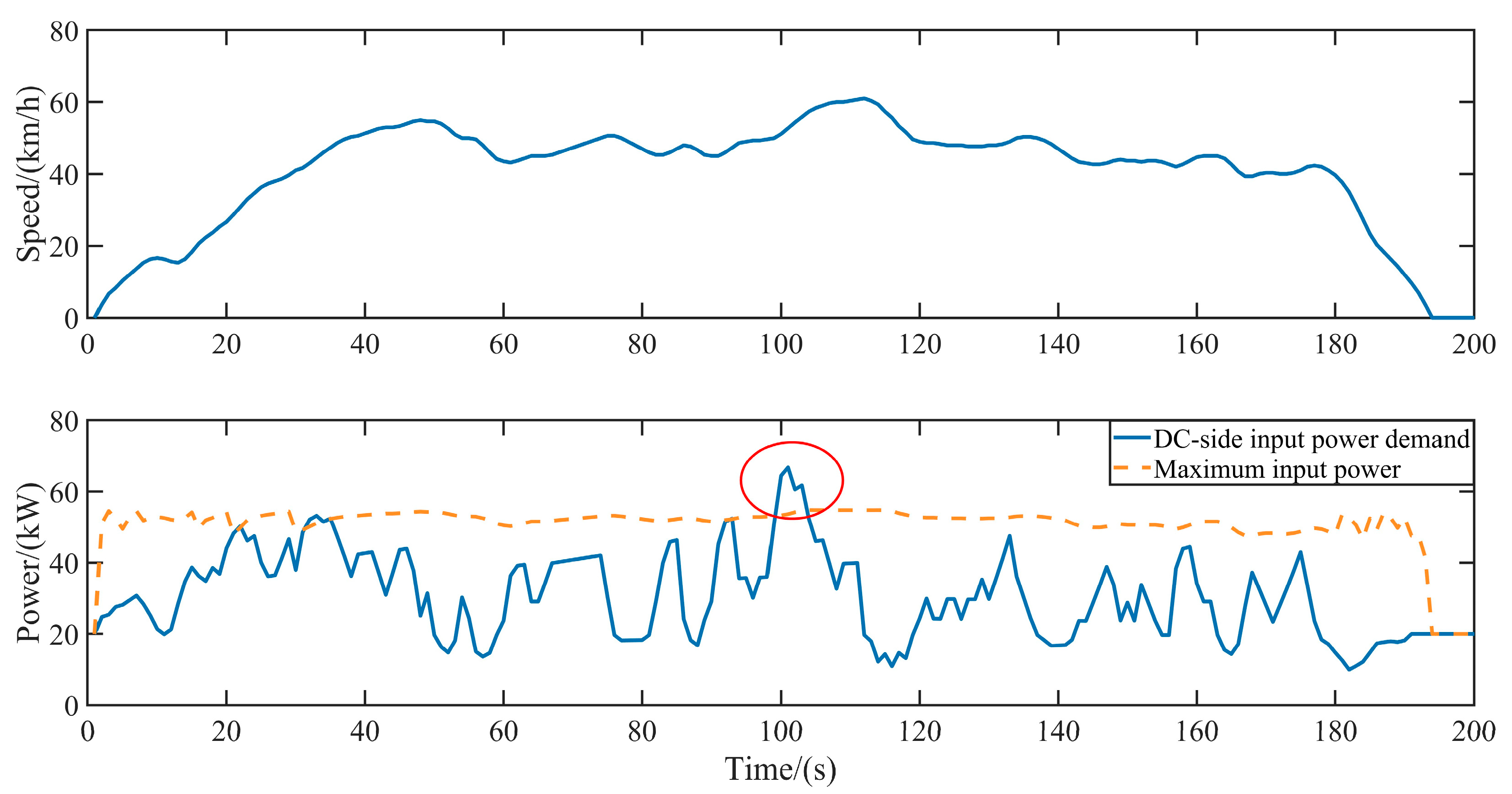
- According to relevant CTM standards, speed is limited to 50 km/h when fully loaded during transporting. However, no specific speed limit applies to empty returning.
- (c)
- All micro-trips in the established database for CTMs should be validated against the studied powertrain. Thus, the DC-side power demand sequence of the drive motor controller for each micro-trip is calculated, discarding any micro-trip where power demand exceeds the drive motor’s external characteristic curve at any point.
- (2)
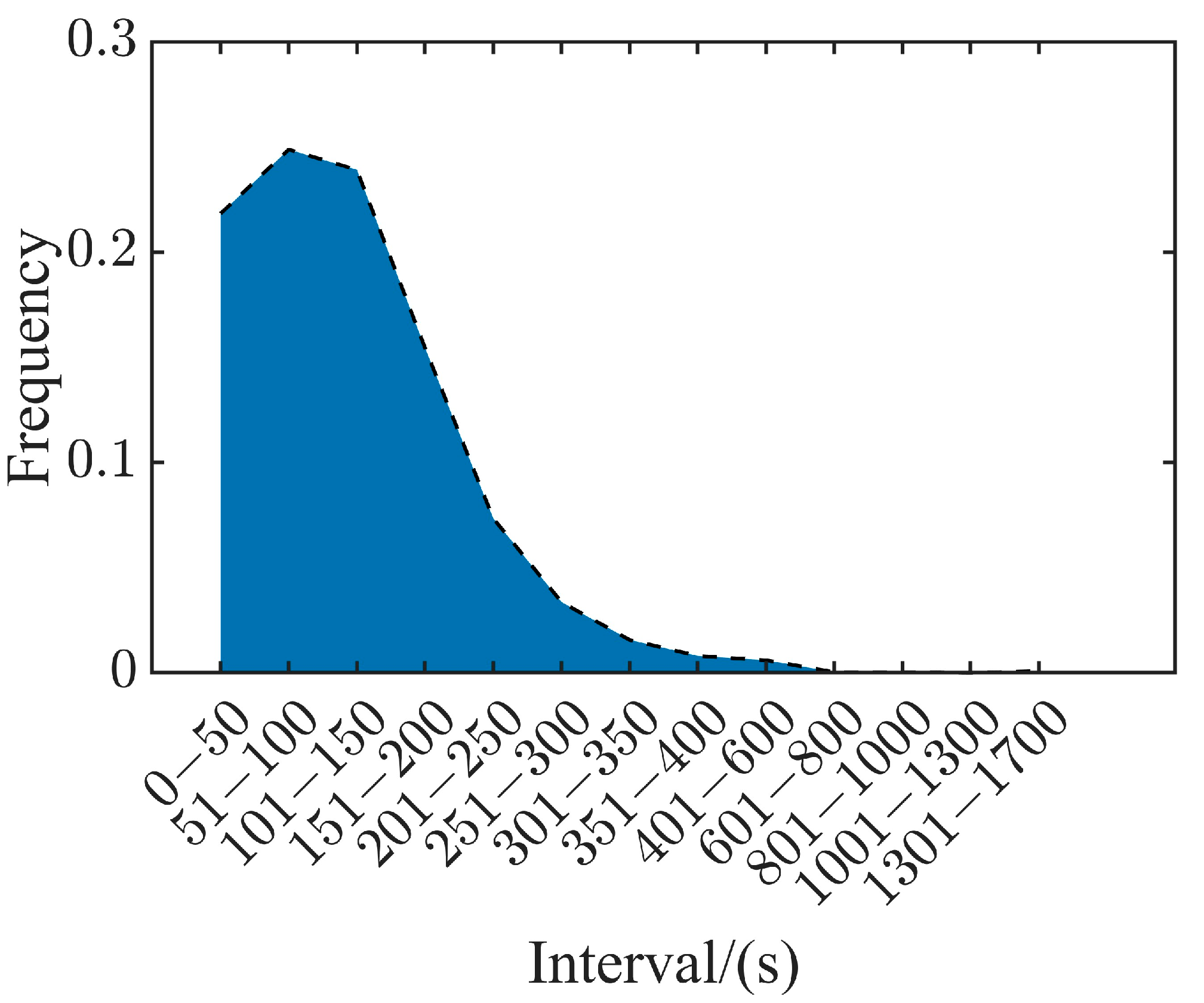
- Due to the requirement of fixed input dimensions for SSAE, it is necessary to unify the duration of micro-trips. Divide the time interval and calculate the frequency distribution of the micro-trips, and select the average of the time interval with the highest frequency as time length .
- (3)
- Cut or fill driving data in each micro-trip according to the established division criteria: if the real-time length of the micro-trip is less than , cut the micro-trip and divide it into multiple sub-segments with time length ; otherwise, fill the micro-trip to time length with the last speed. Additionally, it should be noted to delete all segments with zero values.
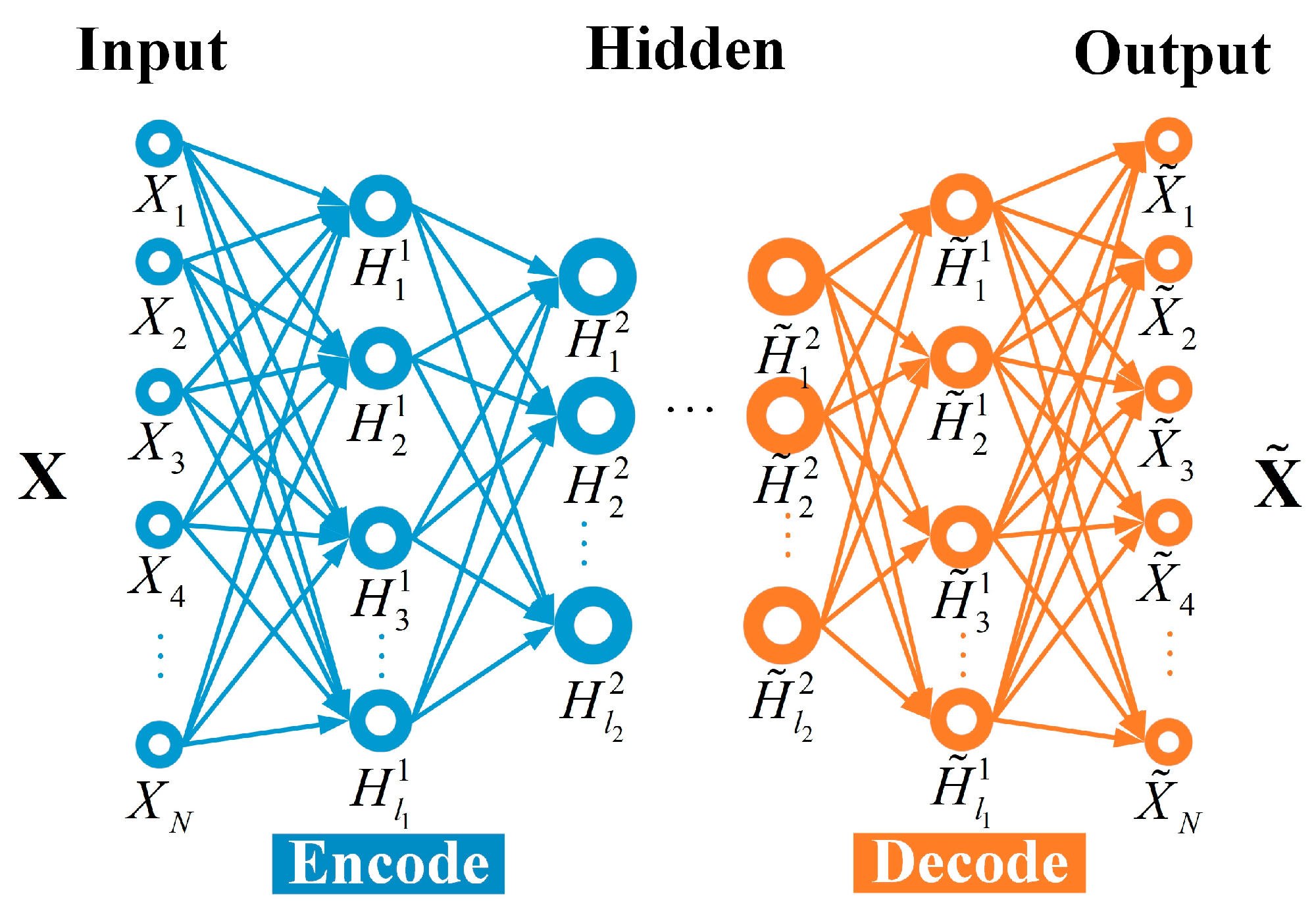
2.3. Deep Feature Extraction
3. Deep Adaptive Clustering Method for CTMs Driving Conditions
3.1. Adaptive Cluster Method
- (1)
- Input the feature samples extracted by the SSAE algorithm, and initialize parameters, mainly including the maximum allowable error ε and the range of the number of clusters , where takes the value of [35].
- (2)
- Randomly initialize the cluster center . Then, update the cluster center by calculating the centers and the mean of the samples’ features of each class.
- (3)
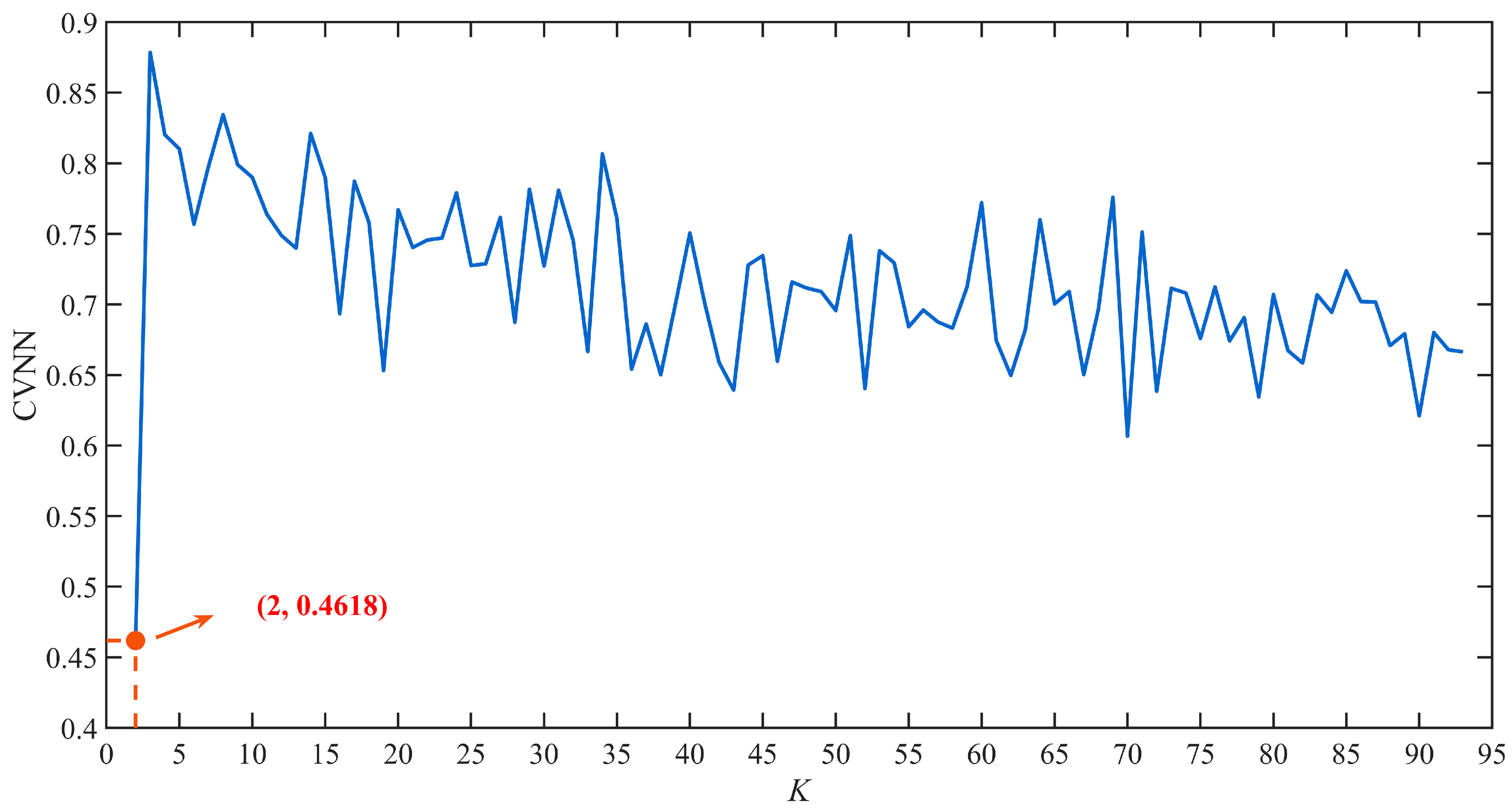
- Check whether the change in cluster centers before and after updating is less than . If it does, output the optimal number of clusters , the corresponding CVNN under the optimal number, and the cluster labels; Otherwise, increase the number of clusters until the error condition is satisfied or the predefined maximum number of clusters is reached. The calculation method of the indicator CVNN is as follows,
3.2. Fine Turning Process
4. Simulation Analysis
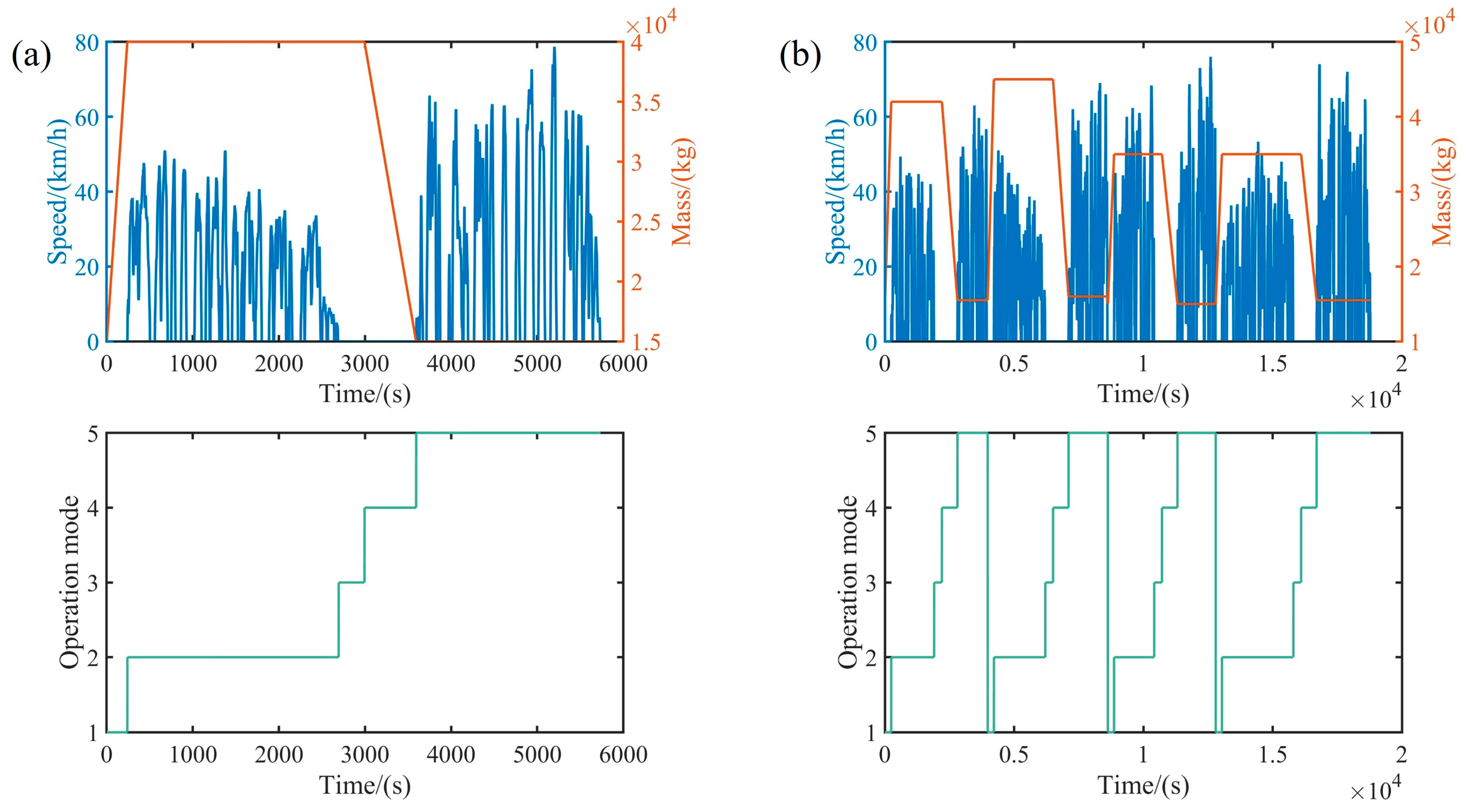
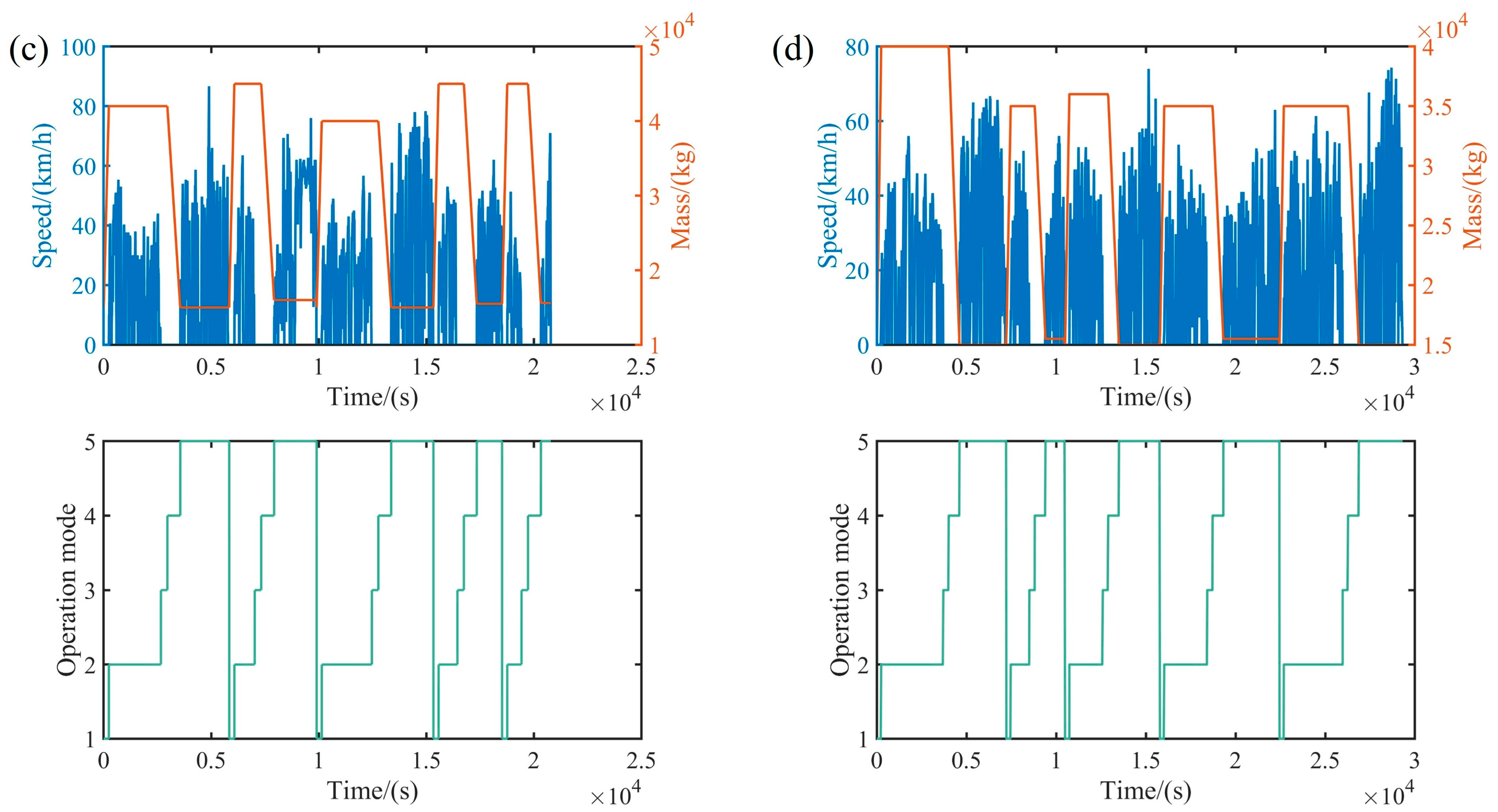
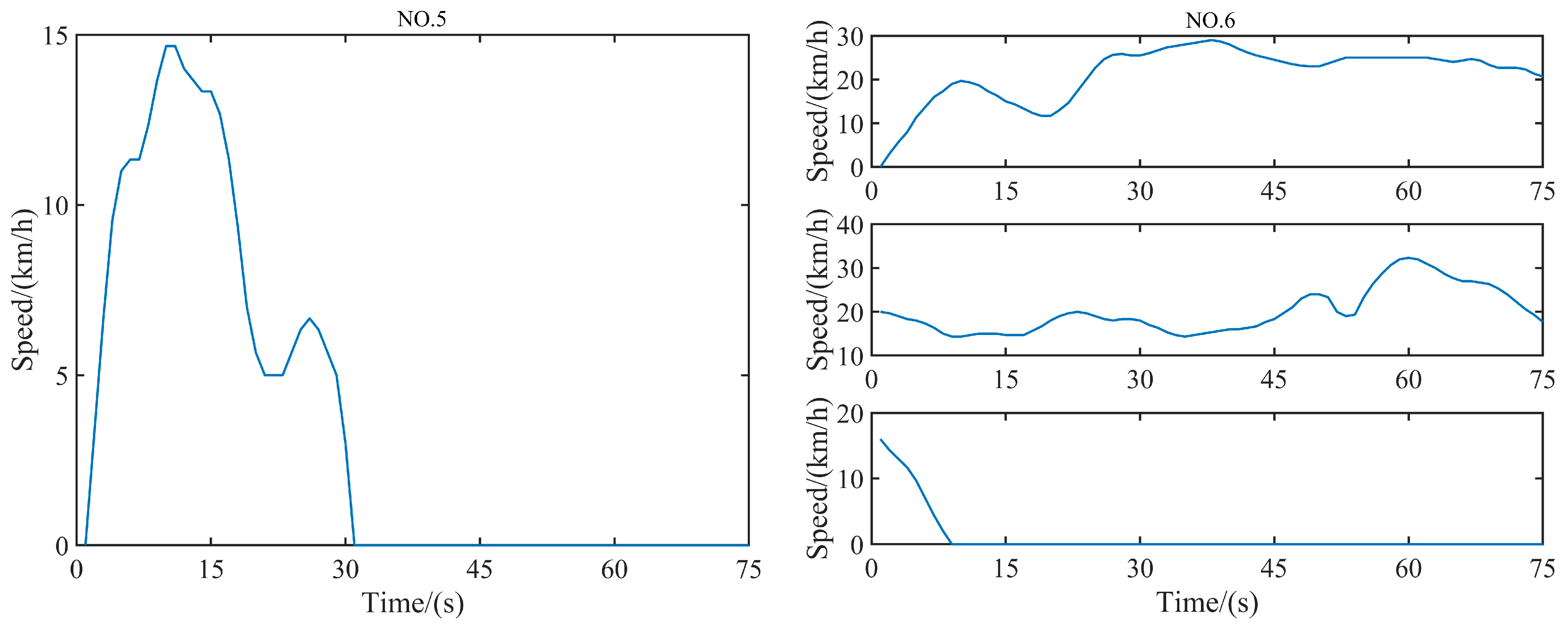
4.1. Data Collection and Preprocessing
4.2. Feature Extraction Results Analysis
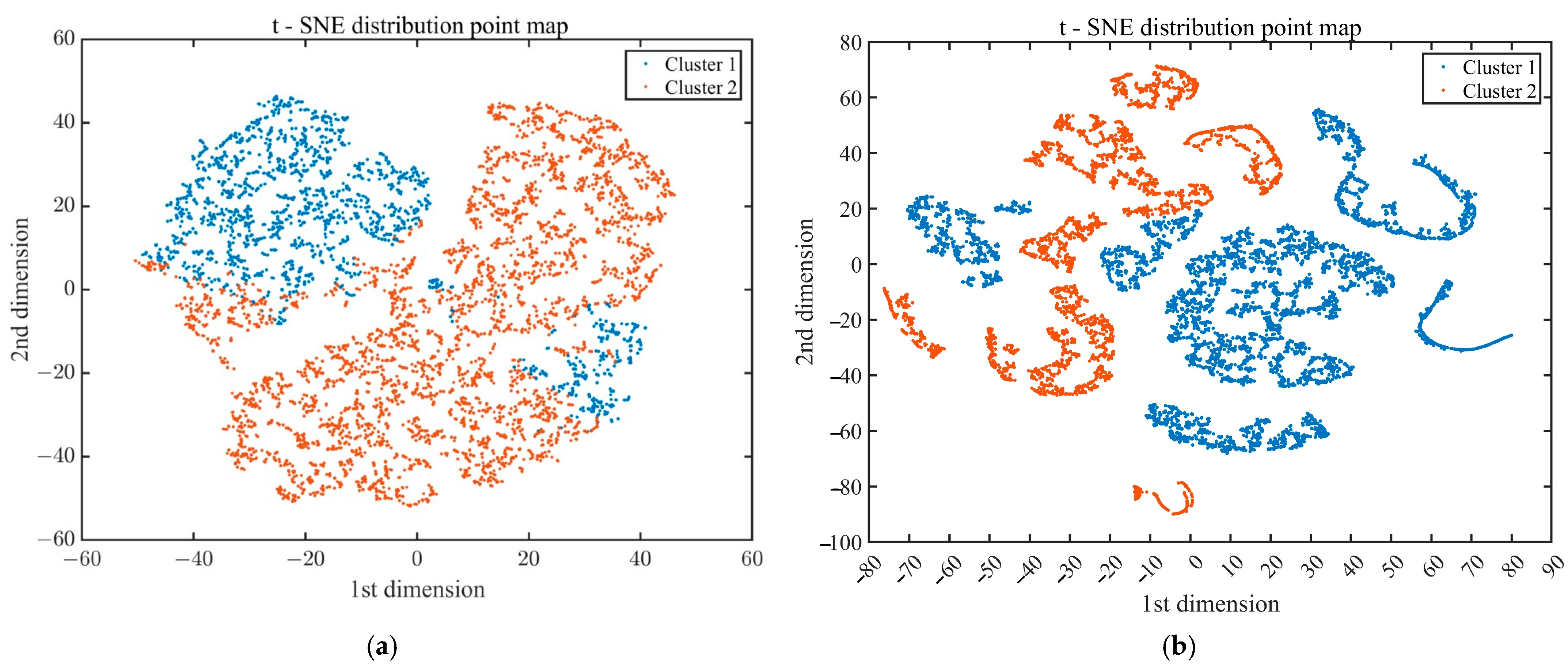
4.3. Clustering Results Analysis
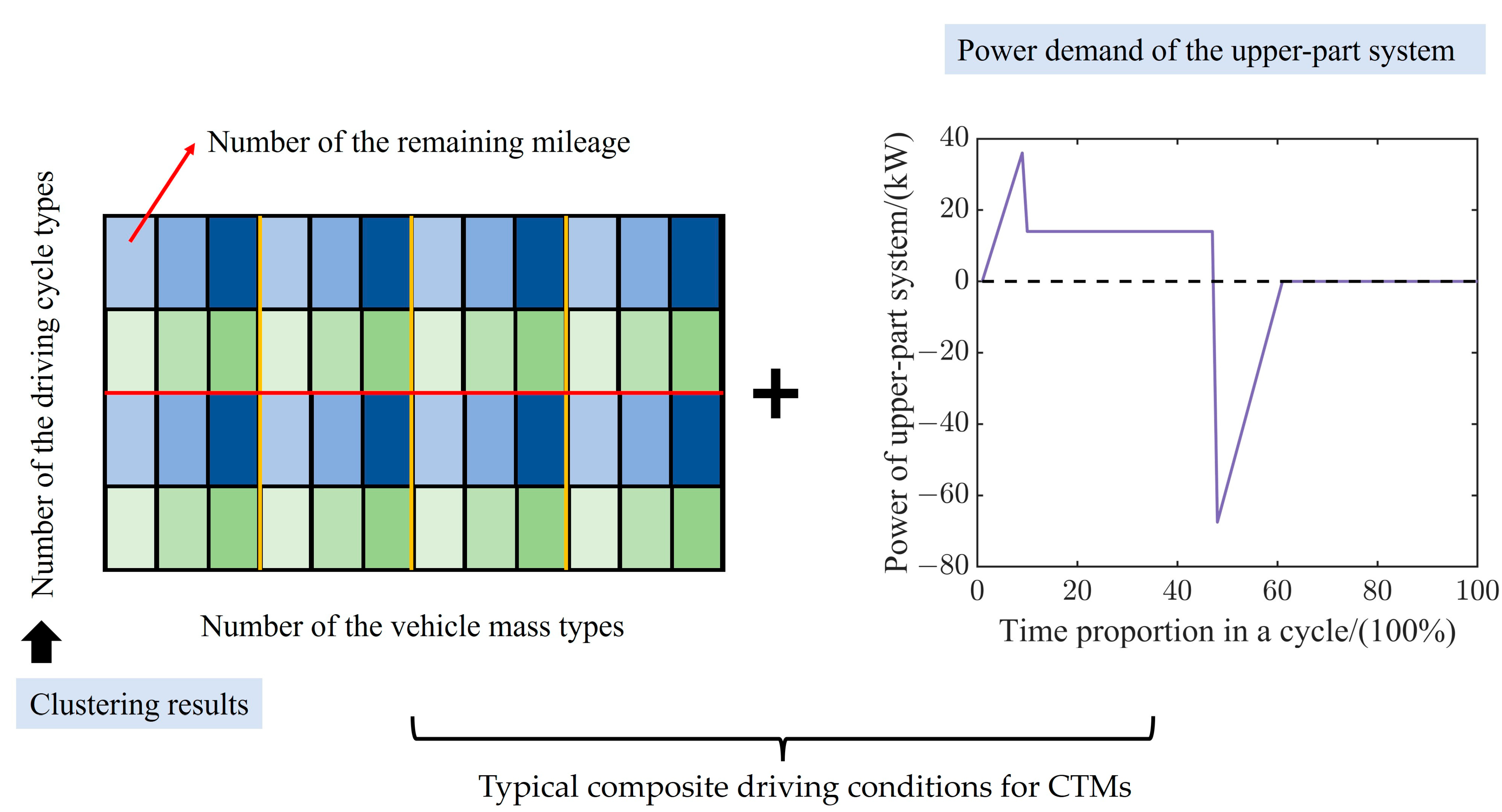
4.4. Future Research
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CTMs | Concrete truck mixers |
| SSAE | Stacked sparse autoencoders |
| PCA | Principal component analysis |
| SAE | Stacked autoencoders |
| DB | Davies–Bouldin index |
| CH | Calinski–Harabasz index |
| SH | Silhouette coefficient |
References
- He, L.; Mo, H.; Wu, L.; Zhang, Y.; Tang, J.; Wu, H. Optimization on motor control strategy for a pure electric heavy truck with dual motor. J. Braz. Soc. Mech. Sci. Eng. 2025, 47, 530. [Google Scholar] [CrossRef]
- Liu, C.N.; Liu, Y. Energy Management Strategy for Plug-In Hybrid Electric Vehicles Based on Driving Condition Recognition: A Review. Electronics 2022, 11, 342. [Google Scholar] [CrossRef]
- Kemper, P.; Rehlaender, P.; Witkowski, U.; Schwung, A. Competitive Evaluation of Energy Management Strategies for Hybrid Electric Vehicle Based on Real World Driving. In Proceedings of the 2017 European Modelling Symposium (EMS), Manchester, UK, 20–21 November 2017; pp. 151–156. [Google Scholar]
- Liu, T.; Tan, W.; Tang, X.; Zhang, J.; Xing, Y.; Cao, D. Driving conditions-driven energy management strategies for hybrid electric vehicles: A review. Renew. Sustain. Energy Rev. 2021, 151, 111521. [Google Scholar] [CrossRef]
- Wu, H.S.; Li, L.; Wang, X.Y. A Combined Energy Management Strategy for Heavy-Duty Trucks Based on Global Traffic Information Optimization. Sustainability 2025, 17, 6361. [Google Scholar] [CrossRef]
- Chen, R.; Yang, C.; Wang, W.; Zha, M.; Du, X.; Wang, M. Efficient Adaptive Power Coordination Control for Heavy-Duty Series Hybrid Electric Vehicles with Model and Weight Transfer Awareness. IEEE Trans. Transp. Electrif. 2025, 11, 9404–9415. [Google Scholar] [CrossRef]
- Moghadasi, S.; Yasami, A.; Munshi, S.; McTaggart-Cowan, G.; Shahbakhti, M. Real-world steep drive cycles and gradeability performance analysis of hybrid electric and conventional class 8 regional-haul truck. Energy 2025, 320, 135128. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, S.; Li, K.; Fan, Z.; Xie, H.; Jiang, F. Multi-parameter adaptive online energy management strategy for concrete truck mixers with a novel hybrid powertrain considering vehicle mass. Energy 2023, 277, 12770. [Google Scholar] [CrossRef]
- Huang, Y.; Jiang, F.C.; Xie, H.M. Adaptive hierarchical energy management design for a novel hybrid powertrain of concrete truck mixers. J. Power Sources 2021, 509, 230325. [Google Scholar] [CrossRef]
- Yan, Q.-D.; Chen, X.-Q.; Jian, H.-C.; Wei, W.; Wang, W.-D.; Wang, H. Design of a deep inference framework for required power forecasting and predictive control on a hybrid electric mining truck. Energy 2022, 238, 121960. [Google Scholar] [CrossRef]
- Tang, Q.; Hu, M.; Bian, Y.; Wang, Y.; Lei, Z.; Peng, X.; Li, K. Optimal energy efficiency control framework for distributed drive mining truck power system with hybrid energy storage: A vehicle-cloud integration approach. Appl. Energy 2024, 374, 123989. [Google Scholar] [CrossRef]
- Seunarine, M.B.; King, G. Representative Driving Cycles for Trinidad and Tobago with Slope Profiles for Electric Vehicles. Transp. Res. Rec. 2023, 2677, 1007–1016. [Google Scholar]
- Qiu, H.; Cui, S.; Wang, S.; Wang, Y.; Feng, M. A Clustering-Based Optimization Method for the Driving Cycle Construction: A Case Study in Fuzhou and Putian, China. IEEE Trans. Intell. Transp. Syst. 2022, 23, 18681–18694. [Google Scholar] [CrossRef]
- Wang, P.Y.; Pan, C.Y.; Sun, T.J. Control strategy optimization of plug-in hybrid electric vehicle based on driving data mining. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 237, 333–346. [Google Scholar] [CrossRef]
- He, H.; Guo, J.; Peng, J.; Tan, H.; Sun, C. Real-time global driving cycle construction and the application to economy driving pro system in plug-in hybrid electric vehicles. Energy 2018, 152, 95–107. [Google Scholar]
- Topi, J.; Kugor, B.; Deur, J. Neural network-based prediction of vehicle fuel consumption based on driving cycle data. Sustainability 2022, 14, 744. [Google Scholar] [CrossRef]
- Cui, Y.; Zou, F.; Xu, H.; Chen, Z.; Gong, K. A novel optimization-based method to develop representative driving cycle in various driving conditions. Energy 2022, 247, 123455. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.; Shao, P.; Li, Z.; Song, W. Study on Components Durability Test Conditions Based on Combined Clustering and Markov Chain Method. Int. J. Automot. Technol. 2021, 22, 553–560. [Google Scholar] [CrossRef]
- Guo, J.; Xie, D.; Jiang, Y.; Li, Y. A novel construction and evaluation framework for driving cycle of electric vehicles based on energy consumption and emission analysis. Sustain. Cities Soc. 2024, 117, 105951. [Google Scholar] [CrossRef]
- Lin, J.X.; Liu, B.; Zhao, X.; Zhang, L. Intelligent Construction Method of Vehicle Condition Based on Hybrid Constrained Autoencoder. J. Transp. Syst. Eng. Inf. Technol. 2022, 22, 109–116. (In Chinese) [Google Scholar]
- Chen, Z.; Zhang, Q.; Lu, J.; Bi, J. Optimization-based method to develop practical driving cycle for application in electric vehicle power management: A case study in Shenyang, China. Energy 2019, 186, 115766.1–115766.13. [Google Scholar] [CrossRef]
- Wang, Y.; Li, K.; Zeng, X.; Gao, B.; Hong, J. Energy consumption characteristics based driving conditions construction and prediction for hybrid electric buses energy management. Energy 2022, 245, 123189. [Google Scholar] [CrossRef]
- Yang, D.; Liu, T.; Zhang, X.; Zeng, X.; Song, D. Construction of high-precision driving cycle based on Metropolis-Hastings sampling and genetic algorithm. Transp. Res. Part D Transp. Environ. 2023, 118, 103715. [Google Scholar] [CrossRef]
- Tong, Z.M.; Guan, S. Developing high-precision battery electric forklift driving cycle with variable cargo weight. Transp. Res. Part D Transp. Environ. 2024, 136, 104443. [Google Scholar] [CrossRef]
- Zhang, H.L.; Kong, D.; Yu, T.; Ao, G.; Shao, Y. Construction of urban driving cycle of light-duty vehicle based on LLEKM and Markov chain. J. Chang’an Univ. (Nat. Sci. Ed.) 2021, 41, 118–126. (In Chinese) [Google Scholar]
- Tufail, S.; Iqbal, H.; Tariq, M.; Sarwat, A.I. A Hybrid Machine Learning-Based Framework for Data Injection Attack Detection in Smart Grids Using PCA and Stacked Autoencoders. IEEE Access 2025, 13, 33783–33798. [Google Scholar] [CrossRef]
- Bi, J.; Guan, Z.; Yuan, H.; Yang, J.; Zhang, J. Network Anomaly Detection with Stacked Sparse Shrink Variational Autoencoders and Unbalanced XGBoost. IEEE Trans. Sustain. Comput. 2025, 10, 28–38. [Google Scholar] [CrossRef]
- Shi, C.; Luo, B.; He, S.; Li, K.; Liu, H.; Li, B. Tool Wear Prediction Via Multi-Dimensional Stacked Sparse Autoencoders with Feature Fusion. IEEE Trans. Ind. Inform. 2019, 16, 5150–5159. [Google Scholar] [CrossRef]
- Wang, B.L.; Tian, Y.; Yuan, J.K.; Wang, L.M.; Zhou, Y.C. Improvement method of semitrailer driving cycle construction based on clustering. J. Shandong Univ. Technol. (Nat. Sci. Ed.) 2023, 37, 26–33. (In Chinese) [Google Scholar]
- Zhu, D.; Xiao, B.; Xie, H.; Li, D.; He, H.; Zhai, W. Exploring trans-regional harvesting operation patterns based on multi-scale spatiotemporal partition using GNSS trajectory data. Int. J. Digit. Earth 2025, 18, 2466027. [Google Scholar] [CrossRef]
- Ggarwal, S.; Singh, P. Cuckoo, Bat and Krill Herd based k-means++ clustering algorithms. Clust. Comput. 2019, 22, 14169–14180. [Google Scholar] [CrossRef]
- Min, Y.Z.; Hao, D.Y.; Wang, G.; He, Y.; He, J. Reactor voiceprint clustering method based on deep adaptive K-means++ algorithm. Power Syst. Prot. Control 2025, 53, 1–3. (In Chinese) [Google Scholar]
- Mienye, I.D.; Sun, Y. Improved Heart Disease Prediction Using Particle Swarm Optimization Based Stacked Sparse Autoencoder. Electronics 2021, 10, 2347. [Google Scholar] [CrossRef]
- Wang, J.; Huang, Y.; Gao, X.; Wang, T.; Wang, X.; Hui, J. Blockage Location Algorithm of Multi-cylinder Fuel Injectors Based on Stacked Sparse Autoencoder. Acta Armamentarii 2024, 45, 3706–3717. (In Chinese) [Google Scholar]
- Lei, Y.; He, Z.; Zi, Y.; Chen, X. New clustering algorithm-based fault diagnosis using compensation distance evaluation technique. Mech. Syst. Signal Process. 2008, 22, 419–435. [Google Scholar] [CrossRef]
- Ahmed Al-Kerboly, D.M.; Al-Kerboly, D.Z.F. A Comparative Study of Clustering Algorithms for Profiling Researchers in Universities Through Google Scholar. In Proceedings of the 2024 IEEE 3rd International Conference on Computing and Machine Intelligence (ICMI), Mt Pleasant, MI, USA, 13–14 April 2024; pp. 1–5. [Google Scholar]



| Algorithm | Value |
|---|---|
| PCA | 0.41 |
| Stacked AE | 1.03 |
| Sparse AE | 0.44 |
| SSAE | 2.10 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Hidden layers | 4 | Sparsity rate | 0.1 |
| Nodes | [70, 50, 40, 30] | Weight attenuation parameter | 0.001 |
| Sparse penalty term | 3 | Maximum cluster number | 93 |
| Minimum cluster number | 2 |
| Index | EPKMC | DAKMC |
|---|---|---|
| DB | 1.0620 | 0.9140 |
| CH | ||
| SH | 0.5956 | 0.5562 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Jiang, F.; Xie, H. Research on Deep Adaptive Clustering Method Based on Stacked Sparse Autoencoders for Concrete Truck Mixers Driving Conditions. World Electr. Veh. J. 2025, 16, 581. https://doi.org/10.3390/wevj16100581
Huang Y, Jiang F, Xie H. Research on Deep Adaptive Clustering Method Based on Stacked Sparse Autoencoders for Concrete Truck Mixers Driving Conditions. World Electric Vehicle Journal. 2025; 16(10):581. https://doi.org/10.3390/wevj16100581
Chicago/Turabian StyleHuang, Ying, Fachao Jiang, and Haiming Xie. 2025. "Research on Deep Adaptive Clustering Method Based on Stacked Sparse Autoencoders for Concrete Truck Mixers Driving Conditions" World Electric Vehicle Journal 16, no. 10: 581. https://doi.org/10.3390/wevj16100581
APA StyleHuang, Y., Jiang, F., & Xie, H. (2025). Research on Deep Adaptive Clustering Method Based on Stacked Sparse Autoencoders for Concrete Truck Mixers Driving Conditions. World Electric Vehicle Journal, 16(10), 581. https://doi.org/10.3390/wevj16100581





