Optimized Charging Strategy for Lithium-Ion Battery Based on Improved MFO Algorithm and Multi-State Coupling Model
Abstract
1. Introduction
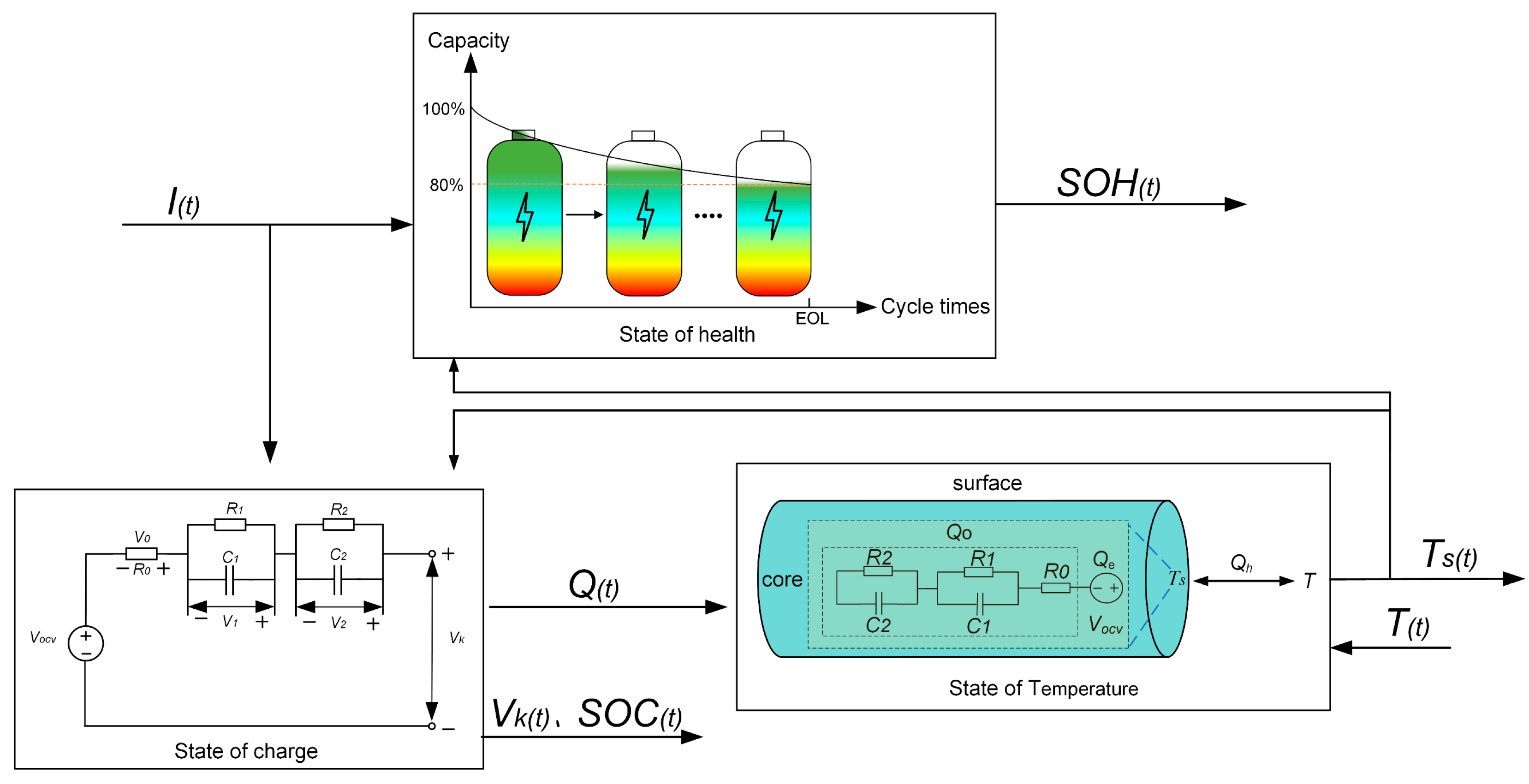
2. Multi-State Coupling Model of Lithium-Ion Battery
2.1. Second-Order RC Circuit Model
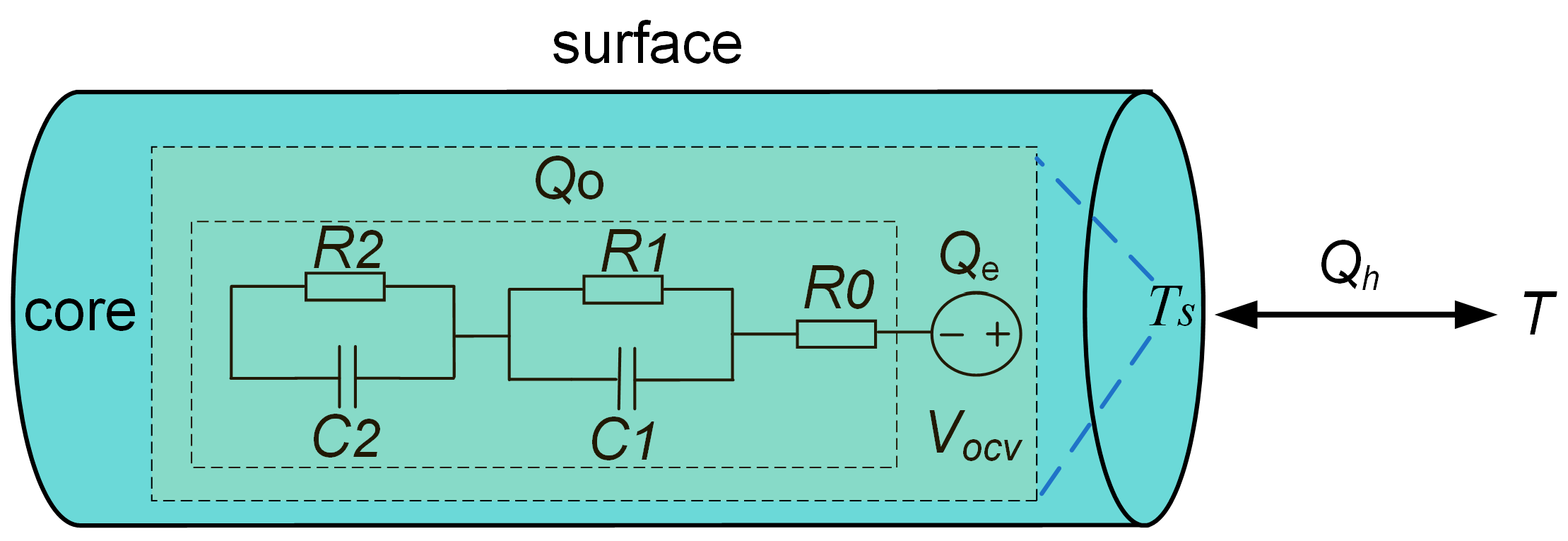
2.2. Thermal Model
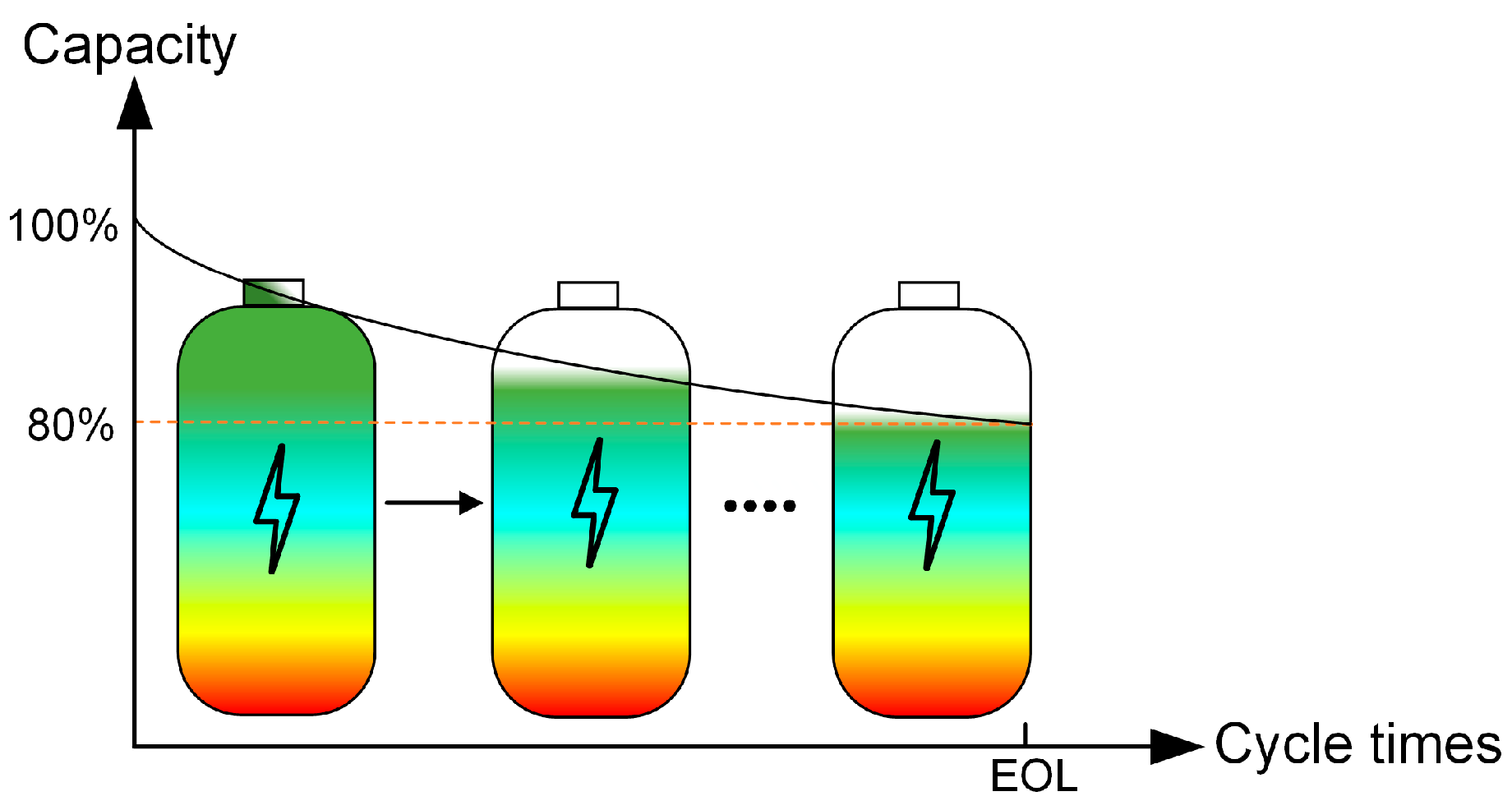
2.3. Aging Model
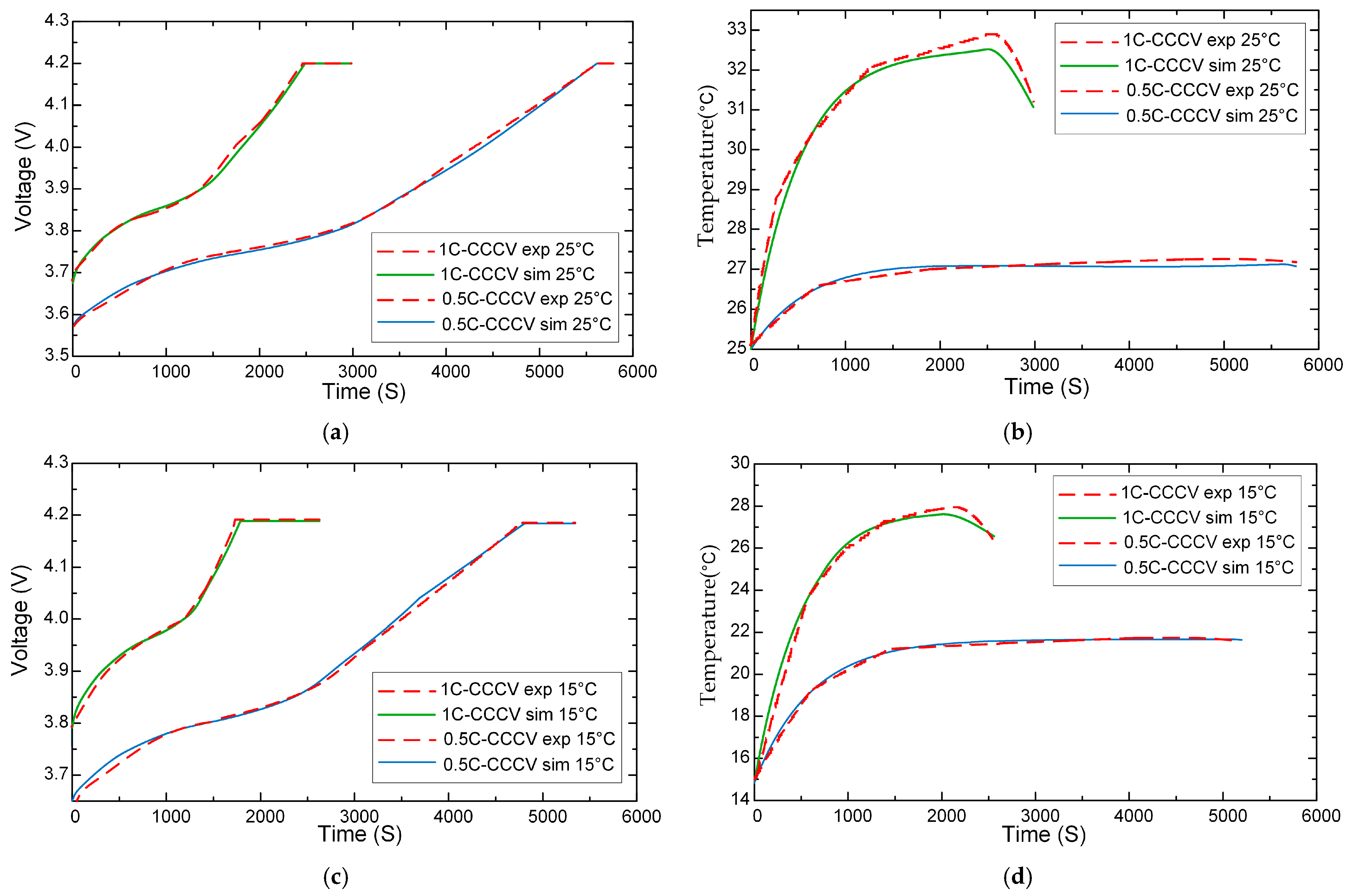
2.4. Multi-State Coupling Model and Model Validation
3. Optimization of Charging Method
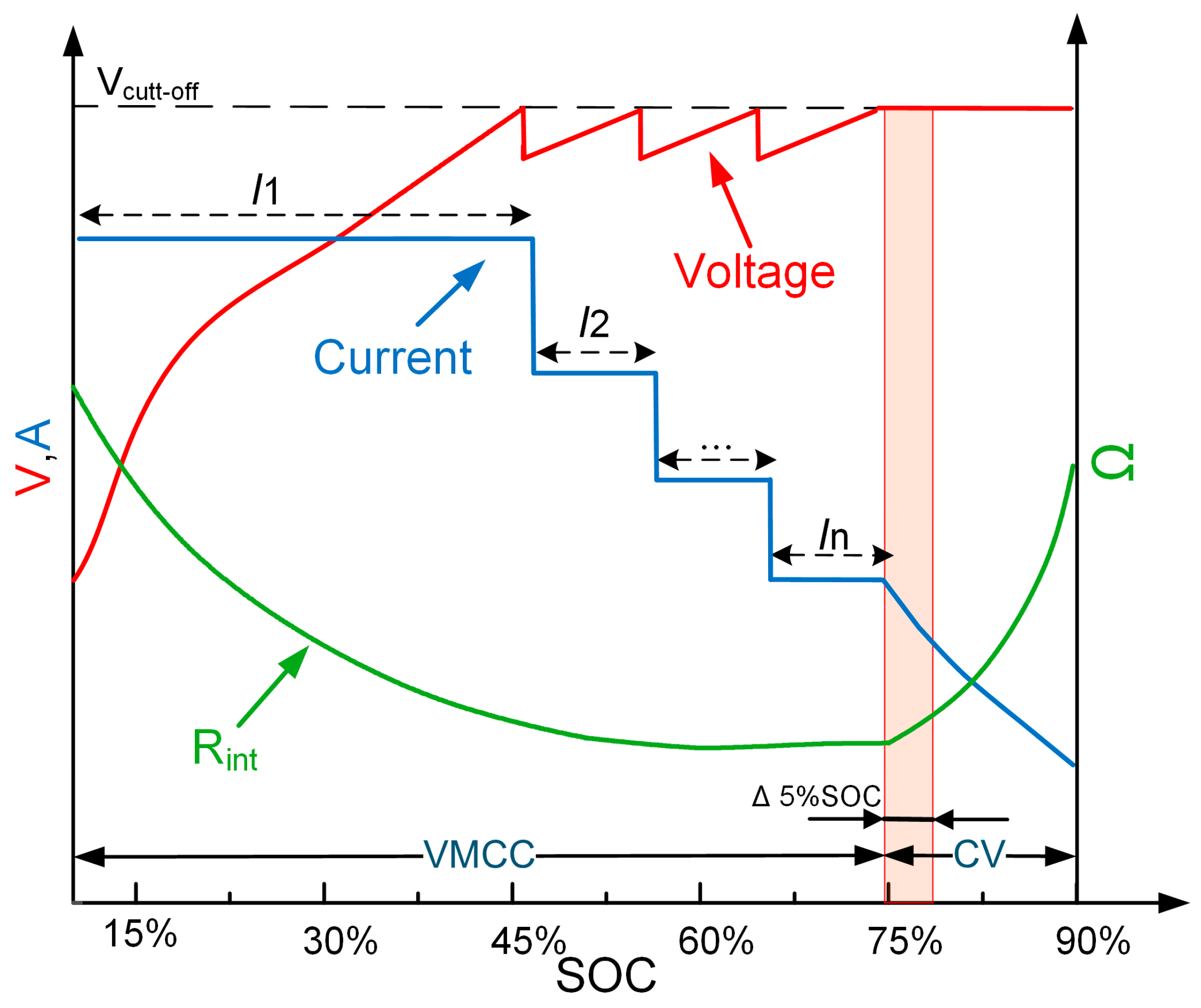
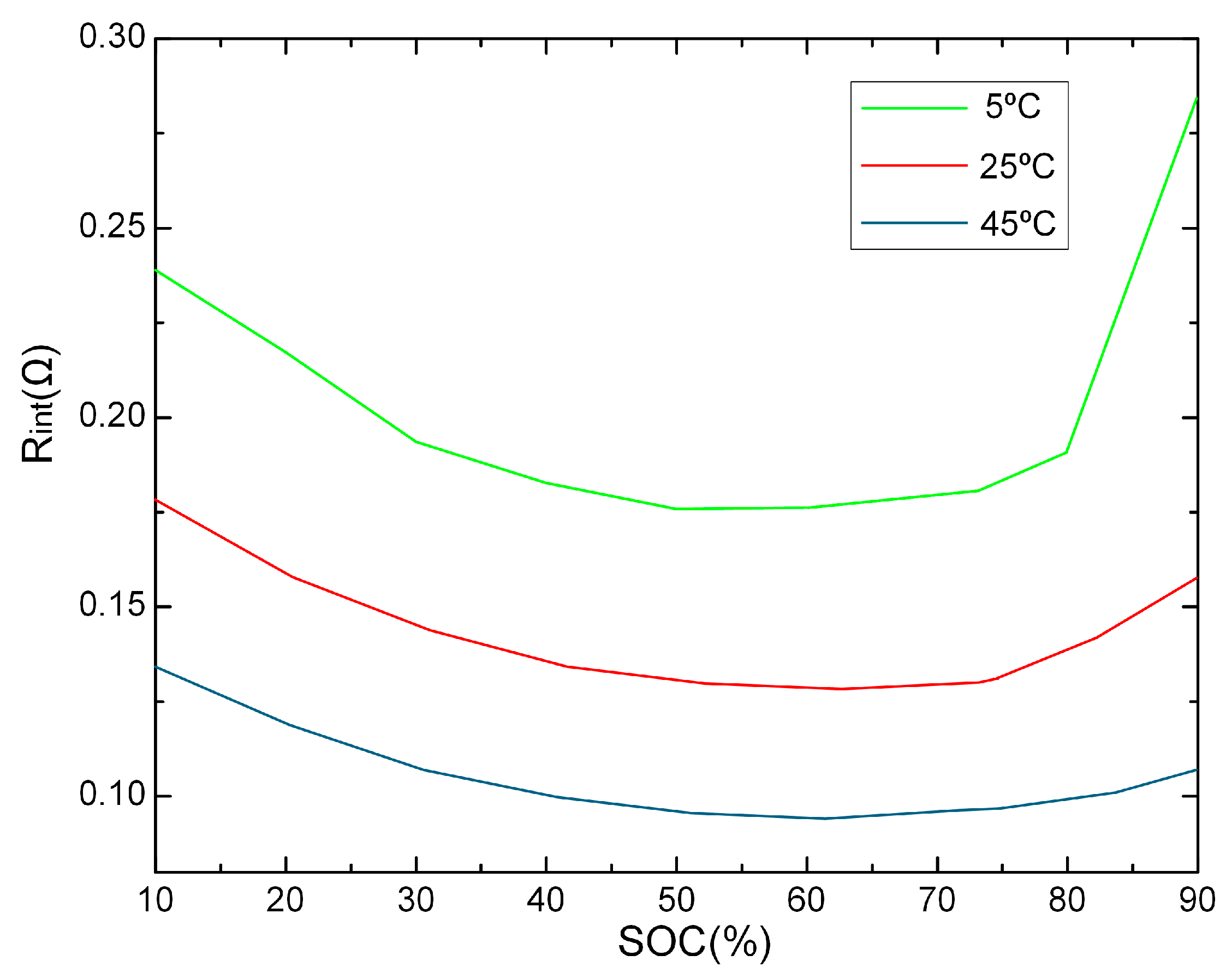
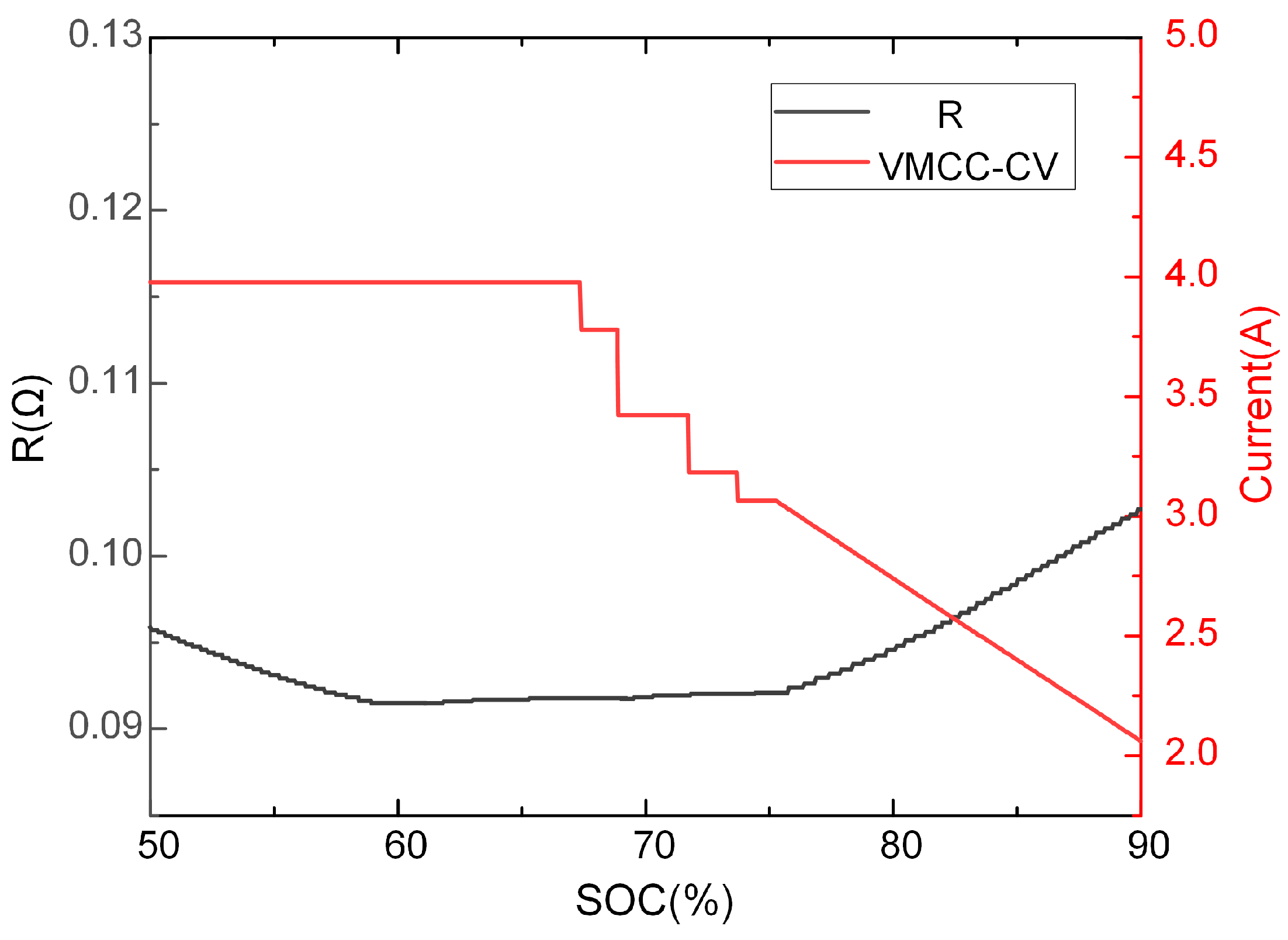
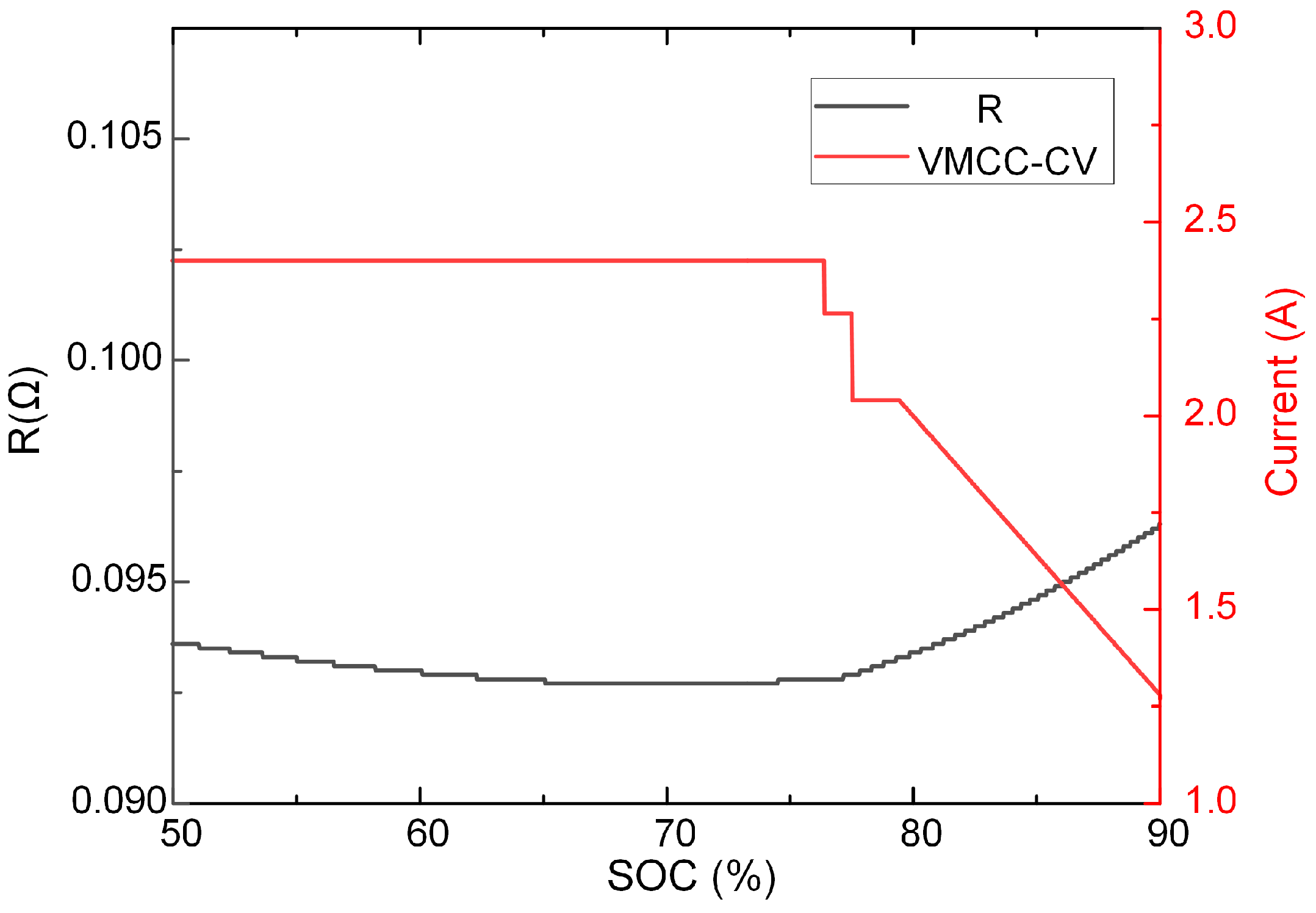
3.1. VMCC-CV Charging Strategy Based on V-SOC-Rint
3.2. Optimization Objective Function
3.3. Traditional MFO Algorithm
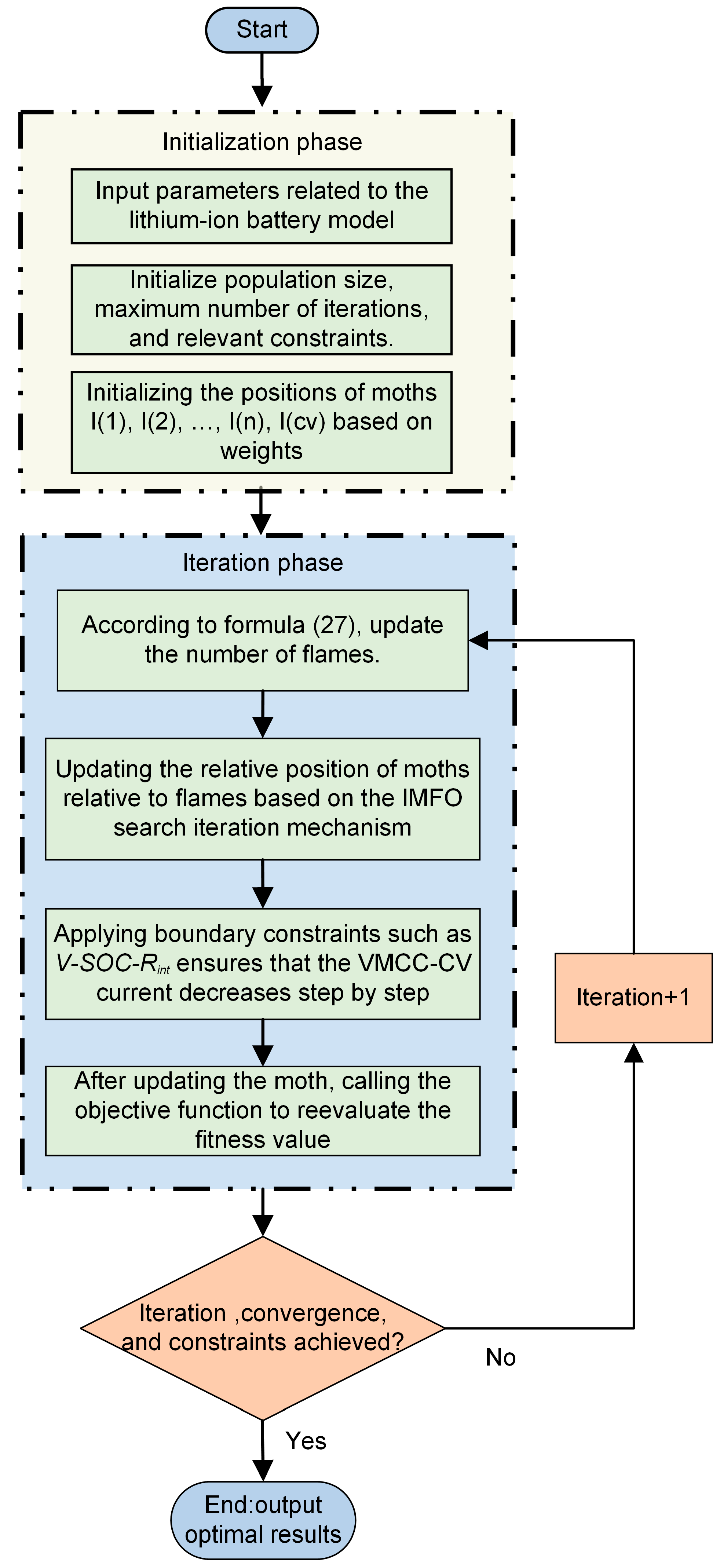
3.4. Improved MFO Algorithm
4. Results and Discussion
4.1. Improved MFO Algorithm Charging Strategy Validation
4.2. Charging Optimization Strategies for Three Charging Scenarios
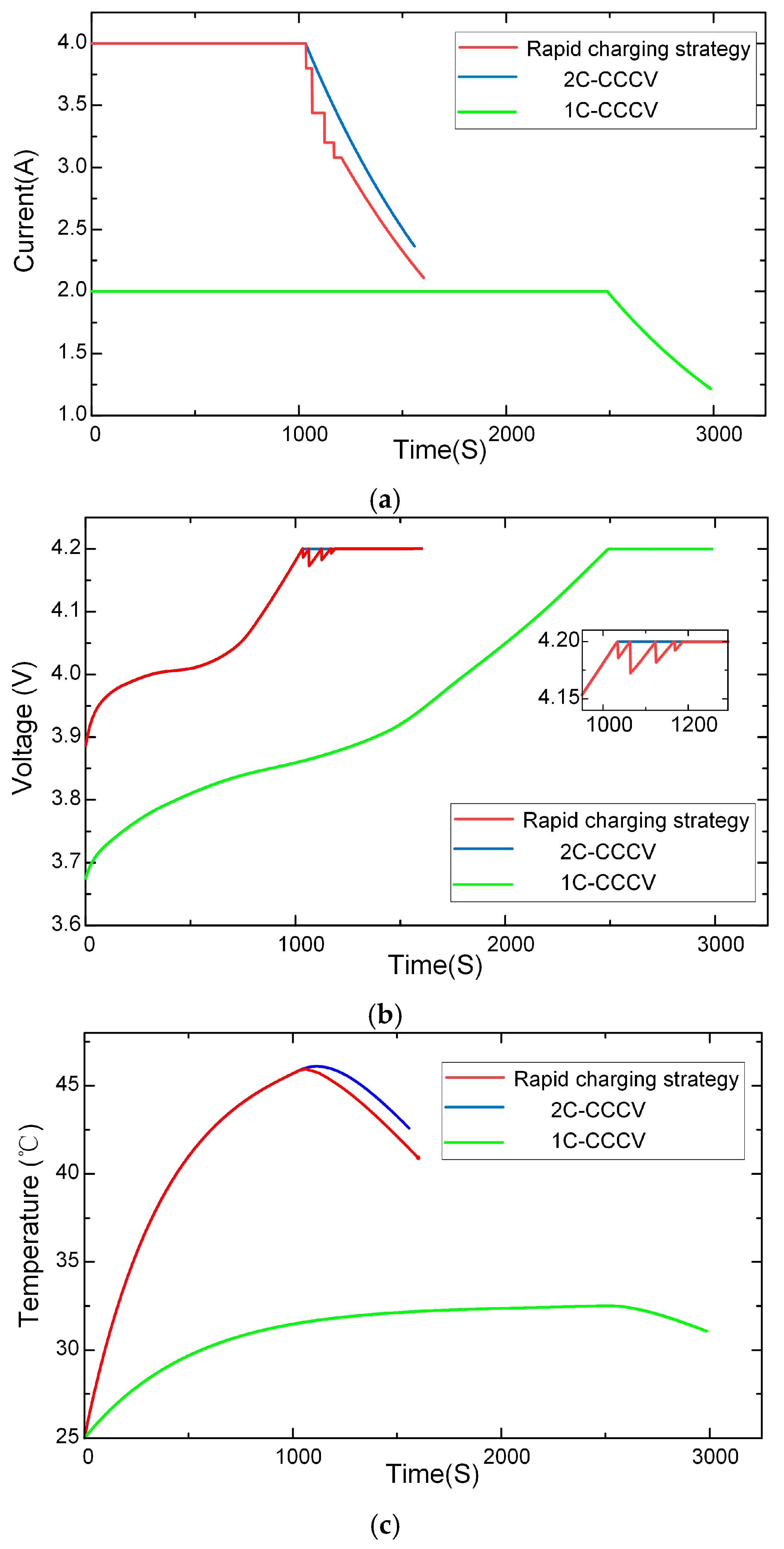
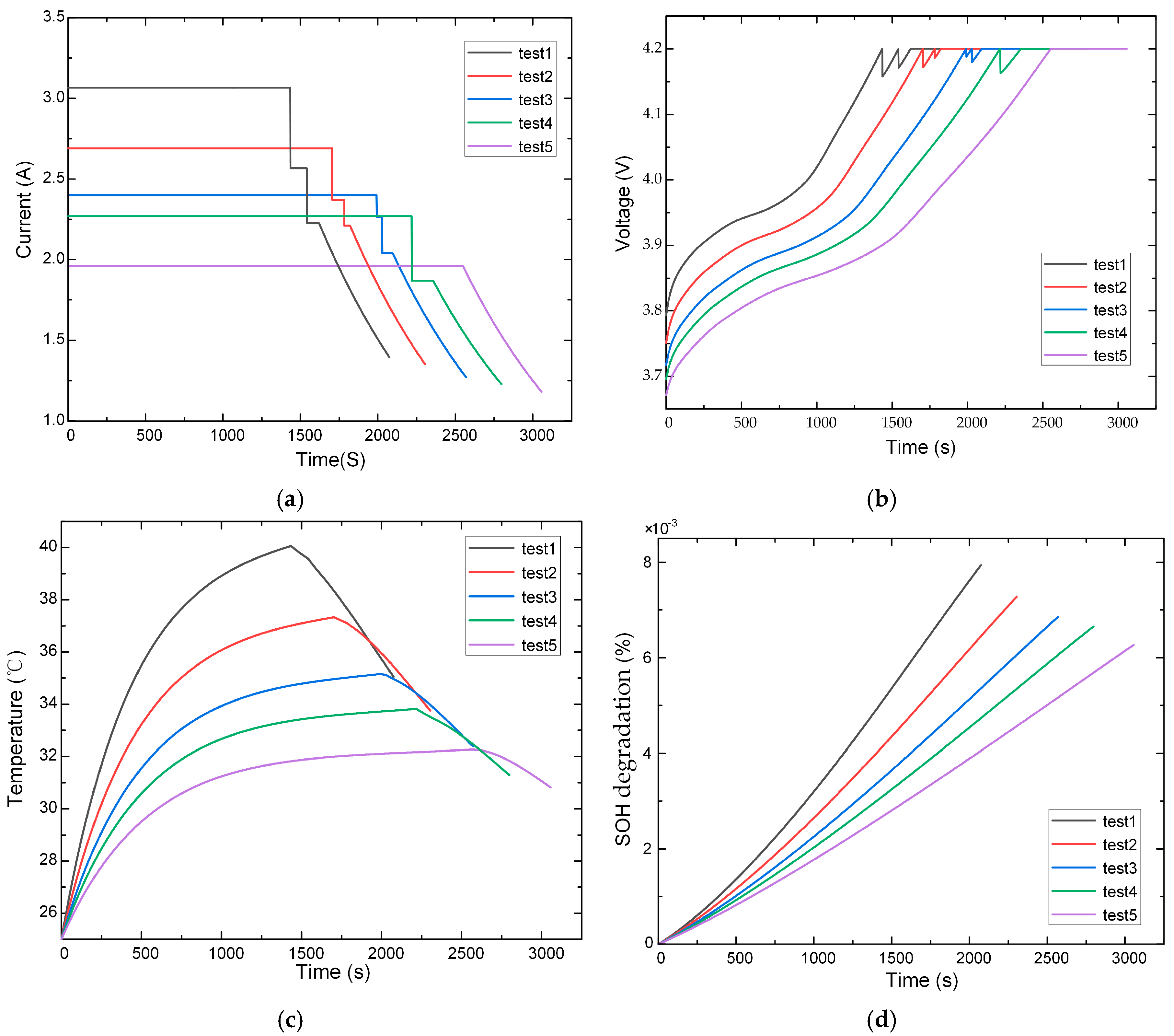
4.2.1. Rapid Charging Strategy
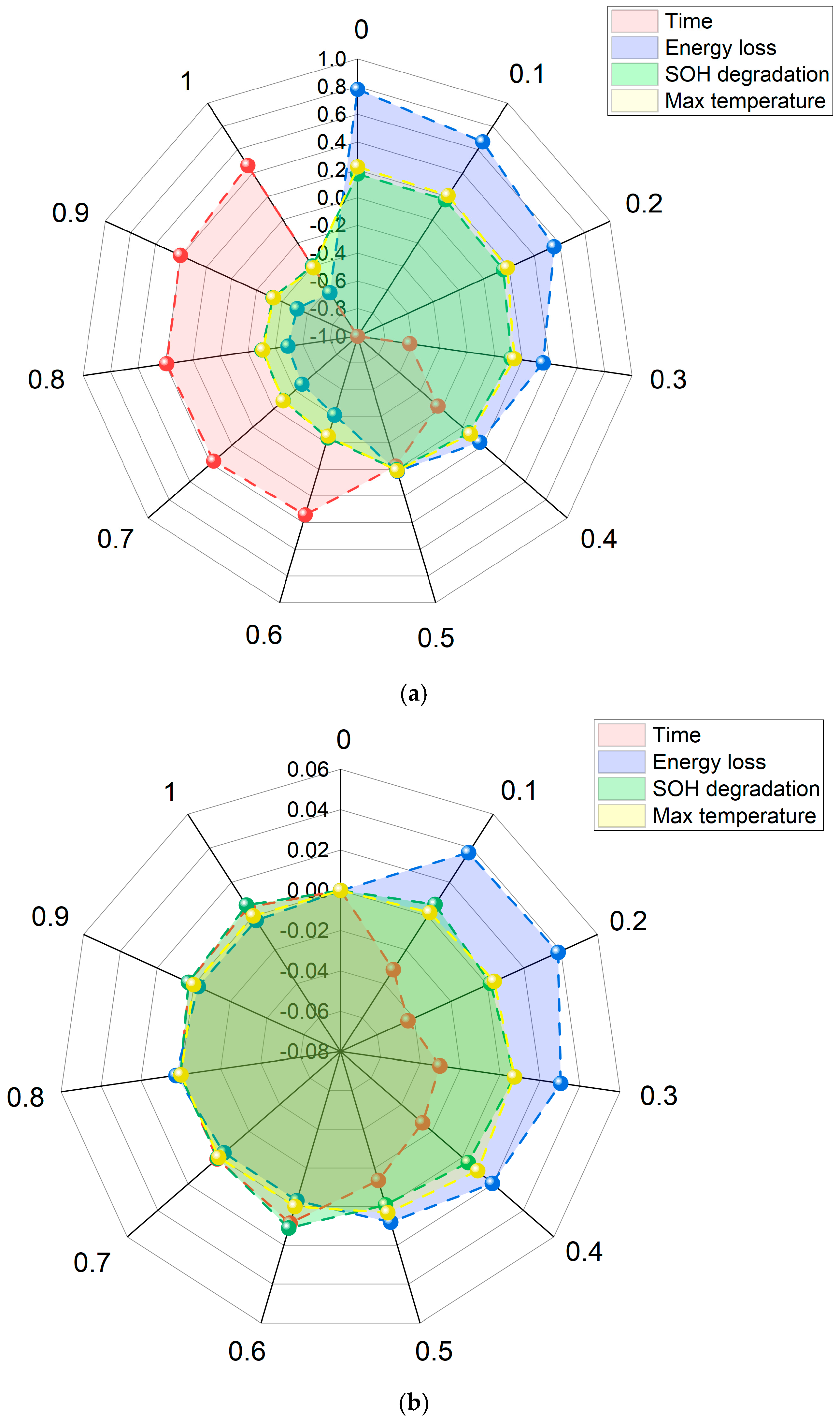
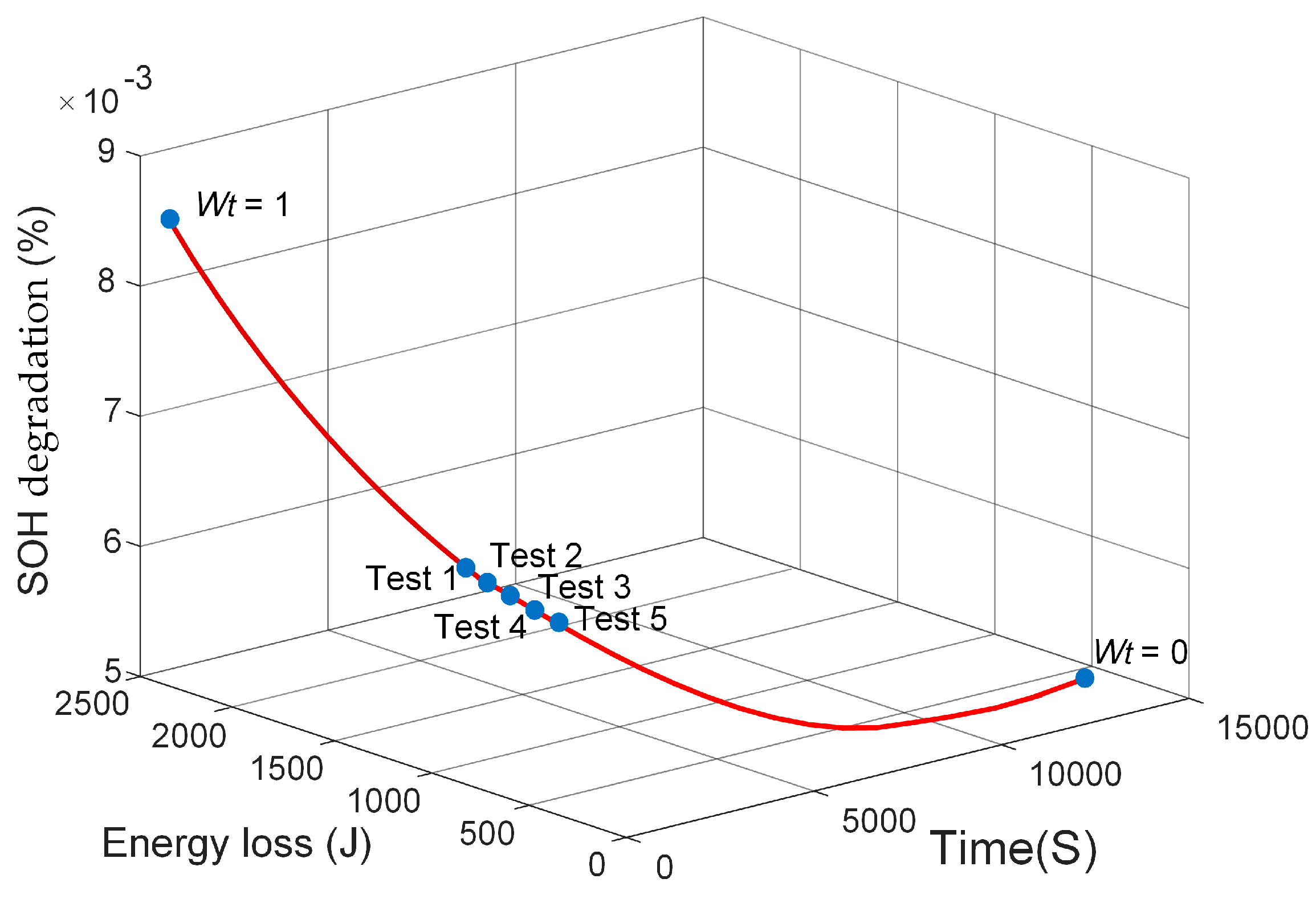
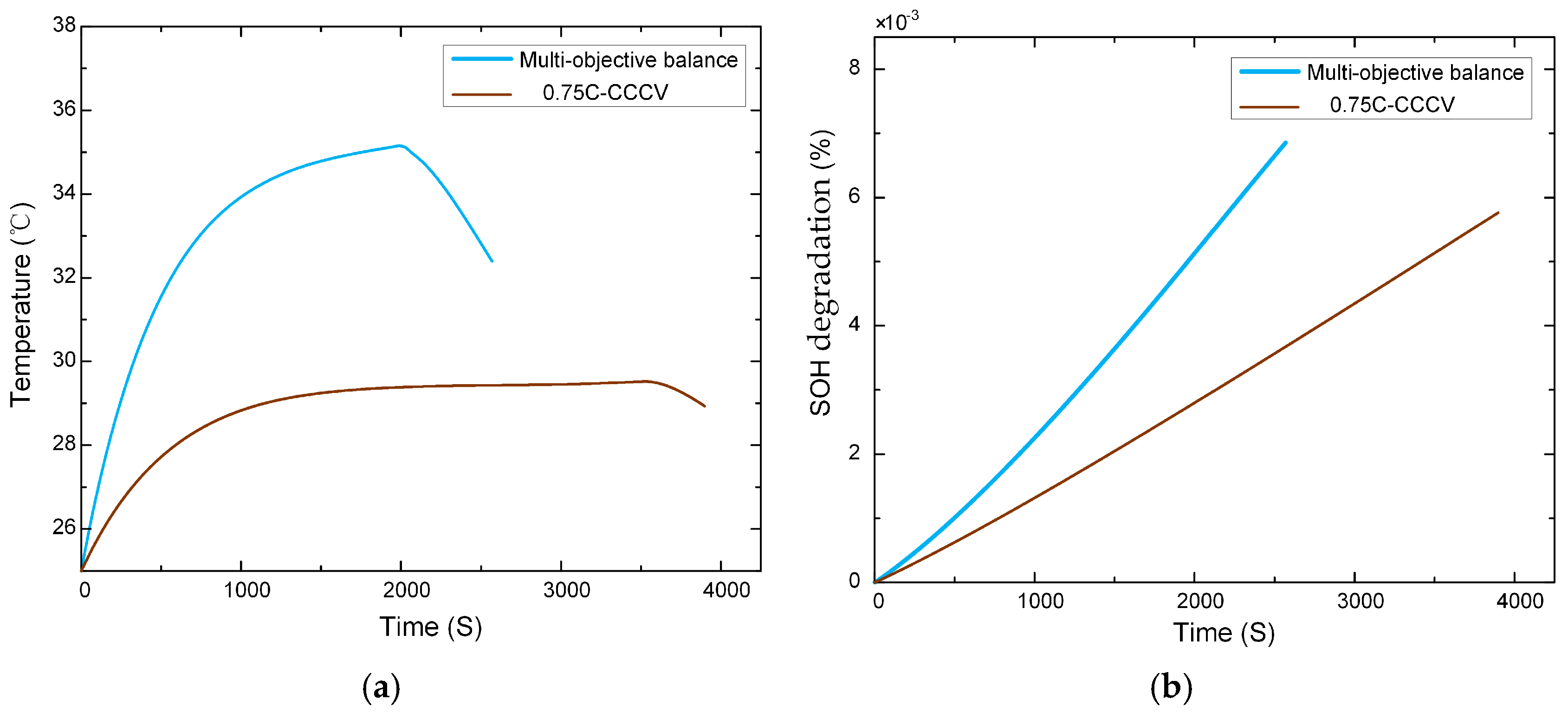
4.2.2. Multi-Objective Balanced Charging Strategy
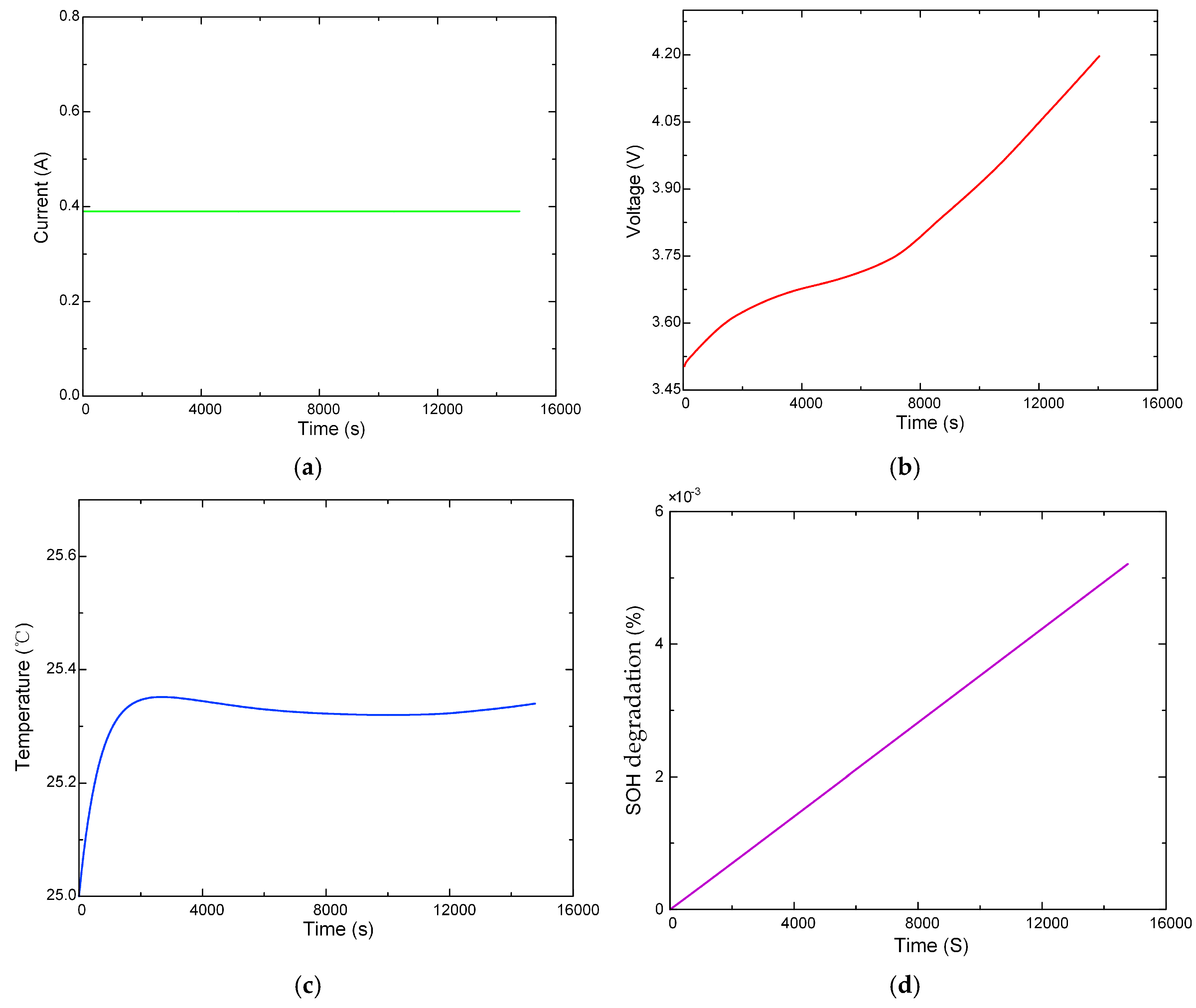
4.2.3. Enhanced Safety Performance Charging Strategy
4.2.4. Limitations and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tahir, M.U.; Anees, M.; Khan, H.A.; Khan, I.; Zaffar, N.; Moaz, T. Modeling and evaluation of nickel manganese cobalt based Li-ion storage for stationary applications. J. Energy Storage 2021, 36, 102346. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Z.; Sun, Z.; Liu, P.; Cui, D.; Deng, J. Data-Driven Lithium-Ion Battery Degradation Evaluation Under Overcharge Cycling Conditions. IEEE Trans. Power Electron. 2023, 38, 10138–10150. [Google Scholar] [CrossRef]
- Xiong, R.; Yang, R.; Chen, Z.; Shen, W.; Sun, F. Online Fault Diagnosis of External Short Circuit for Lithium-Ion Battery Pack. IEEE Trans. Ind. Electron. 2019, 67, 1081–1091. [Google Scholar] [CrossRef]
- Liu, K.; Li, K.; Peng, Q.; Zhang, C. A brief review on key technologies in the battery management system of electric vehicles. Front. Mech. Eng. 2018, 14, 47–64. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, K.; Jow, T. Study of the charging process of a LiCoO2-based Li-ion battery. J. Power Sources 2006, 160, 1349–1354. [Google Scholar] [CrossRef]
- Liu, K.; Li, K.; Yang, Z.; Zhang, C.; Deng, J. An advanced Lithium-ion battery optimal charging strategy based on a coupled thermoelectric model. Electrochim. Acta 2017, 225, 330–344. [Google Scholar] [CrossRef]
- Chen, L.-R.; Hsu, R.C.; Liu, C.-S. A Design of a Grey-Predicted Li-Ion Battery Charge System. IEEE Trans. Ind. Electron. 2008, 55, 3692–3701. [Google Scholar] [CrossRef]
- Liu, J.; Duan, Q.; Chen, H.; Sun, J.; Wang, Q. An optimal multistage charge strategy for commercial lithium ion batteries. Sustain. Energy Fuels 2018, 2, 1726–1736. [Google Scholar] [CrossRef]
- Monem, M.A.; Trad, K.; Omar, N.; Hegazy, O.; Mantels, B.; Mulder, G.; Van den Bossche, P.; Van Mierlo, J. Lithium-ion batteries: Evaluation study of different charging methodologies based on aging process. Appl. Energy 2015, 152, 143–155. [Google Scholar] [CrossRef]
- Li, Y.; Guo, J.; Pedersen, K.; Gurevich, L.; Stroe, D.-I. Investigation of multi-step fast charging protocol and aging mechanism for commercial NMC/graphite lithium-ion batteries. J. Energy Chem. 2023, 80, 237–246. [Google Scholar] [CrossRef]
- Huang, J.-W.; Liu, Y.-H.; Wang, S.-C.; Yang, Z.-Z. Fuzzy-control-based five-step Li-ion battery charger. In Proceedings of the 2009 International Conference on Power Electronics and Drive Systems (PEDS 2009), Taipei, Taiwan, 2–5 November 2009; pp. 1547–1551. [Google Scholar]
- Khan, A.B.; Choi, W. Optimal Charge Pattern for the High-Performance Multistage Constant Current Charge Method for the Li-Ion Batteries. IEEE Trans. Energy Convers. 2018, 33, 1132–1140. [Google Scholar] [CrossRef]
- Lee, C.-H.; Chen, M.-Y.; Hsu, S.-H.; Jiang, J.-A. Implementation of an SOC-based four-stage constant current charger for Li-ion batteries. J. Energy Storage 2018, 18, 528–537. [Google Scholar] [CrossRef]
- Wang, S.-L.; Fernandez, C.; Cao, W.; Zou, C.-Y.; Yu, C.-M.; Li, X.-X. An adaptive working state iterative calculation method of the power battery by using the improved Kalman filtering algorithm and considering the relaxation effect. J. Power Sources 2019, 428, 67–75. [Google Scholar] [CrossRef]
- Wang, S.-C.; Zhang, Z.-Y. Research on Optimum Charging Current Profile with Multi-Stage Constant Current Based on Bio-Inspired Optimization Algorithms for Lithium-Ion Batteries. Energies 2023, 16, 7641. [Google Scholar] [CrossRef]
- Tahir, M.U.; Sangwongwanich, A.; Stroe, D.-I.; Blaabjerg, F. Multi-objective optimization for multi-stage constant current charging for Li-ion batteries. J. Energy Storage 2024, 86, 111313. [Google Scholar] [CrossRef]
- Zou, C.; Hu, X.; Wei, Z.; Wik, T.; Egardt, B. Electrochemical Estimation and Control for Lithium-Ion Battery Health-Aware Fast Charging. IEEE Trans. Ind. Electron. 2017, 65, 6635–6645. [Google Scholar] [CrossRef]
- Klein, R.; Chaturvedi, N.A.; Christensen, J.; Ahmed, J.; Findeisen, R.; Kojic, A. Optimal charging strategies in lithium-ion battery. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 382–387. [Google Scholar]
- Li, X.; Chen, L.; Hua, W.; Yang, X.; Tian, Y.; Tian, J.; Xiong, R. Optimal charging for lithium-ion batteries to avoid lithium plating based on ultrasound-assisted diagnosis and model predictive control. Appl. Energ 2024, 367, 123396. [Google Scholar] [CrossRef]
- Dafeng, S.; Chuqi, S.; Xiaohua, Z.; Nannan, Y. LQR Based Battery Charge Sustaining Strategy for Hybrid Electric Vehicle. IFAC-PapersOnLine 2018, 51, 601–605. [Google Scholar] [CrossRef]
- Fang, H.; Wang, Y.; Chen, J. Health-Aware and User-Involved Battery Charging Management for Electric Vehicles: Linear Quadratic Strategies. IEEE Trans. Control. Syst. Technol. 2016, 25, 911–923. [Google Scholar] [CrossRef]
- Patnaik, L.; Praneeth, A.V.J.S.; Williamson, S.S. A Closed-Loop Constant-Temperature Constant-Voltage Charging Technique to Reduce Charge Time of Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2018, 66, 1059–1067. [Google Scholar] [CrossRef]
- Mohamed, M.M.; Hardianto, Y.P.; Hussain, A.; Ganiyu, S.A.; Gondal, M.; Aziz, A. Laser modified MnO2 cathode for augmented performance aqueous zinc ion batteries. Appl. Surf. Sci. 2024, 669, 160472. [Google Scholar] [CrossRef]
- Wang, S.-C.; Liu, Y.-H. A PSO-Based Fuzzy-Controlled Searching for the Optimal Charge Pattern of Li-Ion Batteries. IEEE Trans. Ind. Electron. 2014, 62, 2983–2993. [Google Scholar] [CrossRef]
- Liu, C.; Liu, L. Optimizing Battery Design for Fast Charge through a Genetic Algorithm Based Multi-Objective Optimization Framework. ECS Trans. 2017, 77, 257–271. [Google Scholar] [CrossRef]
- Liu, Y.-H.; Teng, J.-H.; Lin, Y.-C. Search for an Optimal Rapid Charging Pattern for Lithium–Ion Batteries Using Ant Colony System Algorithm. IEEE Trans. Ind. Electron. 2005, 52, 1328–1336. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, G.; Zhou, C.; Li, M.; Chen, Z. Lithium-Ion Battery Optimal Charging Using Moth-Flame Optimization Algorithm and Fractional-Order Model. IEEE Trans. Transp. Electrif. 2022, 9, 4981–4989. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H.; Sun, F. Charging time and loss optimization for LiNMC and LiFePO4 batteries based on equivalent circuit models. J. Power Sources 2013, 239, 449–457. [Google Scholar] [CrossRef]
- Wang, J.; Liu, P.; Hicks-Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Cycle-life model for graphite-LiFePO4 cells. J. Power Sources 2011, 196, 3942–3948. [Google Scholar] [CrossRef]
- Li, Y.; Li, K.; Xie, Y.; Liu, J.; Fu, C.; Liu, B. Optimized charging of lithium-ion battery for electric vehicles: Adaptive multistage constant current–constant voltage charging strategy. Renew. Energy 2020, 146, 2688–2699. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle Swarm Optimization: A Comprehensive Survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable Multi-Objective Optimization Test Problems. In Proceedings of the 2002 Congress on Evolutionary, Honolulu, HI, USA, 12–17 May 2002; pp. 825–830. [Google Scholar]
- Coello, C.A.C.; Toscano-Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Goldberg, D.E. The Design of Innovation: Lessons from Genetic Algorithms, Lessons for the Real World. Technol. Forecast. Soc. Chang. 2000, 64, 7–12. [Google Scholar] [CrossRef]
- Das, S.; Suganthan, P.N. Differential Evolution: A Survey of the State-of-the-Art. IEEE Trans. Evol. Comput. 2011, 15, 4–31. [Google Scholar] [CrossRef]

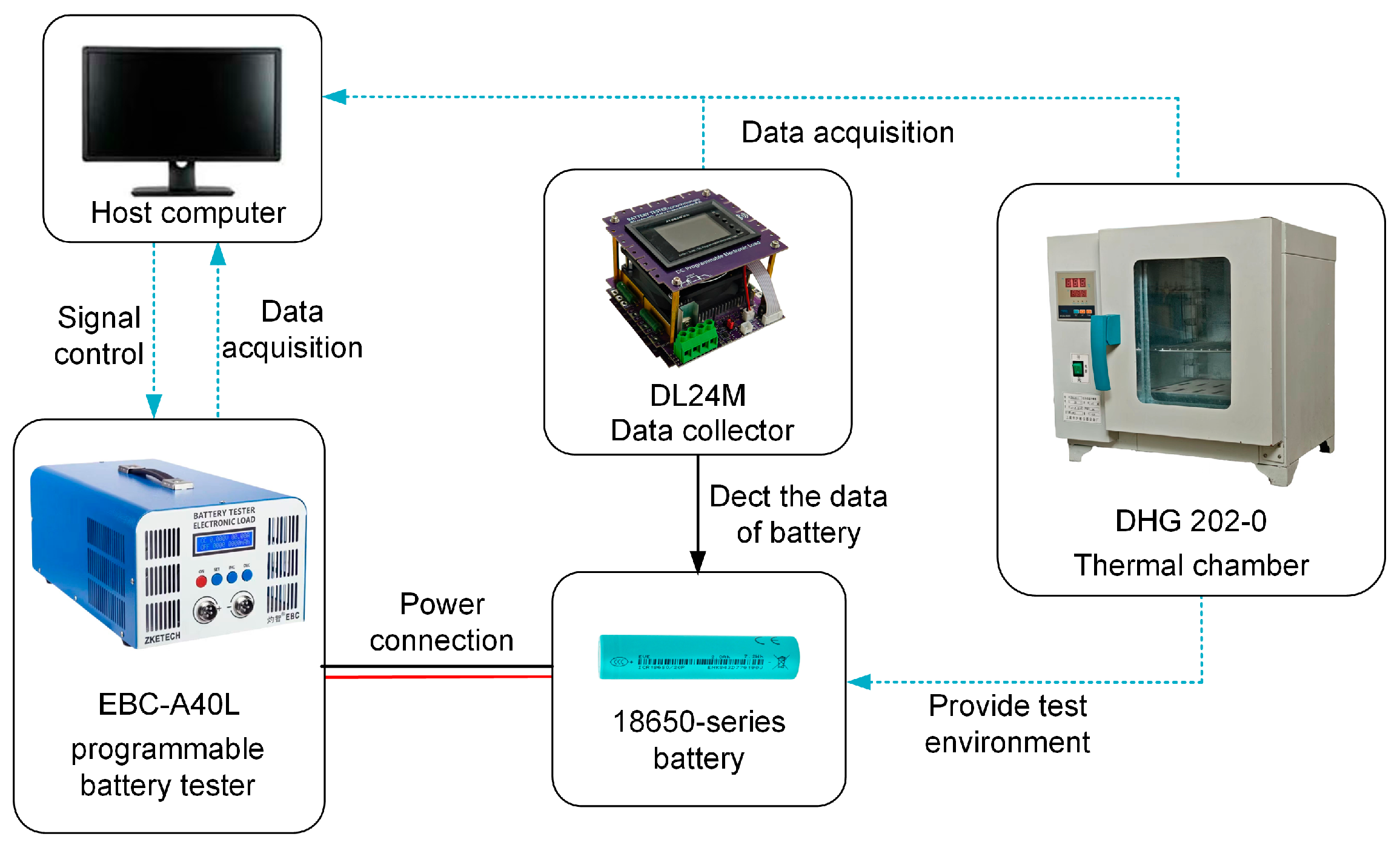

| Parameters | Specification |
|---|---|
| Model name | ICR18650-20P |
| Nominal capacity | 2000 mAh |
| Mass | 43 g |
| Material | LiNixCoyMn1-x-yO2//Graphite |
| cut-off voltage | 4.2 V |
| Maximum charging current | 2C(4 A) |
| Working temperature | 5–50 °C |
| Parameters | Value | Unit |
|---|---|---|
| I | [0, 4] | A |
| Vk | [2.5, 4.2] | V |
| SOC | [10, 90] | % |
| SOH | [80, 100] | % |
| Ts | [5, 50] | °C |
| t | [0, 15,000] | s |
| Baseline Functions | Algorithms | FP | SP | ICN | CT (S) | SD (×10−3) | EL (J) | CTI (%) | SDI (%) | ELI (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| DTLZ1 | IMFO | 78 ± 4 | 0.008 ± 0.001 | 35 ± 4 | 1650 ± 40 | 8.0 ± 0.1 | 1950 ± 15 | 18.80% | 15.05% | 6.75% |
| MFO | 65 ± 5 | 0.012 ± 0.002 | 45 ± 5 | 1800 ± 50 | 8.5 ± 0.2 | 2000 ± 20 | 10.00% | 10.75% | 4.58% | |
| MOPSO | 70 ± 4 | 0.010 ± 0.002 | 40 ± 5 | 1750 ± 45 | 8.2 ± 0.2 | 1975 ± 18 | 12.50% | 13.98% | 5.69% | |
| NSGA-II | 68 ± 5 | 0.011 ± 0.002 | 42 ± 5 | 1770 ± 50 | 8.3 ± 0.2 | 1980 ± 20 | 11.30% | 12.90% | 5.54% | |
| GA | 50 ± 6 | 0.018 ± 0.003 | 60 ± 6 | 2030 ± 60 | 9.0 ± 0.3 | 2050 ± 25 | 0.00% | 0.00% | 0.00% | |
| DE | 55 ± 5 | 0.015 ± 0.002 | 50 ± 5 | 1900 ± 55 | 8.8 ± 0.2 | 2025 ± 22 | 6.40% | 7.53% | 3.47% | |
| DTLZ2 | IMFO | 75 ± 5 | 0.009 ± 0.001 | 38 ± 5 | 1700 ± 45 | 8.1 ± 0.1 | 1960 ± 18 | 16.30% | 14.89% | 6.18% |
| MFO | 60 ± 6 | 0.014 ± 0.002 | 50 ± 6 | 1850 ± 55 | 8.7 ± 0.2 | 2010 ± 22 | 8.60% | 9.57% | 3.96% | |
| MOPSO | 65 ± 5 | 0.012 ± 0.002 | 45 ± 5 | 1800 ± 50 | 8.4 ± 0.2 | 1985 ± 20 | 11.30% | 12.77% | 5.07% | |
| NSGA-II | 63 ± 6 | 0.013 ± 0.002 | 47 ± 6 | 1820 ± 50 | 8.5 ± 0.2 | 1990 ± 21 | 10.30% | 11.70% | 4.89% | |
| GA | 45 ± 7 | 0.020 ± 0.003 | 65 ± 7 | 2030 ± 65 | 9.0 ± 0.4 | 2050 ± 20 | 0.00% | 0.00% | 0.00% | |
| DE | 52 ± 6 | 0.016 ± 0.002 | 55 ± 6 | 1950 ± 60 | 8.9 ± 0.2 | 2030 ± 23 | 3.90% | 7.45% | 3.04% | |
| DTLZ3 | IMFO | 72 ± 5 | 0.010 ± 0.001 | 40 ± 5 | 1750 ± 50 | 8.2 ± 0.1 | 1970 ± 20 | 13.80% | 14.74% | 6.16% |
| MFO | 58 ± 7 | 0.015 ± 0.002 | 55 ± 6 | 1900 ± 60 | 8.8 ± 0.2 | 2020 ± 23 | 6.50% | 9.47% | 3.90% | |
| MOPSO | 72 ± 5 | 0.013 ± 0.002 | 48 ± 6 | 1850 ± 55 | 8.5 ± 0.2 | 1995 ± 22 | 8.90% | 14.46% | 5.05% | |
| NSGA-II | 62 ± 6 | 0.014 ± 0.002 | 50 ± 6 | 1870 ± 55 | 8.6 ± 0.2 | 2000 ± 22 | 7.90% | 12.63% | 4.81% | |
| GA | 60 ± 6 | 0.022 ± 0.003 | 70 ± 7 | 2030 ± 70 | 9.0 ± 0.5 | 2050 ± 28 | 0.00% | 0.00% | 0.00% | |
| DE | 40 ± 8 | 0.017 ± 0.002 | 60 ± 6 | 1980 ± 65 | 8.9 ± 0.2 | 2035 ± 24 | 2.50% | 9.20% | 2.07% |
| Charging Strategies | Time (S) | Energy Loss (J) | SOH Degradation (%) | Max Temperature (°C) | |||||
|---|---|---|---|---|---|---|---|---|---|
| wt -related charging strategies | wt | IMFO | MFO | IMFO | MFO | IMFO | MFO | IMFO | MFO |
| 0 | 14,769 | 14,769 | 301 | 301 | 0.005211 | 0.005211 | 25.3 | 25.3 | |
| 0.1 | 9599 | 9305 | 458.6 | 476.4 | 0.005213 | 0.005248 | 25.8 | 25.85 | |
| 0.2 | 7216 | 6917 | 611 | 635.5 | 0.005305 | 0.005314 | 26.4 | 26.5 | |
| 0.3 | 4838 | 4696 | 892.1 | 920 | 0.005529 | 0.005569 | 27.9 | 28.1 | |
| 0.4 | 3683 | 3589 | 1148 | 1171 | 0.005882 | 0.005904 | 30 | 30.3 | |
| 0.5 | 3056 | 3015 | 1357 | 1368 | 0.006269 | 0.006263 | 32.2 | 32.3 | |
| 0.6 | 1962 | 1979 | 1938 | 1932 | 0.00776 | 0.007847 | 40.6 | 40.6 | |
| 0.7 | 1872 | 1874 | 2024 | 2017 | 0.008104 | 0.00811 | 41.9 | 41.9 | |
| 0.8 | 1816 | 1816 | 2055 | 2060 | 0.008187 | 0.008188 | 42.6 | 42.6 | |
| 0.9 | 1775 | 1780 | 2093 | 2088 | 0.00834 | 0.008365 | 43.3 | 43.3 | |
| 1 | 1602 | 1610 | 2242 | 2236 | 0.00877 | 0.008826 | 45.9 | 45.9 | |
| 1C-CCCV | 2985 | 1377 | 0.00628 | 32.5 | |||||
| Charging Strategies | Weights | ||
|---|---|---|---|
| wt | wS | wE | |
| Test 1 | 0.58 | 0.21 | 0.21 |
| Test 2 | 0.56 | 0.22 | 0.22 |
| Test 3 | 0.54 | 0.23 | 0.23 |
| Test 4 | 0.52 | 0.24 | 0.24 |
| Test 5 | 0.50 | 0.25 | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, S.; Chen, L. Optimized Charging Strategy for Lithium-Ion Battery Based on Improved MFO Algorithm and Multi-State Coupling Model. World Electr. Veh. J. 2025, 16, 565. https://doi.org/10.3390/wevj16100565
Duan S, Chen L. Optimized Charging Strategy for Lithium-Ion Battery Based on Improved MFO Algorithm and Multi-State Coupling Model. World Electric Vehicle Journal. 2025; 16(10):565. https://doi.org/10.3390/wevj16100565
Chicago/Turabian StyleDuan, Shuangming, and Linglong Chen. 2025. "Optimized Charging Strategy for Lithium-Ion Battery Based on Improved MFO Algorithm and Multi-State Coupling Model" World Electric Vehicle Journal 16, no. 10: 565. https://doi.org/10.3390/wevj16100565
APA StyleDuan, S., & Chen, L. (2025). Optimized Charging Strategy for Lithium-Ion Battery Based on Improved MFO Algorithm and Multi-State Coupling Model. World Electric Vehicle Journal, 16(10), 565. https://doi.org/10.3390/wevj16100565





