An Intelligent Control Framework for High-Power EV Fast Charging via Contrastive Learning and Manifold-Constrained Optimization

Abstract

To address the complex trade-offs among charging efficiency, battery lifespan, energy efficiency, and safety in high-power electric vehicle (EV) fast charging, this paper presents an intelligent control framework based on contrastive learning and manifold-constrained multi-objective optimization. A multi-physics coupled electro-thermal-chemical model is formulated as a Mixed-Integer Nonlinear Programming (MINLP) problem, incorporating both continuous and discrete decision variables—such as charging power and cooling modes—into a unified optimization framework. An environment-adaptive optimization strategy is also developed. To enhance learning efficiency and policy safety, a contrastive learning–enhanced policy gradient (CLPG) algorithm is proposed to distinguish between high-quality and unsafe charging trajectories. A manifold-aware action generation network (MAN) is further introduced to enforce dynamic safety constraints under varying environmental and battery conditions. Simulation results demonstrate that the proposed framework reduces charging time to 18.3 min—47.7% faster than the conventional CC–CV method—while achieving 96.2% energy efficiency, 99.7% capacity retention, and zero safety violations. The framework also exhibits strong adaptability across wide temperature (−20 °C to 45 °C) and aging (SOH down to 70%) conditions, with real-time inference speed (6.76 ms) satisfying deployment requirements. This study provides a safe, efficient, and adaptive solution for intelligent high-power EV fast-charging.

1. Introduction

The global energy transition and the pursuit of “dual carbon” goals—carbon peaking and neutrality—have accelerated the growth of the electric vehicle (EV) industry. Among the key enablers for large-scale EV adoption, high-power fast charging (typically 150–350 kW) has emerged as a critical technology to significantly shorten charging time and enhance user convenience. However, the introduction of high-power charging also presents substantial challenges: increased risk of thermal runaway, accelerated battery degradation due to lithium plating, and reduced energy efficiency, especially under dynamic environmental conditions. These issues highlight the need for a comprehensive, system-level control strategy that balances performance, safety, and longevity.

Existing charging strategies can be broadly classified into three categories: rule-based, model-based, and data-driven. Rule-based methods like constant current–constant voltage (CC–CV) are simple to implement but lack adaptability to dynamic conditions. Model-based methods that explicitly encode constraints but struggle with parameter drift and computational complexity [1,2,3,4,5]. Data-driven approaches, especially reinforcement learning (RL), offer adaptability but suffer from poor sample efficiency and lack of safety guarantees [6,7,8,9,10].

The core challenge of high-power EV fast charging lies in complex constrained optimization under strong multi-physics coupling. The charging process involves tightly coupled electrochemical reactions, heat transfer, and electrical dynamics, where high power levels can trigger thermal runaway [11]. High currents also accelerate lithium plating, degrading battery lifespan [12]. The trade-offs among charging time, battery life, and energy efficiency make it difficult for traditional methods to find a globally optimal solution [13]. Thus, improving charging efficiency while guaranteeing safety remains a critical unresolved problem.

To address these challenges, this paper proposes an intelligent control framework for high-power EV fast charging that integrates contrastive learning-enhanced policy optimization and manifold-constrained safe action generation. The main contributions are summarized as follows:

• A multi-physics coupled MINLP model that incorporates electrochemical, thermal, and electrical dynamics is developed, and it encodes lithium plating risk and temperature limits as hard constraints and supports an environment-adaptive optimization strategy.
• A contrastive learning–enhanced policy gradient (CLPG) algorithm is designed to improve policy learning efficiency by incorporating a novel trajectory-level contrastive learning mechanism that distinguishes between safe/efficient and unsafe/inefficient charging patterns.
• Unlike existing safe RL methods that operate at the reward or constraint optimization level, we introduce manifold-aware action generation that directly projects actions onto a safe manifold, providing intrinsic safety guarantees at the action generation stage.

2. Related Work

The optimization and control of electric vehicle (EV) charging have evolved from simple rule-based strategies to intelligent decision-making. Early studies primarily adopted fixed charging schemes such as constant current–constant voltage (CC–CV), which lacked adaptability to battery conditions and environmental variations. With the development of optimization theory, model-based approaches gradually became mainstream. Reference [4] proposed a nonlinear Model Predictive Control (MPC) framework that explicitly considered battery temperature constraints; however, the computational burden of online optimization limited its real-time applicability. To reduce computational complexity, linearized MPC has been widely employed, albeit at the cost of model accuracy [5]. Mixed-integer programming methods are capable of handling discrete decisions in the charging process, such as power level selection [14] and charging mode switching [15], but their computational efficiency deteriorates rapidly with increasing problem size.

In recent years, data-driven approaches—particularly Deep Reinforcement Learning (DRL)—have shown great potential in charging control. Reference [16] proposed a DQN (Deep Q-Network)-based large-scale EV charging scheduling method that achieved model-free adaptive control. Actor-Critic algorithms designed for continuous action spaces further improved control precision [6,7]. Nevertheless, traditional reinforcement learning algorithms suffer from low sample efficiency and struggle to handle hard constraints. Constrained reinforcement learning approaches, such as Constrained Policy Optimization (CPO) [17] and Safety Layer mechanisms [18], have incorporated constraints but at the cost of increased algorithmic complexity.

Multi-objective optimization and constraint handling are key challenges in charging control. Traditional weighted-sum methods lack theoretical guidance for weight selection [19], while Pareto optimization can obtain a set of non-dominated solutions. Studies have shown that algorithms like NSGA-II and NSGA-III perform well in the optimal configuration of charging stations [20]. For constraint handling, the penalty function method adds penalty terms to the objective [21]; in reinforcement learning frameworks, CPO ensures safe policy updates within a trust region [17], and the Safety Layer introduces a safety filter at the output layer [18]. However, these methods still exhibit limitations when addressing state-dependent dynamic constraints.

Research on battery aging and safety provides important constraints for charging optimization. The growth of the solid electrolyte interface (SEI) film is a major cause of capacity degradation. Reference [22] developed an aging model incorporating SEI growth. Lithium plating presents significant safety risks during high-current charging. Reference [23] found that the risk significantly increases when the anode potential drops below 0 V versus Li/Li⁺. In terms of thermal management, Reference [24] established a 3D thermal model for battery packs, while Reference [25] proposed an active thermal management system. However, existing studies often consider thermal management and charging control separately.

In summary, existing research faces several limitations: model-based methods struggle to accurately describe nonlinear and time-varying characteristics; data-driven approaches lack safety guarantees; multi-objective optimization often lacks adaptive weight adjustment mechanisms; and environmental factors are not sufficiently accounted for. To address these issues, this paper formulates the charging optimization problem as an MINLP model and adopt a DRL-based solution. The proposed method introduces a contrastive learning mechanism and manifold awareness to design an environment-adaptive multi-objective optimization strategy. This approach offers a novel technological pathway for safe, efficient, and adaptive high-power fast charging, with significant implications for advancing the EV industry.

3. Materials and Methods

3.1. Multi-Physics Coupled MINLP Model

3.1.1. Charging Requirements and Physical Modeling

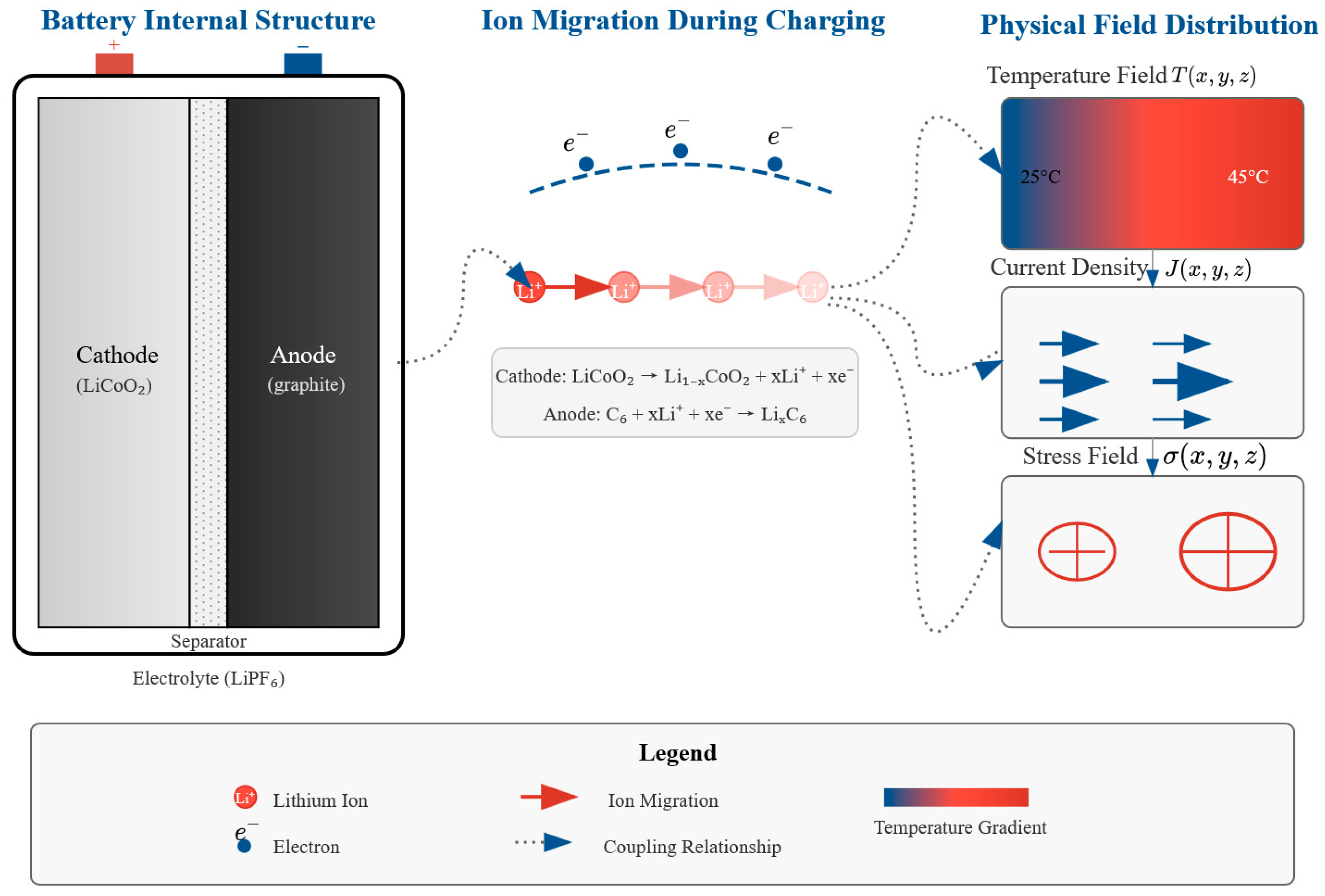
The battery charging process involves the multi-physics coupling of electrochemical reactions, thermodynamic processes, and electrical characteristics, as shown in Figure 1. During the charge transfer process—comprising lithium-ion deintercalation, migration, and intercalation—the generation of Joule heat, polarization heat, and heat from side reactions causes dynamic changes in internal resistance and drifts in electrode potential. The strong coupling effects of these processes cause the system to exhibit significant nonlinear and time-varying characteristics. Figure 2 illustrates the charging system circuit diagram, showing the power conversion stages from AC grid to battery pack, with the proposed CL-PG+MAN controller managing both charging power and cooling system operation.

Consequently, balancing charging speed and battery lifespan is not a simple static trade-off. Instead, it requires a dynamic decision-making framework capable of sensing the battery’s state and environmental conditions in real-time. This framework must seek a dynamic optimal solution among conflicting objectives, including minimizing charging time, maximizing battery lifespan, optimizing energy efficiency, and ensuring safety margins. This constitutes a complex optimization problem that continuously evolves with the system’s state and boundary conditions.

This study aims to solve the multi-objective optimization control problem for high-power fast charging of EVs. Our core design objectives are: (1) To establish an environment-adaptive, layered decision mechanism. This mechanism uses integer variables to represent the selection of power levels and cooling modes, combined with continuous variables to describe the charging dynamics, enabling adaptation across a wide temperature range of −20 °C to 45 °C. (2) To construct an optimization model with embedded safety constraints. Protections against lithium plating and temperature limits are integrated as hard constraints within the MINLP framework. (3) To design a multi-objective optimization strategy with dynamic weights. This strategy automatically adjusts the priority of charging speed, battery protection, and energy efficiency based on the ambient temperature.

The dynamic weight adjustment mechanism operates through a temperature-dependent function that prioritizes different objectives based on operational conditions. At nominal temperatures, the system emphasizes charging speed to maximize user convenience. Under extreme conditions, the weights shift to prioritize battery preservation and energy efficiency, reflecting the increased stress on battery chemistry at these temperatures. This adaptive strategy ensures optimal performance across varying environmental conditions while maintaining battery health.

3.1.2. Decision Variable Definition

The charging process is discretized into N time intervals, each with a duration of t $\mathit{\Delta }t=10 \mathrm{s}$. The model’s decision variables include two categories: continuous and integer variables. Continuous variables represent physical system states and control inputs, including charging power $P_k\in [0,P_{max}]$, charging current $I_k\in \left[0,I_{max}\right]$, charging voltage $V_k\in [V_{min},V_{max}]$, battery core temperature $T_k^{core}\in {\mathbb{R}}^{+}$, surface temperature $T_k^{surf}\in {\mathbb{R}}^{+}$, and cooling system power $Q_{cool,k}\in [0,Q_{cool}^{max}]$. Integer variables correspond to discrete system decisions, including the charging state ${\alpha }_k\in \left\{0,1\right\}$, where 1 indicates active charging and 0 indicates charging is paused; power level selection ${\beta }_k^j\in \left\{0,1\right\} \mathrm{for} j\in \left\{1,2,3,4,5\right\}$, where each j corresponds to a distinct power level; the cooling mode ${\gamma }_k\in \left\{0,1,2\right\}$, representing natural convection, fan cooling, and liquid cooling, respectively; and the preheating flag ${\delta }_k\in \left\{0,1\right\}$, which indicates if the preheating mode is active. Details of the definitions and units for all variables employed in the MINLP model formulation are provided in Appendix A,

Table A1. This is a notation table.

Symbol	Definition	Unit/Range
$P_k$	Charging power at time step k	$[0,P_{max}]$ kW
$I_k$	Charging current	$\left[0,I_{max}\right]$ A
$V_k$	Charging voltage	$[V_{min},V_{max}]$ V
${\alpha }_k$	Charging state (binary)	$\left\{0,1\right\}$
${\beta }_k^j$	Power level selection	$\left\{0,1\right\}$, $j\in \left\{1,2,3,4,5\right\}$
${\gamma }_k$	Cooling mode	$\left\{0,1,2\right\}$
${\delta }_k$	Preheating flag	$\left\{0,1\right\}$
$T_k^{core}$	Battery core temperature	°C
$T_k^{surf}$	Battery surface temperature	°C
$SO{C}_k$	State of charge	$[0,1]$
$SO{H}_k$	State of health	$[0,1]$
$T_{env}$	Ambient temperature	°C
$Q_{\mathrm{cool}}$	Cooling power	kW
$C_{th}$	Core thermal capacitance	J/°C
$h_{conv}$	Internal convection coefficient	W/°C
$E_a$	Activation energy	24,500 J/mol
$R_g$	Universal gas constant	8.314 J/(mol·K)
$w_i\left(T_{env}\right)$	Temperature-dependent weights	$[0,1]$
${\eta }_{\mathrm{loss}}(P_k,T_k^{\mathrm{core}})$	Energy loss rate function	-
$R_{int}(SO{C}_k,T_k^{core})$	Internal resistance	mΩ
${\eta }_{anode}$	Anode potential	V vs. Li/Li+

.

Practical charging infrastructure exhibits discrete power level configurations, while thermal management systems operate according to predetermined modalities. The incorporation of integer decision variables accurately captures inherent system discretization, precludes infeasible solutions arising from purely continuous optimization formulations, and facilitates the enforcement of logical constraint structures.

3.1.3. Multi-Objective Optimization Function Design

A dynamically weighted objective function is used that considers three key metrics: charging time, battery aging, and energy consumption. The goal is to minimize the total cost $J$:

$$minJ=w_1\left(T_{env}\right)\cdot J_{time}+w_2\left(T_{env}\right)\cdot J_{aging}+w_3\left(T_{env}\right)\cdot J_{energy}$$

(1)

Each component of the objective function represents critical operational and economic factors in EV charging. The charging time cost $J_{time}$ directly impacts user satisfaction and charging station throughput, as reduced charging duration significantly improves station utilization rates and customer experience. The aging cost $J_{aging}$ captures long-term battery degradation effects, where aggressive charging strategies without proper thermal management can substantially reduce battery lifespan, leading to premature replacement costs. The energy cost $J_{energy}$ encompasses both electricity consumption and auxiliary system operation, particularly cooling, which represents a non-negligible portion of operational expenses. The adaptive weighting mechanism ensures these competing objectives are balanced according to environmental conditions. where the weighting coefficients $w_i\left(T_{env}\right)$ are adaptively adjusted according to the ambient temperature $T_{env}$:

$$w_i(T_{env})=\{\begin{array}{cc}0.6& \mathrm{if} T_{env}\in [15,25{]}^{ \circ }\mathrm{C}\\ 0.4& \mathrm{if} T_{env}\in [5,15)\cup (25,35{]}^{ \circ }\mathrm{C}\\ 0.3& \mathrm{otherwise}\end{array}$$

(2)

The temperature-dependent weight coefficients in Equation (2) are designed based on extensive battery degradation studies and thermal safety research. According to reference [26], lithium-ion batteries exhibit optimal performance and minimal degradation within the 15–25 $°\mathrm{C}$ temperature range, where lithium plating risk is negligible and ion mobility is sufficient. This supports our assignment of $w_1\left(T_{env}\right)=0.6$ to prioritize charging speed in this range.

For moderate temperature deviations ($T_{env}\in [5,15)\cup (25,35] °\mathrm{C}$), reference [13] demonstrated that capacity fade rate increases by approximately 15% per $10 °\mathrm{C}$ deviation from optimal temperature. Therefore, we increase the battery protection weight to $w_2\left(T_{env}\right)=0.4$ to compensate for accelerated aging. Under extreme conditions ($T_{env}<5 °\mathrm{C}$ or >35 °C), the risk of lithium plating at low temperatures and thermal runaway at high temperatures necessitates a conservative strategy with $w_2\left(T_{env}\right)=0.5$ and $w_3\left(T_{env}\right)=0.2$ [27,28].

The charging time cost accounts not only for the actual charging duration but also incorporates a penalty for overtime to ensure completion within the target time:

$$J_{time}=\sum _{k=1}^N\mathit{\Delta }t\cdot \left(1-{\alpha }_k\right)+{\lambda }_{time}\cdot \mathit{max}\left(0,t_{total}-t_{target}\right)$$

(3)

where ${\lambda }_{time}$ denotes the overtime penalty coefficient, $t_{total}$ is the total charging time, and $t_{target}$ is the target charging duration.

The battery aging cost $J_{aging}$ is formulated based on the Arrhenius aging model and stress factor theory, comprehensively considering the effects of thermal stress, current stress, and state-of-charge (SOC) stress:

$$J_{\mathrm{aging} }=\sum _{k=1}^N{\alpha }_k\cdot [A_1\cdot exp({\displaystyle \frac{-E_a}{R_g{T}_k^{\mathrm{core} }}})\cdot {\left({\displaystyle \frac{I_k}{I_{\mathrm{nom} }}}\right)}^{n_1}+A_2\cdot exp({\displaystyle \frac{T_k^{\mathrm{core} }-T_{\mathrm{ref} }}{T_{\mathrm{stress} }}})\cdot f_{SOC}(SO{C}_k\left)\right]$$

(4)

The parameters in Equation (4) are defined as follows: $A_1$ and $A_2$ are the pre-exponential factors for aging; $E_a$ is the activation energy (J/mol); $R_g$ is the universal gas constant (8.314 J/(mol·K)); $I_{nom}$ is the nominal charging current; $n_1$ is the current stress exponent; $T_{ref}$ is the reference temperature (298.15 K); and $T_{stress}$ is the temperature stress scale.

In the model, an exponential temperature stress term $\mathrm{e}\mathrm{x}\mathrm{p}\left({\displaystyle \frac{T_k^{core}-T_{ref}}{T_{stress}}}\right)$ is introduced to reflect the accelerated aging under elevated temperatures; the current stress term ${\left({\displaystyle \frac{I_k}{I_{nom}}}\right)}^{n_1}$ captures the adverse effects of high charging currents; and the SOC-related stress function $f_{SOC}\left(SO{C}_k\right)$ characterizes the aging acceleration at high state-of-charge levels.

The energy cost $J_{\mathrm{energy}}$ accounts not only for energy losses during the charging process but also for the energy consumed by the cooling system, as defined in Equation (5):

$$J_{\mathrm{energy}}=\sum _{k=1}^N\left[{\eta }_{\mathrm{loss}}\right(P_k,T_k^{\mathrm{core} })\cdot P_k+Q_{\mathrm{cool},k}\cdot {\eta }_{\mathrm{cool}}({\gamma }_k\left)\right]\cdot \Delta t$$

(5)

Here, ${\eta }_{loss}\left(P_k,T_k^{core}\right)$ denotes the energy loss rate as a function of power and temperature, and ${\eta }_{cool}\left({\gamma }_k\right)$ denotes the efficiency factor for each cooling mode. Specifically, the energy loss rate is expressed as

$${\eta }_{loss}\left(P_k,T_k^{core}\right)={\displaystyle \frac{I_k^2\cdot R_{int}\left(SO{C}_k,T_k^{core}\right)}{P_k}}$$

(6)

$${\eta }_{cool}({\gamma }_k)=\{\begin{array}{cc}0& \mathit{if} {\gamma }_k=0 (\mathit{natural} \mathit{cooling})\\ 0.3& \mathit{if} {\gamma }_k=1 (\mathit{air} \mathit{cooling})\\ 0.6& \mathit{if} {\gamma }_k=2 (\mathit{liquid} \mathit{cooling})\end{array}$$

(7)

Here, $R_{int}(SO{C}_k,T_k^{core})$ denotes the internal resistance as a function of SOC and core temperature.

3.1.4. Constraint Conditions and Safety Mechanisms

Power Balance and Limitation:

$$P_k=V_k\cdot I_k\cdot {\alpha }_k$$

(8)

$$P_k\le \sum _{j=1}^5{\beta }_k^j\cdot P_{level}^j\left(T_{env}\right)$$

(9)

where $P_{level}^j\left(T_{env}\right)$ denotes the available power at the j-th level under the ambient temperature $T_{env}$.

Uniqueness of Power Level Selection:

$$\sum _{j=1}^5{\beta }_k^j={\alpha }_k,\forall k$$

(10)

The dynamic thermal constraints are keys to ensuring charging safety. The proposed model captures these dynamics using a two-state thermal model for the core and surface temperatures:

$$C_{th}{\displaystyle \frac{d{T}_k^{core}}{dt}}=P_{loss,k}-h_{conv}\left(T_k^{core}-T_k^{surf}\right)-Q_{cool,k}$$

(11)

$$C_{th}^{surf}{\displaystyle \frac{d{T}_k^{surf}}{dt}}=h_{conv}\left(T_k^{core}-T_k^{surf}\right)-h_{amb}\left(T_k^{surf}-T_{env}\right)$$

(12)

where $C_{th}$ and $C_{th}^{surf}$ denote the core and surface thermal capacitance (J/°C), respectively; $h_{conv}$ and $h_{amb}$ represent the internal and ambient convective heat transfer coefficients (W/°C). The heat loss power $P_{loss,k}$ in time step $k$ considers both Joule heating and charging efficiency loss:

$$P_{loss,k}=I_k^2\cdot R_{int}\left(SO{C}_k,T_k^{core}\right)+P_k\cdot \left(1-{\eta }_{charge}\left(I_k\right)\right)$$

(13)

Temperature Safety Constraint:

$$T_k^{core}\le T_{max}^{safe}-{ϵ}_{temp}\cdot \left(1+0.5\cdot \mathbb{I}\left(T_{env}>35\right)\right)$$

(14)

where $T_{max}^{safe}$ is the maximum allowable core temperature ($55 °\mathrm{C}$), ${ϵ}_{temp}$ is the temperature safety margin ($3 °\mathrm{C}$), and $\mathbb{I}(\cdot )$ is the indicator function.

Lithium Plating Protection Constraint:

$${\eta }_{anode}\left(SO{C}_k,I_k,T_k^{core}\right)>V_{{\displaystyle \frac{Li}{L{i}^{+}}}}+{ϵ}_{plating}$$

(15)

where ${\eta }_{anode}$ is the anode potential, ${\displaystyle \frac{Li}{L{i}^{+}}}$ is the lithium metal potential (0 V), and ${ϵ}_{plating}$ is the safety margin (0 V) to prevent lithium plating. The lithium plating constraint is particularly critical as it shares mechanistic similarities with dendrite formation in lithium metal batteries. Recent research has shown that effective suppression of lithium dendrites requires careful management of current distribution and interface stability [29]. In this fast charging context, the manifold constraint mechanism ensures that the charging current never creates conditions conducive to metallic lithium deposition, thereby preventing both capacity fade and potential safety hazards associated with dendrite growth.

SOC Evolution Equation:

$$SO{C}_{k+1}=SO{C}_k+{\displaystyle \frac{{\eta }_{coulombic}(I_k,T_k^{core})\cdot I_k\cdot \Delta t}{Q_{capacity}\left(SO{H}_k\right)}}$$

(16)

where ${\eta }_{coulombic}$ is the coulombic efficiency, and $Q_{capacity}$ represents the capacity of the battery.

Power Derating Coefficient:

$$\mu (T_{env})=\{\begin{array}{cc}0.3+0.7\cdot {\displaystyle \frac{T_{env}+20}{20}}& \mathrm{if} T_{env}<0 °C\\ 1.0& \mathrm{if} T_{env}\in \left[0,30\right] °C\\ 1.0-0.5\cdot {\displaystyle \frac{T_{env}-30}{15}}& \mathrm{if} T_{env}>30 °C\end{array}$$

(17)

Low-Temperature Preheating Logic:

$${\alpha }_k\le M\cdot \left(1-{\delta }_k\cdot \mathbb{I}\left(T_k^{core}<T_{preheat}^{min}\right)\right)$$

(18)

where $M$ is a sufficiently large constant and $T_{preheat}^{min}$ denotes the minimum preheating temperature.

High-Temperature Cooling Control:

$${\gamma }_k\ge {\gamma }_{k-1}-M\cdot (1-\mathbb{I}(T_k^{core}>T_{cool}^{trigger}\left)\right)$$

(19)

where $T_{cool}^{trigger}$ represents the cooling trigger temperature.

3.2. Solution Framework with Contrastive Learning and Manifold Constraints

3.2.1. DRL Framework and Problem Mapping

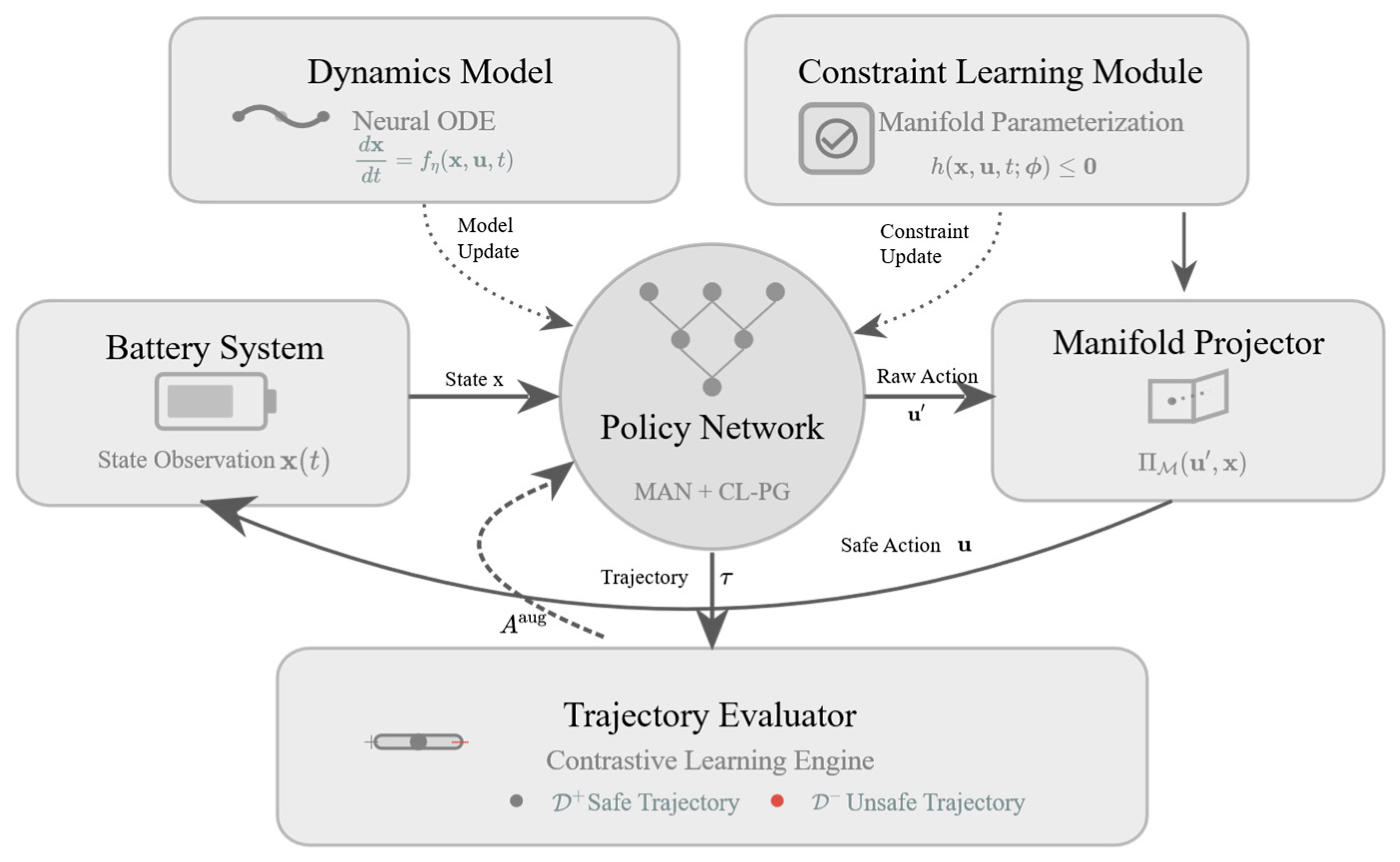
The proposed algorithmic framework learns an optimal charging strategy from scratch through the coordination of three core modules: dynamics modeling, constraint learning, and policy optimization, as shown in Figure 3. In each learning cycle, the system employs Neural Ordinary Differential Equations (Neural ODEs) to model the battery’s dynamic behavior.

The objective function for learning the dynamics model is defined as:

$${\mathcal{L}}_{dynamics}={\mathbb{E}}_{\left({\mathit{x}}_t,{\mathit{u}}_t,{\mathit{x}}_{t+1}\right)\sim \mathcal{D}}\left[{\parallel {\mathit{x}}_{t+1}-{\int }_t^{t+\mathit{\Delta }t}{f}_{\eta }\left(\mathit{x}\left(s\right),\mathit{u}\left(s\right),s\right)ds\parallel }_2^2\right]$$

(20)

The integral is computed using a numerical ODE solver (e.g., Runge-Kutta method), ensuring that state predictions are continuous and differentiable, which provides reliable gradient information for the subsequent policy optimization.

Meanwhile, the constraint manifold is learned by analyzing safe and unsafe patterns from historical charging trajectories. The system maintains two trajectory buffers: ${\mathcal{B}}_{\mathrm{safe}}$, which stores trajectories that complete successfully without triggering any safety alerts, ${\mathcal{B}}_{\mathrm{unsafe}}$, which contains trajectories that lead to overheating, voltage violations, or other hazardous signals.

$${\mathcal{L}}_{\mathrm{constraint}}={\mathbb{E}}_{\left(\mathbf{x},\mathbf{u}\right)\sim {\mathcal{B}}_{\mathrm{safe}}}\left[\mathrm{ReLU}\left(\mathbf{h}\left(\mathbf{x},\mathbf{u},t;\varphi \right)\right)\right]+{\mathbb{E}}_{\left(\mathbf{x},\mathbf{u}\right)\sim {\mathcal{B}}_{\mathrm{unsafe}}}\left[\mathrm{ReLU}\left(-\mathbf{h}\left(\mathbf{x},\mathbf{u},t;\varphi \right)+ϵ\right)\right]$$

(21)

where $ϵ>0$ is a safety margin parameter that ensures the learned constraint boundary is conservative.

The policy network update leverages both the predictive capability of the dynamics model and the safety guarantees provided by the learned manifold. During action generation, the manifold-aware module computes a parameterized representation of the feasible action space given the current state. Policy search is then conducted within this constrained region, ensuring the exploration process remains within safe operational bounds.

The algorithm modulates the exploration level by adjusting the output covariance matrix Σ(x)$\mathsf{\Sigma }\left(\mathbf{x}\right)$ of the manifold parameterization network. Early in training or in unexplored state regions, a higher covariance encourages broader exploration. As confidence grows with accumulated experience, the covariance gradually shrinks, enabling fine-grained control. The state-dependent exploration strategy is formulated as:

$$\mathsf{\Sigma }\left(\mathbf{x}\right)={\mathsf{\Sigma }}_{\mathrm{base}}\left(\mathit{x}\right)\cdot \exp \left(-\beta \cdot N\left(\mathit{x}\right)\right)$$

(22)

where $N\left(\mathbf{x}\right)$ is the visitation count near state x, and β is a decay coefficient.

The learning process uses an asynchronous update schedule: the dynamics model is updated most frequently (every episode), the constraint function at a moderate frequency (every 10 episodes), and the policy network least frequently (every 20 episodes).

The overall algorithm flow is illustrated in Figure 4, which shows the iterative learning process with environmental adaptation.

3.2.2. Contrastive Learning-Enhanced Policy Gradient (CLPG) Algorithm

The CLPG algorithm introduced in this paper incorporates a trajectory-level contrastive learning mechanism, as shown in Figure 5. Let $\mathit{\theta }$ denote the parameters of the policy network, and ${\pi }_{\mathit{\theta }}\left(\mathbf{u}\right|\mathbf{x})$ represent the policy function. A trajectory encoder $E_{\psi }:\mathcal{T}\to {\mathbb{R}}^d$ maps trajectories into an embedding space, where $\mathcal{T}$ denotes the trajectory space and $d$ represents the embedding dimension. For trajectories ${\tau }_i$ and ${\tau }_j$, the contrastive learning loss function is defined as:

$${\mathcal{L}}_{CL}=-{\mathbb{E}}_{\begin{array}{c}{\tau }_i\sim {\mathcal{D}}^{+}\\ {\tau }_j\sim {\mathcal{D}}^{-}\end{array}}\left[\mathit{log}{\displaystyle \frac{\mathit{exp}\left(s\left(E_{\psi }\left({\tau }_i\right),E_{\psi }\left({\tau }_j\right)\right)\right)}{\sum _{k=1}^K\mathit{exp}\left(s\left(E_{\psi }\left({\tau }_i\right),E_{\psi }\left({\tau }_k\right)\right)\right)}}\right]$$

(23)

where ${\mathcal{D}}^{+}$ and ${\mathcal{D}}^{-}$ denote the distributions of positive (safe and efficient trajectories) and negative (violation or inefficient trajectories) samples, respectively. $s\left(·,·\right)$ is the similarity function, and $K$ is the number of negative samples.

The policy gradient update rule is modified as:

$${\nabla }_{\mathit{\theta }}J(\mathit{\theta })={\mathbb{E}}_{\tau \sim {\pi }_{\mathit{\theta }}}\left[\sum _{t=0}^T{\mathsf{\nabla }}_{\mathit{\theta }}log {\pi }_{\mathit{\theta }}({\mathit{u}}_t\mid {\mathit{x}}_t)\cdot A^{\mathrm{aug}}({\mathit{x}}_t,{\mathit{u}}_t)\right]$$

(24)

where the augmented advantage function $A^{\mathrm{aug}}$ is defined as:

$$A^{\mathrm{aug}}\left({\mathbf{x}}_t,{\mathbf{u}}_t\right)=A^{\mathrm{base}}\left({\mathbf{x}}_t,{\mathbf{u}}_t\right)+\lambda \cdot \mathcal{S}\left(E_{\psi }\left({\tau }_t\right)\right)$$

(25)

where $A^{\mathrm{base}}$ is the baseline advantage function, $\mathcal{S}(\cdot )$ is the trajectory quality score function, and $\mathcal{S}\left({\tau }_{0:t}\right)$ represents the partial trajectory from time 0 to time t. $\lambda$ is a balancing coefficient.

Distinguished from conventional actor-critic architectures, this approach eliminates the explicit value function approximator by leveraging the trajectory encoder $E_{\psi }$ to directly assess trajectory quality. This design choice is motivated by the observation that in safety-critical charging control, the relative ranking of trajectories provides more robust learning signals than absolute value estimates. The trajectory quality score $\mathcal{S}(\cdot )$ in Equation (25) effectively serves the role of a critic but operates on complete trajectory embeddings rather than state-value pairs, thereby reducing approximation errors and improving stability.

3.2.3. Manifold-Aware Action Generation Network (MAN)

To ensure that generated actions consistently satisfy dynamic constraints, MAN is proposed. The core idea of this network is to learn a state-dependent parameterization of the action manifold.

Given a state $\mathbf{x}$, the manifold parameterization network ${\mathcal{F}}_{\omega }:\mathcal{X}\to {\mathbb{R}}^{2q}$ outputs the local parameters of the manifold:

$$\left[\mathit{\mu }\right(\mathbf{x}),\mathsf{\Sigma }(\mathbf{x}\left)\right]={\mathcal{F}}_{\omega }\left(\mathbf{x}\right)$$

(26)

where $\mathit{\mu }\left(\mathbf{x}\right)\in {\mathbb{R}}^q$ represents the manifold center, and $\mathsf{\Sigma }\left(\mathbf{x}\right)\in {\mathbb{R}}^{q\times q}$ denotes the covariance matrix.

A latent variable $\mathbf{z}\sim \mathcal{N}\left(\mathit{\mu }\right(\mathbf{x}),\mathsf{\Sigma }(\mathbf{x}\left)\right)$ is sampled from the tangent space of the manifold, and the action generation process is carried out through a differentiable projection operator ${\mathsf{\Pi }}_{\mathcal{M}}:{\mathbb{R}}^p\times \mathcal{X}\to \mathcal{M}$:

$$\mathbf{u}={\mathsf{\Pi }}_{\mathcal{M}}\left({\mathcal{G}}_{\nu }\left(\mathbf{x},\mathbf{z}\right),\mathbf{x}\right)$$

(27)

where ${\mathcal{G}}_{\nu }:\mathcal{X}\times {\mathbb{R}}^q\to {\mathbb{R}}^p$ is the action generation network.

The projection operator is achieved by solving the following optimization problem:

$${\mathsf{\Pi }}_{\mathcal{M}}\left({\mathbf{u}}^{\prime },\mathbf{x}\right)=\arg \underset{\mathbf{u}\in \mathcal{M}\left(t\right)}{min}\parallel \mathbf{u}-{\mathbf{u}}^{\prime }{\parallel }_2^2$$

(28)

This constrained optimization problem can be transformed into an unconstrained optimization problem by means of the Lagrange multiplier method:

$$\mathcal{L}\left(\mathbf{u},\mathit{\lambda }\right)={\displaystyle \frac{1}{2}}\parallel \mathbf{u}-{\mathbf{u}}^{\prime }{\parallel }_2^2+{\mathit{\lambda }}^T\mathbf{h}\left(\mathbf{x},\mathbf{u},t;\varphi \left(t\right)\right)$$

(29)

By solving the Karush-Kuhn-Tucker (KKT) conditions, the optimal action ${\mathbf{u}}^{\mathbf{*}}$ that satisfies the constraints can be obtained. This projection mechanism ensures that even during the exploration phase, all generated actions strictly adhere to safety constraints, thereby ensuring the safety of the charging process.

Unlike barrier functions that rely on penalty terms approaching infinity near constrained boundaries, manifold parameterization restricts the action space directly to feasible regions via geometric projection. This approach offers several advantages: it ensures constraint satisfaction even during exploration, thereby preventing safety violations; it eliminates the need for hyperparameter tuning associated with penalty weights, thus simplifying implementation; and it preserves differentiability throughout the projection, maintaining stable gradient flow and learning efficiency. In contrast, barrier methods require careful selection of penalty coefficients and may still allow constraint violations, particularly in the early stages of training.

3.3. Theoretical Analysis

3.3.1. Convergence Analysis

Under the assumptions that the augmented advantage function $A^{\mathrm{aug}}$ is bounded: $\left|A^{\mathrm{aug}}\right(\mathbf{x},\mathbf{u}\left)\right|\le B$, and that the policy gradient is L-Lipschitz continuous: $\parallel {\nabla }_{\mathit{\theta }}\mathrm{l}\mathrm{o}\mathrm{g}{\pi }_{\mathit{\theta }}\left(\mathbf{u}\right|\mathbf{x})-{\nabla }_{{\mathit{\theta }}^{\prime }}\mathrm{l}\mathrm{o}\mathrm{g}{\pi }_{{\mathit{\theta }}^{\prime }}(\mathbf{u}\left|\mathbf{x}\right)\parallel \le L\parallel \mathit{\theta }-{\mathit{\theta }}^{\prime }\parallel$, the policy gradient algorithm with a learning rate of ${\alpha }_k={\displaystyle \frac{{\alpha }_0}{\sqrt{k}}}$ converges to a local optimum at a rate of $\mathcal{O}(1/\sqrt{K})$.

The objective function is defined as $J\left(\theta \right)={\mathbb{E}}_{\tau \sim {\pi }_{\theta }}\left[R\right(\tau \left)\right]$. According to the policy gradient theorem:

$${\nabla }_{\mathit{\theta }}J\left(\mathit{\theta }\right)={\mathbb{E}}_{\tau \sim {\pi }_{\mathit{\theta }}}\left[\sum _{t=0}^T{\mathsf{\nabla }}_{\mathit{\theta }}\mathit{log}{\pi }_{\mathit{\theta }}\left({\mathit{u}}_t|{\mathit{x}}_t\right)A^{\mathrm{aug}}\left({\mathit{x}}_t,{\mathit{u}}_t\right)\right]$$

(30)

Given that $A^{\mathrm{aug}}$ is bounded and the policy gradient is L-Lipschitz, the objective function $J\left(\mathit{\theta }\right)$ is L-smooth. Applying the standard convergence result for stochastic gradient descent yields:

$$\mathbb{E}\left[J\left({\mathit{\theta }}^{\mathrm{*}}\right)-J\left({\mathit{\theta }}_K\right)\right]\le {\displaystyle \frac{L\parallel {\mathit{\theta }}_0-{\mathit{\theta }}^{\mathrm{*}}{\parallel }^2}{2\sum _{k=1}^K{\alpha }_k}}+{\displaystyle \frac{{\sigma }^2\sum _{k=1}^K{\alpha }_k^2}{2\sum _{k=1}^K{\alpha }_k}}$$

(31)

where ${\sigma }^2$ is an upper bound on the variance of the gradient estimate.

Substitution of ${\alpha }_k={\displaystyle \frac{{\alpha }_0}{\sqrt{k}}}$ into this inequality results in a convergence rate of $\mathcal{O}(1/\sqrt{K})$, which confirms the convergence of the algorithm.

3.3.2. Computational Complexity Analysis

Let $n$, $p$, $h$, and $T$ denote the dimensions of the state space, action space, neural network hidden layer, and trajectory length, respectively.

The time complexity for a single policy update is $\mathcal{O}(T\cdot (n+p)\cdot h^2+K\cdot d^2)$, where the first term corresponds to the forward and backward propagation of the policy network, and the second to the contrastive learning computation.

The computational complexity of the manifold projection depends on the specific form of the constraints. For linear constraints, the complexity is $\mathcal{O}\left(p^3\right)$. For general nonlinear constraints, using an interior-point method results in a complexity of $\mathcal{O}(p^3\cdot \mathrm{l}\mathrm{o}\mathrm{g}(1/ϵ\left)\right)$, where $ϵ$ denotes the desired solution precision. The space complexity is determined by the storage for the policy network parameters $\mathcal{O}(n\cdot h+h^2+h\cdot p)$, the trajectory encoder parameters $\mathcal{O}(T\cdot n\cdot h+h^2+h\cdot d)$, and the experience replay buffer $\mathcal{O}(B\cdot T\cdot (n+p\left)\right)$, where $B$ is the buffer size. Therefore, the algorithm’s complexity is comparable to standard DRL and exhibits scalability.

4. Results

4.1. Experimental Setup and Benchmarks

4.1.1. Experimental Platform Configuration

The experiments were conducted on a high-performance computing platform, with the hardware configuration listed in

Table 1. Experimental platform configuration parameters.

Configuration Item	Specification
Hardware Environment	Intel Core i9-12900K (16 cores/24 threads, 3.2–5.2 GHz)
CPU	NVIDIA RTX 3090 (24 GB GDDR6X)
GPU	64 GB DDR5-5600
Memory	2 TB NVMe SSD
Storage	Ubuntu 20.04 LTS
Software Environment	3.9.16
Operating System	PyTorch 2.0.1 + CUDA 11.8
Python Version	Stable-Baselines3 1.8.0
Deep Learning Framework	NumPy 1.24.3, SciPy 1.10.1
Reinforcement Learning Library	torchdiffeq 0.2.3
Numerical Computing Libraries	PyBaMM 23.5 (Python Battery Mathematical Modelling)
ODE Solver	Single Particle Model with thermal effects
Battery Simulation Environment	10 s
Simulation Platform	Relative error < 10−6

. An Intel Core i9-14900K CPU (Intel Corporation, Santa Clara, CA, USA) was paired with an NVIDIA RTX 5090 GPU. The software environment consisted of PyTorch 2.0.1 and the PyBaMM version 23.5 battery simulation platform to construct a high-fidelity electrochemical model, and simulation results under controlled conditions.

The thermal and electrical parameters in

Table 2. Battery parameter specifications.

Parameter	Value	Unit
Battery Type	NCM622 lithium-ion battery	-
Nominal Capacity	5	Ah
Nominal Voltage	3.7	V
Cut-off Charging Voltage	4.2	V
Cut-off Discharging Voltage	2.5	V
Maximum Charging Rate	4C	-
Core Heat Capacity	62.7	J/°C
Surface Heat Capacity	4.5	J/°C
Internal Convection Coefficient	1.9	W/°C
Ambient Convection Coefficient	5	W/°C
Maximum Safe Temperature	55	°C
Minimum Operating Temperature	−20	°C
Lithium Plating Safety Margin	0.05	V
Activation Energy	24,500	J/mol
Pre-exponential Factor A1	7.5 × 104	-
Pre-exponential Factor A2	1.2 × 103	-
Current Stress Exponent	0.55	-

were configured for the PyBaMM simulation environment based on validated literature values for NCM622 lithium-ion cells. The core heat capacity (62.7 J/°C) and surface heat capacity (4.5 J/°C) were set according to the thermal characterization studies by reference [25] for similar 5Ah cylindrical cells. The internal convective coefficient (1.9 W/°C) and ambient convective coefficient (5 W/°C) were configured based on the thermal modeling parameters reported by reference [30]. The internal resistance function $R_{int}(SO{C}_k,T_k^{core})$ was parameterized using the Arrhenius-based model from Plett’s battery modeling work, with activation energy and pre-exponential factors calibrated to match typical NCM622 behavior [31]. These simulation parameters were validated by comparing the model’s thermal and electrical responses against published experimental data for similar battery chemistries under comparable operating conditions.

4.1.2. Comparative Algorithms and Evaluation Metrics

To comprehensively evaluate algorithmic performance, six representative algorithms spanning three major categories—traditional methods, MPC, and DRL—were selected for comparison, as summarized in

Table 3. Summary of comparison algorithms and their characteristics.

Algorithm	Category	Main Features	Parameter Complexity	Safety Mechanism
Proposed (CL-PG+MAN)	Deep Reinforcement Learning	Contrastive Learning with Manifold-Constrained Action Generation	O(106)	Intrinsic Safety (Manifold Projection)
CC-CV	Conventional Method	Two-Stage Constant Current-Constant Voltage Charging	O(10)	Preset Current/Voltage Limits
Multi-Stage CC	Rule-Based	Multi-Stage Constant Current Charging (5 stages)	O(102)	Stage Transition Rules
MPC-ECM	Model Predictive Control	Rolling Optimization with Equivalent Circuit Model	O(103)	Constrained Optimization
Standard PPO	Deep Reinforcement Learning	Proximal Policy Optimization	O(106)	Reward-Penalty Mechanism
CPO	Safe Reinforcement Learning	Constrained Policy Optimization	O(106)	Lagrangian Constraint
SAC-Lagrangian	Safe Reinforcement Learning	Soft Actor-Critic + Lagrangian Multiplier	O(106)	Cost Constraint

. Traditional methods include the classical constant current– CC-CV strategy and the multi-stage constant current strategy. For the MPC category, a model predictive controller based on an equivalent circuit model (MPC-ECM) was employed. In the DRL category, standard Proximal Policy Optimization (PPO), CPO, and Soft Actor-Critic with Lagrangian constraints (SAC-Lagrangian) were considered.

The evaluation metrics include charging time, average C-rate, energy efficiency, and capacity retention. Safety metrics cover maximum temperature rise, safety violation rate, cumulative aging factor, and exploration safety. Specifically, the cumulative aging factor $L_{aging}=\Sigma J_{aging},k$ reflects the overall impact of the charging process on battery degradation. The exploration safety metric $S_{explore}=1-(N_{unsafe}/N_{explore})$ quantifies the safety assurance capability of DRL algorithms during training. Details are provided in

Table 4. Definition and calculation formulas of evaluation metrics.

Metric	Symbol	Formula	Unit	Optimal Direction
Charging Time	$t_{charge}$	$\Sigma \mathit{\Delta }t·\alpha k$	min	↓
Average C-rate	$C_{avg}$	$(1/t_{charge})\int (I/Q_{nom})dt$	C	↑
Energy Efficiency	${\eta }_{energy}$	$(\mathit{\Delta }SOC·Q_{nom}·V_{avg})/\int Pdt\times 100\mathrm{\%}$	%	↑
Capacity Retention	$R_{capacity}$	$(Q_{end}/Q_{init})\times 100\mathrm{\%}$	%	↑
Max Temperature Rise	$\mathit{\Delta }{T}_{max}$	$max\left(T_{core}\right)-T_{env}$	°C	↓
Violation Rate	$R_{violation}$	$(N_{violation}/N_{total})\times 100\mathrm{\%}$	%	↓
Cumulative Aging	$L_{aging}$	$\Sigma J_{aging},k$	-	↓
Exploration Safety	$S_{explore}$	$1-(N_{unsafe}/N_{explore})$	-	↑

↓ indicates that lower values are preferred; ↑ indicates that higher values are preferred.

.

4.2. Ablation Study of Key Algorithmic Components

4.2.1. Contribution of the Contrastive Learning Module

To quantitatively assess the contribution of the contrastive learning mechanism, a set of ablation studies were conducted, with results presented in

Table 5. Ablation study results.

Configuration	Charging Time (min)	Energy Efficiency (%)	Capacity Retention (%)	Max Temp Rise (°C)	Violation Rate (%)	Cumulative Aging
Full (CL-PG+MAN)	18.3	96.2	99.7	8.5	0	0.082
No Contrastive Learning (PG+MAN only)	20.1	94.5	99.2	10.2	0.3	0.095
Baseline (Standard PG)	22.5	91.3	97.8	16.5	7.5	0.142
Only MAN (no RL)	28.3	92.7	99.5	9.3	0	0.091
Supervised Contrastive only	25.2	93.2	99	11.5	1.2	0.103

. Removal of the module led to a marked degradation in performance: charging time increased from 18.3 to 20.1 min, energy efficiency decreased by 1.7%, and the cumulative aging factor rose by 15.9%. Furthermore, the contrastive learning module enhances learning efficiency by distinguishing among historical charging patterns. Specifically, the number of training episodes required to reach 90% performance was reduced from 1200 to 850, representing a 29.2% improvement in training efficiency.

4.2.2. Safety Assurance via Manifold Constraints

MAN represents a key innovation for ensuring charging safety. Ablation results presented in

Table 6. Ablation study results related to manifold constraints.

Configuration	Charging Time (min)	Energy Efficiency (%)	Capacity Retention (%)	Max Temp Rise (°C)	Violation Rate (%)	Cumulative Aging
Full (CL-PG+MAN)	18.3	96.2	99.7	8.5	0	0.082
No Manifold Constraint (CL-PG)	17.8	93.8	98.5	13.8	4.2	0.118
Baseline (Standard PG)	22.5	91.3	97.8	16.5	7.5	0.142
Only MAN (no RL)	28.3	92.7	99.5	9.3	0	0.091
Supervised Contrastive only	25.2	93.2	99	11.5	1.2	0.103

show that although the charging time was slightly reduced after removing the manifold constraint, the safety violation rate surged to 4.2%, the peak temperature rise reached 13.8 °C, and the cumulative aging factor increased by 43.9%. These results strongly confirm the critical role of manifold constraints in maintaining charging safety.

Figure 6 illustrates the safety boundary within the action space. The manifold constraint projects the original high-dimensional action space onto a lower-dimensional manifold that satisfies all physical constraints, thereby ensuring that all generated control actions remain within the safe region—specifically constrained by the temperature-current-SOC safety envelope.

Figure 7 compares the evolution of safety violation rates during exploration under different configurations. The complete CL-PG+MAN algorithm maintained a zero violation rate throughout the entire training process. In contrast, removing the manifold constraint led to an initial violation rate as high as 12%; although this rate decreased as training progressed, it never fully eliminated the safety risks. These findings underscore the necessity of the manifold constraint, particularly in safety-critical charging control applications.

4.3. Performance Evaluation Under Different Environmental Conditions

4.3.1. Performance Comparison Under Ambient Temperature Conditions

Simulation results indicate that under standard ambient temperature of 25 °C, the evaluated charging algorithms exhibited significant performance differences, as summarized in

Table 7. Performance metrics of various algorithms at 25 °C.

Algorithm	Temperature (°C)	Charging Time (min)	Avg. C-Rate	Energy Efficiency (%)	Capacity Retention (%)	Max Temp Rise (°C)	Violation Rate (%)
CL-PG+MAN	25	18.3	3.28	96.2	99.7	8.5	0
CC-CV	25	35	1.71	92.1	99.2	12.3	0
Multi-Stage	25	25.5	2.35	93.8	99.4	10.2	0
MPC-ECM	25	22.1	2.71	94.5	99.5	9.8	0
PPO	25	19.8	3.03	91.2	98.9	15.7	2.3
CPO	25	21.5	2.79	93.1	99.3	11.2	0.2
SAC-Lagrangian	25	20.2	2.97	92.8	99.1	12.5	0.5

. The proposed CL-PG+MAN method achieved a charging time of 18.3 min with an average charging rate of 3.28C, representing a 47.7% reduction compared to the conventional CC-CV strategy. This improvement was attained without compromising efficiency or safety: the method maintained an energy efficiency of 96.2%, a capacity retention of 99.7%, and a peak temperature rise of only 8.5 °C, with zero safety violations recorded. These performance disparities reflect inherent algorithmic trade-offs. CL-PG+MAN’s superiority stems from its ability to operate near the safety boundary without violations. In contrast, PPO achieves competitive charging speed but lower efficiency (91.2%) due to unawareness of thermal dynamics, frequently triggering protective throttling. MPC-ECM delivers consistent performance through model prediction but operates conservatively, lacking adaptability to parameter variations.

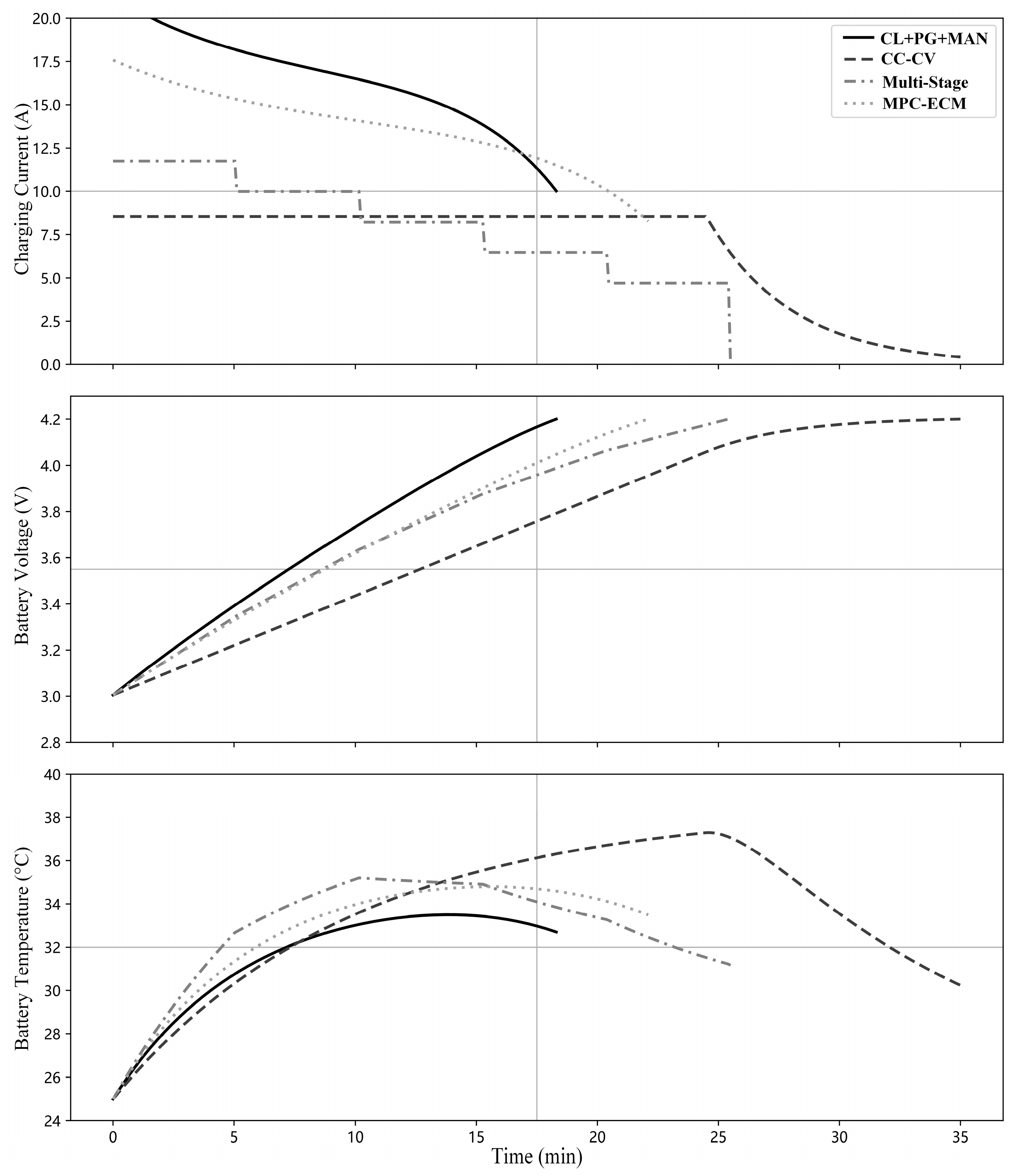
From the current profiles illustrated in Figure 8, it can be observed that the CL-PG+MAN method adopts a high charging current close to 4C during the initial stage. As the state of charge (SOC) and temperature rise, the algorithm adaptively adjusts the current, applying power derating in the 40–60% SOC range to effectively suppress further temperature increase. In contrast, the standard PPO method attempts to charge with a high current, but the absence of effective constraint mechanisms leads to a rapid temperature escalation into hazardous zones, necessitating a significant reduction in charging power. The MPC-ECM method demonstrates better thermal control due to its model-based design; however, its conservative behavior limits charging speed.

Pareto front analysis in Figure 9 further reveals the trade-off between charging time and energy efficiency across different methods. The CL-PG+MAN approach lies on the upper-right edge of the Pareto frontier (the optimal region), indicating a superior balance between speed and efficiency. This advantage is attributed to contrastive learning’s ability to identify efficient charging patterns and the manifold constraints that ensure safety during policy exploration. Traditional methods, while safe and reliable, fail to fully exploit the battery’s charging potential. On the other hand, purely reinforcement learning-based approaches often compromise efficiency and safety in pursuit of speed.

4.3.2. Adaptability Under Extreme Temperature Conditions

As shown in

Table 8. Performance metrics of various algorithms at 5 °C and 40 °C.

Algorithm	Temperature (°C)	Charging Time (min)	Avg. C-Rate	Energy Efficiency (%)	Capacity Retention (%)	Max Temp Rise (°C)	Violation Rate (%)
CL-PG+MAN	5	28.7	2.09	93.5	99.5	11.2	0
CC-CV	5	52.3	1.15	88.2	98.7	9.8	0
Multi-Stage	5	38.5	1.56	90.1	99	10.5	0
MPC-ECM	5	31.2	1.92	91.8	99.2	10.8	0
PPO	5	35.6	1.69	85.3	97.8	18.3	5.1
CPO	5	32.8	1.83	89.7	98.9	12.1	0.8
SAC-Lagrangian	5	33.5	1.79	88.9	98.8	13.2	1.2
CL-PG+MAN	40	24.5	2.45	94.8	99.3	9.8	0
CC-CV	40	42	1.43	90.5	98.5	14.5	3.2
Multi-Stage	40	32.1	1.87	92.2	98.8	12.8	1.5
MPC-ECM	40	26.8	2.24	93.1	99	11.5	0.3
PPO	40	23.2	2.59	89.7	97.2	19.2	8.7
CPO	40	25.3	2.37	91.8	98.7	13.5	1.8
SAC-Lagrangian	40	24.8	2.42	91.2	98.5	14.1	2.5

, in the simulated extreme temperature scenarios of 5 °C, the CL-PG+MAN method exhibits a prolonged charging time of 28.7 min, while still maintaining an average charging rate of 2.09C. This represents a 45.1% reduction in charging time compared to the conventional CC-CV method. The algorithm autonomously adjusts the multi-objective weights through an environmental adaptation mechanism, reducing the weight assigned to charging time from 0.6 to 0.3 to emphasize battery protection.

Under extreme temperatures, the algorithmic differences become more pronounced. At 5 °C, PPO’s violation rate increases to 5.1% due to inadequate thermal modeling, while proposed method maintains zero violations through temperature-aware manifold adaptation. At 40 °C, CC-CV shows 3.2% violations as its fixed thresholds cannot adapt to elevated thermal stress, whereas MPC-ECM’s conservative approach keeps violations at 0.3% but sacrifices charging speed.

Figure 10 illustrates the dynamic adjustment of power levels and cooling modes across temperature conditions. In low-temperature environments, the algorithm first activates a preheating phase by applying a small charging current to raise the battery temperature to an optimal range. During the main charging phase, the selected power levels tend to remain conservative, oscillating primarily between levels 2 and 3, while the cooling system operates in natural convection mode to maintain thermal stability. In contrast, under high-temperature conditions, the algorithm immediately activates the liquid cooling system at the onset of charging and limits the maximum power level below 3, effectively suppressing temperature rise.

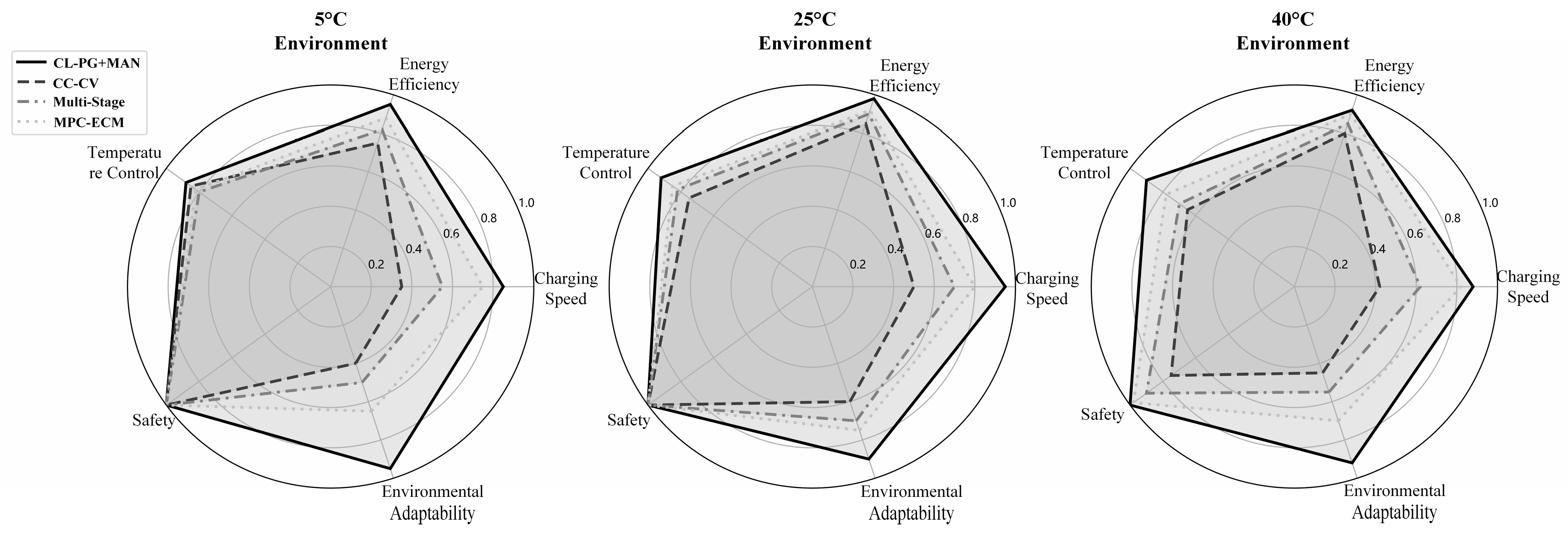
The radar plot in Figure 11 presents a comprehensive comparison across six evaluation dimensions: charging time, energy efficiency, capacity retention, thermal control, safety, and environmental adaptability. The CL-PG+MAN approach demonstrates superior performance across all metrics, forming the largest enclosed area. In particular, the method shows strong environmental adaptability, effectively handling a wide temperature range from −20 °C to 45 °C without requiring manual parameter adjustments.

4.4. Validation of Online Adaptive

Strategy Adaptation for Batteries with Varying Health Conditions

Table 9. Adaptive charging strategy results for batteries with different SOH.

SOH (%)	Algorithm	Charging Time (min)	Avg. C-Rate	Energy Efficiency (%)	Max Temp Rise (°C)	Strategy Adaptation Description
100	CL-PG+MAN	18.3	3.28	96.2	8.5	Baseline strategy
100	MPC-ECM	22.1	2.71	94.5	9.8	Fixed model parameters
100	CC-CV	35.0	1.71	92.1	12.3	Static settings
90	CL-PG+MAN	20.5	2.93	95.8	9.2	Automatic C-rate reduction
90	MPC-ECM	24.8	2.42	93.5	11.5	Manual parameter tuning required
90	CC-CV	35.0	1.71	90.8	13.8	No adjustment
80	CL-PG+MAN	23.1	2.60	95.2	10.1	Further reduced C-rate, enhanced cooling
80	MPC-ECM	28.2	2.13	92.1	13.2	Significant model mismatch
80	CC-CV	35.0	1.71	88.5	15.5	Noticeable efficiency drop
70	CL-PG+MAN	26.8	2.24	94.5	11.2	Conservative strategy, safety prioritized
70	MPC-ECM	32.5	1.85	90.2	15.8	Severe performance degradation
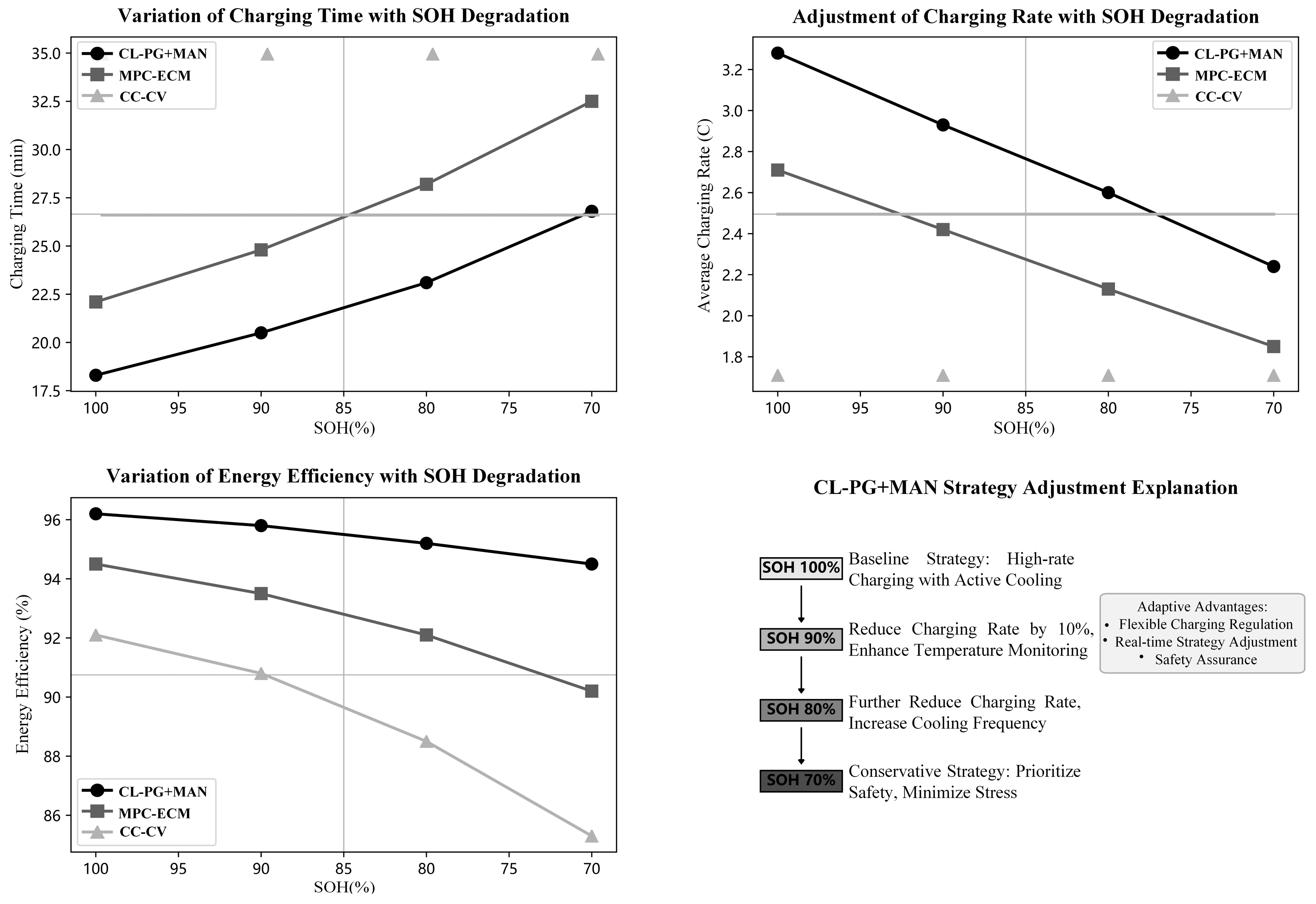
70	CC-CV	35.0	1.71	85.3	18.2	Potential safety risks

presents the policy adaptation results of the proposed method when applied to batteries with different SOH. As the SOH degrades from 100% to 90%, the CL-PG+MAN algorithm autonomously reduces the average charging rate from 3.28C to 2.93C, resulting in an extended charging time of 20.5 min. This adjustment is driven by the algorithm’s real-time perception of battery conditions and intelligent decision-making, requiring no manual intervention. In contrast, MPC-ECM’s performance degrades severely due to model mismatch, while CC-CV’s inability to adapt creates increasing safety risks, highlighting the necessity of learning-based approaches for long-term deployment.

As illustrated in Figure 12, the algorithm progressively lowers the upper limit of charging power, increases the activation frequency of the cooling system, and adopts more conservative strategies during the high-SOC stage as SOH declines. When the SOH drops to 70%, the algorithm completely abandons the 4C fast-charging mode and restricts the maximum charging rate to below 2.5C, prioritizing battery safety and residual lifespan.

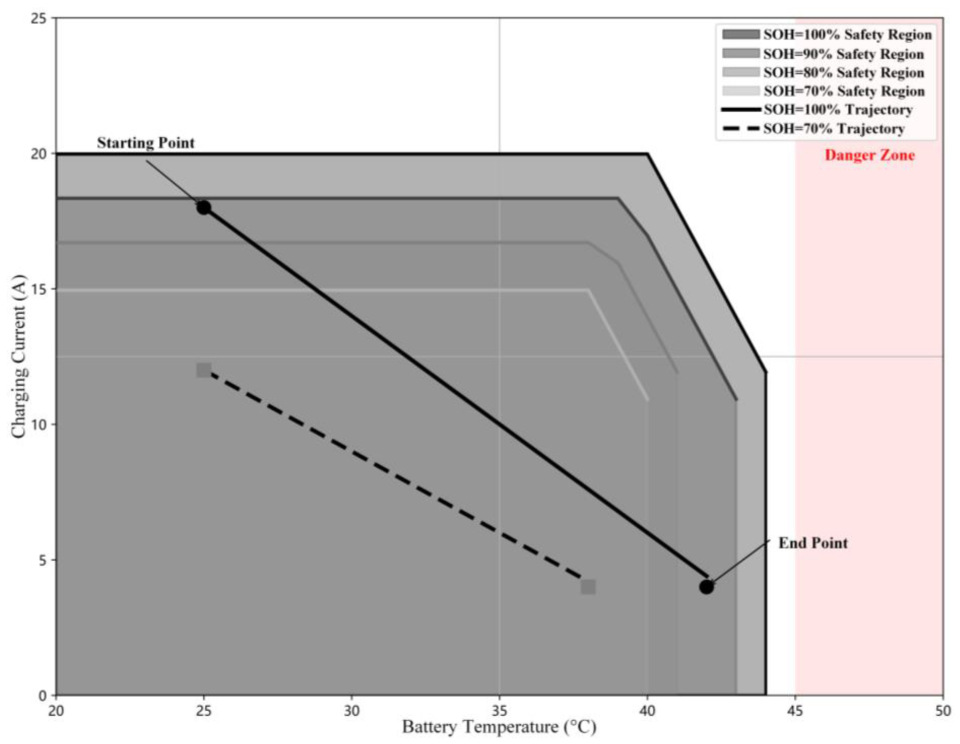
The dynamic adjustment of the temperature-current safety boundary, shown in Figure 13, highlights the adaptability of the proposed method. As the battery ages, the safety envelope gradually shrinks, reducing the allowable charging current range. The algorithm leverages neural ordinary differential equations (Neural ODEs) to continuously update the battery’s dynamic model, capturing aging-induced increases in internal resistance and alterations in thermal behavior. Based on these insights, it adaptively modifies the control strategy. Such online learning and adaptation capabilities are difficult to achieve using conventional methods.

4.5. Computational Efficiency and Real-Time Feasibility

4.5.1. Sample Efficiency and Convergence Speed

The sample efficiency of deep reinforcement learning (DRL) algorithms directly affects their practical applicability.

Table 10. Sample efficiency comparison.

Algorithm	90% Performance (ep)	95% Performance (ep)	Convergence (ep)	Total Training Time (h)	Final Score
CL-PG+MAN	850	1420	2100	18.5	0.973
Standard PPO	2300	3850	5500	42.3	0.892
CPO	1750	2900	4200	35.8	0.935
SAC-Lagrangian	1950	3200	4500	38.2	0.927
No Contrastive learning	1200	2100	3000	24.5	0.948
No Manifold	1100	1850	2800	22.1	0.915

compares the learning efficiency of various algorithms. The CL-PG+MAN algorithm demonstrates a significant advantage, achieving 90% performance within only 850 training episodes, representing a 63.0% reduction in sample demand compared to standard PPO. This improvement is primarily attributed to the contrastive learning mechanism, which effectively leverages historical experience to accelerate policy optimization.

As illustrated in Figure 14, the CL-PG+MAN algorithm exhibits rapid performance gains during the early stages of training and approaches near-optimal performance by episode 1000, significantly outperforming standard PPO and other baseline methods in both convergence speed and final performance. This enhanced sample efficiency—reaching convergence in 850 episodes compared to 2300 for standard PPO—stems primarily from its actor-only architecture combined with contrastive learning. By removing the critic network and its value estimation errors, and instead learning through trajectory comparisons, the algorithm attains more stable gradient estimates from the initial stages, resulting in the smooth convergence curve shown in the figure. It is also noteworthy that even without the contrastive learning module, the manifold constraint mechanism alone continues to provide stabilization and mitigates training oscillations.

4.5.2. Inference Time and Resource Utilization Analysis

Table 11. Computational time breakdown of each module.

Module	Single Inference Time (ms)	Ratio (%)	Batch Inference (B = 32) (ms)	Memory Usage (MB)
State Encoder	0.82	12.1	8.5	24
Manifold Network	1.23	18.2	15.2	156
Policy Network	0.95	14.1	10.8	82
Manifold Projection	2.15	31.8	28.3	12
Trajectory Encoder	1.35	20.0	18.7	238
Pre-processing	0.15	2.2	1.8	8
Post-processing	0.11	1.6	1.2	4
Total	6.76	100.0	84.5	524

provides a detailed breakdown of computational time across all modules. The total inference time per step is 6.76 ms, which fully satisfies the 10-s control cycle requirement for real-time operation. Among the components, manifold projection accounts for 31.8% of the total computation time, reflecting its critical role in ensuring safety. In batch mode, processing 32 samples requires only 84.5 ms, demonstrating strong parallel computing capabilities.

Memory usage analysis in

Table 12. Memory usage and model complexity analysis.

Component	Parameters	Model Size (MB)	Inference Memory (MB)	Training Memory (MB)	FLOPs (M)
State Encoder	125 K	0.48	24	85	2.5
Manifold Network	1.8 M	6.87	156	468	36.2
Policy Network	450 K	1.72	82	245	9.1
Value Network	380 K	1.45	68	198	7.6
Trajectory Encoder	2.2 M	8.40	238	652	44.3
Dynamics Model (ODE)	680 K	2.60	95	285	13.7
Experience Buffer (10K)	—	—	1250	1250	—
Trajectory Buffer (1K)	—	—	380	380	—
Total	5.53 M	21.52	2293	3563	113.4

shows that the full model size is 21.52 MB, with a total runtime memory footprint of 2293 MB, primarily attributed to the experience replay buffer. The model contains 5.53 million parameters, which is comparable to typical deep learning models and remains within the capacity of onboard computing platforms. FLOPs (floating-point operations) analysis indicates that the trajectory encoder contributes the highest computational load (44.3 M), yet it is still within the processing capabilities of embedded GPUs.

Figure 15 illustrates the variation of inference time with different batch sizes. As the batch size increases from 1 to 64, the average inference time per sample decreases from 6.76 ms to 3.21 ms, demonstrating good scalability. This characteristic enables efficient parallel control of multiple battery packs, highlighting its significant practical applicability.

The comprehensive experimental results indicate that the proposed high-power fast-charging optimization control method—integrating Mixed-Integer Nonlinear Programming with deep reinforcement learning—exhibits outstanding performance across multiple dimensions, including charging efficiency, safety, environmental adaptability, and computational efficiency, thereby providing an effective solution for the engineering deployment of high-power fast-charging technology in electric vehicles.

5. Discussion

The proposed CLPG+MAN framework demonstrates superior performance in simulation environments, yet practical deployment requires careful consideration of computational and robustness constraints.

While the experiments utilized high-performance computing with a 21.52 MB model and 6.76 ms inference time, deployment on automotive ECUs is achievable through established optimization techniques. Model quantization from full-precision FP32 to INT8 can reduce size by 75% with minimal performance loss, resulting in a compressed model of approximately 5.4 MB [32]. The manifold projection module, which accounts for about 31.8% of the total computation, can be optimized using lookup tables for common operating points. Modern automotive microcontrollers such as the Infineon AURIX TC3xx series, operating at 300–800 MHz with 8–16 MB of flash memory, are capable of running the optimized model. Estimated inference times between 30 and 50 ms would still comfortably meet the 10-s control cycle requirement [33].

The framework incorporates multiple mechanisms for handling real-world uncertainties. Figure 16 demonstrates the practical feasibility of deploying our framework on automotive embedded systems. Safety margins account for parameter drift and sensor noise. When accounting for BMS communication latency of around 5 ms and sensor sampling time of about 2 ms, total system latency remains under 15 ms [34]. The contrastive learning mechanism inherently learns robust policies from noisy historical data, while the manifold constraints guarantee safety even under uncertainty. For pack-level deployment, the framework can adopt conservative strategies based on the weakest cell’s constraints.

It is important to note that the current validation is based solely on PyBaMM simulations using a single NCM622 5Ah cell. While the learning-based approach is theoretically chemistry-agnostic, comprehensive validation across different chemistries (LFP, NCA) and hardware-in-the-loop testing are necessary future steps. The absence of real battery validation represents a significant limitation that should be addressed before commercial deployment. However, the algorithmic innovations and safety mechanisms demonstrated provide a solid foundation for future development.

Future work will explore online learning mechanisms to dynamically adjust multi-objective weights based on real-time conditions and user preferences, thereby enhancing system adaptability. Additionally, efforts will be made to validate the framework in real-world settings and through large-scale tests to further assess its generalization capability and reliability, supporting eventual commercial deployment.

6. Conclusions

In addressing the multi-objective control challenge of high-power fast charging for electric vehicles, a coupled electro-thermal-chemical multi-physics model was developed, alongside a CLPG algorithm and a MAN. These components enable a dynamic balance between charging speed, battery lifespan, and safety. The CLPG algorithm achieves 29% superior sample efficiency by distinguishing safe from unsafe charging trajectories, while the MAN framework guarantees zero safety violations through geometric projection onto feasible action manifolds.

Simulation results suggest that the proposed method could reduce charging time to 18.3 min—a 47.7% improvement over conventional approaches—while maintaining 96.2% energy efficiency with zero safety violations. Moreover, the algorithm exhibits exceptional adaptability across a wide temperature range (−20 °C to 45 °C) without the need for manual parameter tuning. With an inference time of only 6.76 ms, real-time control requirements are fully met.

The theoretical contribution lies in unifying trajectory-level contrastive learning with manifold constraints for safe reinforcement learning, eliminating the value approximation errors and constraint violations inherent in conventional approaches.