An Efficient Coordinated Observer LQR Control in a Platoon of Vehicles for Faster Settling Under Disturbances
Abstract
1. Introduction
2. Autonomous Vehicle Platooning System
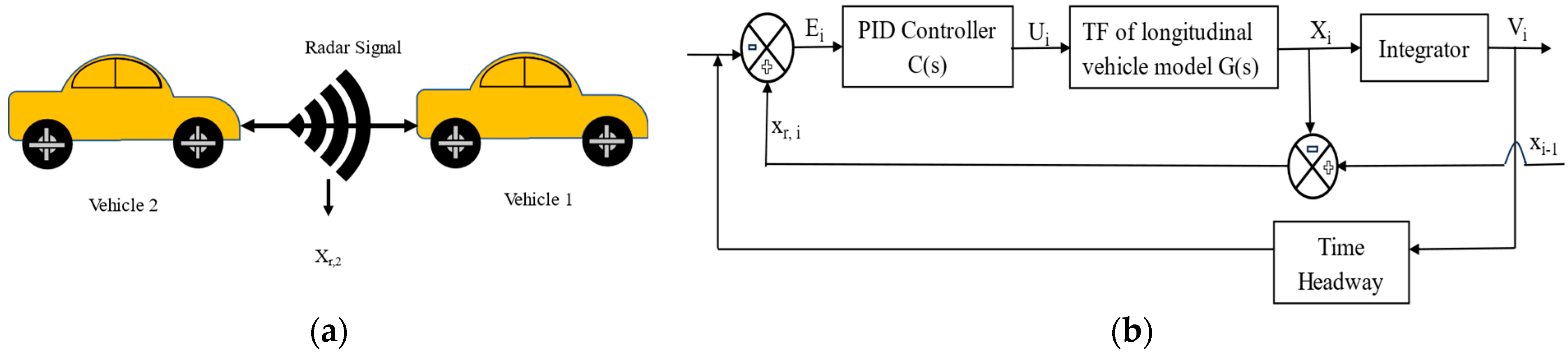
2.1. ACC Assisted Platoon
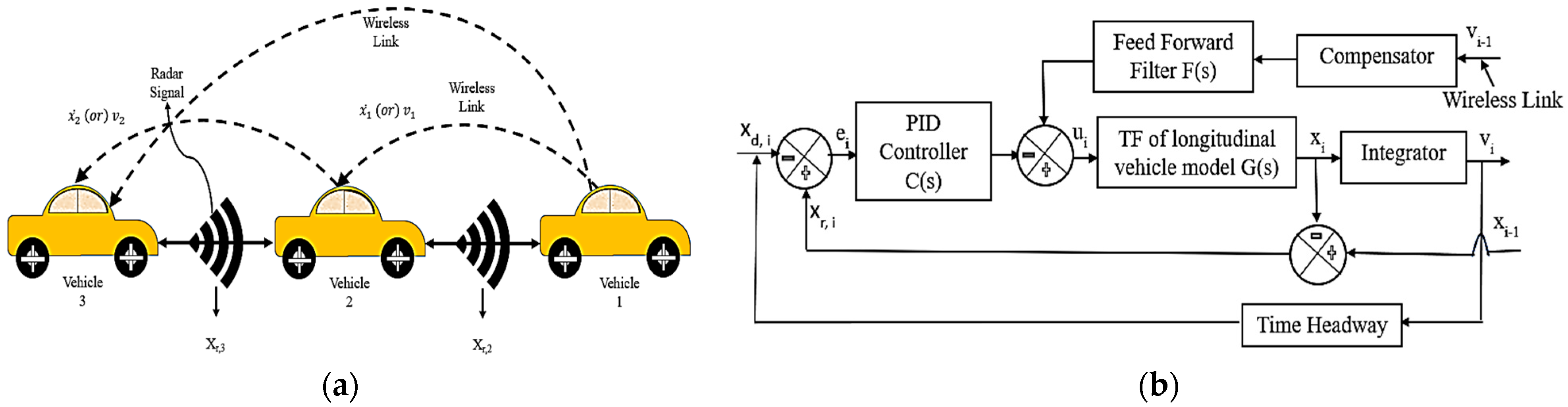
2.2. CACC Assisted PLATOON
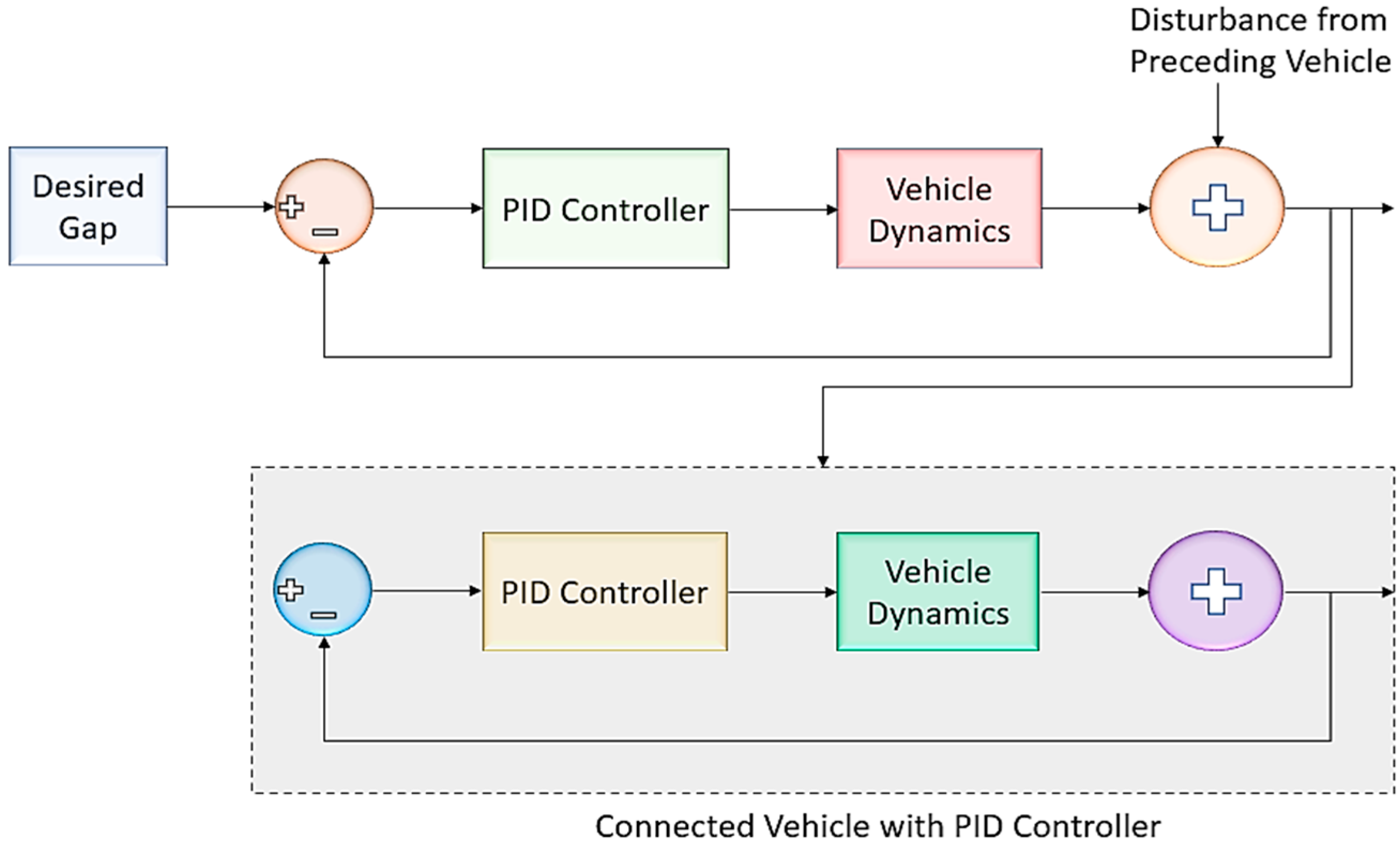
2.3. Implementation of PID Controller
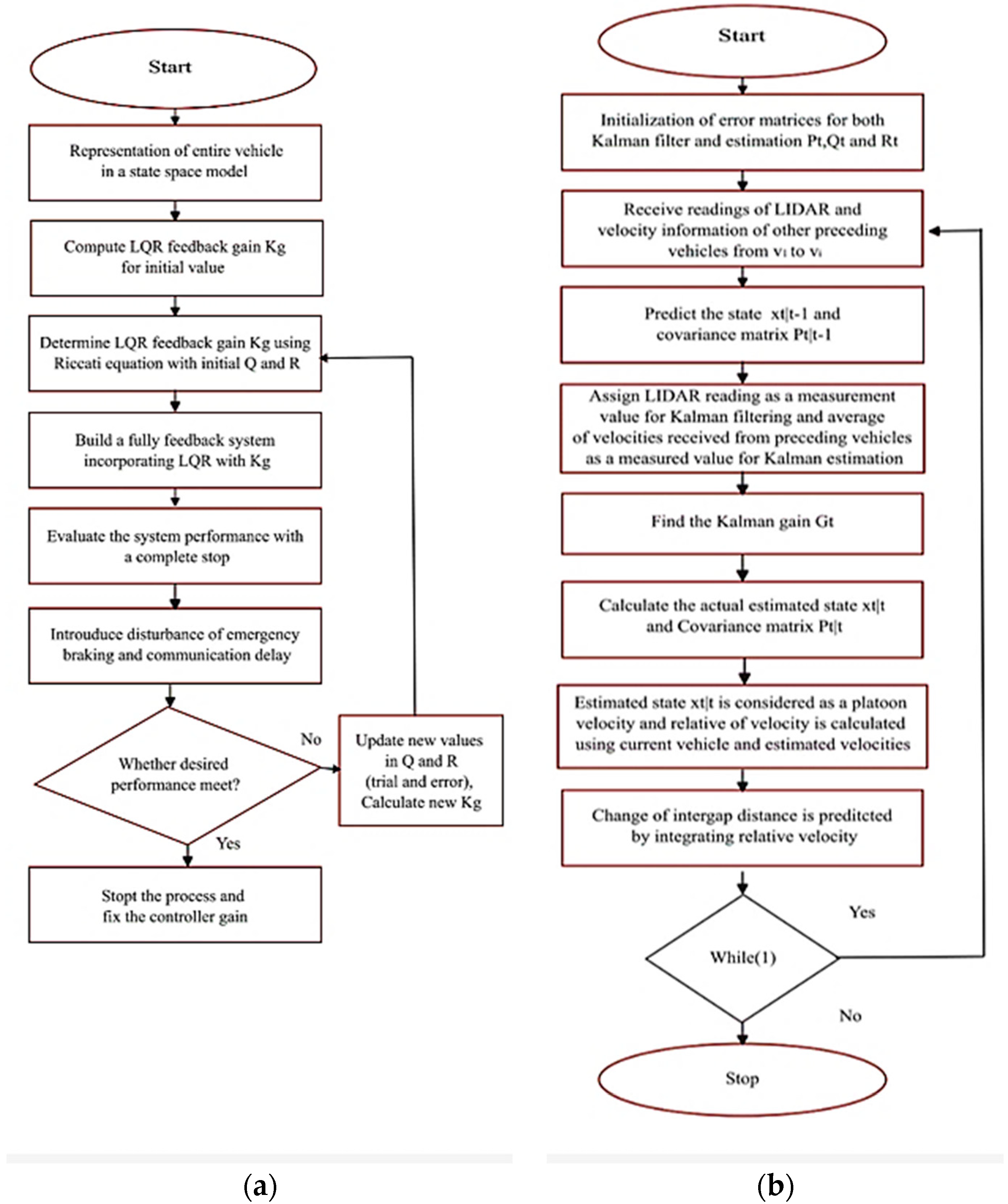
3. LQR Controller for Platoon
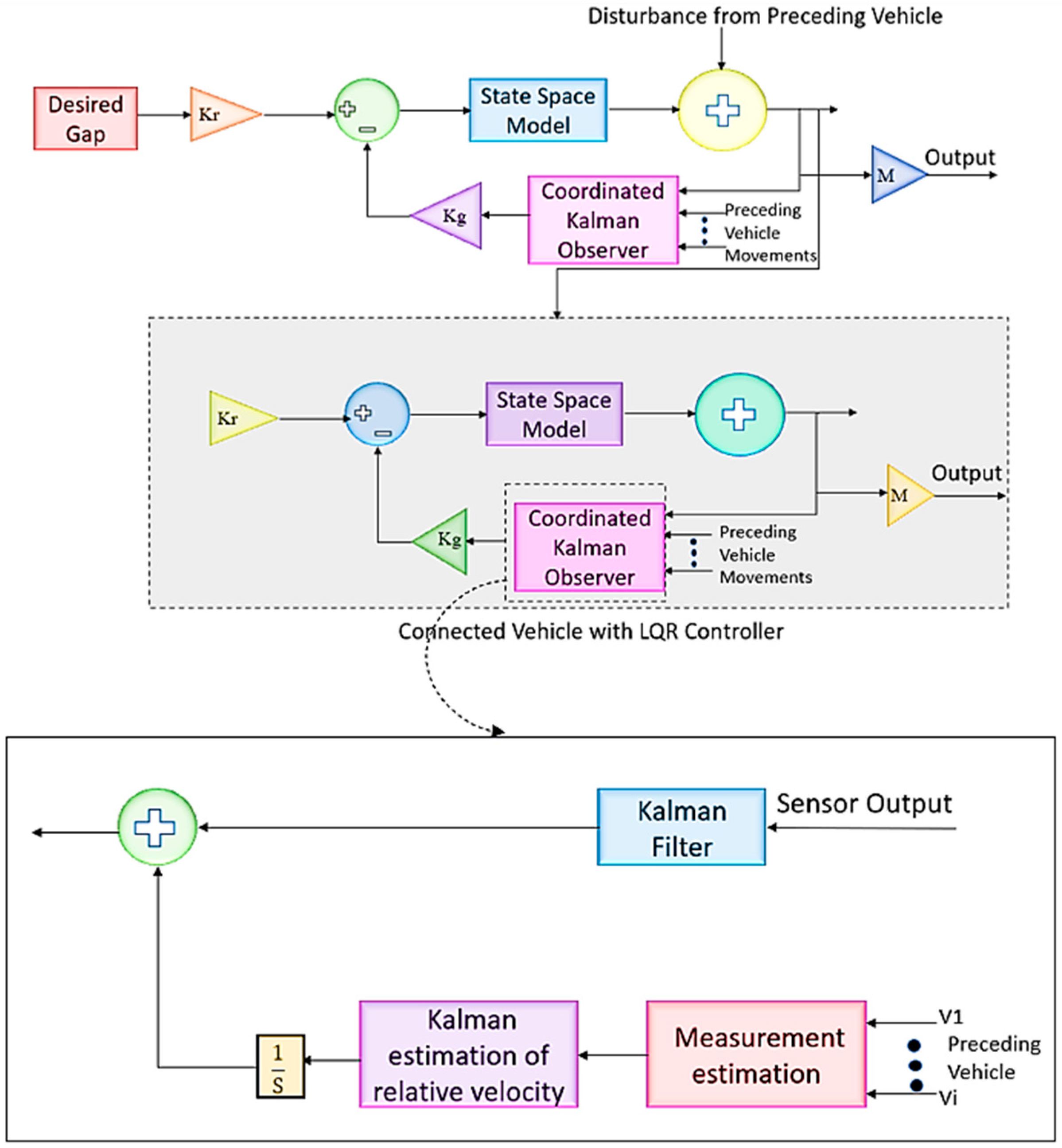
4. Coordinated Kalman Observer–LQR Controller for Platoon (CKO-LQR)
5. Results and Discussions
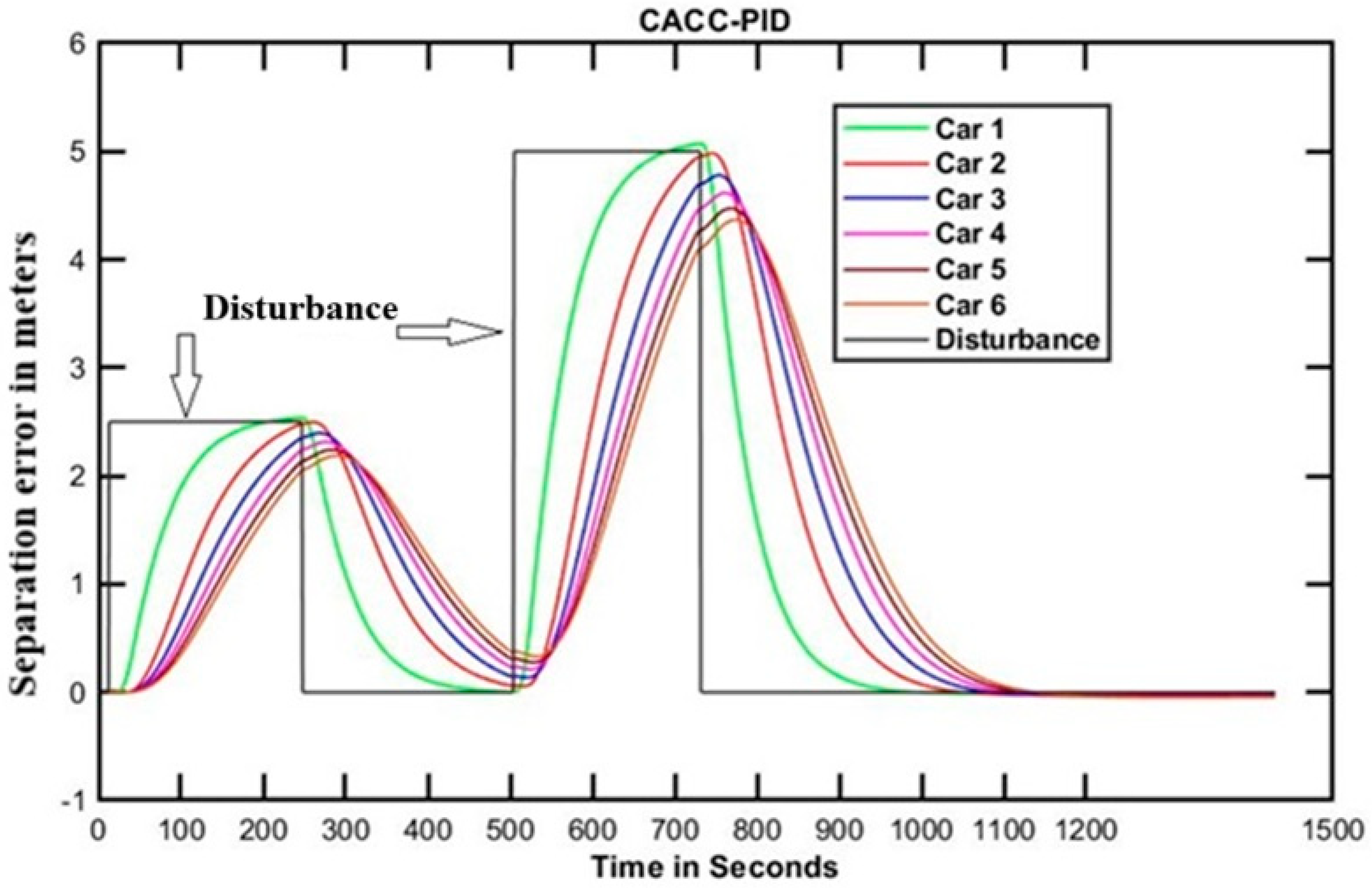
5.1. CACC Using PID Controller
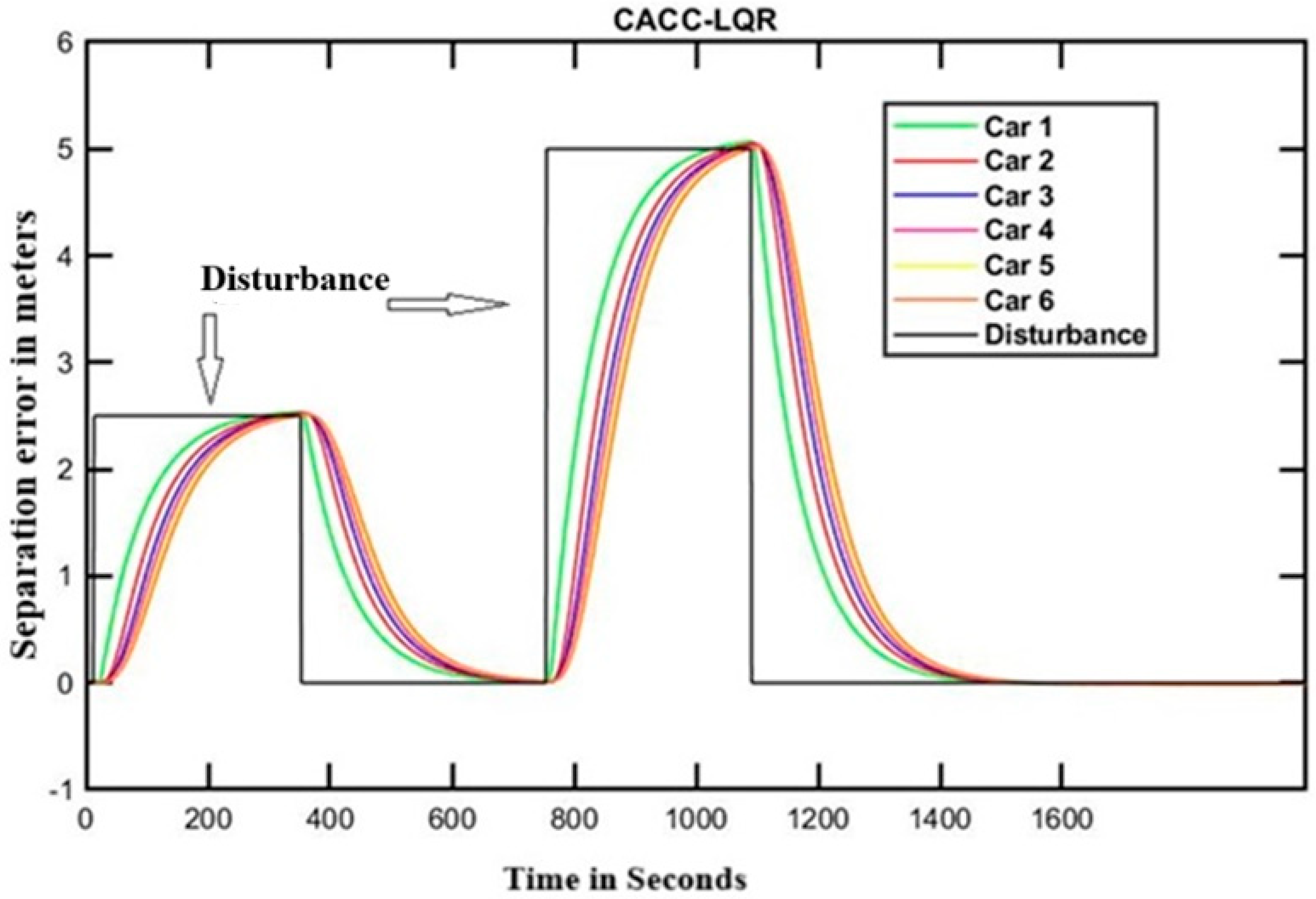
5.2. Performance of LQR Controller in a Platoon
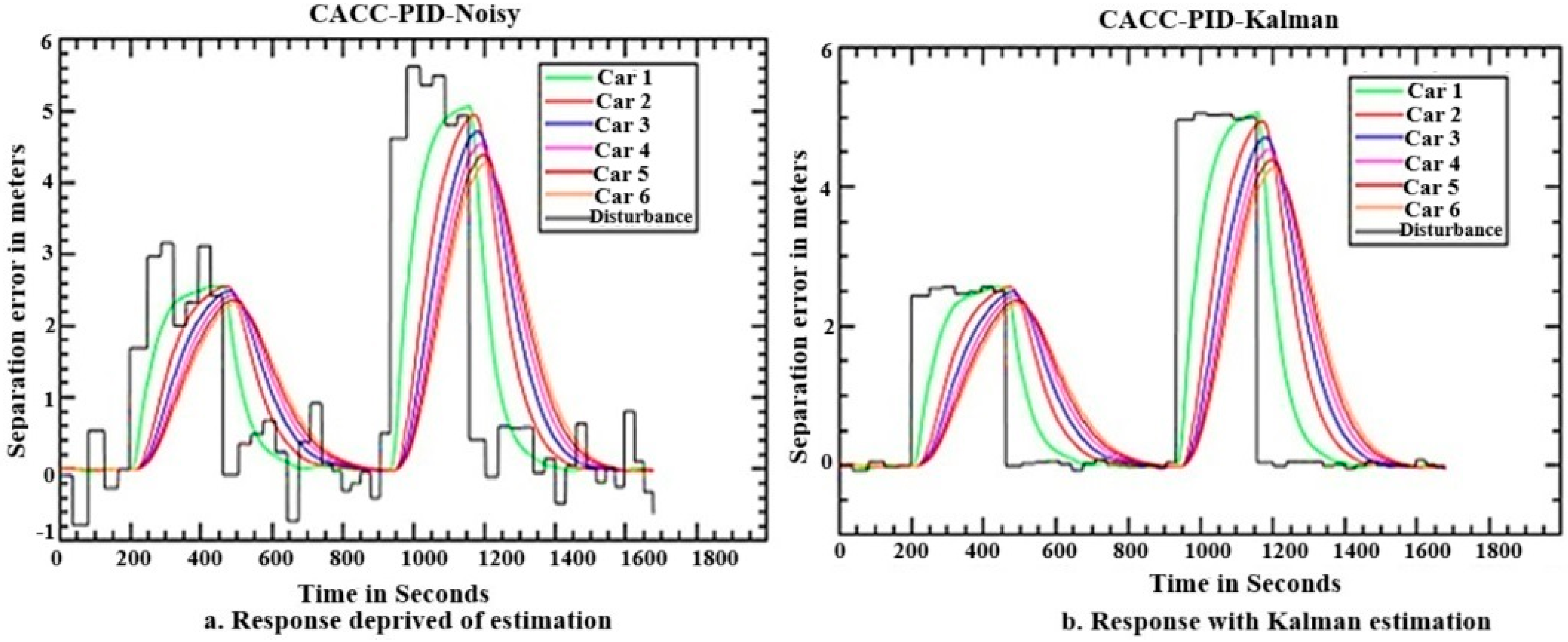
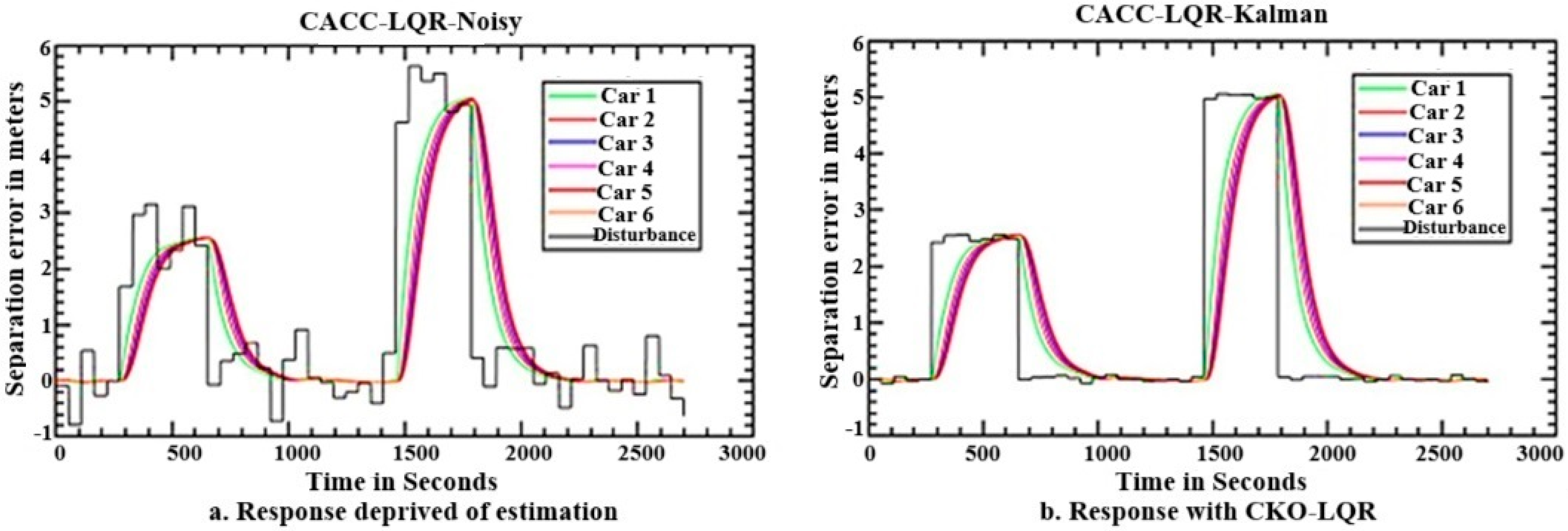
5.3. Performance of CKO-PID and CKO-LQR in a Platoon
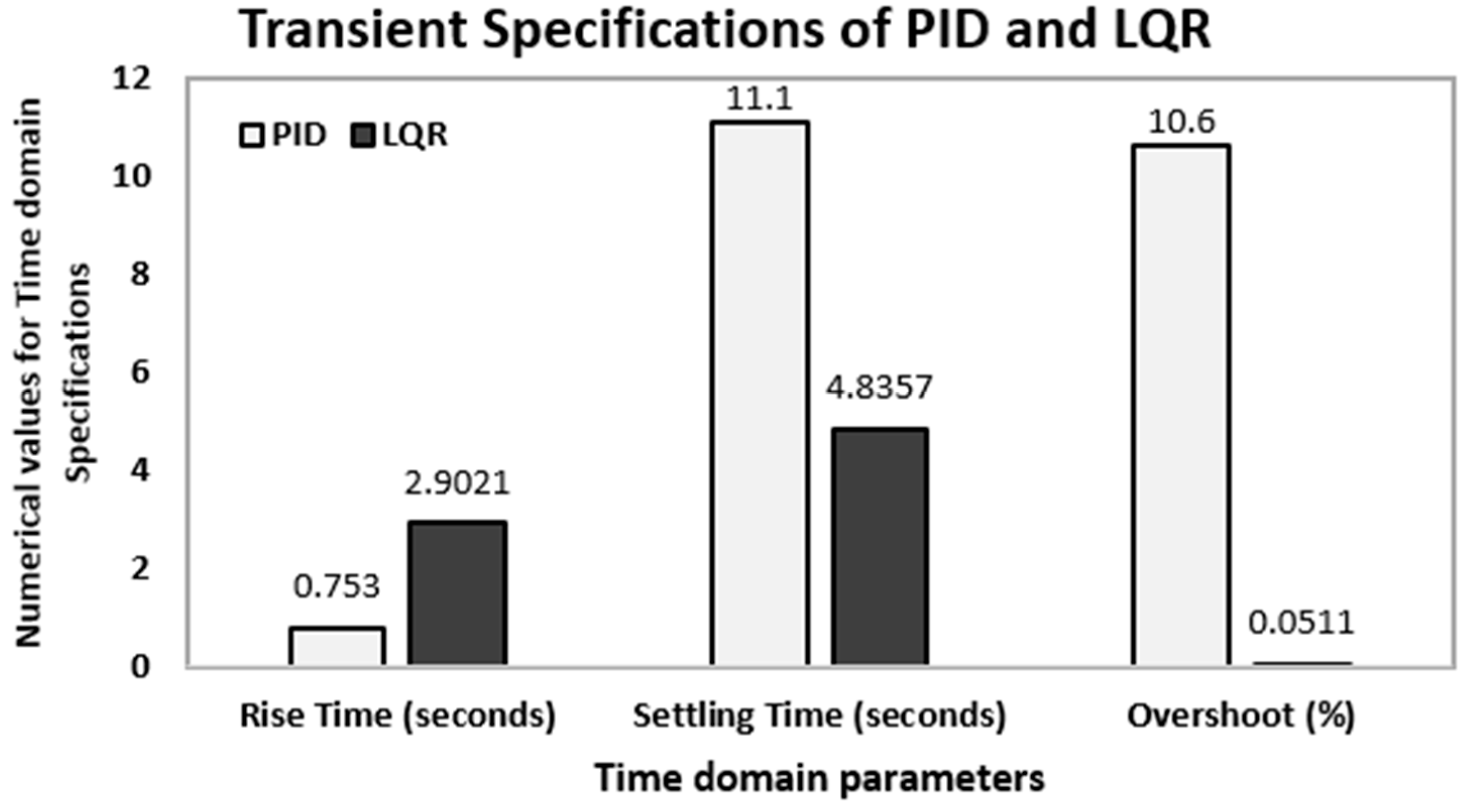
5.4. Comparison of Time-Domain Responses of PID and LQR
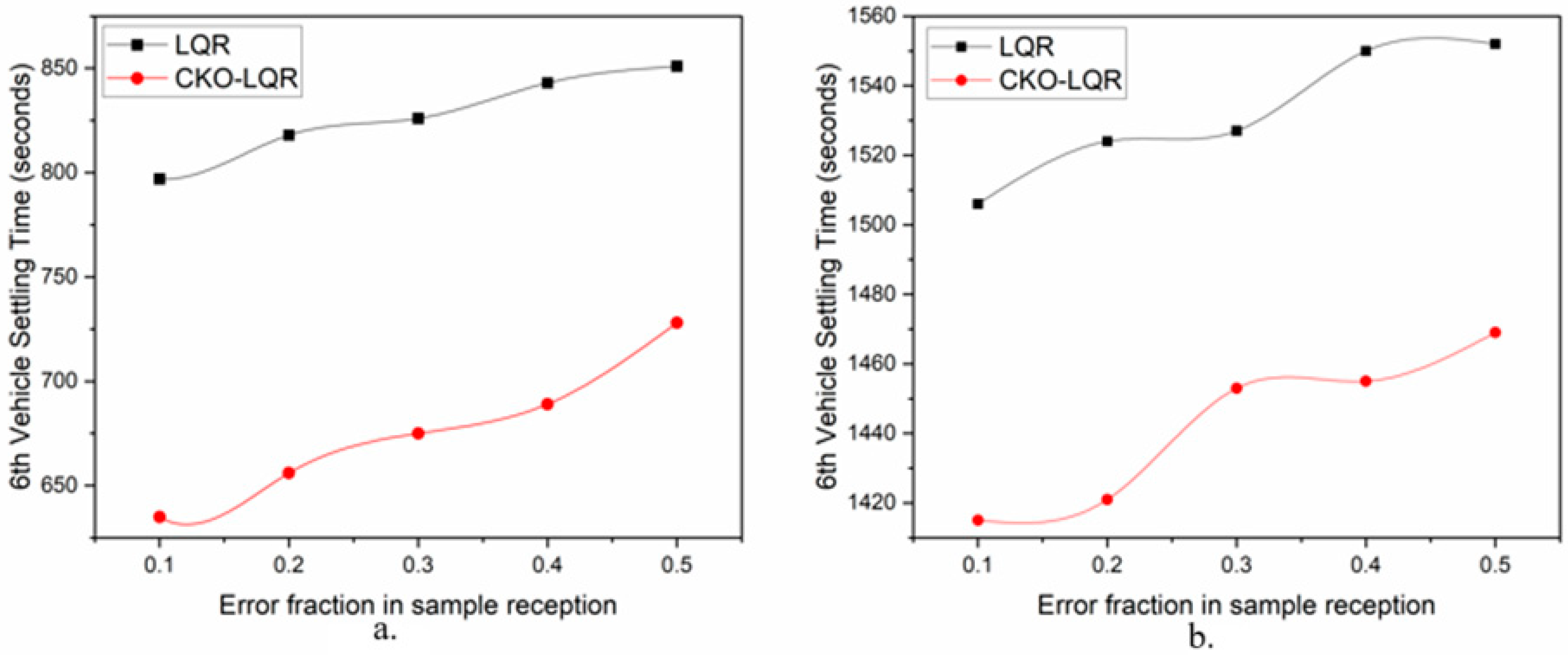
5.5. Performance of CKO-LQR in the 6th Vehicle
6. Conclusions
- The PID and LQR controllers are designed to form a platoon.
- The experimental results show that LQR offers faster settling under disturbance over the PID controller.
- A CKO-LQR is proposed to estimate platoon velocity in a noisy wireless medium.
- CKO outperforms conventional controllers even in the presence of communication errors and uncertainties.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, F.; Wang, J.; Zhu, S.; Gelbal, S.Y.; Yang, Y.; Aksun-Guvenc, B.; Guvenc, L. Distributed Control of Cooperative Vehicular Platoon with Nonideal Communication Condition. IEEE Trans. Veh. Technol. 2020, 69, 8207–8220. [Google Scholar] [CrossRef]
- Ju, Z.; Zhang, H.; Tan, Y. Distributed Deception Attack Detection in Platoon-Based Connected Vehicle Systems. IEEE Trans. Veh. Technol. 2020, 69, 4609–4620. [Google Scholar] [CrossRef]
- Liu, D.; Baldi, S.; Hirche, S. Collision Avoidance in Longitudinal Platooning: Graceful Degradation and Adaptive Designs. IEEE Control Syst. Lett. 2023, 7, 1694–1699. [Google Scholar] [CrossRef]
- Hidayatullah, M.R.; Juang, J.C. Centralized and distributed control framework under homogeneous and heterogeneous platoon. IEEE Access 2021, 9, 49629–49648. [Google Scholar] [CrossRef]
- Flores, C.; Merdrignac, P.; De Charette, R.; Navas, F.; Milanes, V.; Nashashibi, F. A Cooperative Car-Following/Emergency Braking System with Prediction-Based Pedestrian Avoidance Capabilities. IEEE Trans. Intell. Transp. Syst. 2019, 20, 1837–1846. [Google Scholar] [CrossRef]
- Rosenstatter, T.; Englund, C. Modelling the Level of Trust in a Cooperative Automated Vehicle Control System. IEEE Trans. Intell. Transp. Syst. 2018, 19, 1237–1247. [Google Scholar] [CrossRef]
- Groelke, B.; Earnhardt, C.; Borek, J.; Vermillion, C. A Predictive Command Governor-Based Adaptive Cruise Controller With Collision Avoidance for Non-Connected Vehicle Following. IEEE Trans. Intell. Transp. Syst. 2022, 23, 12276–12286. [Google Scholar] [CrossRef]
- Tian, B.; Deng, X.; Xu, Z.; Zhang, Y.; Zhao, X. Modeling and Numerical Analysis on Communication Delay Boundary for CACC String Stability. IEEE Access 2019, 7, 168870–168884. [Google Scholar] [CrossRef]
- Nandhini, M.; Mohamed Rabik, M. A new spacing policy in a platoon using extremum-seeking controller on an anti-lock braking system. Trans. Inst. Meas. Control July 2024. [Google Scholar] [CrossRef]
- Wang, Z.; Gao, Y.; Fang, C.; Liu, L.; Zeng, D.; Dong, M. State-Estimation-Based Control Strategy Design for Connected Cruise Control with Delays. IEEE Syst. J. 2023, 17, 99–110. [Google Scholar] [CrossRef]
- Dahal, P.; Mentasti, S.; Arrigoni, S.; Braghin, F.; Matteucci, M.; Cheli, F. Extended Object Tracking in Curvilinear Road Coordinates for Autonomous Driving. IEEE Trans. Intell. Veh. 2023, 8, 1266–1278. [Google Scholar] [CrossRef]
- Deng, Q. A General Simulation Framework for Modeling and Analysis of Heavy-Duty Vehicle Platooning. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3252–3262. [Google Scholar] [CrossRef]
- Hussain, R.; Zeadally, S. Autonomous cars: Research results issues and future challenges. In IEEE Communications Surveys & Tutorials; IEEE: New York, NY, USA, 2019; Volume 21, pp. 1275–1313. [Google Scholar]
- Zhou, Z.; Li, L.; Qu, X.; Ran, B. PACC: A platoon-based adaptive cruise control strategy based on leader-following information topology to mitigate traffic oscillations under CAV environment. Phys. A Stat. Mech. Its Appl. 2024, 654, 130117. [Google Scholar] [CrossRef]
- Viadero-Monasterio, F.; Meléndez-Useros, M.; Jiménez-Salas, M.; Boada, B.L. Robust adaptive heterogenous vehicle platoon control based on disturbances estimation and compensation. IEEE Access 2024, 12, 96924–96935. [Google Scholar] [CrossRef]
- Chaurasia, V.; Tiwari, A.N.; Tripathi, S.M. Optimal hybrid strategy in adaptive cruise control system for enhanced autonomous vehicle stability and safety. Comput. Electr. Eng. 2024, 118, 109377. [Google Scholar] [CrossRef]
- Liang, Y.; Dong, H.; Li, D.; Song, Z. Adaptive eco-cruising control for connected electric vehicles considering a dynamic preceding vehicle. eTransportation 2024, 19, 100299. [Google Scholar] [CrossRef]
- Jiang, Y.; Cong, H.; Chen, H.; Wu, Y.; Yao, Z. Adaptive cruise control design for collision risk avoidance. Phys. A Stat. Mech. Its Appl. 2024, 640, 129724. [Google Scholar] [CrossRef]
- Lopez, J.; Sanchez-Vilarino, P.; Sanz, R.; Paz, E. Efficient Local Navigation Approach for Autonomous Driving Vehicles. IEEE Access 2021, 9, 79776–79792. [Google Scholar] [CrossRef]
- Mwaffo, V.; Curry, J.S.; Iudice, F.L.; De Lellis, P. Pause-and-Go Self-Balancing Formation Control of Autonomous Vehicles Using Vision and Ultrasound Sensors. IEEE Trans. Control Syst. Technol. 2021, 29, 2299–2311. [Google Scholar] [CrossRef]
- Djouadi, H.; Ouari, K.; Belkhier, Y.; Lehouche, H. Real-Time HIL Simulation of Nonlinear Generalized Model Predictive-Based High-Order SMC for Permanent Magnet Synchronous Machine Drive. Int. Trans. Electr. Energy Syst. 2024, 2024, 5536555. [Google Scholar] [CrossRef]
- Guo, G.; Li, P.; Hao, L.Y. A New Quadratic Spacing Policy and Adaptive Fault-Tolerant Platooning with Actuator Saturation. IEEE Trans. Intell. Transp. Syst. 2022, 23, 1200–1212. [Google Scholar] [CrossRef]
- Lan, J.; Zhao, D.; Tian, D. Data-Driven Robust Predictive Control for Mixed Vehicle Platoons Using Noisy Measurement. IEEE Trans. Intell. Transp. Syst. 2023, 24, 6586–6596. [Google Scholar] [CrossRef]
- Dutta, R.G.; Hu, Y.; Yu, F.; Zhang, T.; Jin, Y. Design and Analysis of Secure Distributed Estimator for Vehicular Platooning in Adversarial Environment. IEEE Trans. Intell. Transp. Syst. 2022, 23, 3418–3429. [Google Scholar] [CrossRef]
- Devika, K.B.; Rohith, G.; Yellapantula VR, S.; Subramanian, S.C. A Dynamics-Based Adaptive String Stable Controller for Connected Heavy Road Vehicle Platoon Safety. IEEE Access 2020, 8, 209886–209903. [Google Scholar] [CrossRef]
- Guo, G.; Li, P.; Hao, L.Y. Adaptive Fault-Tolerant Control of Platoons with Guaranteed Traffic Flow Stability. IEEE Trans. Veh. Technol. 2020, 69, 6916–6927. [Google Scholar] [CrossRef]
- Dey, K.C.; Yan, L.; Wang, X.; Wang, Y.; Shen, H.; Chowdhury, M.; Yu, L.; Qiu, C.; Soundararaj, V. A Review of Communication, Driver Characteristics, and Controls Aspects of Cooperative Adaptive Cruise Control (CACC). IEEE Trans. Intell. Transp. Syst. 2016, 17, 491–509. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, K.; Ma, S.; Sun, L.; Gao, W.; Dong, Z. Improved Linear Quadratic Regulator Lateral Path Tracking Approach Based on a Real-Time Updated Algorithm with Fuzzy Control and Cosine Similarity for Autonomous Vehicles. Electronics 2022, 11, 3703. [Google Scholar] [CrossRef]
- Coppola, A.; Lui, D.G.; Petrillo, A.; Santini, S. Eco-Driving Control Architecture for Platoons of Uncertain Heterogeneous Nonlinear Connected Autonomous Electric Vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 24220–24234. [Google Scholar] [CrossRef]
- Zhang, H.; Li, L.; Xu, J.; Fu, M. Linear quadratic regulation and stabilization of discrete-time systems with delay and multiplicative noise. IEEE Trans. Autom. Control 2015, 60, 2599–2613. [Google Scholar] [CrossRef]
- Harfouch, Y.A.; Yuan, S.; Baldi, S. An adaptive switched control approach to heterogeneous platooning with intervehicle communication losses. IEEE Trans. Control Netw. Syst. 2018, 5, 1434–1444. [Google Scholar] [CrossRef]
- Stankovic, S.S.; Stanojevic, M.J.; Siljak, D.D. Decentralized overlapping control of a platoon of vehicles. IEEE Trans. Control. Syst. Technol. 2000, 8, 816–832. [Google Scholar] [CrossRef]
- Feng, S.; Zhang, Y.; Li, S.E.; Cao, Z.; Liu, H.X.; Li, L. String stability for vehicular platoon control: Definitions and analysis methods. Annu. Rev. Control 2019, 47, 81–97. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, B.; Yu, L.; Ho, D.W.C. Distributed Kalman Filtering for Interconnected Dynamic Systems. IEEE Trans. Cybern. 2022, 52, 11571–11580. [Google Scholar] [CrossRef]
- Sun, C.; Vianney, J.M.U.; Li, Y.; Chen, L.; Li, L.; Wang, F.-Y.; Khajepour, A.; Cao, D. Proximity based automatic data annotation for autonomous driving. IEEE/CAA J. Autom. Sin. 2020, 7, 395–404. [Google Scholar] [CrossRef]
- Da Silva, G.R.G.; Bazanella, A.S.; Lorenzini, C.; Campestrini, L. Data-Driven LQR Control Design. IEEE Control Syst. Lett. 2019, 3, 180–185. [Google Scholar] [CrossRef]
- Kanieski, J.M.; Tambara, R.V.; Pinheiro, H.; Cardoso, R.; Grundling, H.A. Robust Adaptive Controller Combined With a Linear Quadratic Regulator Based on Kalman Filtering. IEEE Trans. Autom. Control 2016, 61, 1373–1378. [Google Scholar] [CrossRef]
- Li, X.; Guvenc, L.; Aksun-Guvenc, B. Vehicle State Estimation and Prediction for Autonomous Driving in a Round Intersection. Vehicles 2023, 5, 1328–1352. [Google Scholar] [CrossRef]
- Ghahestani, M.; Vali, A.; Siahi, M.; Moarefianpour, A. Stabilization of an Uncertain Maglev Train System Using Finite Time Adaptive Back-stepping Controller. Int. J. Control Autom. Syst. 2024, 22, 744–752. [Google Scholar] [CrossRef]
- Wei, C. Modeling and Simulation of Active Half-vehicle Suspension Based on a New Output-feedback H∞ Controller. Int. J. Control Autom. Syst. 2024, 22, 775–784. [Google Scholar] [CrossRef]
- Zhao, C.; Cai, L.; Cheng, P. Stability Analysis of Vehicle Platooning with Limited Communication Range and Random Packet Losses. IEEE Internet Things J. 2021, 8, 262–277. [Google Scholar] [CrossRef]
- Prakash, N.P.S.; Horowitz, R. Data-Driven Robust Feedback Control Design for Multi-Actuator Hard Disk Drives. IFAC-PapersOnLine 2022, 55, 131–138. [Google Scholar] [CrossRef]
- Viadero-Monasterio, F.; Alonso-Rentería, L.; Pérez-Oria, J.; Viadero-Rueda, F. Radar-Based Pedestrian and Vehicle Detection and Identification for Driving Assistance. Vehicles 2024, 6, 1185–1199. [Google Scholar] [CrossRef]
- Wang, B.; Liao, Z.; Guo, S. Adaptive Curve Passing Control in Autonomous Vehicles with Integrated Dynamics and Camera-Based Radius Estimation. Vehicles 2024, 6, 1648–1660. [Google Scholar] [CrossRef]
- Jee, G.; Yalagach, A.; Brinda, V.; Lalithambika, V.; Dhekane, M.V. Controller Design for Lateral Dynamics of Reusable Launch Vehicle by H-infinity Mixed Sensitivity approach. IFAC Proc. Vol. 2014, 47, 171–175. [Google Scholar] [CrossRef]
- Kassarian, E.; Sanfedino, F.; Alazard, D.; Montel, J.; Chevrier, C.A. Robust integrated control/structure co-design for stratospheric balloons. IFAC-PapersOnLine 2022, 55, 13–18. [Google Scholar] [CrossRef]
- Monnet, D.; Ninin, J.; Clement, B. Robust structured H2 synthesis for linear systems subject to time-invariant uncertainties with global optimization. IFAC-PapersOnLine 2021, 54, 341–347. [Google Scholar] [CrossRef]
- Lian, J.; Dimirovski, G.M.; Zhao, J. Switched Uncertain Linear Systems Control by Robust H∞ Smc Synthesis1. IFAC Proc. Vol. 2007, 40, 78–83. [Google Scholar] [CrossRef]
- Furenes, B.; Lie, B. Robust Control of a Solidification Process with Parametric Uncertainty. IFAC Proc. Vol. 2007, 40, 225–230. [Google Scholar] [CrossRef]
| Parameters | Values |
|---|---|
| Mass of the vehicle (in kg) | 1049 |
| Radius of the wheel (in m) | 0.33 |
| Moment of Inertia (I) | 0.5 × (1049) × (0.332) |
| Acc. due to gravity (g in ms−2) | 9.81 |
| Velocity (V0 in ms−1) | 13.889/20.833/27.778 |
| Specifications | Values |
|---|---|
| P | 0.1342 |
| I | 0.0015782 |
| D | 1.9203 |
| N | 195.428 |
| Rise Time | 0.753 s |
| Settling Time | 11.1 s |
| Overshoot | 10.6% |
| Peak | 1.11 |
| Gain Margin | 40.1 dB @ 25.2 rad/s |
| Phase Margin | 60 deg @ 1.71 rad/s |
| Specifications | Values |
|---|---|
| Q | 100*eye (3) |
| R | 0.5 |
| Rise Time | 2.9021 s |
| Settling Time | 4.8357 s |
| Settling Min | 45.0828 s |
| Settling Max | 50.0255 s |
| Overshoot | 0.0511 |
| Undershoot | 0 |
| Transient Specifications | PID | LQR |
|---|---|---|
| Rise Time | 0.753 s | 2.9021 s |
| Settling Time | 11.1 s | 4.8357 s |
| Overshoot | 10.6% | 0.0511% |
| Error Fraction | Time Taken to Settling Down by nth Vehicle, Here 6th Vehicle (Seconds) | |||
|---|---|---|---|---|
| LQR | CKO-LQR | |||
| Disturbance I | Disturbance II | Disturbance I | Disturbance II | |
| 0.5 | 851 | 1552 | 728 | 1469 |
| 0.4 | 843 | 1550 | 689 | 1455 |
| 0.3 | 826 | 1527 | 675 | 1453 |
| 0.2 | 818 | 1524 | 656 | 1421 |
| 0.1 | 797 | 1506 | 635 | 1415 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murugan, N.; Mohamed Ismail, M.R. An Efficient Coordinated Observer LQR Control in a Platoon of Vehicles for Faster Settling Under Disturbances. World Electr. Veh. J. 2025, 16, 28. https://doi.org/10.3390/wevj16010028
Murugan N, Mohamed Ismail MR. An Efficient Coordinated Observer LQR Control in a Platoon of Vehicles for Faster Settling Under Disturbances. World Electric Vehicle Journal. 2025; 16(1):28. https://doi.org/10.3390/wevj16010028
Chicago/Turabian StyleMurugan, Nandhini, and Mohamed Rabik Mohamed Ismail. 2025. "An Efficient Coordinated Observer LQR Control in a Platoon of Vehicles for Faster Settling Under Disturbances" World Electric Vehicle Journal 16, no. 1: 28. https://doi.org/10.3390/wevj16010028
APA StyleMurugan, N., & Mohamed Ismail, M. R. (2025). An Efficient Coordinated Observer LQR Control in a Platoon of Vehicles for Faster Settling Under Disturbances. World Electric Vehicle Journal, 16(1), 28. https://doi.org/10.3390/wevj16010028






