Game-Based Vehicle Strategy Equalization Algorithm for Unsignalized Intersections

Abstract

To address the coordination issue of connected autonomous vehicles (CAVs) at unsignalized intersections, this paper proposes a game-theory-based distributed strategy equalization algorithm. To begin, the vehicles present in the scene are conceptualized as participants in a game theory. The decision-payoff function takes into account three critical performance indicators: driving safety, driving comfort, and driving efficiency. Then, virtual logic lines connect the front and rear extremities of vehicles with odd and even numbers at the intersection to create a virtual logic ring. By dividing the virtual logic ring into numerous overlapping game groups, CAVs can engage in negotiation and interaction within their respective game groups. This enables the revision of action strategies and facilitates interaction between the overlapping game groups. A further application of the genetic algorithm (GA) is the search for the optimal set of strategies in constrained multi-objective optimization problems. The proposed decision algorithm is ultimately assessed and certified through a collaborative simulation utilizing Python and SUMO. In comparison to the first-come, first-served algorithm and the cooperative driving model based on cooperative games, the average passing delay is decreased by 40.7% and 6.17%, respectively, resulting in an overall improvement in the traffic system’s passing efficiency.

1. Introduction

Traditional urban intersections regulate the flow of traffic using traffic signals to facilitate the orderly and efficient movement of vehicles and pedestrians within the intricate intersection setting. While this control method has the potential to enhance road safety and traffic efficiency to a certain degree, the incidence of intersection accidents in urban areas is concurrently escalating due to the rising traffic volume. From 2001 to 2010, over 20% of traffic accidents in European countries took place at intersections [1]. Meanwhile, in the United States [2], approximately 40% of accidents took place at intersections.

In urban intersections, drivers face various traffic disruptions and conflicts, making it extremely challenging to navigate complex urban traffic patterns. In addressing this issue, it is crucial to incorporate decision-making processes that enhance fuel efficiency and safety within the transportation system, particularly at intersections lacking traffic signals. The defining feature of an unsignalized intersection is the absence of traffic lights, resulting in ambiguity regarding the right of way for traffic flow [3]. Novel prospects arise from the implementation of wireless communication technology and autonomous driving technology to improve traffic flow management at urban intersections. Using vehicle-road collaboration technology, autonomous vehicles can regulate traffic flow at intersections lacking traffic signals. This is achieved through the integration of advanced vehicle-to-infrastructure (V2I), vehicle-to-vehicle (V2V), and vehicle-to-pedestrian (V2P) technologies. The technology mentioned is used to detect and collect data related to the surrounding environment and adjacent vehicles [4]. Through the implementation of these technologies, autonomous vehicles can collaborate with other vehicles in real-time communication and make decisions, therefore facilitating their navigation of the right of way at uncontrolled intersections. In this process, the autonomous vehicle navigates the intersection area by employing speed guidance and other strategies to avoid conflicts over space and time resources with other vehicles. This enables the vehicle to cross the intersection safely and efficiently without the need to come to a stop.

1.1. Related Work

Researchers have employed a variety of approaches to investigate how vehicles interact when making decisions at intersections. These approaches can be broadly divided into two categories:

Centralized Management Approach: The coordination and optimization of scheduling for all vehicles rely on V2I communication technology to exchange information and interaction. The central processor within the system establishes the optimal path for each vehicle to navigate the control area [5]. Dongxin et al. [6] proposed a priority tree-based method for vehicle coordination at unsignalized intersections. The results of the simulation demonstrate that the proposed algorithm not only prevents vehicle collisions but also increases the intersection’s efficiency. The centralized management approach improves traffic efficiency. The rise in the number of vehicles is associated with a growth in computing complexity, leading to challenges concerning dependability and robustness [7].

Distributed Management Approach: The CAVs depend on the V2X network for collaborative decision-making, operating without a central controller [8,9]. This strategy encompasses rule-based, model-based, data-driven, and game-theoretic approaches. The rule-based strategy stands out as the most straightforward and comprehensible among all strategies. A collision graph tree search (CGTS) algorithm is used for vehicle traffic management at unsignalized intersections. In addition, a motion control strategy based on a heuristic threshold is proposed to control the vehicles to arrive at the intersection at the specified time [10]. Despite this, strategies based on rules are incapable of ensuring safe and efficient driving in intricate traffic scenarios. Additionally, model-based approaches are frequently employed. To enhance safety and efficiency, Zheng et al. [11] employed a composite spring model to evaluate the level of driving risk, aiding in the decision-making process regarding driving behavior. The model was subsequently tested and validated at a T-shaped intersection. The test results indicated that the behavioral decision-making model was able to consistently avert collision incidents while ensuring a specific level of efficiency. The effectiveness of learning-based systems is contingent upon the quantity and quality of the dataset, which are commonly referred to as data-driven approaches [12]. Zhang et al. [13] for the decision-making process of self-driving cars at unsignalized T-intersections. In general, learning-based solutions are more appropriate for addressing complex dynamic situations. Despite this, the training of learning-based techniques is expensive and demands significant effort to attain semantic interpretation [14].

Moreover, techniques grounded in game theory have proven to be superior and effective in modeling vehicle interactions and decision-making. Tian et al. [15] describe a level-k-based game theory framework that integrates game theory, backward horizon optimization, and imitation learning to obtain control strategies for urban environments with unsignalized intersections. Chen et al. [16] constructed a model for resolving conflicts involving intelligent vehicles by integrating game theory and fuzzy logic. Simulation investigations have validated the decision model’s efficacy and dependability. Hang et al. [17] employed cooperative game methods in the development of cooperative decision frameworks. This process entails the consideration of comfort, safety, and driving efficiency, incorporating a range of driving style features into decision algorithms. The test results illustrate the potential of this method, which entails making logical choices, to improve driving performance and safety.

1.2. Contribution

While numerous scholars have employed diverse methods to address the issue of the vehicle-interaction decision-making problem at unsignalized intersections, the aspect of optimality in vehicle strategy selection is seldom taken into account. Consequently, a proposed solution addresses the issue of vehicle-interaction decision-making at unsignalized intersections to guarantee the optimality of strategies in the decision-making process concerning vehicle interactions. The primary contributions of this paper are:

(1)

The study considers three distinct performance metrics: driving safety, driving comfort, and driving efficiency. Additionally, various constraints are established to formulate a strategy payoff function for vehicles.

(2)

A virtual logic ring is established for vehicles operating at unsignalized intersections, and a virtual game group is segmented. Subsequently, the strategy deviation function is formulated and integrated with the strategy payoff function to address the cooperative decision-making challenges encountered by CAVs at unsignalized intersections.

(3)

This work presents a distributed vehicle strategy equalization technique that is based on cooperative game theory and is implemented using a genetic algorithm. The algorithm is ultimately compared with two additional algorithms. The results indicate that the algorithm suggested has the potential to enhance intersection traffic efficiency and alleviate traffic delays.

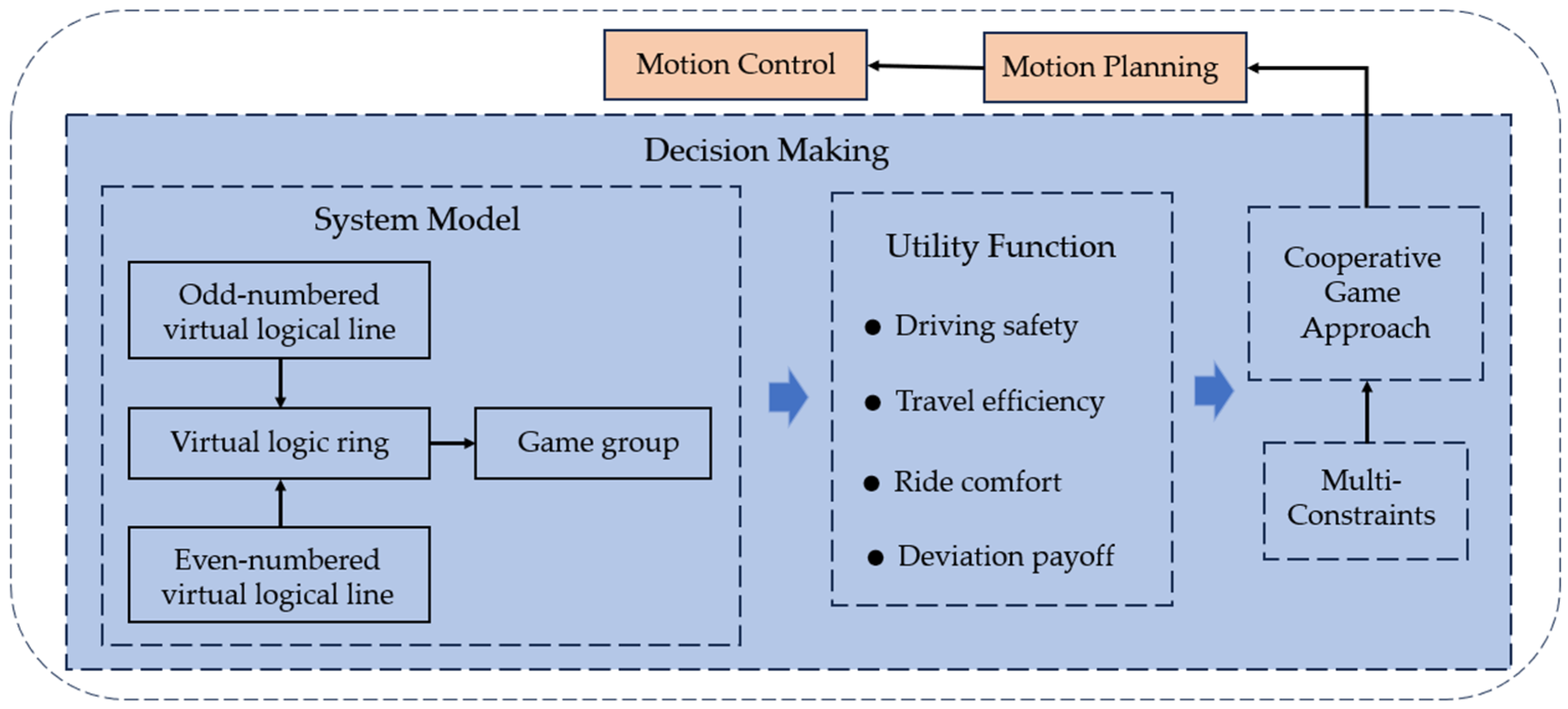
This study presents a distributed game equilibrium algorithm based on game theory to tackle the interactive game dilemma that emerges as vehicles navigate signal-less intersections. The algorithm creates a closed virtual logic ring, divides a collection of interconnected game groups on it, and designates all vehicles in the unsignalized intersection scenario as participants. The text further outlines three performance indicators: driving efficiency, driving safety, and comfort. Through the implementation of this methodology, vehicles participate in an ongoing exchange of strategic information within the virtual logic loop. They revise and adjust their strategies in response to feedback received, ultimately converging to the Nash equilibrium state.

This paper is organized as follows: Section 2 introduces the system model, establishes the unsignalized intersection scenario, and deduces the vehicle decision income function from three different perspectives. Section 3 introduces equalization algorithm strategies that rely on virtual logical rings. Section 4 uses segmented virtual game groups to construct the deviation income function and applies it together with the decision income function to address the vehicle cooperative decision problem. Section 5 delineates the experimental parameters and discusses the experimental results. Finally, Section 6 is the summary of this article.

2. System Model

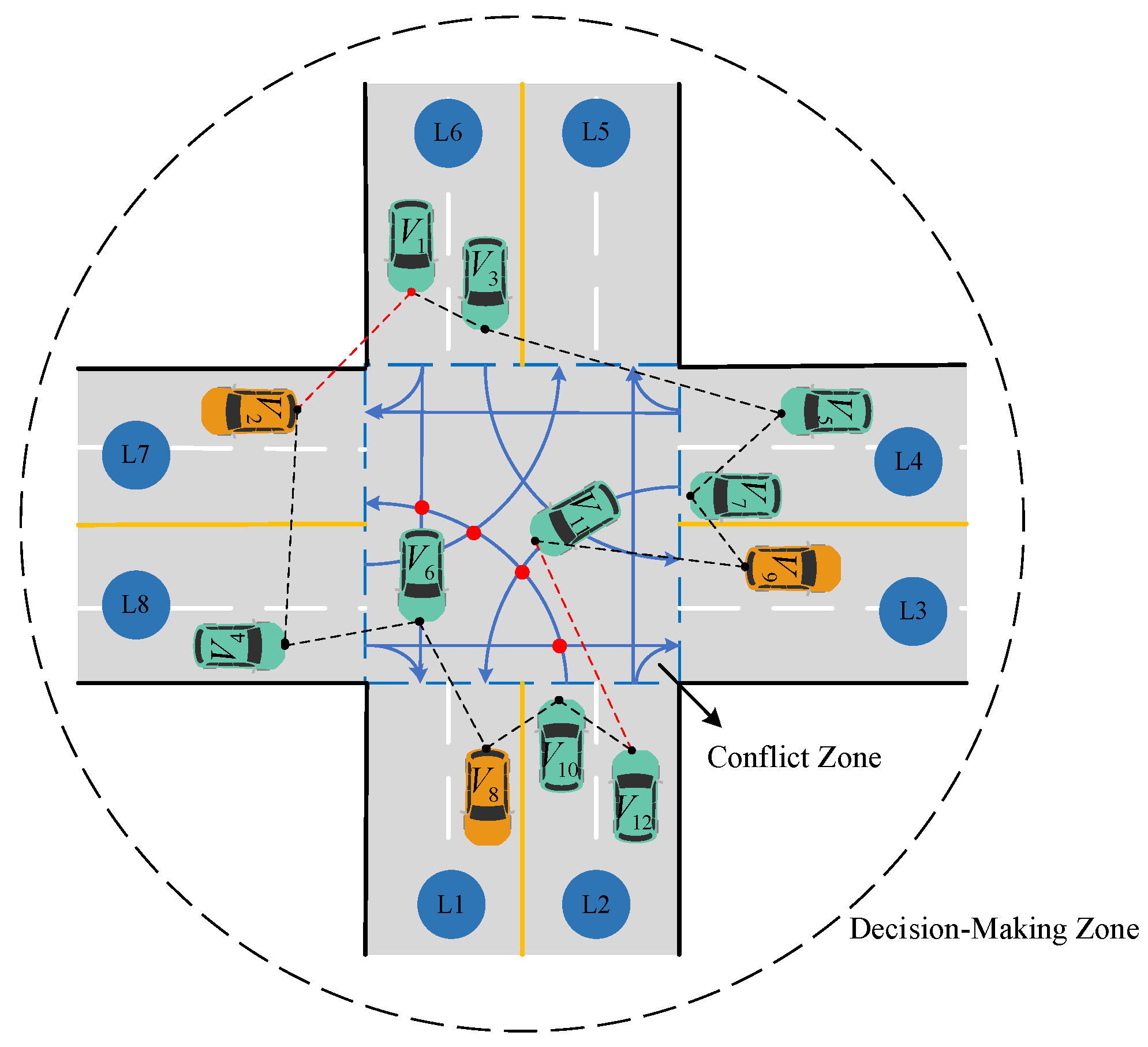
As depicted in Figure 1, consider an unsignalized intersection scenario where n vehicles coexist concurrently. Each vehicle is a Connected Automated Vehicle (CAV) capable of interacting and exchanging vehicle state information, such as position, speed, and driving intent, via a V2X network. The concept of a decision region with a radius R is introduced to encompass a broad spectrum of areas where spatio-temporal conflicts may arise while vehicles are in transit. The linear network topology of intelligent vehicles is depicted through an undirected graph $G=\left(V,L\right)$, where the set $V=\left\{V_i|i\le n,i\in N^{+}\right\}$ represents the vehicles within the intersection region, and the set $L=\left\{l_{ij}|V_i,V_j\in V\right\}$ signifies the wireless communication link between vehicles $V_i$ and $V_j$.

In the unsignalized intersection scenario shown in Figure 1, there is a conflict area and eight dual lanes labeled L1–L8 in a counterclockwise direction. These vehicles are equipped with autonomous decision-making capabilities, enabling them to make informed decisions and execute actions based on environmental cues and predetermined objectives once they have entered the decision-making zone, as illustrated by the green vehicles. Once the vehicle starts moving away from the conflict area, as indicated by the yellow vehicle, it is categorized as a moving-away vehicle. This type of vehicle maintains a safe distance from other vehicles until it exits the decision area. Every vehicle within the intersection region makes use of the V2X network to communicate with neighboring vehicles, share information regarding their operational statuses and perceived local road conditions, and follow the designated route, which is visually represented by the solid blue line. Nevertheless, during the interaction game among vehicles, various conflict points are evident, illustrated by the red dots, which may lead to instances of conflict and deadlock. Furthermore, with the rise in the number of vehicles, ensuring vehicle safety becomes increasingly challenging, leading to a notable decrease in intersection passing efficiency. To address the collaborative decision-making issue faced by CAVs at unsignalized intersections, this paper presents the development of a game theory decision-making framework, which is visually represented in Figure 2.

In the context of an unsignalized intersection scenario, a coordinated set of decision strategies denoted as $U^t=\left\{u_1^t,u_2^t,\cdots ,u_n^t\right\}$, encompasses all the strategies that must be implemented by the vehicles at a given time $t$. The decision strategy $a_i^t$ represents the specific strategy that must be implemented by vehicle $V_i$ at time $t$, denoted as $u_i^t=a_i^t$. The strategy space of a vehicle is defined as the collection of all feasible decision strategies, denoted as $U_i=\left\{u_i^t|i\in V,t=0,1,2,\cdots \right\}$.

Definition 1 (Driving Safety Index). 

Let $v_i^t$ denote the traveling speed of the vehicle, $a_i^t$ represents the acceleration of the vehicle $V_i$, and $L_i^t$ be the distance of vehicle $V_i$ from the conflict point. Define the time for vehicle $V_i$ to reach the conflict point as depicted in Equation (1):

$$T_i=\sqrt{{\left(\frac{v_i^t}{a_i^t}\right)}^2+\frac{2L_i^t}{a_i^t}}-\frac{v_i^t}{a_i^t}$$

(1)

The formula used to determine the distance between vehicle $V_i$ and the conflict point is as follows:

$$L_i^t=\sqrt{{(x_i^t-x_{cpk}^t)}^2+{(y_i^t-y_{cpk}^t)}^2}-L_v$$

(2)

where: $\left(x_i^t,y_i^t\right)$ represents the coordinate position of vehicle $V_i$ at time $t$; $\left(x_{cpk}^t,y_{cpk}^t\right)$ denotes the coordinate position of the k-th conflict point of vehicle $V_i$ along the driving route; $L_v$ denotes a safety factor that considers the length of the vehicle.

Based on Formula (1), the moment at which vehicle $V_j$ arrives at the k-th conflict point can be determined similarly. The driving safety index is defined as the Time Difference to Collision (TDTC) between vehicle $V_i$ and $V_j$, as depicted in Formula (3):

$$s_{i\sim cp}^t=|T_i-T_j|$$

(3)

Among these vehicles, vehicle $V_i$ is identified as having multiple conflict points along its driving path. To assess the potential conflicts between vehicles, Time-to-Collision (TTC) is chosen as the criterion, formulated as:

$$\left|\frac{L_i^t}{v_i^t}-\frac{L_j^t}{v_j^t}\right|<T_M$$

(4)

The variable $T_M$ represents the threshold used to assess the potential conflict between vehicles. The validity of the formula mentioned above indicates the presence of a potential collision risk between two vehicles.

TDTC is primarily established to address cross-conflicts and confluent conflicts within conflict zones. Assuming that vehicle $V_i$ has m conflict points on its driving path, the safety index of the vehicle at the j-th conflict point can be further defined as:

$$s_i^t=e^j\cdot s_{i\sim cp}^t$$

(5)

where the vector $e^j={\left[0,0,\cdots ,1,\cdots ,0\right]}_{m\times 1}^T$, at the j-th conflict point, the elements are 1 and the others are 0. If potential conflicts exist at other conflict points according to Formula (4), the element is 1.

Definition 2 (Travel Efficiency Index). 

Travel Efficiency Index $e_i^t$ is defined as a function of vehicle speed. The speed of a vehicle $V_i$ at time $t+1$ is denoted as $v_i^{t+1}$, where the maximum driving speed is represented by $v_i^{max}$. The driving efficiency index is expressed as:

$$e_i^t=1/\left[\left(v_i^{t+1}-v_i^{\max }\right)+\epsilon \right]$$

(6)

where the parameter$\epsilon$represents a minuscule value, ensuring that the denominator does not approach zero.

Definition 3 (Comfort Index). 

Driving comfort is associated with the rate of acceleration of the vehicle, which is defined as the change in the vehicle over some time $\Delta t$, as depicted below:

$$c_i^t=1/\left[\left|a_i^t-a_i^{t-1}\right|+\epsilon \right]$$

(7)

The decision-payoff function considers three performance indicators and the strategy payoff in the interactive game of vehicle $V_i$ is expressed as follows:

$$\begin{array}{c}{J}_i=\alpha f\left(s_i^t\right)+\beta f\left(e_i^t\right)+\gamma f\left(c_i^t\right)\\ s.t.\hspace{1em}{v}_i^{\min }\le v_i^t\le v_i^{\max },\forall i\in V\\ \hspace{1em}\hspace{1em}{a}_i^{\min }\le a_i^t\le a_i^{\max },\forall i\in V\\ \frac{d{a}_i^t}{dt}\ne 0,\forall i\in V\\ \left|\left(x_i^t,y_i^t\right)-\left(x_j^t,y_j^t\right)\right|\ge d,\forall i,j\in V\end{array}$$

(8)

where: $\alpha$, $\beta$, and $\gamma$ are used as weight coefficients, while the function $f\left(·\right)$ represents a normalization operation that applies zero mean normalization. Constraints limit the allowable range of vehicle speed and acceleration, and stipulate that vehicle acceleration should not occur abruptly. $\left(x_i^t,y_i^t\right)$ and $\left(x_j^t,y_j^t\right)$ denote the locations of vehicles $V_i$ and $V_j$ at time $t$, respectively. The variable d represents the minimum safe distance necessary to maintain a safe distance between vehicles.

3. Vehicle Strategy Equalization Algorithm

This paper introduces an algorithm for distributed vehicle strategy equalization. In the unsignalized intersection scenario, vehicles are allocated unique numerical identifiers upon entering the decision-making zone. Subsequently, a virtual logic ring is established among the vehicles within the intersection area, which is segmented into multiple intersecting game groups. Within these game groups, collaborative decisions are reached among vehicles, leading to the attainment of Nash equilibrium through the interaction and adjustment of strategies among neighboring game groups.

Once the vehicle reaches the decision area, a unique identification number is assigned to each vehicle. First, odd-numbered vehicles are sequentially linked in a virtual logical line, while even-numbered vehicles are processed similarly. Finally, the two virtual logic lines are interconnected end-to-end to create a closed virtual logic ring, as illustrated in Figure 1.

In Figure 1, only 12 vehicles are included in the decision area. As illustrated in Figure 1, the vehicles in the virtual logic line comprised of odd numbers are sequentially labeled from $V_1$ to $V_{11}$, while the vehicles in the virtual logic line formed by even numbers are sequentially labeled from $V_2$ to $V_{12}$. Furthermore, vehicles $V_1$ and $V_2$, as well as $V_{12}$ and $V_{11}$, are interconnected, forming a virtual logic ring with two virtual logic lines. Based on the concept of the virtual logic ring, the vehicles within it are categorized into overlapping game groups, with each group consisting of three vehicles. In the context of the game group, the terms “first car”, “middle car”, and “last car” refer to the vehicles in their respective positions within the sequence. In the depicted scenario illustrated in Figure 1, the game groups are segregated into $\left\{\left(V_1,V_3,V_5\right),\left(V_3,V_5,V_7\right),\right.\left(V_5\right., \left.V_7,V_9\right),\left(V_7,V_9,V_{11}\right),\left(V_9,V_{11},\right.$$\left.V_{12}\right)\left(V_{11},\right.\left.V_{12},V_{10}\right),\left(V_{12},V_{10},V_8\right),\left(V_{10},V_8,V_6\right),\left(V_8,V_6,V_4\right),\left(V_6,V_4,V_2\right), \left.\left(V_4\right.,V_2,\left.V_1\right),\left(V_2,V_1,V_3\right)\right\}$.

Following the establishment of the virtual logic ring, vehicles engage in interactions and negotiations concerning strategic information within their respective game groups. Subsequently, this information is disseminated to other vehicles within the virtual logic ring to attain a state of strategic equilibrium. In the specified procedure, vehicle $V_i$ assumes the position of the front car within the game group while $V_j$ and $V_k$ function as the middle and trailing cars in the same game group. Likewise, $V_j$ can be seen as the middle car within the latter game group, while $V_k$ can be seen as the trailing car in the latter game group. By segmenting the intersecting game groups, the vehicles can transmit information for navigation within the virtual logic loop. Moreover, each vehicle acquires the status and strategic information of other vehicles. Through ongoing information transmission and interaction, vehicles will autonomously adjust and refresh their strategic information, ultimately attaining a state of strategic equilibrium among all vehicles.

4. Cooperative Decision-Making Based on Cooperative Game

In a distributed communication environment, intelligent vehicles are limited to acquiring only partial information, which may result in deviations in strategy and incomplete decision-making. In response to these challenges, a cooperative strategy is implemented to facilitate collaborative decision-making. The strategy set $B_i^t$ is assumed to be formulated at time $t$ after the vehicle enters the decision region. The set consists of two components: the first part is the strategy proposal $S_i^t$, which includes its own strategy $s_{ii}^t$ and the strategy proposal $s_{ij}^t$ for other vehicles; the second part is the bidding proposal $P_i^t$ corresponding to each strategy proposal. The priority of the strategy proposal increases with the increase in the bid proposal $p_{ij}^t$ associated with the strategy proposal $s_{ij}^t$.

A virtual logic loop is established among vehicles within the intersection area, enabling the transmission of each vehicle’s policy set $B_i^t,i\in V$ after its generation by the vehicle. In the game group $\left(V_i,V_j,V_k\right)$, vehicle $V_i$ serves as the head vehicle of the game group, and the strategy deviation is calculated using the strategy set $B_j^t$ generated by the intermediate vehicle $V_j$. If the strategy deviation is small, it indicates that the strategy between the two cars is close to the same. The term “strategy deviation” is defined as follows:

Definition 4 (Strategy Deviation). 

At time $t$, let vehicles $V_i$ and $V_j$ generate the policy sets $B_i^t=\left(S_i^t,P_i^t\right)$ and $B_j^t=\left(S_j^t,P_j^t\right)$. The strategy deviation ${\Phi }_{ij}^t$ is defined as the variance in strategy configurations between vehicle $V_i$ and vehicle $V_j$, expressed by the following formula:

$${\mathsf{\Phi }}_{ij}^t=\left(P_i^t-P_j^t\right){\left(1\right)}^T+\left(S_i^t-S_j^t\right)diag\left(P_i^t\right){\left(S_i^t-S_j^t\right)}^T$$

(9)

where: $diag\left(·\right)$ represents a diagonal matrix.

According to Equation (9), it is evident that when the strategy sets produced by vehicles $V_i$ and $V_j$ are identical, the strategy deviation is 0, and conversely.

Definition 5 (Deviation Payoff). 

In the game group $\left(V_i,V_j,V_k\right)$ on the virtual logic ring, the deviation payoff $V\left(B_i^t\right)$ of vehicle $V_i$ is defined as the deviation between ${\Phi }_{ij}^t$ and ${\Phi }_{jk}^t$, expressed as follows:

$$\begin{array}{c}V\left(B_i^t\right)={\mathsf{\Phi }}_{ij}^t-{\mathsf{\Phi }}_{jk}^t\\ =\left(P_i^t-P_j^t\right){\left(1\right)}^T+\left(S_i^t-S_j^t\right)diag\left(P_i^t\right){\left(S_i^t-S_j^t\right)}^T\\ -\left(P_j^t-P_k^t\right){\left(1\right)}^T+\left(S_j^t-S_k^t\right)diag\left(P_j^t\right){\left(S_j^t-S_k^t\right)}^T\end{array}$$

(10)

Based on the equation provided, when the strategy deviation between the front vehicle $V_i$ and the middle vehicle $V_j$ is smaller than the deviation between the middle vehicle $V_j$ and the rear vehicle $V_k$, the front vehicle $V_i$ will receive a positive payoff, denoted as $V\left(B_i^t\right)>0$. Conversely, the front car $V_i$ will receive a negative payoff, indicated as $V\left(B_i^t\right)<0$.

Within the virtual logic ring, every game group establishes an interconnected communication network, where the strategic choices of each participant progressively engage and circulate within this ring structure. This interaction process aims to eliminate strategy deviation and promote balanced strategies among all vehicles. Nevertheless, it is crucial to acknowledge that the elimination of strategy deviation does not necessarily indicate the optimality of the strategy set. Nevertheless, numerous additional factors must be taken into account in the collaborative decision-making process, including efficiency, safety, and comfort. To address the aforementioned issues, the deviation benefit $V\left(B_i^t\right)$ can be integrated with the strategy benefit within the strategy proposal $S_i^t$. The utility function $R\left(B_i^t\right)$ of participant $V_i$ can be formulated as follows:

$$R\left(B_i^t\right)=V\left(B_i^t\right)+J_i\left(B_i^t\right)$$

(11)

Within the virtual logic loop, participants engage in cooperation to optimize their profits. Through ongoing interaction and negotiation, participants strive to reach the Nash equilibrium point to enhance safety, improve driving efficiency, and increase ride comfort. Consequently, the Nash equilibrium problem can be reformulated as a constrained multi-objective optimization problem, as demonstrated below:

$$\left(u_1^{t*},u_2^{t*},\cdots ,u_n^{t*}\right)=\arg \max {\displaystyle {\sum }_{i=1}^{n}R\left(B_i^t\right)}$$

(12)

According to the definition of Nash equilibrium, an equilibrium state arises among the strategy sets of participants, wherein each participant’s chosen strategy maximizes its utility function, and any unilateral deviation from this strategy by other participants would result in decreased returns.

Nash equilibrium denotes a state of stability. In the context of cooperative decision-making among vehicles, the attainment of a consensus among all vehicles in the game results in the formation of a set of strategy proposals, which represents a Nash equilibrium point.

Let $S^t=\left\{S_1^t,S_2^t,\cdots ,S_n^t\right\}$ denote the set of strategy proposals produced by all vehicles at time $t$, and $P^t=\left\{P_1^t,P_2^t,\cdots ,P_n^t\right\}$ represent the bidding proposals associated with each strategy proposal in the set $S^t$. If the strategy proposal at the Nash equilibrium point is $B{N}^{t*}=\left\{B_i^{t*}=\left(S_i^{t*},P_i^{t*}\right)|i\in V\right\}$, the corresponding strategy proposal is $S^{t*}=\left\{S_1^{t*},S_2^{t*},\cdots ,S_n^{t*}\right\}$, and the bidding proposal is $P^{t*}=\left\{P_1^{t*},P_2^{t*},\cdots ,P_n^{t*}\right\}$. According to the definition provided above, when all vehicles adopt the same strategy set at the Nash equilibrium point, the total benefits from deviating obtained by all vehicles amount to 0, denoted as ${{\displaystyle \sum }}_{\forall i\in V}V\left(B_i^{t*}\right)=0$.

According to Equation (12), the total utility function $R\left(·\right)$ for all vehicles can be computed, leading to the derivation of the following equation.

$${\displaystyle {\sum }_{\forall i\in V}R\left(B_i^t\right)}={\displaystyle {\sum }_{\forall i\in V}V\left(B_i^t\right)}+{\displaystyle {\sum }_{\forall i\in V}{J}_i\left(B_i^t\right)}$$

(13)

$$\begin{array}{cc}\hfill {\displaystyle {\sum }_{\forall i\in V}{J}_i\left(B_i^{t*}\right)}& ={\displaystyle {\sum }_{\forall i\in V}\left(R\left(B_i^{t*}\right)-V\left(B_i^{t*}\right)\right)}\hfill \\ & ={\displaystyle {\sum }_{\forall i\in V}R\left(B_i^{t*}\right)}-{\displaystyle {\sum }_{\forall i\in V}V\left(B_i^{t*}\right)}\hfill \\ & ={\displaystyle {\sum }_{\forall i\in V}R\left(B_i^{t*}\right)}\hfill \end{array}$$

(14)

Since the utility function attains a Nash equilibrium at $B{N}^{t*}=\left\{B_i^{t*}=\left(S_i^{t*},P_i^{t*}\right)|i\in V\right\}$, it can be deduced from the equation above that the strategy payoff function also reaches a Nash equilibrium at $B{N}^{t*}=\left\{B_i^{t*}=\left(S_i^{t*},P_i^{t*}\right)|i\in V\right\}$.

Upon entering the decision-making zone, intelligent vehicles are designated as participants. Each participant engages in interactive negotiations within the game group on the virtual logic ring, ultimately achieving strategic equilibrium on the virtual logic ring. Algorithm 1 is presented as follows:

Algorithm 1: Distributed strategy balancing algorithm based on cooperative game

Initialize: Get vehicle status information $m$;

1:   Assignment number $V_i\leftarrow$ID

2:   Construct virtual logic ring and divide game group $\left(V_i,V_j,V_k\right),i,j,k\in V$

3:   Generation policy set $B_i^t=\left(S_i^t,P_i^t\right),i\in V$

4:   for iteration in range(max_iterations):

5:   Gets policy sets for other vehicles $B_j^t=\left(S_j^t,P_j^t\right),j\ne i,j\in V$

6:   Optimal utility function $argmax{{\displaystyle \sum }}_{i=1}^{n}R\left(B_i^t\right)$

7:   Adjustment strategy set $B_i^t\leftarrow B_i^{t*}$

8:   if ${\mathsf{\Phi }}_{ij}^t==0$

9:   break

10: end if

11: end for

12: Output the optimal policy set $B_i^{t*}=\left(S_i^{t*},P_i^{t*}\right)$

5. Simulation

5.1. Simulation Environment Setup

To assess the proposed algorithm, this study constructs an unsignalized intersection scenario using SUMO, as illustrated in Figure 1. The pertinent parameters are detailed in

Table 1. Parameter Settings of unsignalized intersection.

Parameters	Description	Value
Scene parameters	Decision area radius/(m)	150
	Number of lanes	2
	Road width/(m)	3.5
Control parameters	$\Delta t$/(s)	0.2
	$v^{max}$/(m/s)	15
	$v^{min}$/(m/s)	0
	$a^{max}$/(m/s2)	3
	$a^{min}$/(m/s2)	−3

. The game strategy balancing algorithm presented in this study is implemented through co-simulation with Python.

To implement the game strategy equilibrium algorithm as proposed, this study employs a genetic algorithm to address the nonlinear optimization model with constraints. The genetic algorithm is an optimization technique rooted in the principles of biological evolution. It operates by emulating natural selection, genetic variation, and other biological processes to search for the most optimal solution. In this study, the genetic algorithm is utilized to address the game equilibrium problem, aiming to identify the optimal game equilibrium solution through the modification of individual gene codes.

Table 2. Genetic algorithm parameters.

Parameters	Description	Value
pop_size	Number of population	30
generations	Number of iterations	30
code_number	Binary code length	6
chrome_length	Chromosome length	54
pm	Crossover rate	0.6
pc	Variation rate	0.01

presents the parameters of the genetic algorithm.

5.2. Simulation Result Analysis

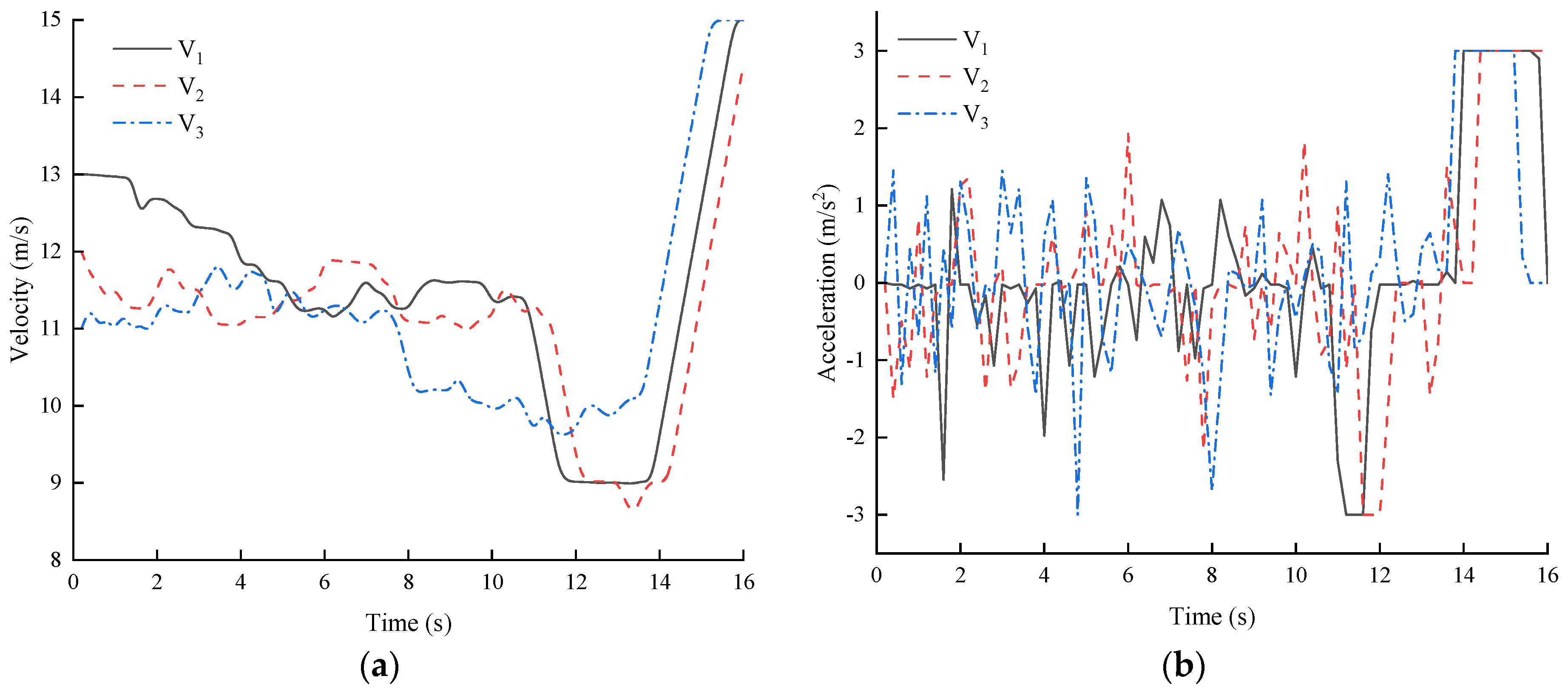
To investigate the interaction among vehicles in the game, only three vehicles were selected to validate the rationality and effectiveness of the proposed algorithm. In this scenario, vehicle $V_1$ will make a left turn from lane L8 to lane L5, vehicle $V_2$ will also make a left turn from lane L2 to lane L7, and vehicle $V_3$ will proceed straight from lane L4 to lane L7. In conflict zones, it is imperative for $V_1$ must interact with $V_2$ and $V_3$ to make informed decisions aimed at conflict prevention. In this instance, the conflict points are located at coordinates (−3.81, 0.05) and (0.61, 4.8). The initial coordinates of $V_1$, $V_2$, and $V_3$ are (−144.9, −1.6), (1.6, −144.9), and (144.9, 4.8), respectively. The initial speeds are set at 13 m/s, 12 m/s, and 11 m/s, respectively.

Figure 3 illustrates the variation in strategy deviation among three vehicles as the number of iterations increases. In the virtual logic ring, $V_1$, $V_3$, and $V_2$ are arranged clockwise, with policy deviations between the three cars denoted as ${\mathsf{\Phi }}_{13}$, ${\mathsf{\Phi }}_{32}$, and ${\mathsf{\Phi }}_{21}$. As illustrated in Figure 2, initially, the strategy deviation values of the three vehicles are substantial, suggesting significant disparities in the cooperation proposals among the vehicles. Nevertheless, as the number of iterations increases, the policy deviation value gradually diminishes and eventually converges to zero. It is important to acknowledge that during the initial iteration, the policy bias may vary, as the optimal individual chosen by the genetic algorithm may not necessarily represent the global optimal solution. As the iteration progresses, the optimization algorithm incrementally discovers improved solutions, resulting in the stabilization of the strategy deviation.

A graph illustrating the variations in vehicle speed and acceleration is presented in Figure 4. According to the data presented in the figure, it is evident that starting from 10.8 s, the speed of vehicle $V_1$ started to decrease gradually to safely navigate through the conflict area. At 11.8 s, vehicle $V_1$ entered the conflict zone. At 11.4 s, to avoid a collision with vehicle $V_1$, vehicle $V_2$ initiated deceleration as it entered the conflict zone. Simultaneously, at the 12-s mark, vehicle $V_2$ also entered the area of conflict. In the conflict zone, vehicle $V_1$ traversed the area at a consistent speed and exited successfully after 13.6 s. Nevertheless, the $V_2$ decelerated within the conflict zone to enhance security measures and exited the area within 14 s. It is crucial to acknowledge that $V_1$ exits conflict point 2 before the entry of $V_3$ into the conflict zone. Hence, $V_3$ did not collide with $V_1$. Unaffected by the collision, vehicle $V_3$ experienced a gradual acceleration at 13.6 s.

Three decision algorithms are implemented to enhance the validation of the model’s validity: algorithm A, which is the first−come, first−served decision algorithm [18]; algorithm B, which is the cooperation−driven model grounded in cooperative game theory [19]; and algorithm C, which is the game−based strategy balance algorithm. The first−come, first−served algorithm is a prevalent and straightforward traffic flow control scheme that efficiently improves traffic flow and alleviates congestion without taking into account the coordination and interaction among traffic participants. An advanced algorithm for traffic flow control, the cooperative drive model is founded upon the concept of cooperative games. Its primary objective is to enhance the overall traffic efficacy of the system while simultaneously guaranteeing driver safety and comfort. Furthermore, these two algorithms are representative and extensively implemented in the domain of autonomous driving; thus, we selected them as benchmark algorithms to assess the efficacy and benefits of our proposed algorithms.

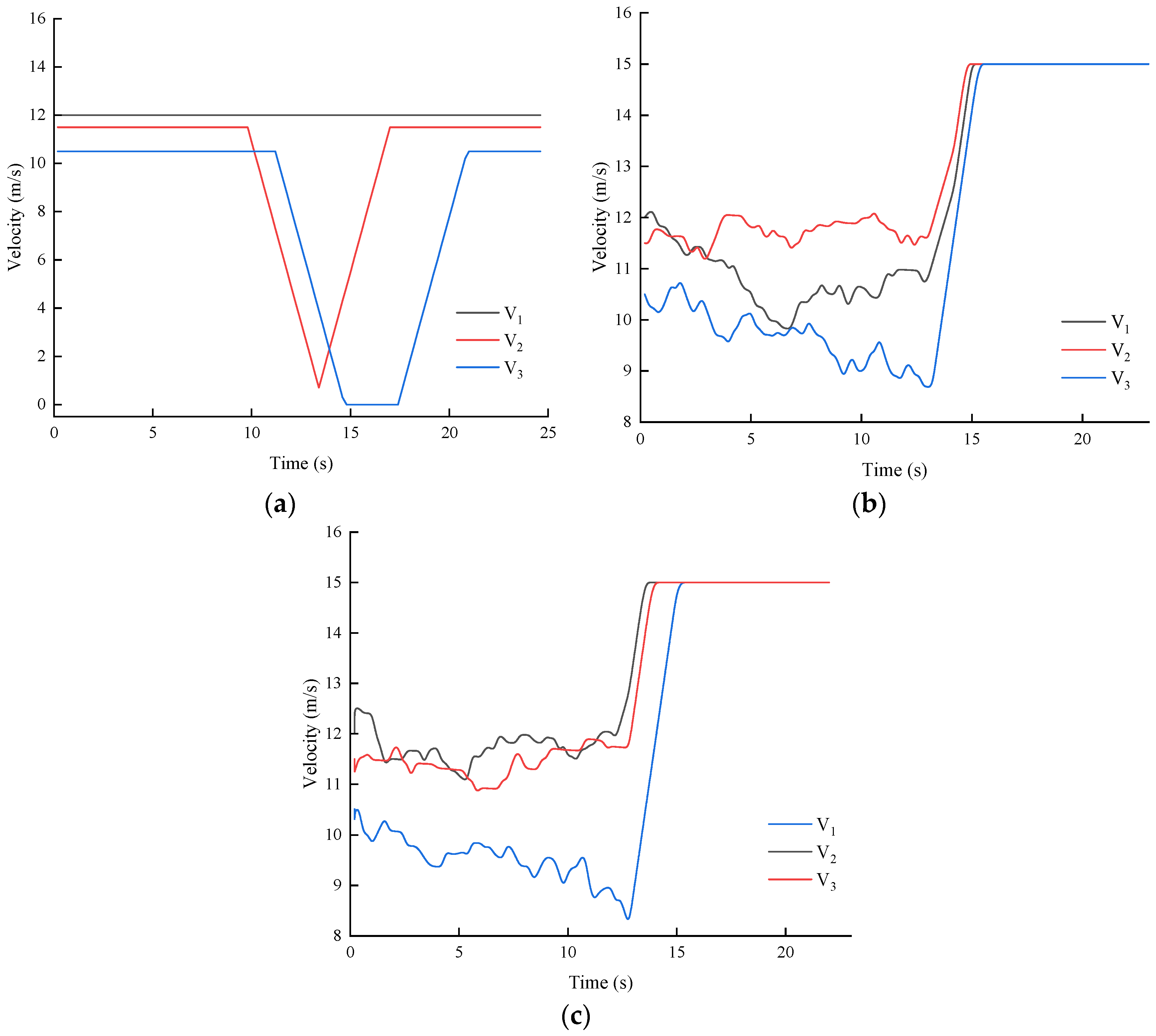
In this scenario, vehicle $V_1$ is transitioning from the L8 lane to the L3 lane in a straight path, while vehicle $V_2$ intends to proceed straight and engage with vehicles $V_1$ and $V_3$ to optimize decision-making. Vehicle $V_3$ transitions into lane L7 from lane L4. $V_1$, $V_2$, and $V_3$ exhibit initial velocities of 12 m/s, 11.5 m/s, and 10.5 m/s, respectively.

According to the results of the strategy depicted in Figure 5 and

Table 3. Data of different comparison algorithms.

Test Result	Algorithm A	Algorithm B	Algorithm C
Average transit time/(s)	29.49	23.89	23.65
Average transit delay/(s)	6.16	3.89	3.65
Average travel speed/(m/s)	10.36	12.57	12.71

, the curves illustrating the change in vehicle speed under the three decision algorithms exhibit distinct characteristics. Decision algorithm A dictates that vehicles must always wait for conflicting vehicles to vacate the conflict area before proceeding. While this measure can enhance vehicle safety to some degree, it evidently diminishes traffic efficiency and leads to increased traffic delays, which are not favorable in scenarios involving large-scale traffic flow. In contrast, Algorithm B and Algorithm C are iterative processes where decisions are not made as one-time events but are repeated at regular intervals to achieve the optimal decision variable. In comparison to algorithm B, algorithm C exhibits superior advantages in terms of average transit time, average transit delay, and other related factors. This phenomenon occurs in Algorithm C, where participants can continuously engage and adjust their strategies within the virtual logic ring. This process aims to minimize policy deviation and ultimately reach a Nash equilibrium state. In comparison to the other two decision algorithms, algorithm C demonstrates a reduction in the average passage time at the intersection by 5.84 s and 0.24 s, respectively. Additionally, the average passage delay is decreased by 40.7% and 6.17%, respectively. Furthermore, Algorithm C exhibits a superior average travel speed.

6. Conclusions

This paper introduces a distributed vehicle strategy equalization algorithm for unsignalized intersections. By establishing a virtual logic loop, the algorithm links all vehicles within the area of the unsignalized intersection. Additionally, it divides them into game groups that overlap to facilitate the sharing and application of strategic information among the vehicles. Thus, to achieve a Nash equilibrium state, vehicles situated at the intersection can adapt their strategies in response to the actions of other vehicles. Vehicles can select the most advantageous strategy based on their individual information and the actions of other vehicles in a game-theoretic interaction, therefore enhancing the efficiency of the overall traffic flow.

Three performance indices have been developed, encompassing driving safety, driving comfort, and driving efficiency. To facilitate game interaction, a strategy set is devised for each vehicle. The text comprises various strategy proposals and bidding strategies. Each vehicle selects the optimal strategy and places bids to ascertain its course of action. The design of this strategy set facilitates effective game interaction for vehicles, aiming to attain a Nash equilibrium state.

In small-scale scenarios, the algorithm proposed in this paper is shown to improve traffic efficiency and reduce traffic delays. In addition, the algorithm is applicable to various research scenarios, including traffic situations involving unsignalized roundabouts and highways. Also, the bidding strategy illustrated in this paper can be implemented and cited in similar studies. However, the limitation of this paper is that only small-scale traffic flow scenarios are considered to evaluate the performance and feasibility of the algorithm more comprehensively. It may be necessary to implement the algorithm in scenarios involving a large number of traffic flows in order to validate the algorithm at a subsequent stage. In addition, for the proposed algorithm, a higher number of parameters need to be optimized, which need to be improved in later work. For future proposals, the combination of machine learning and reinforcement learning can be considered to be an additional method to advance the progress of autonomous driving systems. It is also worth investigating how to integrate into the human driving ecosystem, ensure driving safety, and improve the efficiency of the transportation system, as interaction with human drivers may also be required in the future.