A Rotor Position Detection Method for Permanent Magnet Synchronous Motors Based on Variable Gain Discrete Sliding Mode Observer
Abstract
1. Introduction
- (1)
- The problem of rotor position estimation buffeting in sliding mode observers is addressed by proposing a novel observer control law based on the supersonic sliding mode. By using this method, the gain can be adjusted in real-time depending on the rotor speed, which ensures that the error between the actual value and estimated value stays within a small range.
- (2)
- An adaptive phase-locked loop (PLL) approach is used to account for phase delay and other challenges when estimating rotor position. The PLL gain is adjusted adaptively based on the operating state of the rotor, thereby improving issues such as slow fixed bandwidth response during speed switching in high-speed permanent magnet synchronous motors.
- (3)
- The proposed position-independent observation method is demonstrated by numerical simulation results to effectively reduce buffeting and enhance corresponding speed during speed switching. Validating the system’s stability under load conditions involves subjecting it to different loads at different times.
2. Mathematical Model of a Permanent Magnet Synchronous Motor
3. Design of a Sliding Mode Observer for Gain of a Discrete Variable
3.1. Design of a Conventional Super-Twisting Sliding Mode Observer
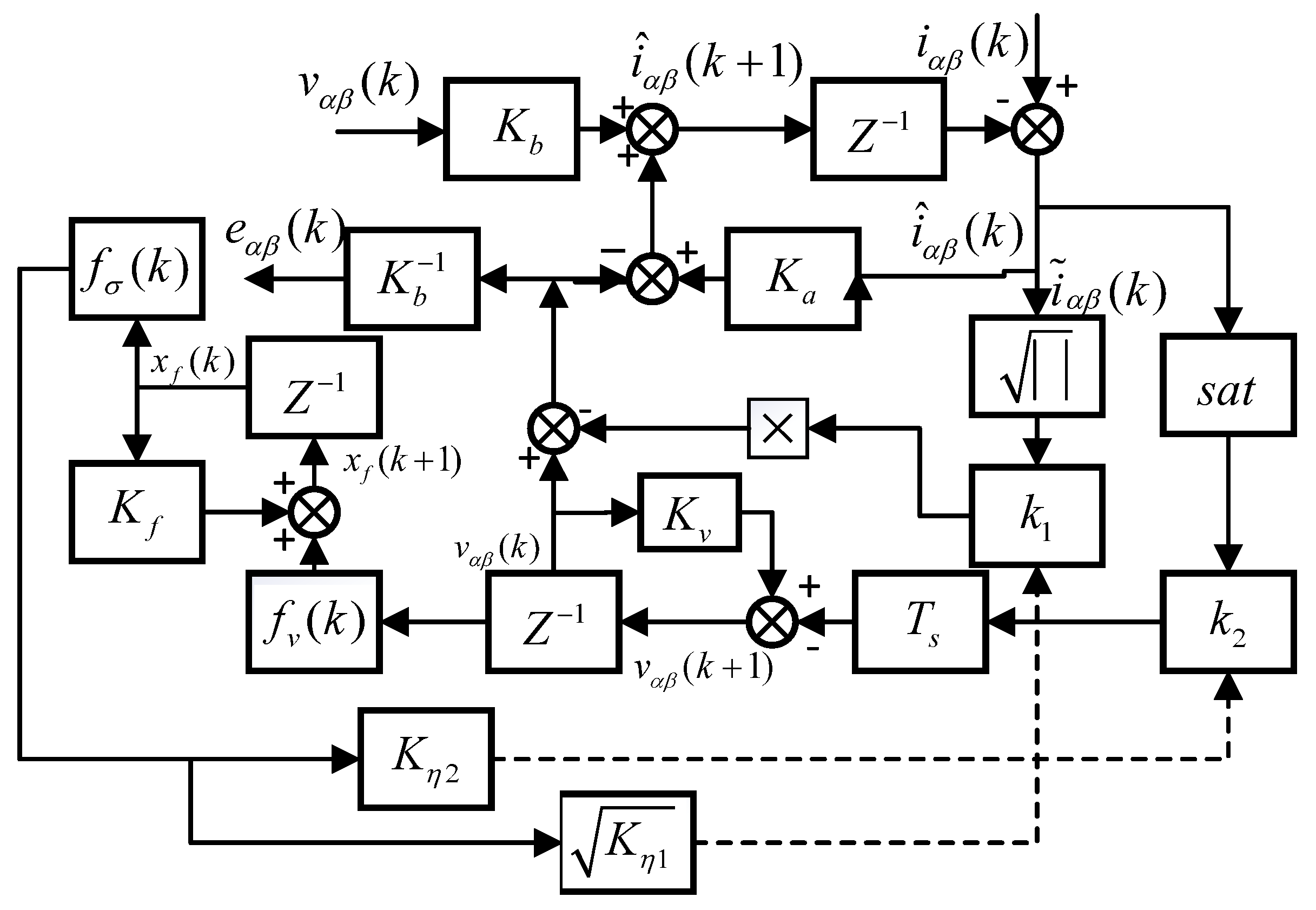
3.2. Design of a Sliding Mode Observer for Discrete Variable Gain
3.3. Feasibility and Convergence Analysis
3.3.1. Proof of Feasibility
3.3.2. Proof of Convergence
4. Phase-Locked Loop Performance Improvement
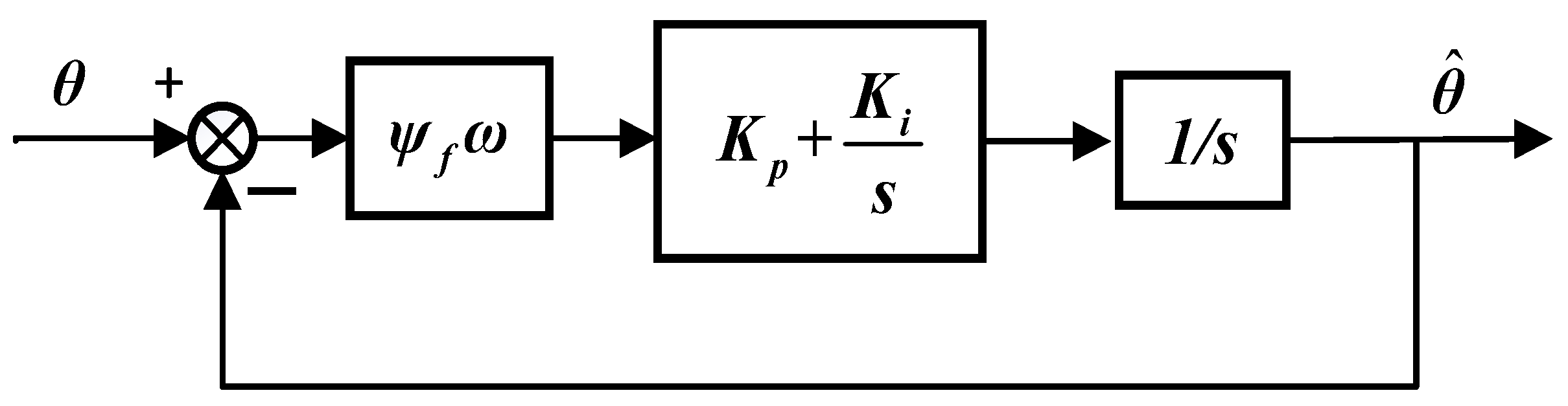
4.1. Design and Analysis of Basic Phase-Locked Loop
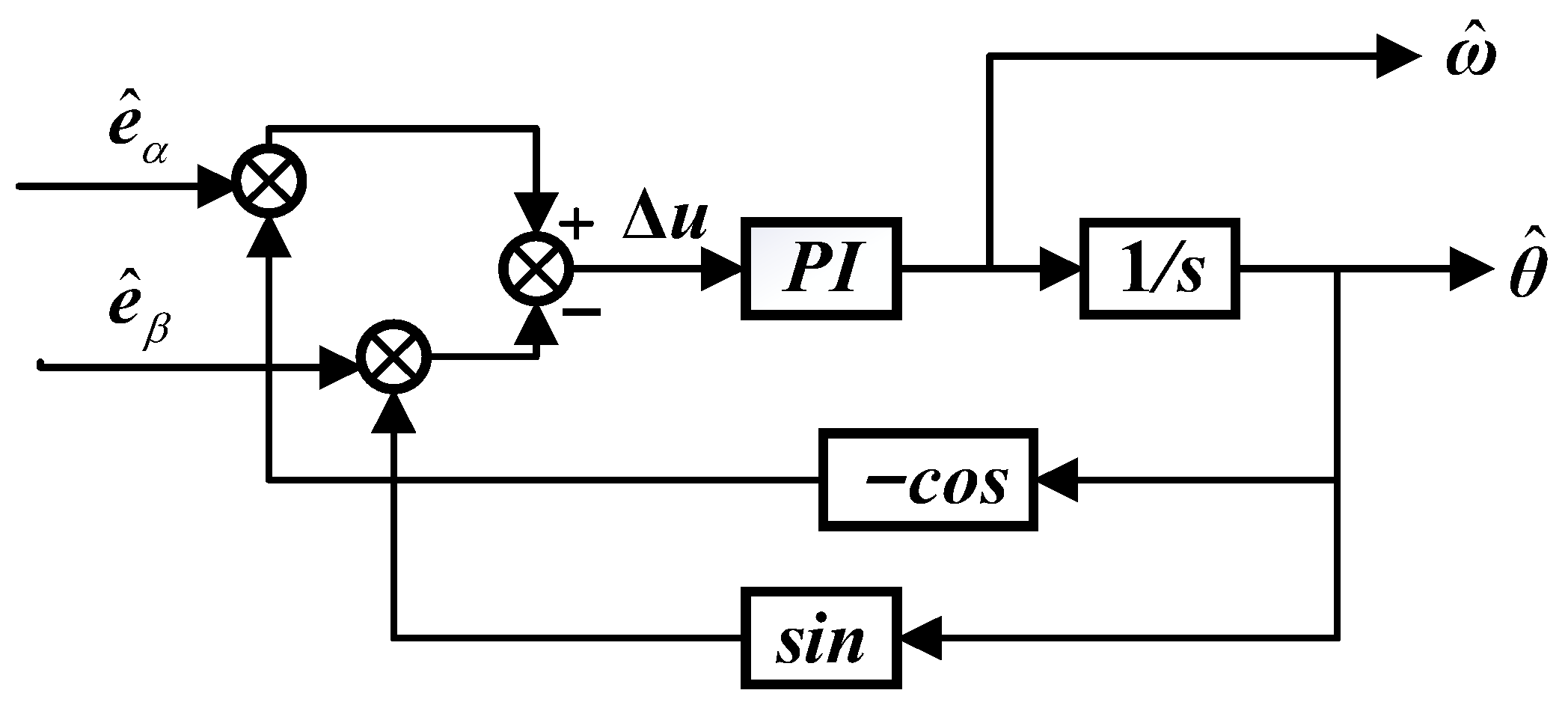
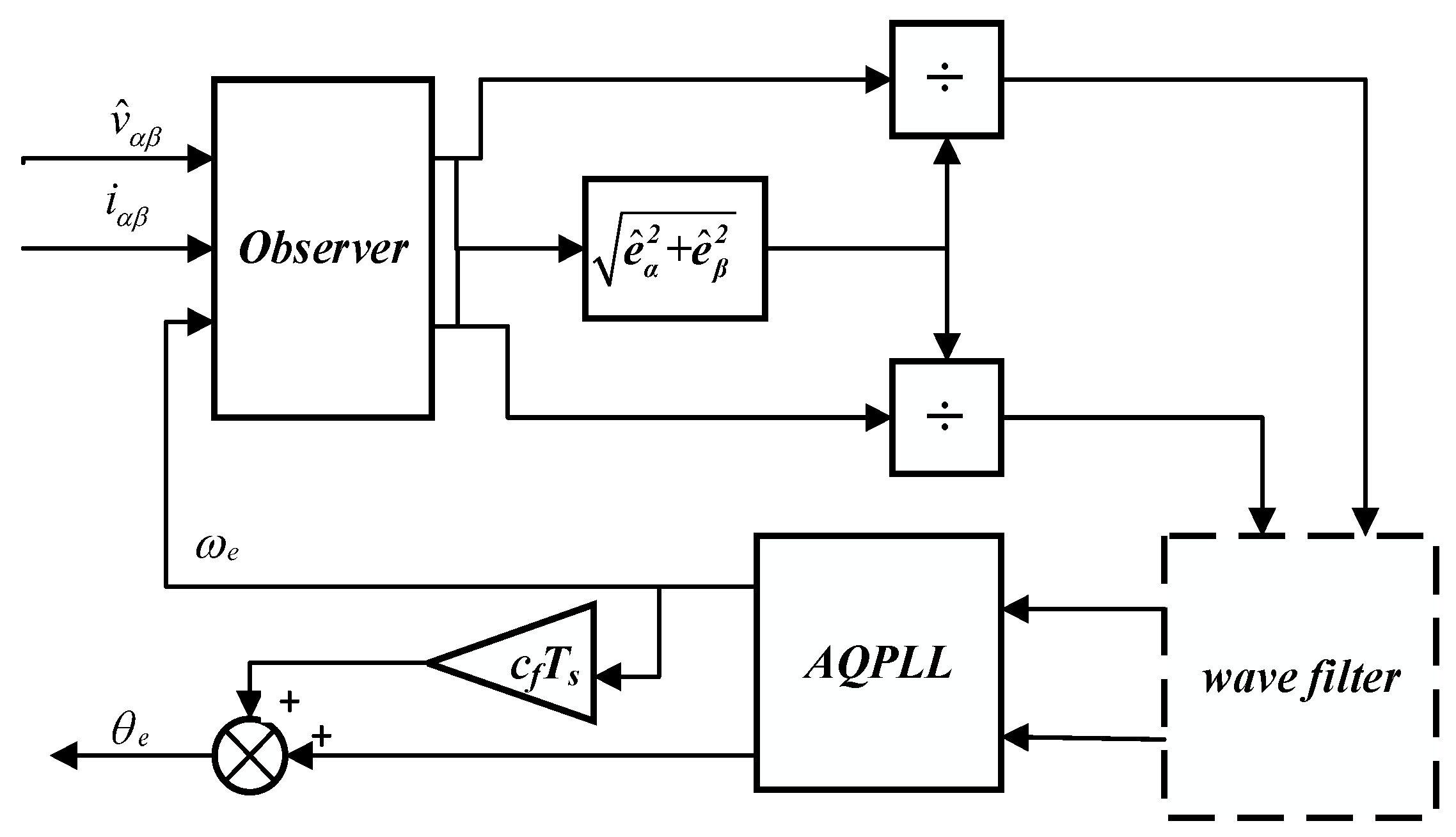
4.2. Design of Adaptive Quadrature Phase-Locked Loop
4.3. Stability Analysis
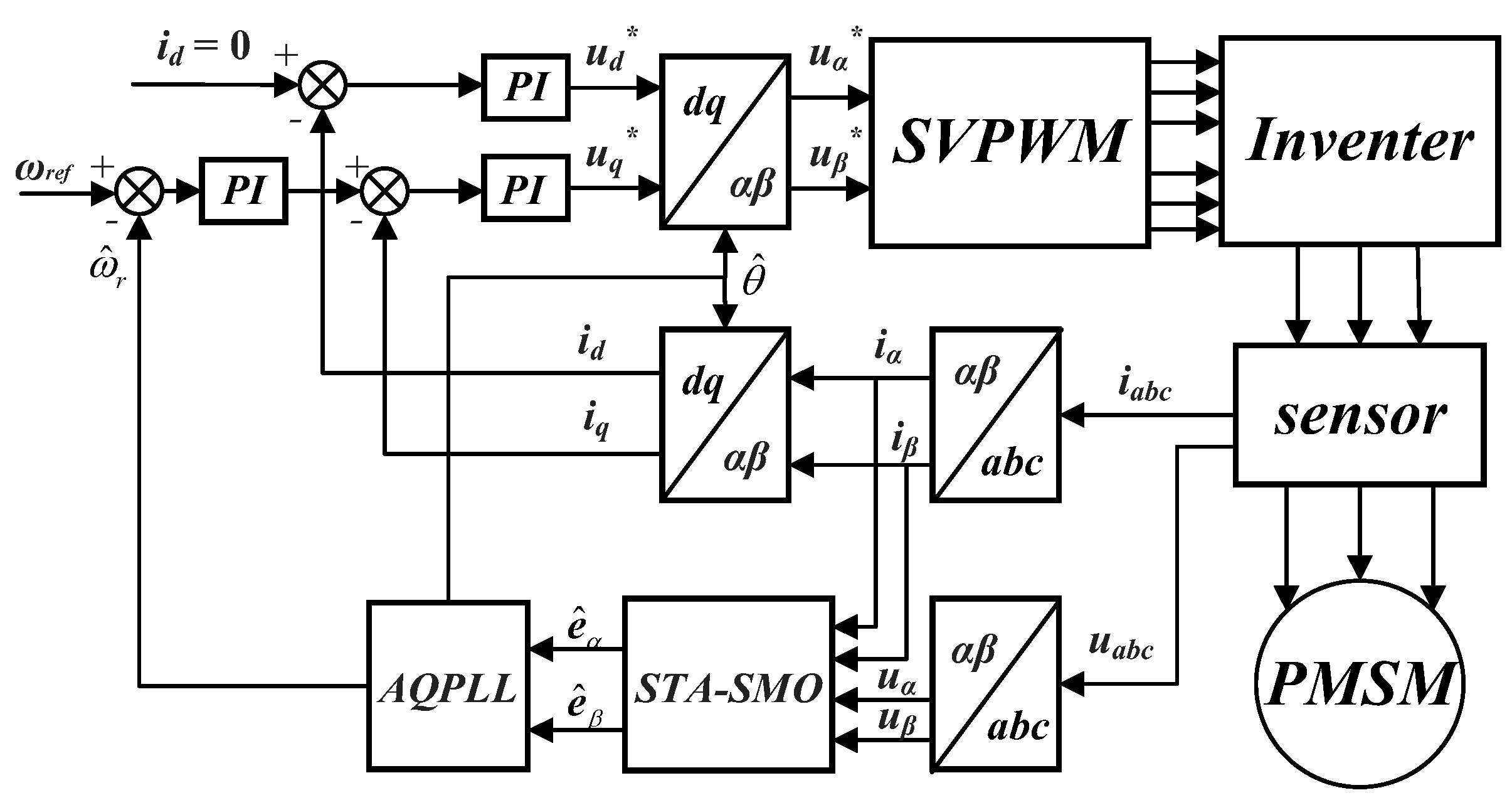
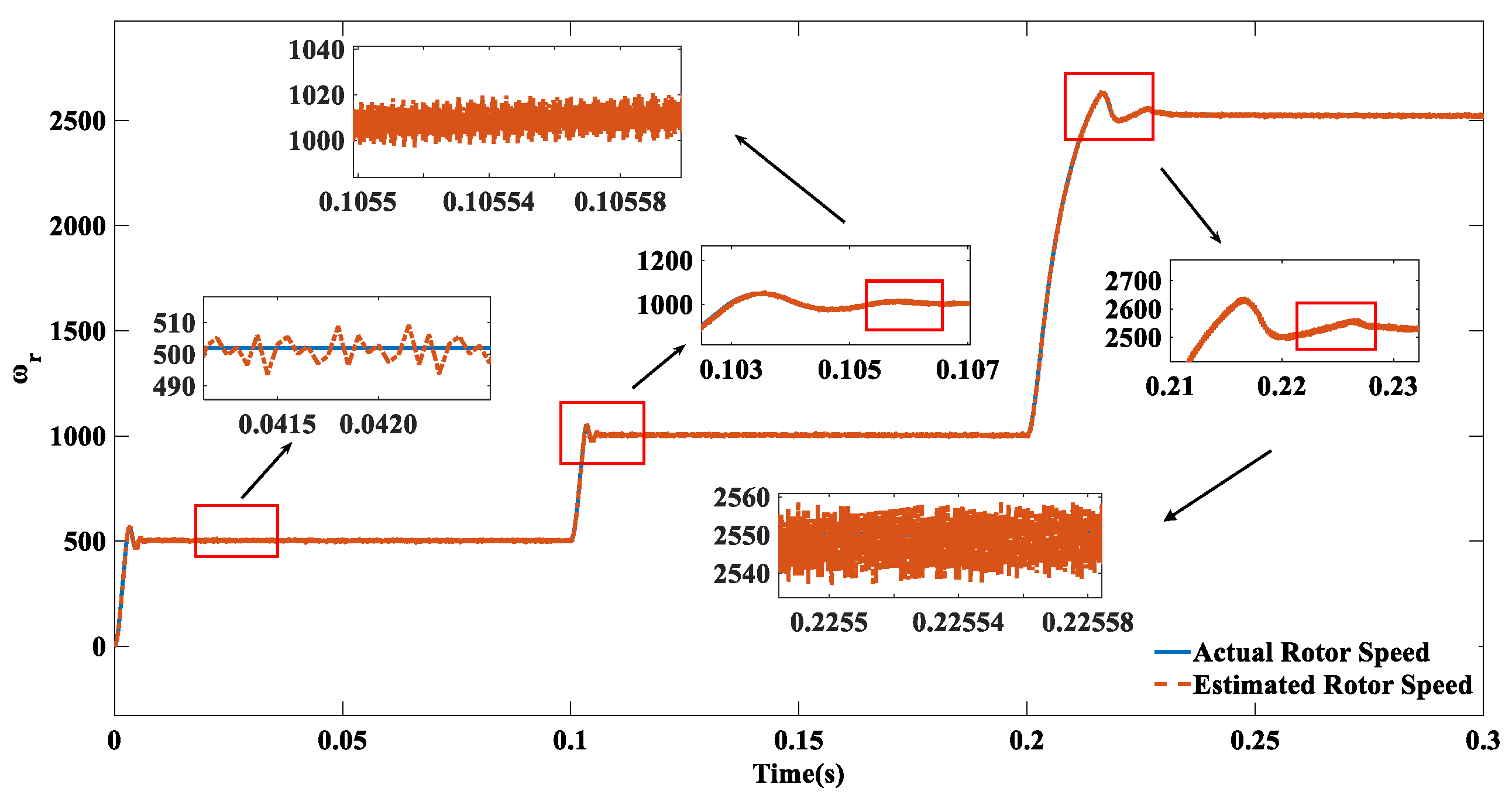
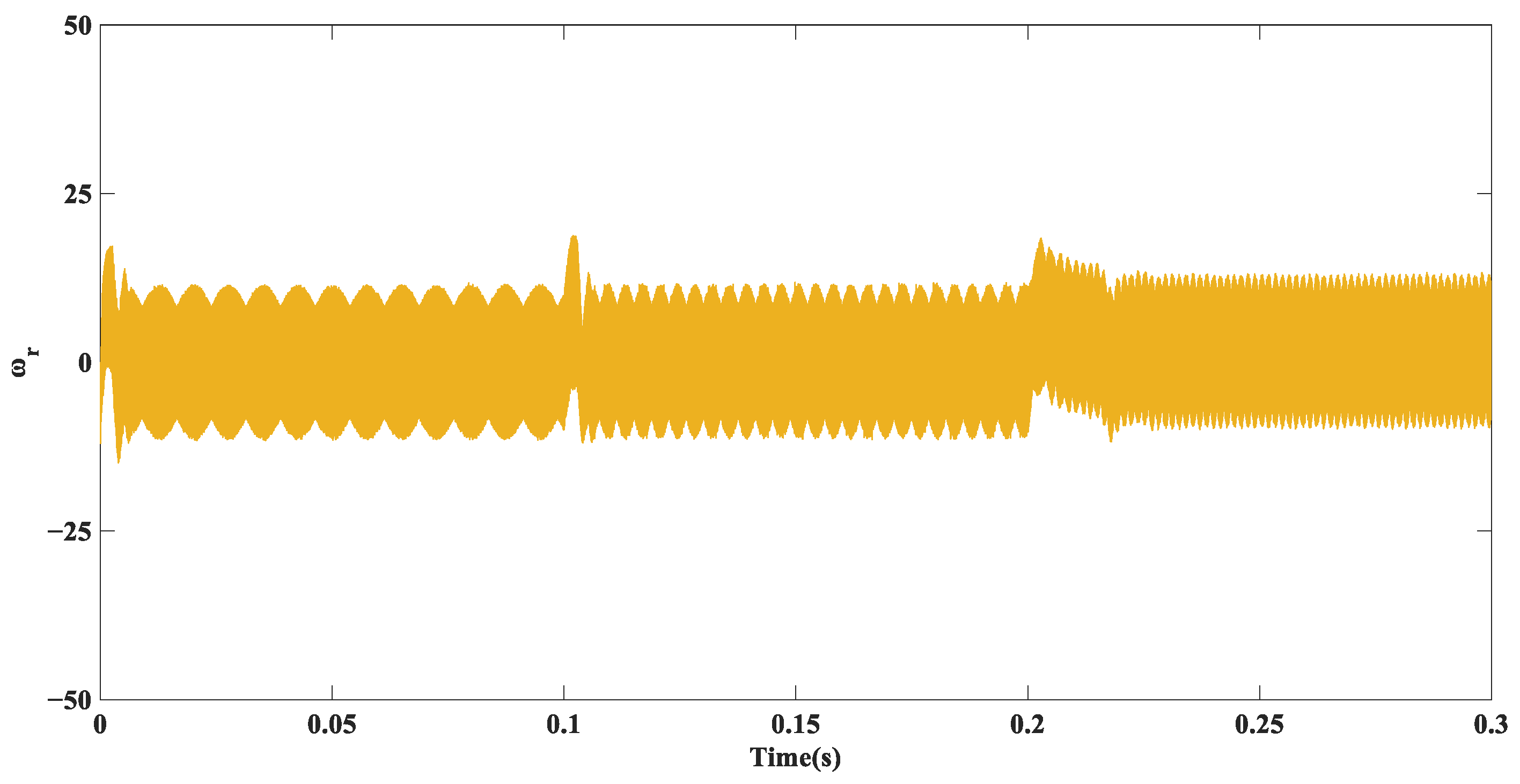
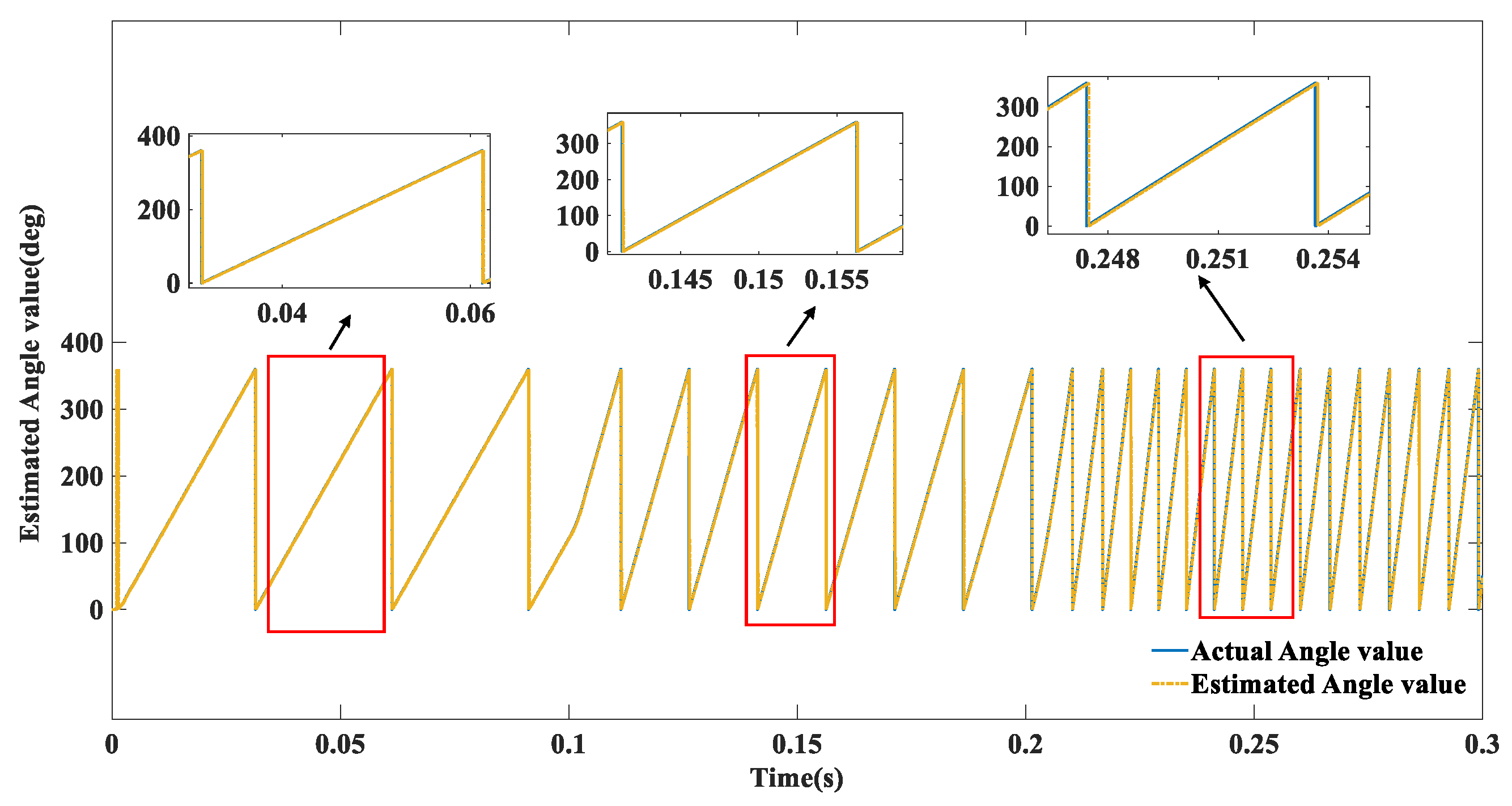
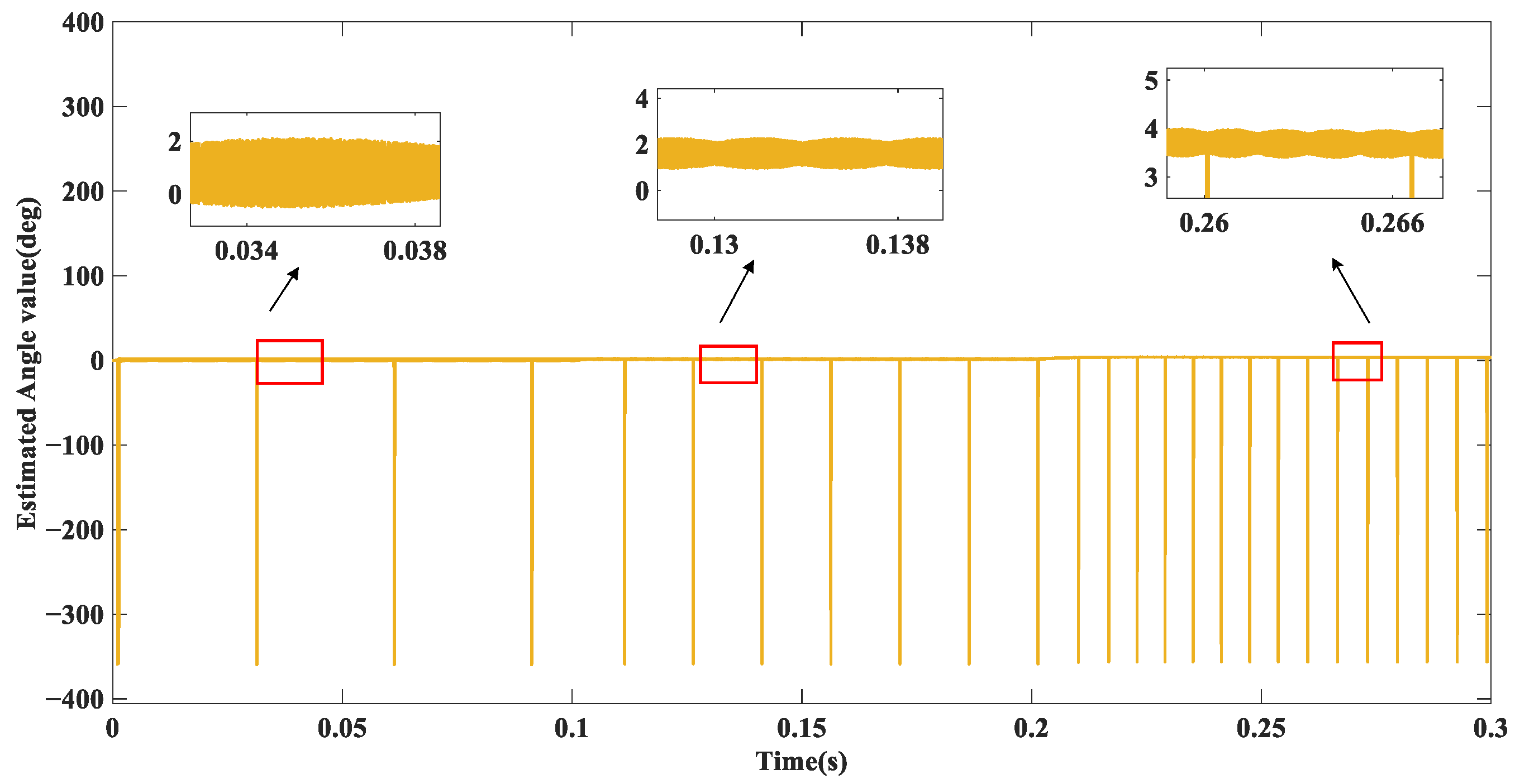
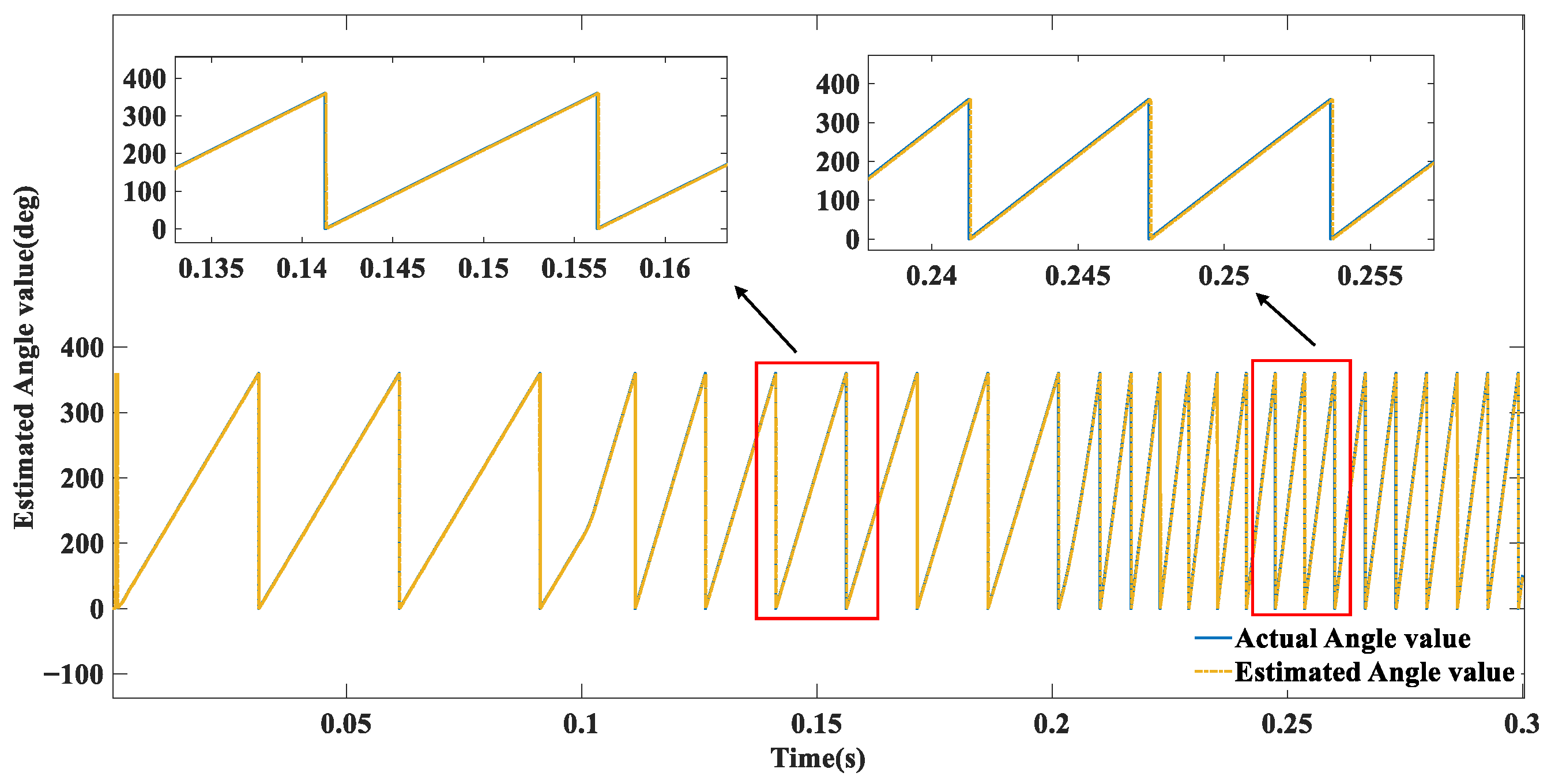
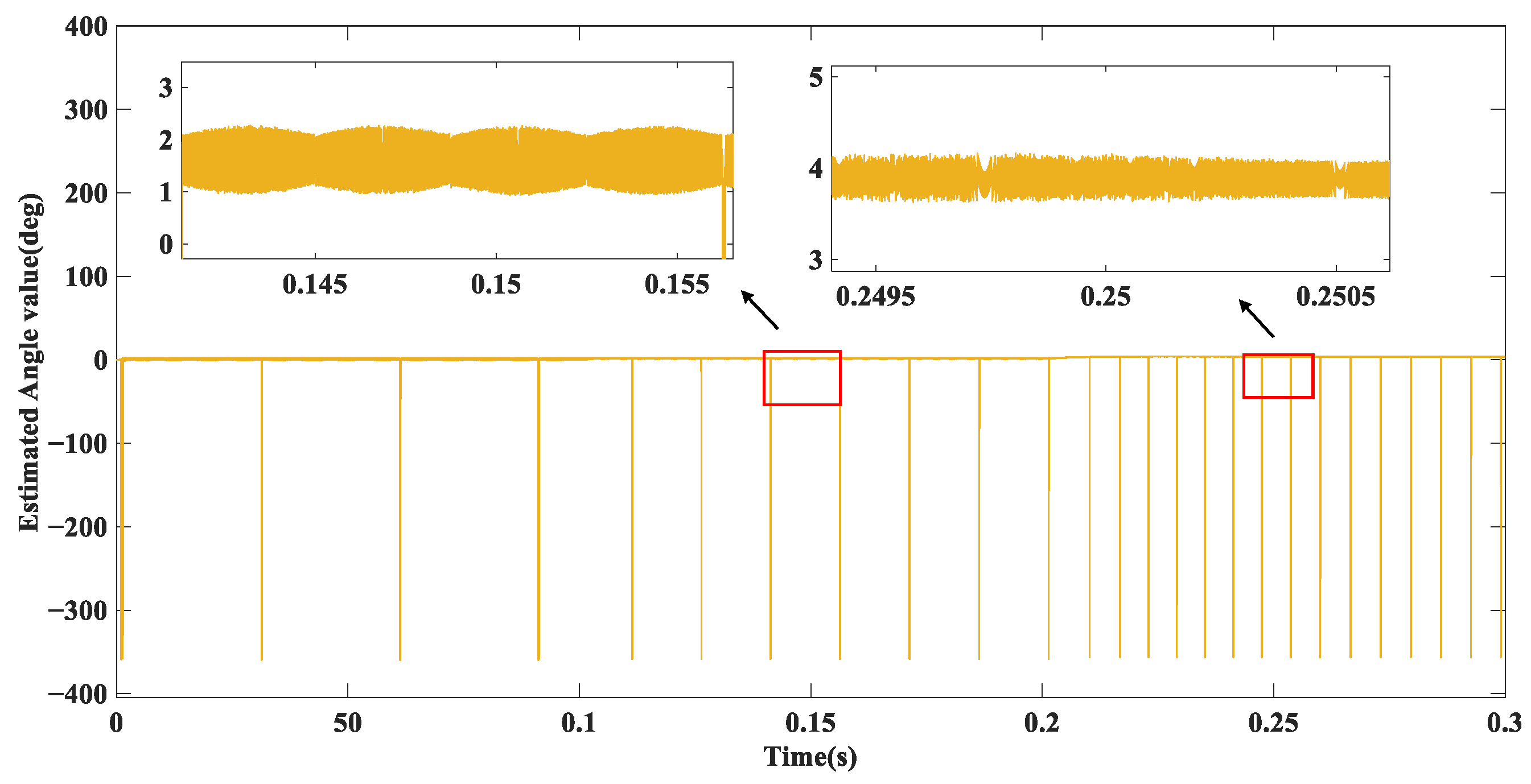
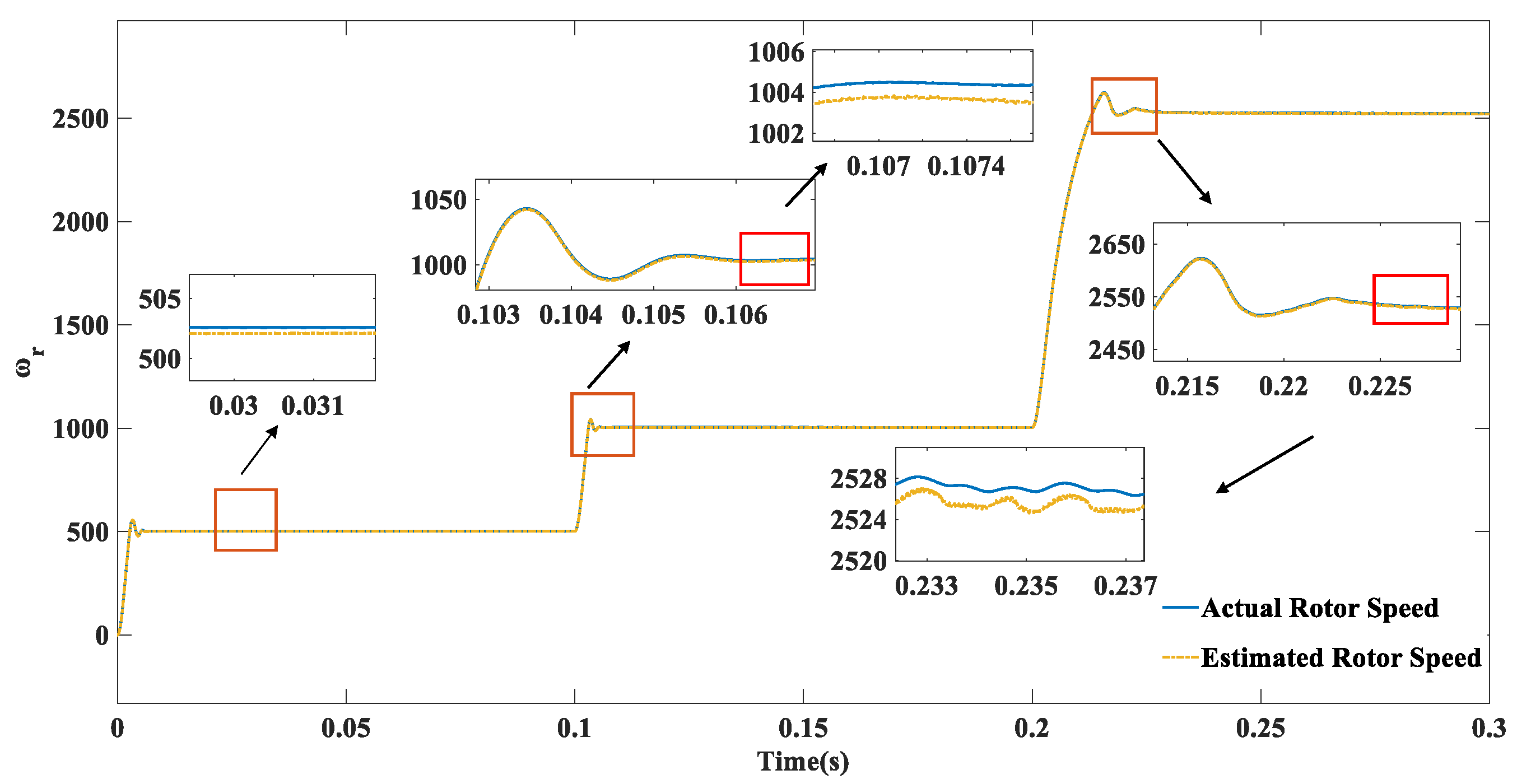
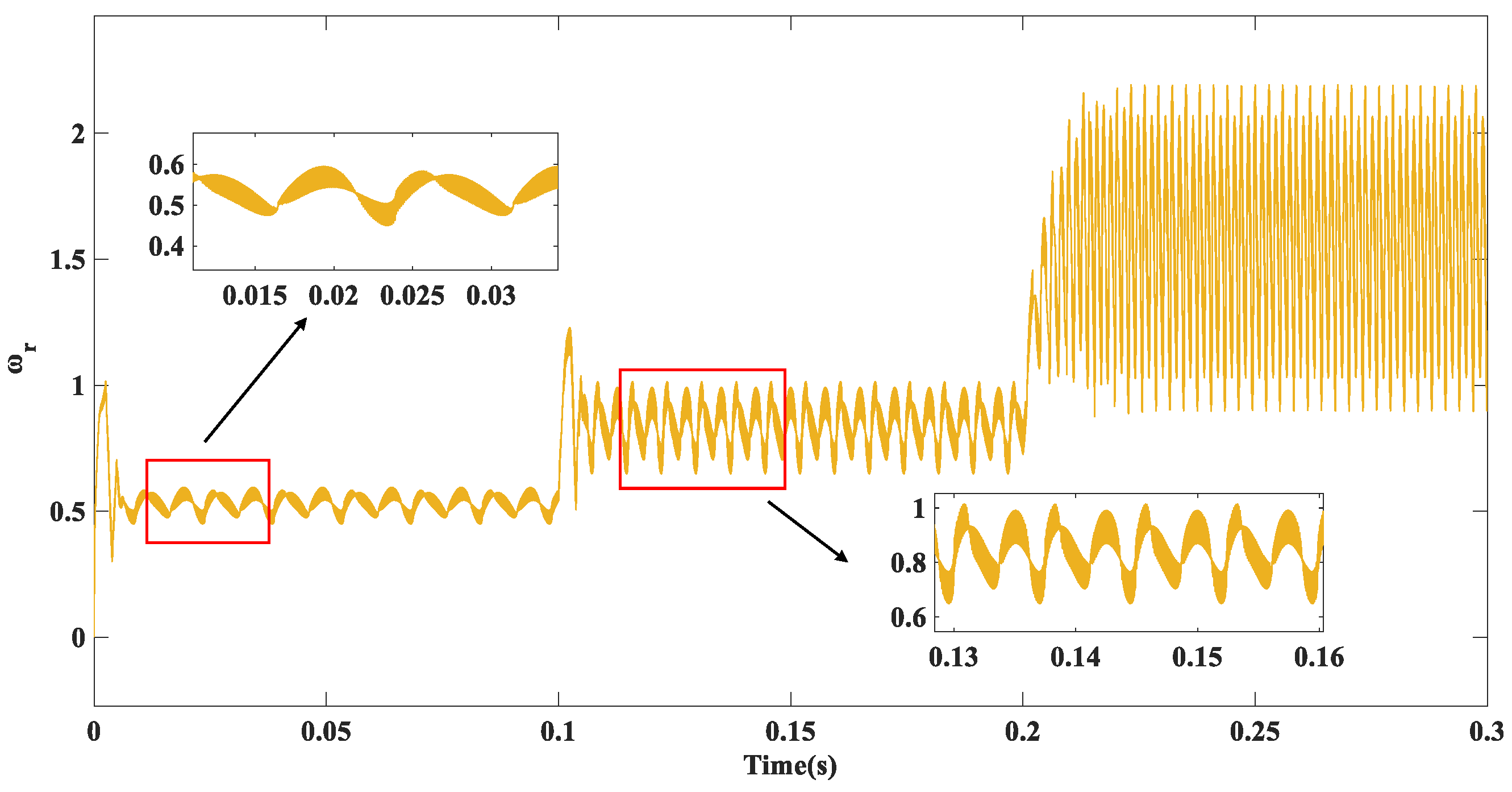
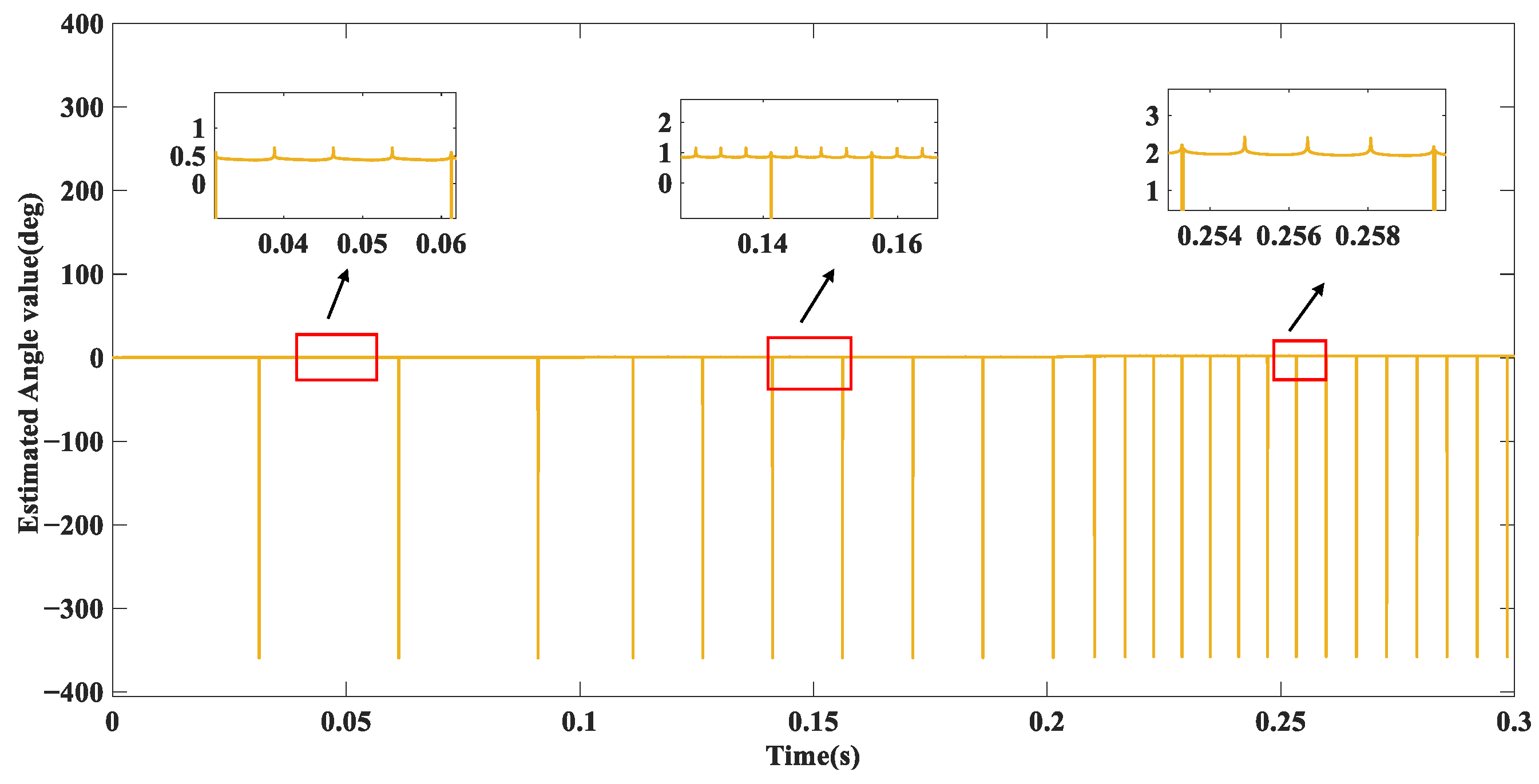
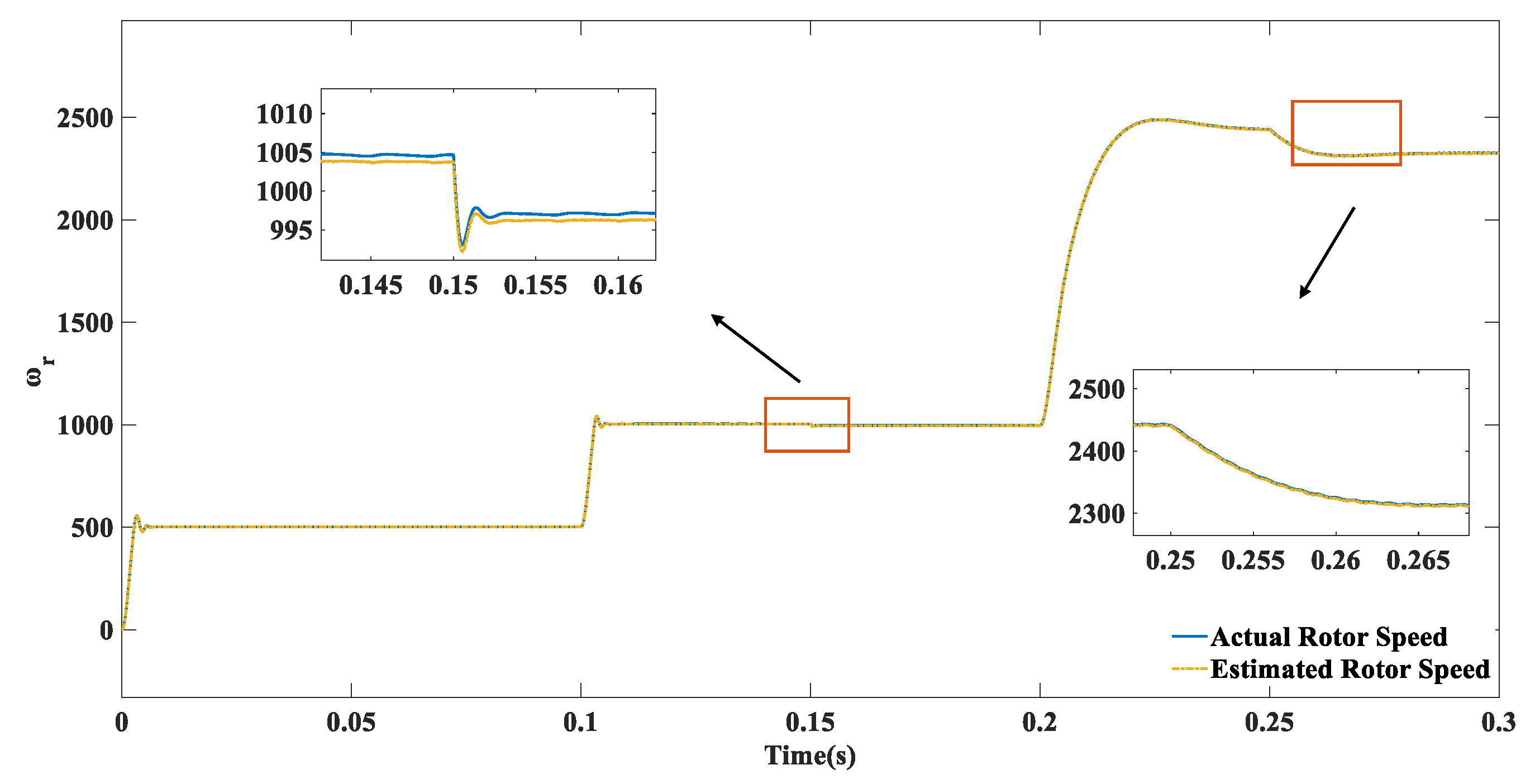
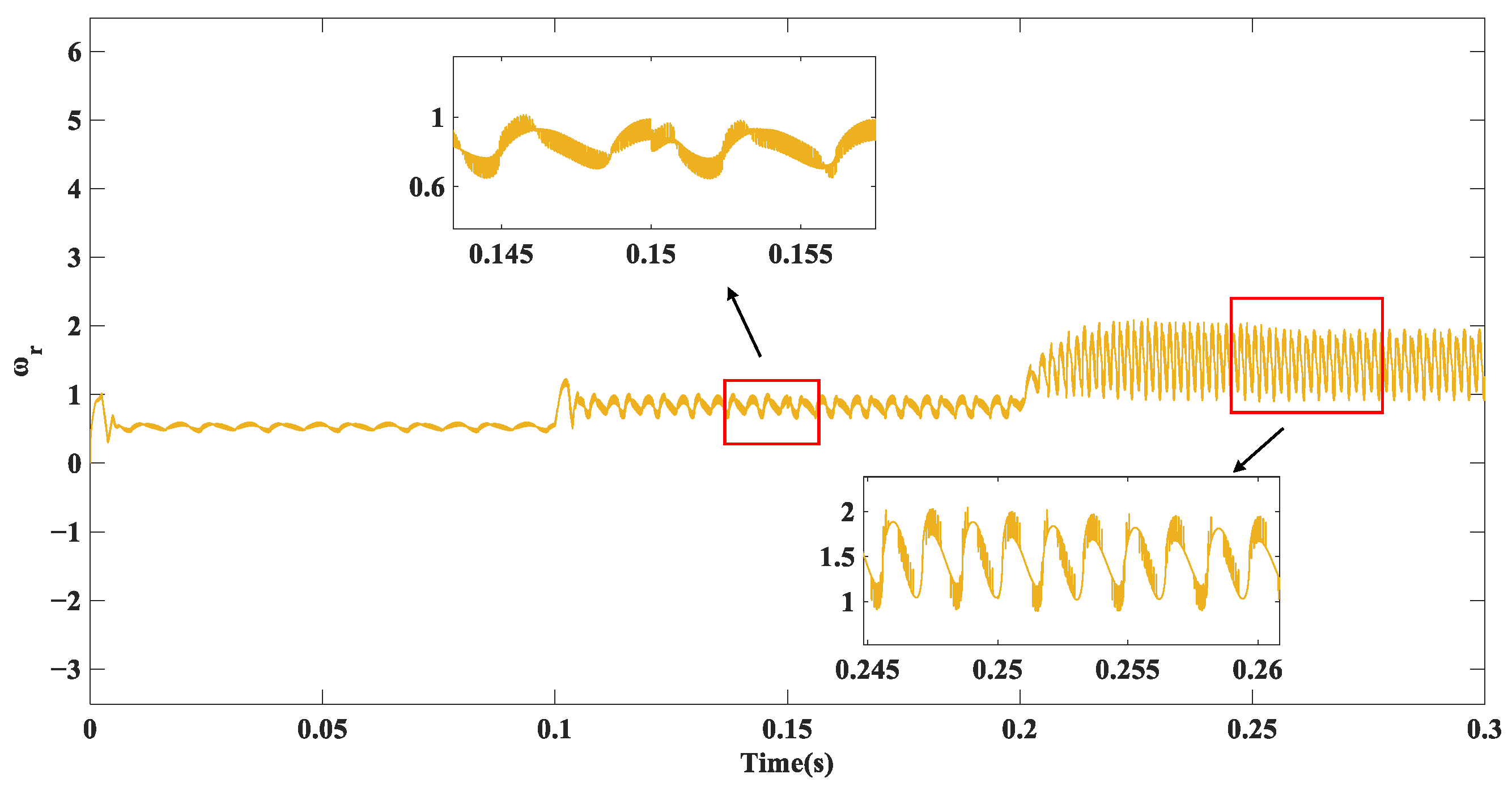
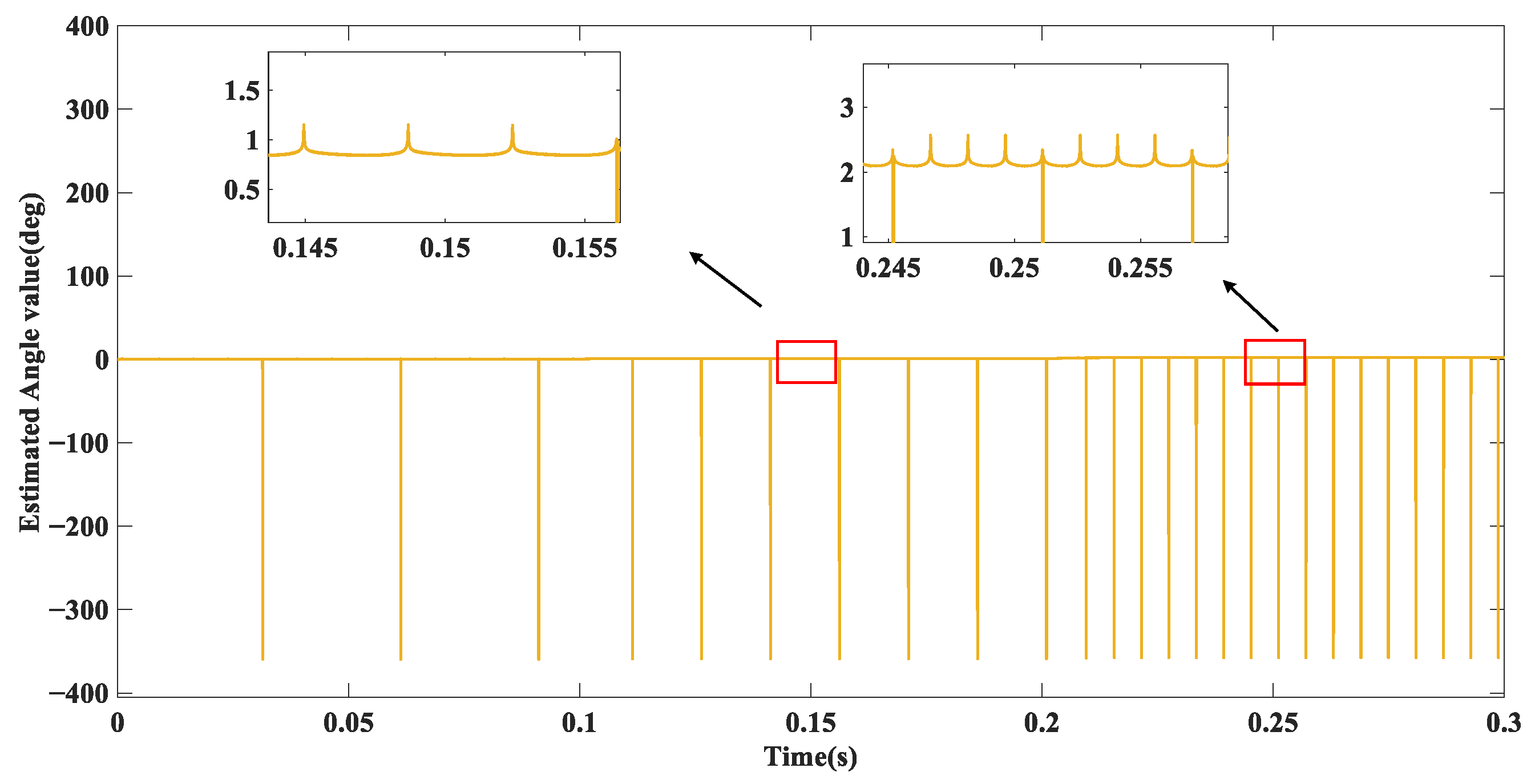
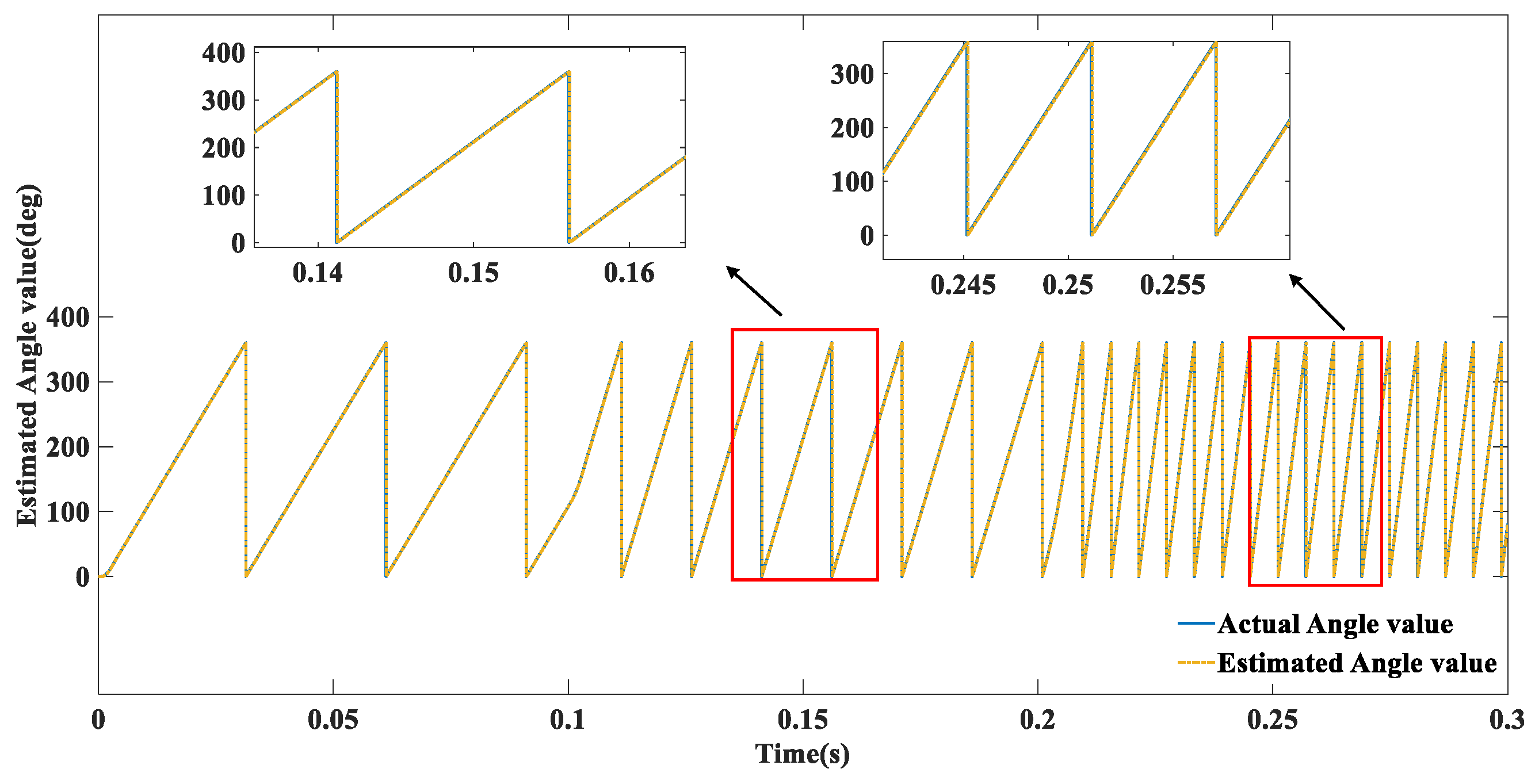
5. Simulation Experiments
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, B.; Shen, A.; Chen, B.; Luo, X.; Tang, Q.; Xu, J.; Zhu, M. A compensation strategy of flux linkage observer in SPMSM sensor-less drives based on linear extended state observer. IEEE Trans. Energy Convers. 2021, 37, 824–831. [Google Scholar] [CrossRef]
- Yang, Y. Research on Position Sensor-Less Control System of Permanent Magnet Synchronous Motor; Harbin Institute of Technology: Harbin, China, 2018. [Google Scholar]
- Shen, Y.; Liu, A.; Cui, G.; Yang, X.; Zheng, Z. Sensor-less vector control of permanent magnet synchronous motor with extended sliding mode observer. J. Electr. Mach. Control. 2020, 24, 8. [Google Scholar] [CrossRef]
- Volpato Filho, C.J.; Xiao, D.; Vieira, R.P.; Emadi, A. Observers for high-speed sensor-less pmsm drives: Design methods, tuning challenges and future trends. IEEE Access 2021, 9, 56397–56415. [Google Scholar] [CrossRef]
- Wu, Z.; Li, R. Sensor-less control of PMSM based on sliding mode variable structure control and adaptive sliding mode observer. In Proceedings of the 2021 24th International Conference on Electrical Machines and Systems (ICEMS), Gyeongju, Republic of Korea, 31 October–3 November 2021; pp. 2015–2019. [Google Scholar]
- Zribi, M.; Chiasson, J. Position control of a PM stepper motor by exact linearization. IEEE Trans. Autom. Control 1991, 36, 620–625. [Google Scholar] [CrossRef]
- Yao, Y.; Huang, Y.; Peng, F.; Dong, J.; Zhu, Z. Compensation method of position estimation error for high-speed surface-mounted PMSM drives based on robust inductance estimation. IEEE Trans. Power Electron. 2021, 37, 2033–2044. [Google Scholar] [CrossRef]
- Tang, Q.; Yu, B.; Luo, P.; Luo, X.; Shen, A.; Xia, Y.; Xu, J. Second Harmonic Seamless Splicing Technique Based on Maximum Active-Voltage Vector for Online MTPA Tracking Control of SynRM. IEEE Trans. Ind. Electron. 2021, 69, 10958–10968. [Google Scholar] [CrossRef]
- Luo, X.; Shen, A.; Tang, Q.; Liu, J.; Xu, J. Two-step continuous-control set model predictive current control strategy for SPMSM sensor-less drives. IEEE Trans. Energy Convers. 2020, 36, 1110–1120. [Google Scholar] [CrossRef]
- Ding, S.; Hou, Q.; Wang, H. Disturbance-observer-based second-order sliding mode controller for speed control of PMSM drives. IEEE Trans. Energy Convers. 2022, 38, 100–110. [Google Scholar] [CrossRef]
- Wang, M.; Sun, D.; Zheng, Z.; Nian, H. A novel lookup table based direct torque control for OW-PMSM drives. IEEE Trans. Ind. Electron. 2020, 68, 10316–10320. [Google Scholar] [CrossRef]
- Xiong, Y.; Wang, A.; Zhang, T. Sensor-Less Complex System Control of PMSM Based on Improved SMO. In Proceedings of the 2021 6th International Conference on Automation, Control and Robotics Engineering (CACRE), Dalian, China, 15–17 July 2021; pp. 228–232. [Google Scholar]
- Guo, L.; Wang, H.; Jin, N.; Dai, L.; Cao, L.; Luo, K. A speed sensor-less control method for permanent magnet synchronous motor based on super-twisting sliding mode observer. In Proceedings of the 2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; pp. 1179–1184. [Google Scholar]
- Zhang, J.; Tian, J.; Alcaide, A.M.; Leon, J.I.; Vazquez, S.; Franquelo, L.G.; Luo, H.; Yin, S. Lifetime Extension Approach Based on Levenberg-Marquardt Neural Network and Power Routing of DC-DC Converters. IEEE Trans. Power Electron. 2023, 38, 10280–10291. [Google Scholar] [CrossRef]
- Ke, W.; Sun, D.; Zhang, X.; Nian, H.; Hu, B. Adaptive Capacitor Voltage-Based Model Predictive Control for Open-Winding PMSM System with a Floating Capacitor. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 11, 442–452. [Google Scholar] [CrossRef]
- Sun, C.; Sun, D.; Chen, W.; Nian, H. Improved model predictive control with new cost function for hybrid-inverter open-winding PMSM system based on energy storage model. IEEE Trans. Power Electron. 2021, 36, 10705–10715. [Google Scholar] [CrossRef]
- Chen, W.; Sun, D.; Wang, M.; Nian, H. Modeling and control for open-winding PMSM under open-phase fault based on new coordinate transformations. IEEE Trans. Power Electron. 2020, 36, 6892–6902. [Google Scholar] [CrossRef]
- Wang, M.; Sun, D.; Ke, W.; Nian, H. A universal lookup table-based direct torque control for OW-PMSM drives. IEEE Trans. Power Electron. 2020, 36, 6188–6191. [Google Scholar] [CrossRef]
- Sun, D.; Chen, W.; Cheng, Y.; Nian, H. Improved direct torque control for open-winding PMSM system considering zero-sequence current suppression with low switching frequency. IEEE Trans. Power Electron. 2020, 36, 4440–4451. [Google Scholar] [CrossRef]
- Zheng, Z.; Sun, D.; Wang, M.; Nian, H. A dual two-vector-based model predictive flux control with field-weakening operation for OW-PMSM drives. IEEE Trans. Power Electron. 2020, 36, 2191–2200. [Google Scholar] [CrossRef]
- Hu, W.; Ruan, C.; Nian, H.; Sun, D. An improved modulation technique with minimum switching actions within one PWM cycle for open-end winding PMSM system with isolated DC bus. IEEE Trans. Ind. Electron. 2019, 67, 4259–4264. [Google Scholar] [CrossRef]
- Cheng, Y.; Sun, D.; Chen, W.; Nian, H. Model predictive current control for an open-winding PMSM system with a common DC bus in 3-D space. IEEE Trans. Power Electron. 2020, 35, 9597–9607. [Google Scholar] [CrossRef]
- Zheng, Z.; Sun, D.; Wang, M.; Nian, H. Model predictive control with a novel cost function evaluation scheme for OW-PMSM drives. Electron. Lett. 2020, 56, 655–657. [Google Scholar] [CrossRef]
- Zheng, Z.; Sun, D. Model predictive flux control with cost function-based field weakening strategy for permanent magnet synchronous motor. IEEE Trans. Power Electron. 2019, 35, 2151–2159. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, Y.; Shi, K.; Zhang, F.; Du, H. High-frequency pulsating voltage injection PMSM position sensor-less control based on generalized second-order integrator. J. Electr. Mach. Control 2023, 1–10. [Google Scholar]
- Chen, B. Research on Medium and High Speed Control Technology and Starting Strategy of Permanent Magnet Synchronous Motor without Position Sensor; Huazhong University of Science and Technology: Wuhan, China, 2021. [Google Scholar]
- Liu, G.; Zhang, H.; Song, X. Position-estimation deviation-suppression technology of PMSM combining phase self-compensation SMO and feed-forward PLL. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 335–344. [Google Scholar] [CrossRef]
- Chen, S. Research on Position Sensor-Less Control Strategy of Permanent Magnet Synchronous Motor in Full Speed Domain; China University of Mining and Technology: Beijing, China, 2020. [Google Scholar]
- Lascu, C.; Andreescu, G.D. PLL position and speed observer with integrated current observer for sensor-less PMSM drives. IEEE Trans. Ind. Electron. 2020, 67, 5990–5999. [Google Scholar] [CrossRef]
- Tang, Q.; Chen, D.; He, X. Integration of improved flux linkage observer and I–f starting method for wide-speed-range sensorless SPMSM drives. IEEE Trans. Power Electr. 2019, 35, 8374–8383. [Google Scholar] [CrossRef]
- Chen, D.; Liu, X.; Yu, W.; Zhu, L.; Tang, Q. Neural-network based adaptive self-triggered consensus of nonlinear multi-agent systems with sensor saturation. IEEE Trans. Netw. Sci. Eng. 2021, 8, 1531–1541. [Google Scholar] [CrossRef]
- Hu, W.; Ruan, C.; Nian, H.; Sun, D. Zero-sequence current suppression strategy with common-mode voltage control for open-end winding PMSM drives with common DC bus. IEEE Trans. Ind. Electron. 2020, 68, 4691–4702. [Google Scholar] [CrossRef]
- Novak, Z.; Novak, M. Adaptive PLL-based sensor-less control for improved dynamics of high-speed PMSM. IEEE Trans. Power Electron. 2022, 37, 10154–10165. [Google Scholar] [CrossRef]
- Wang, H.; Yang, Y.; Ge, X.; Zuo, Y.; Yue, Y.; Li, S. PLL-and FLL-based speed estimation schemes for speed-sensor-less control of induction motor drives: Review and new attempts. IEEE Trans. Power Electron. 2021, 37, 3334–3356. [Google Scholar] [CrossRef]




| Parameter | Value | Parameter | Value |
| Rs | 2.875 Ω | λpm | 0.175 Wb |
| Ts | 0.1 ms | J | 0.85 mKgm2 |
| Ls | 85 mH | B | 0.373 mNms |
| Kη1 | 0.3861 | Kη2 | 750 |
| ωrmax | 3000 rpm | ωf | 2π10 rad/s |
| Kv | 0.999 | Tioad(ωr) | (0.00142ωr) Nm |
| VDC | 300 V | Pole Pairs | 4 |
| Power | 100 W | Q | 50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luan, M.; Zhang, Y.; Li, X.; Xu, F. A Rotor Position Detection Method for Permanent Magnet Synchronous Motors Based on Variable Gain Discrete Sliding Mode Observer. World Electr. Veh. J. 2024, 15, 87. https://doi.org/10.3390/wevj15030087
Luan M, Zhang Y, Li X, Xu F. A Rotor Position Detection Method for Permanent Magnet Synchronous Motors Based on Variable Gain Discrete Sliding Mode Observer. World Electric Vehicle Journal. 2024; 15(3):87. https://doi.org/10.3390/wevj15030087
Chicago/Turabian StyleLuan, Mingchen, Yun Zhang, Xiaowei Li, and Fenghui Xu. 2024. "A Rotor Position Detection Method for Permanent Magnet Synchronous Motors Based on Variable Gain Discrete Sliding Mode Observer" World Electric Vehicle Journal 15, no. 3: 87. https://doi.org/10.3390/wevj15030087
APA StyleLuan, M., Zhang, Y., Li, X., & Xu, F. (2024). A Rotor Position Detection Method for Permanent Magnet Synchronous Motors Based on Variable Gain Discrete Sliding Mode Observer. World Electric Vehicle Journal, 15(3), 87. https://doi.org/10.3390/wevj15030087








