Sizing of Autonomy Source Battery–Supercapacitor Vehicle with Power Required Analyses
Abstract
1. Introduction
2. System Modeling
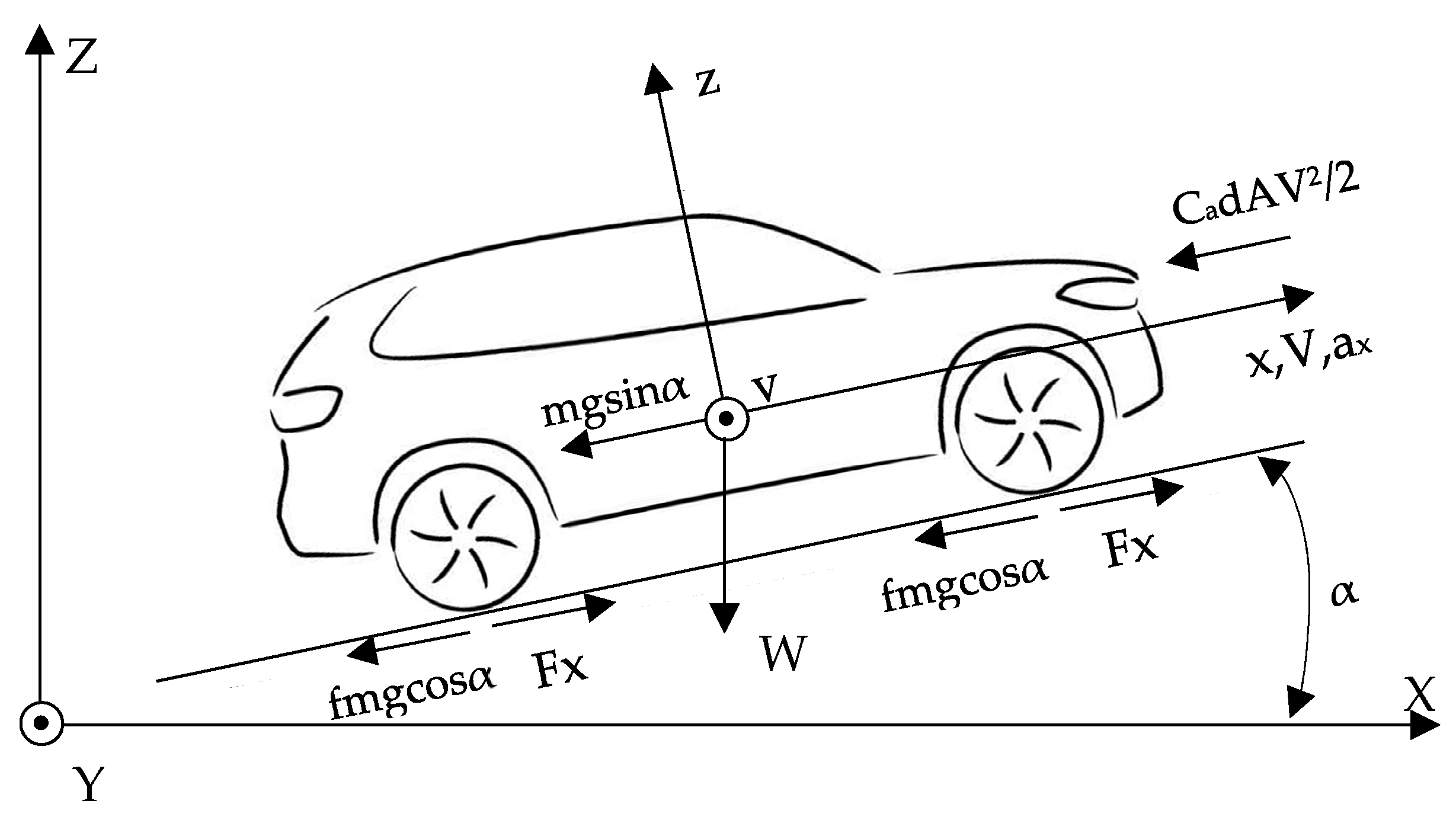
2.1. Vehicular Dynamic Modeling
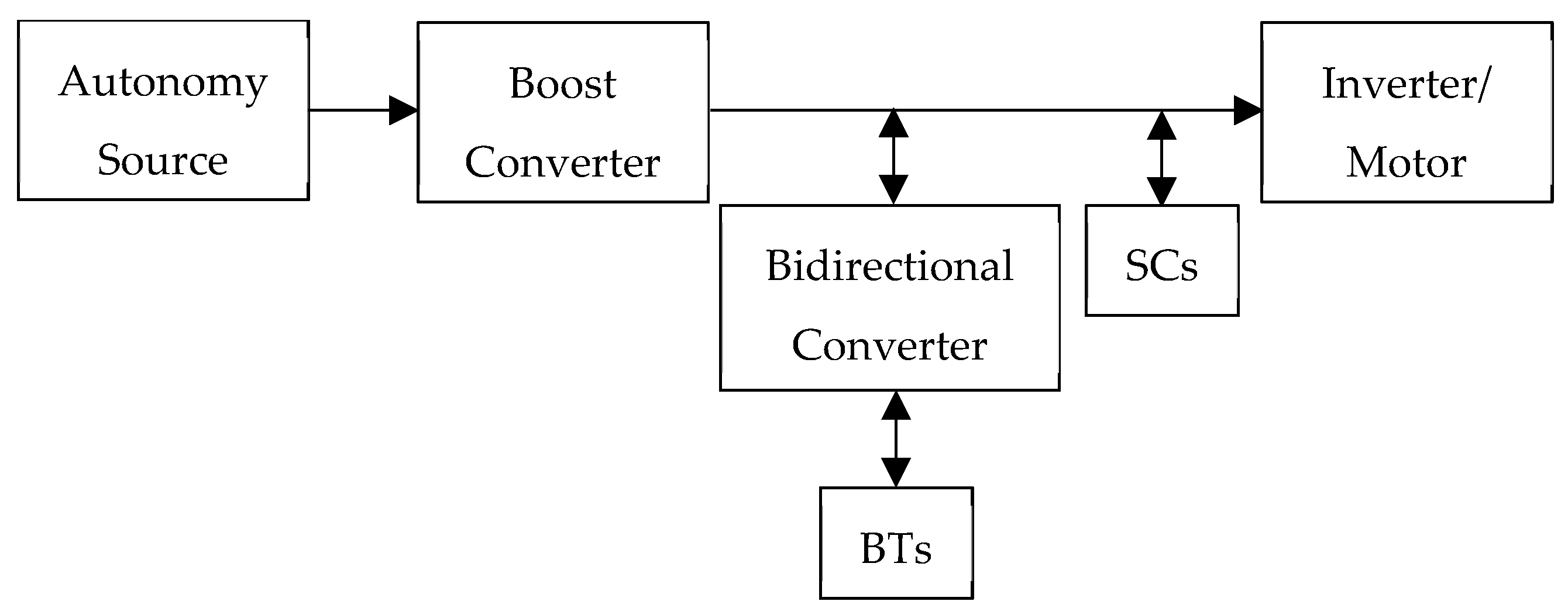
2.2. EV’s Powertrain Topology
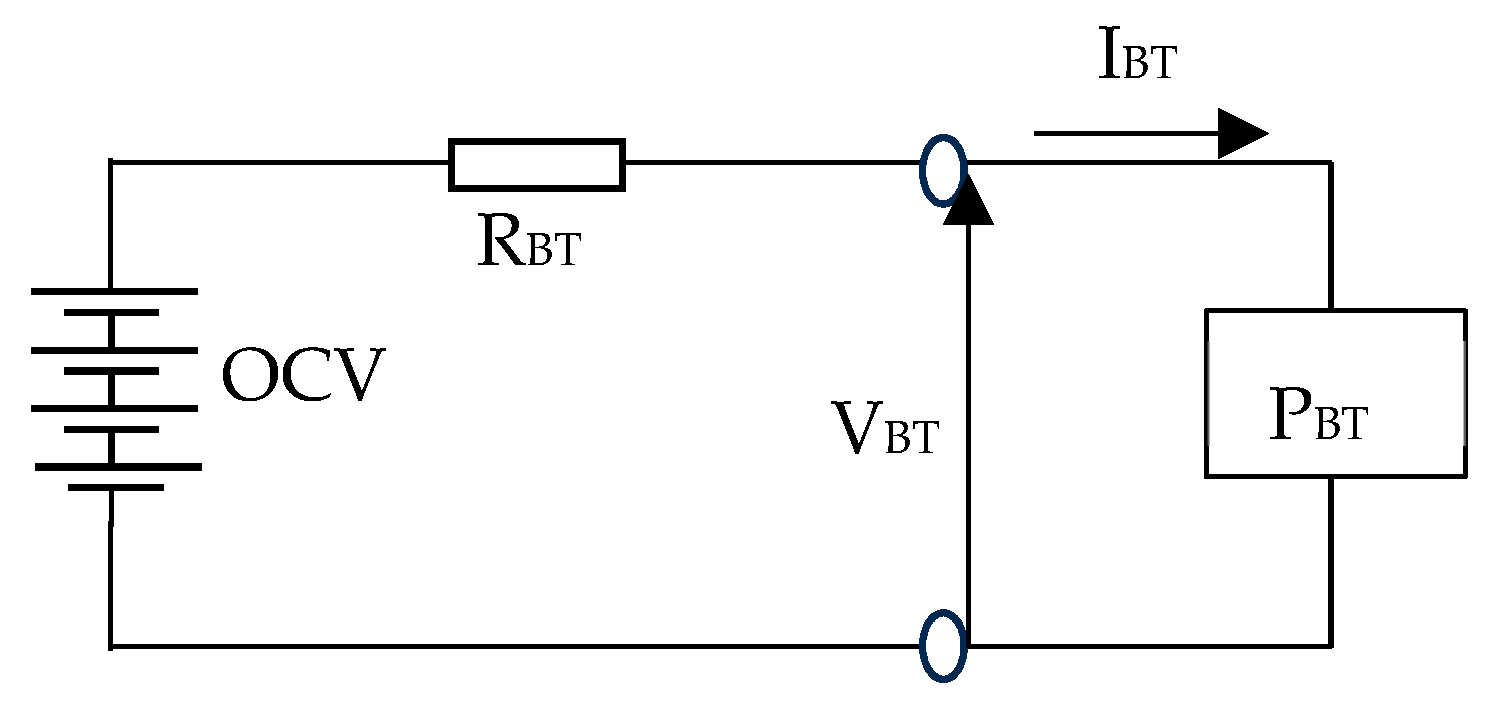
2.3. Battery Model
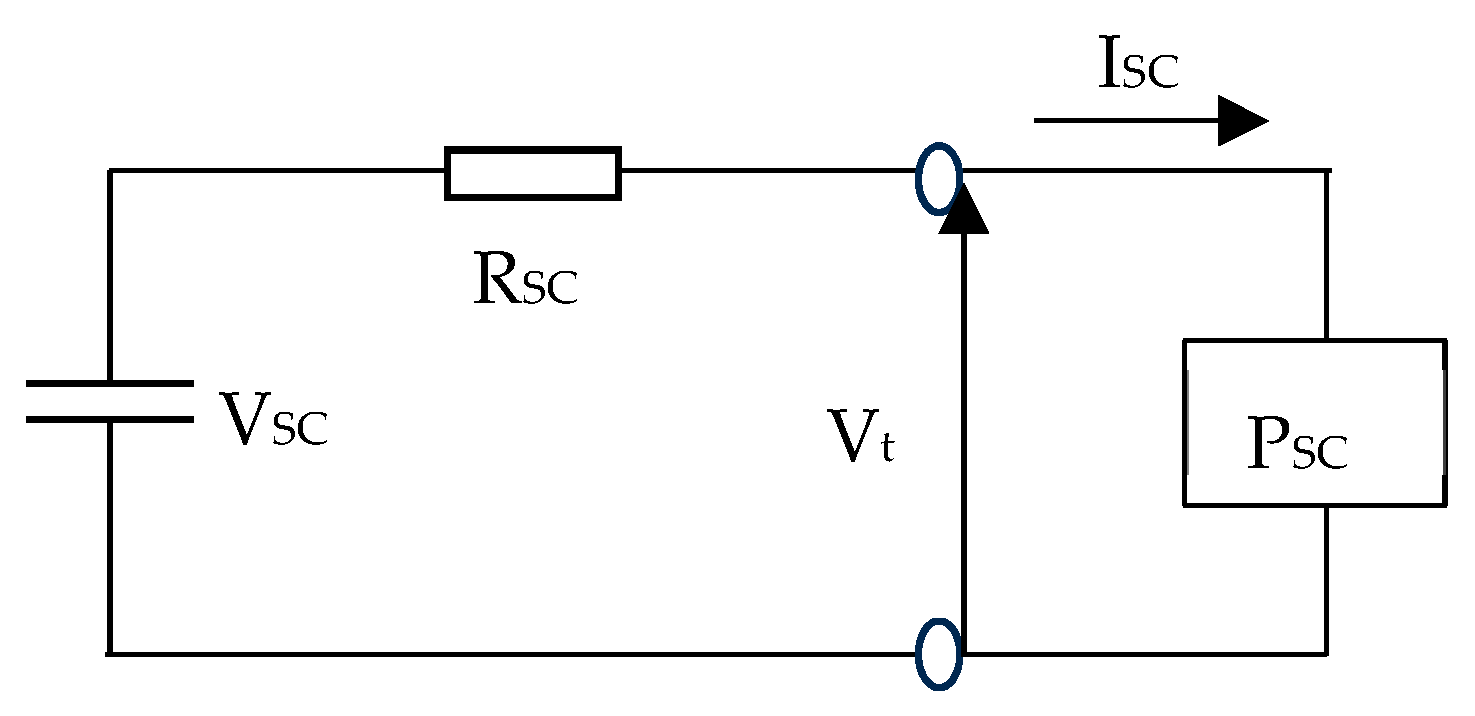
2.4. Supercapacitor Modeling
3. Methodology
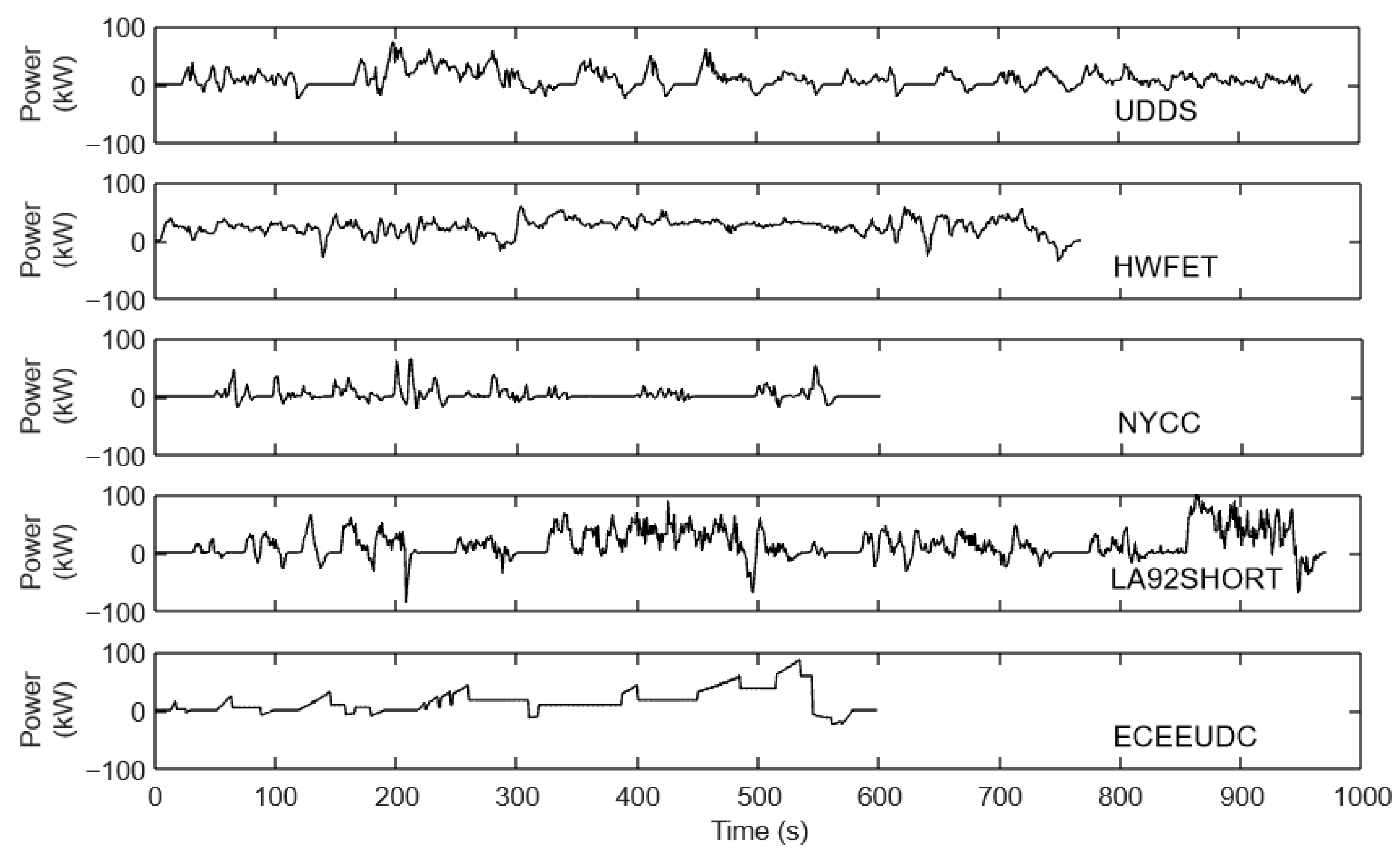
3.1. Driving Cycles Used in the ESS Sizing Methodology
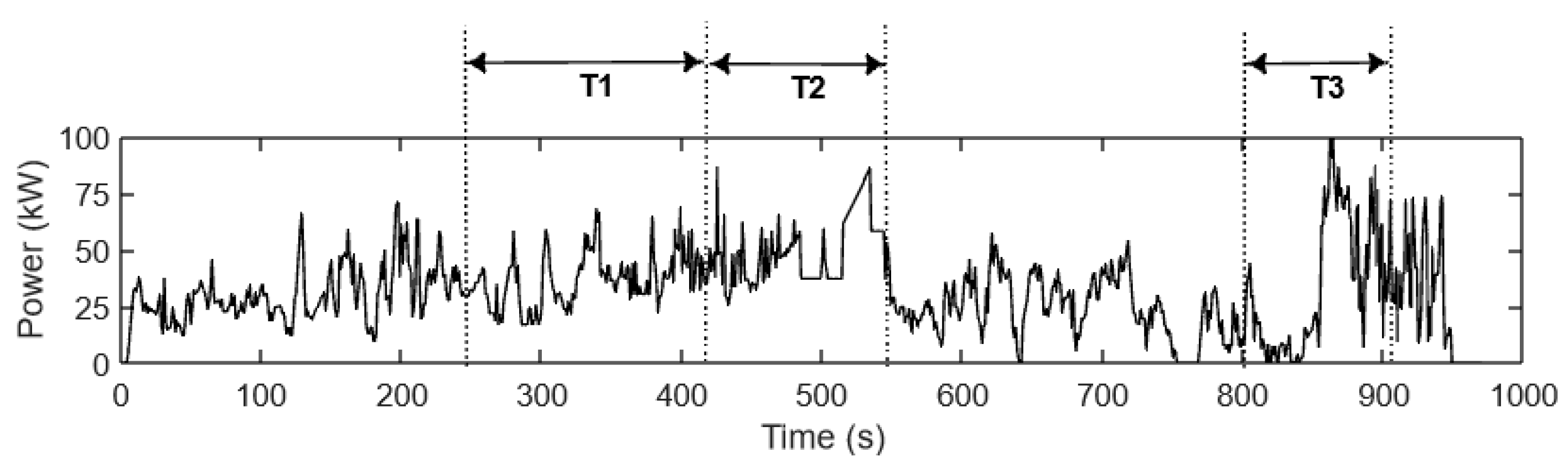
3.2. Envelope Power Profile
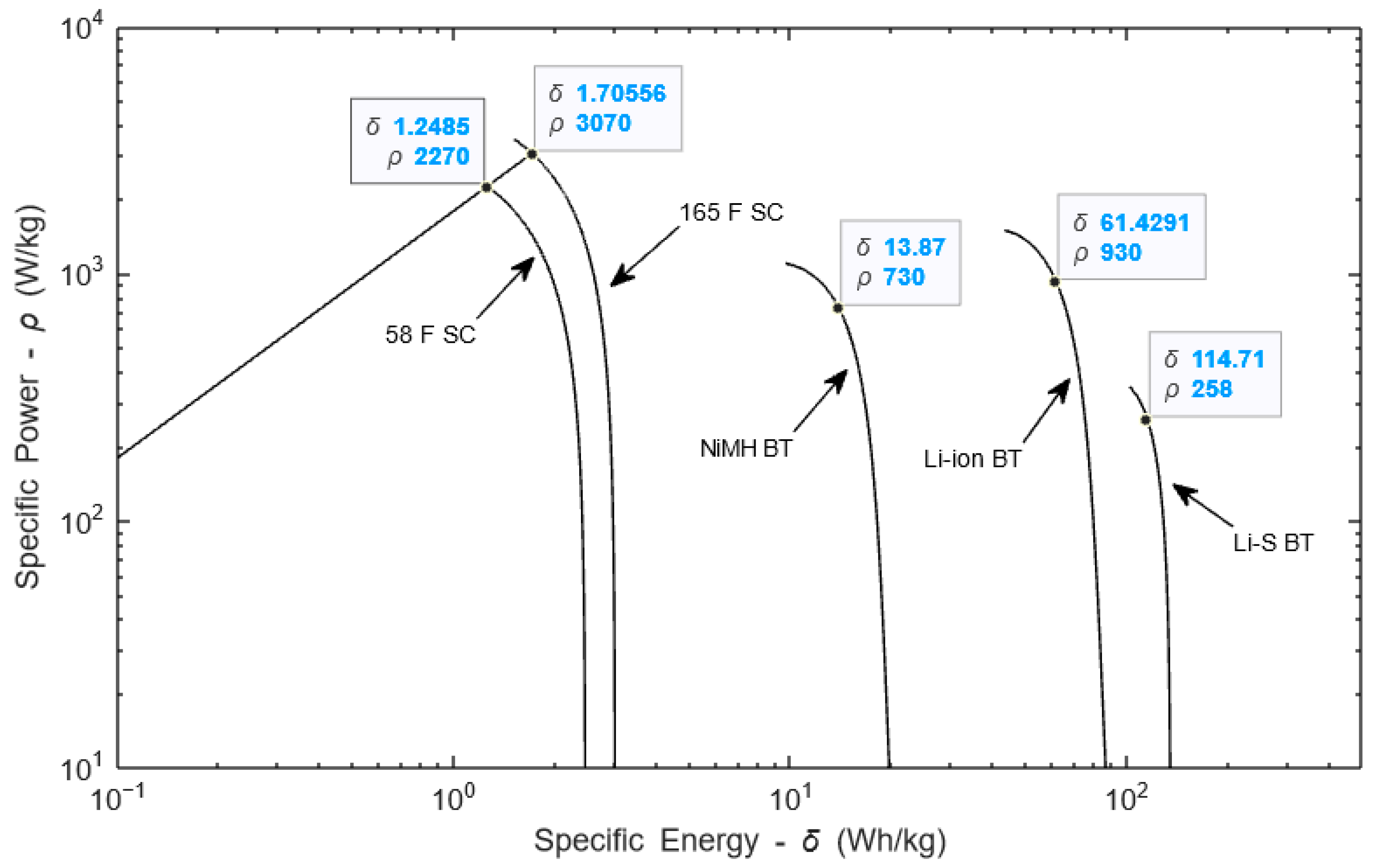
3.3. Ragone Coefficients
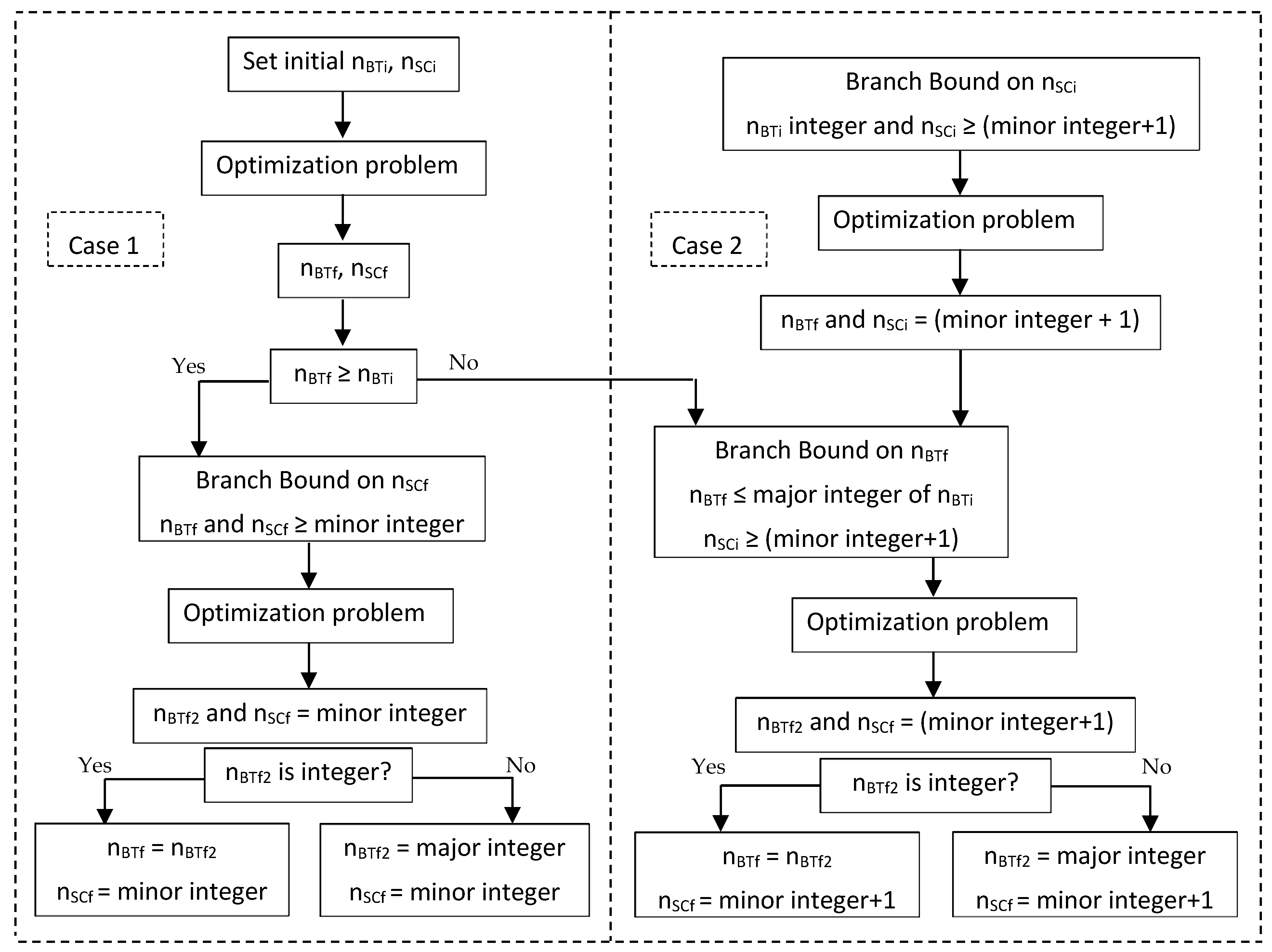
3.4. Optimization Problem—ESS Sizing Methodology
- The power required of the envelope power profile (Figure 7) is equal to the power delivered by the ESS, PESS, plus the power produced by the autonomy source, Pautonomy:
- The ESS power cannot exceed the maximum available power in the BT and SC strings. This available power was estimated considering the coefficients of maximum specific power, ρBT, ρSC, taken from the BT’s/SC’s Ragone plots in Figure 8.
- The SC voltage is between Vtmax (400 V) and Vtmin (250 V):
- The BT state of charge, between the maximum, SoCBTmax (100%), and the minimum, SoCBTmin (60%), values is as follows:
3.4.1. ESS Sizing Methodology Input Data
3.4.2. ESS Sizing Methodology Overview
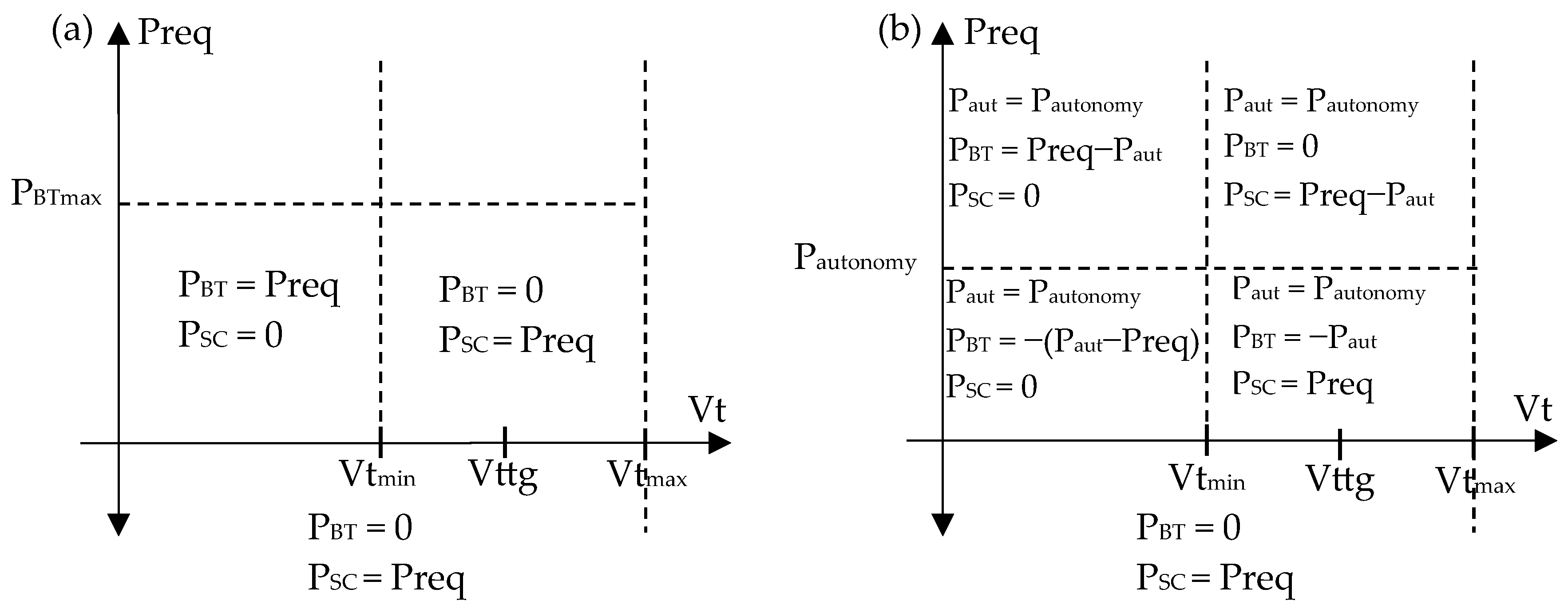
3.5. Rules-Based Energy Management
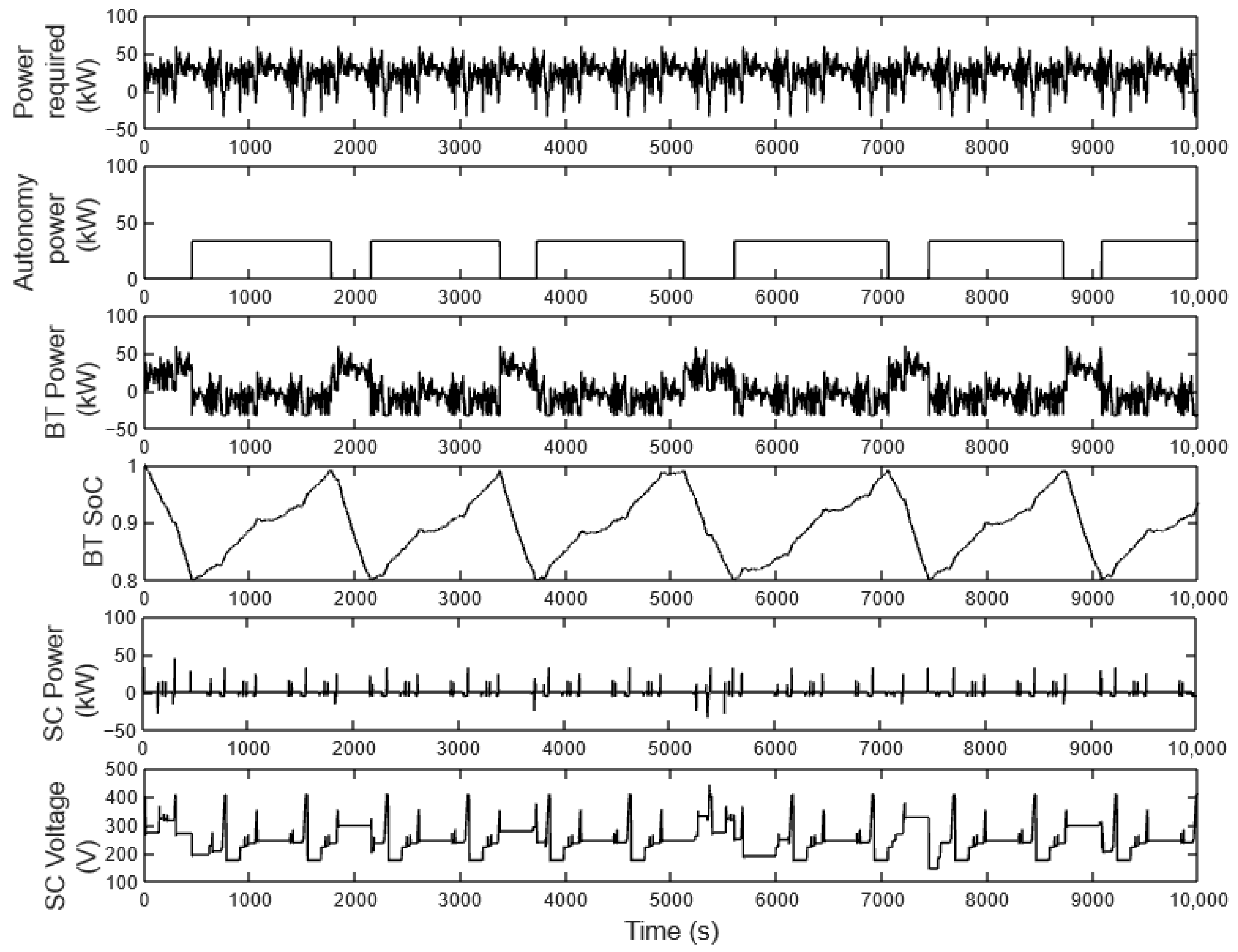
- Power deliverable by the autonomy source must be equal to the average power of the envelope power profile in Figure 7, i.e., 33 kW.
- The autonomy source has an on/off control. When PBTmax is reached, the autonomy source is turned on to provide a power system, reducing the BT demand. Once SoCBTmax is reached, the autonomy source is turned off.
- The SC voltage should be kept around its half load (Vttg ≈ 330 V). At this voltage, the SC can provide extra power in acceleration or accept power from regenerative braking. The voltage regulation is controlled via the BT bidirectional converter.
- The SC absorbs the regenerative braking energy.
4. Results and Discussion
4.1. Simulation Procedure
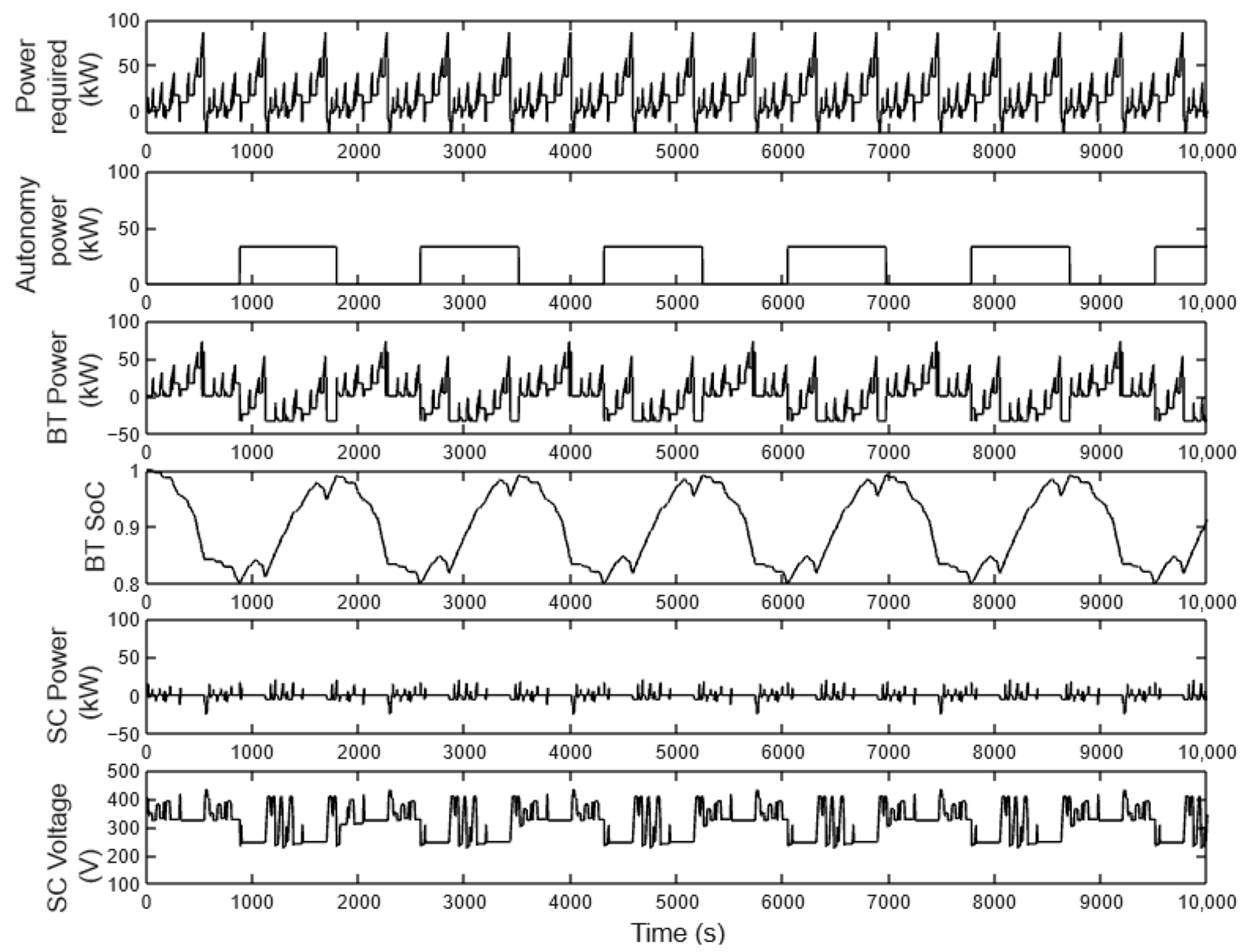
4.2. Rule-Based Energy Management
4.3. A Brief Analysis of ESS’s Cost
- The definition of the location.
- Types and models of batteries available.
- Definition or estimation of where and how the vehicle will be driven.
- Considering sizing and management, how many cycles can these batteries withstand?
- The local energy and fuel costs.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Koengkan, M.; Fuinhas, J.A.; Teixeira, M.; Kazemzadeh, E.; Auza, A.; Dehdar, F.; Osmani, F. The Capacity of Battery-Electric and Plug-in Hybrid Electric Vehicles to Mitigate CO2 Emissions: Macroeconomic Evidence from European Union Countries. World Electr. Veh. J. 2022, 13, 58. [Google Scholar] [CrossRef]
- Lopes, J.; Pomílio, J.A.; Ferreira, P.A.V. Optimal Sizing of Batteries and Ultracapacitors for Fuel Cell Electric Vehicles. In Proceedings of the IECON 2011—37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, Australia, 7–10 November 2011. [Google Scholar]
- Gurkaynak, Y.; Khaligh, A.A.; Emadi, A. State of the Art Power Management Algorithms for Hybrid Electric Vehicles. In Proceedings of the IEEE Vehicle Power Propulsion Conference, Dearborn, MI, USA, 7–10 September 2009. [Google Scholar]
- Li, M.; Xu, H.; Li, W.; Liu, Y.; Li, F.; Hu, Y.; Li, L. The Structure and Control Method of Hybrid Power Source for Electric Vehicle. Energy 2016, 112, 1273–1285. [Google Scholar] [CrossRef]
- Thounthong, P.; Raël, S.; Davat, B. Energy Management of Fuel Cell/Battery/Supercapacitor Hybrid Power Source for Vehicle Applications. J. Power Sources 2009, 193, 376–385. [Google Scholar] [CrossRef]
- Mahmoudi, C.; Flah, A.; Sbita, L. An overview of electric vehicle concept and power management strategies. In Proceedings of the International Conference on Electrical Sciences and Technologies in Maghreb, Tunis, Tunisia, 3–6 November 2014. [Google Scholar]
- Becker, J.; Schaeper, C.; Sauer, D. Energy management system for a multi-source storage system electric vehicle. In Proceedings of the IEEE Vehicle Power Propulsion Conference, Seoul, Republic of Korea, 9–12 October 2012. [Google Scholar]
- Liu, F.; Wang, C.; Luo, Y. Parameter Matching Method of a Battery-Supercapacitor Hybrid Energy Storage System for Electric Vehicles. World Electr. Veh. J. 2021, 12, 253. [Google Scholar] [CrossRef]
- Larminie, J.; Lowry, J. Electric Vehicle Technology Explained; John Wiley & Sons Ltd.: Chichester, UK, 2003; ISBN 0-470-85163-5. [Google Scholar]
- Lopes, J. Optimal Sizing and Power Management Methodologies of Energy Sources for Electric Vehicles. Available online: http://repositorio.unicamp.br/bitstream/REPOSIP/260868/1/Lopes_Juliana_D.pdf (accessed on 2 July 2019).
- Christen, T.; Carlen, M.W. Theory of Ragone Plots. J. Power Sources 2000, 91, 210–216. [Google Scholar] [CrossRef]
- Schupbach, R.; Balda, J.; Zolot, M.; Kramer, B. Design Methodology of a Combined Battery-Ultracapacitor Energy Storage Unit for Vehicle Power Management. In Proceedings of the IEEE 34th Annual Conference on Power Electronics Specialist, Acapulco, Mexico, 15–19 June 2003. [Google Scholar]
- Tu, J.; Bai, Z.; Wu, X. Sizing of a Plug-In Hybrid Electric Vehicle with the Hybrid Energy Storage System. World Electr. Veh. J. 2022, 13, 110. [Google Scholar] [CrossRef]
- KoteswaraRao, K.V.; Srinivasulu, G.N.; Rahul, J.R.; Velisala, V. Optimal component sizing and performance of Fuel Cell—Battery powered vehicle over world harmonized and new european driving cycles. Energy Convers. Manag. 2024, 300, 117992. [Google Scholar] [CrossRef]
- Bauman, J.; Kazerani, M. A Comparative Study of Fuel-Cell–Battery, Fuel-Cell–Ultracapacitor, and Fuel-Cell–Battery–Ultracapacitor Vehicles. IEEE Trans. Veh. Technol. 2008, 57, 760–769. [Google Scholar] [CrossRef]
- Huilong, Y.; Cao, D. Multi-objective Optimal Sizing and Real-time Control of Hybrid Energy Storage Systems for Electric Vehicles. In Proceedings of the IEEE Intelligent Vehicle Symposium, Changshu, China, 26–30 June 2018. [Google Scholar]
- Araújo, R.E.; Castro, R.; Pinto, C.; Melo, P.; Freitas, D. Combined Sizing and Energy Management in EVs With Batteries and Supercapacitors. IEEE Trans. Veh. Technol. 2014, 63, 3062–3076. [Google Scholar] [CrossRef]
- Souffran, G.; Miegeville, L.; Guerin, P. Simulation of Real-World Vehicle Missions Using a Stochastic Markov Model for Optimal Powertrain Sizing. IEEE Trans. Veh. Technol. 2012, 61, 3454–3465. [Google Scholar] [CrossRef]
- Schwarzer, V.; Ghorbani, R.; Rocheleau, R. Drive cycle generation for stochastic optimization of energy management controller for hybrid vehicles. In Proceedings of the IEEE International Control Applications Conference, Yokohama, Japan, 8–10 September 2010. [Google Scholar]
- Banvait, H.; Anwar, S.; Chen, Y. A rule-based energy management strategy for Plug-in Hybrid Electric Vehicle (PHEV). In Proceedings of the American Control Conference, St. Louis, MO, USA, 10–12 June 2009. [Google Scholar]
- Wu, J.; Peng, J.; He, H.; Luo, J. Comparative Analysis on the Rule-based Control Strategy of Two Typical Hybrid Electric Vehicle Powertrain. Energy Procedia 2016, 104, 384–389. [Google Scholar] [CrossRef]
- Gillespie, T. Fundamentals of Vehicle Dynamics; SAE International: Warrendale, PA, USA, 1992; ISBN 978-1-4686-0176-3. [Google Scholar]
- Ulitskaya, J. Which Electric Vehicles Are Most Available Right Now? Available online: https://www.cars.com/articles/which-electric-vehicles-are-most-available-right-now-448044/ (accessed on 23 January 2023).
- Goodwin, A. Best Electric Cars and EVs for 2024. Available online: https://www.cnet.com/roadshow/news/best-ev-electric-car/ (accessed on 23 January 2023).
- Best Electric Cars. Available online: https://www.truecar.com/best-cars-trucks/cars/fuel-electric/ (accessed on 23 January 2023).
- Electric Vehicle Research and Development. Available online: https://afdc.energy.gov/fuels/electricity_research.html#battery (accessed on 23 January 2023).
- Volvo Car Group Signs Multi-Billion-Dollar Battery Supply Deals with CATL and LG Chem. Available online: https://www.media.volvocars.com/global/en-gb/media/pressreleases/252485/volvo-car-group-signs-multi-billion-dollar-battery-supply-deals-with-catl-and-lg-chem (accessed on 23 January 2023).
- Saw, L.; Yonghuang, Y.; Tay, A. Integration Issues of Lithium-ion Battery into Electric Vehicles Battery Pack. J. Clean. Prod. 2016, 113, 1032–1045. [Google Scholar] [CrossRef]
- Jaguemont, J.; Boulon, L.; Dubé, Y. A Comprehensive Review of Lithium-ion Batteries Used in Hybrid and Electric Vehicles at Cold Temperatures. J. Appl. Energy 2016, 164, 99–114. [Google Scholar] [CrossRef]
- Chen, M.; Ma, X.; Chen, B.; Arsenault, R.; Karlson, P.; Simon, N.; Wang, Y. Recycling End-of-Life Electric Vehicle Lithium-Ion Batteries. J. Joule 2019, 3, 2622–2646. [Google Scholar] [CrossRef]
- Xie, W.; Liu, X.; He, R.; Li, Y.; Gao, X.; Li, X.; Peng, Z.; Feng, S.; Feng, X.; Yang, S. Challenges and Opportunities Toward Fast-Charging of Lithium-ion Batteries. J. Energy Storage 2020, 32, 101837. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, L.; Sun, F.; Wang, Z. An Overview on Thermal Safety Issues of Lithium-ion Batteries for Electric Vehicle Application. IEEE Access 2018, 6, 23848–23863. [Google Scholar] [CrossRef]
- Batteries for Electric Vehicles. Available online: https://afdc.energy.gov/vehicles/electric_batteries.html (accessed on 23 January 2023).
- Torabi, F.; Ahmadi, P. Simulation of Battery Systems; Academic Press: Cambridge, MA, USA, 2020; Chapter 1; pp. 1–54. ISBN 978-0-12-816212-5. [Google Scholar]
- Abdin, Z.; Khalilpour, K.R. Polygeneration with Polystorage for Chemical and Energy Hubs; Academic Press: Cambridge, MA, USA, 2019; Chapter 4; pp. 77–131. ISBN 978-0-12-813306-4. [Google Scholar]
- Tsai, P.; Chan, L. Nickel-Based Batteries: Materials and Chemistry, Electricity Transmission, Distribution and Storage Systems; Woodhead Publishing: Sawston, UK, 2013; pp. 309–397. ISBN 978-1-84569-784-6. [Google Scholar]
- Ameur, A.; Berrada, A.; Loudiyi, K.; Adomatis, R. Hybrid Energy System Models; Academic Press: Cambridge, MA, USA, 2021; pp. 195–238. ISBN 978-0-12-821403-9. [Google Scholar]
- Merrifield, R. Cheaper, Lighter and More Energy-Dense: The Promise of Lithium-Sulphur Batteries. Available online: https://ec.europa.eu/research-and-innovation/en/horizon-magazine/cheaper-lighter-and-more-energy-dense-promise-lithium-sulphur-batteries (accessed on 23 January 2023).
- Patel, P. Long-lasting Lithium-Sulfur Battery Promises to Double EV Range. Available online: https://spectrum.ieee.org/lithium-sulfur-battery-news-ev-electric-vehicle-range (accessed on 23 January 2023).
- Lisa Project|Developing the New Generation of LIs Battery Cells. Available online: https://lisaproject.eu/ (accessed on 23 February 2023).
- Karthik, M.; Vijayachitra, S. Numerical Study on the Detailed Characterization of Ni-MH Battery Model for its Dynamic Behavior using Multi-Regression Analysis—MRA. IJSCE 2015, 4, 34–43. [Google Scholar]
- Propp, K.; Marinescu, M.; Auger, D.J.; O’Neill, L.; Fotouhi, A.; Somasundaram, K.; Offer, G.J.; Minton, G.; Longo, S.; Wild, M.; et al. Multi-Temperature State-Dependent Equivalent Circuit Discharge Model for Lithium-Sulfur Batteries. J. Power Sources 2016, 328, 289–299. [Google Scholar] [CrossRef]
- datasheets.com. Available online: https://www.datasheets.com/en/part-details/hhr650d-panasonic-31361681#datasheet (accessed on 3 October 2022).
- Kroeze, R.; Krein, P.T. Electrical battery model for use in dynamic electric vehicle simulations. In Proceedings of the IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008. [Google Scholar]
- Omar, N.; Verbrugge, B.; Mulder, G.; van den Bossche, P.; van Mierlo, J.; Daowd, M.; Dhaens, M.; Pauwels, S. Evaluation of performance characteristics of various lithium-ion batteries for use in BEV application. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010. [Google Scholar]
- Chau, K.; Wong, Y. Overview of power management in hybrid electric vehicles. Energy Convers. Manag. 2002, 43, 1953–1968. [Google Scholar] [CrossRef]
- maxwell.com. Available online: https://www.maxwell.com/images/documents/datasheet_16v_small_cell_module.pdf (accessed on 18 August 2019).
- maxwell.com. Available online: https://www.maxwell.com/images/documents/hq_48v_ds10162013.pdf (accessed on 18 August 2019).
- epa.gov. Available online: https://www.epa.gov/vehicle-and-fuel-emissions-testing/dynamometer-drive-schedules (accessed on 18 August 2019).
- Sadoun, R.; Rizoug, N.; Bartholomeüs, P.; Barbedette, B.; le Moigne, P. Optimal sizing of hybrid supply for electric vehicle using Li-ion battery and supercapacitor. In Proceedings of the IEEE Vehicle Power Propulsion Conference, Chicago, IL, USA, 6–9 September 2011. [Google Scholar]
- Eldeeb, H.H.; Elsayed, A.T.; Lashway, C.R.; Mohammed, O. Hybrid Energy Storage Sizing and Power Splitting Optimization for Plug-In Electric Vehicles. IEEE Trans. Ind. Appl. 2019, 55, 2252–2262. [Google Scholar] [CrossRef]
- Bertsekas, D.P. Nonlinear Programming; Athena Scientific: Belmont, CA, USA, 1999; ISBN 1886529051. [Google Scholar]
- Kouchachvili, L.; Yaïci, W.; Entchev, E. Hybrid Battery/Supercapacitor Energy Storage System for the Electric Vehicles. J. Power Sources 2018, 374, 237–248. [Google Scholar] [CrossRef]
- Fathabadi, H. Novel Fuel Cell/Battery/Supercapacitor Hybrid Power Source for Fuel Cell Hybrid Electric Vehicles. Energy 2018, 143, 467–477. [Google Scholar] [CrossRef]
- Zou, K.; Luo, W.; Lu, Z. Real-Time Energy Management Strategy of Hydrogen Fuel Cell Hybrid Electric Vehicles Based on Power Following Strategy–Fuzzy Logic Control Strategy Hybrid Control. World Electr. Veh. J. 2023, 14, 315. [Google Scholar] [CrossRef]
- Panaparambil, V.S.; Kashyap, Y.; Castelino, R.V. A Review on Hybrid Source Energy Management Strategies for Electric Vehicle. Int. J. Energy Res. 2021, 45, 19819–19850. [Google Scholar] [CrossRef]
- Global EV Outlook 2023, IEA, Paris. Available online: https://www.iea.org/reports/global-ev-outlook-2023 (accessed on 20 November 2023).
- Whitehead, J.; Washington, S.P.; Franklin, J.P. The Impact of Different Incentive Policies on Hybrid Electric Vehicle Demand and Price: An International Comparison. World Electr. Veh. J. 2019, 10, 20. [Google Scholar] [CrossRef]



| Parameter | Nomenclature | Value |
|---|---|---|
| Vehicle’s Gross Mass | M | 2050 kg |
| Vehicle’s Rotating Components’ Mass | Mr | 154.8 kg |
| Drag Coefficient | Ca | 0.45 |
| Vehicle’s Frontal Area | A | 3.16 m2 |
| Coefficient of Rolling Resistance | f | 0.015 |
| Manufacturer/Model | Type | Terminal Voltage [V] | Capacity [Ah] | Peukert Coefficient | Resistance [Ω] | Cell Mass [kg] | ρBT [W/kg] |
|---|---|---|---|---|---|---|---|
| Panasonic/CGR18650A | Li-ion | 3.7 [44] | 2.2 [44] | 1.03 [45] | Equation (18) | 0.045 | 930 |
| Panasonic/HHR650D | NiMH | 1.2 | 6.5 | 1.027 | 0.002 | 0.170 | 730 |
| Oxis Energy pouch cell | Li-S | 2.1 | 14 | 1 | Equation (21) | 0.140 | 258 |
| Manufacturer/Model | Nominal Voltage [V] | Capacitance [F] | Resistance [Ω] | Mass [kg] | ρSC [W/kg] |
|---|---|---|---|---|---|
| Maxwell/BMOD0058 E016 B02 [47] | 16 | 58 | 0.022 | 0.63 | 2270 |
| Maxwell/BMOD0165 P048 [48] | 48.6 | 165 | 0.0063 | 13.5 | 3070 |
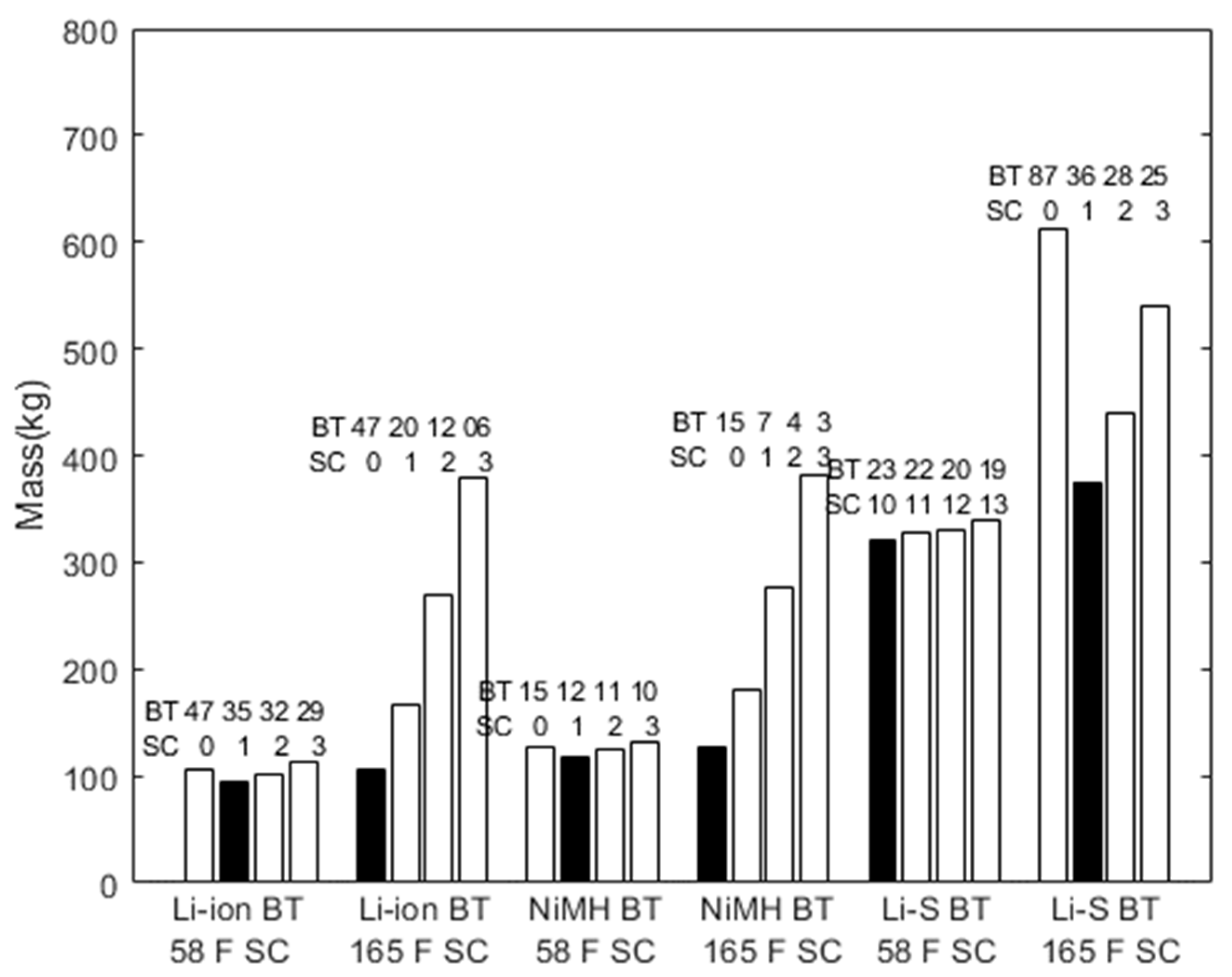
| Li-ion | Li-S | NiMH | SC of 58 F | SC of 165 F | |
|---|---|---|---|---|---|
| Number of elements per string | 50 cells | 50 cells | 50 cells | 25 packs | Nine packs |
| String mass, mBT,SC (kg) | 2.25 | 7.05 | 8.50 | 15.75 | 121.5 |
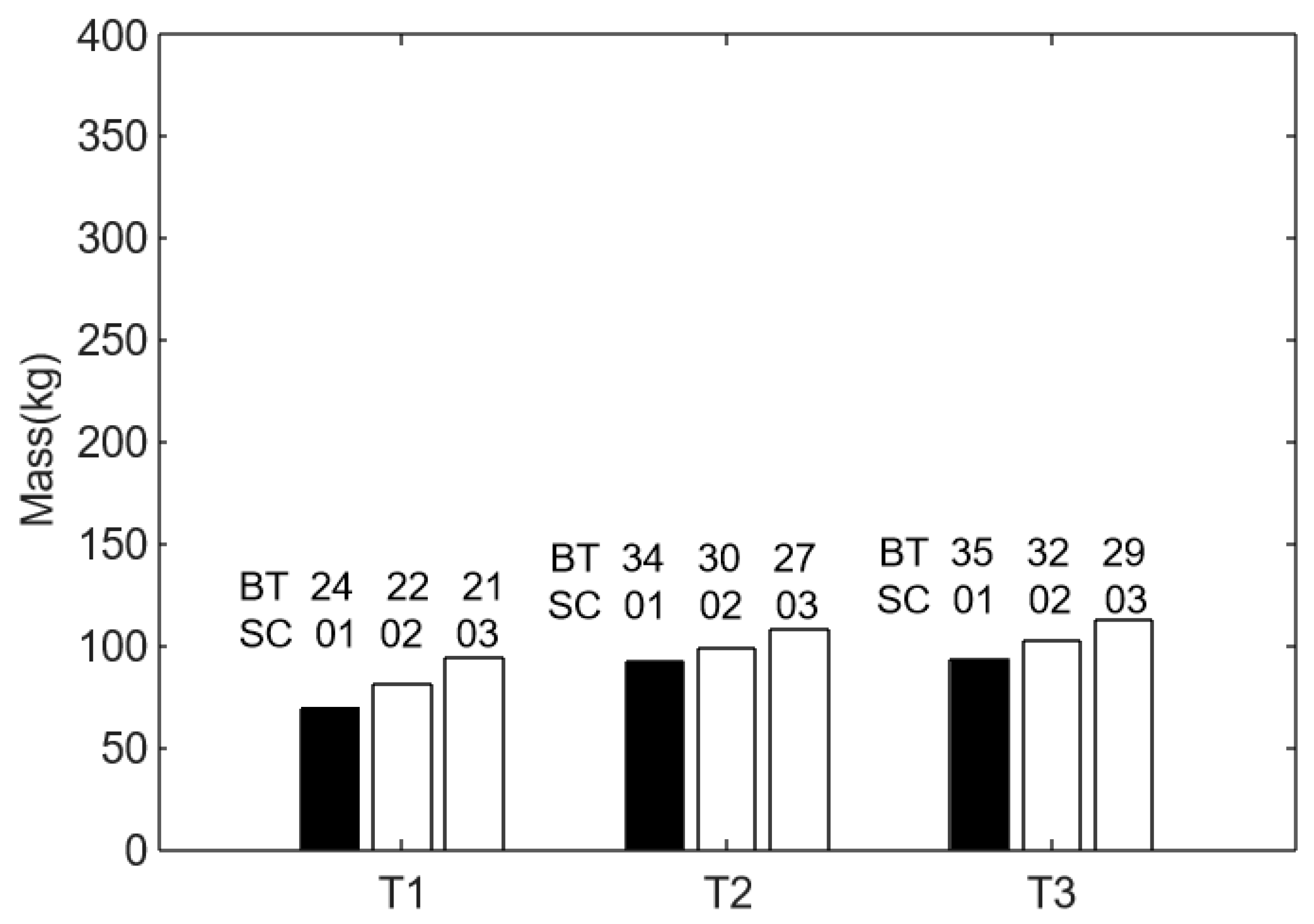
| nBTi | nSCi | nBTf | nSCf | Mass (kg) | |
|---|---|---|---|---|---|
| Case 1 | 2 | 30 | 34.57 | 1.02 | 93.85 |
| 34.57 | ≥1 | 34.65 | 1 | 93.71 | |
| - | - | 35 | 1 | 94.5 | |
| Case 2 | 33 | ≥2 | 32.87 | 2 | 105.46 |
| ≤33 | ≥2 | 31.55 | 2 | 102.49 | |
| - | - | 32 | 2 | 103.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopes, J.; Pomilio, J.A.; Ferreira, P.A.V. Sizing of Autonomy Source Battery–Supercapacitor Vehicle with Power Required Analyses. World Electr. Veh. J. 2024, 15, 76. https://doi.org/10.3390/wevj15030076
Lopes J, Pomilio JA, Ferreira PAV. Sizing of Autonomy Source Battery–Supercapacitor Vehicle with Power Required Analyses. World Electric Vehicle Journal. 2024; 15(3):76. https://doi.org/10.3390/wevj15030076
Chicago/Turabian StyleLopes, Juliana, José Antenor Pomilio, and Paulo Augusto Valente Ferreira. 2024. "Sizing of Autonomy Source Battery–Supercapacitor Vehicle with Power Required Analyses" World Electric Vehicle Journal 15, no. 3: 76. https://doi.org/10.3390/wevj15030076
APA StyleLopes, J., Pomilio, J. A., & Ferreira, P. A. V. (2024). Sizing of Autonomy Source Battery–Supercapacitor Vehicle with Power Required Analyses. World Electric Vehicle Journal, 15(3), 76. https://doi.org/10.3390/wevj15030076






