Long Downhill Braking and Energy Recovery of Pure Electric Commercial Vehicles
Abstract
1. Introduction
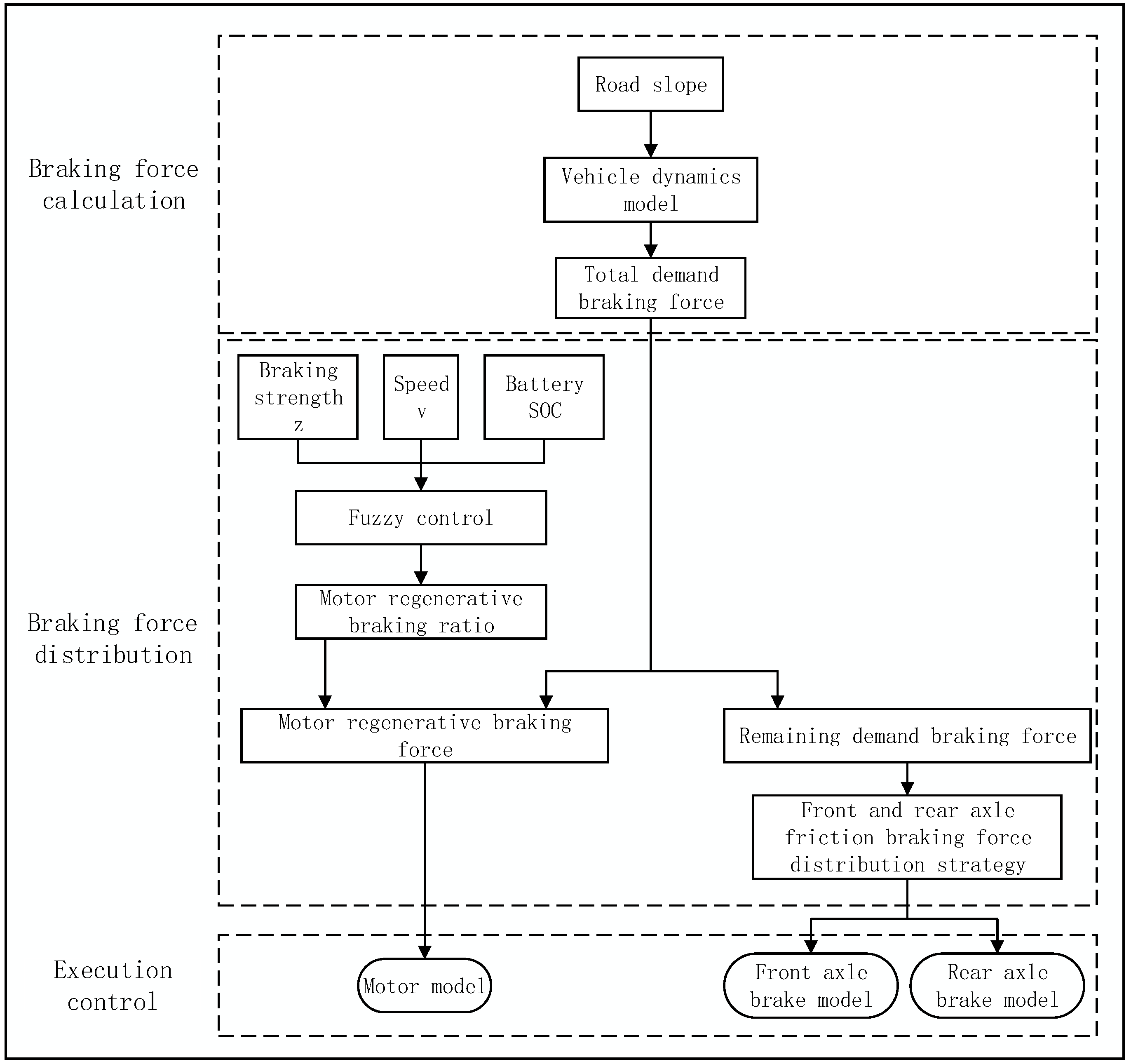
2. Long Downhill Braking Control Strategy
- (1)
- Braking force calculation: Referring to the vehicle dynamics model, calculate the required braking force of the entire vehicle based on the road slope I;
- (2)
- Braking force distribution: A fuzzy controller is established by taking the braking strength z, vehicle speed v and the state of charge (SOC) of the battery as inputs, and the proportion of regenerative braking force of the motor to the required braking force of the entire vehicle k as output, and the remaining required braking force is distributed to the front and rear axles;
- (3)
- The regenerative braking force and friction braking force of the motor are input into the established model, and the control strategy is verified by joint simulation using Simulink and Cruise(R2019.2) software.
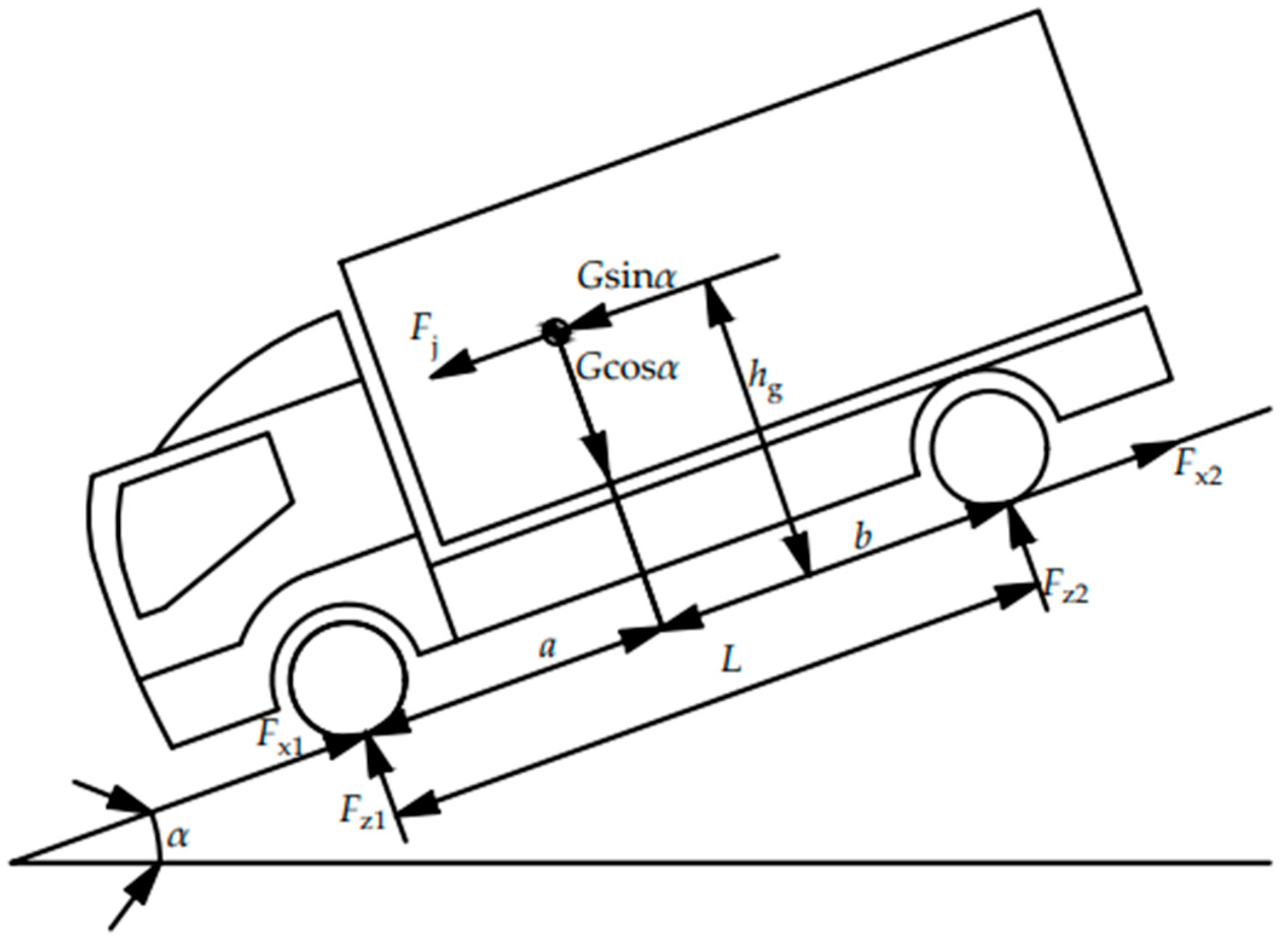
2.1. Vehicle Demand Braking Force
2.2. Fuzzy Control
2.3. Calculation of Regenerative Braking Force for Motor
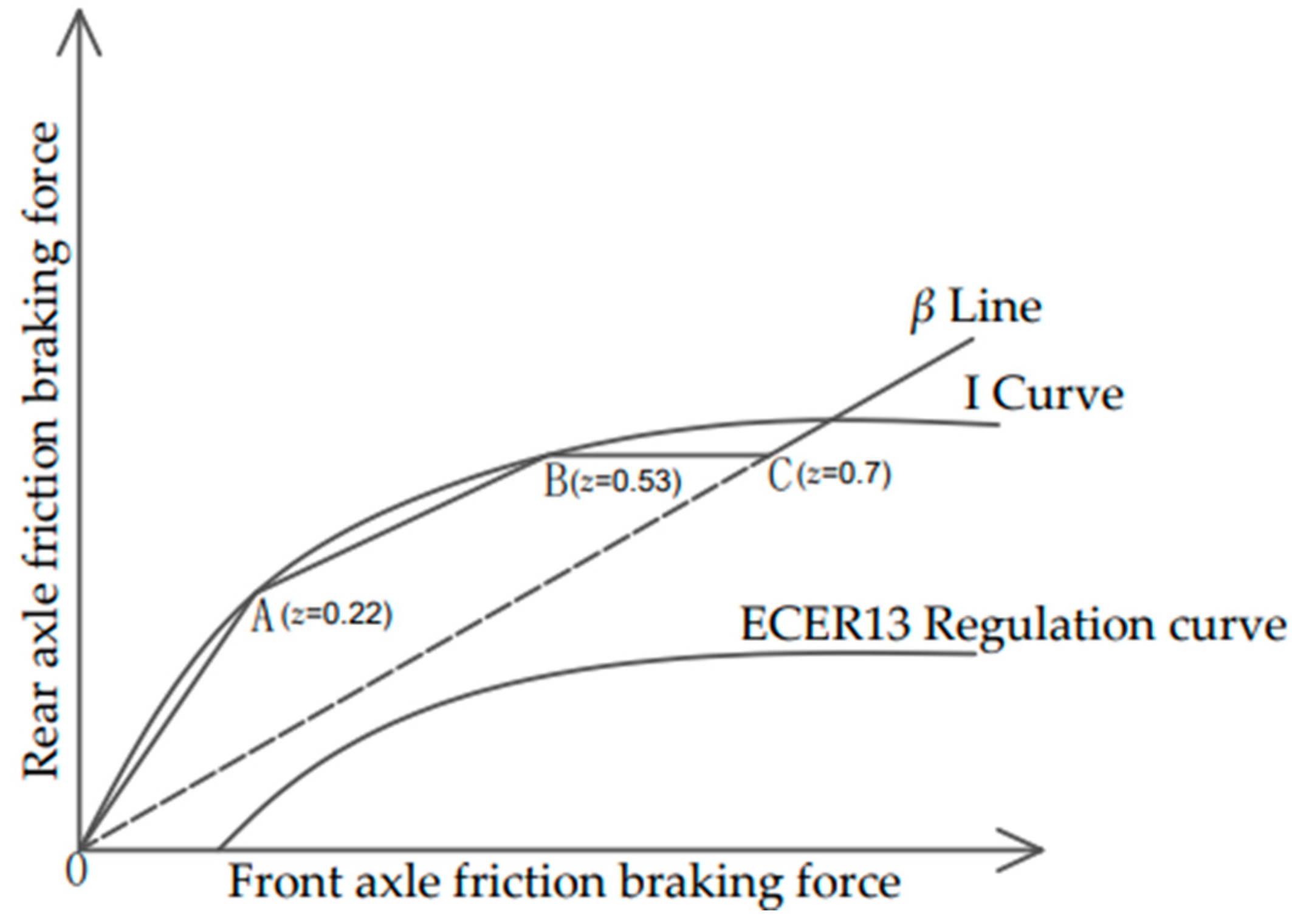
2.4. Remaining Demand Braking Force Distribution
2.5. Execution Control Constraint
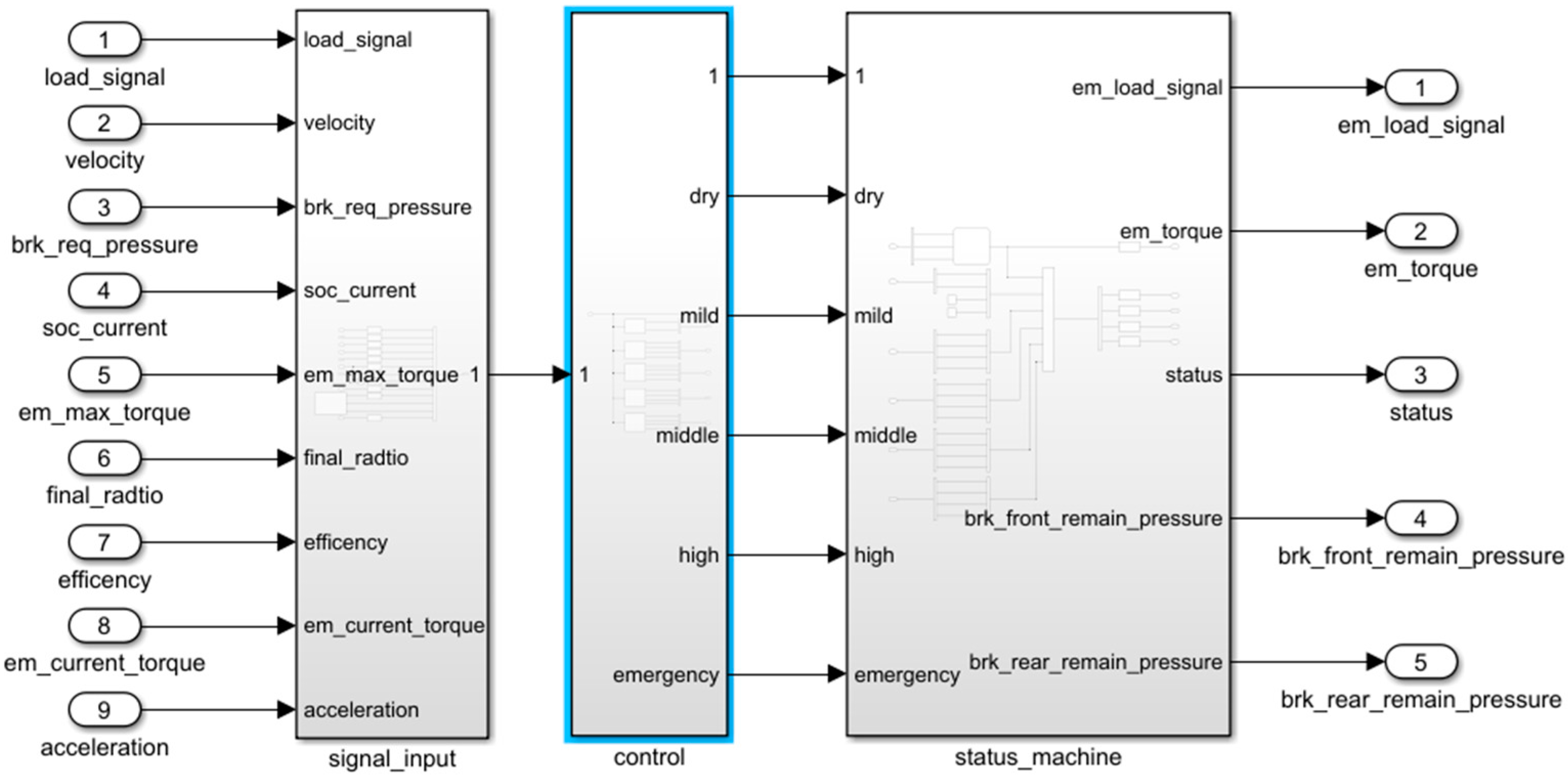
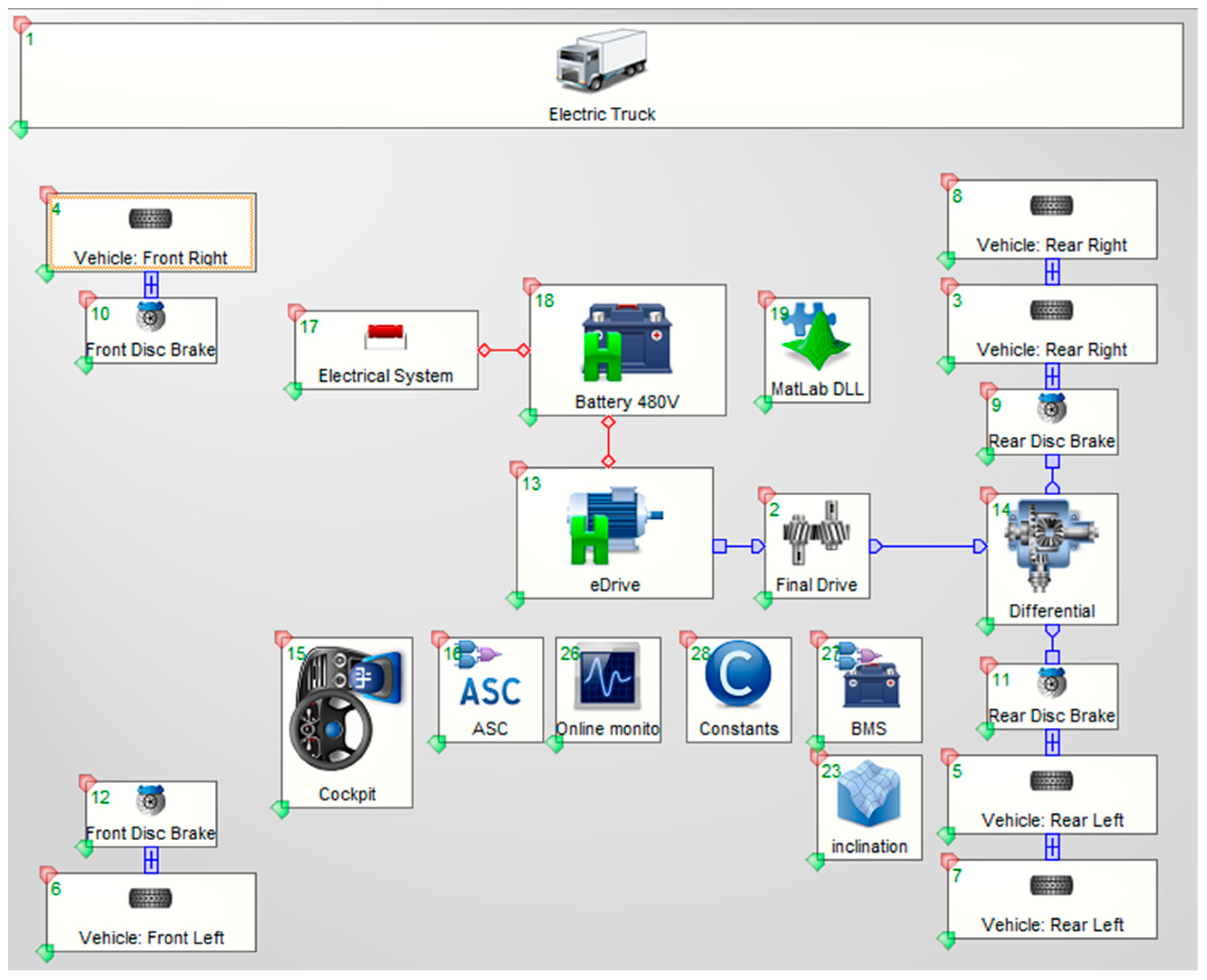
3. Establish Control Strategies and Vehicle Models
4. Results and Discussion
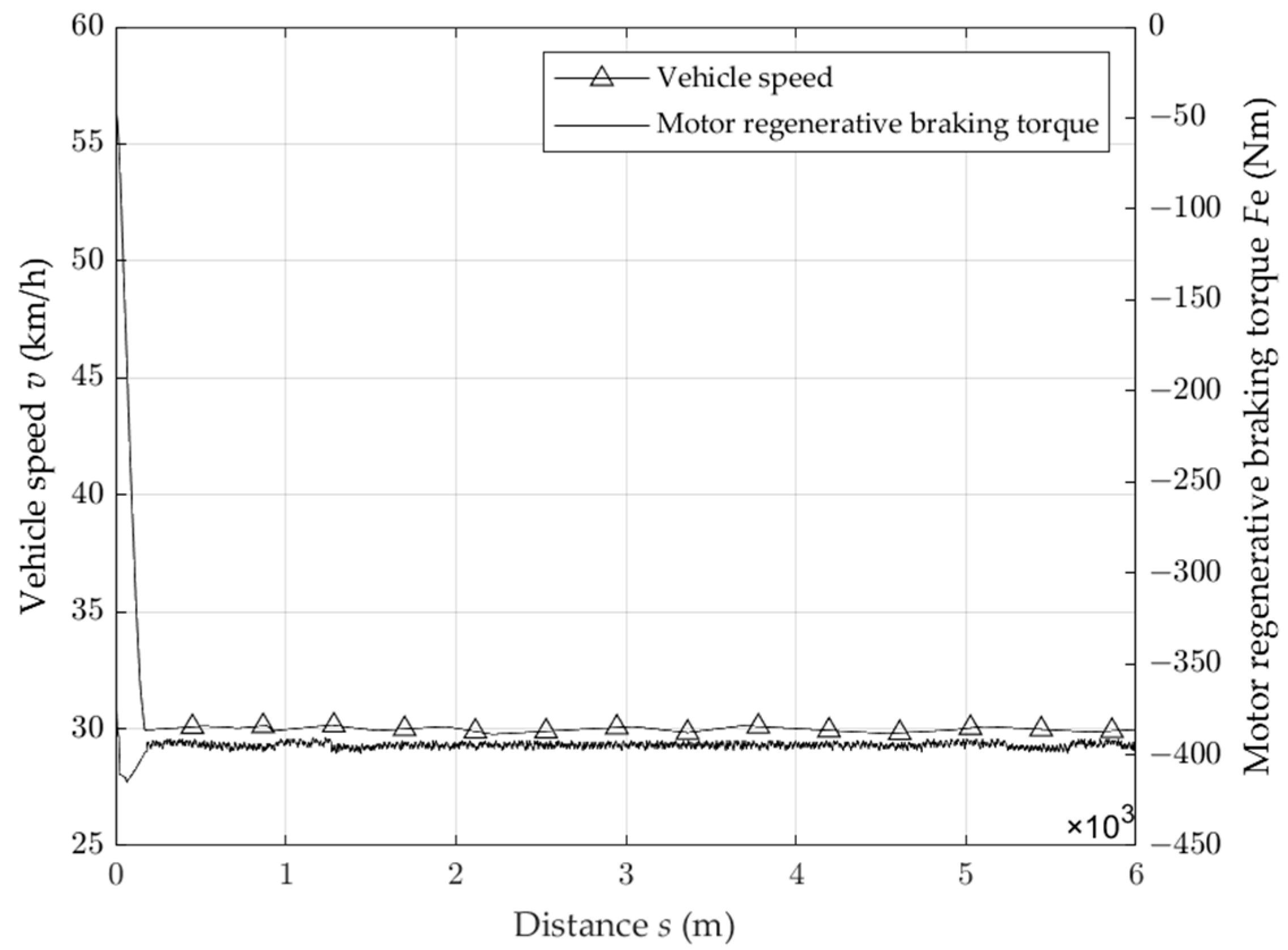
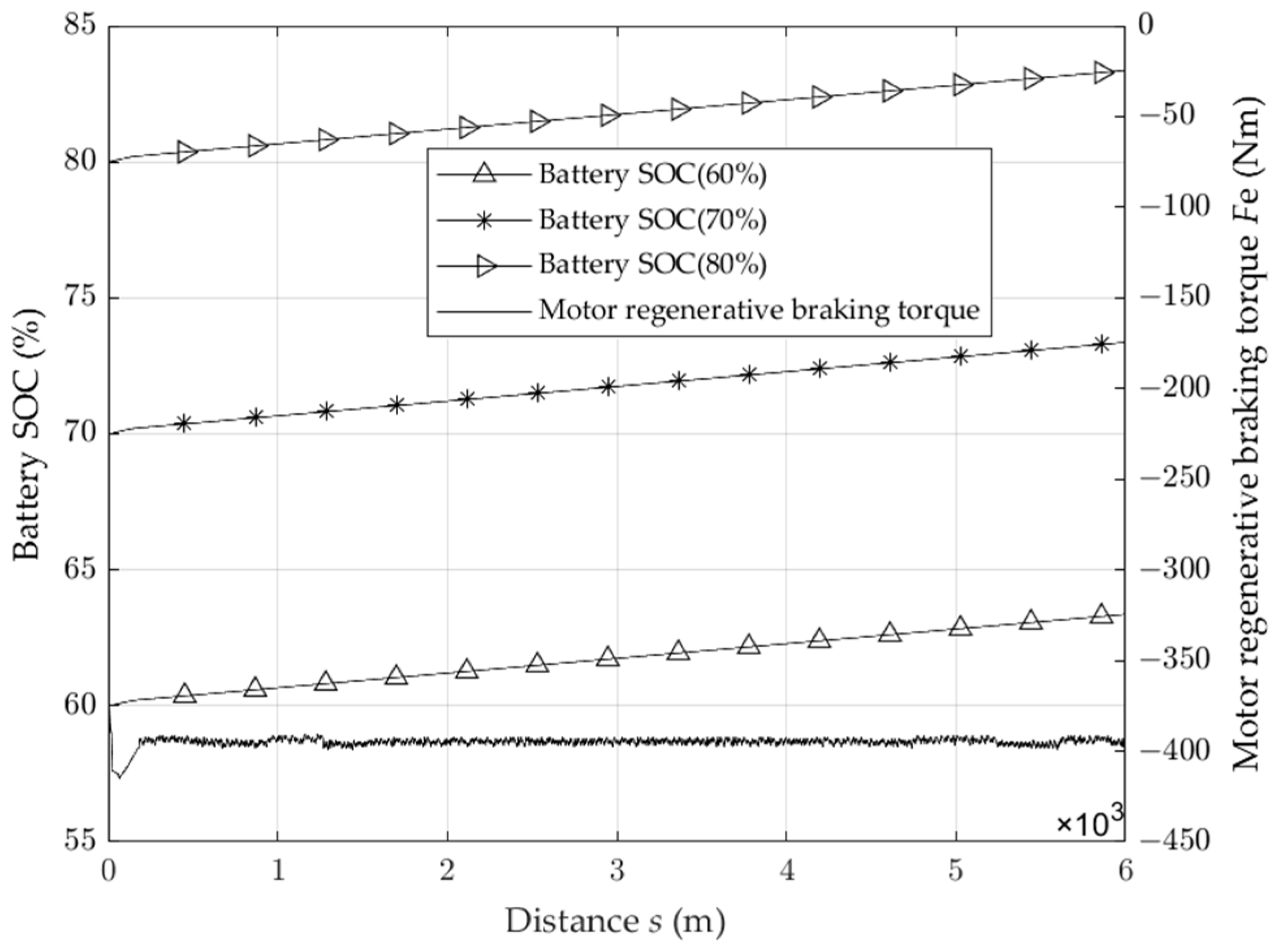
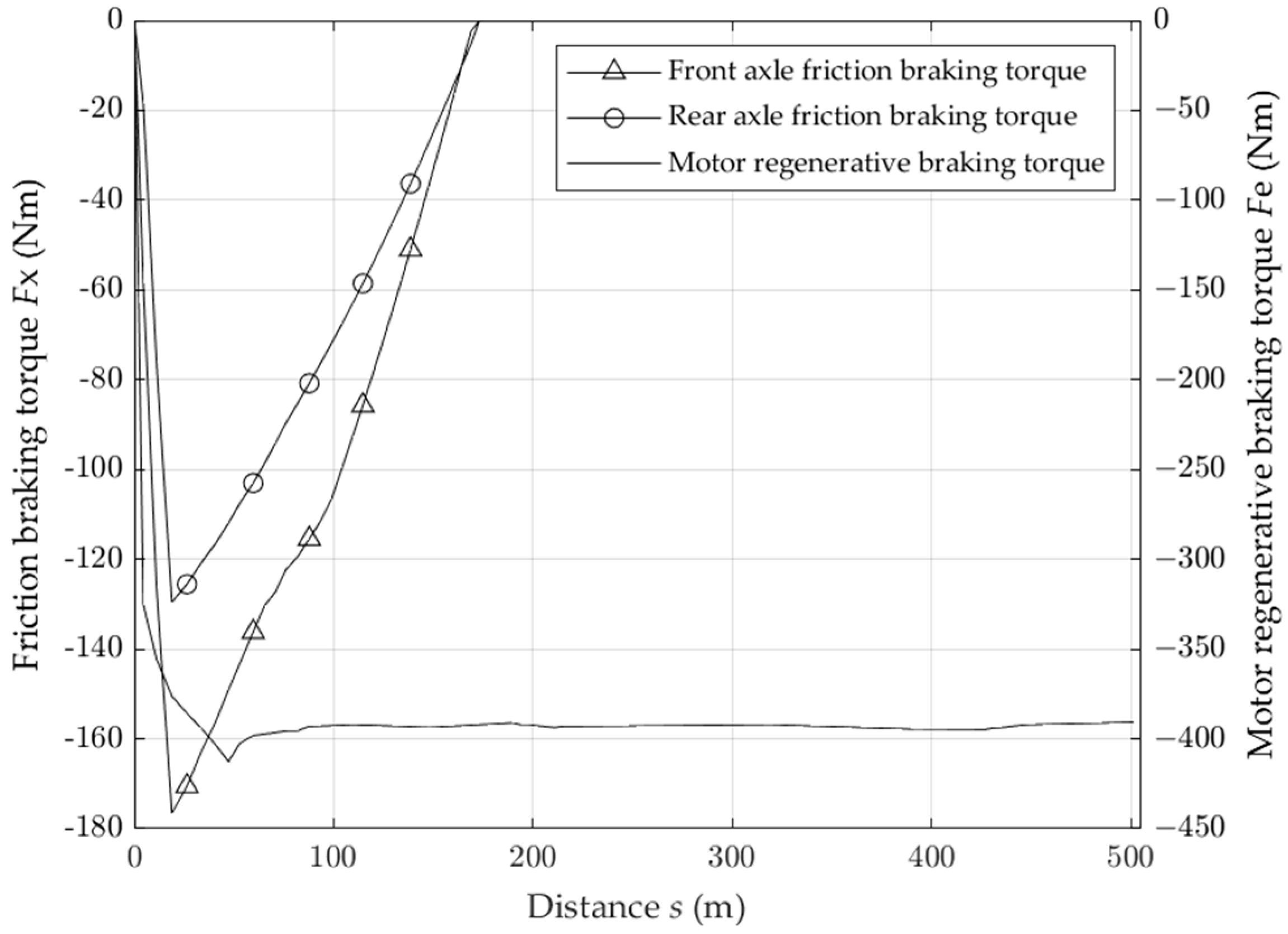
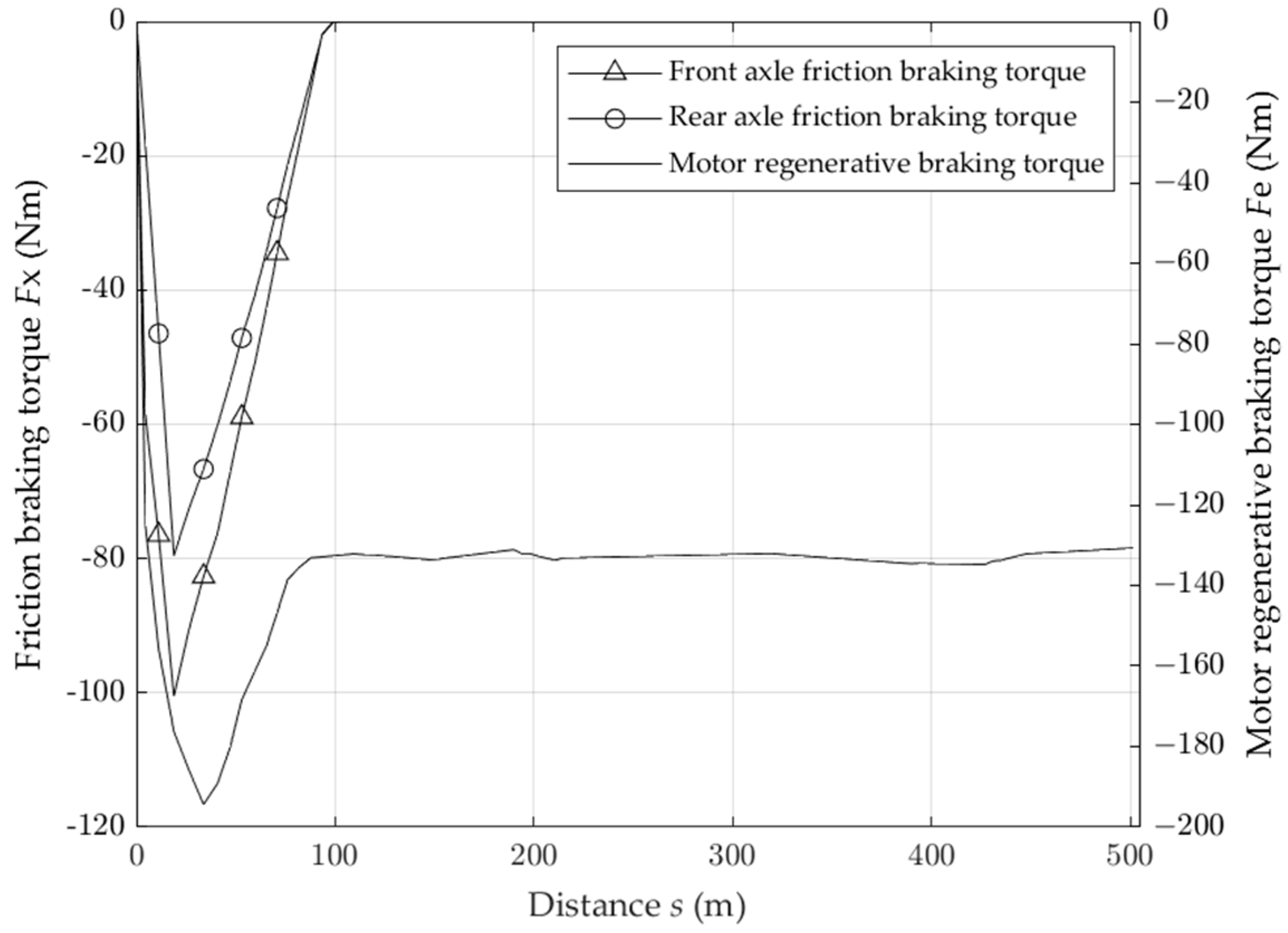
4.1. Analysis of Driving Conditions and Results of Fixed Slope and Long Downhill Driving
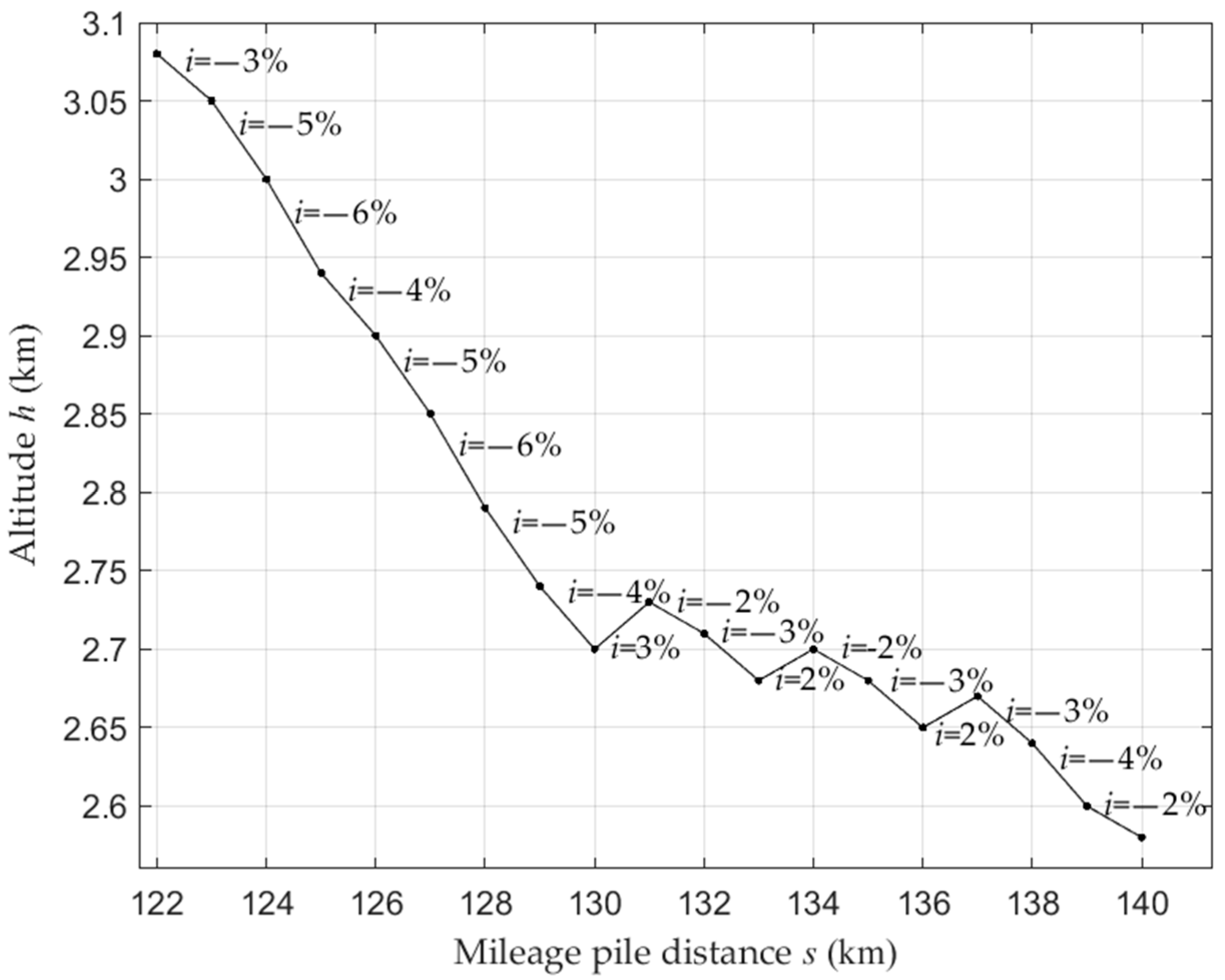
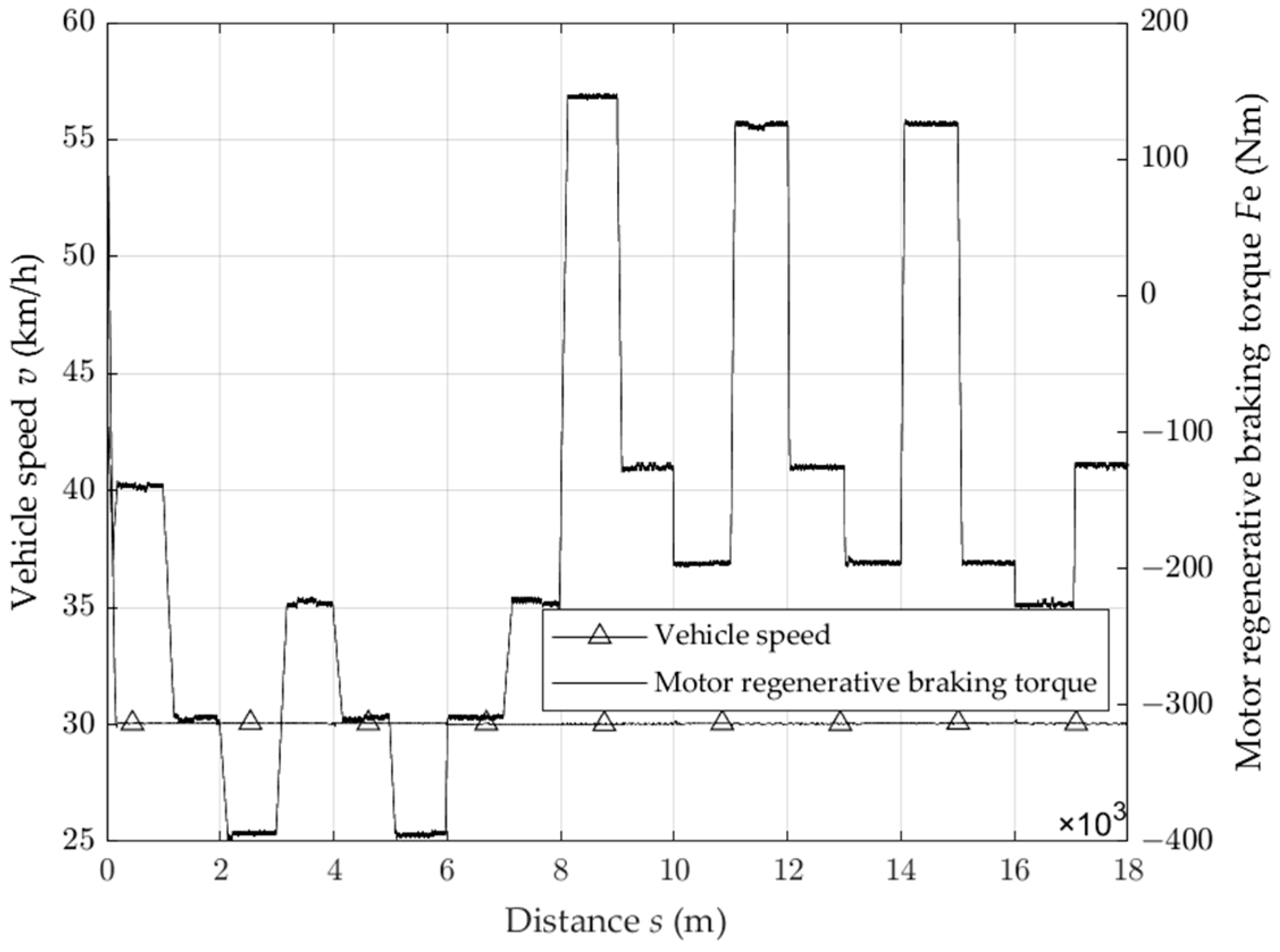
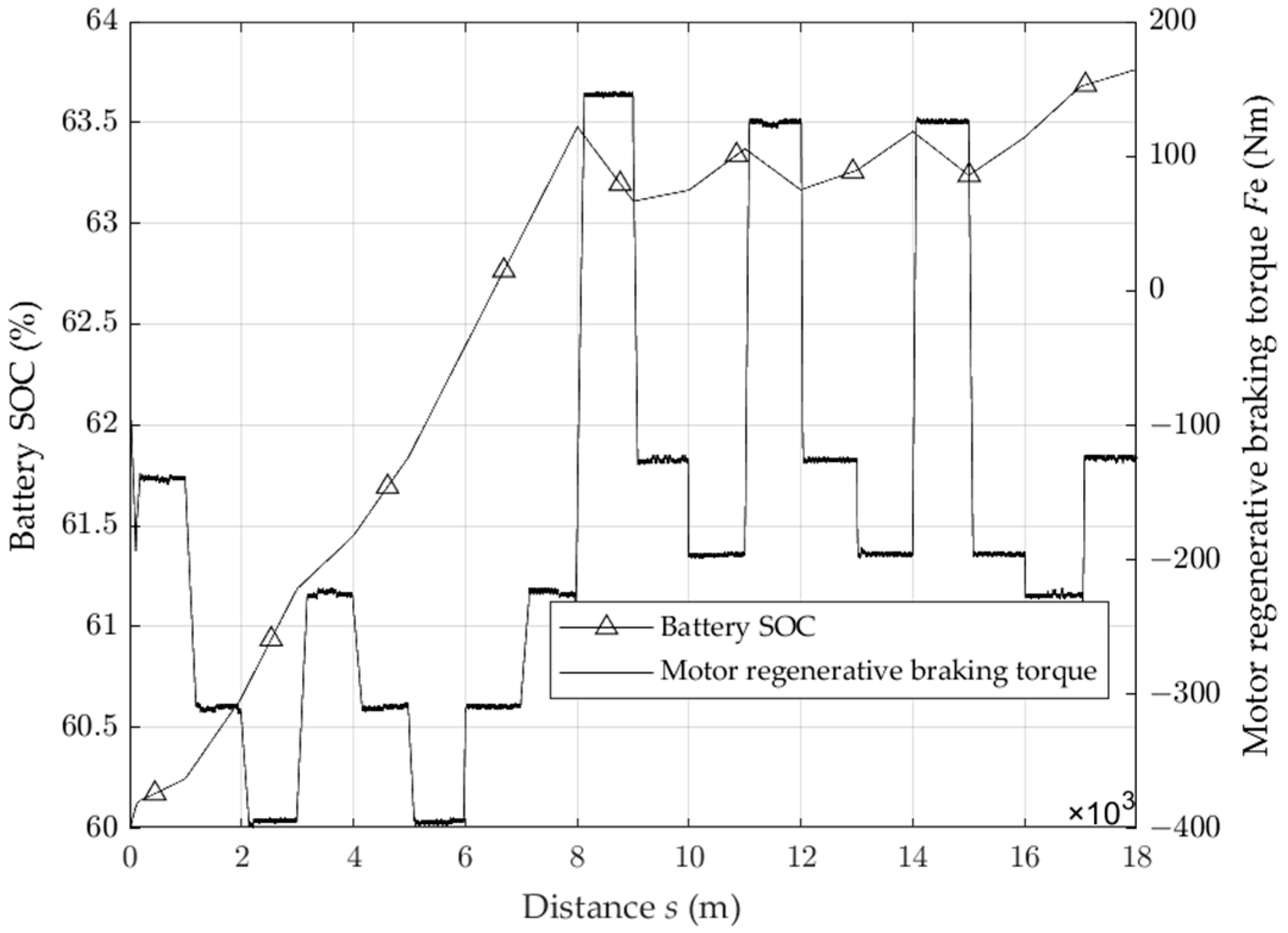
4.2. Analysis of Driving Conditions and Results of Variable Slope and Long Downhill Driving
5. Conclusions
- (1)
- Under the condition of constant slope driving, the motor provides continuous braking so that the vehicle can maintain a constant speed of 30 km/h downhill driving, and the braking energy recovery rate reaches 50.93% under the initial 60% battery SOC. The braking energy recovery rate reaches 50.89% under the initial 70% battery SOC, and the braking energy recovery rate reaches 50.81% under the initial 80% battery SOC. It is concluded that when the battery SOC reaches 80%, the braking energy recovery rate will decrease, and in order to improve the battery service life, the braking energy recovery will be stopped when the battery SOC reaches 90%;
- (2)
- Under the condition of variable slope driving, the motor regenerative braking torque is determined by the size of the road slope: when the slope changes, the regenerative braking torque decreases, and the braking energy recovery speed decreases. When the slope increases, the regenerative braking torque increases, and the braking energy recovery speed increases. At the same time, after adjusting the power torque of the electric mechanism, the vehicle can still be kept at a constant speed of 30 km/h, and the braking energy recovery rate reaches 49.96%;
- (3)
- When the vehicle is kept at a constant driving speed of 30 km/h, the friction braking force is no longer involved in braking, which can effectively prevent the brake from generating thermal degradation phenomenon and improve the braking stability of the vehicle;
- (4)
- The continuous braking joint control strategy for pure electric commercial vehicles mentioned in the introduction mainly utilizes the electric motor to take part of the auxiliary braking to reduce the temperature of the retarder, and the main continuous braking part is still provided by the retarder. Compared with this paper, it is more complicated in structure and the braking energy recovery rate is not very high. The use of motor anti-drag characteristics for sustained braking is theoretically possible; there are authors using simulation to verify this, but in the case of high battery SOC for sustained braking is still lacking. In order to avoid overcharging the battery and still need the motor for sustained braking, the vehicle will inevitably need to be retrofitted with other energy storage devices or direct energy directly provided to the vehicle’s horn, air conditioning and other equipment.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wager, G.; Whale, J.; Braunl, T. Performance Evaluation of Regenerative Braking Systems. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2018, 232, 1414–1427. [Google Scholar] [CrossRef]
- Ni, C.; Gao, H.; Kong, F. Design of downhill travel assist braking system for electric trucks. Light Veh. Technol. 2019, 3–4, 12. [Google Scholar]
- Lan, H.; Ma, Z.; Li, X. Long downhill joint braking control strategy for electric commercial vehicles based on dynamic planning. J. Northwest Univ. Nat. Sci. Ed. 2020, 50, 987–995. [Google Scholar]
- Chang, J.; Zhang, Y. Research on optimal control strategy of braking energy recovery for pure electric vehicles based on EMB. Automot. Eng. 2022, 44, 64–72. [Google Scholar]
- Shi, P.; Gao, Y.; Zhang, Z. Recognition of long downhill braking conditions of heavy-duty trucks. J. Automot. Saf. Energy Conserv. 2023, 14, 299–309. [Google Scholar]
- Yabe, T.; Akatsu, K.; Okui, N.; Niikuni, T.; Kawai, T. Efficiency Improvement of Regenerative Energy for an EV. World Electr. Veh. J. 2012, 5, 494–500. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, J.; Zhang, W.; Ma, F. Research on Regenerative Braking of Pure Electric Mining Dump Truck. World Electr. Veh. J. 2019, 10, 39. [Google Scholar] [CrossRef]
- Li, Z.; Shi, Z.; Gao, J.; Xi, J. Research on Regenerative Braking Control Strategy for Single-Pedal Pure Electric Commercial Vehicles. World Electr. Veh. J. 2023, 14, 229. [Google Scholar] [CrossRef]
- Wei, L. Research on Long Downhill Composite Braking Control Strategy and Braking Energy Recovery for Pure Electric Commercial Vehicles. Master’s Thesis, Chang’an University, Xi’an, China, 2021. [Google Scholar]
- Trovão, J.P.; Santos, V.D.N.; Pereirinha, P.G.; Jorge, H.M.; Antunes, C.H. Comparative Study of Different Energy Management Strategies for Dual-Source Electric Vehicles. World Electr. Veh. J. 2013, 6, 523–531. [Google Scholar] [CrossRef]
- Miri, I.; Fotouhi, A.; Ewin, N. Electric Vehicle Energy Consumption Modelling and Estimation—A Case Study. Int. J. Energy Res. 2021, 45, 501–520. [Google Scholar] [CrossRef]
- Khanra, M.; Chakraborty, D.; Nandi, A.K. Improvement of Regenerative Braking Energy of Fully Battery Electric Vehicle through Optimal Driving. J. Asian Electr. Veh. 2018, 16, 1789–1798. [Google Scholar] [CrossRef]
- Yu, Y.; Jiang, J.; Min, Z.; Wang, P.; Shen, W. Research on Energy Management Strategies of Extended-Range Electric Vehicles Based on Driving Characteristics. World Electr. Veh. J. 2020, 11, 54. [Google Scholar] [CrossRef]
- Krishnamoorthy, K.; Pazhamalai, P.; Mariappan, V.K.; Manoharan, S.; Kesavan, D.; Kim, S. Two-Dimensional Siloxene–Graphene Heterostructure-Based High-Performance Supercapacitor for Capturing Regenerative Braking Energy in Electric Vehicles. Adv. Funct. Mater. 2021, 31, 2008422. [Google Scholar] [CrossRef]
- Chen, B.; Evangelou, S.A.; Lot, R. Series Hybrid Electric Vehicle Simultaneous Energy Management and Driving Speed Optimization. IEEE/ASME Trans. Mechatron. 2019, 24, 2756–2767. [Google Scholar] [CrossRef]
- Zhao, L.; Cao, Q.; Li, Y.; Gao, N. An Optimization Technique of Braking Force Distribution Coefficient for Truck. In Proceedings of the Proceedings 2011 International Conference on Transportation, Mechanical, and Electrical Engineering (TMEE), Changchun, China, 16–18 December 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1784–1787. [Google Scholar]
- Goodarzi, A.; Mehrmashhadi, J.; Esmailzadeh, E. Optimised Braking Force Distribution Strategies for Straight and Curved Braking. Int. J. Heavy Veh. Syst. 2009, 16, 78. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, X. Optimization Algorithm for Vehicle Braking Force Distribution of Front and Rear Axles Based on Brake Strength. In Proceedings of the 2016 12th World Congress on Intelligent Control and Automation (WCICA), Guilin, China, 12–15 June 2016; IEEE: Piscataway, NJ, USA; pp. 3353–3360. [Google Scholar]
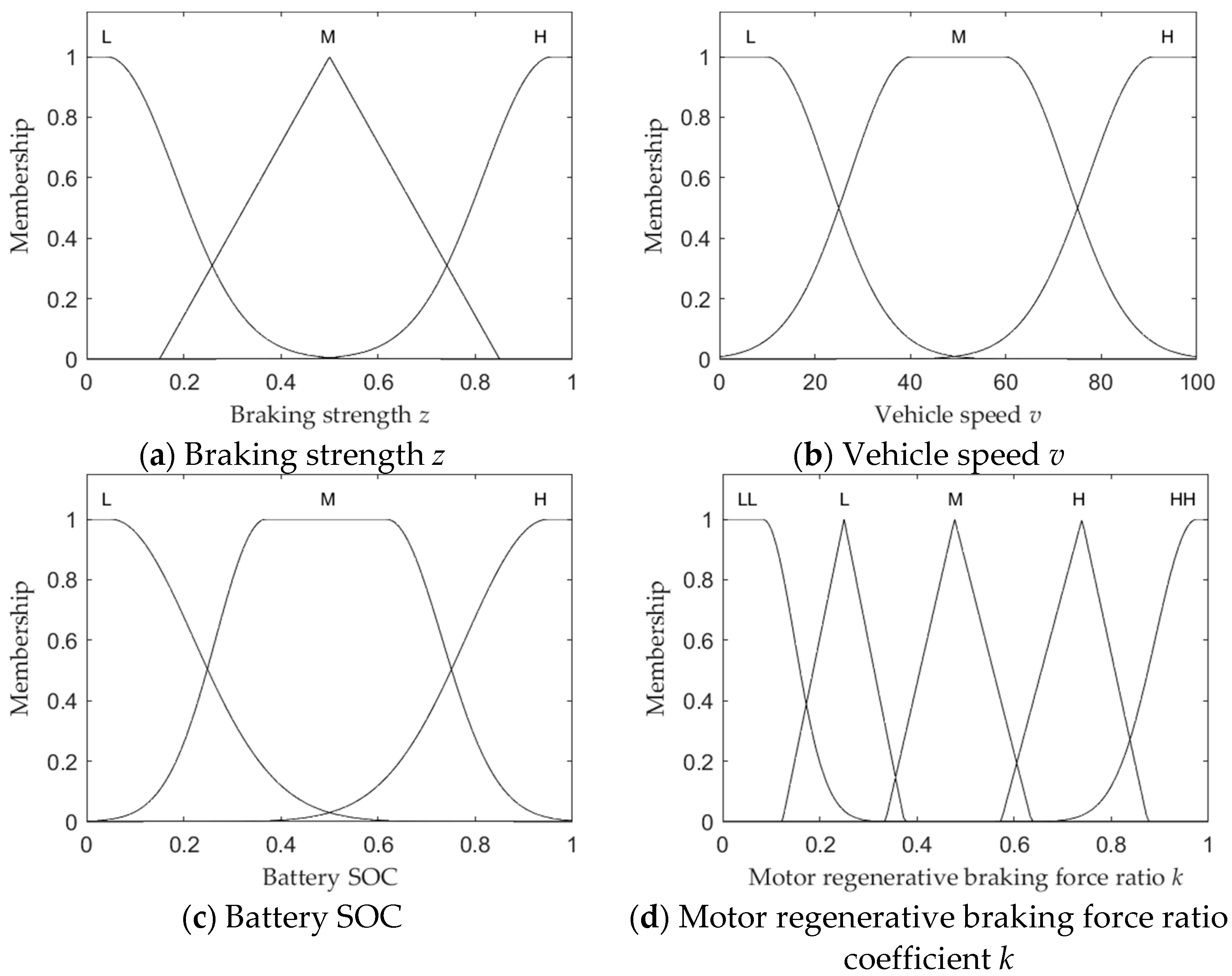
| Number | z | v | SOC | k |
|---|---|---|---|---|
| 1 | L | L | L | HH |
| 2 | M | L | L | H |
| 3 | H | L | L | M |
| 4 | L | M | L | H |
| 5 | M | M | L | M |
| 6 | H | M | L | L |
| 7 | L | H | L | M |
| 8 | M | H | L | L |
| 9 | H | H | L | LL |
| 10 | L | L | M | HH |
| 11 | M | L | M | H |
| 12 | H | L | M | M |
| 13 | L | M | M | H |
| 14 | M | M | M | M |
| 15 | H | M | M | L |
| 16 | L | H | M | M |
| 17 | M | H | M | L |
| 18 | H | H | M | LL |
| 19 | L | L | H | L |
| 20 | M | L | H | L |
| 21 | H | L | H | LL |
| 22 | L | M | H | L |
| 23 | M | M | H | L |
| 24 | H | M | H | LL |
| 25 | L | H | H | L |
| 26 | M | H | H | L |
| 27 | H | H | H | LL |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Vehicle curb weight m/t | 3.05 | Rolling resistance coefficient f | 0.08 |
| Vehicle full weight m1/t | 6.15 | Main reducer reduction ratio i0 | 7.05 |
| Vehicle test mass m2/t | 4.05 | transmission efficiency ηt | 0.95 |
| Wheelbase L/m | 4.96 | Motor peak power pm/kw | 320 |
| Distance from front axle to center of mass a/m | 2.05 | Motor peak torque Tm/N·m | 500 |
| Distance from rear axle to center of mass b/m | 2.91 | Rated power of motor pe/kw | 250 |
| Centroid height hg/m | 0.94 | Rated torque of motor Te/N·m | 420 |
| Windward area A/m2 | 5.3 | Maximum battery voltage U/V | 480 |
| Drag coefficient CD | 0.67 | Minimum battery voltage U/V | 400 |
| Wheel radius r/mm | 515 | Number of battery packs | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, W.; Liu, C. Long Downhill Braking and Energy Recovery of Pure Electric Commercial Vehicles. World Electr. Veh. J. 2024, 15, 51. https://doi.org/10.3390/wevj15020051
Cai W, Liu C. Long Downhill Braking and Energy Recovery of Pure Electric Commercial Vehicles. World Electric Vehicle Journal. 2024; 15(2):51. https://doi.org/10.3390/wevj15020051
Chicago/Turabian StyleCai, Weisheng, and Chengye Liu. 2024. "Long Downhill Braking and Energy Recovery of Pure Electric Commercial Vehicles" World Electric Vehicle Journal 15, no. 2: 51. https://doi.org/10.3390/wevj15020051
APA StyleCai, W., & Liu, C. (2024). Long Downhill Braking and Energy Recovery of Pure Electric Commercial Vehicles. World Electric Vehicle Journal, 15(2), 51. https://doi.org/10.3390/wevj15020051






