Topology Optimization Design and Dynamic Performance Analysis of Inerter-Spring-Damper Suspension Based on Power-Driven-Damper Control Strategy
Abstract
:1. Introduction
2. Model Building and Power-Driven-Damper Control Strategy Design
2.1. Quarter Suspension Model
2.2. Power-Driven-Damper Control Strategy Design
3. Topological Design and Dynamic Performance Optimization of Suspension Structure
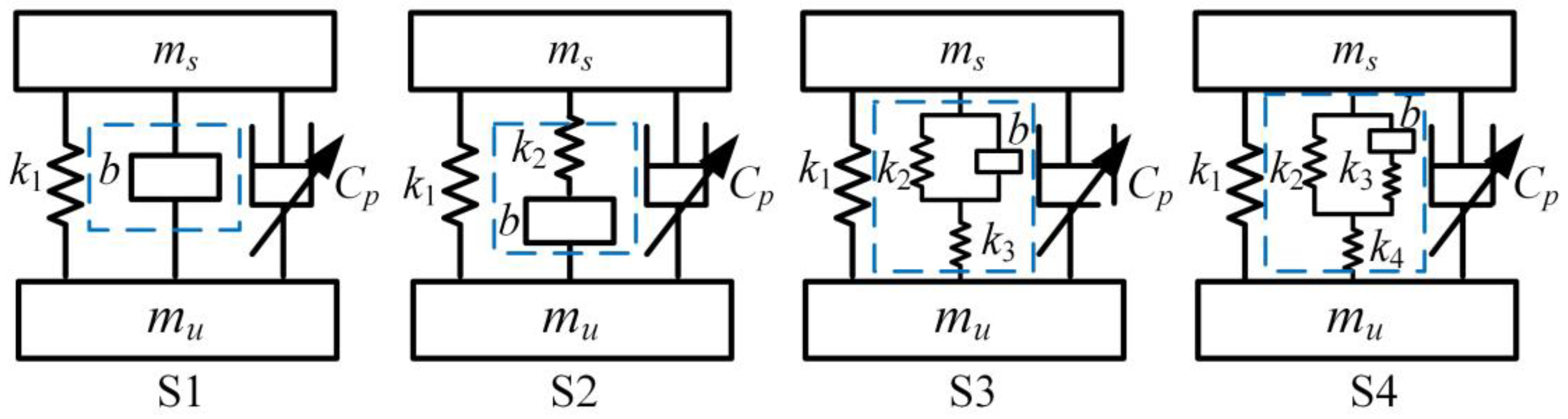
3.1. Suspension Structure Topology Design
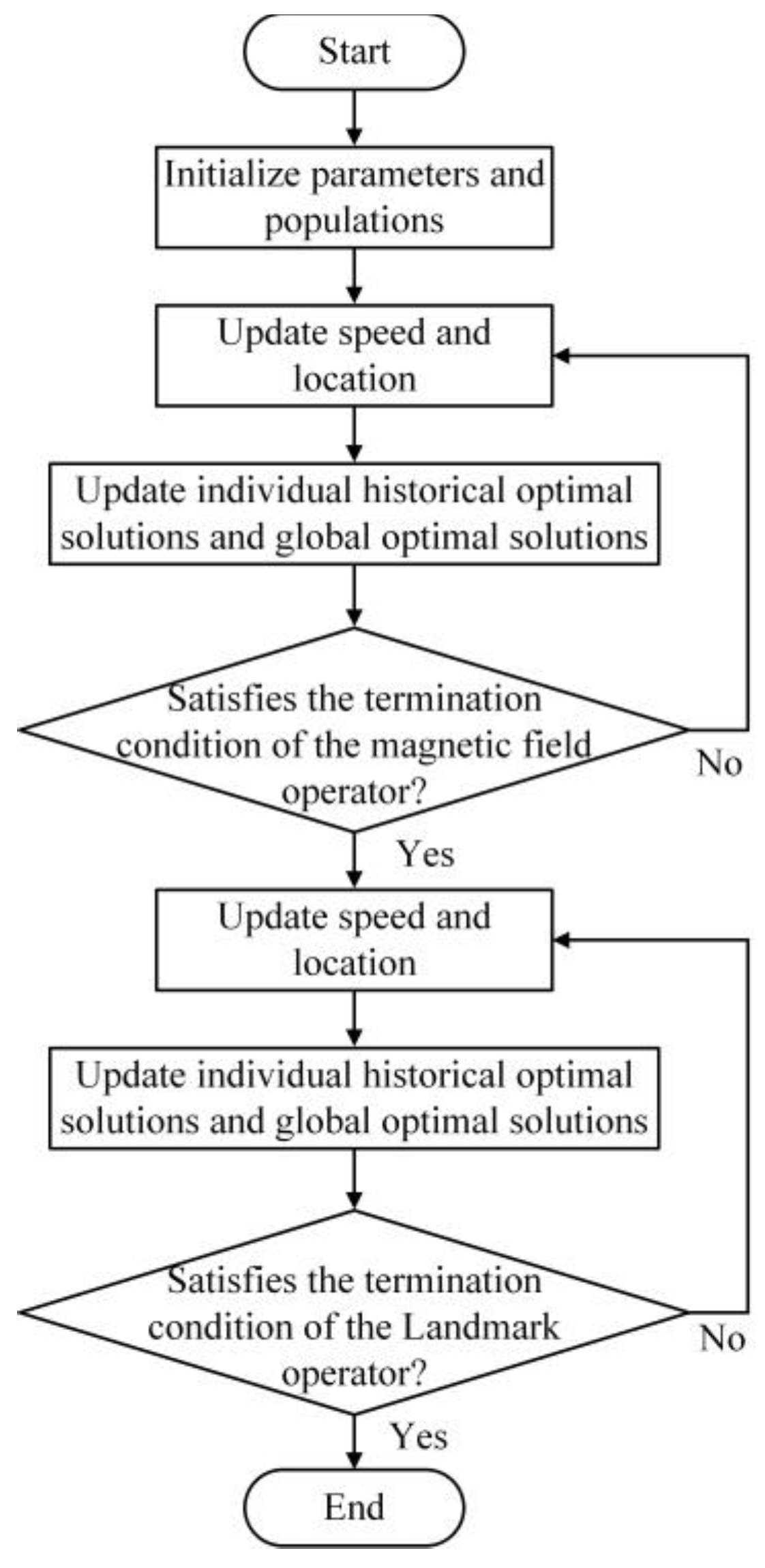
3.2. Dynamic Performance Optimization
4. Dynamic Performance Analysis
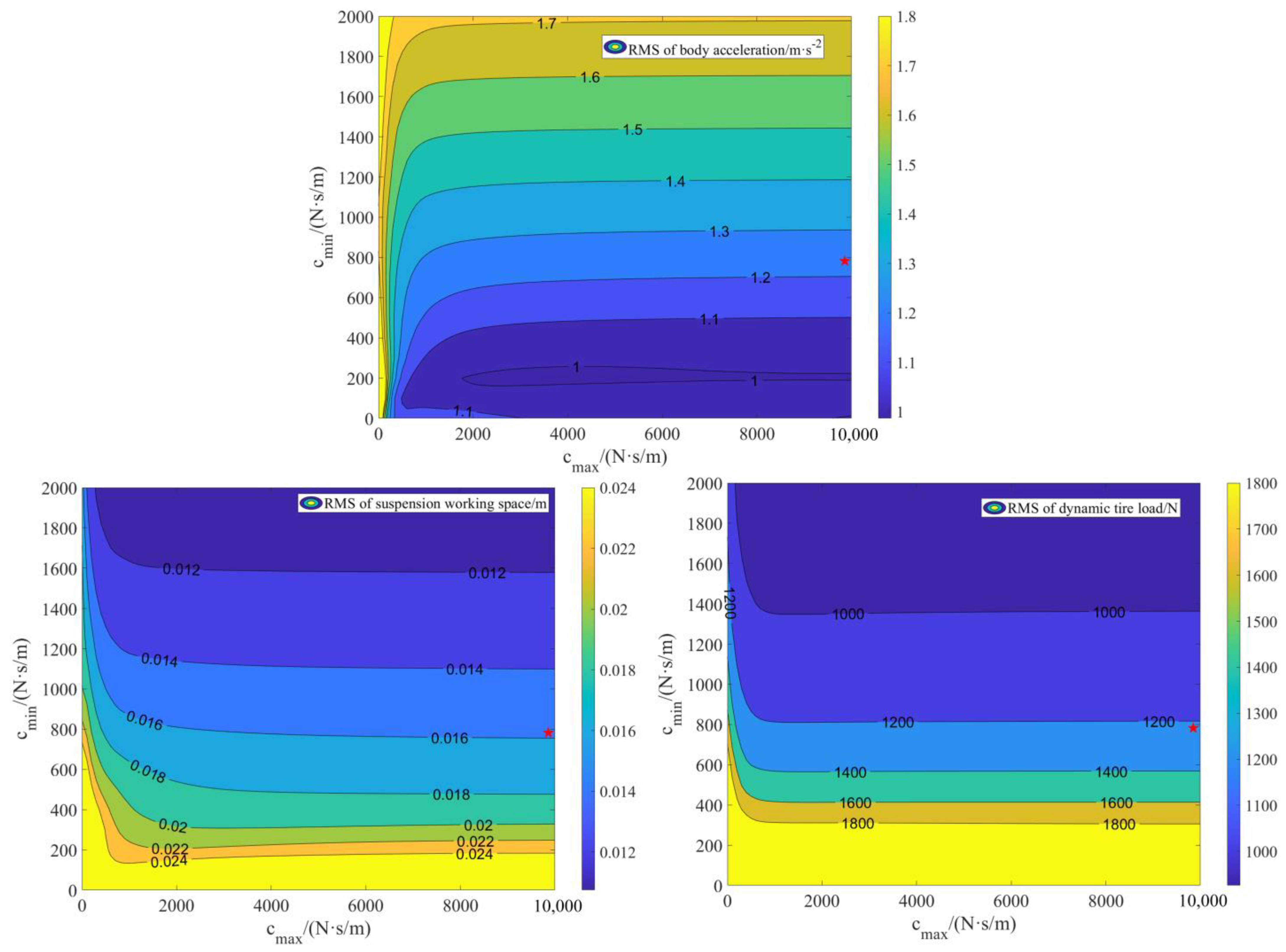
4.1. Influence of Damping Coefficient Variation on Dynamic Performance
4.2. Research on Vibration Suppression Mechanism in Wide Frequency Domain
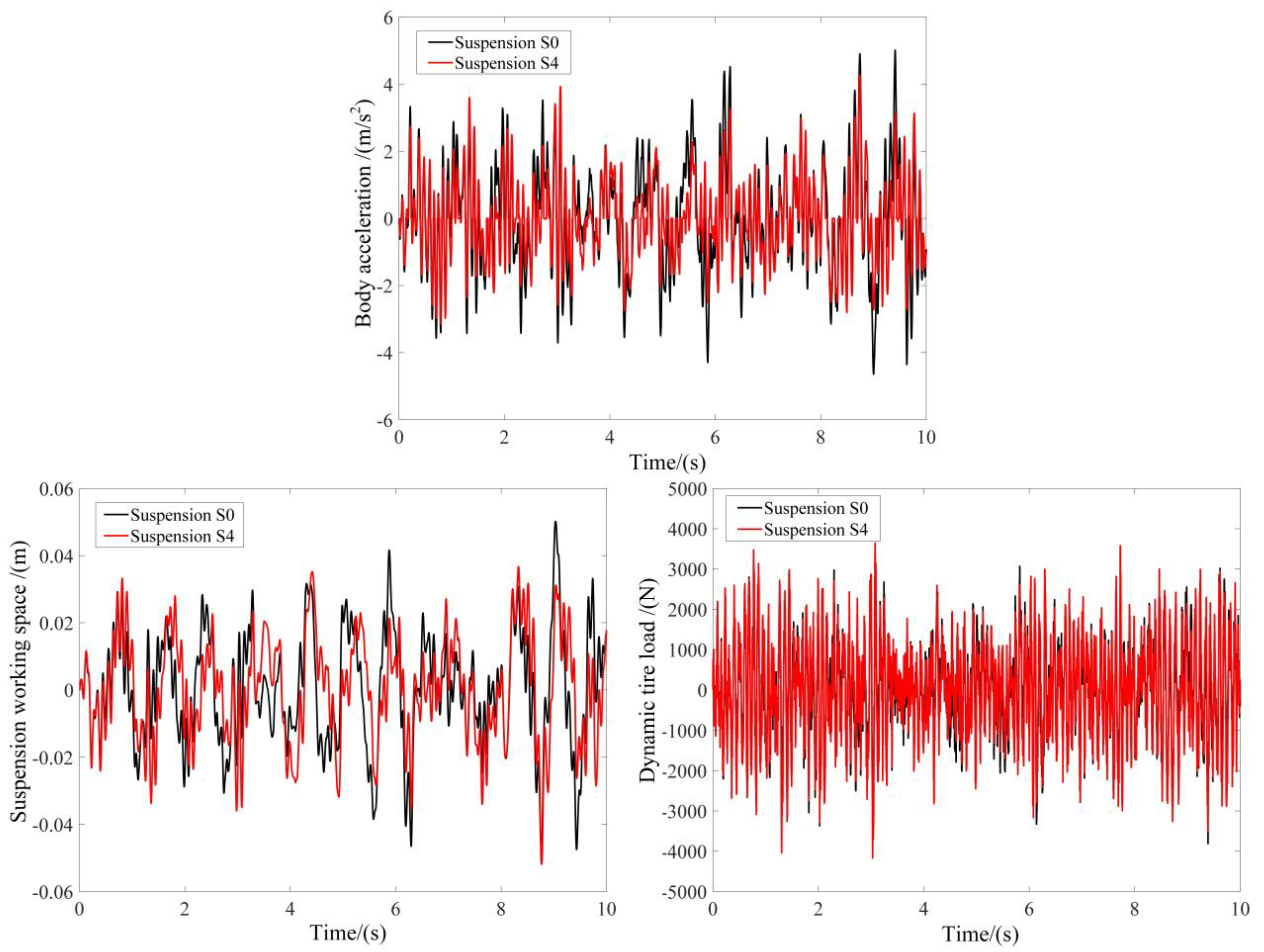
4.3. Time Domain Simulation
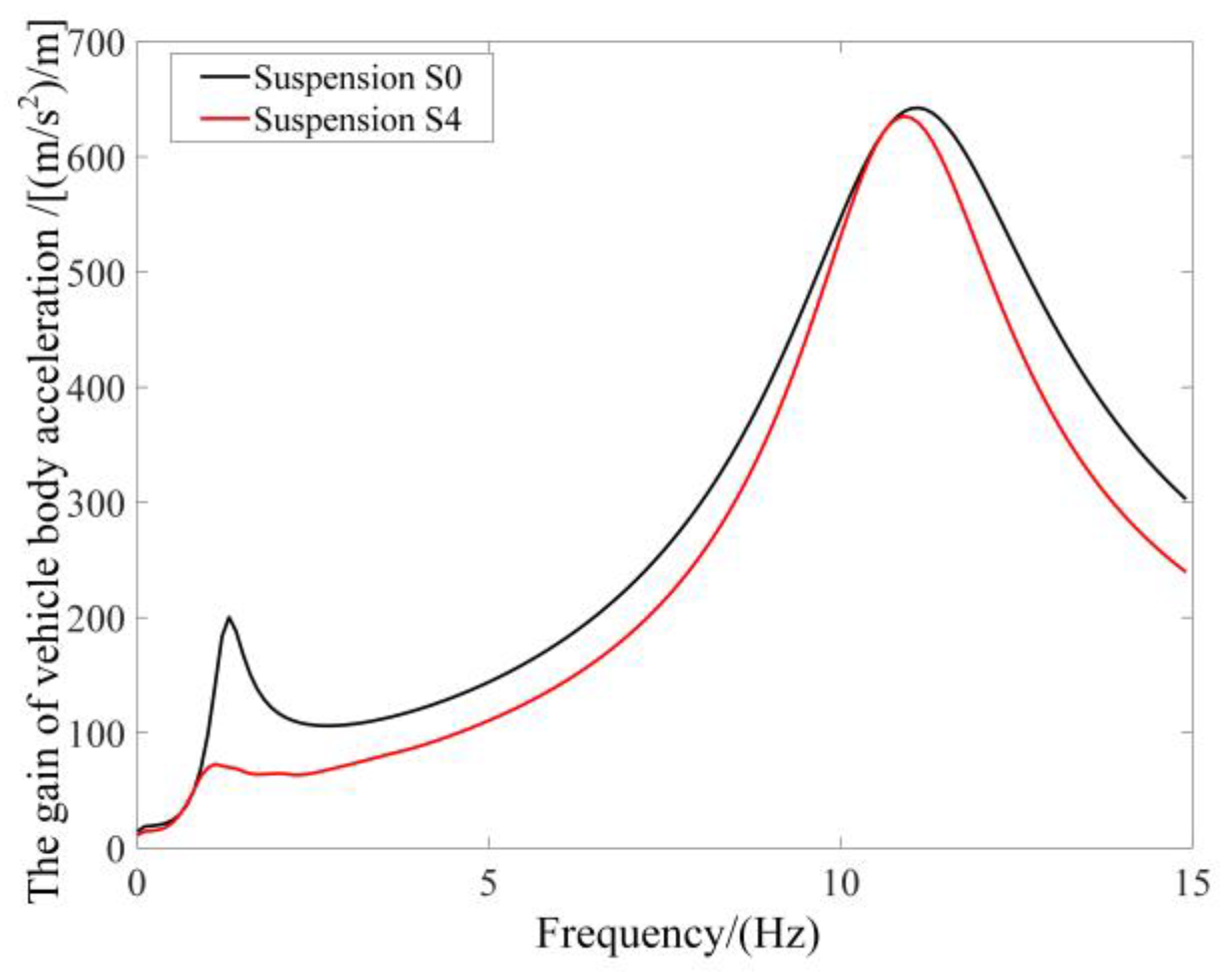
4.4. Frequency Domain Simulation
4.5. Discussion of the Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviation
| Abbreviation | Meaning |
| ISD | Inerter-Spring-Damper |
| PDD | Power-driven-damper |
| ADD | Acceleration-driven-damper |
| SH | Skyhook |
| LQR | Liner-quadratic-regulator |
References
- Wen, X.; Li, Y.N.; Yang, C. Design, Modeling, and Characterization of a Tubular Linear Vibration Energy Harvester for Integrated Active Wheel System. Automot. Innov. 2021, 4, 413–429. [Google Scholar] [CrossRef]
- Sun, W.C.; Zhang, J.H.; Pan, H.H. Heavy vehicle air suspension control considering ride comfort and height regulation. Control Theory Appl. 2022, 39, 1002–1010. [Google Scholar]
- Qin, Y.Z.; Zhao, Z.; Wang, Z.F.; Li, G.F. Study of Longitudinal–Vertical Dynamics for In-Wheel Motor-Driven Electric Vehicles. Automot. Innov. 2021, 4, 227–237. [Google Scholar] [CrossRef]
- Issa, M.; Samn, A. Passive vehicle suspension system optimization using Harris Hawk Optimization algorithm. Math. Comput. Simul. 2021, 191, 328–345. [Google Scholar] [CrossRef]
- Kumar, S.; Medhavi, A.; Kumar, R. Optimization of Nonlinear Passive Suspension System to Minimize Road Damage for Heavy Goods Vehicle. Int. J. Acoust. Vib. 2021, 26, 56–63. [Google Scholar] [CrossRef]
- Abut, T.; Salkim, E. Control of Quarter-Car Active Suspension System Based on Optimized Fuzzy Linear Quadratic Regulator Control Method. Appl. Sci. 2023, 13, 8802. [Google Scholar] [CrossRef]
- Nie, J.; Wang, F.; Zhang, X.; Yang, Y. Design and test of hydro-pneumatic ISD suspension in heavy multi-axle vehicles. Adv. Mech. Eng. 2021, 13, 16878140211064737. [Google Scholar] [CrossRef]
- Wang, K.; Chen, M.Z.Q.; Li, C.; Chen, G. Passive Controller Realization of a Biquadratic Impedance with Double Poles and Zeros as a Seven-Element Series-Parallel Network for Effective Mechanical Control. IEEE Trans. Autom. Control 2018, 63, 3010–3015. [Google Scholar] [CrossRef]
- Li, F.J.; Li, X.P.; Shang, D.Y.; Wang, Z. Dynamic modeling and damping performance improvement of two stage ISD suspension system. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 236, 2259–2271. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, X.L.; Nie, J.M.; Wang, R.C. Performance Analysis of Two-stage Series-connected Inerter-spring-damper Suspension Based on Half-car Model. J. Mech. Eng. 2012, 48, 102–108. [Google Scholar] [CrossRef]
- Du, F.; Mao, M.; Chen, Y.J.; Wang, Y.J.; Zhang, Y.F. Structure design and performance analysis of inerter-spring-damper suspension structure based on dynamic model and parameter optimization. J. Vib. Shock 2014, 33, 59–65. [Google Scholar]
- Xu, L.; Mao, M.; Chen, Y.J.; Du, F. Configuration Design and Analysis of two-stage tandem ISD suspension. J. Ordnance Equip. Eng. 2020, 41, 7–12. [Google Scholar]
- Nie, J.M.; Zhang, X.L.; Sun, X.Q.; Wang, R.C. Modeling and Parameter Optimization of a New Hybrid ISD Suspension. Automot. Eng. 2015, 2, 44–47. [Google Scholar]
- Paageorgiou, C.; Smith, M.C. Positive real synthesis using matrix inequalities for mechanical networks: Application to vehicle suspension. IEEE Trans. Control Syst. Technol. 2006, 14, 423–435. [Google Scholar] [CrossRef]
- Jiang, J.Z.; Smith, M.C. Series-Parallel Six-Element Synthesis of Biquadratic Impedances. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 2543–2554. [Google Scholar] [CrossRef]
- Zhang, S.Y.; Jiang, J.Z.; Neild, S.A. Passive vibration control: A structure-immittance approach. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20170011. [Google Scholar]
- Ioan-Cozmin, M.R.; Cornel, S.; Ioan, M. Analysis of passive vs. semi-active quarter car suspension model. In Proceedings of the Conference on Advanced Topics in Optoelectronics, Microelectronics and Nanotechnologies, Constanta, Romania, 20–23 August 2020; p. 11718. [Google Scholar]
- Jayaraman, T.; Palanisamy, S.; Thangaraj, M. Hydraulic control valve integrated novel semi active roll resistant interconnected suspension with vertical and roll coordinated control scheme. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 2022, 237, 98–111. [Google Scholar] [CrossRef]
- Ma, T.; Bi, F.; Wang, X.; Tian, C.; Lin, J.; Wang, J.; Pang, G. Optimized Fuzzy Skyhook Control for Semi-Active Vehicle Suspension with New Inverse Model of Magnetorheological Fluid Damper. Energies 2021, 14, 1674. [Google Scholar] [CrossRef]
- Karnopp, D.; Crosby, M.J.; Harwood, R.A. Vibration control using semi-active force generators. J. Eng. Ind. 1974, 96, 619–626. [Google Scholar] [CrossRef]
- Karnopp, D.; Crosby, M.J. The active damper a new concept for shock and vibration control. Shock Vib. Bull. 1973, 143, 119–133. [Google Scholar]
- Zhu, B.L.; Qing, W.; ShangGuan, W.B.; Rakheja, S. Modeling and control of a quarter-car model with double wishbones and its equivalent two degrees of freedom model. J. Vib. Shock 2019, 10, 6–14. [Google Scholar]
- Lin, C.B.; Wang, Y.; Xu, E.Y.; Liu, F.Y.; Zhao, L.L.; Tang, Z.T. Study on improved ADD control Strategy for semi-active Suspensions. Noise Vib. Control 2023, 43, 197–202. [Google Scholar]
- Wang, Y.; Liu, F.Y.; Deng, J.C.; Zhao, L.L.; Tang, Z.T. Simulation Analysis of SH-LQR Damping Control Strategy for Semi-active Suspensions. Noise Vib. Control 2022, 42, 68–72. [Google Scholar]
- Savaresi, S.M.; Spelta, C. Mixed Sky-Hook and ADD: Approaching the Filtering Limits of a Semi-Active Suspension. J. Dyn. Syst. Meas. Control 2007, 129, 382–392. [Google Scholar] [CrossRef]
- Liu, Y.L.; Zuo, L. Mixed Skyhook and Power-Driven-Damper: A New Low-Jerk Semi-Active Suspension Control Based on Power Flow Analysis. J. Dyn. Syst. Meas. Control 2016, 138, 081009. [Google Scholar] [CrossRef]
- Morselli, R.; Zanasi, R. Control of port Hamiltonian systems by dissipative devices and its application to improve the semi-active suspension behaviour. Mechatronics 2008, 18, 364–369. [Google Scholar] [CrossRef]
- Talebitooti, R.; Gohari, H.D.; Zarastvand, M.R. Multi objective optimization of sound transmission across laminated composite cylindrical shell lined with porous core investigating Non-dominated Sorting Genetic Algorithm. Aerosp. Sci. Technol. 2017, 69, 269–280. [Google Scholar] [CrossRef]
- Qiu, H.X.; Duan, H.B. Multi-objective pigeon-inspired optimization for brushless direct current motor parameter design. Sci. China-Technol. Sci. 2015, 58, 1915–1923. [Google Scholar] [CrossRef]
- Sun, X.Q.; Chen, L.; Wang, S.H. Nonlinear modeling and parameter optimization of two-stage series ISD suspension. Trans. Chin. Soc. Agric. Mach. 2014, 45, 7–13. [Google Scholar]
- Liu, Y.L.; Yan, L.; Yang, X.F.; Shen, Y.; Liu, C. Optimization design and performance of vehicle ISD suspension based on ADD positive real network. J. Vib. Shock 2021, 40, 262–268. [Google Scholar]
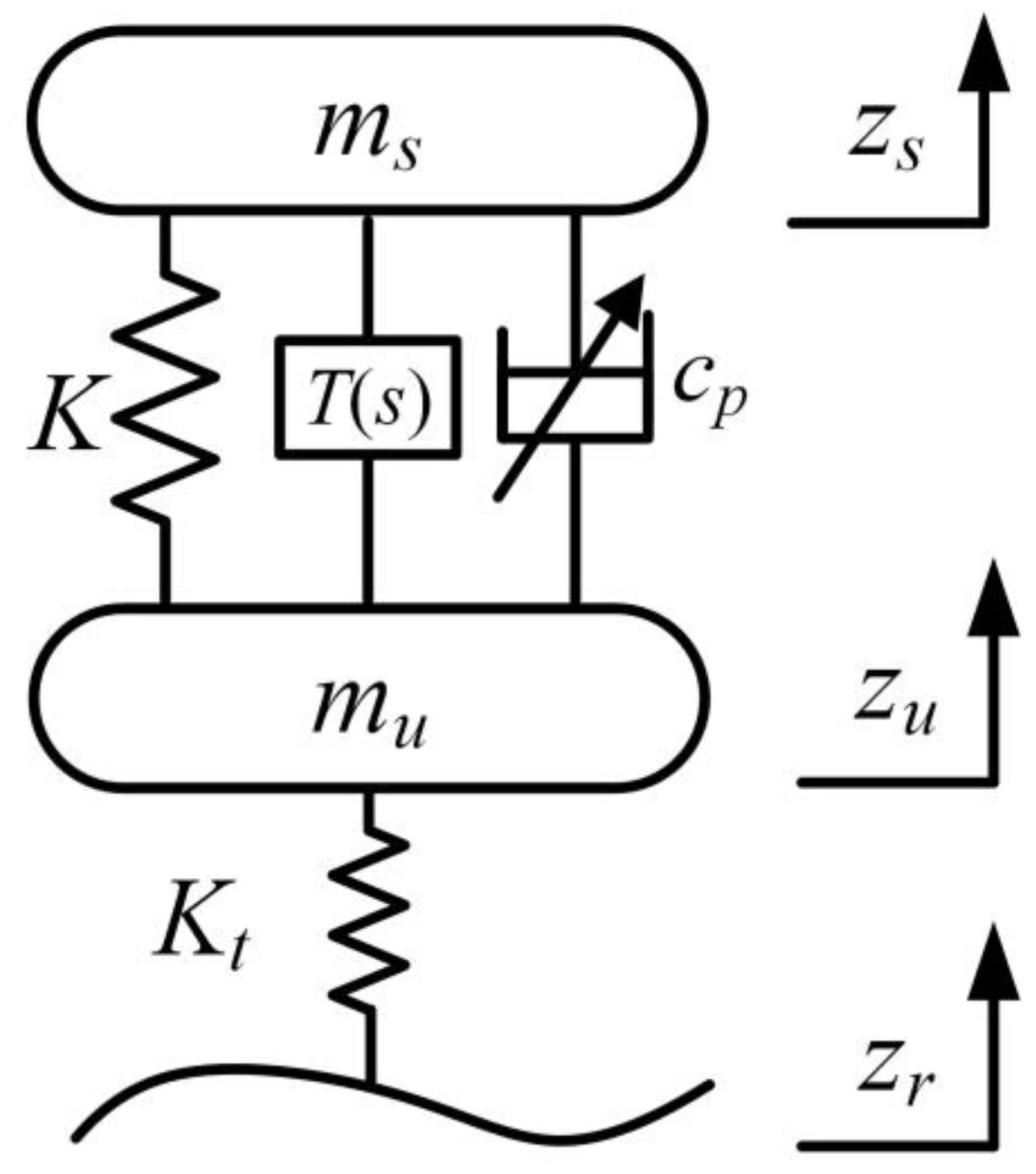

| Parameters | Symbol | Unit | Value |
|---|---|---|---|
| Sprung mass | ms | kg | 320 |
| Unsprung mass | mu | kg | 45 |
| Support spring stiffness | K | N·m−1 | 22,000 |
| Damper coefficient | C | N·s·m−1 | 1000 |
| Tire stiffness | kt | N·m−1 | 190,000 |
| Speed of vehicle | u | m·s−1 | 20 |
| Grade C Road roughness coefficient | Gq(n0) | m3·cycle−1 | 2.56 × 10−4 |
| Layouts | Optimized Parameters | J1 | J2 | J3 |
|---|---|---|---|---|
| S0 | k1 = 22,000, C = 1000 | 1.607 | 0.0169 | 1150.3 |
| S1 | k1 = 15,160, b = 16, cmax = 9293, cmin = 1025 | 1.4247(11.4%↓) | 0.0139(17.8%↓) | 1216.7 |
| S2 | k1 = 15,337, k2 = 2544, b = 5, cmax = 9617, cmin = 750 | 1.3883(13.7%↓) | 0.0152(9.5%↓) | 1216.7 |
| S3 | k1 = 15,128, k2 = 9814, k3 = 2122, b = 1936, cmax = 9817, cmin = 777 | 1.2986(20.0%↓) | 0.0163(3.6%↓) | 1216.7 |
| S4 | k1 = 15,011, k2 = 7424, k3 = 9778, k4 = 5, b = 3665, cmax = 9961, cmin = 788 | 1.2359(23.1%↓) | 0.0158(6.6%↓) | 1216.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Shen, Y.; Du, F.; Li, M.; Yang, X. Topology Optimization Design and Dynamic Performance Analysis of Inerter-Spring-Damper Suspension Based on Power-Driven-Damper Control Strategy. World Electr. Veh. J. 2024, 15, 8. https://doi.org/10.3390/wevj15010008
Wang J, Shen Y, Du F, Li M, Yang X. Topology Optimization Design and Dynamic Performance Analysis of Inerter-Spring-Damper Suspension Based on Power-Driven-Damper Control Strategy. World Electric Vehicle Journal. 2024; 15(1):8. https://doi.org/10.3390/wevj15010008
Chicago/Turabian StyleWang, Jinsen, Yujie Shen, Fu Du, Ming Li, and Xiaofeng Yang. 2024. "Topology Optimization Design and Dynamic Performance Analysis of Inerter-Spring-Damper Suspension Based on Power-Driven-Damper Control Strategy" World Electric Vehicle Journal 15, no. 1: 8. https://doi.org/10.3390/wevj15010008
APA StyleWang, J., Shen, Y., Du, F., Li, M., & Yang, X. (2024). Topology Optimization Design and Dynamic Performance Analysis of Inerter-Spring-Damper Suspension Based on Power-Driven-Damper Control Strategy. World Electric Vehicle Journal, 15(1), 8. https://doi.org/10.3390/wevj15010008







