Parameter Optimization of the Power and Energy System of Unmanned Electric Drive Chassis Based on Improved Genetic Algorithms of the KOHONEN Network
Abstract
:1. Introduction
2. Establishment of the Simulation Model and Optimization Model
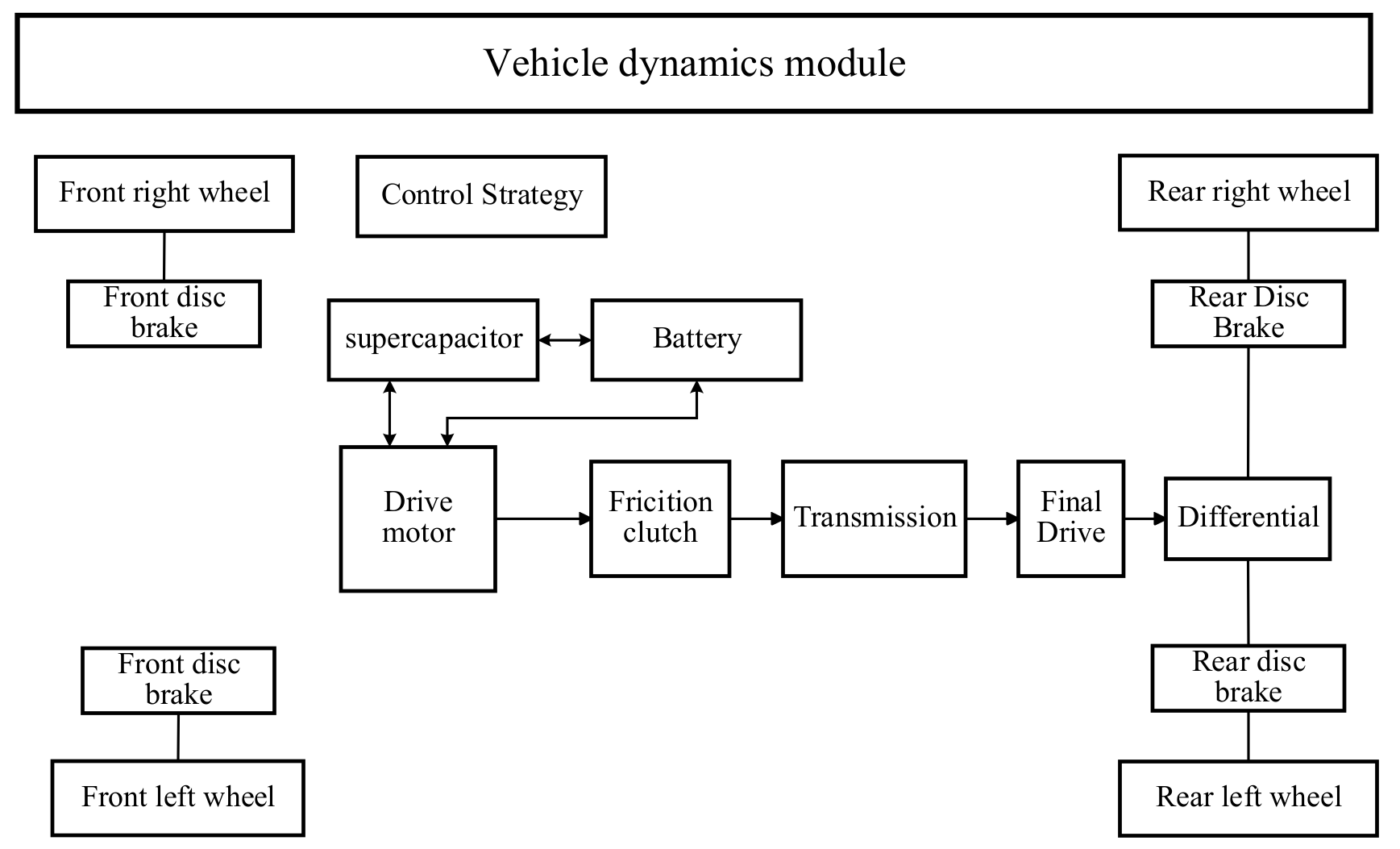
2.1. Establishment of Unmanned Electric Drive Chassis Simulation Model Based on AVL CRUISE
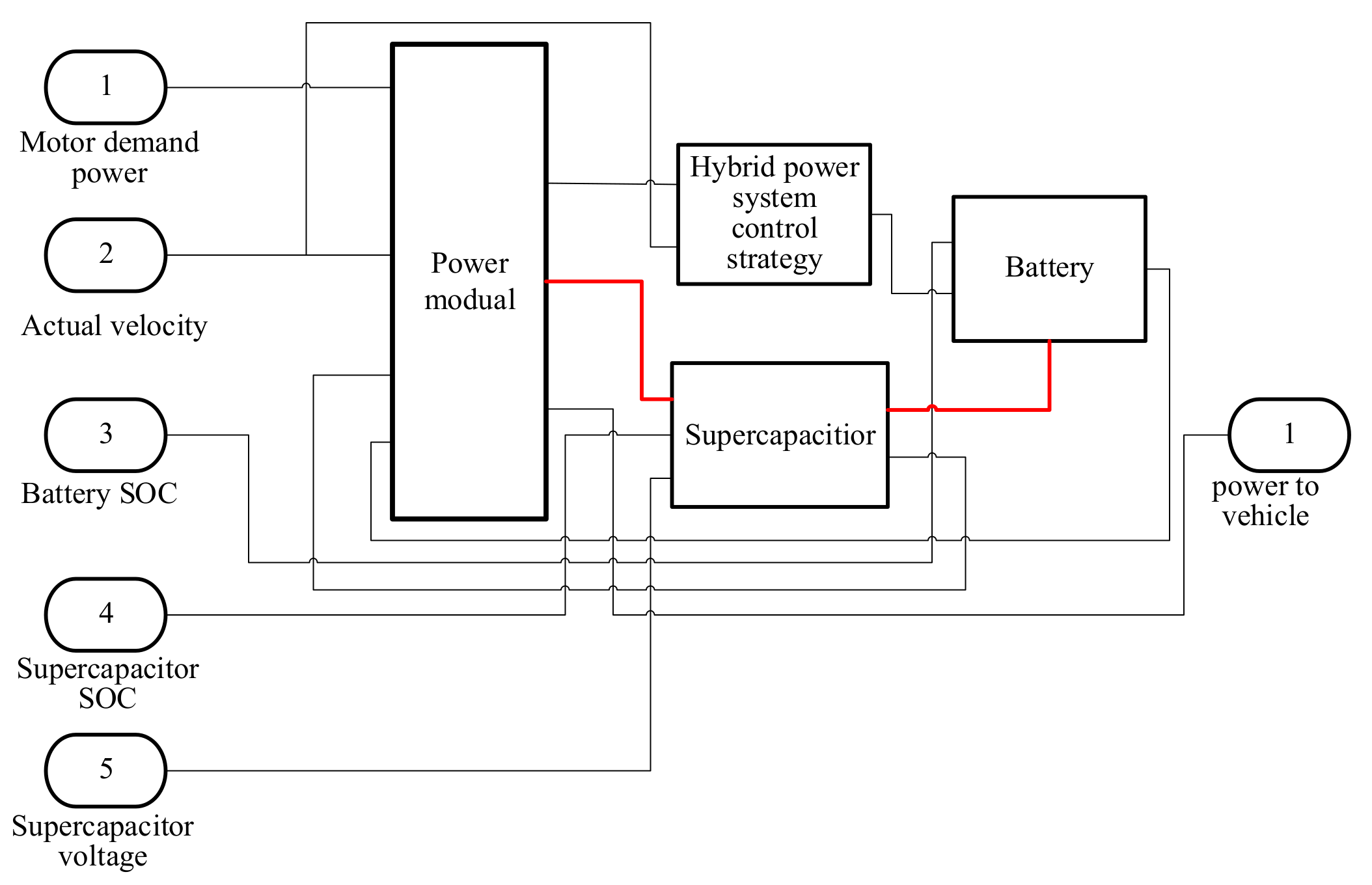
2.2. Modeling of Power System and Energy System
2.2.1. Motor Model
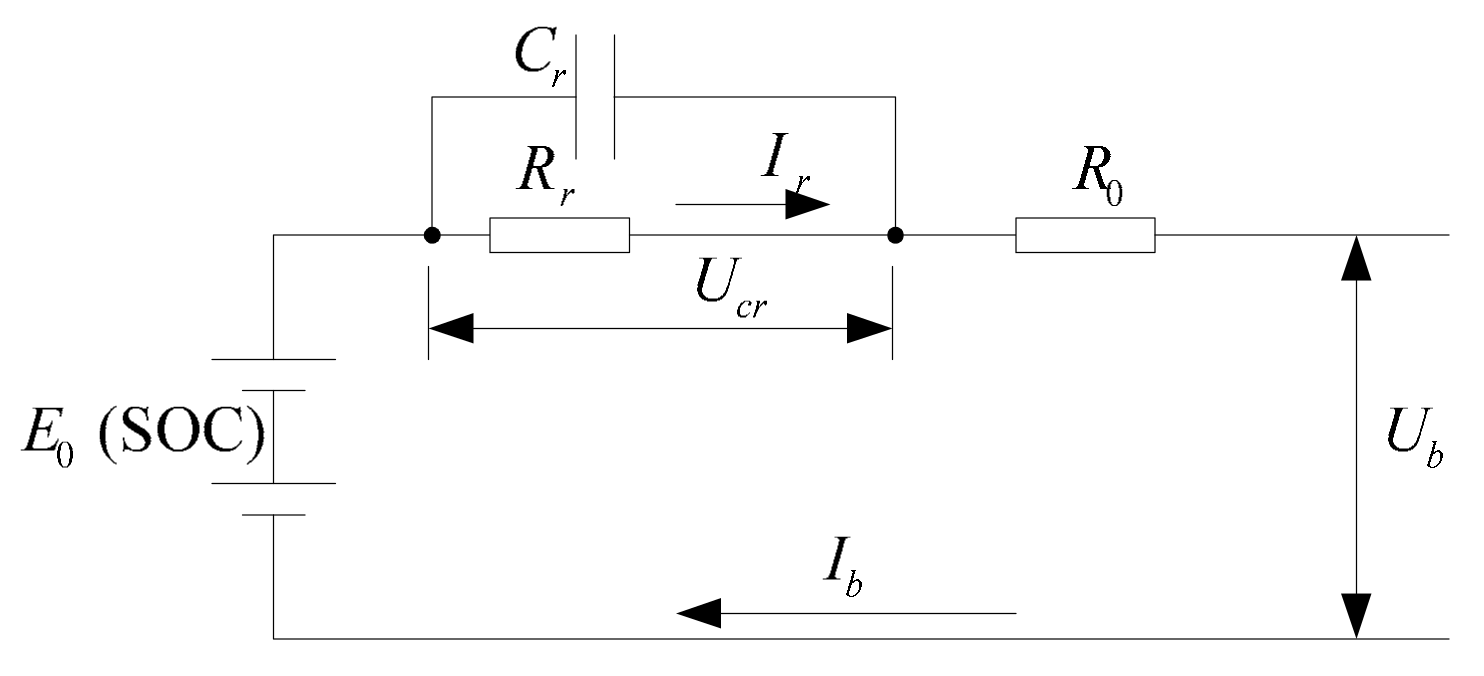
2.2.2. Battery Model
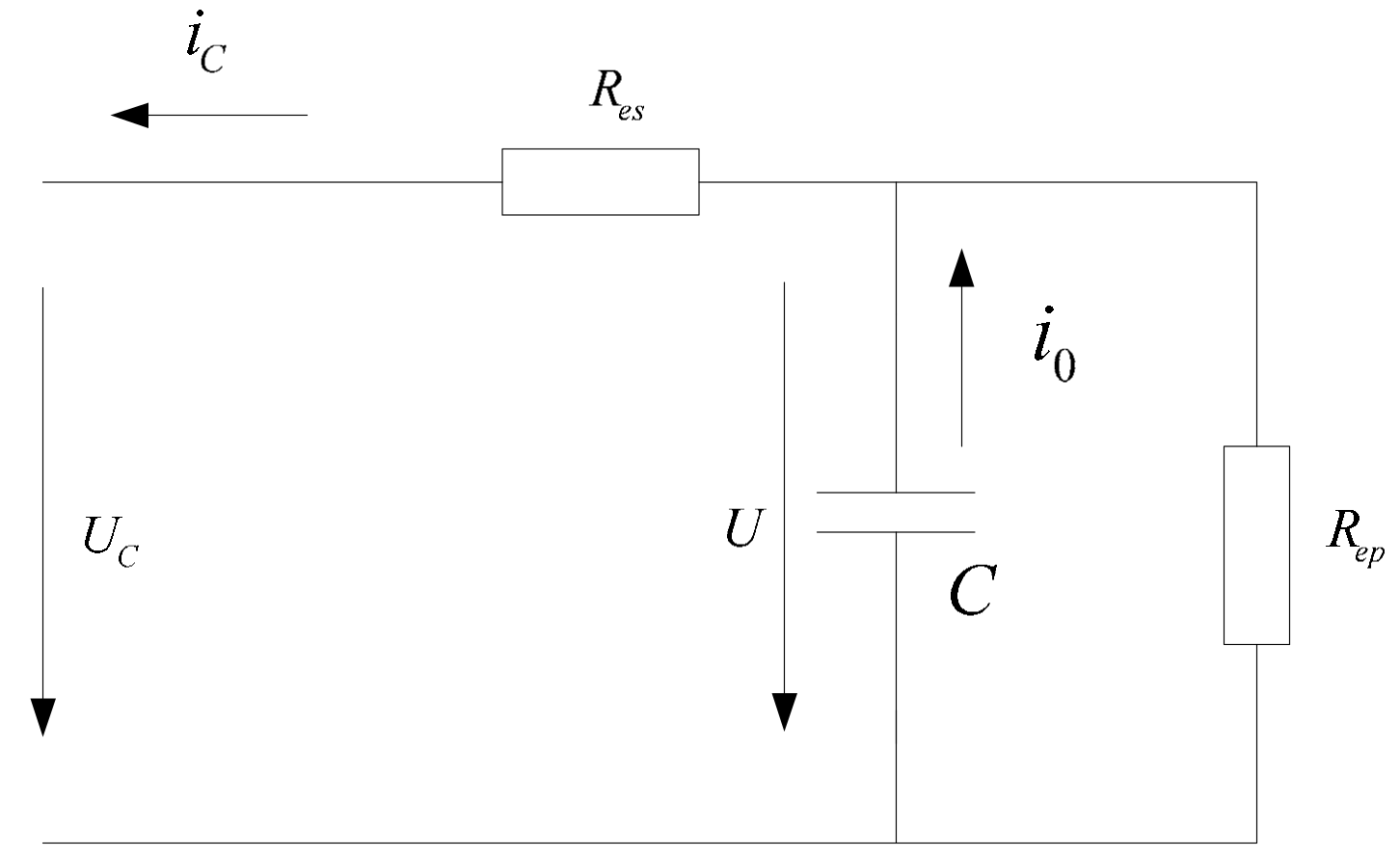
2.2.3. Supercapacitor Model
2.3. Parameter Optimization of Unmanned Electric Drive Chassis with Power-Energy Coupling
2.4. Optimization Objective
2.5. Optimization Variables
2.6. Constraint Condition
- The difference between the simulated speed at any moment and the speed required by the working condition shall be ≤2 km/h;
- Maximum speed requirement: vmax ≥ 90 km/h;
- Driving range: ≥100 km;
- Variation range of supercapacitor’s SOC: 20~90%;
- Variation range of battery’s SOC: 30~80%.
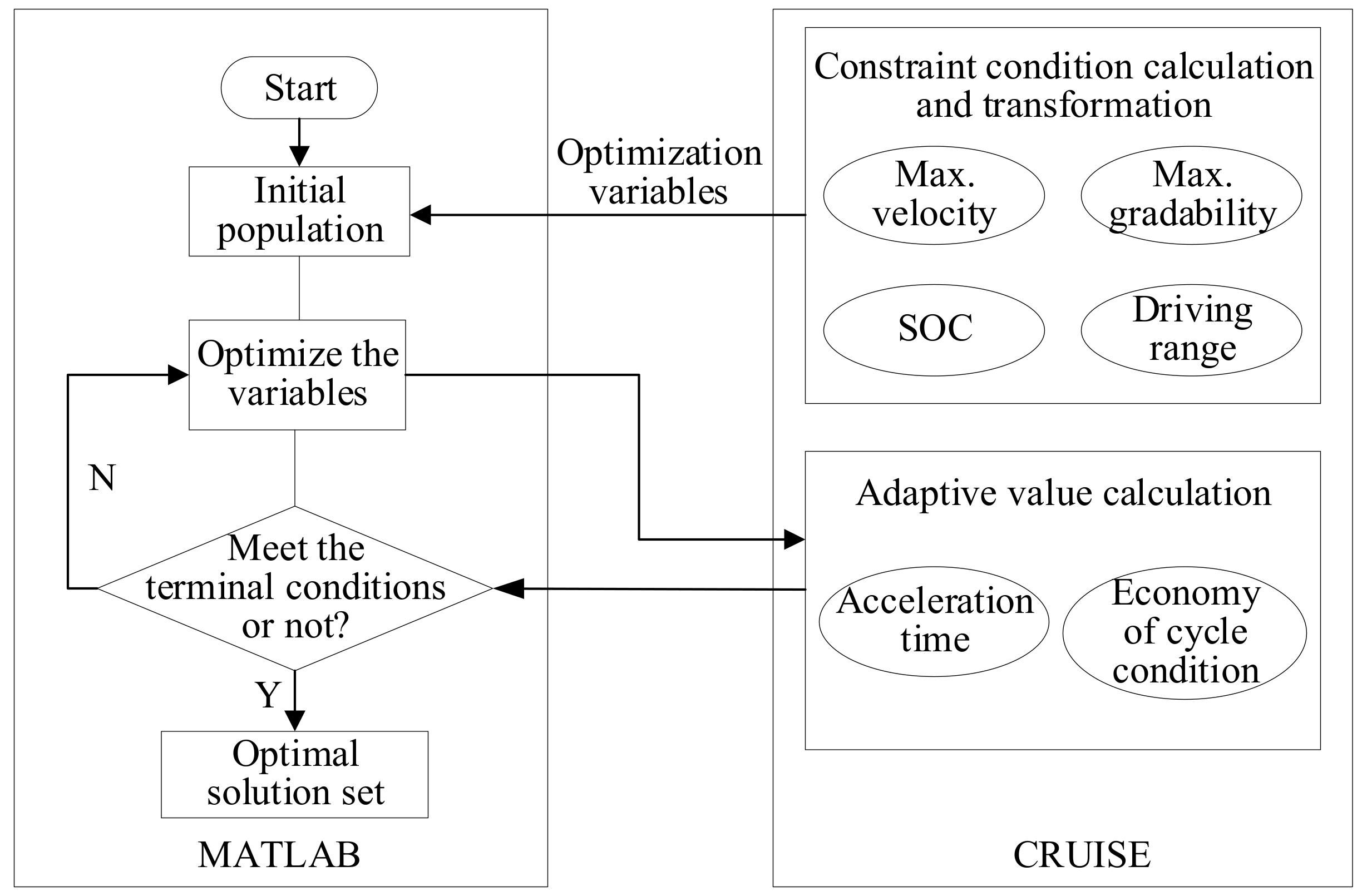
3. Process Design of Model-in-the-Loop Optimization
4. An Improved Isolated Niche Genetic Algorithm Based on the KOHONEN Network (KIGA)
4.1. General Overview of KIGA
- (a)
- The KOHONEN network clustering algorithm is used to divide the initial subpopulation to achieve a more reasonable division of the initial niche;
- (b)
- Two external archives are established to store the individual with the highest fitness and the Pareto solution set found at the initial stage, respectively, to guide the direction of evolution of the algorithm;
- (c)
- The weight of the subobjective function is determined by using the combination method based on the least squares method, and the Pareto solution set is optimized.
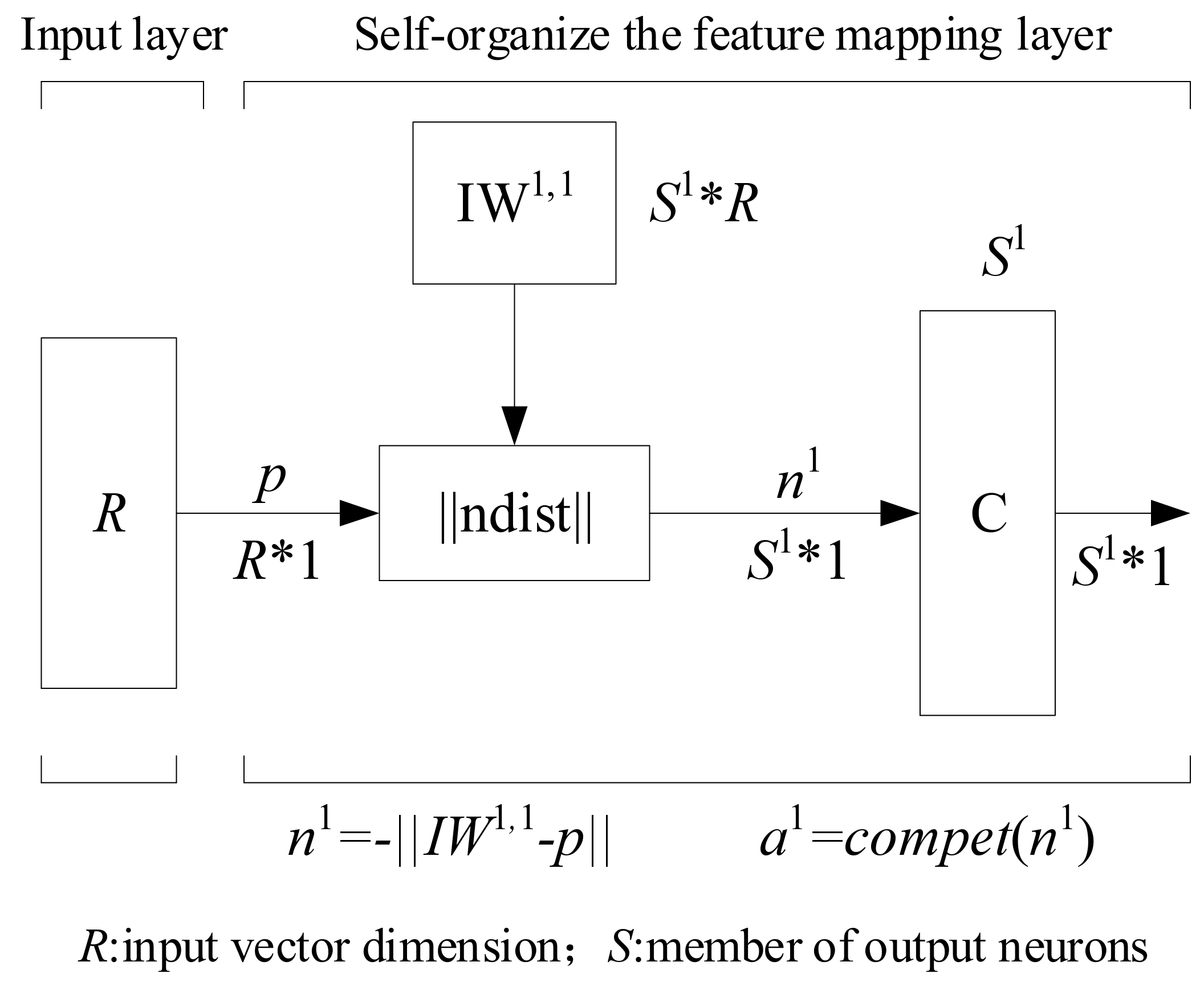
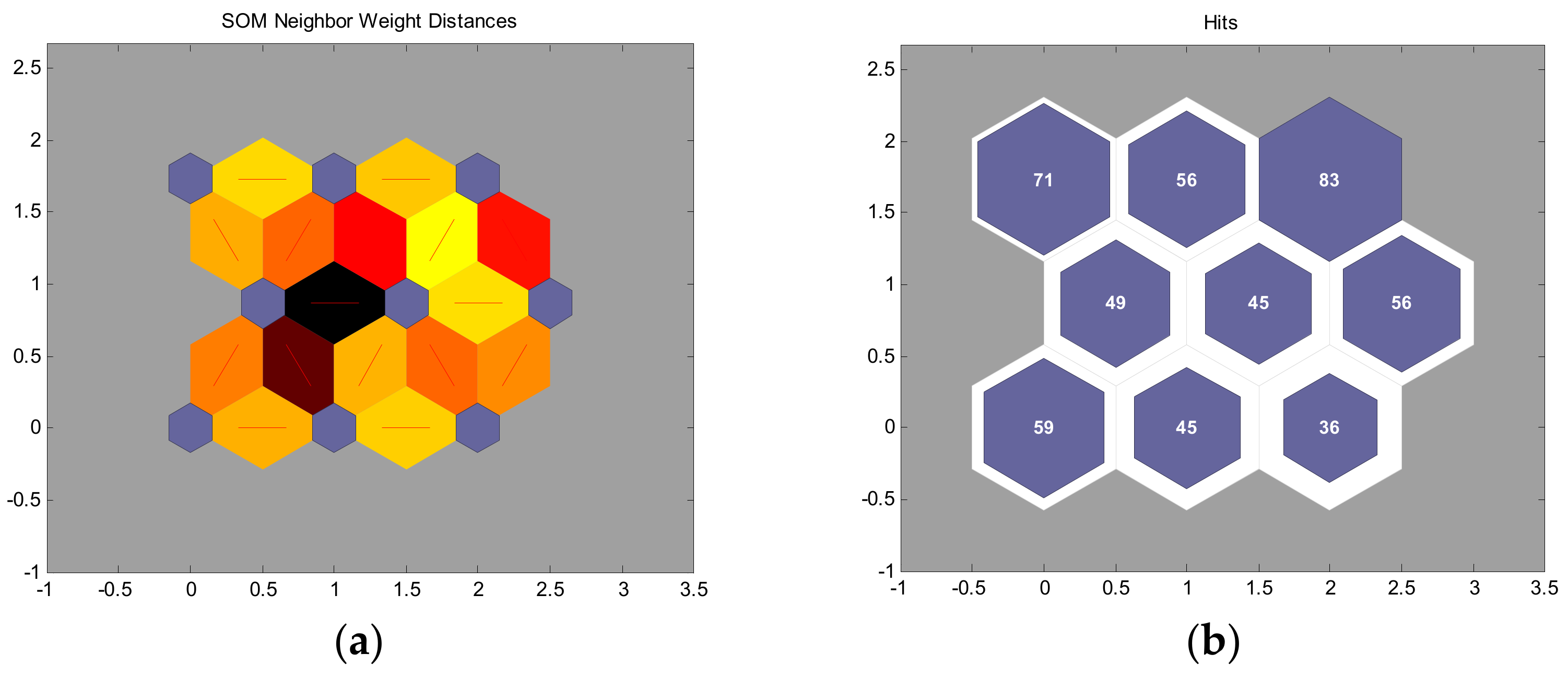
4.2. Establishment of the Initial KIGA Niche Subpopulation Based on KOHONEN Network Clustering
4.2.1. Selection of Sample Feature Vectors
4.2.2. Design of the Output Layer
4.2.3. Design of the Learning Rate
4.3. Establishment of External Archives
4.4. Pareto Selection Based on Least Squares Combination Weighting
- Using the AHP (analytic hierarchy process) to determine the subjective weight of each index;
- The determination of objective weight by the coefficient of variation method;
- Combining the weight of each index;
- Standardizing the scheme set with n schemes and m evaluation indicators to obtain the decision matrix. Then, the evaluation value of the i-th evaluation object isThe optimal combination model obtained by the least squares method is as follows:
- The objective function in this model is taken as a Lagrangian function, and then the partial derivatives of wj and λ (λ is a Lagrangian operator) are calculated, respectively, to calculate the comprehensive evaluation value of each scheme. The best scheme is the one with the highest comprehensive evaluation value. The comprehensive evaluation value is
4.5. Algorithm Flow
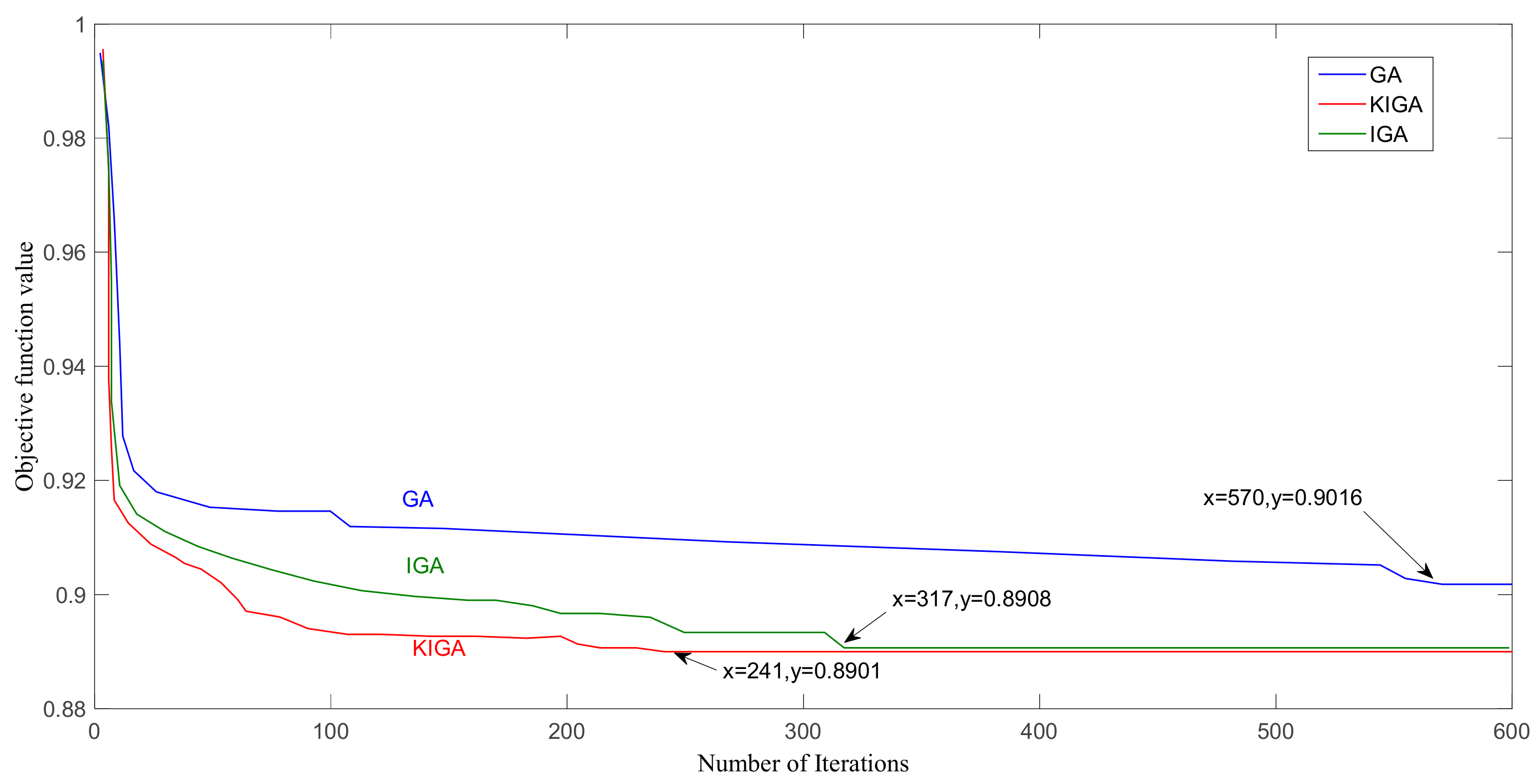
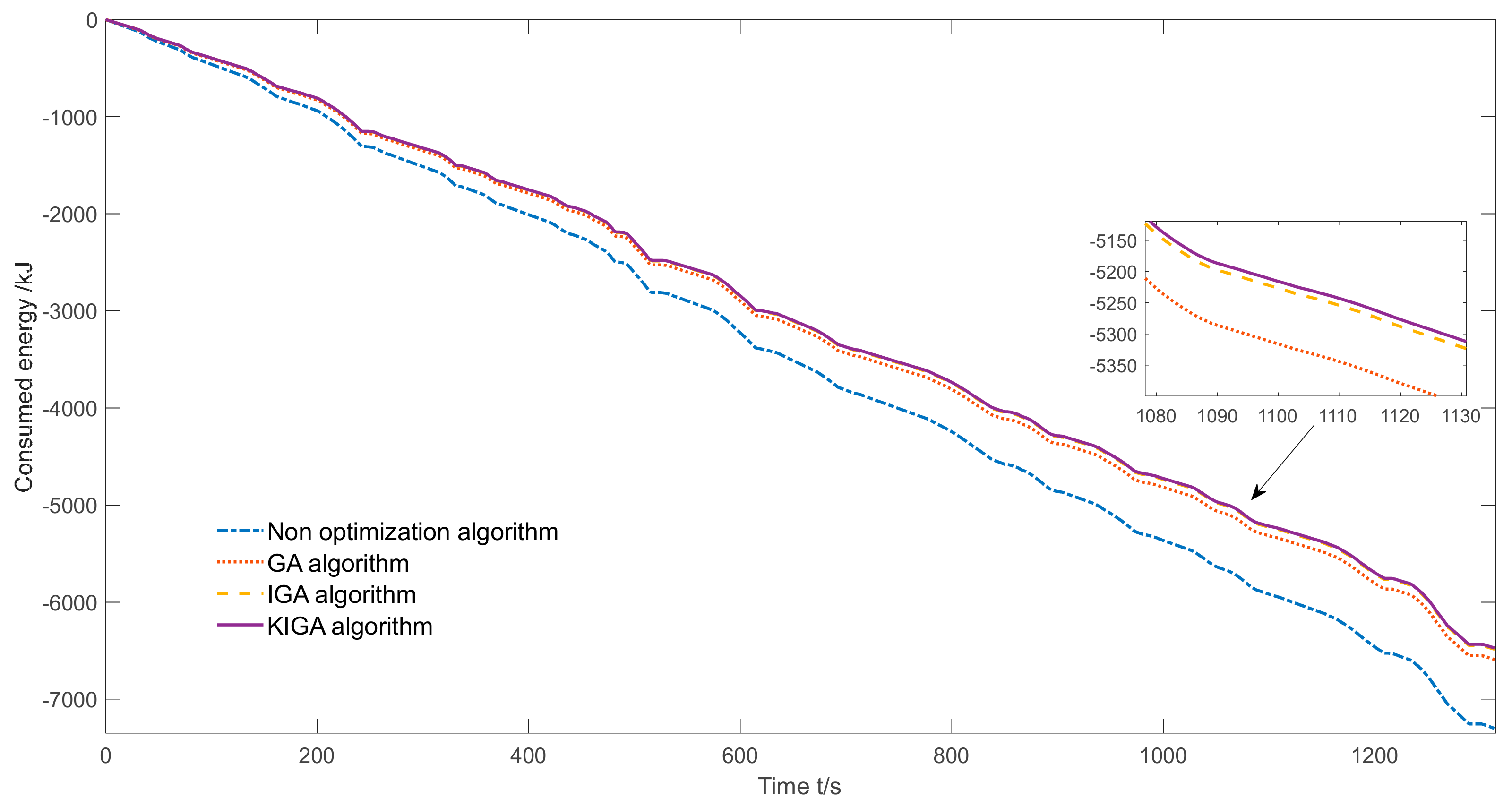
5. Optimization Results and Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Çağatay Bayindir, K.; Gözüküçük, M.A.; Teke, A. A comprehensive overview of hybrid battery vehicle: Powertrain configurations, powertrain control techniques and electronic control units. Energy Convers. Manag. 2011, 52, 1305–1313. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Y.; Yang, C.; Jiao, X.; Zhang, L.; Song, J. Hybrid genetic algorithm-based optimization of powertrain and control parameters of plug-in hybrid electric bus. J. Frankl. Inst. 2015, 352, 776–801. [Google Scholar] [CrossRef]
- Hegazy, O.; Van Mierlo, J.; Barrero, R.; Omar, N.; Lataire, P. PSO algorithm-based optimal power flow control of fuel cell/supercapacitor and fuel cell/battery hybrid battery vehicles. Compel-Int. J. Comput. Math. Electr. Electron. Eng. 2013, 32, 86–107. [Google Scholar] [CrossRef]
- Montazeri-Gh, M.; Poursamad, A.; Ghalichi, B. Application of genetic algorithm for optimization of control strategy in parallel hybrid battery vehicles. J. Frankl. Inst. 2006, 343, 420–435. [Google Scholar] [CrossRef]
- Dong, B. Energy Management System Control Strategy and Optimization for Battery Vehicle Based on the Lithium-Ion Power Battery; Jilin University: Changchun, China, 2014. [Google Scholar]
- Deng, Y.-w.; Gong, J.-k.; Wang, Y.-n. Energy Optimization and Simulation of HEV Using Mild Hybrid Control Strategy. China J. Highw. Transp. 2008, 21, 114–120. [Google Scholar]
- Lei, F.; Bai, Y.; Zhu, W.; Liu, J. A novel approach for electric powertrain optimization considering vehicle power performance, energy consumption and ride comfort. Energy 2019, 167, 1040–1050. [Google Scholar] [CrossRef]
- Morozov, A.; Humphries, K.; Rahman, T.; Zou, T.; Angeles, J. Drivetrain Analysis and Optimization of a Two-Speed Class-4 Electric Delivery Truck. SAE Tech. Paper 2019. [Google Scholar] [CrossRef]
- Puma-Benavides, D.S.; Izquierdo-Reyes, J.; Calderon-Najera JD, D.; Ramirez-Mendoza, R.A. A Systematic Review of Technologies, Control Methods, and Optimization for Extended-Range Electric Vehicles. Appl. Sci. 2021, 11, 7095. [Google Scholar] [CrossRef]
- Tan, S.; Yang, J.; Zhao, X.; Hai, T.; Zhang, W. Gear ratio optimization of a multi-speed transmission for electric dump truck operating on the structure route. Energies 2018, 11, 1324. [Google Scholar] [CrossRef]
- Kwon, K.; Jo, J.; Min, S. Multi-objective gear ratio and shifting pattern optimization of multi-speed transmissions for electric vehicles considering variable transmission efficiency. Energy 2021, 236, 121419. [Google Scholar] [CrossRef]
- Lin, Y.; Hao, J.M.; Ji, Z.S.; Dai, Y.S. A study of genetic algorithm based on isolation niche technique. J. Syst EMS Eng. 2000, 15, 86–91. [Google Scholar]
- Chen, X.-D.; He, R.; Yang, Z.-L. Development of hybrid battery vehicles (HEV) performance simulation software. J. Traffic Transp. Eng. 2002, 2, 114–117. [Google Scholar]
- Wang, Q.-N.; Yu, Y.-T.; Zeng, X.-H.; Yu, Y.-B. Development of forward-looking simulation platform for hybrid battery vehicle based on software CRUISE. J. Jilin Univ. (Eng. Technol. Ed.) 2009, 39, 1413–1419. [Google Scholar]
- Qiao, H.M. Research on Two-Wheel Drive Electric Vehicle Motor Control System; Shandong University of Technology: Zibo, China, 2008. [Google Scholar]
- Sun, X.X.; Wang, Y.C.; Xiang, L.Y.; Wang, R. A Research on the Braking Control Strategy with Energy Consuming Braking for Power-split HEV. Automot. Eng. 2012, 34, 46–50. [Google Scholar]
- BimaI, K. Bose Modern Power Electronics And AC Drives; Prentice Hall PTR: Hoboken, NJ, USA, 2001. [Google Scholar]
- Li, B.; Chen, Q. Research on battery characteristics in hybrid electric vehicles. Automob. Technol. 1999, 10, 11–14. [Google Scholar]
- Massimo, C. New Dynamical Models of Leads-Acid Batteries. IEEE Trans. Power Syst. 2000, 15, 1184–1190. [Google Scholar]
- Wang, H.; Cui, S. Modeling of the characteristics of charge and discharge of lead-acid battery based on test. Chin. Labat Man 2005, 42, 38–41. [Google Scholar]
- Zhang, B.Y. Battery Inner Resistance Test during Battery Maintenance. Telecom Power Technol. 2002, 2, 26–29. [Google Scholar]
- Endo, M.; Takeda, T.; Kim, Y.J. High Power Electric Double Layer Capacitor (EDLC’s) from Operation Principle to Pore Size Control in Advanced Activated Carbons. Carbon Sci. 2001, 1, 117–128. [Google Scholar]
- Wendy, G.; Pell, B.E.; Conway, W.A. Electrochemical efficiency in multiple discharge/recharge cycling of super capacitors in hybrid EV applications. J. Power Sources 1999, 80, 134–141. [Google Scholar]
- Liu, X.-B.; Ma, J.; Hao, R.-R.; Song, Q.-S. Design of regenerative braking energy feedback system for ultracapacitor heavy-duty tractor. J. Traffic Transp. Eng. 2013, 13, 60–65. [Google Scholar]
- Zhou, Y.; Jia, J. Parameters optimization of hybrid battery vehicle based on orthogonal experimental design and multi-objective genetic algorithm. J. Automot. Saf. Energy 2014, 5, 324–330. [Google Scholar]
- Xu, J.; Liu, J. A new genetic algorithm based on niche technique. Pattern Recognit. Artif. Intell. 1999, 12, 104–108. [Google Scholar]
- Jiang, J.-G.; Li, J.; Long, X.-P.; Shen, J.-L.; Tian, M. A shuffled frog leaping algorithm using niche technology. Chin. J. Comput. Mech. 2012, 29, 960–965. [Google Scholar]
- Cheol, G.L.; Cho, D.-H.; Jung, A.H.-K. Niching Genetic Algorithm with Restricted Competition Selection for Multimodal Function Optimization. IEEE Trans. Magn. 1999, 35, 1722–1725. [Google Scholar] [CrossRef]
- Ban, S.-H.; Yang, H.-Z. Niche genetic algorithms applied in inversion of pore media. Pet. Explor. Dev. 2005, 32, 78–81. [Google Scholar]
- Dragomir, O.E.; Dragomir, F.; Radulescu, M. Matlab Application of Kohonen Self-organizing Map to Classify Consumers’ Load Profiles. Procedia Comput. Sci. 2014, 31, 474–479. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, A.C. JADE: Adaptive differential evolution with optional external archive. Evol. Comput. IEEE Trans. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Ma, J.; Jia, X. Comprehensive Evaluation of Power Quality Based on the Method of Consistent between Subjective and Objective in the Least-squares Sense. Electr. Power Sci. Eng. 2013, 29, 18–23. [Google Scholar]



| Parameters | Numerical Value | Unit |
|---|---|---|
| Total mass | 5244 | m/kg |
| Air drag coefficient | 0.6 | CD |
| Windward area | 6.0168 | A/m2 |
| Rolling resistance coefficient | 0.019 | f |
| Wheel radius | 0.357 | r/m |
| Driveline efficiency | 85 | ηT/% |
| Transmission ratio | [5.568, 2.360, 1.634, 1] | ign |
| Final drive ratio | 6.43 | i0 |
| Rated power of motor | 40 | Pe/kW |
| Maximum power of motor | 70 | Pm/kW |
| Rated torque of motor | 124 | Te/N·m |
| Maximum torque of motor | 300 | Tm/N·m |
| Rated speed of motor | 3000 | ne/(r·min−1) |
| Maximum speed of motor | 5000 | nm/(r·min−1) |
| Battery capacity | 120 | C/Ah |
| Variable Name | Optimization Parameters | Lower Limit | Upper Limit |
|---|---|---|---|
| x1 | Motor power/kW | 30 | 60 |
| x2 | First-gear transmission ratio | 2.8 | 5.7 |
| x3 | Second-gear transmission ratio | 1.5 | 2.6 |
| x4 | Third-gear transmission ratio | 0.9 | 1.1 |
| x5 | Final drive ratio | 3.5 | 7.5 |
| x6 | Battery capacity | 100 Ah | 200 Ah |
| x7 | Supercapacitor energy storage | 100 Wh | 300 Wh |
| Parameter | Numeric Value |
|---|---|
| Number of variables | 7 |
| Population size | 500 |
| Iterations to terminate evolution | 600 |
| Crossover probability/Pc | 0.4 |
| Mutation probability/Pm | 0.01 |
| Maximum allowable size of subpopulation/Smax | 80 |
| Minimum allowable size of subpopulation/Smin | 30 |
| Optimization Project | Before and after Optimization | |||||||
|---|---|---|---|---|---|---|---|---|
| Before Optimization | GA | IGA | KIGA | |||||
| Optimization Value | Rate of Change | Optimization Value | Rate of Change | Optimization Value | Rate of Change | |||
| Optimization variables | First-gear transmission ratio | 5.568 | 5.384 | −3.30% | 5.352 | −3.88% | 5.352 | −3.88% |
| Second-gear transmission ratio | 2.605 | 2.714 | 4.18% | 2.652 | 1.80% | 2.643 | 1.46% | |
| Third-gear transmission ratio | 1 | 1 | 0.00% | 0.984 | −1.60% | 0.984 | −1.60% | |
| Final drive ratio | 6.43 | 6.32 | −1.71% | 6.24 | −2.95% | 6.24 | −2.95% | |
| Battery capacity/Ah | 132 | 126 | −4.55% | 120 | −9.09% | 120 | −9.09% | |
| Supercapacitor energy storage/Wh | 162 | 178 | 9.88% | 186 | 14.81% | 189 | 16.67% | |
| Power | Maximum speed (km/h) | 91 | 92.2 | 1.32% | 92.5 | 1.65% | 92.5 | 1.65% |
| Maximum gradient/% | 36.22 | 35.37 | −2.35% | 35.14 | −2.98% | 35.14 | −2.98% | |
| 0~50 km/h Acceleration time/s | 11.5 | 11.12 | −3.30% | 11.04 | −4.0% | 11.04 | −4.0% | |
| Economy | 100 km power consumption (kWh/100 km) | 34.25 | 30.94 | −9.66% | 30.46 | −11.07% | 30.42 | −11.18% |
| Driving range/km | 106.3 | 109.7 | 3.20% | 113.9 | 7.15% | 114.7 | 7.90% | |
| Comprehensive performance | Acceleration time + 100 km power consumption | 0.970 | 0.902 | −7.07% | 0.891 | −8.18% | 0.890 | −8.26% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Xu, S.; Ouyang, H.; Zeng, X. Parameter Optimization of the Power and Energy System of Unmanned Electric Drive Chassis Based on Improved Genetic Algorithms of the KOHONEN Network. World Electr. Veh. J. 2023, 14, 260. https://doi.org/10.3390/wevj14090260
Wang W, Xu S, Ouyang H, Zeng X. Parameter Optimization of the Power and Energy System of Unmanned Electric Drive Chassis Based on Improved Genetic Algorithms of the KOHONEN Network. World Electric Vehicle Journal. 2023; 14(9):260. https://doi.org/10.3390/wevj14090260
Chicago/Turabian StyleWang, Weina, Shiwei Xu, Hong Ouyang, and Xinyu Zeng. 2023. "Parameter Optimization of the Power and Energy System of Unmanned Electric Drive Chassis Based on Improved Genetic Algorithms of the KOHONEN Network" World Electric Vehicle Journal 14, no. 9: 260. https://doi.org/10.3390/wevj14090260
APA StyleWang, W., Xu, S., Ouyang, H., & Zeng, X. (2023). Parameter Optimization of the Power and Energy System of Unmanned Electric Drive Chassis Based on Improved Genetic Algorithms of the KOHONEN Network. World Electric Vehicle Journal, 14(9), 260. https://doi.org/10.3390/wevj14090260






