Computer Vision for DC Partial Discharge Diagnostics in Traction Battery Systems
Abstract
1. Introduction
2. Related Work
- Potential root causes can be identified by different patterns.
- Partial discharges in the volume of the defect can be detected.
- Depending on the application, one can simulate the working load of the test object.
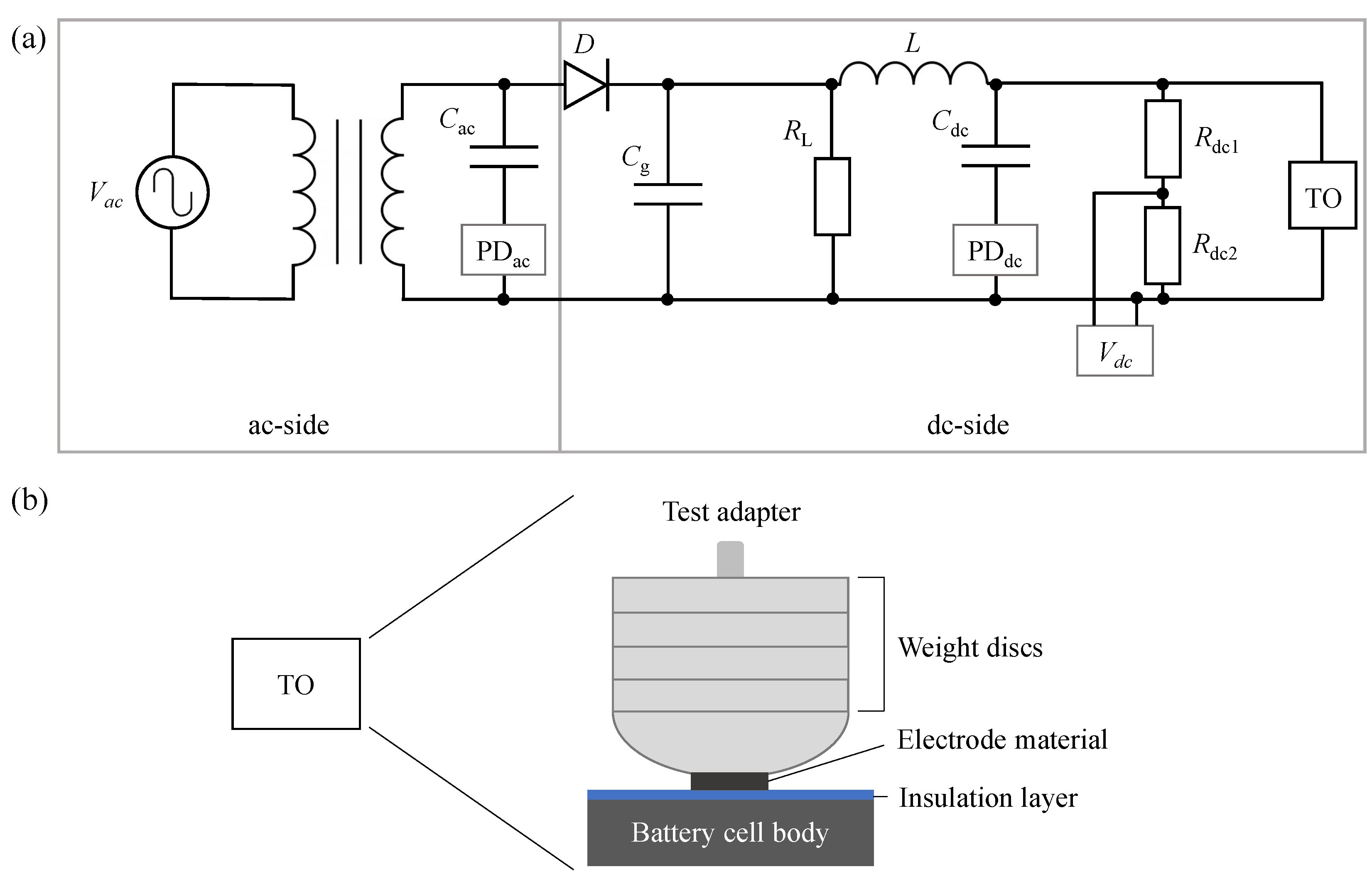
3. Technical Background
- The area;
- A threshold for the number of discharges in that area, above which we assign the diagram to a specific pattern.
4. Machine Learning Approach
4.1. Dataset Description
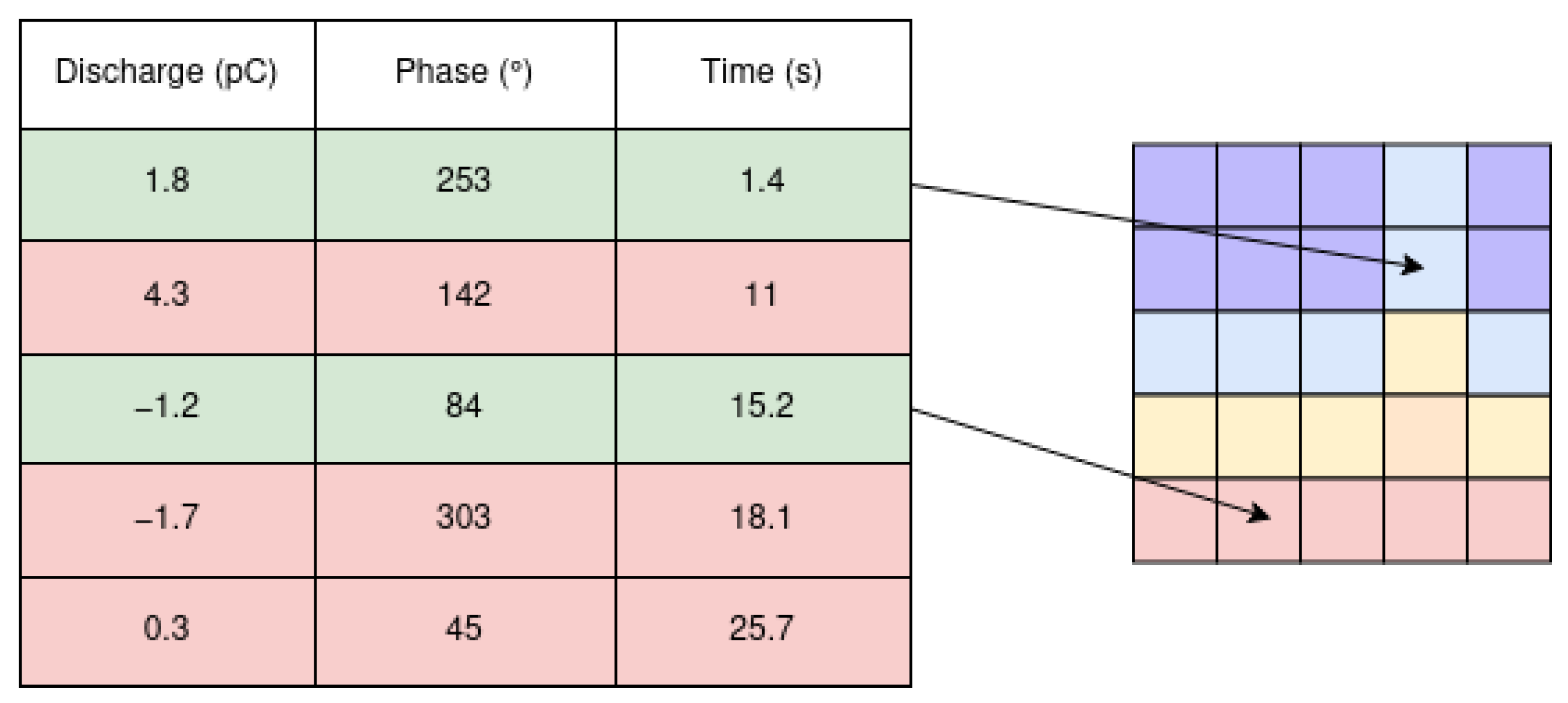
4.2. Creation of PRPD Diagrams
4.3. Algorithms
4.3.1. Classifiers
Logistic Regression
Support Vector Machine
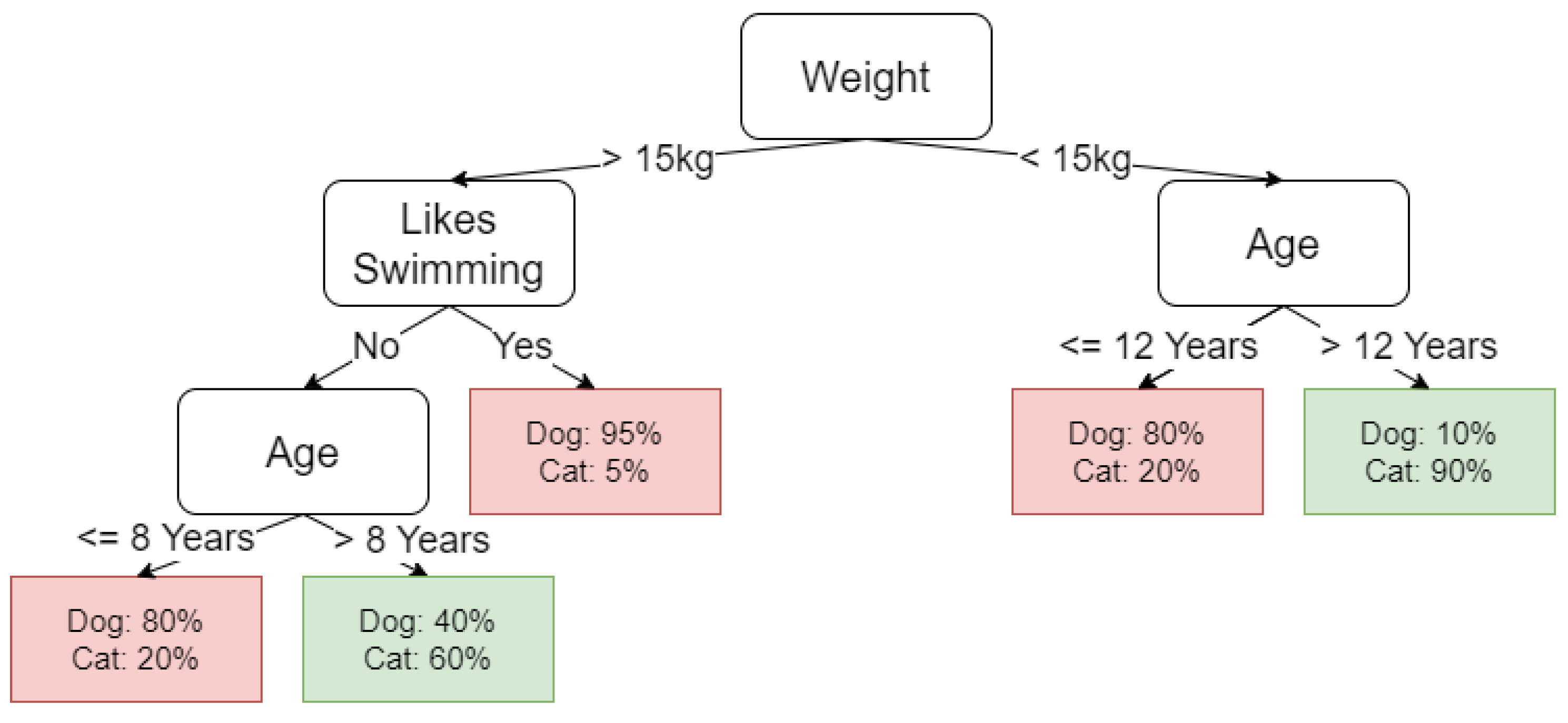
Random Forest
XGBoost
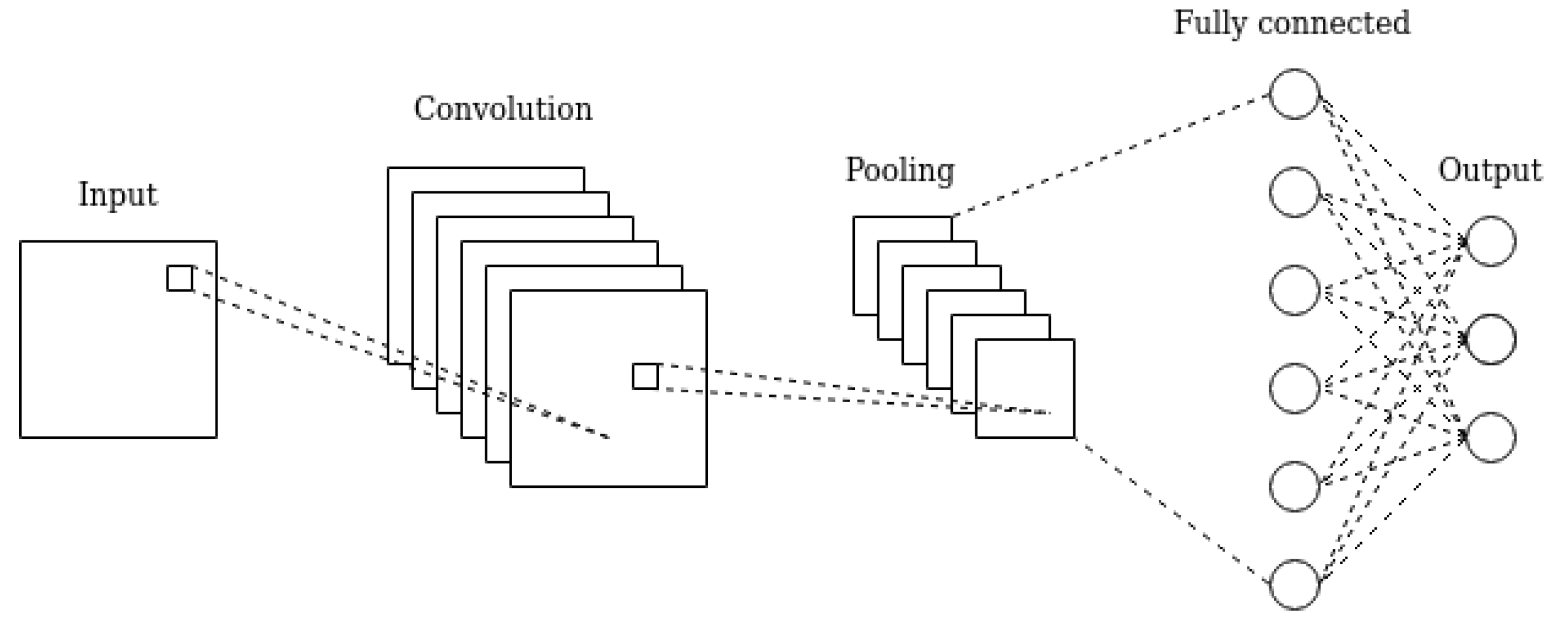
Convolutional Neural Networks
4.3.2. Dimension Reduction Techniques
Principal Component Analysis
Non-Negative Matrix Factorization
4.4. Evaluation Methodology
4.4.1. Classification Metrics
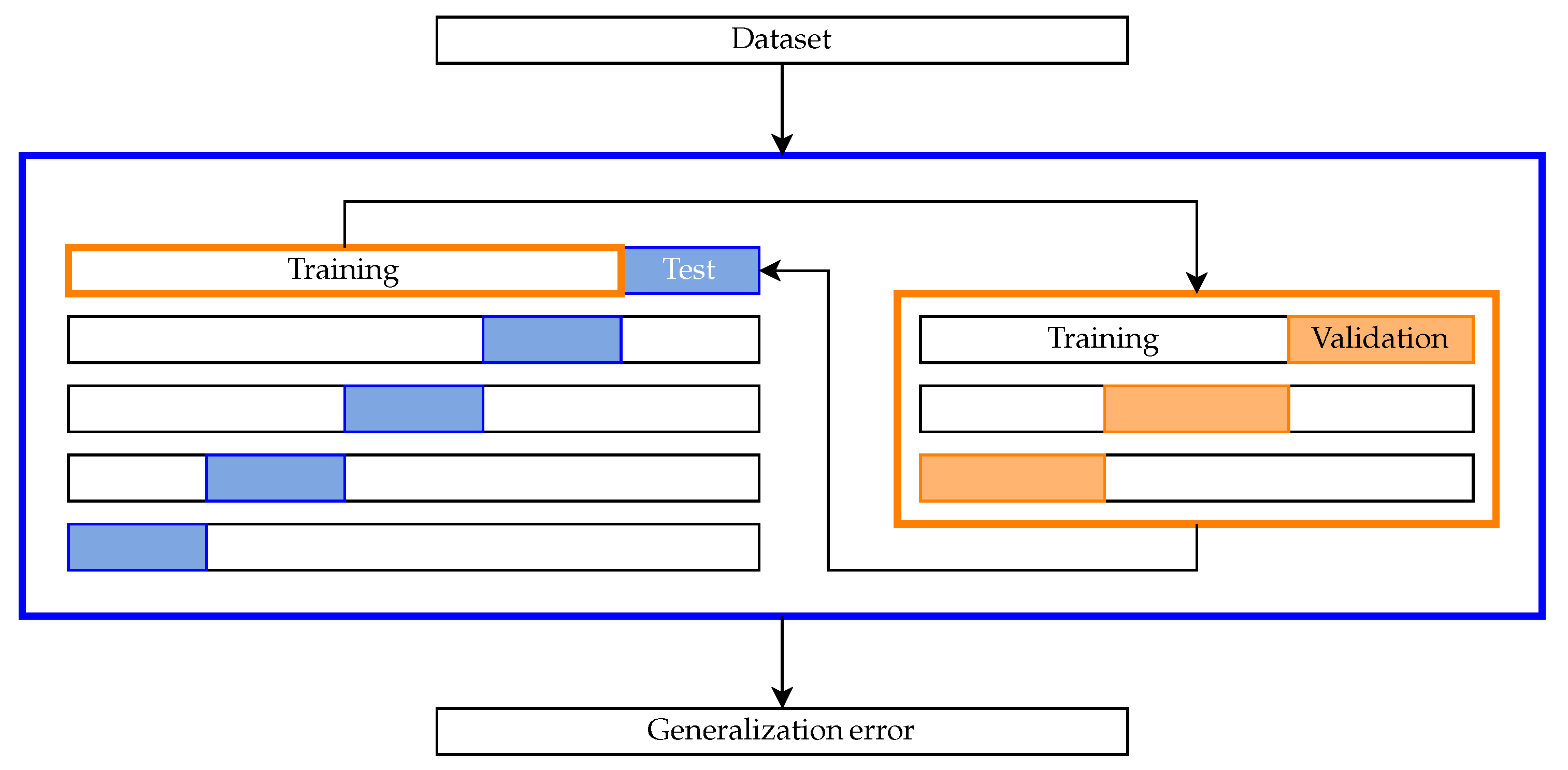
4.4.2. Nested Cross-Validation Methodology
5. Results
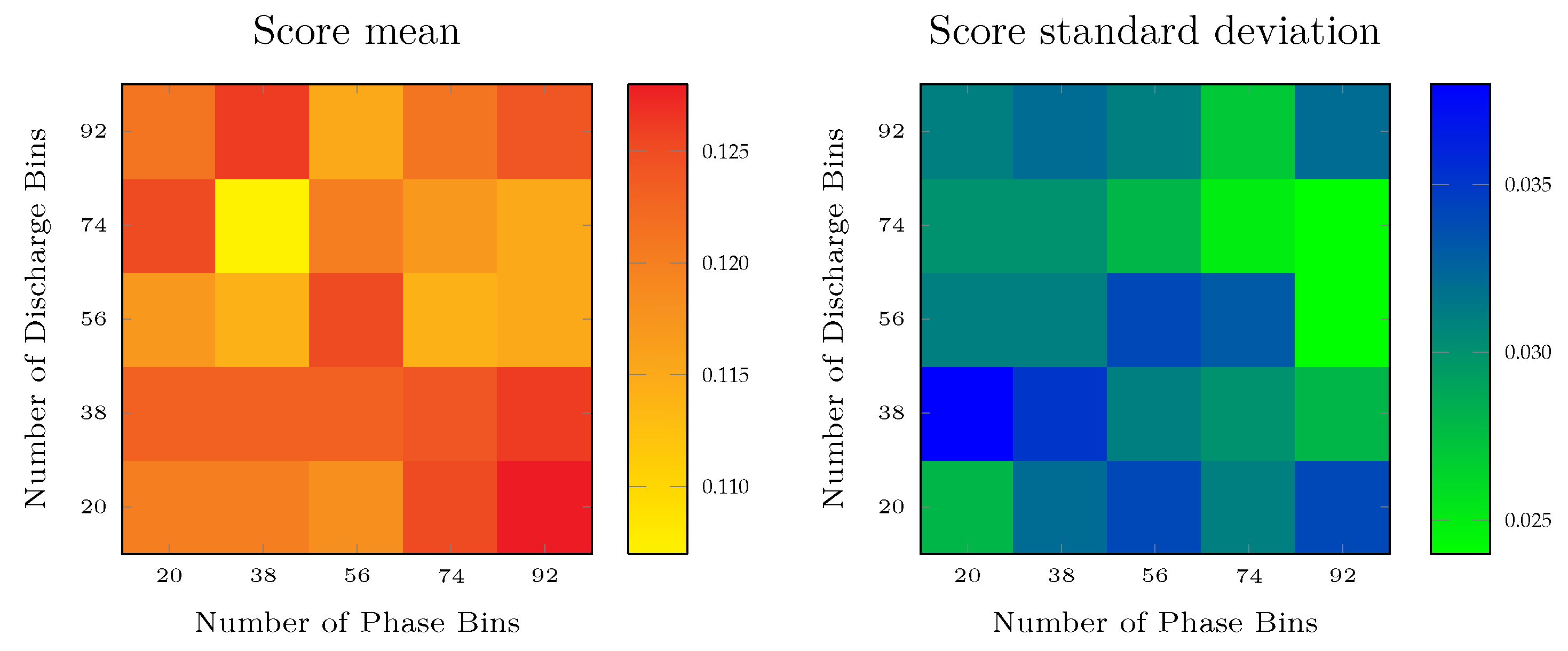
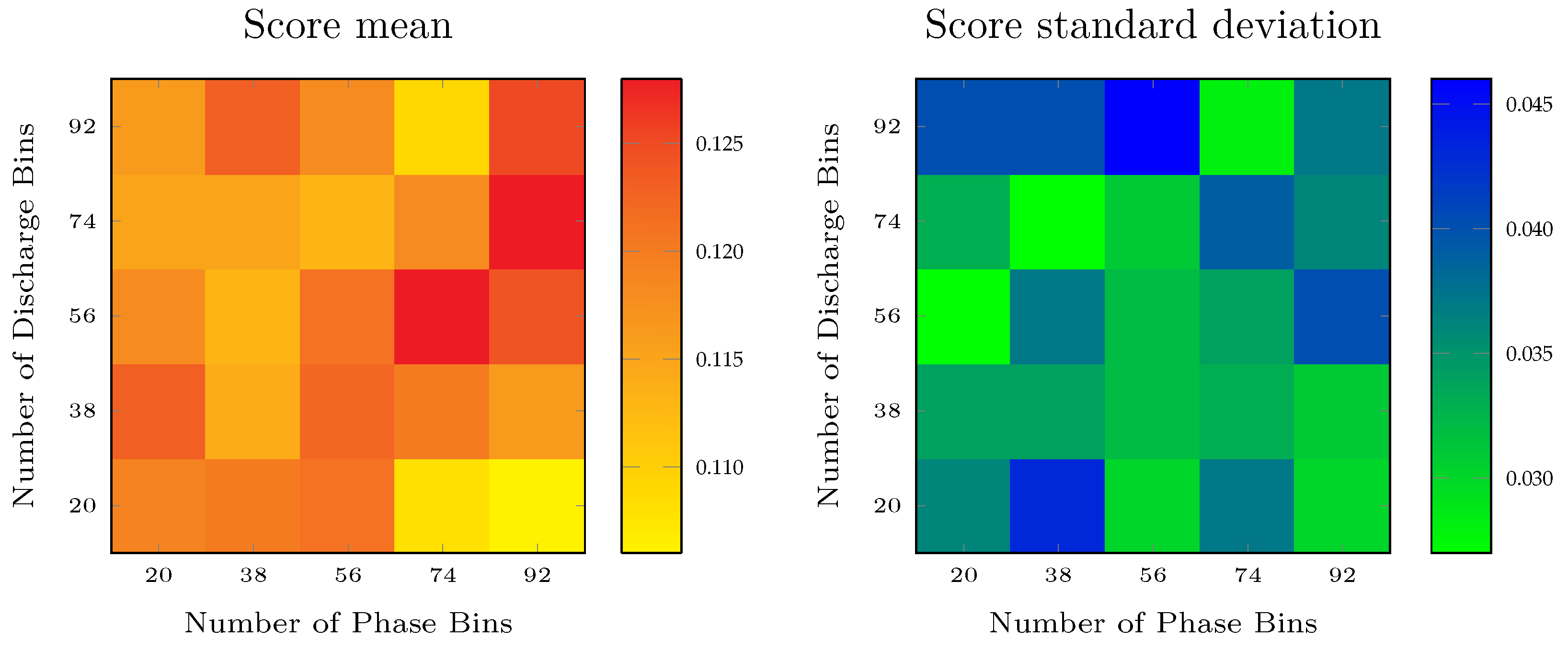
5.1. Choosing the Image Resolution
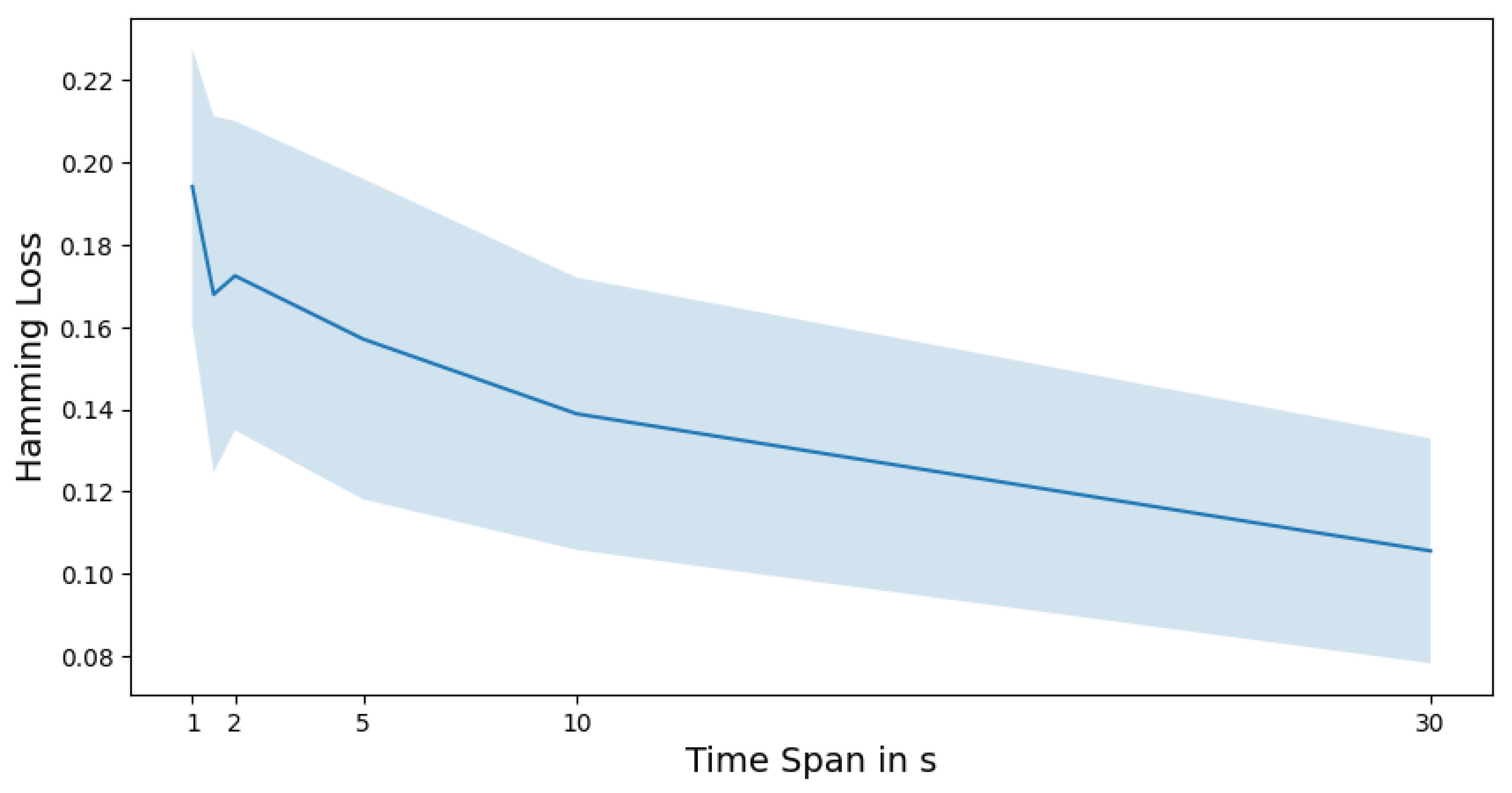
5.2. Short-Term Identification Ability of PRPD Patterns
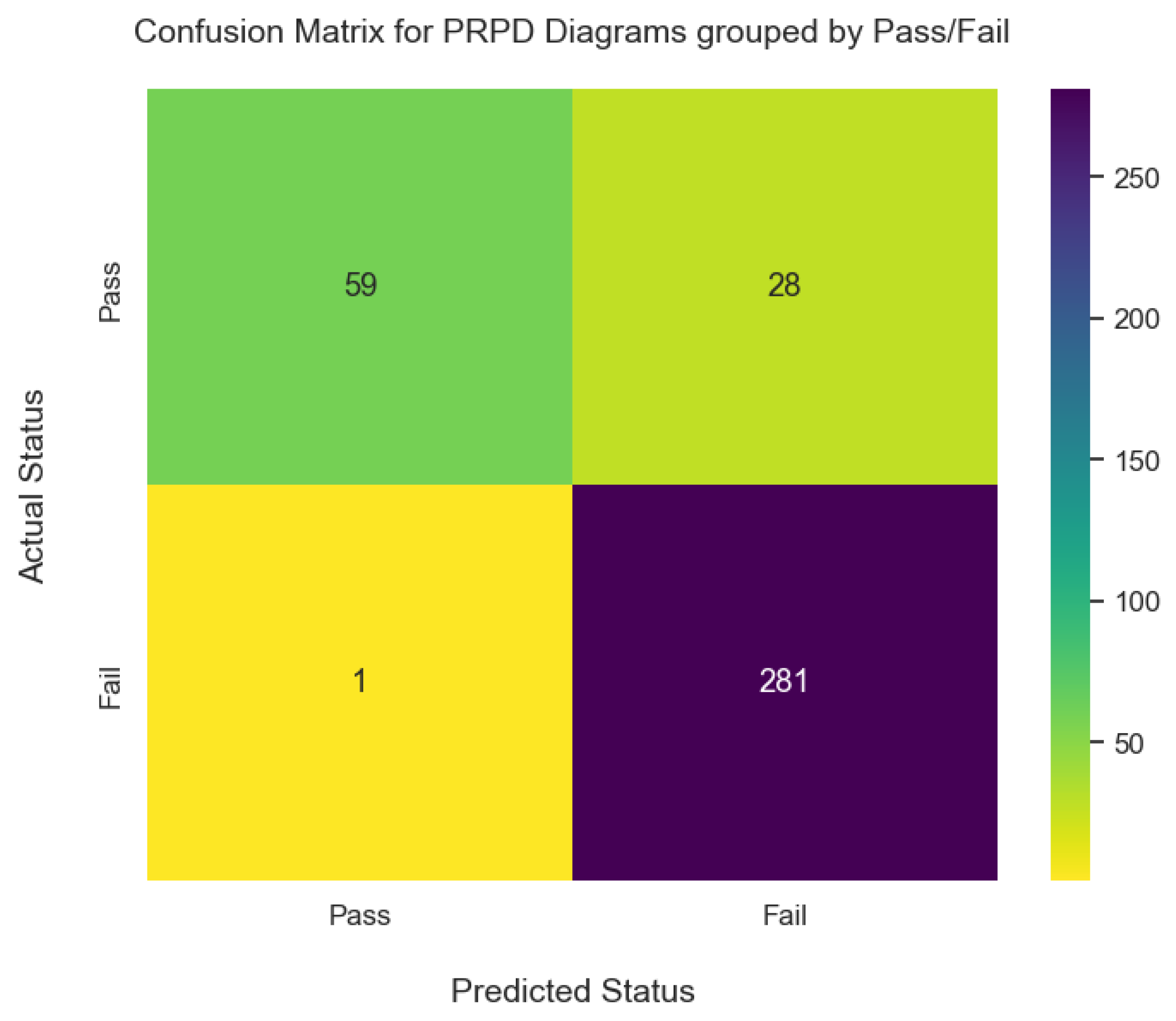
5.3. Performance by Label
5.4. Explainability
- In cases where the explanations of the model match those of the expert, one can be confident that the algorithm has learned the correct patterns and the model will also apply them to unseen images.
- It is important to rule out that the algorithm has not learned specific artifacts in the training images, which have a high predictive power but contain no information for unseen data [35].
5.4.1. Local Interpretable Model-Agnostic Explanations (LIME)
5.4.2. Interpretation of the Classifier
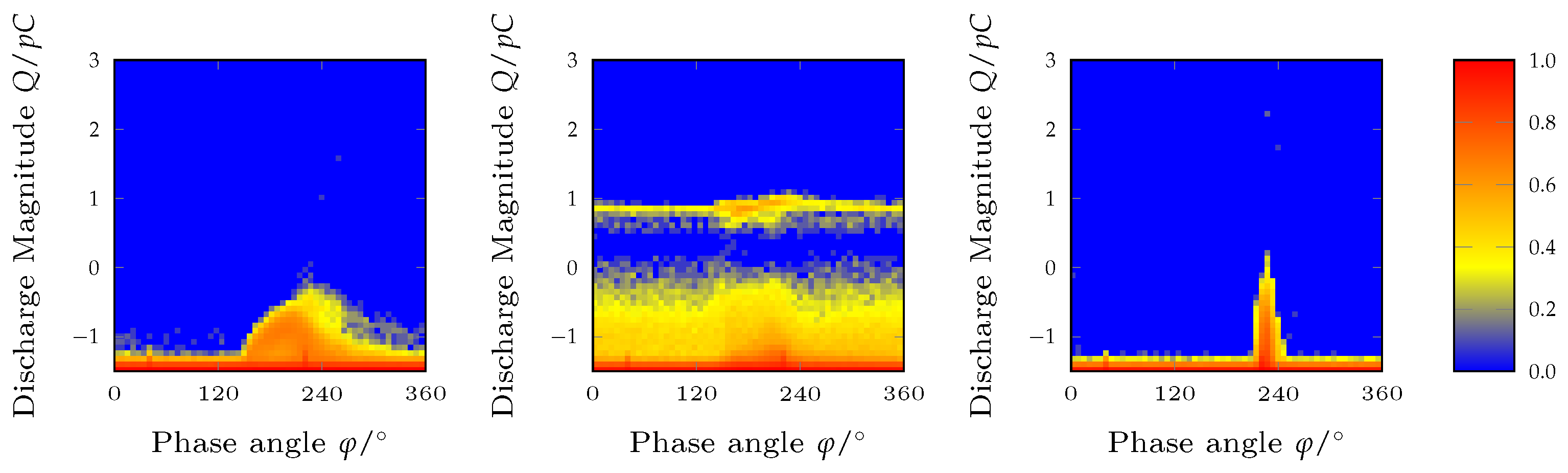
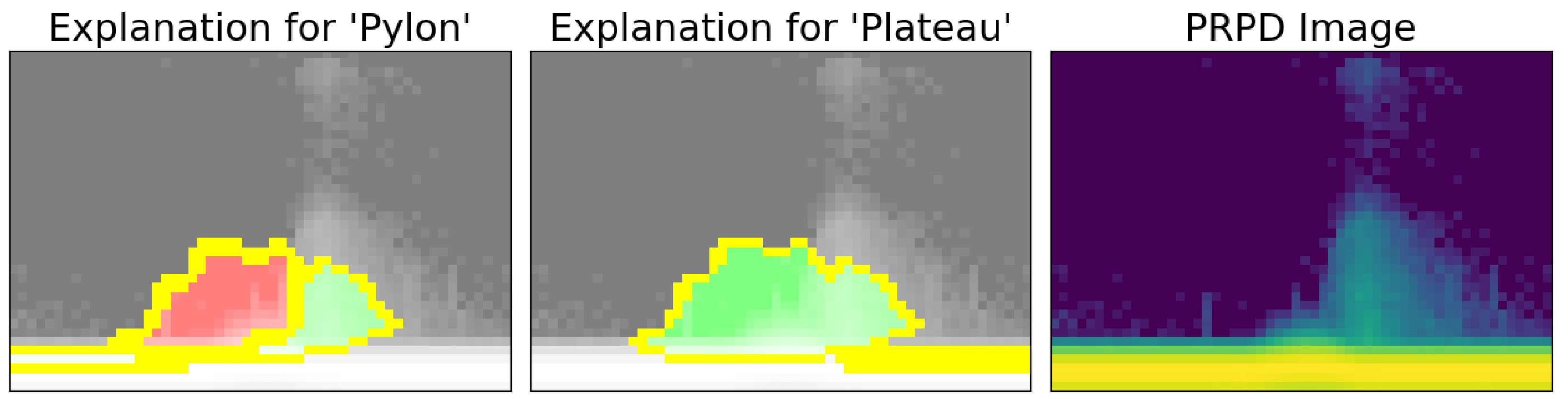
5.4.3. “Pylon” Predicted, True Label Is “Pylon”
5.4.4. “Plateau” Predicted, True Labels Are “Pylon” and “Plateau”
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BEV | Battery electric vehicles |
| CNN | Convolutional neural network |
| CO | Carbon dioxide |
| LIME | Local interpretable model-agnostic explanations |
| NMF | Non-negative matrix factorization |
| PCA | Principal component analysis |
| PD | Partial discharge |
| PoC | Proof of concept |
| PRPD | Phase-resolved partial discharge |
| RF | Random forest |
| SHAP | Shapley additive explanations |
| SVM | Support vector machine |
| TO | Test object |
| xAI | Explainable artificial intelligence |
Appendix A. Hyperparameter Search Spaces
| Algorithm | Hyperparameter Search Space |
|---|---|
| CNN | Batch Size: |
| Dense Layer Width: | |
| Kernel Size: | |
| Learning Rate: | |
| Number of Filters | |
| Logistic Regression | Regularizer: |
| Dimensions Projection: | |
| Support Vector Machine | Regularizer: |
| Parameter Kernel: | |
| Dimensions Projection: | |
| Random Forest | Maximal Depth Trees: |
| Dimensions Projection: | |
| XGBoost | Maximal Depth Trees: |
| Dimensions Projection: | |
| Learning Rate: |
References
- Cozzi, L.; Bouckaert, S. CO2 Emissions in 2022; Technical Report; International Energy Agency: Paris, France, 2023. [Google Scholar]
- Xiong, R.; Sun, W.; Yu, Q.; Sun, F. Research progress, challenges and prospects of fault diagnosis on battery system of electric vehicles. Appl. Energy 2020, 279, 115855. [Google Scholar] [CrossRef]
- Küchler, A. High Voltage Engineering: Fundamentals-Technology-Applications; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Guo, J.; Zheng, Z.; Caprara, A. Partial Discharge Tests in DC Applications: A Review. In Proceedings of the 2020 IEEE Electrical Insulation Conference (EIC), Knoxville, TN, USA, 22 June–3 July 2020; pp. 225–229. [Google Scholar] [CrossRef]
- Freudenberg, I.; Betz, T.; Gillilan, S.; Hild, D. Early fault detection of thin insulation layers in traction battery systems using dc partial discharge diagnostics. In Proceedings of the VDE High Voltage Technology; 4. ETG-Symposium, Berlin, Germany, 8–10 November 2022; pp. 1–6. [Google Scholar]
- Fu, M.; Dissado, L.A.; Chen, G.; Fothergill, J.C. Space charge formation and its modified electric field under applied voltage reversal and temperature gradient in XLPE cable. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 851–860. [Google Scholar] [CrossRef]
- Florkowski, M. Partial Discharges in High-Voltage Insulating Systems—Mechanisms, Processing, and Analytics; Wydawnictwa AGH: Kraków, Poland, 2021. [Google Scholar]
- Morshuis, P.; Jeroense, M.; Beyer, J. Partial discharge. Part XXIV: The analysis of PD in HVDC equipment. IEEE Electr. Insul. Mag. 1997, 13, 6–16. [Google Scholar] [CrossRef]
- Sahoo, N.; Salama, M.; Bartnikas, R. Trends in partial discharge pattern classification: A survey. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 248–264. [Google Scholar] [CrossRef]
- Müller, A.; Beltle, M.; Tenbohlen, S. Automated PRPD pattern analysis using image recognition. Int. J. Electr. Eng. Inform. 2012, 4, 483. [Google Scholar] [CrossRef]
- Janani, H.; Kordi, B. Towards automated statistical partial discharge source classification using pattern recognition techniques. High Volt. 2018, 3, 162–169. [Google Scholar] [CrossRef]
- Florkowski, M. Classification of Partial Discharge Images Using Deep Convolutional Neural Networks. Energies 2020, 13, 5496. [Google Scholar] [CrossRef]
- Do, T.D.; Tuyet-Doan, V.N.; Cho, Y.S.; Sun, J.H.; Kim, Y.H. Convolutional-neural-network-based partial discharge diagnosis for power transformer using UHF sensor. IEEE Access 2020, 8, 207377–207388. [Google Scholar] [CrossRef]
- Soh, D.; Krishnan, S.B.; Abraham, J.; Xian, L.K.; Jet, T.K.; Yongyi, J.F. Partial Discharge Diagnostics: Data Cleaning and Feature Extraction. Energies 2022, 15, 508. [Google Scholar] [CrossRef]
- Dezenzo, T.; Betz, T.; Schwarzbacher, A. (Eds.) Phase resolved partial discharge measurement at dc voltage obtained by half wave rectification. In Proceedings of the VDE High Voltage Technology 2018; ETG-Symposium, Berlin, Germany, 12–14 November 2018; CD-ROM, Berlin and Offenbach. VDE Verlag: Berlin, Germany, 2018; Volume 157. [Google Scholar]
- IEC 60270; High Voltage Test Techniques: Partial Discharge Measurements. International Electrotechnical Commission: Geneva, Switzerland, 2001.
- Teyssedre, G.; Laurent, C. Charge transport modeling in insulating polymers: From molecular to macroscopic scale. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 857–875. [Google Scholar] [CrossRef]
- Frenkel, J. On pre-breakdown phenomena in insulators and electronic semi-conductors. Phys. Rev. 1938, 54, 647. [Google Scholar] [CrossRef]
- Read, J.; Pfahringer, B.; Holmes, G.; Frank, E. Classifier chains: A review and perspectives. J. Artif. Intell. Res. 2021, 70, 683–718. [Google Scholar] [CrossRef]
- Hearst, M.; Dumais, S.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Their Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Zhang, M.L.; Zhou, Z.H. A Review on Multi-Label Learning Algorithms. IEEE Trans. Knowl. Data Eng. 2014, 26, 1819–1837. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the KDD ’16: 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef]
- Raschka, S. Model evaluation, model selection, and algorithm selection in machine learning. arXiv 2018, arXiv:1811.12808. [Google Scholar]
- Varma, S.; Simon, R. Bias in error estimation when using cross-validation for model selection. BMC Bioinform. 2006, 7, 91. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2, pp. 241–248. [Google Scholar]
- Kurakin, A.; Goodfellow, I.J.; Bengio, S. Adversarial examples in the physical world. In Artificial Intelligence Safety and Security; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018; pp. 99–112. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should i trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Adadi, A.; Berrada, M. Peeking Inside the Black-Box: A Survey on Explainable Artificial Intelligence (XAI). IEEE Access 2018, 6, 52138–52160. [Google Scholar] [CrossRef]
- Guidotti, R.; Monreale, A.; Ruggieri, S.; Turini, F.; Giannotti, F.; Pedreschi, D. A survey of methods for explaining black box models. ACM Comput. Surv. 2018, 51, 93. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Kampker, A.; Wessel, S.; Fiedler, F.; Maltoni, F. Battery pack remanufacturing process up to cell level with sorting and repurposing of battery cells. J. Remanuf. 2021, 11, 1–23. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]

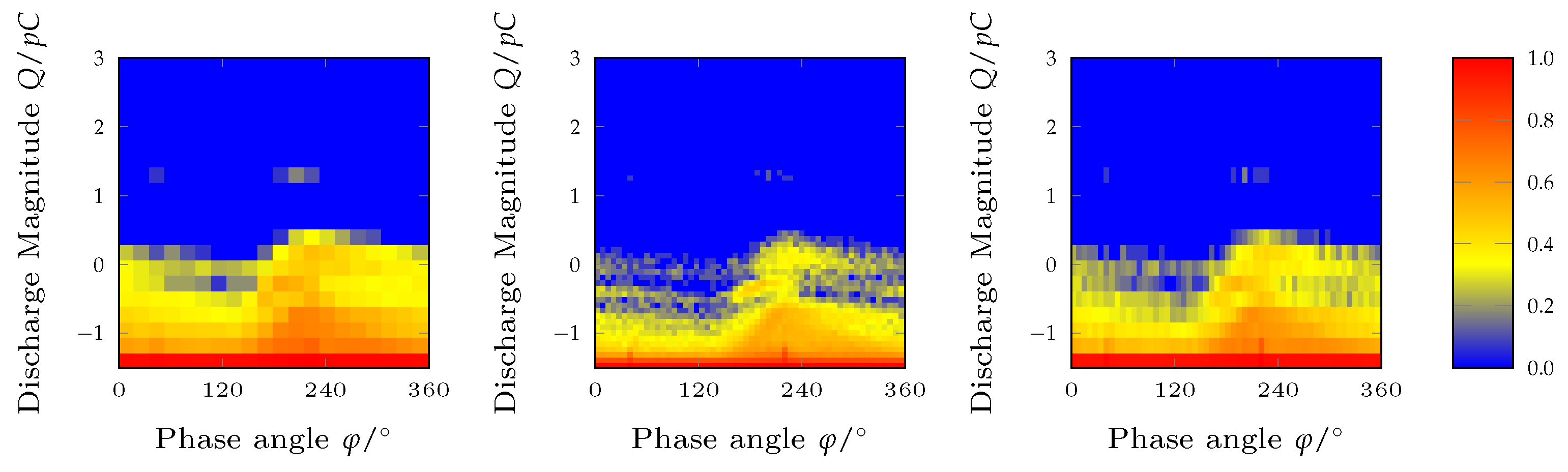



| Plateau | ¬ Plateau | |||
|---|---|---|---|---|
| Pylon | ¬ Pylon | Pylon | ¬ Pylon | |
| Hill | 20 | 75 | 4 | 5 |
| ¬ Hill | 80 | 98 | 77 | 10 |
| Algorithm | Optimal Shape | Mean (Hamming Loss) in Outer CV | Preferred Hyperparameters (on Separate CV) |
|---|---|---|---|
| Batch Size: 8 | |||
| Dense Layer Width: 128 | |||
| CNN | 0.107 | Kernel Size: 4 | |
| Learning Rate: | |||
| Number of Filters: 48 | |||
| Dimension Reduction: NMF | |||
| Logistic Regression | 20 × 20 | 0.118 | Regularization: 100 |
| Dimensions Projection: 37 | |||
| Support Vector Machine | 0.128 | Dimension Reduction: NMF | |
| Regularization: 10 | |||
| Kernel Coefficient: 10 | |||
| Dimensions Projection: 25 | |||
| Dimension Reduction: NMF | |||
| Random Forest | 92 × 20 | 0.106 | Maximal Depth Trees: 20 |
| Dimensions Projection: 45 | |||
| XGBoost | 0.106 | Dimension Reduction: NMF | |
| Maximal Depth Trees: 11 | |||
| Dimensions Projection: 45 | |||
| Learning Rate: |
| Label | Diagrams with Pattern | Diagrams without Pattern | False Positive | False Negative |
|---|---|---|---|---|
| Plateau | 273 | 96 | 18 | 12 |
| Pylon | 181 | 188 | 18 | 25 |
| Hill | 105 | 264 | 10 | 45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sangouard, R.; Freudenberg, I.; Kertel, M. Computer Vision for DC Partial Discharge Diagnostics in Traction Battery Systems. World Electr. Veh. J. 2023, 14, 222. https://doi.org/10.3390/wevj14080222
Sangouard R, Freudenberg I, Kertel M. Computer Vision for DC Partial Discharge Diagnostics in Traction Battery Systems. World Electric Vehicle Journal. 2023; 14(8):222. https://doi.org/10.3390/wevj14080222
Chicago/Turabian StyleSangouard, Ronan, Ivo Freudenberg, and Maximilian Kertel. 2023. "Computer Vision for DC Partial Discharge Diagnostics in Traction Battery Systems" World Electric Vehicle Journal 14, no. 8: 222. https://doi.org/10.3390/wevj14080222
APA StyleSangouard, R., Freudenberg, I., & Kertel, M. (2023). Computer Vision for DC Partial Discharge Diagnostics in Traction Battery Systems. World Electric Vehicle Journal, 14(8), 222. https://doi.org/10.3390/wevj14080222







