Electric Logistics Vehicle Path Planning Based on the Fusion of the Improved A-Star Algorithm and Dynamic Window Approach

Abstract

The study of path-planning algorithms is crucial for an electric logistics vehicle to reach its target point quickly and safely. In light of this, this work suggests a novel path-planning technique based on the improved A-star (A*) fusion dynamic window approach (DWA). First, compared to the A* algorithm, the upgraded A* algorithm not only avoids the obstruction border but also removes unnecessary nodes and minimizes turning angles. Then, the DWA algorithm is fused with the enhanced A* algorithm to achieve dynamic obstacle avoidance. In addition to RVIZ of ROS, MATLAB simulates and verifies the upgraded A* algorithm and the A* fused DWA. The MATLAB simulation results demonstrate that the approach based on the enhanced A* algorithm combined with DWA not only shortens the path by 4.56% when compared to the A* algorithm but also smooths the path and has dynamic obstacle-avoidance capabilities. The path length is cut by 8.99% and the search time is cut by 16.26% when compared to the DWA. The findings demonstrate that the enhanced method in this study successfully addresses the issues that the A* algorithm’s path is not smooth, dynamic obstacle avoidance cannot be performed, and DWA cannot be both globally optimal.

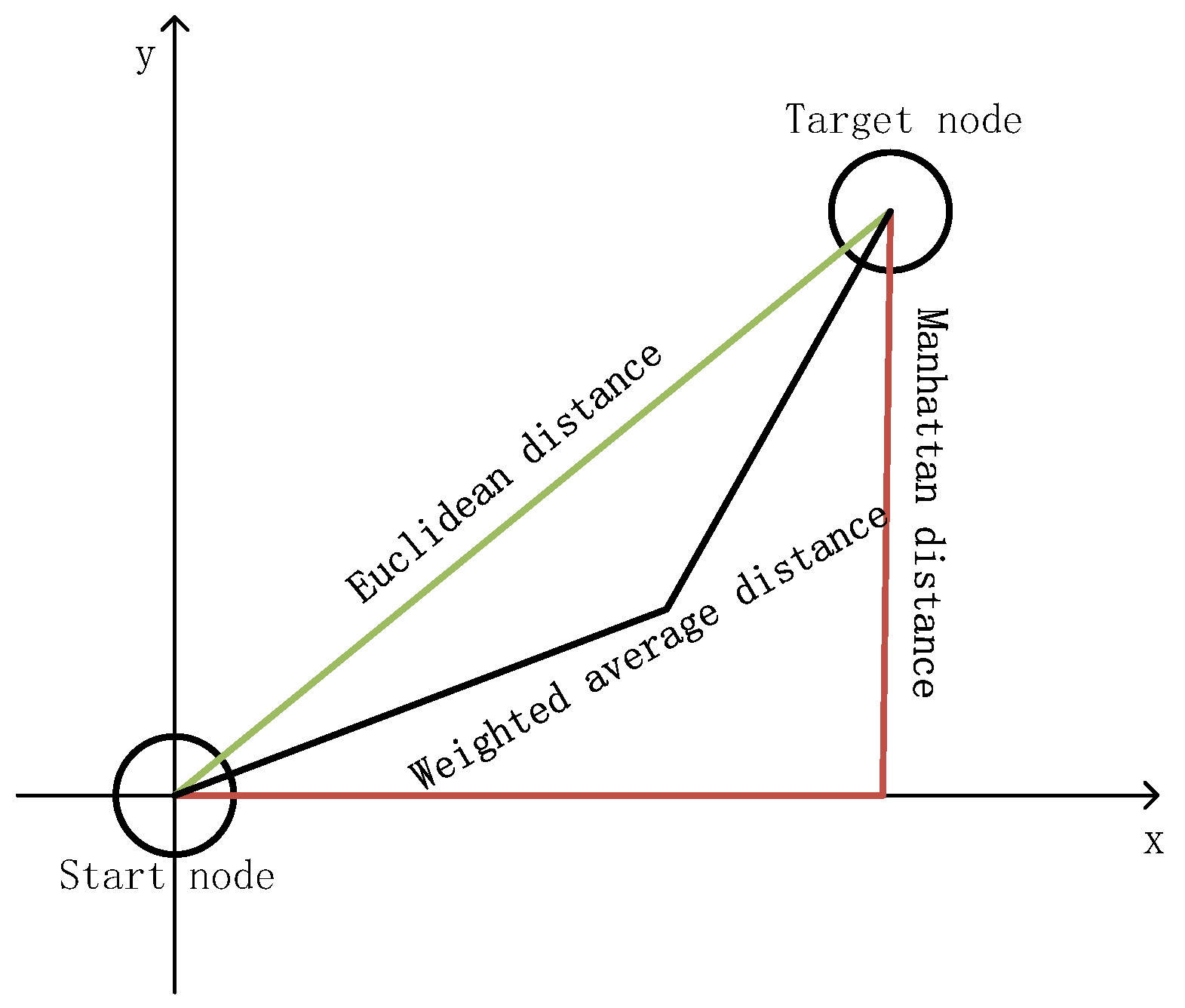
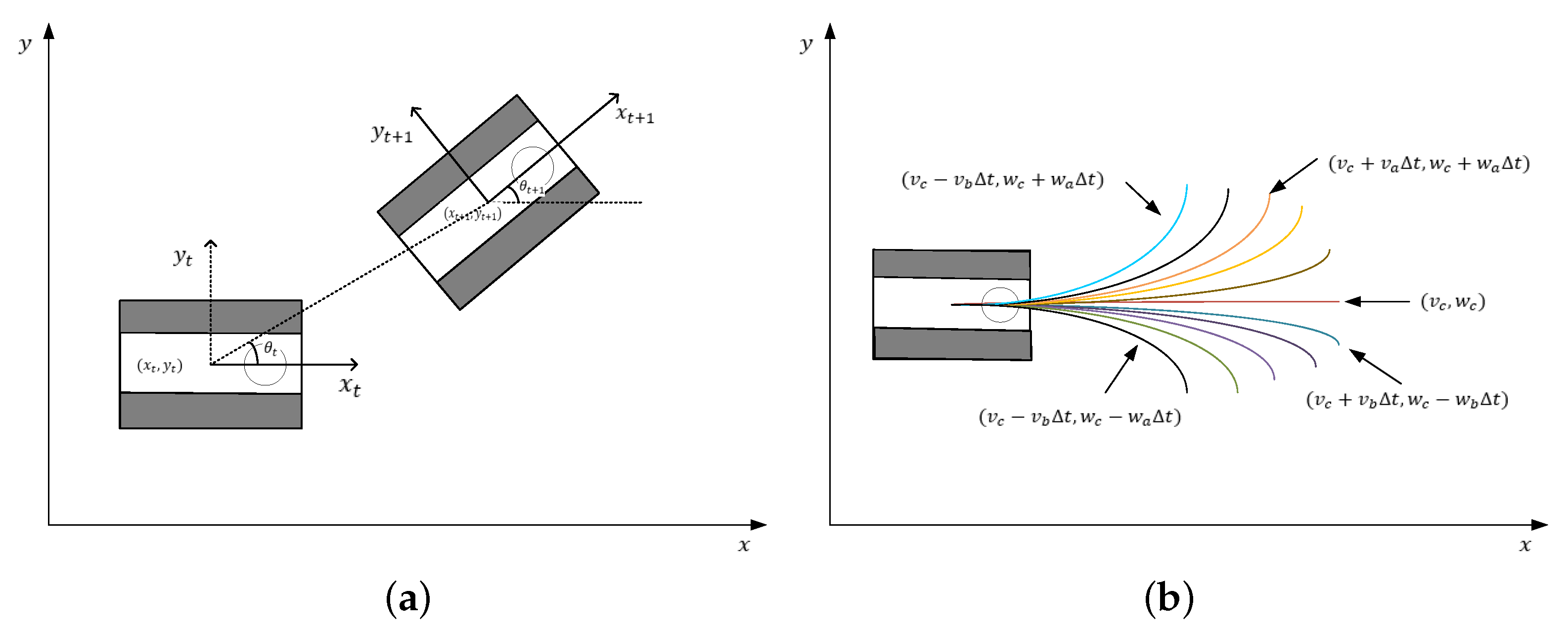
1. Introduction

With the wide application of electric logistics vehicles and the rapid development of automatic navigation technology, dynamic obstacle-avoidance algorithms play a crucial role in realizing the navigation of electric logistics vehicles. In practical application scenarios, electric logistics vehicles need to be able to identify and avoid obstacles instantly and accurately to ensure safe delivery of goods to their destinations [1]. With existing technologies, safety can only be guaranteed in static obstacle environments or predefined specific environments. Due to this technical limitation, a challenging element of navigation is dynamic obstacle avoidance. Dynamic obstacle avoidance is necessary for the autonomous operation of electric logistics vehicles in real situations with dynamic and unpredictable factors like pedestrians and other logistics vehicles [2,3,4]. To achieve efficient dynamic obstacle-avoidance capabilities, researchers have proposed various algorithms, among which the A* algorithm and DWA are two commonly used approaches.

Path-planning issues frequently use the A* algorithm, a heuristic search technique [5,6]. By analyzing the nodes’ cost functions, it determines the optimum route to the destination [7]. The A* algorithm, however, has several drawbacks when it comes to dealing with dynamic obstacle-avoidance issues. First, the A* algorithm must take into account global path planning while doing a search, which increases computing complexity. Second, the A* algorithm lacks real-time performance and cannot handle immediate changes in dynamic obstacles. To address the limitations of the A* algorithm, researchers have introduced DWA as a real-time path-planning and dynamic obstacle-avoidance method [8,9]. DWA selects the best travel path by evaluating the trajectory within the motion window based on the vehicle motion model and environment-aware information. This motion window-based approach has real-time and low computational complexity for dynamic obstacle-avoidance problems, but suffers from local optimality, resulting in low efficiency.

For the aforementioned issues, numerous improved algorithms have been put forth by both domestic and international researchers. There are four main solutions based on dynamic obstacle avoidance; the first is a variant of the A* algorithm. Tsatcha et al. proposed an innovative dynamic routing method utilizing hexagonal lattices and the Iterative Deepening A* (IDA*) algorithm, along with a front-end-to-front-end strategy using dynamic graphs, which enhances data accessibility [10]. This approach reduces memory usage but may result in higher search time. Huang et al. introduced a unique search approach, Lifelong Planning A* (LPA*), which is a modified version of the A* algorithm [11]. This method dynamically adjusts to changing traffic conditions and utilizes previous search outcomes to find the shortest path between a moving object and its destination. The second is to use Artificial Potential Field (APF) [12,13]. In an improved APF that Zang et al. presented, the distance parameter between the vehicle and the target point is introduced to address the issue of unreachable targets in APF [14]. The repulsive potential field function of the obstacle is optimized for the problem of unreachable targets in APF. Then comes the use of DWA for obstacle avoidance, in an attempt to address the issues of poor stability and excessive energy consumption of vehicle DWA, Lai et al. suggested a new enhanced DWA that employs the function of distance as the weight of the target guidance coefficient and suggests a new assessment function to maximize the azimuth angle [15]. Yang et al.’s enhanced A and DWA proposal increased automatic parking for tracked cars’ accuracy and speed [16]. Within a small deviation range, the place-to-park position has been greatly optimized. Finally, using a prediction model, in unstructured situations with stationary and moving impediments, Brito et al.’s method for local motion planning was developed. They calculated a local trajectory based on an improved backward horizon approach that avoids obstacles while reducing tracking errors given a reference path and speed [17]. A four-wheeled MECANUM omnidirectional electric vehicle’s motion control in a dynamic environment was researched by Azizi et al. [18]. The Kane approach was used to extract the differential equations of motion for the electric car and transform them into discrete state space form. A nonlinear model predictive control (NMPC) technique is created to stabilize the electric vehicle at the intended position and direction based on the mathematical model that is deduced from it. These methods address local dynamic obstacle avoidance from different perspectives, but these methods have a common constraint that they do not consider global path planning, and the use of APF or DWA may fall into local optimality, leading to long search time and low efficiency in the path planning of electric logistics vehicles. In addition, the prediction model cannot solve the problems that occur during actual operation in time [19,20].

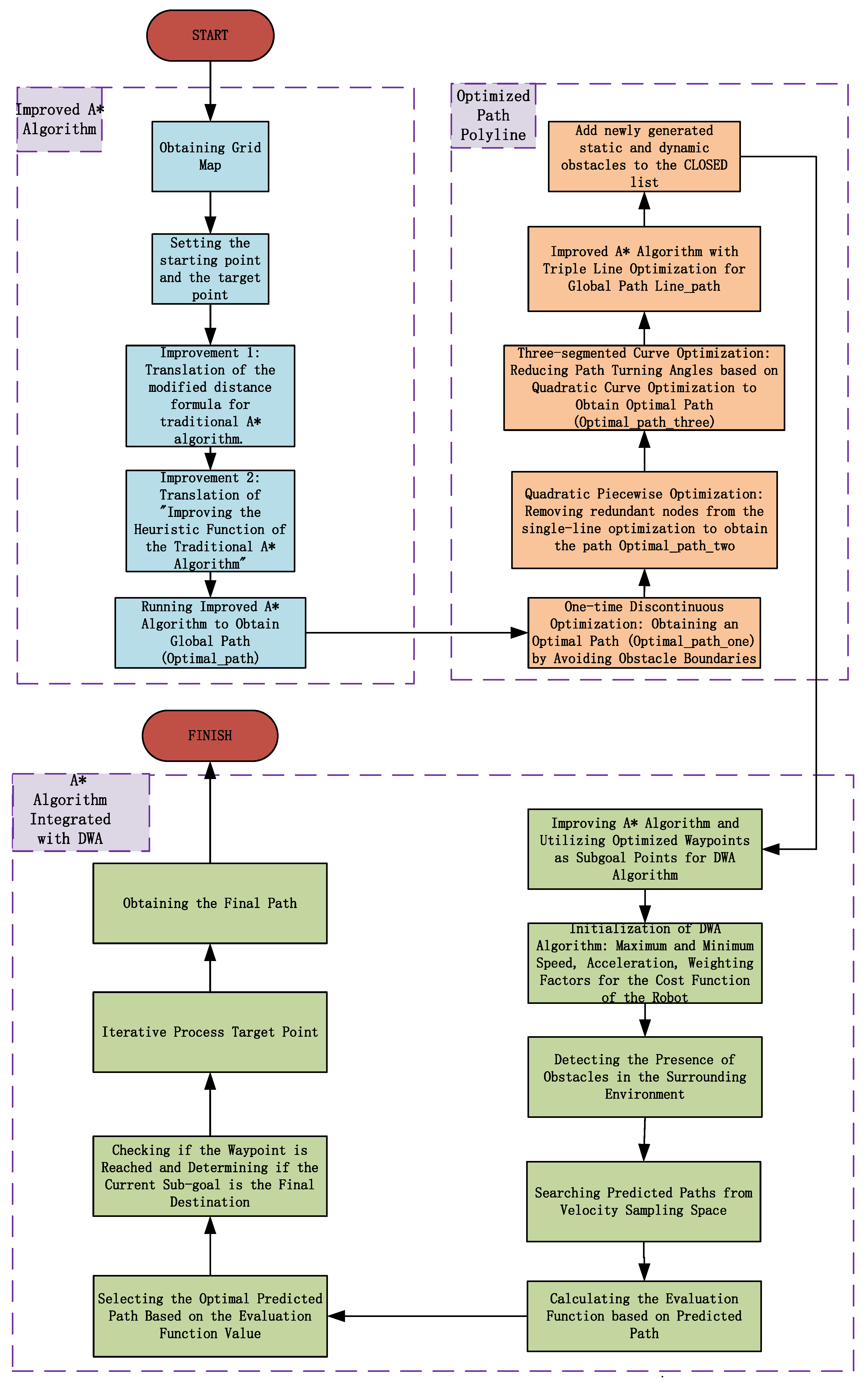
To overcome the issues with the A* algorithm and DWA and enhance the impact of dynamic obstacle avoidance, this research suggests an enhanced A* fusion DWA algorithm. This study proposes an innovative approach for path planning by combining the enhanced A* algorithm with DWA. The upgraded A* algorithm improves obstacle avoidance and reduces unnecessary nodes and turning angles. Subsequently, the DWA algorithm is integrated with the enhanced A* algorithm to enable dynamic obstacle avoidance. The fundamentals of the enhanced A* algorithm are introduced in Section 2. Section 3 combines DWA with the enhanced A* algorithm. In MATLAB and ROS, simulation verification and result analysis are carried out in Section 4 of this study to confirm the viability and efficacy of the enhanced path planning method. The key research findings of this paper’s analysis are summarized, along with predictions for future study trends.

2. Improved the A* Algorithm

2.1. A* Algorithm

In this study, we opt for the raster map approach [20]. Path planning and graph search issues frequently use the A* algorithm, a heuristic search algorithm. It is effective and precise in determining the shortest route between the starting location and the desired node. The fundamental idea behind the A* algorithm is to choose the next node to be expanded by analyzing the nodes’ cost functions to incrementally find the best path [21,22]. In Equation (1), its expression is displayed:

$$f\left(n\right)=g\left(n\right)+h\left(n\right)$$

(1)

where $f\left(n\right)$ represents the anticipated cost from the starting point through n intermediate nodes to the target node m, and n represents the current searched node. The cost function consists of two components, the actual path length $g\left(n\right)$ that has been traveled and the heuristically estimated remaining path length $h\left(n\right)$. $h\left(n\right)$ is often chosen to be calculated by Euclidean distance or Manhattan distance, and its corresponding expressions are shown in Equations (2) and (3):

$$h_{Euclidean}=\sqrt{{(x_{node}-x_{goal})}^2+{(y_{node}-y_{goal})}^2}$$

(2)

$$h_{Manhattan}=|x_{node}-x_{goal}|+|y_{node}-y_{goal}|$$

(3)

where $h_{Euclidean}$ represents the Euclidean distance, $h_{Manhattan}$ represents the Manhattan distance, $x_{node}$ and $y_{node}$ represent the horizontal and vertical coordinates of the node, and $x_{goal}$ and $y_{goal}$ represent the horizontal and vertical coordinates of the target point.

2.2. Improvement of Heuristic Function

First, the distance formula $h\left(n\right)$ of the heuristic function is improved, from Equation (1), $g\left(n\right)$ is constant and the algorithm’s performance is significantly impacted by the value of $h\left(n\right)$, the smaller the $h\left(n\right)$, the slower the search speed, but the accuracy of the search to the optimal path is higher, on the contrary, the larger the $h\left(n\right)$, the faster the search speed, but there is a certain chance of not searching the optimal path. Therefore, in this paper, based on the Euclidean distance and Manhattan distance, we propose the weighted average distance, as shown in Figure 1, and the corresponding expression is shown in Equation (4):

$$h_{WA}=(h_{Euclidean}+\beta ·h_{Manhattan})/2$$

(4)

where $h_{WA}$ is the improved weighted average distance formula in this paper, and $\beta$ is the balance coefficient, which is used to reasonably allocate the advantageous proportion between the Euclidean distance and the Manhattan distance, and $\beta$ can be reasonably adjusted in raster maps with different scales and different obstacle densities.

$\beta$ ranges from 0 to 1. $\beta$ can be appropriately enlarged when wanting to arrive at the target point quickly, but it may not be able to find the optimal path and $\beta$ can be appropriately reduced when wanting to find the optimal path. $\beta$ can be appropriately reduced, but the search time may be too long, so it is necessary to appropriately adjust the size of $\beta$ according to the map environment to ensure that the algorithm’s final results are well optimized.

Second, the heuristic function formula $f\left(n\right)$ to improve the A* algorithm itself does not consider the influence of obstacles, but in the actual operation process, obstacles play a greater impact, the more obstacles, the need to increase the proportion of $h\left(n\right)$, so the heuristic function in the improvement of the distance formula based on the addition of the obstacle rate P. The equation for the obstacle P is shown in Equation (5),the improvement formula as shown in Equation (6):

$$P=\frac{N_o}{|x_T-x_N\left|\right|y_T-y_N|}$$

(5)

$$f\left(n\right)=g\left(n\right)+e^P·h_{average}\left(n\right)$$

(6)

where $x_T$ and $y_T$ are the horizontal and vertical coordinates of the target node, and $x_N$ and $y_N$ are the horizontal and vertical coordinates of the current node, P is a proportion of the number of obstacle grids to the number of all raster maps, $N_o$ is the number of obstacles in the raster map, and so forth.

2.3. Three Optimizations of the Path

(1) First path optimization: avoiding obstacle boundaries;

For the optimized path diagram shown in Figure 2a.The obstacle’s up and down nodes are deleted when it is in the parent node’s left and right directions, and its left and right nodes are deleted when it is in the parent node’s up and down directions. This method can avoid the obstacle boundary perfectly, and the primary path optimization is shown in Figure 2b.

(2) Second path optimization: remove redundant nodes in the path;

Start from the starting point to connect with other nodes in turn, if the three nodes are in the same line, delete the second redundant node; find out whether there are any impediments at the point where the two nodes link if they are not in a straight line, if there are obstacles do not change the node, if there is no obstacle to change the node, the secondary path optimization diagram is shown in Figure 2c.

(3) Third path optimization: reduce the turning angle.

To establish whether the distance between the connecting line and the obstruction is larger than the predetermined safety distance, segmentation between the two nodes is assessed, if greater than that point can be selected, if less than then stop selection. Three times the path optimization is seen in Figure 2d.

3. Improved A* Algorithm to Fuse DWA

3.1. Dynamic Window Approach

To plan the trajectory of e-logistics vehicles, DWA, a route planning algorithm, is typically used. DWA combines the dynamic window approach with robot motion dynamics models and selects the best trajectory within the feasible window [23,24]. The kinematic equations are shown in Equation (7). It enables electric logistics vehicles to generate real-time safe and efficient paths in dynamic and unknown environments. This method has been widely applied in the field of electric logistics vehicles and mobile robot navigation, addressing to some extent the issue of high computational complexity in traditional path-planning algorithms in dynamic environments. Figure 3a and Figure 3b depict the velocity sampling space and the electric logistics vehicle motion model, respectively.

$$\left\{\begin{array}{c}{x}_{t+1}=x_t+v_x\Delta tcos\left({\theta }_t\right)-v_y\Delta tsin\left({\theta }_t\right)\\ y_{t+1}=y_t+v_x\Delta tsin\left({\theta }_t\right)-v_y\Delta tcos\left({\theta }_t\right)\\ {\theta }_{t+1}={\theta }_t+w\Delta t\end{array}\right.$$

(7)

(1) Speed limit of electric logistics vehicles as in Equation (8):

$$V_m=\left\{(v,w)|v={[v_{min},v_{max}]}^w\in [w_{min},w_{max}]\}\right.$$

(8)

where $V_m$ denotes the speed of electric logistics vehicle, $v_{min}$, $v_{max}$ denotes the minimum and maximum linear speed, and $w_{min}$, $w_{max}$ denotes the minimum and maximum angular speed.

(2) Electric logistics vehicles of their own conditions constraints as in Equation (9):

$$V_d=\left\{(v,w)|v\in [v_c-{\dot{v}}_b\Delta t,\right.v_c+{\dot{v}}_a{]}^w\in [w_c-{\dot{w}}_b\Delta t,w_c+{\dot{w}}_a\Delta t]\}$$

(9)

where $\Delta t$ denotes the time interval $v_c$, $w_c$ denotes the current velocity of the electric logistics vehicle. ${\dot{v}}_a$ and ${\dot{w}}_a$ the maximum acceleration, ${\dot{v}}_b$ and ${\dot{w}}_a$ are the maximum deceleration.

(3) Electric logistics vehicle safety distance constraint as in Equation (10):

$$V_a=\left\{(v,w)|v\le {\left(2dist(v,w){\dot{v}}_b\right)}^{1/2},\right.w\le {\left(2dist(v,w){\dot{w}}_b\right)}^{1/2}\}$$

(10)

where $dist(v,w)$ indicates when the electric logistics vehicle speed is $(v,w)$, the speed of the electric logistics vehicle operating trajectory is projected to be the nearest safety distance from the obstacles [25].

(4) The following is a definition of the DWA evaluation function as in Equation (11):

$$G(v,w)=\sigma \left[\alpha head\right(v,w)+\beta dist(v,w)+\gamma vel(v,w\left)\right]$$

(11)

where $head(v,w)$ denotes the difference between the azimuth of the current electric logistics vehicle and the azimuth of the final target point. At speed $(v,w)$, $dist(v,w)$ represents the distance between the expected trajectory of the electric logistics vehicle and the closest barrier. $vel(v,w)$ is used to calculate the electric logistics vehicle’s current velocity, $\theta$ is the smoothing coefficient and $\alpha$, $\beta$, $\gamma$ are the weighting coefficients of the corresponding functions.

Typically, the values for the three coefficients $\alpha$, $\beta$ and $\gamma$ are in the interval of 0 to 1. $\alpha$ represents the weight of heading score. If you want to have a shorter path and reach the target point faster, you can increase the weight of the heading score, but you may enter the dead end of the obstacles and cannot reach the target point. If you want to try to avoid the obstacles in the direction of the line connecting the start point and the endpoint, you can reduce the weight of the heading score, but the search time may be too long, so you need to modify it according to the actual map situation.

(5) Setting of the DWA initial position formula as in Equation (12):

$$S_{angle}=arctan\frac{y_{node}-y_{start}}{x_{node}-x_{start}}$$

(12)

where $x_{node}$ and $y_{node}$ represent the horizontal and vertical coordinates of the first selected node, while $x_{start}$ and $y_{start}$ represent the coordinates of the starting point. $S_{angle}$ denotes the angle between the starting point and the next node. The setup of the initial position formula allows the electric logistics vehicle to pre-rotate to an appropriate angle, facilitating its operation, reducing the time required for path planning, and ensuring more accurate navigation.

When improving DWA, the initial angle is an important consideration. The initial angle in DWA is usually the current orientation of the electric logistics vehicle. In certain specific application scenarios, the handling of the initial angle can significantly affect the effectiveness of path planning. Before using the DWA algorithm, perform calibration of the initial angle. Rotate the electric logistics vehicle to align the radar with the mapping, and then calibrate the initial angle of the electric logistics vehicle using Formula (12), ensuring the accuracy of the initial orientation to avoid path-planning issues caused by incorrect initial orientation.

3.2. Improved A* Algorithm Fused with Dynamic Window Approach

The A* algorithm is a global path-planning algorithm, which is often used for path planning of electric logistics vehicles under known maps, and the improved A* algorithm is a solution to the problems of the A* algorithm, which makes the algorithm more effective. However, the A* algorithm cannot achieve dynamic obstacle avoidance, so it needs to join the local path-planning algorithm [26]. The dynamic windowing approach can successfully avoid local obstacles, but it is simple to settle for the local optimum and is unable to produce the global optimum path. To achieve accurate destination and dynamic obstacle avoidance, the global path-planning algorithm A* is paired with the local path-planning algorithm dynamic window approach. The pseudo-code is shown in Algorithms 1 and 2. The following are the precise steps for implementation:

• First, we obtain the map information and convert the map into a raster(1) $MAP=\left[\begin{array}{ccccc}0& 0& 1& \dots & 0\end{array}\right]$, 0 denotes the doable area, while 1 denotes the area with obstacles;
• Set the start point $(x_{start},y_{start})$, target point $(x_{target},y_{target})$ and the obstacle representation, with the start point position marked as $\Delta$ and the target position marked as o;
• For path planning, use the A* algorithm with an enhanced heuristic function to obtain the global planning path $Optima{l}_{path}=\left\{X_i\right|i=0,1,2,\dots ,n\}$;
• Based on improving the A * algorithm, further optimize the path three times, the first time to achieve the path optimization of avoiding obstacle boundaries, and the path $Optima{l}_{path1}=\left\{O_i\right|i=0,1,2,\dots ,m\}$; the second time to achieve the path optimization of removing redundant nodes, and the path $Optima{l}_{path2}=\left\{P_i\right|i=0,1,2,\dots ,n\}$; the third implementation of the path optimization to reduce the turning angle, to obtain the optimized final path $NewOptima{l}_{path0}=\left\{W_i\right|i=0,1,2,\dots ,o\}$;
• Set unknown static obstacles and unknown dynamic obstacles $Ob{s}_{dj}=\left[\begin{array}{ccccc}0& 0& 1& \dots & 0\end{array}\right]$, put the newly generated temporary obstacles into CLOSED and display them on the map;
• Initialize the initial values of the maximum and minimum values, acceleration, and evaluation function weights of the DWA algorithm’s electric logistics vehicle;
• Run the DWA algorithm for speed sampling and search the predicted trajectory $Pr{e}_{path}=\left\{{PT}_i\right|i=0,1,2,\dots ,k\}$, calculate the evaluation function according to the predicted trajectory, and select the optimal path according to the evaluation function $Bes{t}_{path}=\left\{{BT}_i\right|i=0,1,2,\dots ,j\}$;
• The electric logistics vehicle proceeds to the end of the optimal path $Bes{t}_{path}$ and determines whether the current node is the target point. If the current node is not the target point, steps (7) and (8) are repeated until the electric logistics vehicle reaches the target point. Figure 4 depicts the path-planning flowchart of the enhanced A* fusion DWA algorithm.

Algorithm 1: Improved A* Algorithm

Algorithm 2: Improved A* Algorithm Integrated with DWA

4. Simulation Experiment Verification and Analysis

To verify the efficacy of the enhanced A* algorithm has been improved A* fusion DWA algorithm, simulations were conducted in MATLAB2020b and RVIZ of ROS, respectively, with the parameters listed in

Table 1. A* algorithm: key parameter settings.

Parameters	Values
Maximum speed	2 m/s
Maximum rotation speed	20 rad/s
Maximum rotational acceleration	50 rad/s2
Time to simulate trajectory forward	3 s
Weighting of heading scores	0.05
Distance score weighting	0.2
Speed score weighting	0.5

. After simulation experiments are concluded, the obtained experimental results are analyzed.

To evaluate the performance of the enhanced A* algorithm, the A* algorithm, the improved A* algorithm in the literature [5], the A* algorithm with improved heuristic function without optimized folds in this paper, and the A* algorithm with improved heuristic function with optimized folds in this paper are simulated and verified in MATLAB 2020b for 20 × 20 map scene 1, 20 × 20 map scene 2, and 50 × 50 map scene, and the experimental. The results are analyzed.

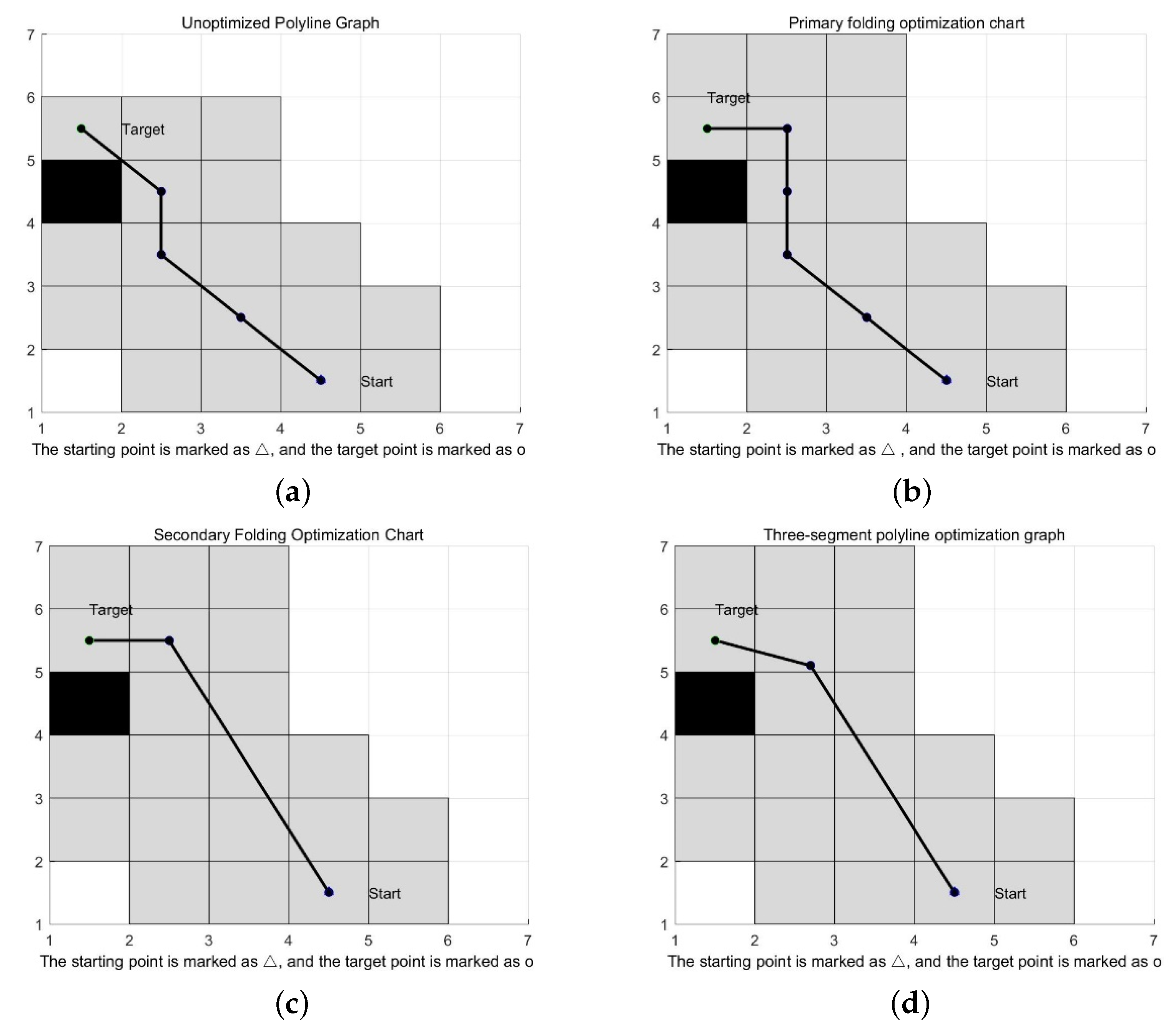
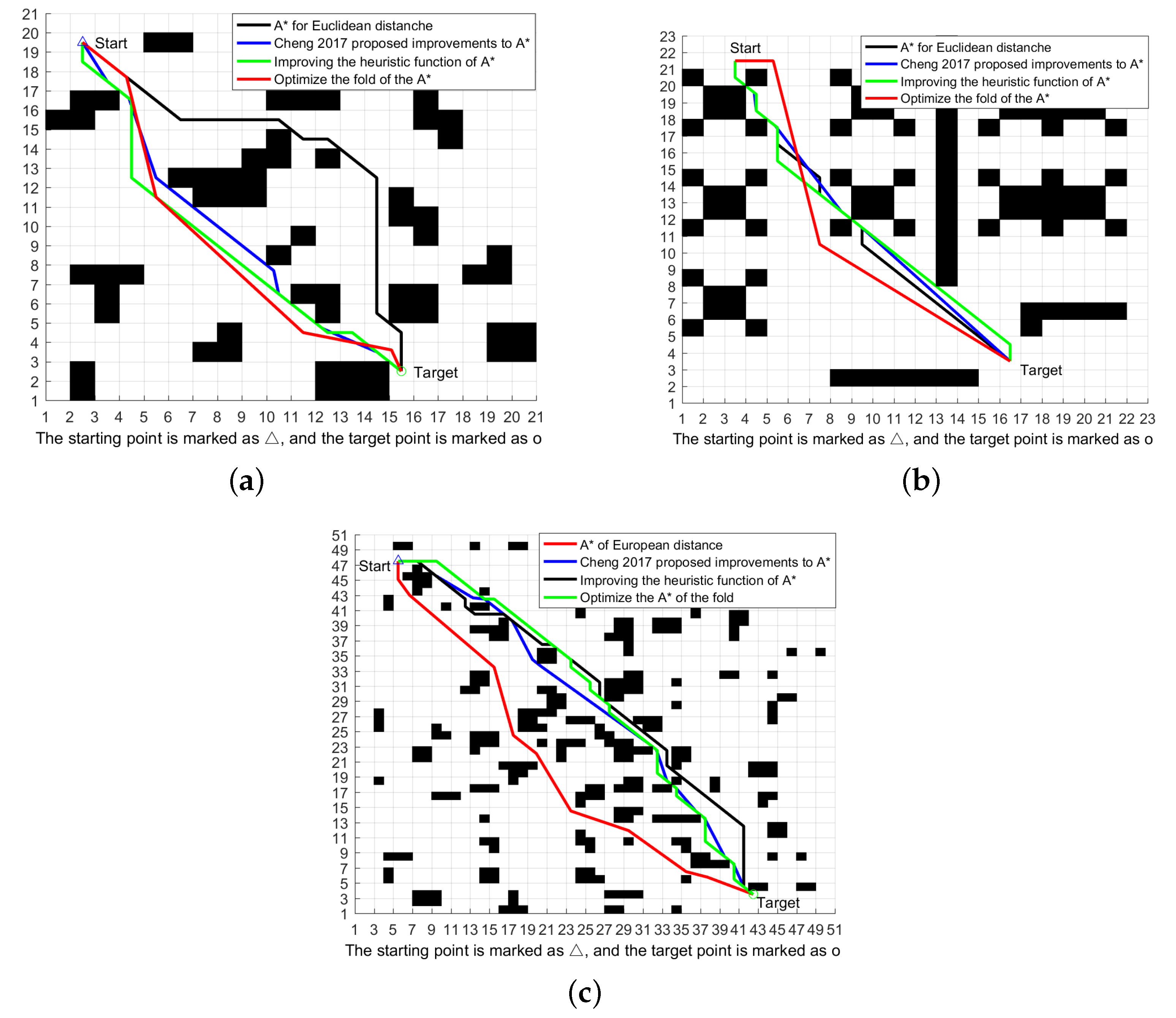
The simulation results in Figure 5 and

Table 2. Simulation experiment results (20 × 20 scene1).

Algorithm Name	Turning Points Number/Each	Number of Nodes Traversed/Each	Path Length/m	Search Time/s
A* algorithm using Euclidean distance	5	108	27.0026	79.904031
Cheng 2017 proposed improvements to A*	8	247	27.9319	85.142965
A* algorithm with improved heuristic function	5	172	26.0413	77.020405
A* algorithm with improved heuristic function and optimized folds	4	88	24.8729	66.907335

demonstrate that the improved A* algorithm presented in this paper has been optimized further than the A* algorithm and the improved algorithm presented in the literature [5]. In the 20 × 20 scene 1 raster map, the number of turning points is decreased by 20%, the traversed nodes are decreased by 18.51%, the path length is decreased by 8.99%, and the search duration is decreased by 16.27%. In all four aspects, the efficacy of the enhanced algorithm was demonstrated. In the 20 × 20 scenario 2 raster map, from

Table 3. Simulation experiment results (20 × 20 scene 2).

Algorithm Name	Turning Points Number/Each	Number of Nodes Traversed/Each	Path Length/m	Search Time/s
A* algorithm using Euclidean distance	9	112	23.3848	61.042
Cheng 2017 proposed improvements to A*	5	201	22.6624	109.136
A* algorithm with improved heuristic function	5	95	25.7279	48.357
A* algorithm with improved heuristic function and optimized folds	2	92	24.3454	47.867

it is clear that the number of turning points is decreased by 77.78%, the number of traversing nodes is decreased by 17.86%, the path length is increased by 4.11%, and the search time is decreased by 21.58% due to the bypassing of obstacle boundaries. Consequently, the improved A* path length is slightly longer than the A* algorithm, but the number of traversing nodes, search time, and the number of turning points are significantly decreased. Significant reductions are made to the number of nodes traversed, the search duration, and the number of turning points. In the 50 × 50 raster map, from

Table 4. Simulation experiment results (50 × 50).

Algorithm Name	Turning Points Number/Each	Number of Nodes Traversed/Each	Path Length/m	Search Time/s
A* algorithm using Euclidean distance	13	820	62.2548	491.858
Cheng 2017 proposed improvements to A*	12	1976	59.9827	1367.009
A* algorithm with improved heuristic function	14	225	64.0122	118.024
A* algorithm with improved heuristic function and optimized folds	8	211	60.0237	118.618

it is clear that the number of turning points, traversing nodes, path length, and search time are reduced by 38.46%, 74.27%, 3.58%, and 75.88%, respectively. With substantially fewer traversing nodes, shorter path lengths, shorter search times, and fewer turning points, the improved algorithm is more efficient.

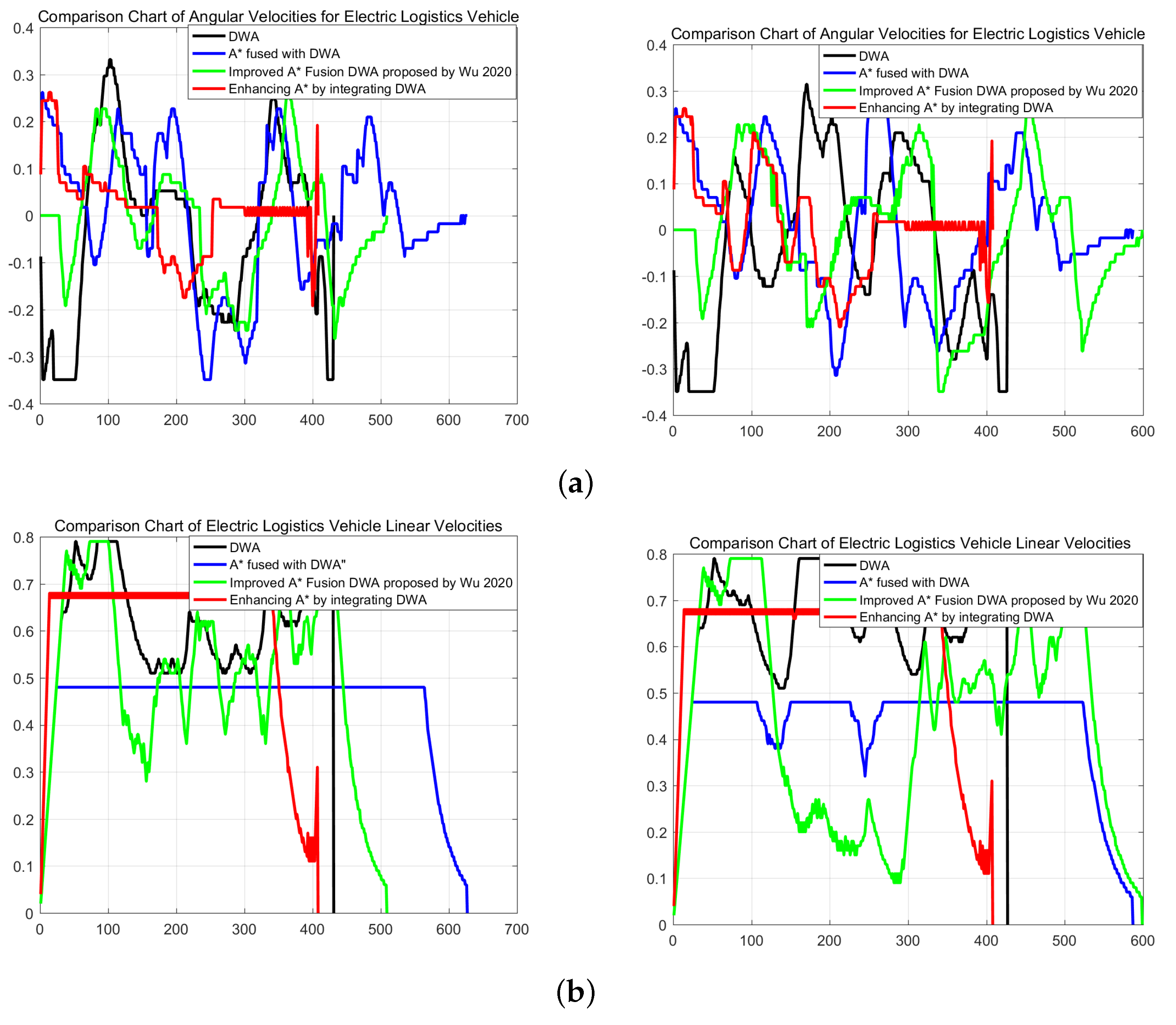
The DWA algorithm, the A* fusion DWA algorithm, the improved A* fusion DWA algorithm from the literature [27] and the improved A* fusion DWA algorithm from this paper are validated through simulations. The simulation comparison image in Figure 6 demonstrates that the improved algorithm presented in this paper not only avoids the original obstacle boundary, but also can avoid unknown static and dynamic obstacles, and is the shortest and smoothest one among all paths, therefore proving the effectiveness of the improved algorithm.

From Figure 6 above, we can learn that all four algorithms can perfectly avoid the static obstacles that appear, but the A* fusion DWA algorithm is ineffective and does not improve compared to the DWA algorithm; the literature [27] has a considerable reduction in both path length and search time; the improved A* fusion DWA algorithm presented in this paper has the shortest path length and the least amount of search time. and the improvement is significant, with a reduction in path length of 8.99%, and the search time is reduced by 16.27%. From

Table 5. Operational data for the DWA algorithm as well as the fusion algorithm (Static obstacle avoidance).

Algorithm Name	Path Length/m	Search time/s
Dynamic Window Approach	27.0026	79.904031
A* Algorithm Fusion DWA	27.9319	85.142965
Improved A* Fusion DWA proposed by Wu 2020	26.0413	77.020405
In this paper, we improve the A* algorithm to fuse DWA	24.5729	66.907335

and

Table 6. Operational data of the DWA algorithm as well as the fusion algorithm (dynamic obstacle avoidance).

Algorithm Name	Path Length/m	Search time/s
Dynamic Window Approach	28.4446	79.300621
A* Algorithm Fusion DWA	25.4588	94.402967
Improved A* Fusion DWA proposed by Wu 2020	26.3942	88.878559
In this paper, we improve the A* algorithm to fuse DWA	24.6606	66.881723

, we can know that for unknown dynamic obstacles, The A* fusion DWA algorithm and the algorithm of literature [27] to improve the A* fusion DWA both shorten the path length, but the search time is longer, whereas this paper to improve the A* fusion DWA algorithm not only reduces the path length but also the search time significantly, the path length is shortened by 13.30% and the search time is reduced by 15.66%, and both simulation experiments demonstrate that this improvement is effective.

As shown in Figure 7 above, the side plot of Figure 7 shows obstacle avoidance under unknown static obstacles, and the right plot shows obstacle avoidance under unknown static and dynamic obstacles. Figure 7a is the angular velocity graph of the four algorithms of the electric logistics vehicle; from the graph, it can be seen that the angular velocity of the improved algorithm in this paper has the fastest convergence speed among all the algorithms and is the most stable at the same time. 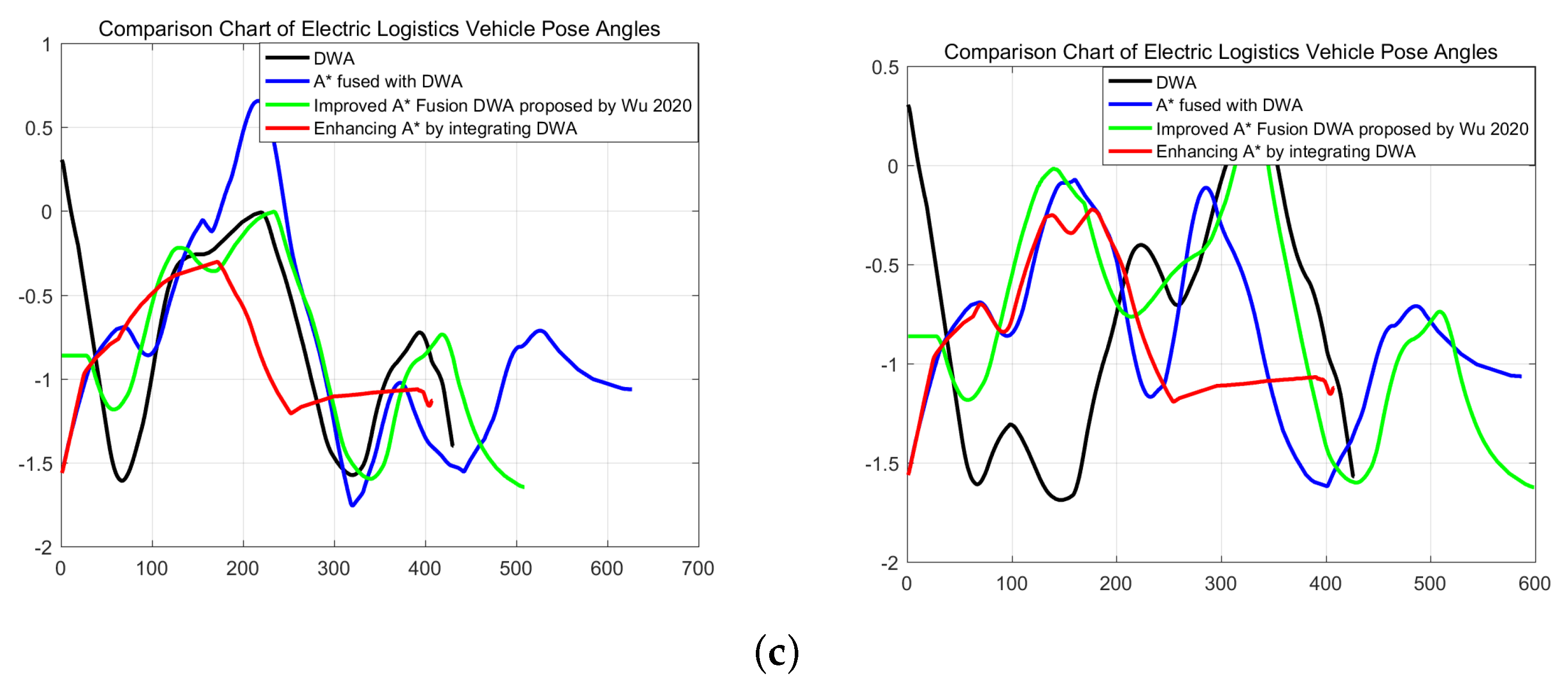Figure 7b is the linear velocity graph of the algorithm of the electric logistics vehicle; from the graph, it can be seen that the angular velocity of the algorithm in this paper is the fastest convergence speed among all the algorithms. From the pose angle of Figure 7c, it can be seen that the improved algorithm has a smooth pose and reaches the target point faster. The three angle comparison graphs above demonstrate that the A* fusion DWA algorithm presented in this paper is effective.

Simulation Verification of RVIZ in ROS

First, the simulation was verified in RVIZ in the ROS system. The same 20 × 20 map as MATLAB was built with GAZEO, and then the map in RVIZ was obtained by slam building as shown in the Figure 8.

Table 7. A* Algorithmic Fusion DWA: key parameter settings.

Parameters	Values
Initial position	(−1.95, −1.95, 0)
Initial target point	(13.5, 16.5, 90)
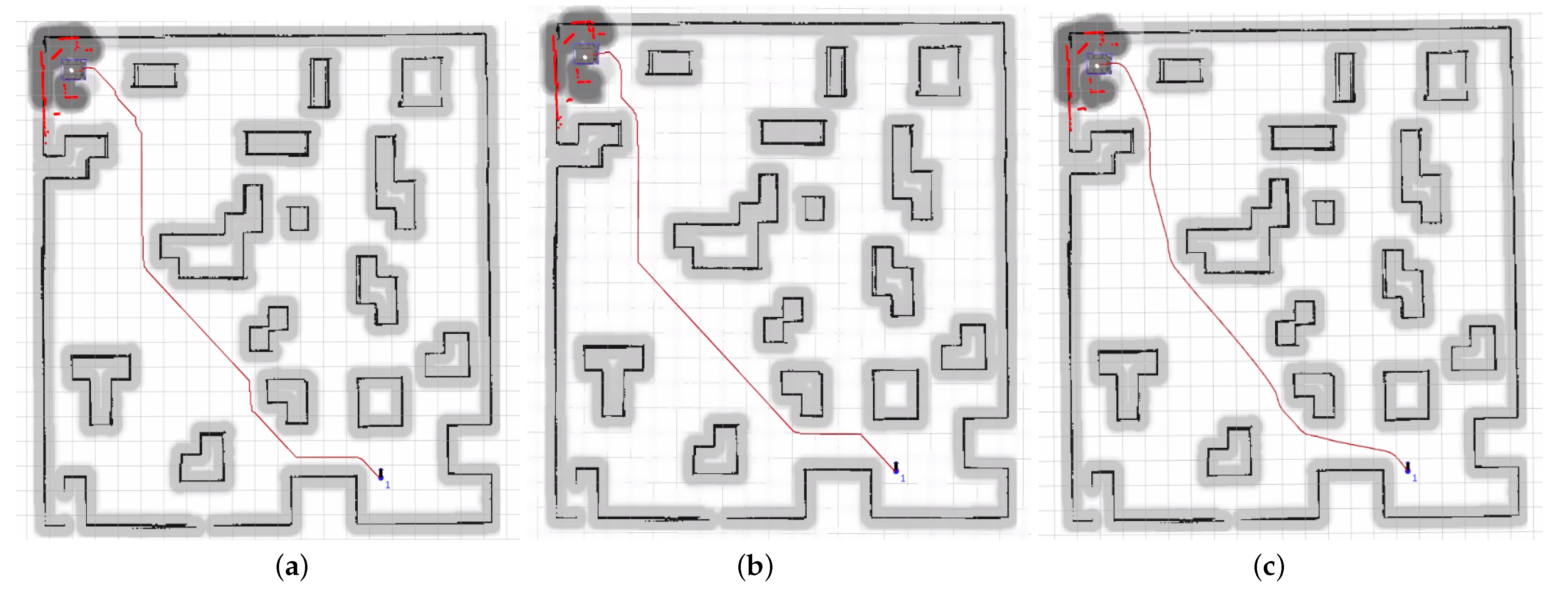
Straight line width	0.05

shows the main parameter settings of the A* algorithm fusing DWA.From the three path-planning graphs in Figure 8, it can be observed that the improved A* algorithm has fewer turning points compared to the traditional A*. Furthermore, the integration of the improved A* algorithm with the DWA algorithm results in smoother paths and smaller turning angles compared to the traditional A* algorithm. This evidence demonstrates the effectiveness of the improved algorithm. 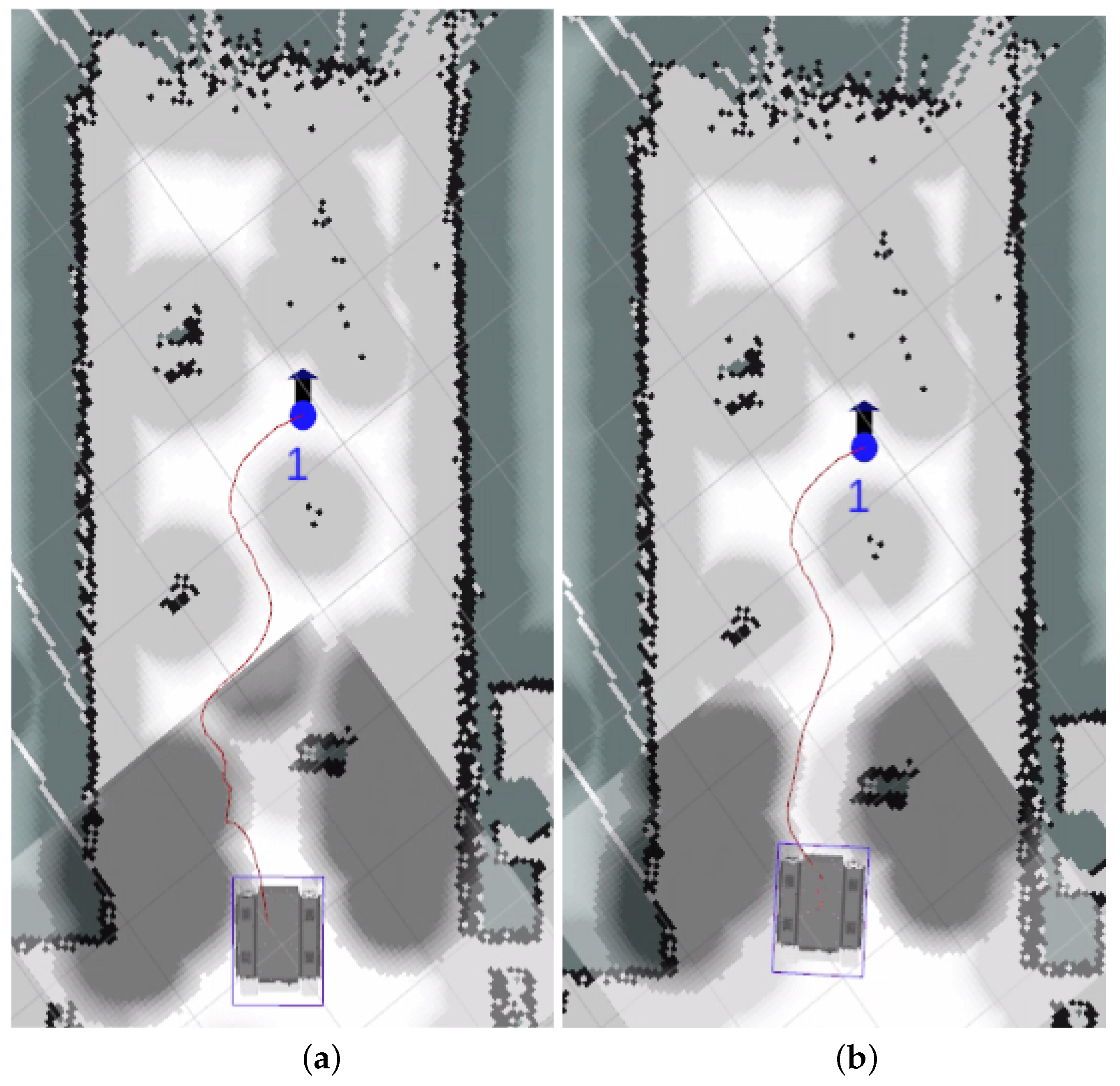Figure 9 shows the path-planning maps after SLAM-based mapping. The left map displays the path-planning results using the original algorithm, while the right map represents the path-planning results using the improved algorithm. A comparison between the two maps reveals that the modified algorithm not only avoids perfect convergence to the target point but also achieves smoother local path planning while avoiding obstacles. The path-planning maps obtained through both simulation and actual mapping confirm the effectiveness of the proposed algorithm in this paper.

The blue dots in Figure 9 indicate the location of the target points, "1" indicates the first target point, and the black arrows represent the orientation of the electric transporter at the target point.

5. Conclusions

In this paper, a new algorithm to improve A* fusion DWA is proposed for the problem that the path is not smooth and cannot be dynamically avoided when the A* algorithm is used alone for electric logistics vehicles and the problem that the global optimum cannot be considered when the DWA algorithm is used alone.

(1) The enhanced A* algorithm is used by the global path-planning algorithm. Improving the heuristic function of the A* algorithm can reduce the number of path nodes that require judgment, therefore decreasing the time required for electric logistics vehicles to find the optimal route. In three-fold optimization of the path, primary path optimization can avoid the obstacle boundary; secondary discount optimization can eliminate redundant path nodes, and the third path optimization can reduce the path’s turning angle. The improved A* algorithm increases the electric logistics vehicle’s operational efficacy.

(2) The DWA algorithm is utilized by the local path-planning algorithm. The improved A* algorithm is integrated with the DWA algorithm, and the globally optimal path is first obtained using the improved A* algorithm, then the generated path collection points are used as sub-target points of the DWA algorithm, and finally, the DWA algorithm is executed to search the predicted path from the speed sampling space to generate the final electric logistics vehicle driving path.

(3) Simulation experiments are conducted in MATLAB and RVIZ of ROS, and the simulation results show that while achieving global path optimality, path smoothing can be allowed to achieve local dynamic obstacle avoidance. The algorithm based on the improved A* algorithm fused with DWA not only reduces the path length by 4.56% while the path is smooth and can avoid dynamic obstacles compared to the A* algorithm but also reduces the path length by 8.99% and the search time by 16.26% compared to the DWA algorithm. Real-world operation results demonstrate that the enhanced A* fusion DWA algorithm is effective and practicable and that the fused algorithm outperforms the A* algorithm and the DWA algorithm.

This article combines both the A* algorithm and the DWA algorithm, which may result in a relatively high computational load in complex environments. However, it enhances robustness, as the A* algorithm performs well in static environments but may encounter issues in dynamic or partially observable environments. On the other hand, DWA is more robust in local motion planning but exhibits higher uncertainty in global path planning. Therefore, integrating both algorithms may strengthen their robustness. Additionally, the choice of parameters has an impact on both the computational load and robustness of the algorithm. Thus, careful tuning of these parameters is necessary for practical implementations to strike a balance between computational load and robustness. Further improvements and refinements to this integrated algorithm will be pursued in the future.