A Game Lane Changing Model Considering Driver’s Risk Level in Ramp Merging Scenario

Abstract

A ramp merging decision as an important part of the lane change model plays a crucial role in the efficiency and safety of the entire merging process. However, due to the inevitability of on-ramp merging, the limitations of the road environment, and the conflict between the merging vehicle and the following vehicle on the main road, it is difficult for human drivers to make optimal decisions in complex merging scenarios. First, based on the NGSIM dataset, a gain function is designed to represent the interaction between the ego vehicle (EV) and the surrounding vehicles, and the gain value is then used as one of the characteristic parameters. The K-means algorithm is employed to conduct a cluster analysis of the driving style under the condition of changing lanes. This paper models the interaction and conflict between the ego vehicle (vehicle merging) and the mainline lagging vehicle as a complete information non-cooperative game process. Further, various driving styles are coupled in the ramp decision model to mimic the different safety and travel efficiency preferences of human drivers. After EV decision-making, a quintic polynomial method with multi-constraints is proposed to implement merging trajectory planning. The proposed algorithm is tested and analyzed in an on-ramp scenario, and the results demonstrate that drivers with different driving styles can make correct decisions and complete the ramp merging. The changing trend of the speed and trajectory tests are also in line with the features of the driver’s driving style, offering a theoretical foundation for individualized on-ramp merging decisions.

1. Introduction

1.1. Literature Review

The development of autonomous driving faces significant obstacles because of the numerous complicated driving situations that exist in the actual world. For instance, in the ramp merging scenario, the vehicle must modify its speed and location on the merge lane to enter the main road [1]. Due to the frequent lane changes, complex geometric design, and diversity of driving behaviors in this area, the risk of collision and conflict is high, so the drivers must make the right decision in a short time [2,3]. The wrong decision often reduces the travel efficiency of the vehicle, increases fuel consumption, and even causes serious security risks. Therefore, how to make a safe and effective on-ramp merging decision is of great significance [4,5]. Human drivers combine driving experience and perception of the driving environment to make merging maneuvers. However, wrong judgment and fuzzy perception make it difficult for the self-vehicle to make optimal decisions in complex and changeable scenarios [6,7]. With the rapid development of technologies such as artificial intelligence and machine vision, autonomous driving technology is a promising technology for solving traffic congestion and driving safety [8]. Autonomous vehicles (AVs) can precisely perceive the driving environment because they are equipped with comprehensive sensors and networking technology. Additionally, information interaction and sharing between vehicles can be realized, allowing AVs to make correct decisions quickly and effectively.

Control methods based on intelligent on-ramps have been intensively researched by academia and industry to solve the problem of merging AVs onto on-ramps in complex scenarios [9]. Lu et al. [10] proposed the concept of virtual parking space and provided an algorithm for general merging. The algorithm provides merged trajectory planning for on-ramp vehicles using mainline vehicle state information. When the vehicle in the main line changes velocity, the merging vehicle’s control variables are adjusted consistently. Xu [11] proposed a cooperative merging strategy for intelligent connected vehicles. The cooperative merging issue is transformed into an optimized problem and then solved using a genetic algorithm to minimize the travel time of mainline vehicles and maximize the number of merging vehicles. Under the condition of an intelligent network connection, Wang et al. [12] proposed a control algorithm for vehicle on-ramp merging on motorways. A collaborative driving algorithm based on the Internet of Vehicles is designed to perform collision-free ramp merging based on the characteristics of vehicles in the merging process. Dong et al. [13] proposed three off-ramp path control strategies for autonomous vehicles. The risk factor is incorporated into the autonomous lane change model, and the processes of an early lane change and forced lane change are thoroughly investigated. Lee and Park [14] believe that under the condition of the Internet of Vehicles, vehicle–vehicle communication, and vehicle–road communication can make the variable velocity limit a highly effective measure to alleviate traffic congestion. In addition, a microscopic simulation model is used to analyze the bottleneck section of the expressway under the condition of the Internet of Vehicles. The results show that the variable velocity limit effect under the Internet of Vehicles can reduce traffic congestion by 7–12% with the increase in the proportion of connected vehicles. Zhang [15] proposed a cooperative merging model that considers the location of vehicles arriving at the merging point and provides a stable gap for merging vehicles by changing lanes beforehand.

Other types of lane-changing methods, except the game theory model, only investigate lane-changing operations from the perspective of merging vehicles and rarely consider the dynamic interaction between merging vehicles and surrounding vehicles [16]. In fact, for the lane-changing motion of the merging vehicle, the lagging vehicle in the main lane will respond accordingly, including accelerating to prevent, decelerating to allow, or disregarding the merging vehicle’s lane-changing intention. Alireza Talebpour [17] developed a vehicle autonomous lane-changing decision-making model in a vehicle–vehicle communication environment employing game theory. In this model, the impact of the vehicle’s lane-changing behavior on the vehicle following it on the main road is considered. Kita simulated merging behavior under slope scenarios using a discrete choice model and then estimated the probability of concession with game theory [18,19]. In [20], the cooperative game method was applied to the CAVs on-ramp merging control problem. This method can reduce the vehicle’s fuel consumption and travel time as well as enhance the vehicle’s comfort and travel efficiency. Combining the definition of receding horizon control (RHC) with the accessibility analysis method and game theory, Meng et al. [21]. proposed a dynamic decision-making model for intelligent vehicle lane-changing games based on RHC theory. Liu et al. [22] constructed a model of how vehicles interact when merging based on an enhanced game theory framework. The test results prove that the model is capable of predicting the driving behavior of vehicles and correctly reflects the interaction between vehicles on the highway ramp.

Regarding the testing and verification of decision-making algorithms, various nations have developed pertinent policies and regulations for autonomous driving vehicles in recent years due to the continuous advancement of autonomous driving technology and growing social demand, providing more options for the testing and verification of autonomous driving decision-making algorithms. Included in these tests are simulation tests, HIL (hardware-in-the-loop) tests, proving grounds tests, and real road tests, all of which are very helpful in the advancement of automated driving [23,24].

In addition, drivers and passengers with different driving styles in real life show different preferences for safety, comfort, and travel efficiency under normal driving conditions. The strategies employed by game ego vehicles with different driving styles to interact with obstacle vehicles will be quite different [25]. Hence, when designing the decision algorithm for merging vehicles to change lanes, it is necessary to consider the various driving style factors of merging vehicles and investigate the characteristics and rules of AVs with different driving styles in dynamic interaction and decision-making. Consequently, the acceptance of ADAS by people with different driving styles can be improved during the development phase of autonomous driving.

In summary, most of the existing studies regarding on-ramp merging decisions do not take into account the micro-interaction and dynamic game behavior between the main vehicle and the surrounding vehicles during the ramp merging process, which is difficult to get close to the actual lane-changing situation; secondly, the existing research on intelligent vehicle ramp merging decision-making does not consider the factors of human drivers enough. The ramp merging decision-making of aggressive and conservative drivers are significantly different, and the interaction and game of different types of driving styles will have a great impact on decision-making. Given the limitations mentioned above, we combine the aggressiveness indicators of different driving styles, which has the potential to increase the adaptability of intelligent vehicles to various types of drivers.

1.2. Contribution

The highlights of this paper can be summarized as follows. First, based on the NGSIM dataset, a clustering study on driving styles under lane-changing conditions was carried out. Secondly, based on the complete information non-cooperative game theory, introducing driving style into the decision-making model of ramp merging provides a theoretical basis for the development of personalized autonomous driving. Then, considering the limited distance of the acceleration lane and the domestic and foreign research on the ramp merging model based on game theory mainly focus on making lane change decisions, a quintic polynomial trajectory planning algorithm under the constraints of multiple conditions is designed so that the EV can complete the ramp merge. Finally, the effectiveness of the algorithm is verified in a typical ramp merge scenario.

1.3. Paper Organization

The remainder of this paper is organized as follows. In Section 2, the driving style under lane-changing conditions is studied based on the NGSIM dataset. In Section 3, based on the complete information non-cooperative game theory, the ego vehicle’s ramp merge decision model is established. In Section 4, an optimal quintic polynomial trajectory planning algorithm under multiple conditional constraints is designed. In Section 5, we design a typical expressway ramp merge scenario for simulation testing and discuss the simulation results. Finally, the conclusions are drawn in Section 6.

2. Research on Driving Style under Lane-Changing Conditions

The identification and clustering of driving styles play a crucial role in the development of human-like driving algorithms. In this section, the driving style clustering research is carried out on the real traffic dataset, and the differences in motion characteristics, such as velocity and acceleration reflected by drivers with different driving styles in the process of changing lanes, are analyzed. It offers a theoretical foundation for the development of a decision-making algorithm for ramp merging, which is based on interactive game theory and takes driver attributes into account.

2.1. Extraction of Driving Style Features

There is no standard index for choosing features that evaluate driving styles, but generally speaking, the more comprehensive the index is chosen, the more thoroughly it can reflect the actions of drivers with various driving styles. This paper selected 16 driving style indexes, including lane-changing gains, lane-changing time, lateral and longitudinal velocities, lateral and longitudinal accelerations, time headway, spacing headway, and so on.

For normal and rational drivers, lane-changing behavior is a process of pursuing the maximization of gains. This paper adopted an approach that considers the environmental vehicles in the lane-changing scenario as a mutually dependent and interacting entity to provide a more accurate representation of the differences between various driving styles. Additionally, the travel efficiency of the EV, the collision risk of the EV and the surrounding vehicles, and the impact of comfort are taken into account in the feature extraction of lane-changing. This standard comes from the research of Xiaolin, S. et al. [26]. Different from other driving style feature extraction, the income feature needs to be further calculated by combining the motion parameters of the EV and the environment vehicle at the current moment of lane-changing.

The parameters $l_e$ and $d_e$ denote the length and width of the lane-changing vehicle EV, respectively. Similarly, the parameters $l_{env}$ and $d_{env}$ represent the length and width of the environment vehicle $V_{env}$. At a certain moment, the positional coordinates and heading angles of two vehicles in frame k are denoted by $(x_e^t,{\mathrm{y}}_e^t,{\phi }_e^t)$ an $(x_{env}^t,{\mathrm{y}}_{env}^t,{\phi }_{env}^t)$, respectively. The disparity between the heading angles of the two automobiles is represented by $\Delta \phi ={\phi }_e^t-{\phi }_{env}^t$. The benefits of the EV’s comfort, traffic efficiency, and collision risk during lane changes are denoted by $U_{comfort}$, $U_{efficiency}$, and $U_{comflict}$, respectively, which are all thoroughly considered in this paper and are expressed as follows:

$$\{\begin{array}{l}{U}_e{}_{fficiency}=(V_{E,t}-V_f)/(V_t-V_f)\\ U_{comfort}=-{\displaystyle {\int }_0^T(a_x^2}+a_y^2)dt\\ U_{conflict}={\displaystyle \sum _{t\in T,t\ne 0}{U}_{EV,V_{env}}}\end{array}$$

(1)

where for $U_{efficiency}$, $V_{E,t}$ denotes the velocity of the vehicle that is changing lanes while $V_f$ represents the velocity of traffic flow in the current road section. Moreover, $V_t$ signifies the permitted speed of the current road section, which is assumed to be 80 km/h in this instance. The comfort gain for $U_{comfort}$ is equal to the negative value of the sum of the squares of the lateral acceleration $a_x$ and the longitudinal acceleration $a_y$ integrated over a period of T.

For $U_{comflict}$, refer to the research in [27]; the condition that the EV and the environment vehicle do not collide at any moment k frame in the prediction period is as follows:

$$|(x_e^t-x_{env}^t)\cos {\phi }_{env}^t+(y_e^t-y_{env}^t)\sin {\phi }_{env}^t|\ge \frac{\sqrt{l_e+d_e}}{2}\sin (a+|\Delta \phi |)+\frac{l_{env}}{2}+\Delta S$$

(2)

The benefit of the collision between the lane-changing vehicle EV and the surrounding vehicle $V_{env}$ is as follows:

$$U_{EV,V_{env}}=\{\begin{array}{l}0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}satisfied\\ \frac{-1}{d_{min}^{EV,V_{env}}}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}failed\end{array}$$

(3)

where $d_{min}^{EV,V_{env}}$ represents the shortest distance between the lane-changing vehicle EV and the environment vehicle $V_{env}$ (${}_{env}$=1, 2, …, m) during the prediction period T.

The total benefit can be calculated as follows:

$$U_{Total}={\omega }_1{U}_{efficiency}+{\omega }_2{U}_{comflict}+{\omega }_3{U}_{comfort}$$

(4)

where ${\omega }_1=0.2634$, ${\omega }_2=0.6126$, and ${\omega }_3=0.3482$ are the weight coefficients of each gain [28].

2.2. Cluster Analysis by K-Means

In this study, I-80 and US-101 highway data are used. The NGSIM data include the trajectories of every vehicle on the road; vehicles that exhibit lane-changing behavior are screened out, and 17 feature quantities are selected. The K-means algorithm is a classic clustering algorithm. Its basic idea is to find a division scheme of K clusters iteratively, so that the loss function corresponding to the clustering result is minimized. Among them, the loss function can be defined as the sum of squared errors of each sample from the center point of the cluster to which it belongs:

$$J(c,u)={\displaystyle {\sum }_{i=1}^M\parallel }{x}_i-u_{ci}{\parallel }^2$$

(5)

where $x_i$ represents the sample, $c_i$ is the cluster to which $x_i$ belongs, $u_{ci}$ represents the center point corresponding to the cluster, and M is the total number of samples.

To avoid information redundancy among the feature quantities, the K-means algorithm can be optimized based on the clustering effect corresponding to different feature combinations, and unnecessary feature quantities can be removed to achieve the optimal driving style classification effect. In addition, we presume that the driving style of each lane-changing EV does not alter during the execution of a particular lane-changing operation. Based on the K-means algorithm for cluster analysis, 281 driving behavior samples were classified as aggressive, 386 as moderate, and the remaining 304 as conservative to enable a more intuitive observation and analysis of the variations in motion characteristic parameters during lane-changing maneuvers among drivers with distinct driving styles. The generation of a box plot, as depicted in Figure 1, can be achieved through statistical analysis and visualization of the feature samples about the three distinct driving styles exhibited by lane-changing EV.

According to the analysis of the visualization results of the K-means driving style classification, it is not difficult to see that there are obvious gaps between aggressive drivers and conservative drivers in terms of velocity, acceleration, spacing headway, and THW during lane changes. For the vehicle’s horizontal and vertical speeds, because conservative drivers pursue safety, they will complete the ramp merging process at a lower speed while aggressive drivers often complete the lane change at a higher speed. Similarly, aggressive drivers pursue travel efficiency and complete lane changes with greater acceleration, resulting in greater changes in lateral and longitudinal acceleration, while conservative drivers change lanes relatively smoothly. At the same time, aggressive drivers tend to have a smaller distance from the vehicle in front than conservative drivers. It is clear from the study’s results above that drivers with varied driving preferences would choose different strategies for ramp merging. Aggressive drivers tend to pay attention to travel efficiency and complete the ramp merging process faster at the cost of driving safety. Conservative drivers are just the opposite. As a result, different driving styles have varying preferences for travel efficiency and driving safety. To offer a theoretical foundation for individualized ramp merging decisions, these two factors can be introduced to the game decision cost function.

3. Ramp Merge Decision Modeling

Game theory is a powerful tool for studying interactions between decision-makers. Game players make optimal decisions that maximize their payoffs during the interaction and gaming process. By modeling the interaction and competition process as a mathematical formula, it provides a theoretical basis and solutions for decision-makers. The process of mutual exploration between vehicles changing lanes is very similar to a game. In this section, the interaction between them is constructed as a non-cooperative game process, which is a form of the game under the topic of game theory. In this model, there are no external rules that force players to cooperate. A game is a well-defined mathematical object consisting of the following elements: game players, strategy space of the players, information, payoff function (utility), and equilibrium [29].

3.1. Ramp Merging Decision Modeling

A merging maneuver occurs because there is an obstacle ahead or the road is about to end, and the vehicle must adopt a lane change strategy. This paper concentrates on the game decision between the merging vehicle EV and the mainline lagging vehicle FV in the on-ramp merging scenario and the trajectory planning stage after decision-making.

As illustrated in Figure 2a, the vehicles involved in the game are the EV and FV. The PV is not a player, but it impacts the longitudinal safety cost of the EV and FV. Since the limited distance of the acceleration lane, the EV must complete the merging operation within a limited distance in this scenario. Before starting a lane change, the EV detects the status of encircling vehicles. At this time, if there is an FV and it is relatively near to the EV, the EV will interact with the FV through the turn signal or a small lateral displacement before changing lanes and observe its response to the lane-changing intention. This paper assumes that the FV reacts to the EV by accelerating or decelerating, respectively. As shown in Figure 2c,d, it is clear that the actions of the EV will have a greater influence on the decision-making strategy of the FV. In this paper, the ramp merging decision-making process is modeled as a two-vehicle Nash game. The EV and FV are considered equal and independent participants in the game, and when solving the player’s payoff function, they each aim to maximize their payoffs.

Figure 2b displays the decision cost functions for the four interaction cases between the EV and FV. According to the example game cost matrix in the Figure, when the EV chooses to change lanes, the FV will choose to yield to the EV. In the same way, the EV chooses lane keeping, and the FV will optimally choose the appropriate acceleration according to the cost function. Thus, both sides of the game find the optimal strategy pair (wait, accelerate) in the game by evaluating and searching the decision-making costs corresponding to the strategy pair. Finally, this paper models the lane-changing decision problem as a two-vehicle game with different decision cost functions and always has a Nash equilibrium.

The cost matrix of the two-vehicle game is shown in

Table 1. Game payoff function matrix.

Decision Making	The Following Vehicle
	Strategy	Yield $[{\mathit{a}}_{\mathit{m}\mathit{i}\mathit{n}},{\mathit{a}}_{\mathit{m}\mathit{a}\mathit{x}}]$	Block $[{\mathit{a}}_{\mathit{m}\mathit{i}\mathit{n}},{\mathit{a}}_{\mathit{m}\mathit{a}\mathit{x}}]$
Ego vehicle $[a_{min},a_{max}]$	Lane-changing	$(U_{\mathrm{L}c},U_{Yield})$	$(U_{Lc},U_{Block})$
	Wait	$(U_{\mathrm{Wait}},U_{Yield})$	$(U_{Wait},U_{Block})$

, where $a$ represents the possible longitudinal acceleration of the two vehicles, and $U$ is the decision cost corresponding to different strategy pairs. The EV not only decides whether to change lanes, but also calculates the optimal longitudinal acceleration required at the current sampling step. Note that longitudinal acceleration is a control variable for longitudinal motion planning. Since acceleration is continuous, the EV has infinite combinations of strategies. Similarly, the FV also has infinite policy combinations, which can choose any acceleration within the constraints (i.e., $[a_{min},a_{max}]$). During the game, both players are trying to minimize their costs. Therefore, the design of the decision cost function plays a crucial role in Avs making reasonable decisions.

To better understand the interaction behavior between Avs and human-driving vehicles and, moreover, highlight the key points of the research, this paper makes the following assumptions:

(1)

The vehicles studied are all cars, excluding other types of vehicles, such as trucks;

(2)

We assumed that the FV is a human-driven vehicle equipped with V2X and V2V equipment;

(3)

We assumed that the merging vehicle EV studied in this paper is an autonomous vehicle and has been equipped with complete on-board sensors and wireless communication modules;

(4)

Only the acceleration and deceleration behavior of the FV is considered, and its lane-changing behavior is not considered.

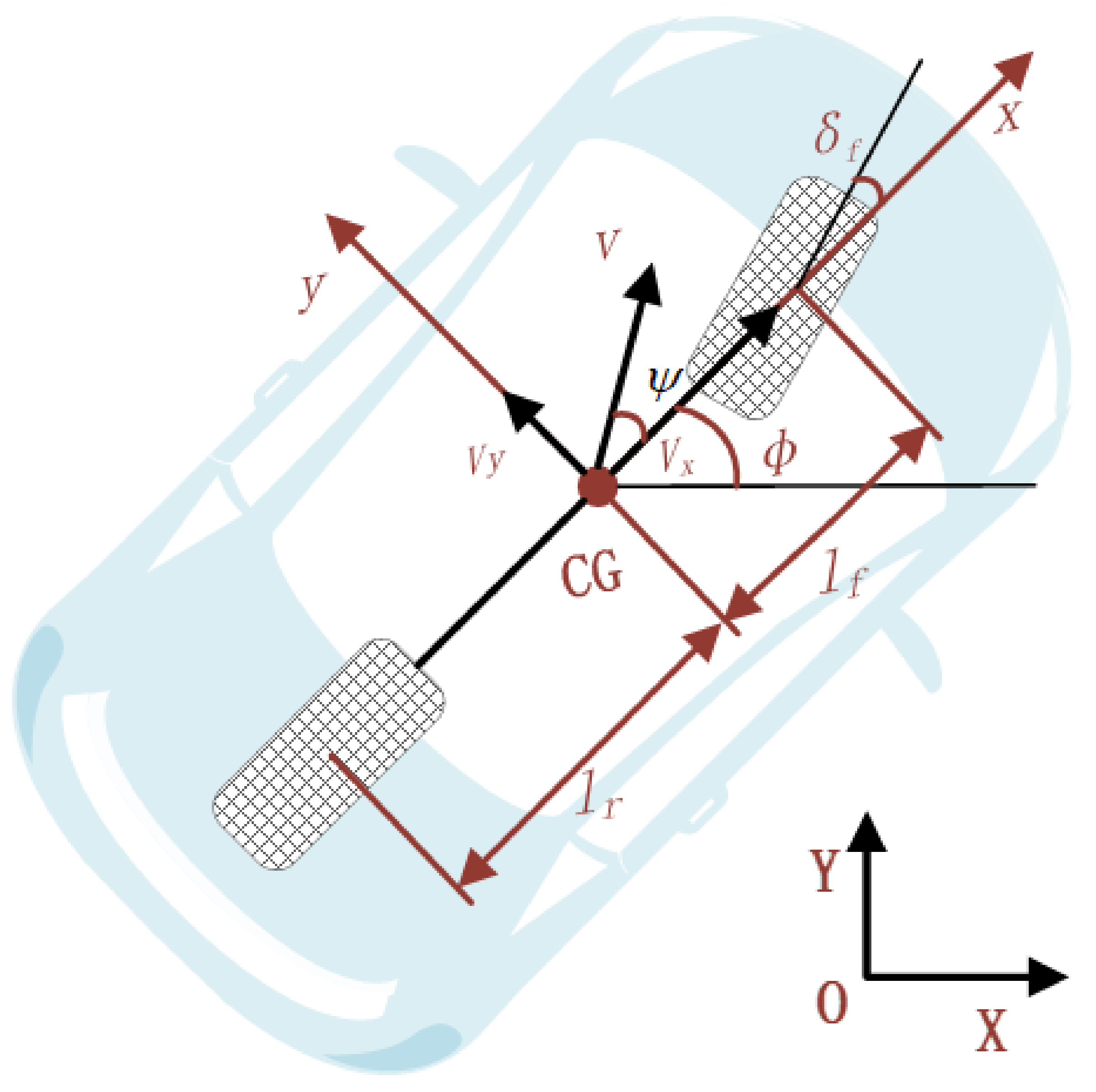
3.2. Vehicle Kinematics Model

In this paper, a simplified vehicle kinematics model is applied [30], as shown in Figure 3. Then, the kinematics model is discretized and used for the design of the decision-making algorithm.

$$\chi =[v_x\hspace{0.17em}\phi \hspace{0.17em}X\hspace{0.17em}Y{]}^T={[a_x/v_x,\tan \psi /{\mathrm{l}}_r,\cos \theta /\cos \psi ,\hspace{0.17em}\sin \theta /\cos \psi ]}^T\cdot v_x$$

(6)

$$\theta =\phi +\psi$$

(7)

$$\psi =\arctan (l_r/(l_r+l_f)\cdot tan{\delta }_f)$$

(8)

where the system state vector is $\chi =[v_x\hspace{0.17em}\phi \hspace{0.17em}X\hspace{0.17em}Y{]}^T$; the control vector is $u={\delta }_f$; and $\phi$, $\psi$, and $\theta$ are the vehicle yaw angle, side slip angle, and heading angle, respectively. ${\delta }_f$, ($X$,$Y$) are the front wheel angle and center of gravity (CG) position coordinates of the vehicle, respectively; $a_x$ and $v_x$ are the longitudinal acceleration and longitudinal velocity of the vehicle; and $l_f$ and $l_r$ are the distances from the front and rear axle to the CG, respectively.

3.3. Definition of EV Cost-Function

Based on the research on vehicle driving style under lane-changing conditions in the second section, it can be analyzed that there are significant differences in the vehicle motion characteristic parameters under different driving style modes. In this section, the aggressiveness coefficient β is introduced into the design of the game cost function to simulate the preference characteristics of different driving styles on travel efficiency and driving safety. It is worth noting that the decision-making algorithm developed in this way can better simulate the interaction between the AV and the human driver and achieve the effect of human-like decision-making.

A reliable game cost function plays a crucial role in decision-making. The decision cost in this paper considers three aspects [31,32]. The first is safety cost, $U_{ds}^{EV}$, which quantifies the level of safety for vehicles changing lanes and keeping lanes. The second is the cost of travel efficiency, $U_{te}^{EV}$, which quantifies the speed benefits that vehicles can obtain in the game. The third is $U_{dc}^{EV}$, which can guarantee the comfort of the vehicle during the game process. Therefore, the total decision-making cost function of the EV can be expressed as the following:

$$U^{EV}=\beta \cdot U_{ds}^{EV}+(1-\beta )\cdot U_{te}^{EV}+k_A{}_{cc}\cdot U_{dc}^{EV}$$

(9)

where $U_{ds}^{EV}$, $U_{te}^{EV}$, and $U_{dc}^{EV}$ represent the corresponding driving safety cost, travel efficiency cost, and comfort cost when the EV adopts a specific strategy, respectively; $\beta$ is a coefficient indicating the level of EV aggressiveness, which is used to characterize the EV-specific driving style; and $k_A{}_{cc}$ is the comfort cost weight coefficient.

The driving safety cost of EVs has different forms in the two conditions of lane keeping and lane changing. When choosing a strategy for lane keeping, the safety cost is mainly related to the relative velocity and relative distance between the EV and the PV of the vehicle ahead on the on-ramp. On the contrary, when an EV changes lanes, the safety cost between the EV and FV is mainly considered. The safety cost can be uniformly expressed as follows:

$$U_{ds}^{EV}=(1-|\gamma |)U_{ds-lk}^{EV}+\left|\gamma \right|U_{ds-lc}^{EV}$$

(10)

where $U_{ds-lc}^{EV}$ and $U_{ds-lk}^{EV}$ are the corresponding driving safety costs of the EV lane changing and lane keeping, respectively; $\gamma$ denotes the results of EV decision-making (i.e., $\gamma \in \{1,0\}\hspace{0.17em}=${lane change to the main road, lane keeping}).

$U_{ds-lk}^{EV}$ is related to the relative distance and relative velocity of the EV and PV, which is expressed as follows:

$$U_{ds-lk}^{EV}=\{\begin{array}{l}{\psi }_{v-lk}^{EV}\times \mathrm{sgn}[-\Delta V_{lk}^{P{V}_{\kappa }-EV}]\times (\Delta V_{lk}^{P{V}_{\kappa }-EV}){}^2\\ \hspace{1em}\hspace{1em}+{\psi }_{s-lk}^{EV}/[\Delta S_{lk}^{P{V}_{\kappa }~EV}+\varsigma ],\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}\exists \hspace{0.17em}P{V}_{\kappa }^i\\ {\varpi }_{lk}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}otherwise\end{array}$$

(11)

where $P{V}_k$ denotes the vehicle ahead in the on-ramp, and $\kappa \in \{1,2\}$ indicates the lane ID of the EV. $\Delta V_{lk}^{P{V}_{\kappa }-EV}$ and $\Delta V_{lk}^{P{V}_{\kappa }-EV}$ are the relative velocity and relative distance between the EV and $P{V}_k$. ${\psi }_{v-lk}^{EV}$ and ${\psi }_{s-\mathrm{l}\mathrm{k}}^{EV}$ are the respective weight coefficients for the velocity and distance terms. ${\varpi }_{lk}$ is a small number that represents the cost of selecting a lane-keeping strategy when the EV driving lane lacks $P{V}_k$, and $\varsigma$ is a very small value to avoid a denominator of 0. $U_{lc}^{EV}$ is related to the relative distance and relative velocity between the EV and FV, defined as follows:

$$U_{ds-lc}^{EV}=\hspace{0.17em}\{\begin{array}{l}{\psi }_{v-lc}^{EV}\cdot \hspace{0.17em}\mathrm{sgn}\hspace{0.17em}[-\Delta V_{lc}^{EV-F{V}_{\kappa }}]\cdot \hspace{0.17em}\hspace{0.17em}(\Delta V_{lk}^{EV-F{V}_{i\kappa }}){}^2\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+{\psi }_{s-lc}^{FV}\hspace{0.17em}/\hspace{0.17em}[\Delta S_{lc}^{EV-F{V}_{\kappa }}+\varsigma ],\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}\exists \hspace{0.17em}F{V}_{\kappa }\\ {\varpi }_{lc},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}otherwise\end{array}$$

(12)

where $F{V}_{\kappa }$ represents the competing vehicle on the main road; $\Delta V_{lc}^{EV-F{V}_{\kappa }}$ and $\Delta S_{lc}^{EV-F{V}_{\kappa }}$ are the relative velocity and relative distance between the EV and FV; ${\psi }_{v-\mathrm{lc}}^{EV}$ and ${\psi }_{s-lc}^{EV}$ are the respective weight coefficients for the velocity and distance terms; and ${\varpi }_{lc}$ is a small number that represents the cost of selecting a lane-changing strategy when the main road lacks $F{V}_{\kappa }$.

EV ride comfort is primarily determined by acceleration, which is defined as follows:

$$U_{\mathrm{dc}}^{EV}={\psi }_{acc}^{EV}{(a_x^{EV})}^2$$

(13)

where $U_{\mathrm{dc}}^{EV}$ is the longitudinal acceleration of the EV, and ${\psi }_{acc}^{EV}$ is the comfort weight factor.

The travel efficiency of the EV is mainly related to the expected velocity gain in the game, which is represented as follows:

$$U_{te}^{EV}=\{\begin{array}{l}{(\Delta V_{}^{v_x^{max}-EV})}^2,\hspace{0.17em}\hspace{0.17em}\Delta s\ge d_{free}\\ {(\Delta V_{}^{P{V}_{\kappa }-EV})}^2,\hspace{0.17em}\hspace{0.17em}\Delta s\le d_{free}\end{array}$$

(14)

where $\Delta s$ is the relative distance between the EV and the vehicle in front, $v_x^{max}$ represents the maximum vehicle velocity, and $d_{free}$ is the safe distance threshold for the EV to accelerate freely.

3.4. Definition of Game Equilibrium

For the decision-making model of ramp merging developed in this paper, the game players generate optimal decisions by minimizing their respective cost functions. The definition for the two-vehicle Nash game problem is as follows:

$$(a_x^{\mathrm{E}V*},{\gamma }^{*})=\underset{a_x^{EV},\hspace{0.17em}\gamma }{\mathrm{argmin}}{U}^{EV}(a_x^{EV},\gamma ,a_x^{FV}))$$

(15)

$$(a_x^{\mathrm{F}V*})=\underset{a_x^{FV},\hspace{0.17em}\gamma }{\mathrm{argmin}}{U}^{FV}(a_x^{EV},\gamma ,a_x^{FV}))$$

(16)

$$s.\mathrm{t}.\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\gamma \in \{0,1\},\hspace{0.17em}\gamma (\gamma -1)\hspace{0.17em}=0$$

(17)

$$\hspace{0.17em}{a}_x^{EV}\in [a_x^{min},a_x^{max}],\hspace{0.17em}\hspace{0.17em}{a}_x^{FV}\in [a_x^{min},a_x^{max}]$$

(18)

$$v_x^{EV}\in [v_x^{min},v_x^{max}],\hspace{0.17em}\hspace{0.17em}{v}_x^{FV}\in [v_x^{min},v_x^{max}]\hspace{0.17em}$$

(19)

where $U^{EV}$ and $U^{FV}$ indicate the decision-making cost of the EV and FV, respectively; $a_x^{EV*}$ and $a_x^{FV*}$ represent the optimal longitudinal acceleration for the EV and FV; $\gamma *$ is the optimal merge decision for the EV; $[a_x^{min},a_x^{max}]$ and $[v_x^{min},v_x^{max}]$ are the acceleration and velocity boundaries of the vehicle, respectively; and $v_x^{EV}$ and $v_x^{FV}$ represent the driving velocity of the EV and FV.

For the equilibrium solution of the above Nash game optimization problem, if a high-precision equilibrium solution is not required, the optimization problem can be solved by extensively searching the discrete cost matrix. The matrix has a finite composition, and finding a Nash equilibrium is relatively easy. It should be noted that, to meet real-time decision-making, the optimal equilibrium is calculated at every sampling step.

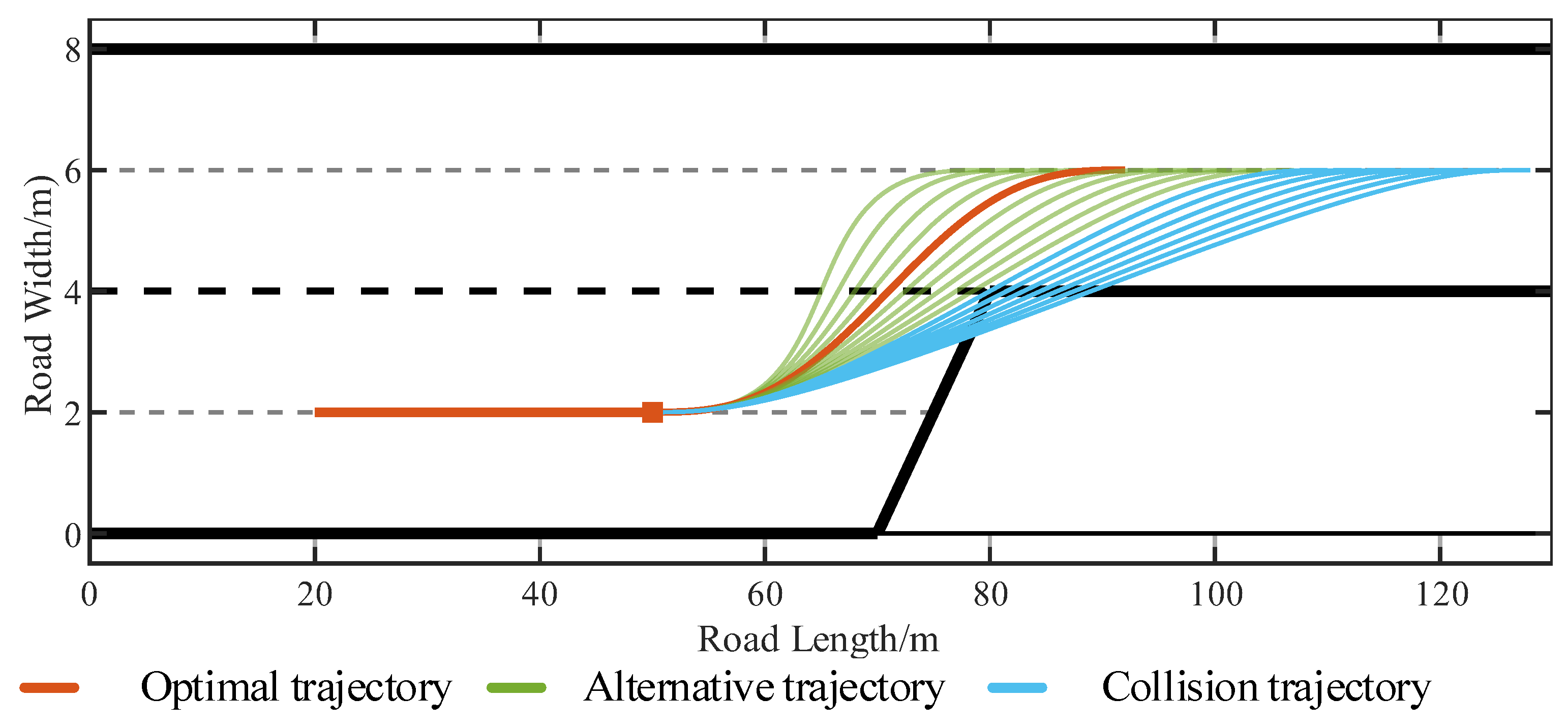
4. Quintic Polynomial Trajectory Planning with Multi-Constraints

Ramp merging trajectories can be modeled as common lane-free trajectory planning. The quintic polynomial trajectory planning has high real-time performance and strong practicability, and the generated trajectory meets the requirements of vehicle dynamics.

The longitudinal distance and time of the lane change in the traditional trajectory planning algorithm based on quintic polynomials are set artificially. With limited ramp distance, such methods have great shortcomings. An inappropriate longitudinal distance and lane change time will cause the planned trajectory to exceed the ramp boundary and become unfeasible. The blue track in Figure 4 crosses the road boundary, making it impractical. As a result, the trajectory needs to be optimized. Additionally, AVs need to meet multiple constraints during merging, including stability, safety, and comfort [33]. To address the aforementioned issues, this paper establishes a quintic polynomial trajectory planning algorithm that can automatically optimize the longitudinal distance and duration of ramp merging and satisfy numerous constraints.

The initial state and target state of the vehicle must be obtained for the quintic polynomial’s lane-changing trajectory model to serve as boundary conditions. The defined $S_0$ and $S_z$ are, respectively, as follows:

$$\{\begin{array}{l}{S}_0=\left[x_0{\dot{x}}_0{\ddot{x}}_0{y}_0{\dot{y}}_0{\ddot{y}}_0\right]\hfill \\ S_{\mathrm{z}}=\left[x_z{\dot{x}}_z{\ddot{x}}_z{y}_z{\dot{y}}_z{\ddot{y}}_z\right]\hfill \end{array}$$

(20)

where $x$, $\dot{x}$, $y$, $\dot{y}$, $\ddot{y}$, and $\ddot{y}$ are the EV’s longitudinal displacement, longitudinal velocity, longitudinal acceleration, lateral displacement, lateral velocity, and lateral acceleration, respectively.

The quintic polynomial is chosen to represent the lane change trajectory function in both the x and y directions based on its properties:

$$\{\begin{array}{l}f(x,t)={\displaystyle \sum _{i=0}^5{a}_i}{t}^i\hfill \\ f(y,t)={\displaystyle \sum _{i=0}^5{b}_i}{t}^i\hfill \end{array}$$

(21)

The time parameter matrix is defined as follows:

$$T=\left[\begin{array}{rrrrrr}\hfill t_0^5& \hfill t_0^4& \hfill t_{0 }^3& \hfill t_0^2& \hfill t_{0 }& \hfill 1\\ \hfill 5t_0^4& \hfill 4t_0^3& \hfill 3t_0^2& \hfill 2t_0& \hfill 1& \hfill 0\\ \hfill 20t_0^3& \hfill 12t_0^2& \hfill 6t_{0 }& \hfill 2& \hfill 0& \hfill 0\\ \hfill t_z^5& \hfill t_z^4& \hfill t_z^3& \hfill t_z^2& \hfill t_z& \hfill 1\\ \hfill 5t_z^4& \hfill 4t_z^3& \hfill 3t_z^2& \hfill 2t_z& \hfill 1& \hfill 0\\ \hfill 20t_z^3& \hfill 12t_z^2& \hfill 6t_z& \hfill 2& \hfill 0& \hfill 0\end{array}\right]$$

(22)

where $t_0$ and $t_z$ are the initial time of lane change and the time of completion of lane change, respectively.

The definition of the coefficient matrices is as follows:

$$\{\begin{array}{l}A=\left[\begin{array}{llllll}{a}_5\hfill & a_4\hfill & a_3\hfill & a_2\hfill & a_1\hfill & a_0\hfill \end{array}\right]\hfill \\ B=\left[\begin{array}{llllll}{b}_5\hfill & b_4\hfill & b_3\hfill & b_2\hfill & b_1\hfill & b_0\hfill \end{array}\right]\hfill \end{array}$$

(23)

To guarantee the EV’s smooth lane change, the following boundary conditions need to be provided for the lane change trajectory function:

$$\{\begin{array}{l}\begin{array}{lll}x(0)=0\hfill & \dot{x}(0)={\dot{x}}_0\hfill & \ddot{x}(0)=0\hfill \\ x\left(t_z\right)=x_z\hfill & \dot{x}\left(t_z\right)={\dot{x}}_z\hfill & \ddot{x}\left(t_z\right)=0\hfill \end{array}\\ \begin{array}{lll}y(0)=y_0\hfill & \dot{y}(0)=0\hfill & \ddot{y}(0)=0\hfill \\ y\left(t_z\right)=y_z\hfill & \dot{y}\left(t_z\right)=0\hfill & \ddot{y}\left(t_z\right)=0\hfill \end{array}\end{array}$$

(24)

Combining the aforementioned formulas, we obtain the following:

$$\{\begin{array}{l}{\left[\begin{array}{llllll}{x}_{0 }\hfill & {\dot{x}}_{0 }\hfill & {\ddot{x}}_{0 }\hfill & x_{\mathrm{z} }\hfill & {\dot{x}}_{\mathrm{z} }\hfill & {\ddot{x}}_{\mathrm{z} }\hfill \end{array}\right]}^T=T{A}^T\\ {\left[\begin{array}{llllll}{y}_{0 }\hfill & {\dot{y}}_{0 }\hfill & {\ddot{y}}_{0 }\hfill & y_{\mathrm{z} }\hfill & {\dot{y}}_{\mathrm{z} }\hfill & {\ddot{y}}_{\mathrm{z} }\hfill \end{array}\right]}^T=T{B}^T\end{array}$$

(25)

The coefficient matrices A and B are computed using the aforementioned equations, and the EV’s lane-changing trajectory is subsequently determined.

In order to make the trajectory planning algorithm obtain the adaptive optimal lane change time and lane change the longitudinal distance for different vehicle motion states, the longitudinal lane-changing distance and lane-changing time are used as optimization variables in this paper to construct a normalized trajectory evaluation function that takes into account numerous performance restrictions, such as EV lane-changing efficiency, driving stability, and comfort. The function can be expressed as follows:

$$J={\omega }_1\frac{\max \left(x_z\right)}{x_{z\max }}+{\omega }_2\frac{\max \left(\ddot{y}\right)}{a_{y\max }}+{\omega }_3\frac{\max \left({\omega }_r\right)}{{\omega }_{r\max }}+{\omega }_4\frac{\max (\psi )}{{\psi }_{\max }}+{\omega }_5\frac{\max ({\delta }_f)}{{\delta }_{f\max }}$$

(26)

where ${\omega }_r$ is the yaw rate; ${\omega }_1$, ${\omega }_2$, ${\omega }_3$, ${\omega }_4$, and ${\omega }_5$ are weight coefficients, and ${\omega }_1+{\omega }_2+{\omega }_3+{\omega }_4+{\omega }_5=1$. $x_{z\max }$ is maximum longitudinal lane change distance; $a_{y\max }$ is maximum lateral acceleration; ${\omega }_{r\max }$ is maximum yaw rate, (${\omega }_{rmax}=\left|\mu g/v\right|$); ${\psi }_{\max }$ is maximum side slip angle; and ${\delta }_{f\max }$ is maximum front wheel rotation angle.

In order to improve the comfort of the lane-changing process, this paper constrains the lateral acceleration of the EV in conjunction with the restrictions of vehicle dynamics in the real motion process and the description of comfort in GB/T13441.1-2007 [34]. Then, the multi-performance limitations represented by the front wheel rotation angle, side slip angle, lateral acceleration, and yaw rate are established. It can be expressed as follows:

$$\{\begin{array}{l}\ddot{y}\le a_{ymax}\\ {\omega }_r\le {\omega }_{rmax}\\ \psi \le {\psi }_{max}\\ {\delta }_f\le {\delta }_{fmax}\end{array}$$

(27)

5. Simulation and Verification

In order to validate the ramp merging decision algorithm and trajectory planning algorithm proposed in this paper, a typical test scenario is designed. All the simulation tests are constructed in the MATLAB-Simulink platform.

5.1. Simulation Parameter Setting

Table 2. Model parameters.

Decision Making				Trajectory Planning
${\psi }_{v-\log }^{EV}$	0.32	${\psi }_{ay}^{EV}$	0.6	$\mu$	0.7	$a$,$b$/(m)	1.4, 1.65
${\psi }_{s-\log }^{EV}$	8 × 103	$\varsigma$	1 × 10−5	${\psi }_{max}$ (°)	10	$i$	17
${\psi }_{v-\mathrm{lat}}^{EV}$	0.4	$d_m$/(m)	20	${\delta }_{fmax}$ (°)	2	$k_1$,$k_2$ (N/rad)	−264,570, −240,000
${\psi }_{s-\mathrm{lat}}^{EV}$	7 × 103	$a_x^{EV}$	[−3, 5]	${\omega }_{rmax}$ (rad/s)	3	$a_{ymax}$ (m/s2)	0.4g
${\psi }_{ax}^{EV}$	0.45	$a_y^{EV}$	[−4, 5]	$m$ (kg)	1650	$x_{zmax}$ (m)	60
$v_x^{EV}$ (m/s)	30	$k_A{}_{cc}$	2.1	$l$ (m)	3.05	$t_{zmax}$ (s)	14

displays the game decision-making and trajectory planning model parameters used in this paper. For the parameters of the decision-making module, through continuous optimization of the simulation results of the decision-making model, the parameters in the model are calibrated to obtain the optimal setting parameters; for the trajectory planning module, these parameters are based on previous research results [35].

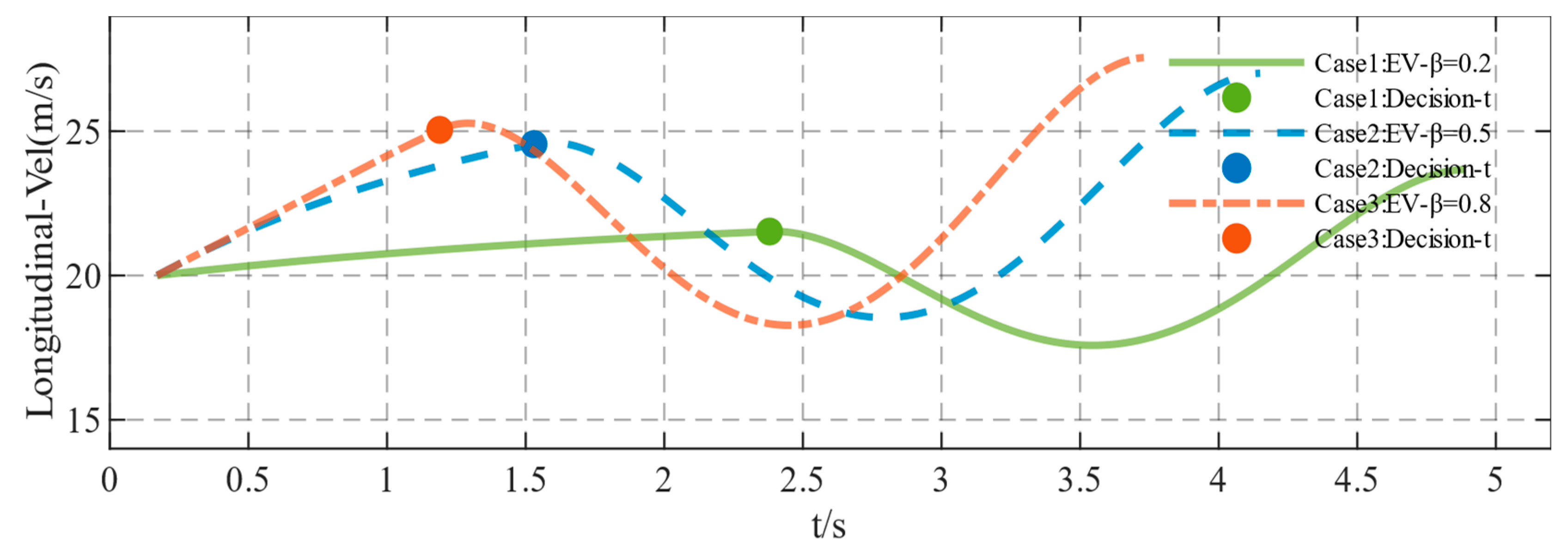
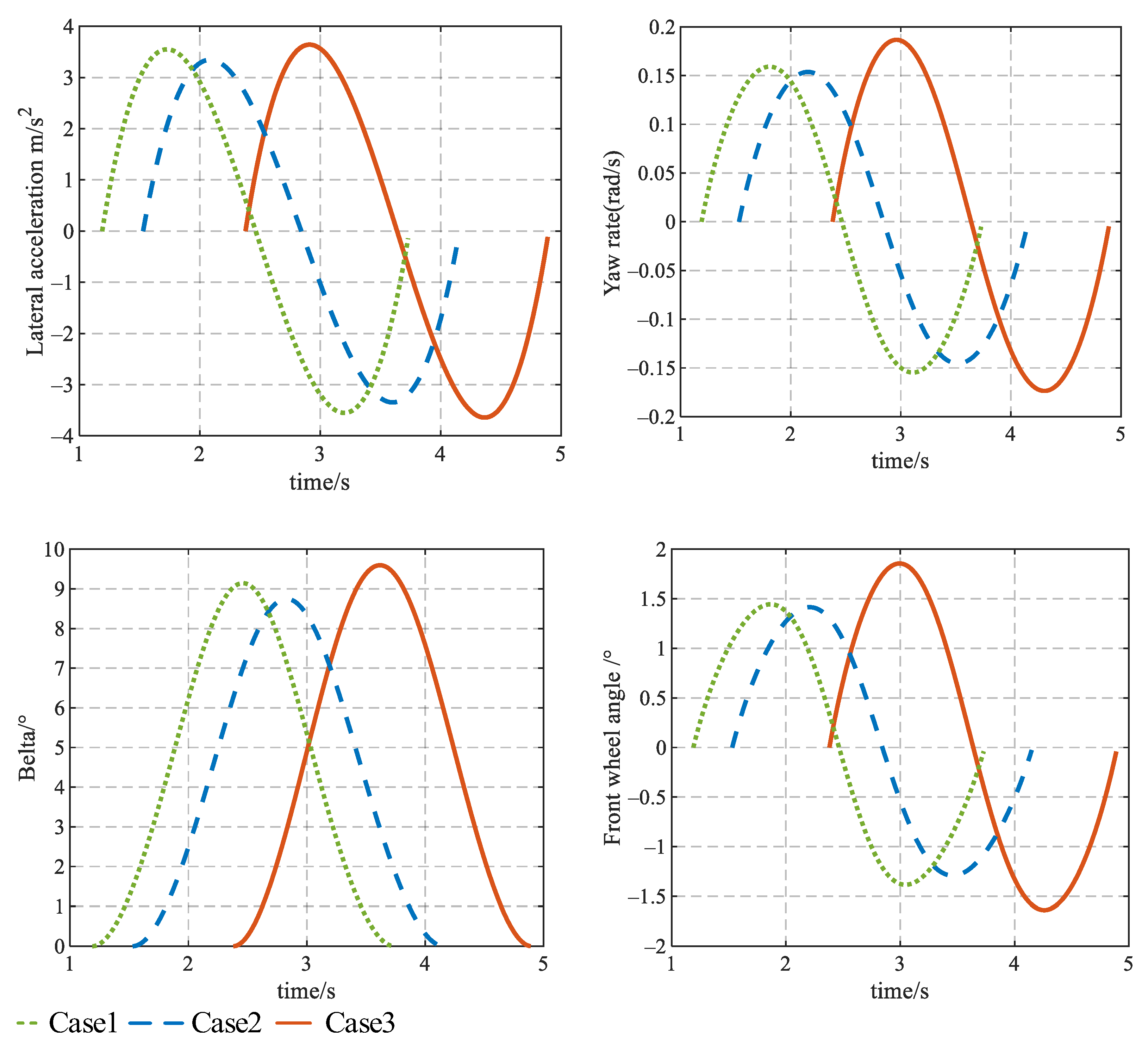
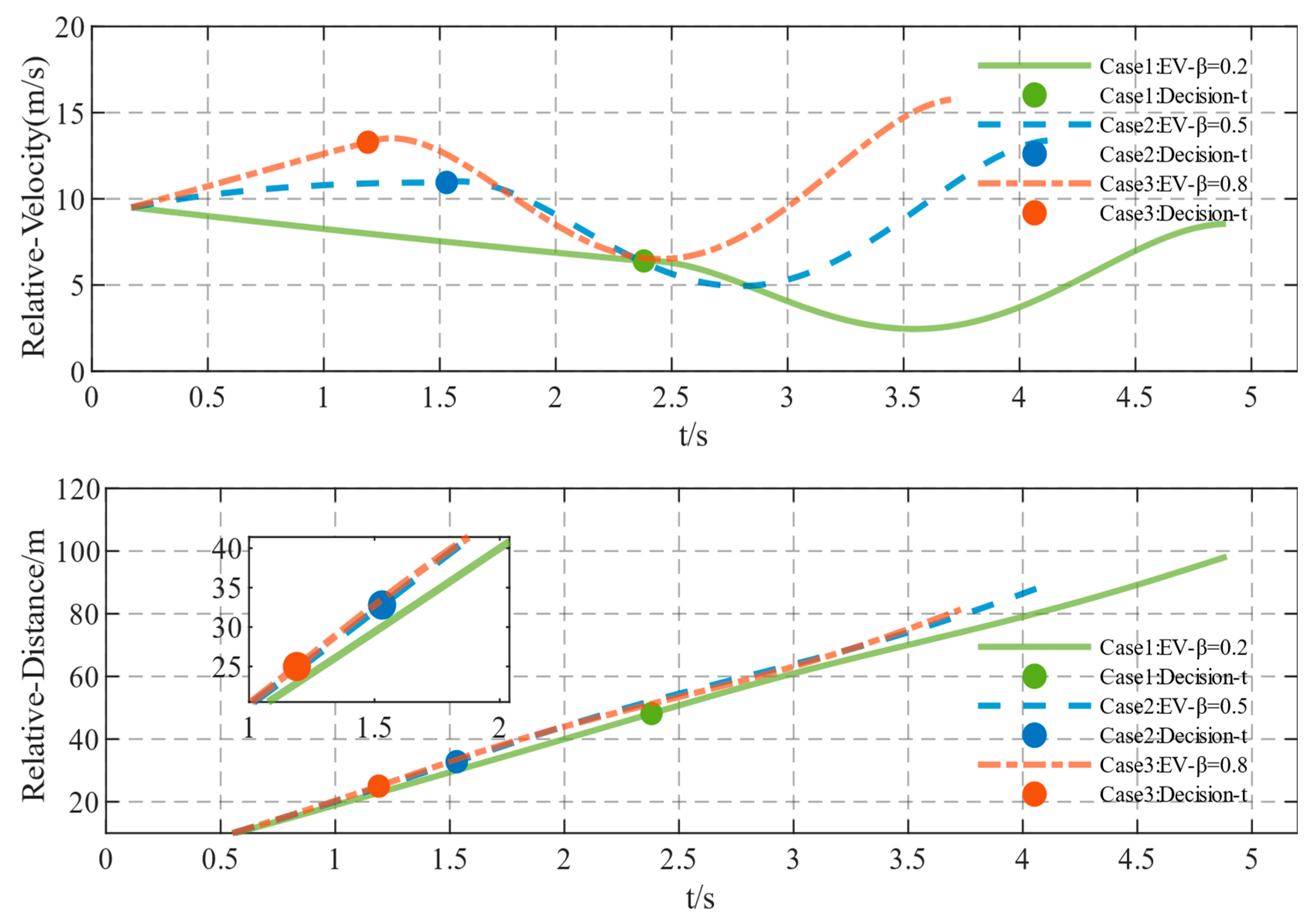
5.2. Model Simulation Test

As shown in Figure 5, a typical on-ramp merging scenario is constructed in this section; the EV must change lanes due to the limited distance of the ramp. Information and conditions of the vehicles in the target lane environment, particularly the rear and front vehicles, must be taken into account when the EV intends to change lanes. When the distance between the PV and the EV satisfies the lane change condition, the EV may evaluate the FV’s reaction to the ramping merge action by making a slight lateral displacement or turning on the turn signal. If the FV prevents the EV from changing lanes, the EV will wait for the next merging opportunity; on the contrary, the merging game decision model built in this paper will solve the optimum merger opportunity.

The aggressiveness coefficients of the EV in the scenario are set to 0.2, 0.4, 0.6, and 0.8, respectively, to explore the effects of various aggressiveness coefficients on AV’s decision-making. The driving style of the EV grows more aggressive as the aggression coefficient increases, but on the contrary, it becomes more conservative and attentive to travel safety. The paper assumes that the FV continues to drive in the same style to more thoroughly validate the effect of aggression on the EV. As shown in Table 2, the state parameters of the game-related vehicles in the scenario are at the beginning of the simulation. The initial relative distance between the two vehicles is maintained small in the present study to confirm the impact of the FV’s reaction on the EV’s decision. If the FV is far behind the EV, whether or not it intends to block the EV’s lane change, it will not have a significant bearing on the EV’s final decision or the safety of the lane change.

In the course of the game, EVs with varying degrees of aggressiveness demonstrate distinct outcomes in their decision-making processes and lane-changing trajectories, as shown in Figure 6. The shades of the colors in the figure represent the trajectories of the EV before and during the lane-changing, respectively. In Case 1, the EV’s aggressiveness coefficient is denoted as EV_β = 0.2, indicating a conservative driving style. In the game against the FV, the prioritization of collision safety led to a decrease in acceleration, ultimately resulting in a disadvantage in both speed and position. In comparison to alternative driving styles, the driver’s timing for changing lanes is comparatively delayed. Setting the aggressiveness coefficient EV_β to 0.8 in Case 3 indicates that the EV is currently driving aggressively. Compared with safety, it is more biased towards travel efficiency, which is reflected in the cost function as the weight value of this item is greater. Simultaneously, owing to the more assertive safety evaluation of the ramp merge, it can promptly execute a lane-changing maneuver and accomplish the lane-changing procedure in the shortest duration. In Case 2, the EV aggressiveness coefficient is at a moderate level, and the passing velocity is also increased while travel safety is ensured. The EV is a moderate driving style at this time.

The simulation results of the longitudinal velocity for the EV with varying aggressiveness coefficients during testing are presented in Figure 7. The figure illustrates a positive correlation between the longitudinal velocity increase and the aggressiveness coefficient value before the merging decision. In other words, in the game, the EV with the higher aggressiveness coefficient is likely to demonstrate greater velocity, may take a dominant position, and can make choices that maximize its interests. Before the decision is made, the EV travels in a straight line, so its lateral stability is unaffected. The simulation results for front wheel rotation angle, side-slip angle, lateral acceleration, and yaw angle that match trajectory planning are displayed in Figure 8. The stability indicators under the various driving styles meet the restrictions, as seen in the figure, and the EV can complete the merging process safely and comfortably.

Figure 9 displays the simulation outcomes of the relative velocity curve and relative distance throughout the game involving the EV and FV. The aggressive drivers (EV_β = 0.8) had the least relative distance and relative velocity from the FV when they decide to change lanes in comparison to the moderate and conservative drivers. In this case, the aggressive driver rapidly increases the relative distance and velocity with the FV through a large acceleration and decides to merge and change to the target lane after meeting the safety conditions. In contrast to the acceleration strategy of aggressive drivers, conservative drivers tend to use a gradual acceleration approach while observing the relative distance and velocity of the FV. Additionally, they delay their merging decision until they have reached a certain psychological threshold.

6. Conclusions

This paper proposed a game-merging model of coupled driver characteristics in on-ramp scenarios. First of all, based on the NGSIM dataset, a K-means clustering algorithm was used to study the driving style under lane-changing conditions. The difference of motion parameters of various driving style modes under lane-changing conditions was analyzed and provided a theoretical foundation for the design of personalized decision-making algorithms. Then, a Nash game model was used to simulate the interaction and conflict between the EV and the FV in the main lane. The influence of different levels of aggression on the decision to ramp merge was studied. Finally, a quintic polynomial merging trajectory planning technique with multi-constraints was proposed, taking into account the particularity of the acceleration lane.

It is concluded that EVs that have different driving styles can make the right decision and successfully finish the ramp merging in a common ramp conflict interaction scenario. The results from the velocity and trajectory tests demonstrate that the decision-making characteristics of varied driving styles are consistent with the NGSIM driving style cluster analysis outcomes, thereby validating the effectiveness of the integrated decision-making algorithm. Additionally, the proposed ramp trajectory planning algorithm can quickly plan a safe and comfortable trajectory for the EV.

Affected by the data conditions, there was no consideration of the weather factor in this paper’s decision to ramp merge. The impact of these uncertain factors on decision-making can be explored by collecting data under different weather conditions in the future. Additionally, comparing the ramp merging model with other decision-making models could provide valuable insights for improving overall decision-making processes.