Adaptive Constant-Current/Constant-Voltage Charging of a Battery Cell Based on Cell Open-Circuit Voltage Estimation
Abstract
1. Introduction
1.1. Motivation
1.2. State-of-the-Art Methods in Battery Charging
1.3. Research Gap and the Proposed Solution
2. Materials and Methods
2.1. Battery Cell-Equivalent Circuit Dynamic Model
2.2. Damping Optimum Criterion
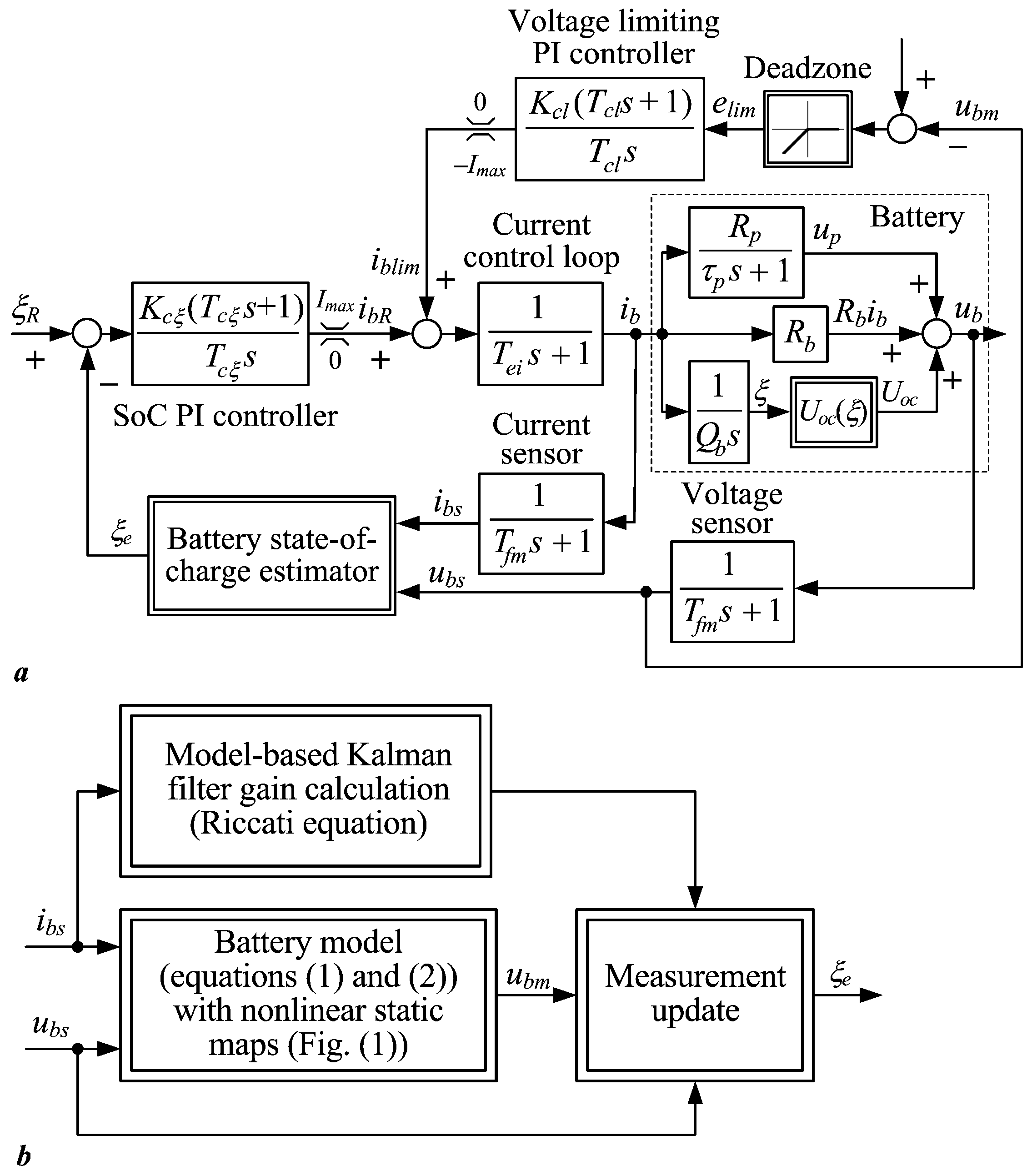
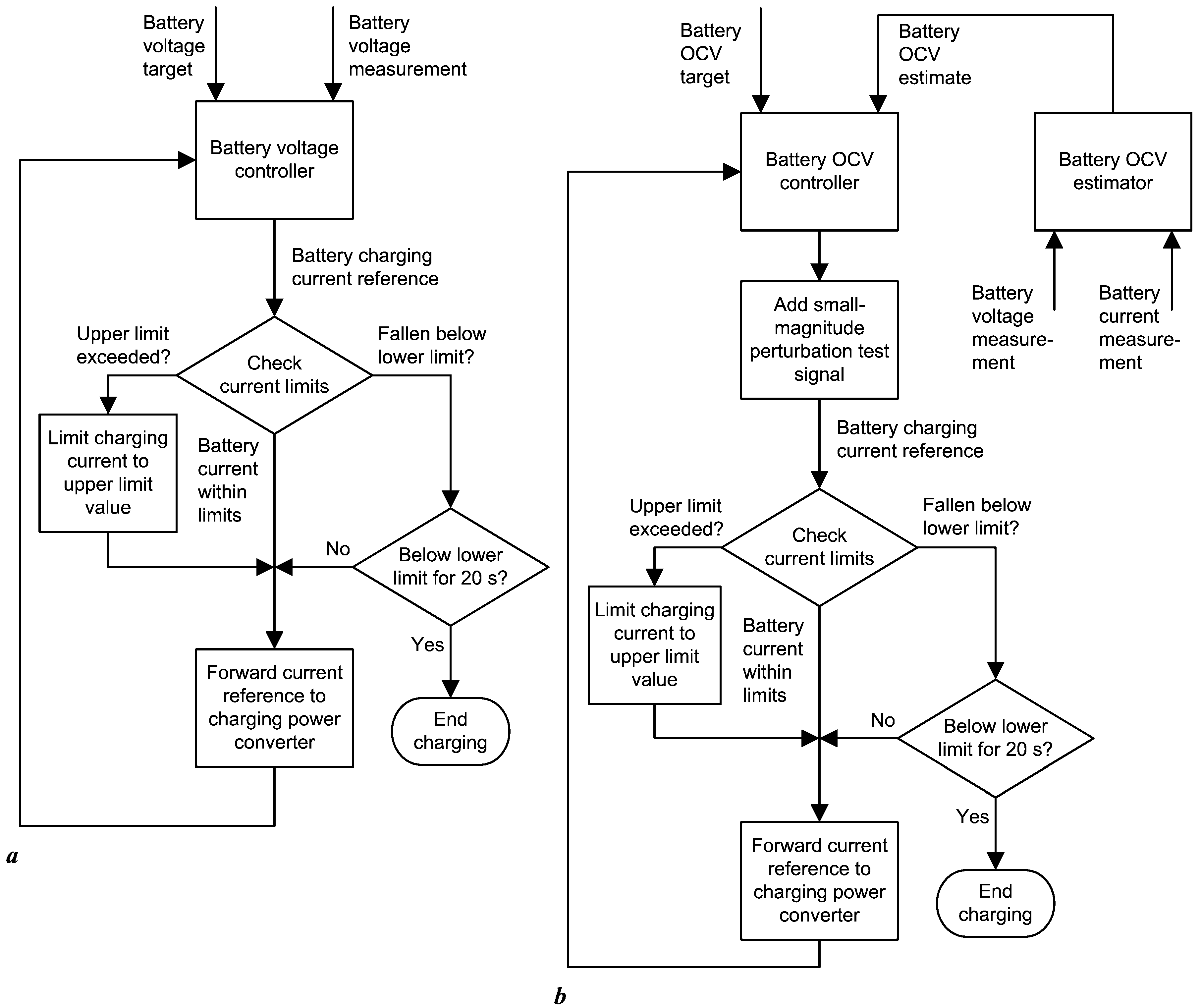
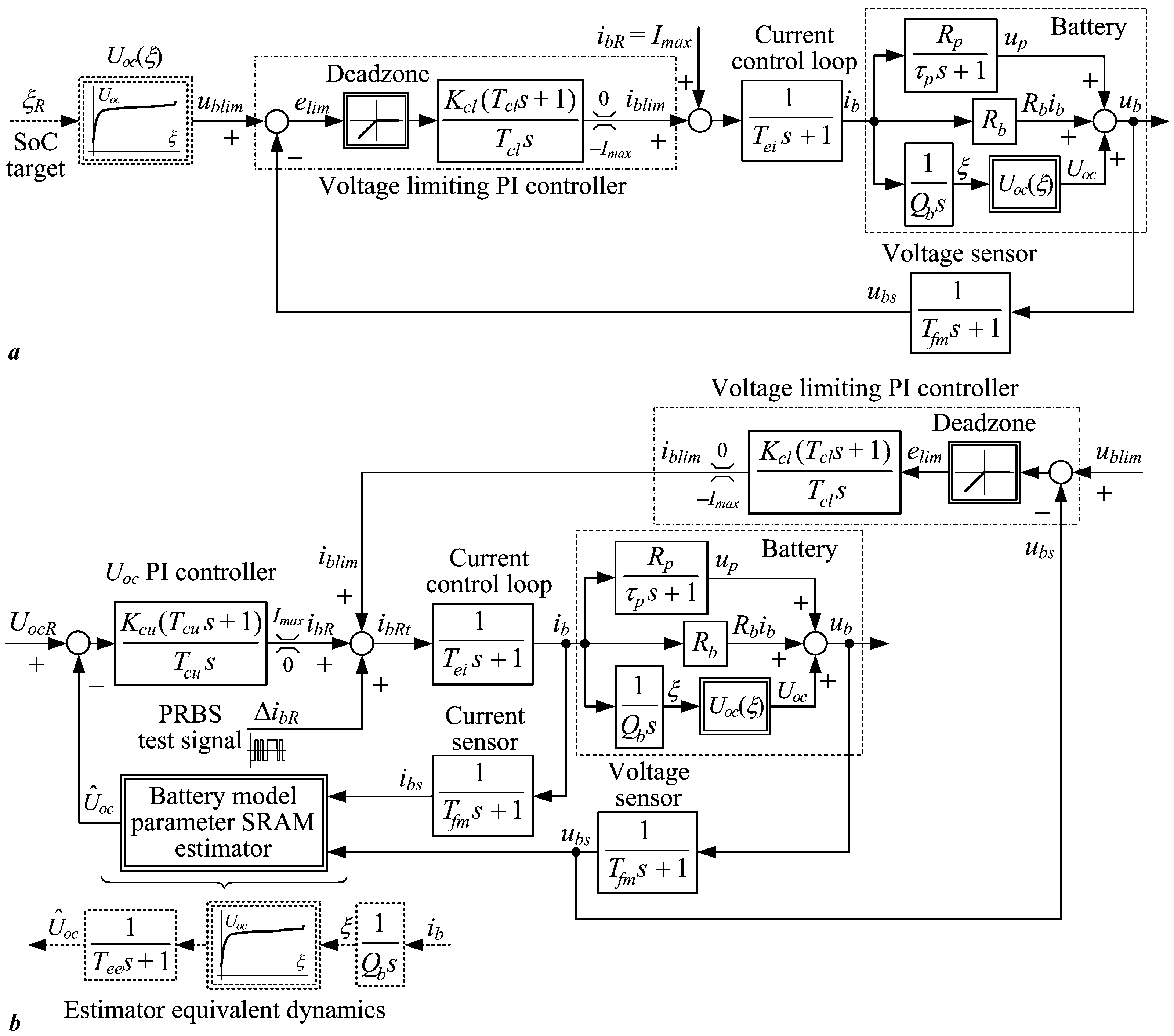
2.3. Conventional and Adaptive Cascade Control Systems for Battery Charging
2.4. Feedback Controller Tuning Rules
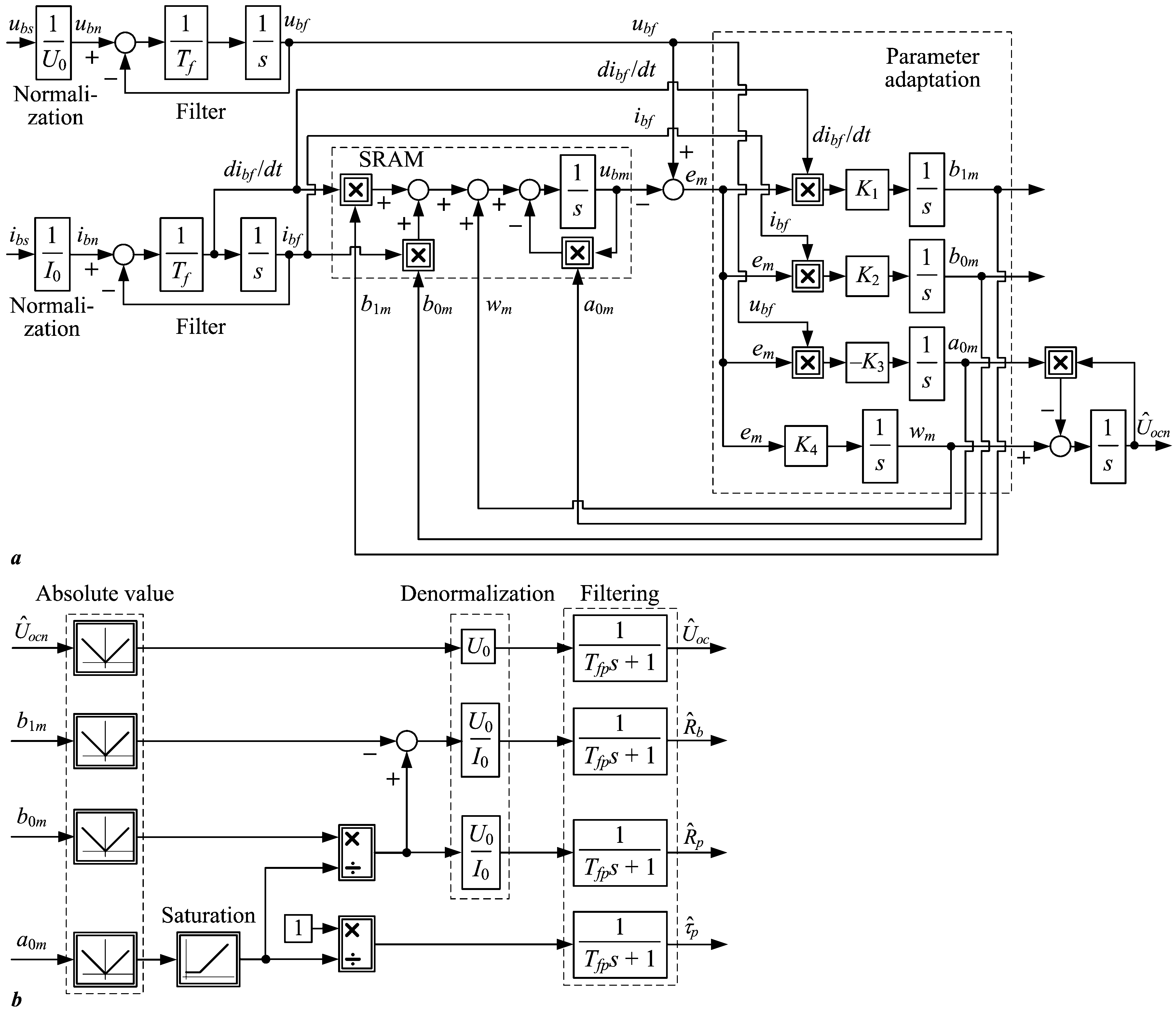
2.5. Parameter Estimator Design Based on the Lyapunov Stability Theory
3. Simulation Results
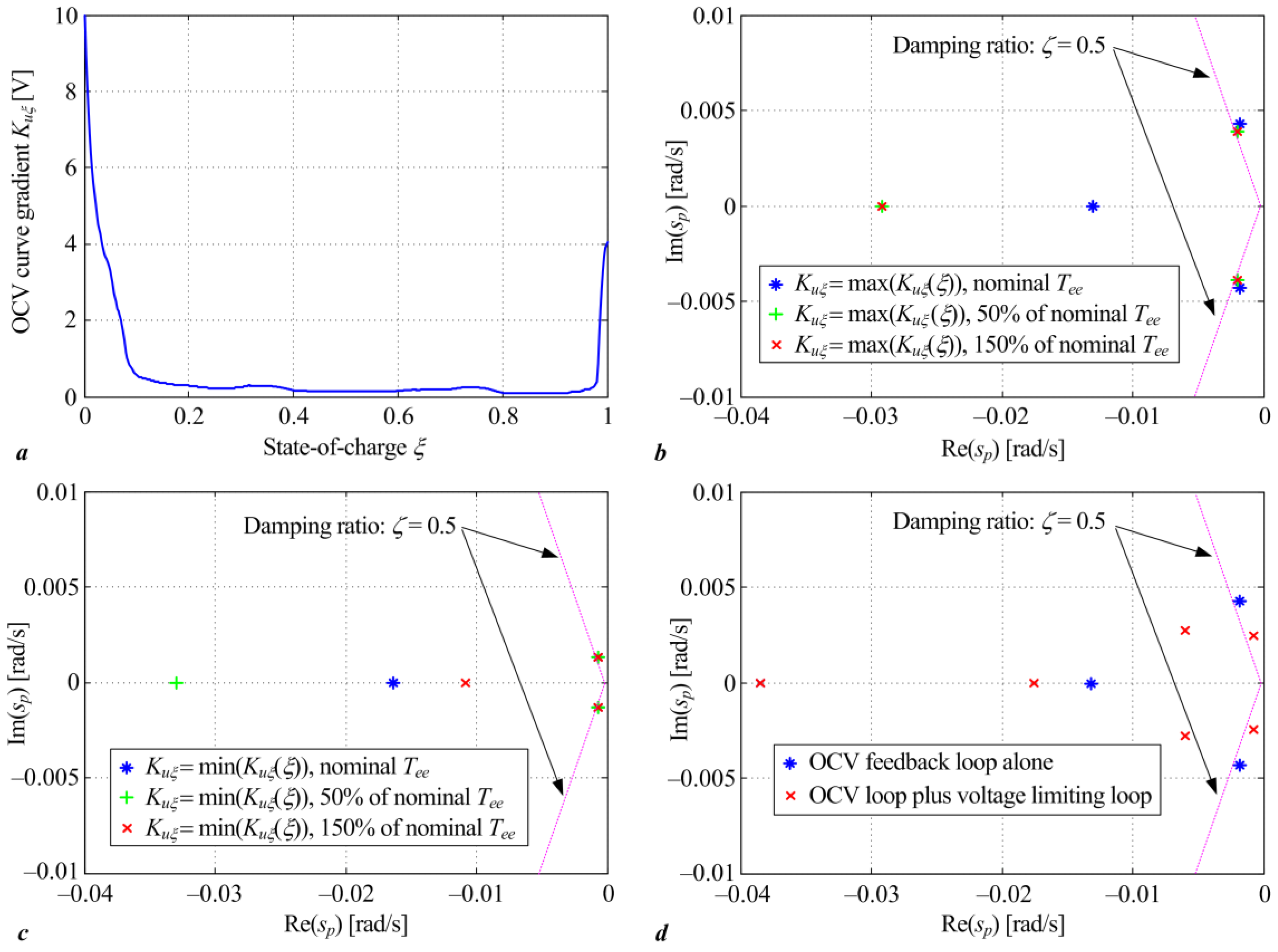
3.1. Control System Robustness Analysis
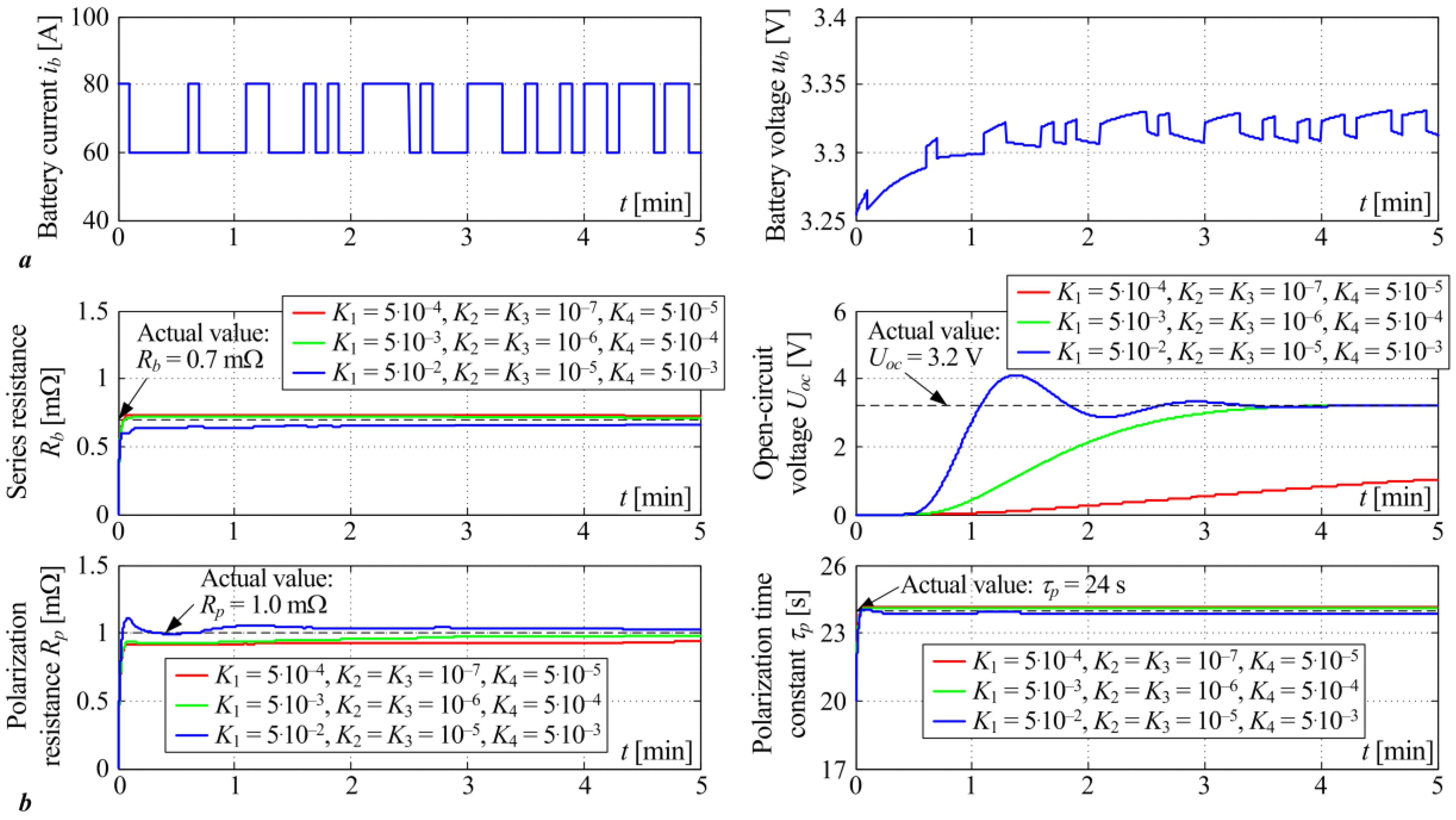
3.2. Illustration of Parameter Estimator Convergence
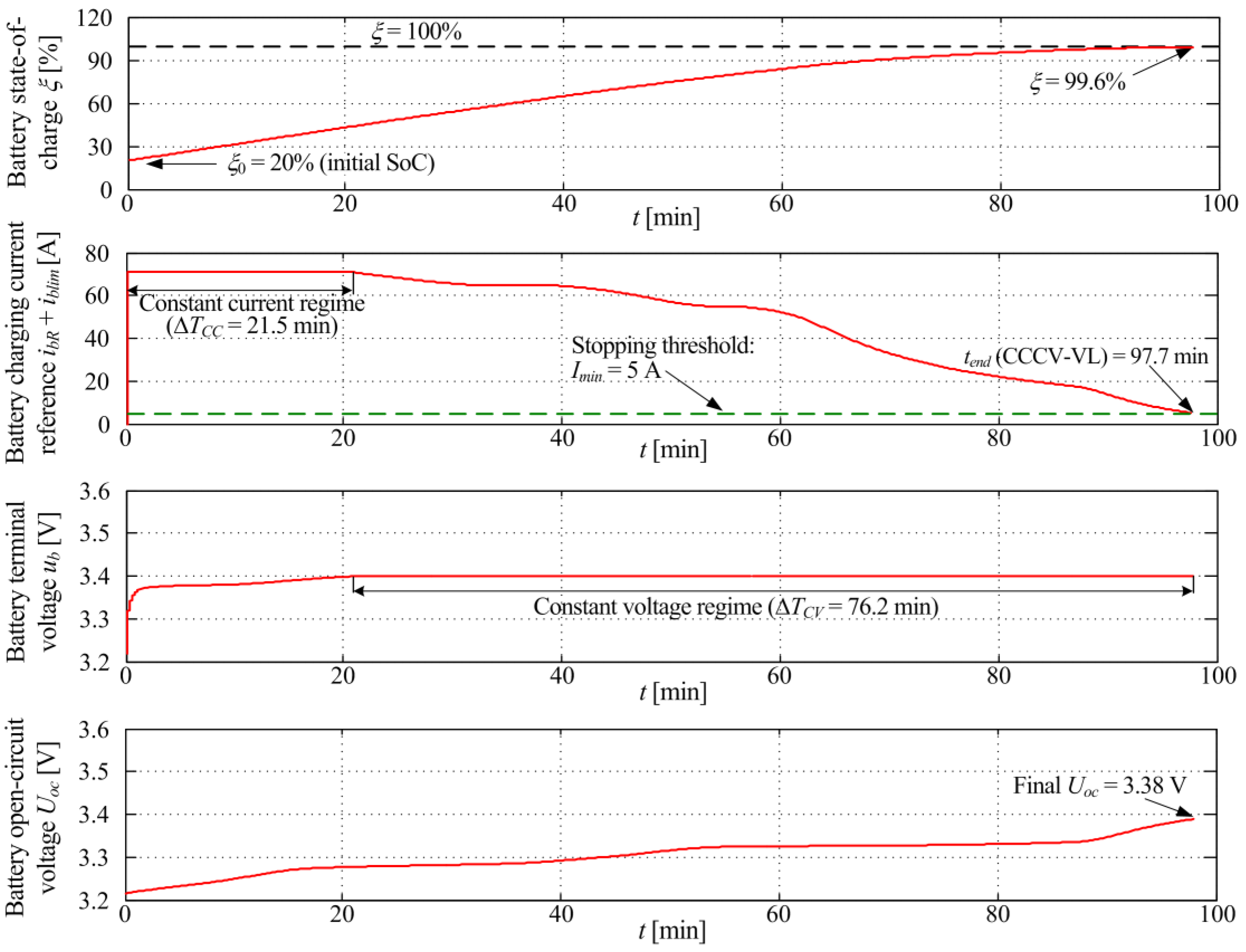
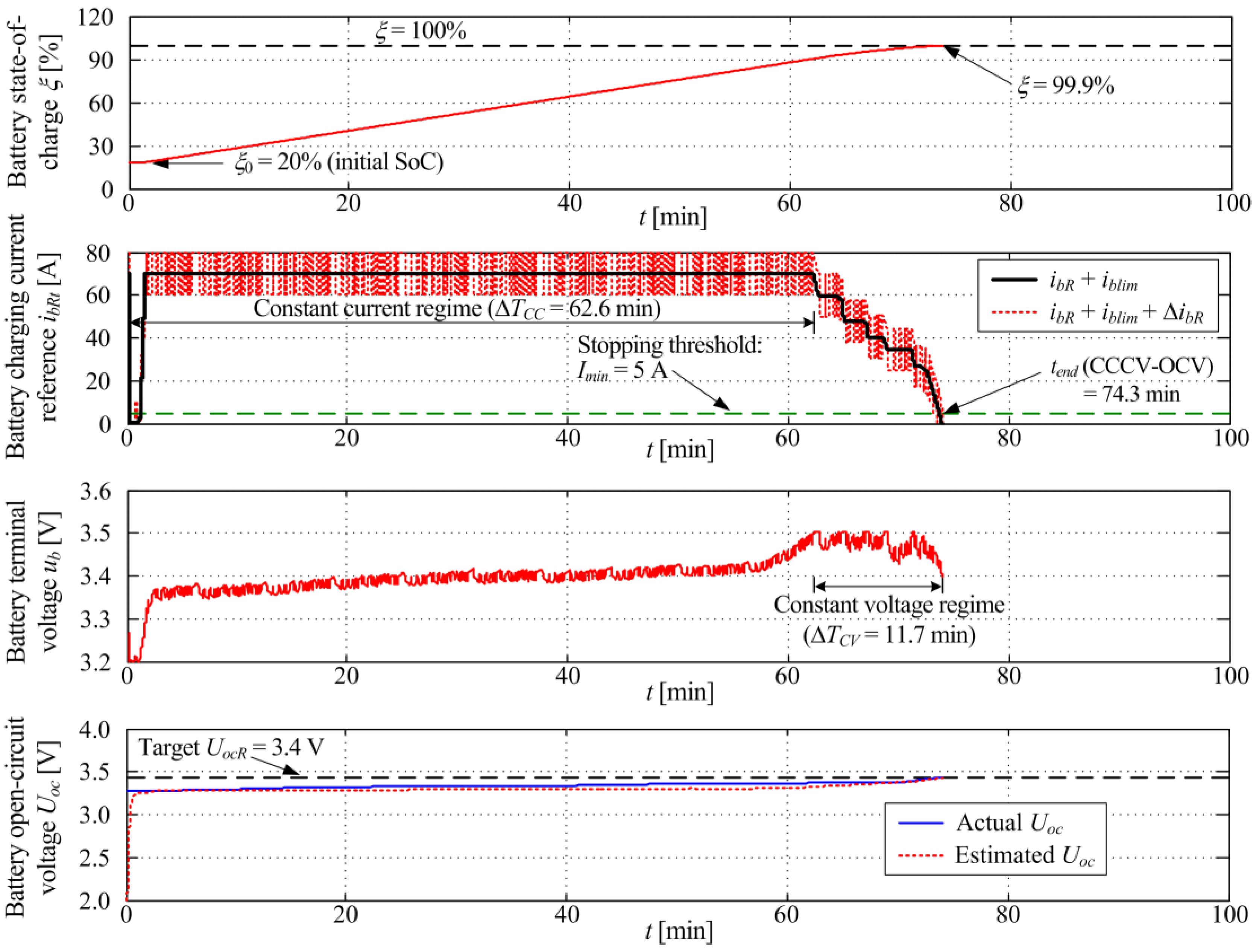
3.3. Charging Control Strategy Results
4. Discussion of Obtained Results and Comparison with Other Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- McCollum, D.; Krey, V.; Kolp, P.; Nagai, Y.; Riahi, K. Transport electrification: A key element for energy system transformation and climate stabilization. Clim. Chang. 2014, 123, 651–664. [Google Scholar] [CrossRef]
- Deur, J.; Škugor, B.; Cipek, M. Integration of Electric Vehicles into Energy and Transport Systems, Automatika. J. Control. Meas. Electron. Comput. Commun. 2015, 56, 395–410. [Google Scholar]
- Komnos, D.; Tsiakmakis, S.; Pavlovic, J.; Ntziachristos, L.; Fontaras, G. Analysing the real-world fuel and energy consumption of conventional and electric cars in Europe. Energy Convers. Manag. 2022, 270, 116161. [Google Scholar] [CrossRef]
- Goodall, G.; Scioletti, M.; Zolan, A.; Suthar, B.; Newman, A.; Kohl, P. Optimal design and dispatch of a hybrid microgrid system capturing battery fade. Optim. Eng. 2019, 20, 179–213. [Google Scholar] [CrossRef]
- Chinese, D.; Pinamonti, P.; Mauro, C. A spatially explicit optimization model for the selection of sustainable transport technologies at regional bus companies. Optim. Eng. 2021, 22, 1921–1954. [Google Scholar] [CrossRef]
- Mohanty, A.K.; Perli, S.B. Fuzzy logic based multi-objective approach for optimal allocation of charging stations for electric vehicles, e-Prime—Advances in Electrical Engineering. Electron. Energy 2022, 2, 100089. [Google Scholar]
- Cipek, M.; Pavković, D.; Kljaić, Z.; Mlinarić, T.J. Assessment of Battery-Hybrid Diesel-electric Locomotive Fuel Savings and Emission Reduction Potentials based on a Realistic Mountainous Rail Route. Energy 2019, 173, 1154–1171. [Google Scholar] [CrossRef]
- Cipek, M.; Pavković, D.; Krznar, M.; Kljaić, Z.; Mlinarić, T.J. Comparative Analysis of Conventional Diesel-Electric and Hypothetical Battery-Electric Heavy Haul Locomotive Operation in terms of Fuel Savings and Emissions Reduction Potentials. Energy 2021, 232, 121097. [Google Scholar] [CrossRef]
- Ahmad, S.; Spiryagin, M.; Cole, C.; Wu, Q.; Wolfs, P.; Bosomworth, C. Analysis of positioning of wayside charging stations for hybrid locomotive consists in heavy train operations. Railw. Eng. Sci. 2021, 23, 285–298. [Google Scholar] [CrossRef]
- Karlušić, J.; Cipek, M.; Pavković, D.; Šitum, Ž.; Benić, J. Efficiency comparison of different powertrain structures intended for a hybrid skidder by utilizing a novel cascade optimization algorithm, e-Prime—Advances in Electrical Engineering. Electron. Energy 2022, 2, 100079. [Google Scholar]
- Di Ilio, G.; Di Giorgio, P.; Tribioli, L.; Bella, G.; Jannelli, E. Preliminary design of a fuel cell/battery hybrid powertrain for a heavy-duty yard truck for port logistics. Energy Convers. Manag. 2021, 243, 114423. [Google Scholar] [CrossRef]
- Hoenicke, P.; Ghosh, D.; Muhandes, A.; Bhattacharya, S.; Bauer, C.; Kallo, J.; Willich, C. Power management control and delivery module for a hybrid electric aircraft using fuel cell and battery. Energy Convers. Manag. 2021, 244, 114445. [Google Scholar] [CrossRef]
- Peprah, F.; Gyamfi, S.; Effah-Donyina, E.; Amo-Boateng, M. Evaluation of reactive power support in solar PV prosumer grid, e-Prime—Advances in Electrical Engineering. Electron. Energy 2022, 2, 100057. [Google Scholar] [CrossRef]
- Udeh, G.T.; Michailos, S.; Ingham, D.; Hughes, K.J.; Ma, L.; Pourkashanian, M. Optimal sizing of a hybrid PV-WT-battery storage system: Effects of split-ST and combined ST + ORC back-ups in circuit charging and load following. Energy Convers. Manag. 2022, 256, 115370. [Google Scholar] [CrossRef]
- Pavković, D.; Sedić, A.; Guzović, Z. Oil Drilling Rig Diesel Power-plant Fuel Efficiency Improvement Potentials through Rule-Based Generator Scheduling and Utilization of Battery Energy Storage System. Energy Convers. Manag. 2016, 121, 194–211. [Google Scholar] [CrossRef]
- Pavković, D.; Lobrović, M.; Hrgetić, M.; Komljenović, A. A Design of Cascade Control System and Adaptive Load Compensator for Battery/Ultracapacitor Hybrid Energy Storage-based Direct Current Microgrid. Energy Convers. Manag. 2016, 114, 154–167. [Google Scholar] [CrossRef]
- Pavković, D.; Cipek, M.; Kljaić, Z.; Mlinarić, T.-J.; Hrgetić, M.; Zorc, D. Damping Optimum-Based Design of Control Strategy Suitable for Battery/Ultracapacitor Electric Vehicles. Energies 2018, 11, 2854. [Google Scholar] [CrossRef]
- International Renewable Energy Agency (IRENA): “Road Transport: The Cost of Renewable Solutions”. IRENA’s Costing Study. 2013. Available online: http://www.irena.org/publications (accessed on 15 November 2015).
- Omar, N.; Monem, M.A.; Firouz, Y.; Salmien, J.; Smekens, J.; Hagazy, O.; Gaulous, H.; Mulder, G.; Van den Bossche, P.; Coosemans, T.; et al. Lithium Iron Phosphate Based Battery—Assessment of Aging Parameters and Development of Life Cycle Model. Appl. Energy 2014, 113, 1575–1585. [Google Scholar] [CrossRef]
- GWL/Power Group: “SE100AHA Cell Specification”. 2015. Available online: https://www.ev-power.eu (accessed on 15 November 2016).
- Wai, R.J.; Jhung, S.J. Design of energy-saving adaptive fast-charging control strategy for Li-Fe-PO4 battery module. IET Power Electron. 2012, 5, 1684–1693. [Google Scholar] [CrossRef]
- Hussein, A.A.H.; Batarseh, I. A Review of Charging Algorithms for Nickel and Lithium Battery Chargers. IEEE Trans. Veh. Technol. 2011, 60, 830–838. [Google Scholar] [CrossRef]
- James, M.; Grummett, J.; Rowan, M.; Newman, J. Application of Pulse Charging Techniques to Submarine Lead-Acid Batteries. J. Power Sources 2006, 162, 878–883. [Google Scholar] [CrossRef]
- Chen, M.; Rincón-Mora, G.A. Accurate, Compact, and Power-Efficient Li-Ion Battery Charger Circuit. IEEE Trans. Circuits Syst. Express Briefs 2006, 53, 1180–1184. [Google Scholar] [CrossRef]
- Lee, S.; Han, U.; Lee, H. Development of a hybrid battery thermal management system coupled with phase change material under fast charging conditions. Energy Convers. Manag. 2022, 268, 116015. [Google Scholar] [CrossRef]
- Chen, L.-R. PLL-Based Battery Charge Circuit Topology. IEEE Trans. Ind. Electron. 2004, 51, 1134–1136. [Google Scholar] [CrossRef]
- Chen, L.-R.; Liu, C.-S.; Chen, J.-J. Improving Phase-Locked Battery Charger Speed by Using Resistance Compensated Technique. IEEE Trans. Ind. Electron. 2009, 56, 1205–1211. [Google Scholar] [CrossRef]
- Pavković, D.; Lobrović, M.; Hrgetić, M.; Komljenović, A.; Smetko, V. Battery Current and Voltage Control System Design with Charging Application. In Proceedings of the 2014 IEEE Multi-Conference on Systems and Control, Antibes, France, 8–10 October 2014; pp. 1133–1138. [Google Scholar] [CrossRef]
- Vermeer, W.; Stecca, M.; Mouli, G.R.C.; Bauer, P. A Critical Review on The Effects of Pulse Charging of Li-ion Batteries. In Proceedings of the 19th IEEE International Power Electronics and Motion Control Conference (PEMC 2021), Gliwice, Poland, 25–29 April 2021; pp. 217–224. [Google Scholar] [CrossRef]
- Arabsalmanabadi, B.; Tashakor, N.; Javadi, A.; Al-Haddad, K. Charging Techniques in Lithium-Ion Battery Charger: Review and New Solution. In Proceedings of the 44th Annual Conference of the Industrial Electronics Society (IEEE IECON 2018), Washington, DC, USA, 21–23 October 2018; pp. 5731–5738. [Google Scholar] [CrossRef]
- Amanor-Boadu, J.M.; Guiseppi-Elie, A. Improved Performance of Li-ion Polymer Batteries Through Improved Pulse Charging Algorithm. Appl. Sci. 2020, 10, 895. [Google Scholar] [CrossRef]
- Huang, X.; Li, Y.; Acharya, A.B.; Sui, X.; Meng, J.; Teodorescu, R.; Stroe, D.-I. A Review of Pulsed Current Technique for Lithium-ion Batteries. Energies 2020, 13, 2458. [Google Scholar] [CrossRef]
- Collin, R.; Miao, Y.; Yokochi, A.; Enjeti, P.; von Jouanne, A. Advanced Electric Vehicle Fast-Charging Technologies. Energies 2019, 12, 1839. [Google Scholar] [CrossRef]
- Hsieh, G.-C.; Chen, L.-R.; Huang, K.-S. Fuzzy-Controlled Li-Ion Battery Charge System with Active State-of-Charge Controller. IEEE Trans. Ind. Electron. 2001, 48, 585–593. [Google Scholar] [CrossRef]
- Zou, C.; Hu, X.; Wei, Z.; Wik, T.; Egardt, B. Electrochemical Estimation and Control for Lithium-Ion Battery Health-Aware Fast Charging. IEEE Trans. Ind. Electron. 2018, 65, 6635–6645. [Google Scholar] [CrossRef]
- Jiang, L.; Huang, Y.; Li, Y.; Yu, J.; Qiao, X.; Huang, C.; Cao, Y. Optimization of Variable-Current Charging Strategy Based on SOC Segmentation for Li-ion Battery. IEEE Trans. Intell. Transp. Syst. 2021, 22, 622–629. [Google Scholar] [CrossRef]
- Vo, T.T.; Chen, X.; Shen, W.; Kapoor, A. New charging strategy for lithium-ion batteries based on the integration of Taguchi method and state of charge estimation. J. Power Sources 2015, 273, 413–422. [Google Scholar] [CrossRef]
- Chen, Z.; Xia, B.; Mi, C.C.; Xiong, R. Loss-Minimization-Based Charging Strategy for Lithium-Ion Battery. IEEE Trans. Ind. Appl. 2015, 51, 4121–4129. [Google Scholar] [CrossRef]
- Liu, K.; Li, K.; Ma, H.; Zhang, J.; Peng, Q. Multi-objective optimization of charging patterns for lithium-ion battery management. Energy Convers. Manag. 2018, 159, 151–162. [Google Scholar] [CrossRef]
- Lee, K.-T.; Dai, M.-J.; Chuang, C.-C. Temperature-Compensated Model for Lithium-Ion Polymer Batteries with Extended Kalman Filter State-of-Charge Estimation for an Implantable Charger. IEEE Trans. Ind. Electron. 2018, 65, 589–596. [Google Scholar] [CrossRef]
- Rai, R.; Gaglani, M.; Das, S.; Panigrahi, T. Multi-Level Constant Current Based Fast Li-Ion Battery Charging Scheme with LMS Based Online State of Charge Estimation. In Proceedings of the 2020 IEEE Kansas Power and Energy Conference (KPEC 2020), Manhattan, KS, USA, 13–14 July 2020. [Google Scholar] [CrossRef]
- Lin, Q.; Wang, J.; Xiong, R.; Shen, W.; He, H. Towards a smarter battery management system: A critical review on optimal charging methods of lithium ion batteries. Energy 2019, 183, 220–234. [Google Scholar] [CrossRef]
- Wassiliadis, N.; Schneider, J.; Frank, A.; Wildfeuer, L.; Lin, X.; Jossen, A.; Lienkamp, M. Review of fast charging strategies for lithium-ion battery systems and their applicability for battery electric vehicles. J. Energy Storage 2021, 44, 103306. [Google Scholar] [CrossRef]
- Xie, W.; Liu, X.; He, R.; Li, Y.; Gao, X.; Li, X.; Peng, Z.; Feng, S.; Feng, X.; Yang, S. Challenges and opportunities toward fast-charging of lithium-ion batteries. J. Energy Storage 2020, 32, 101837. [Google Scholar] [CrossRef]
- de Hoog, J.; Jaguemont, J.; Abdel-Monem, M.; Van Den Bossche, P.; Van Mierlo, J.; Omar, N. Combining an Electrothermal and Impedance Aging Model to Investigate Thermal Degradation Caused by Fast Charging. Energies 2018, 11, 804. [Google Scholar] [CrossRef]
- Szumanowski, A.; Chang, Y. Battery Management System Based on Battery Nonlinear Dynamics Modeling. IEEE Trans. Veh. Technol. 2008, 57, 1425–1432. [Google Scholar] [CrossRef]
- Pavković, D.; Krznar, M.; Komljenović, A.; Hrgetić, M.; Zorc, D. Dual EKF-based State and Parameter Estimator for a LiFePO4 Battery Cell. J. Power Electron. 2017, 17, 398–410. [Google Scholar] [CrossRef]
- Mastali, M.; Vasquez-Arenas, J.; Fraser, R.; Fowler, M.; Afshar, S.; Stevens, M. Battery state of charge estimation using Kalman filtering. J. Power Sources 2013, 239, 294–307. [Google Scholar] [CrossRef]
- Ceraolo, M.; Lutzemberger, G.; Huria, T. Experimentally-Determined Models for High-Power Lithium Batteries, SAE 2011-01-1365. In Proceedings of the 2011 SAE World Congress, Detroit, MI, USA, 12–14 April 2011. [Google Scholar] [CrossRef]
- Pavković, D.; Premec, A.; Krznar, M.; Cipek, M. Current and voltage control system designs with EKF-based state-of-charge estimator for the purpose of LiFePO4 battery cell charging. Optim. Eng. 2022, 23, 2335–2363. [Google Scholar] [CrossRef]
- Dey, S.; Mohon, S.; Pisu, P.; Ayalew, B.; Onori, S. Online State and Parameter Estimation of Battery-Double Layer Capacitor Hybrid Energy Storage System. In Proceedings of the IEEE 54th Annual Conference on Decision and Control (CDC 2015), Osaka, Japan, 15–18 December 2015; pp. 676–681. [Google Scholar] [CrossRef]
- Pavković, D.; Komljenović, A.; Hrgetić, M.; Krznar, M. Experimental Characterization and Development of a SoC/SoH Estimator for a LiFePO4 Battery Cell. In Proceedings of the IEEE EUROCON 2015, Salamanca, Spain, 8–11 September 2015; pp. 397–402. [Google Scholar] [CrossRef]
- Rao, G.P.; Unbehauen, H. Identification of Continuous-Time Systems; IEE Proceedings Control Theory Applications; Springer: Berlin/Heidelberg, Germany, 2006; Volume 153, pp. 185–220. [Google Scholar] [CrossRef]
- Roscher, M.A.; Sauer, D.U. Dynamic electric behavior and open-circuit-voltage modeling of LiFePO4-based lithium-ion secondary batteries. J. Power Sources 2011, 196, 331–336. [Google Scholar] [CrossRef]
- Naslin, P. Essentials of Optimal Control; Illife Books Ltd.: London, UK, 1968. [Google Scholar]
- Schröder, D. Elektrische Antriebe—Regelung von Antriebssystemen, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Unbehauen, H.; Rao, G.P. Identification of Continuous Systems; North Holland: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Isermann, R. Digital Control Systems 1; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]


| Parameter | Value |
|---|---|
| Battery model series resistance Rb | 0.7 mΩ |
| Battery model polarization resistance Rp | 1.0 mΩ |
| Battery model polarization time constant τp | 24 s |
| Battery model open-circuit voltage Uoc | 3.2 V |
| Parameter | Value |
|---|---|
| Inner current control-loop lag Tei | 20 ms |
| Current/voltage sensor time constant Tfm | 5 ms |
| LiFePO4 battery cell charge capacity Qb | 100 Ah |
| Battery charging current upper limit Imax | 70 A |
| Battery charging turn-off current Imin | 5 A |
| Initial battery state of charge ξ0 | 20 % |
| Target battery state of charge ξR | 100 % |
| CCCV-VL battery limit voltage value ublim | 3.4 V |
| CCCV-OCV open-circuit voltage target value UocR | 3.4 V |
| CCCV-OCV battery limit voltage value ublim | 3.5 V |
| Parameter | Value |
|---|---|
| Voltage-limiting PI controller proportional gain Kcl | 157.8 |
| Voltage-limiting PI controller integral time constant Tcl | 5.4 ms |
| OCV PI controller proportional gain Kcu | 16,325 |
| OCV PI controller integral time constant Tcu | 44.1 s |
| SRAM parameter estimator gain K1 | 5·10−3 |
| SRAM parameter estimator gain K2 | 10−6 |
| SRAM parameter estimator gain K3 | 10−6 |
| SRAM parameter estimator gain K4 | 5·10−4 |
| SRAM parameter estimator pre-filtering time constant Tf | 1 s |
| SRAM parameter estimator post-filtering time constant Tpf | 5 s |
| Voltage normalization parameter U0 | 3.2 V |
| Current normalization parameter I0 | 100 A |
| Control strategy sampling period T | 4 ms |
| Charging Method and Reference | Speed-Up vs. Conventional Charging |
|---|---|
| Fuzzy logic charging controller [34] | 13.2% |
| MCC charging with offline optimization [37] | 19.1% to 29.7% |
| MPC with moving horizon estimation [35] | 17.5% |
| GA-based offline optimization [36] | 39.7% |
| MCC charging with LMS estimator of OCV [41] | 39.3% |
| EKF-based SoC estimation plus CCCV (CCCV-SoC) [50] | 25.0% |
| SRAM-based OCV estimation plus CCCV (CCCV-OCV) | 23.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavković, D.; Kasać, J.; Krznar, M.; Cipek, M. Adaptive Constant-Current/Constant-Voltage Charging of a Battery Cell Based on Cell Open-Circuit Voltage Estimation. World Electr. Veh. J. 2023, 14, 155. https://doi.org/10.3390/wevj14060155
Pavković D, Kasać J, Krznar M, Cipek M. Adaptive Constant-Current/Constant-Voltage Charging of a Battery Cell Based on Cell Open-Circuit Voltage Estimation. World Electric Vehicle Journal. 2023; 14(6):155. https://doi.org/10.3390/wevj14060155
Chicago/Turabian StylePavković, Danijel, Josip Kasać, Matija Krznar, and Mihael Cipek. 2023. "Adaptive Constant-Current/Constant-Voltage Charging of a Battery Cell Based on Cell Open-Circuit Voltage Estimation" World Electric Vehicle Journal 14, no. 6: 155. https://doi.org/10.3390/wevj14060155
APA StylePavković, D., Kasać, J., Krznar, M., & Cipek, M. (2023). Adaptive Constant-Current/Constant-Voltage Charging of a Battery Cell Based on Cell Open-Circuit Voltage Estimation. World Electric Vehicle Journal, 14(6), 155. https://doi.org/10.3390/wevj14060155







