Optimal Electric Vehicle Fleet Charging Management with a Frequency Regulation Service
Abstract
1. Introduction
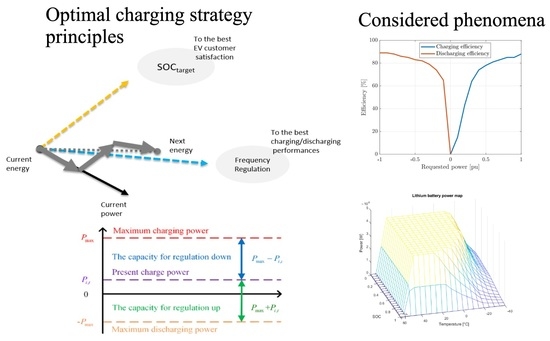
- Maximize the regulatory reserve by using an EV charging algorithm based on preventive actions, replacing the planning problem with one on the fly;
- Avoid the use of hard constraints, as well as reducing the number of decision variables and the number of constraints to reduce computation time and memory usage;
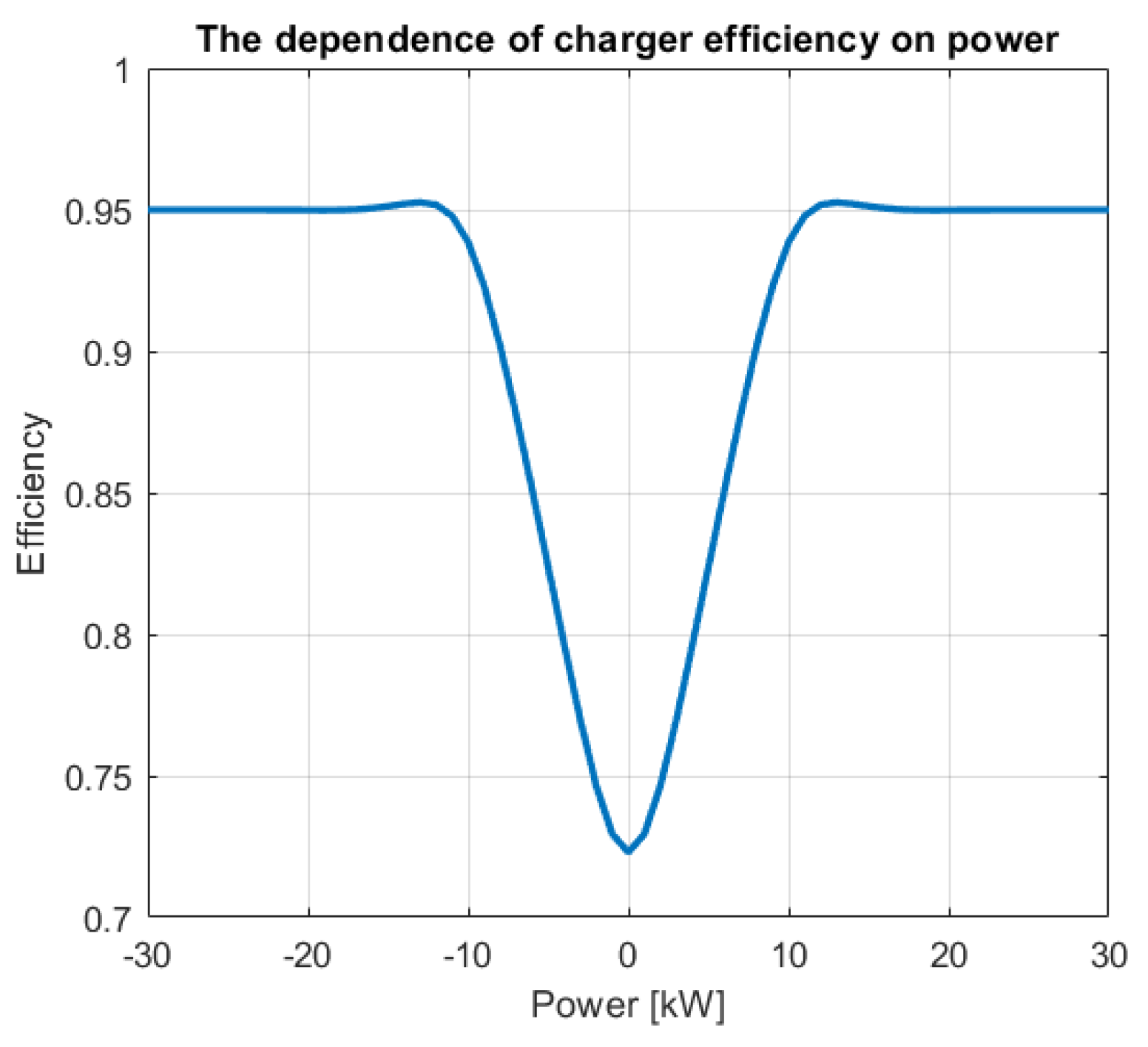
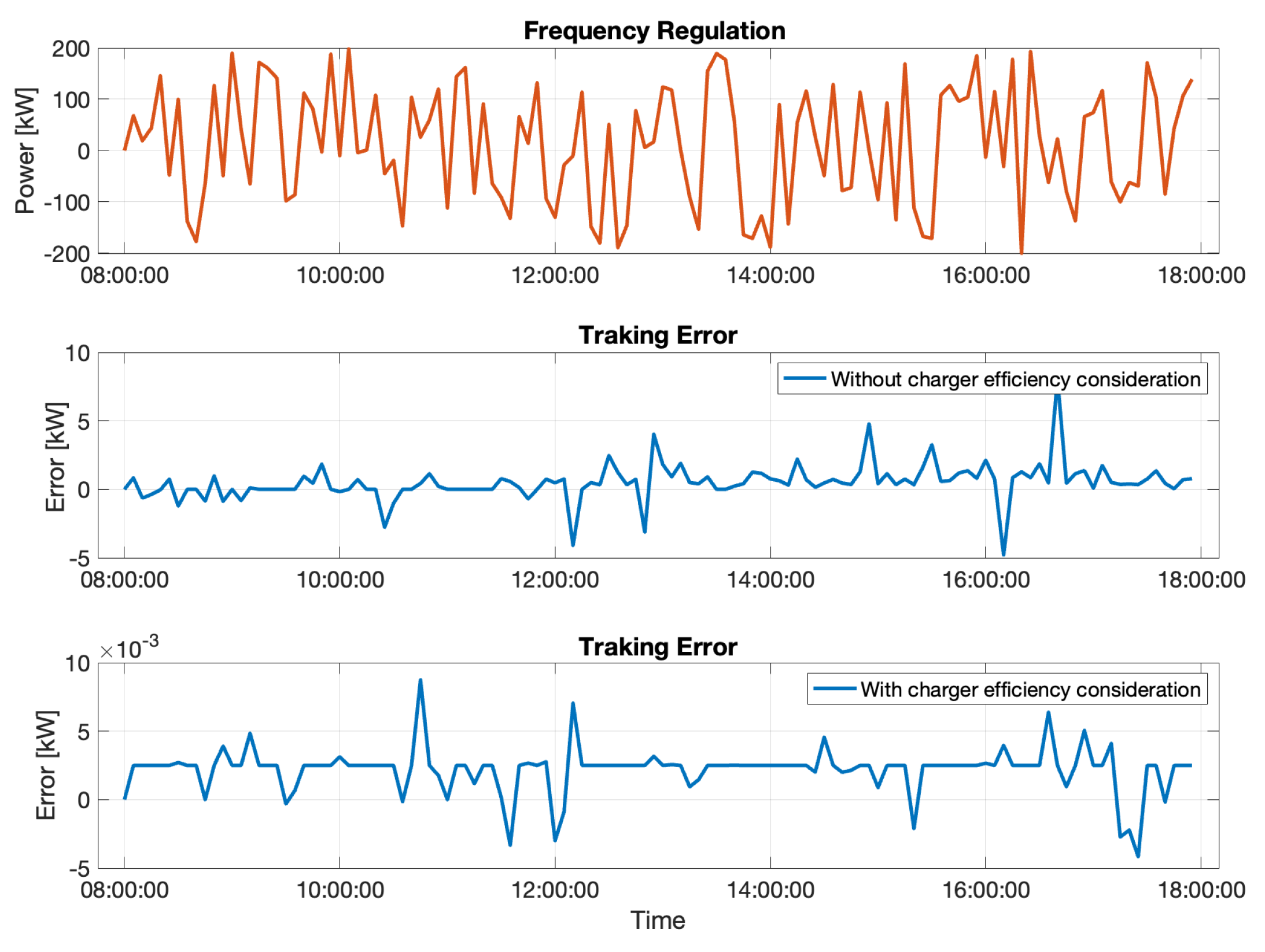
- Take into account the efficiency of the charger and its dependence on power and therefore maximizing charging efficiency;
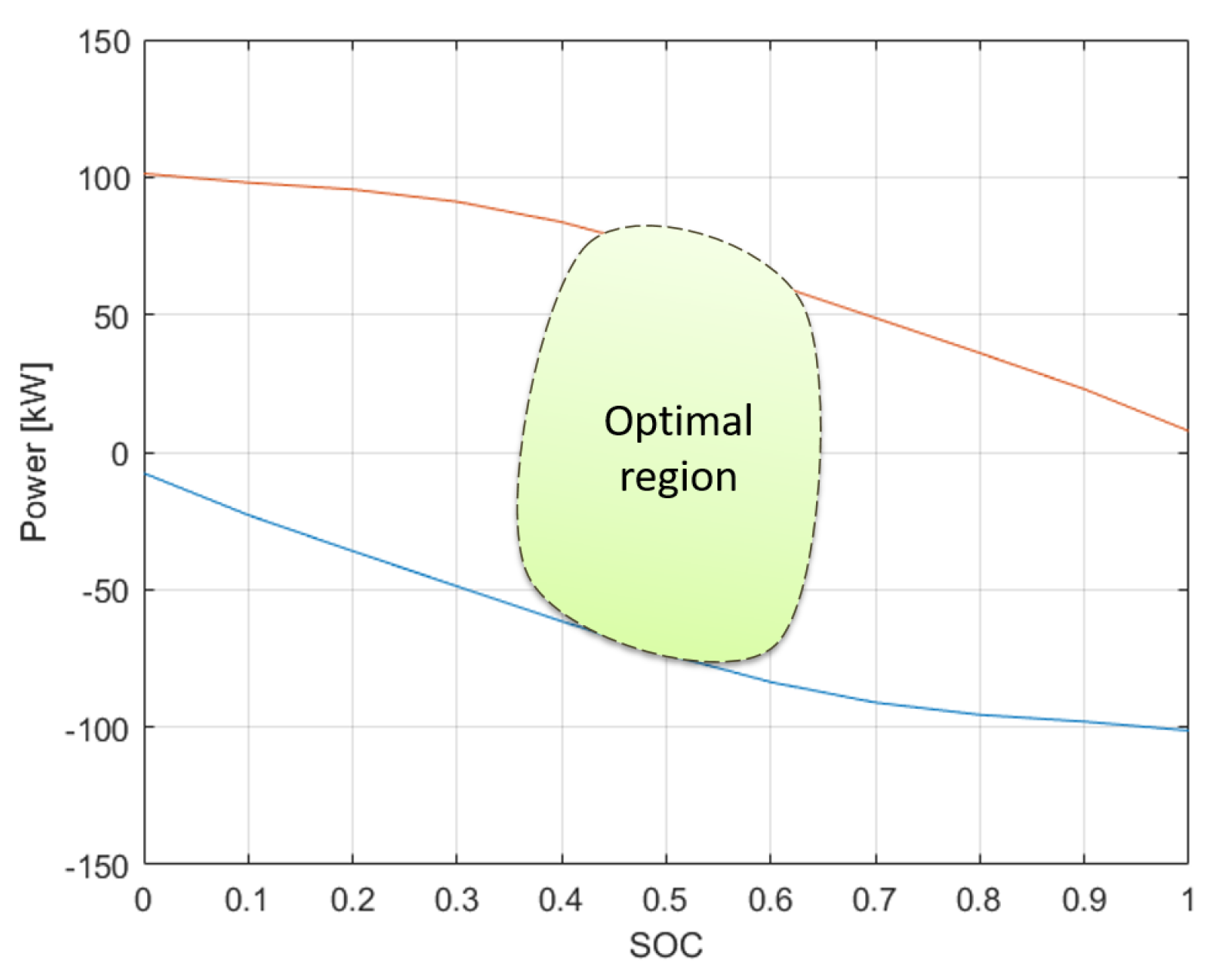
- Take into account the SoC and temperature dependence of regulation capacity and keeping the total regulation capacity in the optimal zone;
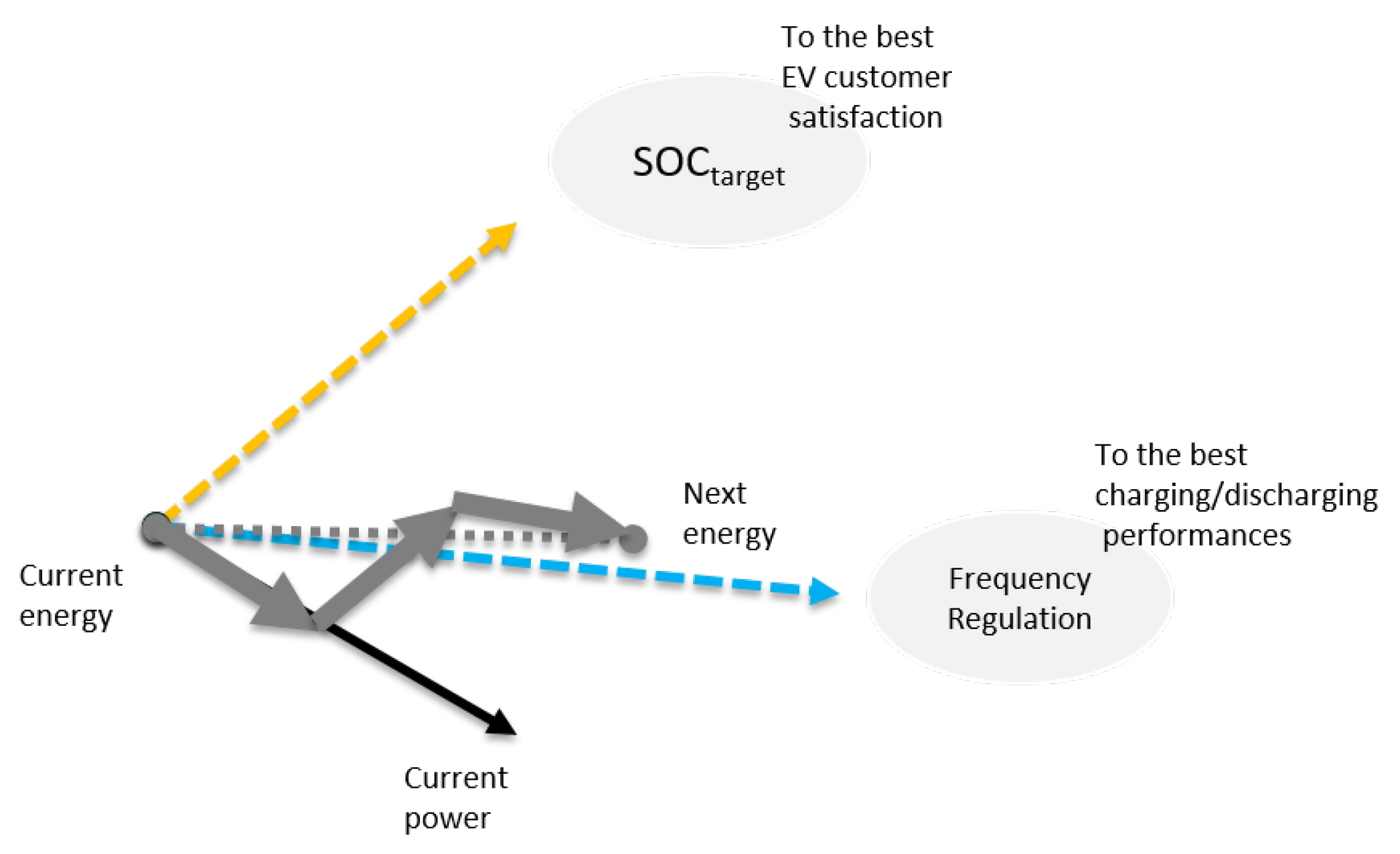
- Control the bi-directional charging of EVs (V2G), taking into account both the power demand of the grid operator and the satisfaction of the SoC target of the EVs’ users.
2. Optimization Problem Modeling
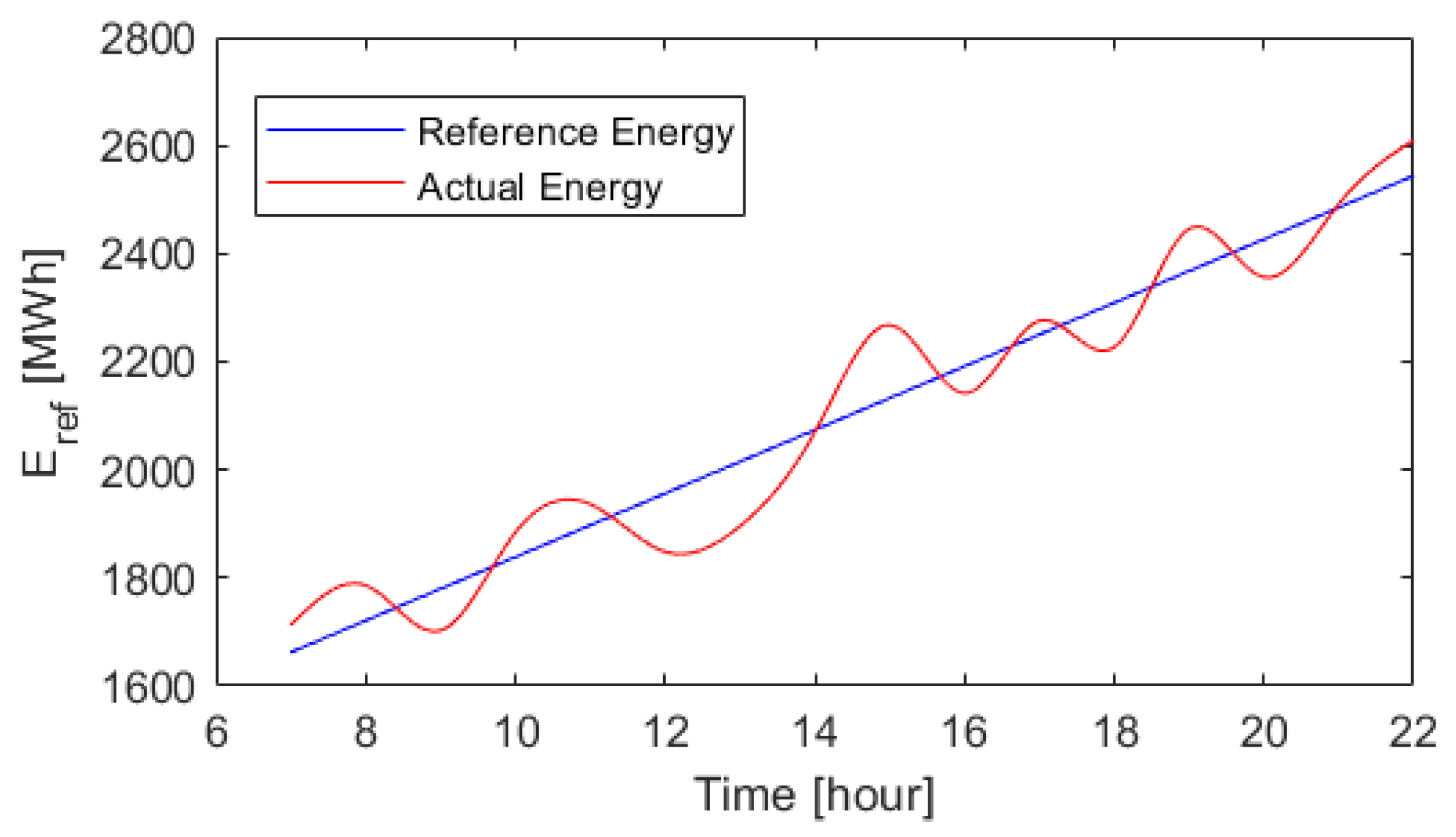
- Case 1 (namely P1): the standard power dispatch problem with a frequency disturbance. In this context, the main goal is to charge EVs, but the idea is to also keep a regulation capability of up and down, i.e., to keep EVs in an optimal region to be able to better face the second case;
- Case 2 (namely P2): the frequency regulation problem with a power request from or to the power grid. The main goal, then, becomes to answer this power demand emerging from the power grid, while trying to consider EVs charging expectations.
- To charge its battery in order to obtain a high SoC to meet the EV owner needs (>0.7);
- To keep the SoC within an optimal range to improve the capability of the fleet to answer a frequency control request (>0.4 and <0.6).
3. Simulations and Results
3.1. Impacts of the Charger Efficiency
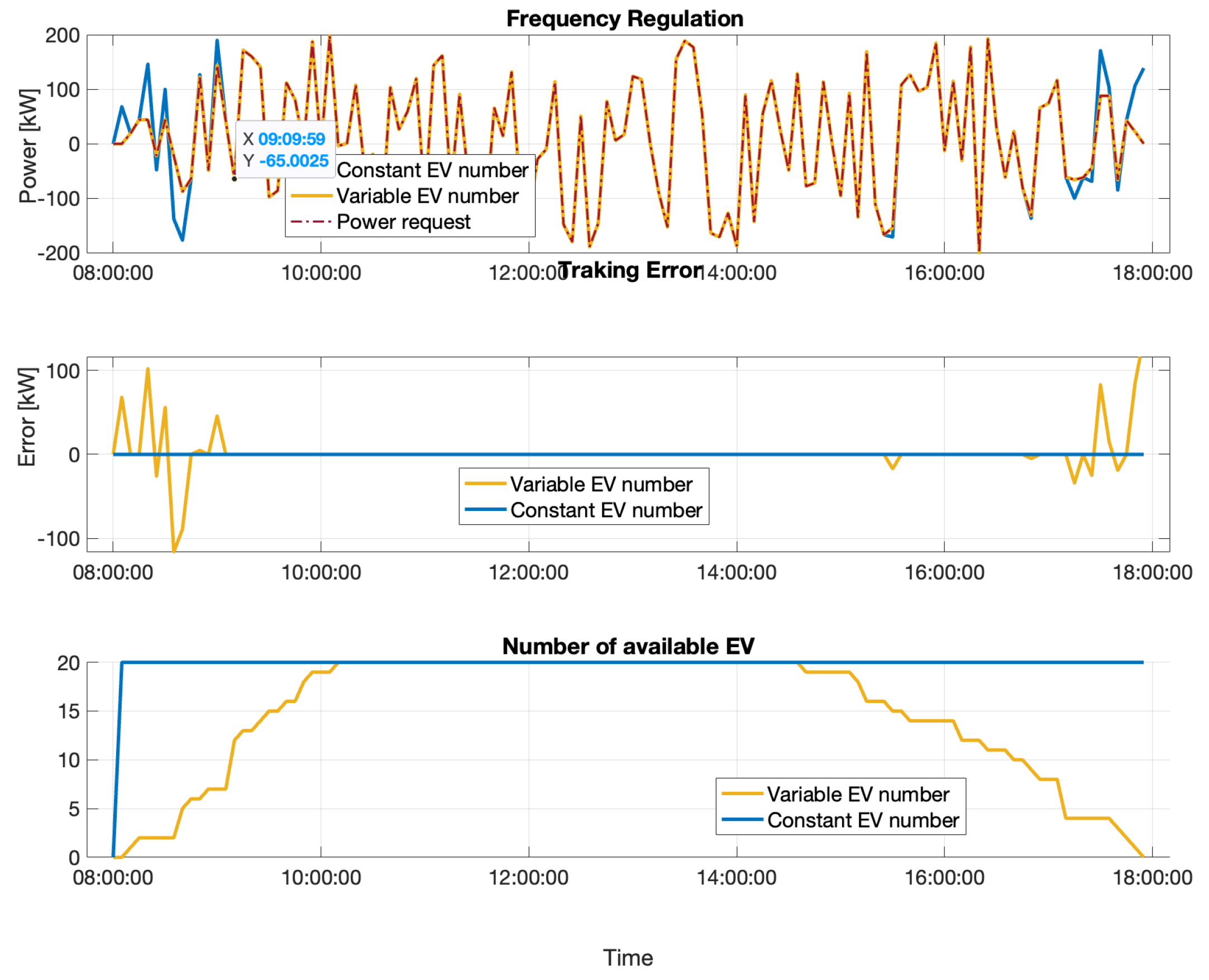
3.2. Impacts of the Number of EVs
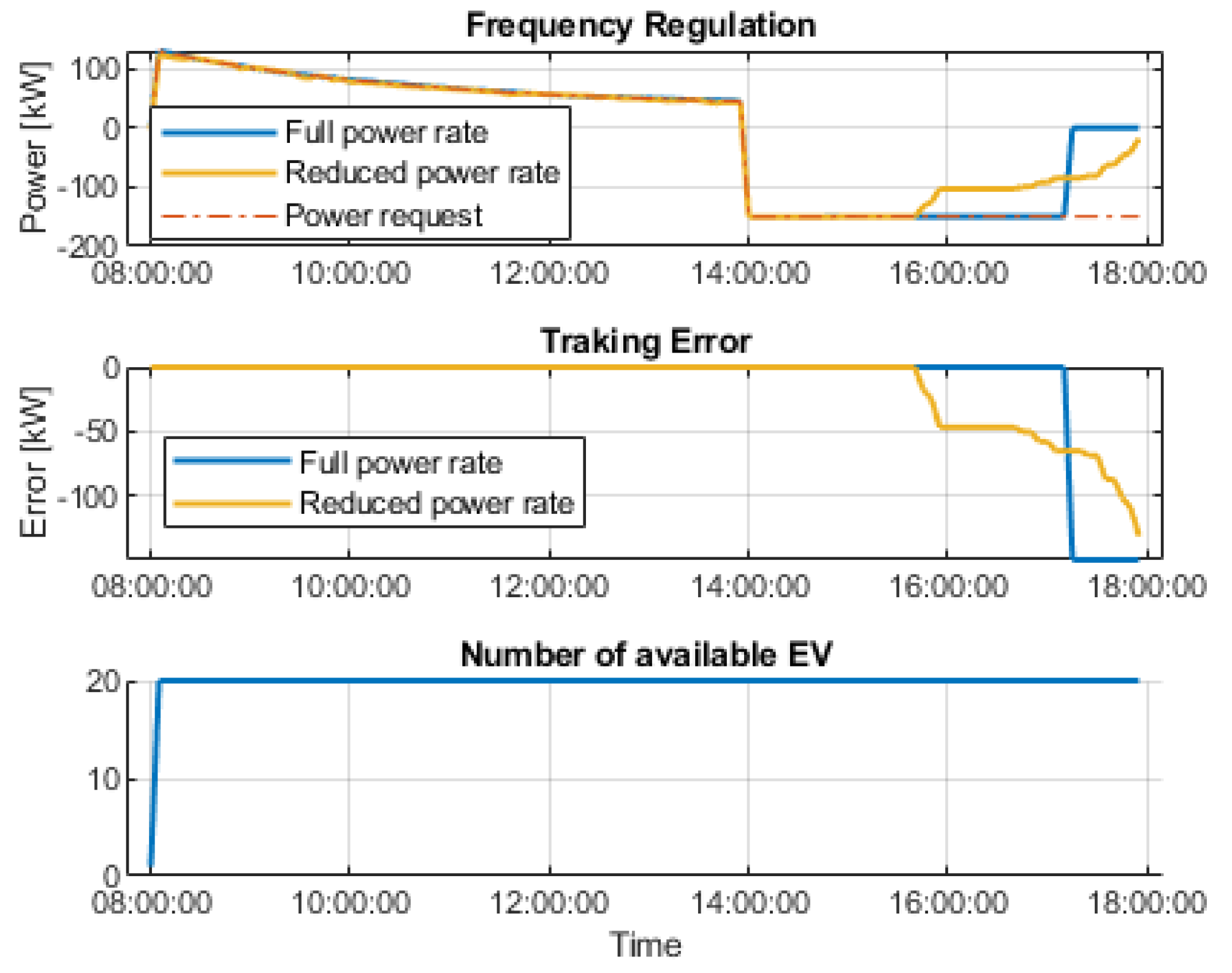
3.3. Impact of Long Frequency Drops and the Maximum Charging Rate
3.4. Discussions about EV Usage in the Frequency Regulation Market
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Weighting factors | |
| Total available energy stored in the EVs | |
| Number of EVs | |
| Charging power of the j-th EV at time i | |
| Sampling time | |
| Energy reference at time i | |
| State of charge of the j-th EV in time step i | |
| Battery capacity of the j-th EV | |
| State of health of the j-th EV’ battery | |
| SoC reference at time i | |
| Power reference at time i | |
| Energy threshold of the charging station | |
| Maximum SoC limit | |
| Remaining energy before reaching | |
| time i | |
| Station opening hours | |
| Power request at time i | |
| Charger efficiency | |
| , | Power upper/lower bound of the j-th EV during time step i |
| ] | State of the j-th EV at time i |
| , | Binary variables depending on the SoC of the j-th EV at time i |
| , | Maximal authorized charging/discharging rate for j-th EV at time step i |
| , | Maximum charging/discharging power of the charging point of the j-th EV |
| , | Maximum power of the j-th charger in charging or discharging mode |
| , | Maximum accepted/delivered battery’s power of the j-th EV at time i |
| depending on the SoC and the battery’s temperature | |
| Maximum transformer power of the charging station | |
| Mass of the j-th EV battery | |
| Specific heat coefficient of the j-th EV battery | |
| Temperature of the j-th EV battery at time i | |
| Power dissipated by the joule effect of the j-th EV battery at time i | |
| Power heat transfer between the battery and the outside of the j-th EV battery | |
| at time i | |
| Thermal factor depending on the thermal inertia of the j-th EV battery | |
| Outside temperature at time i | |
| Heat convection coefficient between the j-th EV battery and outside |
References
- Amamra, S.A.; Marco, J. Vehicle-to-Grid Aggregator to Support Power Grid and Reduce Electric Vehicle Charging Cost. IEEE Access 2019, 7, 178528–178538. [Google Scholar] [CrossRef]
- Tchagang, A.; Yoo, Y. V2B/V2G on Energy Cost and Battery Degradation under Different Driving Scenarios, Peak Shaving, and Frequency Regulations. World Electr. Veh. J. 2020, 11, 14. [Google Scholar] [CrossRef]
- Calearo, L.; Marinelli, M. Profitability of frequency regulation by electric vehicles in Denmark and Japan considering battery degradation costs. World Electr. Veh. J. 2020, 11, 48. [Google Scholar] [CrossRef]
- Liu, H.; Hu, Z.; Song, Y.; Lin, J. Decentralized vehicle-to-grid control for primary frequency regulation considering charging demands. IEEE Trans. Power Syst. 2013, 28, 3480–3489. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, C.; Gu, L. Decentralized primary frequency regulation control strategy for vehicle-to-grid. In Proceedings of the 2016 3rd International Conference on Systems and Informatics (ICSAI), Shanghai, China, 19–21 November 2016; pp. 217–222. [Google Scholar]
- Liu, H.; Qi, J.; Wang, J.; Li, P.; Li, C.; Wei, H. EV dispatch control for supplementary frequency regulation considering the expectation of EV owners. IEEE Trans. Smart Grid 2018, 9, 3763–3772. [Google Scholar] [CrossRef]
- Izadkhast, S.; Garcia-Gonzalez, P.; Frías, P. An aggregate model of plug-in electric vehicles for primary frequency control. IEEE Trans. Power Syst. 2015, 30, 1475–1482. [Google Scholar] [CrossRef]
- Liu, H.; Huang, K.; Yang, Y.; Wei, H.; Ma, S. Real-time vehicle-to-grid control for frequency regulation with high frequency regulating signal. Prot. Control. Mod. Power Syst. 2018, 3, 13. [Google Scholar] [CrossRef]
- Iqbal, S.; Habib, S.; Khan, N.H.; Ali, M.; Aurangzeb, M.; Ahmed, E.M. Electric Vehicles Aggregation for Frequency Control of Microgrid under Various Operation Conditions Using an Optimal Coordinated Strategy. Sustainability 2022, 14, 3108. [Google Scholar] [CrossRef]
- Sahu, P.C.; Prusty, R.C.; Panda, S. Frequency regulation of an electric vehicle-operated micro-grid under WOA-tuned fuzzy cascade controller. Int. J. Ambient. Energy 2022, 43, 2900–2911. [Google Scholar] [CrossRef]
- Hajiakbari Fini, M.; Golshan, M.E.H.; Martí, J.R. Coordinated Participation of Electric Vehicles and Generating Units in Primary Frequency Control in the Presence of Renewables. IEEE Trans. Transp. Electrif. 2023, 9, 130–141. [Google Scholar] [CrossRef]
- Yao, E.; Wong, V.W.S.; Schober, R. Robust Frequency Regulation Capacity Scheduling Algorithm for Electric Vehicles. IEEE Trans. Smart Grid 2017, 8, 984–997. [Google Scholar] [CrossRef]
- Wenzel, G.; Negrete-Pincetic, M.; Olivares, D.E.; MacDonald, J.; Callaway, D.S. Real-time charging strategies for an electric vehicle aggregator to provide ancillary services. IEEE Trans. Smart Grid 2018, 9, 5141–5151. [Google Scholar] [CrossRef]
- Liu, H.; Huang, K.; Wang, N.; Qi, J.; Wu, Q.; Ma, S.; Li, C. Optimal dispatch for participation of electric vehicles in frequency regulation based on area control error and area regulation requirement. Appl. Energy 2019, 240, 46–55. [Google Scholar] [CrossRef]
- Kaur, K.; Kumar, N.; Singh, M. Coordinated power control of electric vehicles for grid frequency support: MILP-based hierarchical control design. IEEE Trans. Smart Grid 2019, 10, 3364–3373. [Google Scholar] [CrossRef]
- Kaur, K.; Singh, M.; Kumar, N. Multiobjective optimization for frequency support using electric vehicles: An aggregator-based hierarchical control mechanism. IEEE Syst. J. 2019, 13, 771–782. [Google Scholar] [CrossRef]
- Jeong, H.; Jeong, M.; Lee, S. Vehicle-To-Grid Based Frequency Regulation Method In An Isolated Microgrid Considering Charging Requests Of Electric Vehicles. In Proceedings of the 2019 International Conference and Exhibition on Electricity Distribution (CIRED), Madrid, Spain, 3–6 June 2019; pp. 1–5. [Google Scholar]
- Wang, M.; Mu, Y.; Li, F.; Jia, H.; Li, X.; Shi, Q.; Jiang, T. State Space Model of Aggregated Electric Vehicles for Frequency Regulation. IEEE Trans. Smart Grid 2019, 11, 981–994. [Google Scholar] [CrossRef]
- Khooban, M.H.; Gheisarnejad, M. A Novel Deep Reinforcement Learning Controller Based Type-II Fuzzy System: Frequency Regulation in Microgrids. IEEE Trans. Emerg. Top. Comput. Intell. 2020, 5, 689–699. [Google Scholar] [CrossRef]
- Dahmane, Y.; Ghanes, M.; Chenouard, R.; Alvarado-Ruiz, M. Coordinated Charging of Large Electric Vehicle Fleet in a Charging Station With Limited Transformer Power. In Proceedings of the 2020 4th IEEE Conference on Control Technology and Applications (IEEE CCTA), Montreal, QC, Canada, 24–26 August 2020; pp. 1–6. [Google Scholar]
- Dahmane, Y.; Ghanes, M.; Chenouard, R.; Alvarado-Ruiz, M. Decentralized Control of Electric Vehicle Smart Charging for Cost Minimization Considering Temperature and Battery Health. In Proceedings of the 2019 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Beijing, China, 21–23 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Ziras, C.; Zecchino, A.; Marinelli, M. Response accuracy and tracking errors with decentralized control of commercial v2g chargers. In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; pp. 1–7. [Google Scholar]
- Ye, X.; Ji, T.; Li, M.; Wu, Q. Optimal control strategy for plug-in electric vehicles based on reinforcement learning in distribution networks. In Proceedings of the 2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, 6–8 November 2018; pp. 1706–1711. [Google Scholar]
- Zeller, M.; Blake, S.; Cedillos, D.; Gertz, A.; Boyd, E. Flexibility within the Electrical Systems through Demand Side Response: Introduction to Balancing Products and Markets in Germany, France, and the UK; Technical Report 3027514; European Commission: Brussels, Belgium, 2017.
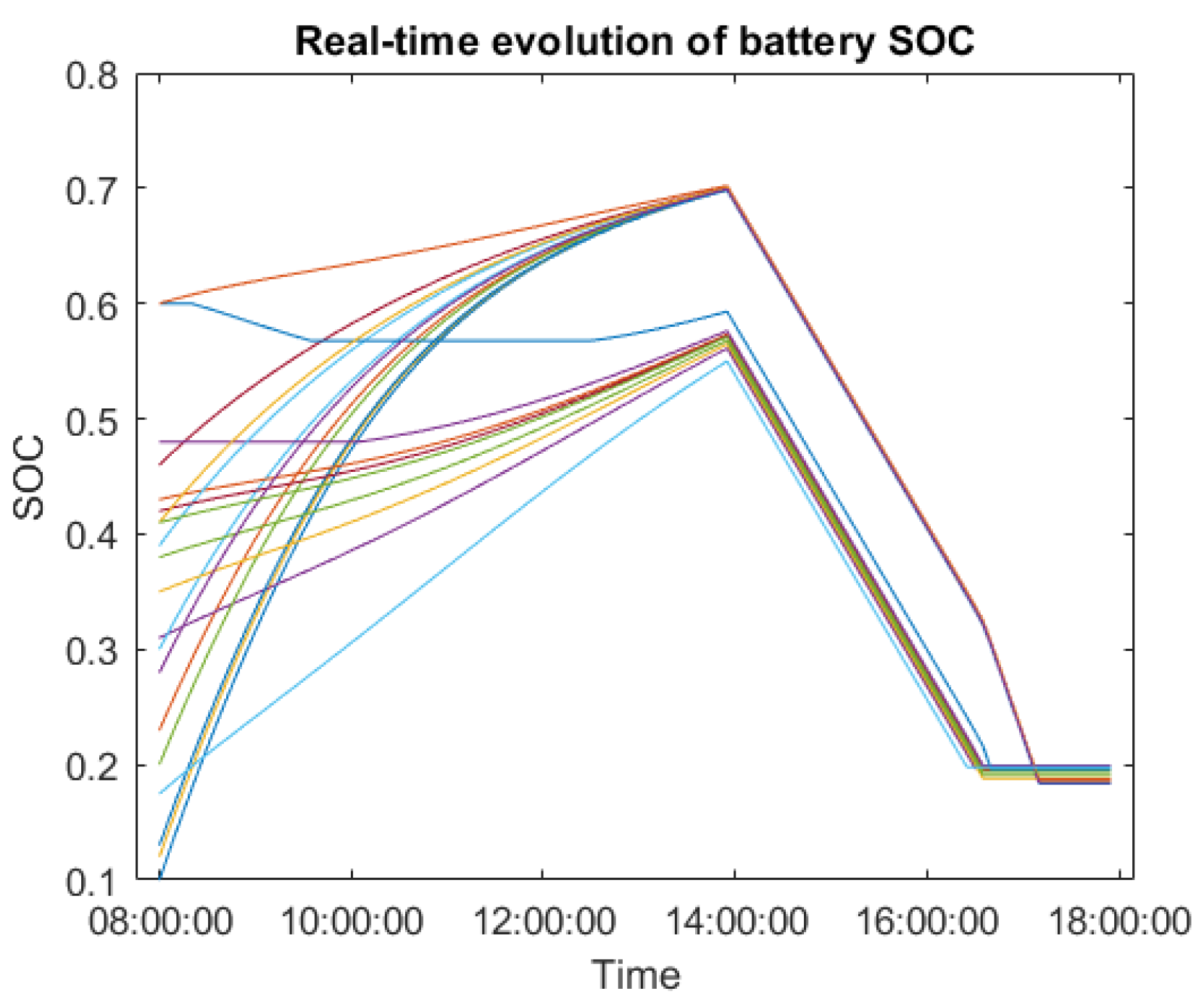
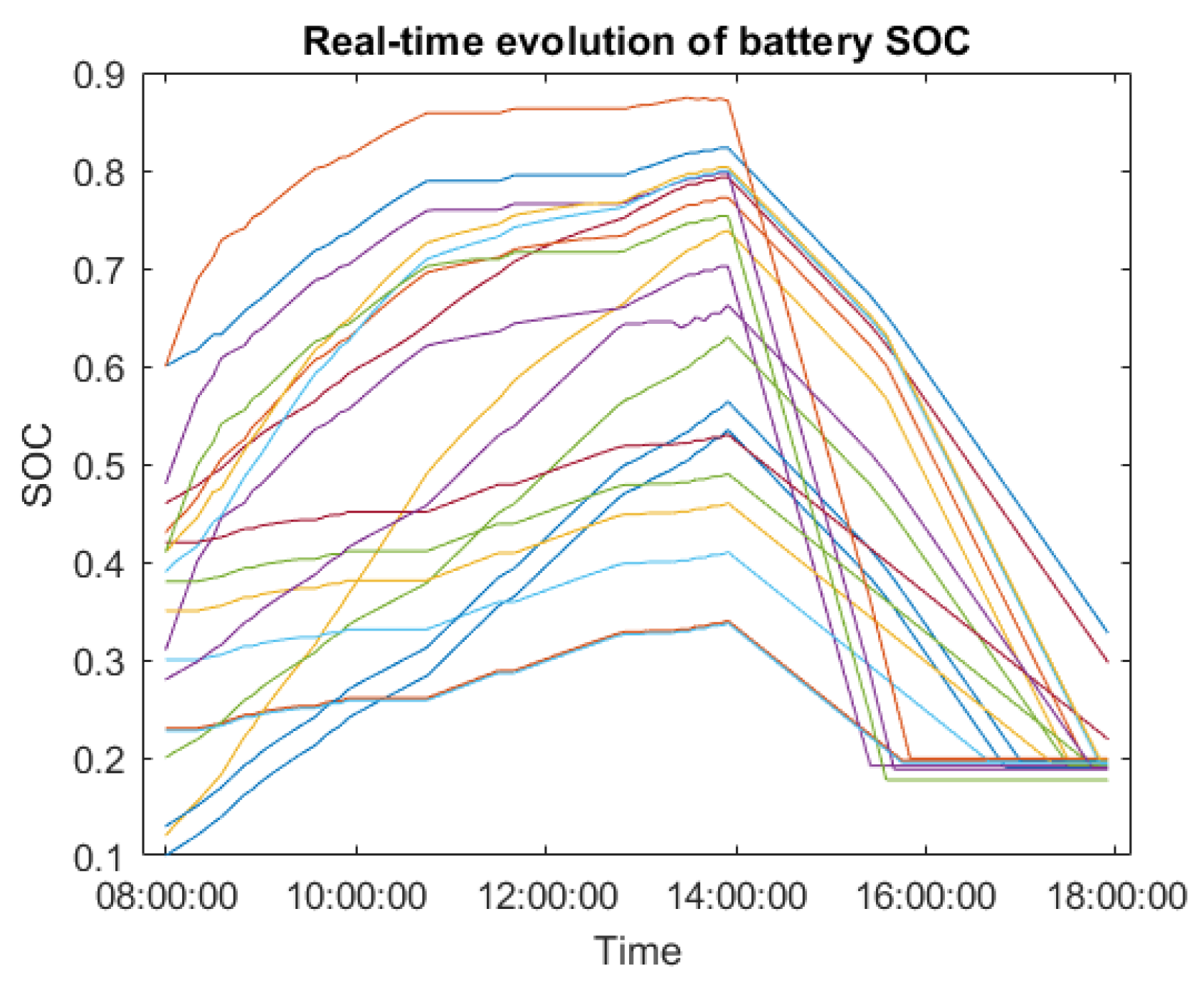
| Parameters | Value |
|---|---|
| Sampling time | 5 min |
| Maximum number of EVs | 20 |
| Battery capacity | 60 kWh |
| Starting SoC | |
| Desired SoC | |
| Maximum/minimum SoC | 0.9/0.2 |
| Parameters | Time (h) |
|---|---|
| Arrival times | 8 h |
| Departure times | 18 h |
| Parameters | Time (h) |
|---|---|
| Arrival times | |
| Departure times |
| Primary Reserve | Secondary Reserve | |
|---|---|---|
| Dynamic of activation | within 15 s and of the reserve enabled within 30 s | of the reserve activated within 5 min |
| Duration of activation | Maximum of 15 min | unlimited during the duration of the contract |
| Minimum power | 1 MW | 5 MW |
| Power direction | Negative AND Positive | Negative OR Positive |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dahmane, Y.; Chenouard, R.; Ghanes, M.; Alvarado Ruiz, M. Optimal Electric Vehicle Fleet Charging Management with a Frequency Regulation Service. World Electr. Veh. J. 2023, 14, 152. https://doi.org/10.3390/wevj14060152
Dahmane Y, Chenouard R, Ghanes M, Alvarado Ruiz M. Optimal Electric Vehicle Fleet Charging Management with a Frequency Regulation Service. World Electric Vehicle Journal. 2023; 14(6):152. https://doi.org/10.3390/wevj14060152
Chicago/Turabian StyleDahmane, Yassir, Raphaël Chenouard, Malek Ghanes, and Mario Alvarado Ruiz. 2023. "Optimal Electric Vehicle Fleet Charging Management with a Frequency Regulation Service" World Electric Vehicle Journal 14, no. 6: 152. https://doi.org/10.3390/wevj14060152
APA StyleDahmane, Y., Chenouard, R., Ghanes, M., & Alvarado Ruiz, M. (2023). Optimal Electric Vehicle Fleet Charging Management with a Frequency Regulation Service. World Electric Vehicle Journal, 14(6), 152. https://doi.org/10.3390/wevj14060152