Robust H∞ Output Feedback Trajectory Tracking Control for Steer-by-Wire Four-Wheel Independent Actuated Electric Vehicles
Abstract
1. Introduction
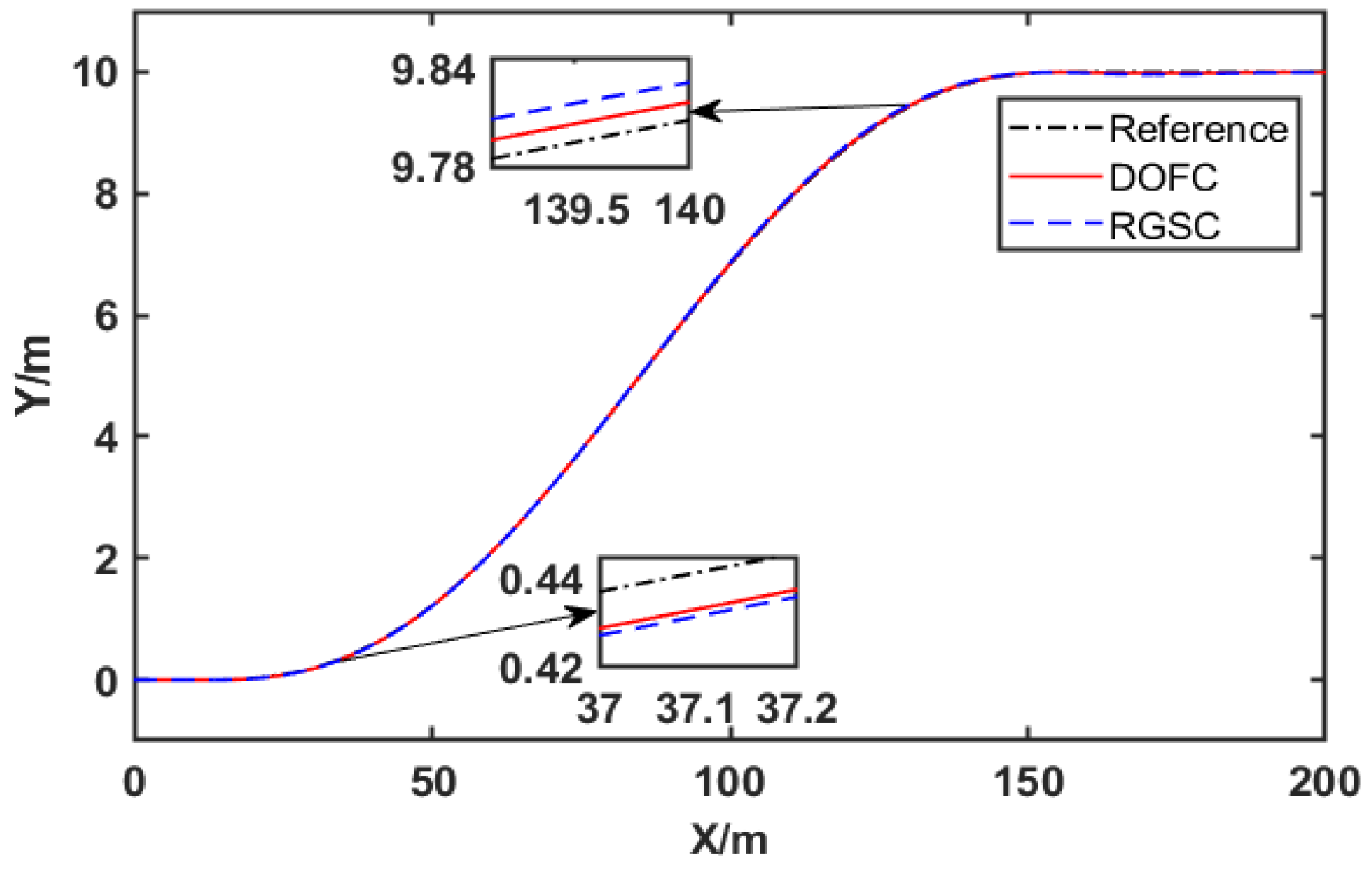
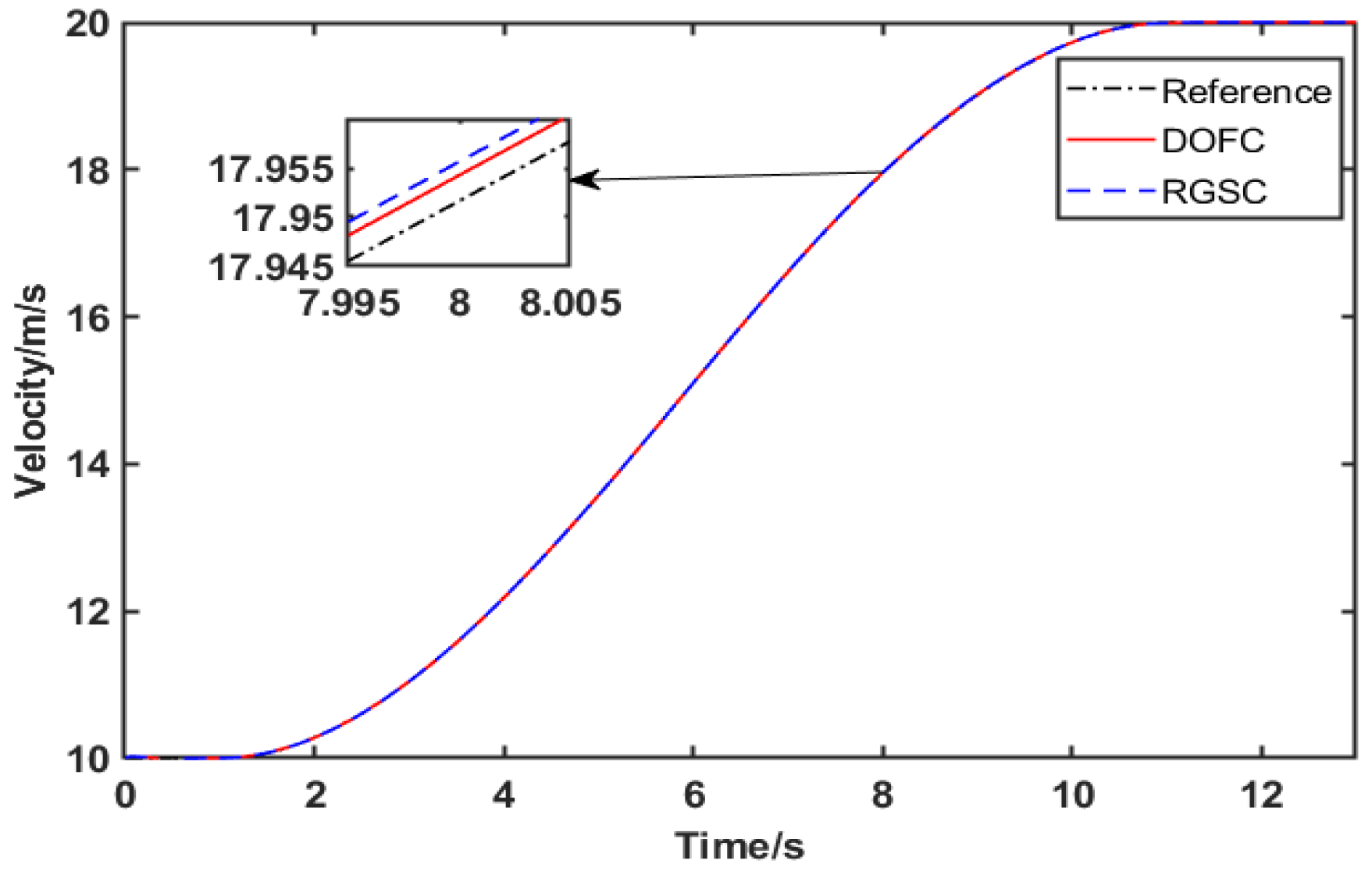
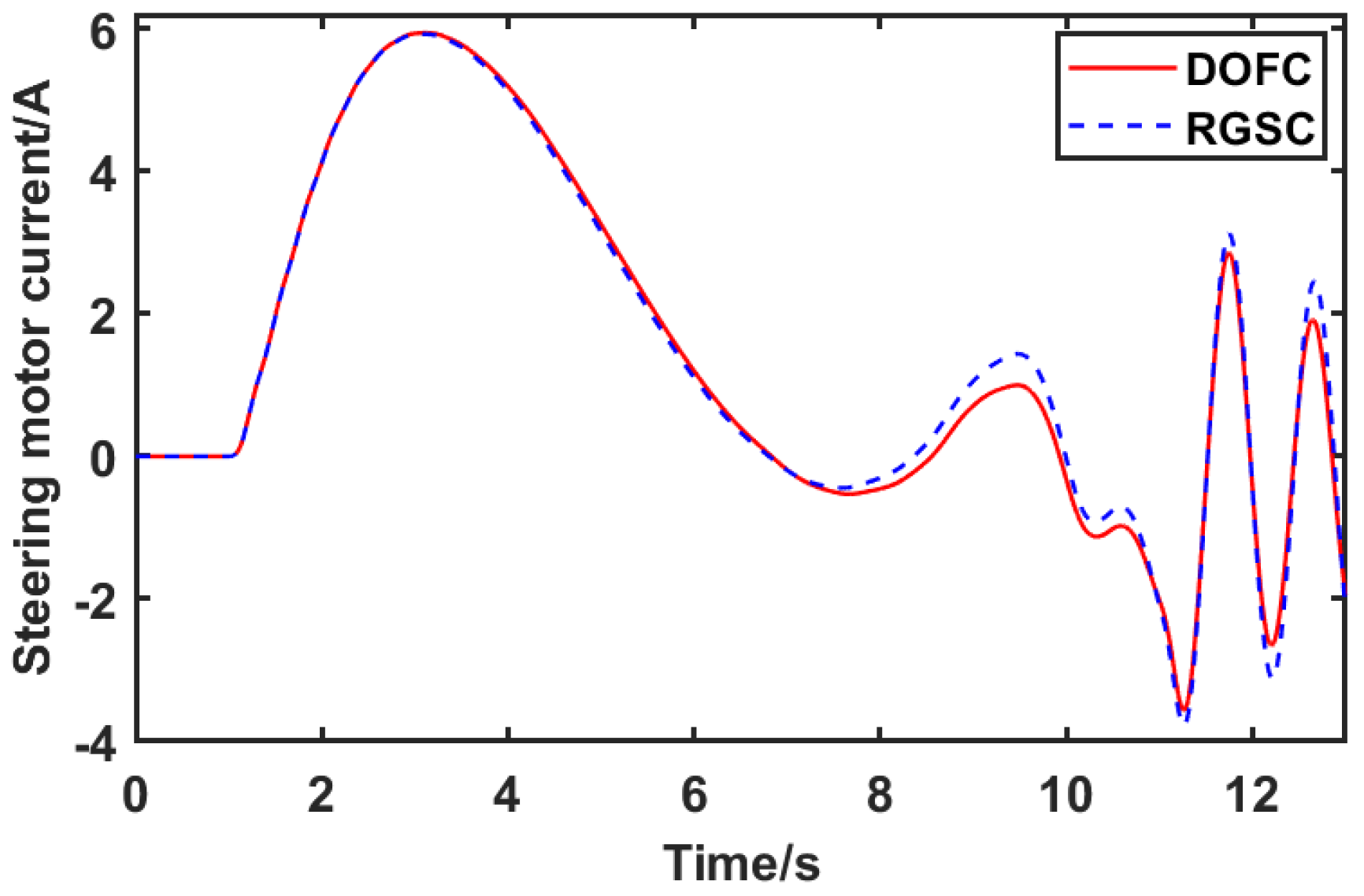
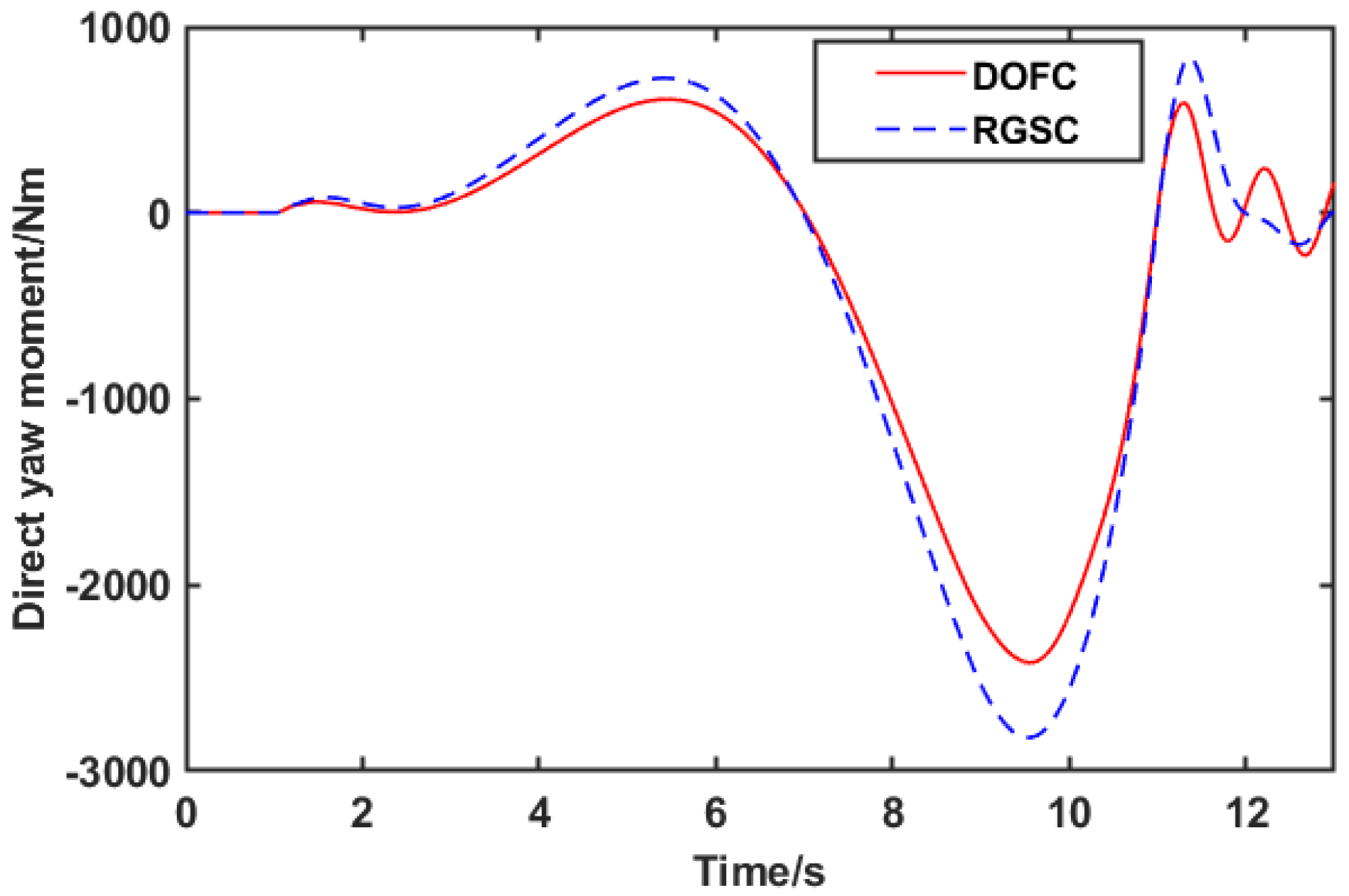
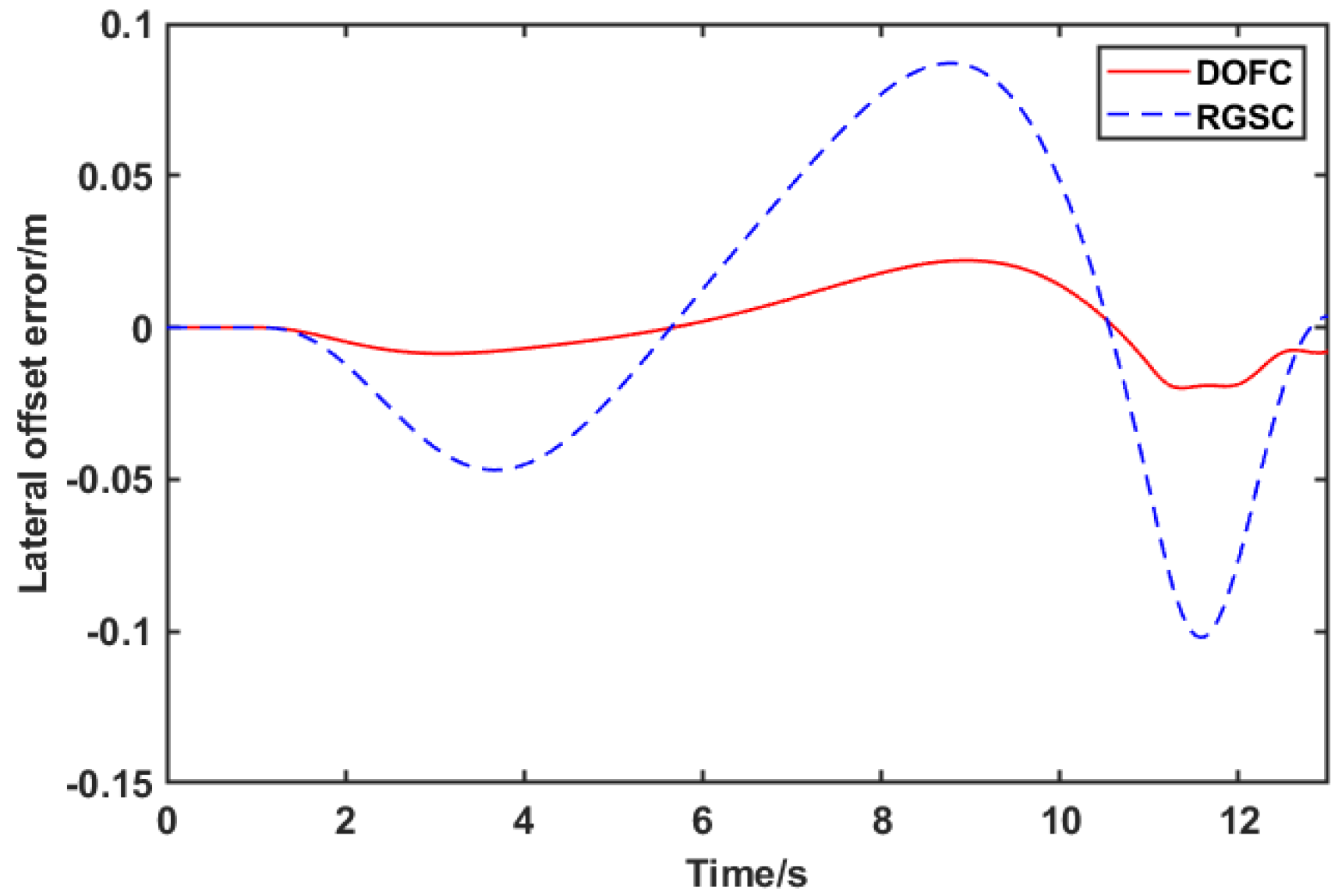
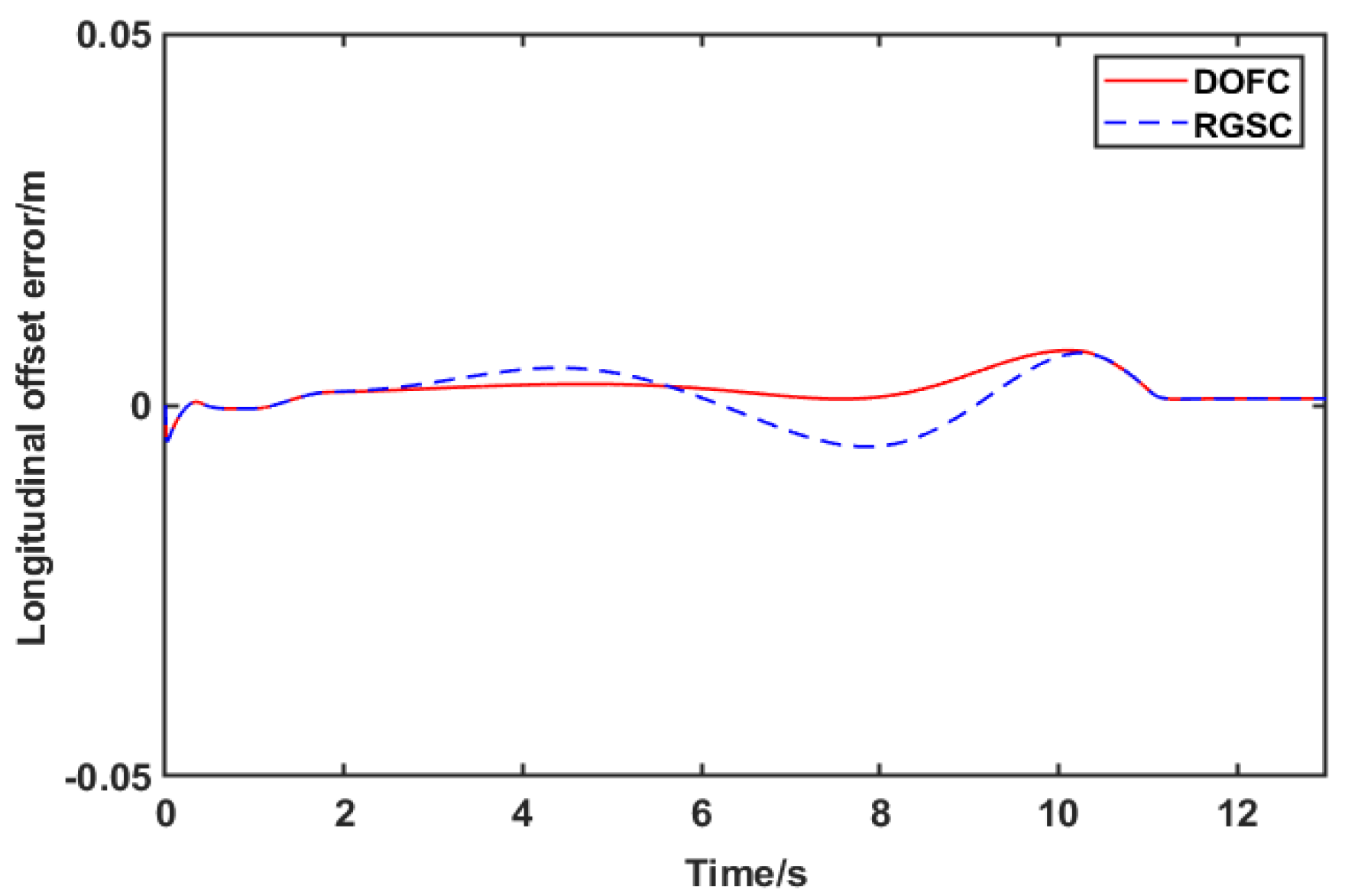
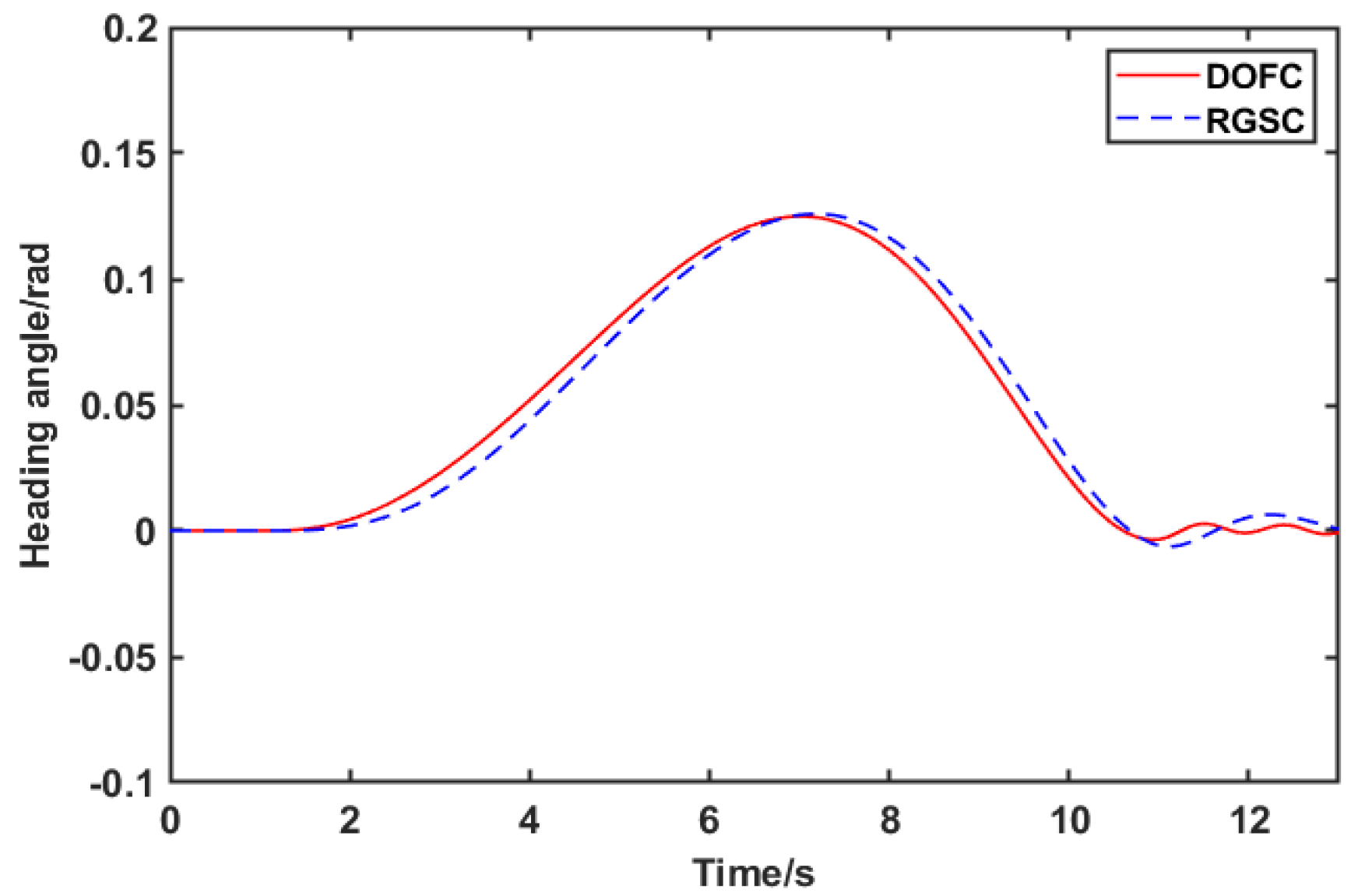
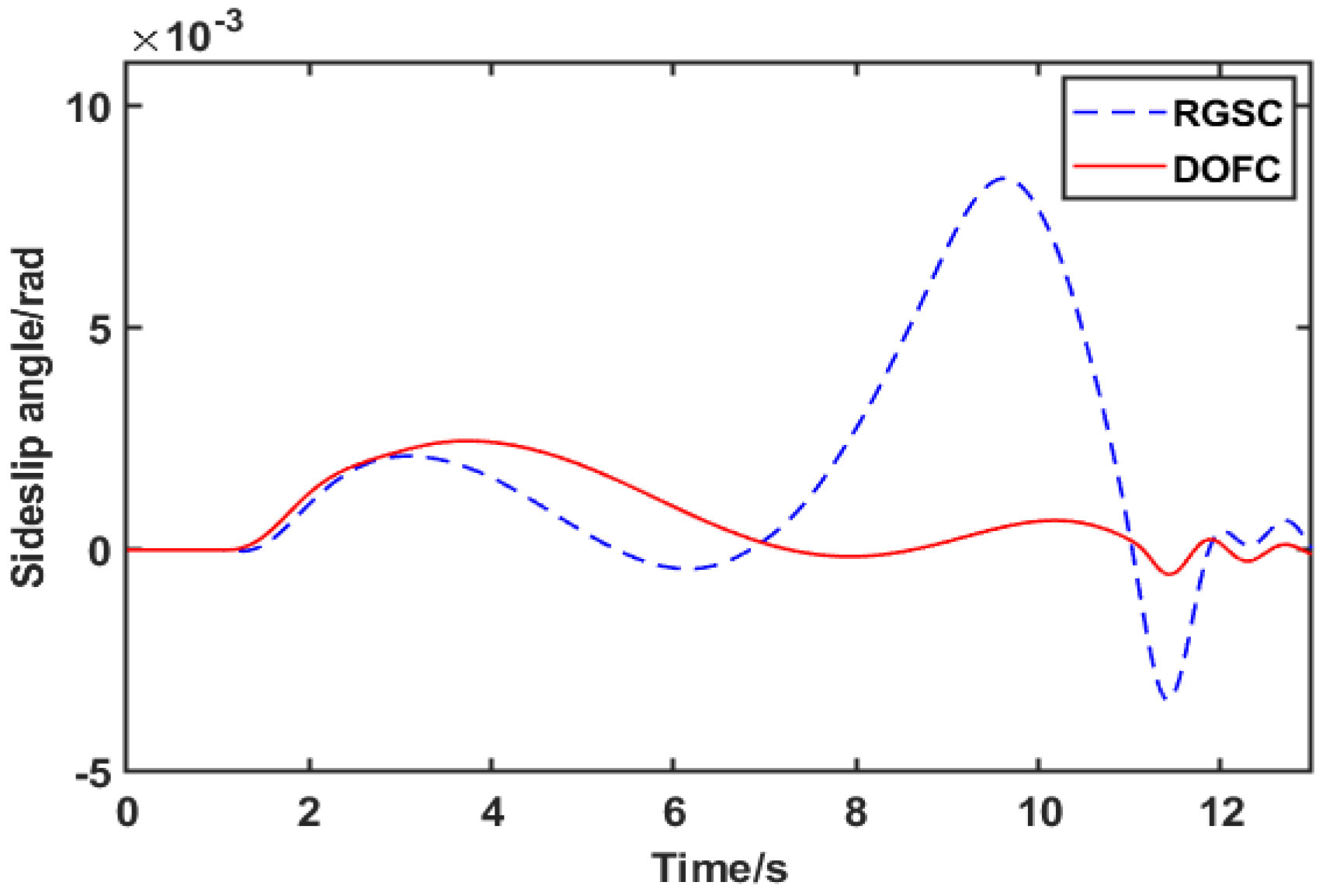
- A trajectory tracking control method with integrated AFS and DYC is proposed for the steer-by-wire FWIA EV, involving the dynamic of steer-by-wire, which is more closely related to the control actuation of the steer-by-wire FWIA EV in reality. Compared with the robust gain-scheduling control (RGSC) strategy not considering the dynamic of the steer-by-wire system, the proposed control strategy can guarantee higher tracking accuracy and better comfort.
- In the proposed integrated control framework, a polyhedral LPV model with eight vertices is established for all the states of the steer-by-wire FWIA EV by considering the time-varying longitudinal velocity and selecting , and as scheduling parameters.
- A robust dynamic output feedback controller without using the vehicle sideslip angle is designed by solving the linear matrix inequalities integrating robust stability, performance, and actuator constraint, which meets the stability and maneuverability, tracking accuracy, and driving safety requirements in the trajectory tracking process.
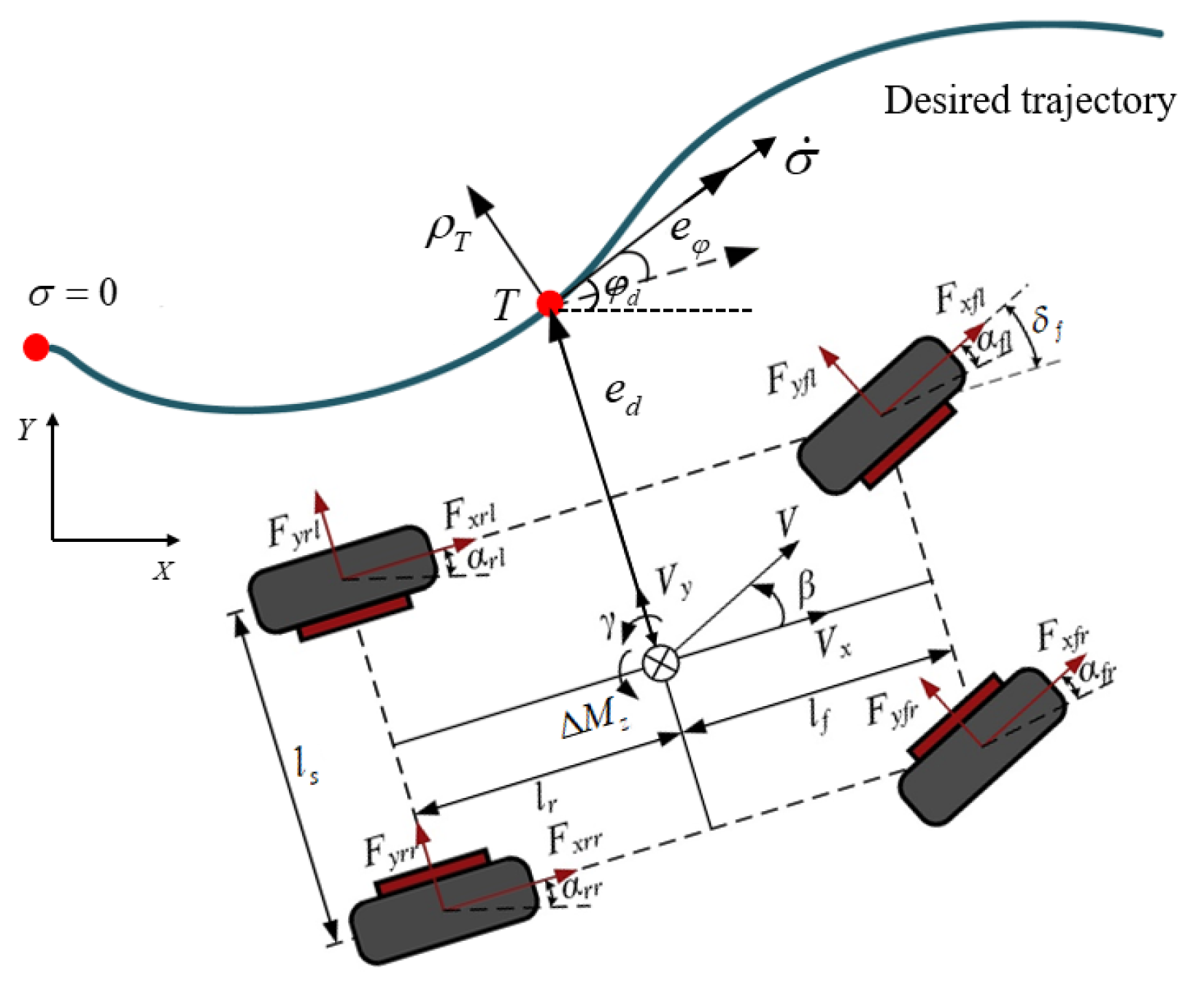
2. System Modeling and Problem Statement
2.1. System Modeling Considering Dynamic Characteristics of Steer-by-Wire
2.2. Polytopic Model Establishment for System Uncertainty
2.3. Control Problem Formulation
3. Robust Output Feedback Trajectory Tracking Control
4. Simulation Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, R.; Zhang, H.; Wang, J. Linear parameter-varying controller design for four-wheel independently actuated electric ground vehicles with active steering systems. IEEE Trans. Control Syst. Technol. 2013, 22, 1281–1296. [Google Scholar]
- Chen, T.; Cai, Y.; Chen, L.; Xu, X.; Sun, X. Trajectory tracking control of steer-by-wire autonomous ground vehicle considering the complete failure of vehicle steering motor. Simul. Model. Pract. Theory 2020, 109, 102235. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, H.; Wang, J.; Yan, F.; Chen, N. Robust lateral motion control of four-wheel independently actuated electric vehicles with tire force saturation consideration. J. Frankl. Inst. Eng. Appl. Math. 2015, 352, 645–668. [Google Scholar] [CrossRef]
- Guo, J.; Wang, J.; Luo, Y.; Li, K. Robust lateral control of autonomous four-wheel independent drive electric vehicles considering the roll effects and actuator faults. Mech. Syst. Signal Process. 2020, 143, 106773. [Google Scholar] [CrossRef]
- Zhang, W. A robust lateral tracking control strategy for autonomous driving vehicles. Mech. Syst. Signal Process. 2021, 150, 107238. [Google Scholar] [CrossRef]
- Shi, K.; Yuan, X.; Liu, L. Model predictive controller-based multi-model control system for longitudinal stability of distributed drive electric vehicle. ISA Trans. 2018, 72, 44–55. [Google Scholar] [CrossRef]
- Guo, J.; Li, K.; Luo, Y. Coordinated control of autonomous four drive electric wheels for platooning and trajectory tracking using a hierarchical architecture. ASME J. Dyna. Syst. Meas. Control 2015, 137, 100101. [Google Scholar] [CrossRef]
- Guo, J.; Luo, Y.; Li, K. An adaptive hierarchical trajectory following control approach of autonomous four-wheel independent drive electric vehicles. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2482–2492. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, H.; Li, Y. Displacement and force coupling control design for automotive active front steering system. Mech. Syst. Signal Process. 2018, 106, 76–93. [Google Scholar] [CrossRef]
- Zhang, H.; Liang, J.; Jiang, H.; Cai, Y.; Xu, X. Stability research of distributed drive electric vehicle by adaptive direct yaw moment control. IEEE Access 2019, 7, 106225–106237. [Google Scholar] [CrossRef]
- Jin, X.; Yin, G.; Zeng, X.; Chen, J. Robust gain-scheduled output feedback yaw stability control for in-wheel-motor-driven electric vehicles with external yaw-moment. J. Frankl. Inst. Eng. Appl. Math. 2018, 355, 9271–9297. [Google Scholar] [CrossRef]
- Ahmadian, N.; Khosravi, A.; Sarhadi, P. Integrated model reference adaptive control to coordinate active front steering and direct yaw moment control. ISA Trans. 2020, 106, 85–96. [Google Scholar] [CrossRef]
- Cheng, S.; Li, L.; Liu, C.; Wu, X.; Fang, S.N.; Yong, J.W. Robust LMI-based H-Infinite controller integrating AFS and DYC of autonomous vehicles with parametric uncertainties. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 6901–6910. [Google Scholar] [CrossRef]
- Liang, J.; Lu, Y.; Yin, G.; Fang, Z.; Zhuang, W.; Ren, Y.; Xu, L.; Li, Y. A distributed integrated control architecture of AFS and DYC based on MAS for distributed drive electric vehicles. IEEE Trans. Veh. Technol. 2021, 70, 5565–5577. [Google Scholar] [CrossRef]
- Liu, H.; Liu, C.; Han, L.; Xiang, C. Handling and stability integrated control of AFS and DYC for distributed drive electric vehicles based on risk assessment and prediction. IEEE Trans. Intell. Transp. Syst. 2022, 23, 23148–23163. [Google Scholar] [CrossRef]
- Jing, H.; Wang, R.; Wang, J.; Chen, N. Robust H∞ dynamic output-feedback control for four-wheel independently actuated electric ground vehicles through integrated AFS/DYC. J. Frankl. Inst. Eng. Appl. Math. 2018, 355, 9321–9350. [Google Scholar] [CrossRef]
- Ahmadian, N.; Khosravi, A.; Sarhadi, P. Driver assistant yaw stability control via integration of AFS and DYC. Veh. Syst. Dyn. 2022, 60, 1742–1762. [Google Scholar] [CrossRef]
- Zou, S.; Zhao, W. Synchronization and stability control of dual-motor intelligent steer-by-wire vehicle. Mech. Syst. Signal Process. 2020, 145, 106925. [Google Scholar] [CrossRef]
- Hu, C.; Wang, R.; Yan, F.; Chen, N. Output constraint control on path following of four-wheel independently actuated autonomous ground vehicles. IEEE Trans. Veh. Technol. 2015, 65, 4033–4043. [Google Scholar] [CrossRef]
- Guo, J.; Luo, Y.; Li, K.; Dai, Y. Coordinated path-following and direct yaw-moment control of autonomous electric vehicles with sideslip angle estimation. Mech. Syst. Signal Process. 2018, 105, 183–199. [Google Scholar] [CrossRef]
- Guo, J.; Luo, Y.; Li, K. Robust gain-scheduling automatic steering control of unmanned ground vehicles under velocity-varying motion. Veh. Syst. Dyn. 2019, 57, 595–616. [Google Scholar] [CrossRef]
- Peng, H.; Wang, W.; An, Q.; Xiang, C.; Li, L. Path tracking and direct yaw moment coordinated control based on robust MPC with the finite time horizon for autonomous independent-drive vehicles. IEEE Trans. Veh. Technol. 2020, 69, 6053–6066. [Google Scholar] [CrossRef]
- Xie, J.; Xu, X.; Wang, F.; Tang, Z.; Chen, L. Coordinated control based path following of distributed drive autonomous electric vehicles with yaw-moment control. Control Eng. Pract. 2021, 106, 104659. [Google Scholar] [CrossRef]
- Cao, X.; Xu, T.; Tian, Y.; Ji, X. Gain-scheduling LPV synthesis H∞ robust lateral motion control for path following of autonomous vehicle via coordination of steering and braking. Veh. Syst. Dyn. 2023, 61, 968–991. [Google Scholar] [CrossRef]
- Rego, F.; Hung, N.; Pascoal, A. Cooperative Path-Following of Autonomous Marine Vehicles: Theory and Experiments. In Proceedings of the 2018 IEEE/OES Autonomous Underwater Vehicle Workshop (AUV), Porto, Portugal, 6–9 November 2018; pp. 1–6. [Google Scholar]
- Ghabcheloo, R.; Aguiar, A.; Pascoal, A.; Silvestre, C.; Kaminer, I.; Hespanha, J. Coordinated path-following in the presence of communication losses and time delays. SIAM J. Control Optim. 2009, 48, 234–265. [Google Scholar] [CrossRef]
- Chang, S. Synchronization in a steer-by-wire vehicle dynamic system. Int. J. Eng. Sci. 2007, 45, 628–643. [Google Scholar] [CrossRef]

| Symbol | Definition | Value |
|---|---|---|
| m | Vehicle mass | 1830 kg |
| Vehicle yaw moment of inertia | 3234 kg m | |
| Moment of inertia in steering system | 10.0035 kg m | |
| Viscous damping | 350.1 Nm s/rad | |
| Motor constant | 0.078 Nm/A | |
| Aerodynamic trajectory | 0.036 m | |
| Mechanical trajectory | 0.024 m | |
| Motor efficiency | 0.7 | |
| Steering ratio | 30 | |
| Distance of CG from front axle | 1.4 m | |
| Distance of CG from rear axle | 1.65 m | |
| Cornering stiffness of front tires | −134.843 kN/rad | |
| Cornering stiffness of rear tires | −124.337 kN/rad | |
| Vehicle tread | 1.5 m | |
| R | Tire radius | 0.3 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Jiao, X.; Zhang, T. Robust H∞ Output Feedback Trajectory Tracking Control for Steer-by-Wire Four-Wheel Independent Actuated Electric Vehicles. World Electr. Veh. J. 2023, 14, 147. https://doi.org/10.3390/wevj14060147
Li Z, Jiao X, Zhang T. Robust H∞ Output Feedback Trajectory Tracking Control for Steer-by-Wire Four-Wheel Independent Actuated Electric Vehicles. World Electric Vehicle Journal. 2023; 14(6):147. https://doi.org/10.3390/wevj14060147
Chicago/Turabian StyleLi, Zhiwen, Xiaohong Jiao, and Ting Zhang. 2023. "Robust H∞ Output Feedback Trajectory Tracking Control for Steer-by-Wire Four-Wheel Independent Actuated Electric Vehicles" World Electric Vehicle Journal 14, no. 6: 147. https://doi.org/10.3390/wevj14060147
APA StyleLi, Z., Jiao, X., & Zhang, T. (2023). Robust H∞ Output Feedback Trajectory Tracking Control for Steer-by-Wire Four-Wheel Independent Actuated Electric Vehicles. World Electric Vehicle Journal, 14(6), 147. https://doi.org/10.3390/wevj14060147






