Coordinated Control Strategy for Drive Mode Switching of Double Rotor In-Wheel Motor Based on MPC and Control Allocation

Abstract

To overcome the problems existing in the practical application of traditional in-wheel motors used for electric vehicles, an integrated double rotor in-wheel motor was proposed, which can realize three drive modes to meet variable operating condition requirements of the vehicle. The process of switching between different drive modes affects the ride comfort of a vehicle. Taking the mode switching from a single inner motor drive to a dual-motor coupling drive as a research object, a dynamic modeling method of drive mode switching based on the switching system was proposed. According to the critical conditions of each state transition, the switching rules expressed by the segmental constant function were designed. At the engagement stage of electromagnetic clutch II, the torque coordination control strategy based on model predictive control (MPC) and control allocation was proposed. The simulation results show that the proposed strategy can effectively reduce the impact degree of a vehicle and the slipping-friction work of the clutch on the premise of ensuring the fast response of mode switching and the steady increase in vehicle speed. The switching quality of the mode-switching process is effectively improved. In addition, the drive mode switching control of the double rotor in-wheel motor prototype was tested, which proves its ability to operate in multi-drive mode.

1. Introduction

Double rotor motor (DRM) is a new type of electric power coupling mechanism proposed more than ten years ago, which has the functions of continuously variable speed, variable torque and starting engine and can realize all the operating modes of traditional series–parallel hybrid electric vehicles (HEV). Therefore, it is considered a feasible alternative to the mechanical power coupling system. Zheng et. al. [1] proposed the concept of using a four-quadrant transducer (4QT) in the power train of HEV, which was integrated radially by two permanent-magnet synchronous machines. Xu et. al. [2] explored a dual mechanical port (DMP) electric machine and discussed the salient features and suitability of a DMP machine for HEVs. Pisek et. al. [3] presented a double-rotor permanent magnet synchronous machine used in HEVs as a four-quadrant drive system. The no-load, load and temperature rise characteristics were analyzed. Xiang et. al. [4] proposed a dual mechanical port flux-switching permanent magnet motor used potentially for HEVs. With the advantages of a compact structure and efficient transmission, an in-wheel motor-driven electric vehicle has become a typical representative of the development direction of future electric vehicles [5,6,7]. However, the existing inner-rotor and outer-rotor in-wheel motors have some problems in practical application, which have limited applications. In particular, their operating points cannot always be maintained in the high-efficiency zone under full driving conditions. Therefore, an integrated double rotor in-wheel motor (DRIWM) is proposed in this paper. It has three drive modes, such as single drive and coupling drive for the inner and outer motors, which can give full play to the high-efficiency characteristics of the two motors under different driving conditions. Now, there are few research reports about the DRIWM, and there are only some patent applications. Literature [8] presented a DRM applied to an in-wheel driven electric vehicle, and only the outer rotor was used for driving. Literature [9] proposed an electric wheel based on DRM, but its inner rotor was used for driving and the outer rotor was used for recovering braking energy. Literature [10] proposed a wheel-side power drive system based on DRM, which also had only one drive mode. There are no specific descriptions of the drive mode of in-wheel motor drive systems based on DRM in Literature [11] and Literature [12]. Only one drive mode is provided in the structural schemes mentioned above, which cannot meet the requirements of actual driving conditions. For electric vehicles with multiple drive modes, impact and vibration of the transmission system will be caused in the process of mode switching. In order to improve the ride comfort of vehicles, scholars at home and abroad have conducted relevant studies on torque coordination control in the mode-switching process. Huang et al. [13] presented a model reference adaptive controller for series–parallel HEVs during the mode shift, which decreases the vehicle jerk and frictional loss of clutch. He et al. [14] divided the mode-switching process of parallel HEV into three stages based on the switching system, and designed a fuzzy-PI controller and an adaptive sliding-mode controller to coordinate the torque of the engine and motor, which realize the continuity of power transmission. Zhang et al. [15] took a dual-mode series–parallel electromechanical compound transmission system as object and proposed a control strategy based on MPC for torque coordination, which effectively reduces the torque ripple of the output shaft and the sliding friction loss of clutch. Lin et al. [16] proposed a coordinated control strategy based on MPC for the mode-switching process of HEVs with clutch engagement, which effectively suppresses the vehicle jerk and improves the ride comfort. Hu et al. [17] took the jerk as an optimization objective and proposed a torque control strategy for a dual-motor coupled drive system during mode switching, which realized an interruption-free transmission of power. Zeng et al. [18] proposed a dynamic coordinated switching strategy for the dual-motor system of electric CVT according to the torque compensation characteristics of the motor, which significantly reduced the jerk of the vehicle.

When the three drive modes of the DRIWM switch, it is necessary to control the engagement or disengagement of different electromagnetic clutches. The mode-switching processes show the hybrid characteristics of both continuous and discrete dynamic variables. During the drive mode switching process of the DRIWM, how to achieve torque coordination control of the inner motor, outer motor and electromagnetic clutch so as to ensure the switching quality is the key problem to be solved. Considering these problems, a dynamic model of mode switching was established according to the switching system theory, and a torque coordination control strategy based on MPC and control allocation was proposed.

The rest of this paper is organized as follows: the structure and drive modes of the DRIWM are first introduced in Section 2. Taking the mode switching from a single inner motor drive to a dual-motor coupling drive as the research object, the model of the mode switching dynamic system is established based on the switching system theory in Section 3. The torque coordination control strategy based on MPC and control allocation is proposed for the engagement stage of electromagnetic clutch II in Section 4. The effectiveness of the proposed strategy is verified by simulation in Section 5. The DRIWM prototype is made and the drive mode switching control is tested in Section 6. Section 7 draws a conclusion and points out the direction of further research.

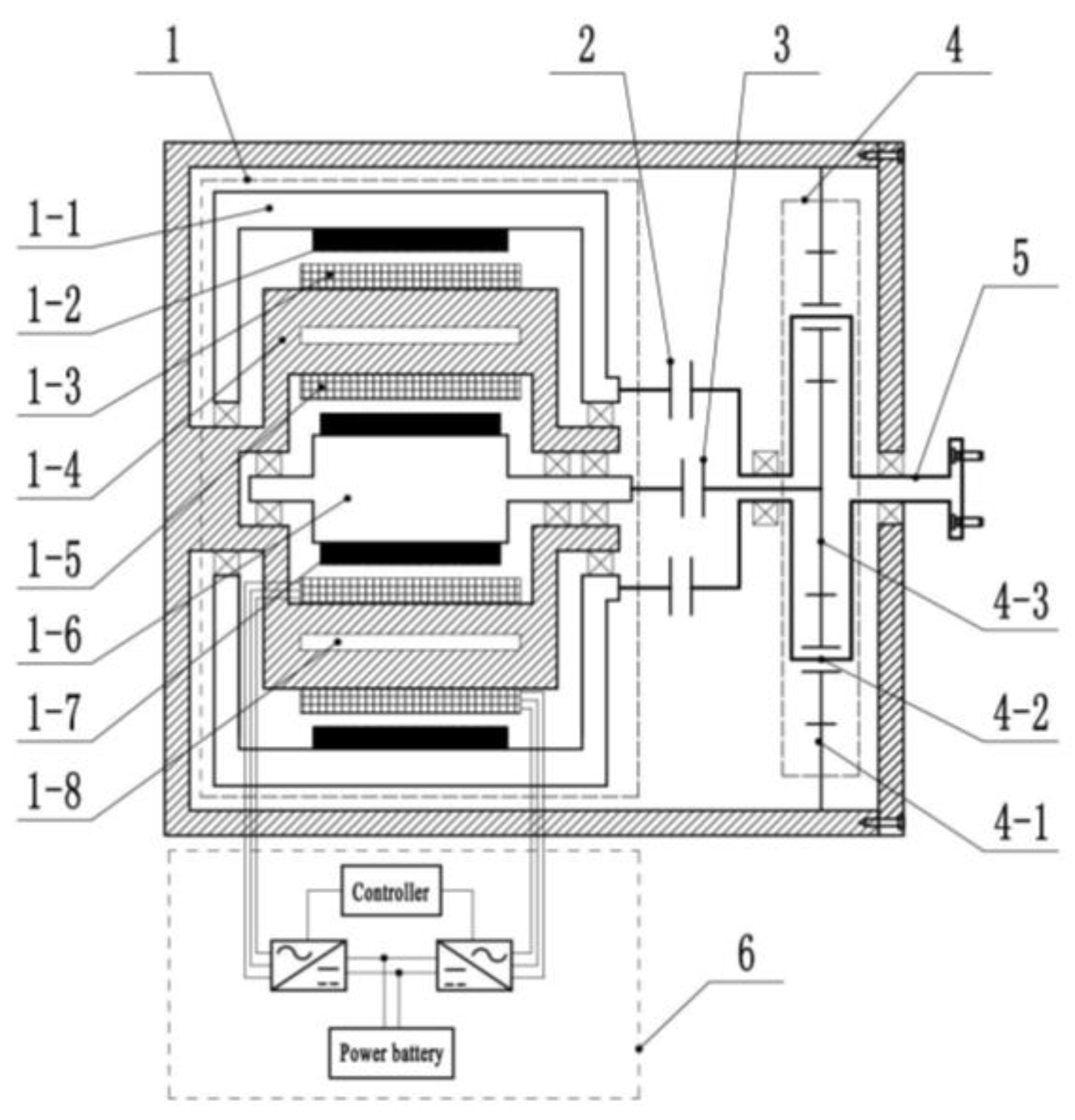
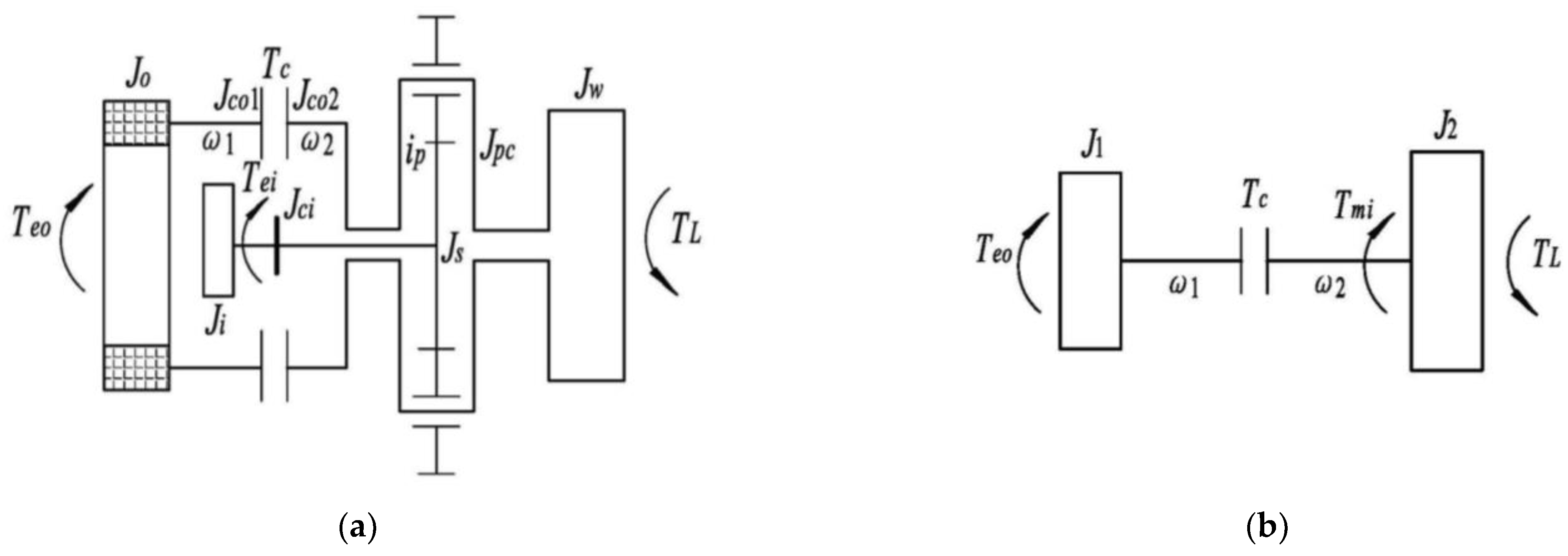
2. Structure and Drive Modes of the DRIWM

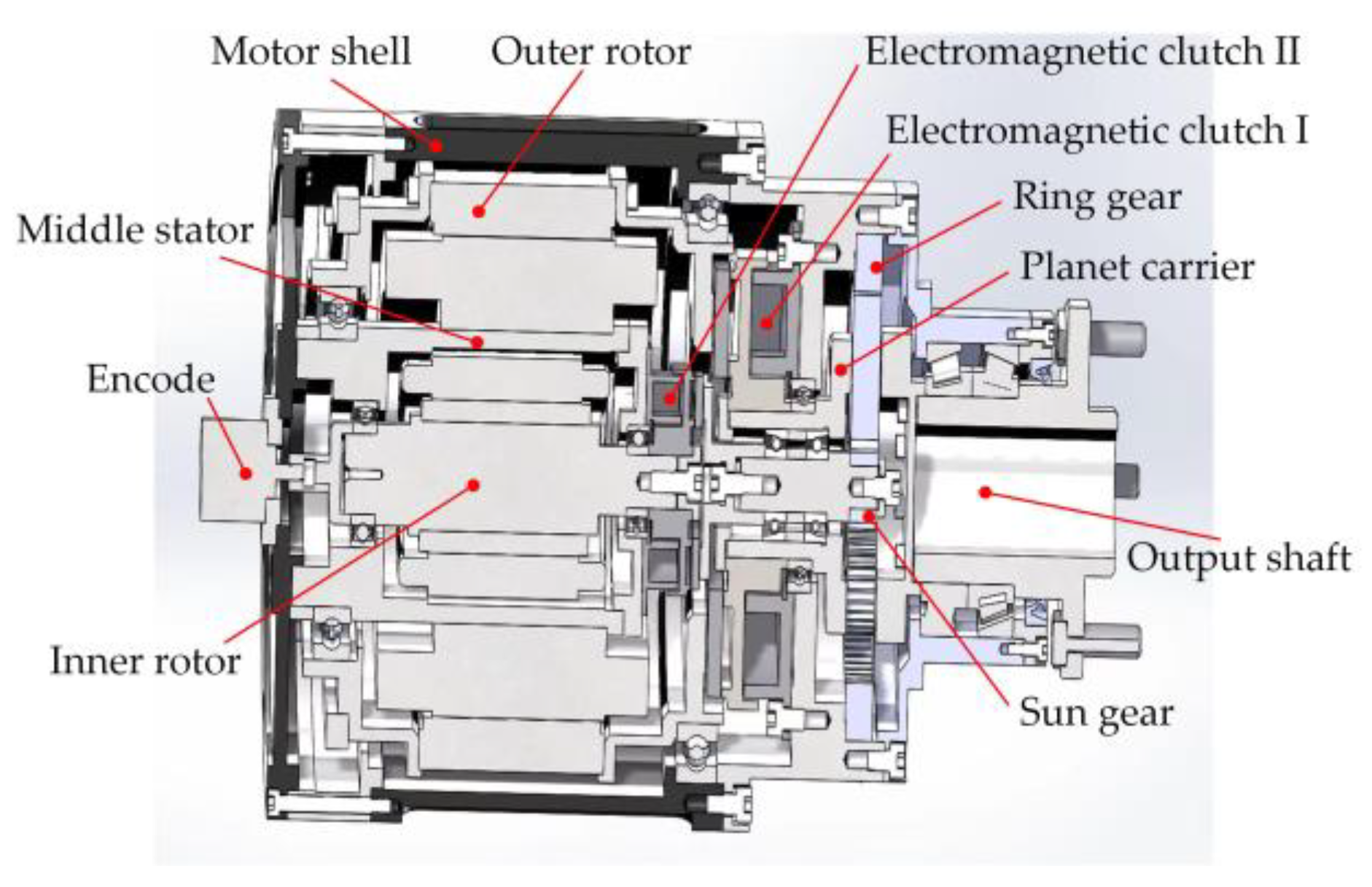
2.1. Structural Scheme

The structure of the proposed DRIWM is shown in Figure 1, which integrates the DRM, electromagnetic clutch I/II, planetary gears and output shaft. The inner rotor and outer rotor of the DRM are arranged, respectively, on the inner and outer sides of the middle stator. Figure 2 shows the cross-section of the DRM. From the perspective of structure, it can be regarded as the combination of an inner rotor motor and an outer rotor motor in radial space. The ring gear is fixedly connected to the inner wall of the motor shell. Electromagnetic clutch II is arranged between the inner rotor and the sun gear, and electromagnetic clutch I is arranged between the outer rotor and the planet carrier. The powers of the inner and outer motors are transferred to the output shaft through the planet carrier.

2.2. Drive Modes Analyses

As shown in

Table 1. Drive modes of the DRIWM.

Drive Mode	Inner Motor	Outer Motor	Electromagnetic Clutch I	Electromagnetic Clutch II
SIM	●	○	○	●
SOM	○	●	●	○
DMC	●	●	●	●

Note: “●” represents that the motor is working or the clutch is engaged, “○” represents that the motor is not working or the clutch is disengaged.

, by controlling the engagement and disengagement of electromagnetic clutch I and electromagnetic clutch II, the DRIWM can operate in three different drive modes, such as single inner motor drive (SIM), single outer motor drive (SOM), and dual-motor coupling drive (DMC).

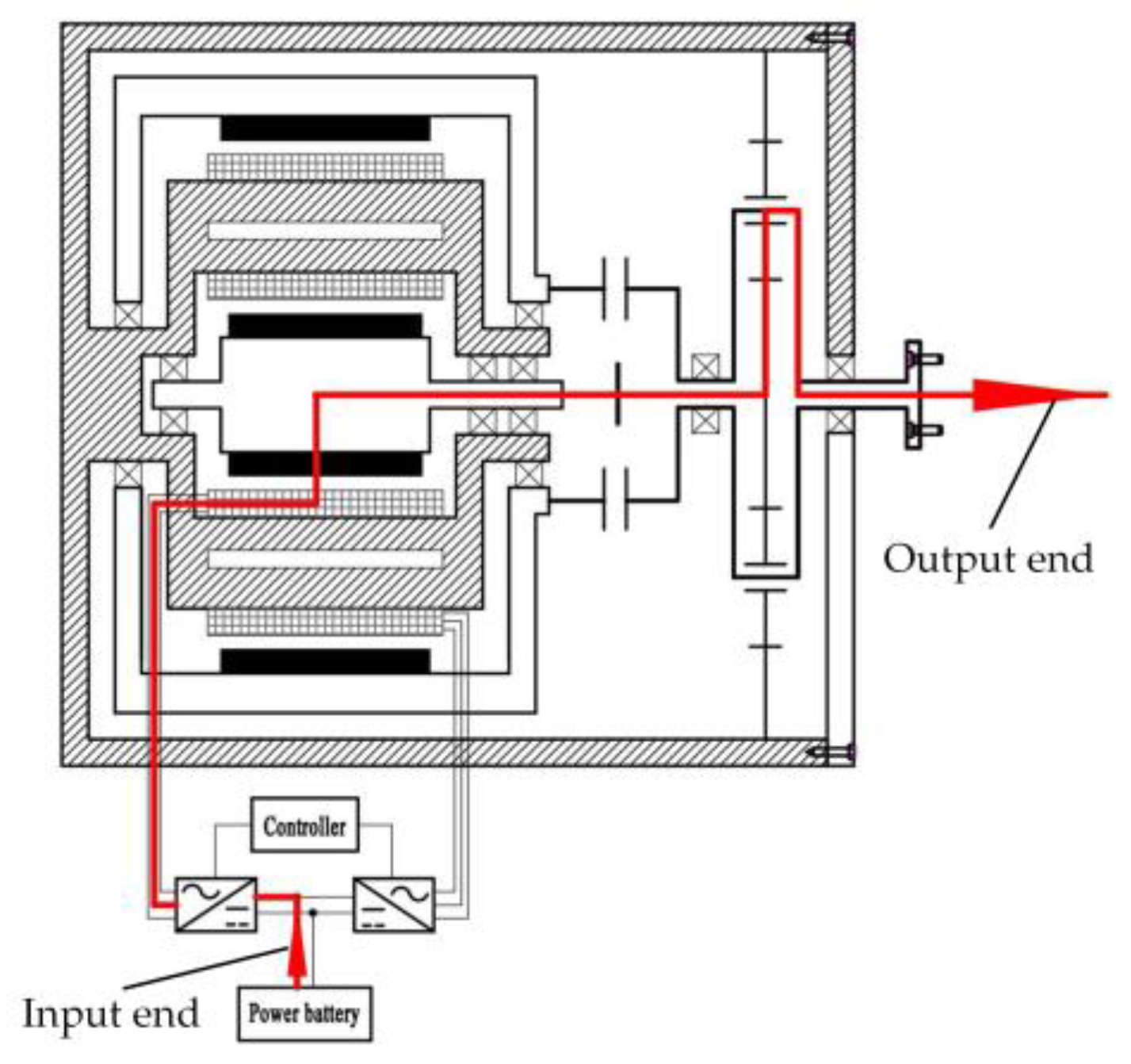
• Single inner motor drive. In this mode, electromagnetic clutch I and electromagnetic clutch II are disengaged and engaged, respectively. As shown in Figure 3, the power of the inner motor is transferred to the wheel through the sun gear, the planet carrier and the output shaft. The inner motor can be regarded as a deceleration-driven in-wheel motor. It is mainly suitable for driving conditions with general torque demand, such as vehicle starting and low-speed driving.

2.

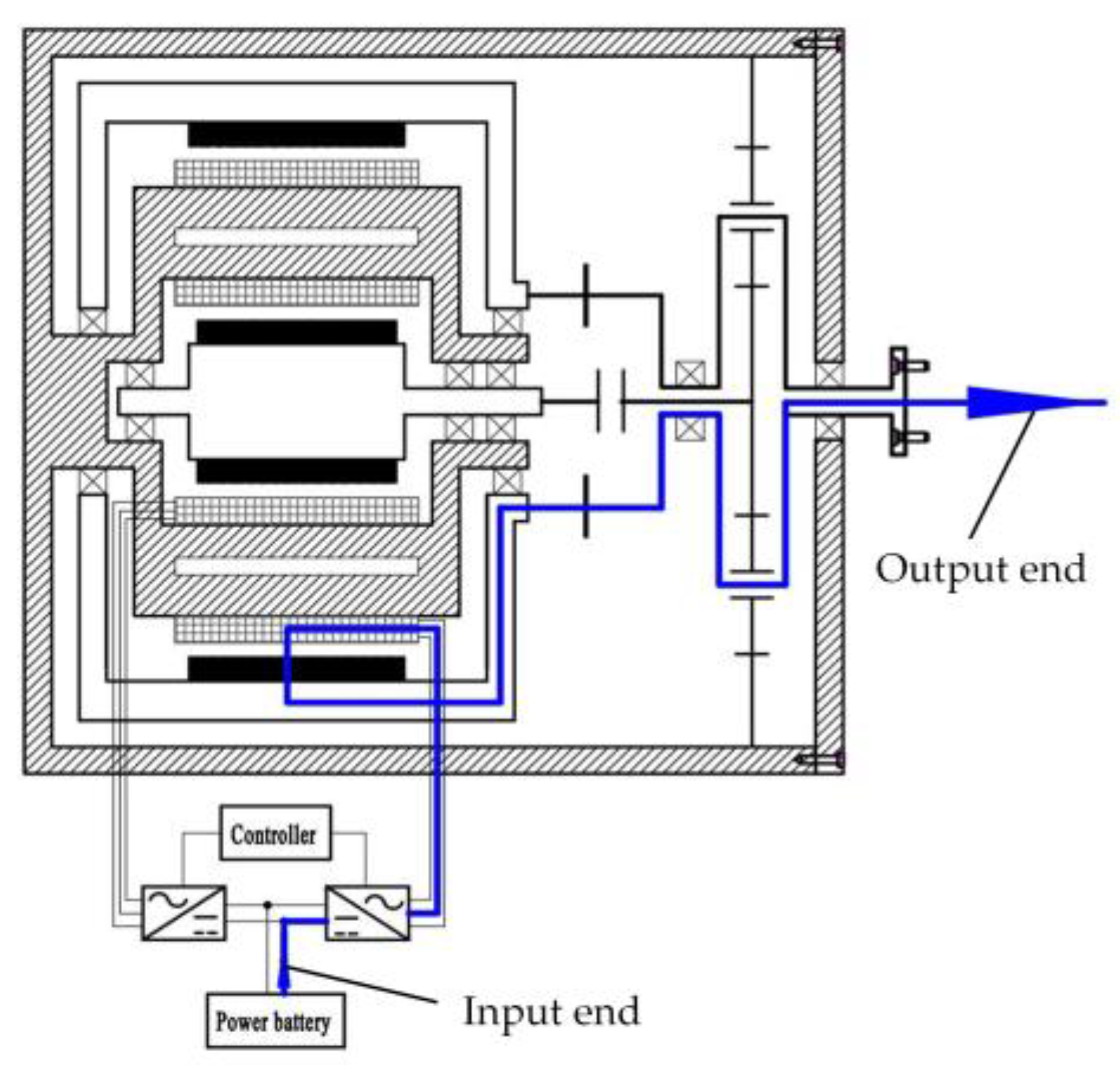
Single outer motor drive. In this mode, electromagnetic clutch I and electromagnetic clutch II are engaged and disengaged, respectively. As shown in Figure 4, the power of the outer motor is transferred to the wheel through the planet carrier and the output shaft. The outer motor can be regarded as a direct drive in-wheel motor. It is mainly suitable for high-speed driving conditions.

3.

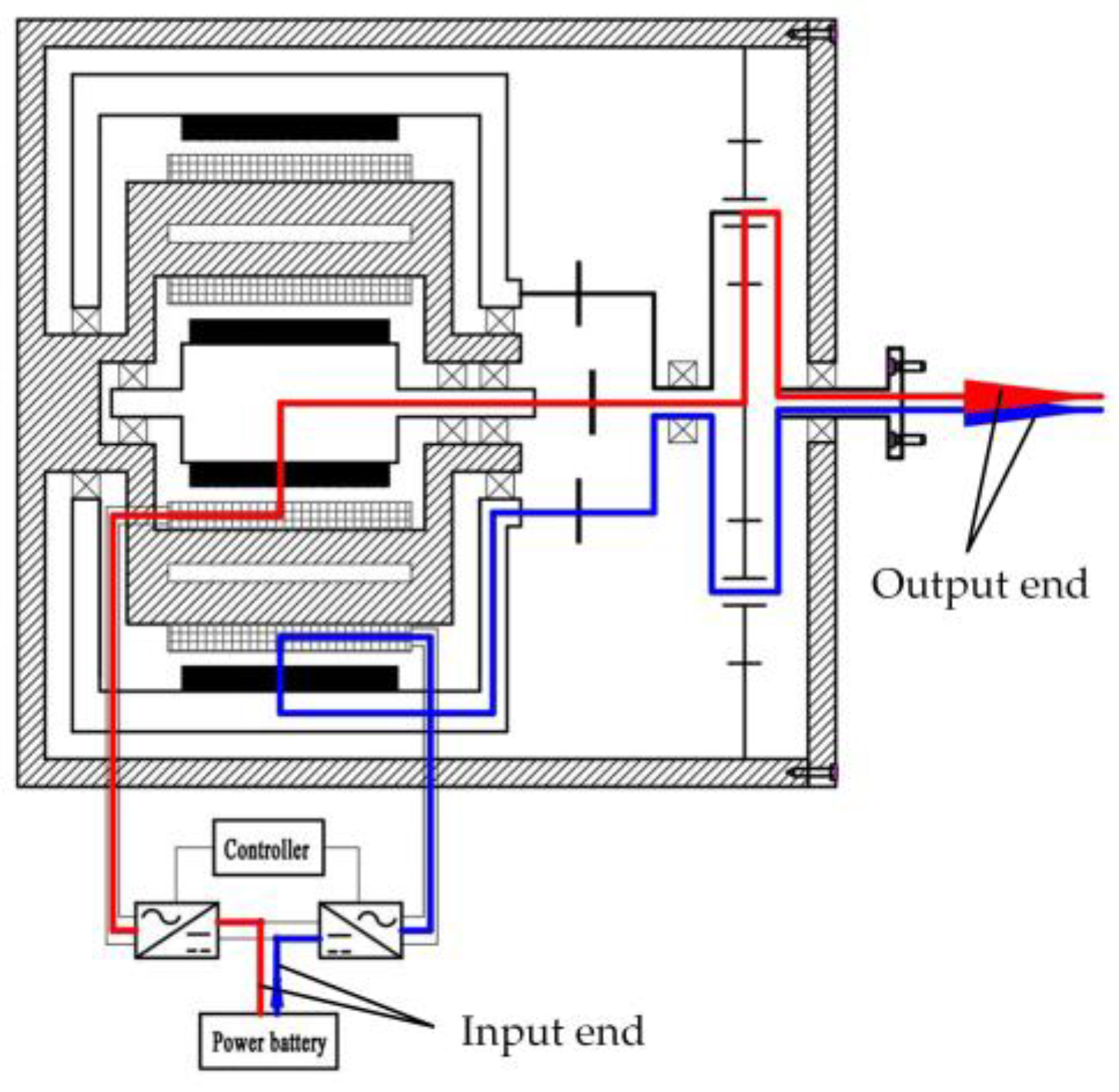
Dual-motor coupling drive. In this mode, both electromagnetic clutch II and electromagnetic clutch I are engaged, the power flows of the inner and outer motors are shown in Figure 5. The driving torques of two motors are coupled at the planet carrier and then transferred to the wheel. It is mainly suitable for driving conditions with high torque demand, such as the vehicle climbing or acceleration at a low speed.

3. Dynamic Modeling of Drive Mode Switching Process of the DRIWM

3.1. Description of the Drive Mode Switching

During the switching processes of the three drive modes of the DRIWM, not only continuous variable dynamic behaviors are included, such as vehicle speed, SOC of battery, etc., but also some discrete event actions are included, such as engagement/disengagement of electromagnetic clutch I and electromagnetic clutch II, operation/stop of inner and outer motor, etc. These variables with different characteristics affect each other so that the drive modes switching processes of the DRIWM show typical hybrid characteristics.

In the mode switching process of the SIM drive to the DMC drive, electromagnetic clutch II will experience two working states of “slipping-friction” and “synchronous locking” at the engagement stage, and the torque transmission is non-linear. When the current torques of the inner and outer motors change to the target torque, the output torque will change greatly if the conventional control strategy is adopted. It will result in a large impact on the vehicle. Therefore, this paper takes the impact degree of the vehicle and the slipping-friction work of the clutch to evaluate the smoothness of power transmission during the mode switching, and the expressions are:

$$j=\frac{da}{dt}=\frac{d^{2}v}{d{t}^2},$$

(1)

where, a is vehicle acceleration; v is vehicle speed.

$$W_d={\displaystyle \underset{0}{\overset{t_c}{\int }}\left({\omega }_2-{\omega }_1\right)}{T}_{c}dt,$$

(2)

where, ω₁ and ω₂ are, respectively, the angular velocities of the active and driven ends of electromagnetic clutch II; T_c is the friction torque of electromagnetic clutch II; t_c is the moment of the clutch locking.

3.2. Hybrid Dynamic Modeling of the Drive Mode Switching Process

The transmission system model of the mode switching from the SIM drive to the DMC drive is shown in Figure 6. When the mode-switching model is established, the transmission efficiency of each moving part is not considered, and they are regarded as rigid bodies. J_o and J_i are, respectively, the moments of inertia of the outer and inner motors; J_co1 and J_co2 are, respectively, the moment of inertia of the active and driven ends of electromagnetic clutch II; J_s is the moment of inertia of the sun gear; J_ci is the moment of inertia of electromagnetic clutch I (engaged state); J_pc is the moment of inertia of the planet carrier; i_p is the transmission ratio of planetary gears, T_eo and T_ei are, respectively, the electromagnetic torque produced by the outer and inner motors; T_mi is the torque acting on the planet carrier by the inner motor, and T_mi = (1+p)T_ei; T_L is the load torque; p is the characteristic parameter of planetary gears.

In order to facilitate the study of torque coordination control with the consideration of the friction torque of electromagnetic clutch II, Figure 6a can be further simplified into the equivalent model shown in Figure 6b. J₁ and J₂ are, respectively, the equivalent moment of inertia simplified to the active and driven ends of electromagnetic clutch II, and the calculation expressions are as follows:

$$J_1=J_o+J_{co1,}$$

(3)

$$J_2=\frac{J_i+J_{ci}+J_s}{i_p^2}+J_{pc}+J_{co2}+\frac{1}{4}m{r}^2,$$

(4)

where, m is vehicle mass; r is wheel radius.

3.2.1. Discrete Event Dynamic System

When the SIM drive mode switches to the DMC drive mode, the whole switching process goes through three stages: single inner motor drive, engagement of electromagnetic clutch II and dual-motor torque coupling drive, as shown in Figure 7.

Because the three stages correspond to different discrete states, the system structure and dynamic characteristics of each state are different. According to the modeling method of the switching system, set I is a finite set of discrete states, which is used to describe different states of the mode switching of the DRIWM. Therefore, set I of discrete states can be expressed as:

$$I=\left\{i_1,i_2,i_3\right\},$$

(5)

where, i₁ represents the SIM drive mode, i₂ represents the engagement stage of electromagnetic clutch II, and i₃ represents the DMC drive mode.

The discrete event set E can be expressed as:

$$E=\left\{\left(i_1,i_2\right),\left(i_2,i_3\right)\right\},$$

(6)

where, e₁ = (i₁, i₂) represents the transition from the SIM drive mode to the engagement stage of electromagnetic clutch II; e₂ = (i₂, i₃) represents the transition from the engagement stage of electromagnetic clutch II to the DMC drive mode.

3.2.2. Continuous Variable Dynamic System

This system is used to describe the variation of vehicle speed under different drive torques. In the process of the SIM drive mode switching to the DMC drive mode, the dynamic equations of three different stages can be expressed as:

1.

Single inner motor drive: electromagnetic clutch II is disengaged.

$$J_2{\dot{\omega }}_2=\left(1+p\right)T_{ei}-T_L,$$

(7)

2.

Engagement stage of electromagnetic clutch II: electromagnetic clutch II is in the engagement.

$$\{\begin{array}{l}{J}_1{\dot{\omega }}_1=T_{eo}-T_c\hfill \\ J_2{\dot{\omega }}_2=\left(1+p\right)T_{ei}+T_c-T_L\hfill \end{array},$$

(8)

2.

Dual-motor coupling drive: electromagnetic clutch II is locked.

$$\left(J_1+J_2\right){\dot{\omega }}_0=T_{eo}+\left(1+p\right)T_{ei}-T_L,$$

(9)

where, ω₀ is the common angular velocity of the active and driven ends of electromagnetic clutch II after it is locked, and ω₁ = ω₂. The corresponding sets of state variables and control variables are selected as:

$$\{\begin{array}{l}x\left(t\right)=\left[{\omega }_1,{\omega }_2\right]\hfill \\ u\left(t\right)=\left[T_{eo},T_{mi},T_c\right]\hfill \end{array},$$

(10)

Since there are three different working states in the mode-switching process, the differential equation is also different when the selected state is different. Then, the mapping relationship between the discrete states and the dynamic system with continuous variables can be expressed as:

$$i_k\to f_k:\dot{x}\left(t\right)=A_{k}x\left(t\right)+B_{k}u\left(t\right)\begin{array}{cc}& \left(k=1,2\right)\end{array},$$

(11)

where, A_k is the matrix of the state variable, B_k is the matrix of the control variable, and f_k is the state mapping function.

3.3. Determination of the Mode Switching Rule

Combined with the applicable working conditions of the three drive modes of the DRIWM and the switching system idea, the specific mode-switching process from the SIM drive to the DMC drive can be described as follows: when the vehicle speed is less than 60 km/h and the vehicle demand torque is less than the critical value of the mode switching torque, the system is in the SIM drive mode. When the vehicle speed is less than 60 km/h and the demand torque of the vehicle is greater than the critical value of the mode-switching torque, the outer motor starts. When the speed difference between the active and driven ends of electromagnetic clutch II is less than the threshold, the discrete event e₁ is triggered and the system enters the engagement stage of electromagnetic clutch II. When the speed difference between the active and driven ends of electromagnetic clutch II is about 0, electromagnetic clutch II is locked, the discrete event e₂ is triggered, and the system enters the DMC drive mode. The control flow chart of the mode switching is shown in Figure 8.

The speed difference of electromagnetic clutch II in the engagement process can be expressed as:

$$\Delta {\omega }_c=\left|{\omega }_1-{\omega }_2\right|=\left|{\omega }_{mo}-\frac{1}{1+p}{\omega }_{mi}\right|,$$

(12)

where, ω_mo is the angular velocity of the outer motor, and ω_mo = ω₁; ω_mi is the angular velocity of the inner motor, and ω_mi = (1 + p)ω_2○.

According to the control flow of the mode switching, the switching signal is represented by a segmental constant function, and then the drive mode switching rules of the DRIWM are formulated as follows:

$$\sigma (t^{+})=\{\begin{array}{l}1\hfill \\ 2,\left\{\sigma (t^{-})=1,v<60,T_{req}>T_{v\max },\left|{\omega }_{mo}-\frac{1}{1+p}{\omega }_{mi}\right|\le {\overline{\omega }}_c\right\}\hfill \\ 3,\left\{\sigma (t^{-})=2,v<60,T_{req}>T_{v\max },\left|{\omega }_{mo}-\frac{1}{1+p}{\omega }_{mi}\right|\approx 0\right\}\hfill \end{array},$$

(13)

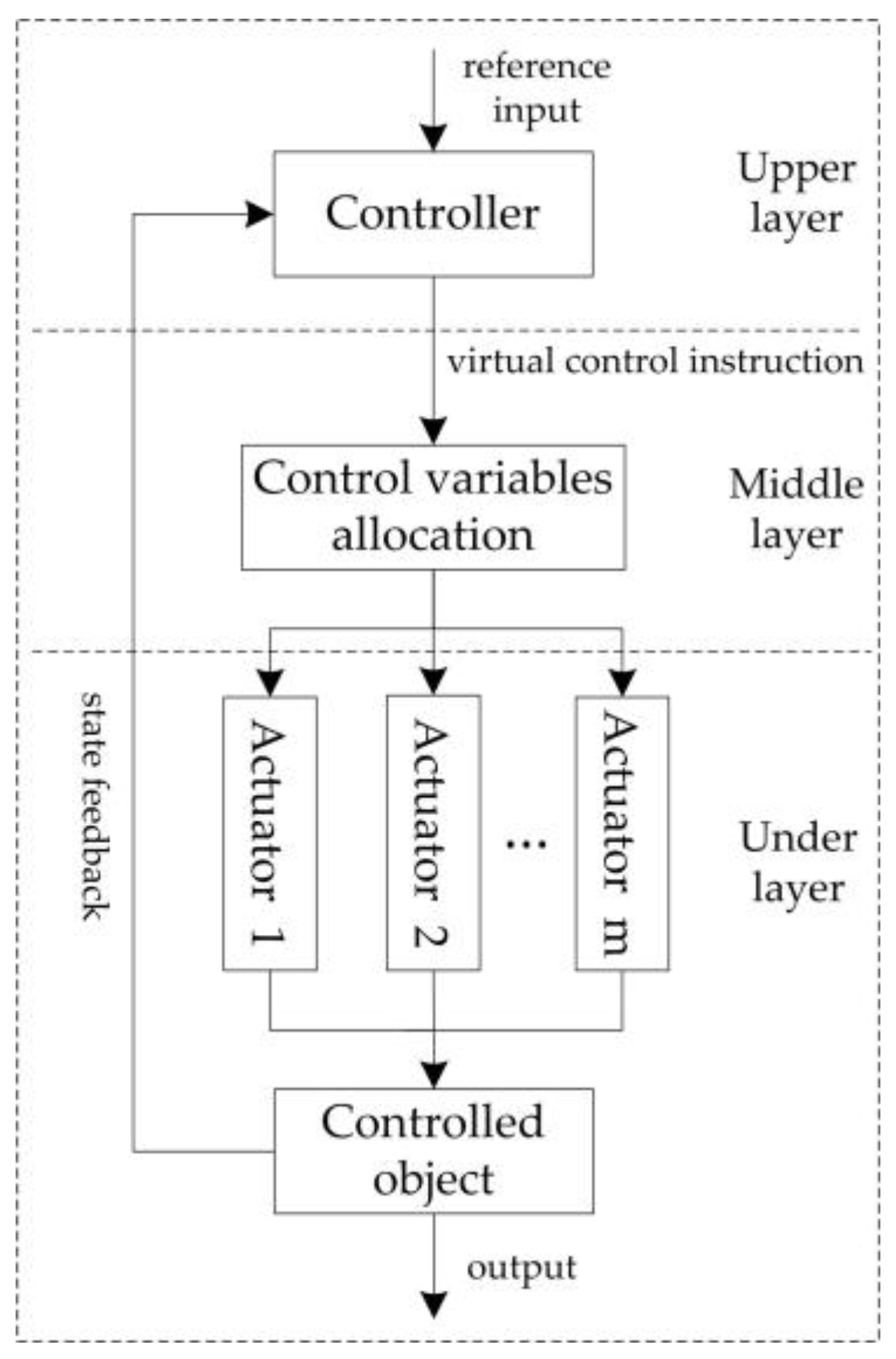
4. Torque Coordination Control Strategy for the Mode Switching Based on MPC and Control Allocation

From the above analysis, we will focus on the engagement stage of electromagnetic clutch II in this section. Combined with its dynamics model, the torque coordination control strategy based on MPC and control allocation was designed.

4.1. Description of the Control Allocation Problem

Equation (8) shows the relationship between the speed of the active and driven ends and the torque of the driving system in the engagement stage of electromagnetic clutch II. In order to prevent the deadlock phenomenon and algebraic loop problem in the online optimization process of model predictive control, the damping coefficients δ₁ and δ₂ were introduced into the active and driven ends of electromagnetic clutch II. The state variables are selected as x₁(t) = ω₁(t), x₂(t) = ω₂(t); the input variable are selected as u₁(t) = T_eo(t), u₂(t) = T_mi(t), u₃(t) = T_c(t); the output variable are selected as y₁(t) = x₁(t), y₂(t) = x₂(t); the load disturbance is d(t) = T_L(t). Therefore, the state space expression of the engagement stage of electromagnetic clutch II can be written as:

$$\{\begin{array}{l}\dot{x}=Ax+Bu+\tilde{B}d\hfill \\ y=Cx\hfill \end{array},$$

(14)

where, $x={\left[x_1(t)\begin{array}{c}\end{array}{x}_2(t)\right]}^T$, $u={\left[u_1(t)\begin{array}{c}\end{array}{u}_2(t)\begin{array}{c}\end{array}{u}_3(t)\right]}^T$, $y={\left[y_1(t)\begin{array}{c}\end{array}{y}_2(t)\right]}^T$, $d={\left[0\begin{array}{c}\end{array}d(t)\right]}^T$, $A=\left[\begin{array}{cc}-\frac{{\delta }_1}{J_1}& 0\\ 0& -\frac{{\delta }_2}{J_2}\end{array}\right]$, $B=\left[\begin{array}{ccc}\frac{1}{J_1}& 0& -\frac{1}{J_1}\\ 0& \frac{1}{J_2}& \frac{1}{J_2}\end{array}\right]$, $\tilde{B}=\left[\begin{array}{cc}-\frac{1}{J_1}& 0\\ 0& -\frac{1}{J_2}\end{array}\right]$, $C=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$.

Meanwhile, the input variables are constrained by the following constraints:

$$\{\begin{array}{c}{T}_{eo\min }\le u_1(t)\le T_{eo\max }\\ T_{mi\min }\le u_2(t)\le T_{mi\mathrm{m}ax}\\ T_{c\min }\le u_3(t)\le T_{c\max }\end{array},$$

(15)

where, T_eomin, T_mimin and T_cmin are, respectively, the minima of the electromagnetic torque of the outer motor, the torque acted on the planet carrier by the inner motor, and the friction torque of electromagnetic clutch II. T_eomax, T_mimax and T_cmax are, respectively, the maxima of the electromagnetic torque of the outer motor, the torque acted on the planet carrier by the inner motor, and the friction torque of electromagnetic clutch II.

Since there are three control input variables and two output variables in the state space of the above system, this is an overdriven system with input constraints and control redundancy. At present, the modularized scheme based on control allocation is mostly adopted when the drive control system is designed [15,19,20]. By adding the control distribution layer between the controller and actuator, the actual control variables are represented by virtual control variables with smaller dimensions, as shown in Figure 9.

Based on the idea of control allocation, the virtual control instruction ν = [ν₁ ν₂]^T was introduced, ν₁ and ν_2, respectively, represent the virtual torque of the active and driven ends of electromagnetic clutch II. Then, the relationship between the actual control input variables and the virtual control instruction can be expressed as:

$$v=B_{u}u,$$

(16)

where, $B_u=\left[\begin{array}{ccc}1& 0& -1\\ 0& 1& 1\end{array}\right]$, so the control matrix B can be decomposed into:

$$B=B_v{B}_u,$$

(17)

where, $B_v=\left[\begin{array}{cc}\frac{1}{J_1}& 0\\ 0& \frac{1}{J_2}\end{array}\right]$, then the equivalent state space corresponding to the state space expression of electromagnetic clutch II in the engagement stage can be expressed as:

$$\begin{array}{l}\dot{x}=Ax+B_{v}v+\tilde{B}d\\ s.t.\begin{array}{c}\end{array}{v}_{\min }\le v\le v_{\max }\end{array},$$

(18)

Aiming at the overdrive problem existing in the engagement process of electromagnetic clutch II, the MPC and control allocation algorithm will be adopted, as shown in Figure 10. The basic idea is that the optimal virtual control variables will be firstly calculated by MPC based on the reference speed and the actual speed. Then, the optimal virtual control variables are allocated according to the idea of control allocation. After the actual control variables are obtained, they act on the vehicle together with the external disturbance. In addition, by adjusting the weight relation of the control matrix, the impact on the system caused by the discontinuity of the friction torque of the clutch can be reduced to ensure the smooth transition of the mode-switching process.

4.2. Building of Reference Model

The dynamic model after the mode switching was selected as the reference model. At this time, electromagnetic clutch II is locked. The system is driven by both inner and outer motors. The actual output speed of the controlled object tracks the target speed of the reference model in real time. Therefore, the dynamic equation of the reference model can be expressed as:

$$\left(J_1+J_2\right){\dot{\omega }}_{ref}=T_{eo}+\left(1+p\right)T_{ei}-T_L,$$

(19)

where, ω_ref is the reference speed.

4.3. Design of Model Predictive Controller

Here the discrete-time model prediction algorithm was adopted, and the sampling time interval was set as τ_s. Then, the discrete form of the state equation in the engagement stage of electromagnetic clutch II can be written as:

$$x_d\left(k+1\right)=A_d{x}_d\left(k\right)+B_d{v}_d\left(k\right)+B_{\xi }d\left(k\right),$$

(20)

where, $x_d(k)={\left[x_1(k)\begin{array}{c}\end{array}{x}_2(k)\right]}^T$, $v_d(k)={\left[v_1(k)\begin{array}{c}\end{array}{v}_2(k)\right]}^T$, $d(k)={\left[0\begin{array}{c}\end{array}d(k)\right]}^T$, $A_d=\left[\begin{array}{cc}1-\frac{{\delta }_1{\tau }_s}{J_1}& 0\\ 0& 1-\frac{{\delta }_2{\tau }_s}{J_2}\end{array}\right]$, $B_d=\left[\begin{array}{cc}\frac{{\tau }_s}{J_1}& 0\\ 0& \frac{{\tau }_s}{J_2}\end{array}\right]$, $B_{\xi }=\left[\begin{array}{cc}-\frac{{\tau }_s}{J_1}& 0\\ 0& -\frac{{\tau }_s}{J_2}\end{array}\right]$.

Rewrite Equation (20) into an incremental model:

$$\Delta x_d\left(k+1\right)=A_d\Delta x_d\left(k\right)+B_d\Delta v_d\left(k\right),$$

(21)

where, the state increment is Δx_d(k) = x_d(k) − x_d(k − 1), the control increment is Δν_d(k) = ν_d(k) − ν_d(k − 1). Define a new state variable:

$$\overline{x}(k)={\left[\Delta x_d{(k)}^T\begin{array}{c}\end{array}{x}_d{(k)}^T\right]}^T=\left[\begin{array}{c}\Delta x_1(k)\\ \Delta x_2(k)\\ x_1(k)\\ x_2(k)\end{array}\right],$$

(22)

Then the new augmented model is:

$$\{\begin{array}{l}\overline{x}\left(k+1\right)=A_{aug}\overline{x}\left(k\right)+B_{aug}\Delta v_d\left(k\right)\hfill \\ \overline{y}\left(k\right)=C_{aug}\overline{x}\left(k\right)\hfill \end{array},$$

(23)

where, $A_{aug}=\left[\begin{array}{cccc}1-\frac{{\delta }_1{\tau }_s}{J_1}& 0& 0& 0\\ 0& 1-\frac{{\delta }_2{\tau }_s}{J_2}& 0& 0\\ 1-\frac{{\delta }_1{\tau }_s}{J_1}& 0& 1& 0\\ 0& 1-\frac{{\delta }_2{\tau }_s}{J_2}& 0& 1\end{array}\right]$, $B_{aug}=\left[\begin{array}{cc}\frac{{\tau }_s}{J_1}& 0\\ 0& \frac{{\tau }_s}{J_2}\\ \frac{{\tau }_s}{J_1}& 0\\ 0& \frac{{\tau }_s}{J_2}\end{array}\right]$, $C_{aug}=\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$.

Because the calculation amount of the system is determined by the size of the prediction time domain N and the control time domain M, N = 10 and M = 6 are taken here after comprehensive consideration. Therefore, $\overline{v}(k)=\overline{v}(k+1)=\cdots =\overline{v}(k+9)$, the predicted output variable of Equation (23) can be expressed by iterative operation as:

$$Y_p=S_x\overline{x}\left(k\right)+S_v\Delta V\left(k\right),$$

(24)

where, $Y_p=\left[\begin{array}{c}\overline{y}(k+1|k)\\ \overline{y}(k+2|k)\\ ⋮\\ \overline{y}(k+10|k)\end{array}\right]$, $S_x=\left[\begin{array}{c}{C}_{aug}{A}_{aug}\\ C_{aug}{A}_{aug}^2\\ ⋮\\ C_{aug}{A}_{aug}^{10}\end{array}\right]$, $S_v=\left[\begin{array}{c}{C}_{aug}{B}_{aug}\\ C_{aug}{A}_{aug}^{}{B}_{aug}\\ ⋮\\ C_{aug}{A}_{aug}^9{B}_{aug}\end{array}\right]$.

r(k) = [ω_ref(k) ω_ref(k)]^T is assumed to be the reference signal of output variable y₁(k) and y₂(k) in the model prediction controller so that the speed of the active and driven ends of electromagnetic clutch II can track the reference signal in real time and realize the clutch transition from slipping-friction to locking stage. Hence the control objective of the system is to find the optimal control increment ΔV that minimizes the error between the reference signal and the predicted output. The objective function can be expressed as:

$$J={(R-Y_p)}^T(R-Y_p)+\Delta V^T{R}_v\Delta V,$$

(25)

where, R is the reference signal matrix, and R_v is the weight matrix of the control variables. When the objective function is minimum, the necessary condition is:

$$\frac{\partial J}{\partial \Delta V}=0,$$

The optimal control increment can be obtained by solving:

$$\Delta V(k)={(S_v^T{S}_v+R_v)}^{-1}{S}_v^T(R-S_x\overline{x}(k)),$$

(26)

Therefore, the optimal virtual control variables of the current system can be expressed as:

$$v_d\left(k\right)=v_d\left(k-1\right)+\Delta v\left(k\right),$$

(27)

4.4. Control Allocation Method

In order to ensure a well-coordinated control effect of the mode switching, the optimization method is usually adopted to allocate virtual control variables. This paper adopts the allocation method based on the minimization of control variables, which can be expressed as:

$$\begin{array}{l}\underset{u}{\min }{J}_u=\frac{1}{2}{\Vert W_u(u-u_d)\Vert }_2^2\\ s.t.\begin{array}{c}\begin{array}{cc}& \end{array}\end{array}{v}^{*}=B_{u}u\\ \begin{array}{cc}& \end{array}{u}_{\min }\le u\le u_{\max }\end{array},$$

(28)

where, $W_u=W_u^T>0$ represents the actual control weight matrix, $W_u=\left[\begin{array}{ccc}{w}_1& 0& 0\\ 0& w_2& 0\\ 0& 0& w_3\end{array}\right]$, and w₁ > 0, w₂ > 0, w₃ > 0; u_d indicates the target value of the control variable.

The Lagrange function of the above optimization problem can be written as:

$$L(u,\lambda ,\mu )=J_u+{\displaystyle \sum _{i=1}^2{\lambda }_i{h}_i(u)}+{\displaystyle \sum _{k=1}^6{\mu }_k{g}_k(u)},$$

(29)

where, h_i(u)(i = 1, 2) represents the equality constraint, and its expression is:

$$\{\begin{array}{c}{h}_1(u)=u_1-u_3-v_1^{*}\\ h_2(u)=u_2+u_3-v_2^{*}\end{array},$$

(30)

where, g_k(u)(k = 1, 2, ∙∙∙, 6) represents inequality constraint, and its expression is:

$$\{\begin{array}{l}{g}_i(u)=u_i-u_{i\max }(i=1,2,3)\hfill \\ g_{j+3}(u)=u_{j\min }-u_j(j=1,2,3)\hfill \end{array},$$

(31)

The Kuhntucker (KKT) condition is usually used to solve the optimization problems with both equality and inequality constraints.

$$\{\begin{array}{l}\frac{\partial L}{\partial u}|{}_{u=u^{*}}=0\hfill \\ {\lambda }_i\ne 0,{\mu }_k\ge 0,\begin{array}{c}i=1,2;k=1,2,\cdots ,6\end{array}\hfill \\ {\mu }_k{g}_k(u^{*})=0\hfill \\ h_i(u^{*})=0\hfill \\ g_k(u^{*})\le 0\hfill \end{array},$$

(32)

Finally, the actual optimal control input variables u* are obtained:

$$\{\begin{array}{l}{u}_1^{*}=\frac{(w_2^2+w_3^2)v_1^{*}+w_2^2{v}_2^{*}}{w_1^2+w_2^2+w_3^2}\hfill \\ u_2^{*}=\frac{w_1^2{v}_1^{*}+(w_1^2+w_3^2)v_2^{*}}{w_1^2+w_2^2+w_3^2}\hfill \\ u_3^{*}=\frac{-w_1^2{v}_1^{*}+w_2^2{v}_2^{*}}{w_1^2+w_2^2+w_3^2}\hfill \end{array},$$

(33)

4.5. Stability Analysis of the Mode Switching Based on Lyapunov Method

When the virtual control variables are allocated in the control distribution layer, the actual control variables can reach the optimal value of the virtual control variables due to the consideration of the constraints of control variables. Therefore, the stability of the system is only determined by the stability of the model predictive controller used to solve the virtual control variables.

For the incremental system and any state $\overline{x}$ shown in Equation (24), its objective function can be written in discrete form:

$$\underset{\Delta v_d}{\min }J(k)={\displaystyle \sum _{i=1}^N{\Vert \overline{y}(k+i|k)-r(k+i|k)\Vert }_{Q_i}^2+{\displaystyle \sum _{i=1}^M{\Vert \Delta v_d(k+i-1|k)\Vert }_{R_i}^2}},$$

(34)

$$s.t.\{\begin{array}{l}{\overline{x}}_0-\overline{x}=0\hfill \\ v_d{}_{\min }(k+i|k)\le v_d(k+i|k)\le v_d{}_{\mathrm{m}ax}(k+i|k)\hfill \\ \Delta v_d{}_{\min }(k+i|k)\le \Delta v_d(k+i|k)\le \Delta v_d{}_{\mathrm{m}ax}(k+i|k)\hfill \\ {\overline{y}}_{\min }(k+i|k)\le \overline{y}(k+i|k)\le {\overline{y}}_{\max }(k+i|k)\hfill \\ \overline{x}(k+N|k)=0\hfill \end{array},$$

(35)

where, Q_i and R_i are weighted matrices of the system output error and control increment; r(k + i|k) is the system reference at the current moment; $\overline{x}(k+N|k)=0$ is a terminal equality constraint introduced to ensure the system stability.

To simplify writing, the right part of the equal sign of Equation (23) is marked as $f(\overline{x},\Delta v_d)$, and the control time domain and prediction time domain are assumed to be the same and equal to N, then Equation (34) can be further expressed as [21,22]:

$$\underset{\Delta v_d}{\min }J(k)={\displaystyle \sum _{i=1}^{N}l\left(\overline{x}(k+i|k),\Delta v_d(k+i-1|k)\right)},$$

(36)

Without considering external interference, and assuming that the model is unbiased, the predicted system state is the same as the state of the actual controlled object, whereupon:

$$\begin{array}{l}{J}^{*}(k+1)=\underset{\Delta v_d}{\min }{\displaystyle \sum _{i=1}^{N}l\left(\overline{x}(k+1+i),\Delta v_d(k+i)\right)}\\ \begin{array}{c}\hspace{1em}\hspace{1em}\hspace{1em} =\end{array}\underset{\Delta v_d}{\min }\left\{{\displaystyle \sum _{i=1}^{N}l\left(\overline{x}(k+i),\Delta v_d(k+i-1)\right)-l\left(\overline{x}(k+1),\Delta v_d(k)\right)+l\left(\overline{x}(k+1+N),\Delta v_d(k+N)\right)}\right\}\\ \hspace{1em}\hspace{1em}\hspace{1em} \le -l\left(\overline{x}(k+1),\Delta v_d^{*}(k)\right)+J^{*}(k)+\underset{\Delta v_d}{\min }\left\{l\left(\overline{x}(k+1+N),\Delta v_d(k+N)\right)\right\}\end{array},$$

(37)

Under the constraint of terminal equality,

$$\underset{\Delta v_d}{\min }\left\{l\left(\overline{x}(k+1+N),\Delta v_d(k+N)\right)\right\}=0,$$

(38)

Because of $l\left(\overline{x}(k+1),\Delta v_d^{*}(k)\right)\ge 0$, substituting Equation (38) into Equation (37), we can obtain:

$$J^{*}(k+1)\le J^{*}(k),$$

(39)

Therefore, J*(k) is a Lyapunov function of the system, and it is convergent. The system is asymptotically stable.

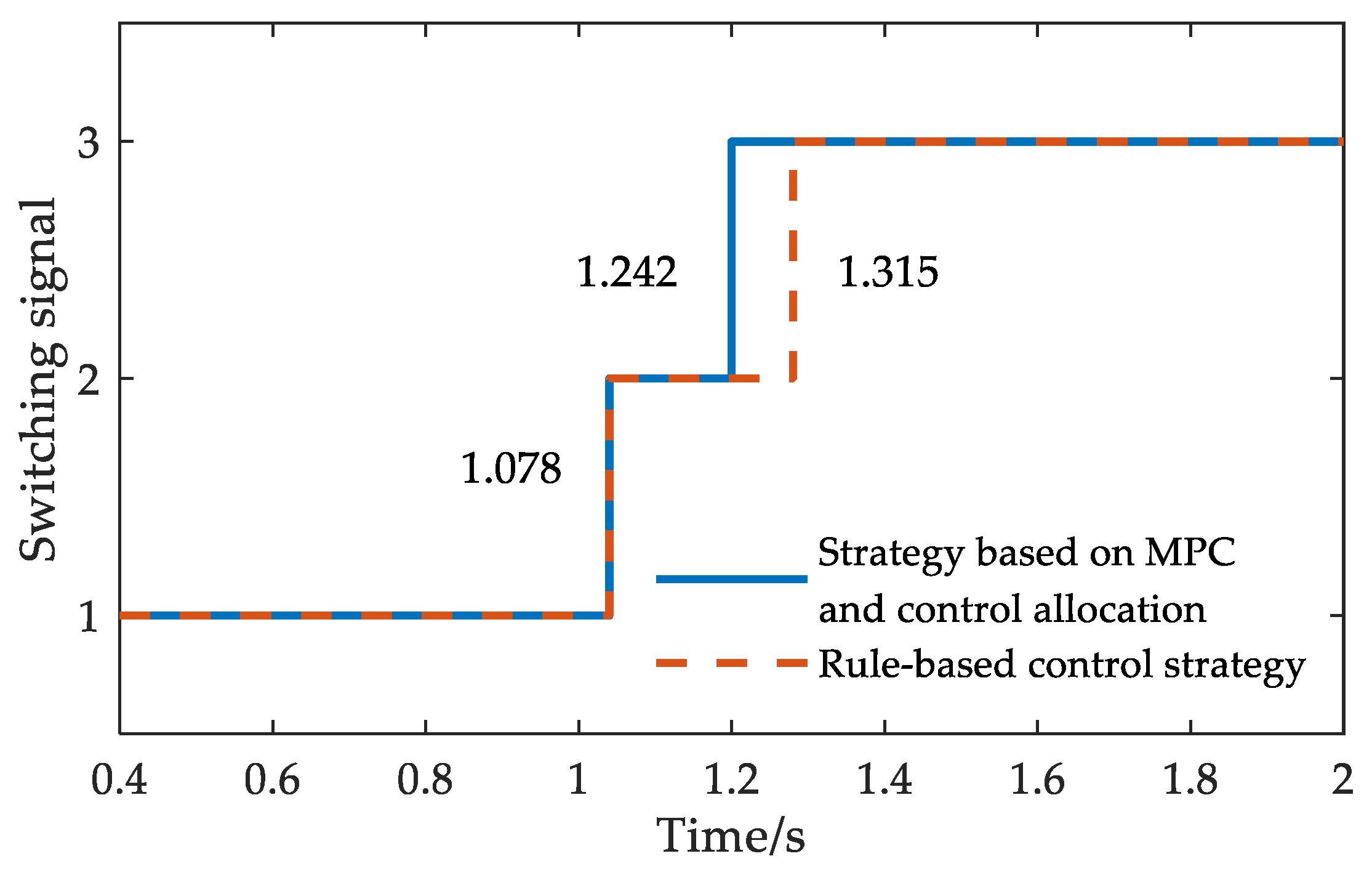
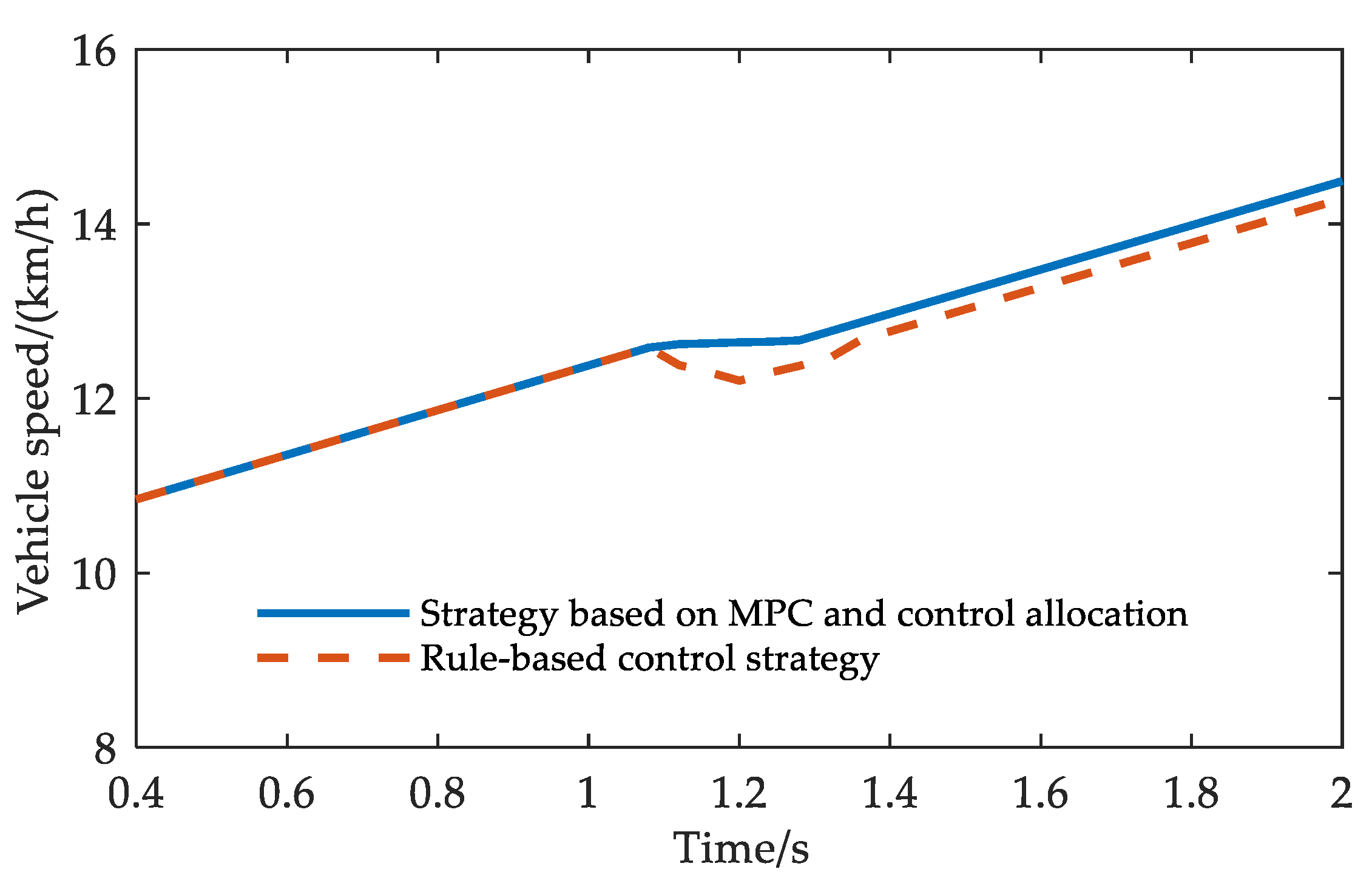
5. Simulation Analysis

To verify the effectiveness of the proposed torque coordination control strategy for mode switching, a rule-based control strategy was used for comparison. The simulation model was built by Matlab/Simulink/Stateflow. The simulation analysis was carried out in a stage of acceleration. The sampling interval of the MPC controller is set to 0.001 s. After several debugging, the control time domain and prediction time domain are, respectively, set as M = 6 and N = 10. The weight matrices of the virtual and actual control variables are R_v = diag(4, 5) and W_u = diag(2, 2, 1), respectively. The speed difference threshold of electromagnetic clutch II in the engagement process is set to 12.6 rad/s, which is converted to a speed of 120 r/min.

Figure 11 shows the mode switching changes under two control strategies. The whole switching process is divided into three stages. Switching signals 1, 2 and 3, respectively, represent SIM drive mode, engagement stage of electromagnetic clutch II and DMC drive mode. By calculation, the mode switching duration is, respectively, 0.164 s and 0.237 s under the torque coordination control strategy based on MPC and control allocation and the rule-based control strategy. The mode switching response speed increases by 30.8% using the proposed torque coordination control strategy.

Figure 12 shows the changes in the output torque of inner and outer motors, the friction torque of electromagnetic clutch II, and the speed of active and driven ends under two control strategies. As can be seen from Figure 12a–c, during the engagement stage of electromagnetic clutch II, the torque coordination control strategy based on MPC and control allocation can effectively compensate for the change of the friction torque of electromagnetic clutch II by coordinating the torque of inner and outer motors, so that its growth rate changes gently. Figure 12d shows that, after electromagnetic clutch II enters the locking stage, the speed of the driven end decreases slightly compared to that before electromagnetic clutch II is engaged, which is mainly because the speed of the active end (outer motor) is always smaller than that of the driven end during the rising process of speed. Besides, under the proposed torque coordination control strategy, the speed of the active end increases faster than that of the rule-based control strategy, which effectively shortens the mode-switching time.

Figure 13 shows the changes in vehicle speed under two control strategies. During the mode-switching process, there is a large fluctuation of the vehicle speed using the rule-based control strategy, while there is a small fluctuation of the vehicle speed using the torque coordination control strategy based on MPC and control allocation, and the transition of vehicle speed is smoother.

Figure 14 shows the change curve of vehicle impact degree under the two control strategies. During the mode switching, the longitudinal impact degree of the vehicle based on the rule control strategy fluctuates greatly. At the engagement moment of electromagnetic clutch II, the peak value of the absolute impact degree is 8.39 m/s³. In contrast, the impact degree of the vehicle is less fluctuant when the torque coordination control strategy based on MPC and control allocation is adopted, and its absolute peak value is 2.87 m/s³, which better improves the stability of the mode switching process. The main reason is that when the rule-based control strategy is adopted, the rapid current increase can make the active and driven ends of electromagnetic clutch II engage quickly, but it will cause a large instantaneous impact. However, by coordinating the output torque of inner and outer motors, the proposed torque coordination control strategy can effectively compensate for the friction torque of electromagnetic clutch II so as to adapt to the nonlinear changes caused by various uncertain factors in the system, which ensure the continuity of clutch torque change and avoid the impact at the moment of mode switching.

Figure 15 shows the slipping-friction work changes of electromagnetic clutch II under the two control strategies. It can be seen that in the clutch engagement stage, the slipping-friction work generated by the rule-based control strategy is 238 J, while that generated by the torque coordination control strategy based on MPC and control allocation is 104 J. The slipping-friction work of electromagnetic clutch II is mainly related to the speed difference between its active and driven ends, friction torque and slipping-friction time. When the proposed torque coordination control strategy is adopted, the simulation results of the above three factors are smaller than those of the rule-based control strategy, which reduces the slipping-friction work.

6. Experimental Verification

The prototype of the DRIWM with a rated power of 4.7kW was made, which is mainly composed of the DRM body, electromagnetic clutches, planetary gears, output shaft, encoders and motor shell. The design specification parameters are listed in

Table 2. Design specifications of the DRIWM.

Parameter	Value
	Inner Motor	Outer Motor
Rated power (kW)	1	3.7
Rated speed (rpm)	3000	960
Pole pairs number of permanent magnet	2	4
Torque constant (Nm/A)	1.729	5.001
Induced voltage constant (V/krpm)	0.6271	0.581

. The axial section of the general assembly drawing of the DRIWM is shown in Figure 16. Figure 17 shows the experimental test platform of the DRIWM, which is mainly composed of a servo motor, measured motor, torque and speed sensor, the control unit of the motor, measurement and control system, etc. The experimental platform uses a servo motor to simulate the drive load, and the simulation load can be adjusted by the measurement and control system.

Figure 18 shows the changes in output torque, speed and current of the DRIWM during the mode switching from the SIM drive to the DMC drive. Assume that the simulated working condition: the vehicle running on a level road at a constant speed is transformed into climbing on the ramp, and the required torque increases. When the inner motor works alone, the output torque is 40 Nm. After maintaining for a period of time, the load is increased to 56 Nm. According to the mode switching condition, electromagnetic clutch II engages, and the DRIWM enters the coupling drive mode. The engagement time of electromagnetic clutch II is about 0.25 s, and the speed decreases slightly. The phase current of the outer motor increases to a constant value, and the phase current of the inner motor decreases. This is mainly because the outer motor bears a larger load torque.

Furthermore, when the torque coordination control strategy based on MPC and control allocation was adopted, the comparisons between the simulation and experimental results of the vehicle impact degree and the engagement time of electromagnetic clutch II were shown in

Table 3. Comparison between the simulation and experimental results by the proposed strategy.

Parameter	Simulation Results	Experimental Results
Impact degree (m/s3)	2.87	4.31
Engagement time of clutch II (s)	0.164	0.25

. The experimental values are slightly higher than the simulation values, which may be related to the manufacturing factors of the prototype and controller. However, the experimental value of vehicle impact degree is still within the recommended standard range, which verifies the proposed strategy is effective.

7. Conclusions

This paper proposes an integrated structure of the DRIWM, which has multiple drive modes, such as SIM drive, SOM drive, and DMC drive. It can meet the needs of vehicles in variable operating conditions. Aiming at the hybrid characteristics with both continuous and discrete dynamic variables shown during the drive mode switching process of the DRIWM, the mode switching from the SIM drive to the DMC drive was selected as the research object, a dynamic model of the mode switching was built based on the switching system theory. According to the critical conditions of each state transition, the switching rules expressed by the segmental constant function were designed. At the engagement stage of electromagnetic clutch II, the torque coordination control strategy based on MPC and control allocation was proposed, and the stability of the mode switching was analyzed by the Lyapunov method. The simulation results show that the mode-switching duration using the proposed torque-coordinated control strategy is shorter compared with the rule-based control strategy. Through the torque-coordinated control of the inner motor, outer motor and electromagnetic clutch II, the impact degree of the vehicle is reduced, and the slipping-friction work of electromagnetic clutch II is also decreased to a large extent. Under the premise of ensuring the steady increase in vehicle speed, the switching quality of the mode-switching process is effectively improved. In addition, the drive mode switching control of the DRIWM prototype was tested, which proves its ability to operate in multi-drive mode. In the future, the performance test of an electric vehicle equipped with the DRIWM will be carried out, and the coordinated control between multiple electric wheels will be further studied.