Construction of Nitrogen Content Observer for Fuel Cell Hydrogen Circuit Based on Anode Recirculation Mode

Abstract

The anode recirculation mode is increasingly being adopted in today’s fuel cell systems. The recycling of hydrogen gas can effectively improve fuel utilization and the wider economy. However, using the purge strategy for the recirculation exhaust has a significant impact on the operational performance and economic efficiency of fuel cell systems.Experiments have shown that, when the purge interval increases from 6 s to 10 s, the recirculation pump power increases by about 20%, the nitrogen content in the exhaust gas increases, and the stack voltage shows a 10 V attenuation. The accumulation of nitrogen permeation in the anode circuit leads to the degradation of the fuel cell performance. Therefore, it is necessary to discharge the accumulated nitrogen through the purge valve in a timely manner. However, opening the exhaust valve with excessively high frequency can result in the unreacted hydrogen being discharged, which reduces the economic efficiency of the fuel cell. This paper is based on the principle of mass conservation and models each subsystem of the anode circuit in the recirculation pump mode of the fuel cell separately, including the proportional valve model, the hydrogen consumption model of the fuel cell, the nitrogen permeation model of the fuel cell, the neural network model of the circulating pump, and the purge valve model. These submodels are integrated to construct a nitrogen content observer for the hydrogen circuit, which can estimate the nitrogen content. The accuracy of the model is validated through experimental data. The estimation error is less than 5.5%. The nitrogen content in the anode circuit can be effectively estimated, providing a model reference for purge operations and improving hydrogen utilization.

1. Introduction

The proton exchange membrane (PEM) in fuel cells is a very important component that is used to separate the gas between the anode and cathode, ensuring effective proton conduction. However, in actual use, in addition to high proton conduction rates, there is also the phenomenon of the transmembrane permeation of gas molecules [1,2,3,4]. Due to the different gas pressures on both sides of the membrane, a small amount of gas molecules will permeate. When hydrogen molecules from the anode and oxygen molecules from the cathode cross the membrane, they will react with each other to produce heat and water, while nitrogen molecules will not participate in the reaction when they permeate. In the anode recirculation mode of the fuel cell system, nitrogen continuously accumulates when mixed with hydrogen, and with time, the nitrogen concentration gradually increases. When the nitrogen concentration is high, it can dilute the hydrogen, causing local hydrogen deficiency near the catalyst and affecting the performance output of the fuel cell. Therefore, the purge valve of the anode must be opened periodically to discharge high-concentration nitrogen, thereby improving the output performance of the fuel cell [5,6,7].

To investigate the nitrogen permeation characteristics of fuel cells, Baik et al. [8] studied the influence of membrane humidity and temperature on the nitrogen permeation coefficient. With an increasing temperature, the membrane permeation coefficient slowly decreases, while an increase in humidity made nitrogen permeation easier. Mittelsteadt et al. [9] conducted research on the water absorption, gas diffusion, and permeation of proton exchange membranes and established a function of the nitrogen permeation coefficient with the temperature and water content of the membrane. Kocha et al. [6] studied the permeation of hydrogen, oxygen, and nitrogen with respect to temperature, and established a differential equation based on the variation in the anode nitrogen partial pressure along the flow channel and the nitrogen permeation rate. The simulation results showed a large accumulation of nitrogen in the 5–10% segment at the outlet of the flow channel. In addition, the nitrogen concentration at the outlet increased exponentially as the current density decreased. Pukrushpan et al. [10] modeled the hydrogen content in the anode using a proportion valve and nitrogen discharge valve as the hydrogen flow control device, but did not consider the hydrogen circulation process.

There have also been many studies on the estimation of the anode nitrogen content. The nitrogen concentration variation on the anode side of the cell depends on the permeation of nitrogen from the cathode side to the anode side and the flow rate of nitrogen discharged with anode gas. Based on this, Chen et al. [11,12] established a differential equation for the change in nitrogen concentration on the anode side of the cell. With an initial concentration of 0, the nitrogen concentration in the anode can be calculated in real time. They also found that, when the cell voltage decreased by less than 0.5 V, the nitrogen mole fraction increased linearly over time, and the accumulation rate gradually slowed down. Based on the experimental results, a function of nitrogen concentration with the cell current density and time was fitted, and the nitrogen content could be calculated based on the current density and time. Liu et al. [13] combined the dynamic equation of the anode nitrogen partial pressure and nitrogen permeation with the Nernst equation (the functional relationship between voltage difference and nitrogen partial pressure) to construct an anode nitrogen partial pressure observer and proposed using a 25% nitrogen concentration as the standard for purge operation triggering. In addition to the nitrogen concentration, the slope of the voltage drop [14] and the integral value of the current [11,15] are also used in the development of purge strategies. If the gas composition at the purge valve can be known, the fuel utilization can be quantitatively calculated, which can be beneficial for the numerical solution of optimization strategies [16].

In addition to the impact of nitrogen concentration on the performance of the stack, water generated by electrochemical reactions in the fuel cell can also accumulate. As a result of electrochemical reactions, water vapor is generated in the cathode catalyst layer by oxygen and hydrogen ions. Depending on the operating temperature, the water generated in the fuel cell may evaporate or condense [17]. Due to the fact that PEMFC typically operates at low temperatures, the generated water vapor can be condensed into liquid water based on its partial pressure. The generation and accumulation of water creates a water concentration gradient between the anode and cathode, which leads to the reverse diffusion of water towards the anode side. Due to the capillary pressure, liquid water flows from the membrane through the anode gas diffusion layer to the anode flow channel. This liquid water is pushed towards the anode outlet by pressurized hydrogen gas and accumulates in the outlet area. Due to the importance of water accumulation on the anode side of DEA-PEMFC, this issue has received considerable attention and has been extensively studied and reported. Several methods for studying water accumulation in proton exchange membrane fuel cells were also proposed and evaluated [18,19], such as neutron imaging or radiography, gas chromatography, X-ray, and infrared.

The most widely used method for overcoming water and nitrogen accumulation in the anode of DEA-PEMFC is anode purging.This is achieved by opening the valve at the anode outlet to flush the water and nitrogen accumulated in the anode channel. As water and nitrogen accumulate and are removed from the anode, hydrogen can reach the active catalyst area and provide sufficient fuel for the electrochemical reaction of the battery, thereby restoring battery performance and minimizing the battery degradation caused by insufficient fuel [20]. Overall, the purging strategies can be classified into the three following categories: (1) fixed purge intervals with different current density [21,22]; (2) slopes of the voltage decrease [14]; and (3) fuel utilization and voltage drop [23]. Sasmito et al. [21] adopted a fractional factorial approach to examine the effects of cathode air-stoichiometry, the anode purging period, and the purging duration on the performance of a DEA-PEMFC. They found that the optimum operating conditions for their fuel cell stack were constituted of a combination of cathode air-stoichiometry of 200%, a purging period of 3 min, and a purging duration of 4 s. Gomez et al. [24] studied the impact of the purging period and duration on a DEA-PEMFC-powered vehicle subjected to segments of a European driving cycle. A low purging duration was found to eliminate the detrimental deceleration at high currents. Meanwhile, a high purging period could sustain higher performance over time. They concluded that a low cathode stoichiometry is desirable to achieve the balance between the parasitic loads and cell performance.

This article models the various parts of the anode loop of a fuel cell based on the principle of the conservation of mass to construct a nitrogen content observer. For the entire anode loop, the molar flow rates of gas input, consumption, permeation, and purge can be modeled and calculated based on submodels. However, because the gas discharged from the purge valve is a mixture, it is necessary to prioritize the observation of the nitrogen concentration at the purge valve. As shown in Figure 1, for the total amount of gas at the purge valve, the input is the gas flow rate output by the stack (the gas flow rate output by the stack includes: the flow rate input by the proportional valve ${\dot{\mathit{n}}}_{\mathit{i}\mathit{n}}$, the flow rate circulated by the circulation pump in the previous cycle ${\dot{\mathit{n}}}_{\mathit{r}\mathit{p}}$, the permeation flow rate of the stack ${\dot{\mathit{n}}}_{\mathit{c}\mathit{r}\mathit{o}\mathit{s}\mathit{s},{\mathit{N}}_2}$, and the consumption flow rate of the stack reaction ${\dot{\mathit{n}}}_{\mathit{s}\mathit{t}\mathit{a}\mathit{c}\mathit{k},{\mathit{H}}_2}$), and the output is the recirculation flow rate of the recirculation pump ${\dot{\mathit{n}}}_{\mathit{r}\mathit{p}}$ and the discharged flow of the purge valve ${\dot{\mathit{n}}}_{\mathit{o}\mathit{u}\mathit{t}}$. The amount of nitrogen at the nitrogen purge valve is the integral of the nitrogen permeation flow rate of the stack minus the nitrogen circulated by the recirculation pump ${\mathit{\alpha }}_{{\mathit{N}}_2,\mathit{t}-1}{\dot{\mathit{n}}}_{\mathit{i}\mathit{n}}$ and discharged by the purge valve ${\mathit{\alpha }}_{{\mathit{N}}_2,\mathit{t}-1}{\dot{\mathit{n}}}_{\mathit{o}\mathit{u}\mathit{t}}$. After calculating the gas composition at the nitrogen discharge valve, the gas composition of the stack input and the recirculation pump can be calculated.

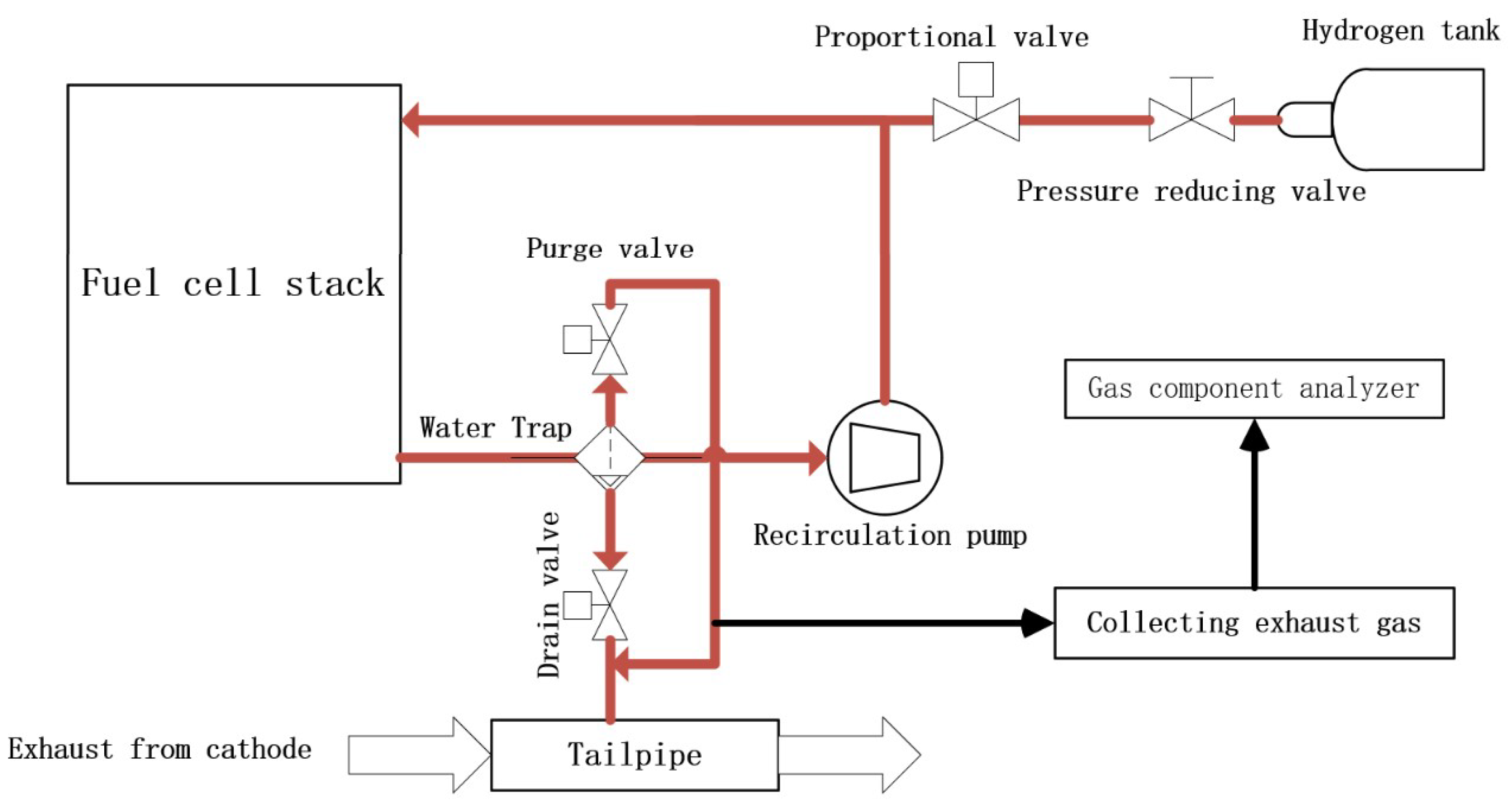
2. System Model Establishment

The topology of the anode circuit of the fuel cell is shown in Figure 2, which includes a proportional valve, a stack, a water trap, a recirculation pump, and a purge valve. Gas flow modeling is carried out for each of the above components, and then submodels such as those of the proportional valve, hydrogen consumption in the stack, nitrogen permeation in the stack, hydrogen circulation pump, and purge valve can be integrated. Additionally, The cathode adopts an open supply mode. The air flows into the stack after passing through the compressor and intercooler, and the gas after reaction flows into the tail pipe to mix with the gas discharged from the anode purge valve. We use the Matlab/Simulink software to study the accumulation process of nitrogen in the anode of the fuel cell under different current densities and the reliability of the observer model is verified with experimental results.

Assumptions:

(1)

The hydrogen in the hydrogen storage tank can be regarded as pure hydrogen, and the mixed gas in the anode circuit is applicable to the ideal gas law and Fick’s law;

(2)

The gas pressure is constant along the channel, and the pressure drop can be ignored for shorter straight channels;

(3)

The fuel cell stack and anode pipe are insulated systems, with each part at the same temperature and humidity;

(4)

The humidity of the proton exchange membrane is good, and the relative humidity of the gas in the pipeline and flow path is maintained at 95%;

(5)

The permeability coefficient of the stack membrane is related to the humidity and temperature of the membrane. When the stack operates stably, and the temperature is stable at around 70${}^{\circ }$–80${}^{\circ }$, C, the humidity of the membrane is stable at 95%. Therefore, the nitrogen permeability coefficient can be approximately constant.

2.1. Proportional Valve Model

The high pressure of the hydrogen supplied by the hydrogen tank in the fuel cell system cannot be directly input into the stack. Therefore, it is necessary to add a pressure reducing valve to reduce the pressure, and at the same time, introduce a proportional valve to control and adjust the gas supply amount. By changing the opening of the proportional valve, a regulating effect on the hydrogen supply of the stack is achieved. The flow coefficient of the proportional valve ${\mathit{K}}_{\mathit{v}}$ is as follows (as obtained from the reference document provided by the proportional valve company [25]):

$${\mathit{K}}_{\mathit{v}}=\left\{\begin{array}{cc}\frac{{\mathit{Q}}_{\mathit{N}}}{514}\sqrt{\frac{{\mathit{T}}_{\mathit{m}}{\mathit{\rho }}_{\mathit{N}}}{{\mathit{P}}_2\left({\mathit{P}}_1-{\mathit{P}}_2\right)}}& {\mathit{P}}_2>\frac{{\mathit{P}}_1}{2}\hfill \\ \frac{{\mathit{Q}}_{\mathit{N}}}{257{\mathit{P}}_1}\sqrt{{\mathit{T}}_{\mathit{m}}{\mathit{\rho }}_{\mathit{N}}}& {\mathit{P}}_2<\frac{{\mathit{P}}_1}{2}\hfill \end{array}\right.$$

(1)

where ${\mathit{Q}}_{\mathit{N}}$ (m${}^3$/h) is the volume flow rate under standard gas conditions; ${\mathit{P}}_1$ and ${\mathit{P}}_2$ (bar) are, respectively, the inlet and outlet pressures of the proportional valve; and ${\mathit{T}}_{\mathit{m}}$ is the medium temperature of the proportional valve.

During the use of fuel cells, the proportional valve inlet is connected to the hydrogen tank, and its inlet pressure is usually much higher than the outlet pressure. Therefore, the proportional valve flow ${\mathit{Q}}_{\mathit{v}}$ (m${}^3$/s) can be calculated as follows:

$${\mathit{Q}}_{\mathit{v}}=\mathit{\alpha }{\mathit{Q}}_{\mathit{N}}=\mathit{\alpha }\frac{257{\mathit{P}}_1{\mathit{K}}_{\mathit{v}}}{\sqrt{{\mathit{T}}_{\mathit{m}}{\mathit{\rho }}_{\mathit{N}}}}$$

(2)

where ${\mathit{Q}}_{\mathit{v}}$ (m${}^3$/h) is the actual outlet volume flow of the proportional valve; and $\mathit{\alpha }$ is the opening degree of the proportional valve, with a value ranging from 0 to 1.

Thus, the molar flow rate of hydrogen at the outlet of the proportional valve $\dot{{\mathit{n}}_{\mathit{i}\mathit{n}}}$ (mol/s) can be calculated as follows:

$$\dot{{\mathit{n}}_{\mathit{i}\mathit{n}}}=\frac{5{\mathit{Q}}_{\mathit{v}}}{18{\mathit{V}}_{\mathit{m}}}$$

(3)

where ${\mathit{V}}_{\mathit{m}}$ is the molar volume of gas under standard conditions, 22.4 L/mol.

2.2. Hydrogen Consumption Model

Based on the law of proton conservation, the amount of hydrogen consumed in the reaction ${\mathit{n}}_{{\mathit{H}}_2}$ can be obtained:

$$\mathit{Q}=2\mathit{e}·{\mathit{n}}_{{\mathit{H}}_2}{\mathit{N}}_{\mathit{A}}$$

(4)

where e is the amount of charge per unit electron ($1.60\times {10}^{-19}\mathit{C}$); ${\mathit{N}}_{\mathit{A}}$ is the Avogadro constant $6.02\times {10}^{23}$; and Q (C) is the number of charges generated corresponding to the hydrogen consumed by the stack reaction.

Thus, the hydrogen consumption per unit time of the stack during the reaction ${\dot{\mathit{n}}}_{\mathit{s}\mathit{t}\mathit{a}\mathit{c}\mathit{k},{\mathit{H}}_2}$ can be calculated as:

$${\dot{\mathit{n}}}_{\mathit{s}\mathit{t}\mathit{a}\mathit{c}\mathit{k},{\mathit{H}}_2}=\frac{\mathit{n}·{\mathit{n}}_{{\mathit{H}}_2}}{\mathit{t}}=\frac{\mathit{n}·\mathit{I}}{2\mathit{F}}$$

(5)

where n is the number of cells in the stack; I (A) is the stack current; and F is the Faraday constant 96,485 C/mol;

2.3. Nitrogen Crossover Model

According to [6], the permeation of nitrogen includes the dissolution process of nitrogen and the diffusion process of nitrogen in the membrane. Furthermore, the driving force of permeation is the concentration gradient across the membrane, as nitrogen diffuses from the higher concentration area on the cathode side to the lower concentration area on the anode side. The molar permeation amount of nitrogen per unit time and area ${\mathit{\alpha }}_{\mathit{s}\mathit{t}\mathit{a}\mathit{c}\mathit{k},{\mathit{N}}_2}$ can be calculated as:

$${\mathit{\alpha }}_{\mathit{s}\mathit{t}\mathit{a}\mathit{c}\mathit{k},{\mathit{N}}_2}={\mathit{k}}_{{\mathit{N}}_2}\frac{{\mathit{P}}_{\mathit{c}\mathit{a},{\mathit{N}}_2}-{\mathit{P}}_{\mathit{a}\mathit{n},{\mathit{N}}_2}}{{\mathit{\delta }}_{\mathit{m}}}$$

(6)

where ${\mathit{\delta }}_{\mathit{m}}$ (m) is the thickness of the membrane in the stack; ${\mathit{P}}_{\mathit{c}\mathit{a},{\mathit{N}}_2}$ and ${\mathit{P}}_{\mathit{a}\mathit{n},{\mathit{N}}_2}$ ($\mathit{P}\mathit{a}$) are the cathode and anode nitrogen partial pressures, respectively; and ${\mathit{K}}_{{\mathit{N}}_2}$ (molm${}^{-1}$s${}^{-1}$Pa${}^{-1}$) is the nitrogen permeability in the membrane, which is determined by the temperature and the water content in the membrane [26,27]:

$${\mathit{K}}_{{\mathit{N}}_2}=(0.0295+1.21{\mathit{f}}_{\mathit{v}}-1.93{\mathit{f}}_{\mathit{v}}^2)·{10}^{-14}·exp\left(\frac{{\mathit{E}}_{{\mathit{N}}_2}}{\mathit{R}}(\frac{1}{{\mathit{T}}_0}-\frac{1}{\mathit{T}})\right)$$

(7)

where ${\mathit{E}}_{{\mathit{N}}_2}$ is the activation energy of nitrogen (${\mathit{E}}_{{\mathit{N}}_2}$ = 24 kJmol${}^{-1}$); ${\mathit{T}}_0$ is the reference temperature (${\mathit{T}}_0$ = 303 K); and ${\mathit{f}}_{\mathit{v}}$ is the volume fraction of water content in the membrane:

$${\mathit{f}}_{\mathit{v}}=\frac{{\mathit{\lambda }}_{\mathit{m}}{\mathit{V}}_{\mathit{w}}}{{\mathit{V}}_{\mathit{m},\mathit{d}\mathit{r}\mathit{y}}+{\mathit{\lambda }}_{\mathit{m}}{\mathit{V}}_{\mathit{w}}}$$

(8)

where ${\mathit{\lambda }}_{\mathit{m}}$ is water content in the membrane; and ${\mathit{V}}_{\mathit{w}}$ and ${\mathit{V}}_{\mathit{m},\mathit{d}\mathit{r}\mathit{y}}$ are molar volumes of the liquid water and dry membrane, respectively.

Thus, the molar flow rate of the nitrogen permeation ${\dot{\mathit{n}}}_{\mathit{c}\mathit{r}\mathit{o}\mathit{s}\mathit{s},{\mathit{N}}_2}$ (mol/s) in stack can be calculated as:

$${\dot{\mathit{n}}}_{\mathit{c}\mathit{r}\mathit{o}\mathit{s}\mathit{s},{\mathit{N}}_2}=\mathit{n}·\mathit{s}·{\mathit{k}}_{{\mathit{N}}_2}\frac{{\mathit{P}}_{\mathit{c}\mathit{a},{\mathit{N}}_2}-{\mathit{P}}_{\mathit{a}\mathit{n},{\mathit{N}}_2}}{{\mathit{\delta }}_{\mathit{m}}}$$

(9)

2.4. Purge Valve Model

The purge valve only has two states: open and closed, so the model can be simplified to only open and close. The flow rate of the purge valve in the open state depends on the pressure difference between both sides of the valve:

$${\mathit{Q}}_{\mathit{V}\mathit{o}}=\left\{\begin{array}{cc}\frac{514{\mathit{K}}_{\mathit{v}2}\sqrt{{\mathit{P}}_2\left({\mathit{P}}_1-{\mathit{P}}_2\right)}}{\sqrt{{\mathit{T}}_{\mathit{m}}{\mathit{\rho }}_{\mathit{N}}}}& \mathrm{Valve}\mathrm{open}\\ 0& \mathrm{Valve}\mathrm{closed}\end{array}\right.$$

(10)

thus, the molar gas flow rate at the outlet of the purge valve ${\dot{\mathit{n}}}_{\mathit{o}\mathit{u}\mathit{t}}$ ($\mathrm{m}\mathrm{o}\mathrm{l}/\mathrm{s}$) can be calculated as:

$${\dot{\mathit{n}}}_{\mathit{o}\mathit{u}\mathit{t}}=\frac{5{\mathit{Q}}_{\mathit{V}\mathit{o}}}{18{\mathit{V}}_{\mathit{m}}}$$

(11)

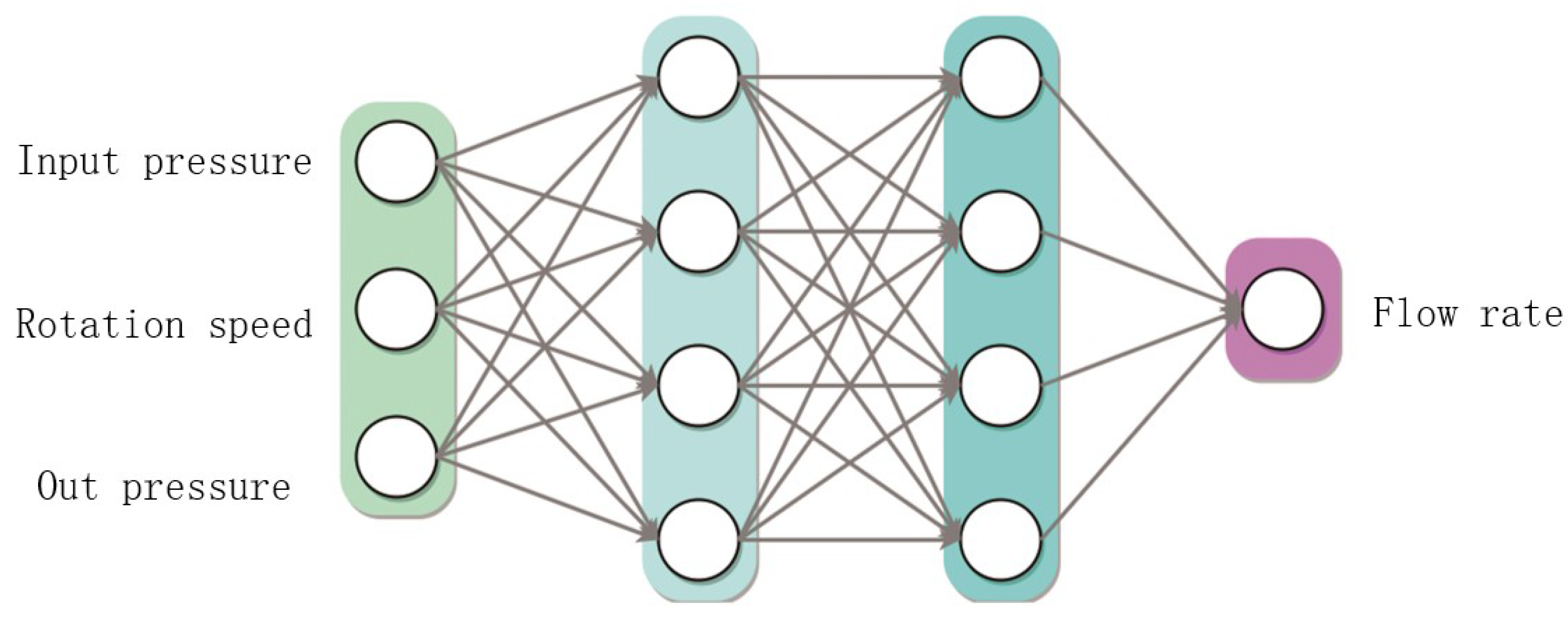
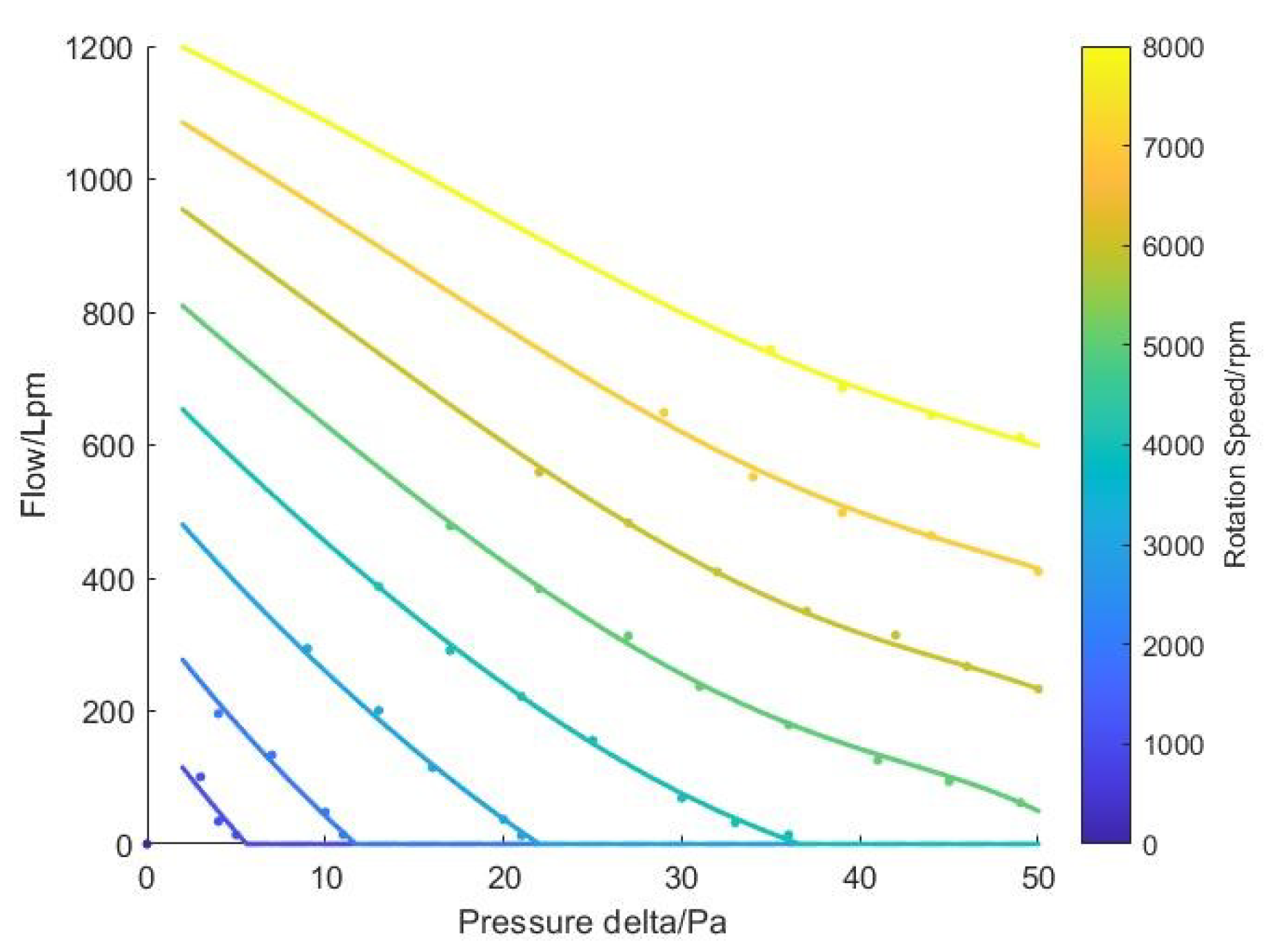
2.5. Recirculation Pump Model

Due to the strong nonlinear characteristics of the recirculation pump, this paper uses a neural network model to establish a model of the volume flow rate with a rotational speed and differential pressure based on the map data of the recirculation pump. Using a three-layer neural network structure, the inputs are the input pressure, rotation speed, and input–output pressure difference of the hydrogen recirculation pump. Therefore, the flow rate of the hydrogen recirculation pump ${\mathit{Q}}_{\mathit{r}\mathit{p}}$ (L/min) can be expressed as follows:

$${\mathit{Q}}_{\mathit{r}\mathit{p}}={\mathit{f}}_{\mathit{n}\mathit{e}\mathit{t}}(\mathit{n},\mathit{\delta }\mathit{p},{\mathit{p}}_{\mathit{i}\mathit{n}})$$

(12)

where ${\mathit{f}}_{\mathit{n}\mathit{e}\mathit{t}}$ is the function mapping of the neural networks, which is showed in Figure 3; n (rpm) is the rotation speed of the pump; and $\mathit{\delta }\mathit{p}$ ($\mathit{P}\mathit{a}$) is the input–output pressure difference of the pump.

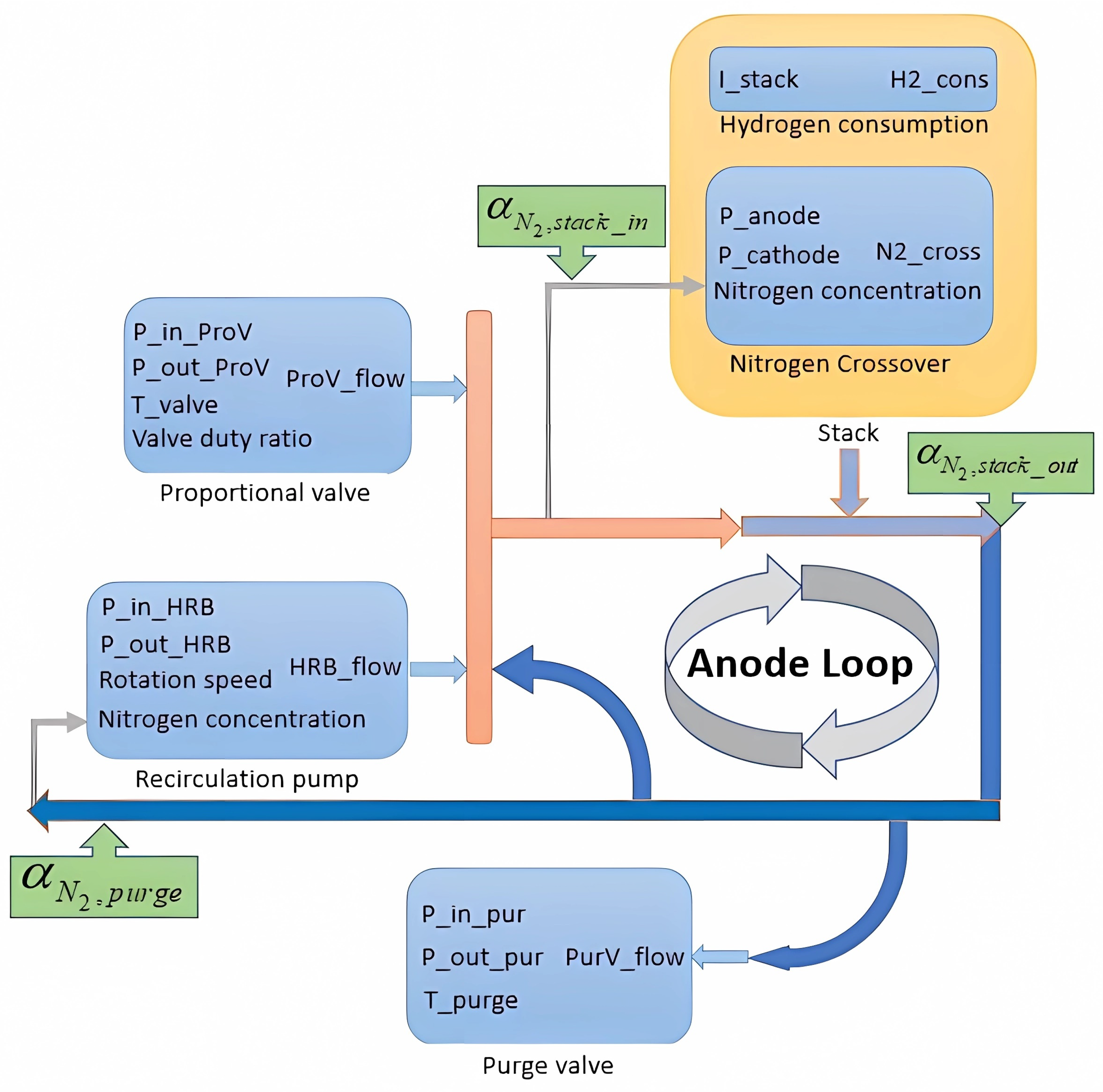
2.6. Integrated Models

By integrating the above submodels into the mass conservation model of the fuel cell hydrogen circuit, a simulation model is established as shown in Figure 4 to analyze the changes in nitrogen content in the anode circuit of the stack.

First, there is the stack input section (as shown in the orange section of Figure 4). The stack input includes the proportional valve input hydrogen and the mixture circulated by the recirculation pump. Therefore, the molar flow rate of the stack input gas can be calculated as:

$${\dot{\mathit{n}}}_{\mathit{s}\mathit{t}\mathit{a}\mathit{c}\mathit{k},\mathit{i}\mathit{n}}={\dot{\mathit{n}}}_{\mathit{i}\mathit{n}}+{\dot{\mathit{n}}}_{\mathit{r}\mathit{p}}$$

(13)

The molar flow rate of the nitrogen input to the stack can be calculated as:

$${\dot{\mathit{n}}}_{{\mathit{N}}_2,\mathit{s}\mathit{t}\mathit{a}\mathit{c}\mathit{k},\mathit{i}\mathit{n}}={\mathit{\alpha }}_{{\mathit{N}}_2,\mathit{t}-1}{\dot{\mathit{n}}}_{\mathit{r}\mathit{p}}$$

(14)

Second, in the output section of the stack (as shown in the light blue section in Figure 4), through the electrochemical reaction of the stack, a portion of the hydrogen is consumed, and due to the permeation of nitrogen, the amount of nitrogen in the output gas increases. Therefore, the molar flow rate of the output gas of the stack can be calculated as:

$${\dot{\mathit{n}}}_{\mathit{s}\mathit{t}\mathit{a}\mathit{c}\mathit{k},\mathit{o}\mathit{u}\mathit{t}}={\dot{\mathit{n}}}_{\mathit{s}\mathit{t}\mathit{a}\mathit{c}\mathit{k},\mathit{i}\mathit{n}}-{\dot{\mathit{n}}}_{\mathit{s}\mathit{t}\mathit{a}\mathit{c}\mathit{k},{\mathit{H}}_2}+{\dot{\mathit{n}}}_{\mathit{c}\mathit{r}\mathit{o}\mathit{s}\mathit{s},{\mathit{N}}_2}$$

(15)

the molar flow rate of the nitrogen in the output gas of the stack can be calculated as:

$${\dot{\mathit{n}}}_{{\mathit{N}}_2,\mathit{s}\mathit{t}\mathit{a}\mathit{c}\mathit{k},\mathit{o}\mathit{u}\mathit{t}}={\dot{\mathit{n}}}_{{\mathit{N}}_2,\mathit{s}\mathit{t}\mathit{a}\mathit{c}\mathit{k},\mathit{i}\mathit{n}}+{\dot{\mathit{n}}}_{\mathit{c}\mathit{r}\mathit{o}\mathit{s}\mathit{s},{\mathit{N}}_2}$$

(16)

By combining the above submodels, the molar concentration of nitrogen in the anode purge valve can be obtained:

$${\mathit{\alpha }}_{{\mathit{N}}_2,\mathit{purge},\mathit{t}}=\frac{\int {\dot{\mathit{n}}}_{\mathit{cross},{\mathit{N}}_2}\mathit{d}\mathit{t}-\int {\mathit{\alpha }}_{{\mathit{N}}_2,\mathit{p}\mathit{u}\mathit{r}\mathit{g}\mathit{e},\mathit{t}-1}\left({\dot{\mathit{n}}}_{\mathit{out}}+{\dot{\mathit{n}}}_{\mathit{r}\mathit{p}}\right)\mathit{d}\mathit{t}}{\int {\dot{\mathit{n}}}_{\mathit{i}\mathit{n}}+{\dot{\mathit{n}}}_{\mathit{r}\mathit{p},\mathit{t}-{\mathit{t}}_0}-{\dot{\mathit{n}}}_{\mathit{s}\mathit{t}\mathit{a}\mathit{c}\mathit{k},{\mathit{H}}_2}+{\dot{\mathit{n}}}_{\mathit{cross},{\mathit{N}}_2}-{\dot{\mathit{n}}}_{\mathit{out}}-{\dot{\mathit{n}}}_{\mathit{r}\mathit{p},\mathit{t}}\mathit{d}\mathit{t}}$$

(17)

where ${\mathit{\alpha }}_{{\mathit{N}}_2,\mathit{purge},\mathit{t}}$ is the nitrogen concentration at the purge valve at time t; ${\mathit{\alpha }}_{{\mathit{N}}_2,\mathit{p}\mathit{u}\mathit{r}\mathit{g}\mathit{e},\mathit{t}-1}$ is the nitrogen concentration at the purge valve at the previous moment; ${\dot{\mathit{n}}}_{\mathit{i}\mathit{n}}$ is the molar flow rate of the input gas to the proportional valve; ${\dot{\mathit{n}}}_{\mathit{s}\mathit{t}\mathit{a}\mathit{c}\mathit{k},{\mathit{H}}_2}$ is the hydrogen consumption rate of the stack; ${\dot{\mathit{n}}}_{\mathit{cross},{\mathit{N}}_2}$ is the nitrogen permeation flow rate of the stack; ${\dot{\mathit{n}}}_{\mathit{out}}$ is the molar flow rate of the exhaust gas from the purge valve; ${\dot{\mathit{n}}}_{\mathit{r}\mathit{p},\mathit{t}}$ is the molar flow rate of return gas from the recirculation pump; and ${\dot{\mathit{n}}}_{\mathit{r}\mathit{p},\mathit{t}-{\mathit{t}}_0}$ is the molar flow rate of the return gas from the recirculation pump of the previous cycle, where ${\mathit{t}}_0$ is the time taken for the gas circulated by the recirculation pump to reach the outlet of the purge valve.

The average nitrogen concentration of the entire anode loop can be calculated as:

$${\mathit{\alpha }}_{\mathit{all},{\mathit{N}}_2,\mathit{t}}=\frac{\int {\dot{\mathit{n}}}_{\mathit{cross},{\mathit{N}}_2}-{\mathit{\alpha }}_{{\mathit{N}}_2,\mathit{p}\mathit{u}\mathit{r}\mathit{g}\mathit{e},\mathit{t}}{\dot{\mathit{n}}}_{\mathit{o}\mathit{u}\mathit{t}}\mathit{d}\mathit{t}}{\int {\dot{\mathit{n}}}_{\mathit{in}}-{\dot{\mathit{n}}}_{\mathit{stack},{\mathit{H}}_2}+{\dot{\mathit{n}}}_{\mathit{cross},{\mathit{N}}_2}-{\dot{\mathit{n}}}_{\mathit{out}}\mathit{d}\mathit{t}}$$

(18)

3. Experiment and Validation

3.1. Experiments and Model Parameter Calibration

Figure 2 shows the structure of the experiment setup which consists of a 125 kw PEM fuel cell and a gas component analyzer. The fuel cell system consists of 396 cells, each with an active area of 275 cm${}^2$. The first step is to calibrate the model parameters of each subsystem of the fuel cell anode loop, including the proportional valve flow coefficient, purge valve flow coefficient, stack nitrogen permeability coefficient, and hydrogen recirculation pump map data. For the flow coefficient of the valve, the flow coefficient is mainly calculated through Equation (1) between the flow measured by the flowmeter and the pressure on both sides of the valve. The nitrogen permeability coefficient of the stack is measured in the straight mode of the stack, that is, when the purge valve is opened and the recirculation pump is stopped. The nitrogen permeability coefficient of the stack is calculated based on the concentration of nitrogen in the exhaust gas in combination with Equation (9). The parameters in the model calculated through bench calibration experiments are shown in

Table 1. Initial parameters of the PEMFC system.

Symbol	Parameter	Value
${\mathit{K}}_{\mathit{v}}$	Proportional valve flow coefficient	$0.34$ m3/h
n	Cell number	396
s	Active area of the single cell	275 cm2
${\mathit{\delta }}_{\mathit{m}}$	Membrane thickness	60 $\mathsf{\mu }\mathrm{m}$
${\mathit{k}}_{{\mathit{N}}_2}$	Nitrogen permeability coefficient	$8.52$ × 10−15 mol/(m s Pa)
V	Stack anode volume	$0.07$ m3
${\mathit{K}}_{\mathit{v}2}$	Purge valve flow coefficient	$0.12$ m3/h
R	Gas constant	$8.314$ K/(mol K)
F	Faraday constant	$96,485$ C/mol
${\mathit{\rho }}_{\mathit{N}}$	Density of hydrogen	$0.089$ g/L
${\mathit{V}}_{\mathit{m}}$	Molar volume of gas	$22.4$ L/mol

.

The second step is to adopt two purge intervals: one purge interval of 6 s and another 10 s, and take different current densities such as 550 A, 495 A, 410 A, 300 A, 190 A, and 80 A to perform a comparative analysis of the different operating conditions of the fuel cell. Additionally, at one current density, the fuel cell is operated four times in order to open the purge valve to collect exhaust gas at 50 s, 100 s, 150 s, and 200 s, then use a gas component analyzer to analyze the gas components as experimental data. At the same time, the constructed model is used to calculate the nitrogen concentration at the fuel cell purge valve, and compared with experimental data to verify the accuracy of the model.

The map data of the recirculation pump measured from the bench experiment are used to train the neural network model of the circulating pump. The fitting results and validation values are shown in Figure 5.

Using a neural network model can effectively characterize the recirculation pump map, with the inlet pump pressure, outlet pump pressure, and rotational speed as input, and the circulating pump flow as output. The model error is within 3%.

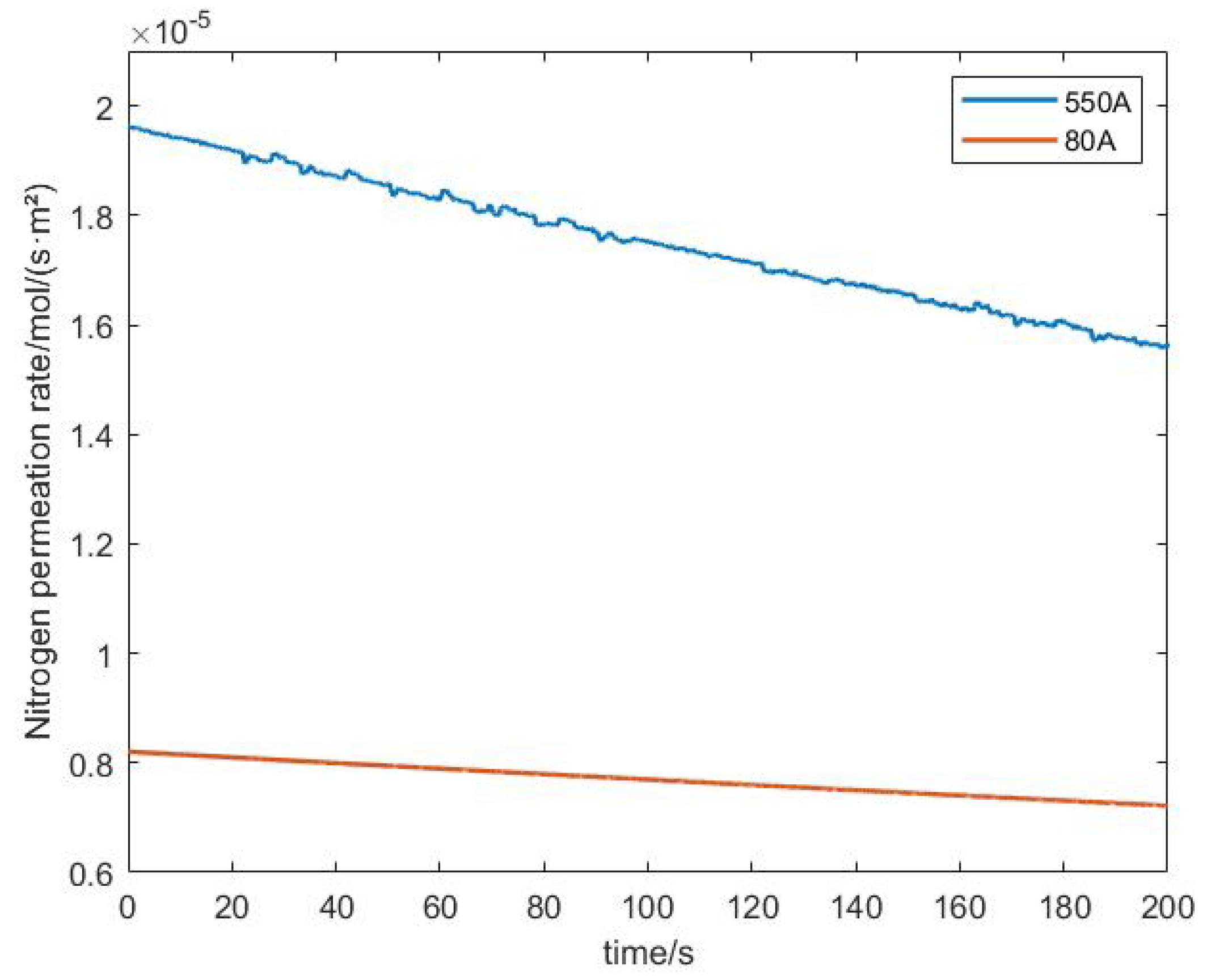
3.2. Analysis of Experimental Results

The state of the purge valve is shown in Figure 6, where 1 means that the purge valve is open, whilst 0 means that it is closed. Two different purge intervals are used to observe the changes in the output performance of the stack, including the output performance of the stack and the characteristics of the recirculation pump, respectively, characterizing the differences in stack performance and the gas density of the anode circuit.

As shown in Figure 7, when different purging intervals are used, the stack output voltage changes significantly.

The stack studied in this article is the product that the company is currently about to install on actual vehicles. The two purge intervals used for high load and low load of are 6 s and 10 s, respectively. Therefore, this experiment mainly uses two typical purge cycles as experimental choices. Figure 7a shows the output raw data of the entire operation process of the stack (without any filtering processing). Figure 7b is a partial magnification of Figure 7a, which takes the main output operating range (50 A–420 A) of the stack. At the same current, the voltage difference is about 10 v, with a performance degradation of 4–6%.

Based on the output data of the stack in Figure 7b, two polarization curves were fitted at purge intervals of 6 s and 10 s, and the relationship between the voltage drop and stack current in Figure 8 was obtained by comparing the two curves. It can be seen that, as the current increases, the voltage drop of the stack increases (the voltage of the stack is 200–300 V). When the purging interval is 6 s, the voltage drop of the stack is about 3 V, while when it is 10 s, the voltage drop of the stack is about 13 V. The voltage drop gradually increases with the increase in the purging interval and the amplitude of the increase also increases.

Figure 9 shows, at same the rotational speed (the rotational speed of the pump is proportional to the stack current), the power of the recirculation pump undergoes a significant change, indicating that the gas density in the anode loop increases and nitrogen accumulation increases. At the same time, according to the polarization curve shown in Figure 7, it can be seen that the nitrogen purge interval is shortened, the stack voltage is increased, and the stack efficiency is improved. The nitrogen content in the stack can have an impact on the operating efficiency of the stack, so the effective estimation of nitrogen content can be of great help to improve the operating efficiency and fuel utilization of the fuel cells.

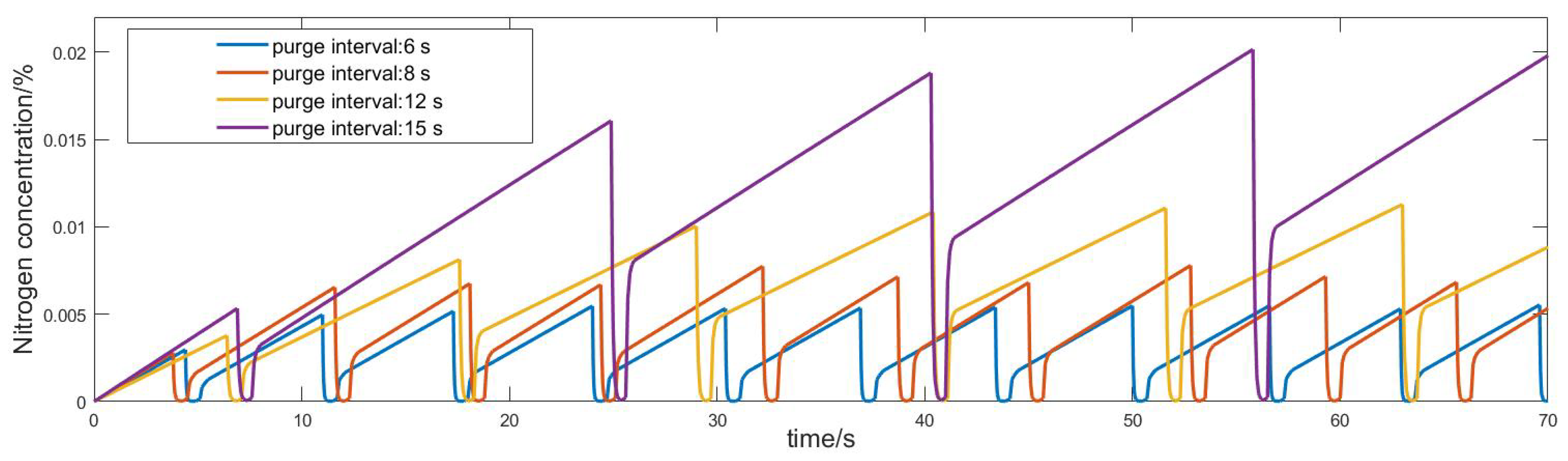
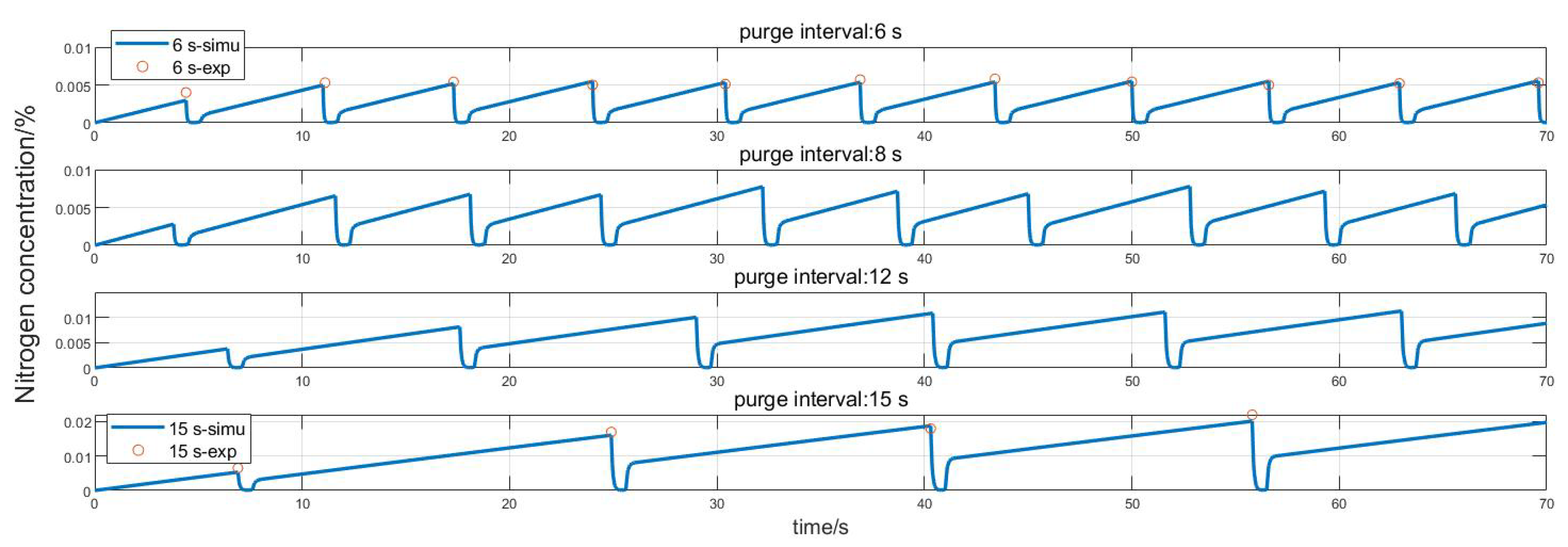
3.3. Validation and Simulation of the Model

According to the operating conditions of the fuel cell, current densities such as 550 A, 495 A, 410 A, 300 A, 190 A, and 80 A are taken to analyze the different operating conditions of the fuel cell. The nitrogen concentration at the purge valve of the fuel cell is calculated based on the model. At the same time, the exhaust gas is collected at 50 s, 100 s, 150 s, and 200 s separately to measure the nitrogen concentration by the gas component analyzer, and the experimental data are compared with the calculated value of the model. Considering that the fluctuation of humidity in the stack can affect the nitrogen permeability coefficient, the model developed in this experiment is based on the good humidity conditions of the membrane. The influence of humidity on the nitrogen permeability coefficient is about 10%, so the measured nitrogen concentration in the experiment may fluctuate by 10%.

Figure 10 shows the comparison between the simulated and experimental data of the nitrogen concentration accumulated over time under different current densities. It can be seen that the predicted values of the model are in good agreement with the experimental data and the model can be used to estimate the nitrogen concentration in the stack. The average error of the model is about 5.5%.

In addition, as shown in Figure 10, under the condition of not opening the purge valve, the nitrogen penetration rate increases with the increasing current density of the stack. Under high current density conditions, the nitrogen concentration can reach about 11% within 200 s, while under low current density conditions, the concentration of nitrogen accumulated within 200 s is about 4.5%. Therefore, it is necessary to adjust the purge strategy under different load conditions. At higher loads, in order to ensure that the performance of the stack meets the use, it is necessary to shorten the purge interval; at lower loads, the nitrogen accumulation is relatively slow, and the purge interval can be appropriately increased to improve fuel utilization. If the load varies, the purge interval can be dynamically adjusted based on the nitrogen concentration observed by the model to meet the high-performance output of the stack while ensuring maximum fuel utilization efficiency. Figure 11 shows that, as nitrogen accumulates, the nitrogen permeation rate gradually decreases, and the greater the current, the faster the nitrogen permeation rate decreases.

Figure 11 shows the non-purging conditions, so the purge valve model has not been validated yet. Therefore, under the 300 A operating condition of the stack, we chose to measure the gas composition of the exhaust gas after each purge interval of 6 s and 15 s, and compared it with the simulation values to obtain Figure 12. It can be seen that, under the conditions of purge intervals of 6 s and 15 s, the model can effectively estimate the nitrogen concentration in the exhaust gas. Figure 13 shows that, when the current density is 300 A, the frequency of opening the purge valve increases, which can significantly reduce the nitrogen content of the anode circuit. When the purge frequency is 15 s and the purge duration is 0.5 s, the nitrogen content fluctuates between around 1% and 2%; however, when the purge frequency is 6 s and the opening time is 0.5 s, the nitrogen content fluctuates between 0.1% and 0.5%.

It can be seen from Figure 12 that increasing the frequency of opening the purge valve can reduce the nitrogen content in the anode circuit of the stack, but opening it too frequently can cause a large amount of hydrogen to be discharged without participating in the reaction, resulting in excessive waste. Therefore, when designing the purge strategy, it is necessary to consider both the performance output and fuel economy. Under high load conditions, in order to ensure that performance does not decay too much, it is necessary to sacrifice some of the fuel’s economic efficiency to increase the opening frequency of the nitrogen removal valve. Under low load conditions, where the performance requirements for the stack are not high, the reaction conditions can be appropriately reduced, that is, operating under a certain concentration of nitrogen input conditions, reducing the opening frequency of the nitrogen removal valve and avoiding unnecessary hydrogen emissions.

4. Discussion

Baik et al. [8] studied the characteristics of nitrogen transmembrane permeation in the proton exchange membrane fuel cells, with a 1 kw stack and an effective monomer reaction area of 25 cm${}^2$. The measured nitrogen permeability coefficient is 7.92 × ${10}^{-14}$ (mol/(m s Pa)), and the operating conditions of the fuel cell are: humidity close to 100%, temperature of 70 °C, hydrogen flow rate of 0.9 L/min, air flow rate of 2 L/min, and a measured nitrogen concentration in the anode outlet of 80 ppm, which is 0.008%. On this basis, Chen et al. [12] also established a flow model for the anode based on the principle of mass conservation, and the calculated nitrogen permeability is as follows in Figure 14:

Wang, B. et al. [16] also used the principle of mass conservation for modeling, but refined the modeling including the anode flow channel, gas diffusion layer, and catalytic layer. They did not provide the nitrogen penetration rate, only the relationship between the nitrogen concentration at the anode outlet and the duty cycle of the purge valve opening in Figure 15.

Their research is mainly focused on modeling cells, and there is a lack of research on large stacks. Additionally, previous studies have considered the anode as a whole, only considering the input of the proportional valve and the output of the purge valve. The calculated nitrogen concentration is the average nitrogen concentration. However, during the actual operation of the stack, the nitrogen concentration varies at different positions in the anode loop, that is, the gas after the electrochemical reaction of the stack has the highest nitrogen concentration, while the nitrogen concentration of the mixture before entering the stack is the lowest. The difference between this article and other researchers lies in the refinement of the model of the anode circuit, in which one can observe the nitrogen concentration at different points in the anode circuit.

Additionally, after knowing the nitrogen concentration, the hydrogen content in the exhaust gas can be calculated in a purging cycle, so fuel loss can be quantified. This equation can be used for calculating fuel loss here:

$${\mathit{\eta }}_{\mathit{fl}}=\frac{{\int }_{\mathit{purge}}{\dot{\mathit{n}}}_{{\mathit{H}}_2,\mathit{o}\mathit{u}\mathit{t}}\mathit{d}\mathit{t}}{{\int }_{\mathit{cycle}}\frac{\mathit{I}}{2\mathit{F}}{\mathit{A}}_{\mathit{act}}\mathit{d}\mathit{t}+{\int }_{\mathit{purge}}{\dot{\mathit{n}}}_{{\mathit{H}}_2,\mathit{o}\mathit{u}\mathit{t}}\mathit{d}\mathit{t}}$$

(19)

where ${\dot{\mathit{n}}}_{{\mathit{H}}_2,\mathit{o}\mathit{u}\mathit{t}}$ is the hydrogen flow rate discharged by the purge valve; and ${\int }_{\mathit{cycle}}\frac{\mathit{I}}{2\mathit{F}}{\mathit{A}}_{\mathit{act}}\mathit{d}\mathit{t}$ is the hydrogen consumption in a purging cycle.

In the present study, we proposed a mass conservation model to observe the nitrogen content in the anode circuit of the fuel cell and studied the accumulation process of nitrogen over time in the anode circuit, as well as the rate of nitrogen accumulation under different currents. The nitrogen content observer proposed in this article can effectively estimate the nitrogen concentration at the purge valve and be used to quantify the fuel’s economic efficiency. The nitrogen content and the attenuation of the fuel cell can serve as the two objectives of purge strategy optimization to design an optimal strategy. 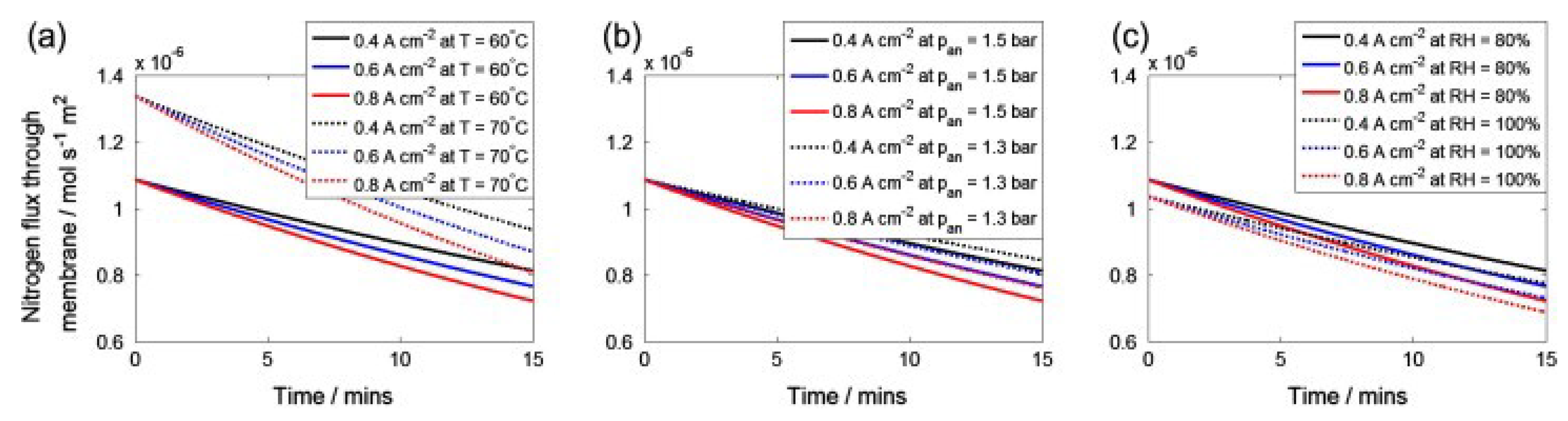Therefore, our next step is to develop a purge strategy based on nitrogen concentration and stack performance degradation.

5. Conclusions

This paper designs a nitrogen content observer for the anode circuit of a fuel cell. Firstly, each component of the fuel cell anode is modeled, and the nitrogen content in the anode circuit is estimated by integrating various component submodels to form a mass conservation model for the hydrogen circuit of the fuel cell. By calibrating the model and verifying the simulation results through experiments, the following conclusions can be obtained:

(1)

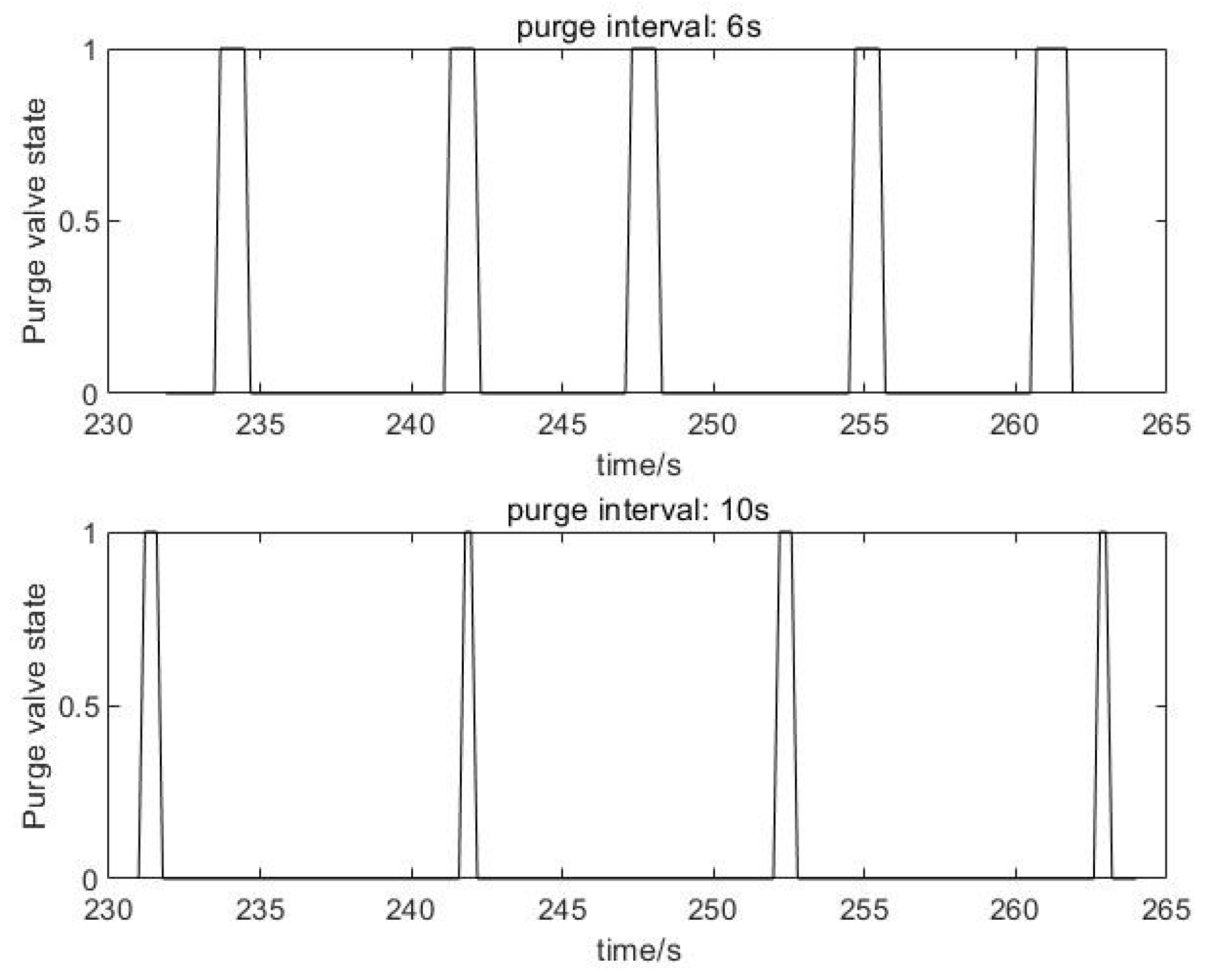
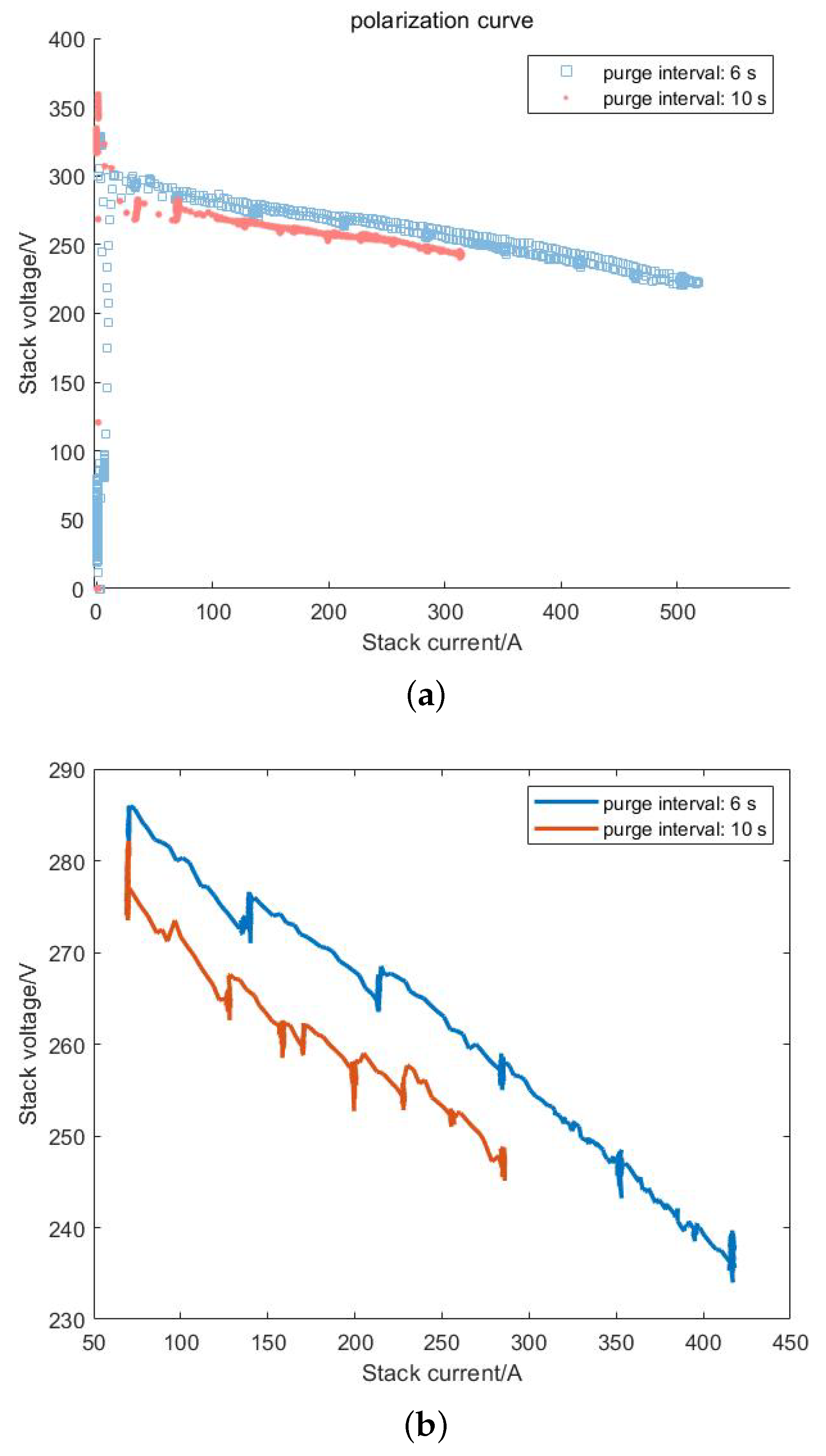
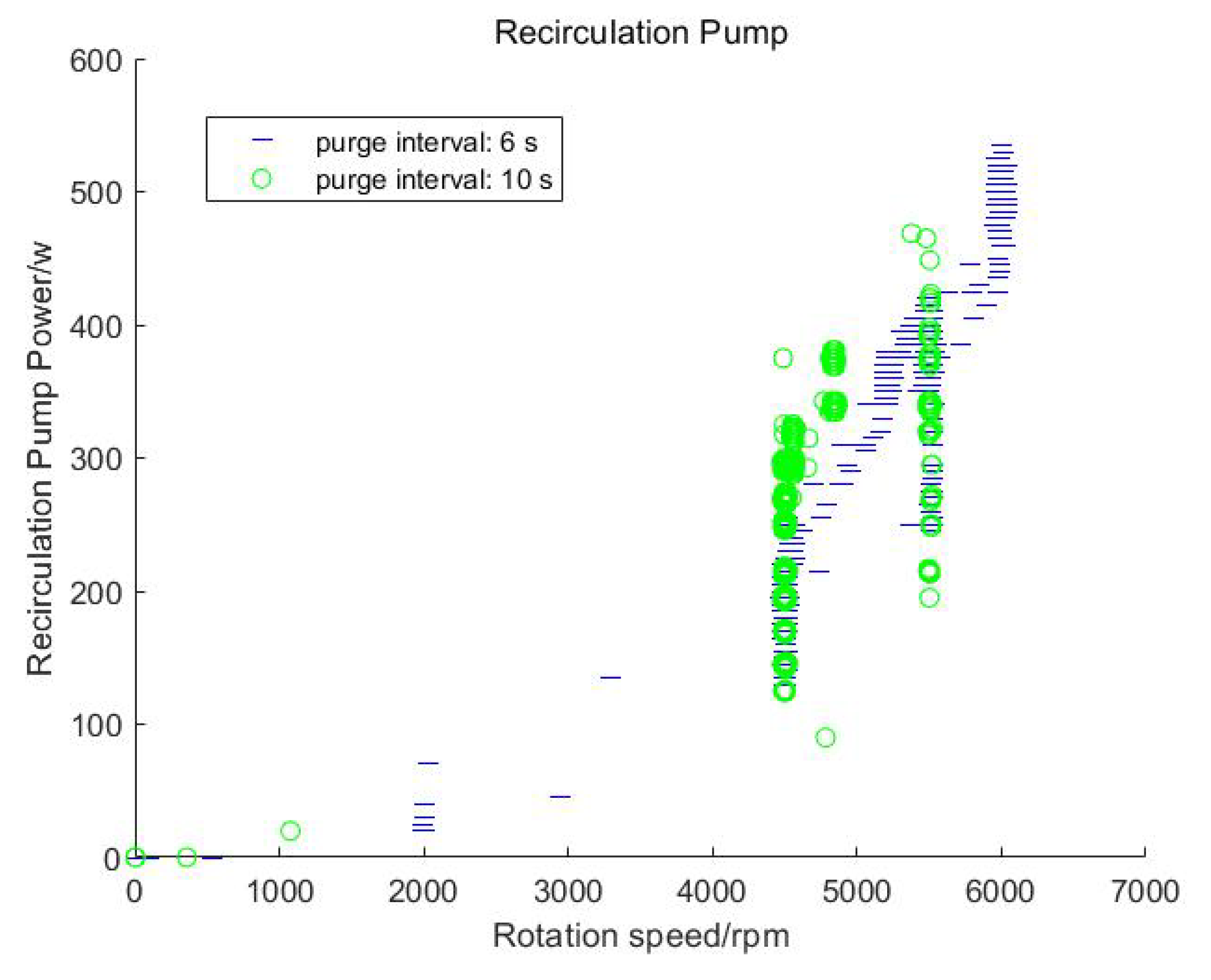
According to experimental data, when the stack adopts two different scavenging intervals (6 s and 10 s), compared to the 10 s scavenging interval, the 6 s scavenging interval can reduce the energy consumption of the hydrogen circulation pump by 20%. Under the same current conditions, the output voltage of the stack is increased by 10 V. Purging can effectively reduce the nitrogen content in the anode, thereby restoring the stack performance.

(2)

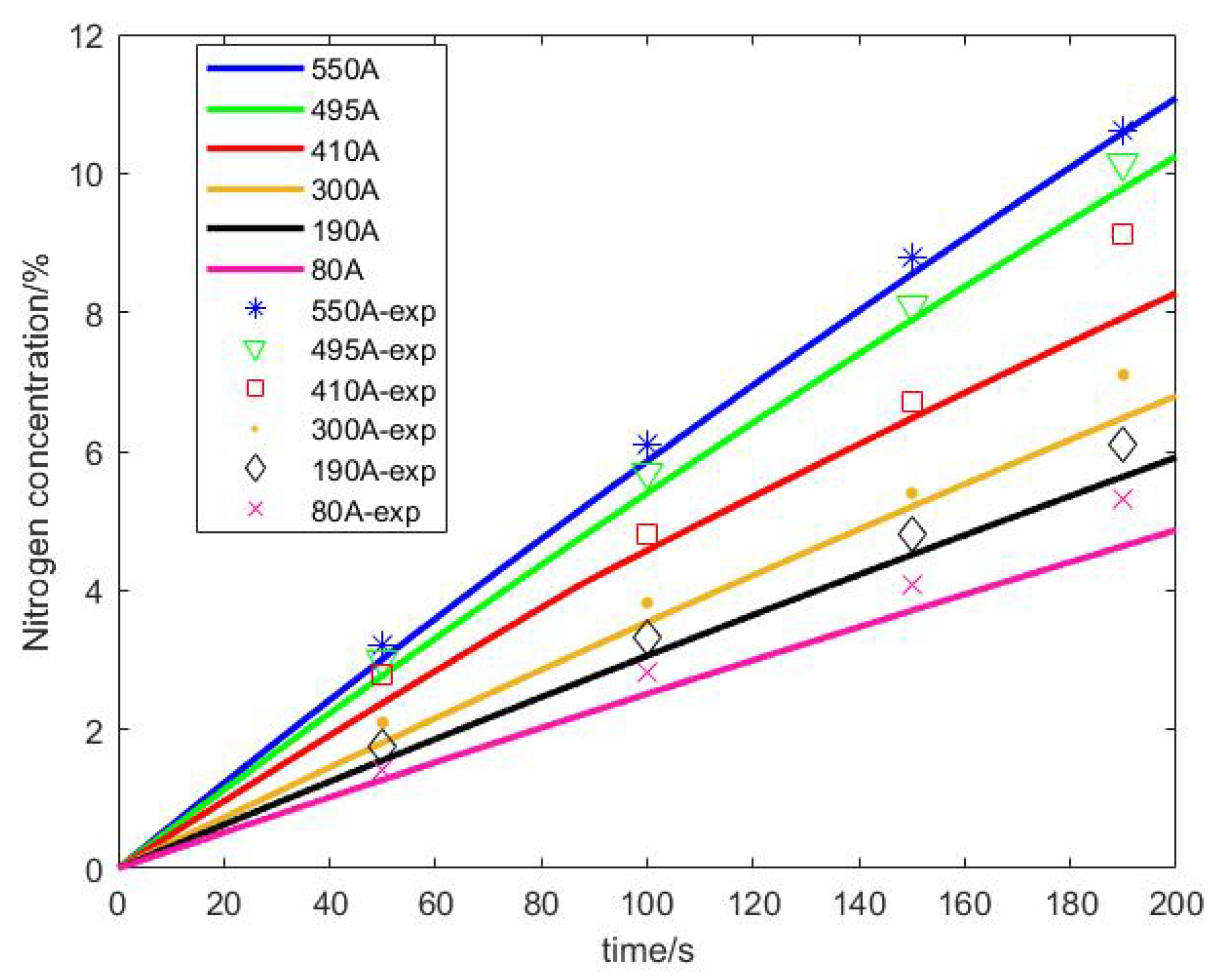
Under different current densities, the rate of nitrogen accumulation varies. Under high load, the nitrogen permeation rate at an output current of 500 A is more than twice that at a low load of 30 A, and the nitrogen permeation rate linearly decreases with the accumulation of nitrogen. Compared to low loads, the nitrogen permeation rate decreases faster under high loads. Additionally, under the condition of 300 A output current, the purge interval gradually increases by 6 s, 8 s, 12 s, and 15 s, and the exponential growth of the nitrogen concentration approximately increases by 0.5%, 0.7%, 1.1%, and 2%, respectively.

(3)

The nitrogen content observer proposed in this article is compared with the experimental results, and the error is less than 5.5%, which can effectively observe the nitrogen content in the anode. The nitrogen observation model combined with Equation (19) can calculate the hydrogen loss rate in a purge cycle, which can be used as a quantitative basis for formulating purge strategies.

The future work is to quantify the relationship between nitrogen content, purge interval, and voltage attenuation, combining the economic losses caused by voltage attenuation and hydrogen loss as quantitative indicators for formulating purge strategies. Then, the state of the purge valve can be adaptively adjusted based on the operating state of the stack to obtain the optimal strategy.