1. Introduction
With the energy dilemma and environmental pollution becoming worse, electric-powered vehicles have attracted considerable attention due to their lower green gas emission and oil consumption [
1]. Recent hybrid electric vehicles (HEVs) provide long-distance operation due to the optimal match between an engine powered by oil and electric motors powered by electricity stored in batteries. HEVs are widely researched by academics and have become dominant commercial products in EV markets [
2,
3]. For micro-hybrid EVs, an integrated starter generator (ISG) is the key component of both driving and generating systems, since it plays two major roles, namely, as a starter and a generator. Due to space and weight limitations, the rotor of an ISG is normally directly coupled to the flywheel of the engine in HEVs, where high torque (power) density, large overload torque capability, and high efficiency are expected. Hence, the flux-switching permanent magnet (FSPM) machine is considered as a promising candidate to be applied in electric vehicles, and aerospace and ship propulsion due to its high torque (power) density, high efficiency, and compact structure [
4].
With the ever-increasing demand for power (torque) density, research on machine loss and temperature has become a hot topic. An accurate thermal model is an essential tool not only at the machine design stage but also for online prediction of temperature distribution [
5]. While finite element method (FEM)-based and computational fluid dynamics (CFD)-based thermal models can achieve high accuracy, a lumped parameter thermal network (LPTN)-based model is often preferred thanks to its lower computational requirement and good accuracy [
6,
7,
8].
In [
9], the thermal influence of vehicle integration on the thermal load of an ISG was discussed by a FEM-based thermal model. In [
10], an axially segmented FEM model of a FSPM machine was proposed to analyze the coupled electromagnetic–thermal performances. A thermal resistance network was established based on a nine-node model for an interior PM (IPM) machine and the transient temperature characteristics were obtained [
11]. In [
12], a numerical approach for estimation of convective heat transfer coefficient in the end region of an ISG was proposed, and both the local and averaged heat transfer coefficients were estimated. A systematic procedure to study the impact of each thermal phenomenon in IPM machines used for ISG was presented in [
13]. In [
14], a reduced model in a multi-physical electric machine optimization procedure was proposed.
The contribution of this paper is to propose two temperature prediction models for a 10 kW FSPM machine as an ISG for micro-hybrid vehicles; namely, a LPTN thermal model, and a one-dimensional (1D) steady heat conduction (SHC) (1D-SHC) model. The two methods can both quickly predict the internal temperature distribution of the FSPM machine. The results were verified by CFD and experiments to prove their accuracy.
Section 2 will propose an improved core loss model considering both the DC-bias component and minor hysteresis loops in iron flux-density, and the core loss of the FSPM machine is calculated and verified by experiments. Then, in
Section 3 a LPTN model is proposed firstly to predict transient thermal behavior. After that, a simplified 1D-SHC thermal model is proposed to reveal the relationship between design parameters of a cooling jacket and thermal distribution of stator, and verified by experiments under different cooling conditions. In
Section 4, both steady and transient thermal predictions are compared with those from ANSYS fluent-based CFD. Experiments with rising temperatures were conducted on a prototyped FSPM machine and are detailed in
Section 5, followed by conclusions in
Section 6.
2. Loss Prediction Model
The key dimensions of the studied FSPM machine are listed in
Table 1. In addition to electromagnetic parameters, the thermal conductivities, the specific heats, and densities of materials used for transient thermal analysis are presented in
Table 2. The employed PM material was N35 and the silicon steel sheet was 35WW310.
The loss of the FSPM machine includes winding joule loss, core loss, eddy current loss in PMs, housing and frictional loss, and excess loss. According to the Bertotti G. model [
15], the core loss of PM machines
PFe consists of hysteresis loss, eddy current loss and excess loss, and the core loss yields:
where
Ph is hysteresis loss in W,
Pc is the classical eddy current loss in W,
Pe is the excess loss in W,
kh,
kc, and
ke are the corresponding coefficient of the above losses, respectively,
f is the fundamental frequency of a magnetizing flux in Hz, and
Bm is the maximum flux density in core in T.
However, Equation (1) only works given a purely sinusoidal magnetizing flux. To exactly obtain the magnetizing flux-density characteristics in the FSPM machine core, eight key points located in stator and rotor respectively are selected, as shown in
Figure 1a. Correspondingly, the resultant loci of the flux-density radial and tangential components (
Bgr/
Bgt) are predicted, as shown in
Figure 1b. Clearly, for the stator points 1 and 2, the surrounded areas by the
Bgr/
Bgt loci are to be almost zero, which means the averaged
Bgr/
Bgt values are nearly zero. However, for points 3 and 4, the corresponding areas (the blue one and the pink one) are not centrosymmetric, which means a DC-biased component exists. For the points 5~8 in the rotor, the
Bgr/
Bgt loci are all centrosymmetric and the averaged values are close to zero. A typically DC-biased component and a minor hysteresis loop are shown in
Figure 1c,d, respectively.
Unfortunately, the influence of magnetized DC-biased components and minor hysteresis loops are not well recognized in the commercial FEM software packages [
16]. Hence, to predict the core loss of FSPM machines more precisely, an improved model considering both DC-biased component and minor hysteresis loops is proposed as follows. Assuming that the minor loop is similar to the major loop, the core loss can be divided into radial and tangential components. The total core loss, including the hysteresis loss [
17], eddy current loss [
18], and excess loss [
19], can be obtained as follows:
where
Nelem is the finite elements number, Δ
Ai is the
ith finite element area in m
2,
Npri and
Npti are the radial and tangential minor loops numbers of the
ith element during one period, respectively,
Nstep is the calculation steps number,
Brmij and
Btmij are the maximum radial and tangential flux-densities of the
jth hysteresis loop in the
ith element in T, respectively,
Brmik and
Btmik are the maximum radial and tangential flux-density of the
ith element in the
kth calculation step in T, and Δ
t is the time step in s.
According to Equations (2)–(5), the core loss can be obtained by a combination platform of ANSYS and MATLAB, where based on ANSYS the detailed
Bgr/
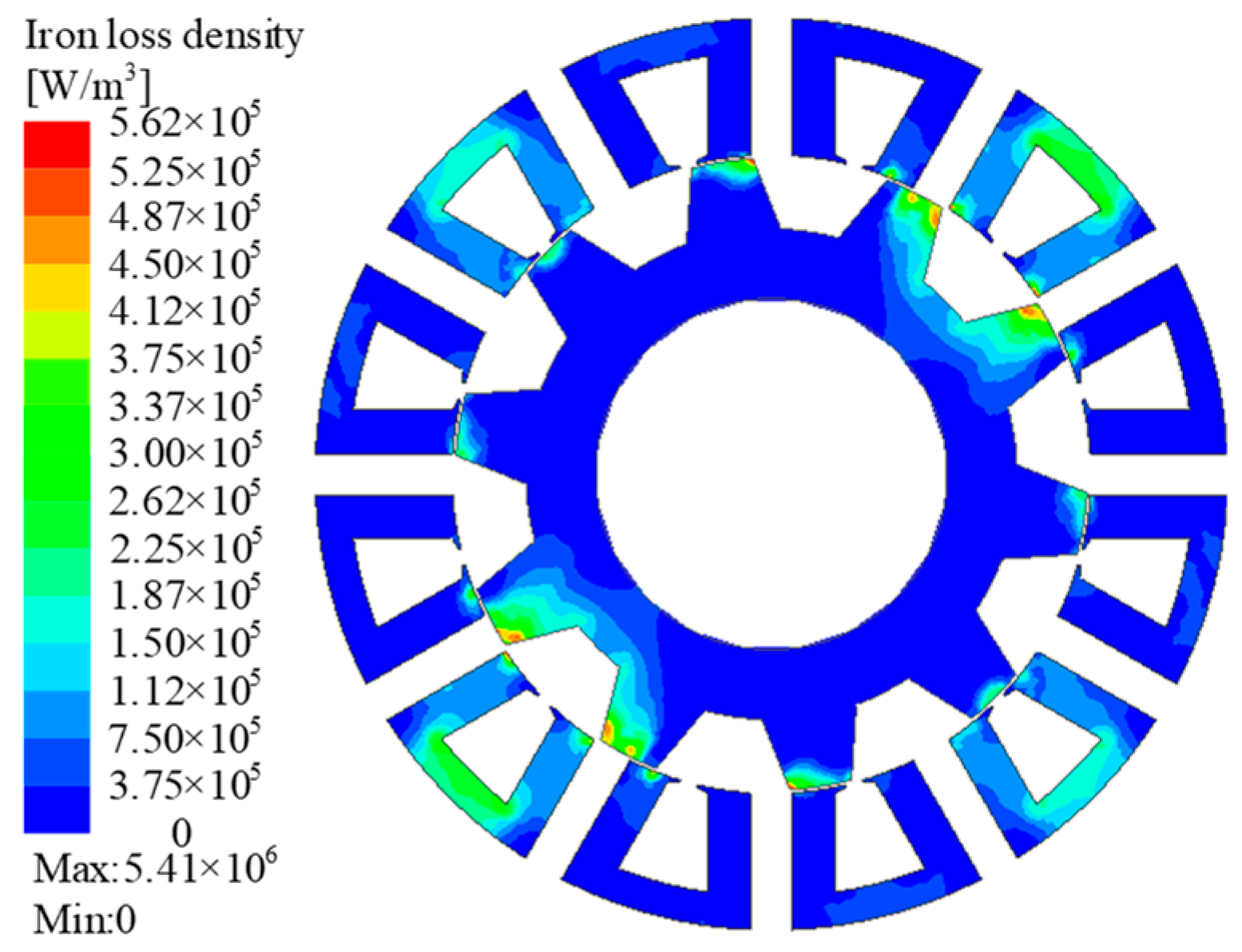
Bgt results of each meshed iron element can be acquired, and based on MATLAB the core loss versus rotating speeds under different conditions can be assessed by a series of data processing calculations according to Equations (2)–(5). The no-load core loss density distribution of the stator and rotor is shown in
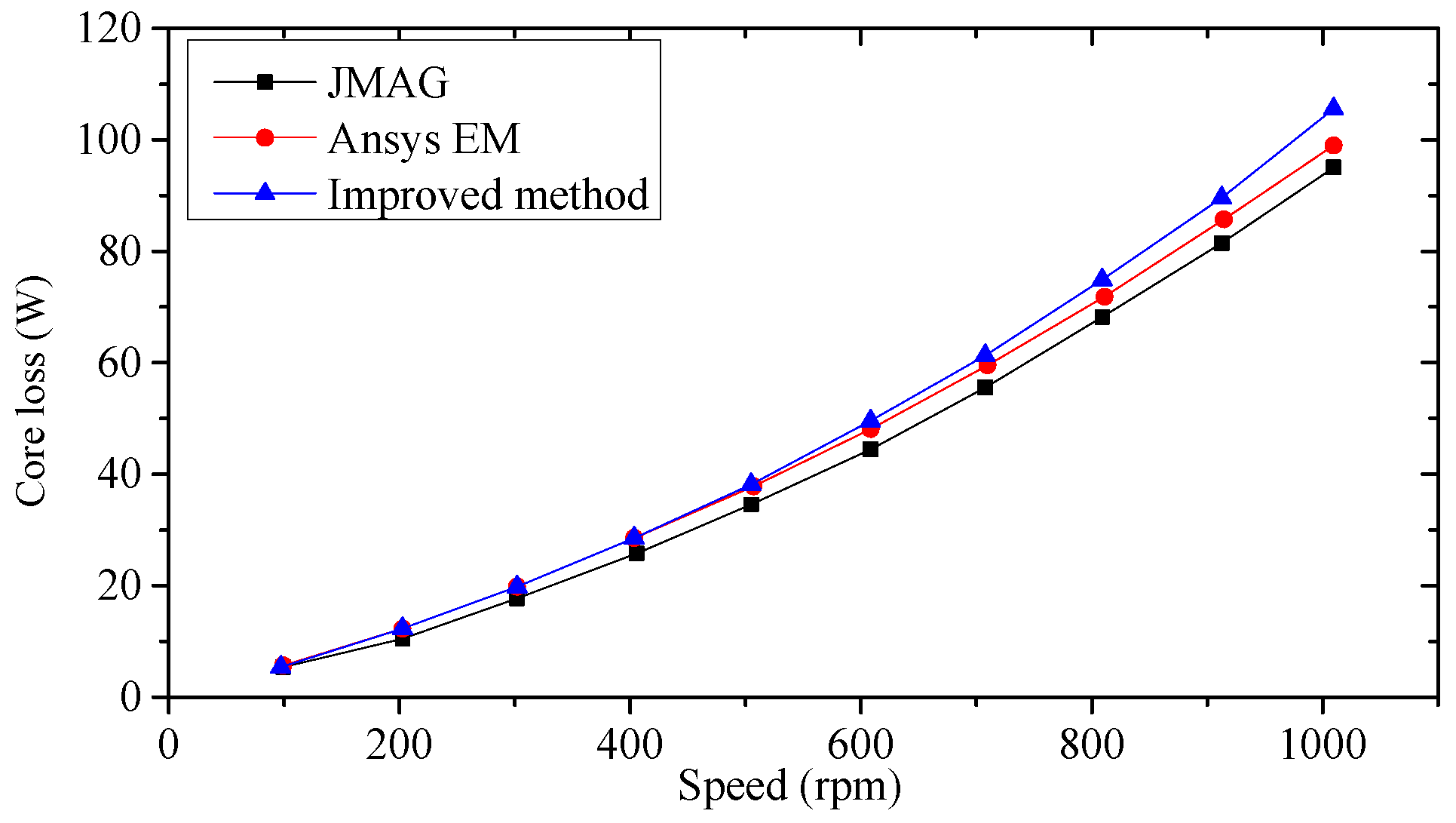
Figure 2. Consequently, the predicted core losses versus rotor speed are compared with those obtained by commercial software, e.g., by JMAG and ANSYS EM as shown in
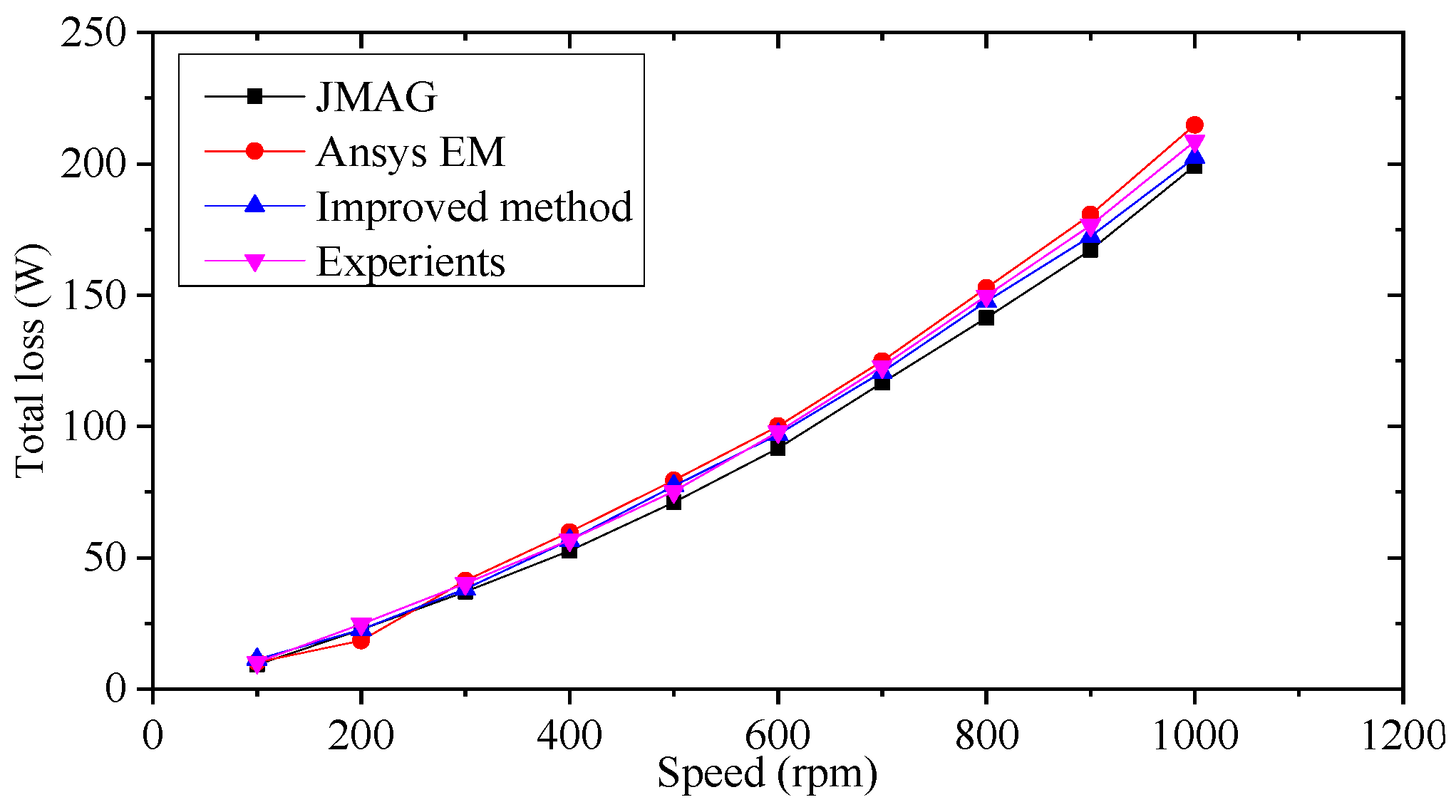
Figure 3. It can be seen that the core losses obtained by the improved method are slightly higher than those from software, which validates the influence of the DC-biased component and minor hysteresis loop, and also validates the feasibility of the improved core loss prediction method.
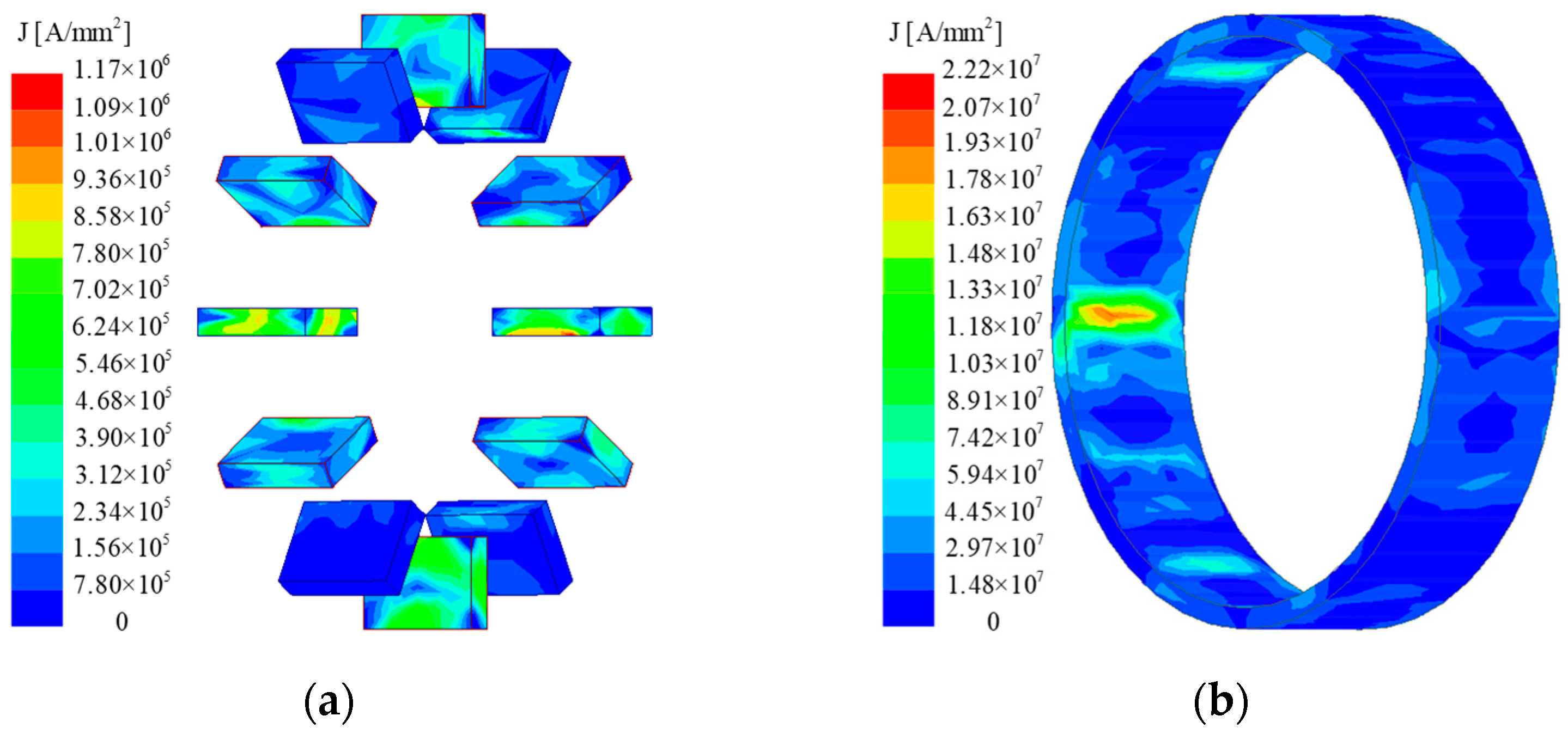
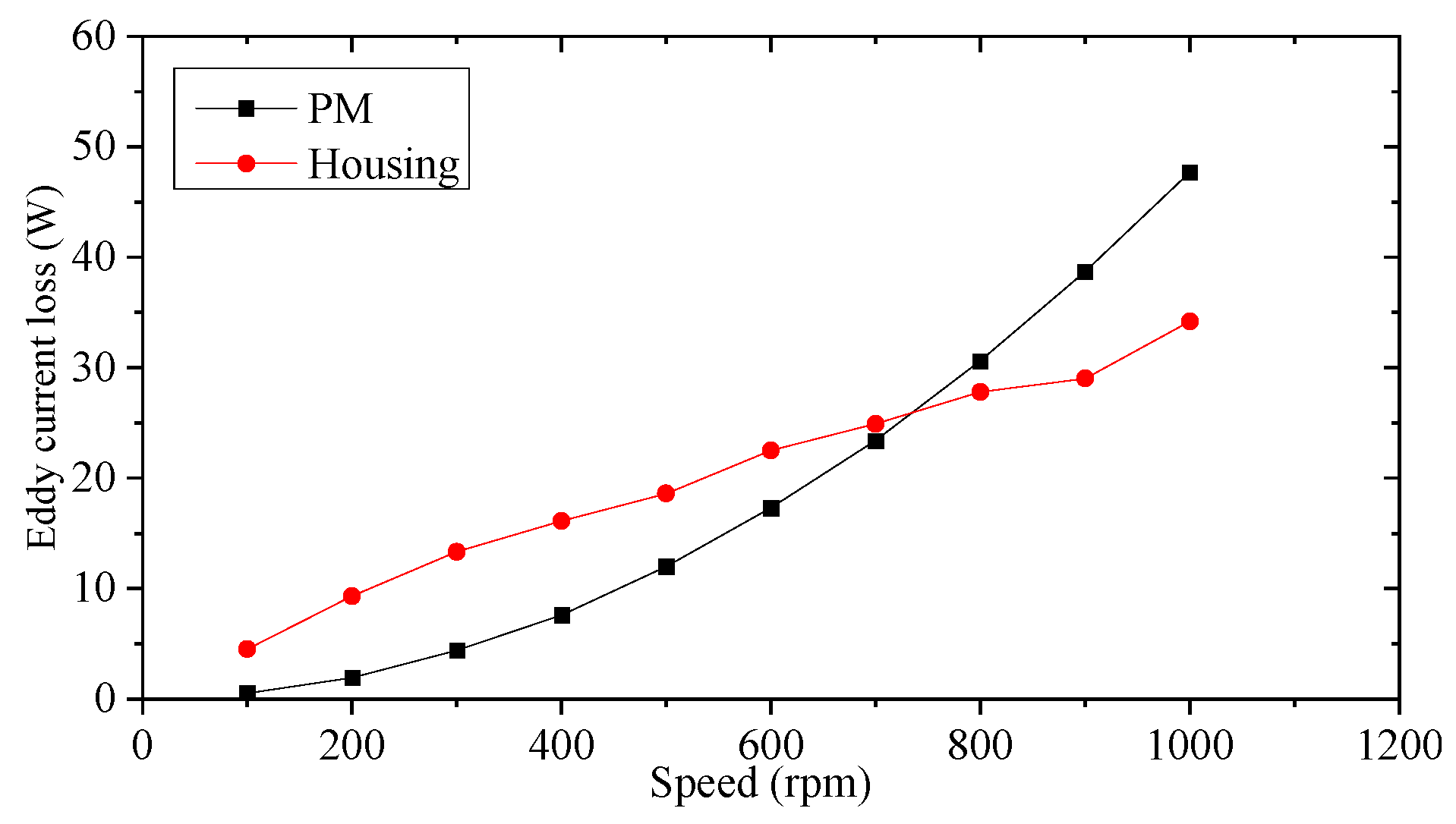
In addition, the no-load eddy current density distribution derived by 3D-FEM is shown in
Figure 4. The resulting no-load eddy loss in PMs
Ppmc and housing
Phc versus rotating speeds are shown in
Figure 5. It can be found that with the increase of the speed, the eddy current losses in PMs and housing increase gradually, which is caused by the air-gap harmonic fields and can be calculated by Equation (6) [
20],
where
Peddy is the eddy current loss in PM and housing in W,
Je is the current density in each element in A/m
2, Δ
Ai is the
ith element area in m
2,
σr is the conductivity of the eddy current zone in S/m, and
tc is the time corresponding to a period in each element in s.
The frictional loss
Pfri of the FSPM machine yields [
21]:
where
vr is the rotor peripheral speed in m/s. It is found that
Pfri = 10.7 W under the rated speed of 1000 r/min.
Finally, a no-load test under different rotation speeds is conducted on a prototyped FSPM machine to verify the predicted results, where the machine is controlled by a DSP-based controller and the input power is obtained by a power analyzer. The frictional loss is so small that it can be neglected. Therefore, the input power is equal to the total loss. The total losses versus rotor speeds by different methods are compared in
Figure 6. Compared with the results obtained by commercial software, the predicted core losses derived by the improved method agree with the measurements with the smallest deviations.
3. Two Thermal Models
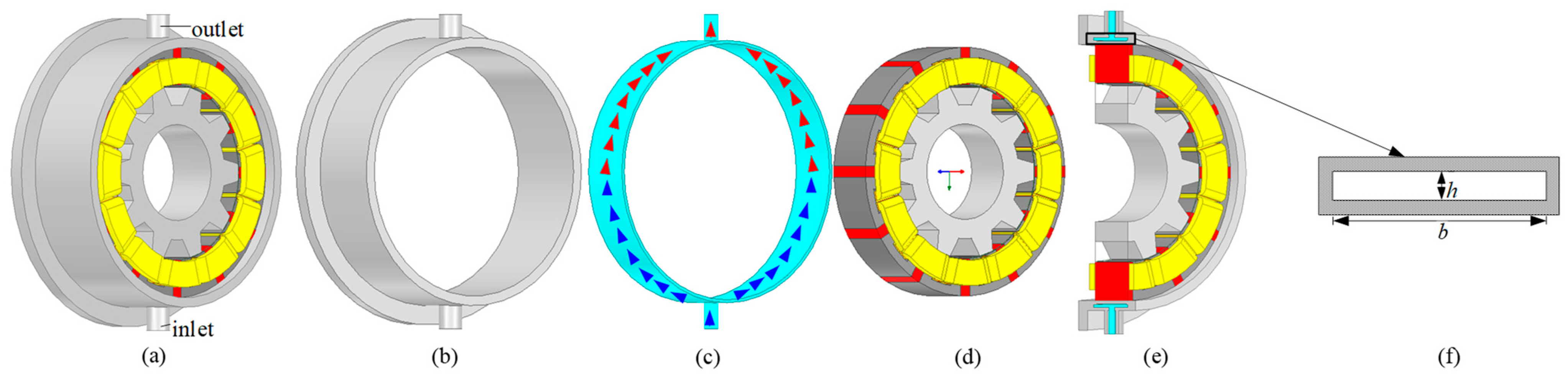
For the prototyped FSPM machine, a circumferential water jacket with one cooling duct is introduced in the stator housing as shown in
Figure 7. The coolant channel of the casing adopts a single-layer water jacket cooling structure.
Figure 7a shows the schematic diagram of the FSPM machine structure.
Figure 7b–d show the housing, coolant flow path, and machine assembly, respectively.
Figure 7b shows the cross-sectional diagram of the machine, and
Figure 7c shows the cross-sectional diagram of the cooling duct. Arrows are used in
Figure 7c to indicate the flow path of the coolant. The blue arrow represents the low temperature coolant near the inlet, while the red arrow represents the coolant that has been heated through heat exchange. The fluid running inside the cooling duct can be modeled as the movement of fluid in a rectangular channel using dimensionless numbers. Consequently, the convection coefficient can be obtained in the following stages.
Firstly, with the cooling jacket cross-section in
Figure 7c, the Prandtl number of the fluid
Prf yields
where
cf is the specific heat capacity of fluid in J/(kg·°C),
ηf is fluid dynamic viscosity in N·s/m
2, and
λf is the fluid thermal conductivity in W/(m·°C).
Secondly, the Reynolds number of fluid
Re yields
where
υ is the velocity of fluid in m/s,
vf is the fluid kinetic viscosity in m
2/s, and
de is the hydraulic radius in m by Equation (10).
where
Acs is a cross-section area of a single cooling duct in m
2.
s,
b, and
h are the wetted perimeter, width, and height of cooling duct in m, respectively.
Approximately, in a circumferential cooling duct, the velocity of fluid can be figured out as
where
Q is the fluid quantity in kg/s.
According to the value of
Re, the fluid flow can be divided into turbulence flow and laminar flow. The Nusselt number of the laminar flow
Nufl yields [
22],
For turbulence flow, the Nusselt number
Nuft yields
where
ηw is the dynamic viscosity of housing in N·s/m
2.
Based on the similarity criterion of fluid [
22], the convection heat transfer coefficient
hf0 yields
Considering that turbulence flow shows a better heat dissipation than laminar flow, the former is employed in the cooling jacket, where the convection heat transfer coefficient
hf of the cooling jacket is affected by the geometric parameters and the velocity of the fluid, and can be given by
From Equation (15), when the fluid quantity keeps constant, as the cross-sectional area of the cooling ducts decreases, the convection coefficient of the cooling jacket increases. However, a small cross-section cooling duct is not only difficult to manufacture, but also may lead to high inlet velocity and high hydraulic pressure, which causes the corrosion of cooling duct and deteriorates the operation stability. In the following, two thermal models are proposed, one a LPTN model and the other a 1D-SHC model.
3.1. Lumped Parameter Thermal Network Model
A LPTN model enables the heat flow and the temperature distribution inside the machine by means of an equivalent thermal circuit, which is composed of heat sources, thermal resistances, and thermal capacitances. For the convenience of calculation and improved accuracy, three assumptions are made as follows [
23,
24,
25]:
Symmetrical temperature distribution and the same cooling conditions along the circumference;
Uniformly distributed thermal capacity and heat generation;
Independent heat flow in radial and axial directions
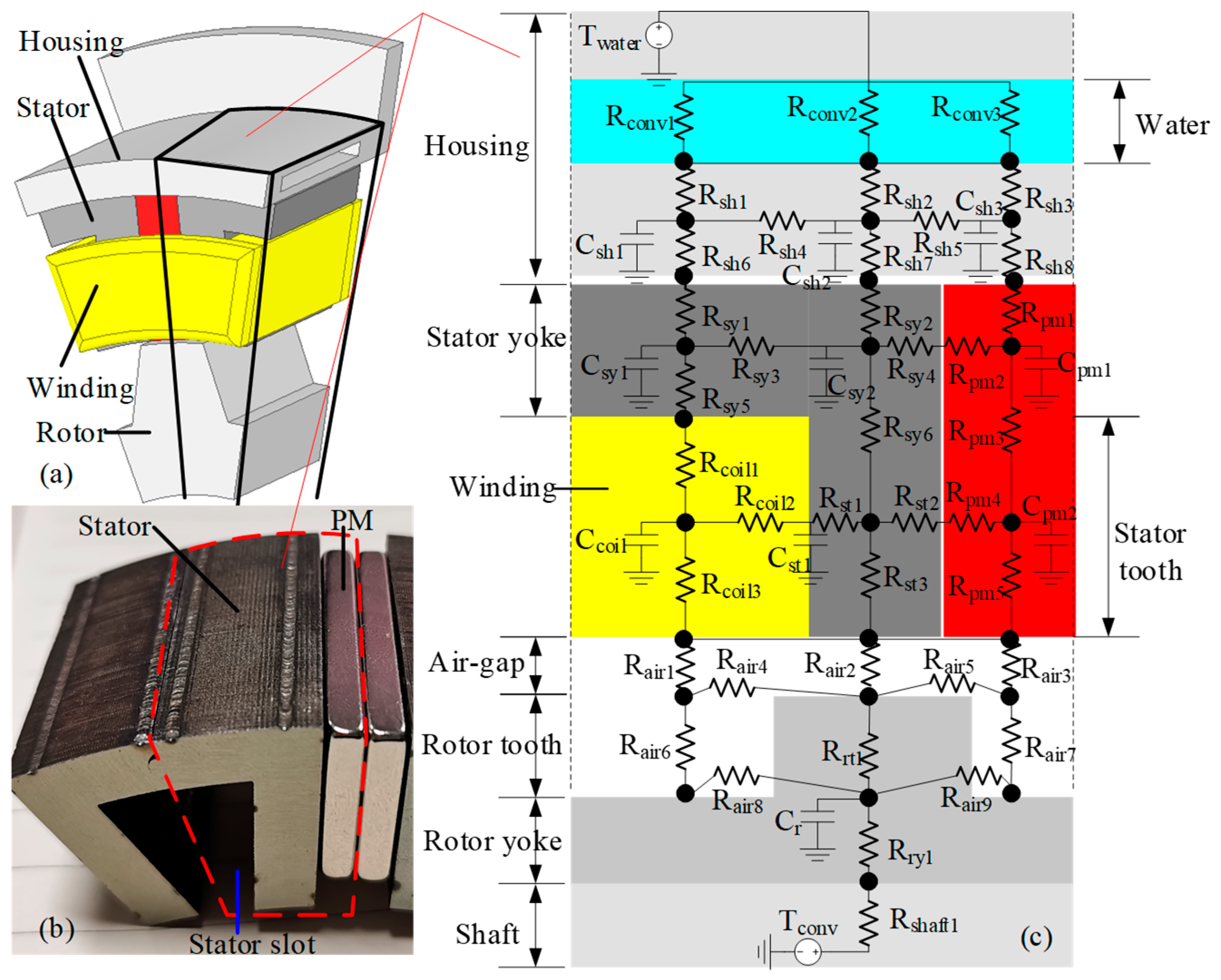
To simplify the calculation load, only 1/24 of the FSPM machine is modeled as shown in
Figure 8 due to symmetry, where the heat sources including stator/rotor core losses, PM/housing eddy current losses, and windings joule loss are considered. The thermal resistances and capacitances can be determined according to the machine geometry and the physical properties of materials.
Table 3 and
Table 4 list the corresponding resistances and capacitances of the LPTN model. A preliminary selection of the resistances and capacitances can be determined according to the machine geometry and physical properties of the materials used [
26].
With the convection heat transfer coefficient, the thermal resistance
Rconvi (
i = 1, 2, 3) representing the heat dissipation by cooling medium convection between the housing external surface and ambient can be calculated by Equation (16) [
25],
where
Rconvi is the thermal resistance due to convection heat transfer in °C/W,
hconvi is the convection heat transfer coefficient in W/(m
2·°C), and
Aconvi is the convective area in m
2. Here, the area of the end-part winding is considered.
Since the heat exchange between stator and rotor through the air-gap is assumed to be only by convection, Equation (16) is also used for the calculation of the thermal resistances Rairi.
In addition to heat convection, heat conduction is also an important way for heat dissipation. The resistance representing the heat flow in the radial direction is modeled by using Equation (17),
where
ro and
ri are the outer and inner diameter of the cylinder in m,
λ is the thermal conductivity of the material in W/m/°C, and
L is the cylinder length in m.
In the tangential direction, the thermal resistance due to conduction heat transfer is given by,
where
l is a portion length of the path considered in m, and
Acond is the area for the conduction in m
2.
Figure 8a,b show the 3D module structure and modular stator element of the FSPM machine. Based on the thermal resistances above, a thermal resistance network of the 1/24 machine is constructed as shown in
Figure 8c, where
Rsh1-
Rsh8,
Rsy1-
Rsy6,
Rair1-
Rair9,
Rst1-
Rst3,
Rcoil1-
Rcoil3, and
Rpm1-
Rpm5 represent the thermal resistances of the housing, stator yoke, air-gap, stator tooth, stator winding coils, and PMs.
Rrt1,
Rry1, and
Rshaft1 represent the thermal resistances of rotor tooth, rotor yoke, and shaft, respectively.
Csh1-
Csh3,
Csy1-C
sy2,
Cst1,
Ccoil1,
Cpm1-
Cpm2, and
Crt represent the thermal capacitances of the housing, stator yoke, stator tooth, winding coils, PMs, and rotor tooth. Here, since the heat dissipated by forced convection is much larger than that by radiation, the radiation heat dissipation is ignored.
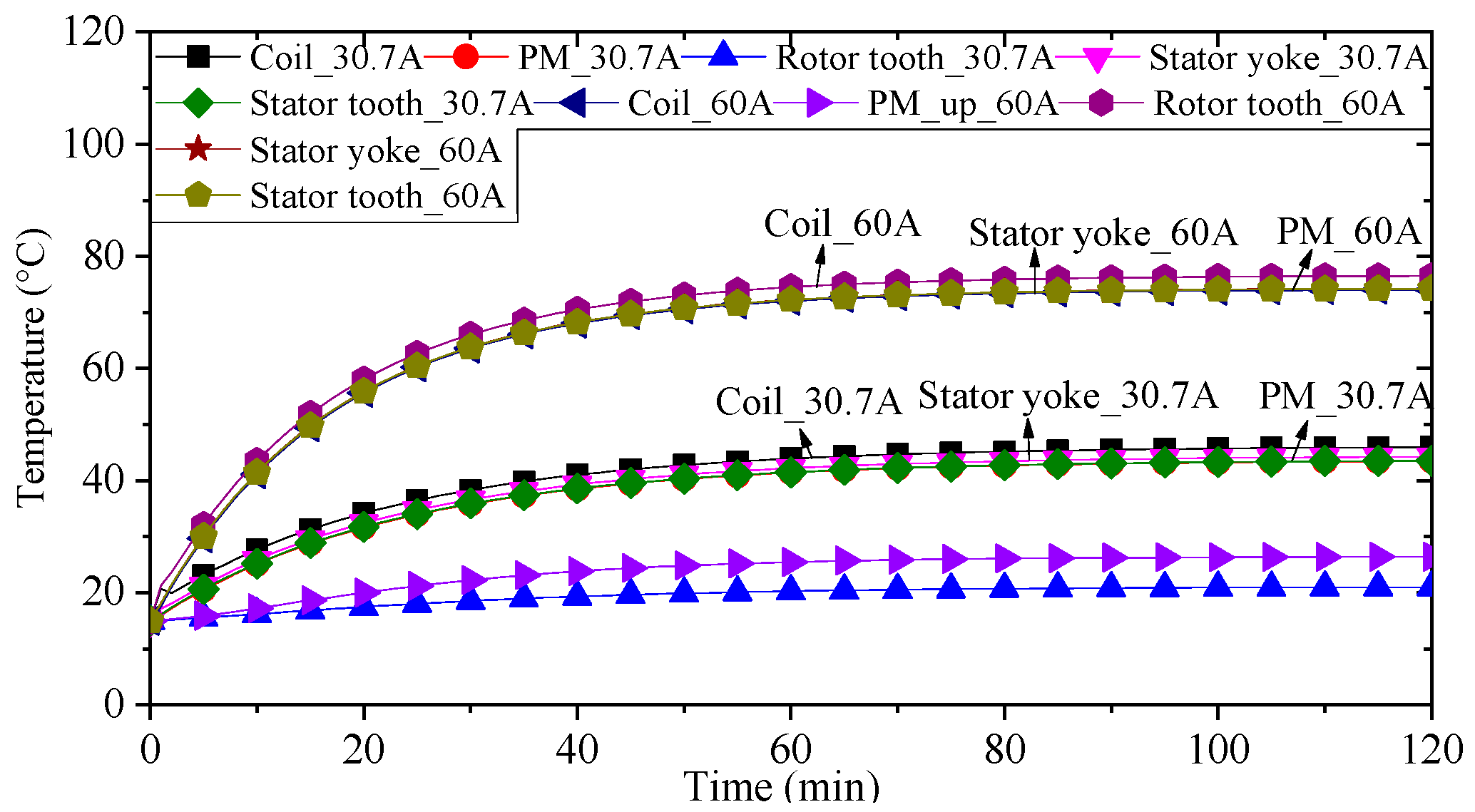
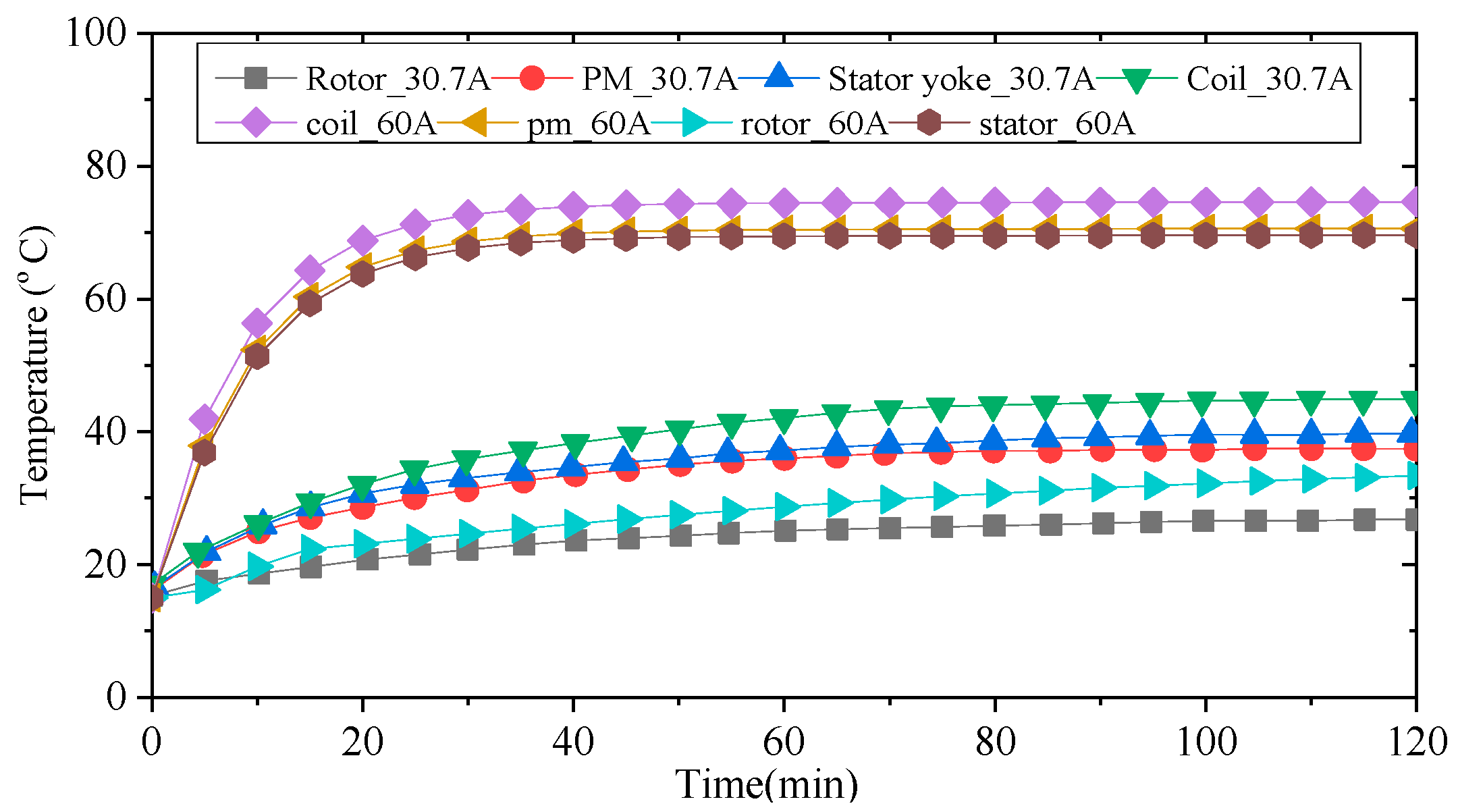
Under two typical operation conditions, i.e., the speed of 1000 r/min and the phase current of 30.7 A (RMS) and 60 A (RMS), the transient temperature rises of different components under forced water cooling are obtained by the LPTN model, and the results are shown in
Figure 9. It takes around 70 min for the machine under water cooling to reach a thermal steady state where the armature windings have the highest temperatures (45.7 °C@30.7 A and 82.8 °C@60 A under water cooling). In addition, since the PMs are mounted on the stator, the temperature of the PMs is very close to that of the stator core, exhibiting the advantage of FSPM machines.
3.2. One-Dimensional Steady Heat Conduction Model
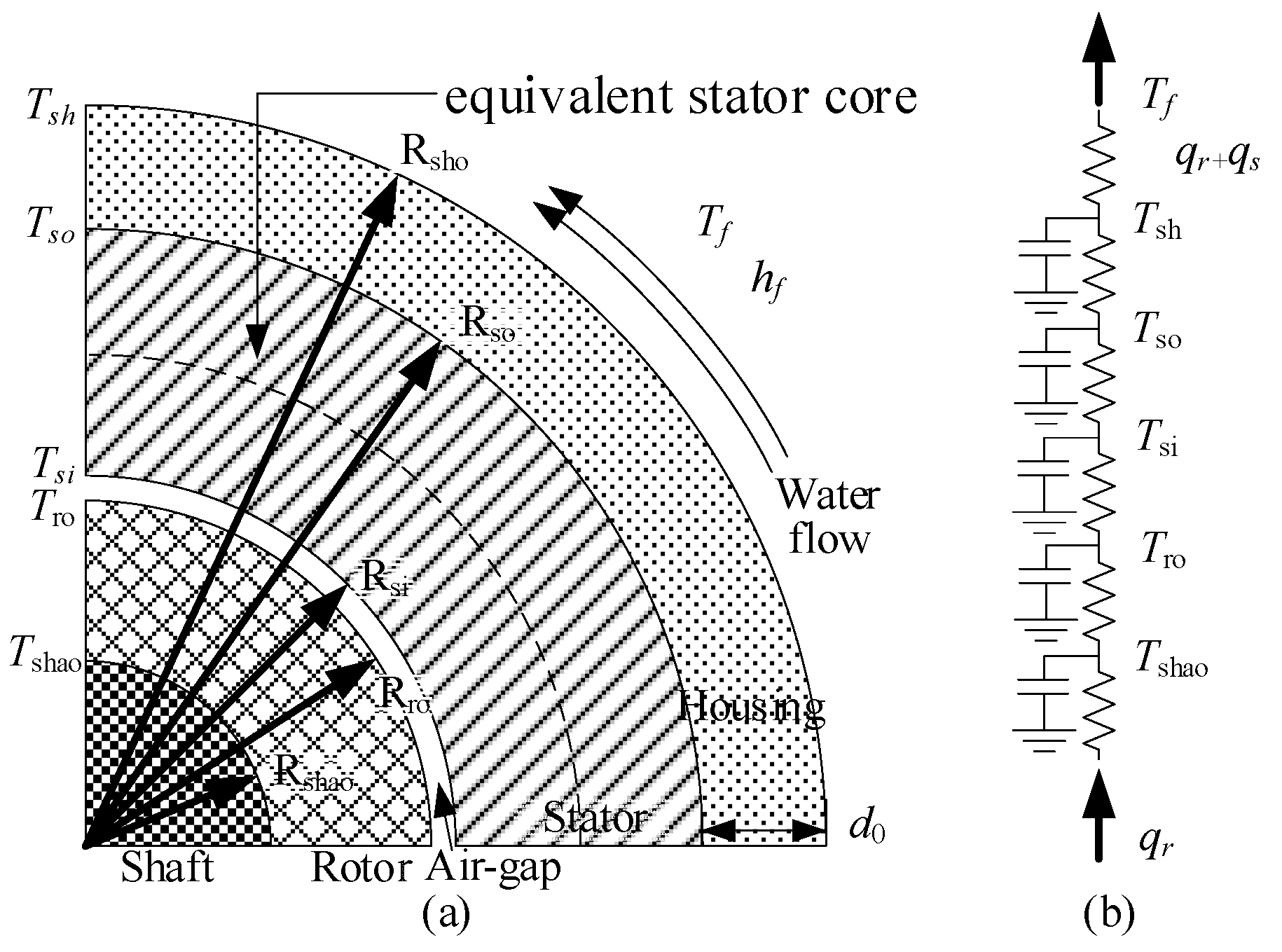
Generally, LPTN and FEM have been widely employed in thermal analysis of electrical machines. However, these two methods are normally time-consuming and require complicated modeling. For water-cooling machines, in order to select a reasonable flow rate of coolant, a 1D-SHC approach is proposed based on heat transfer and fluid mechanics as shown in
Figure 10, and the relationship between the internal temperature of the stator and the coolant flow rate and coolant temperature is obtained.
It should be noted that the 1D-SHC model is based on the following assumptions. (1) The loss is uniformly distributed in each component of the machine. (2) The heat generated by joule loss and stator core loss is only dissipated by the housing. (3) The stator laminations, windings, and PMs are simplified to a homogeneous heating unit and the equivalent averaged thermal conductivity
λavg yields [
26,
27]:
where
As,
Awind, and
Apm are the cross-section area of the stator, windings, and PMs in m
2, respectively,
λs,
λwind, and
λpm are the thermal conductivity of stator, windings, and PMs in W/(m·°C).
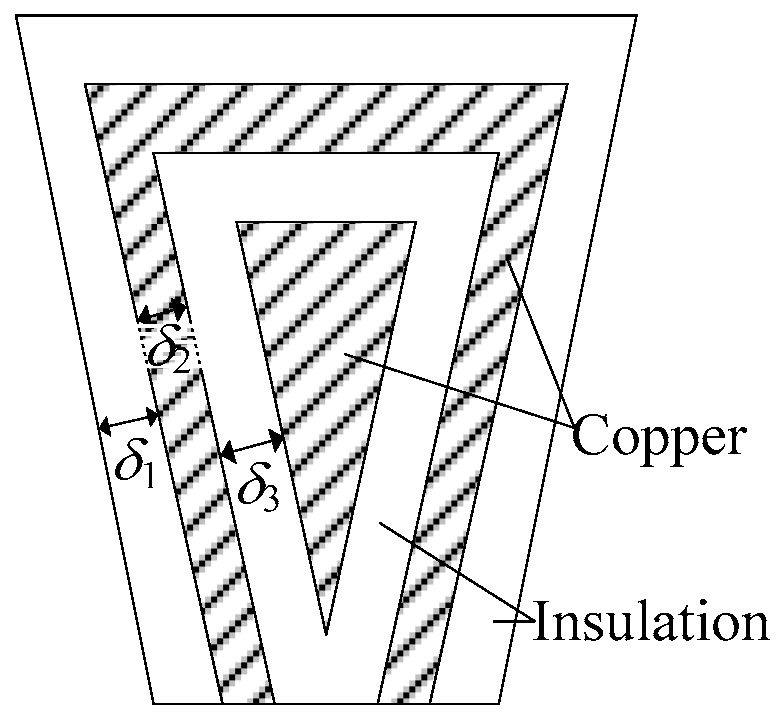
The winding and insulation layering is used to calculate the thermal conductivity of the stator windings.
Figure 11 shows the equivalent diagram of the winding structure, where the insulation and windings are arranged with intervals. The slot filling factor is set as 0.35 according to the prototyped machine. The equivalent winding thermal conductivity yields:
where
δI is the thickness of the
ith layer in m,
λi is the thermal conductivity of the
ith layer in W/(m·°C).
Then, the equivalent volumetric heat generation of stator
qVs and rotor
qVr can be obtained by
where
Peave is equivalent average loss in W,
Ps,
Pcu,
Ppm, and
Pr are the stator core loss, winding joule loss, eddy current loss in PMs, and rotor core loss in W, respectively,
Vs,
Vcu,
Vpm,
Vequ, and
Vr are the volume of stator, winding, PM, equivalent stator, and rotor in m
3, respectively.
Since the thermal model is simplified into a 1D-SHC model, the heat flux density of stator/rotor (
qs/
qr) yields
where
Ss/
Sr is the cross-section area of stator/rotor lamination in m
2.
The inlet and outlet temperature of the cooling fluid can be detected by a hand-held infrared thermometer. Thus, the temperature of the fluid
Tf equals
where
Ti/
To is the inlet/outlet temperature of the fluid in °C.
According to the 1D thermal circuit in
Figure 10b, the temperature of housing
Tsh can be derived by
where
hf is the fluid convection coefficient in W/(m
2·K),
Rsho is the housing outer radius in m,
Rshao is the shaft outer radius in m, and
Rsi is the stator inner radius in m.
The temperature of stator yoke
Tsy yields
where
Rso is the stator outer radius in m, and
hsh is the housing thermal conductivity in W/(m·°C).
The differential equations of the heat conduction and the boundary conditions for a cylinder with uniform heat generation are as follows [
23]:
where
λr is the rotor thermal conductivity in W/(m·°C).
The thermal distribution of the machine can be given by
Hence, the stator teeth temperature can be obtained by
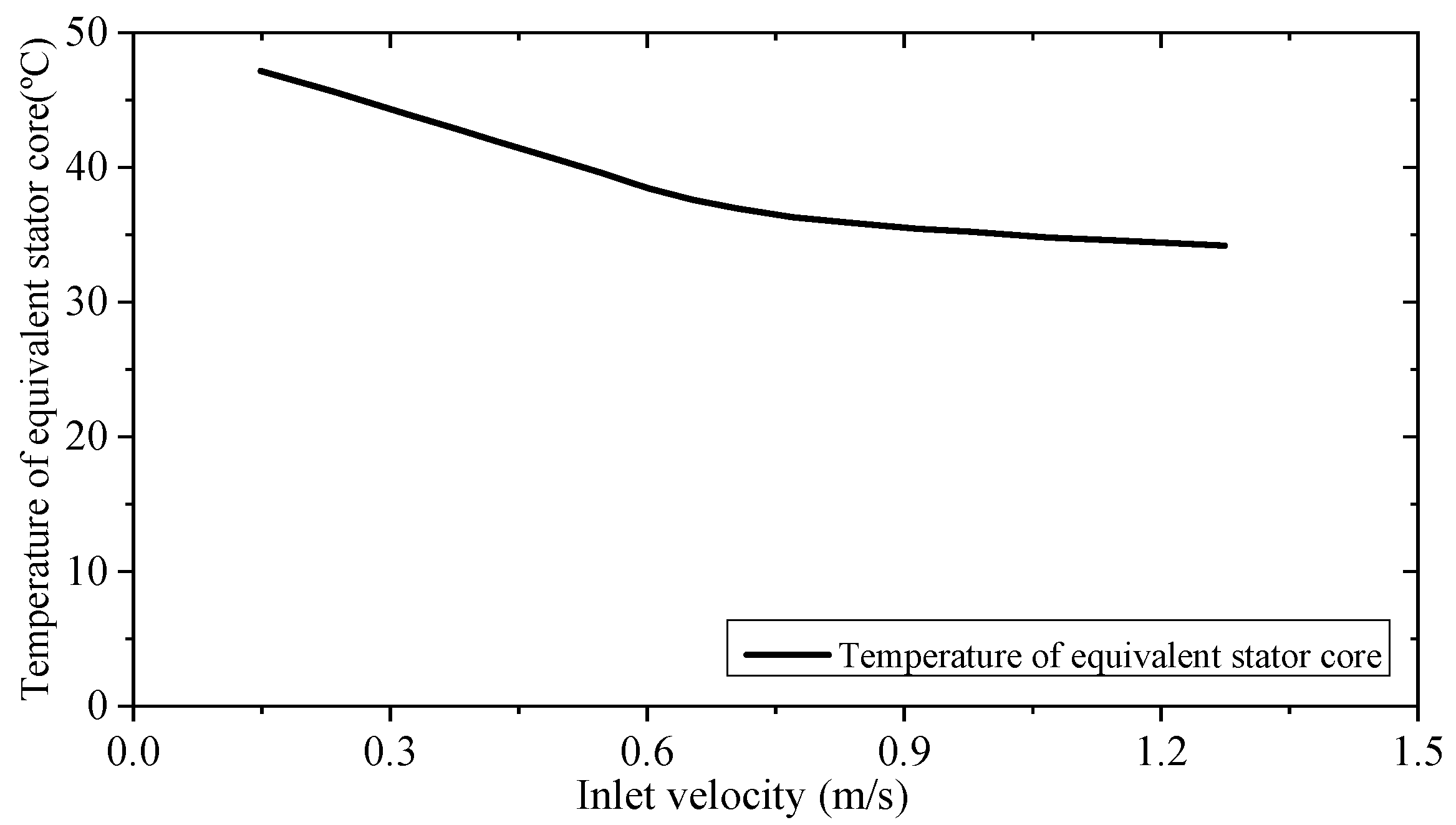
According to Equations (11), (15) and (28), as the average velocity of fluid increases, the convection coefficient of the cooling jacket increases and the stator temperature decreases. According to the prototype dimensions, when the no-load machine is running at the speed of 1000 r/min, the relationship between the temperature of the equivalent stator core (marked in
Figure 10) and the inlet velocity can be obtained as shown in
Figure 12. Obviously, as the inlet velocity of water increases to 0.6 m/s, the equivalent stator core temperature decreases almost linearly. When the inlet velocity increases to 1 m/s, the stator core temperature varies nonlinearly and slowly, so 1 m/s is set as the rated cooling inlet velocity of the FSPM machine, corresponding to a pump flow of 1800 L/h.
4. CFD-Based 3D Temperature Field Verification
In order to verify the proposed LPTN and 1D-SHC models, based on the loss calculated by FEM, a 3D-CFD thermal model is built as shown in
Figure 13a.
Figure 13b corresponds to water cooling.
When the cooling jacket is injected with an total inlet flow of 1800 L/h, a phase current of 30.7 A and 60 A, as well as a speed of 1000 r/min, the transient temperature rises of different components under forced water cooling are obtained as shown in
Figure 14. It can be seen that the armature windings achieve the highest temperature under forced water-cooling conditions, whereas the armature windings temperature difference is 31 °C when the armature current is 30.7 A and 60 A, respectively. In addition, compared with the results obtained by the LPTN model shown in
Figure 9, both the steady-state and transient results agree well.
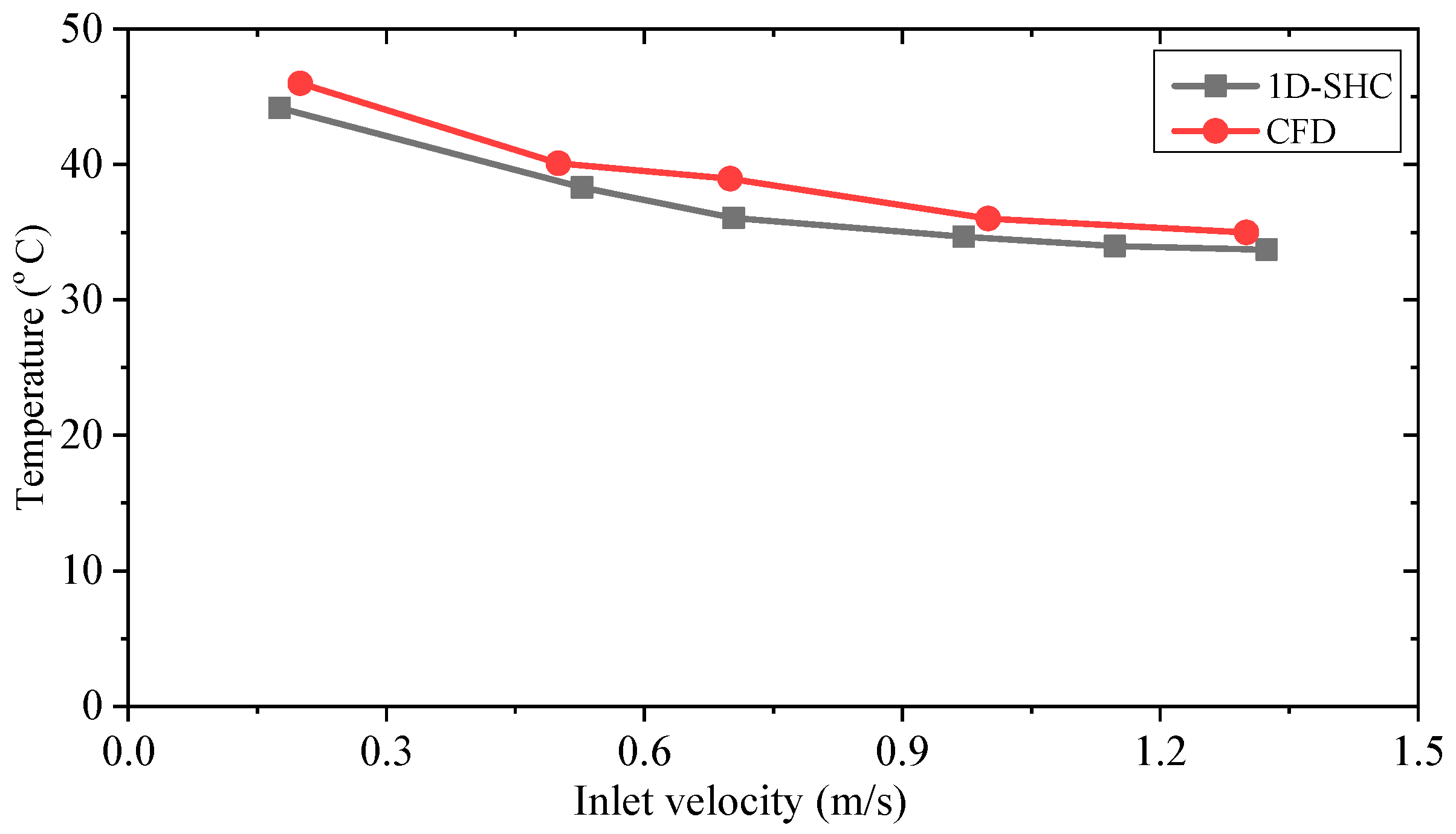
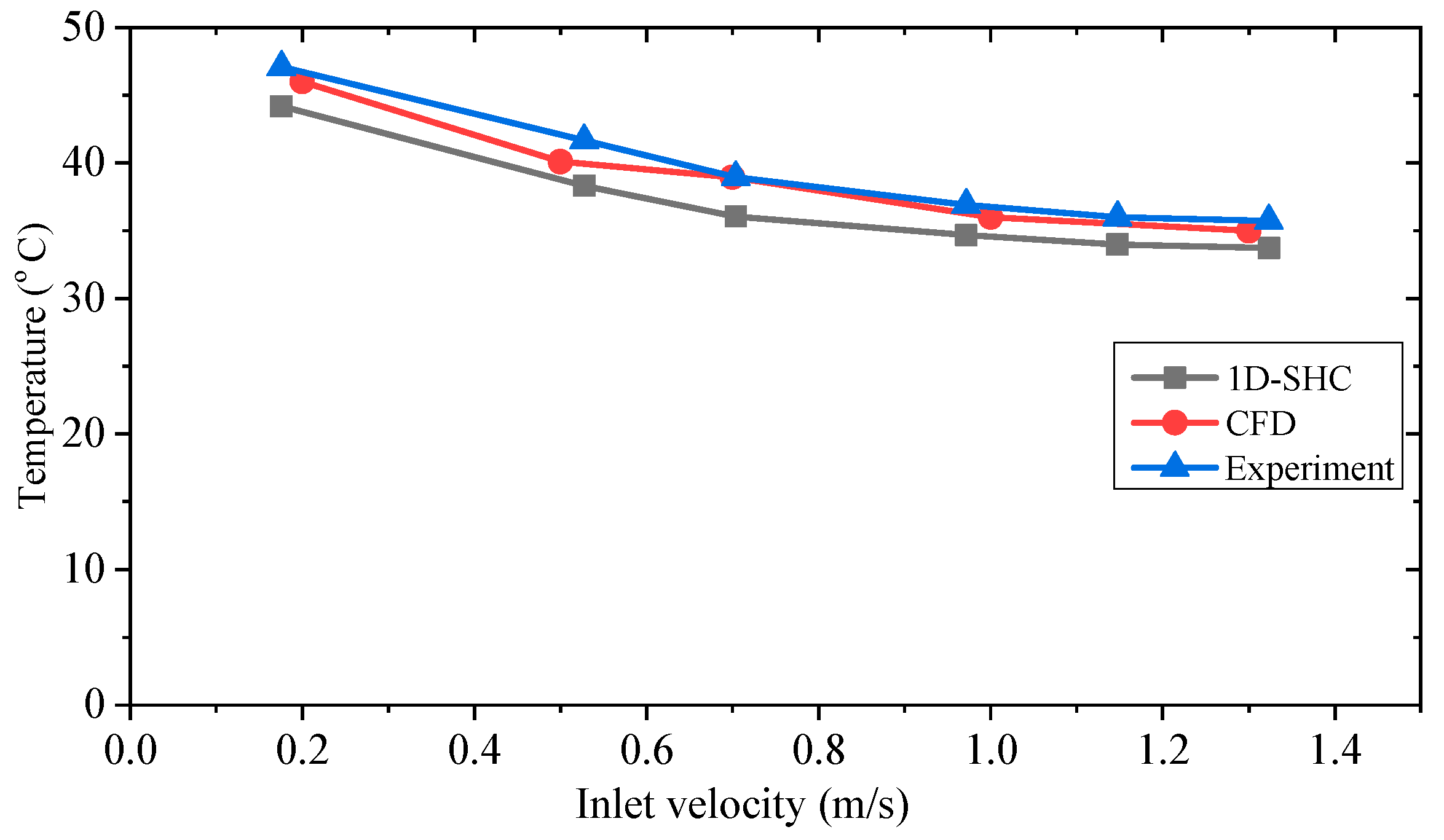
On the other hand, to verify the 1D-SHC model, the predicted equivalent stator core temperatures vs. inlet velocity by 1D-SHC and CFD are compared in
Figure 15, where the operation status and cooling conditions are consistent with the 1D-SHC model. In addition to predicted temperatures, the time consumed by the three methods is compared in
Table 5. Obviously, both the LTPN and 1D-SHC methods can save considerable time, which is favorable for the optimal design of machines.
5. Experiment Verification
To validate the proposed thermal prediction models, a prototyped FSPM machine was manufactured and tested as shown in
Figure 16. The prototyped FSPM machine was driven by an inverter supplied by a DC power source and the output shaft was directly connected with a dynamometer machine, in which a torque transducer and a resolver were equipped to measure torque and (rotor position) speed, respectively.
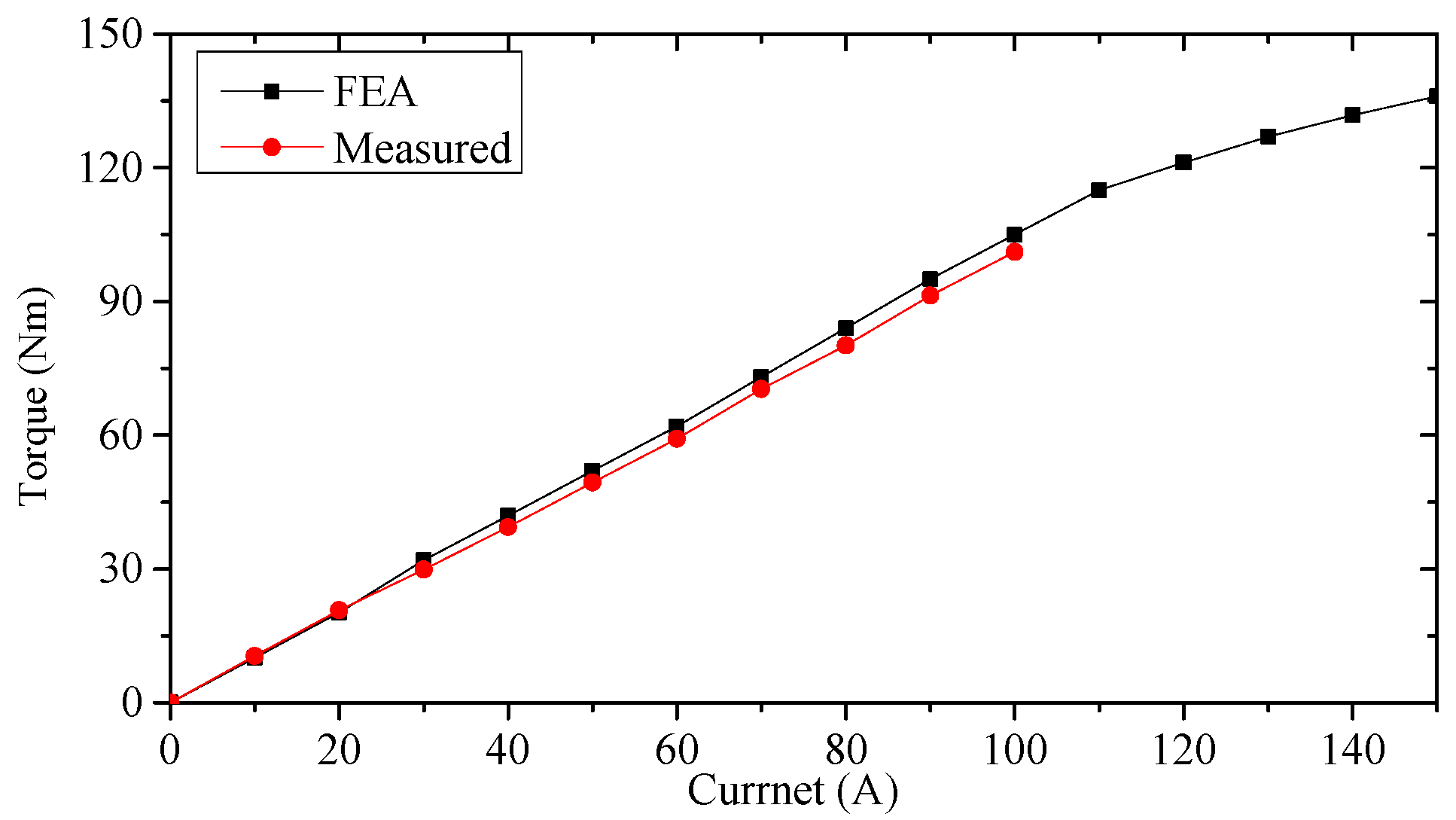
Figure 17 compares the FEA-predicted and experimental results of torque versus phase currents. It can be seen that good agreements can be achieved with a deviation below 8%.
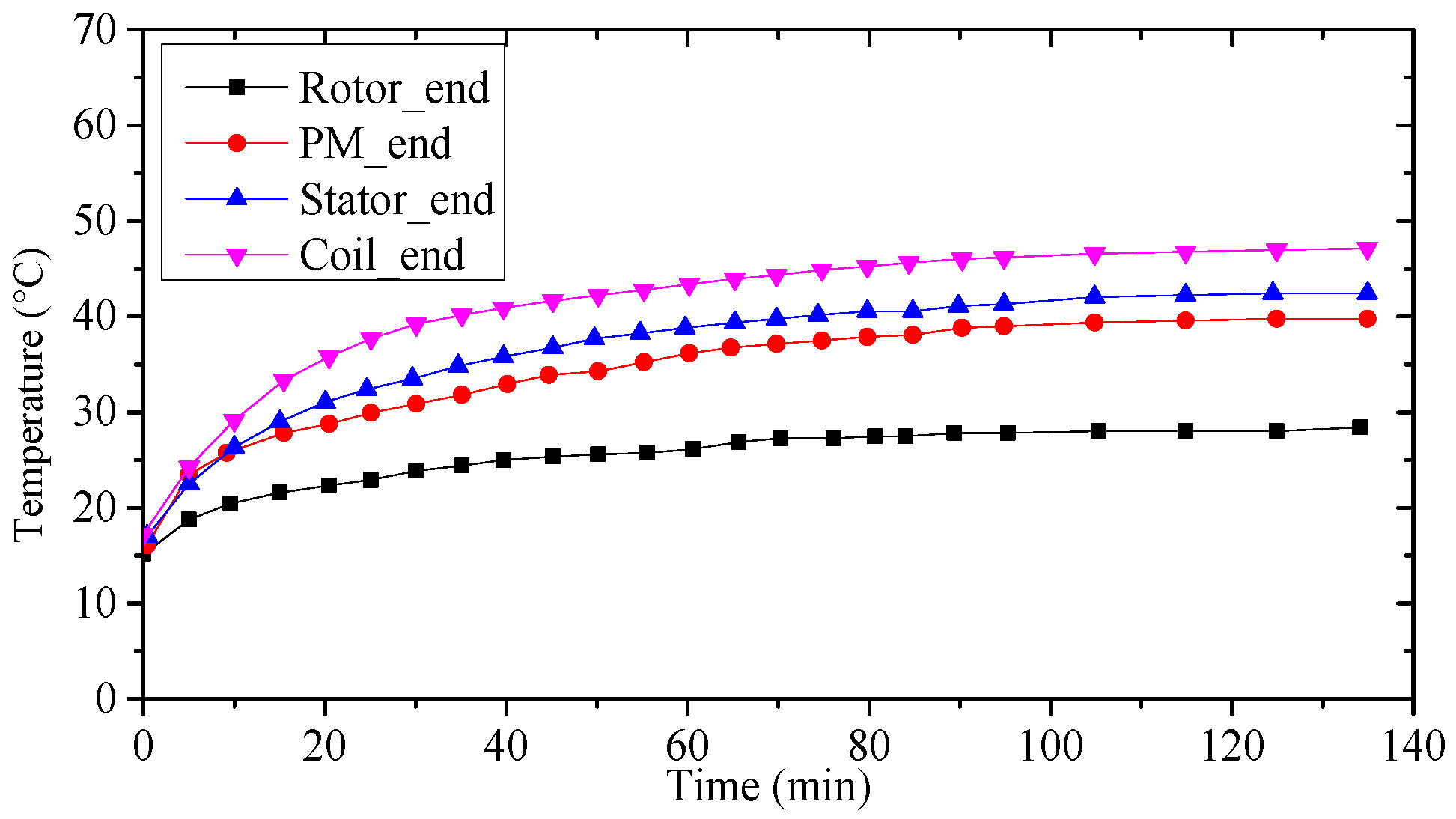
To verify the LPTN model, experiments on transient temperature rise were performed. Under the phase current of 30.7 A and rated speed of 1000 r/min, the transient temperature rises of different components under forced water cooling were obtained as shown in
Figure 18, where the temperature was detected with a hand-held infrared thermometer. Under forced water-cooling conditions, the measured highest temperature was 47.1 °C. Compared with the results obtained by LPTN (
Figure 9) and CFD (
Figure 14), it was found that the steady-state and transient results of the three methods were very close.
Figure 19 shows the experimental steady-state temperatures under forced water cooling. Obviously, agreement between the experiments and LPTN was achieved, validating the effectiveness of the LPTN model.
To verify the 1D-SHC model, experiments with temperature rising and various fluid inlet velocities of the no-load machine at the rated speed of 1000 r/min were conducted, as shown in
Figure 20. It can be seen that when the inlet velocity was bigger than 1.1 m/s, the temperature of the equivalent stator core decreased slowly, which agrees with the simulations giving both 1D-SHC and CFD results.
Overall, satisfactory agreement was achieved between the calculation and measured results, considering manufacturing and testing tolerances.