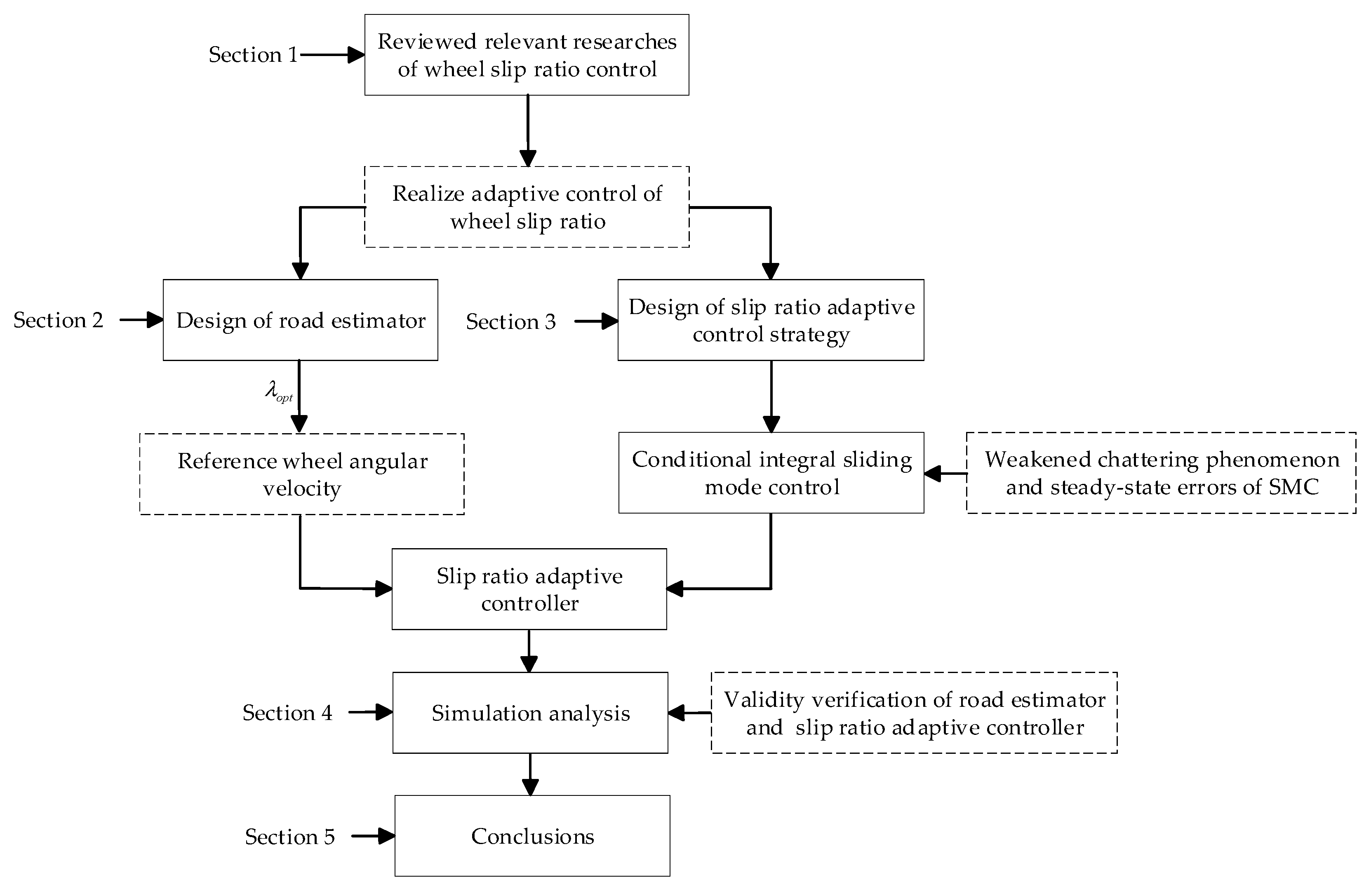
Slip Ratio Adaptive Control Based on Wheel Angular Velocity for Distributed Drive Electric Vehicles
Abstract
1. Introduction
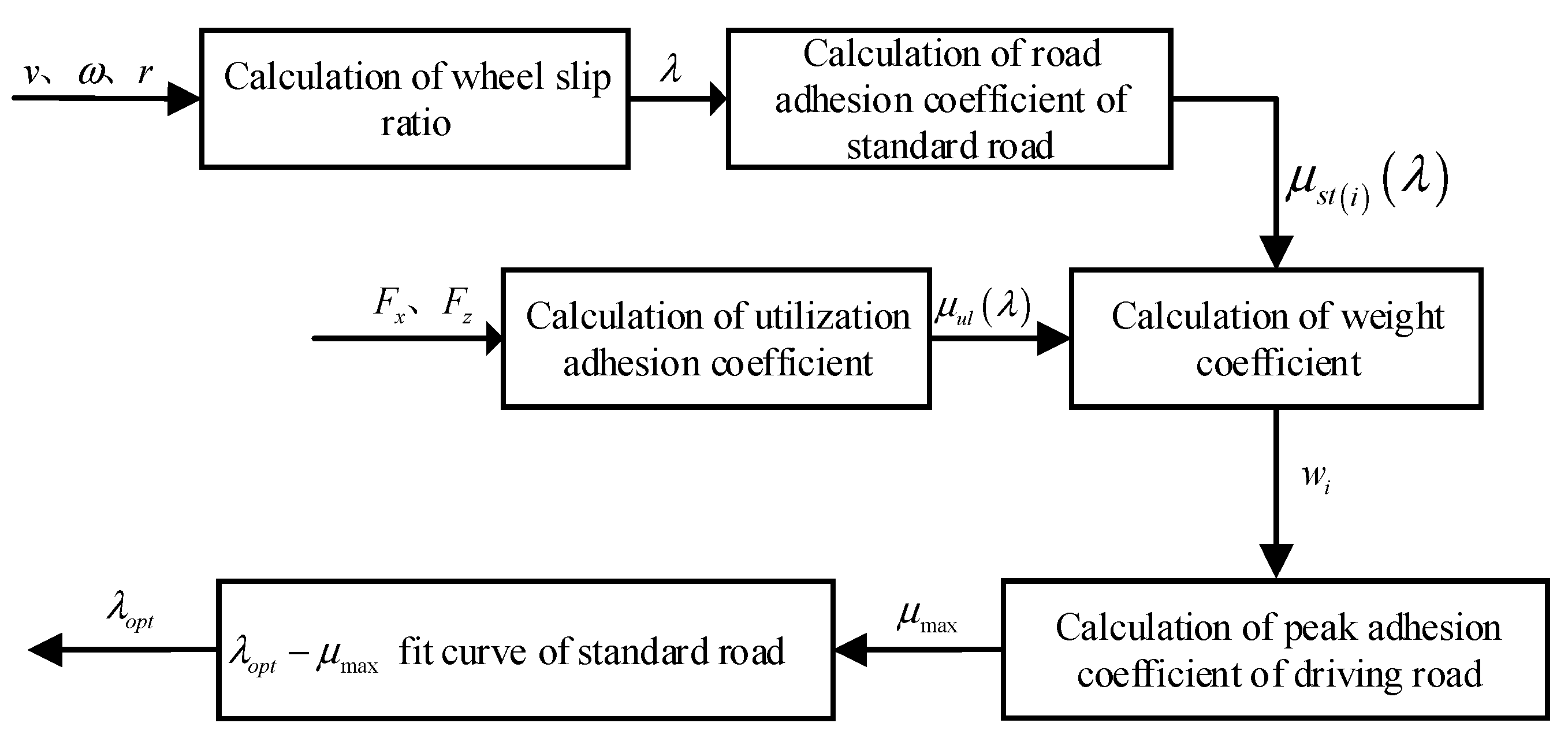
2. Design of the Road Estimation Algorithm
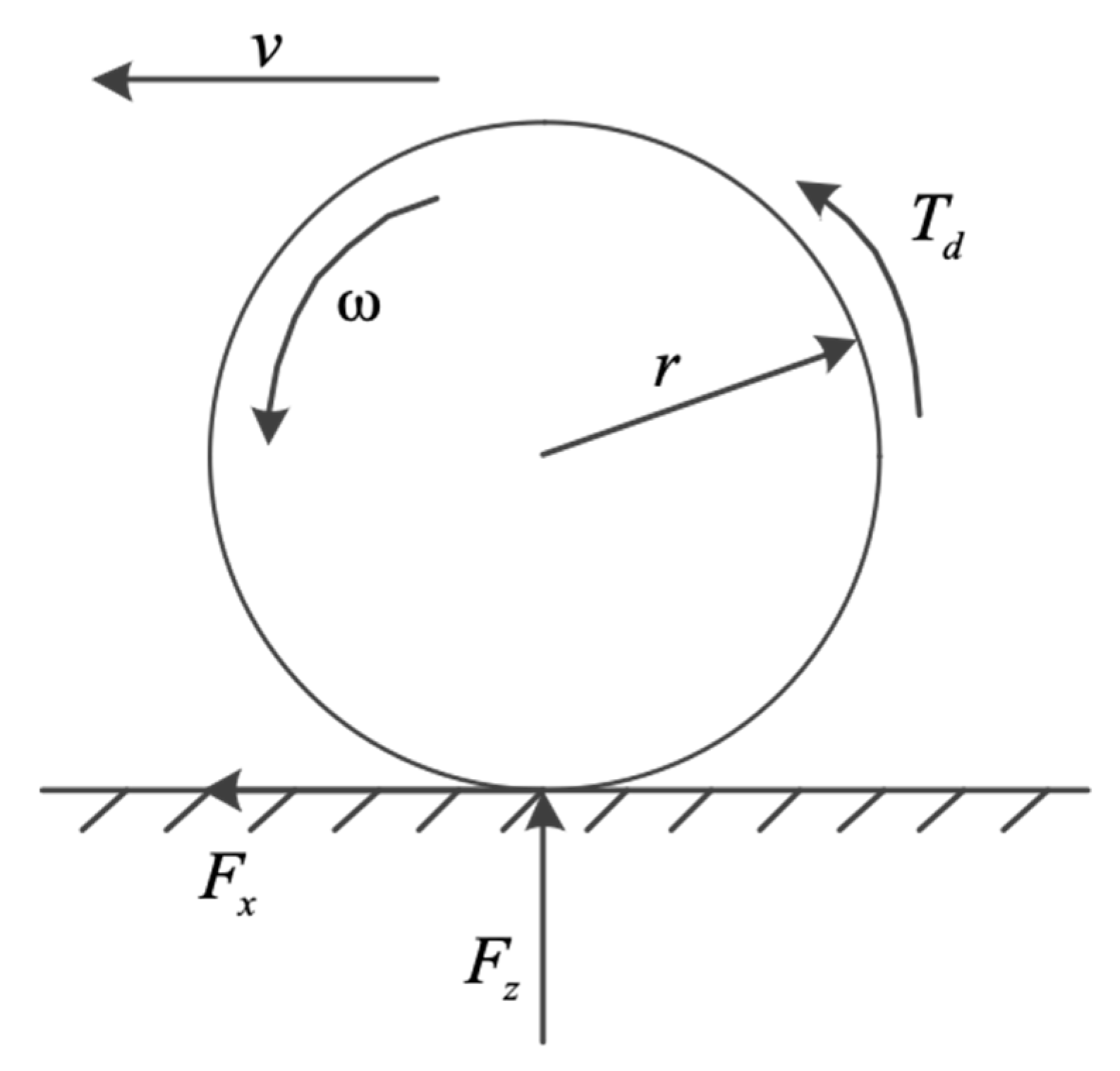
2.1. Establishment of the Tire Model
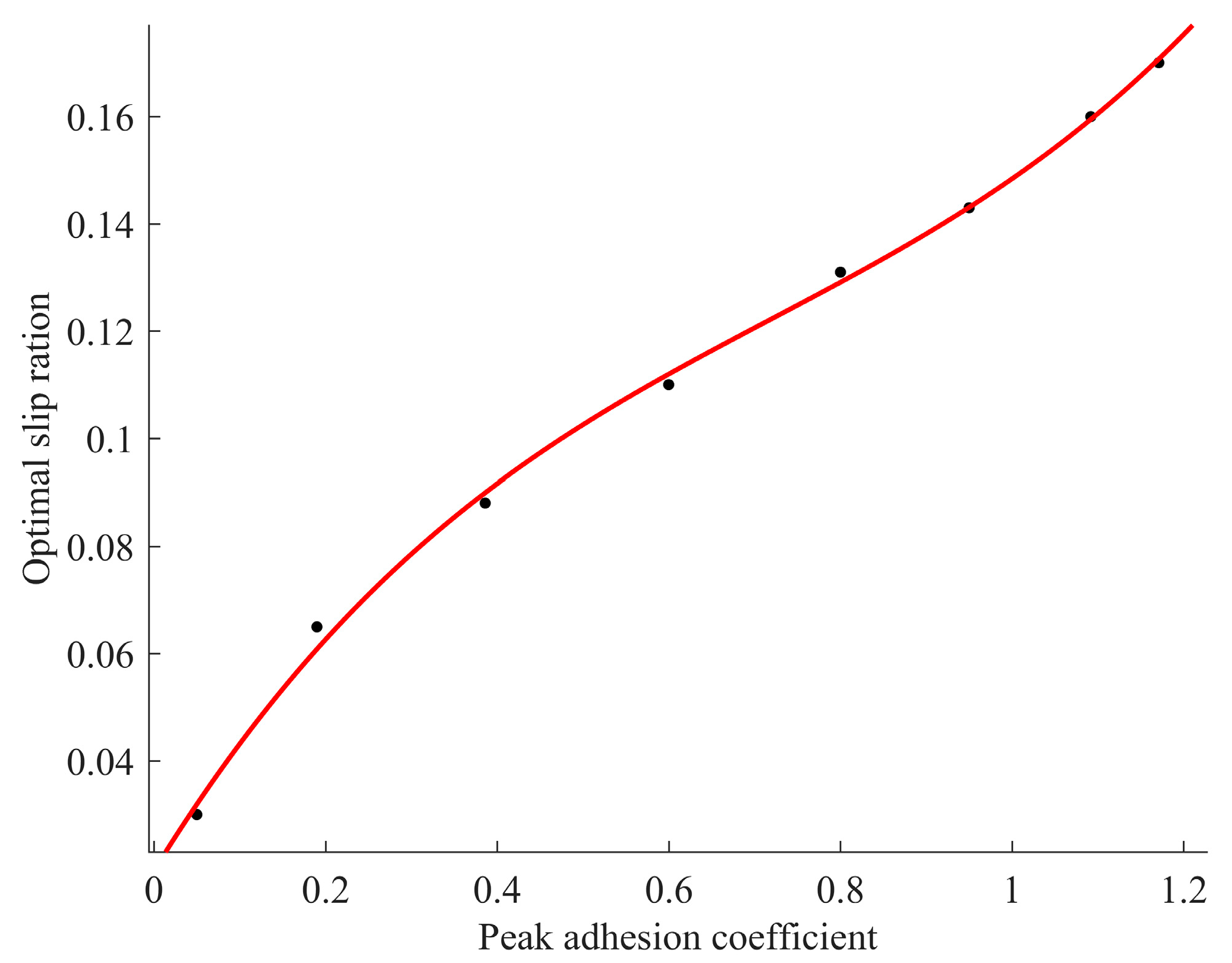
2.2. Estimation of Optimal Slip Ratio
| Algorithm 1 Road estimation algorithm |
| Input: , , , |
| Initialize: , , , , , |
| For do , , , , |
| If , then |
| Elseif |
| Elseif |
| Elseif |
| Elseif |
| Else |
| End if |
| End |
3. Adaptive Control of the Slip Ratio Based on Wheel Angular Velocity
3.1. Design of Conditional Integral Sliding Mode Controller
3.2. Proof of Stability
3.3. Design of Slip Ratio Adaptive Controller Based on Wheel Angular Velocity
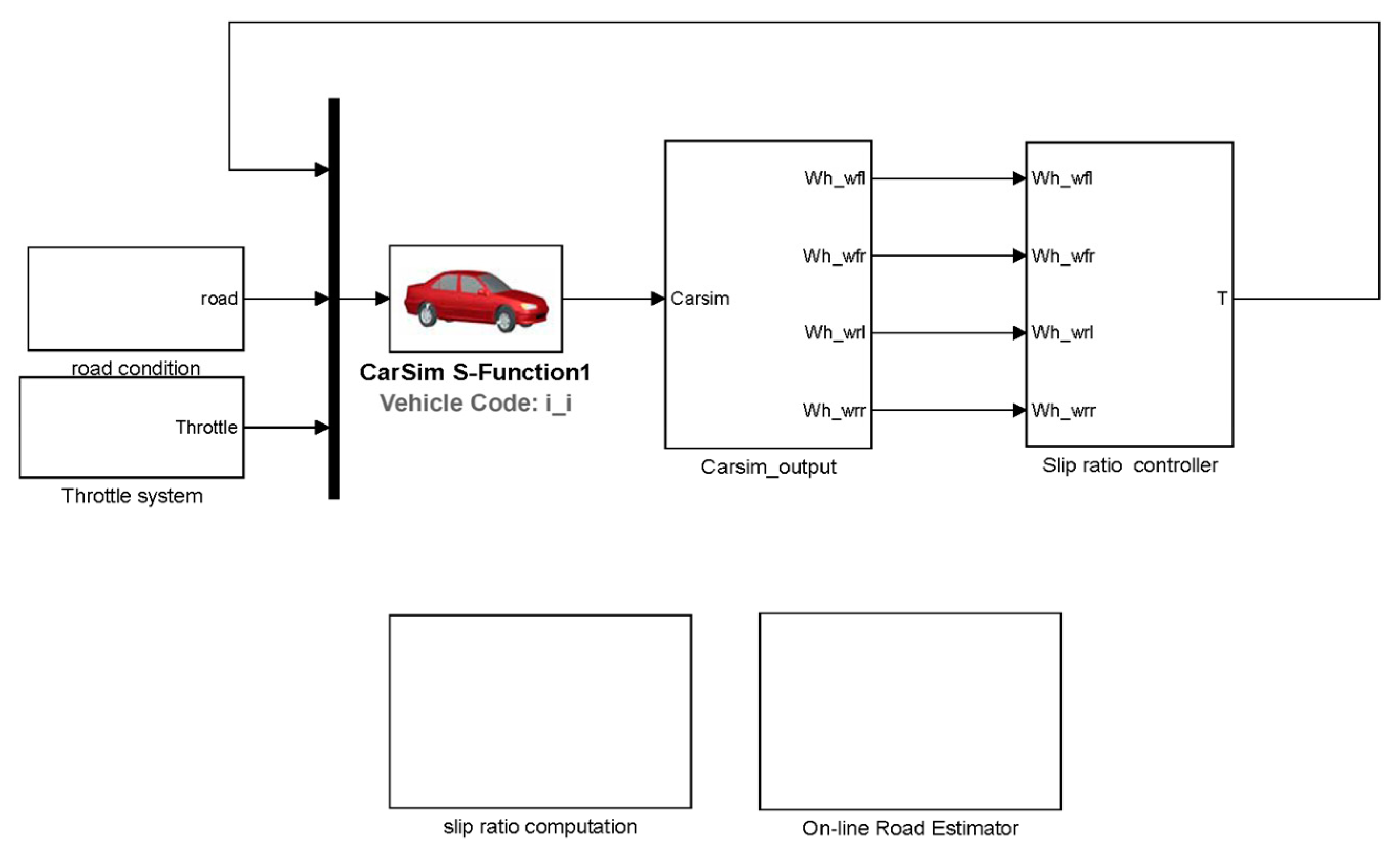
4. Simulation of Slip Ratio Adaptive Control Based on Wheel Angular Velocity
4.1. Simulation of Acceleration on Joint Road
4.2. Simulation of Acceleration on Split Road
5. Conclusions
- (1)
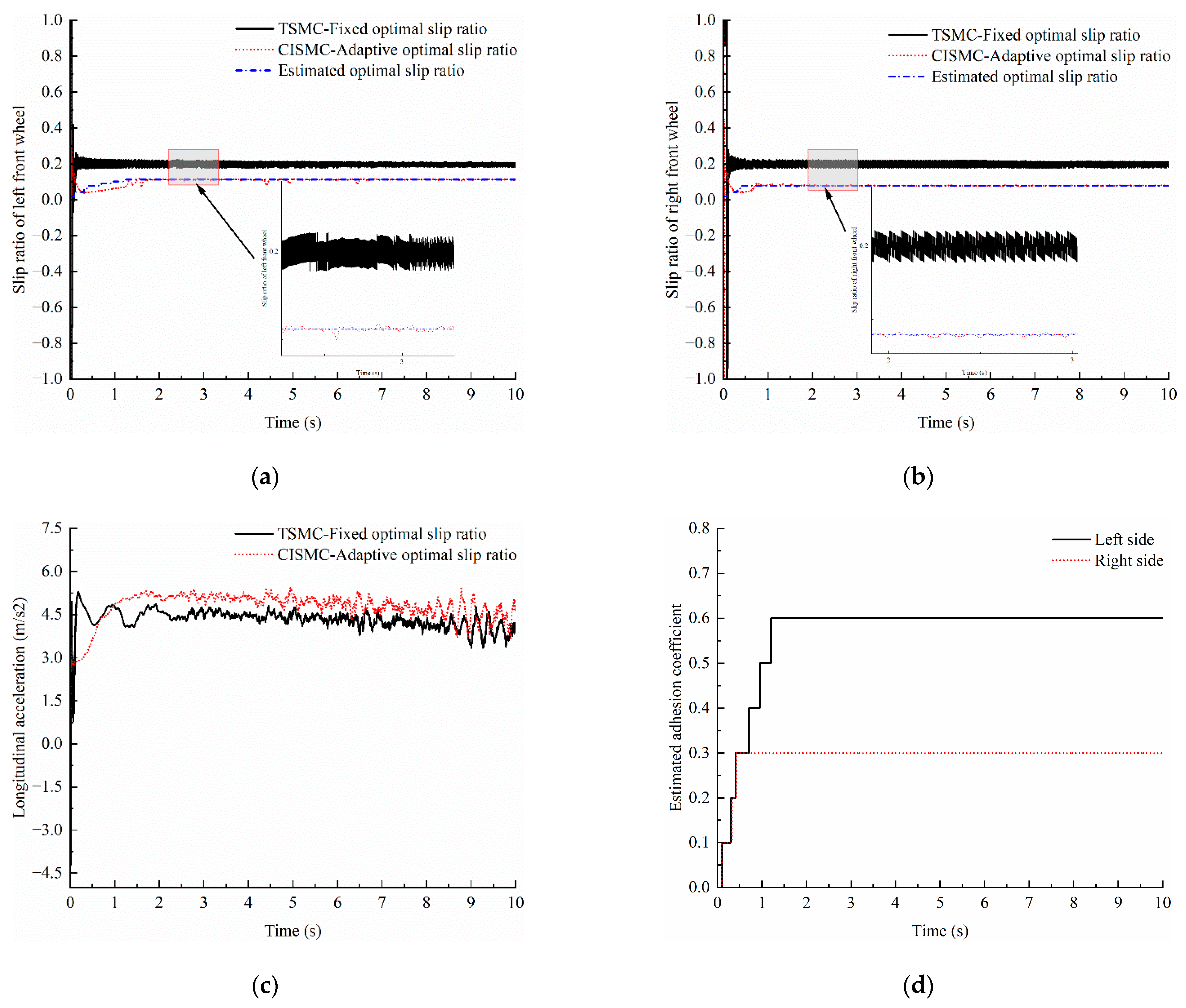
- The designed road estimator can quickly and accurately estimate the road adhesion coefficient and the optimal wheel ratio when the vehicle accelerates on joint road; the road estimator can obtain the road adhesion coefficient and optimal slip ratio within 0.38 , and when the vehicle accelerates on split road, the road estimator can obtain the road adhesion coefficient and optimal slip ratio within 1.20 .
- (2)
- Slip ratio adaptive control based on CISMC can weaken the chattering phenomenon of slip ratio fixed control based on TSMC.
- (3)
- Slip ratio adaptive control based on CISMC can maintain the wheel slip ratio at the optimal value according to the driving road conditions automatically, and the dynamic performance of the vehicle is improved.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Menhour, L.; d’Andréa-Novel, B.; Fliess, M.; Mounier, H. Coupled nonlinear vehicle control: Flatness-based setting with algebraic estimation techniques. Control Eng. Pract. 2014, 22, 135–146. [Google Scholar] [CrossRef]
- Yin, D.; Sun, N.; Hu, J. A wheel slip control approach integrated with electronic stability control for decentralized drive electric vehicles. IEEE Trans. Ind. Inform. 2019, 15, 2244–2252. [Google Scholar] [CrossRef]
- Wang, J.; Yin, D.; Chen, L.; Du, J. Estimation of road adhesion coefficient for four-wheel independent drive electric vehicle. In Proceedings of the 2020 5th International Conference on Mechanical, Control and Computer Engineering (ICMCCE), Harbin, China, 25–27 December 2020. [Google Scholar]
- Leng, B.; Jin, D.; Xiong, L.; Yang, X.; Yu, Z. Estimation of tire-road peak adhesion coefficient for intelligent electric vehicles based on camera and tire dynamics information fusion. Mech. Syst. Signal Process. 2021, 150, 1–15. [Google Scholar] [CrossRef]
- Li, S.; Wang, G.; Yang, Z.; Wang, X. Dynamic joint estimation of vehicle sideslip angle and road adhesion coefficient based on DRBF-EKF algorithm. Chin. J. Theor. Appl. Mech. 2022, 54, 1853–1865. [Google Scholar]
- Zhang, B.; Chen, Z.; Fu, J.; Chen, B. Self-adaption acceleration slip regulation control of four-wheel independently-driving electric vehicle. J. Shandong Univ. (Eng. Sci.) 2018, 48, 96–103. [Google Scholar]
- Guo, W.; Duan, M.; Li, G.; Yu, Q. Study on Acceleration Slip Regulation Control of Electric Vehicle Based on Fuzzy PID Controller. Agric. Equip. Veh. Eng. 2015, 53, 38–42+51. [Google Scholar]
- Tao, W.; Yu, H.; Huang, M. Fuzzy Anti-Slip Regulation Based on Optimal Slip Ratio Recognition for In-wheel Motor Driving Electric Vehicle. J. Wuhan Univ. Technol. 2015, 37, 47–52+70. [Google Scholar]
- Saha, S.; Syed, M. Design of slip-based traction control system for EV and validation using co-simulation between Adams and Matlab/Simulink. Simulation 2020, 96, 537–549. [Google Scholar] [CrossRef]
- Nam, K.; Yoichi, H.; Lee, C. Wheel Slip Control for Improving Traction-Ability and Energy Efficiency of a Personal Electric Vehicle. Energies 2015, 8, 6820–6840. [Google Scholar] [CrossRef]
- Eicke, S.; Busch, A.; Wielitzka, M.; Zemke, S. Tire Road friction estimation for improvements to traction control during drive off maneuvers in vehicles. In Proceedings of the 2016 IEEE Conference on Control Applications (CCA), Buenos Aires, Argentina, 19–22 September 2016. [Google Scholar]
- Yu, D.; Wang, W.; Zhang, H.; Xu, D. Research on anti-lock braking control strategy of distributed-driven electric vehicle. IEEE Access 2020, 8, 162467–162478. [Google Scholar] [CrossRef]
- Guo, L.; Xu, H.; Zou, J.; Xu, H.; Zheng, G. Variable gain control-based acceleration slip regulation control algorithm for four-wheel independent drive electric vehicle. Trans. Inst. Meas. Control 2021, 43, 902–914. [Google Scholar] [CrossRef]
- Peng, M.; Karimi, H.; Yang, S.; Xu, B.; Huang, C. An adaptive fuzzy sliding-mode control for regenerative braking system of electric vehicles. Int. J. Adapt. Control Signal Process. 2022, 36, 391–410. [Google Scholar]
- Hegazy, S.; Sandu, C. Experimental investigation of vehicle mobility using a novel wheel mobility number. J. Terramech. 2013, 50, 303–310. [Google Scholar] [CrossRef]
- Ding, X.; Zhang, L.; Wang, Z.; Liu, P. Acceleration Slip Regulation for Four-Wheel-Independently-Actuated Electric Vehicles Based on Road Identification through the Fuzzy Logic. IFAC-PapersOnLine 2018, 51, 943–948. [Google Scholar] [CrossRef]
- Wang, B.; Guan, H.; Lu, P.; Zhang, A. Road surface condition identification approach based on road characteristic value. J. Terramech. 2014, 6, 103–117. [Google Scholar] [CrossRef]
- Zhou, W.; Li, J.; Zhang, S.; Tang, S. Vehicle Acceleration Slip Regulation Using Extreme Value Search Algorithm to Estimate Adhesion Coefficient. J. Huaqiao Univ. (Nat. Sci.) 2019, 40, 701–706. [Google Scholar]
- Liao, Z.; Liu, D.; Yang, G.; Liu, D. Integrated control of ABS and ASR for multi-wheel independent electric drive vehicle. Mech. Electr. Eng. Mag. 2018, 35, 494–500. [Google Scholar]
- Mehrdad, E.; Yimin, G.; Ali, E. Modern Electric, Hybrid Electric, and Fuel Cell Vehicles: Fundamentals, Theory, and Design; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Ivanov, V.; Savitski, D.; Shyrokau, B. A Survey of Traction Control and Antilock Braking Systems of Full Electric Vehicles With Individually Controlled Electric Motors. IEEE Trans. Veh. Technol. 2014, 64, 3878–3896. [Google Scholar] [CrossRef]
- Incremona, G.; Regolin, E.; Mosca, A.; Incremona, G. Sliding mode control algorithms for wheel slip control of road vehicles. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017. [Google Scholar]
- Guo, H.; Yu, R.; Bai, X.; Chen, H. Vehicle traction control based on optimal slip using sliding mode controller. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014. [Google Scholar]
- Yokoyama, M.; Kim, G.; Tsuchiya, M. Integral Sliding Mode Control with Anti-windup Compensation and its Application to a Power Assist System. J. Vib. Control 2010, 16, 503–512. [Google Scholar] [CrossRef]
- Liu, D.; Liao, Z.; Yang, G.; Chen, L. Acceleration Slip Regulation of Multi-wheel Independent Electric Drive Vehicle Based on Sliding Mode Control. Mod. Manuf. Technol. Equip. 2017, 15–19. [Google Scholar] [CrossRef]
- Maeda, K.; Fujimoto, H.; Hori, Y. Four-wheel driving-force distribution method for instantaneous or split slippery roads for electric vehicle. Autom. Časopis Za Autom. Mjer. Elektron. Računarstvo I Komun. 2013, 54, 103–113. [Google Scholar] [CrossRef]
- Yoshimura, M.; Fujimoto, H. Driving torque control method for electric vehicle with in-wheel motors. Electr. Eng. Jpn. 2012, 181, 49–58. [Google Scholar] [CrossRef]


| Road Type | |||
|---|---|---|---|
| Dry asphalt | 1.281 | 23.993 | 0.520 |
| Dry cement | 1.196 | 25.166 | 0.539 |
| Wet asphalt (big) | 1.027 | 29.494 | 0.442 |
| Wet asphalt (middle) | 0.856 | 33.821 | 0.345 |
| Wet asphalt (small) | 0.628 | 33.768 | 0.200 |
| Wet goose soft stone | 0.400 | 60.010 | 0.120 |
| Snow covered road | 0.195 | 94.129 | 0.065 |
| Ice pavement | 0.050 | 306.390 | 0.001 |
| Parameter | Value |
|---|---|
| Vehicle mass () | 1231 |
| Wheel effective radius () | 0.311 |
| Distance from front axle to CG () | 1.04 |
| Distance from rear axle to CG () | 1.56 |
| Height of CG above ground () | 0.54 |
| Rotational inertia of the wheel () | 0.6 |
| Controller Type | Road Condition | Slip Ratio | ||
|---|---|---|---|---|
| CISMC-Adaptive optimal slip ratio | Joint road | 0.06 (μ = 0.2) | 12.09 | 2.42 |
| 0.11 (μ = 0.6) | 47.28 | 7.04 | ||
| TSMC-Fixed optimal slip ratio | 0.2 (μ = 0.2) | 9.73 | 1.94 | |
| 0.2 (μ = 0.6) | 41.41 | 6.33 | ||
| CISMC-Adaptive optimal slip ratio | Split road | 0.11 (μ = 0.6) | - | 4.76 |
| 0.08 (μ = 0.3) | ||||
| TSMC-Fixed optimal slip ratio | 0.2 (μ = 0.6) | - | 4.32 | |
| 0.2 (μ = 0.3) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, S.; Chen, J.; Qiu, G.; Tong, H. Slip Ratio Adaptive Control Based on Wheel Angular Velocity for Distributed Drive Electric Vehicles. World Electr. Veh. J. 2023, 14, 119. https://doi.org/10.3390/wevj14050119
Kang S, Chen J, Qiu G, Tong H. Slip Ratio Adaptive Control Based on Wheel Angular Velocity for Distributed Drive Electric Vehicles. World Electric Vehicle Journal. 2023; 14(5):119. https://doi.org/10.3390/wevj14050119
Chicago/Turabian StyleKang, Sheng, Junjie Chen, Guangqi Qiu, and Hangkai Tong. 2023. "Slip Ratio Adaptive Control Based on Wheel Angular Velocity for Distributed Drive Electric Vehicles" World Electric Vehicle Journal 14, no. 5: 119. https://doi.org/10.3390/wevj14050119
APA StyleKang, S., Chen, J., Qiu, G., & Tong, H. (2023). Slip Ratio Adaptive Control Based on Wheel Angular Velocity for Distributed Drive Electric Vehicles. World Electric Vehicle Journal, 14(5), 119. https://doi.org/10.3390/wevj14050119







