Investigation and Development of the Brushless and Magnetless Wound Field Synchronous Motor Drive System for Electric Vehicle Application
Abstract
1. Introduction
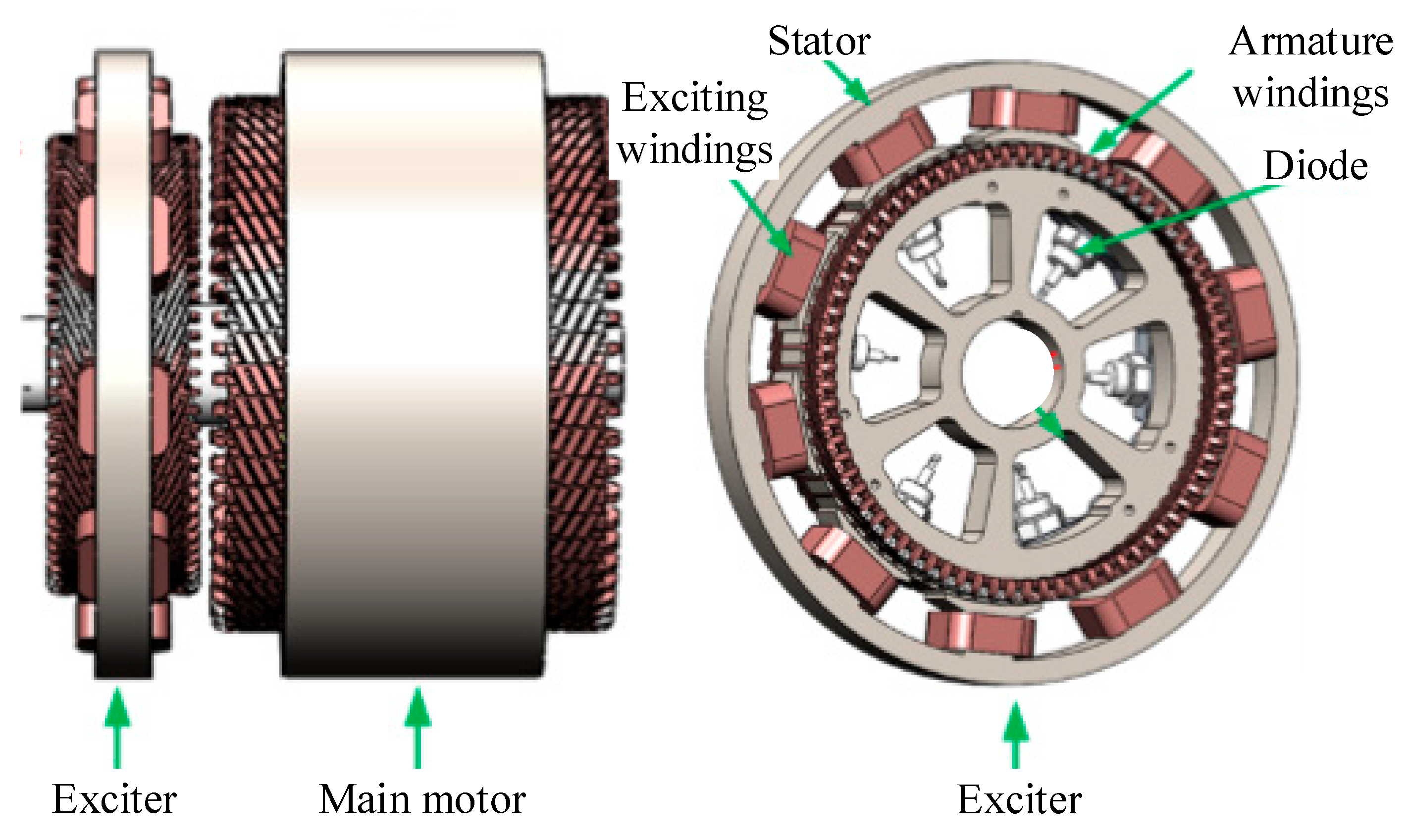
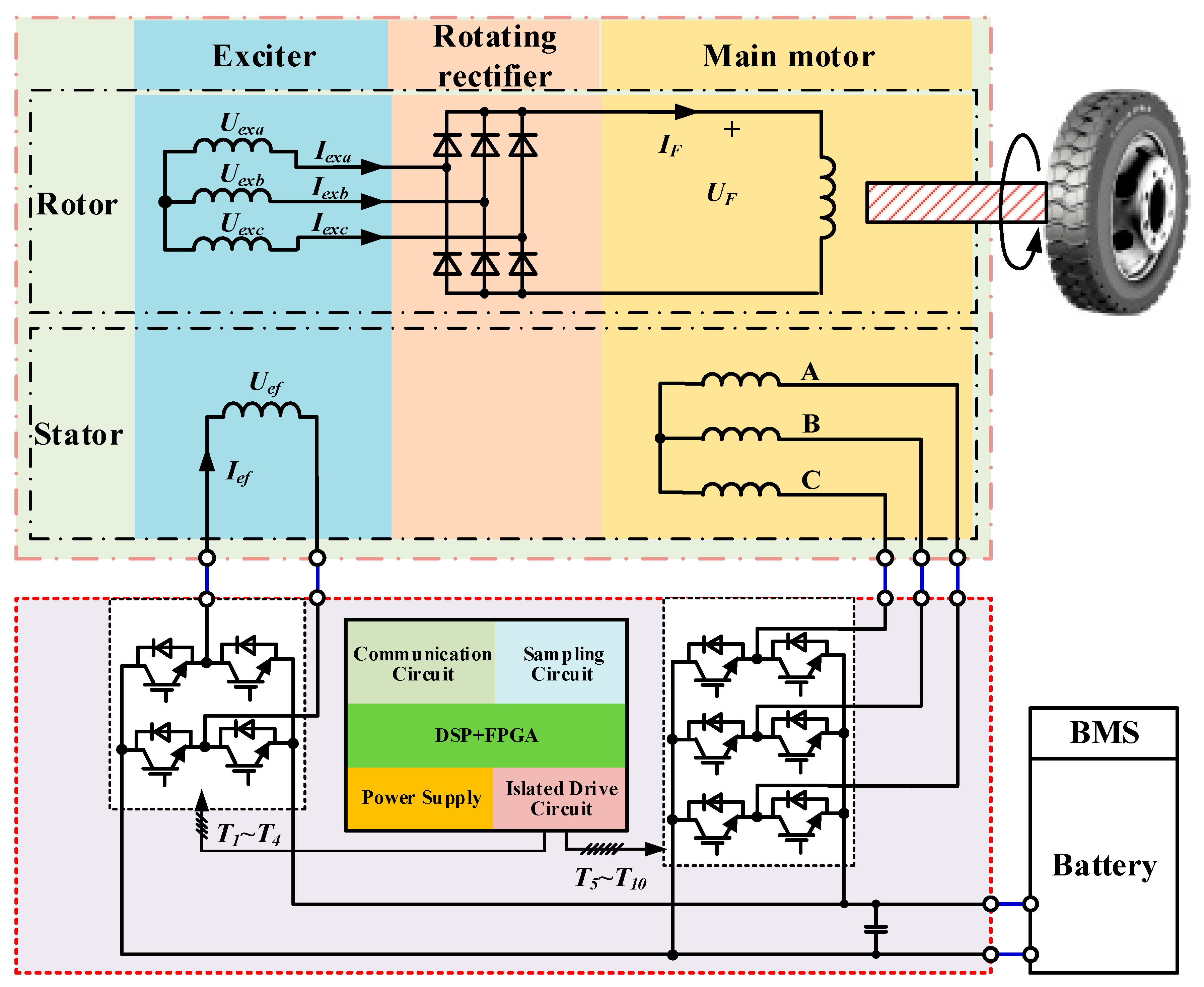
2. Structure and Principle of the Proposed WFSM Drive System
3. System Analysis and Development
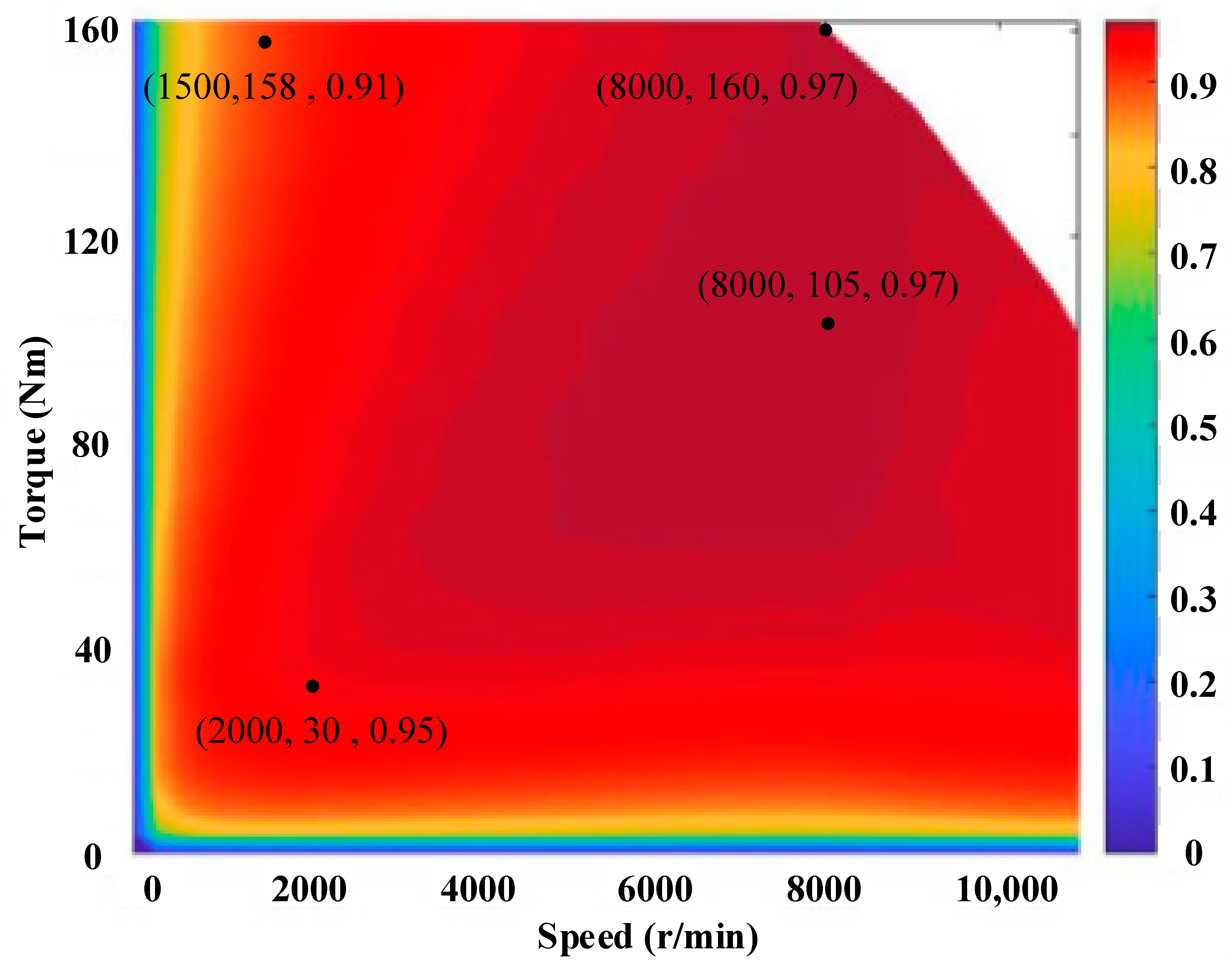
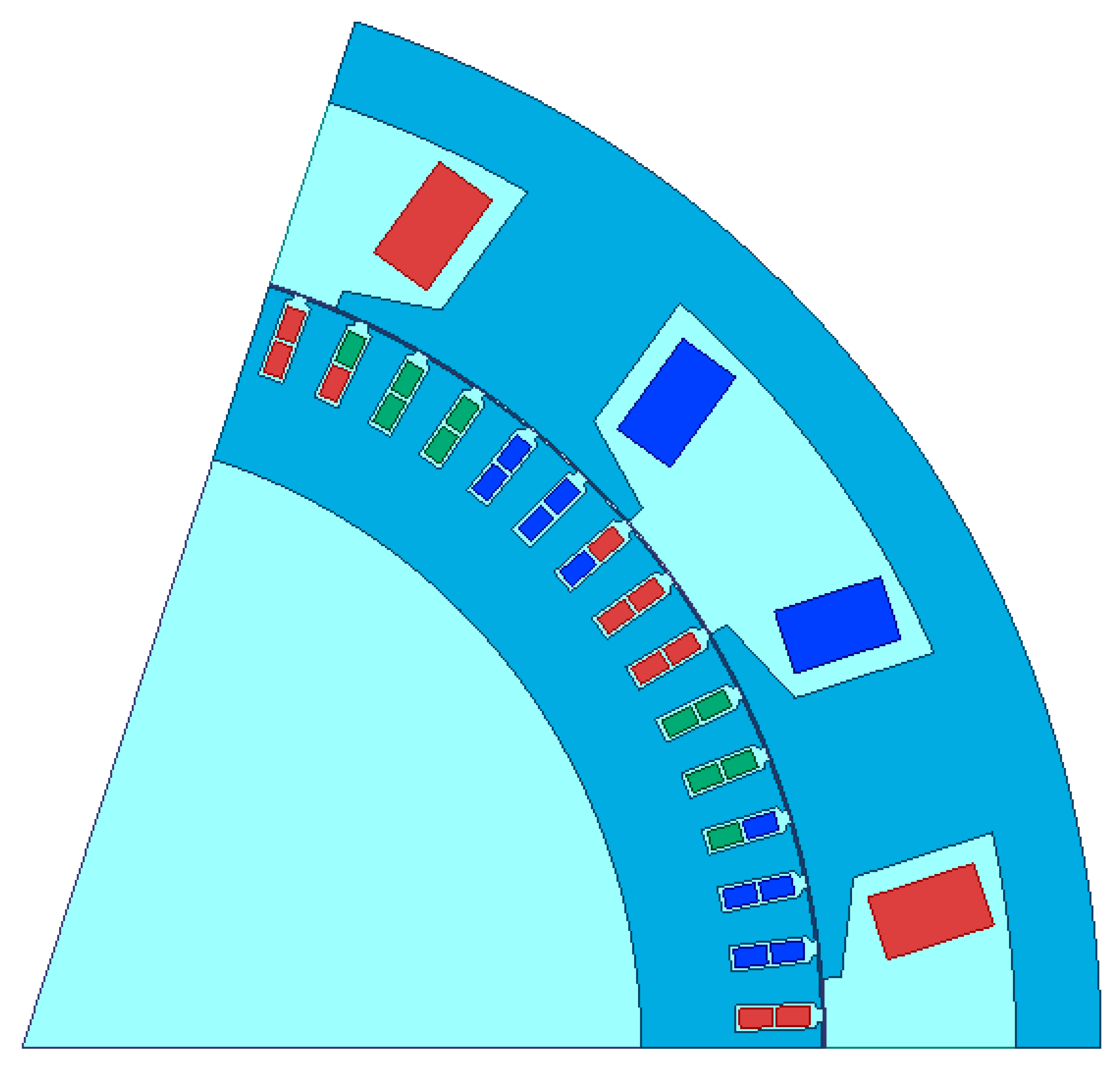
3.1. Investigation and Analysis of the Main Motor
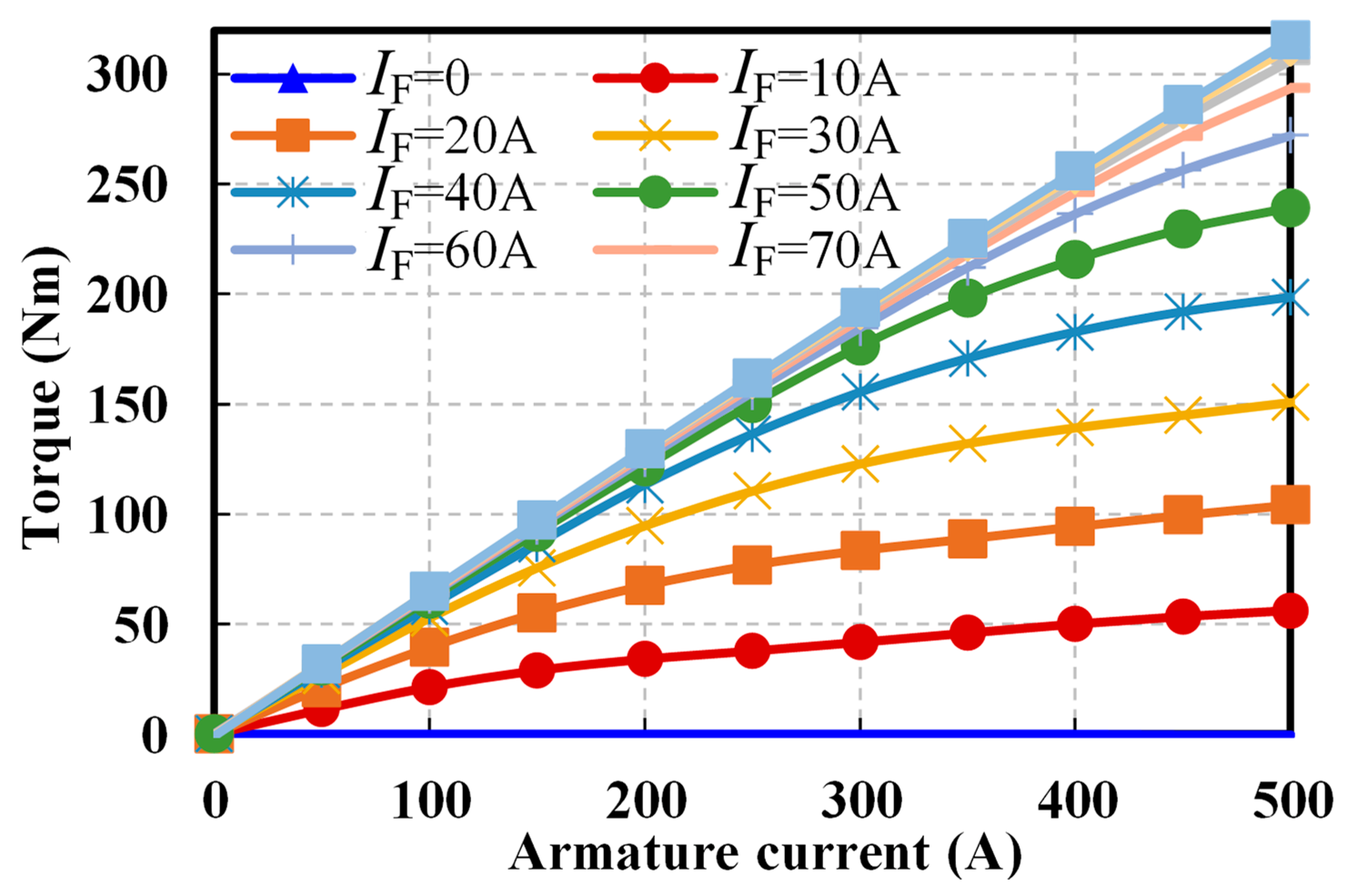
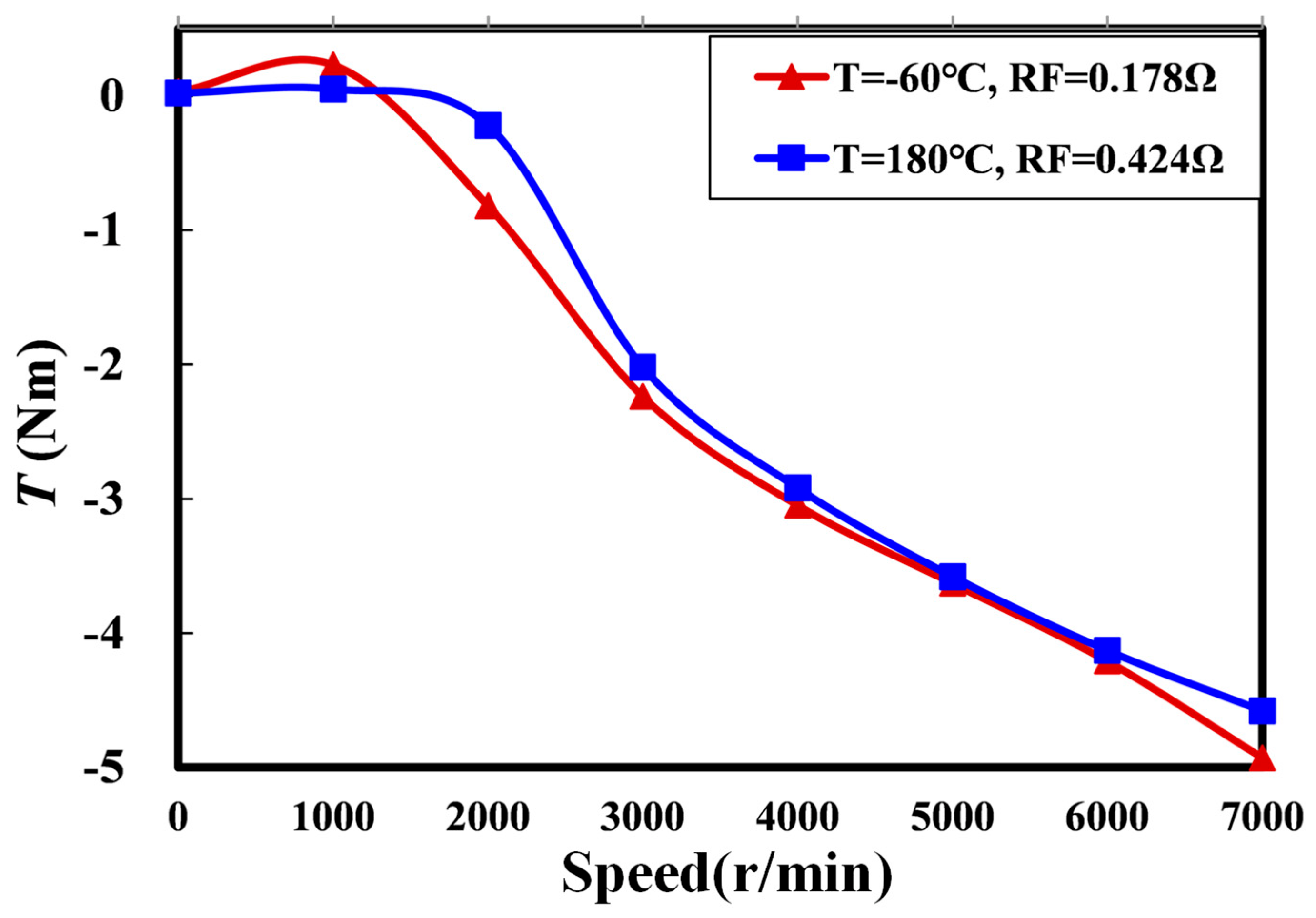
The Torque Characteristics of the Proposed WFSM
3.2. Analysis of the Exciter Characteristics
3.2.1. The Principle of Single-Phase AC Excitation
3.2.2. The FEA Analysis of Single-Phase AC Excitation
3.3. Control Strategy of WFSM Drive System
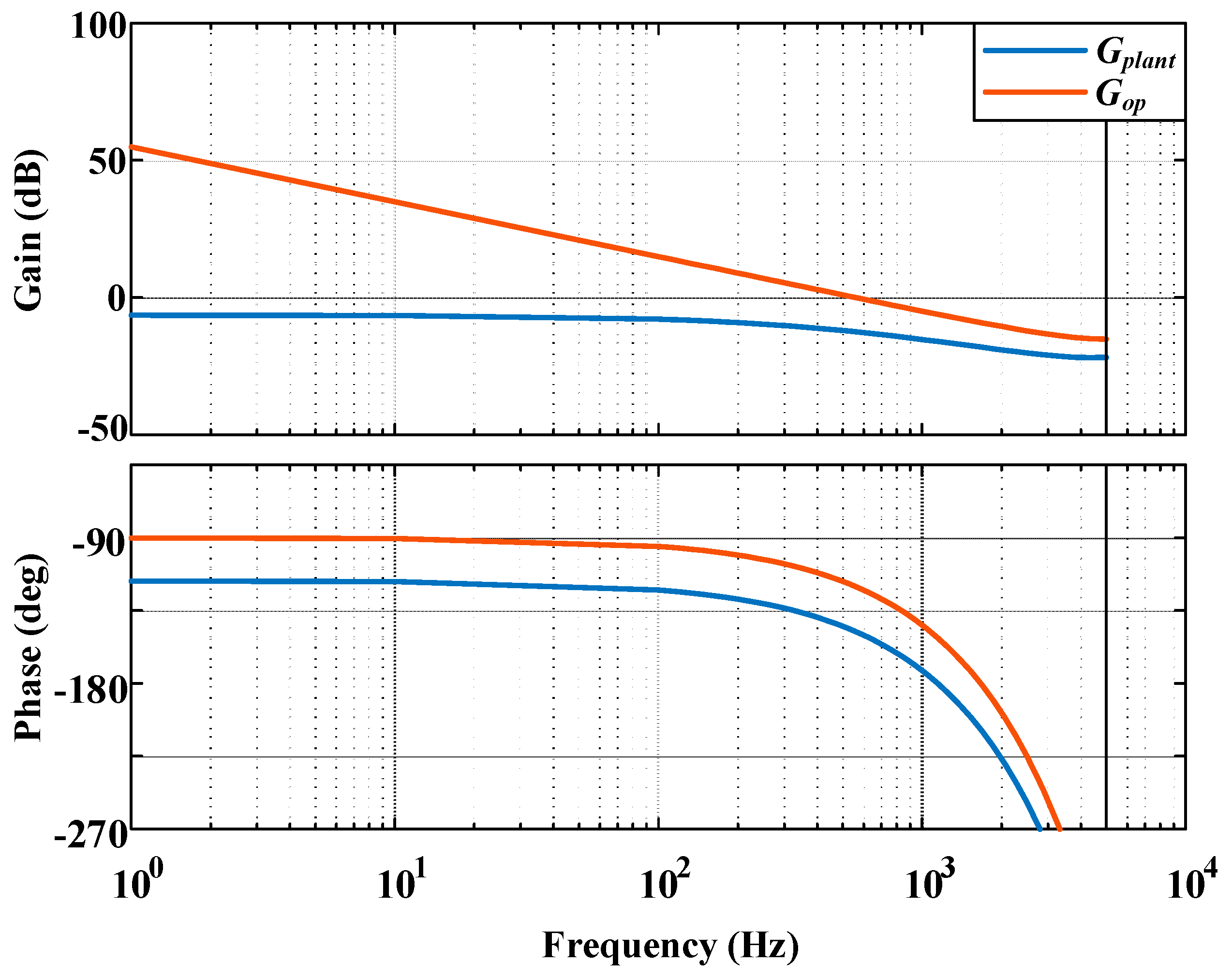
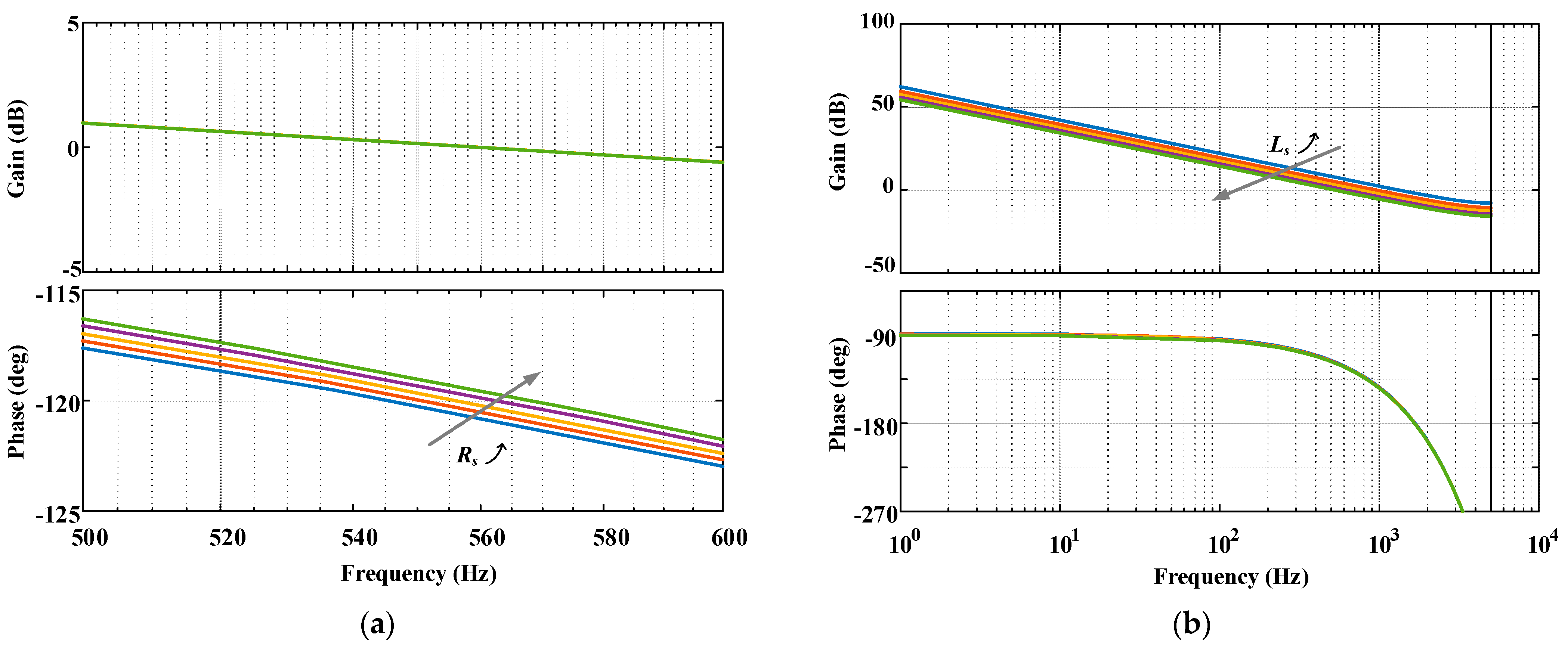
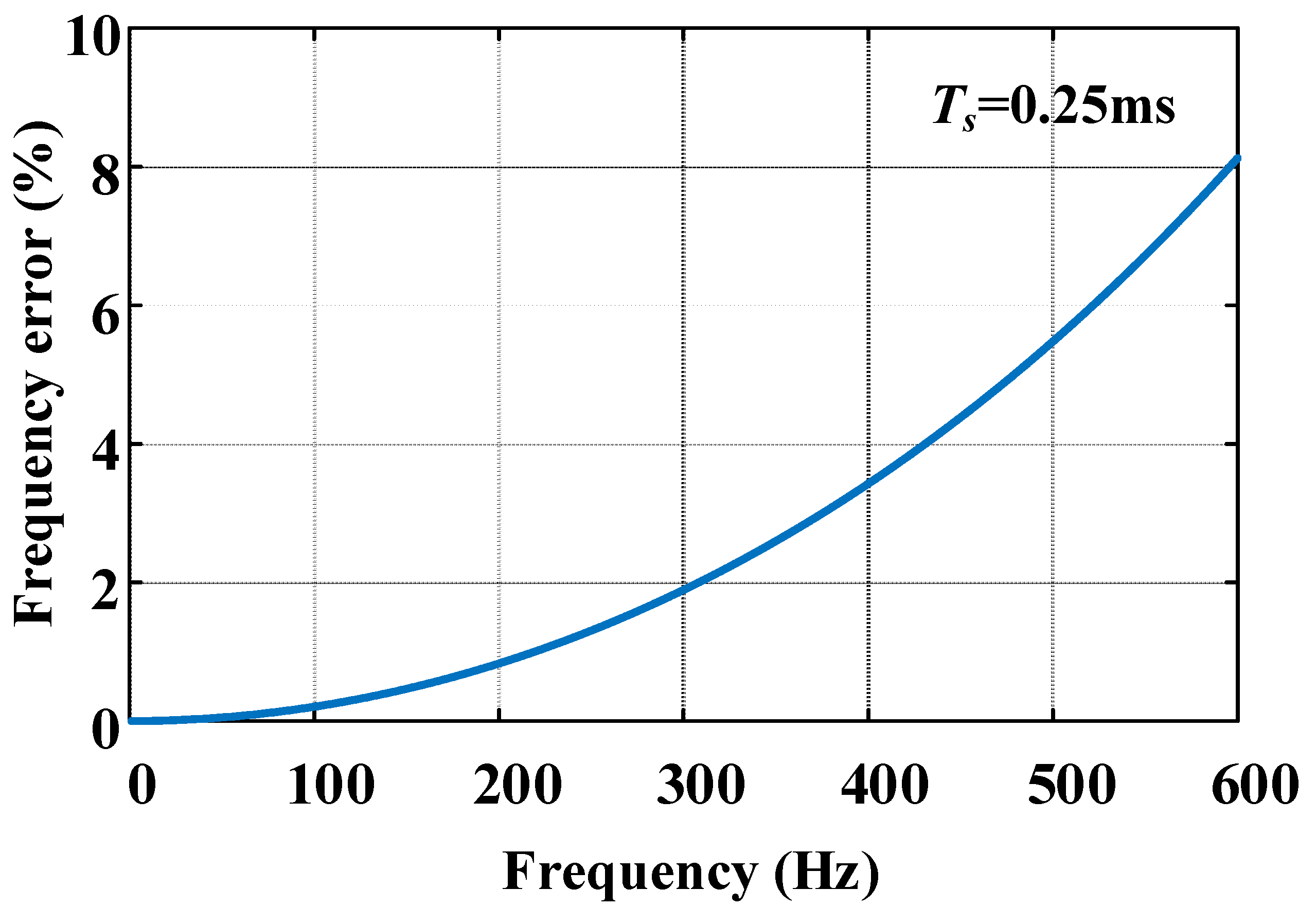
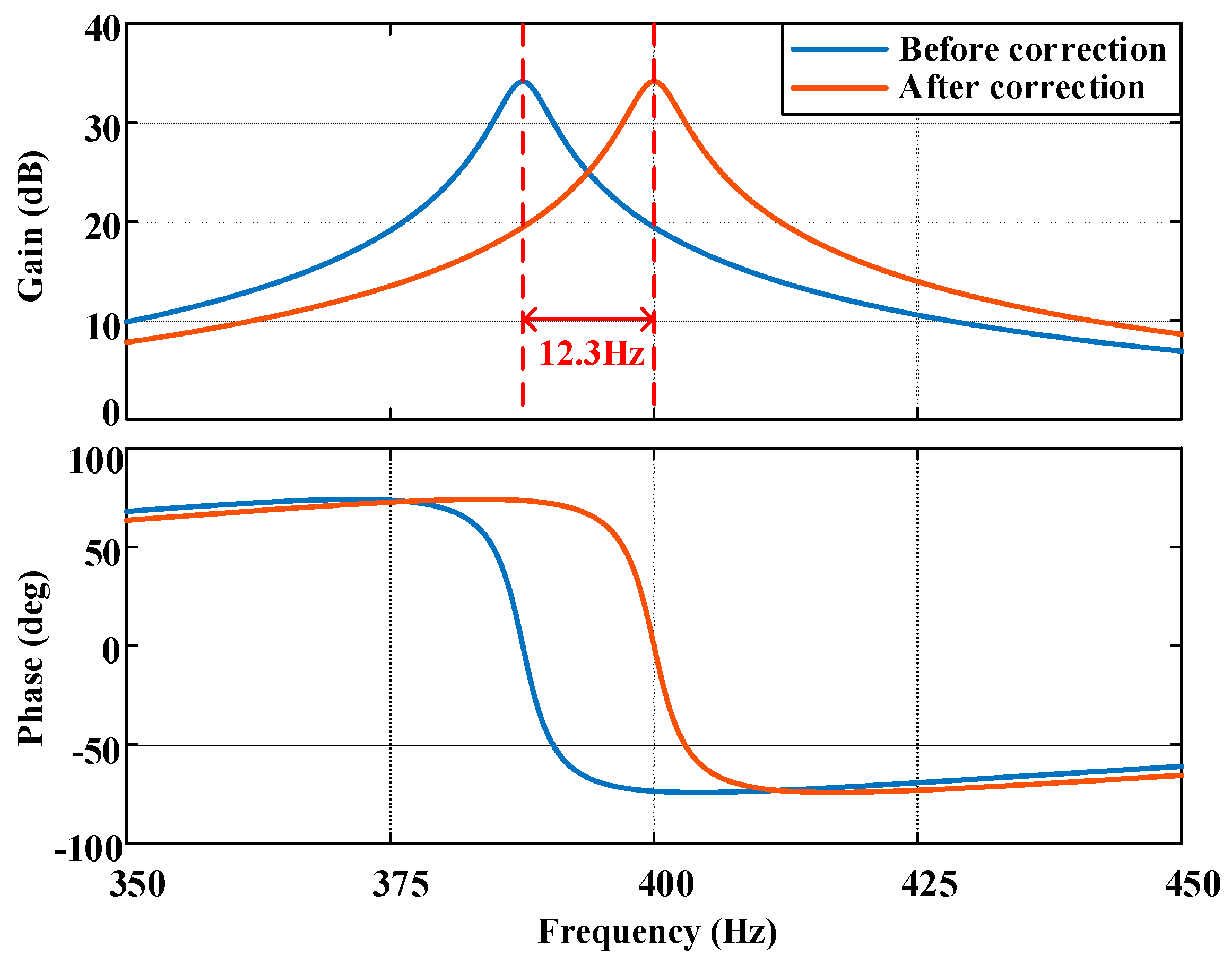
3.3.1. Approaches of Discrete Time Armature Current Regulator Design
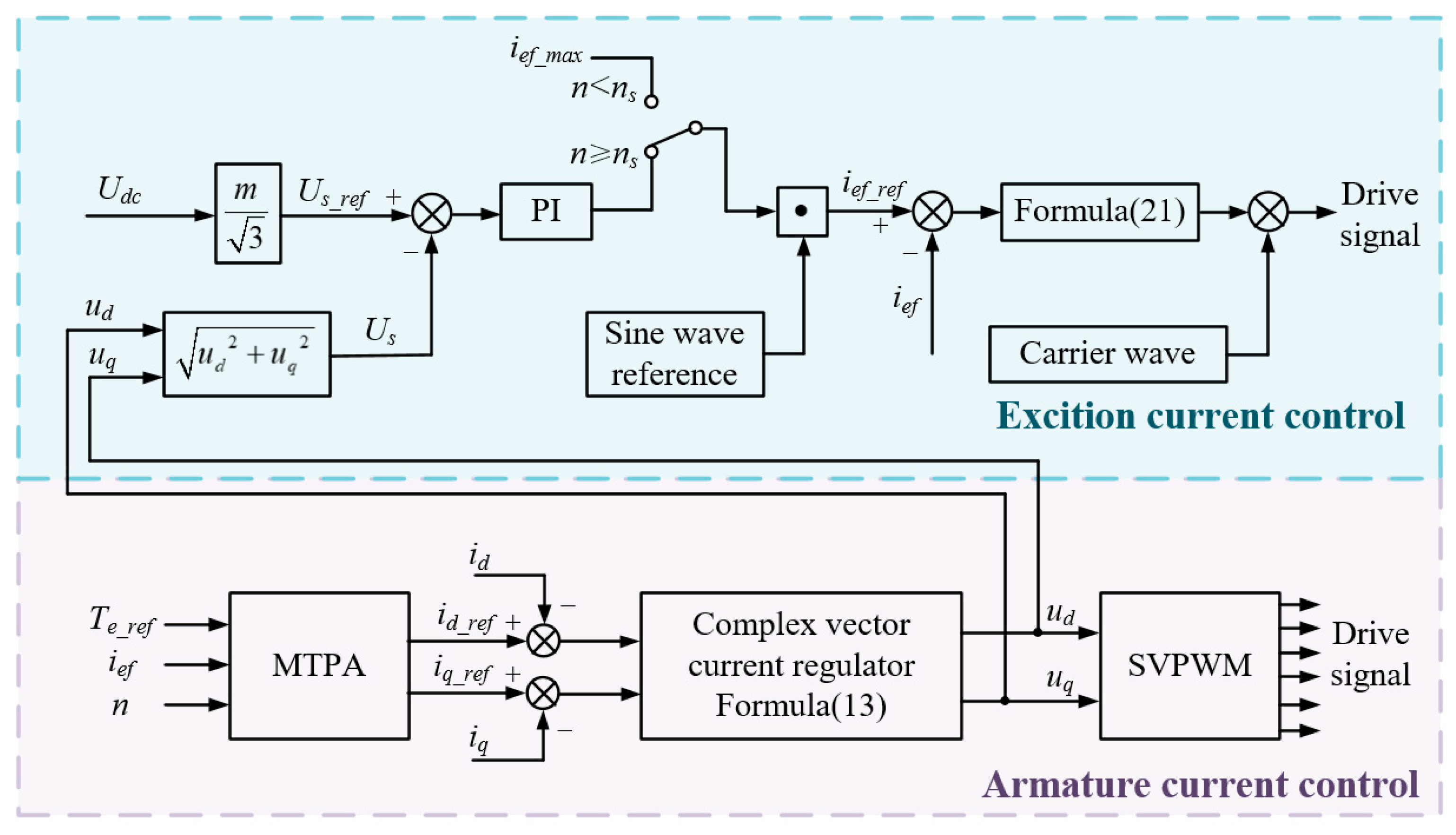
3.3.2. Design of Excitation Current Coordination Control Strategy
4. Experimental Verification
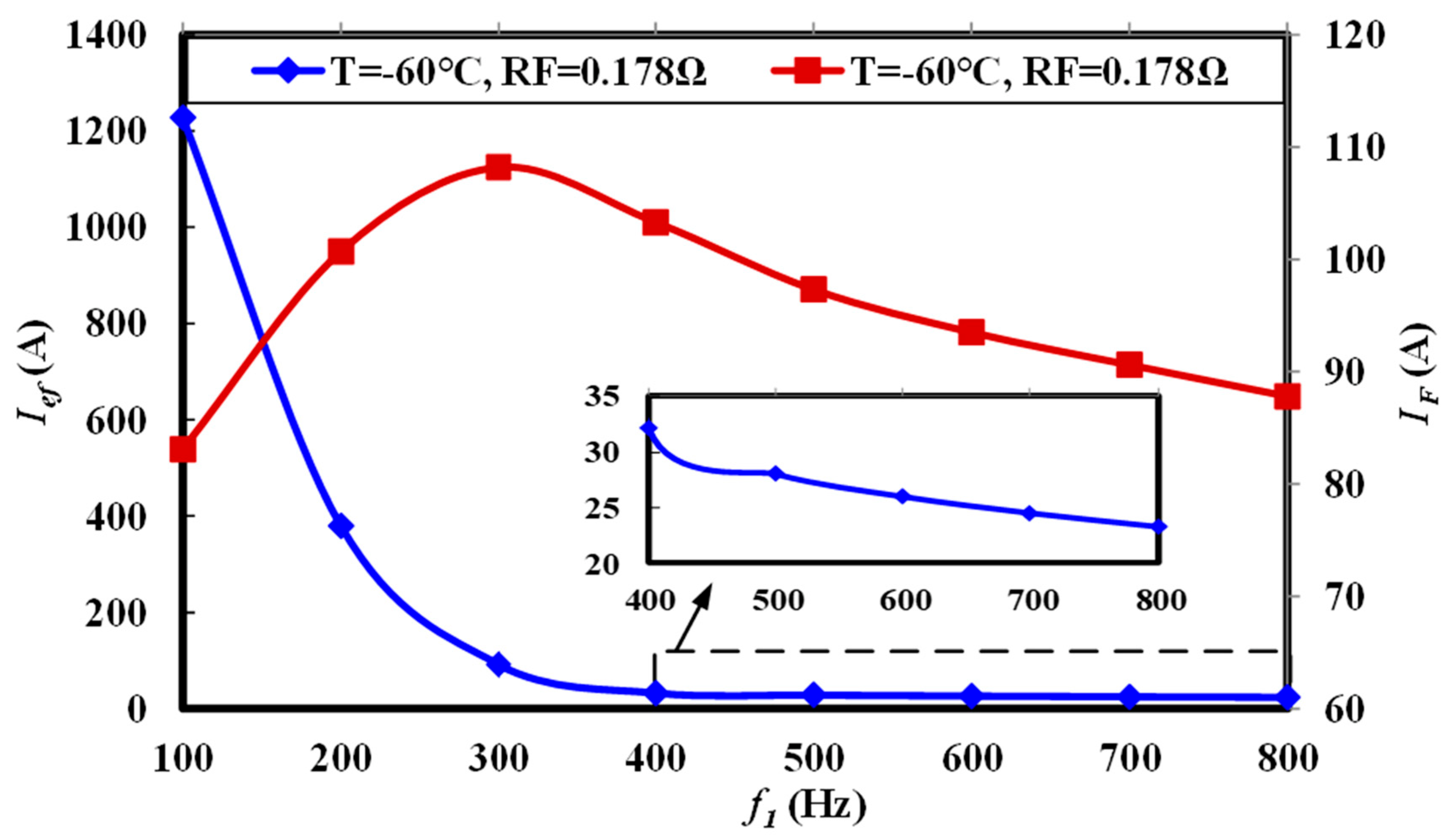
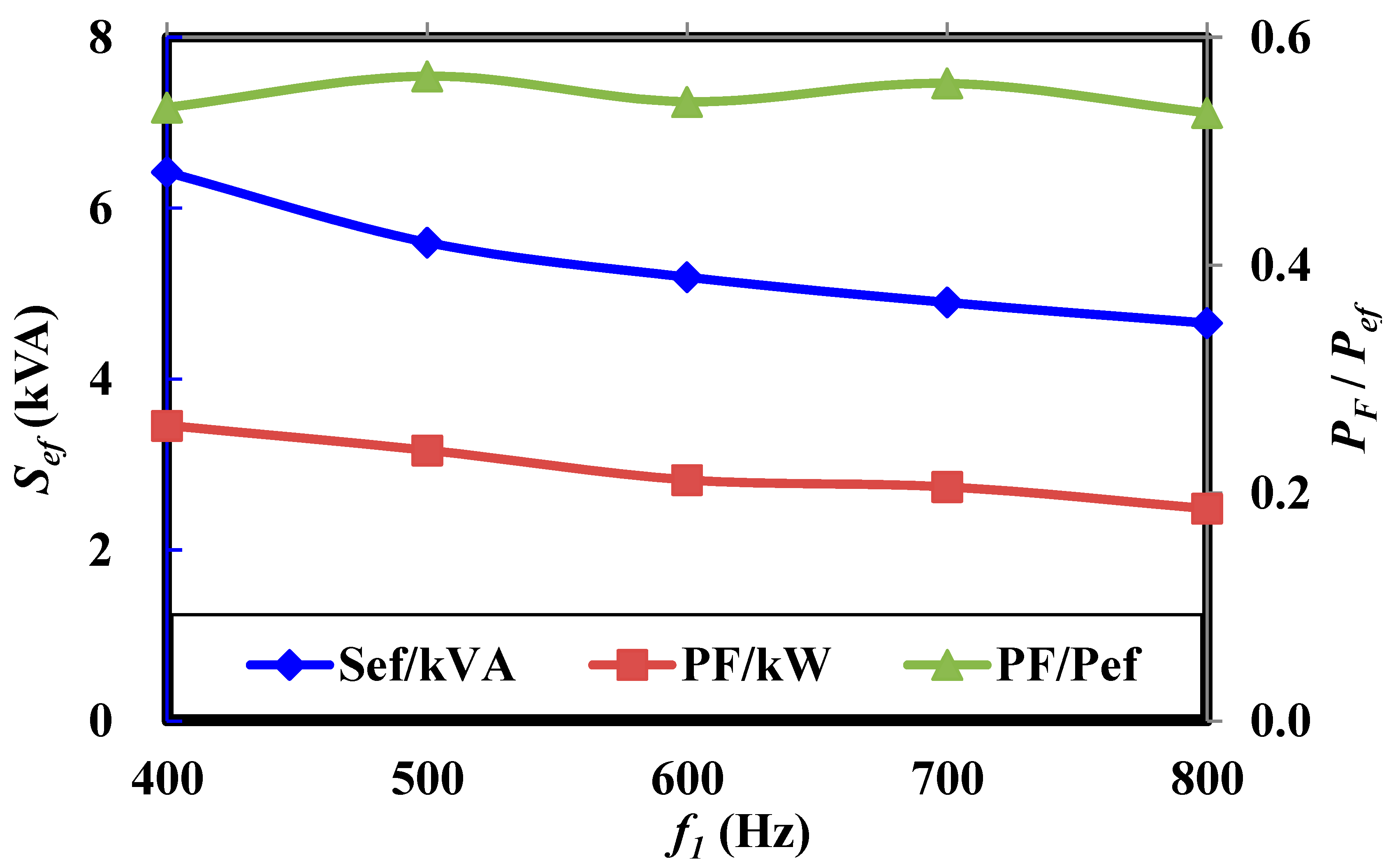
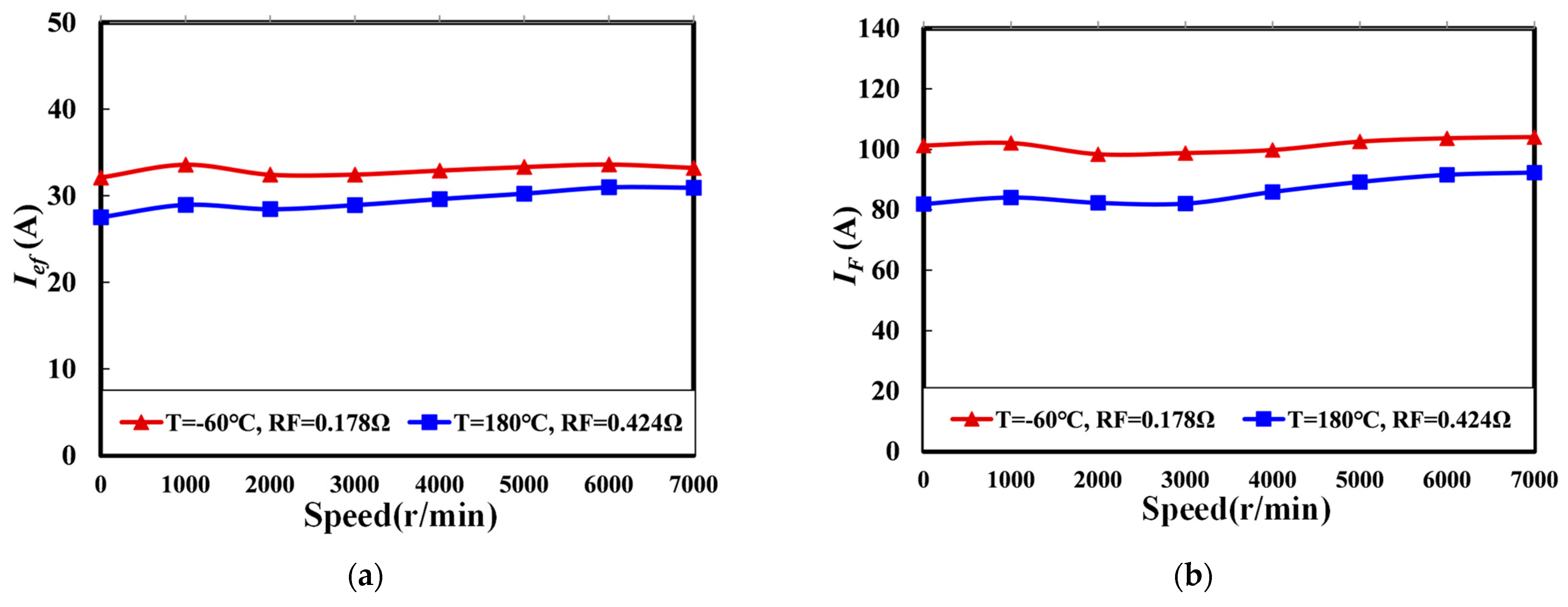
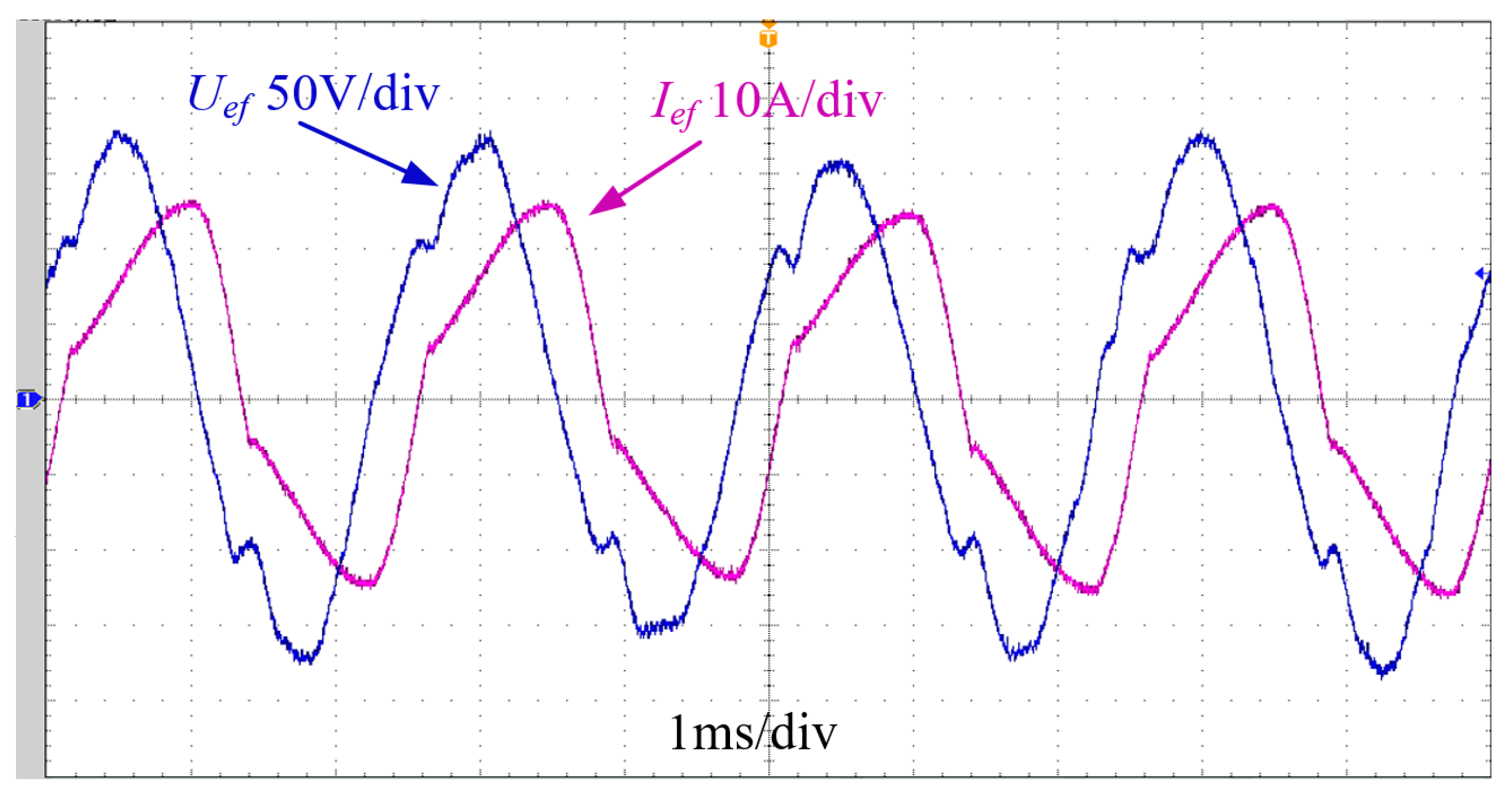
4.1. AC Excitation Characteristics
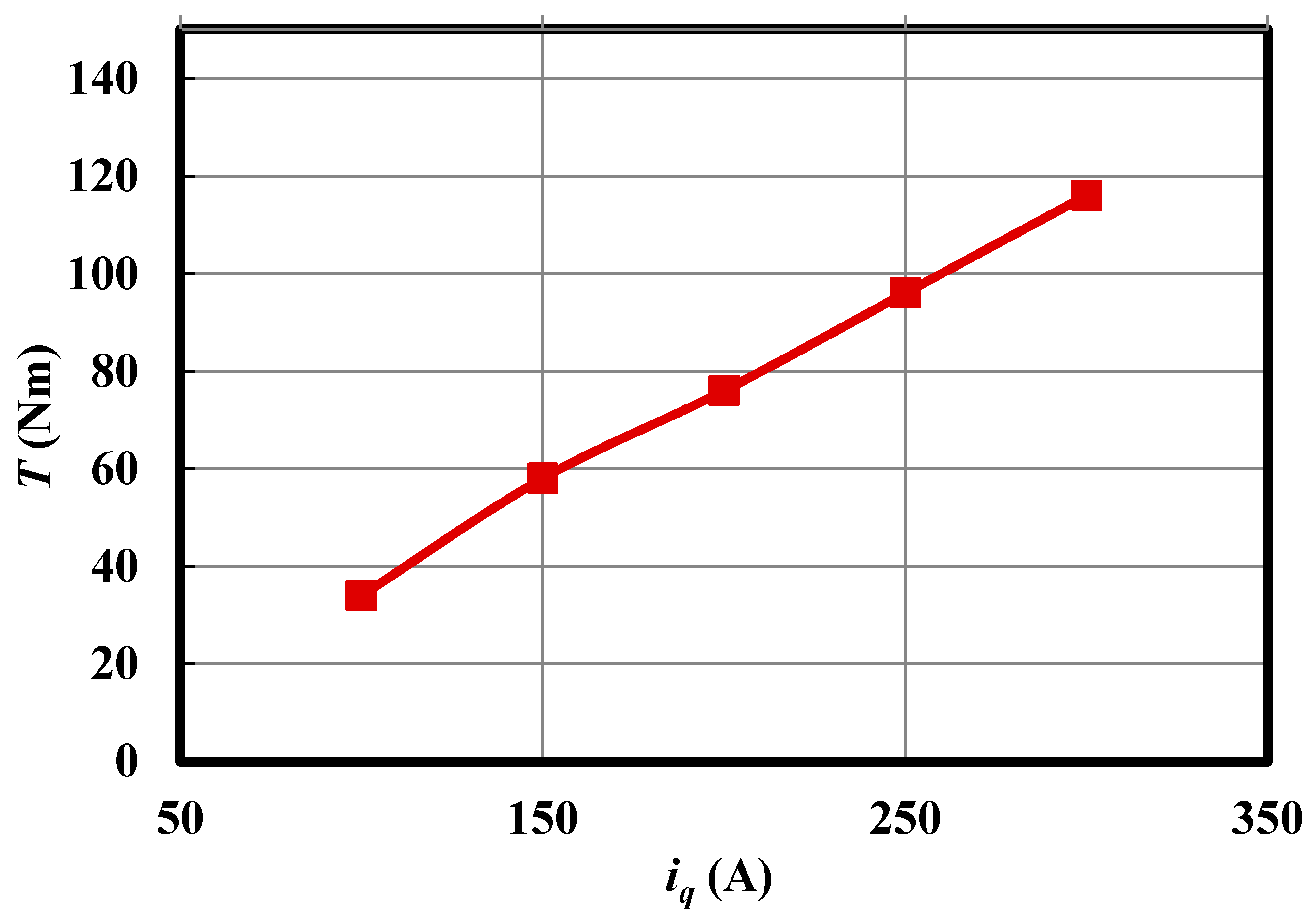
4.2. Torque under Different Armature Current
5. Conclusions
- The exciter excited by single-phase constant frequency current has the characteristics of current amplification and constant current source, and the amplification factor is almost independent of load and speed;
- The torque of the main motor is proportional to the armature current;
- The additional control DOF introduced by the field current is the key for WFSM to obtain high torque capability in the low speed region and to have a wider constant power region.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ruuskanen, V.; Nerg, J.; Rilla, M.; Pyrhonen, J. Iron loss analysis of the permanent magnet synchronous machine based on finite-element analysis over the electrical vehicle drive cycle. IEEE Trans. Ind. Electron. 2016, 63, 4129–4136. [Google Scholar] [CrossRef]
- Jacobs, S.; Hectors, D.; Henrotte, F.; Hafner, M.; Gracia, M.H.; Hameyer, K.; Goes, P. Magnetic material optimization for hybrid vehicle PMSM drives. World Electr. Veh. J. 2009, 3, 875–883. [Google Scholar] [CrossRef]
- Coey, J.M.D. Perspective and Prospects for Rare Earth Permanent Magnets. Engineering 2019, 6, 119–131. [Google Scholar] [CrossRef]
- Zechmair, D.; Steidl, K. Why the Induction Motor Could be the Better Choice for Your Electric Vehicle Program. World Electr. Veh. J. 2012, 5, 546–549. [Google Scholar] [CrossRef]
- Vosswinkel, M.; Lohner, A.; Platte, V.; Hirche, T. Design, Production, and Verification of a Switched-Reluctance Wheel Hub Drive Train for Battery Electric Vehicles. World Electr. Veh. J. 2019, 10, 82. [Google Scholar] [CrossRef]
- Sirewal, G.J.; Bukhari, S.S.H. Cost-Effective Scheme for a Brushless Wound Rotor Synchronous Machine. World Electr. Veh. J. 2021, 12, 194. [Google Scholar] [CrossRef]
- Widmer, J.D.; Martin, R.; Kimiabeigi, M. Electric Vehicle Traction Motors without Rare Earth Magnets. Sustain. Mater. Technol. 2015, 3, 7–13. [Google Scholar] [CrossRef]
- Binnemans, K.; Jones, P.T.; Blanpain, B.; Gerven, T.V.; Yang, Y.; Walton, A.; Buchert, M. Recycling of Rare Earths: A Critical Review. J. Clean. Prod. 2013, 51, 1–22. [Google Scholar] [CrossRef]
- Friedrich, G. Comparative study of three control strategies for the synchronous salient poles and wound rotor machine in automotive applications with on board energy. In Proceedings of the 1994 Fifth International Conference on Power Electronics and Variable-Speed Drives, London, UK, 26–28 October 1994. [Google Scholar]
- Casadei, D.; Rossi, C.; Pilati, A.; Gaetani, A. Traction system for heavy electric vehicles based on the wound rotor salient pole synchronous machine drive. In Proceedings of the 21st Worldwide Battery, Hybrid and Fuel Cell Electric Vehicle Symposium amp; Exhibition (EVS 21), Monte Carlo, Monaco, 2–4 April 2005. [Google Scholar]
- Mao, S.; Liu, W.; Jiao, N.; Gao, F.; Chen, Z. Sensorless Starting Control of Brushless Synchronous Starter/Generators for the Full-Speed Range. IEEE Trans. Power Electron. 2020, 35, 8347–8360. [Google Scholar] [CrossRef]
- Popescu, M.; Goss, J.; Staton, D.A.; Hawkins, D.; Chong, Y.C.; Boglietti, A. Electrical Vehicles-Practical Solutions for Power Traction Motor Systems. IEEE Trans. Ind. Appl. 2018, 54, 2751–2762. [Google Scholar] [CrossRef]
- Park, H.J.; Lim, M.S. Design of High Power Density and High Efficiency Wound-Field Synchronous Motor for Electric Vehicle Traction. IEEE Access 2019, 7, 46677–46685. [Google Scholar] [CrossRef]
- Hwang, S.W.; Sim, J.H.; Hong, J.P.; Lee, J.Y. Torque Improvement of Wound Field Synchronous Motor for Electric Vehicle by PM-Assist. IEEE Trans. Ind. Appl. 2018, 54, 3252–3259. [Google Scholar] [CrossRef]
- Di Gioia, A.; Brown, L.P.; Nie, Y.; Knippel, R.; Ludois, D.C.; Dai, J.J.; Hagen, S.; Alteheld, C. Design and Demonstration of a Wound Field Synchronous Machine for Electric Vehicle Traction With Brushless Capacitive Field Excitation. IEEE Trans. Ind. Appl. 2018, 54, 1390–1403. [Google Scholar] [CrossRef]
- Frias, A.; Pellerey, P.; Lebouc, A.K.; Chillet, C.; Lanfranchi, V.; Friedrich, G.; Albert, L.; Humbert, L. Rotor and stator shape optimization of a synchronous machine to reduce iron losses and acoustic noise. In Proceedings of the 2012 IEEE Vehicle Power and Propulsion Conference, Seoul, Republic of Korea, 9–12 October 2012. [Google Scholar]
- Hall, R.D.; Roberge, R.P. Carbon brush performance on slip rings. In Proceedings of the Conference Record of 2010 Annual Pulp & Paper Industry Technical Conference, San Antonio, TX, USA, 21–23 June 2010. [Google Scholar]
- ANSIIEEE Std 1161975; IEEE Standard Test Procedure for Carbon Brushes. IEEE Standards Department: Piscataway, NJ, USA, 1975.
- Stancu, C.; Ward, T.; Rahman, K.M.; Dawsey, R.; Savagian, P. Separately Excited Synchronous Motor With Rotary Transformer for Hybrid Vehicle Application. IEEE Trans. Ind. Appl. 2018, 54, 223–232. [Google Scholar] [CrossRef]
- Ludois, D.; Reed, J.; Hanson, K. Capacitive power transfer for rotor field current in synchronous machines. IEEE Trans. Power Electron. 2012, 27, 4638–4645. [Google Scholar] [CrossRef]
- Rossi, C.; Casadei, D.; Pilati, A.; Marano, M. Wound rotor salient pole synchronous machine drive for electric traction. In Proceedings of the Conference Record of the 2006 IEEE Industry Applications Conference Forty-First IAS Annual Meeting, Tampa, FL, USA, 8–12 October 2006. [Google Scholar]
- Kim, Y.; Nam, K. Copper-loss-minimizing field current control scheme for wound synchronous machines. IEEE Trans. Power Electron. 2017, 32, 1335–1345. [Google Scholar] [CrossRef]
- Miao, Q.; Li, Q.; Xu, Y.; Lin, Z.; Chen, W.; Li, X. Virtual Constant Signal Injection-Based MTPA Control for IPMSM Considering Partial Derivative Term of Motor Inductance Parameters. World Electr. Veh. J. 2022, 13, 240. [Google Scholar] [CrossRef]
- Kim, H.; Degner, M.W.; Guerrero, J.M.; Briz, F.; Lorenz, R.D. Discrete-Time Current Regulator Design for AC Machine Drives. IEEE Trans. Ind. Electron. 2010, 46, 1425–1435. [Google Scholar]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Wang, Y.; Zhang, Z.; Li, J. Investigation and Development of the Brushless and Magnetless Wound Field Synchronous Motor Drive System for Electric Vehicle Application. World Electr. Veh. J. 2023, 14, 81. https://doi.org/10.3390/wevj14040081
Li Y, Wang Y, Zhang Z, Li J. Investigation and Development of the Brushless and Magnetless Wound Field Synchronous Motor Drive System for Electric Vehicle Application. World Electric Vehicle Journal. 2023; 14(4):81. https://doi.org/10.3390/wevj14040081
Chicago/Turabian StyleLi, Yanhui, Yiwei Wang, Zhuoran Zhang, and Jincai Li. 2023. "Investigation and Development of the Brushless and Magnetless Wound Field Synchronous Motor Drive System for Electric Vehicle Application" World Electric Vehicle Journal 14, no. 4: 81. https://doi.org/10.3390/wevj14040081
APA StyleLi, Y., Wang, Y., Zhang, Z., & Li, J. (2023). Investigation and Development of the Brushless and Magnetless Wound Field Synchronous Motor Drive System for Electric Vehicle Application. World Electric Vehicle Journal, 14(4), 81. https://doi.org/10.3390/wevj14040081








