1. Introduction
Autonomous vehicles have a great potential in improving traffic flow and safety performance, which makes the technology of autonomous vehicle more and more popular, especially in developed countries and emerging markets [
1,
2]. As one of the important components of autonomous vehicles, the trajectory tracking control system aims to track the desired trajectory by controlling the actuators of the steering wheel, brake and throttle [
3]. The high nonlinearity of the vehicle dynamics will make it difficult for the trajectory tracking controller to ensure the tracking accuracy and stability of the vehicle at the same time [
4]. Therefore, a good trajectory tracking control system should fully consider the road information and the nonlinearities characteristics of tires.
In order to address the trajectory tracking problem, much research has been devoted to selecting the suitable control algorithms, such as the linear quadratic regulator (LQR) [
5,
6], fuzzy control [
7,
8], the sliding mode control (SMC) [
9,
10] and the proportional-integrated-differential (PID) control [
11]. However, the constrains caused by tires during trajectory tracking cannot be fully considered in these controller design. In recent years, the model prediction control (MPC) methods have been widely used in trajectory tracking control, which is characterized by rolling optimization and dealing with the optimization problem while considering the input and output constraints [
12]. A large number of researches indicate that the MPC algorithms are good at dealing with the trajectory tracking control problems with the multi-constraints [
13,
14]. Some researches converted the trajectory tracking control problem based on the MPC controller that considering vehicle stability and environmental constraints [
15] or collision avoidance restraints [
16]. Some researches improve trajectory tracking accuracy by adaptively adjusting the weight matrix in the target function [
17,
18]. In addition, a kinematic cascade MPC-PID controller with side slip angle compensation was designed in Ref. [
19] to solve the trajectory tracking control problem of high-speed autonomous vehicles. The authors of [
20] proposed a dead-band penalty function to solve the inequality constraints and guarantee smoothness of the solution.
More precise vehicle models can improve the controller’s ability to predict the future behavior of the vehicle. Banginwar proposed a real-time predictive vehicle controller by using Pontryagin’s optimization method in Ref. [
21]. Meanwhile, Raigoza enhanced the trajectory tracking method with automatic collision avoidance in Ref. [
22]. The authors of [
23] designed a MPC controller, which takes the 8-degree-of-freedom vehicle model as the prediction model and the 14-degree-of-freedom vehicle model as the control object to achieve trajectory tracking. The Unscented Kalman Filter (UKF) was used in Ref. [
24] to estimate the vehicle states, which were used to judge vehicle stability. Although the MPC method with a prediction function could significantly improve the trajectory tracking accuracy, it needed to repeatedly solve optimization problems at each control step, which leads to a heavy computing burden and potential risks in real-time control. In addition, some constraints have a great impact on the trajectory tracking performance of the vehicle, such as the slip and body deviation [
25]. Therefore, a suitable equivalent model of vehicle dynamics should be constructed by considering the reasonable constraints
Ignoring the aerodynamics and gravity, the tire force plays a critical role in improving the vehicle’s handling performance. However, most researches limited the tire model to the linear area [
26]. With increasing the vehicle speed, the nonlinearity caused by the tires’ dynamics had an influence on the trajectory tracking accuracy, even the handling stability. In Ref. [
27], the piecewise linear approximation of the tire characteristic curve method and root mean square error (RMSE) were used to obtain segmented points in different regions to improve the approximate accuracy of the tire models. By combining regularization with continuous linearization, a nonlinear tire model was established to estimate the lateral force of the tire. In addition, Mammar et al. [
28] derived the tire cornering stiffness and slip angle based on the tire characteristics to establish a tire model. However, the piecewise affine (PWA) tire model and tire cornering stiffness estimation are only the approximation of the tire model in a limited area, which could not capture the nonlinearity evident for the trajectory tracking control. Thus, the tires’ dynamics should be fully considered.
It is essential to guarantee the vehicle stability, and it should be mentioned that equilibrium analysis [
29] or empirical judgment methods [
30] are indeed needed to judge vehicle stability, along with the vehicle stability judged using the envelope constraints [
31]. The lateral velocity as a boundary condition for the envelope constraints could not be obtained from the sensors directly. Considering that the lateral velocity can be estimated accurately as presented in Refs. [
32,
33], the lateral velocity could be gained as a configuration, which is set as the input of the envelope constraint of the vehicle swing.
Motivated by the above discussion, this paper presents a trajectory tracking controller design with consideration of the tires’ dynamics and slip constraints. The innovations of the paper are summarized as follows:
Proposing a MPC controller by considering the tires’ dynamics and the road curvature for the trajectory tracking control;
Designing a tire force estimator based on the radial basis function (RBF) neural network to estimate the vehicle driving states, which are used to update the slip constraint.
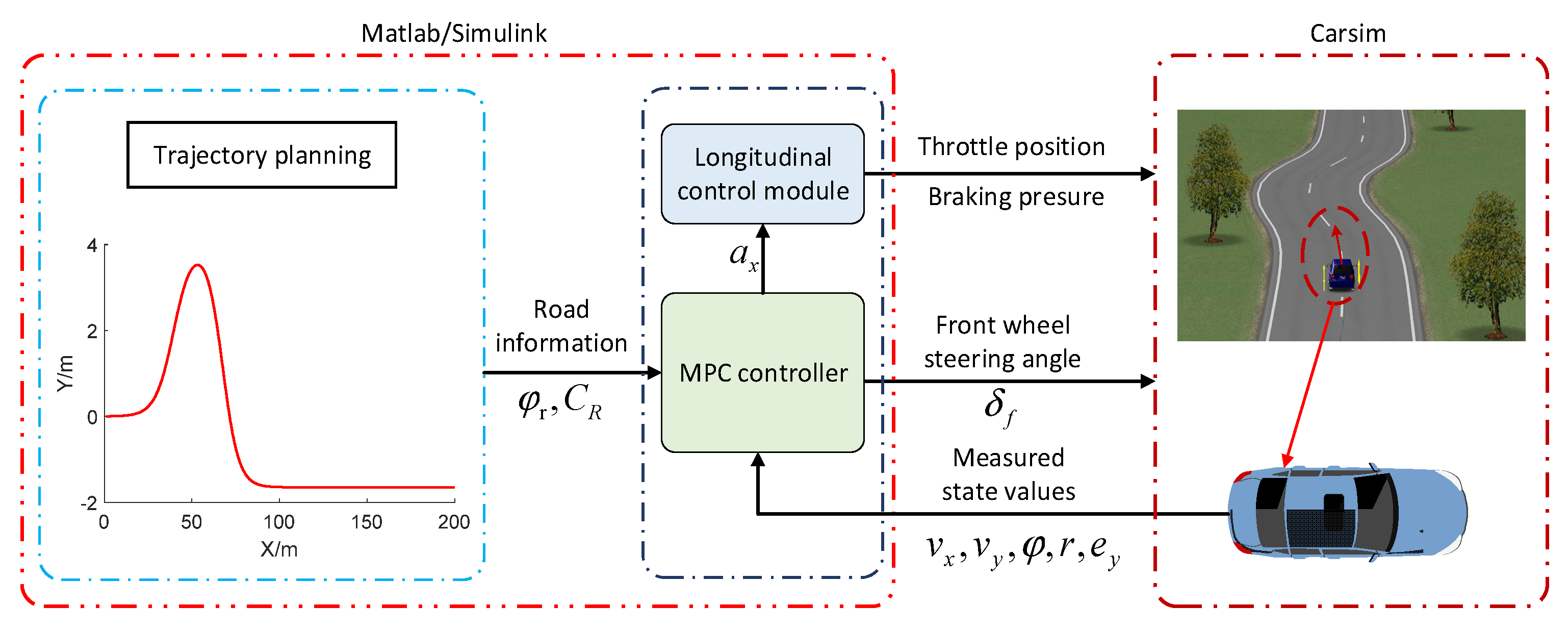
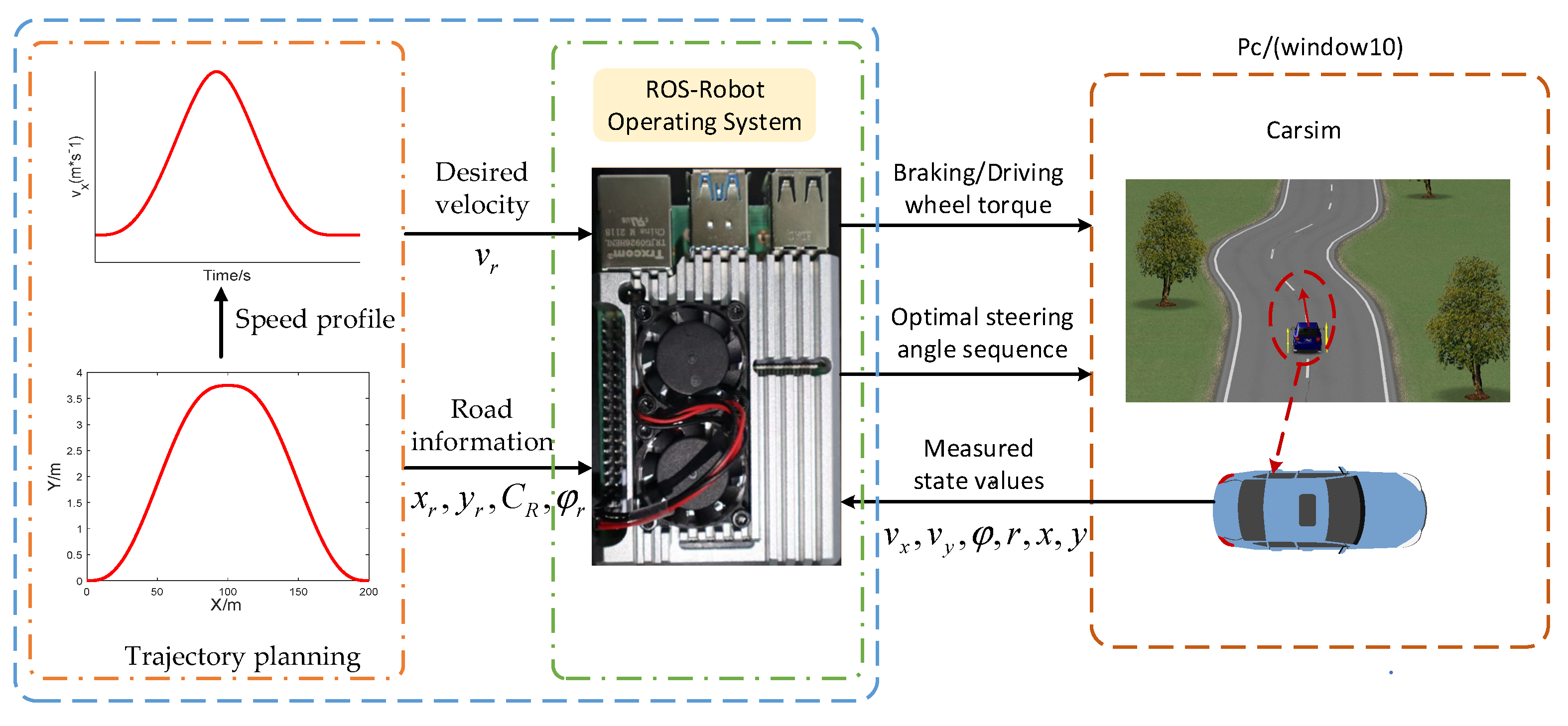
Conducting the co-simulation (CarSim/Simulink) and Hardware-in-loop (HIL) platform to validate the performance of the proposed trajectory tracking control system.
The remainder of this paper is organized as follows. In
Section 2, the control strategy of the trajectory tracking control system is described. In
Section 3, a trajectory tracking model is established based on the trajectory tracking control system. In
Section 4, based on the MPC algorithm, the trajectory tracking problem considering the slip constraint is solved. In
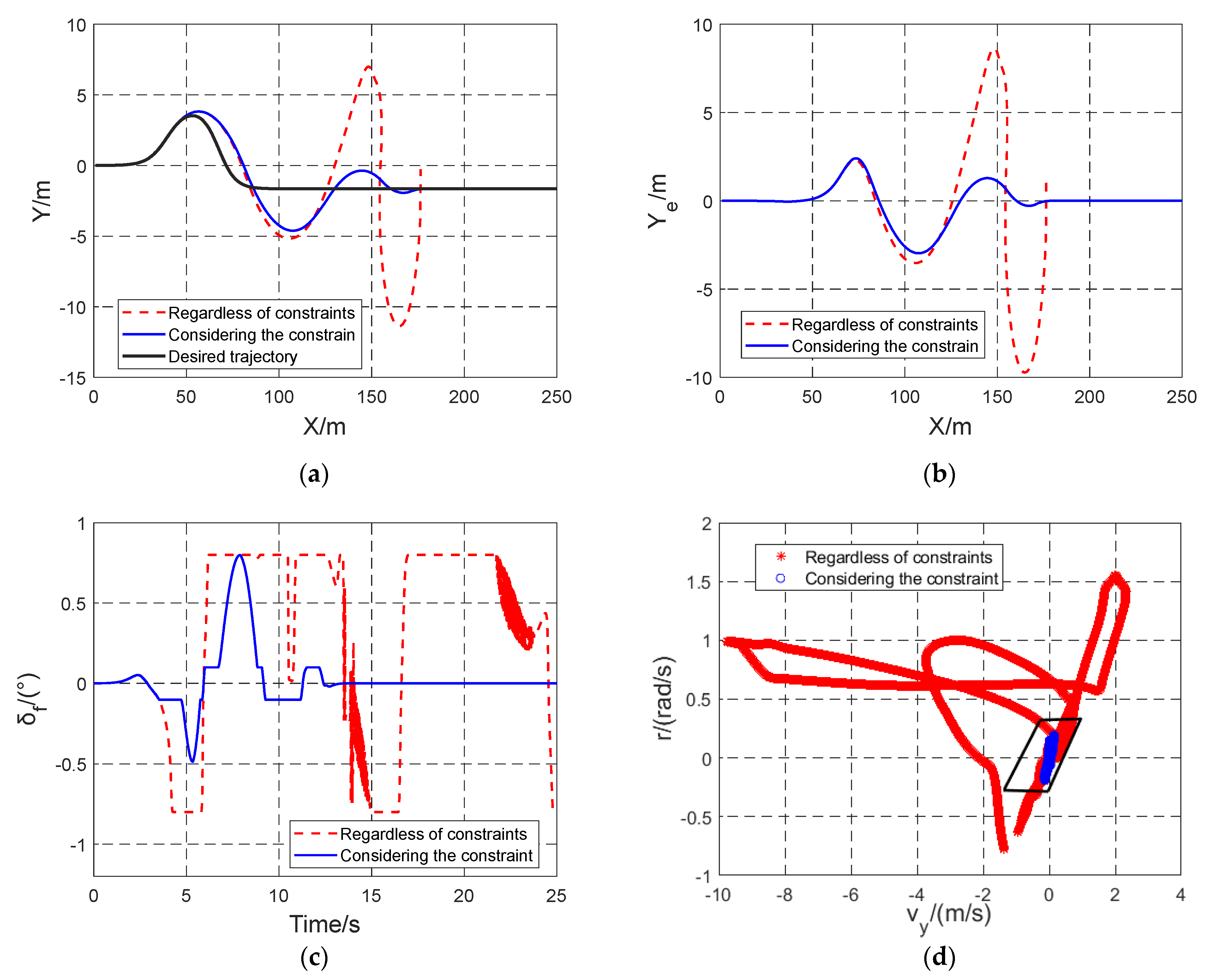
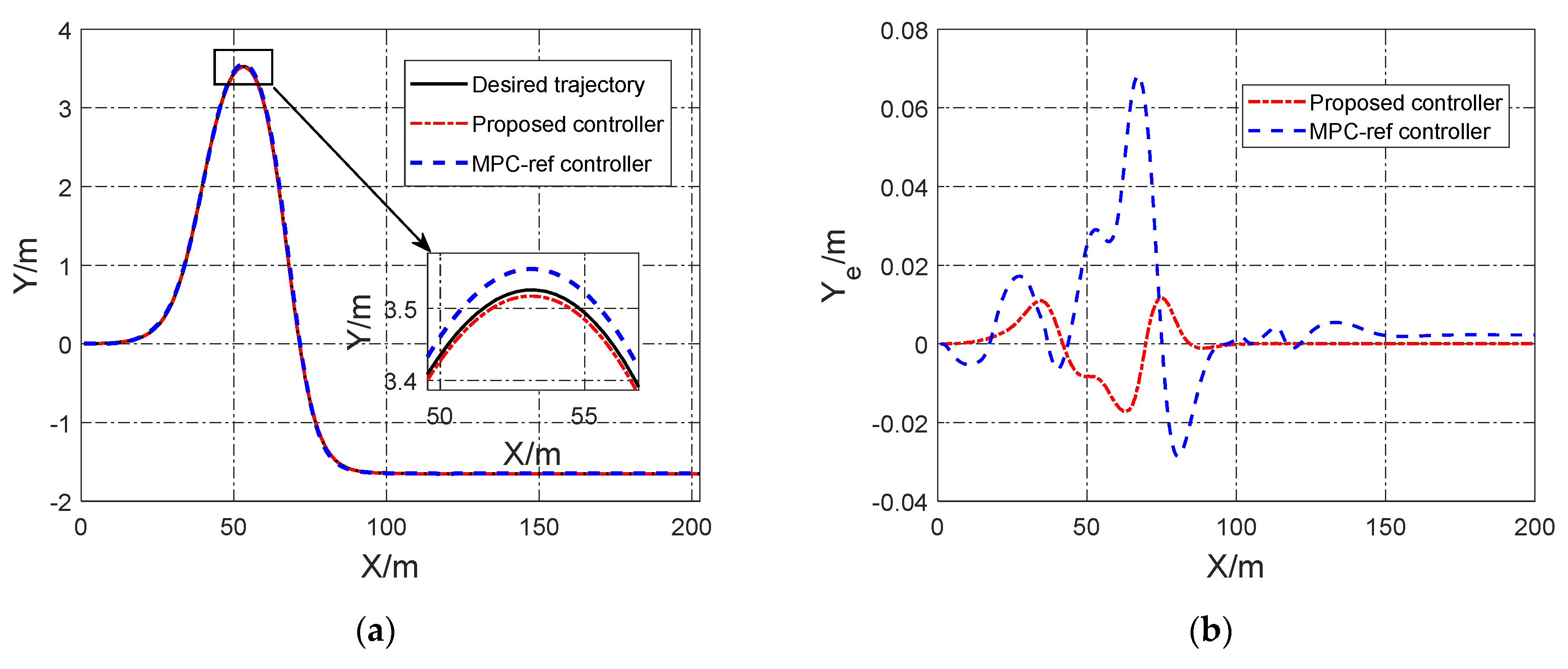
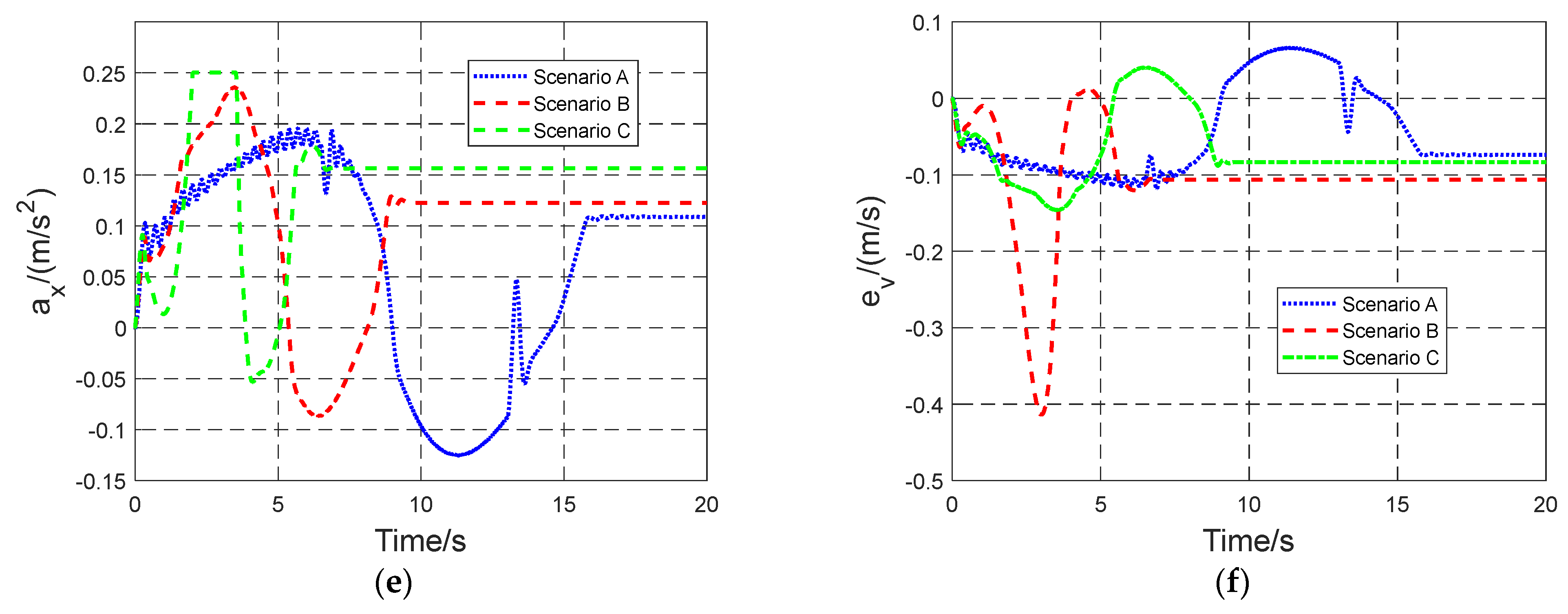
Section 5.1, the CarSim/Simulink co-simulation platform is constructed to verify the effectiveness of the envelope constraint under extreme driving states and test that the vehicle can still drive effectively beyond the nonlinear region of the tire, and it is compared with the algorithm proposed in Ref. [
34]. In
Section 5.2, the HIL platform is built, and the effectiveness of the algorithm is verified based on the quintic polynomial function trajectory planning, and it is compared and verified with the co-simulation.
Section 6 summarizes the contents of this paper.
3. Trajectory Tracking Model
A valuable vehicle model can improve the smoothness of the vehicle during driving and the handling stability of the vehicle during real-time control of autonomous vehicles. Thus, in this section, the trajectory tracking model is established by considering the force of the tires, as shown in
Figure 2.
The model is established based on the following assumptions:
The influence of road slope is not taken into account;
The coupling relationship between longitudinal and lateral forces is ignored; only the pure cornering characteristics of the tire is considered;
The load transfer of the tire is ignored;
The air resistance is ignored;
The heading error
and longitudinal velocity error
are defined as:
where
represents the orientation error of the yaw angle with respect to the desired trajectory, and
is the error between the current and the desired longitudinal velocity.
The desired yaw rate is obtained:
where
is the road curvature.
Thus, combined Equation (1) with Equation (2):
The assumption for the heading error is small;
can be defined as:
The vehicle dynamics model can be described by the following differential equations:
where
is the generalized longitudinal acceleration of the vehicle;
and
are the distance from CG(center of gravity) to the front/real axle;
is the longitudinal force of the front wheel;
is the longitudinal force of the rear wheel; and
is the front-wheel steering angle. The lateral force of the front/rear wheel
and
Fyr are functions of the slip angle of the tire, which can be calculated in the following ways:
where
is the road friction coefficient, and
represents the total vertical load of the vehicle.
The slip angles
and
indicate the angle between the wheel velocity and the direction of the wheel itself:
The total vertical load of the vehicle is distributed between the front and rear wheels according to the geometry of the car model, described by the parameters
and
:
By analyzing Equation (6) and considering tire characteristics, we find that there are three main factors affecting the lateral force
: the vertical load
, the road friction coefficient
, and the slip angle α, which is a complex nonlinear time-varying function with three inputs and one output. It is difficult to establish its accurate mathematical model with traditional methods, so this paper establishes a neural network model of the lateral force by the characteristics of the RBF neural network approximation of nonlinear functions as shown in
Figure 3. The neural network consists of three layers. The first layer is the input layer, which consists of three input quantities:
. The second layer is the hidden layer, and the activation function adopted by the hidden layer is a Gaussian function:
where
is the center width of the hidden layer; X is the input vector;
is the central unit of the jth radial basis function, which is the same as the input vector X dimensionality. The third layer is the output layer, which is the output lateral force
, and its solution is:
where
is the weight.
When the road friction coefficient is fixed, the lateral force is estimated by the RBF neural network as shown in the
Figure 4:
As shown in
Figure 4, the lateral force estimator based on the RBF neural network can estimate the lateral force of the tire well.
Equations (3)–(10) can be combined to obtain the nonlinear vehicle dynamics equations:
where,
,
,
,
,
,
.
Equation (11) is rewritten as a linear state space equation form:
with
,
,
,
where the state variables is
, the control input is
, the output variable the output variable is
, and
is defined as the disturbance.
In real-time control applications, the trajectory tracking model is usually applied to the discrete time domain, and then converted to a discrete time domain through zero-order retention (ZOH) discretization, expressed as:
where
represents the
sampling time,
,
,
and
C are system matrices, which can be expressed as:
where
is sampling time (
),
is an identity matrix, and
y ∈
R5 is the state quantity of vehicle trajectory tracking system.
4. Control Law Allocation
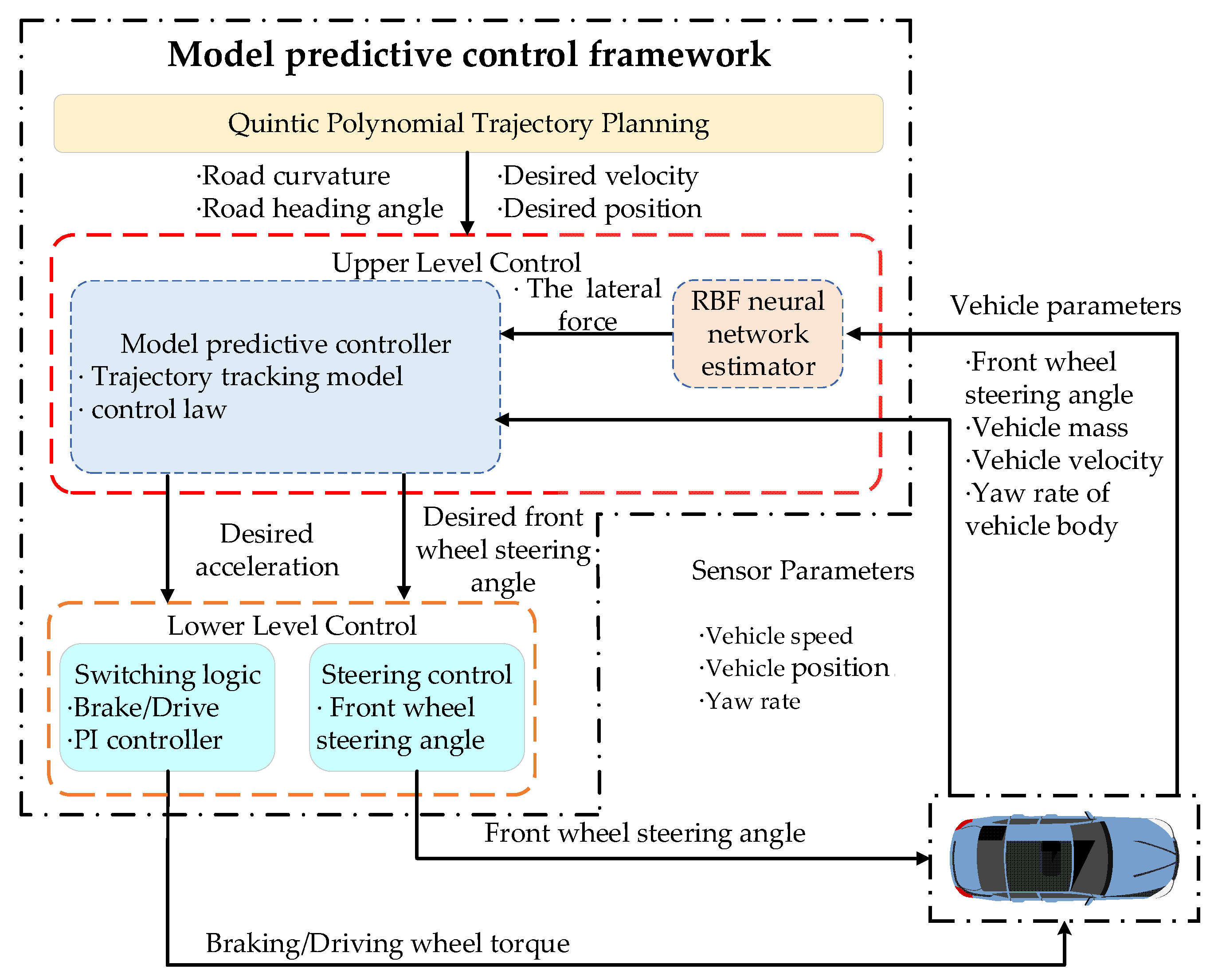
This section describes the proposed control law used for calculating the front-wheel angle and the longitudinal acceleration. The control law is designed to solve the MPC-based trajectory tracking control problem. In addition, this control law takes into account the vehicle’s handling stability, which is defined by the envelope constraint.
4.1. Control Objectives
To improve the lateral tracking accuracy and the vehicle’s handling stability, the lateral position deviation, heading error, and longitudinal velocity error of the vehicle should be minimized, and the yaw rate and lateral velocity of the vehicle should be limited by the maximum lateral force and maximum slip angle that the tire can provide. Therefore, the targets of the trajectory tracking control system can be considered as:
The target of the trajectory tracking behavior can be regarded as the vehicle’s accurate tracking of the desired trajectory:
The controller proposed uses the envelope suggested by Ref. [
35], and the vehicle stability is judged by the vehicle’s velocity state: lateral velocity
and the yaw rate (
), and we estimate the lateral force under different driving conditions through the RBF neural network. Using the lateral force estimated by the RBF neural network, the threshold of the slip angle α under different driving conditions is calculated from the tire model, and the lateral velocity
limit is defined by limiting the slip angle of the rear tire. The maximum slip angle limit of the rear tire can be transformed into the constraint on the lateral velocity
and the yaw rate
of the vehicle by Equation (7):
where the threshold of the yaw rate can be obtained according to the maximum lateral force and Equation (5). In addition, the maximum lateral force of the tire is estimated by the RBF neural network.
The constraints (16) and (17) form a closed envelope, as shown in
Figure 5. Equation (16) limits the control boundary of the yaw rate, and the Equation (17) limits the control boundary of the lateral velocity. When all states are within the envelope, the vehicle stability can be guaranteed.
In order to achieve the required lateral tracking accuracy and control stability, the steering angle and the physical characteristics of the driving and braking should be considered. Apply the following constraints to the vehicle’s variables:
where
are the control input and control input increment of the trajectory tracking control system.
4.2. Trajectory Tracking Controller Based on MPC
The function of the proposed trajectory tracking control system is to calculate the dynamic control command and subsequently manipulate the vehicle to the desired trajectory. This function is achieved with the control law and can be translated into solving an MPC problem. The schematic block diagram of the MPC algorithm is shown in
Figure 6.
During the transitional state, the reference is described as the control objective , and the disturbances are the road curvature and the desired longitudinal acceleration. The output is the lateral velocity, yaw rate, heading error and longitudinal velocity error. The MPC controller consists of three parts: the constraints, the trajectory tracking control model, and the cost function. The trajectory tracking model is designed according to the Equation (11). The constraints are shown in Equations (16)–(18).
To facilitate the design of the controller, the state vector
and the input increment
are usually coupled in a broadening vector that can be expressed as
. Rewriting Equations (13) and (14):
where
,
Nx is the dimension of the state quantity and
Nu means the dimension of the control quantity, and the change of the control input is
. The predicted output performance vector and the sequence of the future incremental inputs at time step
are denoted as
and
, respectively.
where
is the prediction horizon and
means the control horizon,
are the predictive performance at the step
,
are the control input increments for the control time domain.
The MPC controller can predict the state of the next moment according to the state of the current moment, so the prediction equation can be expressed as:
The output vector of the predictive can be expressed in matrix form:
where
,
,
.
To calculate the desired control increment, the trajectory tracking problem is converted to solve the quadratic optimal solution problem:
where
is the weight matrix; and
is the coefficient of relaxation. Combining Equation (20) with Equation (22), and defining
, the objective function can be transformed into a quadratic optimization problem combined with the constraints and the following optimization problems can be solved:
where
,
.
In addition, Equations (12) and (20) transform the slip constraint (16) into a constraint on the control increment
:
where,
.
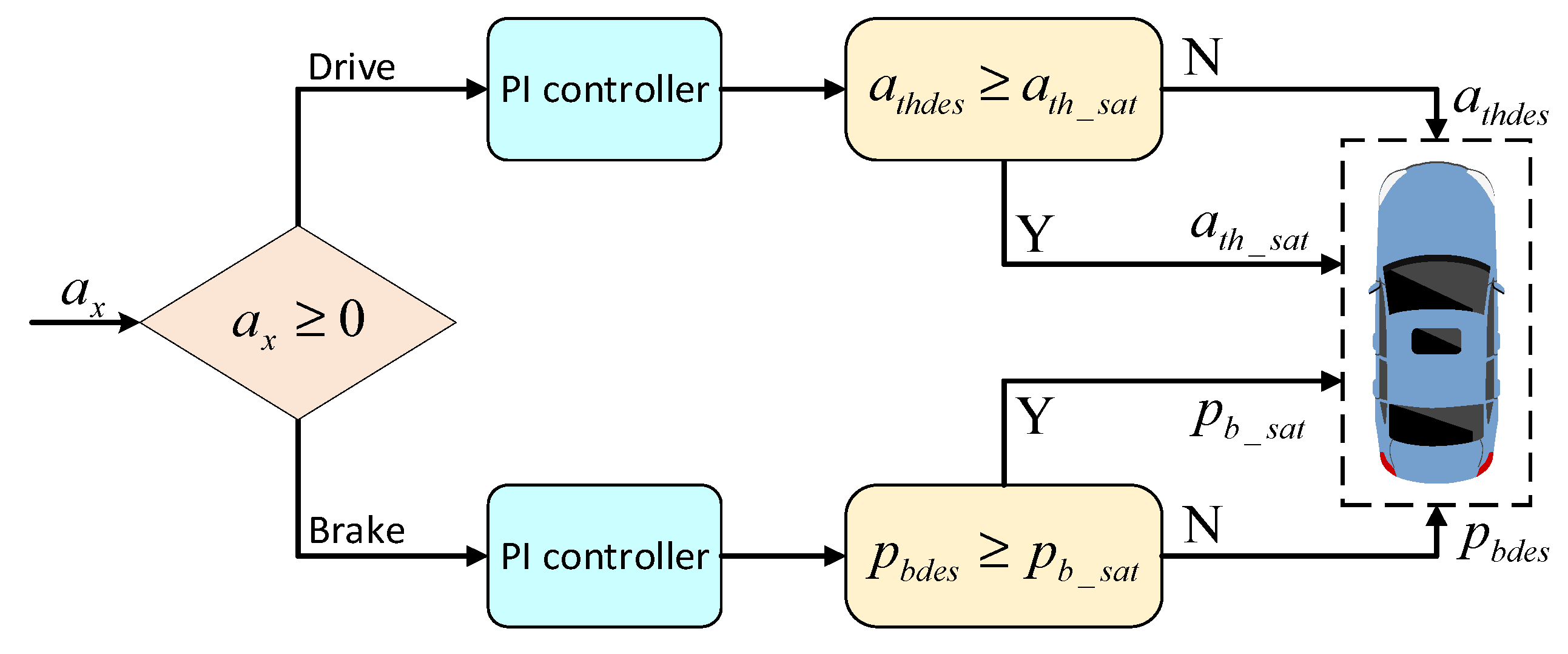
4.3. Lower-level Controller Design
In order to verify the effectiveness of the proposed MPC control algorithm, the lower-level controller needs to be established to convert the output of the MPC controller into the input of the actuator [
36]. Among them, the control input of the steering system of the actuator is the front-wheel steering angle, and the control input of the driving system is the desired throttle opening
and the desired braking master cylinder pressure
. The schematic is shown in
Figure 7. The switching logic of the lower-level controller can be simplified to compare
with 0, to apply the drive control (drive mode) when
, to compare the desired throttle opening
with the throttle opening threshold
and to carry out the PI control. Otherwise, the braking control (braking mode) is applied to compare the desired braking master cylinder pressure
with the braking master cylinder pressure threshold
and carry out the PI control. The switching logic can be formulated as: