Research into the Peculiarities of the Individual Traction Drive Nonlinear System Oscillatory Processes
Abstract
1. Introduction
2. Methods and Materials
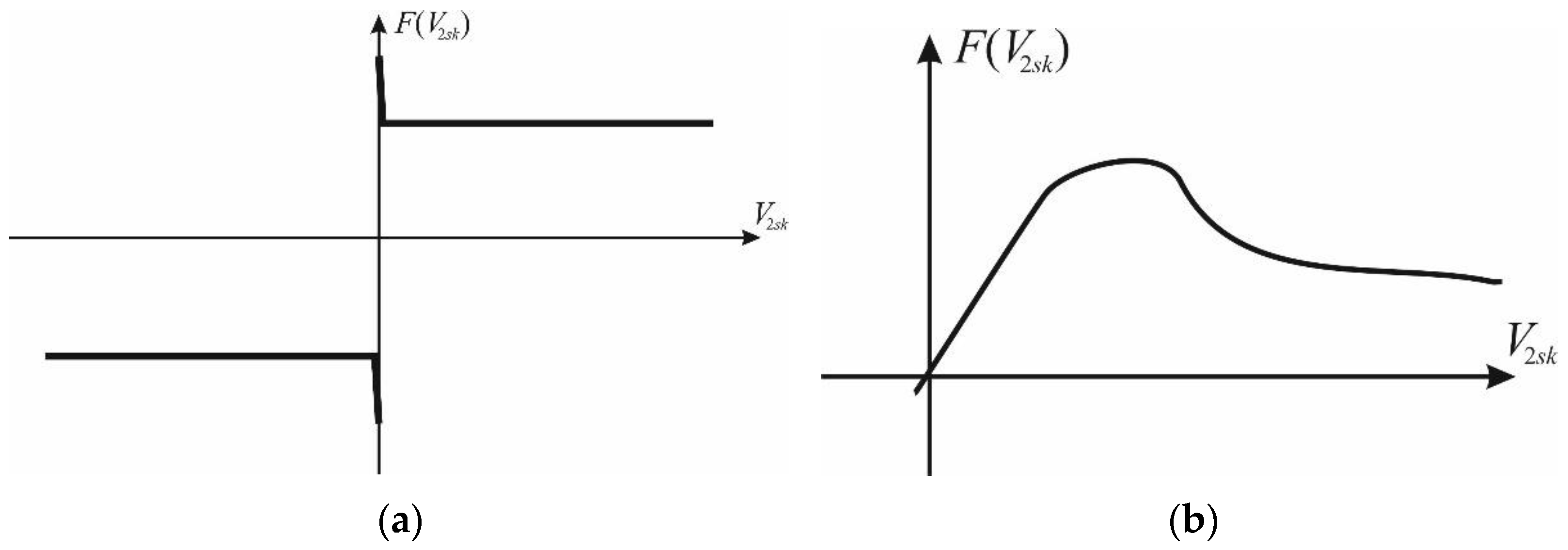
2.1. Criterion for the Occurrence of the Auto-Oscillating Mode
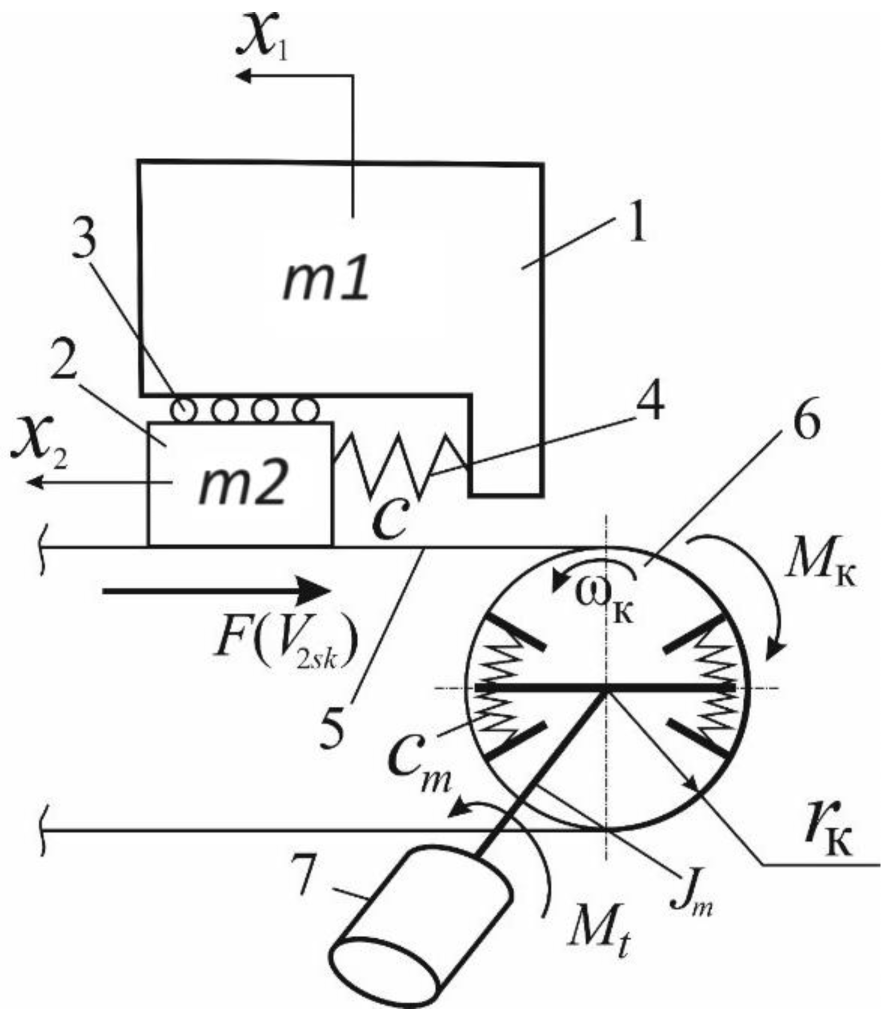
2.2. The Mathematical Model of Frictional Interaction of an Elastic Wheel with a Solid Support Base
2.3. The Mathematical Model of Elastic Wheel Friction against a Solid Support Base
- − for the wheel rolling braking mode:
- − for the wheel rolling traction and driven modes:
2.4. Analysis of the Occurrence of the Auto-Oscillation Mode for the Traction and Slave Modes of Wheel Rolling on a Solid Support Base
2.5. Analysis of the Occurrence of Auto-Oscillation for the Braking Mode of the Wheel Rolling on a Solid Support Base
3. Results
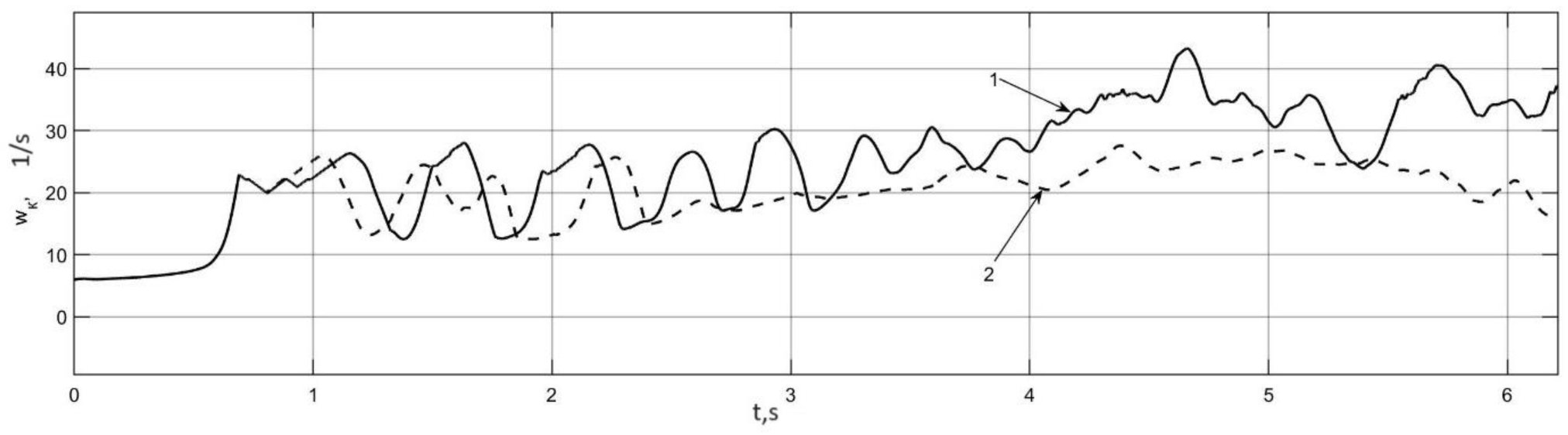
3.1. Research of the Occurrence of the Auto-Oscillation Mode in Individual Traction Electric Drive by Simulation Mathematical Modeling
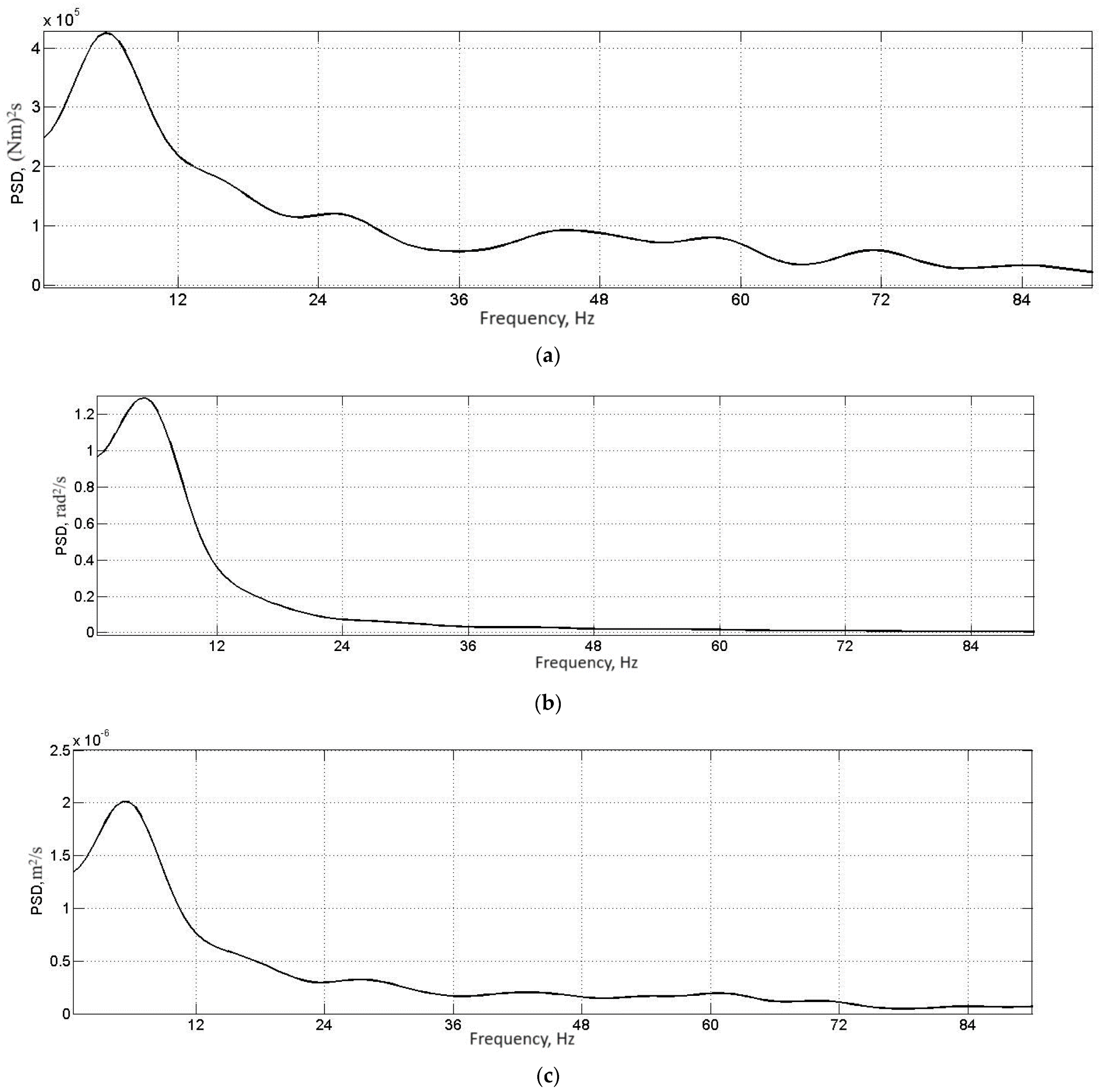
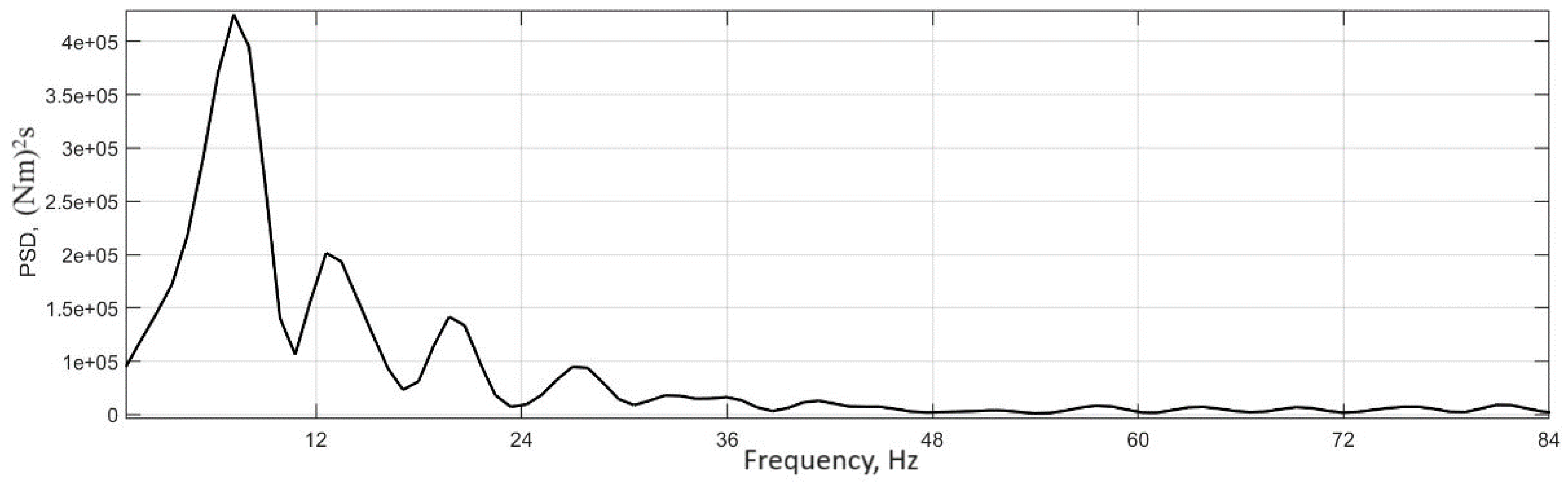
3.2. Determination of the Auto-Oscillation Frequency in a Traction Electric Drive
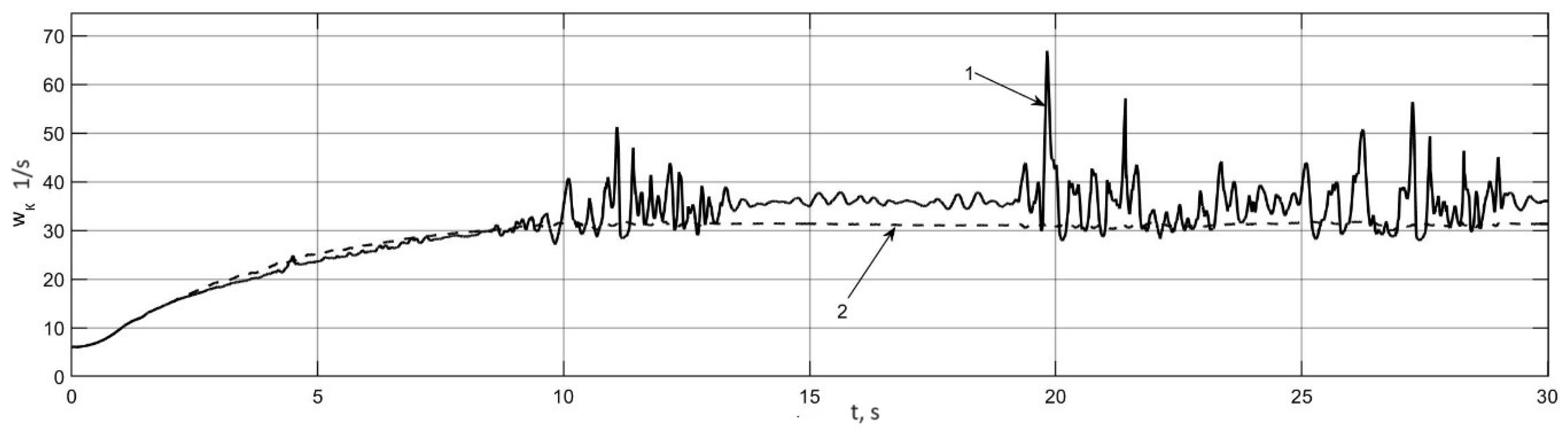
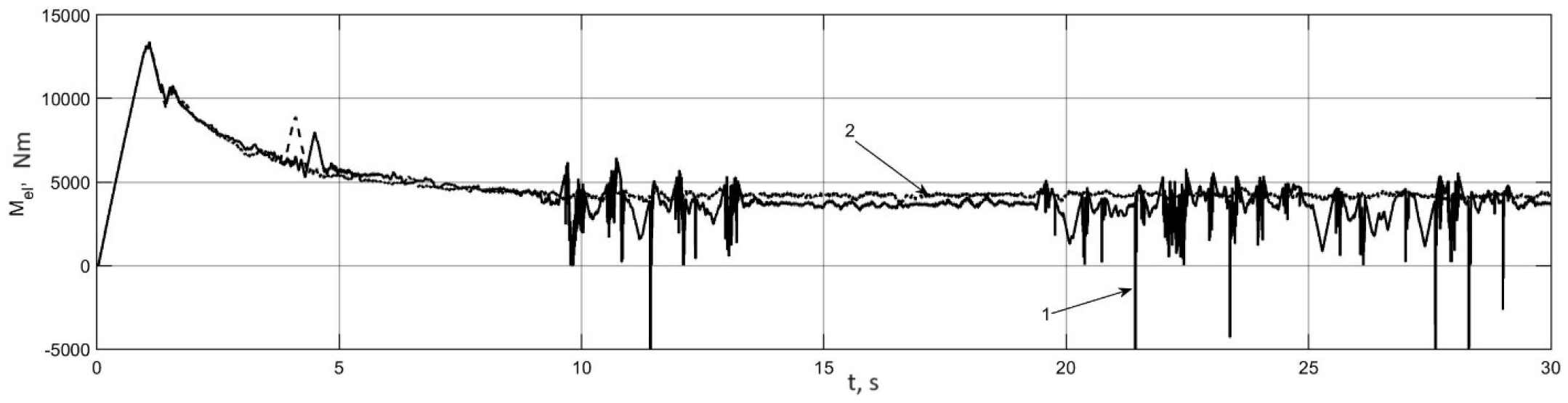
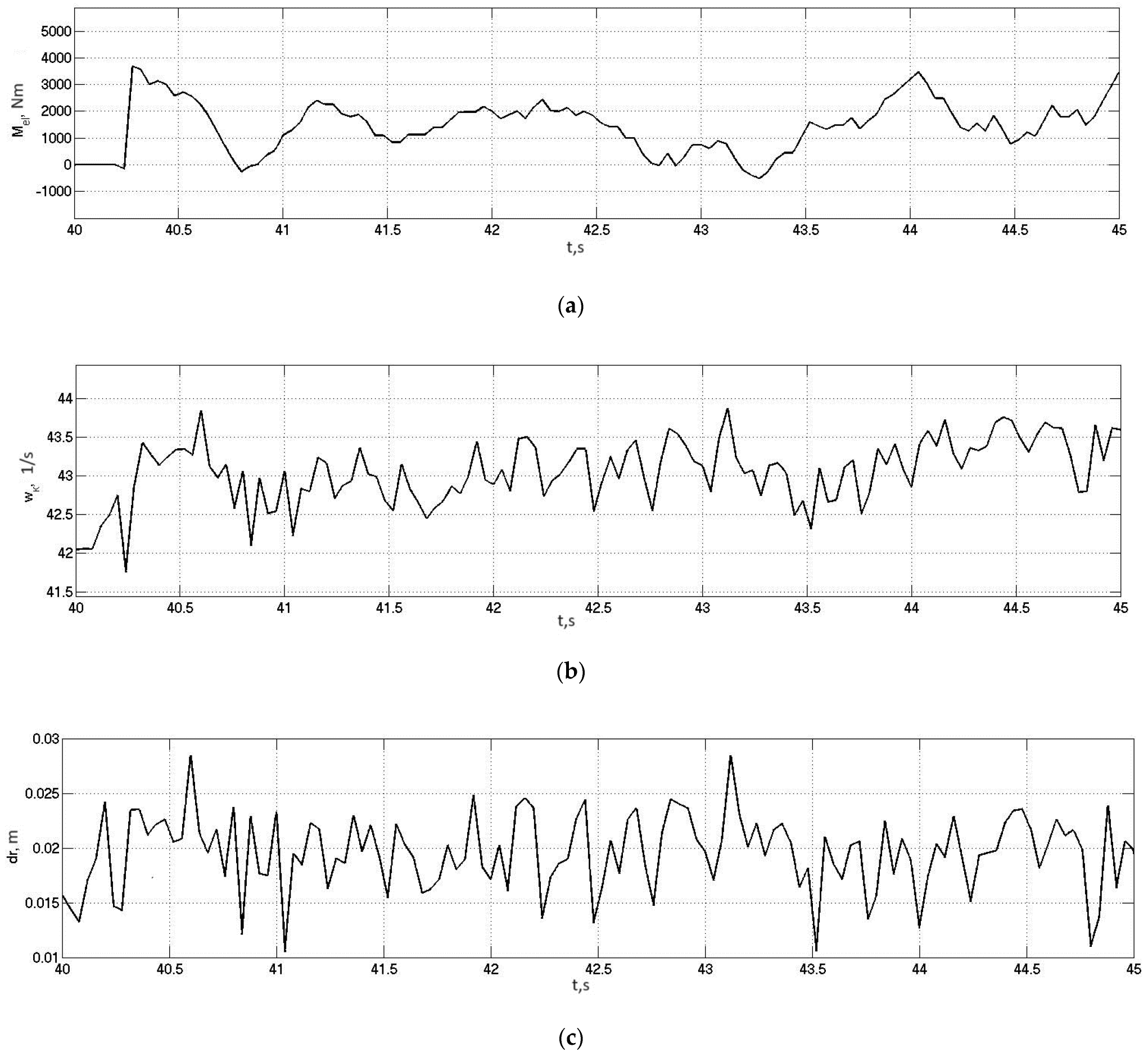
3.3. Experimental Investigation of the Occurrence of the Auto-Oscillation Modes in an Individual Traction Electric Drive
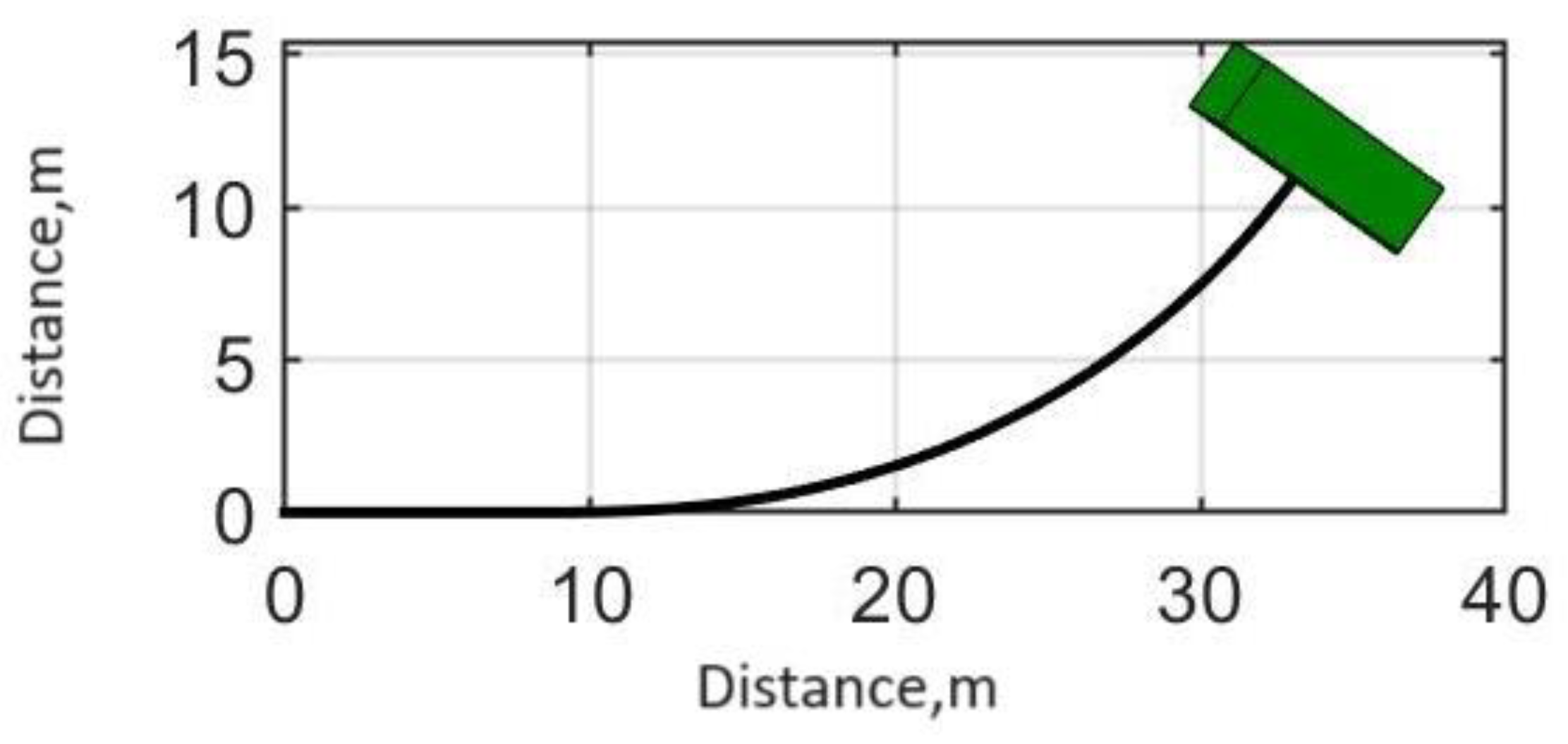
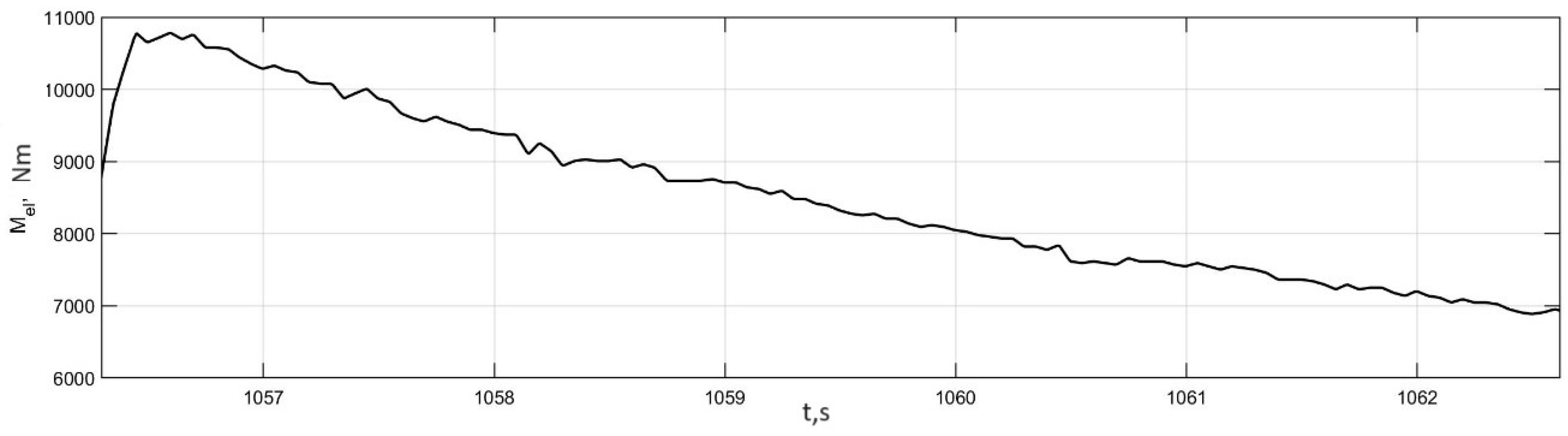
3.4. Investigation of Auto-Oscillation Modes in the Actual Traction Electric Drive of an Electric Bus
4. Conclusions
- The developed mathematical model describing the process of auto-oscillations of an electric vehicle of high reliability (confirmed by test results).
- Based on the results of simulation modeling, the frequencies of tire oscillations are determined, which are 6–7 Hz and coincide with the frequency of auto-oscillations to realize the frequency of rotation of the electric motor shaft.
- Correctness of the results of theoretical research and the results of simulation modeling are confirmed by experimental studies of the process of the occurrence of auto-vibration phenomena in the movement of the vehicle to the support base.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vilke, V.G.; Shapovalov, I.L. Auto Oscillations in the Process of Car Braking; Series 1: Mathematics. Mechanics; Bulletin of Moscow University: Moscow, Russia, 2015; pp. 33–39. [Google Scholar]
- Svetlitsky, V.A. Random Vibrations of Mechanical Systems; Mashinostroenie: Moscow, Russia, 1976; 216p. [Google Scholar]
- Kruchinin, P.A.; Magomedov, M.K.; Novozhilov, I.V. Mathematical Model of an Automobile Wheel on Antiblock Motion Modes; MTT Series; Izvestiya RAN: Moscow, Russia, 2001; pp. 63–69. [Google Scholar]
- Awrejcewicz, J.; Dzyubak, L.; Grebogi, C. Estimation of Chaotic and Regular (Stick–Slip and Slip–Slip) Oscillations Exhibited by Coupled Oscillators with Dry Friction. Nonlinear Dyn. 2015, 42, 383–394. [Google Scholar] [CrossRef]
- Pascal, M. Dynamics and Stability of a Two Degree of Freedom Oscillator with an Elastic Stop. J. Comput. Nonlinear Dyn. 2006, 1, 94–102. [Google Scholar] [CrossRef][Green Version]
- Shin, K.; Brennan, M.J.; Oh, J.E.; Harris, C.J. Analysis of disc brake noise using a two-degree-of-freedom model. J. Sound Vib. 2002, 254, 837–848. [Google Scholar] [CrossRef]
- Kotiev, G.O.; Padalkin, B.V.; Kartashov, A.B.; Dyakov, A.S. Designs and development of Russian scientific schools in the field of cross-country ground vehicles building. ARPN J. Eng. Appl. Sci. 2017, 12, 1064–1071. [Google Scholar]
- Ergin, A.A.; Kolomejtseva, M.B.; Kotiev, G.O. Antiblocking control system of the brake drive of automobile wheel. Prib. Sist. Upr. 2004, 9, 11–13. [Google Scholar]
- Moaaz, A.O.; Ali, A.S.; Ghazaly, N.M. Investigation of Anti-Lock Braking System Performance Using Different Control Systems. Int. J. Control Autom. 2020, 13, 137–153. [Google Scholar]
- Sun, C.; Pei, X. Development of ABS ECU with Hardware-in-the-Loop Simulation Based on Labcar System. SAE Int. J. Passeng. Cars-Electron. Electr. Syst. 2014, 8, 14–21. [Google Scholar] [CrossRef]
- Sabbioni, E.; Cheli, F.; D’alessandro, V. Analysis of ABS/ESP Control Logics Using a HIL Test Bench; SAE International: Warrendale, PA, USA, 2011. [Google Scholar] [CrossRef]
- Hart, P.M. Review of Heavy Vehicle Braking Systems Requirements (PBS Requirements); Draft Report. Available online: https://trid.trb.org/View/1407753 (accessed on 24 April 2003).
- Marshek, K.M.; Cuderman, J.F.; Johnson, M.J. Performance of Anti-Lock Braking System Equipped Passenger Vehicles Part I: Braking as a Function of Brake Pedal Application Force. In Proceedings of the SAE 2002 World Congress, Detroit, MI, USA, 4–7 March 2002. [Google Scholar]
- Kuznetsov, A.P.; Kuznetsov, S.P.; Ryskin, N.M. Nonlinear Oscillations; Fizmatlit: Moscow, Russia, 2002; 292p. [Google Scholar]
- Pacejka, H.B. Tyre and Vehicle Dynamics, 2nd ed.; Butterworth Heinemann: Oxford, UK, 2006; 672p. [Google Scholar]
- Wellstead, P.E.; Pettit, N.B. Analysis and Redesign of an Antilock Brake System Controller. IEE Proc. Control Theory Appl. 1997, 144, 413–426. [Google Scholar] [CrossRef]
- Zhileikin, M.M. Investigation of Autocoletive Processes in the Zone of Interaction of an Elastic Tire with a Solid Support Base. Izvestiya vysshee obrazovaniya vysshee obrazovaniya. Mashinostroenie 2021, 10, 3–15. [Google Scholar] [CrossRef]
- Chelomey, V.N. Vibrations in Engineering; Volume 2: Fluctuations of Nonlinear Mechanical Systems; Blekhman, I.I., Ed.; Mashinostroenie: Moscow, Russia, 1979; 351p. [Google Scholar]
- Kryukov, B.I. Forced Vibrations of Essentially Nonlinear Systems; Mashinostroenie: Moscow, Russia, 1984; 216p. [Google Scholar]
- Nekorkin, V.I. Lectures on the Fundamentals of Vibration Theory: Textbook; Nizhny Novgorod University: Nizhny Novgorod, Russia, 2011; 233p. [Google Scholar]
- Babakov, I.M. Theory of Vibrations, 4th ed.; Drofa: Moscow, Russia, 2004; 591p. [Google Scholar]
- Strelkov, S.P. Introduction to the Theory of Vibrations; Nauka: Moscow, Russia, 1964; 438p. [Google Scholar]
- Yablonsky, A.A.; Noreiko, S.S. Course of the Theory of Vibrations; Lan: Moscow, Russia, 2003; 256p. [Google Scholar]
- Moiseev, N.N. Asymptotic Methods of Nonlinear Mechanics; Izd. “Nauka”, Main Editorial Office of Physical and Mathematical Literature: Moscow, Russia, 1969; 380p. [Google Scholar]
- Bogolyubov, N.N.; Mitropolsky, Y.A. Asymptotic Methods in the Theory of Nonlinear Oscillations; Nauka: Moscow, Russia, 2005; Volume 3, 605p. [Google Scholar]
- Gorelov, V.A.; Komissarov, A.I.; Miroshnichenko, A.V. 8 × 8 wheeled vehicle modeling in a multibody dynamics simulation software. Procedia Eng. 2015, 129, 300–307. [Google Scholar] [CrossRef][Green Version]
- Keller, A.V.; Gorelov, V.A.; Anchukov, V.V. Modeling truck driveline dynamic loads at differential locking unit engagement. Procedia Eng. 2015, 129, 280–287. [Google Scholar] [CrossRef]
- Volskaya, V.N.; Zhileykin, M.M.; Zakharov, A.Y. Mathematical model of rolling an elastic wheel over deformable support base. IOP Conf. Ser. Mater. Sci. Eng. 2018, 315, 012028. [Google Scholar] [CrossRef]
- Belousov, B.; Ksenevich, T.; Vantsevich, V.; Komissarov, D. 8 × 8 Platform for Studing Terrain Mobility and Traction Performance of Unmanned Articulated Ground Vehicles with Steered Wheels. SAE Tech. Pap. 2013, 9. [Google Scholar] [CrossRef]
- Belousov, B.; Shelomkov, S.; Ksenevich, T.; Kupreyanov, A. Experimental verification of a mathematical model of the wheel-supporting surface interaction during nonstationary rolling motion. J. Mach. Manuf. Reliab. 2009, 38, 501–505. [Google Scholar]
- Wong, J.Y. Theory of Ground Vehicles; Wiley: New York, NY, USA, 2001; 560p. [Google Scholar]
- Antonyan, A.; Zhileykin, M.; Eranosyan, A. The algorithm of diagnosing the development of a skid when driving a two-axle vehicle. In Proceedings of the Design Technologies for Wheeled and Tracked Vehicles (MMBC) 2019, Moscow, Russia, 1–2 October 2019; Volume 820. [Google Scholar] [CrossRef]
- Polungyan, A.A.; Fominykh, A.B.; Staroverov, N.N. Dynamics of Wheeled Machines; Polungyan, A.A.A., Ed.; Bauman Moscow State Technical University Publishing House: Moscow, Russia, 2013; 118p, ISBN 978-5-7038-3706-1. [Google Scholar]

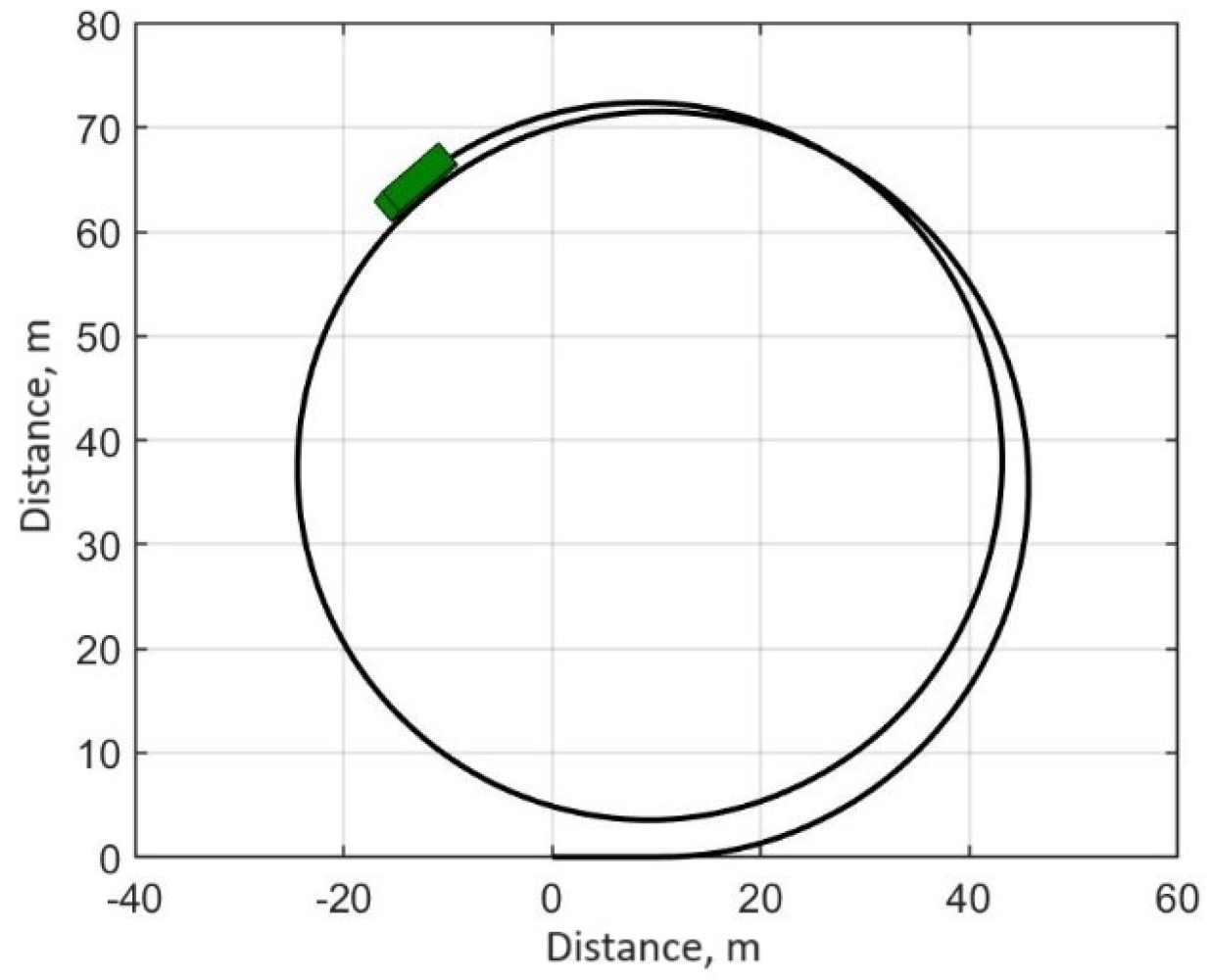
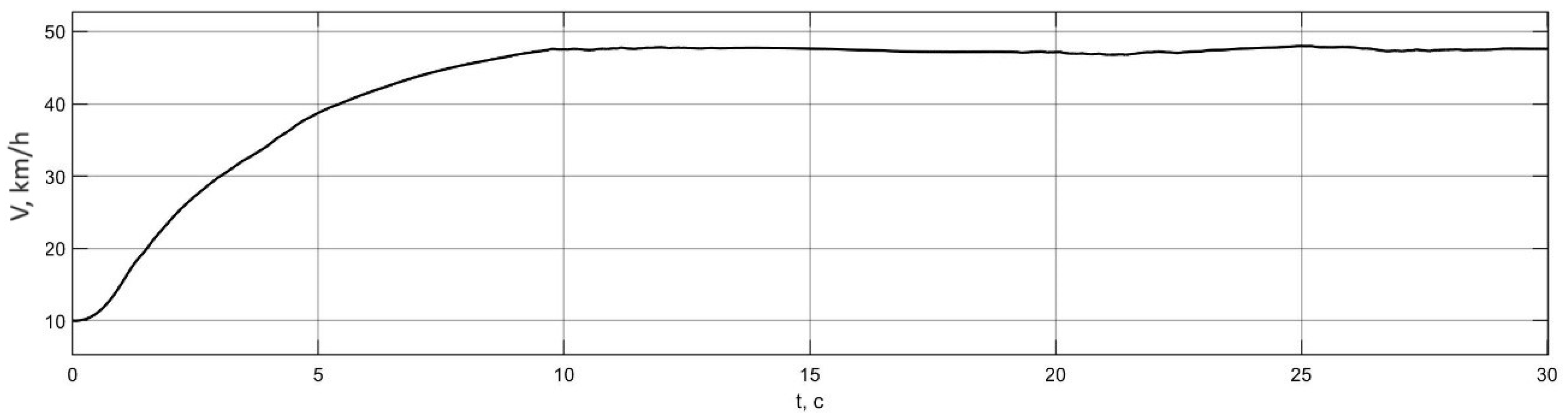

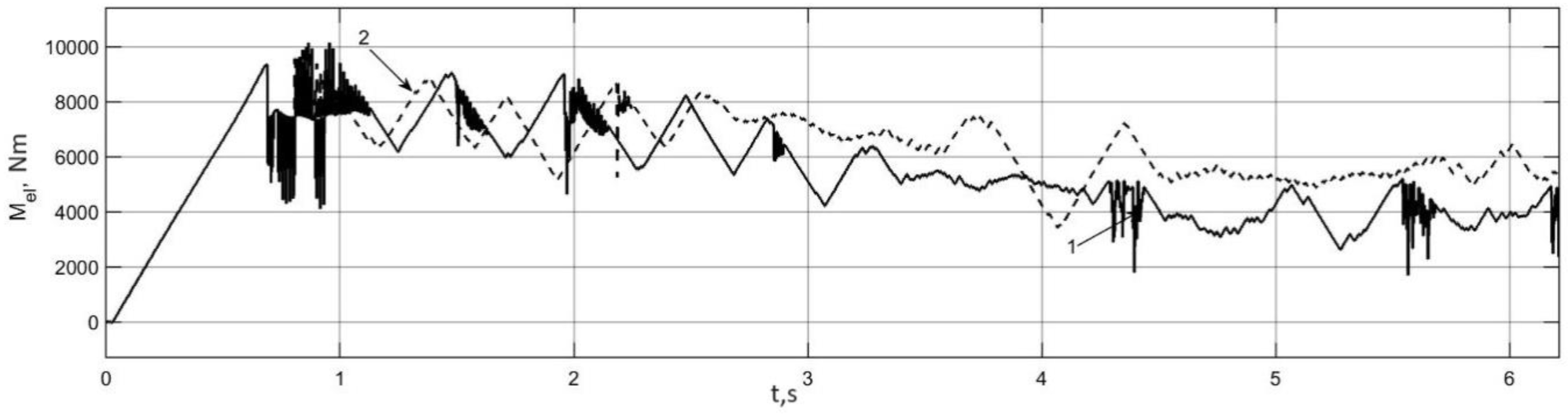

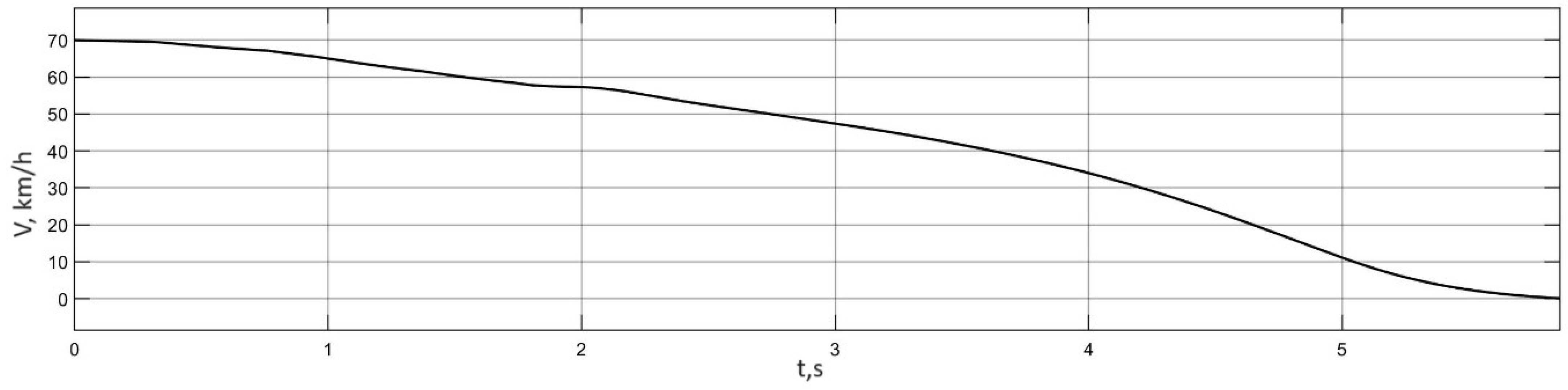
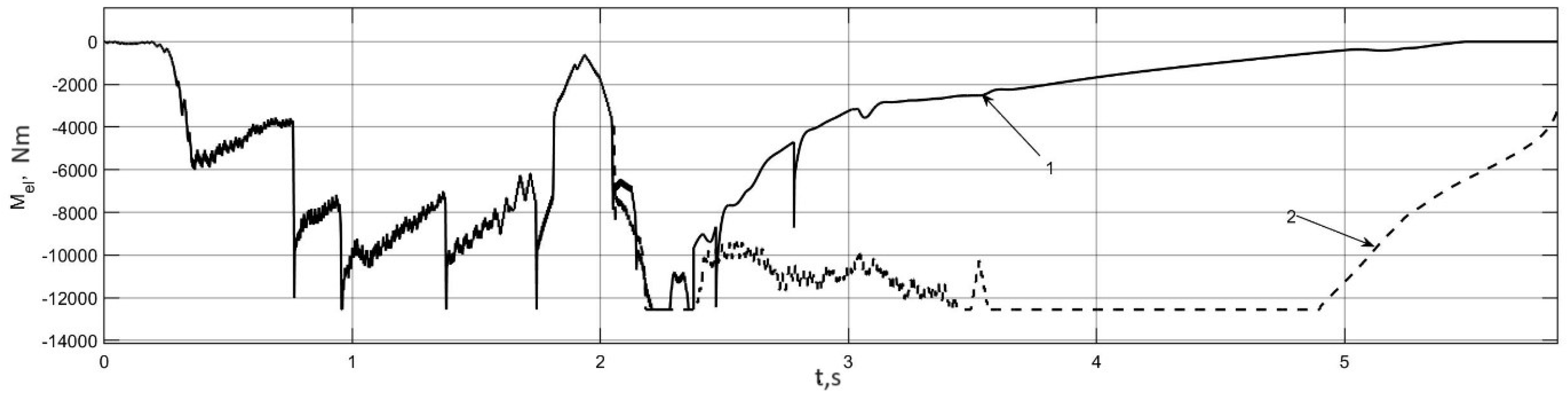
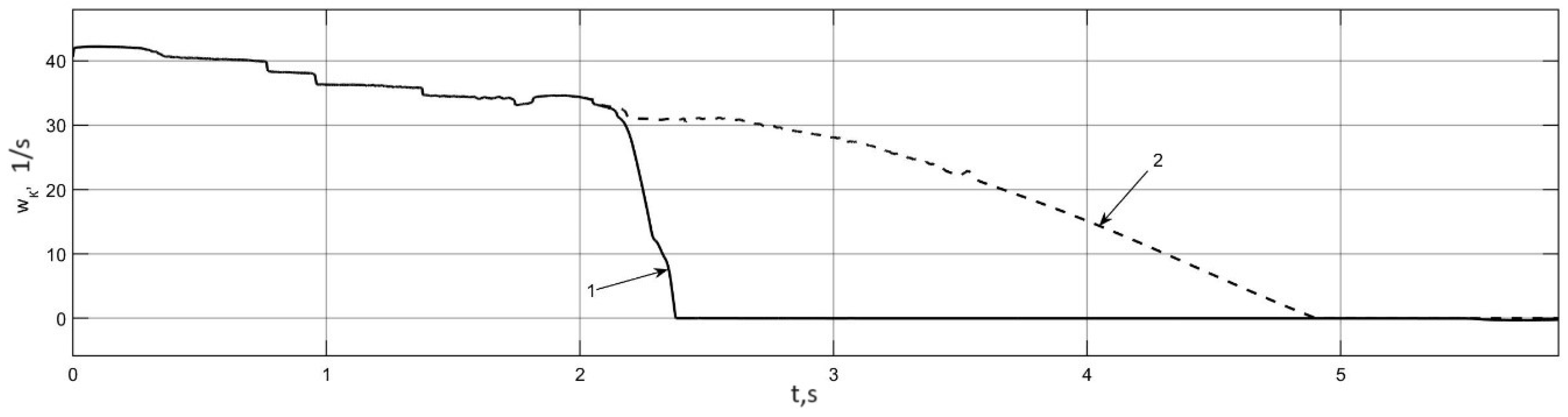


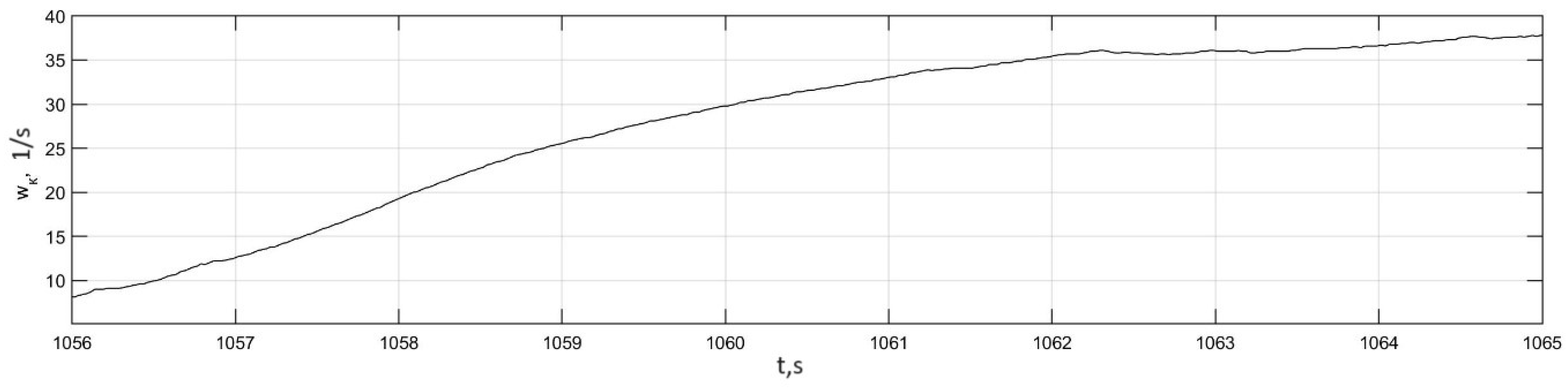


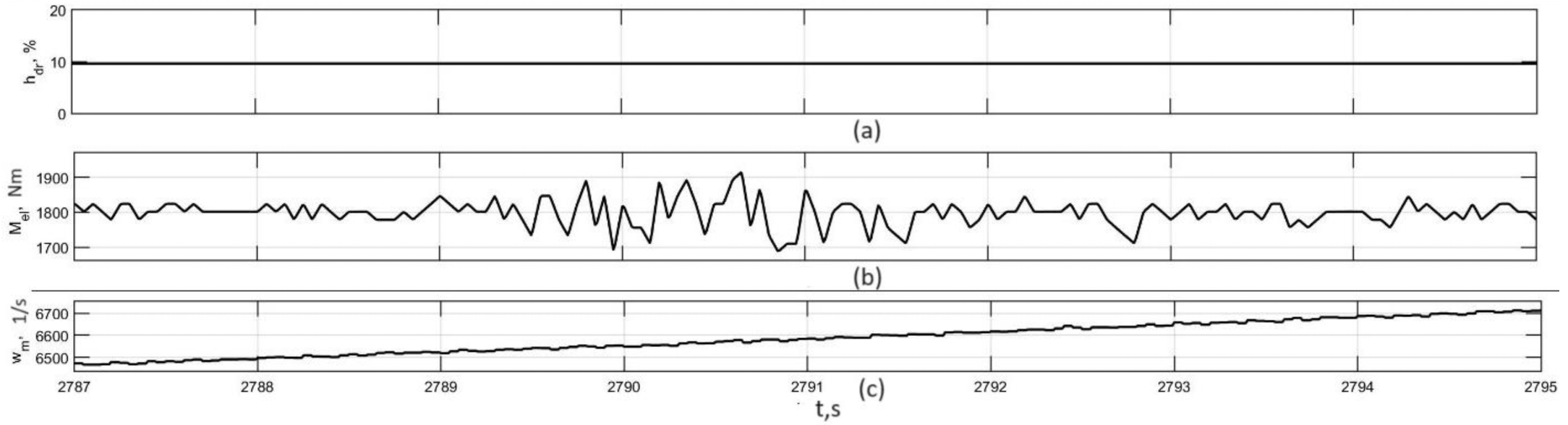
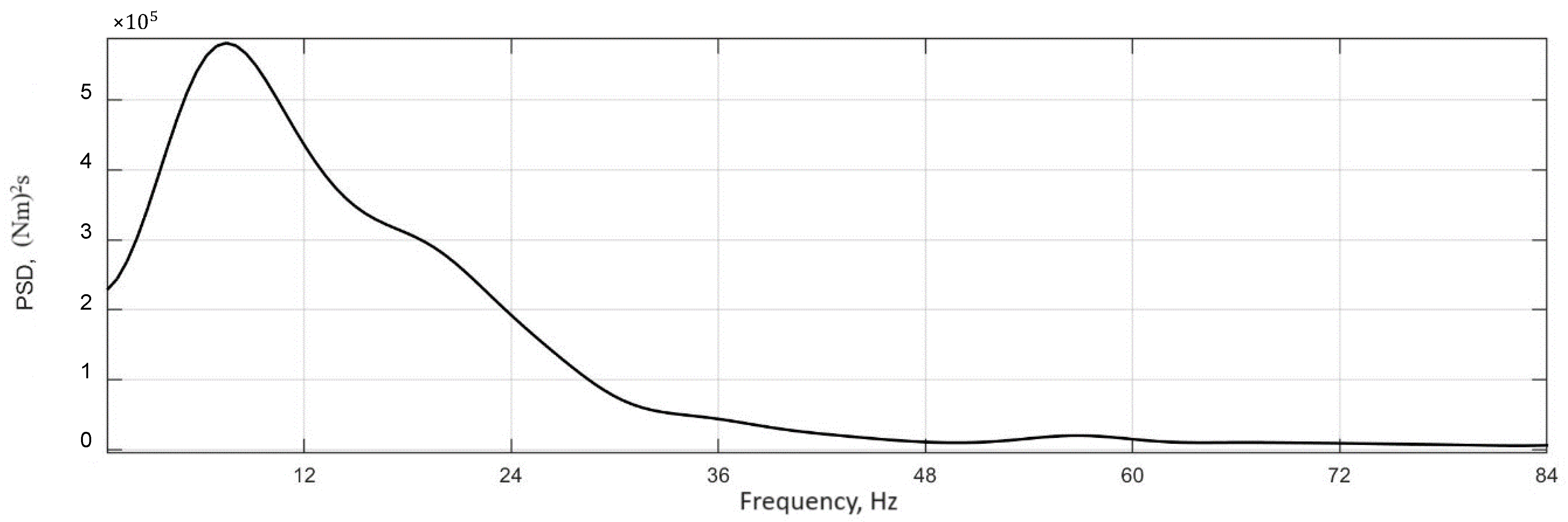
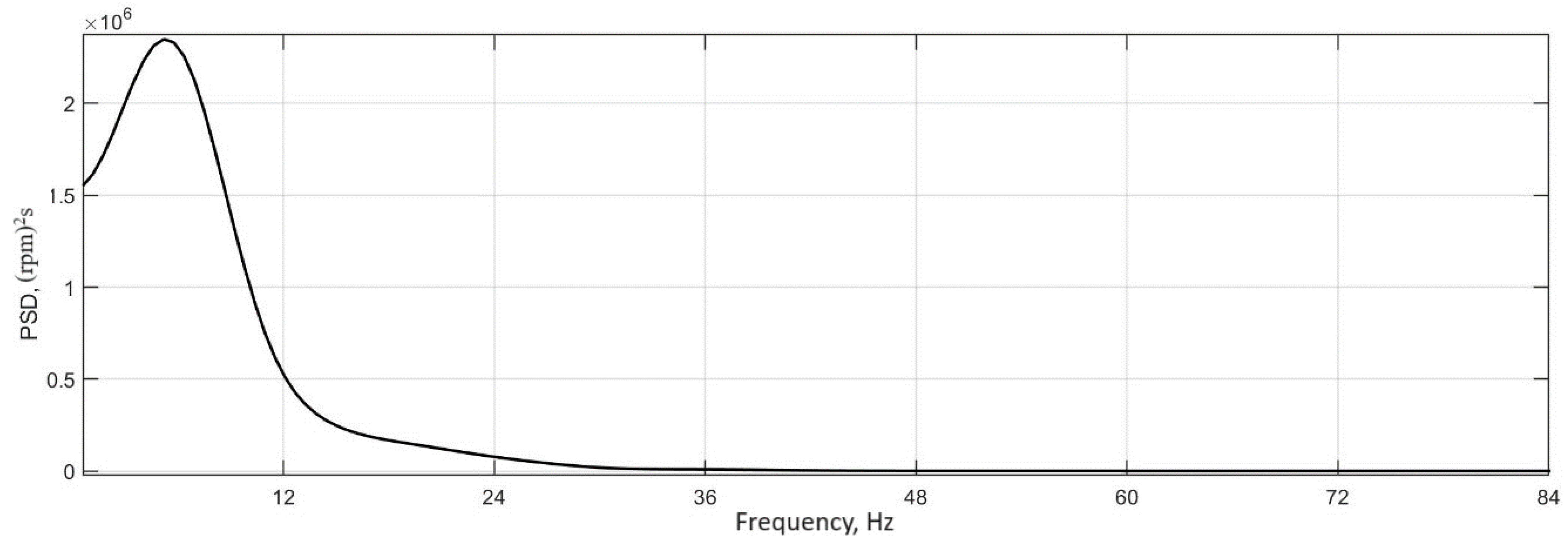
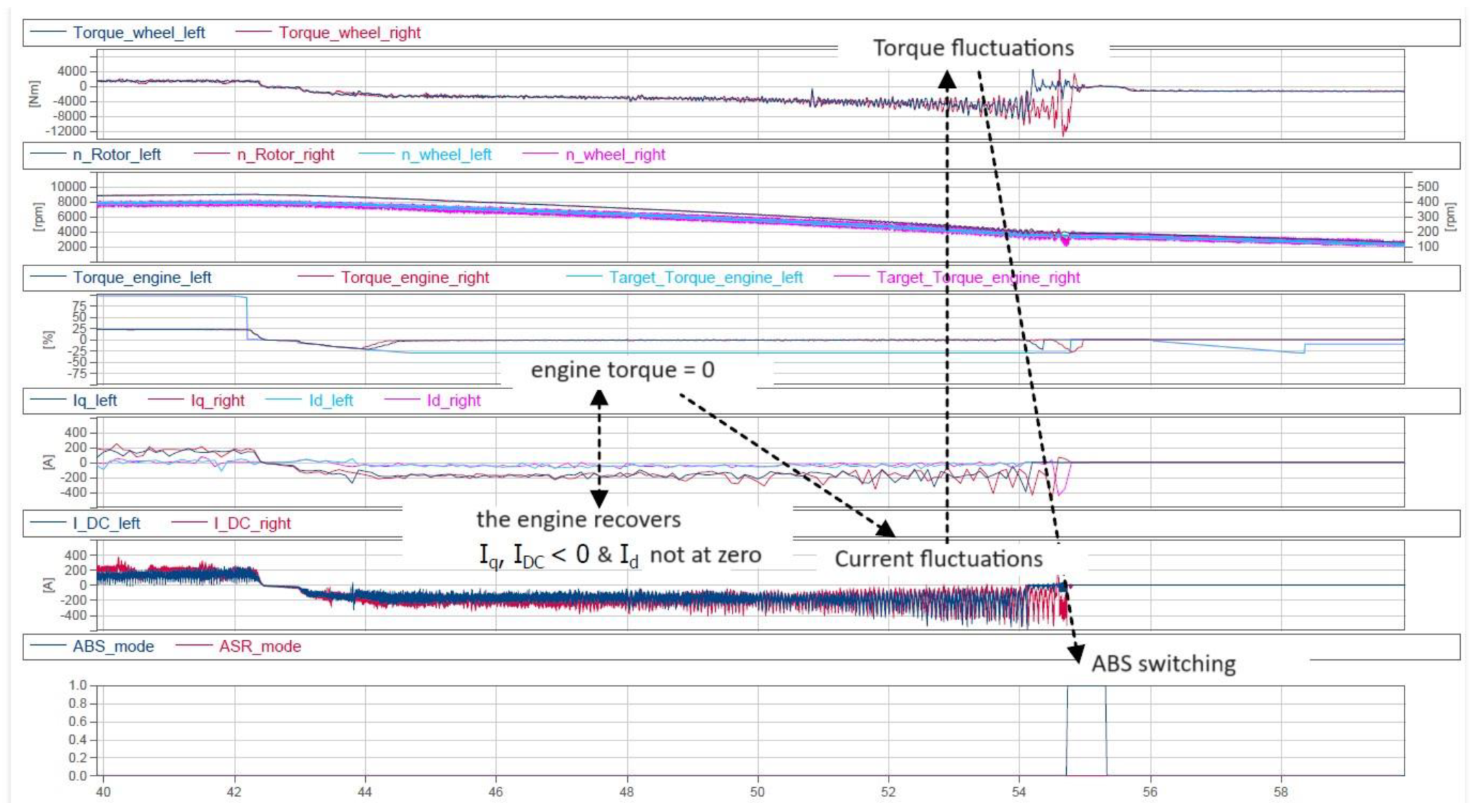
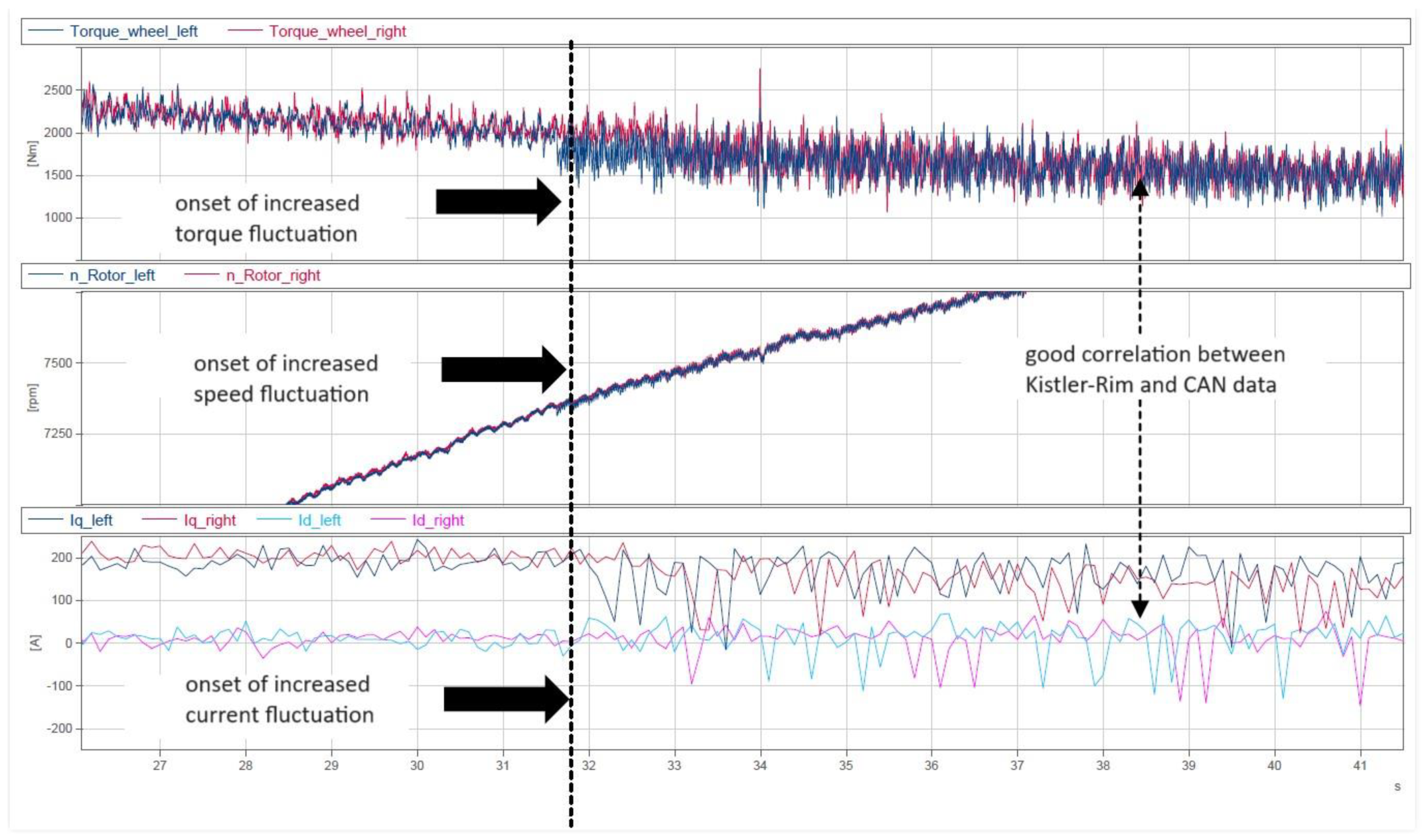
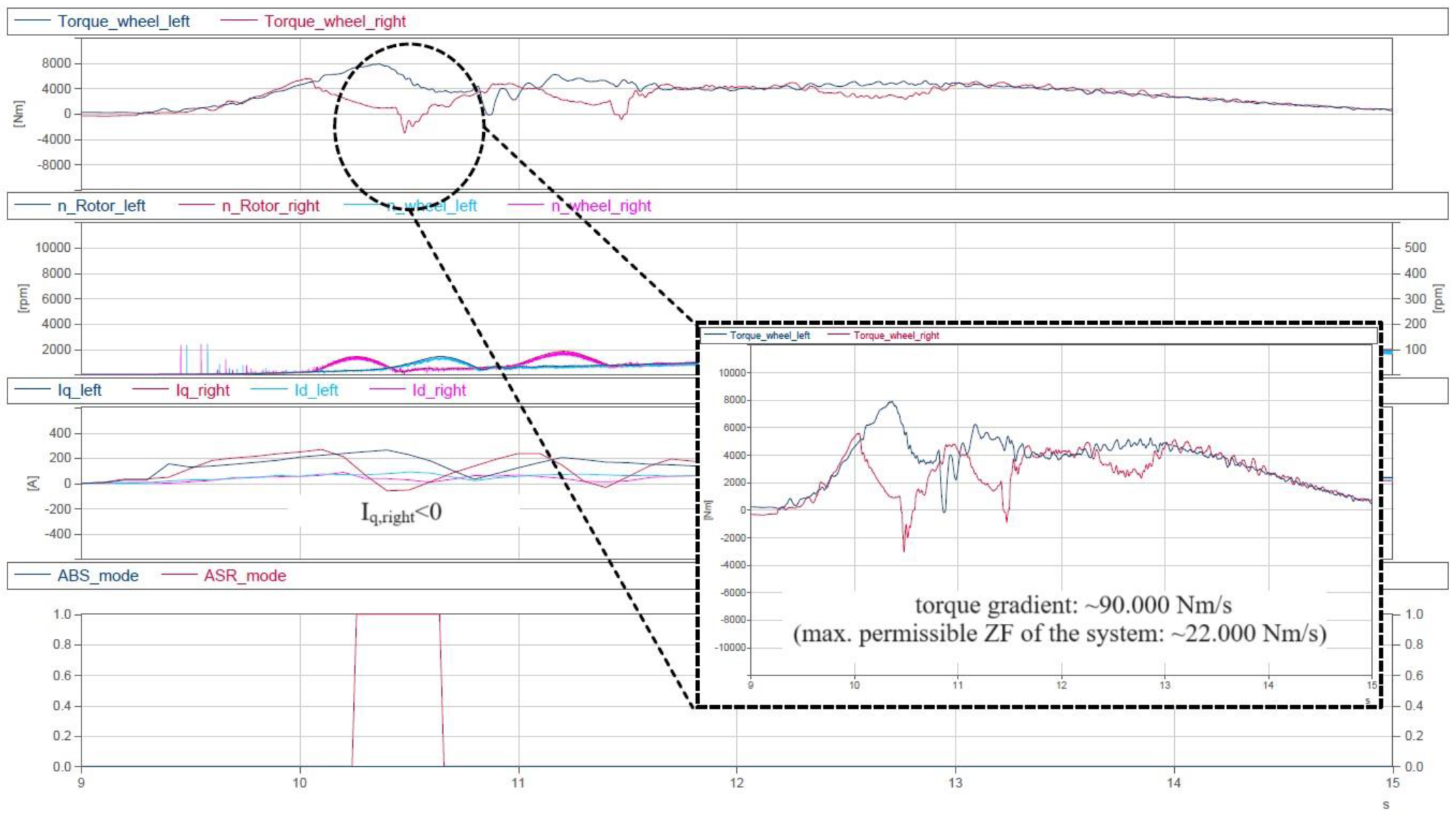

| № | Character of Movement | Wheel Rolling Modes | Traction Properties of the Supporting Surface | Initial Speed, km/h |
|---|---|---|---|---|
| 1 | Acceleration in a left turn with fully depressed accelerator pedal | Traction | Dry asphalt, | 10 |
| 2 | Acceleration in a left turn with fully depressed accelerator pedal | Traction | Ice with snow, | 10 |
| 3 | Regenerative braking in a left turn | Braking | Ice with snow, | 70 |
| Feature | Significance |
|---|---|
| GVW of electric bus, kg | 18,000 |
| GVW distribution by axles, kg | 6400/11,600 |
| Dimensions D × W × H, mm | 12,350 × 2550 × 2770 |
| Wheelbase, mm | 6170 |
| Front track, mm | 2120 |
| Rear track, mm | 1845 |
| Tires | 275/70 R22.5 |
| Front suspension | independent, pneumatic |
| Rear suspension | dependent, pneumatic |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klimov, A.V.; Ospanbekov, B.K.; Keller, A.V.; Shadrin, S.S.; Makarova, D.A.; Furletov, Y.M. Research into the Peculiarities of the Individual Traction Drive Nonlinear System Oscillatory Processes. World Electr. Veh. J. 2023, 14, 316. https://doi.org/10.3390/wevj14110316
Klimov AV, Ospanbekov BK, Keller AV, Shadrin SS, Makarova DA, Furletov YM. Research into the Peculiarities of the Individual Traction Drive Nonlinear System Oscillatory Processes. World Electric Vehicle Journal. 2023; 14(11):316. https://doi.org/10.3390/wevj14110316
Chicago/Turabian StyleKlimov, Alexander V., Baurzhan K. Ospanbekov, Andrey V. Keller, Sergey S. Shadrin, Daria A. Makarova, and Yury M. Furletov. 2023. "Research into the Peculiarities of the Individual Traction Drive Nonlinear System Oscillatory Processes" World Electric Vehicle Journal 14, no. 11: 316. https://doi.org/10.3390/wevj14110316
APA StyleKlimov, A. V., Ospanbekov, B. K., Keller, A. V., Shadrin, S. S., Makarova, D. A., & Furletov, Y. M. (2023). Research into the Peculiarities of the Individual Traction Drive Nonlinear System Oscillatory Processes. World Electric Vehicle Journal, 14(11), 316. https://doi.org/10.3390/wevj14110316






