Topological Optimization of Vehicle ISD Suspension under Steering Braking Condition
Abstract
:1. Introduction
2. Literature Review
3. Construction of Vehicle Nonlinear Dynamics Model
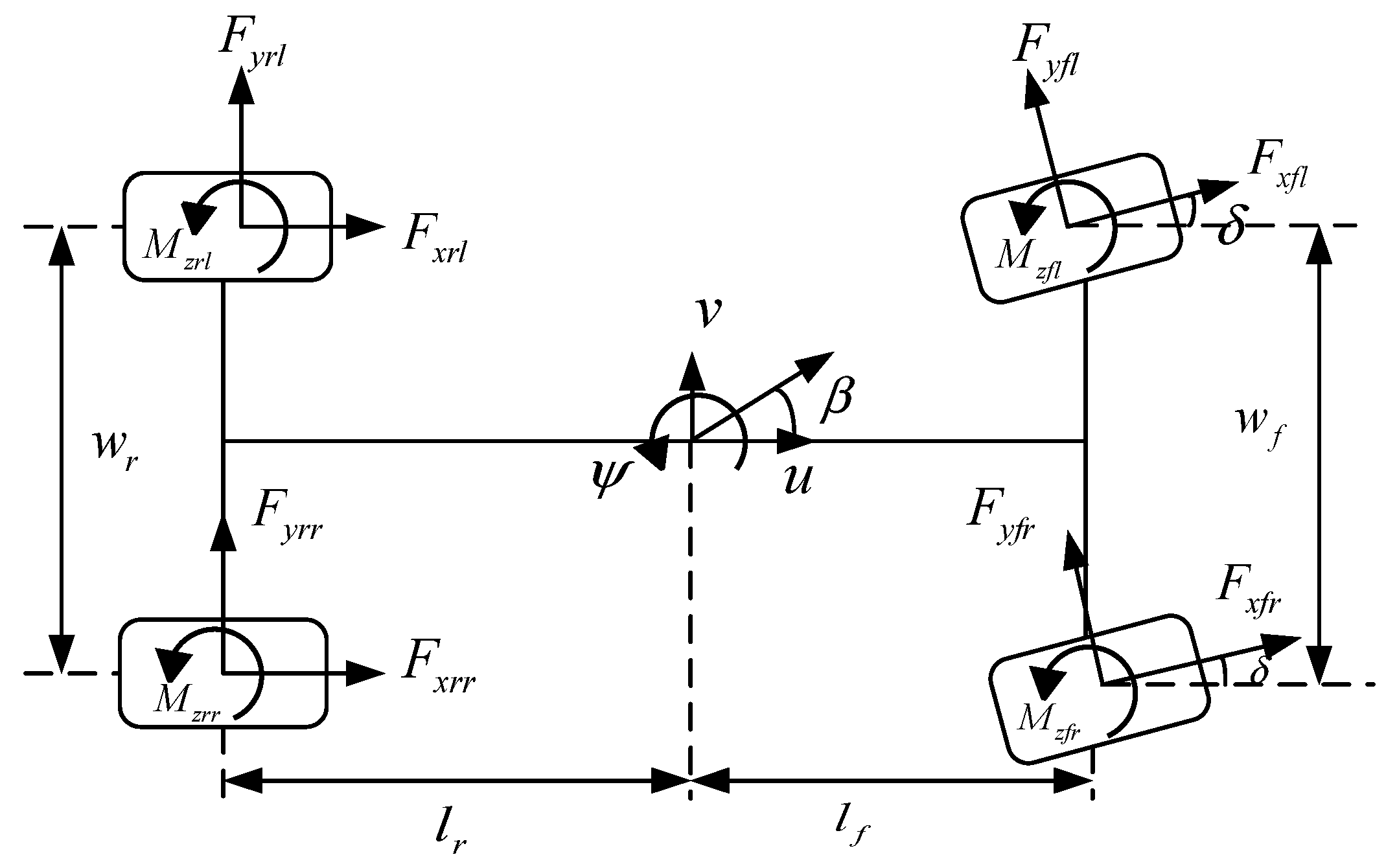
3.1. Vehicle Dynamics Model
- (1)
- Ignore the impact of air resistance and rolling resistance on the car;
- (2)
- Ignore the influence of the steering system and assume that the left and right front wheel angles are the same as the input variables;
- (3)
- Assume that the center of gravity of the car coincides with the origin of the moving coordinate system when the car is driving;
- (4)
- Assume that the four tires have the same characteristics.
3.2. Tire Model
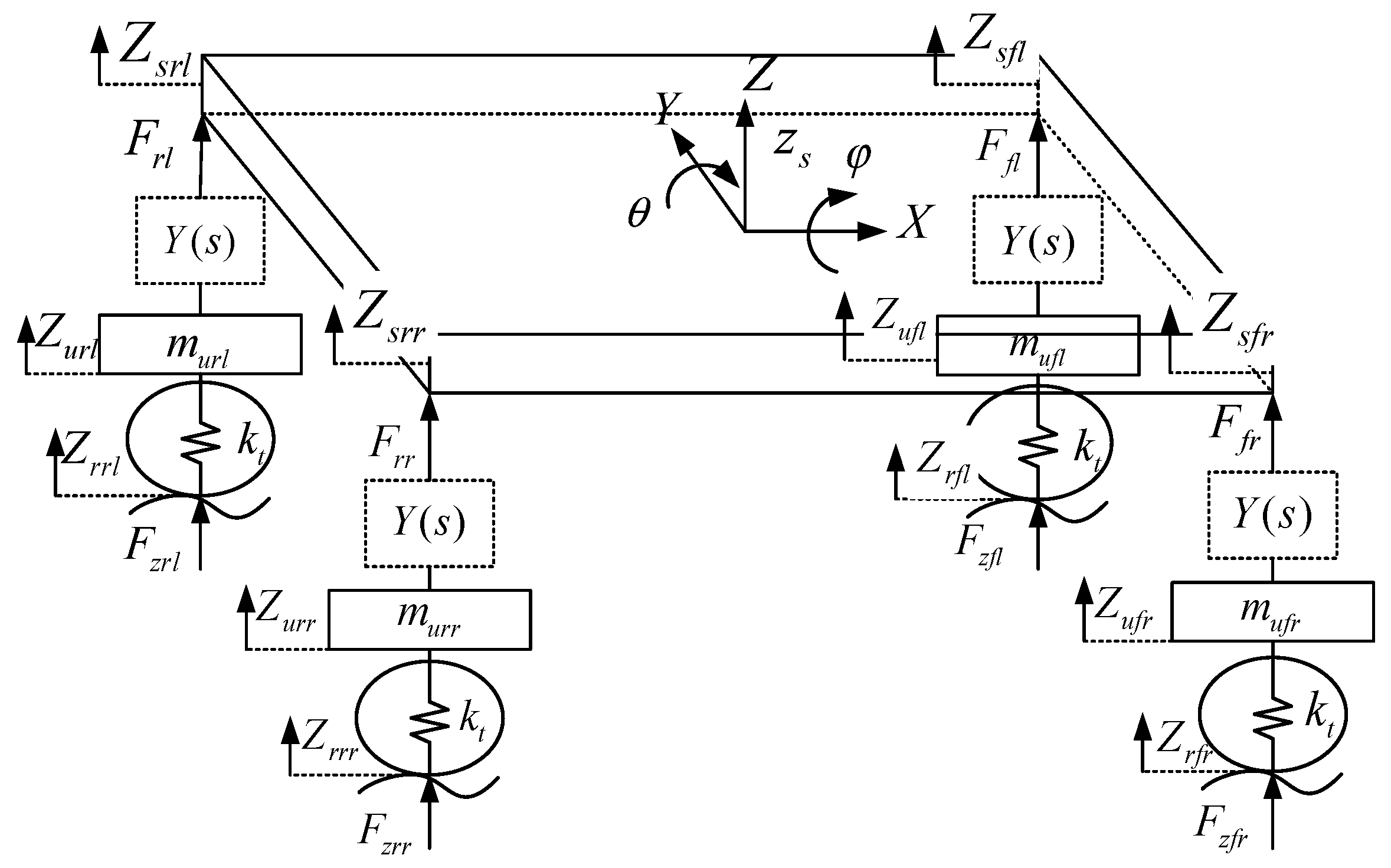
3.3. ISD Suspension Model
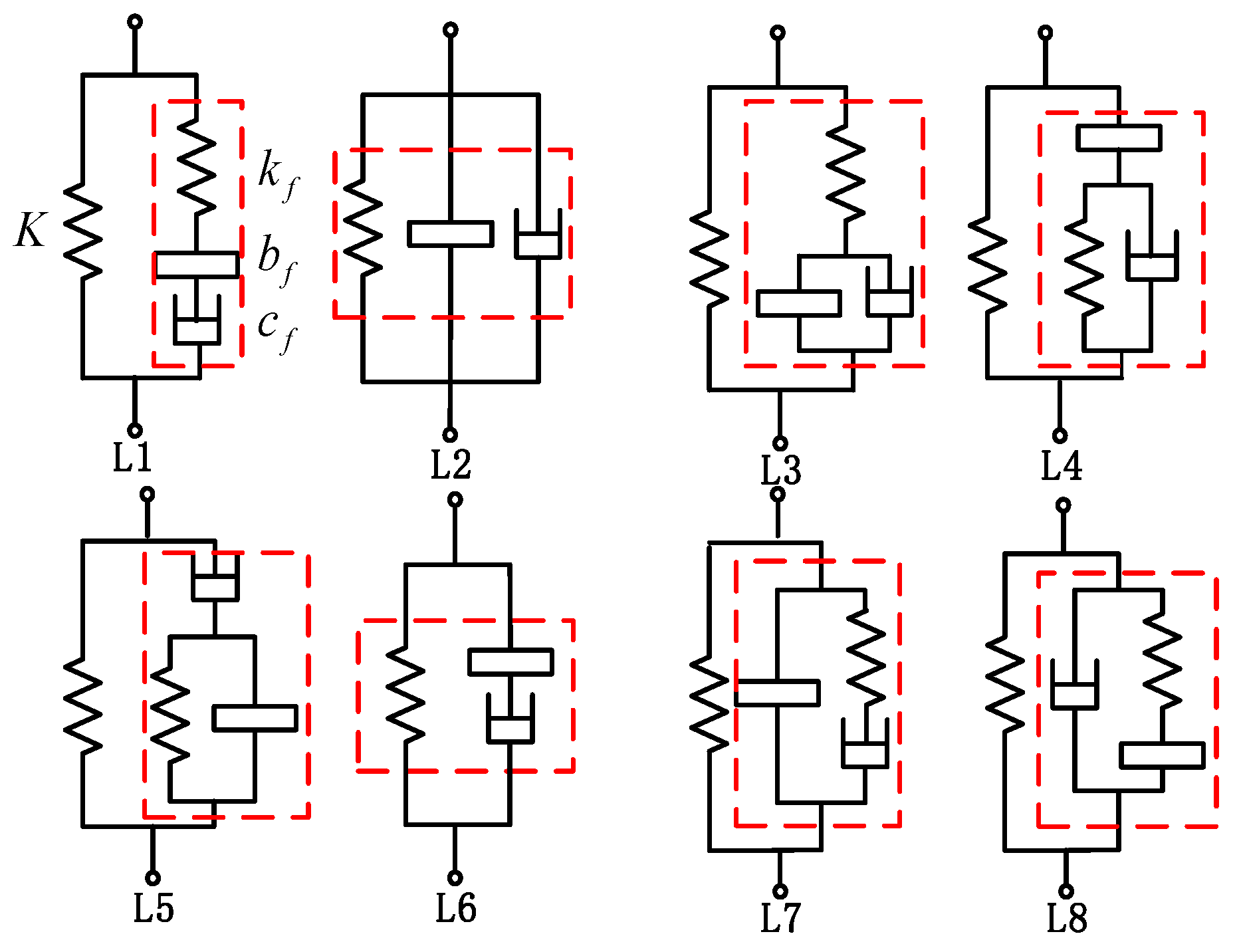
4. Action Law of ISD Suspension Topology
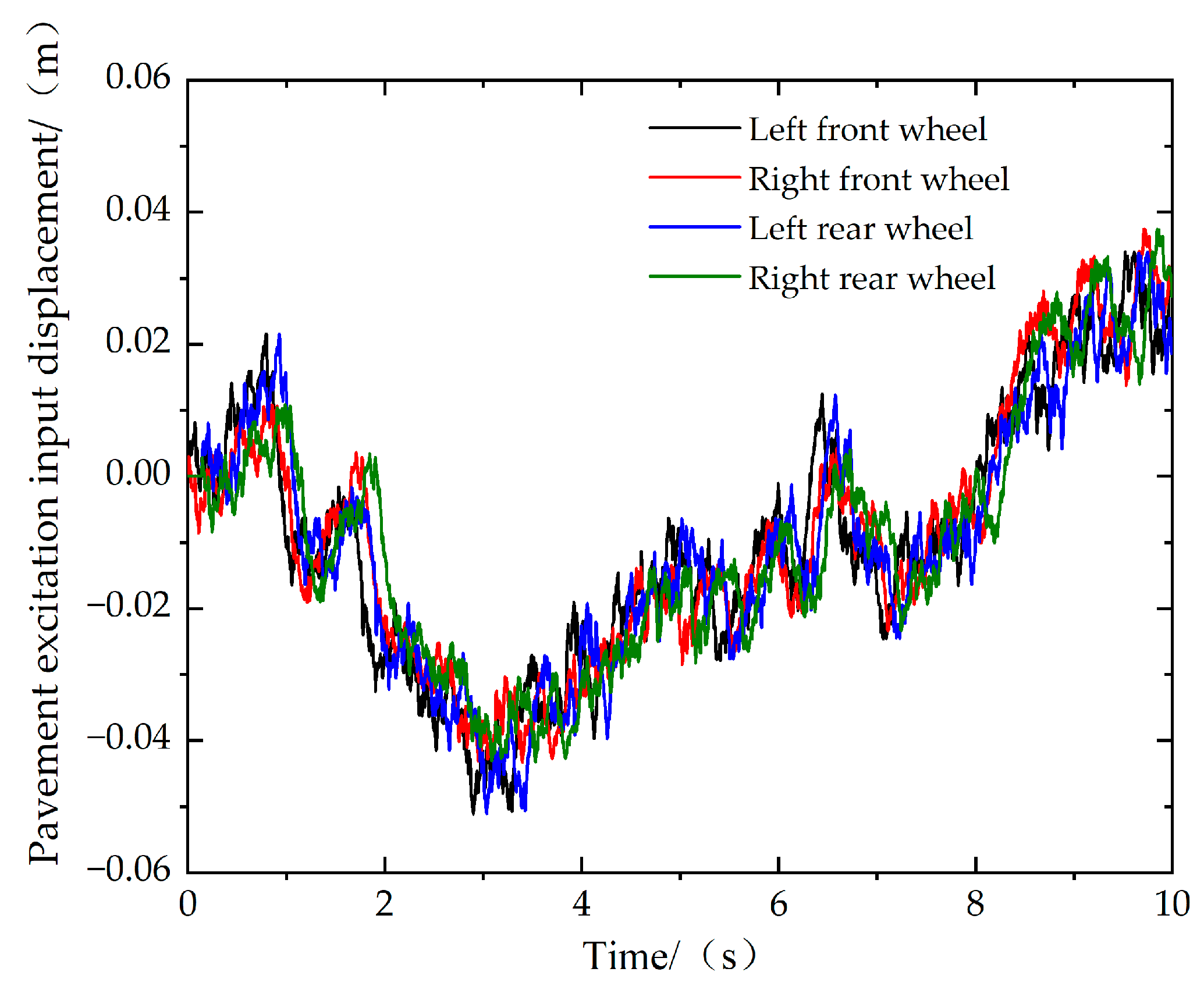
4.1. Pavement Input Model
4.2. The Influence of Eight ISD Suspension Structures on Vehicle Performance
5. Optimization of Vehicle ISD Suspension Parameters Based on NSGA-II
5.1. Optimal Target Selection
5.2. Constraint Selection
5.3. NSGA-Ⅱ Algorithm Steps
5.4. Optimization Result
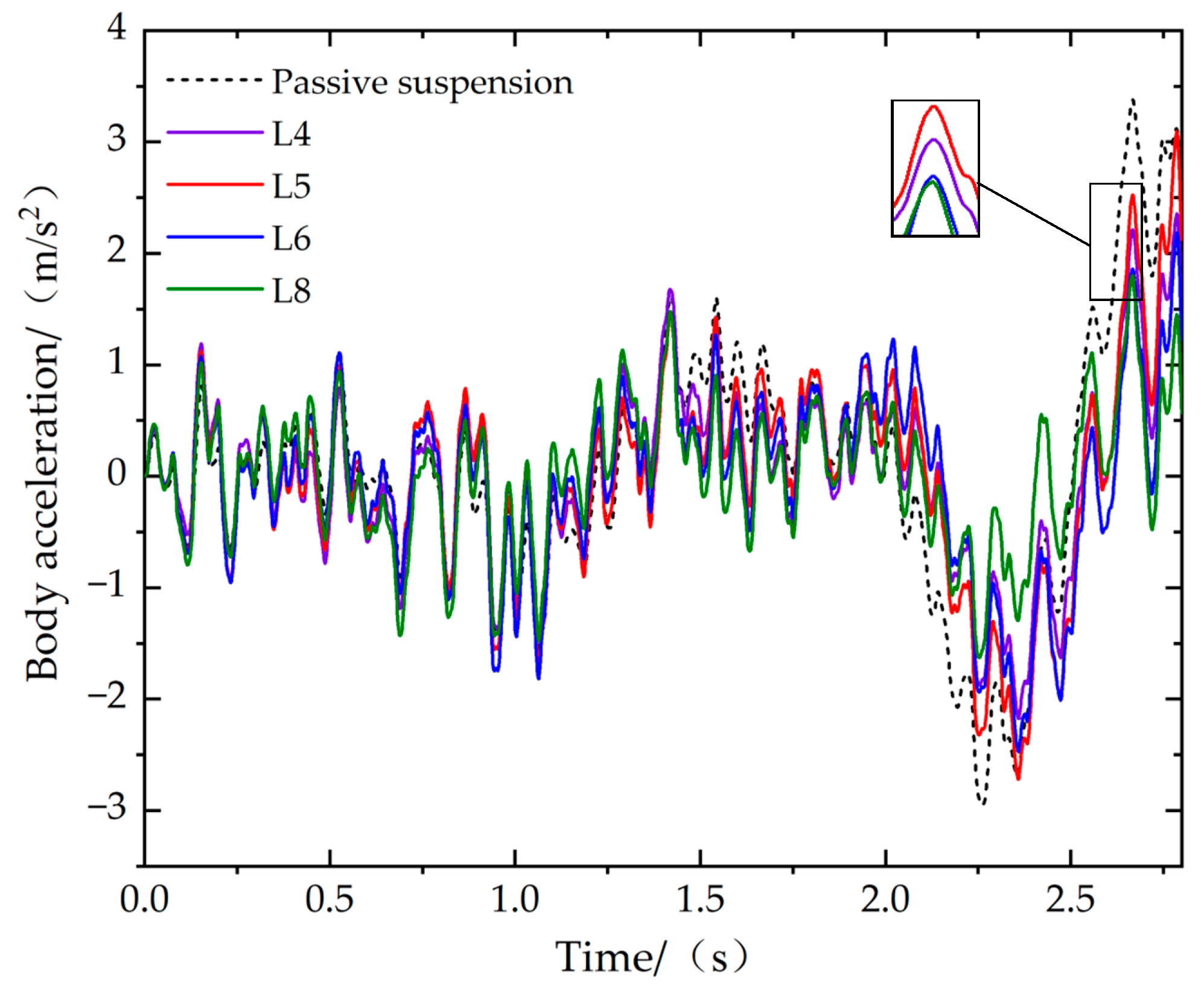
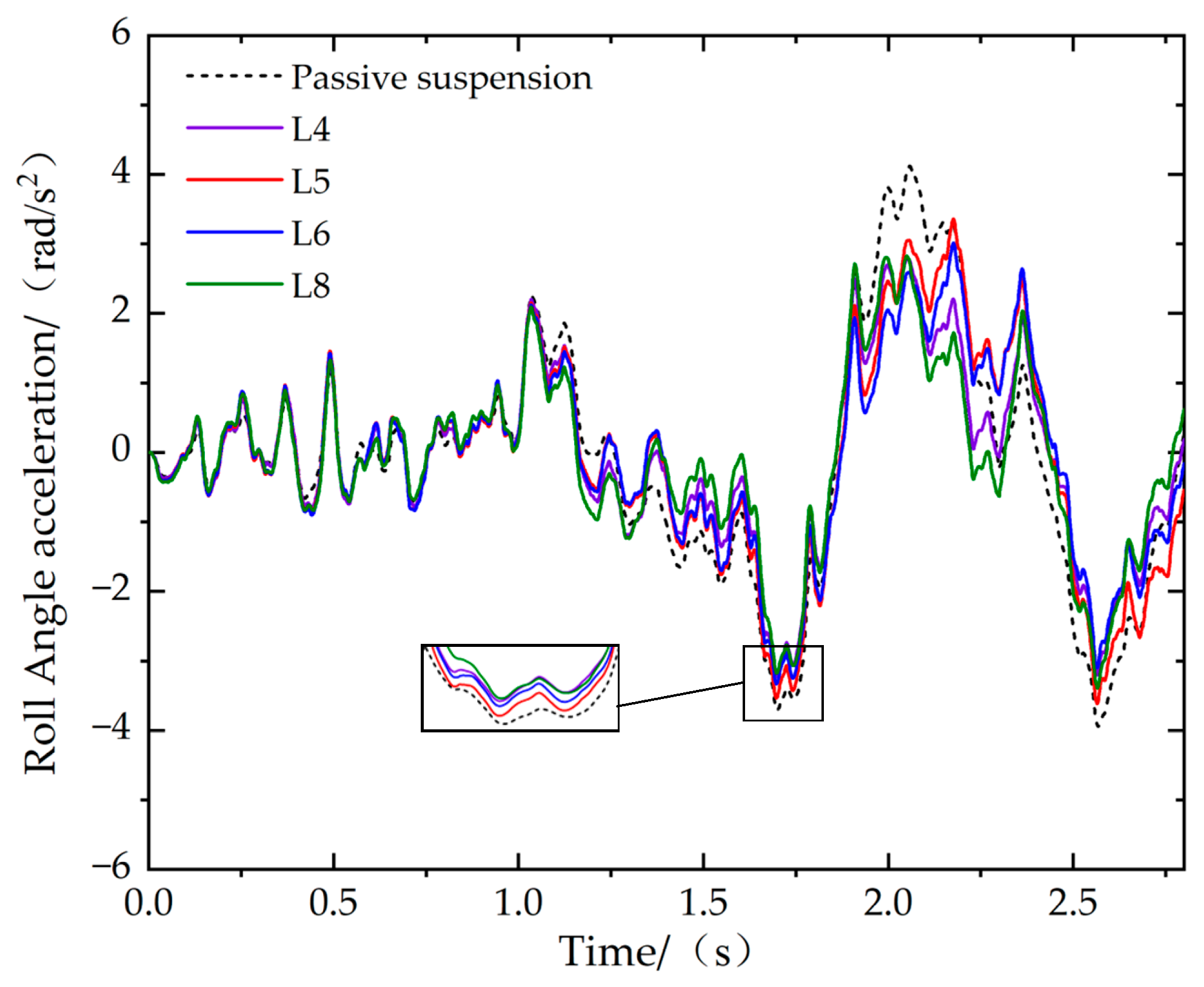
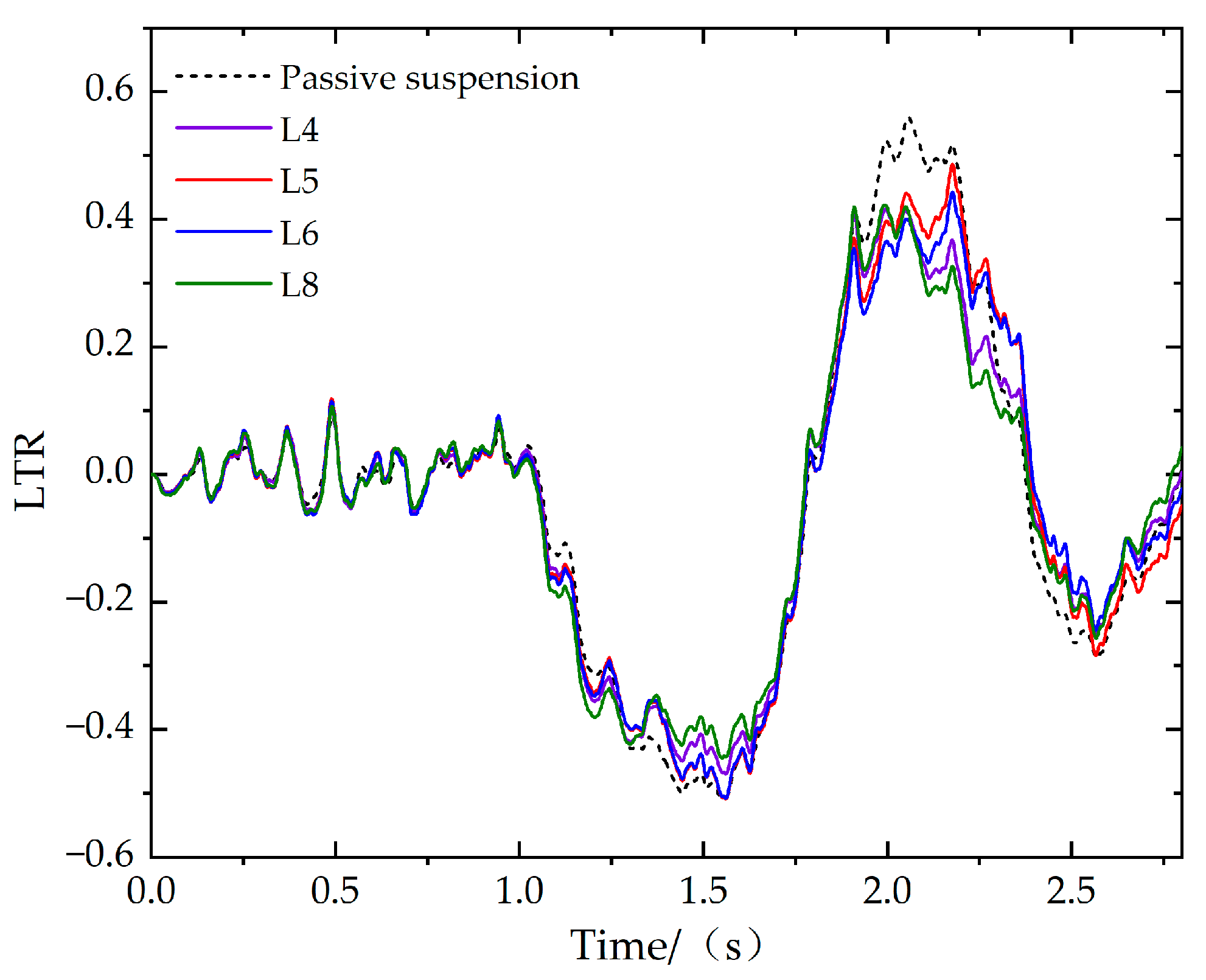
6. Simulation Analysis
6.1. Load Transfer Rate
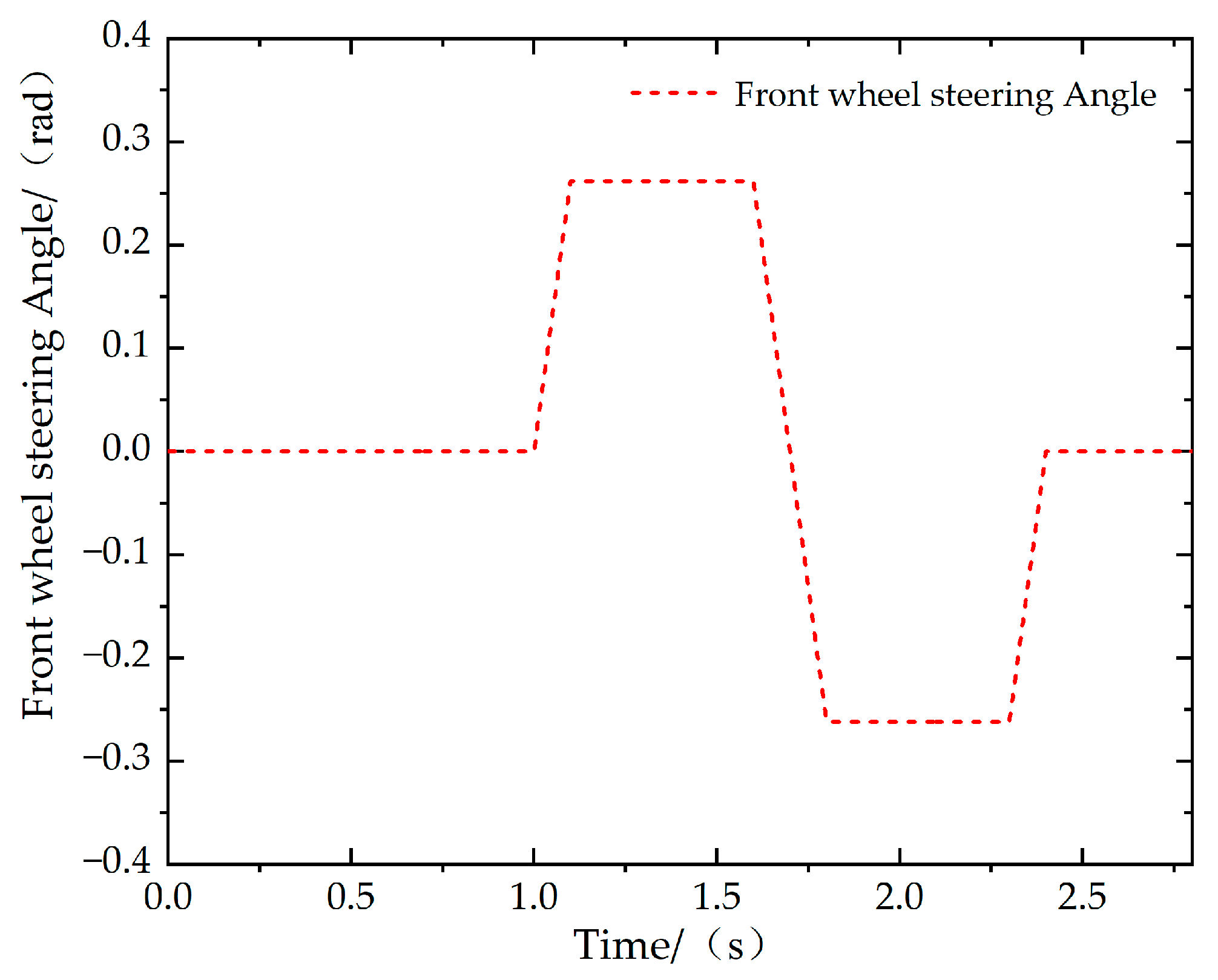
6.2. Step Steering Braking
6.3. Fishhook Steering Braking
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qin, Y.; Zhao, Z.; Wang, Z.; Li, G. Study of Longitudinal—Vertical Dynamics for In-Wheel Motor-Driven Electric Vehicles. Automot. Innov. 2021, 4, 227–237. [Google Scholar] [CrossRef]
- Zhao, D.; Yin, Y.; Ni, T.; Zhang, W. Research review on Chassis Integrated Control of Heavy Truck. J. Yanshan Univ. 2020, 44, 189–197. [Google Scholar]
- Pan, G.; Ding, C.; Wang, W.; Li, A. Application of extended zero moment point in vehicle pitch control evaluation and Active control. J. Jiangsu Univ. 2021, 42, 85–91. [Google Scholar]
- Jiang, Z.; Zheng, M.; Zhang, N. Research on Pitch dynamics of semi-active anti-pitch Hydraulic Interconnected Suspension. J. Vib. Shock. 2020, 39, 272–278. [Google Scholar]
- Wu, X.; Zhou, B.; Wen, G. Research on Anti-roll Control of Hydraulic Interconnected Suspension. China J. Highw. Transp. 2018, 31, 123–132. [Google Scholar]
- Zhang, L.; Meng, Q.; Chen, H.; Huang, Y.; Liu, Y.; Guo, K. Kalman Filter-Based Fusion Estimation Method of Steering Feedback Torque for Steer-by-Wire Systems. Automot. Innov. 2021, 4, 430–439. [Google Scholar] [CrossRef]
- Qin, Y.; Wang, Z.; Yuan, K.; Zhang, Y. Correction to: Comprehensive Analysis and Optimization of Dynamic Vibration-Absorbing Structures for Electric Vehicles Driven by In-Wheel Motors. Automot. Innov. 2020, 3, 192. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Z.; Meng, L.; Fu, T.; Li, J.; Wang, Z. Design and Research of Electro-Hydraulic Suspension System with both Energy Feed and active anti-roll Function. J. Automot. Eng. 2023, 13, 396–407. [Google Scholar]
- Hou, X.; Zhang, J.; Liu, W.; Ji, Y. LuGre Mode-based Longitudinal Ride Comfort Control of Vehicle during the Post-braking Phase. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar]
- Xu, Z.; Liu, H.; Dang, W.; Hu, C.; Long, Y. Research Review of Automobile Brake Comfort Control. Sci. Technol. Eng. 2022, 22, 6790–6801. [Google Scholar]
- Bi, H.; Lu, F.; Duan, S.; Huang, M.; Zhu, J.; Liu, M. Two-level principal–agent model for schedule risk control of IT outsourcing project based on genetic algorithm. Eng. Appl. Artif. Intell. 2020, 91, 103584. [Google Scholar] [CrossRef]
- Wen, H.; Wang, S.; Lu, F.; Feng, M.; Wang, L.; Xiong, J.; Si, M. Colony search optimization algorithm using global optimization. J. Supercomput. 2022, 78, 6567–6611. [Google Scholar] [CrossRef]
- Li, S.; Du, P.; Feng, X. Integrated Control Strategy of anti-rollover Chassis for Minibus. J. Jiangsu Univ. 2022, 43, 131–138. [Google Scholar]
- Zhao, S.; Li, Y.; Yu, Q. Vehicle Stability Control Based on Coordinated Control of Multiple Sub-systems of Chassis. J. Traffic Transp. Eng. 2015, 15, 77–85. [Google Scholar]
- Chen, L.; Chen, M.; Sun, X.; Cai, Y.; Pak, K.W.; Wu, Z. Lateral Dynamics Modeling and Stability Analysis of Air Suspension Bus. Automot. Eng. 2022, 44, 1746–1754. [Google Scholar]
- Huang, K.; Zhao, P.; Chen, J. Research on Improving Performance of Hydraulic Interconnected Suspension with Inertial Vessel. Noise Vib. Control. 2022, 42, 17–22. [Google Scholar]
- Lu, S.; Li, Y.; Zheng, L. Research on Vehicle active Rollover Control based on Brake and Suspension System. Automot. Eng. 2011, 33, 669–675. [Google Scholar]
- Smith, M.C. Synthesis of Networks: The inerter. IEEE Trans. Autom. Control. 2002, 47, 1648–1662. [Google Scholar] [CrossRef]
- Chen, L.; Yang, X.; Wang, R.; Huang, C.; Shen, Y. Study on the Performance of Improved ISD Three-Component Passive Suspension. Automot. Eng. 2014, 36, 340–345. [Google Scholar]
- Ge, Z.; Wang, W.; Li, G.; Rao, D. Design, Parameter Optimisation, and Performance Analysis of Active Tuned Inerter Damper (TID) Suspension for Vehicle. J. Sound Vib. 2022, 525, 116750. [Google Scholar] [CrossRef]
- Shen, Y.; Chen, L.; Liu, Y.; Zhang, X.; Yang, X. Improvement of the lateral stability of vehicle suspension incorporating inerter. Sci. China 2018, 61, 1244–1252. [Google Scholar] [CrossRef]
- Shen, Y.; Hua, J.; Fan, W.; Liu, Y.; Yang, X.; Chen, L. Optimal design and dynamic performance analysis of a fractional-order electrical network-based vehicle mechatronic ISD suspension. Mech. Syst. Signal Process. 2023, 184, 109718. [Google Scholar] [CrossRef]
- Shen, Y.; Jia, M.; Yang, X.; Liu, Y.; Chen, L. Vibration suppression using a mechatronic PDD-ISD-combined vehicle suspension system. Int. J. Mech. Sci. 2023, 250, 108277. [Google Scholar] [CrossRef]
- Luo, J.; Li, P.; Li, P.; Cai, Q. Observer-based multi-objective integrated control for vehicle lateral stability and active suspension design. J. Sound Vib. 2021, 508, 116222. [Google Scholar] [CrossRef]
- Feng, S.; Zhao, Y.; Deng, H.; Wang, Q.; Chen, T. Parameter Identification of Magic Formula Tire Model Based on Fibonacci Tree Optimization Algorithm. J. Shanghai Jiao Tong Univ. 2021, 26, 647–657. [Google Scholar] [CrossRef]
- Meng, L. Research on Active Anti-Roll Control Performance of Automotive Electro-Hydraulic Suspension. Ph.D. Dissertation, Jilin University, Changchun, China, 2023. [Google Scholar]
- Qi, Q.; Wu, T. Multi-objective Production Intelligent Scheduling Based on Improved NSGA-II Algorithm. Comput. Technol. Dev. 2021, 31, 162–168. [Google Scholar]

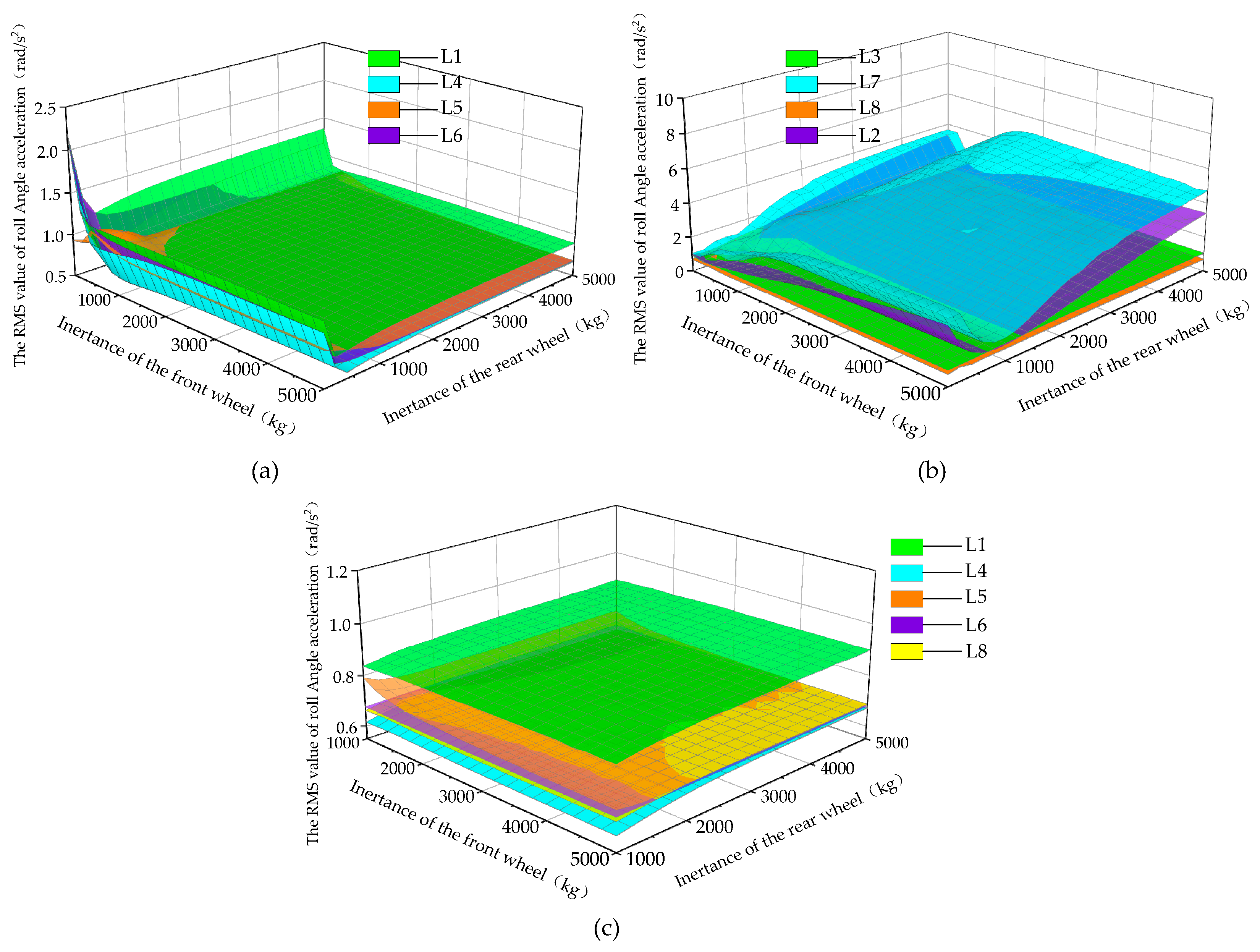
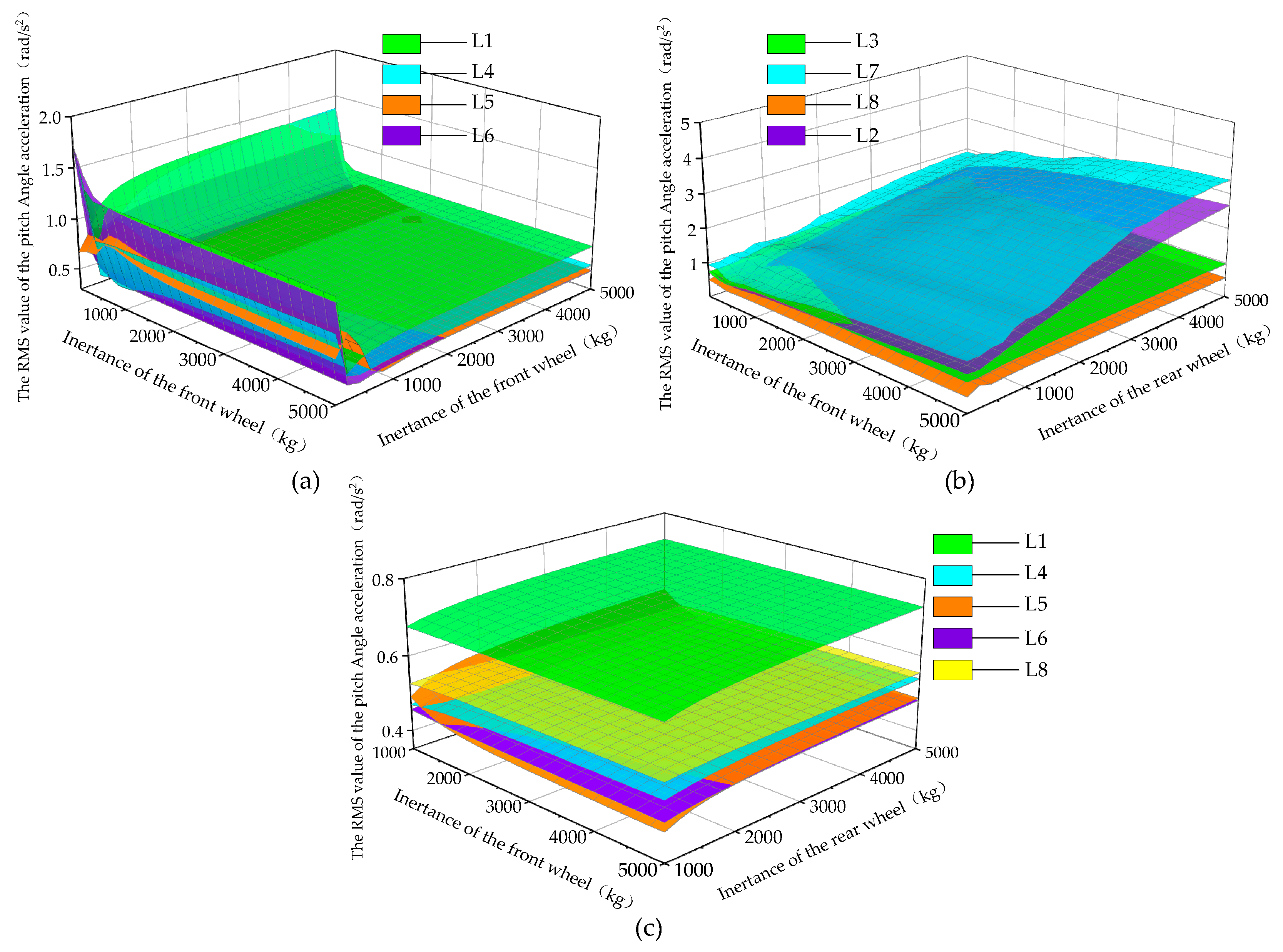
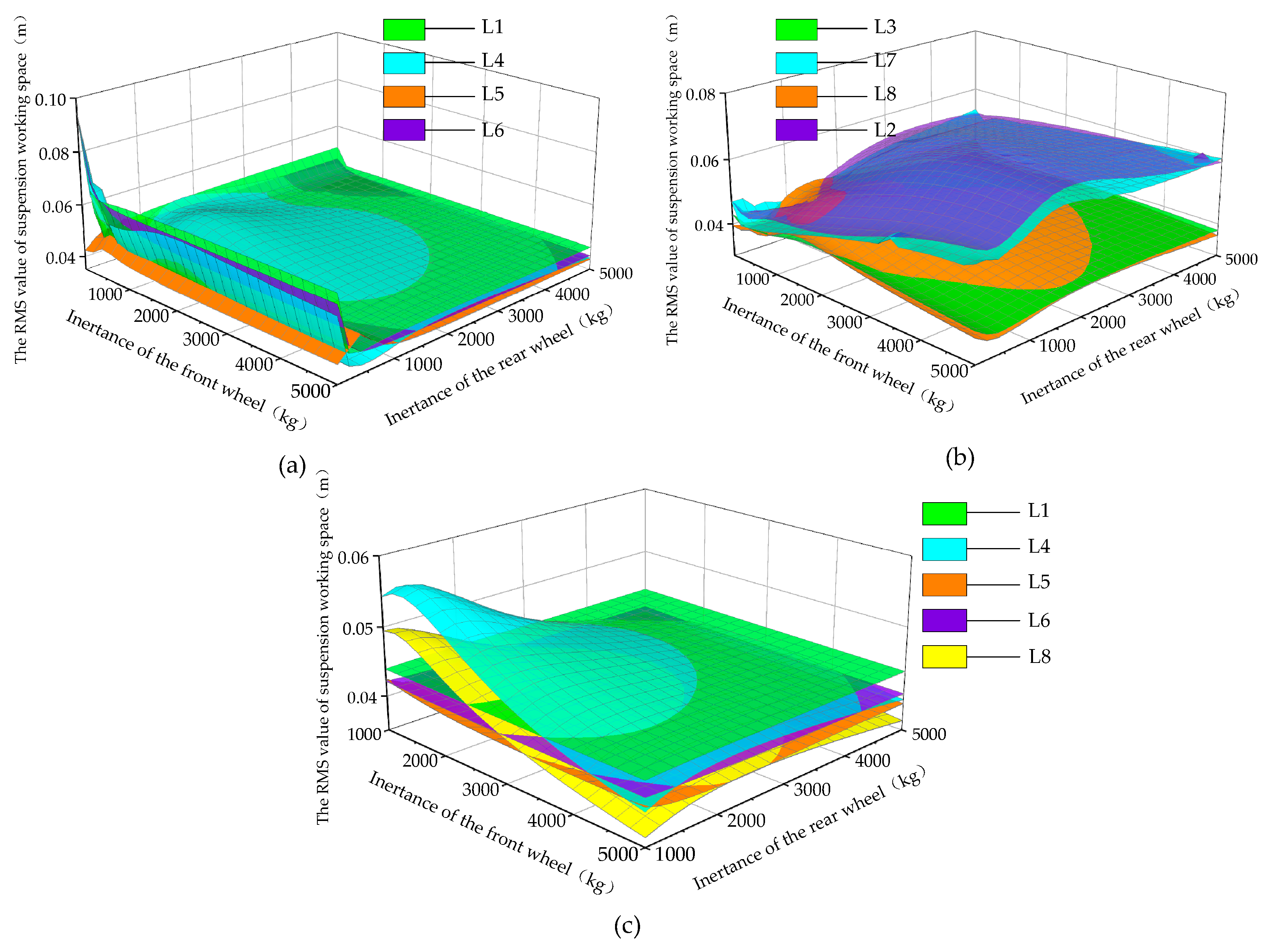
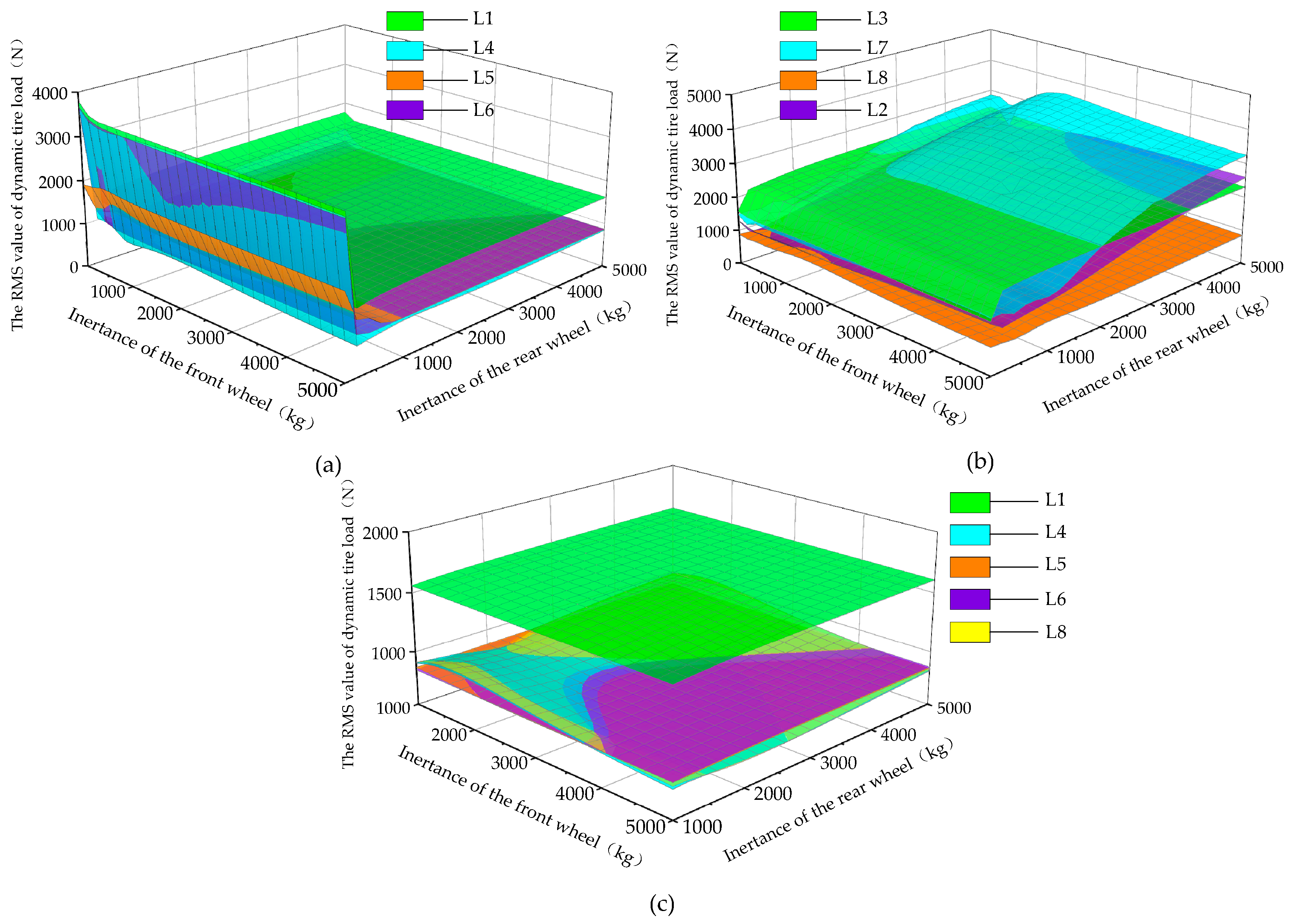



| Parameter | Value |
|---|---|
| Vehicle mass mt/kg | 1659 |
| Sprung mass ms/kg | 1410 |
| Front wheel unsprung mass mufl,mufr/kg | 26.5 |
| Rear wheel unsprung mass murl,murr/kg | 24.4 |
| Left wheel base wf/m | 1.574 |
| Left and right wheel base wr/m | 1.593 |
| Distance from front axle to center of mass lf/m | 1.278 |
| Distance from rear axis to center of mass lr/m | 1.430 |
| Height of center of mass h1/m | 0.50 |
| Roll height h2/m | 0.40 |
| Distance from center of roll to center of mass h3/m | 0.25 |
| Body roll moment of inertia Ix/kg·m2 | 925 |
| Body pitch moment of inertia Iy/kg·m2 | 2577 |
| Body yaw moment of inertia Iz/kg·m2 | 2603 |
| Wheel inertia Iw/kg·m2 | 0.99 |
| Wheel radius Rw/m | 0.345 |
| Front suspension spring stiffness of the original model kf0/kN·m−1 | 25 |
| Rear suspension spring stiffness of the original model kr0/kN·m−1 | 22 |
| Front suspension damping coefficient of the original model cf0/N·s·m−1 | 1800 |
| Rear suspension damping coefficient of the original model cr0/N·s·m−1 | 1500 |
| Tire stiffness kt/kN·m−1 | 192 |
| Front suspension roll stiffness k1/N·m·rad−1 | 47,298 |
| Rear suspension roll stiffness k2/N·m·rad−1 | 37,311 |
| Performance Index | RMS Value |
|---|---|
| Body acceleration/(m·s−2) | 0.8684 |
| Roll angle acceleration/(rad·s−2) | 0.6338 |
| Pitch angle acceleration/(rad·s−2) | 0.4885 |
| Suspension working space/(m) | 0.0395 |
| Dynamic tire load/(KN) | 0.8771 |
| Suspension Structure | (N/m) | (N/m) | (N∙s/m) | (N∙s/m) | (kg) | (kg) |
|---|---|---|---|---|---|---|
| L4 | 11,395 | 17,269 | 2213 | 2895 | 376 | 4514 |
| L5 | 28,708 | 8310 | 2860 | 3406 | 1023 | 3484 |
| L6 | / | / | 2815 | 3425 | 3168 | 3614 |
| L8 | 8583 | 16,313 | 2971 | 2421 | 102 | 2180 |
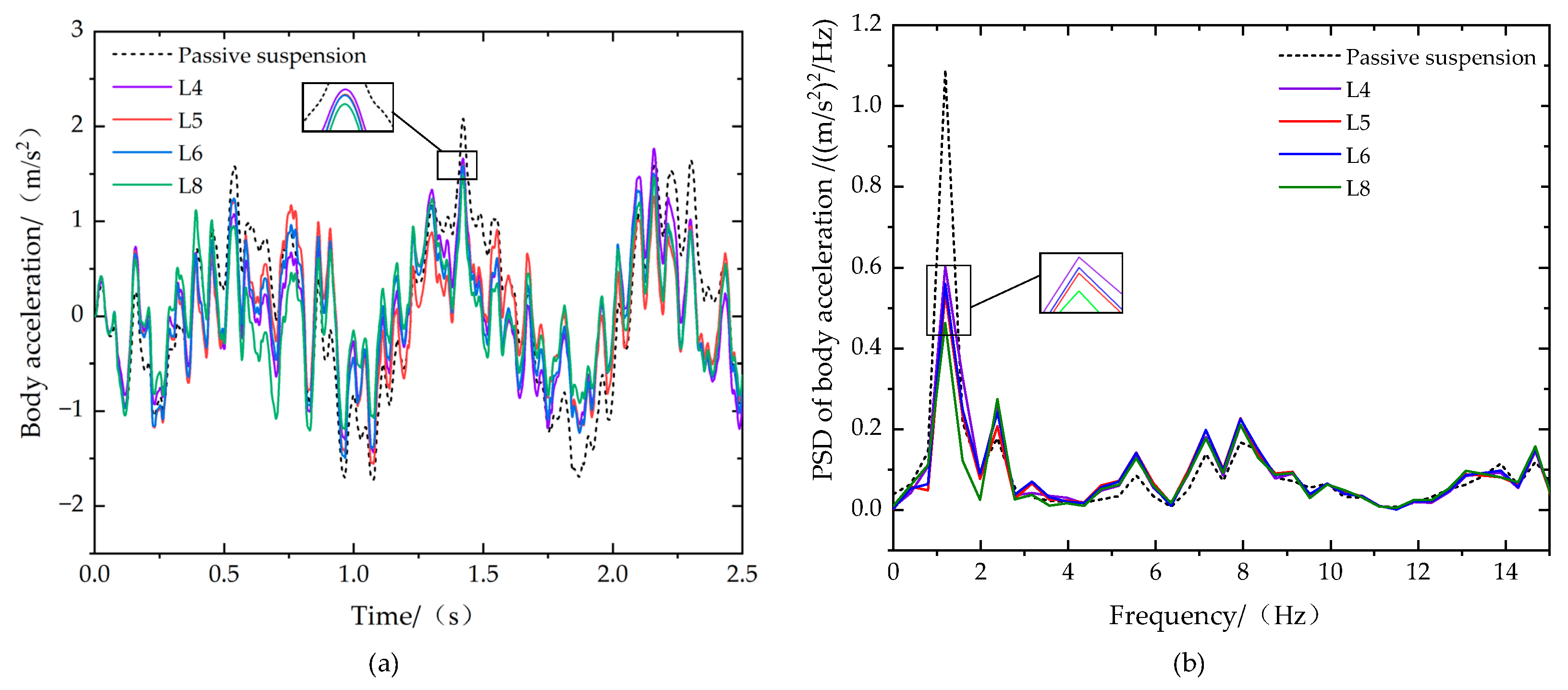
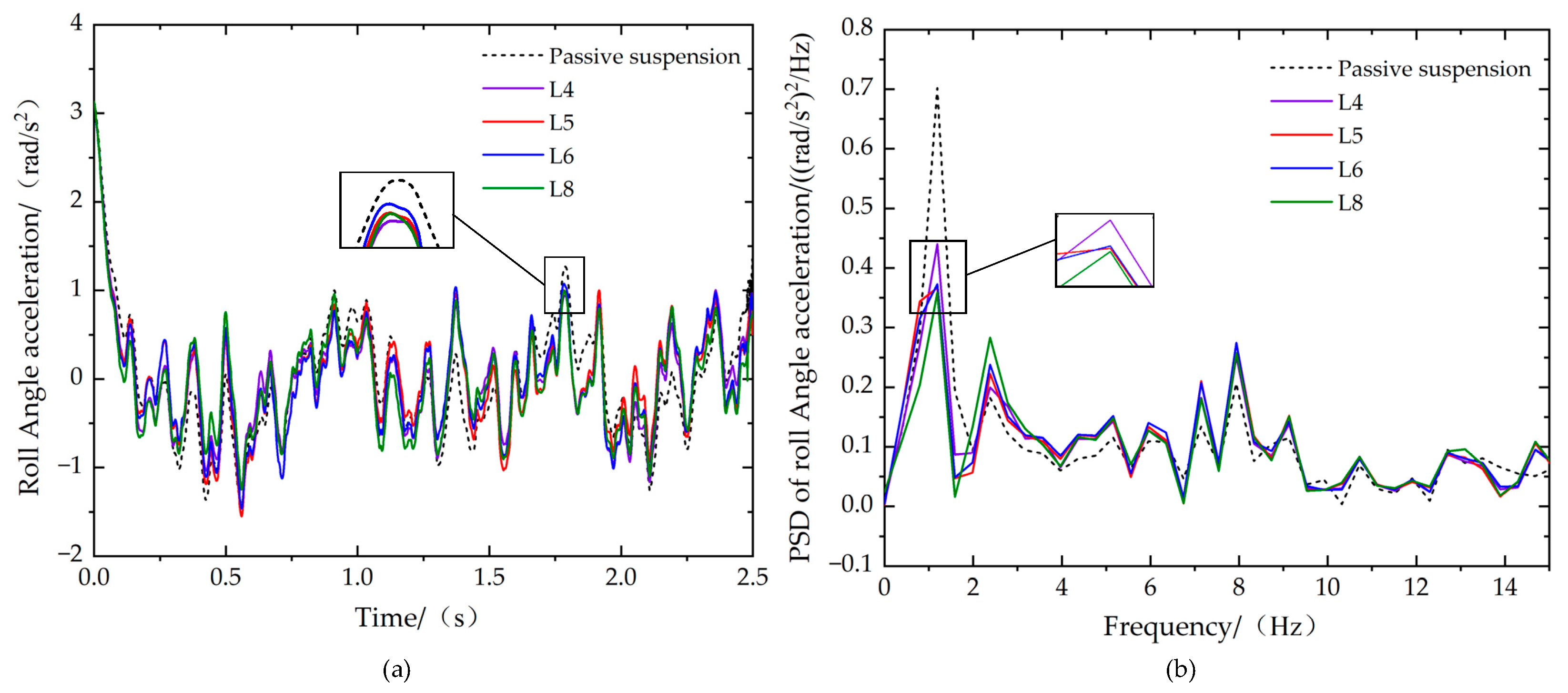
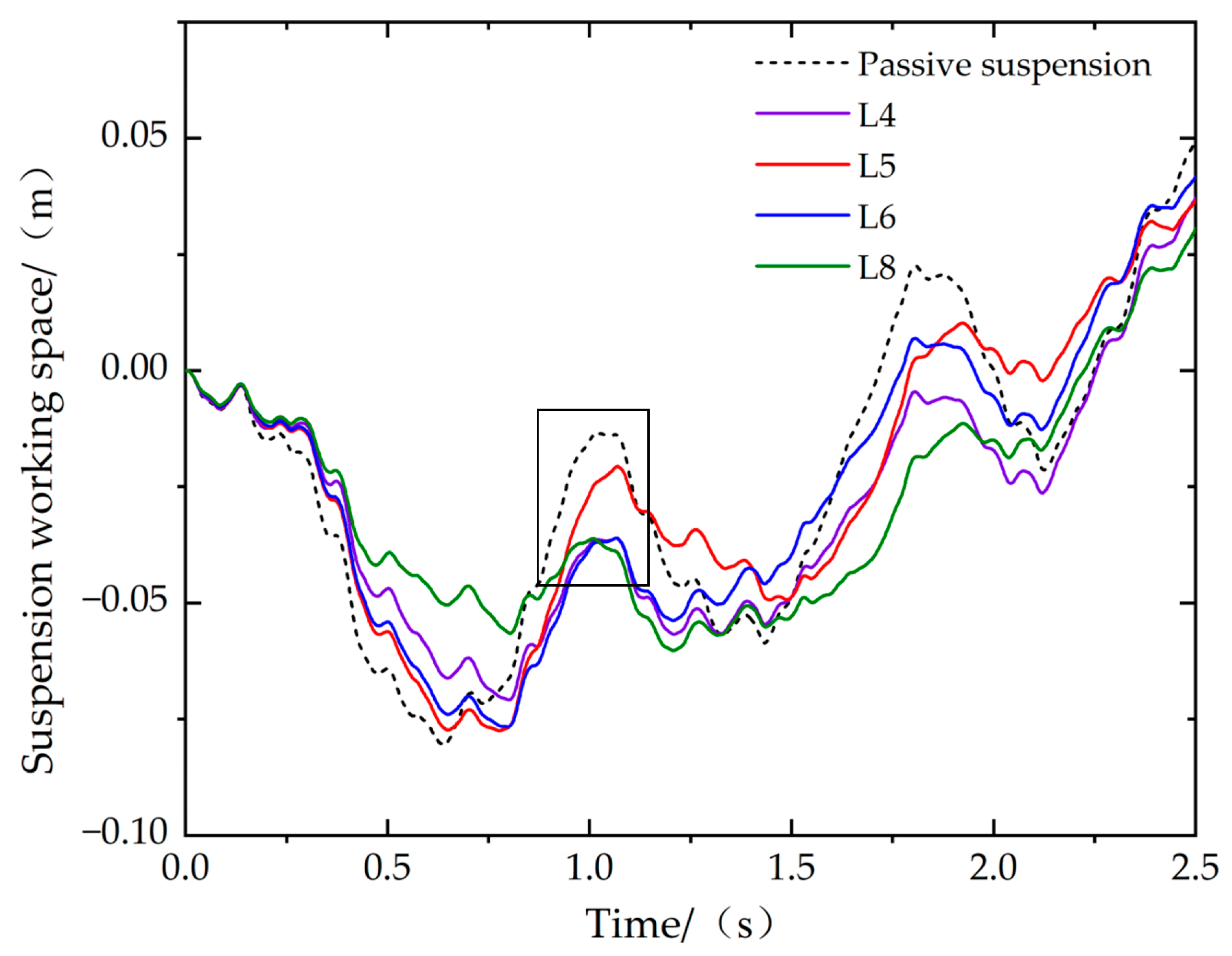
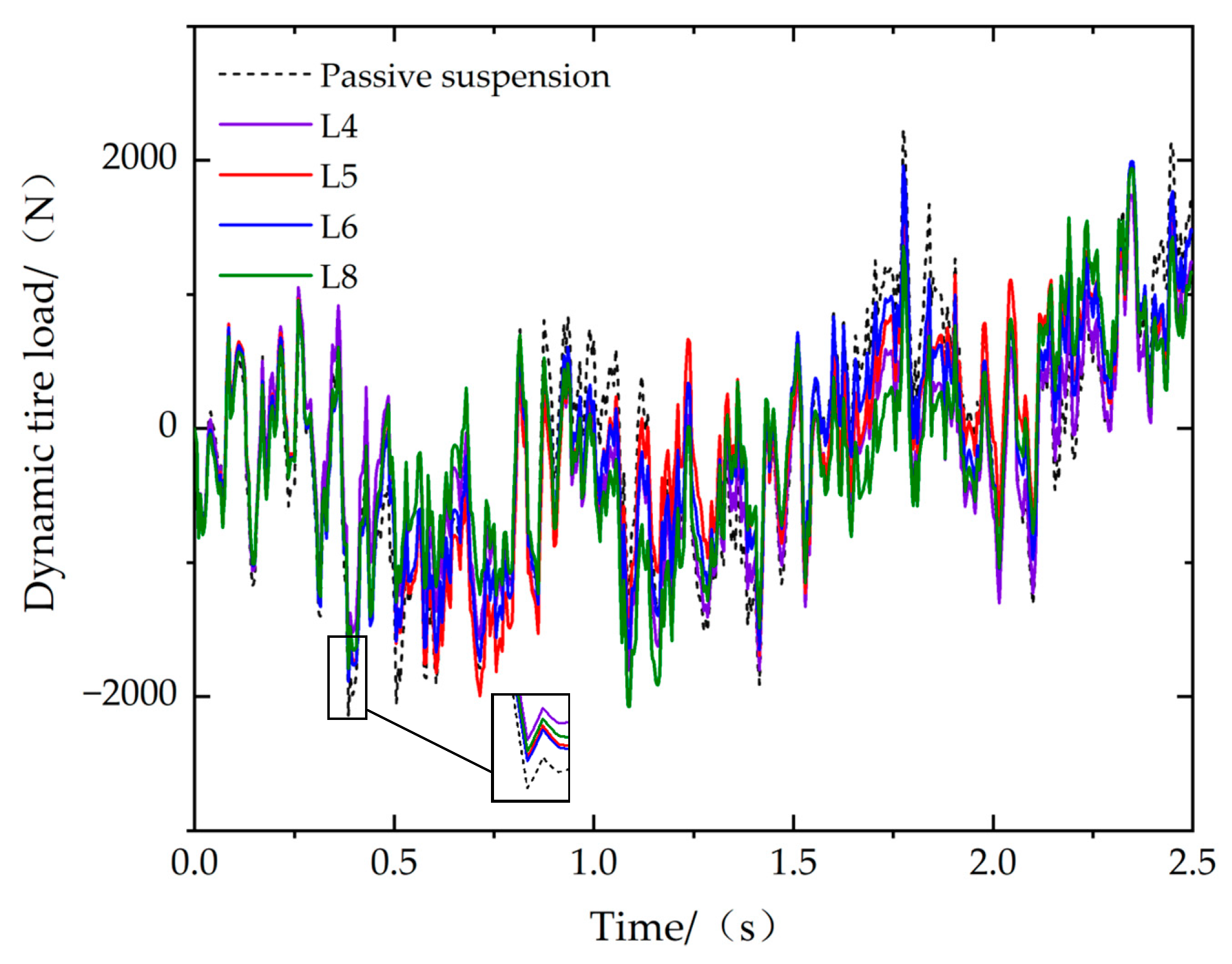
| RMS Value | L4 | Improvement | L5 | Improvement | L6 | Improvement | L8 | Improvement |
|---|---|---|---|---|---|---|---|---|
| Body acceleration/(m·s−2) | 0.6542 | 24.67% | 0.6089 | 29.88% | 0.6230 | 27.51% | 0.5604 | 35.47% |
| Roll angle acceleration/(rad·s−2) | 0.5972 | 12.61% | 0.6126 | 10.35% | 0.6107 | 10.64% | 0.5859 | 14.26% |
| Pitch angle acceleration/(rad·s−2) | 0.3951 | 19.12% | 0.3776 | 10.35% | 0.4077 | 16.54% | 0.4567 | 6.52% |
| Suspension working space/(m) | 0.0389 | 1.44% | 0.0383 | 2.78% | 0.0394 | 0.20% | 0.0368 | 6.92% |
| Dynamic tire load/(kN) | 0.7188 | 18.05% | 0.8033 | 8.42% | 0.7905 | 9.88% | 0.7465 | 14.90% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Shi, D.; Du, F.; Yang, X.; Zhu, K. Topological Optimization of Vehicle ISD Suspension under Steering Braking Condition. World Electr. Veh. J. 2023, 14, 297. https://doi.org/10.3390/wevj14100297
Liu Y, Shi D, Du F, Yang X, Zhu K. Topological Optimization of Vehicle ISD Suspension under Steering Braking Condition. World Electric Vehicle Journal. 2023; 14(10):297. https://doi.org/10.3390/wevj14100297
Chicago/Turabian StyleLiu, Yanling, Dongyin Shi, Fu Du, Xiaofeng Yang, and Kerong Zhu. 2023. "Topological Optimization of Vehicle ISD Suspension under Steering Braking Condition" World Electric Vehicle Journal 14, no. 10: 297. https://doi.org/10.3390/wevj14100297
APA StyleLiu, Y., Shi, D., Du, F., Yang, X., & Zhu, K. (2023). Topological Optimization of Vehicle ISD Suspension under Steering Braking Condition. World Electric Vehicle Journal, 14(10), 297. https://doi.org/10.3390/wevj14100297






