Robust Shared Control for Four-Wheel Steering Considering Driving Comfort and Vehicle Stability
Abstract
:1. Introduction
- To understand the driver’s continuous steering behavior, a driver model with adaptive preview distance is proposed. Meanwhile, to solve the model mismatch problem caused by vehicle parameter perturbation, the fuzzy shared driver-vehicle dynamics model is constructed for steering control.
- The shared steering control method for 4WS is proposed to suppress parametric uncertainties caused by time-varying driver characteristics, cornering stiffness, and vehicle speed. Moreover, constraints on the driver-vehicle system and actuators are considered by using the robust invariant set to enhance the safety of EVs.
2. Mathematical Model of 4WS Vehicle System
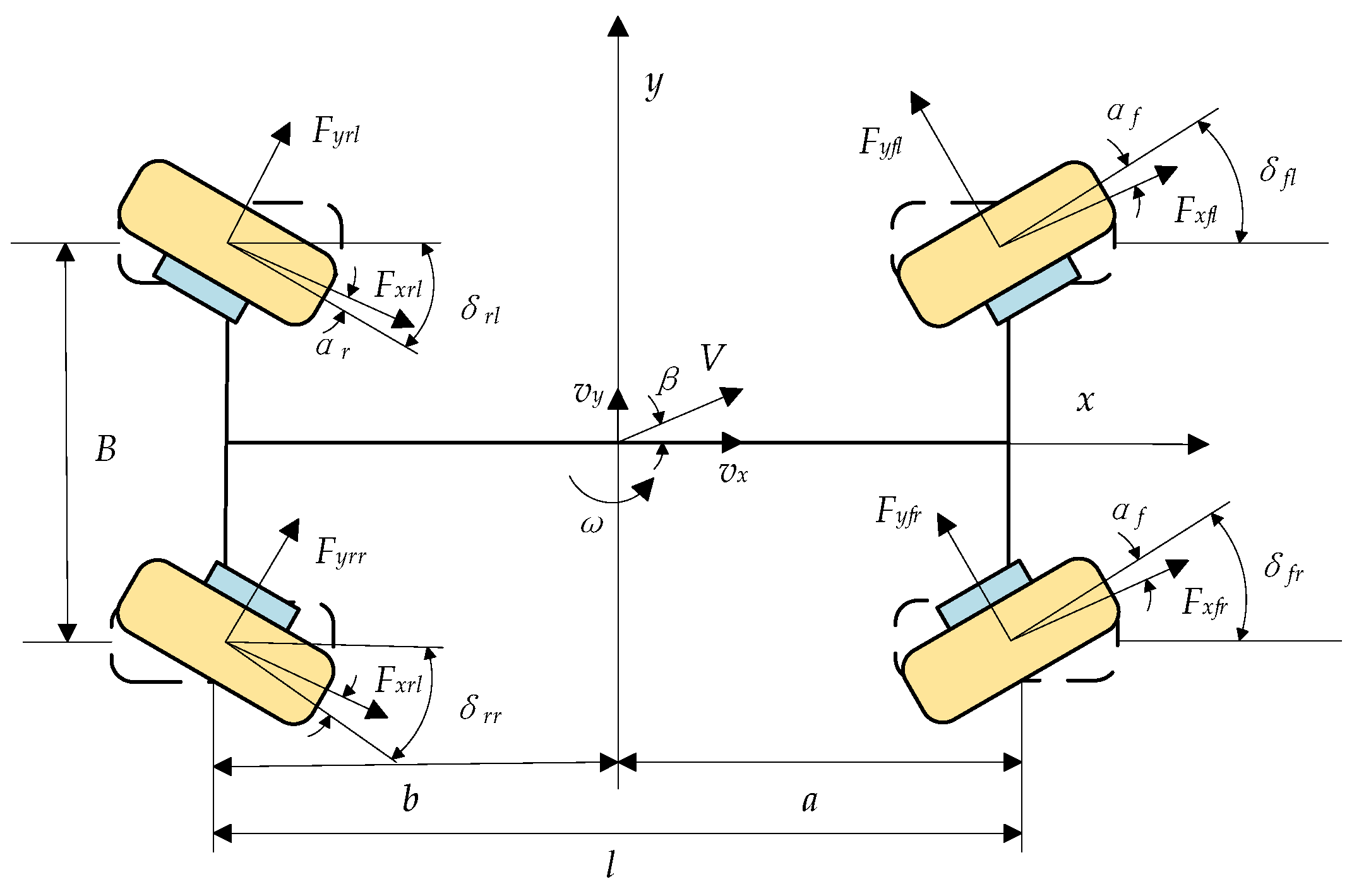
2.1. 4WS Vehicle Dynamics Model
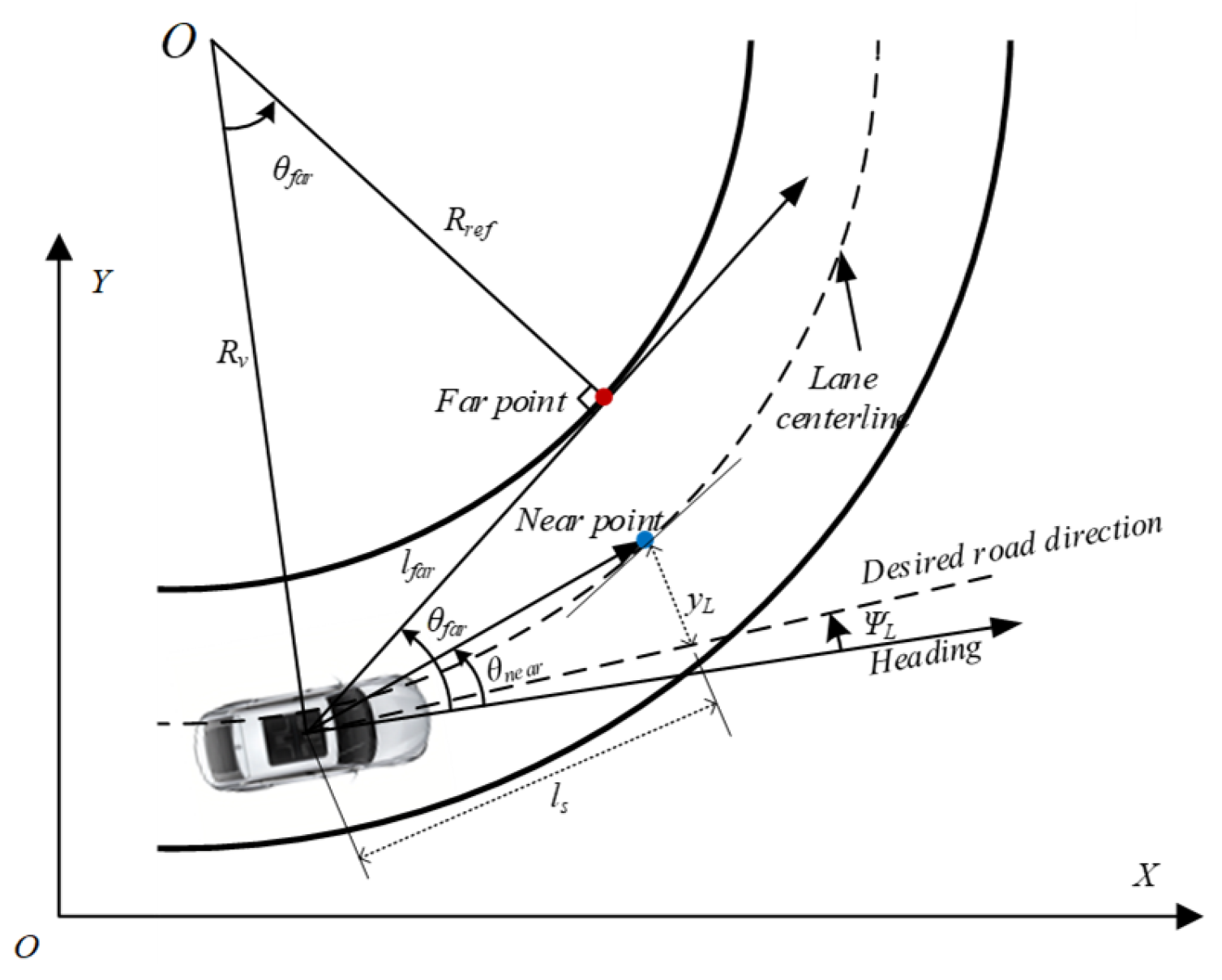
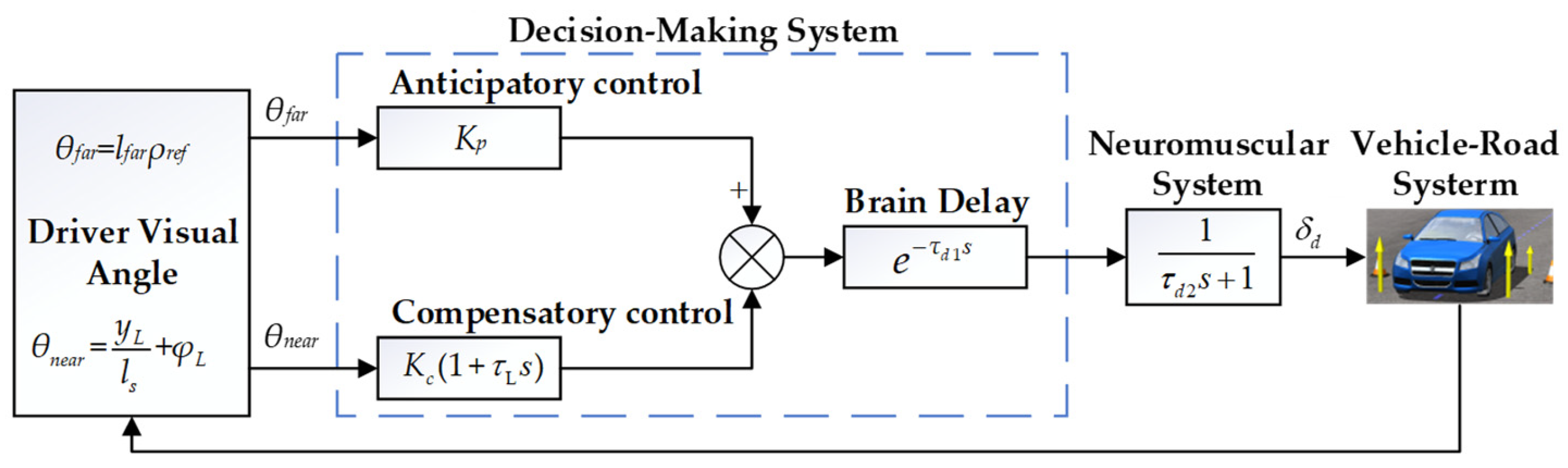
2.2. Driver Model
2.3. Driver-Vehicle Model
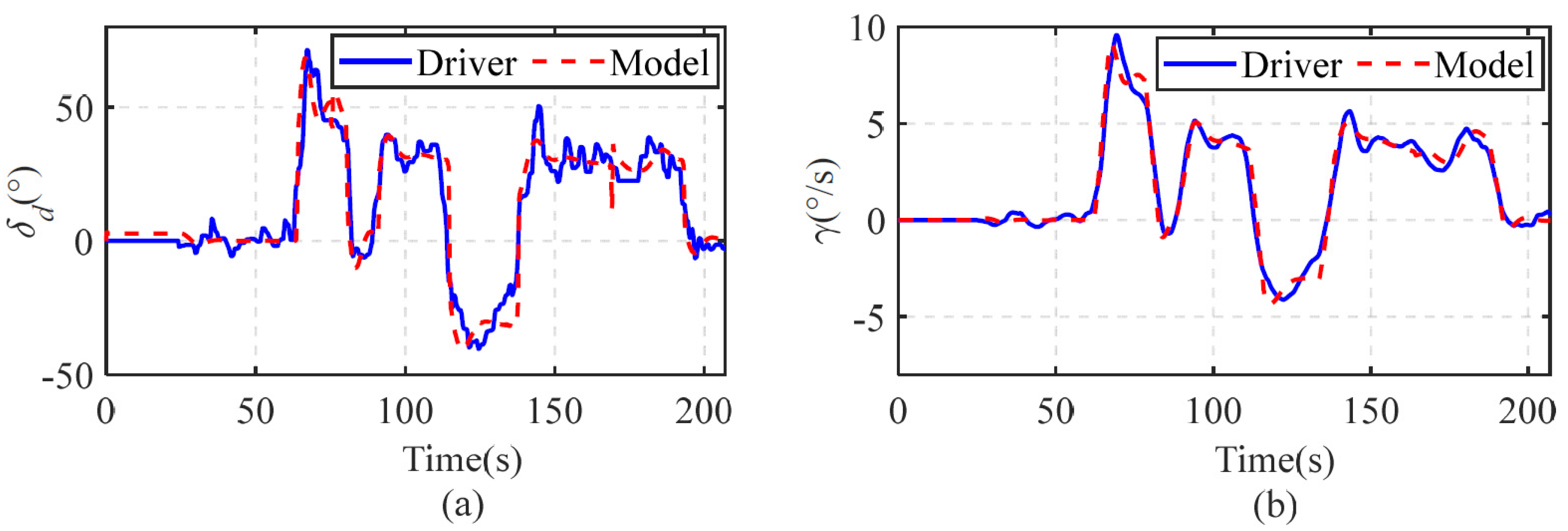
2.4. Validation of the Driver-Vehicle Model
3. Robust Shared Control Design for 4WS Vehicle
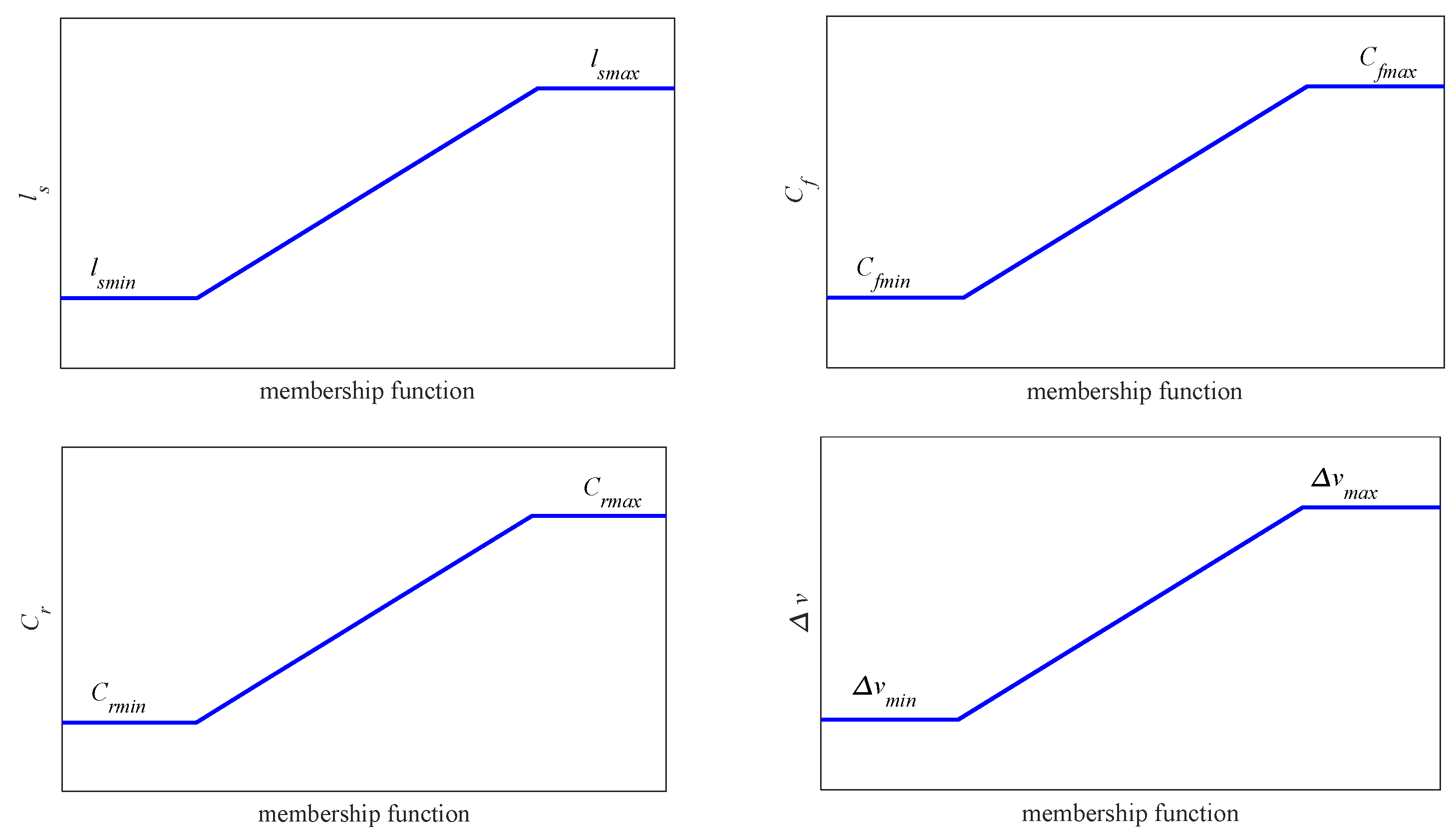
3.1. T-S Fuzzy Description of Parameter Uncertainty
- If ls is S, Cf is S, Cr is S, and vx is S, then lsmin, Cfmin, Crmin, and vxmin replace ls, Cf, Cr, and vx of A1, Bu1, and Bw1 in Equation (18);
- If ls is S, Cf is S, Cr is S, and vx is B, then lsmin, Cfmin, Crmin, and vxmax replace ls, Cf, Cr, and vx of A2, Bu2, and Bw2 in Equation (18);
- If ls is S, Cf is S, Cr is B, and vx is S, then lsmin, Cfmin, Crmax, and vxmin replace ls, Cf, Cr, and vx of A3, Bu3, and Bw3 in Equation (18);
- …
- If ls is B, Cf is B, Cr is B, and vx is S, then lsmax, Cfmax, Crmax, and vxmin replace ls, Cf, Cr, and vx of A15, Bu15, and Bw15 in Equation (18);
- If ls is B, Cf is B, Cr is B, and vx is B, then lsmax, Cfmax, Crmax, and vxmax replace ls, Cf, Cr, and vx of A16, Bu16, and Bw16 in Equation (18).
| Rule No. | Premise Variables | |||
|---|---|---|---|---|
| ls | Cf | Cr | vx | |
| 1 | S | S | S | S |
| 2 | S | S | S | B |
| 3 | S | S | B | S |
| 4 | S | S | B | B |
| … | … | … | … | … |
| 15 | B | B | B | S |
| 16 | B | B | B | B |
3.2. Robust Shared Controller Design for 4WS
3.3. Robust Positive Invariant Set Constraint Design
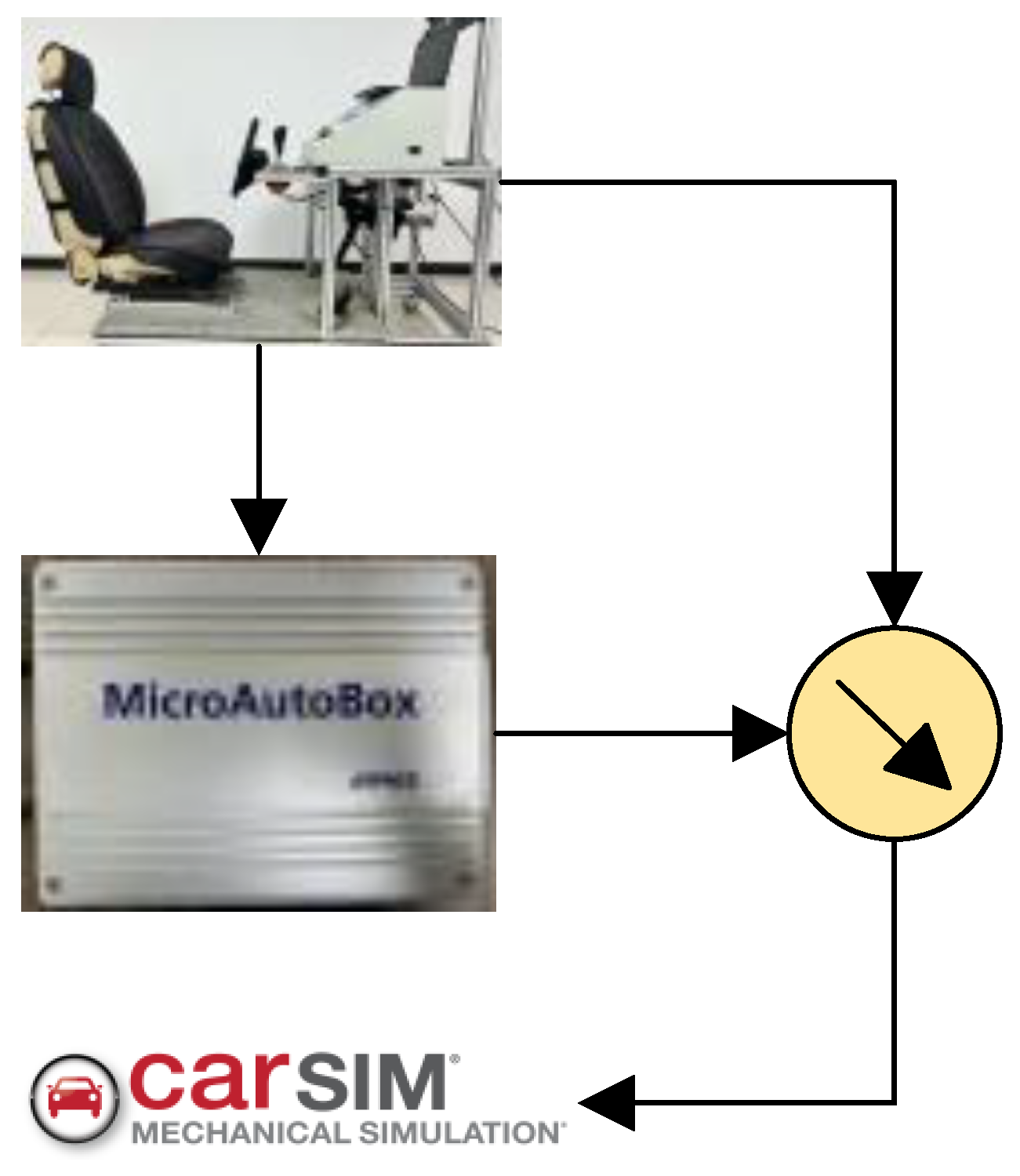
4. Driver-in-the-Loop Experiment
4.1. Experiment Settings
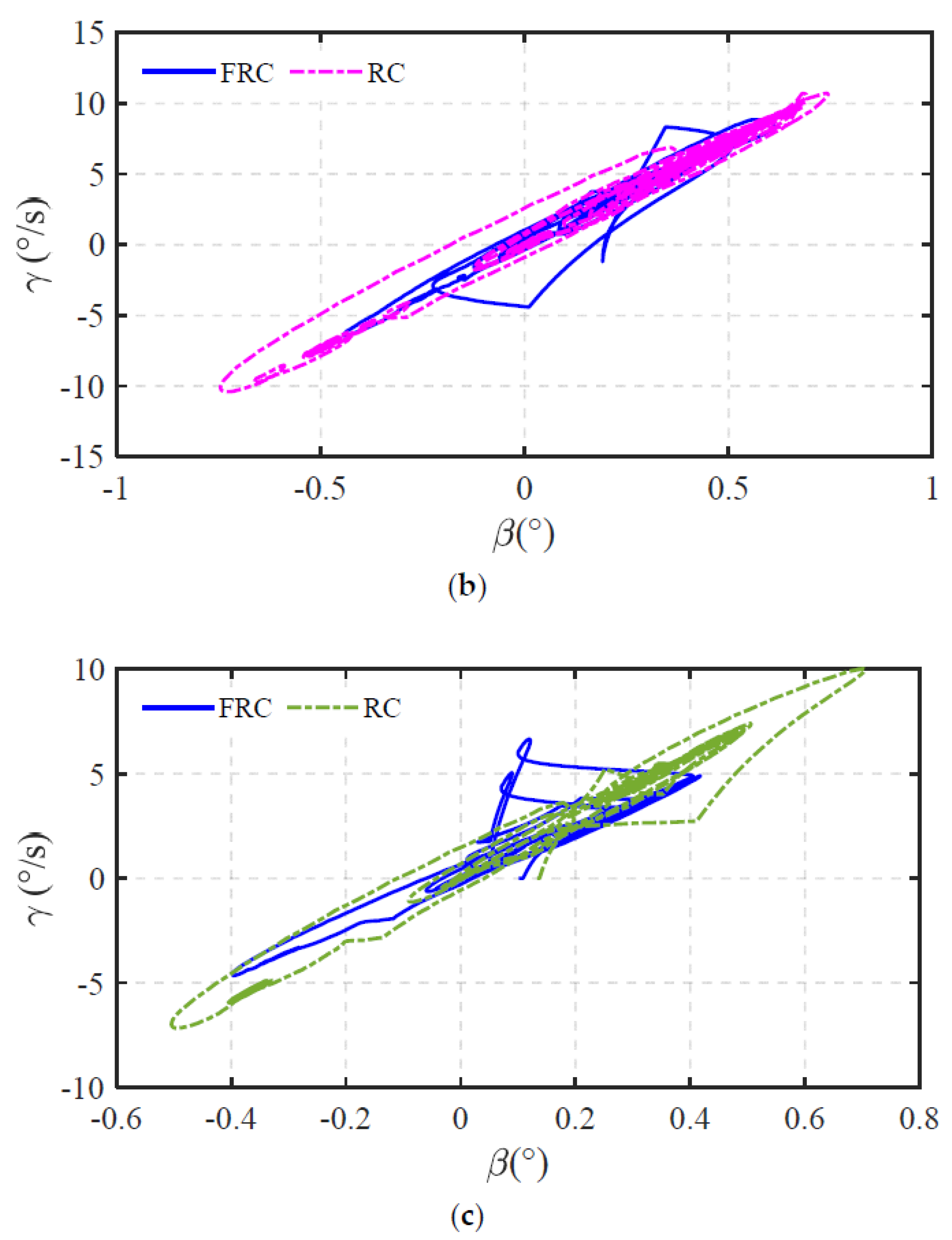
4.2. Performance Analysis of the Proposed Shared Controller
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| B | body width |
| l | wheelbase |
| δf | desired front wheel angle |
| δr | desired rear wheel angle |
| δi (i = fl, fr, rl, rr) | steering angles of each wheel |
| vx | longitudinal vehicle speed |
| vy | lateral vehicle speed |
| r | yaw rate |
| m | vehicle mass |
| Fyi (i = fl, fr, rl, rr) | tire lateral forces |
| CoG | center of gravity |
| lf | distance between CG and front axle |
| lr | distance between CG and rear axle |
| Iz | yaw moment of inertia of the vehicle |
| vehicle yaw moment of inertia | |
| Fxi (i = fl, fr, rl, rr) | tire longitudinal forces |
| front tire slip angle | |
| rear tire slip angle | |
| sideslip angle | |
| θnear | the near point from the near vision angle |
| θfar | the far point from the far vision angle |
| lfar | distance between the far point and CoG |
| ls | distance between the near point and CoG |
| yl | look-ahead lateral error |
| φL | heading error |
| ρref | road curvature of the reference trajectory |
| Kp | feedforward gain |
| Kc | feedback gain |
| τL | differential constant |
| Td | the driver’s total delay time |
| δfd | front wheel steering angle exerted by the driver model |
| Rg | steering ratio |
| measured output | |
| weighting matrix | |
| γ | the vehicle stability |
| z | performance output |
| variation of vx | |
| objective performance function | |
| weighting matrix | |
| ui | control law |
| Ki | state feedback gain of each fuzzy system |
| Lyapunov function | |
| ρ | positive scalar |
| w | system disturbance |
| Cf | Equivalent Cornering Stiffness of front tire |
| Cr | Equivalent Cornering Stiffness of rear tire |
Appendix A
| Driver No. | Age | Driving Years |
|---|---|---|
| 1 | 28 | 5 |
| 2 | 38 | 10 |
| 3 | 45 | 13 |
| 4 | 23 | 1 |
| 5 | 39 | 11 |
| 6 | 57 | 29 |
| 7 | 29 | 3 |
| 8 | 25 | 1 |
| 9 | 27 | 2 |
| 10 | 37 | 7 |
| 11 | 43 | 11 |
| 12 | 51 | 17 |
| 13 | 46 | 16 |
References
- Zhang, L.; Zhang, Z.; Wang, Z.; Deng, J.; Dorrell, D.G. Chassis Coordinated Control for Full X-by-Wire Vehicles-A Review. Chin. J. Mech. Eng. 2021, 34, 42. [Google Scholar] [CrossRef]
- Peng, H.; Chen, X. Active Safety Control of X-by-Wire Electric Vehicles: A Survey. SAE Int. J. Veh. Dyn. Stab. NVH 2022, 6, 115–133. [Google Scholar] [CrossRef]
- Hang, P.; Xia, X.; Chen, X. Handling Stability Advancement with 4WS and DYC Coordinated Control: A Gain-Scheduled Robust Control Approach. IEEE Trans. Veh. Technol. 2021, 70, 3164–3174. [Google Scholar] [CrossRef]
- Zhang, C.; Gao, G.; Zhao, C.; Li, L.; Li, C.; Chen, X. Research on 4WS Agricultural Machine Path Tracking Algorithm Based on Fuzzy Control Pure Tracking Model. Machines 2022, 10, 597. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, J.; Liang, J.; Yan, Y.; Pi, D.; Zhang, H.; Yin, G. Authority Allocation Strategy for Shared Steering Control Considering Human-Machine Mutual Trust Level. IEEE Trans. Intell. Veh. 2023. [Google Scholar] [CrossRef]
- Wang, J.; Fang, Z.; Dai, M.; Yin, G.; Xia, J.; Li, P. Robust steering assistance control for tracking large-curvature path considering uncertainties of driver’s steering behavior. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 2013–2028. [Google Scholar] [CrossRef]
- Qi, H.; Chen, Y.; Zhang, N.; Zhang, B.; Wang, D.; Tan, B. Improvement of both handling stability and ride comfort of a vehicle via coupled hydraulically interconnected suspension and electronic controlled air spring. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 552–571. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, J.; Wang, Z.; Liang, J.; Liu, Y.; Yin, G. A Human-Machine Shared Control Framework Considering Time-Varying Driver Characteristics. IEEE Trans. Intell. Veh. 2023, 8, 3826–3838. [Google Scholar] [CrossRef]
- Wu, J.; Kong, Q.; Yang, K.; Liu, Y.; Cao, D.; Li, Z. Research on the Steering Torque Control for Intelligent Vehicles Co-Driving with the Penalty Factor of Human–Machine Intervention. IEEE Trans. Syst. Man Cybern. Syst. 2022, 53, 59–70. [Google Scholar] [CrossRef]
- Lu, Y.; Liang, J.; Yin, G.; Xu, L.; Wu, J.; Feng, J.; Wang, F. A Shared Control Design for Steering Assistance System Considering Driver Behaviors. IEEE Trans. Intell. Veh. 2022, 8, 900–911. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, Y.; Guo, K.; Li, W. Driving style classification for vehicle-following with unlabeled naturalistic driving data. In Proceedings of the 2019 IEEE Vehicle Power and Propulsion Conference (VPPC), Hanoi, Vietnam, 14–17 October 2019; pp. 1–5. [Google Scholar]
- Wang, W.; Xi, J.; Chong, A.; Li, L. Driving Style Classification Using a Semisupervised Support Vector Machine. IEEE Trans. Hum.-Mach. Syst. 2017, 47, 650–660. [Google Scholar] [CrossRef]
- Deng, Z.; Chu, D.; Wu, C.; Liu, S.; Sun, C.; Liu, T.; Cao, D. A Probabilistic Model for Driving-Style-Recognition-Enabled Driver Steering Behaviors. IEEE Trans. Syst. Man Cybern. Syst. 2020, 52, 1838–1851. [Google Scholar] [CrossRef]
- Freuli, F.; De Cet, G.; Gastaldi, M.; Orsini, F.; Tagliabue, M.; Rossi, R.; Vidotto, G. Cross-cultural perspective of driving style in young adults: Psychometric evaluation through the analysis of the Multidimensional Driving Style Inventory. Transp. Res. Part F Traffic Psychol. Behav. 2020, 73, 425–432. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, J.; Li, P.; Xia, J. Modeling of driver’s steering behavior in large-curvature path following with back propagation neural network. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 6727–6732. [Google Scholar]
- Wang, J.; Zhang, G.; Wang, R.; Schnelle, S.C.; Wang, J. A Gain-Scheduling Driver Assistance Trajectory-Following Algorithm Considering Different Driver Steering Characteristics. IEEE Trans. Intell. Transp. Syst. 2016, 18, 1097–1108. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, H.; Ma, M.; Yu, M.; Yazdani, A.; Chen, L. Active Front Steering-Based Electronic Stability Control for Steer-by-Wire Vehicles via Terminal Sliding Mode and Extreme Learning Machine. IEEE Trans. Veh. Technol. 2020, 69, 14713–14726. [Google Scholar] [CrossRef]
- Benloucif, A.; Nguyen, A.-T.; Sentouh, C.; Popieul, J.-C. Cooperative Trajectory Planning for Haptic Shared Control Between Driver and Automation in Highway Driving. IEEE Trans. Ind. Electron. 2019, 66, 9846–9857. [Google Scholar] [CrossRef]
- Chang, X.-H.; Liu, Y.; Shen, M. Resilient Control Design for Lateral Motion Regulation of Intelligent Vehicle. IEEE/ASME Trans. Mechatron. 2019, 24, 2488–2497. [Google Scholar] [CrossRef]
- Cheng, S.; Li, L.; Liu, C.-Z.; Wu, X.; Fang, S.-N.; Yong, J.-W. Robust LMI-Based H-Infinite Controller Integrating AFS and DYC of Autonomous Vehicles with Parametric Uncertainties. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 6901–6910. [Google Scholar] [CrossRef]
- Goggia, T.; Sorniotti, A.; De Novellis, L.; Ferrara, A.; Gruber, P.; Theunissen, J.; Steenbeke, D.; Knauder, B.; Zehetner, J. Integral Sliding Mode for the Torque-Vectoring Control of Fully Electric Vehicles: Theoretical Design and Experimental Assessment. IEEE Trans. Veh. Technol. 2014, 64, 1701–1715. [Google Scholar] [CrossRef]
- Lu, Y.; Liang, J.; Wang, F.; Yin, G.; Pi, D.; Feng, J.; Liu, H. An Active Front Steering System Design Considering the CAN Network Delay. IEEE Trans. Transp. Electrif. 2023. [Google Scholar] [CrossRef]
- Pugi, L.; Favilli, T.; Berzi, L.; Locorotondo, E.; Pierini, M. Brake blending and torque vectoring of road electric vehicles: A flexible approach based on smart torque allocation. Int. J. Electr. Hybrid Veh. 2020, 12, 87–115. [Google Scholar] [CrossRef]
- Yin, G.-D.; Chen, N.; Wang, J.-X.; Chen, J.-S. Robust control for 4WS vehicles considering a varying tire-road friction coefficient. Int. J. Automot. Technol. 2010, 11, 33–40. [Google Scholar] [CrossRef]
- Yin, G.; Wang, R.; Wang, J. Robust control for four wheel independently-actuated electric ground vehicles by external yaw-moment generation. Int. J. Automot. Technol. 2015, 16, 839–847. [Google Scholar] [CrossRef]
- Jin, X.J.; Yin, G.; Chen, N. Gain-scheduled robust control for lateral stability of four-wheel-independent-drive electric vehicles via linear parameter-varying technique. Mechatronics 2015, 30, 286–296. [Google Scholar] [CrossRef]
- Jin, X.; Yin, G.; Bian, C.; Chen, J.; Li, P.; Chen, N. Gain-Scheduled Vehicle Handling Stability Control via Integration of Active Front Steering and Suspension Systems. J. Dyn. Syst. Meas. Control 2016, 138, 014501. [Google Scholar] [CrossRef]
- Xu, F.-X.; Liu, X.-H.; Chen, W.; Zhou, C.; Cao, B.-W. Improving handling stability performance of four-wheel steering vehicle based on the H2/H∞ robust control. Appl. Sci. 2019, 9, 857. [Google Scholar] [CrossRef]
- Qiao, Y.; Chen, X.; Liu, Z. Trajectory Tracking Coordinated Control of 4WID-4WIS Electric Vehicle Considering Energy Consumption Economy Based on Pose Sensors. Sensors 2023, 23, 5496. [Google Scholar] [CrossRef] [PubMed]
- Zhu, T.; Jin, X.; Yin, G.; Liang, J.; Ren, Z.; Shi, Y. Coordinated control for active 4WS vehicle based on linear quadratic differential game. In Proceedings of the 2019 Chinese Control And Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 5478–5482. [Google Scholar]
- Zhang, Y.; Wang, Z.; Wang, Y.; Zhang, C.; Zhao, B. Research on automobile four-wheel steering control system based on yaw angular velocity and centroid cornering angle. Meas. Control 2022, 55, 49–61. [Google Scholar] [CrossRef]
- Liang, J.; Feng, J.; Fang, Z.; Lu, Y.; Yin, G.; Mao, X.; Wu, J.; Wang, F. An Energy-Oriented Torque-Vector Control Framework for Distributed Drive Electric Vehicles. IEEE Trans. Transp. Electrif. 2023, 9, 4014–4031. [Google Scholar] [CrossRef]
- Liu, H.; Nonami, K.; Hagiwara, T. Active following fuzzy output feedback sliding mode control of real-vehicle semi-active suspensions. J. Sound Vib. 2008, 314, 39–52. [Google Scholar] [CrossRef]
- Cabello, F.; Acuna, A.; Vallejos, P.; Orchard, M.E.; del Solar, J.R. Design and validation of a fuzzy longitudinal controller based on a vehicle dynamic simulator. In Proceedings of the 2011 9th IEEE International Conference on Control and Automation (ICCA), Santiago, Chile, 19–21 December 2011; pp. 997–1002. [Google Scholar] [CrossRef]
- Pugi, L.; Grasso, F.; Pratesi, M.; Cipriani, M.; Bartolomei, A. Design and preliminary performance evaluation of a four wheeled vehicle with degraded adhesion conditions. Int. J. Electr. Hybrid Veh. 2017, 9, 1–32. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, C.; Wang, J. Impaired Driver Assistance Control with Gain-Scheduling Composite Nonlinear Feedback for Vehicle Trajectory Tracking. J. Dyn. Syst. Meas. Control 2020, 142, 071003. [Google Scholar] [CrossRef]
- Nguyen, A.-T.; Sentouh, C.; Popieul, J.-C. Driver-Automation Cooperative Approach for Shared Steering Control Under Multiple System Constraints: Design and Experiments. IEEE Trans. Ind. Electron. 2016, 64, 3819–3830. [Google Scholar] [CrossRef]
- Sentouh, C.; Nguyen, A.-T.; Benloucif, M.A.; Popieul, J.-C. Driver-Automation Cooperation Oriented Approach for Shared Control of Lane Keeping Assist Systems. IEEE Trans. Control Syst. Technol. 2018, 27, 1962–1978. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, J. Vehicle Lateral Dynamics Control through AFS/DYC and Robust Gain-Scheduling Approach. IEEE Trans. Veh. Technol. 2015, 65, 489–494. [Google Scholar] [CrossRef]
- Hu, C.; Chen, Y.; Wang, J. Fuzzy Observer-Based Transitional Path-Tracking Control for Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 22, 3078–3088. [Google Scholar] [CrossRef]
- Tanaka, K.; Wang, H.O. Fuzzy Control Systems Design and Analysis; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2001. [Google Scholar]







| Symbol | Meaning | Value |
|---|---|---|
| m | Vehicle total mass | 1705 kg |
| Mz | Vehicle yaw moment of inertia | 3048 kg·m2 |
| lf | Distance between CG and front axle | 1.035 m |
| lr | Distance between CG and rear axle | 1.665 m |
| Cf | Equivalent Cornering Stiffness of front tire | 103,130 N/rad |
| Cr | Equivalent Cornering Stiffness of rear tire | 73,854 N/rad |
| Parameter | KP | Kc | τL | Td | Driving Style |
|---|---|---|---|---|---|
| Driver I | 2.70 | 1.50 | 0.18 | 0.18 | Experienced |
| Driver II | 3.60 | 2.50 | 0.18 | 0.18 | Aggressive |
| Driver III | 1.90 | 1.10 | 0.19 | 0.19 | Conservative |
| Driver Type | Controller Type | J1 | J2 | J3 | J4 |
|---|---|---|---|---|---|
| Driver I | FRC | 7.5 | 1.2 | 5.2 | 2.0 |
| RC | −6.3 | 6 | 6.8 | 2.5 | |
| MPC | −3 | 8 | 7.0 | 2.2 | |
| Driver II | FRC | −5.3 | 4.1 | 7.5 | 2.4 |
| RC | −40 | 40 | 8.4 | 3.2 | |
| MPC | −36 | 42 | 8.6 | 2.7 | |
| Driver III | FRC | 5.5 | 1.8 | 4.4 | 2.1 |
| RC | 4.2 | 3.2 | 5.6 | 2.3 | |
| MPC | 5.1 | 5 | 5.8 | 2.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Liu, H.; Dang, M. Robust Shared Control for Four-Wheel Steering Considering Driving Comfort and Vehicle Stability. World Electr. Veh. J. 2023, 14, 283. https://doi.org/10.3390/wevj14100283
Zhang C, Liu H, Dang M. Robust Shared Control for Four-Wheel Steering Considering Driving Comfort and Vehicle Stability. World Electric Vehicle Journal. 2023; 14(10):283. https://doi.org/10.3390/wevj14100283
Chicago/Turabian StyleZhang, Chuanwei, Haoxin Liu, and Meng Dang. 2023. "Robust Shared Control for Four-Wheel Steering Considering Driving Comfort and Vehicle Stability" World Electric Vehicle Journal 14, no. 10: 283. https://doi.org/10.3390/wevj14100283
APA StyleZhang, C., Liu, H., & Dang, M. (2023). Robust Shared Control for Four-Wheel Steering Considering Driving Comfort and Vehicle Stability. World Electric Vehicle Journal, 14(10), 283. https://doi.org/10.3390/wevj14100283





