Research on Parameter Optimization Design Method for Dual-Motor Coupled Drive System
Abstract
:1. Introduction
2. Materials and Methods
2.1. Configuration of DMCDS
2.2. Modeling and Mode Analysis
2.2.1. Dynamics Modeling of DMCDS
2.2.2. Driving Mode Analysis
2.3. Parameter Optimization of DMCDS
2.3.1. Mathematical Models
- (1)
- Vehicle model
- (2)
- Motor model
- (3)
- Battery model
- (4)
- Efficiency model
2.3.2. Optimization Problem
- (5)
- Inner-layer optimization
- (6)
- Outer-layer component parameter optimization
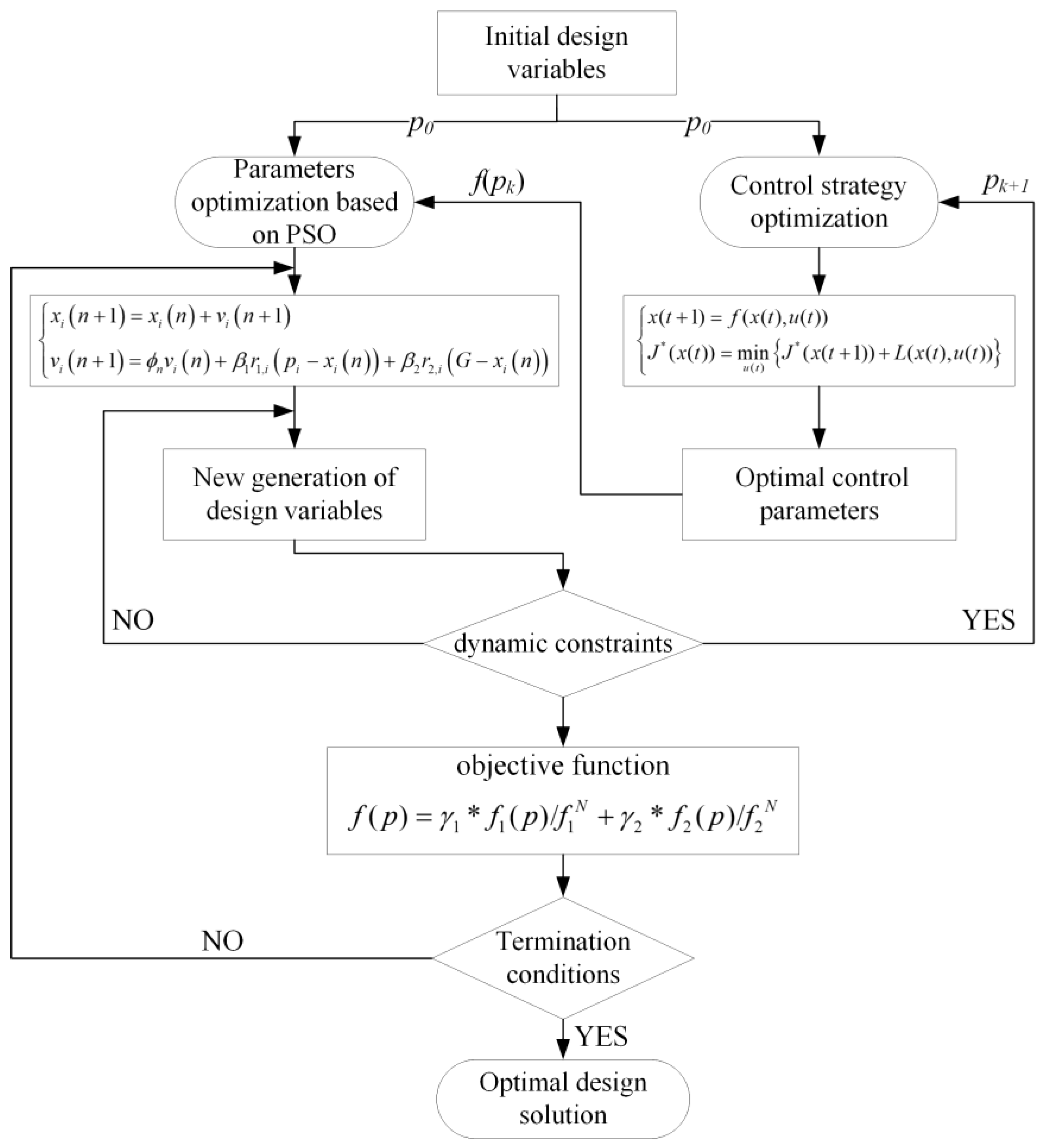
2.3.3. Optimization Process
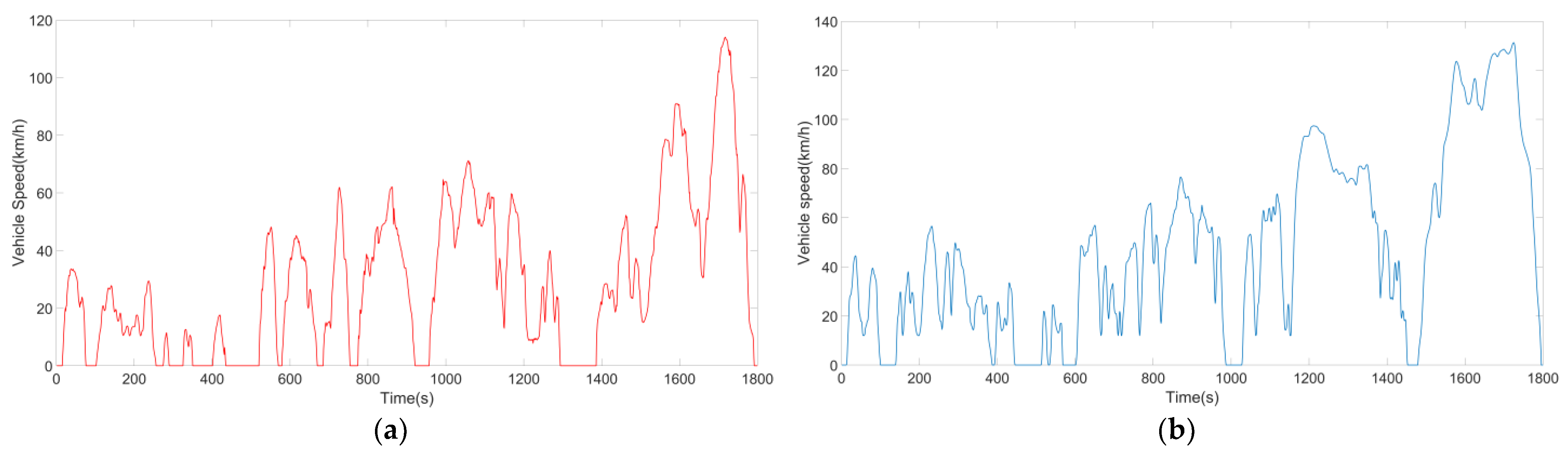
3. Results and Discussion
4. Conclusions
- (1)
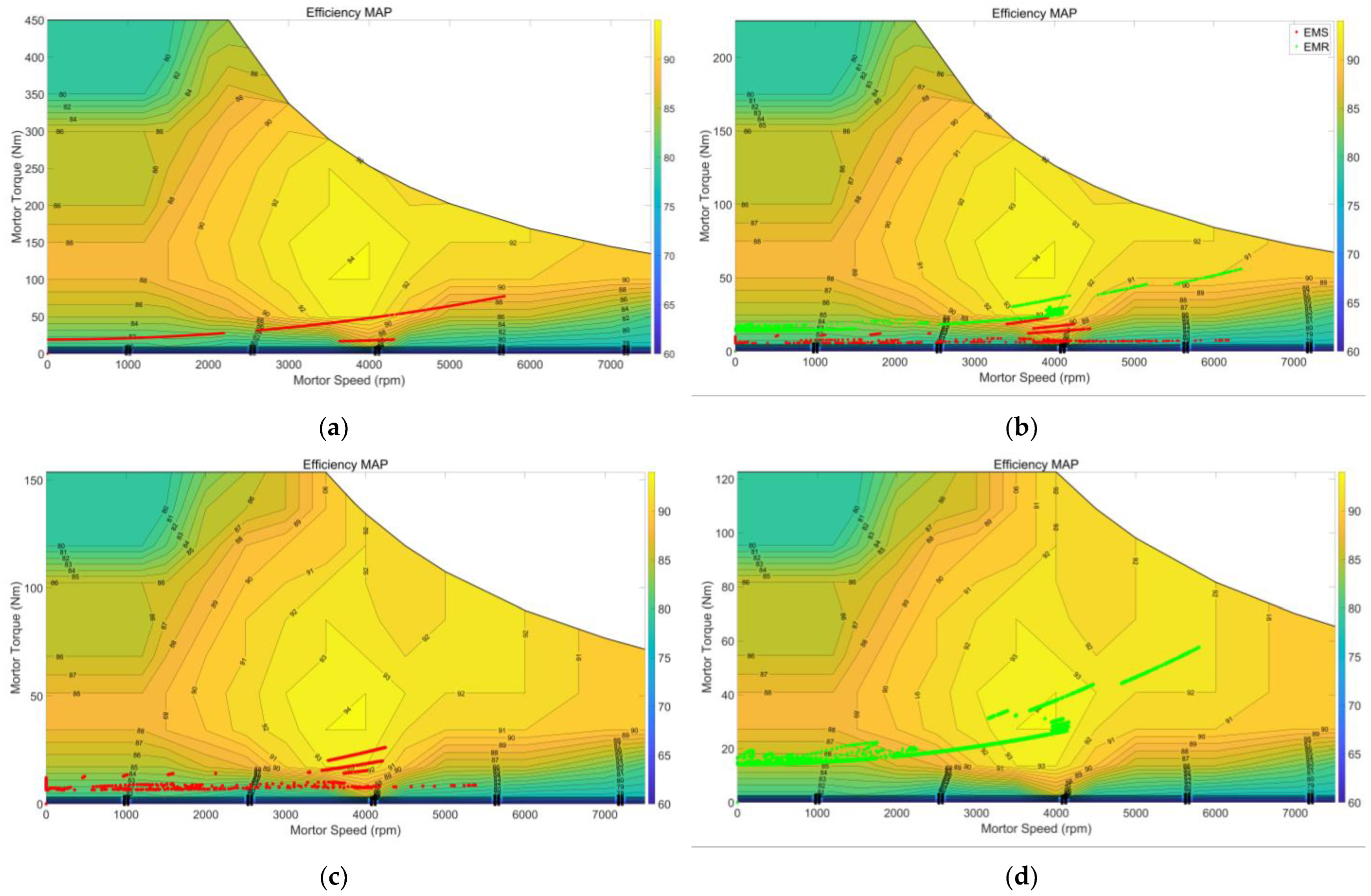
- The selection of motor parameters and gear ratios exerts a substantial influence on the power losses and drive efficiency of the system. While keeping the system maximum output power unchanged, adjustments to the rated power, rated speed, and gear ratios can enhance the utilization efficiency of the high-efficiency region and effectively reduce electrical energy consumption.
- (2)
- The optimized motors exhibit an increase in rated speed and a decrease in peak torque, resulting in a substantial improvement in the utilization efficiency of the high-efficiency region. Compared to the prototype scheme, motors EM_R and EM_S experience an increase of 45% and 48%, respectively. Moreover, the optimized DMCDS achieves an average drive efficiency 2.5% and 4.2% higher than that of DMCDS-pro and SMDS, respectively, leading to DMCDS-opt possessing the lowest energy consumption of 16.95 kWh/100 km.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Smith, W.J. Can EV (electric vehicles) address Ireland’s CO2 emissions from transport? Energy 2010, 35, 4514–4521. [Google Scholar] [CrossRef]
- Nunes, P.; Farias, T.; Brito, M.C. Enabling solar electricity with electric vehicles smart charging. Energy 2015, 87, 10–20. [Google Scholar] [CrossRef]
- Chopra, S.; Bauer, P. Driving range extension of EV with on-road contactless power transfer—A case study. IEEE Trans. Indust. Electron. 2013, 60, 329–338. [Google Scholar] [CrossRef]
- Li, Z.; Khajepour, A.; Song, J. A comprehensive review of the key technologies for pure electric vehicles. Energy 2019, 182, 824–839. [Google Scholar] [CrossRef]
- Walker, P.D. Modelling, Simulations, and Optimisation of Electric Vehicles for Analysis of Transmission Ratio Selection. Adv. Mech. Eng. 2013, 5, 1–13. [Google Scholar] [CrossRef]
- Kamachi, M.; Miyamoto, H.; Sano, Y. Development of power management system for electric vehicle ‘i-MiEV’. In Proceedings of the 2010 International Power Electronics Conference, Sapporo, Japan, 21–24 June 2010; pp. 2949–2955. [Google Scholar] [CrossRef]
- de Santiago, J. Electrical Motor Drivelines in Commercial All-Electric Vehicles: A Review. IEEE Trans. Veh. Technol. 2012, 61, 475–484. [Google Scholar] [CrossRef]
- Wu, J.; Liang, J.; Ruan, J.; Zhang, N.; Walker, P.D. Efficiency comparison of electric vehicles powertrains with dual motor and single motor input. Mech. Mach. Theory 2018, 128, 569–585. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, S.; Han, G.; Liu, H. Power Management Comparison for a Dual-Motor-Propulsion System Used in a Battery Electric Bus. IEEE Trans. Ind. Electron. 2017, 64, 3873–3882. [Google Scholar] [CrossRef]
- Hu, J.; Zu, G.; Jia, M.; Niu, X. Parameter matching and optimal energy management for a novel dual-motor multi-modes powertrain system. Mech. Syst. Signal Process. 2019, 116, 113–128. [Google Scholar] [CrossRef]
- Tseng, S.; Tseng, C.; Liu, T.; Chen, J. Wide-range adjustable speed control method for dual-motor drive system. IET Electr. Power Appl. 2015, 9, 107–116. [Google Scholar] [CrossRef]
- Holdstock, T.; Sorniotti, A.; Everitt, M.; Bertolotto, S. Energy consumption analysis of a novel four-speed dual motor drivetrain for electric vehicles. In Proceedings of the 2012 IEEE Vehicle Power and Propulsion Conference 2012, Seoul, Republic of Korea, 9–12 October 2012; pp. 295–300. [Google Scholar] [CrossRef]
- Xu, L.; Ouyang, M.; Li, J.; Yang, F.; Lu, L.; Hua, J. Optimal sizing of plug-in fuel cell electric vehicles using models of vehicle performance and system cost. Appl. Energy 2013, 103, 477–487. [Google Scholar] [CrossRef]
- Vagg, C.; Akehurst, S.; Brace, C.J. Stochastic dynamic programming in the real-world control of hybrid electric vehicles. IEEE Trans. Control Syst. Technol. 2016, 24, 853–866. [Google Scholar] [CrossRef]
- Kim, N.; Cha, S.W.; Peng, H. Optimal equivalent fuel consumption for hybrid electric vehicles. IEEE Trans. Control Syst. Technol. 2012, 20, 817–825. [Google Scholar] [CrossRef]
- Scordia, J.; Desbois-Renaudin, M.; Trigui, R.; Jeanneret, B.; Badin, F. Global optimisation of energy management laws in hybrid vehicles using dynamic programming. Int. J. Veh. Des. 2005, 39, 349–367. [Google Scholar] [CrossRef]
- Sundström, O.; Ambühl, D.; Guzzella, L. On implementation of dynamic programming for optimal control problems with final state constraints. Oil Gas. Sci. Technol. Rev. Inst. Fr. Pétrole 2010, 65, 91–102. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, C.H.; Cui, N.X. PSO algorithm-based parameter optimization for HEV powertrain and its control strategy. Int. J. Automot. Technol. 2008, 9, 53–59. [Google Scholar] [CrossRef]
- Ebbesen, S.; Dönitz, C.; Guzzella, L. Particle swarm optimisation for hybrid electric drive-train sizing. Int. J. Veh. Des. 2012, 58, 181–199. [Google Scholar] [CrossRef]
- Zeng, X.H.; Wang, Z.W.; Song, D.F. Parameter Optimization of Dual-mode Power-split Hybrid Electric Bus Based on MIGA Algorithm. J. Mech. Eng. 2020, 56, 98–105. [Google Scholar] [CrossRef]
- Nuesch, T.; Ott, T.; Ebbesen, S.; Guzzella, L. Cost and fuel-optimal selection of HEV topologies using particle swarm optimization and dynamic programming. In Proceedings of the 2012 American Control Conference, Montréal, QC, Canada, 27–29 June 2012. [Google Scholar] [CrossRef]
- Bonnans, J.F.; Guilbaud, T.; Ketfi-Cherif, A. Parametric Optimization of Hybrid Car Engines. Optim. Eng. 2004, 5, 395–415. [Google Scholar] [CrossRef]
- Wen, C.; Zhang, S.; Xie, B.; Song, Z.; Li, T.; Jia, F.; Han, J. Design and verification innovative approach of dual-motor power coupling drive systems for electric tractors. Energy 2022, 247, 1–22. [Google Scholar] [CrossRef]
- Bayrak, A.E.; Kang, N.; Papalambros, P.Y. Decomposition-based design optimization of hybrid electric powertrain architectures: Simultaneous configuration and sizing design. J. Mech. Des. 2016, 138, 071405. [Google Scholar] [CrossRef]
- Landolfi, E.; Minervini, F.J.; Minervini, N.; De Bellis, V.; Malfi, E.; Natale, C. Integration of a Model Predictive Control with a Fast Energy Management Strategy for a Hybrid Powertrain of a Connected and Automated Vehicle. World Electr. Veh. J. 2021, 12, 159. [Google Scholar] [CrossRef]
- Coppola, A.; De Tommasi, G.; Motta, C.; Petrillo, A.; Santini, S. Double-layer control architecture for motion and torque optimisation of autonomous electric vehicles. Transp. Res. Interdiscip. Perspect. 2023, 21, 1–15. [Google Scholar] [CrossRef]
- Fathy, H.K.; Reyer, J.A.; Papalambros, P.Y.; Ulsoy, A.G. On the coupling between the plant and controller optimization problems. In Proceedings of the American Control Conference 2001, Arlington, VA, USA, 25–27 June 2001; pp. 1864–1869. [Google Scholar] [CrossRef]
- Fang, L.C.; Qin, S.Y.; Xu, G. Simultaneous optimization for hybrid electric vehicle parameters based on multi-objective Genetic Algorithms. Energies 2011, 4, 532–544. [Google Scholar] [CrossRef]
- Zhuang, W. Optimal Design and Mode Shift Control of Multi-mode Hybrid Electric Vehicles. Ph.D. Thesis, Nanjing University of Science & Technology, Nanjing, China, 2017. [Google Scholar]
- Nguyen, C.T.; Walker, P.D.; Zhou, S.; Zhang, N. Optimal sizing and energy management of an electric vehicle powertrain equipped with two motors and multi-gear ratios. Mech. Mach. Theory 2022, 167, 104513. [Google Scholar] [CrossRef]
- Pennestrì, E.; Mariti, L.; Valentini, P.; Mucino, V. Efficiency evaluation of gearboxes for parallel hybrid vehicles: Theory and applications. Mech. Mach. Theory 2012, 49, 157–176. [Google Scholar] [CrossRef]
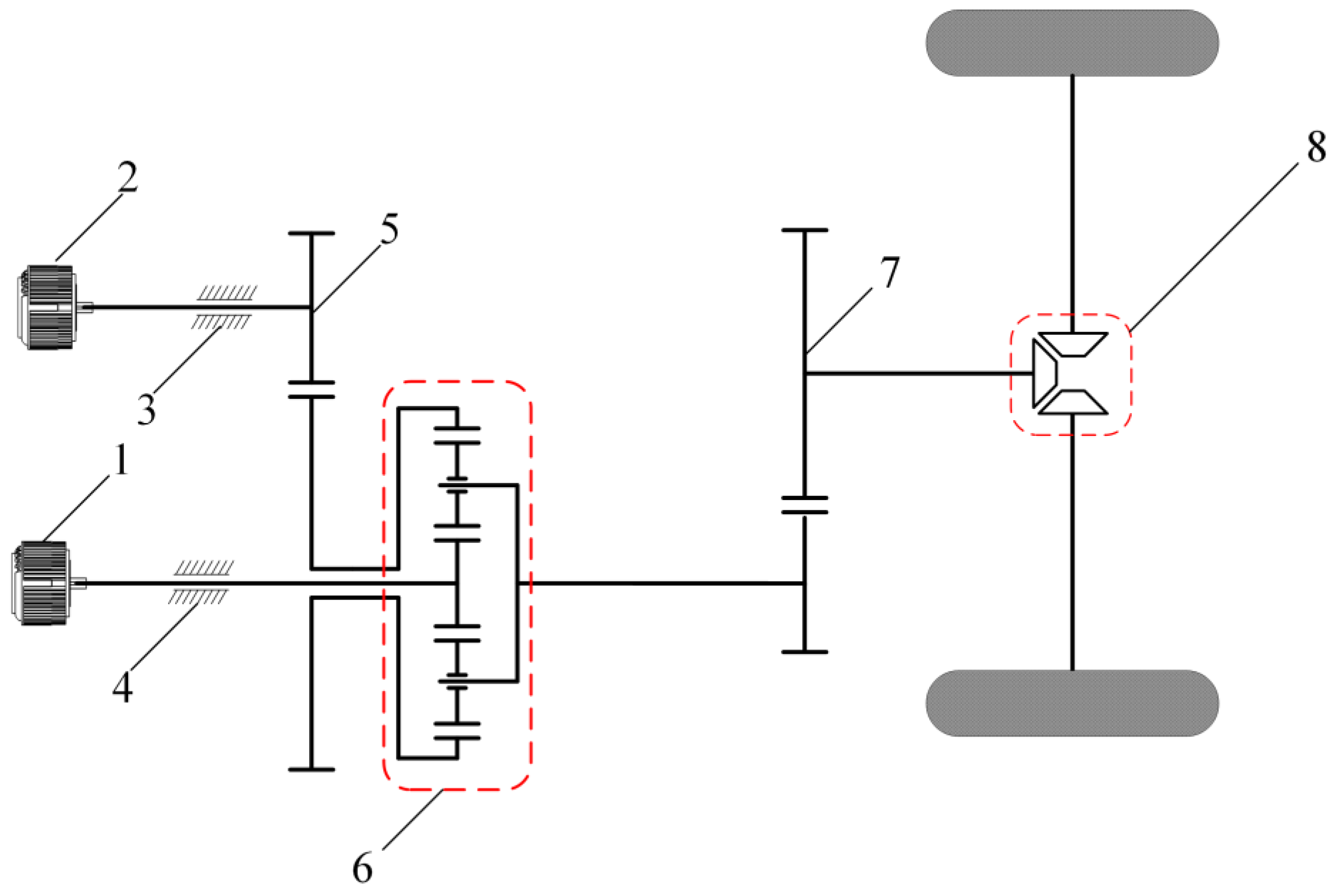
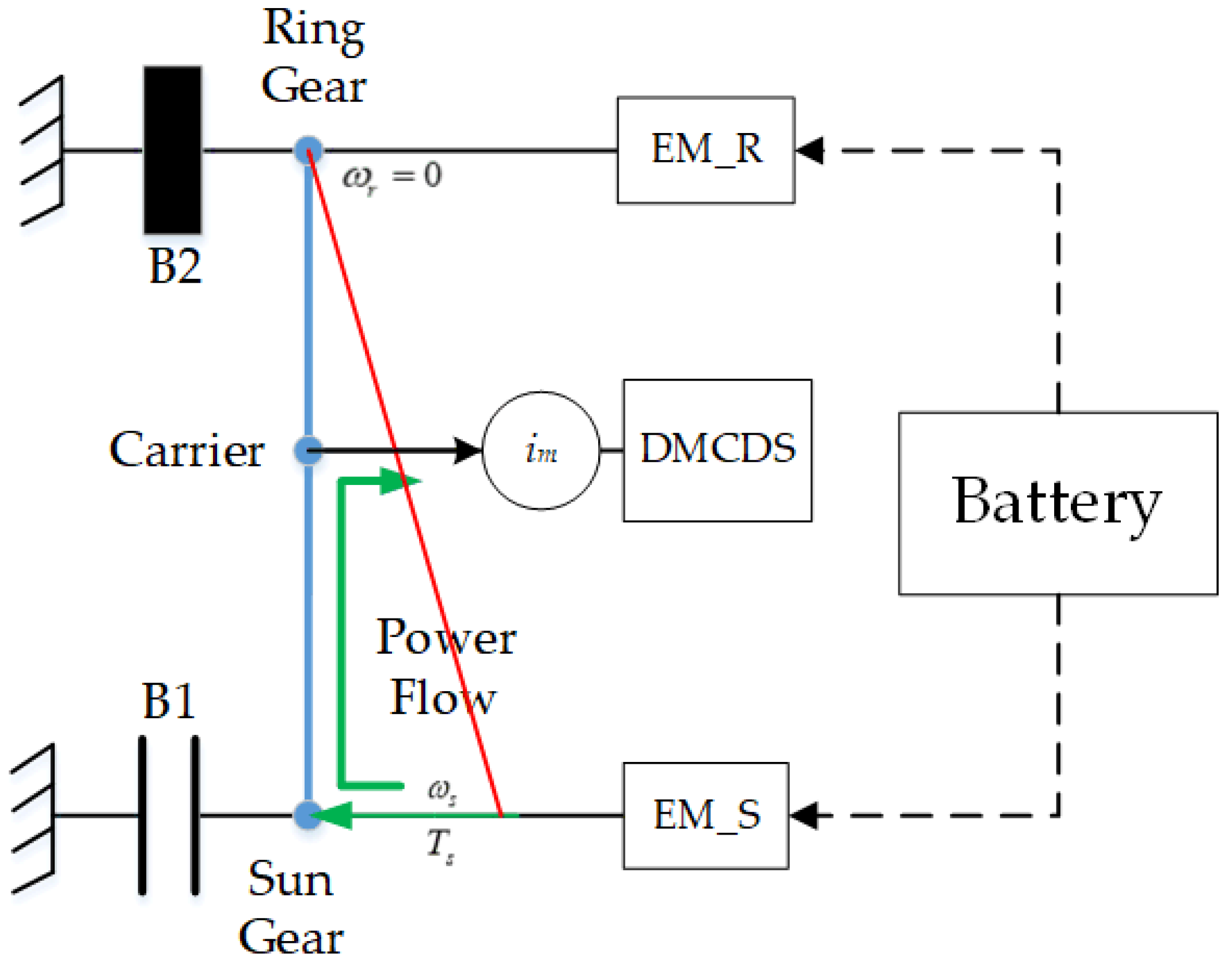

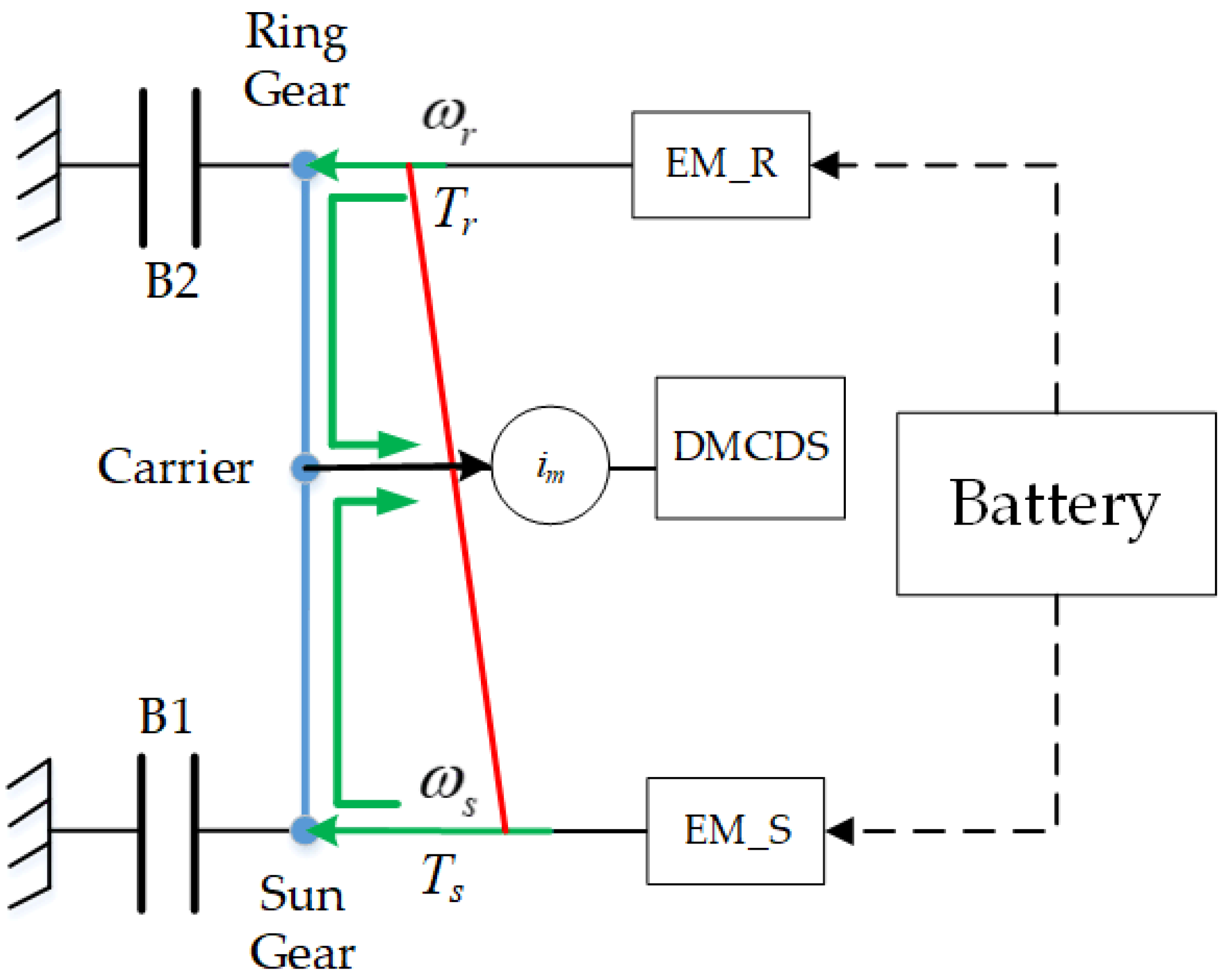


| Working States | Driving Modes | M1 | M2 | B1 | B2 |
|---|---|---|---|---|---|
| Park/Neutral | N/P | ○ | ○ | ○ | ○ |
| Driving states | M1S | ● | ○ | ○ | ● |
| M1R | ○ | ● | ● | ○ | |
| DMC | ● | ● | ○ | ○ |
| Parameter | Meaning | Value |
|---|---|---|
| ms (kg) | Mass of vehicle | 1949 |
| Af (m2) | Frontal area | 2.66 |
| CD | Air resistance coefficient | 0.4 |
| fr | Tire rolling friction coefficient | 0.015 |
| rw (m) | Tire radius | 0.343 |
| vmax (km/h) | Maximum velocity | 150 |
| tacc (s) | 0–100 km/h acceleration time | 9 |
| Parameter | Lower Limit | Upper Limit |
|---|---|---|
| Rated power of EM_S (kW) | 30 | 60 |
| Rated speed of EM_S (r/min) | 2500 | 4000 |
| Rated power of EM_R (kW) | 30 | 60 |
| Rated speed of EM_R (r/min) | 2500 | 4000 |
| Planetary gear ratio | 1.5 | 4 |
| Final drive ratio | 4 | 6.5 |
| Optimization Parameter | Optimized Parameter Value | Prototype Parameter Value |
|---|---|---|
| Rated power of EM_S (kW) | 33.5 | 32 |
| Rated speed of EM_S (r/min) | 3500 | 2250 |
| Rated power of EM_R (kW) | 31.5 | 32 |
| Rated speed of EM_R (r/min) | 4000 | 2250 |
| Planetary gear ratio | 2.26 | 1.86 |
| Final drive ratio | 5.15 | 4.93 |
| Parameter | Value |
|---|---|
| Rated power of motor (kW) | 64 |
| Peak power of motor (kW) | 106 |
| Rated speed of motor (r/min) | 2250 |
| First gear ratio | 3.27 |
| Second gear ratio | 1.98 |
| Final drive ratio | 2.826 |
| Schemes | SMDS | DMCDS-pro | DMCDS-opt | |
|---|---|---|---|---|
| Indicator | ||||
| High-efficiency region utilization (efficiency > 90%) | 6.6% | EM_R 30.2% | EM_R 43.8% | |
| EM_S 8.6% | EM_S 12.8% | |||
| Electricity consumption (kWh/100 km) | 18.18 | 17.58 | 16.95 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Zhang, N.; Gao, X.; Pang, D. Research on Parameter Optimization Design Method for Dual-Motor Coupled Drive System. World Electr. Veh. J. 2023, 14, 282. https://doi.org/10.3390/wevj14100282
Li T, Zhang N, Gao X, Pang D. Research on Parameter Optimization Design Method for Dual-Motor Coupled Drive System. World Electric Vehicle Journal. 2023; 14(10):282. https://doi.org/10.3390/wevj14100282
Chicago/Turabian StyleLi, Tonghui, Nan Zhang, Xiaoyu Gao, and Daqian Pang. 2023. "Research on Parameter Optimization Design Method for Dual-Motor Coupled Drive System" World Electric Vehicle Journal 14, no. 10: 282. https://doi.org/10.3390/wevj14100282
APA StyleLi, T., Zhang, N., Gao, X., & Pang, D. (2023). Research on Parameter Optimization Design Method for Dual-Motor Coupled Drive System. World Electric Vehicle Journal, 14(10), 282. https://doi.org/10.3390/wevj14100282





