Research on Reinforcement-Learning-Based Truck Platooning Control Strategies in Highway On-Ramp Regions
Abstract
:1. Introduction
- (1)
- It uses a MAPPO-based algorithm with centralized training and decentralized execution to control the platoon in the on-ramp area. Each truck only computes its own action, avoiding the data computation delay caused by centralized calculation.
- (2)
- It considers the driving status of the trucks in front and behind each truck, maximizing the overall platoon gain and improving the global operational efficiency.
- (3)
- It does not require communication, and it is scalable to any number of vehicles and communication devices.
2. Related Work
3. Preliminaries and Methods
3.1. Preliminary Knowledge
3.2. Methods
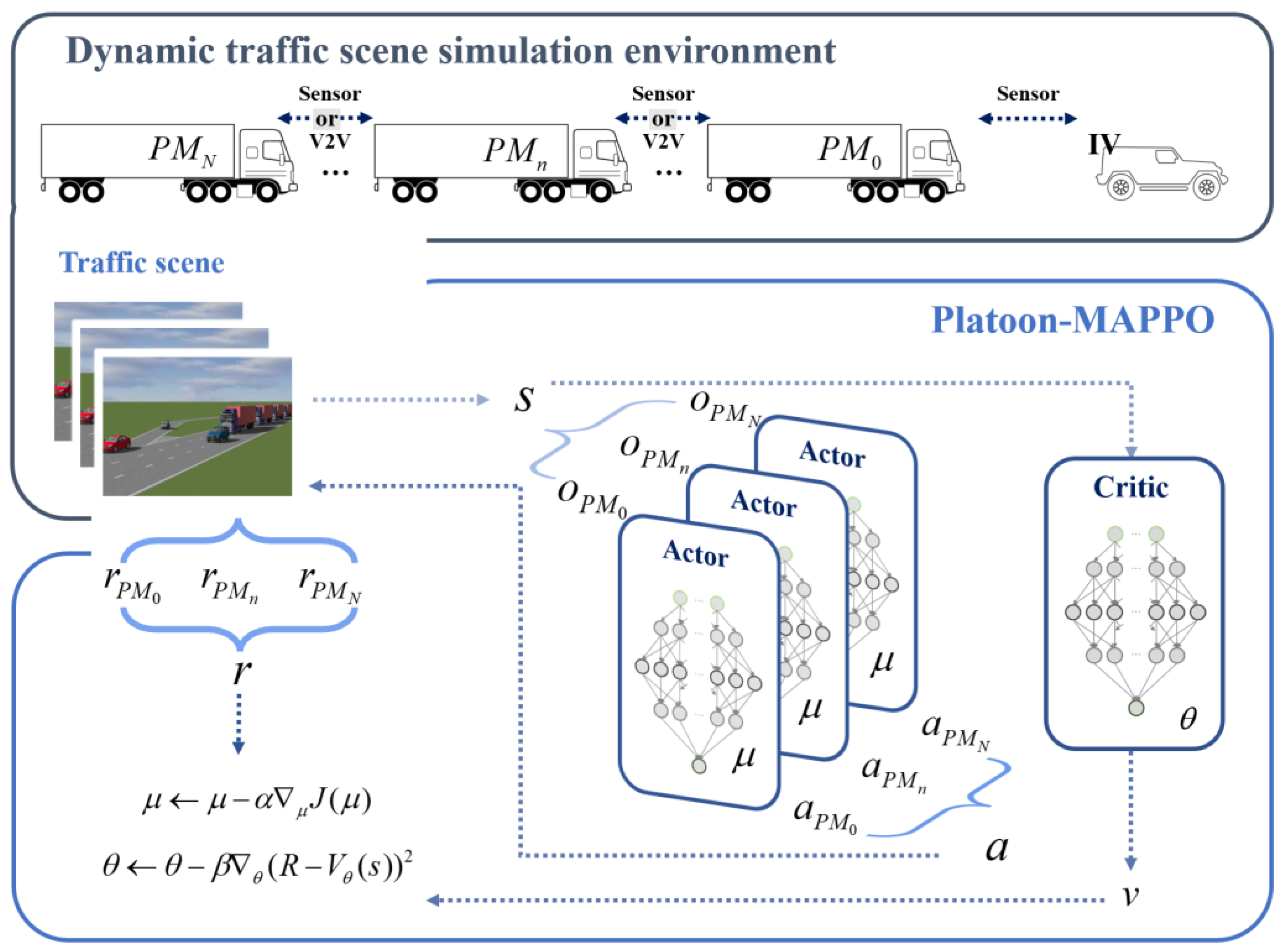
3.2.1. Truck Platoon Communication Topology
3.2.2. Crucial Elements
- (1)
- Observation and state: the observation value of each truck in the platoon is the part of the platoon’s overall state that can be observed by the truck. The observation value of each truck comprises several elements: (a) the type of the truck, which can be , , or , indicating the position of the truck in the platoon; (b) the relative speed of the truck with respect to the vehicle in front of it; (c) the relative speed of the truck with respect to the vehicle behind it; (d) the relative distance between the truck and the vehicle in front of it; (e) the relative distance between the truck and the vehicle behind it; (f) the speed of the truck itself; and (g) if the truck is , it also obtains the relative distance and speed between itself and the IV that is detected within its detection range. RL algorithms are not suitable for applying batch normalization to the input values. Therefore, the input values are scaled directly to [−1, 1] according to their value range. The position identifiers are 0, −1, and 1, representing , , and , respectively. When the platoon consists of more than three trucks, all the position identifiers of the middle trucks, , are set to 1. The training process can accommodate any number of trucks in the platoon.
- (2)
- Action: the main application scenario of truck platoon control technology is on highways, where the traffic environment is relatively simple. To minimize the interference of truck platoons with other human drivers, truck platoons will travel on the rightmost lane. Therefore, this article focuses on the longitudinal control of truck platoons. After obtaining the observation values, the decision-making algorithms will determine the driving force for each truck at each time step. The driving force indicates the acceleration or deceleration of the truck. When the driving force is positive, it means that the truck accelerates forward and is bounded by the maximum driving force value. When the driving force is negative, it means that the truck decelerates.
- (3)
- Reward: autonomous driving is typically a multi-objective optimization problem. These objectives may encompass various aspects, such as speed, travel time, collision, regulations, energy consumption, vehicle wear and tear, and passenger experience. For freight trucks, the main considerations are speed, energy consumption, and safety. The reward function should reflect the goals that autonomous driving vehicles aim to pursue, rather than the methods and techniques used to attain these goals. For instance, adding extra penalties for low speeds to motivate trucks to move forward is known as reward shaping. Reward shaping may facilitate learning in the early stages, but may also constrain the performance potential of the algorithm [36]. Therefore, our reward function only consists of three components: speed, energy consumption, and safety.
| Algorithm 1: Platoon-MAPPO |
| Initialize actor network, , and critic network, , with weights and Initialize batch size B, iterative step ,, and done = 0 for episode = 0, 1, 2, … until convergence do while not done do initialize actor and critic states for all agents i, perform Sampling from normal distribution end for Send to the simulation environment, obtain Save Compute the advantage function, , and return, end for for for k = 0, …, PPO epoch perform Compute Update network parameters using the gradient method end for |
4. Simulation
4.1. Simulation Platform
4.2. Longitudinal Dynamics of Trucks
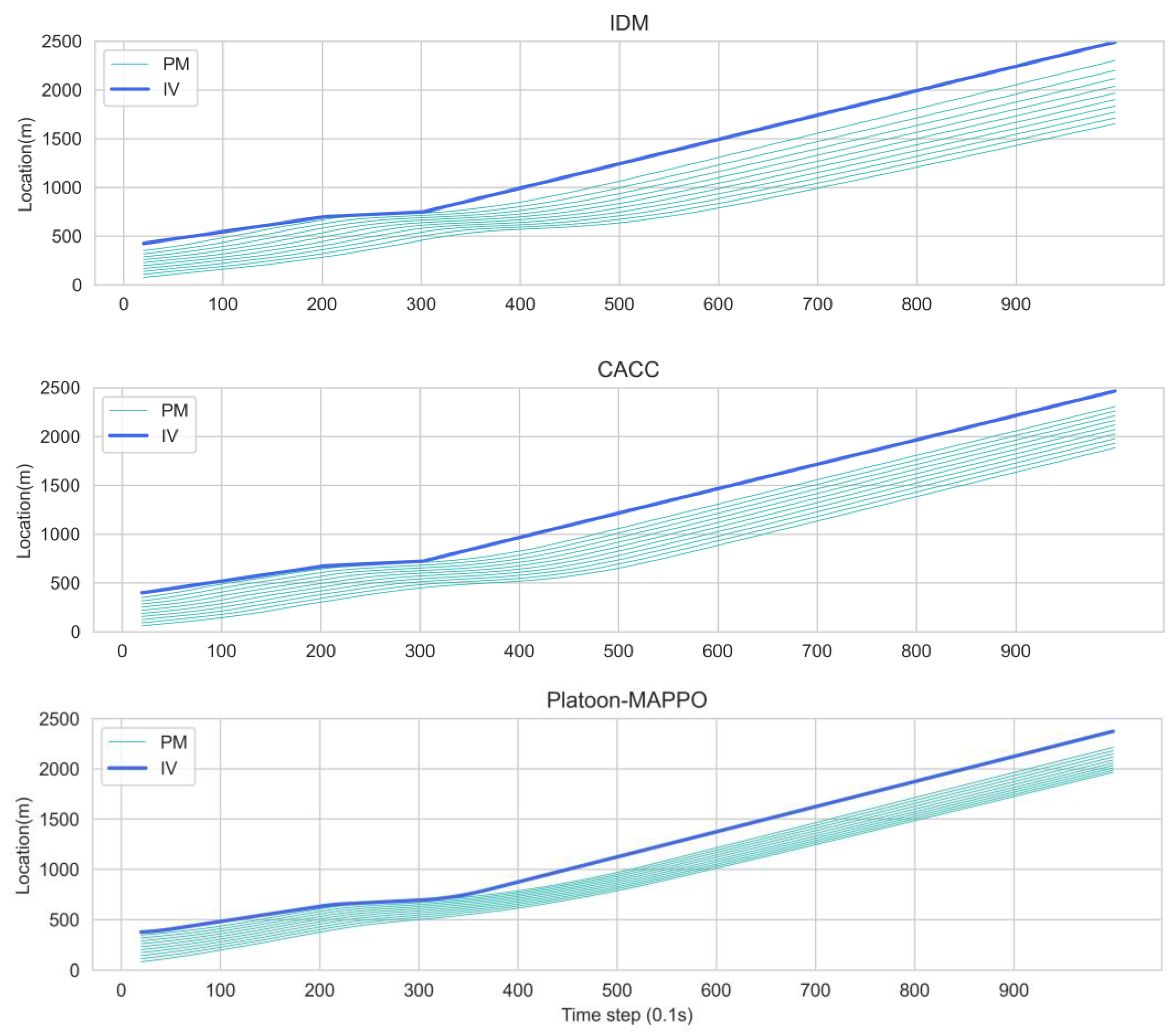
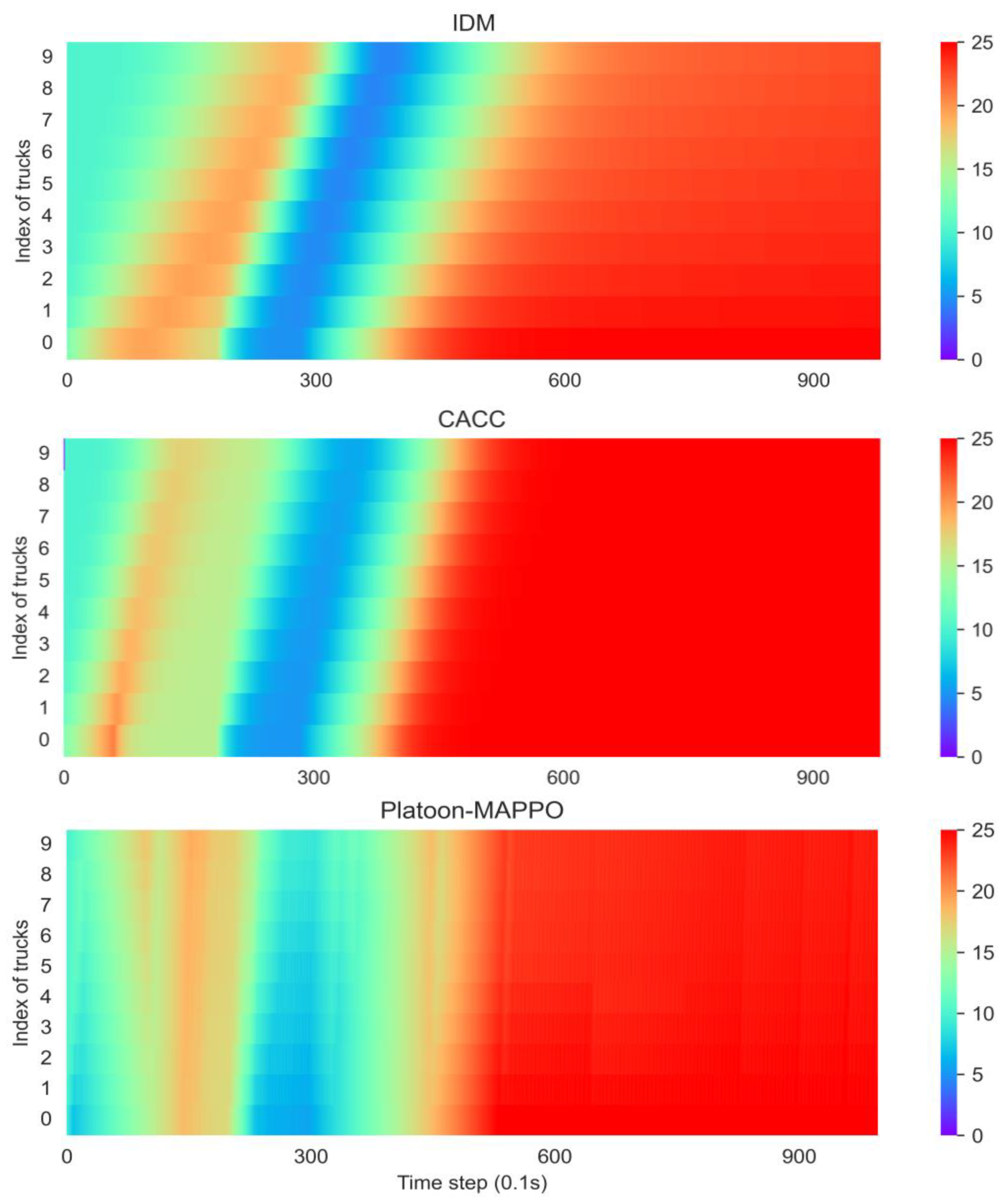
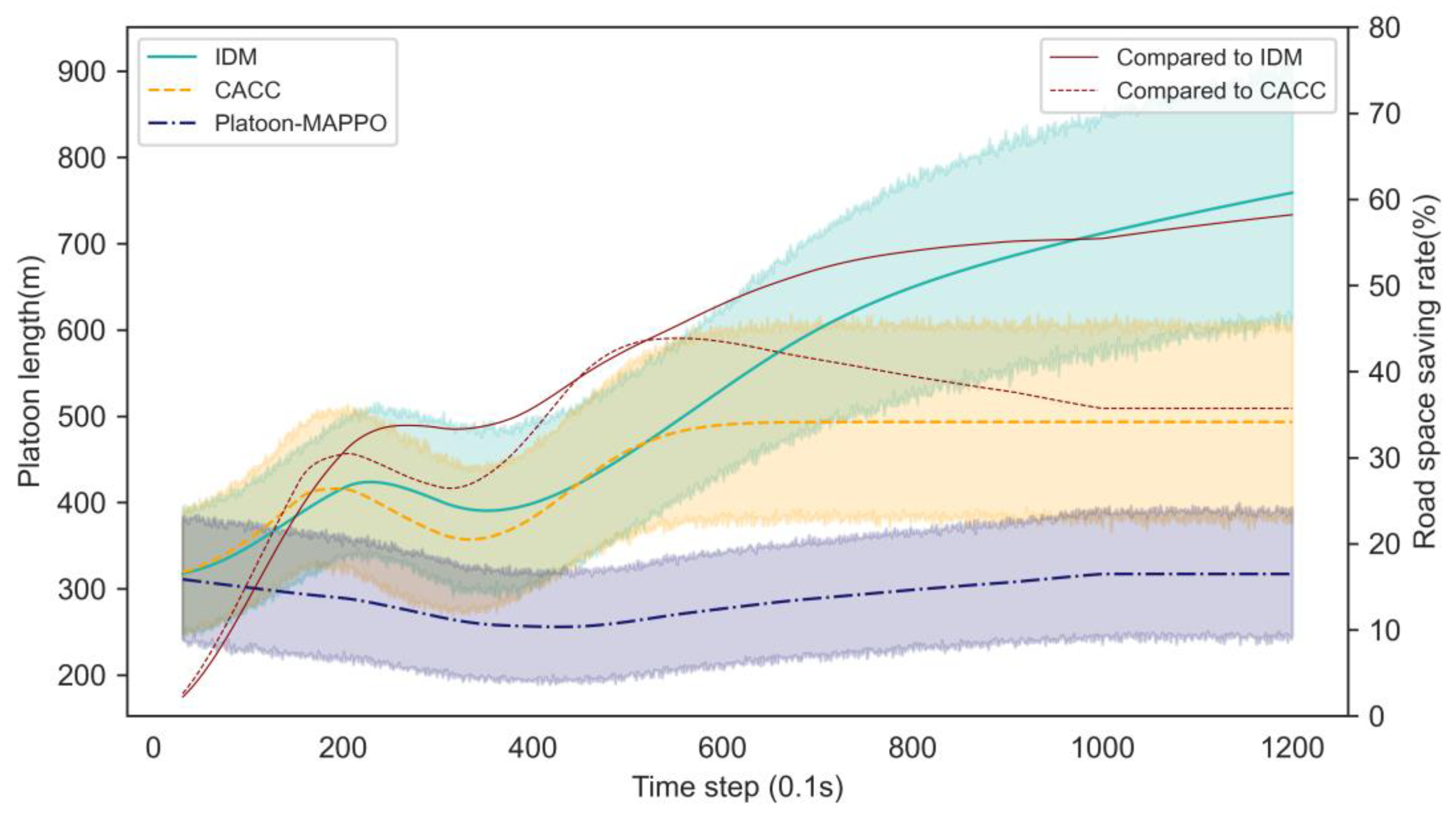
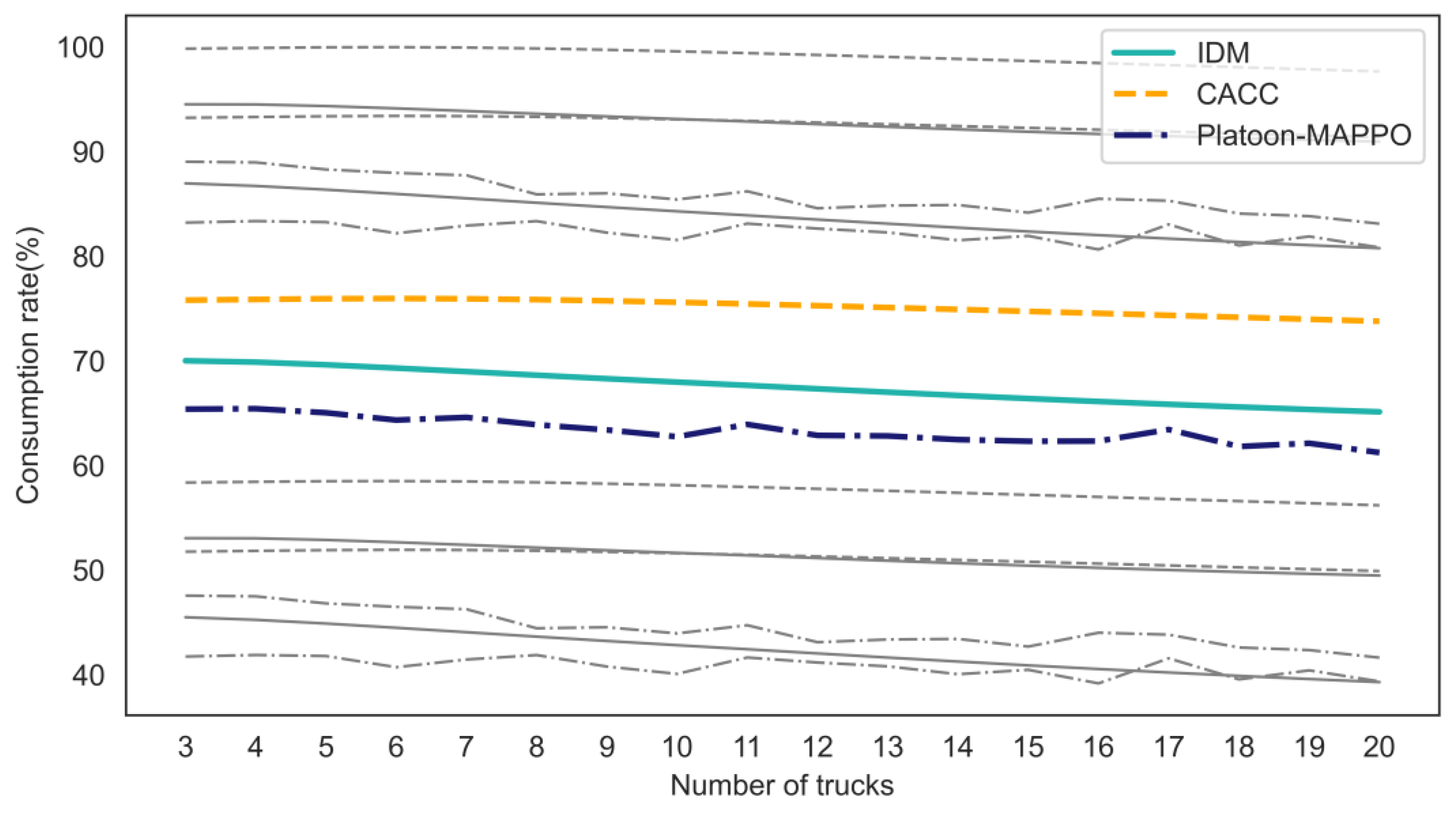
5. Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Harker, B.J. PROMOTE-CHAUFFEUR II & 5.8 GHz vehicle to vehicle communications system. In Proceedings of the 2001 ADAS. International Conference on Advanced Driver Assistance Systems, (IEE Conf. Publ. No. 483), Birmingham, UK, 17–18 September 2001; Available online: https://digital-library.theiet.org/content/conferences/10.1049/cp_20010504 (accessed on 15 August 2023).
- Shladover, S.E. AHS research at the California PATH program and future AHS research needs. In Proceedings of the 2008 IEEE International Conference on Vehicular Electronics and Safety, Columbus, OH, USA, 22–24 September 2008; pp. 4–5. [Google Scholar]
- Shladover, S.E. PATH at 20—History and major milestones. IEEE Trans. Intell. Transp. Syst. 2007, 8, 584–592. [Google Scholar] [CrossRef]
- Kunze, R.; Tummel, C.; Henning, K. Determination of the order of electronically coupled trucks on German motorways. In Proceedings of the 2009 2nd International Conference on Power Electronics and Intelligent Transportation System (PEITS), Shenzhen, China, 19–20 December 2009; pp. 41–46. [Google Scholar]
- Tsugawa, S.; Kato, S.; Aoki, K. An automated truck platoon for energy saving. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 4109–4114. [Google Scholar]
- Robinson, T.; Chan, E.; Coelingh, E. Operating platoons on public motorways: An introduction to the sartre platooning programme. In Proceedings of the 17th World Congress on Intelligent Transport Systems, Busan, Republic of Korea, 25–29 October 2010; p. 12. [Google Scholar]
- Zhao, W.; Ngoduy, D.; Shepherd, S.; Liu, R.; Papageorgiou, M. A platoon based cooperative eco-driving model for mixed automated and human-driven vehicles at a signalised intersection. Transp. Res. Part C Emerg. Technol. 2018, 95, 802–821. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, M.; Ahn, S. Distributed model predictive control approach for cooperative car-following with guaranteed local and string stability. Transp. Res. Part B Methodol. 2019, 128, 69–86. [Google Scholar] [CrossRef]
- Zhou, Y.; Ahn, S.; Wang, M.; Hoogendoorn, S. Stabilizing mixed vehicular platoons with connected automated vehicles: An H-infinity approach. Transp. Res. Part B Methodol. 2020, 132, 152–170. [Google Scholar] [CrossRef]
- Wang, M.; Daamen, W.; Hoogendoorn, S.P.; van Arem, B. Rolling horizon control framework for driver assistance systems. Part II: Cooperative sensing and cooperative control. Transp. Res. Part C Emerg. Technol. 2014, 40, 290–311. [Google Scholar] [CrossRef]
- He, X.; Liu, H.X.; Liu, X. Optimal vehicle speed trajectory on a signalized arterial with consideration of queue. Transp. Res. Part C Emerg. Technol. 2015, 61, 106–120. [Google Scholar] [CrossRef]
- Grigorescu, S.; Trasnea, B.; Cocias, T.; Macesanu, G. A survey of deep learning techniques for autonomous driving. J. Field Robot. 2020, 37, 362–386. [Google Scholar] [CrossRef]
- Hu, Y.; Yang, J.; Chen, L.; Li, K.; Sima, C.; Zhu, X.; Chai, S.; Du, S.; Lin, T.; Wang, W.; et al. Planning-oriented Autonomous Driving. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Online, 1 September 2022. [Google Scholar]
- Ye, F.; Zhang, S.; Wang, P.; Chan, C.Y. A Survey of Deep Reinforcement Learning Algorithms for Motion Planning and Control of Autonomous Vehicles. In Proceedings of the 2021 IEEE Intelligent Vehicles Symposium (IV), Nagoya, Japan, 11–17 July 2021; pp. 1073–1080. [Google Scholar]
- Kiran, B.R.; Sobh, I.; Talpaert, V.; Mannion, P.; Al Sallab, A.A.; Yogamani, S.; Pérez, P. Deep reinforcement learning for autonomous driving: A survey. IEEE Trans. Intell. Transp. Syst. 2021, 23, 4909–4926. [Google Scholar] [CrossRef]
- Talpaert, V.; Sobh, I.; Kiran, B.R.; Mannion, P.; Yogamani, S.; El-Sallab, A.; Perez, P. Exploring applications of deep reinforcement learning for real-world autonomous driving systems. arXiv 2019, arXiv:1901.01536. [Google Scholar]
- Hoel, C.-J.; Wolff, K.; Laine, L. Automated speed and lane change decision making using deep reinforcement learning. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 2148–2155. [Google Scholar]
- Desjardins, C.; Chaib-draa, B. Cooperative Adaptive Cruise Control: A Reinforcement Learning Approach. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1248–1260. [Google Scholar] [CrossRef]
- Li, M.; Cao, Z.; Li, Z. A Reinforcement Learning-Based Vehicle Platoon Control Strategy for Reducing Energy Consumption in Traffic Oscillations. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5309–5322. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Jiang, J.; Lv, N.; Li, S. An Intelligent Path Planning Scheme of Autonomous Vehicles Platoon Using Deep Reinforcement Learning on Network Edge. IEEE Access 2020, 8, 99059–99069. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, Y.; Khosravi, M.R.; Pei, Q.; Wan, S. An Intelligent Platooning Algorithm for Sustainable Transportation Systems in Smart Cities. IEEE Sens. J. 2021, 21, 15437–15447. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, Y.; Pu, Z.; Hu, J.; Wang, X.; Ke, R. Safe, efficient, and comfortable velocity control based on reinforcement learning for autonomous driving. Transp. Res. Part C Emerg. Technol. 2020, 117, 102662. [Google Scholar] [CrossRef]
- Chu, T.; Kalabić, U. Model-based deep reinforcement learning for CACC in mixed-autonomy vehicle platoon. In Proceedings of the 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019; pp. 4079–4084. [Google Scholar]
- Gao, Z.; Wu, Z.; Hao, W.; Long, K.; Byon, Y.J.; Long, K. Optimal Trajectory Planning of Connected and Automated Vehicles at On-Ramp Merging Area. IEEE Trans. Intell. Transp. Syst. 2022, 23, 12675–12687. [Google Scholar] [CrossRef]
- Kumaravel, S.D.; Malikopoulos, A.A.; Ayyagari, R. Decentralized Cooperative Merging of Platoons of Connected and Automated Vehicles at Highway On-Ramps. In Proceedings of the 2021 American Control Conference (ACC), New Orleans, LA, USA, 25–28 May 2021; pp. 2055–2060. [Google Scholar]
- Xue, Y.; Ding, C.; Yu, B.; Wang, W. A Platoon-Based Hierarchical Merging Control for On-Ramp Vehicles Under Connected Environment. IEEE Trans. Intell. Transp. Syst. 2022, 23, 21821–21832. [Google Scholar] [CrossRef]
- Yadavalli, S.R.; Das, L.C.; Won, M. RLPG: Reinforcement Learning Approach for Dynamic Intra-Platoon Gap Adaptation for Highway On-Ramp Merging. arXiv 2022, arXiv:2212.03497. [Google Scholar]
- Jia, D.; Lu, K.; Wang, J.; Zhang, X.; Shen, X. A Survey on Platoon-Based Vehicular Cyber-Physical Systems. IEEE Commun. Surv. Tutor. 2016, 18, 263–284. [Google Scholar] [CrossRef]
- Willke, T.L.; Tientrakool, P.; Maxemchuk, N.F. A survey of inter-vehicle communication protocols and their applications. IEEE Commun. Surv. Tutor. 2009, 11, 3–20. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; Adaptive Computation and Machine Learning; The MIT Press: Cambridge, MA, USA; Cambridge, London, 2018. [Google Scholar]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. In Proceedings of the 33rd International Conference on Machine Learning, Online, 16 June 2016; pp. 1928–1937. [Google Scholar]
- Schulman, J.; Levine, S.; Abbeel, P.; Jordan, M.; Moritz, P. Trust region policy optimization. In Proceedings of the 32nd International Conference on Machine Learning, Online, 6–11 July 2015; pp. 1889–1897. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Yu, C.; Velu, A.; Vinitsky, E.; Gao, J.; Wang, Y.; Bayen, A.; Wu, Y. The surprising effectiveness of ppo in cooperative multi-agent games. Adv. Neural Inf. Process. Syst. 2022, 35, 24611–24624. [Google Scholar]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Abbeel, O.P.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Knox, W.B.; Allievi, A.; Banzhaf, H.; Schmitt, F.; Stone, P. Reward (mis) design for autonomous driving. Artif. Intell. 2023, 316, 103829. [Google Scholar] [CrossRef]
- Alam, A.; Besselink, B.; Turri, V.; Mårtensson, J.; Johansson, K.H. Heavy-duty vehicle platooning for sustainable freight transportation: A cooperative method to enhance safety and efficiency. IEEE Control Syst. Mag. 2015, 35, 34–56. [Google Scholar]
- Hussein, A.A.; Rakha, H.A. Vehicle Platooning Impact on Drag Coefficients and Energy/Fuel Saving Implications. IEEE Trans. Veh. Technol. 2022, 71, 1199–1208. [Google Scholar] [CrossRef]
- Treiber, M.; Hennecke, A.; Helbing, D. Congested traffic states in empirical observations and microscopic simulations. Phys. Rev. E 2000, 62, 1805–1824. [Google Scholar] [CrossRef] [PubMed]
- Milanés, V.; Shladover, S.E. Modeling cooperative and autonomous adaptive cruise control dynamic responses using experimental data. Transp. Res. Part C Emerg. Technol. 2014, 48, 285–300. [Google Scholar] [CrossRef]

| Parameter | Value | Description |
|---|---|---|
| 200,000 N | Gravity of truck | |
| l | 17 m | Length of truck |
| 0.0041 | Rolling resistance coefficient | |
| 0.000025 | Rolling resistance coefficient | |
| (0.3, 0.6) | Adhesion factor of truck | |
| 0.564 | Air resistance coefficient of truck | |
| 5.8 m2 | Front projection area of truck | |
| 1.2258 kg/m3 | Density of air | |
| [−0.05, 0.05] | Road slope | |
| [0 m/s, 25 m/s] | Velocity of truck |
| Control Strategy | Ft (N) | Fw (N) | Fj (N) | Ff (N) |
|---|---|---|---|---|
| IDM | 7368 | 562 | 5690 | 1115 |
| CACC | 8334 | 712 | 6464 | 1157 |
| Platoon-MAPPO | 6278 | 643 | 4480 | 1155 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Zhou, Z.; Duan, Y.; Yu, B. Research on Reinforcement-Learning-Based Truck Platooning Control Strategies in Highway On-Ramp Regions. World Electr. Veh. J. 2023, 14, 273. https://doi.org/10.3390/wevj14100273
Chen J, Zhou Z, Duan Y, Yu B. Research on Reinforcement-Learning-Based Truck Platooning Control Strategies in Highway On-Ramp Regions. World Electric Vehicle Journal. 2023; 14(10):273. https://doi.org/10.3390/wevj14100273
Chicago/Turabian StyleChen, Jiajia, Zheng Zhou, Yue Duan, and Biao Yu. 2023. "Research on Reinforcement-Learning-Based Truck Platooning Control Strategies in Highway On-Ramp Regions" World Electric Vehicle Journal 14, no. 10: 273. https://doi.org/10.3390/wevj14100273
APA StyleChen, J., Zhou, Z., Duan, Y., & Yu, B. (2023). Research on Reinforcement-Learning-Based Truck Platooning Control Strategies in Highway On-Ramp Regions. World Electric Vehicle Journal, 14(10), 273. https://doi.org/10.3390/wevj14100273








