Where to Charge Electric Trucks in Europe—Modelling a Charging Infrastructure Network
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Scenarios
2.2. Methods
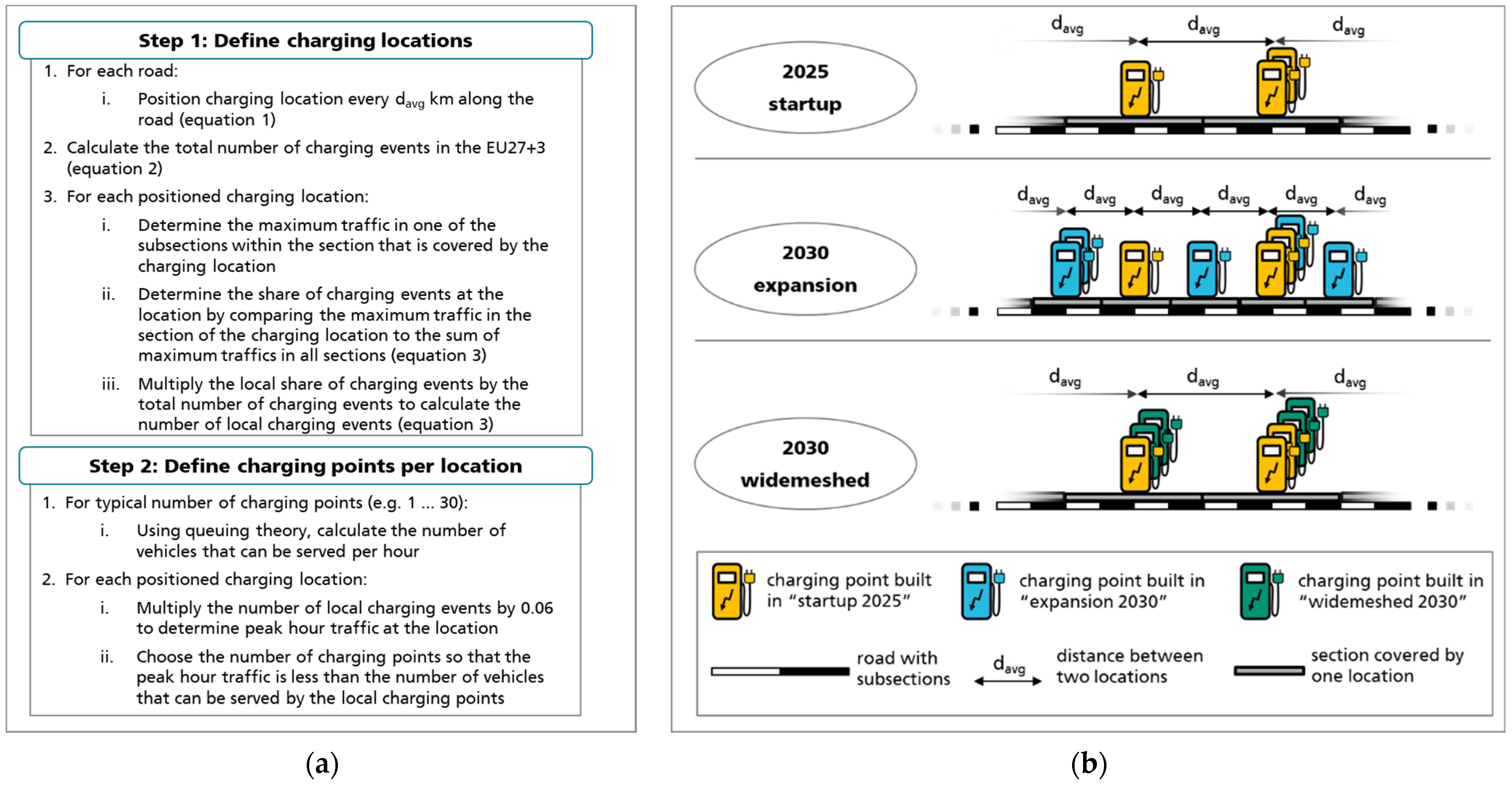
2.2.1. Determine Charging Locations
2.2.2. Dimension Charging Locations
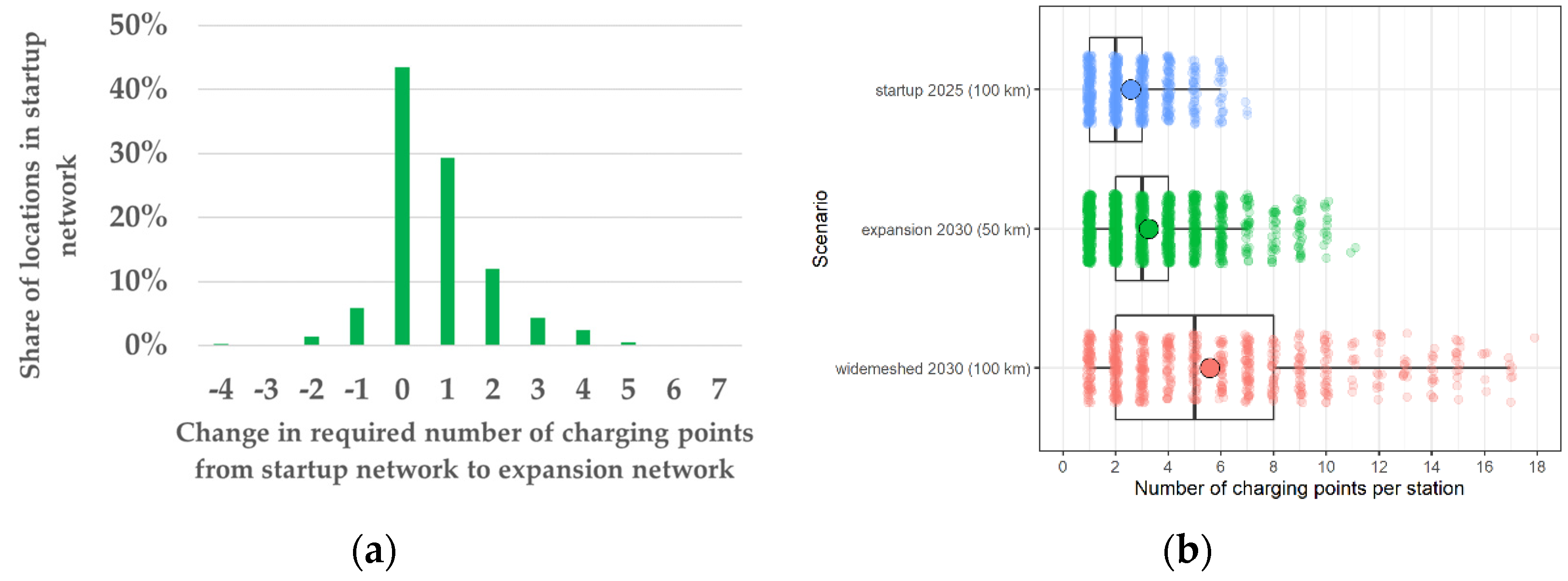
3. Results
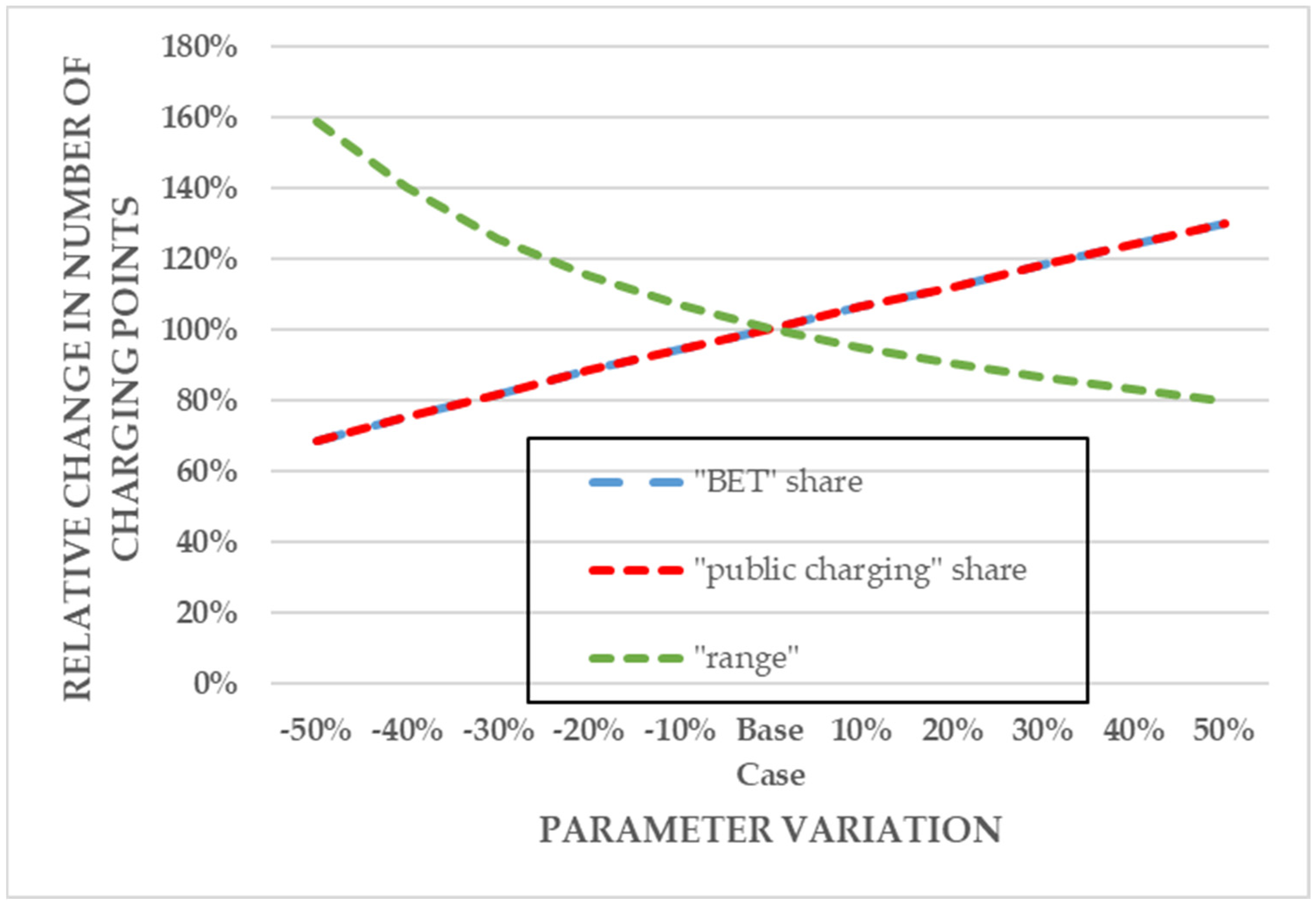
4. Discussion
4.1. Data Limitations
4.2. Model Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Eurostat. Greenhouse Gas Emissions by Source Sector (Source: EEA). Available online: https://ec.europa.eu/eurostat/databrowser/view/ENV_AIR_GGE__custom_1533603/default/table?lang=en (accessed on 8 November 2021).
- European Union. Regulation (EU) 2019/1242 of the European Parliament and of the Council of 20 June 2019 Setting CO2 Emission Performance Standards for New Heavy-Duty Vehicles and Amending Regulations (EC) No 595/2009 and (EU) 2018/956 of the European Parliament and of the Council and Council Directive 96/53/EC. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32019R1242&from=EN (accessed on 22 August 2022).
- Breed, A.K.; Speth, D.; Plötz, P. CO2 fleet regulation and the future market diffusion of zero-emission trucks in Europe. Energy Policy 2021, 159, 112640. [Google Scholar] [CrossRef]
- Speth, D.; Funke, S.Á. Comparing Options to Electrify Heavy-Duty Vehicles: Findings of German Pilot Projects. WEVJ 2021, 12, 67. [Google Scholar] [CrossRef]
- Nykvist, B.; Olsson, O. The feasibility of heavy battery electric trucks. Joule 2021, 5, 901–913. [Google Scholar] [CrossRef]
- Transport & Environment. Unlocking Electric Trucking in the EU: Recharging in Cities: Electrification of Urban and Regional Deliveries; Transport & Environment: Brussels, Belgium, 2020. [Google Scholar]
- European Commission. Proposal for a Regulation of the European Parliament and of the Council on the Deployment of Alternative Fuels Infrastructure, and Repealing Directive 2014/94/EU of the European Parliament and of the Council. Available online: https://eur-lex.europa.eu/resource.html?uri=cellar:dbb134db-e575-11eb-a1a5-01aa75ed71a1.0001.02/DOC_1&format=PDF (accessed on 22 August 2022).
- Metais, M.O.; Jouini, O.; Perez, Y.; Berrada, J.; Suomalainen, E. Too much or not enough? Planning electric vehicle charging infrastructure: A review of modeling options. Renew. Sustain. Energy Rev. 2022, 153, 111719. [Google Scholar] [CrossRef]
- Deb, S.; Tammi, K.; Kalita, K.; Mahanta, P. Review of recent trends in charging infrastructure planning for electric vehicles. WIREs Energy Environ. 2018, 7, e306. [Google Scholar] [CrossRef]
- Hakimi, S.L. Optimum Locations of Switching Centers and the Absolute Centers and Medians of a Graph. Oper. Res. 1964, 12, 450–459. [Google Scholar] [CrossRef]
- Toregas, C.; Swain, R.; ReVelle, C.; Bergman, L. The Location of Emergency Service Facilities. Oper. Res. 1971, 19, 1363–1373. [Google Scholar] [CrossRef]
- Gopalakrishnan, R.; Biswas, A.; Lightwala, A.; Vasudevan, S.; Dutta, P.; Tripathi, A. Demand Prediction and Placement Optimization for Electric Vehicle Charging Stations: In Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence (IJCAI-16). Available online: https://www.ijcai.org/Proceedings/16/Papers/442.pdf (accessed on 22 August 2022).
- Speth, D.; Plötz, P.; Funke, S.; Vallarella, E. Public fast charging infrastructure for battery electric trucks–a model-based network for Germany. Environ. Res. Infrastruct. Sustain. 2022, 2, 025004. [Google Scholar] [CrossRef]
- Funke, S.; Plötz, P. A Techno-Economic Analysis of Fast Charging needs in Germany for Different Ranges of Battery Electric Vehicles. In Proceedings of the European Battery, Hybrid and Fuel Cell Electric Vehicle Congress, Geneva, Switzerland, 17 March 2017. [Google Scholar]
- Hodgson, M.J. A Flow-Capturing Location-Allocation Model. Geogr. Anal. 1990, 22, 270–279. [Google Scholar] [CrossRef]
- Cruz-Zambrano, M.; Corchero, C.; Igualada-Gonzalez, L.; Bernardo, V. Optimal location of fast charging stations in Barcelona: A flow-capturing approach. In Proceedings of the 2013 10th International Conference on the European Energy Market (EEM 2013), Stockholm, Sweden, 27–29 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–6, ISBN 978-1-4799-2008-2. [Google Scholar]
- Kuby, M.; Lim, S. The flow-refueling location problem for alternative-fuel vehicles. Socio-Econ. Plan. Sci. 2005, 39, 125–145. [Google Scholar] [CrossRef]
- He, Y.; Kockelman, K.M.; Perrine, K.A. Optimal locations of U.S. fast charging stations for long-distance trip completion by battery electric vehicles. J. Clean. Prod. 2019, 214, 452–461. [Google Scholar] [CrossRef]
- Jochem, P.; Szimba, E.; Reuter-Oppermann, M. How many fast-charging stations do we need along European highways? Transp. Res. Part D Transport Environ. 2019, 73, 120–129. [Google Scholar] [CrossRef]
- Rose, P.K.; Nugroho, R.; Gnann, T.; Plötz, P.; Wietschel, M.; Reuter-Oppermann, M. Optimal development of alternative fuel station networks considering node capacity restrictions. Transp. Res. Part D Transport Environ. 2020, 78, 102189. [Google Scholar] [CrossRef]
- Xi, X.; Sioshansi, R.; Marano, V. Simulation–optimization model for location of a public electric vehicle charging infrastructure. Transp. Res. Part D Transport Environ. 2013, 22, 60–69. [Google Scholar] [CrossRef]
- Whitehead, J.; Whitehead, J.; Kane, M.; Zheng, Z. Exploring public charging infrastructure requirements for short-haul electric trucks. Int. J. Sustain. Transp. 2021, 1–17. [Google Scholar] [CrossRef]
- Speth, D.; Sauter, V.; Plötz, P.; Signer, T. Synthetic European road freight transport flow data. Data Brief. 2022, 40, 107786. [Google Scholar] [CrossRef] [PubMed]
- Szimba, E.; Kraft, M.; Ihrig, J.; Schimke, A.; Schnell, O.; Kawabata, Y.; Newton, S.; Breemersch, T.; Versteegh, R.; van Meijeren, J.; et al. ETISplus Database Content and Methodology: ETISplus Deliverable D6. In Proceedings of the project co-funded by the European Commission under the 7th Framework Programme, Zoetermeer, The Netherlands, 1 February 2013. [Google Scholar] [CrossRef]
- BAST. Automatische Zählstellen auf Autobahnen und Bundesstraßen: Stundendaten. Available online: https://www.bast.de/BASt_2017/DE/Verkehrstechnik/Fachthemen/v2-verkehrszaehlung/Stundenwerte.html (accessed on 14 December 2019).
- HoLa. HoLa-Hochleistungsladen Lkw-Fernverkehr: Construction, Operation and Accompanying Research for the First Megawatt Charging Systems for Trucks in Europe. Available online: https://www.hochleistungsladen-lkw.de/hola-en/ (accessed on 6 October 2021).
- KiD. Kraftfahrzeugverkehr in Deutschland 2010; Schlussbericht: Braunschweig, Germany; Flensburg, The Netherlands, 2010. [Google Scholar]
- Gnann, T.; Funke, S.; Jakobsson, N.; Plötz, P.; Sprei, F.; Bennehag, A. Fast charging infrastructure for electric vehicles: Today’s situation and future needs. Transp. Res. Part D Transport Environ. 2018, 62, 314–329. [Google Scholar] [CrossRef]
- Funke, S.Á. Techno-ökonomische Gesamtbewertung heterogener Maßnahmen zur Verlängerung der Tagesreichweite von batterieelektrischen Fahrzeugen: Dissertation an der Universität Kassel zur Erlangung des akademischen Grades eines Doktors der Ingenieurwissenschaften (Dr.-Ing.) im Fachbereich 16 Elektrotechnik und Informatik; Universitätsbibliothek Kassel: Kassel, Germany, 2018; Available online: https://d-nb.info/1158692242/34 (accessed on 22 August 2022).
| Parameter | Abbreviation | Value | Reference |
|---|---|---|---|
| Cumulative annual mileage | 188,719 Mio. km (2025) 215,042 Mio. km (2030) | Own calculation, based on [23] | |
| Range in 4.5 h | 300 km | [13] | |
| Share of public charging | 25% | Own estimation, based on [13,26] | |
| Average charging time | 30 min | [13] | |
| Average waiting time | 5 min | [13] | |
| Share of daily charging events in most trafficked hour | 6% | [13] |
| Scenario | Targeted Year | ||
|---|---|---|---|
| Startup | 2025 | 100 km | 5% |
| Expansion | 2030 | 50 km | 15% |
| Widemeshed | 2030 | 100 km | 15% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Speth, D.; Sauter, V.; Plötz, P. Where to Charge Electric Trucks in Europe—Modelling a Charging Infrastructure Network. World Electr. Veh. J. 2022, 13, 162. https://doi.org/10.3390/wevj13090162
Speth D, Sauter V, Plötz P. Where to Charge Electric Trucks in Europe—Modelling a Charging Infrastructure Network. World Electric Vehicle Journal. 2022; 13(9):162. https://doi.org/10.3390/wevj13090162
Chicago/Turabian StyleSpeth, Daniel, Verena Sauter, and Patrick Plötz. 2022. "Where to Charge Electric Trucks in Europe—Modelling a Charging Infrastructure Network" World Electric Vehicle Journal 13, no. 9: 162. https://doi.org/10.3390/wevj13090162
APA StyleSpeth, D., Sauter, V., & Plötz, P. (2022). Where to Charge Electric Trucks in Europe—Modelling a Charging Infrastructure Network. World Electric Vehicle Journal, 13(9), 162. https://doi.org/10.3390/wevj13090162






