The Vertical Force Estimation Algorithm Based on Smart Tire Technology
Abstract
:1. Introduction
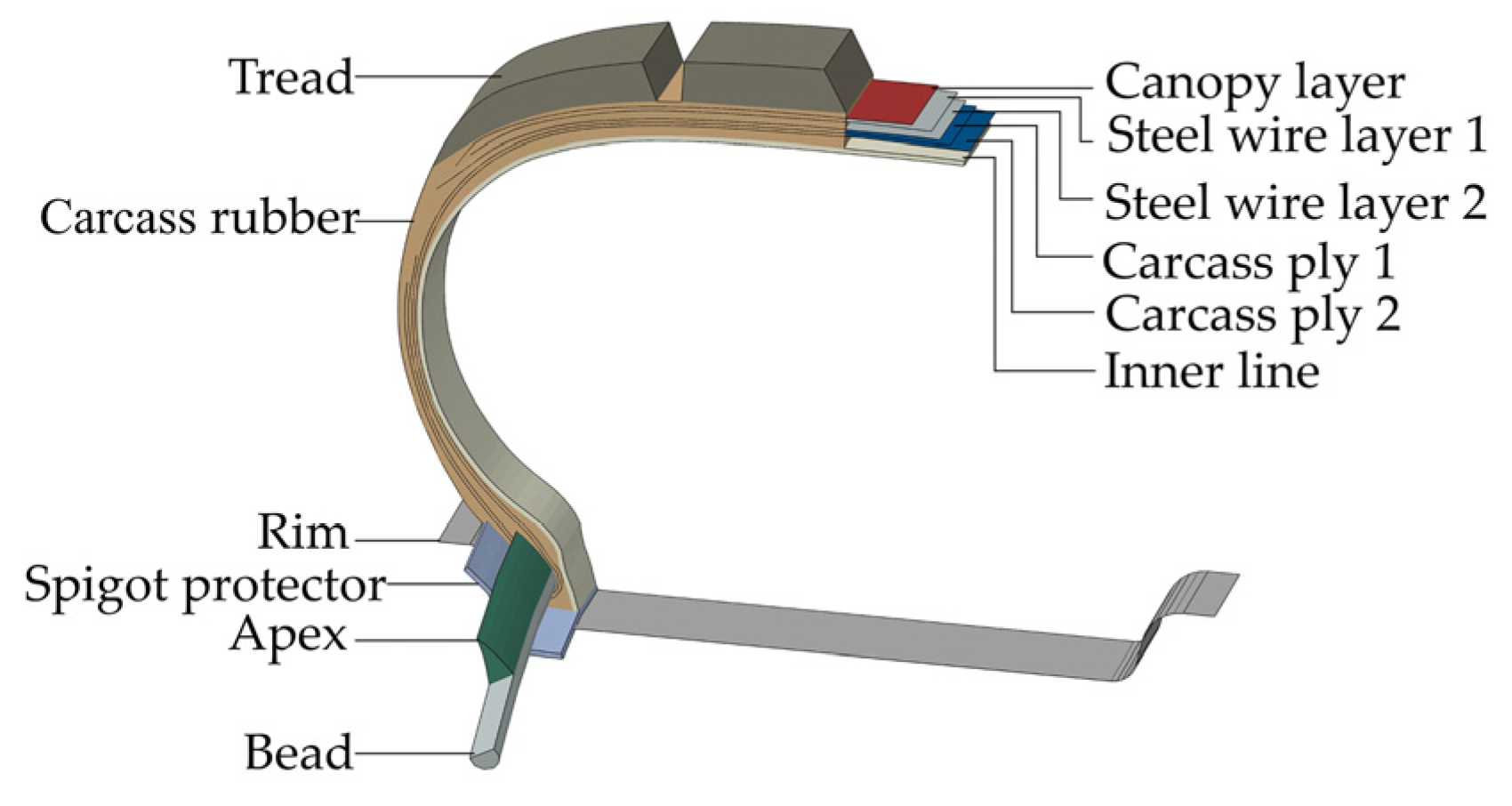
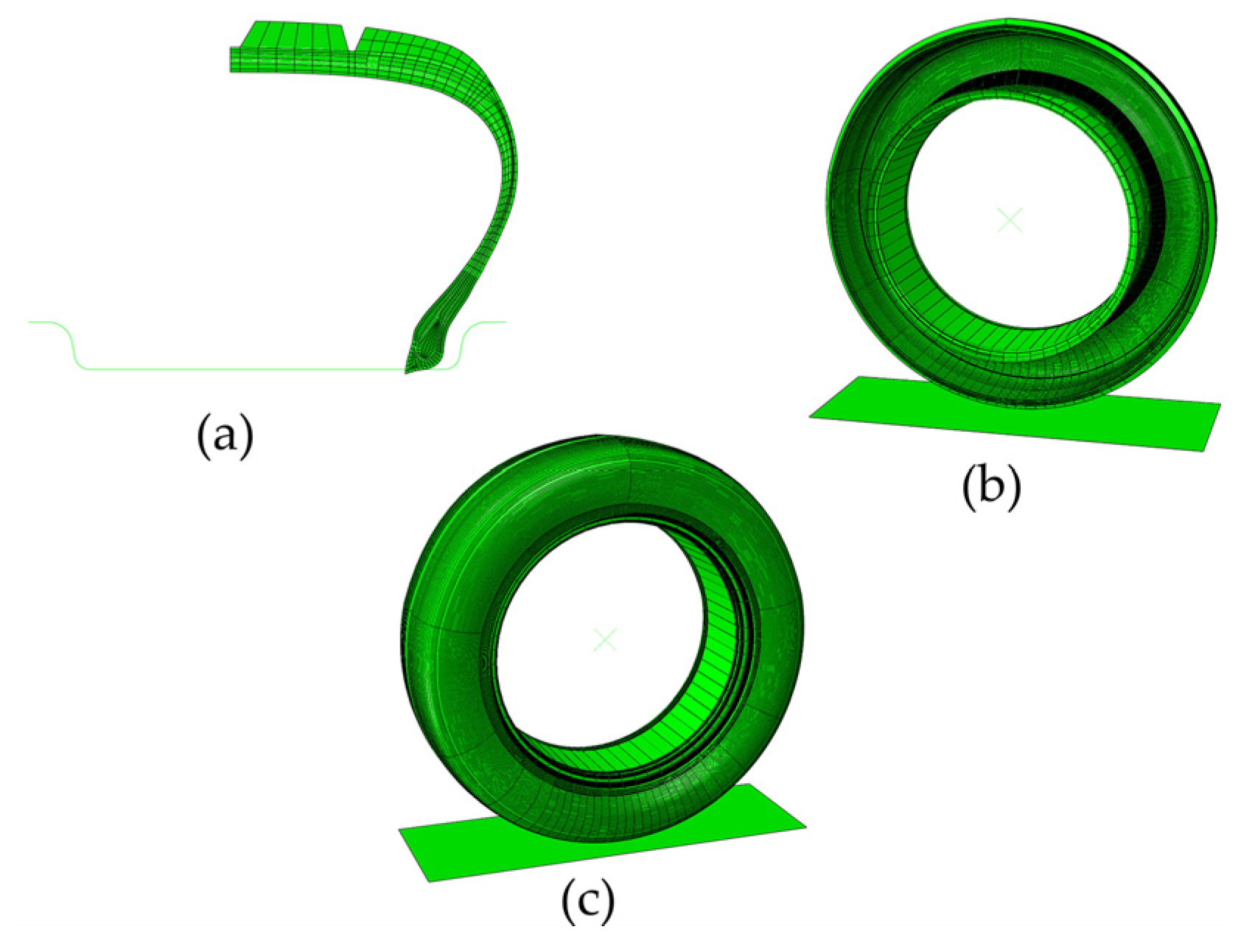
2. Establishment of the Tire Finite Element Model
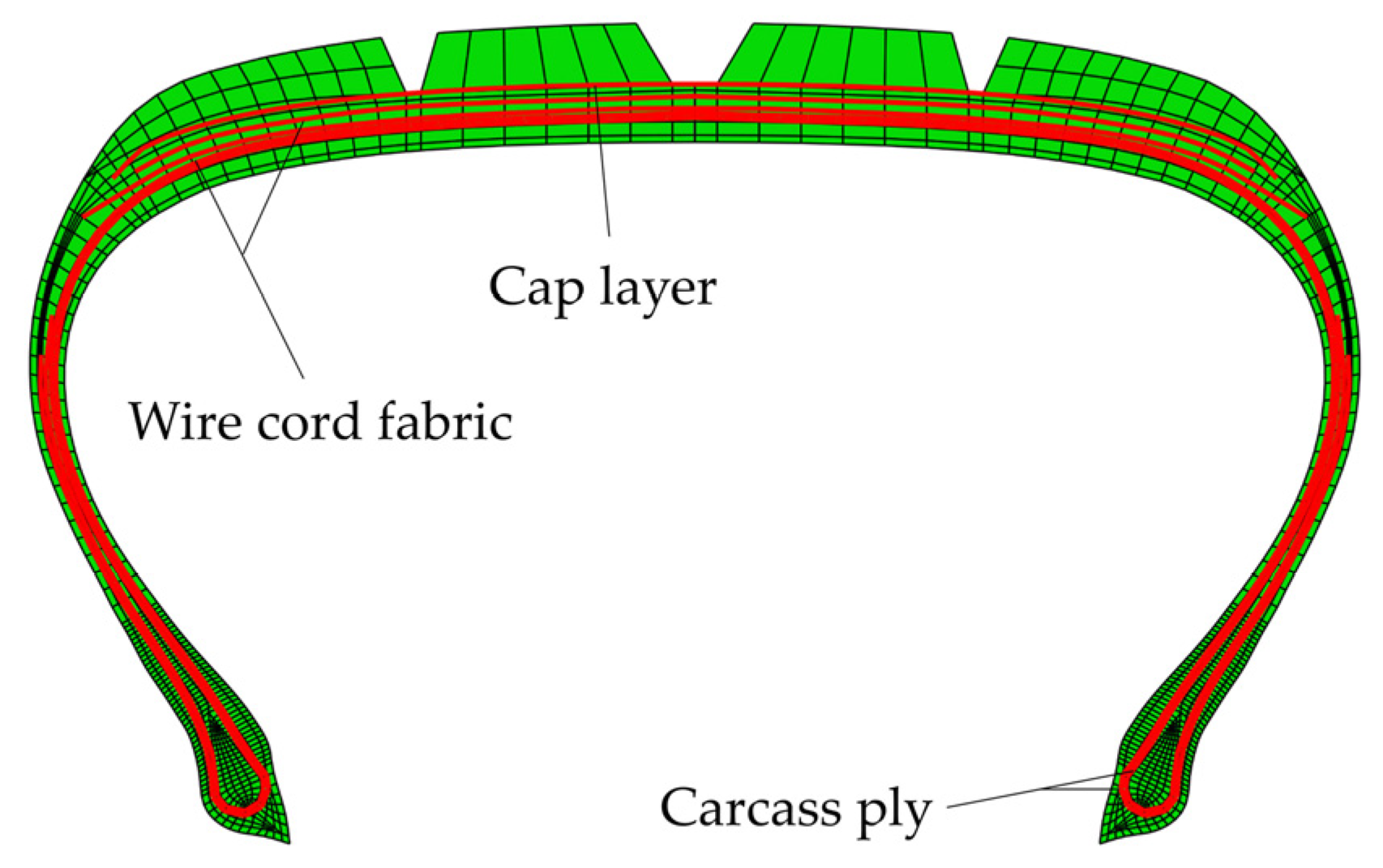
2.1. Element Type
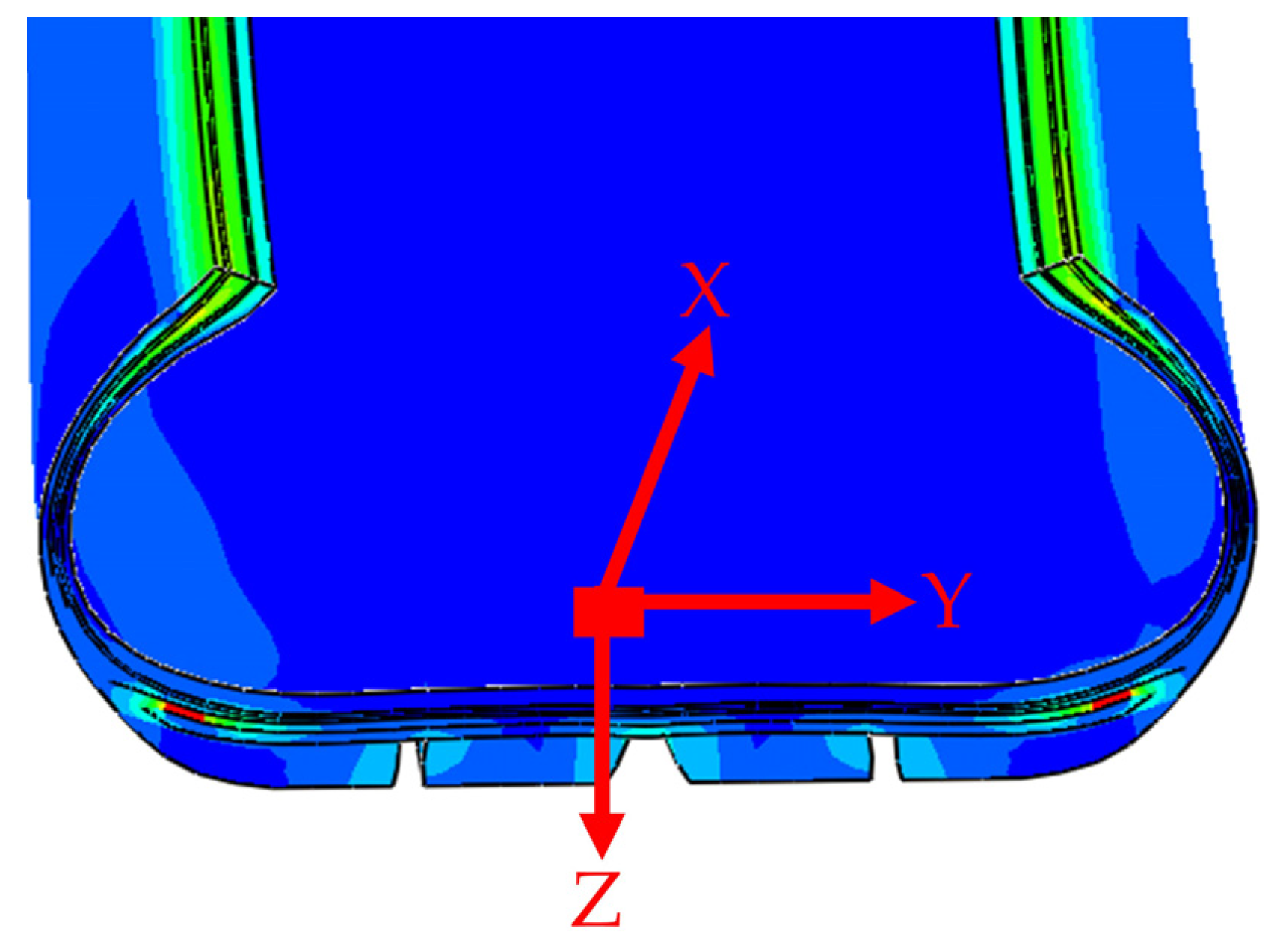
2.2. Material Model and Sensor Positioning
3. Verification of the Tire Finite Element Model
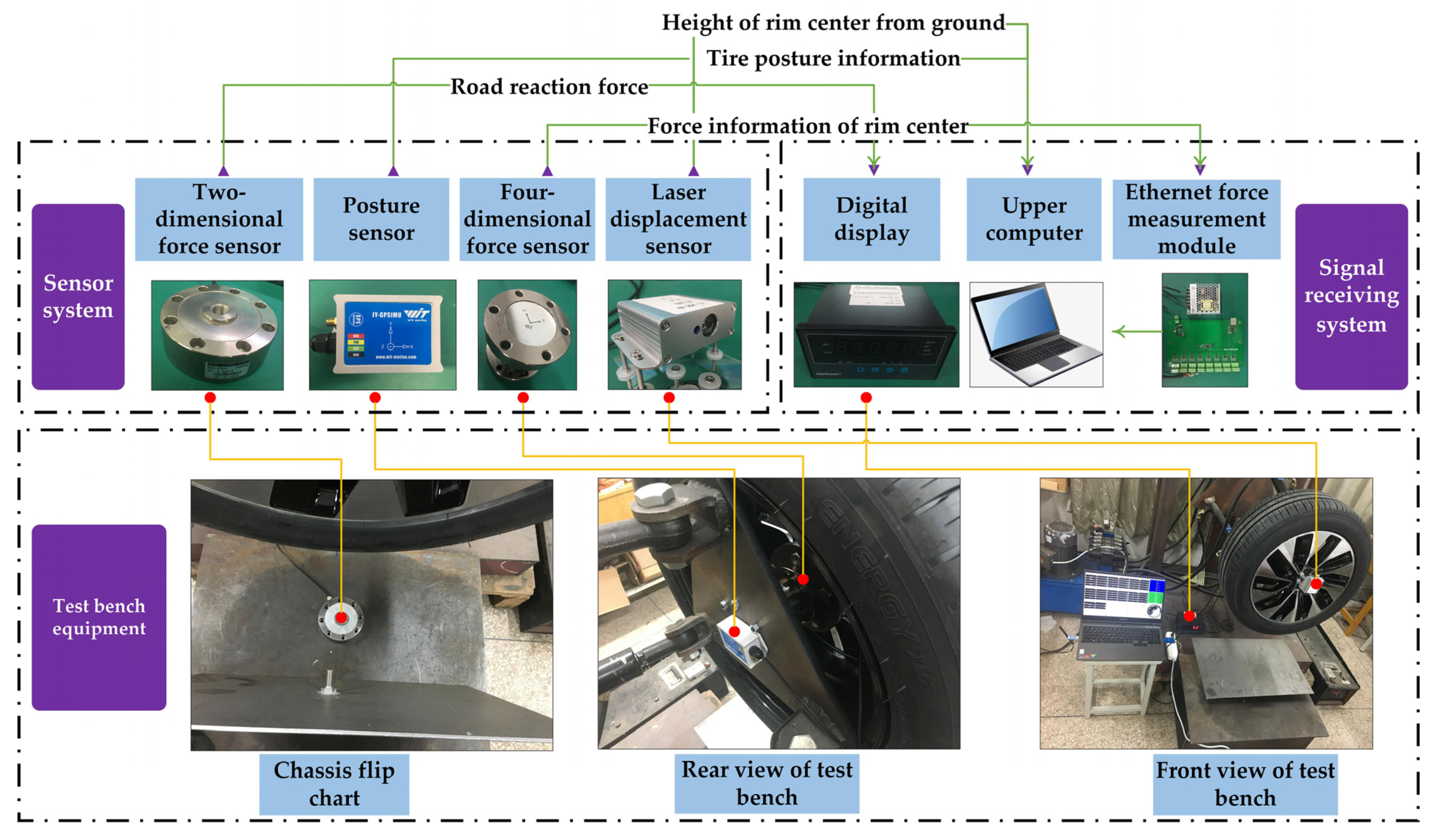
3.1. Statics Experiment Verification
- (a)
- Set tire inflation pressure; the inflation pressure range is 0.181 MPa to 0.281 MPa.
- (b)
- Adjust camber angle to 0° through the attitude sensor and the test bench controller.
- (c)
- Control the tire to move toward the bottom plate until the tire tread lightly touches the bottom plate, at this moment the pressure exerted by the tire on the road surface is 0 N.
- (d)
- Record the distance from the center of the rim to the bottom plate at this moment.
- (e)
- Use the controller to control the tire to move down, and simultaneously record the distance between the tire and the ground and the radial reaction force of the four-dimensional force sensor at the center of the rim.
- (f)
- Draw the radial stiffness curve.
3.2. Dynamic Experiments Validation
4. Simulation Results and Discussion
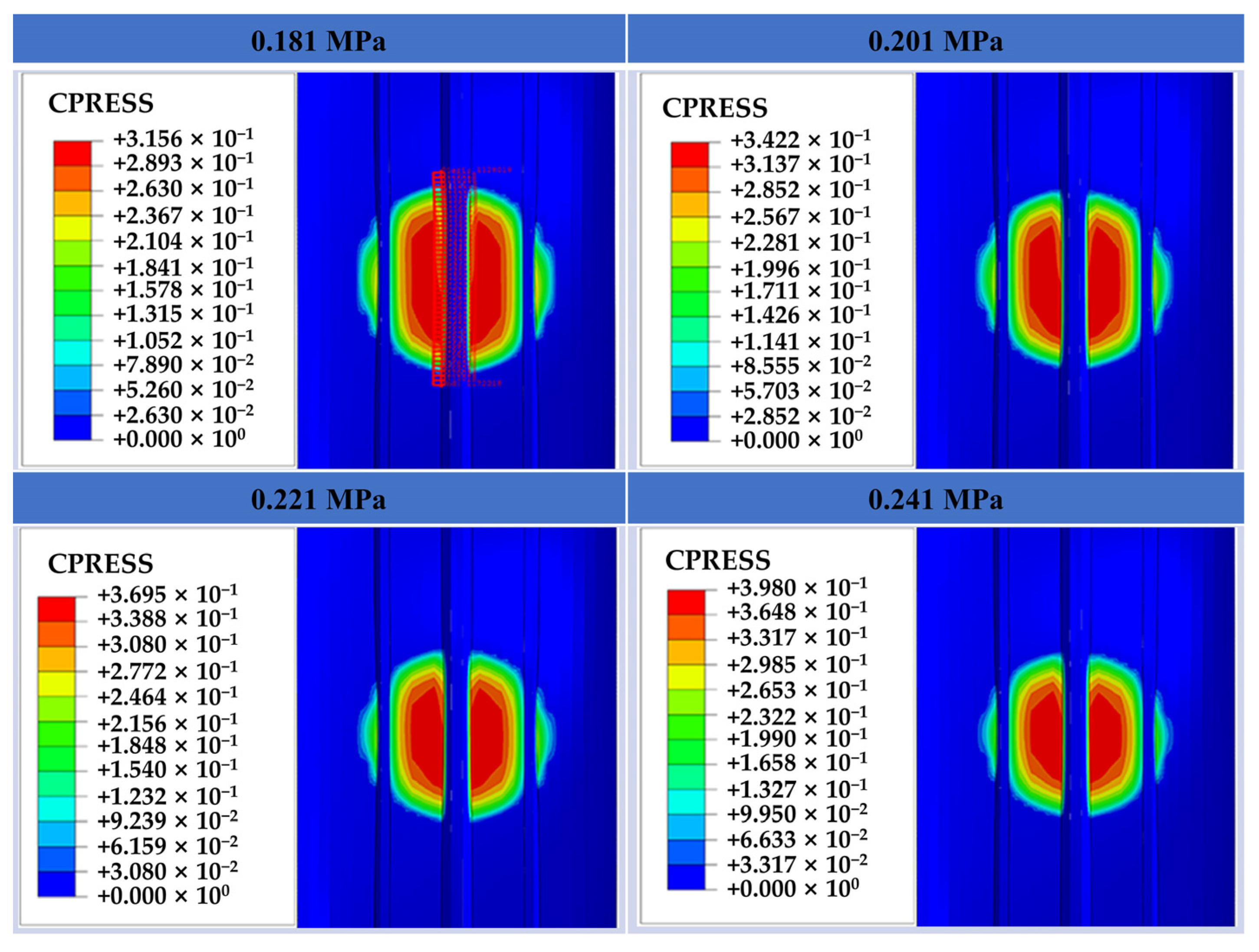
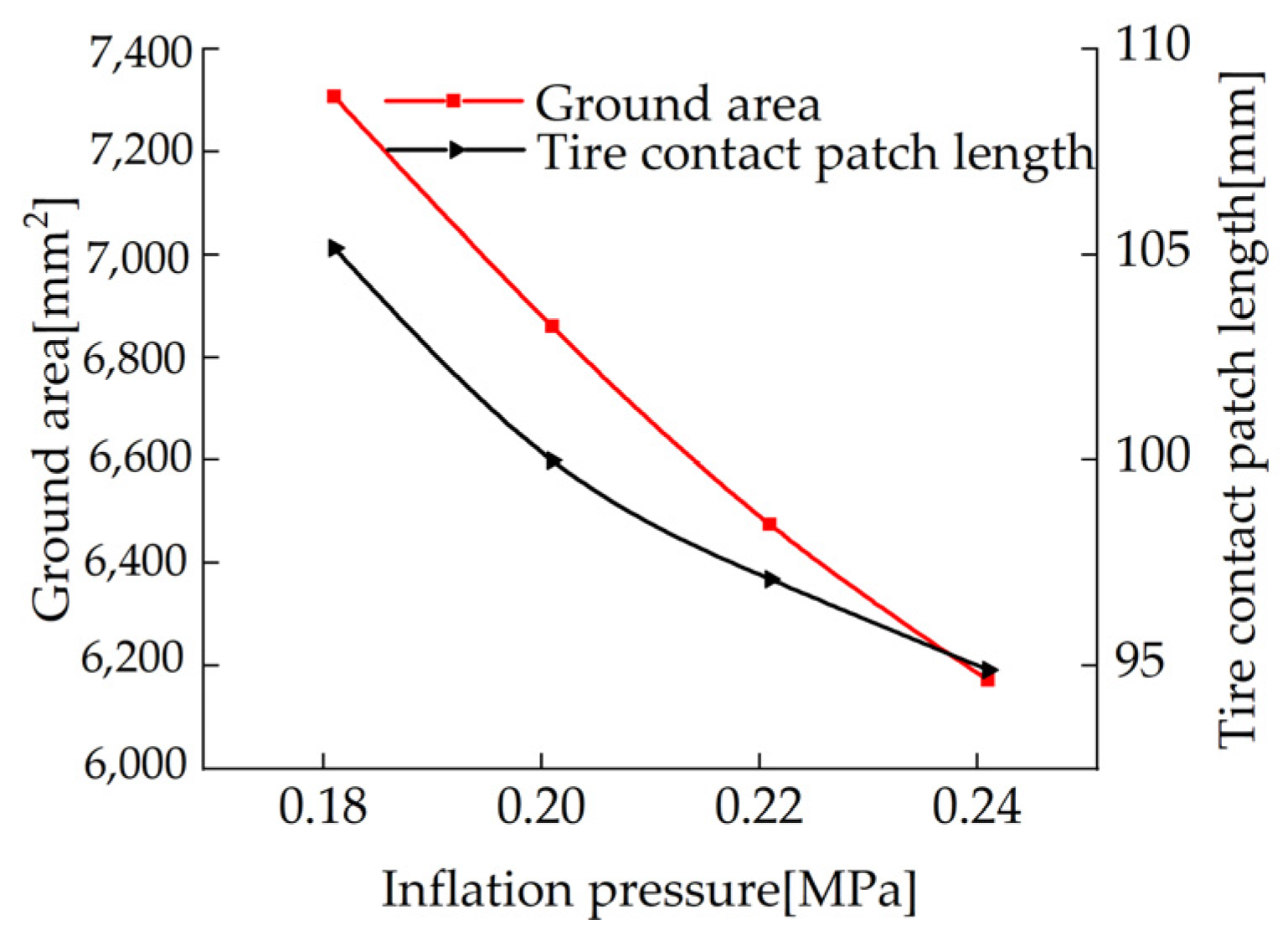
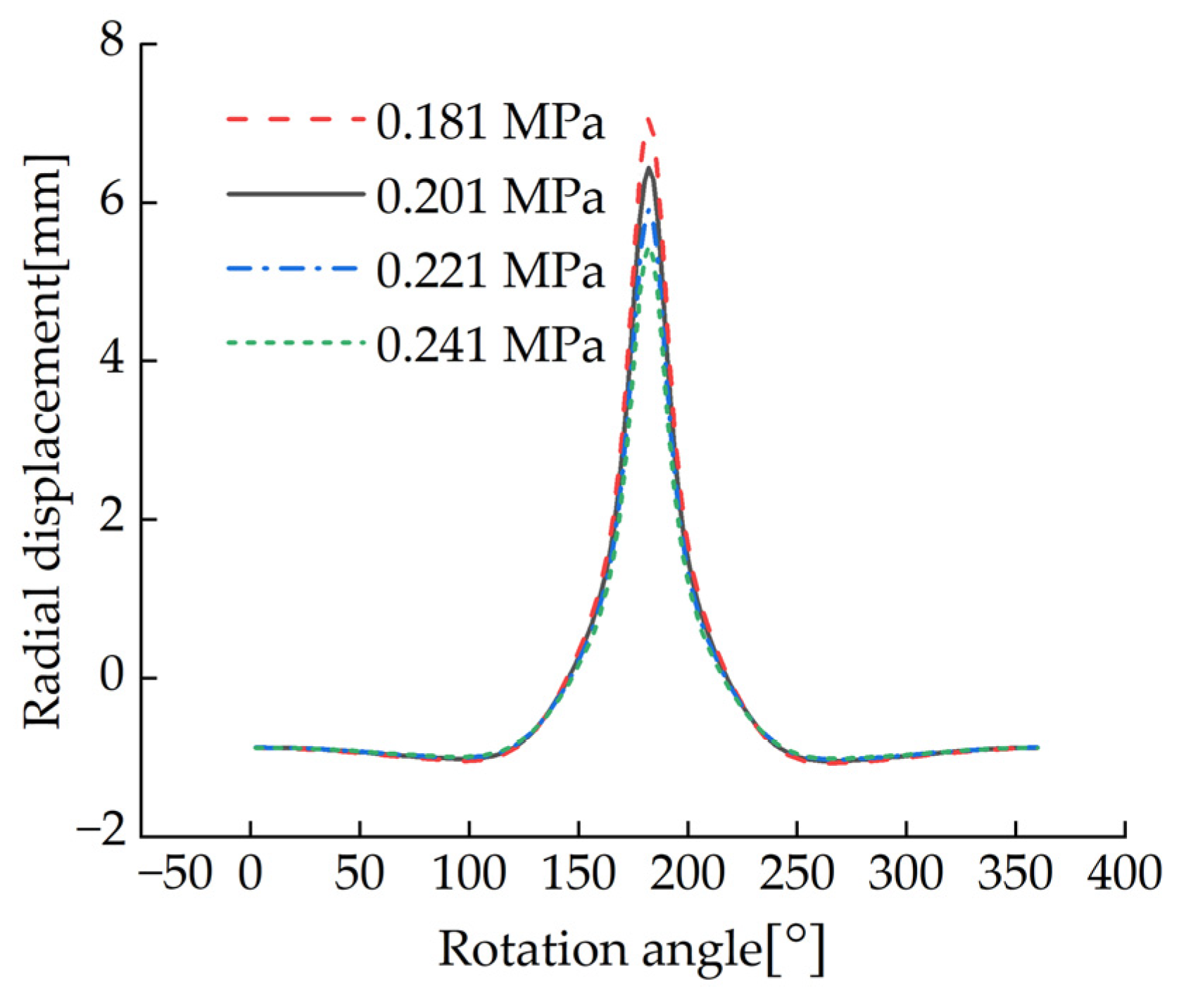
4.1. The Influence of Different Inflation Pressures on the Contact Patch
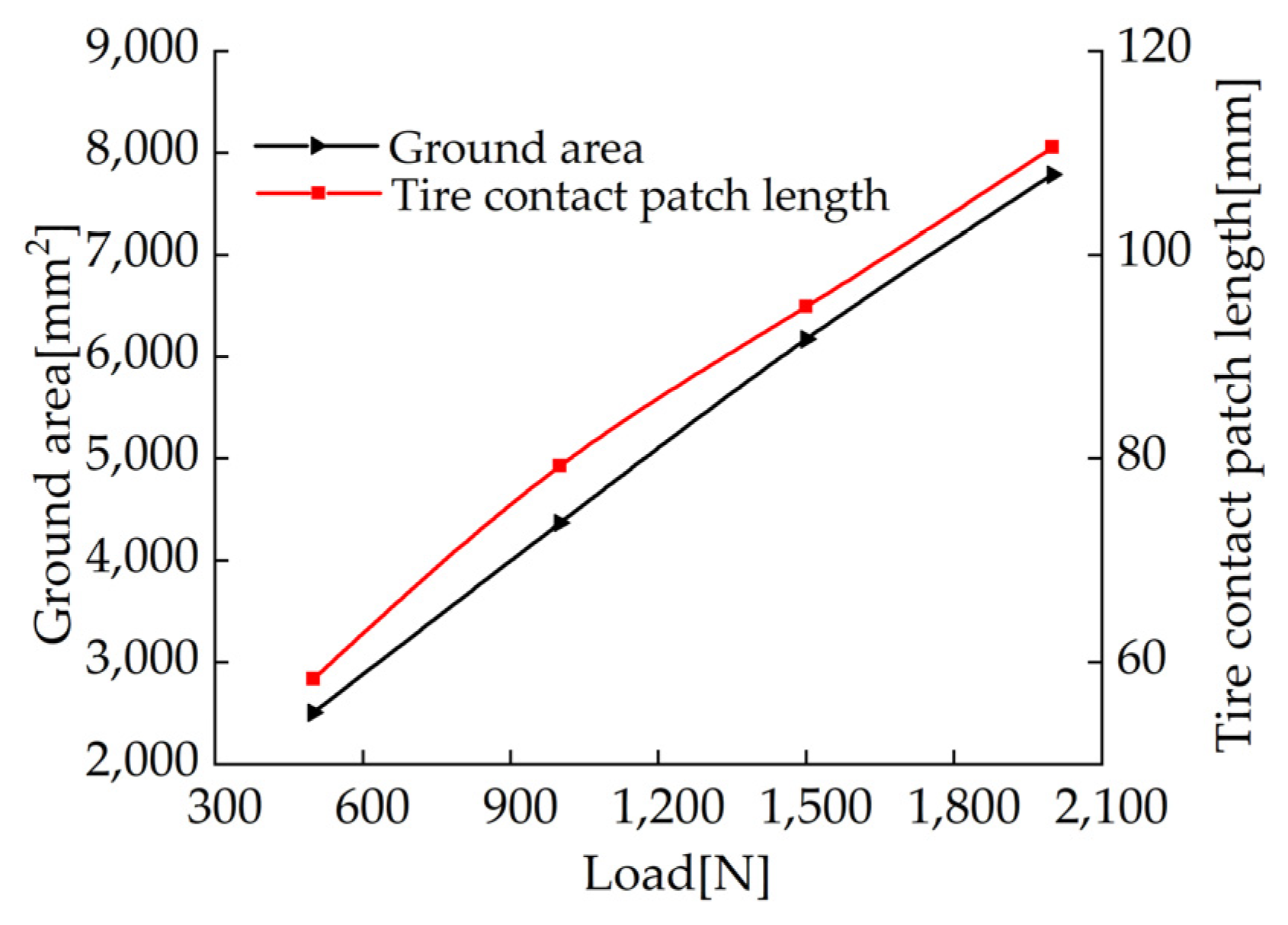
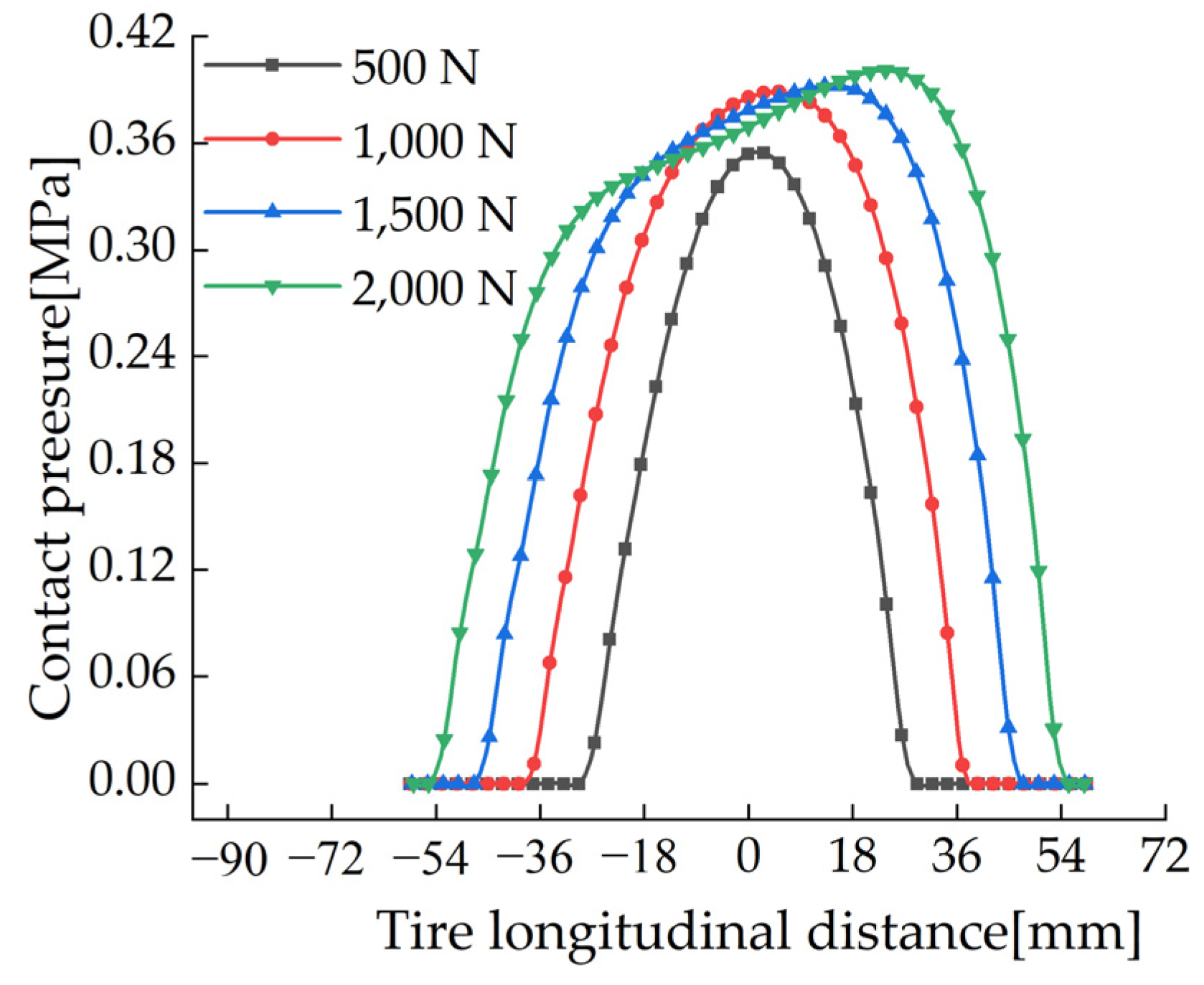
4.2. The Influence of Different Loads on the Contact Patch
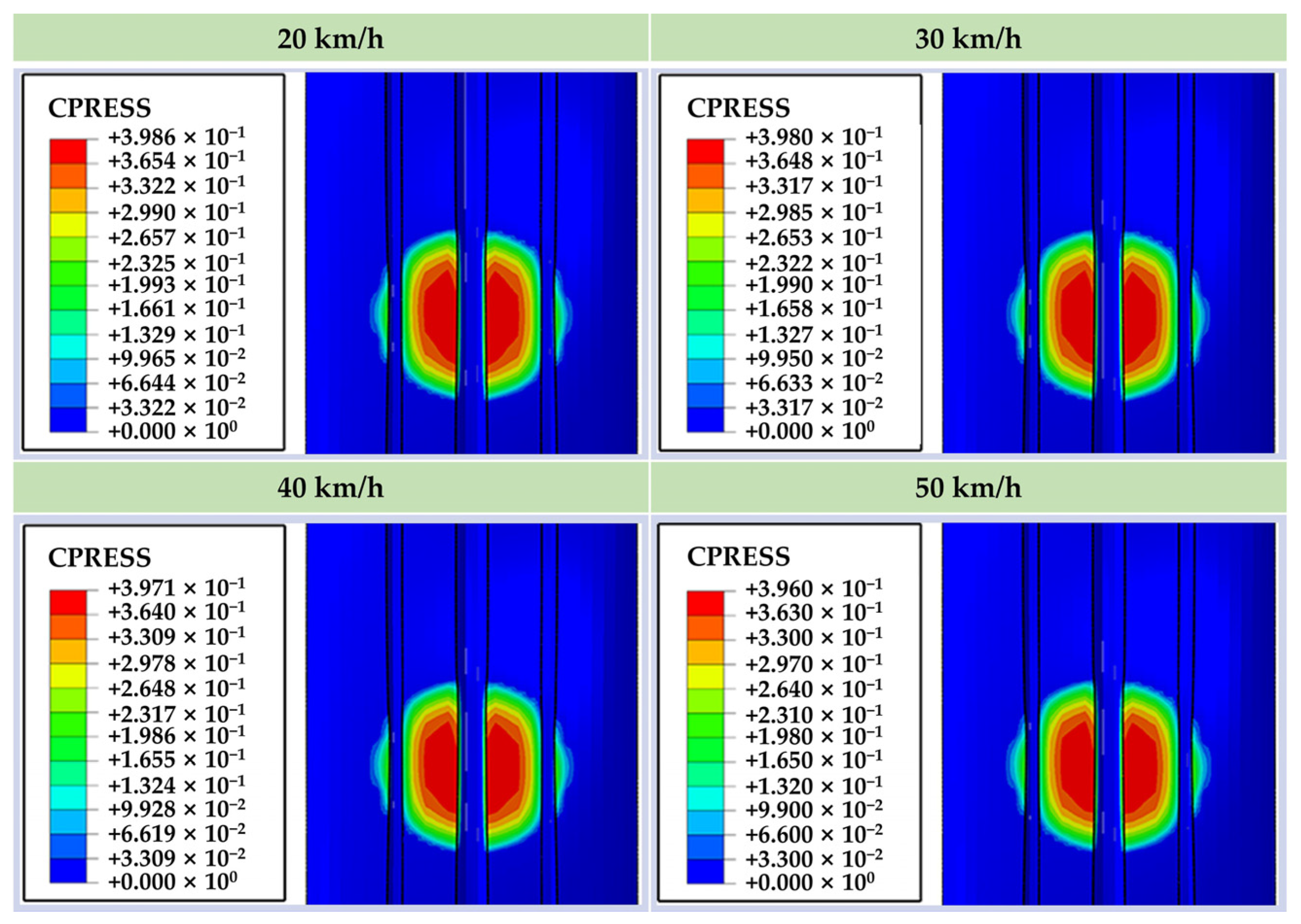
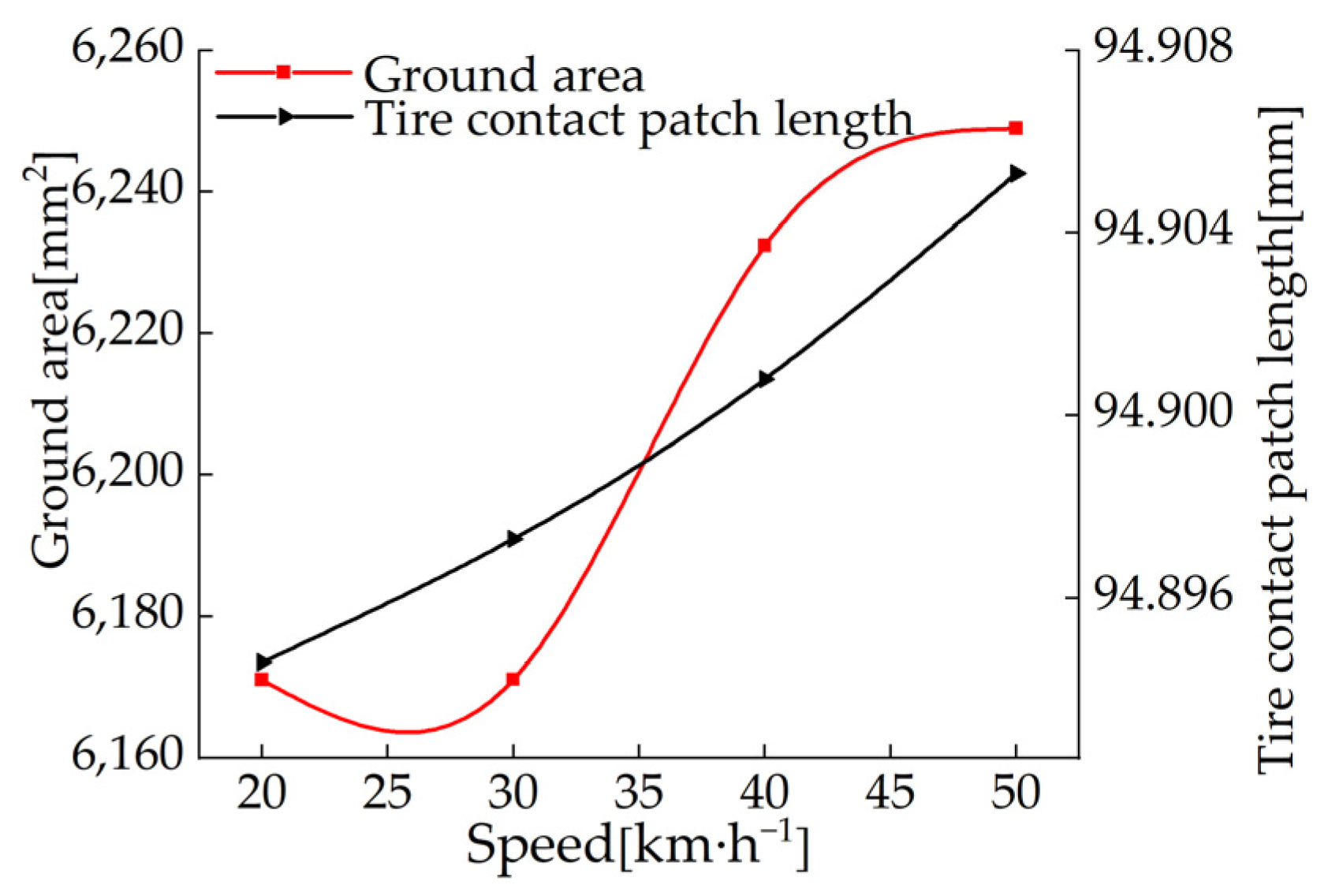
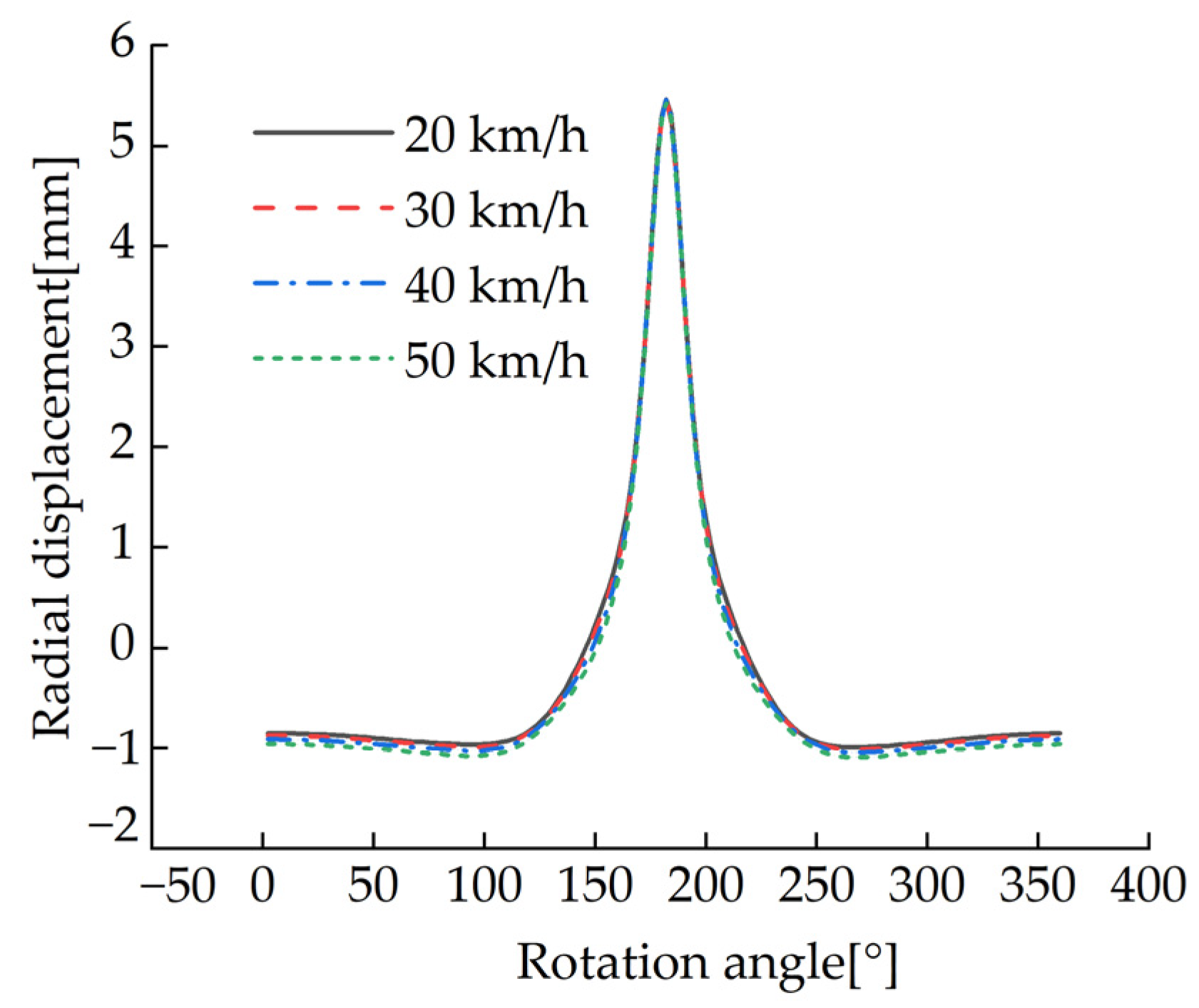
4.3. The Effect of Different Speeds on the Contact Patch
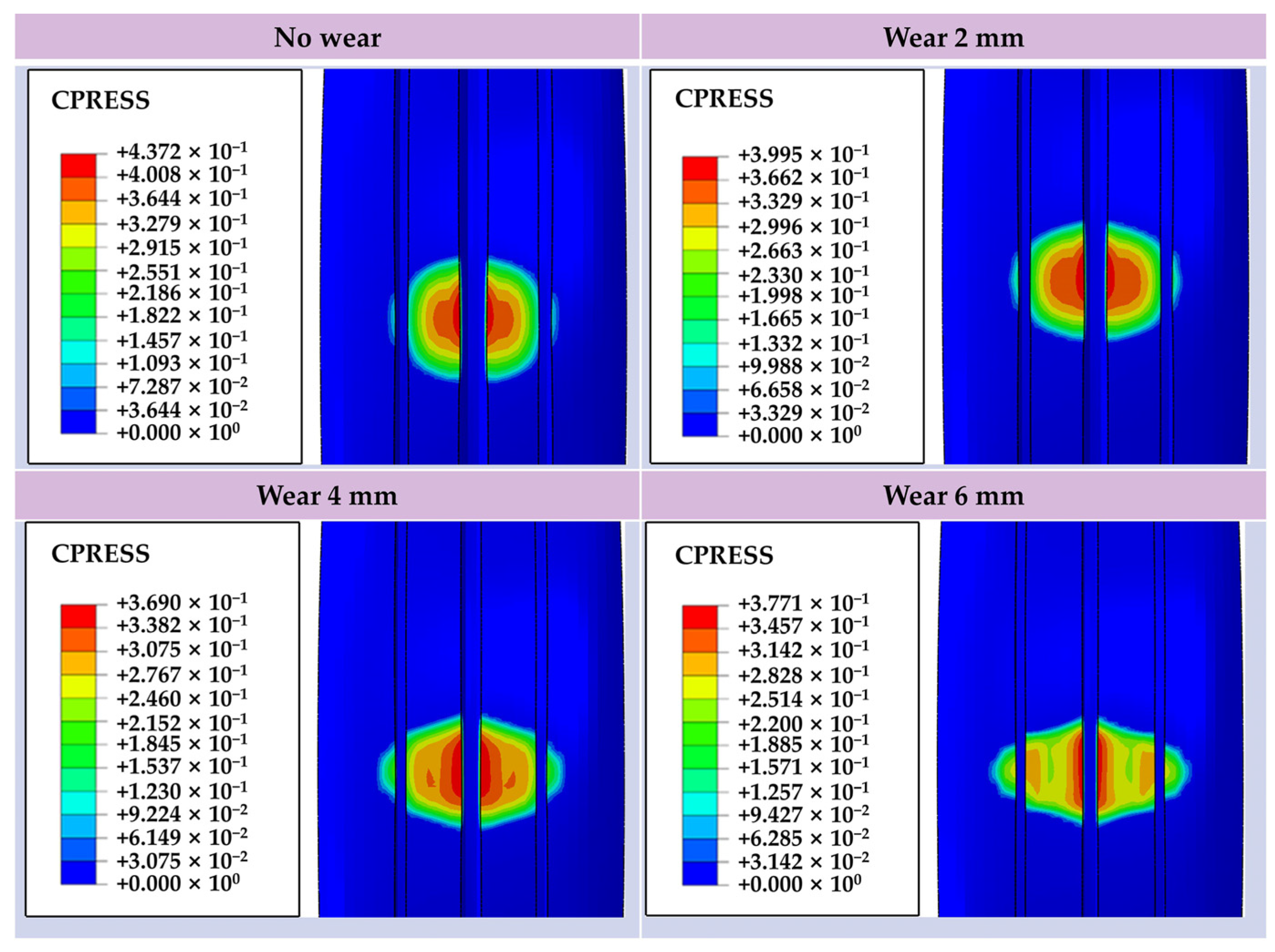
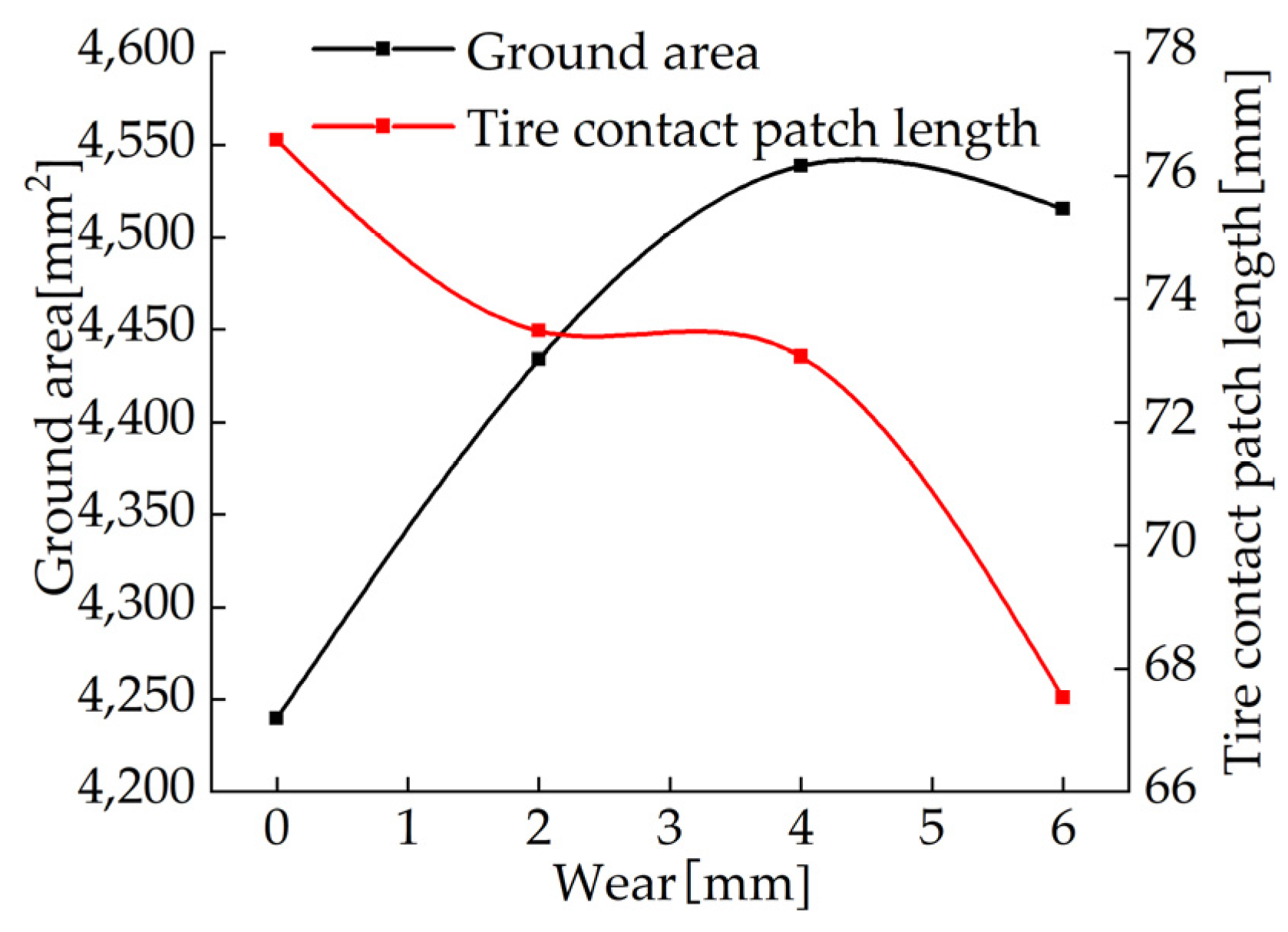
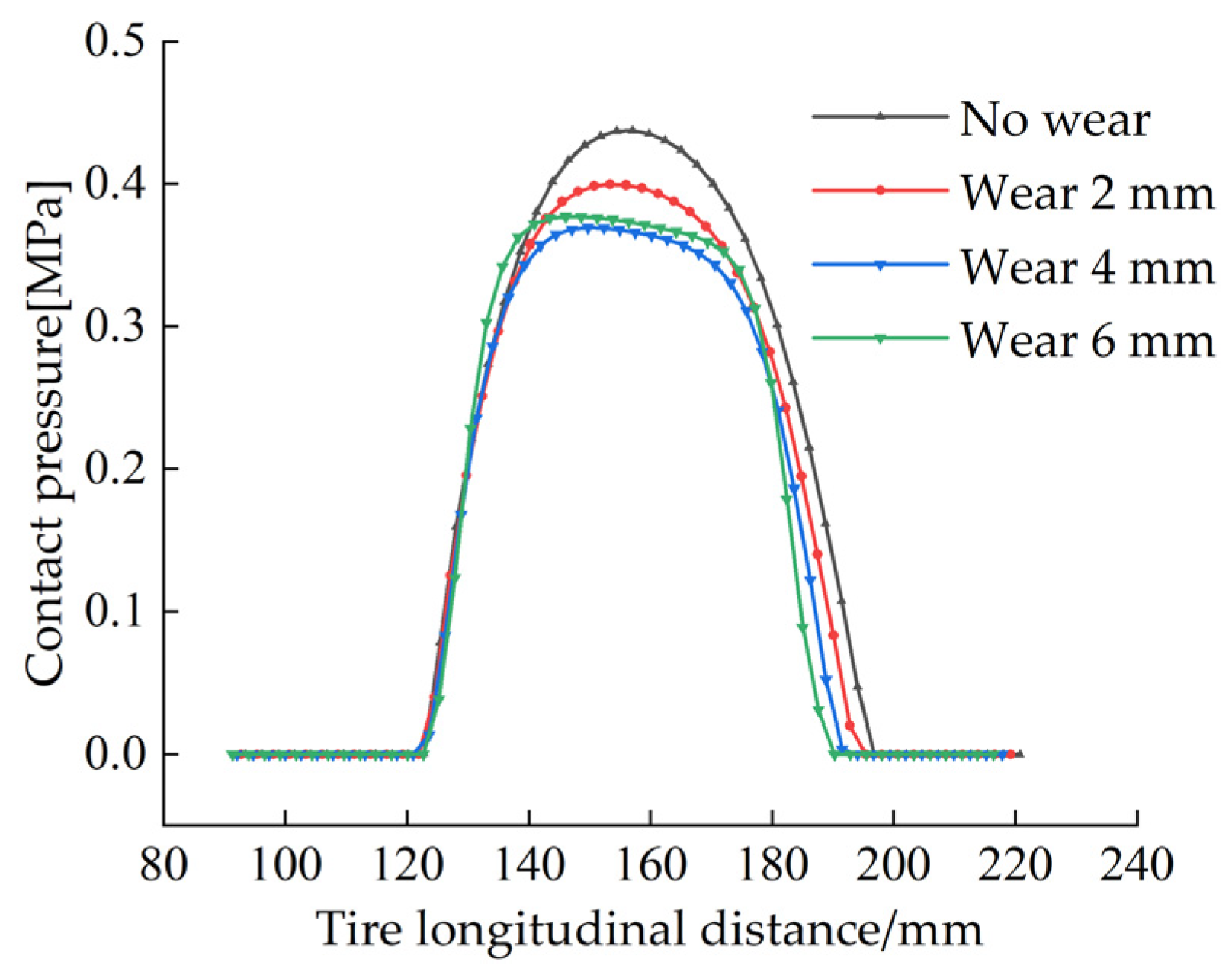
4.4. The Effects of Different Wear Amounts on the Contact Patch
5. Vertical Force Prediction
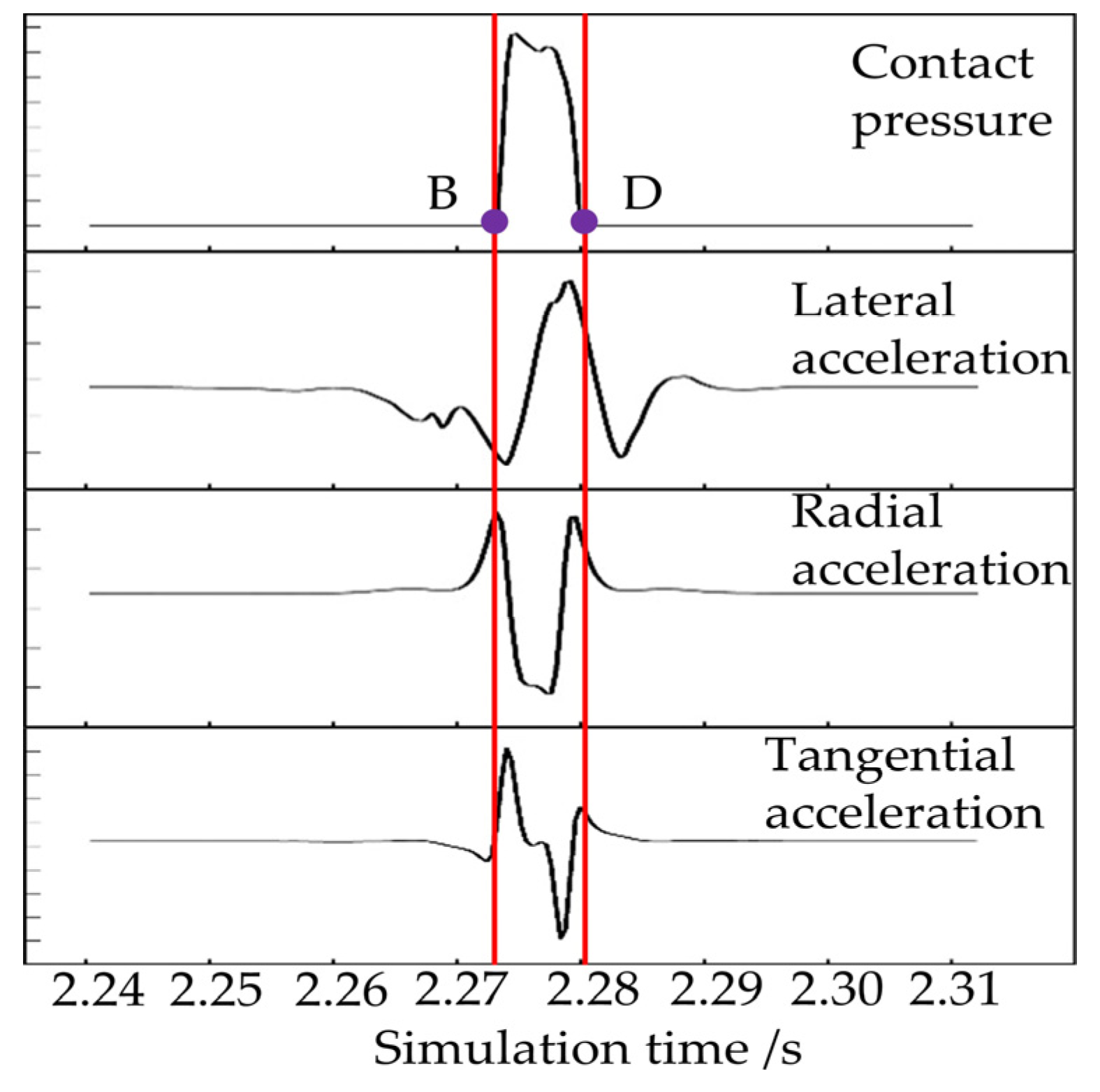
5.1. Determination of Input Characteristic Parameters
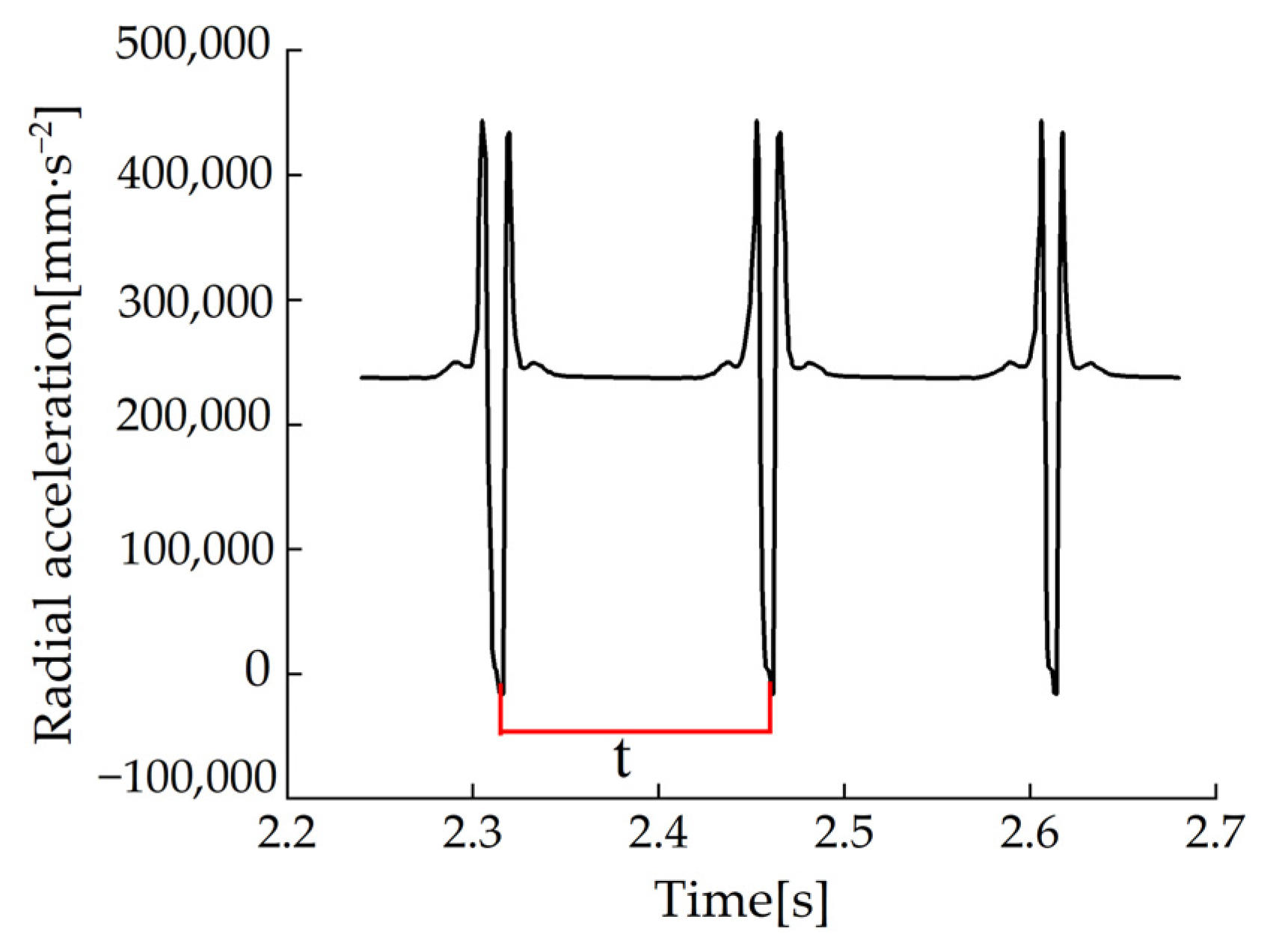
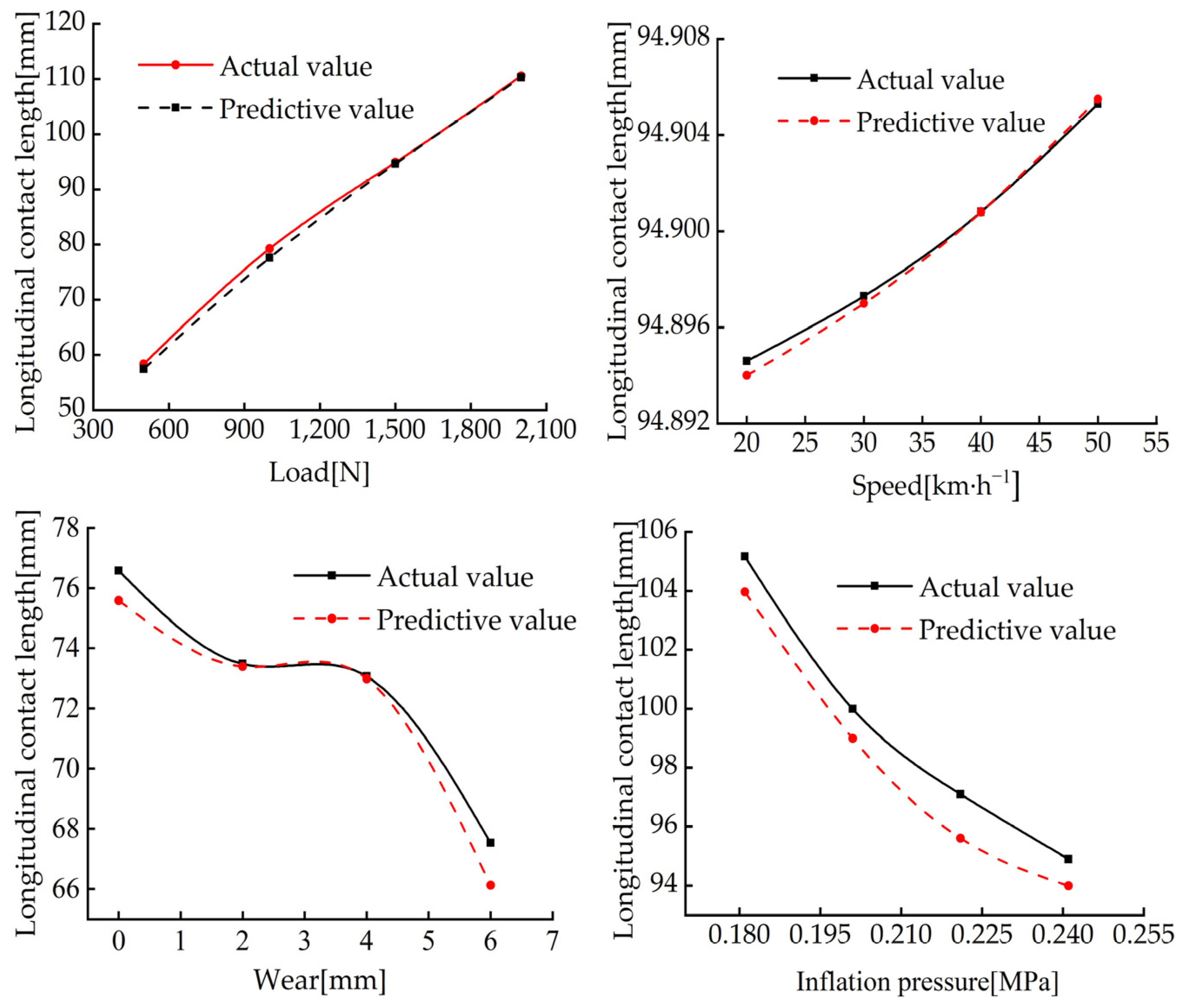
5.2. Estimation of the Length of the Longitudinal Contact Patch Length
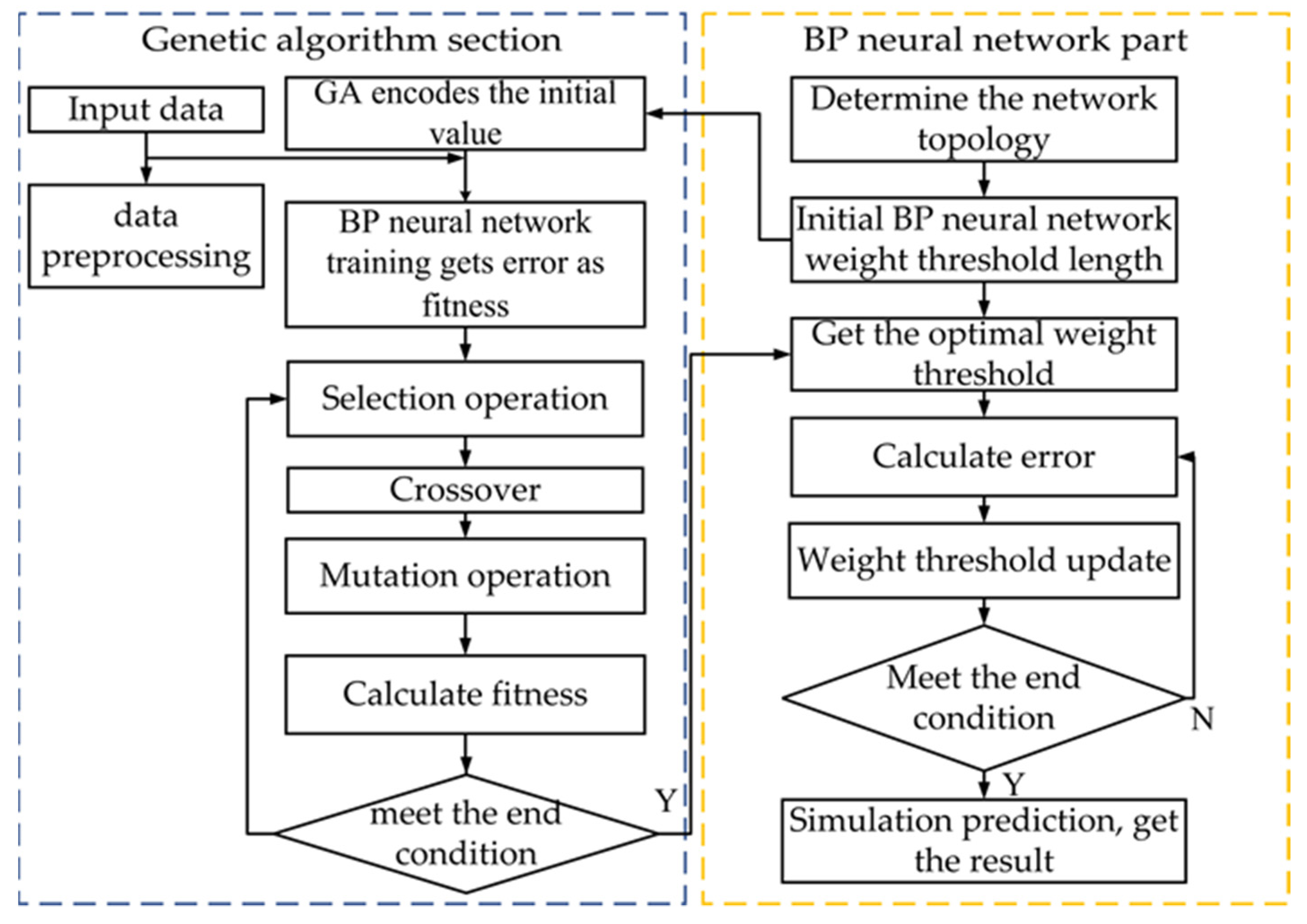
5.3. Vertical Force Calculation Algorithm Based on GA-BP Neural Network Algorithm
- (1)
- BP neural network
- (a)
- The forward propagation of the data flow, from the input layer through the hidden layer, finally reaches the output layer;
- (b)
- The back-propagation of the error, from the output layer to the hidden layer and finally to the input layer, constantly adjusts the weights and thresholds of each layer, when the error of the network output is reduced to the accuracy set according to a certain rule or reaches the set number of learning times stop.
- (2)
- Genetic Algorithm (GA)
- (1)
- Calculation of fitness function
- (2)
- Select operation
- (3)
- Crossover operation
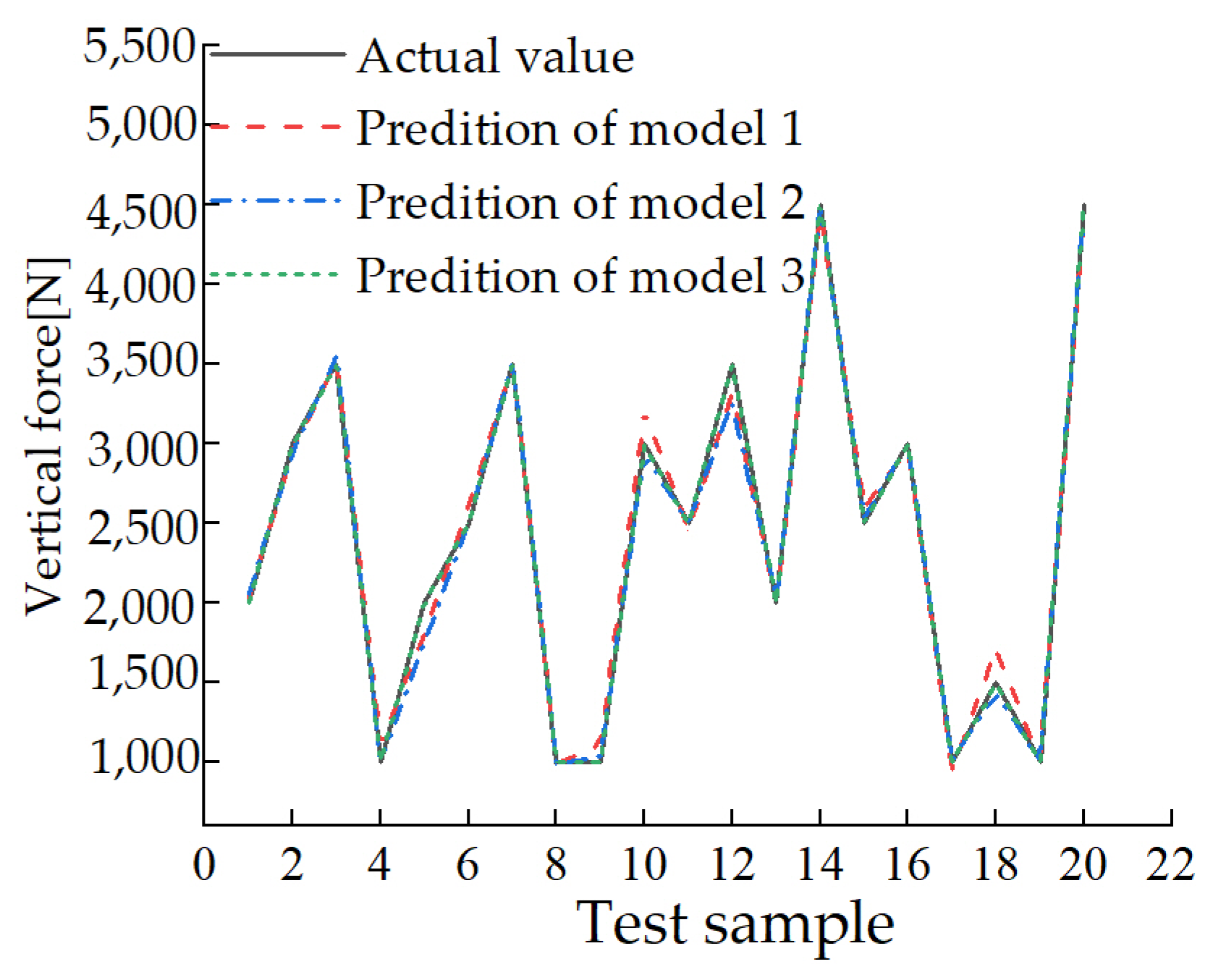
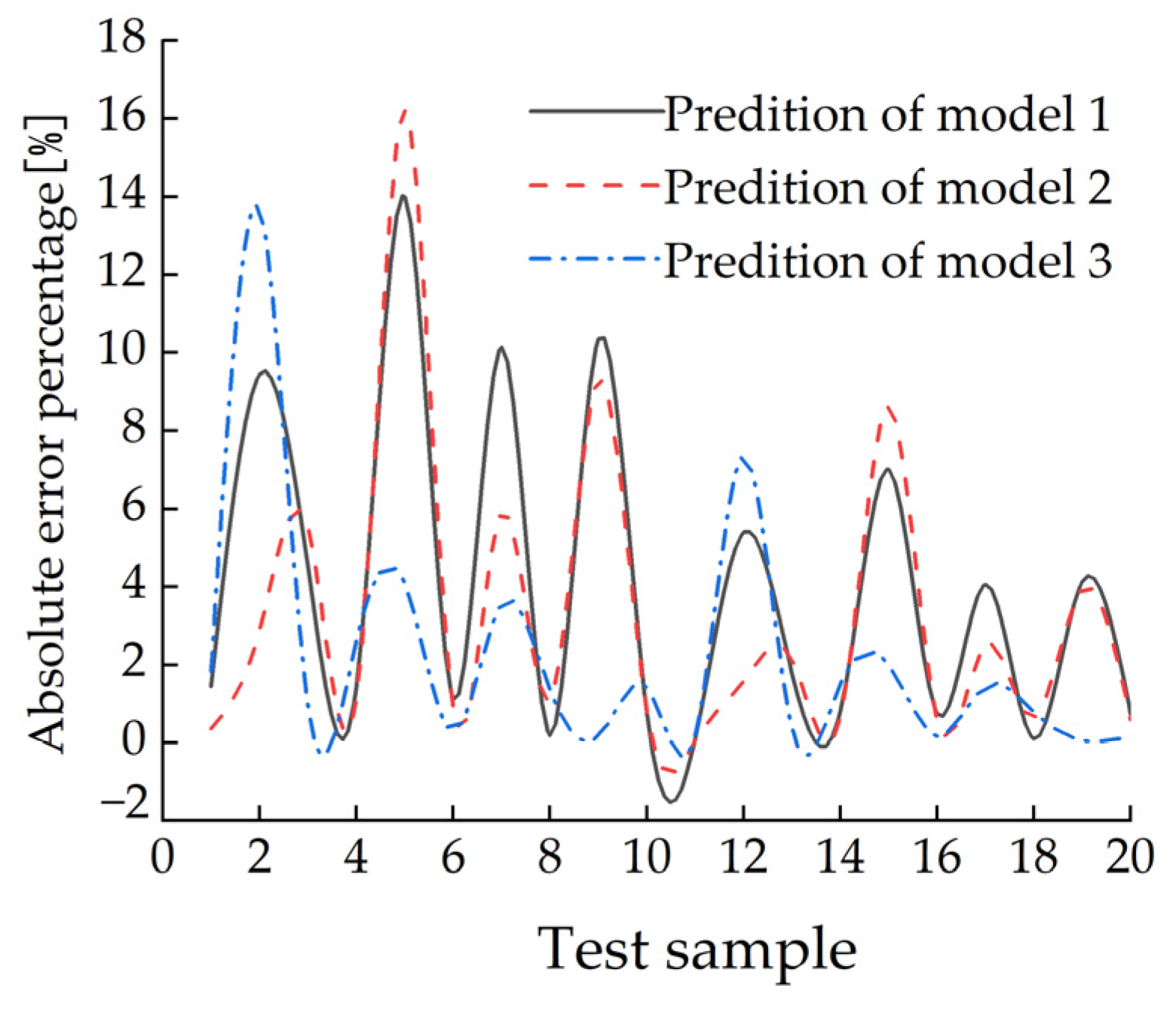
5.4. Analysis of the Estimation of Tire Vertical Force Results
6. Conclusions
- (1)
- The effects of different inflation pressure, speed, load and wear amount on the length of the longitudinal contact patch and the radial displacement at the virtual acceleration sensor are analyzed. The simulation results show that the length of the longitudinal contact patch decreases with the increase of inflation pressure and wear amount and increases with the increase of speed and load. The peak value of the radial displacement wave decreases with the increase of tire pressure and increases with the increase of load, but it is independent of the amount of tread wear and speed.
- (2)
- It was found that the radial acceleration signal of the virtual triaxial acceleration sensor has the highest correlation with the longitudinal length of the tire contact patch. The calculation method of the longitudinal contact patch length built with this signal has high prediction accuracy and good robustness. The mean absolute error is 0.64 mm.
- (3)
- According to the different input characteristic parameters, three vertical force prediction models based on GA-BP neural network algorithm are established. The inputs of Model 1 are inflation pressure, speed and length of longitudinal contact patch; Model 2 considers the influence of tread wear on the basis of Model 1, and its input features are inflation pressure, speed, length of longitudinal contact patch and tread wear. The input quantities of Model 3 are the peak value of radial displacement and inflation pressure. The mean absolute error, mean absolute error percentage and computation time of the three forecasting models were compared. The prediction results show that the three evaluation indicators of the Prediction Model 3 are all optimal, which are more suitable for practical engineering applications, and can further improve vehicle safety, handling stability, fuel economy and ride comfort.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, G.L.; Han, T.; Zhou, H.C.; Ding, J.J. Vertical Force Estimation Algorithm of Intelligent Tires Based on Physical Model. Automot. Eng. 2021, 43, 1865–1870. [Google Scholar]
- Rajendran, S.; Spurgeon, K.S.; Tsampardoukas, G.; Hampson, R. Estimation of road Frictional Force and Wheel Slip for Effective Antilock Braking System (ABS) Control. Int. J. Robust 2019, 29, 736–765. [Google Scholar] [CrossRef] [Green Version]
- Khaleghian, S.; Emami, A.; Taheri, S. A Technical Survey on Tire-Road Friction Estimation. Friction 2017, 5, 123–146. [Google Scholar] [CrossRef] [Green Version]
- Rezaeian, A.; Zarringhalam, R.; Fallah, S.R.; Melek, W.; Khajepour, A.; Chen, S.K.; Moshchuck, N.; Litkouhi, B. Novel Tire Force Estimation Strategy for Real-time Implementation on Vehicle Applications. IEEE Trans. Veh. Technol. 2014, 64, 2231–2241. [Google Scholar] [CrossRef]
- Cho, W.; Yoon, J.; Yim, S.; Koo, B.; Yi, K. Estimation of Tire Forces for Application to Vehicle Stability Control. IEEE Trans. Veh. Technol. 2009, 59, 638–649. [Google Scholar]
- Doumiati, M.; Victorino, A.; Lechner, D.; Baffet, G.; Charara, A. Observers for vehicle tyre/road forces estimation: Experimental validation. Veh. Syst. Dyn. 2010, 48, 1345–1378. [Google Scholar] [CrossRef]
- Ye, H.; Liu, G.H.; Zhang, D.; Wang, Y. Estimating Longitudinal Velocity of Four-Wheel-Independent-Driving Electric Vehicle based on RKF Tire Force Estimator. Mech. Sci. Technol. Aerosp. Eng. 2017, 36, 637–642. [Google Scholar]
- Antonov, S.; Fehn, A.; Kugi, A. Unscented Kalman Filter for Vehicle State Estimation. Veh. Syst. Dyn. 2011, 49, 1497–1520. [Google Scholar] [CrossRef]
- Zhang, X.W.; Wang, F.Y. Opportunities and Challenges for Tires Intelligent Manufacturing from Smart tires. Sci. Technol. 2018, 36, 38–47. [Google Scholar]
- Garcia-Pozuelo, D.; Olatunbosun, O.; Yunta, J.; Yang, X.G.; Diaz, V. A Novel Strain-Based Method to Estimate Tire Conditions Using Fuzzy Logic for Intelligent tires. Sensors 2017, 17, 350. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.J.; Zhang, F.; Zhang, S.W.; Wu, Z.Q.; We, S.; Wang, F. Vertical Load Measurement of Automotive Intelligent Tire. Automot. Eng. 2020, 42, 1270–1276. [Google Scholar]
- Zhao, J.; Lu, Y.H.; Zhu, B.; Liu, S.L. Estimation Algorithm for Longitudinal and Vertical Forces of Smart Tire with Accelerometer Embedded. Automot. Eng. 2018, 40, 137–142. [Google Scholar]
- Xu, N.; Askari, H.; Huang, Y.J.; Zhou, J.F.; Khajepour, A. Tire Force Estimation in Intelligent Tires Using Machine Learning. IEEE Trans. Intell. Transp. 2020, 23, 3565–3574. [Google Scholar] [CrossRef]
- Garcia-Pozuelo, D.; Yunta, J.; Olatunbosun, O.; Yang, X.G.; Diaz, V. A Strain-Based Method to Estimate Slip Angle and Tire Working Conditions for Intelligent tires Using Fuzzy Logic. Sensors 2017, 17, 874. [Google Scholar] [CrossRef] [PubMed]
- Tuononen, A.J.; Matilainen, M.J. Real-time Estimation of Aquaplaning with an Optical Tyre Sensor. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2009, 223, 1263–1272. [Google Scholar] [CrossRef]
- Yilmazoglu, O.; Brandt, M.; Sigmund, J.; Genc, E.; Hartnagel, H.L. Integrated InAs/GaSb 3D magnetic field sensors for “the intelligent Tire”. Sens. Actuators A 2001, 94, 59–63. [Google Scholar] [CrossRef]
- Erdogan, G.; Alexander, L.; Rajamani, R. Estimation of Tire-road Friction Coefficient Using a Novel Wireless Piezoelectric Tire Sensor. IEEE Sens. J. 2011, 11, 267–279. [Google Scholar] [CrossRef]
- Pohl, A.; Steindl, R.; Reindl, L. The “intelligent tire” utilizing passive SAW sensors measurement of tire friction. IEEE Trans. Instrum. Meas. 1999, 48, 1041–1046. [Google Scholar] [CrossRef]
- Xu, N.; Huang, Y.J.; Askari, H.; Tang, Z.P. Tire Slip Angle Estimation Based on the Intelligent Tire Technology. IEEE Trans. Veh. Technol. 2021, 70, 2239–2249. [Google Scholar] [CrossRef]
- Li, B.; Quan, Z.Q.; Bei, S.Y.; Zhang, L.C.; Mao, H.J. An Estimation Algorithm for Tire Wear Using Intelligent Tire Concept. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 2712–2725. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, J.; Gu, Z.Q.; Liu, Z.Z.; Zheng, L.D. Research on Sound Quality Prediction Model of Automobile Wind Buffeting Noise Based on GA-BP. Chin. J. Mech. Eng. 2021, 57, 241–249. [Google Scholar]
- Singh, K.B.; Taheri, S. Accelerometer based Method for Tire Load and Slip angle Estimation. Vibration 2019, 2, 174–186. [Google Scholar] [CrossRef] [Green Version]
- Zhou, M.; Lü, Z.G.; Di, R.H.; Li, Y. BP Neural Network Modeling Based on Small Sample Data. Sci. Technol. Eng. 2022, 22, 2754–2760. [Google Scholar]
- Zheng, D.; Qian, Z.D.; Liu, Y.; Liu, C.B. Prediction and Sensitivity Analysis of Long-Term Skid Resistance of Epoxy Asphalt Mixture Based on GA-BP Neural Network. Constr. Build. Mater. 2018, 158, 614–623. [Google Scholar] [CrossRef]
- Che, Y.; Xiao, W.X.; Chen, L.J.; Huang, Z.C. GA-BP Neural Network Based Tire Noise Prediction. Adv. Mater. Res. 2012, 443–444, 65–70. [Google Scholar] [CrossRef]
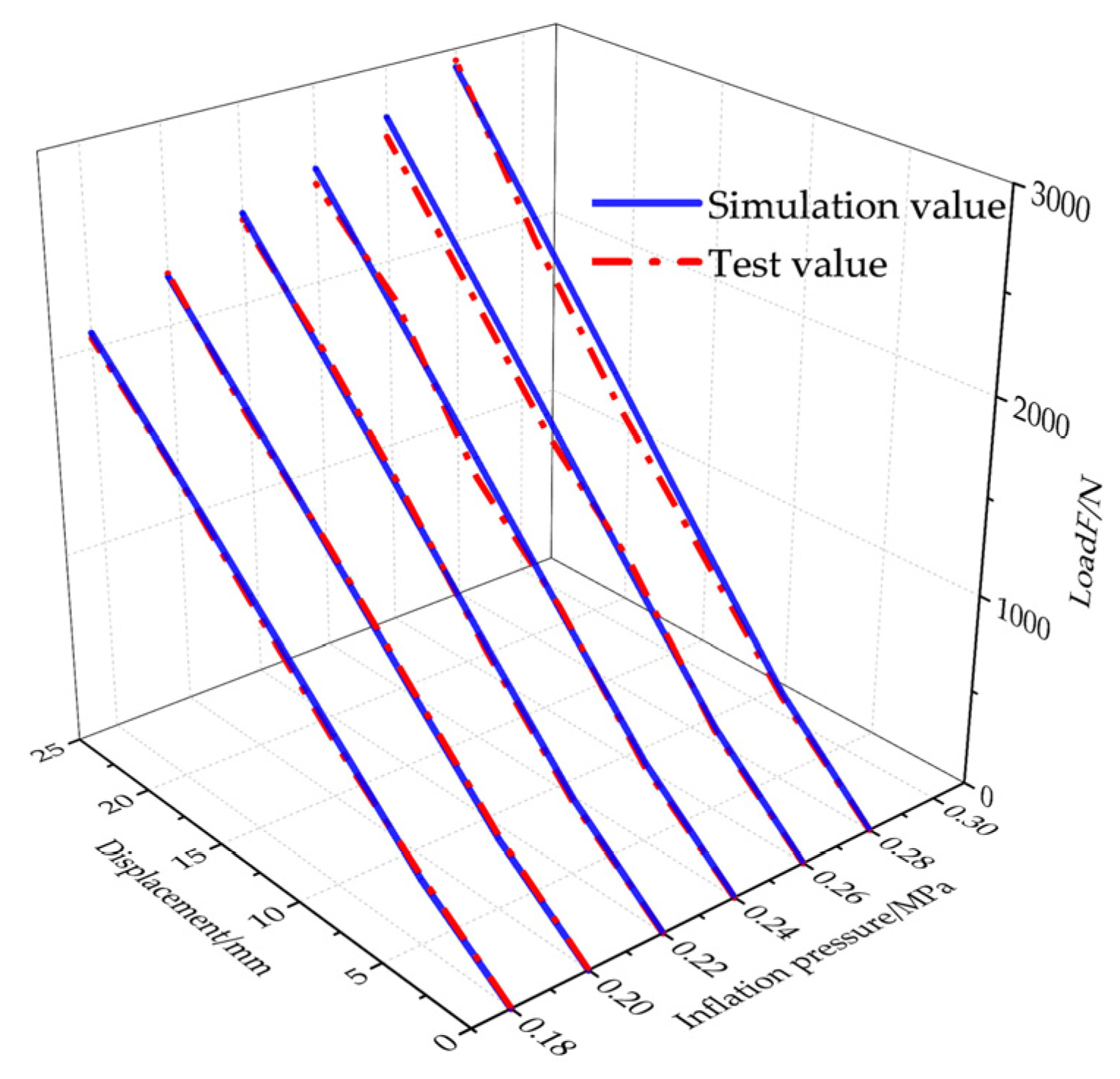









| Inflation Pressure (MPa) | Simulation Value (N) | Test Value (N) | Absolute Error Percentage (%) |
|---|---|---|---|
| 0.18 | 1006 | 993.3 | 1.27 |
| 0.20 | 1087 | 1091.7 | 0.43 |
| 0.22 | 1186 | 1182.3 | 0.31 |
| 0.24 | 1246 | 1224.8 | 1.73 |
| 0.26 | 1324 | 1280.5 | 3.4 |
| 0.28 | 1402 | 1353.3 | 3.6 |
| Predictive Model | Input | Output |
|---|---|---|
| Predictive model 1 | Inflation pressure, speed, longitudinal contact patch length | Vertical force |
| Predictive mode 2 | Inflation pressure, speed, longitudinal contact patch length, wear amount | |
| Predictive mode 3 | Inflation pressure, radial displacement peak value |
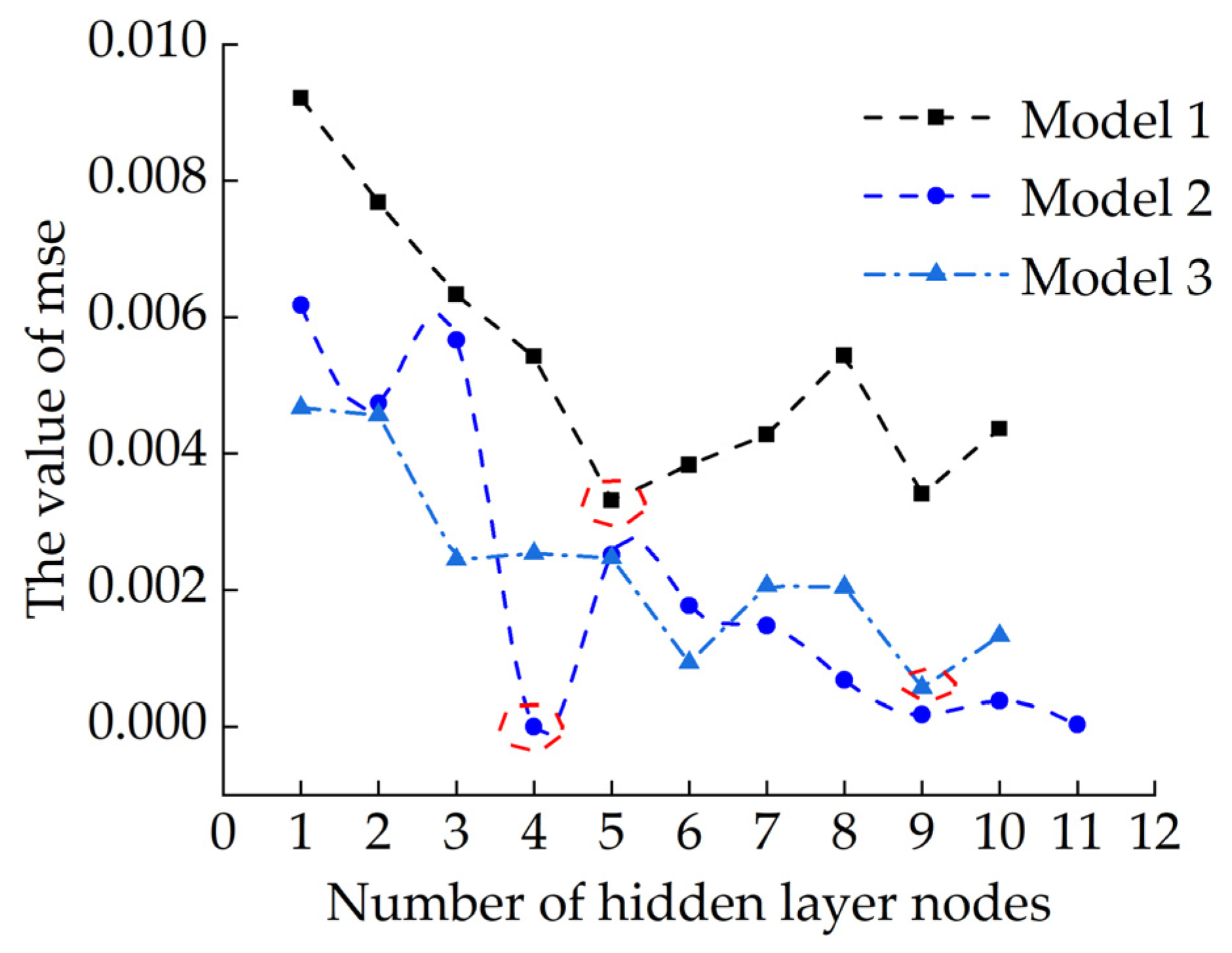
| Method | Parameter | The Number of Neurons in the Hidden Layer | Hidden Layer Activation Function | Output Layer Activation Function | Target Error | Iteration Upper Limit | Learning Rate |
|---|---|---|---|---|---|---|---|
| Model 1 | Value | 5 | 4 × 10−5 | 10,000 | 0.1 | ||
| Model 2 | 4 | ||||||
| Model 3 | 9 |
| Parameter Name | Parameter Value |
|---|---|
| Number of iterations | 200 |
| Population size | 60 |
| Crossover probability | 0.5 |
| Mutation probability | 0.05 |
| Predictive Model | Input | MAE(N) | MPAE (%) | Calculation Time |
|---|---|---|---|---|
| Model 1 | Inflation pressure, speed, longitudinal contact patch length | 75.73 | 3.9% | 0.031 |
| Model 2 | Inflation pressure, speed, longitudinal contact patch length, wear amount | 64.60 | 3.3% | 0.033 |
| Model 3 | Inflation pressure, radial displacement peak value | 47.55 | 2.2% | 0.021 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, T.; Li, B.; Quan, Z.; Bei, S.; Yin, G.; Guo, J.; Zhou, X.; Han, X. The Vertical Force Estimation Algorithm Based on Smart Tire Technology. World Electr. Veh. J. 2022, 13, 104. https://doi.org/10.3390/wevj13060104
Gu T, Li B, Quan Z, Bei S, Yin G, Guo J, Zhou X, Han X. The Vertical Force Estimation Algorithm Based on Smart Tire Technology. World Electric Vehicle Journal. 2022; 13(6):104. https://doi.org/10.3390/wevj13060104
Chicago/Turabian StyleGu, Tianli, Bo Li, Zhenqiang Quan, Shaoyi Bei, Guodong Yin, Jinfei Guo, Xinye Zhou, and Xiao Han. 2022. "The Vertical Force Estimation Algorithm Based on Smart Tire Technology" World Electric Vehicle Journal 13, no. 6: 104. https://doi.org/10.3390/wevj13060104
APA StyleGu, T., Li, B., Quan, Z., Bei, S., Yin, G., Guo, J., Zhou, X., & Han, X. (2022). The Vertical Force Estimation Algorithm Based on Smart Tire Technology. World Electric Vehicle Journal, 13(6), 104. https://doi.org/10.3390/wevj13060104








