Thermal Analysis of Automobile Drive Axles by the Thermal Network Method
Abstract
:1. Introduction
2. Thermal Analysis of a Two-Axle Automobile Drive Axle
2.1. Thermal Network Model of a Two-Axle Automobile Drive Axle
2.1.1. Thermal Network Diagram of a Two-Axle Automobile Drive Axle
2.1.2. Thermal Balance Equations of a Two-Axle Automobile Drive Axle
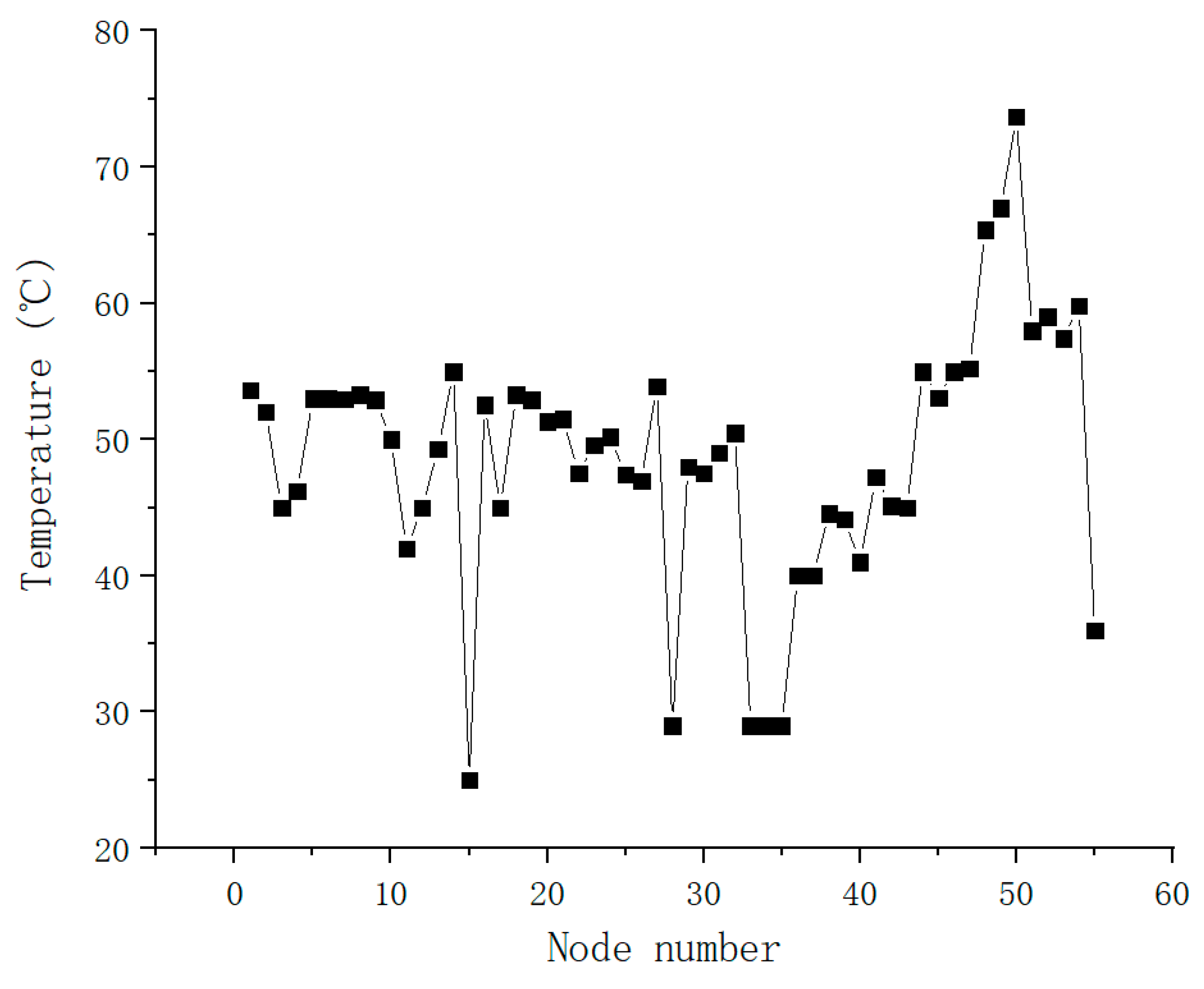
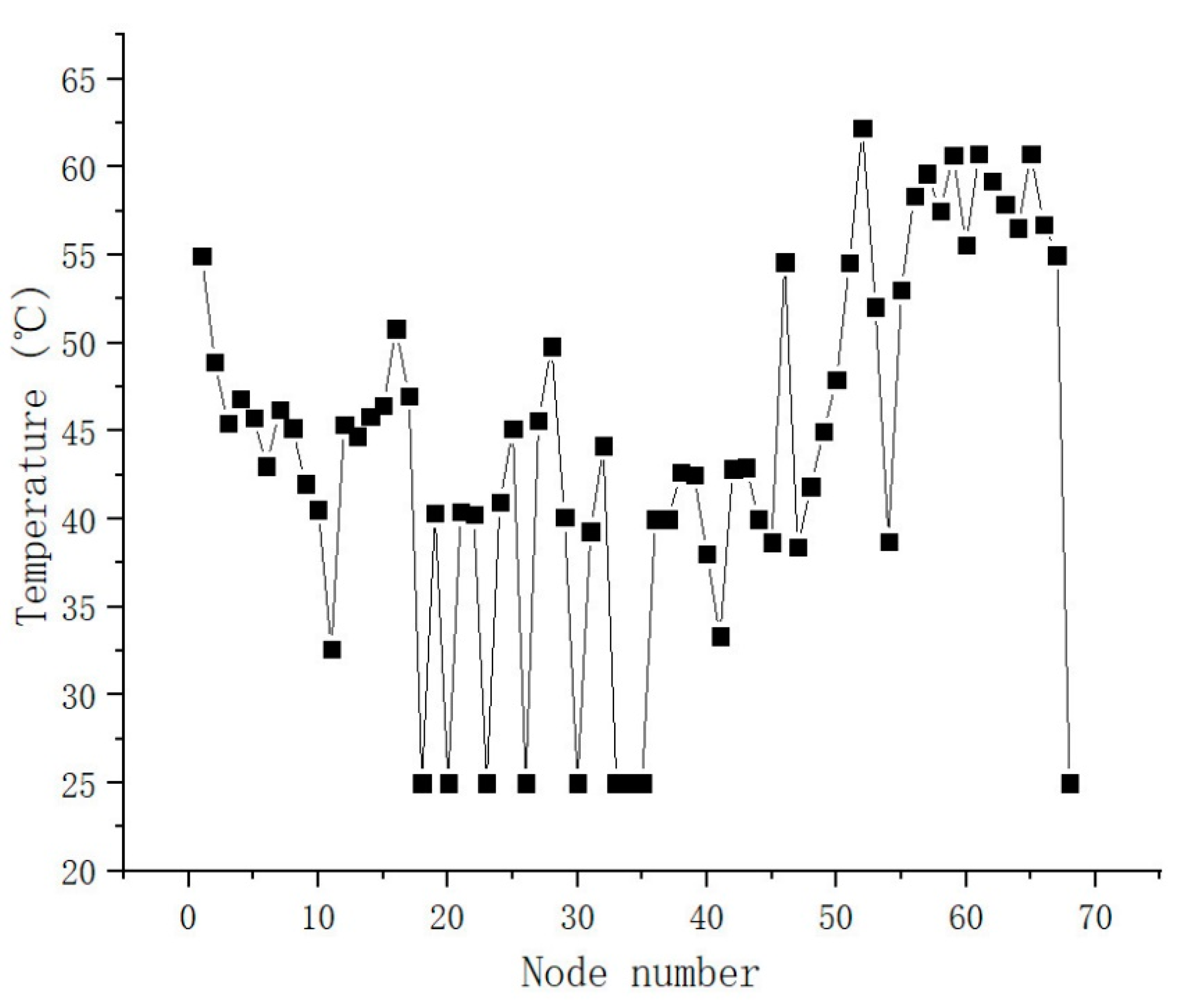
2.2. Thermal Analysis Results of a Two-Axle Automobile Drive Axle
- (1)
- The highest temperatures in the reducer, the motor, and differential are the temperatures of nodes 1, 50, and 14. Notably, the temperature (73.7 °C) of the spindle contacting front-end cover (node 50) is the highest temperature of the two-axle automobile drive axle. The reason is that this part is the uppermost thermal source of the two-axle automobile drive axle, and thermal dissipation is more difficult than in other parts.
- (2)
- The average temperature of the motor is higher than the differential and reducer. The average temperature of the reducer is fiercer than the differential.
- (3)
- The temperature of nodes 1, 5, 14, 18, 19, 38, 42, 43, 46, 50, and 52 are high. These nodes are distributed near the thermal sources of the two-axle automobile drive axle, so these temperatures are higher than others.
- (4)
- The temperature differences among some adjacent nodes are not distinct. However, the temperature differences among different nodes on the shell are apparent.
2.3. Validation of Thermal Network Method
3. Effects of Key Factors on Reducing the Temperature
3.1. Structural Effect of an Automobile Drive Axle
3.2. Parameter Effects of an Automobile Drive Axle
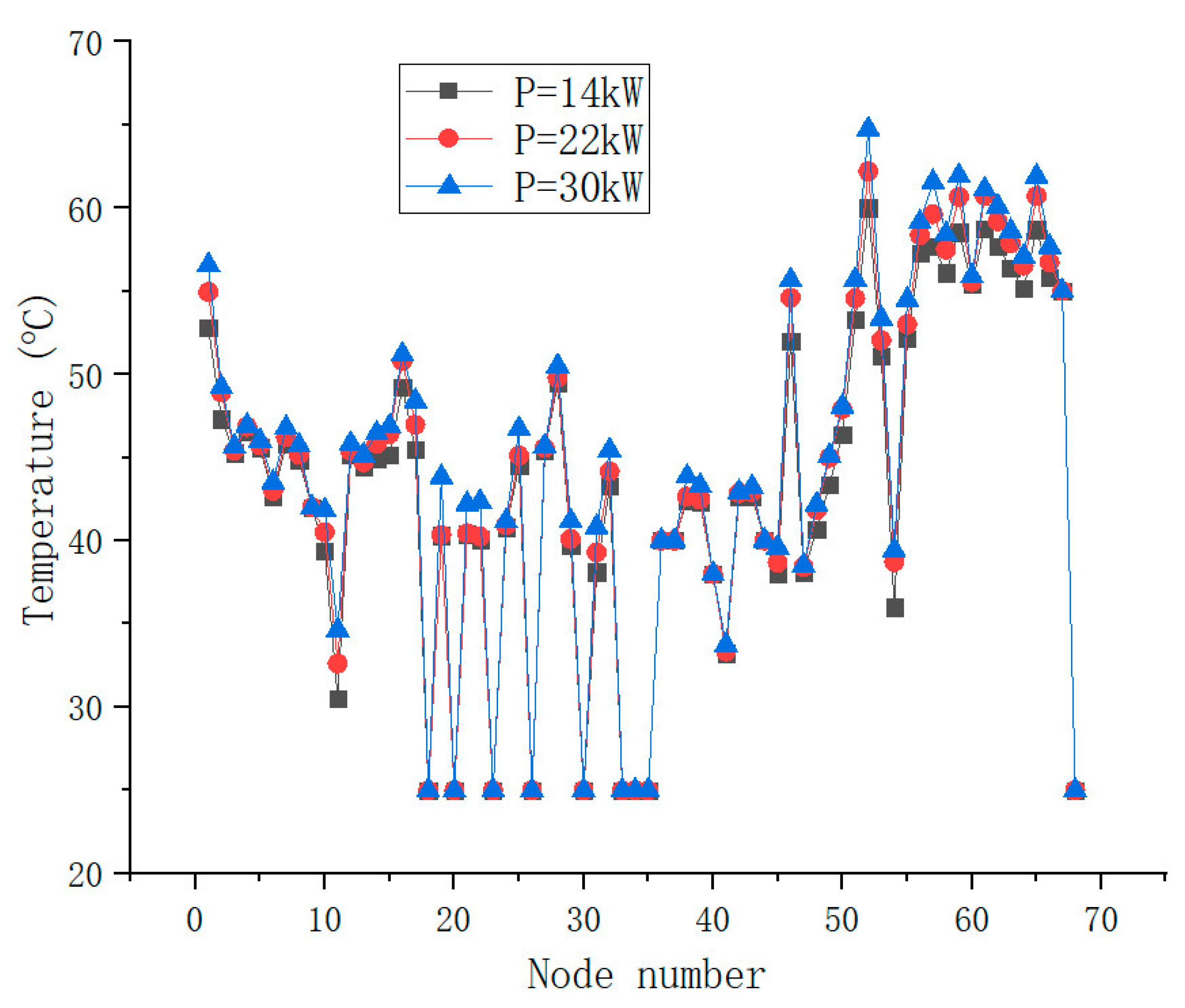
3.2.1. Effect of Motor Output Power
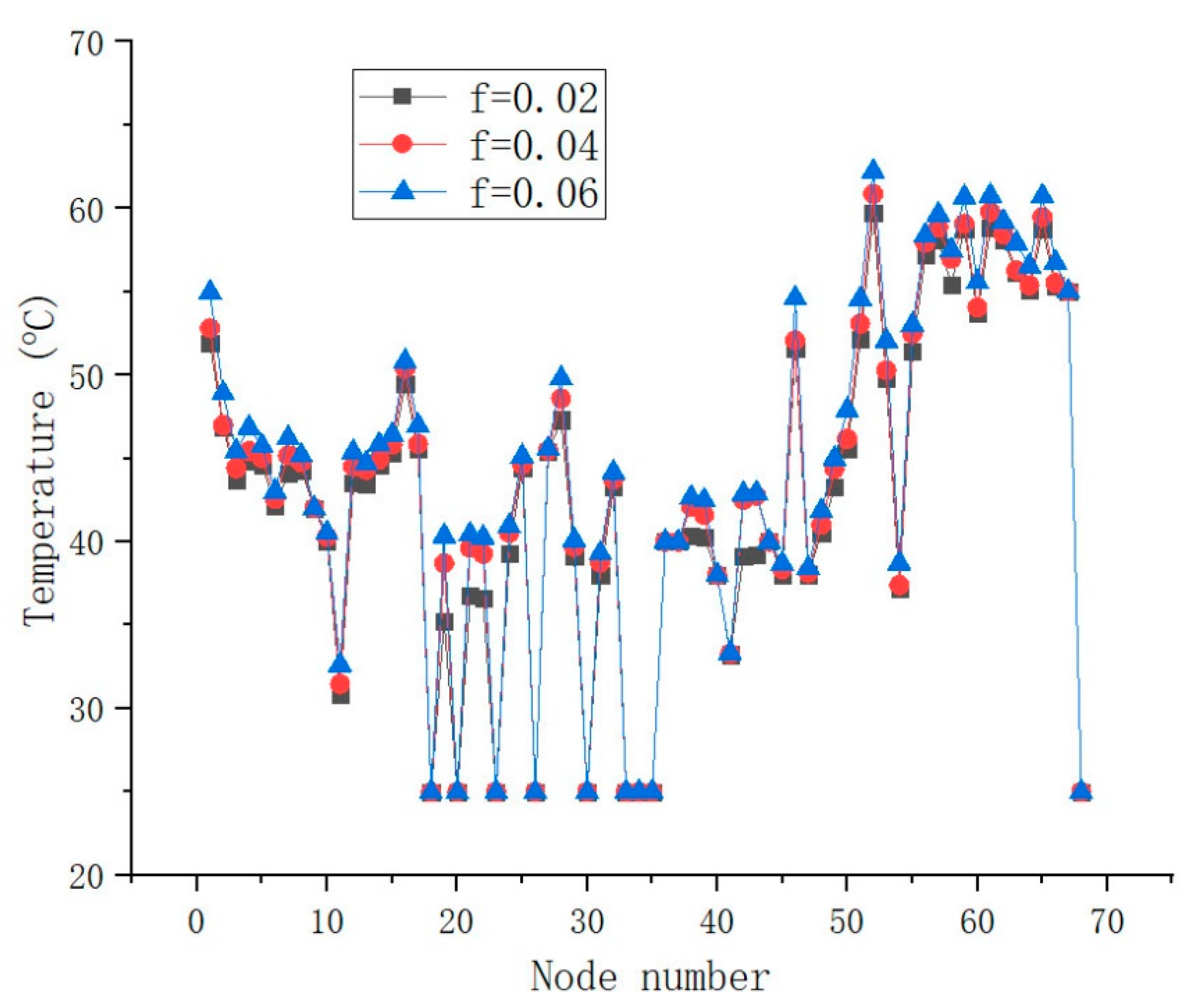
3.2.2. Effect of Friction Coefficient among Teeth
- (1)
- During the process of gears, applying more fashioning or developing the process technology to improve the machining precision.
- (2)
- Further polishing gears after manufacturing.
- (3)
- Replacing gears regularly with new ones
- (4)
- Adopting the lubricating material with good lubrication properties to act as an intermediate medium between gears, and replenishing the lubricating material regularly.
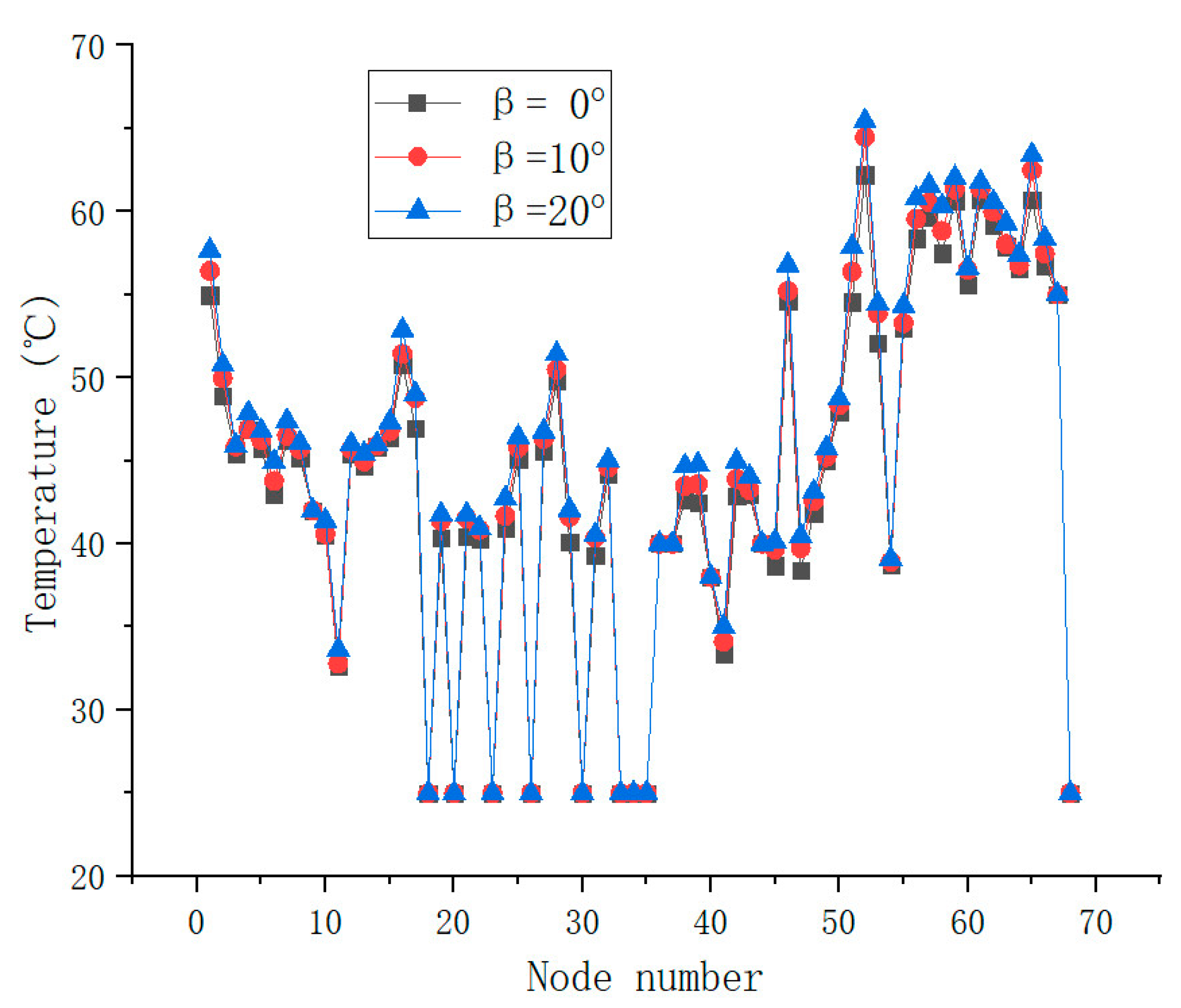
3.2.3. Effect of Helical Angle of Gears
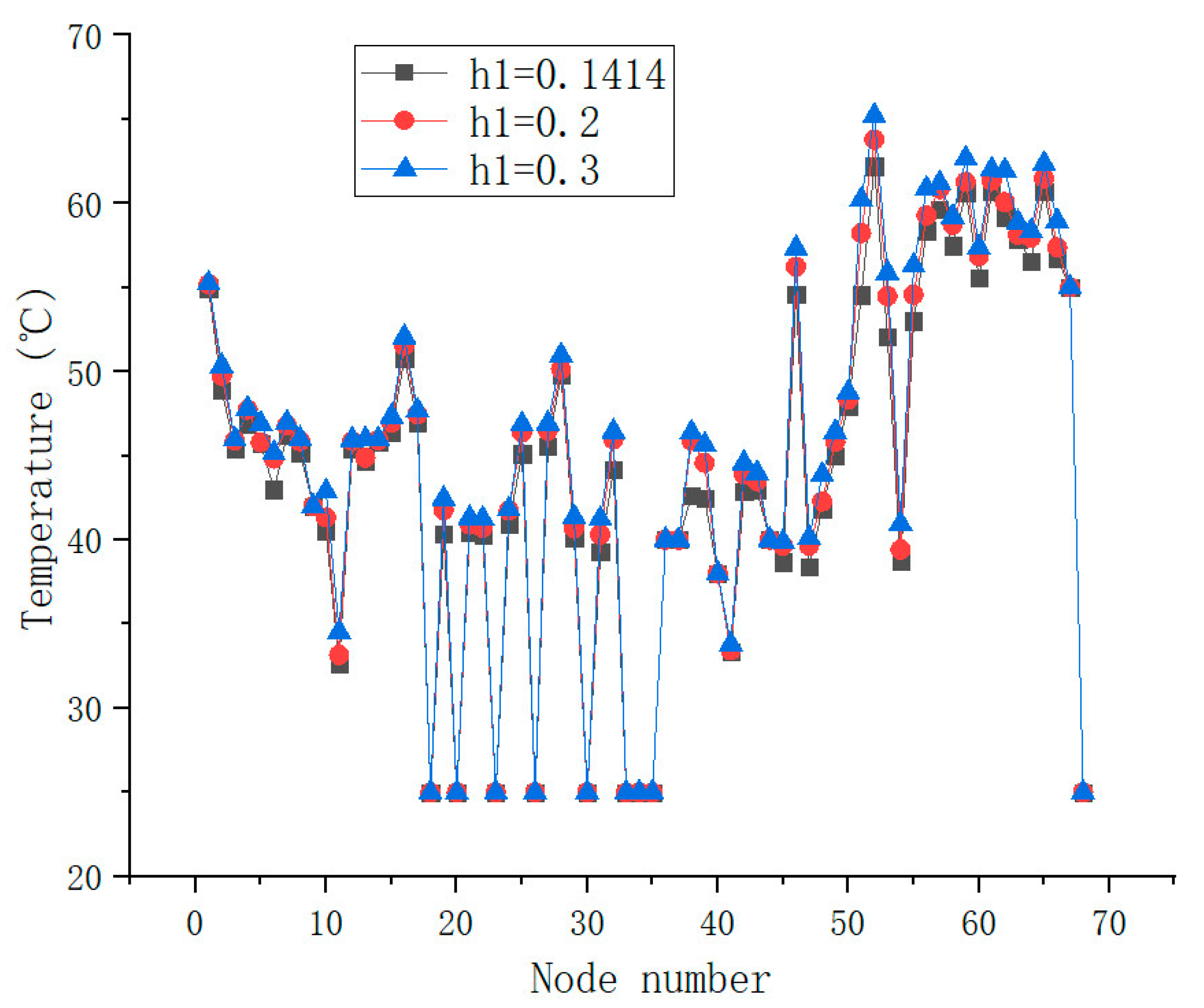
3.2.4. Effect of Lubricating Oil Parameter
4. Conclusions
- (1)
- The highest temperature (73.7 °C) of the two-axle automobile drive axle is located in the motor. In addition, the average temperature of the motor is higher than the differential and reducer, and the average temperature of the reducer is higher than the differential.
- (2)
- The highest temperature (62.2 °C) of the planetary automobile drive axle is also located in the motor. Compared with the two-axle drive axle, the highest temperature of the planetary drive axle is obviously lower. Therefore, as for the planetary drive axle, the possibility of exceeding the limited dangerous temperature is lower.
- (3)
- The corresponding highest temperatures of the planetary automobile drive axle with the motor power of 14 kW, 22 kW, and 30 kW are 60 °C, 62.2 °C, and 64.74 °C. The corresponding highest temperatures with the friction coefficient of 0.02, 0.04, and 0.06 are 59.74 °C, 60.86 °C, and 62.2 °C. The corresponding highest temperatures with the helical angle of 0°, 10°, and 20° are 62.2 °C, 64.47 °C, and 65.43 °C. The corresponding highest temperatures with the thermal transfer coefficient of 0.1414, 0.2, and 0.3 are 62.2 °C, 63.79 °C, and 65.21 °C. On the premise of ensuring normal operation, the motor output power, the friction coefficient among teeth, the helical angle of the gear, and thermal transfer coefficient of the lubricating oil can be optimized to be lower for reducing the temperature of the automobile drive axle.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, M.Z.; Zhuang, W.H.; Deng, S.; Zhu, C. Thermal analysis of the triple-phase asynchronous motor-reducer coupling system by thermal network method. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 2851–2861. [Google Scholar] [CrossRef]
- Hasegawa, T.; Kawashima, N. A new technique to measure the temperature of a rotating motor shaft. Appl. Therm. Eng. 2009, 29, 317–323. [Google Scholar] [CrossRef]
- Li, H.; Chen, W.S.; Tian, X.Q.; Liu, J. An experiment study on temperature characteristics of a linear ultrasonic motor using longitudinal transducers. Ultrasonics 2019, 95, 6–12. [Google Scholar] [CrossRef] [PubMed]
- Wang, X. Thermal imaging experiments of motor vehicles under low visibility at night. In Proceedings of the International Symposium on Photoelectronic Detection and Imaging, Beijing, China, 8 September 2011. [Google Scholar]
- Zhou, X.; Zhang, H.; Hao, X.; Liao, X.; Han, Q. Investigation on thermal behavior and temperature distribution of bearing inner and outer rings. Tribol. Int. 2019, 130, 289–298. [Google Scholar] [CrossRef]
- Takabi, J.; Khonsari, M. Experimental testing and thermal analysis of ball bearings. Tribol. Int. 2013, 60, 93–103. [Google Scholar] [CrossRef]
- Chai, F.; Tang, Y.; Pei, Y.; Liang, P.; Gao, H. Temperature field accurate modeling and cooling performance evaluation of direct-drive outer-rotor air-cooling in-wheel motor. Energies 2016, 9, 818. [Google Scholar] [CrossRef] [Green Version]
- Long, H.; Lord, A.; Gethin, D.; Roylance, B.J. Operating temperatures of oil-lubricated medium-speed gears: Numerical models and experimental results. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2003, 217, 87–106. [Google Scholar] [CrossRef] [Green Version]
- Concli, F. Thermal and efficiency characterization of a low-backlash planetary gearbox: An integrated numerical-analytical prediction model and its experimental validation. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2016, 230, 8. [Google Scholar] [CrossRef]
- Abebe, R.; Vakil, G.; Calzo, G.L.; Cox, T.; Gerada, C.; Johnson, M. FEA based thermal analysis of various topologies for Integrated Motor Drives (IMD). In Proceedings of the Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015. [Google Scholar]
- Huang, Y.K.; Zhu, J.G.; Guo, Y.G. Thermal analysis of high-speed SMC motor based on thermal network and 3-D FEA with rotational core loss included. IEEE Trans. Magn. 2009, 45, 4680–4683. [Google Scholar] [CrossRef]
- Liu, C.S.; Zou, J.B.; Xu, Y.X.; Yu, G. An efficient thermal computation model of PMSM based on FEA results and interpolation. IEEE Trans. Appl. Supercond. 2021, 31, 1–4. [Google Scholar] [CrossRef]
- Fernandes, C.; Rocha, D.; Martins, R.; Magalhães, L.; Seabra, J.H. Finite element method model to predict bulk and flash temperatures on polymer gears. Tribol. Int. 2018, 120, 255–268. [Google Scholar] [CrossRef]
- Roda, V.; Sanchez, F. A 2D finite element based approach to predict the temperature field in polymer spur gear transmissions. Mech. Mach. Theory 2019, 133, 210. [Google Scholar]
- Patil, P.; Kumar, A. Dynamic structural and thermal characteristics analysis of oil-lubricated multi-speed transmission gearbox: Variation of load, rotational speed and convection heat transfer. Iran. J. Sci. Technol. Trans. Mech. Eng. 2016, 41, 281–291. [Google Scholar] [CrossRef]
- Shukla, A.; Kumar, A. Design and thermal characteristic analysis of gearbox system based on finite element analysis (FEA). In Proceedings of the 14th Asia-Pacific Physics Conference, Hyderabad, India, 24–25 July 2020. [Google Scholar]
- Zhu, B.; Wang, X.; Luo, L.; Zhang, N.; Liu, X. Influence of lubricant supply on thermal and efficient performances of a gear reducer for electric vehicles. J. Tribol.-Trans. ASME 2022, 144, 1–22. [Google Scholar] [CrossRef]
- Liu, Y.G.; Peng, J.Y.; Wang, B.; Qin, D.; Ye, M. Bulk temperature prediction of a two-speed automatic transmission for electric vehicles using thermal network method and experimental validation. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2018, 233, 2585–2598. [Google Scholar] [CrossRef]
- Paschold, C.; Sedlmair, M.; Lohner, T.; Stahl, K. Calculating component temperatures in gearboxes for transient operation conditions. Forsch. Ing.-Eng. Res. 2021, 85, 1–14. [Google Scholar] [CrossRef]
- Changenet, C.; Oviedo, X.; Velex, P. Power loss predictions in geared transmissions using thermal networks-application to a six speed manual gearbox. Trans. ASME J. Mech. Des. 2005, 128, 618–625. [Google Scholar] [CrossRef]
- Guo, Y.; Zhu, J.; Wu, W. Thermal analysis of soft magnetic composite motors using a hybrid model with distributed heat sources. IEEE Trans. Magn. 2005, 41, 2124–2128. [Google Scholar]
- Qi, J.; Hua, W.; Zhang, H. Thermal analysis of modular-spoke-type permanent-magnet machines based on thermal network and FEA method. IEEE Trans. Magn. 2019, 55, 1–5. [Google Scholar] [CrossRef]
- Yan, K.; Hong, J.; Zhang, J.; Mi, W.; Wu, W. Thermal-deformation coupling in thermal network for transient analysis of spindle-bearing system. Int. J. Therm. Sci. 2016, 104, 1–12. [Google Scholar] [CrossRef]
- Li, T.J.; Wang, M.Z.; Zhao, C.Y. Study on real-time thermal-mechanical-frictional coupling characteristics of ball bearings based on the inverse thermal network method. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 2335–2349. [Google Scholar] [CrossRef]
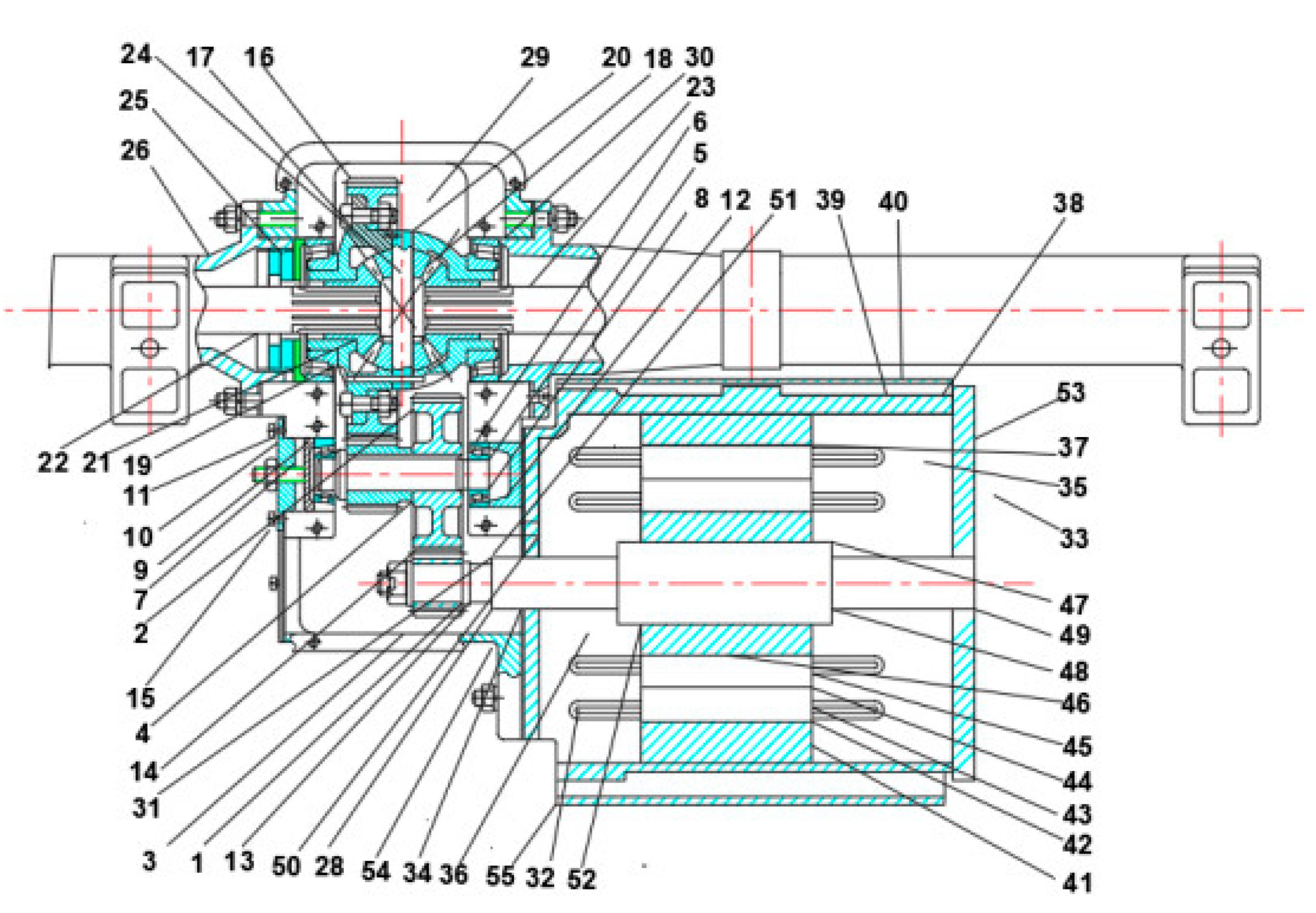
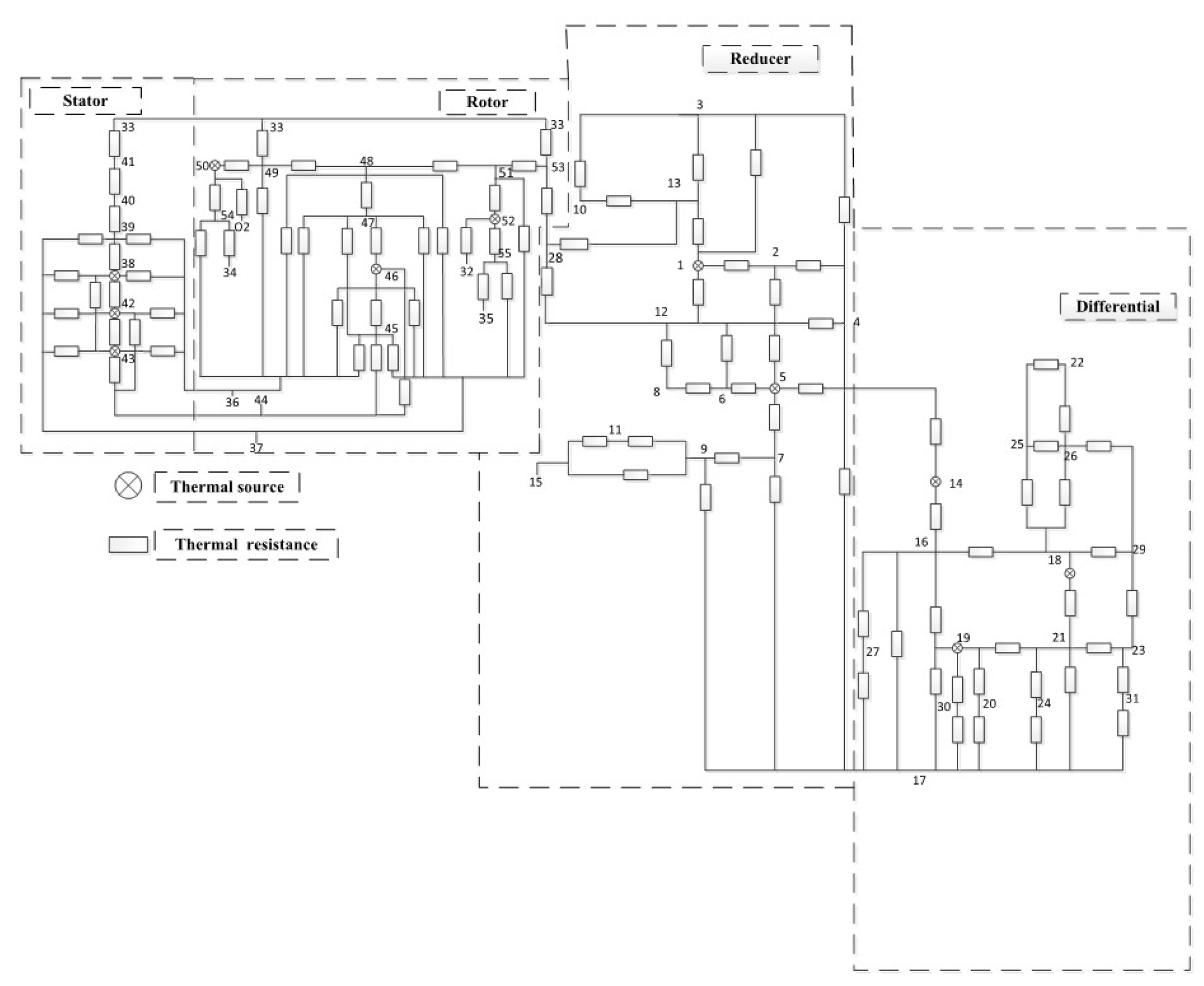


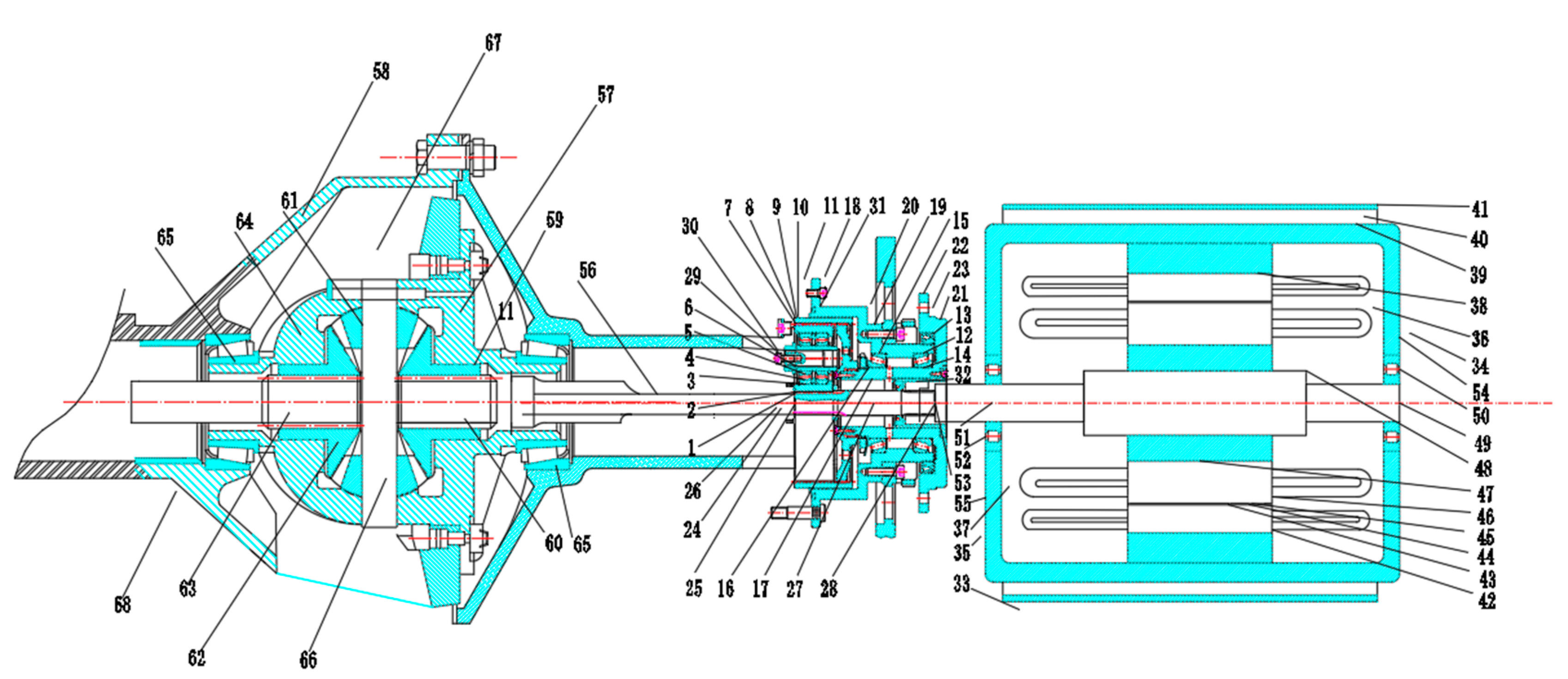
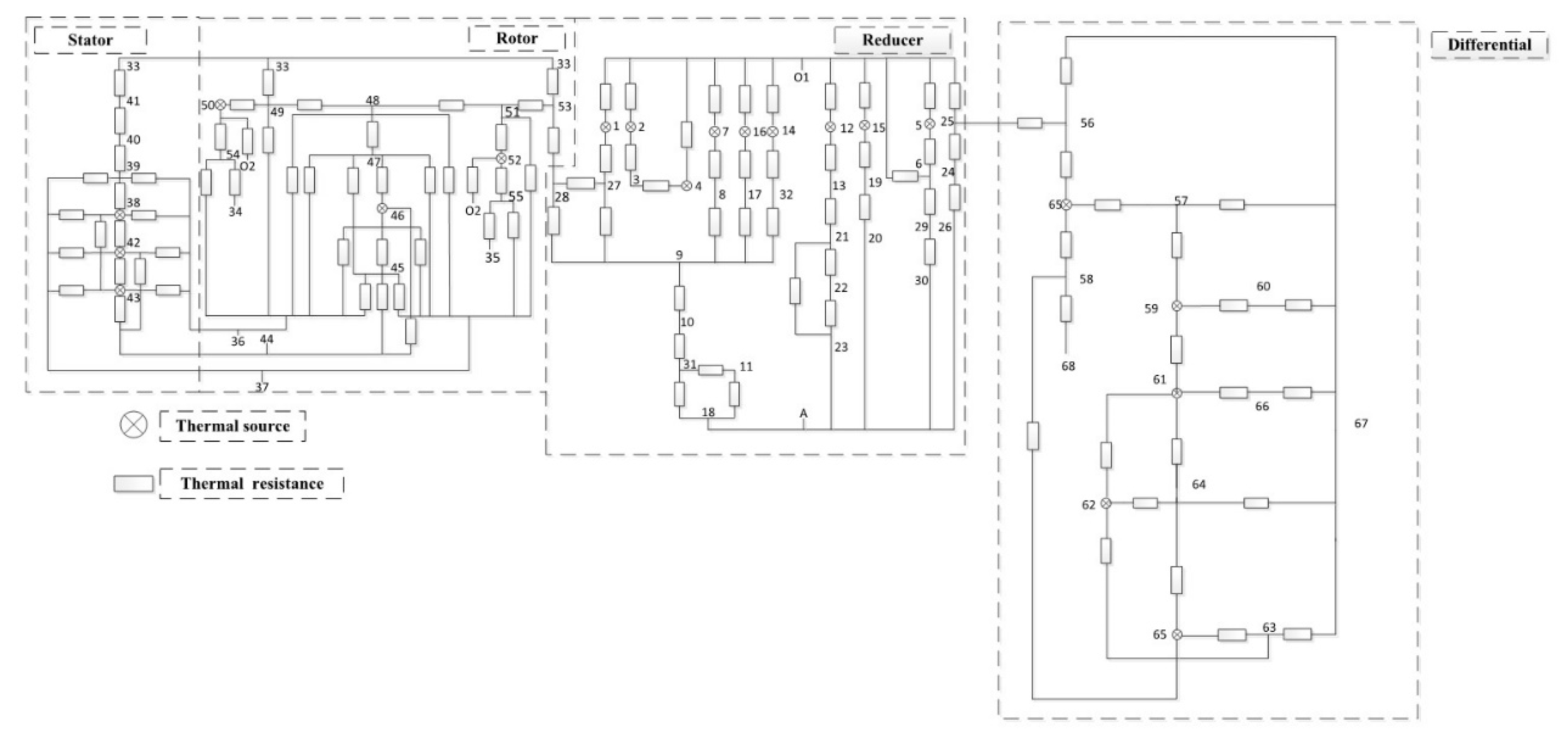
| Node | Name | Node | Name | Node | Name |
|---|---|---|---|---|---|
| 1 | high-speed axle driving gear | 2 | high-speed axle driven gear | 3 | oil–gas mixture in reducer |
| 4 | intermediate axle | 5 | cylindrical bearing | 6 | gasket |
| 7 | fixed sleeve | 8 | bearing clasp | 9 | cover |
| 10 | box cover | 11 | cover | 12 | lubricating oil in reducer |
| 13 | high-speed axle | 14 | intermediate axle driving gear | 15 | air |
| 16 | driven gear | 17 | oil–gas mixture in shell | 18 | side gear |
| 19 | cylindrical bearing on half axle | 20 | differential box | 21 | planetary gear |
| 22 | left half axle | 23 | right half axle | 24 | planet pin |
| 25 | adjuster cover | 26 | drive axle shell | 27 | adjuster gasket |
| 28 | joint of motor and reducer | 29 | oil–gas mixture in differential | 30 | joint of bearing |
| 31 | motor spindle | 32 | oil–gas mixture in motor | 33 | air |
| 34 | front-end of motor | 35 | after end of motor | 36 | air |
| 37 | stator yoke | 38 | base layer of motor cabinet | 39 | air-cooled air duct |
| 40 | upper layer of motor cabinet | 41 | stator winding | 42 | stator tooth |
| 43 | air gap | 44 | superstratum of rotor | 45 | rotor guide rod |
| 46 | substratum of rotor | 47 | axle of motor | 48 | axle contact rear-end cover |
| 49 | bearing near rear-end cover | 50 | axle contact front-end cover | 51 | bearing near front-end cover |
| 52 | axle of motor | 53 | rear-end cover | 54 | front-end cover |
| 55 | air |
| Parameters | Value |
|---|---|
| Motor output power [kW] | 22 |
| Phase voltage [V] | 380 |
| Load current [A] | 19 |
| Speed [rpm] | 1300 |
| Number of poles | 4 |
| Stator slot number | 48 |
| Rotor slot number | 38 |
| Number of the stator winding in parallel | 1 |
| Number of the lead wound | 1 |
| Stator outer diameter [cm] | 38.9 |
| Stator inner diameter [cm] | 24.99 |
| Rotor outer diameter [cm] | 24.82 |
| Rotor inner diameter [cm] | 8.72 |
| Core length [cm] | 17.45 |
| Airgap length [cm] | 0.0834 |
| Insulation layer thickness [cm] | 0.03 |
| Parameters | Value |
|---|---|
| Sun gear teeth number | 19 |
| Planetary gear teeth number | 66 |
| Inner ring gear teeth number | 152 |
| Gear modulus | 1.25 |
| Teeth profile angle [°] | 20 |
| Spiral angle [°] | 0 |
| Tooth width of sun gear [cm] | 4.6 |
| Tooth width of planetary gear [cm] | 4.6 |
| Tooth width of inner ring gear [cm] | 7 |
| Root radius of sun gear [cm] | 1.096 |
| Addendum radius of sun gear [cm] | 1.377 |
| Base radius of sun gear [cm] | 1.115 |
| Pitch radius of sun gear [cm] | 1.201 |
| Root radius of planetary gear [cm] | 3.968 |
| Addendum radius of planetary gear [cm] | 4.25 |
| Base radius of planetary gear [cm] | 3.876 |
| Pitch radius of planetary gear [cm] | 4.173 |
| Root radius of inner ring gear [cm] | 9.656 |
| Addendum radius of inner ring gear [cm] | 9.375 |
| Base radius of inner ring gear [cm] | 8.927 |
| Pitch radius of inner ring gear [cm] | 9.5 |
| Coefficient of friction among teeth | 0.06 |
| Kinematic viscosity of lubricating oil [m2/s] | 0.000006 |
| Thermal conductivity coefficient of lubricating oil [W/m×k] | 0.1414 |
| Parameters | Value |
|---|---|
| Modulus of bevel gear [cm] | 0.5 |
| Main bevel gear teeth number | 10 |
| Side gear teeth number | 16 |
| Radius of main bevel gear [cm] | 2.5 |
| Bevel gear tooth width coefficient | 0.33 |
| Tooth width of bevel gear [cm] | 0.825 |
| Diameter of main bevel gear [cm] | 5 |
| Diameter of side gear [cm] | 8.3 |
| Transmission ratio of main bevel gears | 1.6 |
| Length of gear meshing line [cm] | 0.1 |
| Pressure angle of bevel gear [°] | 20 |
| Contact ratio | 1 |
| Gear oil film thickness [cm] | 0.1 |
| Average diameter of bevel gear indexing circle [cm] | 4.175 |
| Friction coefficient of bevel gear | 0.05 |
| Tangential pressure angle of bevel gear [°] | 23.96 |
| Inner diameter of differential inner cylindrical bearing [cm] | 6 |
| Friction coefficient of bearing | 0.002 |
| Point 1 | Point 2 | Point 3 | Point 4 | Point 5 | |
|---|---|---|---|---|---|
| Temperature in TNM (°C) | 45.9 | 39.5 | 38.0 | 45.7 | 52.4 |
| Temperature in experimentation (°C) | 46.6 | 34.9 | 35.7 | 51.2 | 51.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ning, X.; Chen, M.; Zhou, Z.; Shu, Y.; Xiong, W.; Cao, Y.; Shang, X.; Wang, Z. Thermal Analysis of Automobile Drive Axles by the Thermal Network Method. World Electr. Veh. J. 2022, 13, 75. https://doi.org/10.3390/wevj13050075
Ning X, Chen M, Zhou Z, Shu Y, Xiong W, Cao Y, Shang X, Wang Z. Thermal Analysis of Automobile Drive Axles by the Thermal Network Method. World Electric Vehicle Journal. 2022; 13(5):75. https://doi.org/10.3390/wevj13050075
Chicago/Turabian StyleNing, Xinfei, Mingzhang Chen, Zijian Zhou, Yuwen Shu, Wei Xiong, Yang Cao, Xuebing Shang, and Zixi Wang. 2022. "Thermal Analysis of Automobile Drive Axles by the Thermal Network Method" World Electric Vehicle Journal 13, no. 5: 75. https://doi.org/10.3390/wevj13050075
APA StyleNing, X., Chen, M., Zhou, Z., Shu, Y., Xiong, W., Cao, Y., Shang, X., & Wang, Z. (2022). Thermal Analysis of Automobile Drive Axles by the Thermal Network Method. World Electric Vehicle Journal, 13(5), 75. https://doi.org/10.3390/wevj13050075







