Analysis of DC Winding Induced Voltage in Wound-Rotor Synchronous Machines by Using the Air-Gap Field Modulation Principle

Abstract

In order to analyze the DC winding induced voltage in the wound-rotor synchronous machine, this paper uses the air-gap field modulation principle to investigate its operation mechanism and harmonic order. By establishing the analytical magneto-motive force (MMF)-permeance model, the DC winding induced voltage per electrical cycle under open-circuit condition, armature reaction condition and on-load condition are deduced. Analytical analysis shows that the MMF function, stator and rotor permeance function are critical factors that influence the harmonic order of the DC winding induced voltage. The analysis results are compared with those predicted by the finite element analysis (FEA). Both non-linear steel and linear steel conditions are accounted in the FEA analysis, and the results show that the analytical deduction result agrees well with the FEA analysis result.

1. Introduction

Due to their high torque density and high efficiency, rare earth permanent magnet (PM) machines have been widely applied in modern industry. However, the environmental issue associated with the mining and refining of rare earth PM material, together with the unstable supply and the expensive price, have been the major concerns of using rare earth PM machines [1,2,3]. Compared with the PM machines, the wound-rotor synchronous machines (WRSMs) have field winding on the rotor and armature winding on the stator, which is not only more environmentally friendly due to the elimination of PM material, but also achieves high power density, making it is a potential candidate for the PM machine [4]. BMW IX3 [5], Renault Zoe [6] and a traction motor developed by MAHLE [7] are successful commercial WRSM product applications.

Due to the flexible flux regulation capability and no rare-earth PM material structure, WRSM have been applied in electrical vehicles (EVs) [5,6,7,8,9,10], power generation [11,12,13,14] and aerospace [15,16]. In order to fully utilize the additional control freedom of the DC winding, deadbeat direct torque and flux control was proposed in [8], which can achieve the unity power factor operation and reduce both copper loss and iron loss. The field current estimation method was proposed in [9] for WRSM with high-frequency brushless exciters, which can make it possible to dynamically control the field current by using the high-frequency brushless exciters. The analytical comparison and optimization between WRSM and PM machines were reported in [10], and it showed that the WRSM are more likely to compromise the torque density to meet the thermal constraint. Apart from the analytical method, a novel modeling method of the size-efficient look-up tables [14] and a surrogate-based optimization method [11] have been introduced for the WRSM. For aerospace applications, the WRSM is a consolidated and well-proven option for the generator in more electric aircraft [16]. As reported in [15], by using the integrated damper cage, the output voltage total harmonic distortion performance of the WRSM can be improved to 1% level, which shows a high output power quality.

It should be noted that during the operation of the WRSMs, the field winding is fed with DC current, and the armature windings are fed with symmetrical sinusoidal currents. For the conventional WRSM, brushes and slip rings or additional exciter should be used for the field winding power supply, which needs regular maintenance and will decrease the power density of the machine system [3]. The recently emerging wireless power transmission (WPT) WRSMs have become a promising solution without changing the main flux path and adding auxiliary winding or control complexity [9,17,18]. Although there are still challenges to be overcome, the WPT technique has provided a considerable solution for brushless operation in WRSMs [19].

Although the WRSM can be seen as a potential candidate for PM machines, it has to solve the issue introduced by the DC winding induced voltage. In recent years, DC winding induced voltage in wound field machines has received much attention [20,21,22,23,24,25,26,27]. The pulsating induced voltage of the DC winding will make the machine suffer from high field current ripple and even deteriorate the control performance of the machine [20]. It was found in [21] that due to the DC winding induced voltage, the analyzed DC excited synchronous machine suffers from DC current peak-to-peak variation at 19% of the average current with a rated speed of 500 rpm. Due to the negative impact of DC winding induced voltage, many reduction methods have been proposed. Rotor step skewing was proposed and validated by experiments for open-circuit and on-load DC winding induced voltage in [20,22], and it shows that the reduction methods can suppress the DC winding induced voltage effectively whilst maintaining the torque density at more than 90%. Rotor chamfering and axial pairing were proposed in [23] to suppress the on-load DC winding induced voltage for a five-phase wound field synchronous machine. The proposed method of rotor chamfering and axial pairing are validated on the five-phase prototype machine, which shows that the proposed method can suppress the DC winding induced voltage by more than 50% and 85%, respectively. In [24], the damper wingding was utilized for the DC excitation doubly salient machine to suppress the DC winding induced voltage, and it was found that the damper wingding can reduce the DC winding induced voltage by more than 90%. As for the hybrid excitation wound field synchronous (HEWFS) machine, the step skewing and 2-D pairing methods were analyzed and applied to the prototype, which can suppress the DC winding induced voltage by 96.15% and 89.05%, respectively [25].

The mechanism of the DC winding induced voltage in a flux modulation machine was analyzed in [20,26,27], and it was found that the DC winding self-inductance harmonics are the source of the open-circuit DC winding induced voltage due to the doubly salient structure, whilst the mutual-inductance harmonics between armature winding and DC winding contribute to the on-load DC winding induced voltage. However, for the conventional WRSM, which has a different operating mechanism with the flux modulation machines, the mechanism of the DC winding induced voltage has not been analyzed.

For the WRSM, the current ripple caused by DC winding induced voltage in both AC and DC winding will deteriorate the output power quality and dynamic control performance, which will even influence the stable operation under high-speed operation. Therefore, it is important to take the DC winding induced voltage into consideration during the initial design stage and the control stage. This paper aims at investigating the operation mechanism of the DC winding induced voltage in WRSM, which can be used as the guideline for machine topology optimization at the initial design stage. As for the WRSM control, the operation mechanism can help figure out the source of the winding currents’ fluctuation, and hence, improve the dynamic performance.

This paper will analyze the operation mechanism of the DC winding induced voltage in WRSM by using the air-gap field modulation principle [28,29,30]. The illustration of the analyzed WRSM can be found in Figure 1, and the innovations and contributions of this paper are as follows:

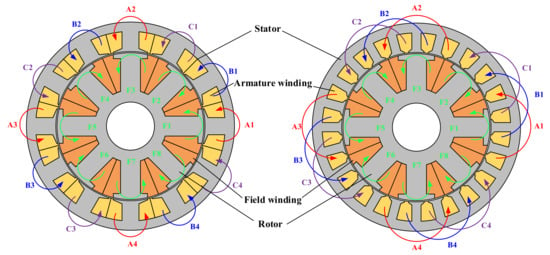
Figure 1. Topology of the analyzed WRSM. (Left: 12-stator slot/4-rotor pole pair, concentrated armature winding. Right: 24-stator slot/4-rotor pole pair, distributed armature winding).

(1)

The analytical MMF-permeance model is established, based on which the spatial–temporal characteristics of the air-gap flux density are analyzed.

(2)

The operating mechanism of the DC winding induced voltage in WRSM is analyzed first, and the harmonic order of the DC winding induced voltage is deduced and compared with that predicted by FEA.

(3)

Winding configurations of concentrated winding and distributed winding are included in the analysis.

2. Magneto-Motive Force-Permeance Modeling for the DC Winding Induced Voltage in WRSM

2.1. Specifications of the Analyzed WRSMs

The specifications of the analyzed WRSMs are shown in Table 1, and the illustration of the parameters can be found in Figure 2. Different stator slots and rotor pole number combinations are included. All the parameters are optimized for maximum electromagnetic torque by using the genetic algorithm (GA). The optimized WRSMs all operate under the brushless alternating current (BLAC) mode, i.e., i_d = 0 control with fixed 60 W copper loss in both armature windings and DC winding. Both DC winding and armature winding also share the same packing factor k_pf = 0.5.

Table 1. Parameters of the Analyzed WRSMs.

Parameters	Unit	WRSM
Stator slot number, Ns	-	12	24
Rotor pole pair number, pr	-	4	4
Stator outer radius, rso	mm	45	45
Stator yoke radius, rsy	mm	40.97	40.75
Stator inner radius, rsi	mm	32.25	32.29
Slot opening arc, θso	deg.	3.196	3.018
Stator tooth arc, θst	deg.	13.15	7.133
Single side air-gap width, g	mm	0.5	0.5
Rotor outer radius, rro	mm	31.75	31.79
Rotor yoke radius, rry	mm	15.61	16.8
Rotor tooth arc, θrt	deg.	15.54	15.85
Rotor tip arc, θrtip	deg.	5.71	6.39
Shaft radius, rsh	mm	10.4	10.4
Stack length, lstk	mm	50	50
Lamination steel type	-	M270-35
Armature coil turns, Nac	-	36	36
DC coil turns, Ndc	-	90	90
Packing factor, kpf	-	0.5	0.5
Rotor speed, nr	rpm	1000	1000
Armature winding copper loss, pcac	W	60	60
DC winding copper loss, pcdc	W	60	60

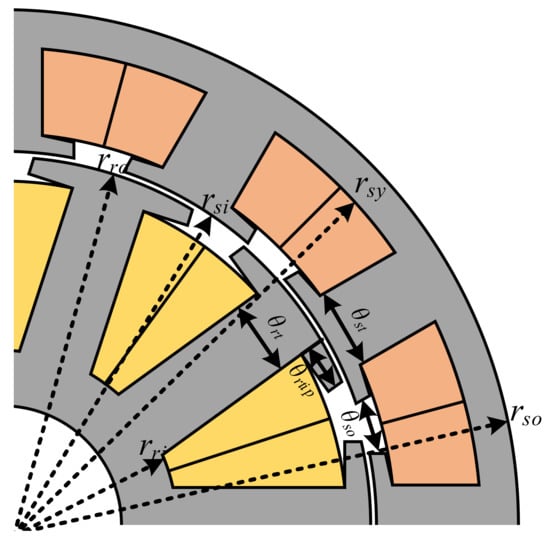
Figure 2. Linear illustrations of the WRSM parameters.

2.2. MMF-Permeance Modelling

This paper will use the MMF-permeance model to analyze the air-gap flux density of the WRSM. Based on the MMF-permeance model, both the spatial and temporal distribution characteristics of the air-gap flux density will be deduced.

Before establishing the MMF-permeance model of the WRSM, some assumptions should be made to simplify the analysis [31]:

• The steel permeability is infinite.
• Flux lines are perpendicular to the steel surface.
• The effect of finite stack length is negligible.

It should be noted that the MMF-permeance model is a 1-D analytical model for analyzing the flux density distribution characteristics. The main purpose is to analyze the spatial and temporal distribution characteristics of the air-gap flux density. Accurate prediction of the magnitude and phase angle of the flux density is not the main purpose of this paper. However, the MMF-permeance model can still shed light on figuring out the physical nature of DC winding induced voltage in WRSM. The impact of the saturation cannot be accounted in the MMF-permeance model, which will be analyzed by the FEA analysis.

2.2.1. Open-circuit condition

The DC winding MMF waveform of the WRSM can be found in Figure 3. By using the Fourier series transformation, the DC winding MMF can be expressed as

$$\left\{\begin{array}{c}{F}_{dc}\left({\theta }_m,t\right)=I_f{N}_{dc}{W}_{dc}\left({\theta }_m,t\right)={\displaystyle {\displaystyle \sum }_{n=1}^{\infty }}{a}_n\cos \left(n{p}_r{\theta }_m-n{p}_r{\omega }_{m}t\right)\hfill \\ a_n=\left\{\begin{array}{cc}\frac{4I_f{N}_{dc}}{n\pi }\left[\sin \left(n{p}_r{\theta }_1\right)\right],\hfill & n is odd number\hfill \\ 0,\hfill & n is even number\hfill \end{array}\right.\hfill \\ {\theta }_1=\left({\theta }_{rt}+{\theta }_{rtip}\right)/2\hfill \end{array}\right.$$

(1)

where F_dc(θ_m,t) is the MMF function of the DC winding, W_dc(θ_m,t) is the winding function of the DC winding, θ_m is the mechanical degree, ω_m is the mechanical rotor angular speed and t is the time; I_f is the DC winding current.

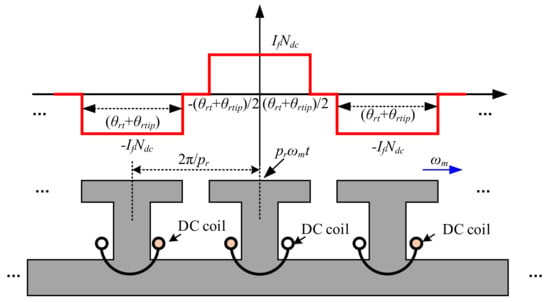
Figure 3. DC winding MMF waveform of the WRSM.

It can be observed from Equation (1) that DC winding MMF has only odd harmonics, which means the spatial order of the DC winding MMF function is the odd times of the rotor poles. The temporal order of the DC winding MMF function is 1, which is caused by the rotation.

The stator relative permeance waveform of the WRSM can be found in Figure 4. By using the Fourier series transformation, the stator relative permeance function can be expressed as

$$\left\{\begin{array}{c}{\Lambda }_s\left({\theta }_m\right)=\frac{N_s{\theta }_2}{\pi }+{\displaystyle {\displaystyle \sum }_{n=1}^{\infty }}{a}_{ns}\cos \left(n{N}_s{\theta }_m\right)\hfill \\ a_{ns}=\frac{1-{\mathsf{\Lambda }}_0}{n\pi }\sin \left(n{N}_s{\theta }_2\right)\hfill \\ {\theta }_2=\left({\theta }_{stip}+{\theta }_{st}\right)/2\hfill \end{array}\right.$$

(2)

where a_ns are Fourier transformation coefficient, Λ_s is the stator permeance function, Λ₀ is the stator average permeance, θ_stip is the stator tooth-tip angle.

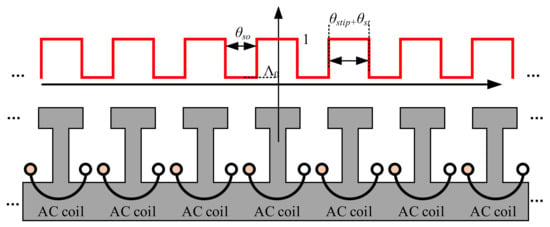
Figure 4. Stator relative permeance waveform of the WRSM.

It can be observed from Equation (2) that the stator permeance function has a spatial order of N_s, 2N_s, 3N_s…. It should be noted that rotor permeance is not modeled in this paper since the DC winding MMF function contained the information on the rotor permeance.

According to [28], the open-circuit air-gap flux density B_goc can be expressed as

$$B_{goc}\left({\theta }_m,t\right)=\frac{{\mu }_0}{g}\left[F_{dc}\left({\theta }_m,t\right){\mathsf{\Lambda }}_s\left({\theta }_m\right)\right]$$

(3)

where B_g is the air-gap flux density, μ₀ is the vacuum permeability.

The open-circuit DC winding flux-linkage can be expressed as

$${\psi }_{dcoc}\left({\theta }_m,t\right)={{\displaystyle \int }}_0^{2\pi }{B}_{goc}\left({\theta }_m,t\right)W_{dc}\left({\theta }_m,t\right)\mathrm{d}{\theta }_m$$

(4)

where ψ_dcoc is the open-circuit DC winding flux-linkage.

It can be observed in Equation (4) that under the open-circuit condition, the DC winding MMF and the stator permeance function are critical factors for the open-circuit DC winding flux-linkage. Equation (4) is an integration equation with 0~2π integration range, therefore the flux density spatial order should satisfy the following equation to contribute to the open-circuit DC winding flux-linkage:

$$p_r\left(2i-1\right)\pm N_{s}j=p_r\left(2k-1\right), i,j,k=1,2,3\dots$$

(5)

In addition, the open-circuit DC winding induced voltage cycle per electrical period N_peopen can be expressed as

$$N_{peopen}=\left|\left(2i-1\right)-\left(2k-1\right)\right|=\left|\frac{N_s}{p_r}j\right|$$

(6)

For WRSM with a 12- or 24-stator slot and 4-rotor pole pair, N_peopen can be calculated based on Equation (6), and the results are listed in Table 2.

Table 2. Predicted N_peopen for the Analyzed WRSMs.

Parameters	WRSM
Stator-slot/Rotor-pole-pair	12/4	24/4
Npeopen	6	6

2.2.2. Armature Reaction Condition

The effect of the armature reaction on DC winding induced voltage is related with the winding configuration [27]. In this paper, the analyzed 12/4 WRSM and 24/4 WRSM have double layer concentrated winding and single layer distributed winding, respectively.

The following analysis is based on the assumption that the armature windings are fed with three-phase symmetrical currents. Therefore, the three-phase currents can be expressed as,

$$\left\{\begin{array}{c}{i}_A\left(t\right)=I_A\sin \left(p_r{\omega }_{m}t+{\theta }_i\right)\hfill \\ i_B\left(t\right)=I_A\sin \left(p_r{\omega }_{m}t-\frac{2}{3}\pi +{\theta }_i\right)\hfill \\ i_C\left(t\right)=I_A\sin \left(p_r{\omega }_{m}t+\frac{2}{3}\pi +{\theta }_i\right)\hfill \end{array}\right.$$

(7)

where θ_i is the current angle, I_A is the phase current amplitude.

The armature winding function can be expressed as

$$\left\{\begin{array}{c}{W}_{aA}\left({\theta }_m\right)=W_{aA0}+{\displaystyle {\displaystyle \sum }_{n=1}^{\infty }}{a}_{nw}\cos \left(n{p}_r{\theta }_m\right)\hfill \\ W_{aB}\left({\theta }_m\right)=W_{aA0}+{\displaystyle {\displaystyle \sum }_{n=1}^{\infty }}{a}_{nw}\cos \left(n{p}_r{\theta }_m-\frac{2}{3}n\pi \right)\hfill \\ W_{aC}\left({\theta }_m\right)=W_{aA0}+{\displaystyle {\displaystyle \sum }_{n=1}^{\infty }}{a}_{nw}\cos \left(n{p}_r{\theta }_m+\frac{2}{3}n\pi \right)\hfill \end{array}\right.$$

(8)

where W_aA, W_aB, and W_aC are armature winding functions, W_aA0 are the average values of the armature winding function, and a_nw are the Fourier transformations for the armature winding. W_aA0 and a_nw for the analyzed 12/4 WRSM and 24/4 WRSM can be expressed as

$$\left\{\begin{array}{c}{a}_{nw}=\left\{\begin{array}{c}\frac{8N_{ac}}{n{p}_r\pi }\sin \left(n{p}_r{\theta }_2\right),12/4 WRSM\hfill \\ \frac{8N_{ac}}{n{p}_r\pi }\sin \left(n{p}_r{\theta }_2\right)\left(1+2\cos \left(\frac{2n\pi p_r}{N_s}\right)\right), 24/4 WRSM\hfill \end{array}\right.\hfill \\ W_{aA0}=\left\{\begin{array}{c}\frac{4{\theta }_2}{\pi },12/4 WRSM\hfill \\ \frac{12{\theta }_2}{\pi },24/4 WRSM \hfill \end{array}\right.\hfill \end{array}\right.$$

(9)

It should be noted that Equation (8) can be easily extended for other winding configurations by calculating the W_aA0 and a_nw for specific windings.

The armature winding MMF can be expressed as

$$\left\{\begin{array}{c}{F}_A\left({\theta }_m,t\right)=W_{aA}\left({\theta }_m\right)i_A\left(t\right)\\ F_B\left({\theta }_m,t\right)=W_{aB}\left({\theta }_m\right)i_B\left(t\right)\\ F_C\left({\theta }_m,t\right)=W_{aC}\left({\theta }_m\right)i_C\left(t\right)\end{array}\right.$$

(10)

where F_A, F_B, and F_C are armature winding MMF for phase A, phase B and phase C.

The total armature winding MMF can be expressed as

$$F_{ac}\left({\theta }_m,t\right)=F_A\left({\theta }_m,t\right)+F_B\left({\theta }_m,t\right)+F_C\left({\theta }_m,t\right)$$

(11)

Equation (11) can be rewritten as

$$F_{ac}\left({\theta }_m,t\right)=\left\{\begin{array}{c}1.5{\displaystyle {\displaystyle \sum }_{n=1}^{\infty }}{I}_A{a}_{nw}\sin \left(p_r{\omega }_{m}t+{\theta }_i-n{p}_r{\theta }_m\right),n=3k+1\\ 1.5{\displaystyle {\displaystyle \sum }_{n=1}^{\infty }}{I}_A{a}_{nw}\sin \left(p_r{\omega }_{m}t+{\theta }_i+n{p}_r{\theta }_m\right),n=3k-1\\ 0, n=3k\end{array}\right.$$

(12)

The armature reaction air-gap flux density B_gar can be expressed as

$$B_{gar}\left({\theta }_m,t\right)=\frac{{\mu }_0}{g}\left[F_{dc}\left({\theta }_m,t\right){\Lambda }_r\left({\theta }_m\right)\right]$$

(13)

where Λ_r is the rotor permeance function, it will be reflected by the DC winding function in the following. Since the armature MMF function contained the information on stator permeance, Equation (13) does not include the stator permeance function. The DC winding flux-linkage ψ_dcar caused by the armature reaction can be expressed as

$${\psi }_{dcar}\left({\theta }_m,t\right)={{\displaystyle \int }}_0^{2\pi }{B}_{gar}\left({\theta }_m,t\right)W_{dc}\left({\theta }_m,t\right)\mathrm{d}{\theta }_m$$

(14)

And it can be rewritten as

$${\psi }_{dcar}\left({\theta }_m,t\right)={{\displaystyle \int }}_0^{2\pi }{\mu }_0{F}_{ac}\left({\theta }_m,t\right)W_{dc}\left({\theta }_m,t\right)/g\mathrm{d}{\theta }_m$$

(15)

It can be observed that in Equation (15) that the armature winding MMF (stator permeance is also included) and the DC winding function are the critical factors for the DC winding flux linkage, and the flux density spatial order should satisfy the following equation to contribute to the open-circuit DC winding flux-linkage:

$$\left\{\begin{array}{c}\left(2i-1\right)p_r\pm \left(-n{p}_r\right)=0,n=3k+1\\ \left(2i-1\right)p_r\pm \left(n{p}_r\right)=0,n=3k-1\end{array}\right.$$

(16)

where (2i − 1)p_r is the spatial order introduced by the DC winding function, and np_r is the spatial order introduced by armature winding MMF. By solving Equation (16), only when n = 6k − 1 or 6k + 1, k = 1,2,3… can the corresponding flux density contribute to the DC winding flux-linkage.

The DC winding induced voltage per cycle under armature reaction condition N_pear can be expressed as

$$N_{pear}=\left\{\begin{array}{c}min\left|-\left(6k-1\right)-1\right|=6,n=6k-1\\ min\left|-\left(6k+1\right)+1\right|=6,n=6k+1\end{array}\right.,k=1,2,3\dots$$

(17)

By using Equation (17), N_pear can be predicted, which is listed in Table 3.

Table 3. Predicted N_pear for the Analyzed WRSMs.

Parameters	WRSM
Stator slot/Rotor pole pair	12/4	24/4
Npear	6	6

2.2.3. On-Load Condition

According to superposition principle, the on-load air-gap flux density is the sum of the open-circuit condition and armature reaction condition, and so is the DC winding flux linkage. Therefore, the on-load DC winding flux linkage is the sum of open-circuit flux linkage and armature reaction flux linkage. The on-load DC winding induced voltage cycle per electrical period N_peol can be expressed as the least common multiple of N_peopen and N_pear. For the analyzed WRSM, the prediction results of N_peol are listed in Table 4,

Table 4. Predicted N_peol for the Analyzed WRSMs.

Parameters	WRSM
Stator slot/Rotor pole pair	12/4	24/4
Npeol	6	6

3. FEA Verification

In order to verify the correctness of the operating mechanism analysis on DC winding induced voltage in WRSM, both 12/4 WRSM and 24/4 WRSM were analyzed by FEA. Both open-circuit and on-load performance, including cogging torque, on-load torque, DC winding flux linkage and DC winding induced voltage are included in the analysis. It should be noted that analysis results between electrical steel material with nonlinear B–H curve characteristic and constant relative permeability characteristic are also compared to analyze the influence of saturation on the DC winding induced voltage.

3.1. Open-Circuit Condition

The cogging torque waveform and spectra for 12/4 WRSM and 24/4 WRSM are shown in Figure 5 and Figure 6. The cogging torque of both 12/4 WRSM and 24/4 WRSM suffers from 6kth (k = 1,2,3…) harmonics. It can be observed from the spectra that the saturation will influence the magnitude of cogging torque harmonics. However, the steel saturation has a different effect on 12/4 and 24/4 WRSM.

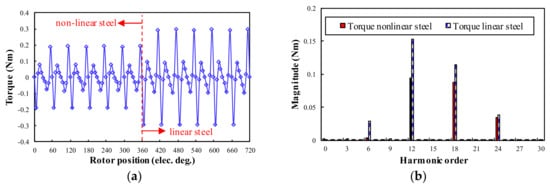
Figure 5. Cogging torque waveforms and spectra for 12/4 WRSM: (a) Waveforms; (b) Spectra.

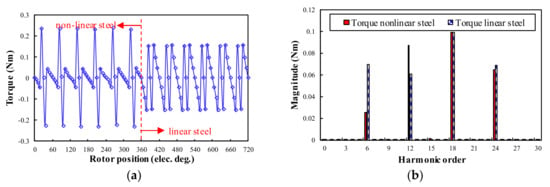
Figure 6. Cogging torque waveforms and Spectra for 24/4 WRSM, (a) Waveforms; (b) Spectra.

As for the open-circuit DC winding induced voltage, it can be seen in Figure 7 and Figure 8 that both 12/4 and 24/4 WRSM have N_peopen = 6, which is the same as the prediction result in Table 2. The influence of steel saturation will not influence the harmonic order of the open-circuit DC winding induced voltage. However, the steel saturation will influence the magnitude of the open-circuit DC winding induced voltage. This is evident for the 24/4 WRSM, which has higher amplitude open-circuit DC winding induced voltage. As for the 12/4 WRSM, the saturation will result in a higher magnitude of the 12th harmonic DC winding induced voltage.

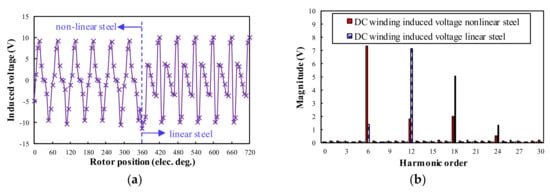
Figure 7. Open-circuit DC winding induced voltage waveforms and spectra for 12/4 WRSM, (a) Waveforms; (b) Spectra.

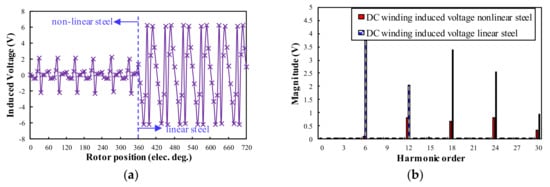
Figure 8. Open-circuit DC winding induced voltage waveforms and spectra for 24/4 WRSM, (a) Waveforms; (b) Spectra.

3.2. On-Load Condition

The on-load torque waveforms and spectra for 12/4 WRSM and 24/4 WRSM can be seen in Figure 9 and Figure 10, respectively. The on-load torque suffers from 6kth (k = 1,2,3…) harmonics. The average on-load torque under the linear steel condition is much higher than that under the non-linear steel condition.

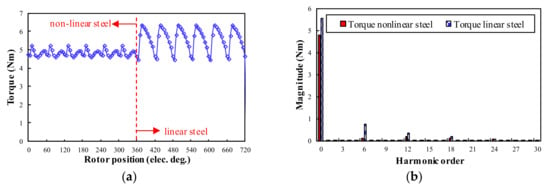
Figure 9. On-load torque waveforms and spectra for 12/4 WRSM: (a) Waveforms; (b) Spectra.

Figure 10. On-load torque waveforms and spectra for 24/4 WRSM: (a) Waveforms; (b) Spectra.

As shown in Figure 11 and Figure 12, the on-load DC winding induced voltage in both 12/4 and 24/4 WRSM has N_peol = 6, which is the same as the prediction result in Table 4. As for the influence of the steel saturation, the on-load DC winding induced voltage has a much higher amplitude for both WRSM machines. However, the steel saturation will not influence the harmonic order of the DC winding induced voltage. The 24/4 WRSM with distributed armature winding has a higher amplitude of DC winding induced voltage than that of 12/4 WRSM with the concentrated armature winding.

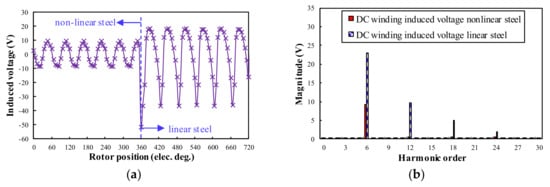
Figure 11. On-load DC winding induced voltage waveforms and spectra for 12/4 WRSM: (a) Waveforms; (b) Spectra.

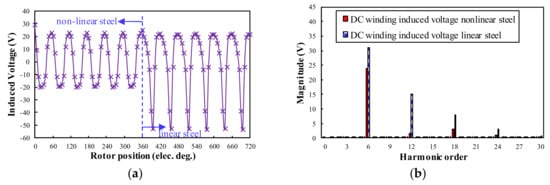
Figure 12. On-load DC winding induced voltage waveforms and spectra for 24/4 WRSM: (a) Waveforms; (b) Spectra.

Finally, the FEA prediction results of both N_peopen and N_peol are listed in Table 5, which agree well with the analysis result of the MMF-permeance model in Table 2 and Table 4.

Table 5. FEA Predicted DC Winding Induced Voltage Cycles per Electrical Period.

Parameters	Linear Steel		Non-Linear Steel
Stator slot/Rotor pole pair	12/4	24/4	12/4	24/4
Npeopen	6	6	6	6
Npeol	6	6	6	6

4. Conclusions

This paper analyzes the operating mechanism of the DC winding induced voltage in both 12/4 WRSM and 24/4 WRSM with concentrated armature winding and distributed armature winding, respectively. By using the air-gap field modulation principle, the MMF-permeance model of the WRSM is established. DC winding MMF, armature reaction MMF and permeance function are modeled analytically in the MMF-permeance model. Then, based on the spatial–temporal characteristics of the effective air-gap flux density for the DC winding, the induced voltage cycle per electrical period N_peopen, N_pear and N_peal are deduced analytically. The deduced results are verified by the FEA with linear steel and non-linear steel, which shows that the analytical prediction results agree well with the FEA analysis results. The analytical model in this paper can give a straightforward insight into the physical nature of the DC winding-induced voltage in WRSM. However, the analytical model cannot predict the magnitude and phase angle of the DC winding induced voltage, since the main purpose of this paper is to analyze the operating mechanism of the DC winding-induced voltage in WRSM. It is different from that in the wound field switched flux machine, which was analyzed in [20,27]. Based on the analysis presented in this paper, reduction methods investigation of the DC winding induced voltage for WRSM is the next stage of work for this paper.