Performance Simulation of Long-Stator Linear Synchronous Motor for High-Speed Maglev Train under Three-Phase Short-Circuit Fault
Abstract
1. Introduction
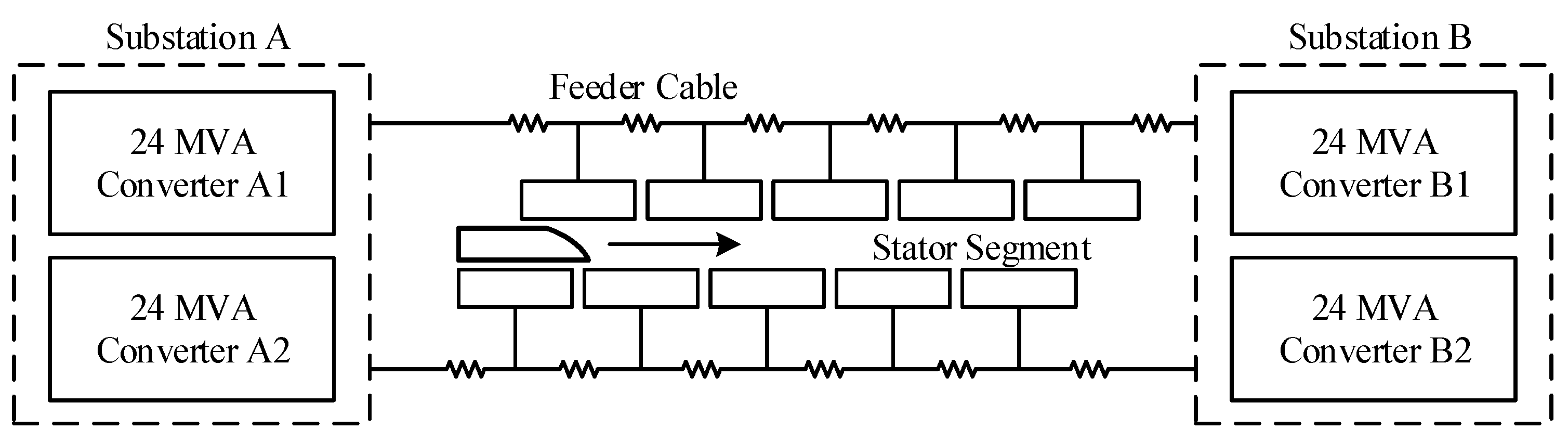
2. Traction Power Supply System of High-Speed Maglev Train
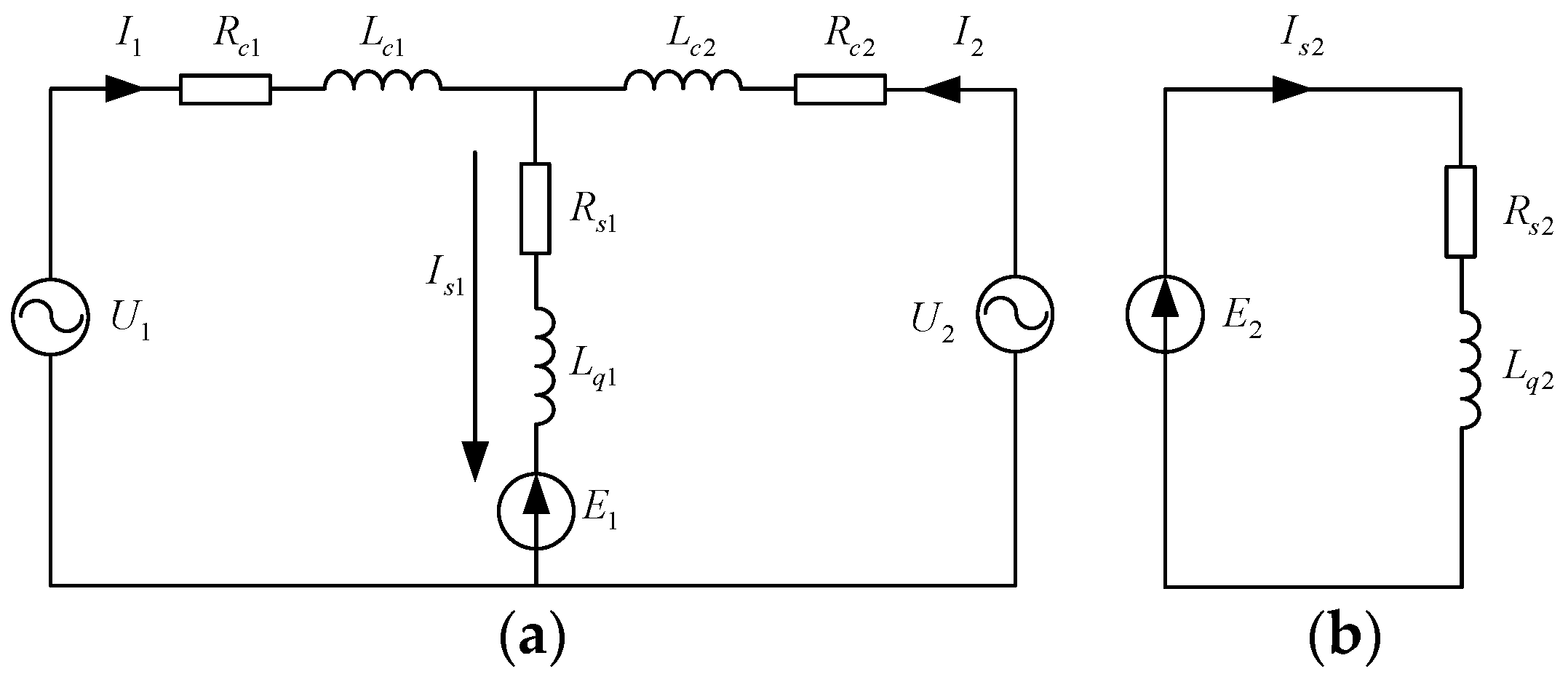
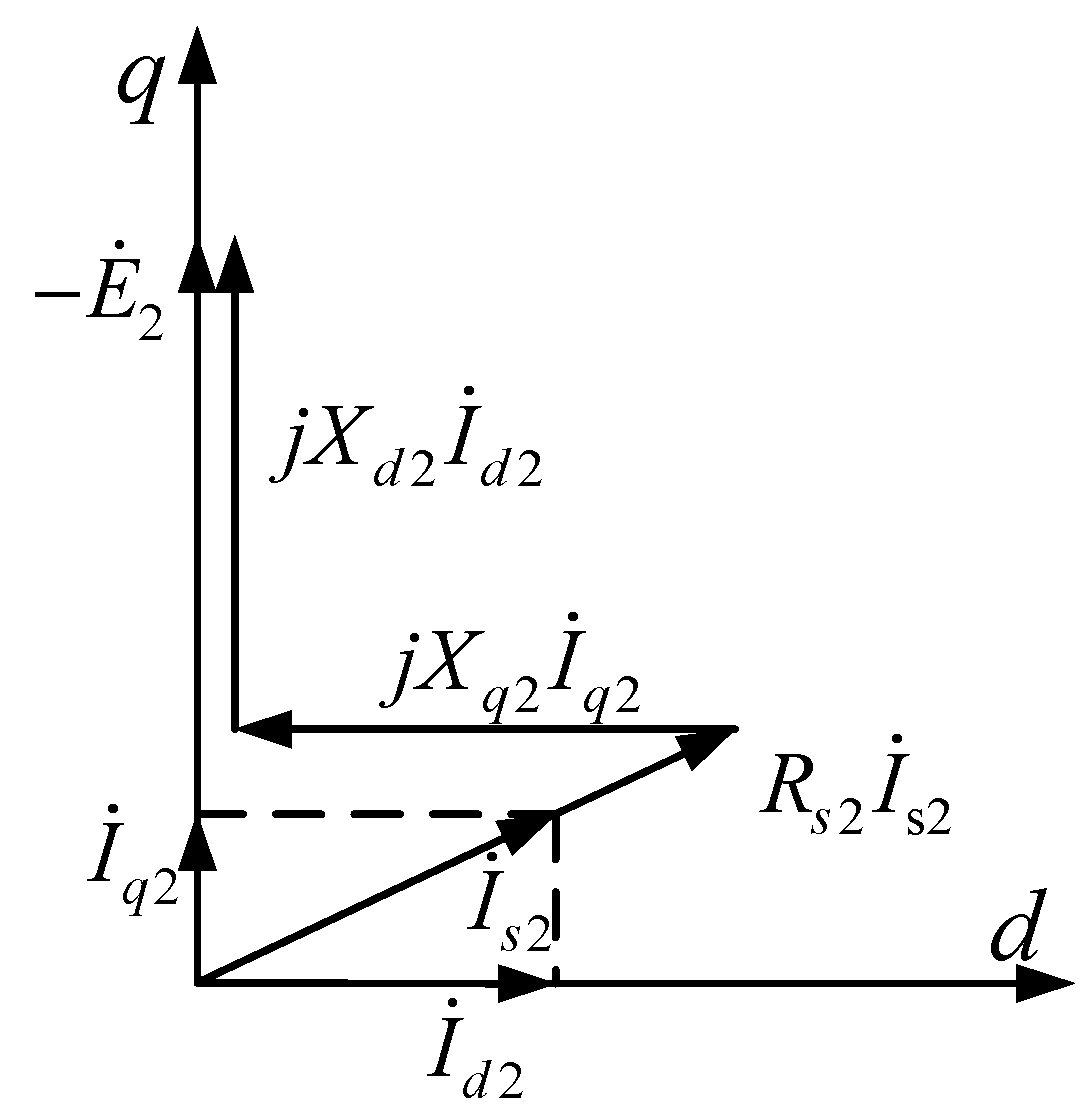
3. Mathematical Model of Three-Phase Short-Circuit Fault of LLSM
4. Simulation of Three-Phase Short-Circuit Fault of LLSM
4.1. Simulation Model
4.2. The Fault Operation Process
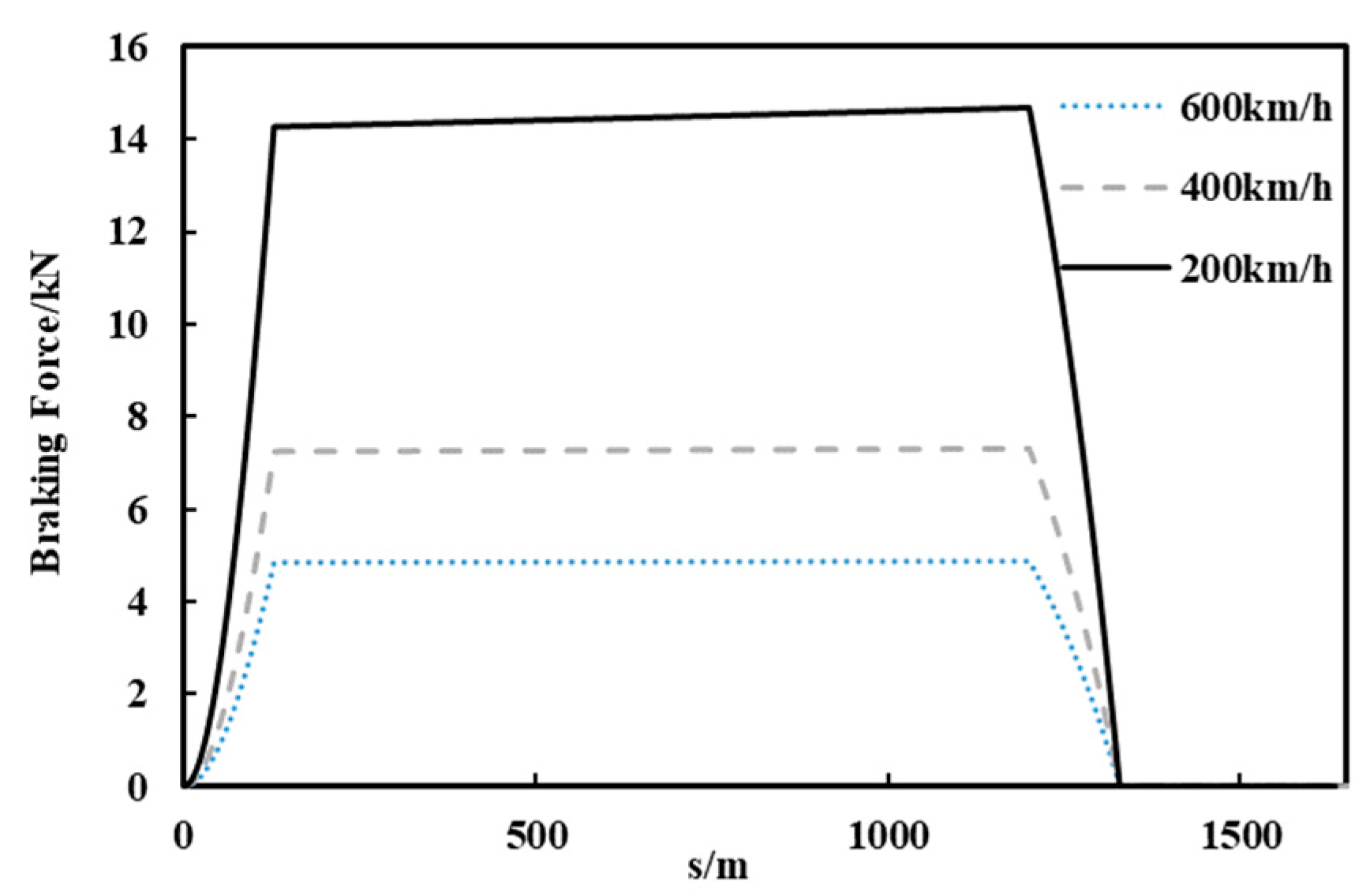
4.3. Failure Performance of the LLSM at Different Speeds
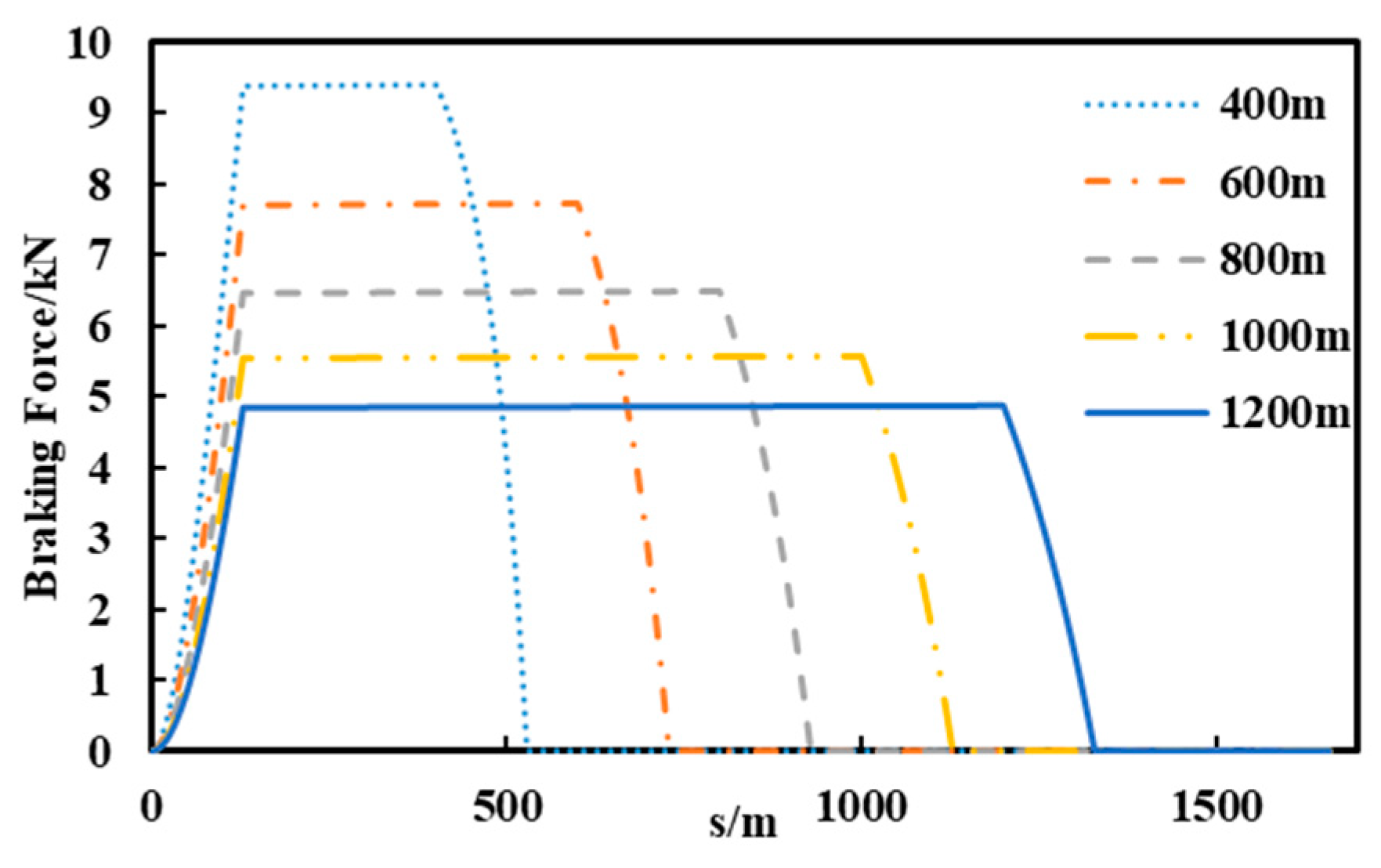
4.4. Failure Performance of the LLSM at Different Lengths of Fault Stator Segment
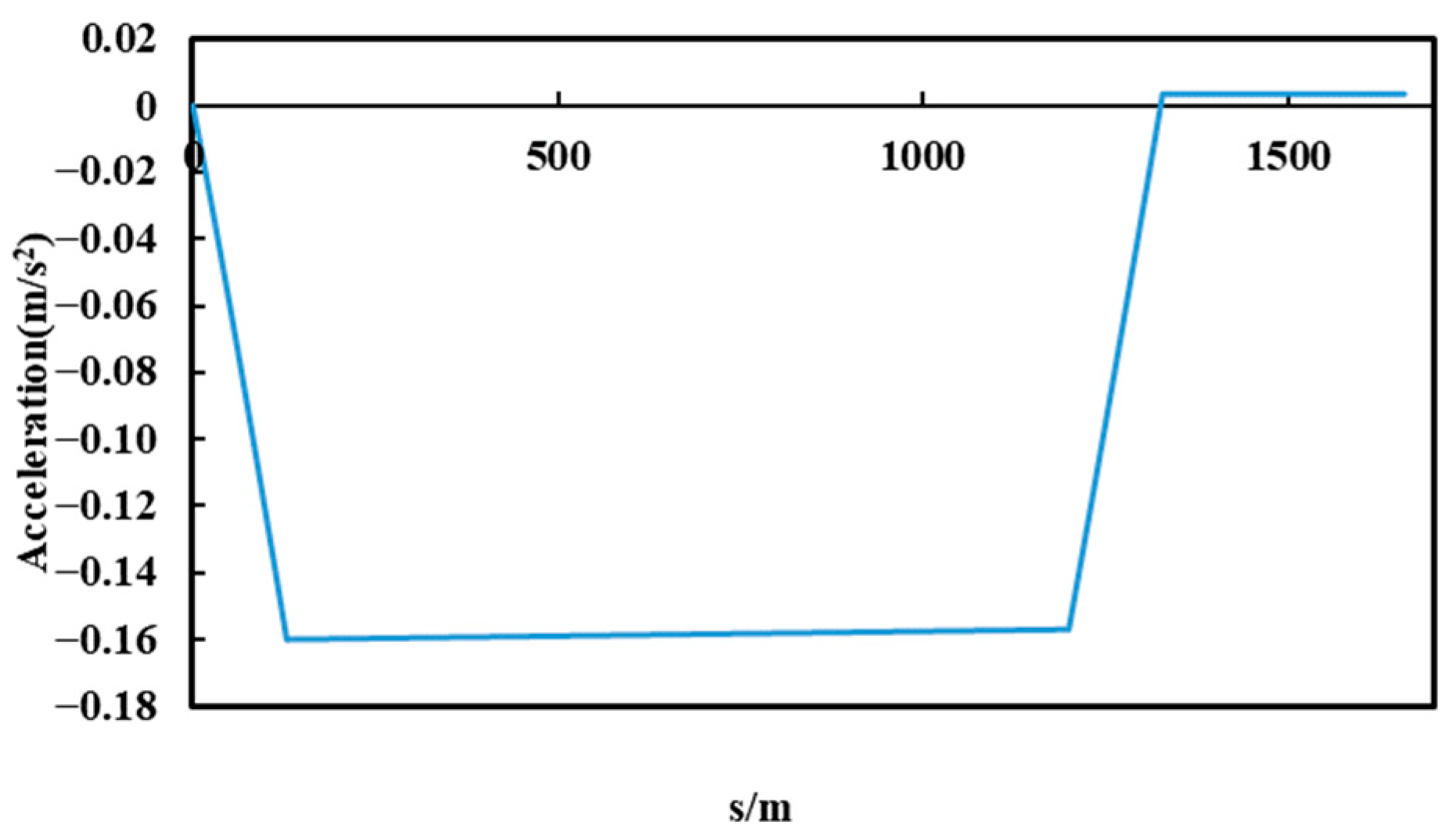
5. Simulation of Three-Phase Short-Circuit Fault during Line Operation
5.1. Simulation Model
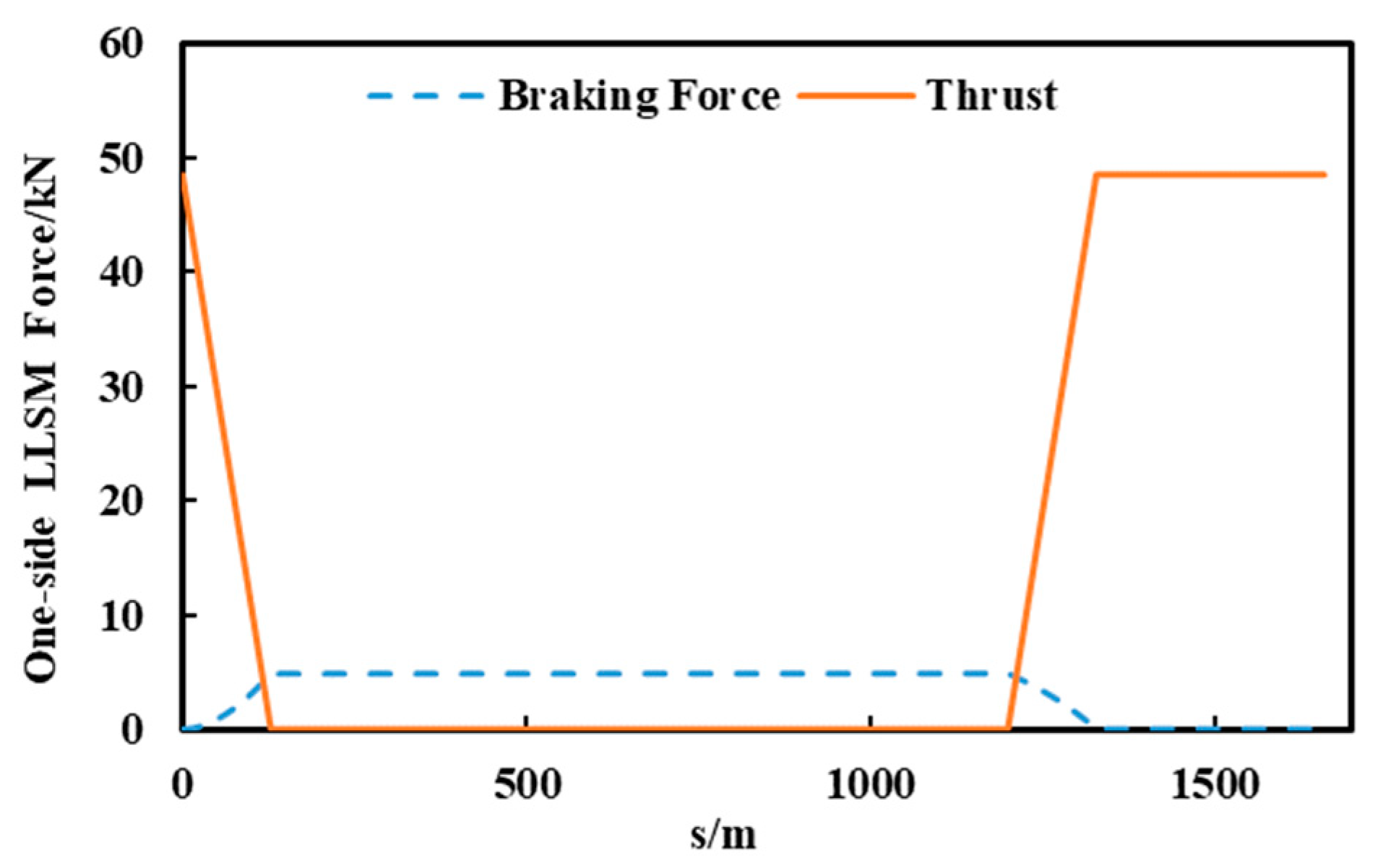
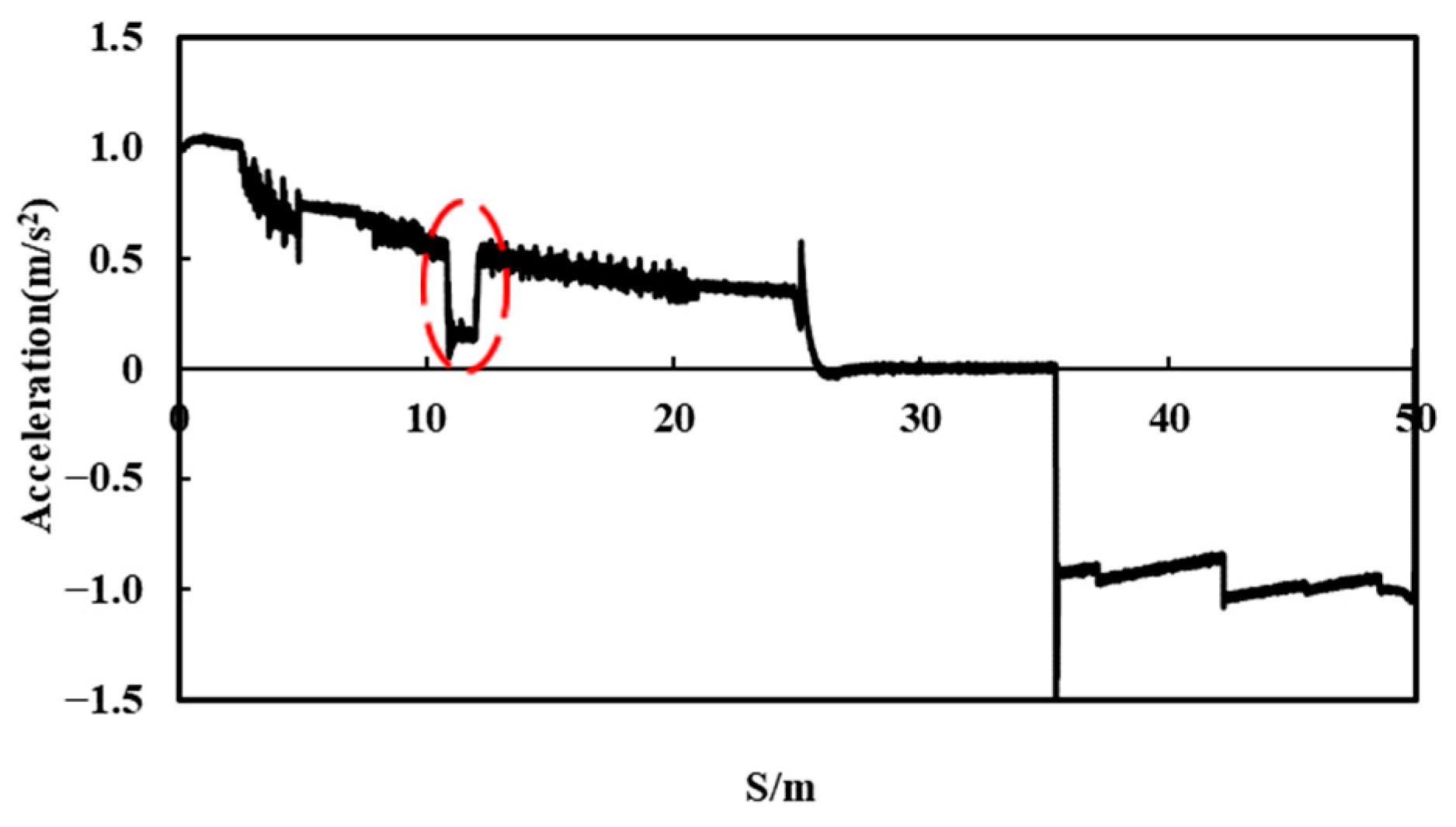
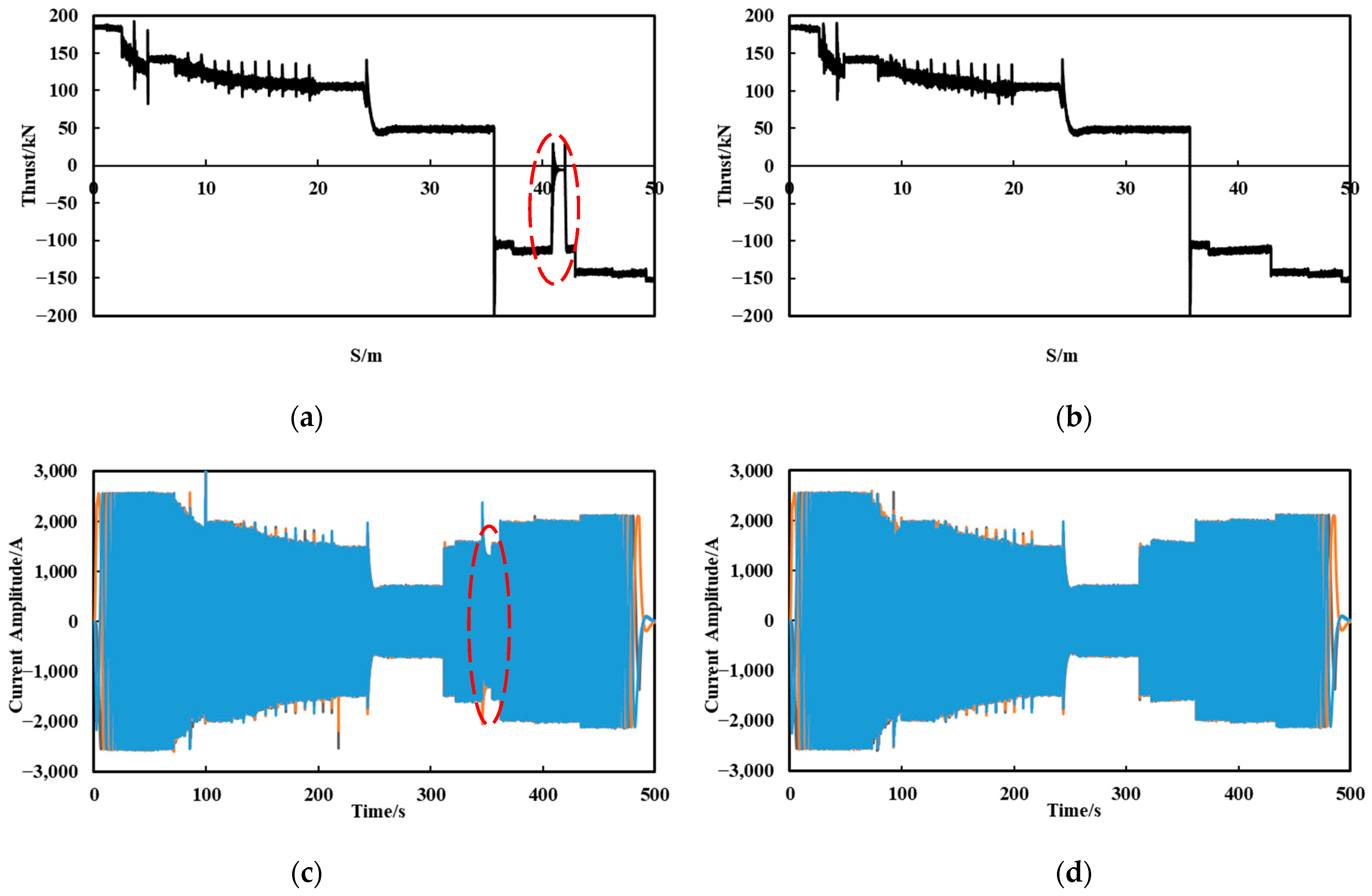
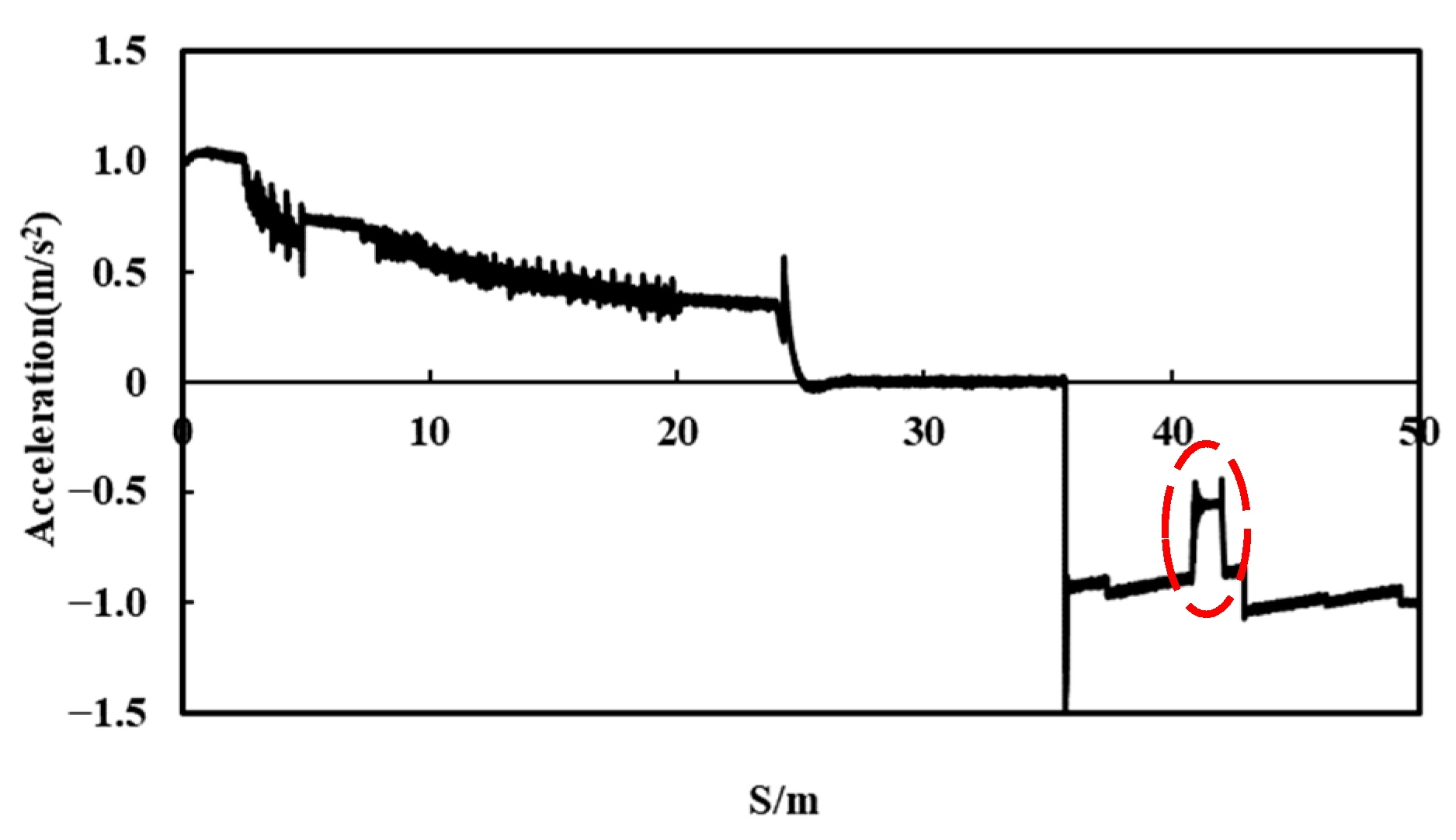
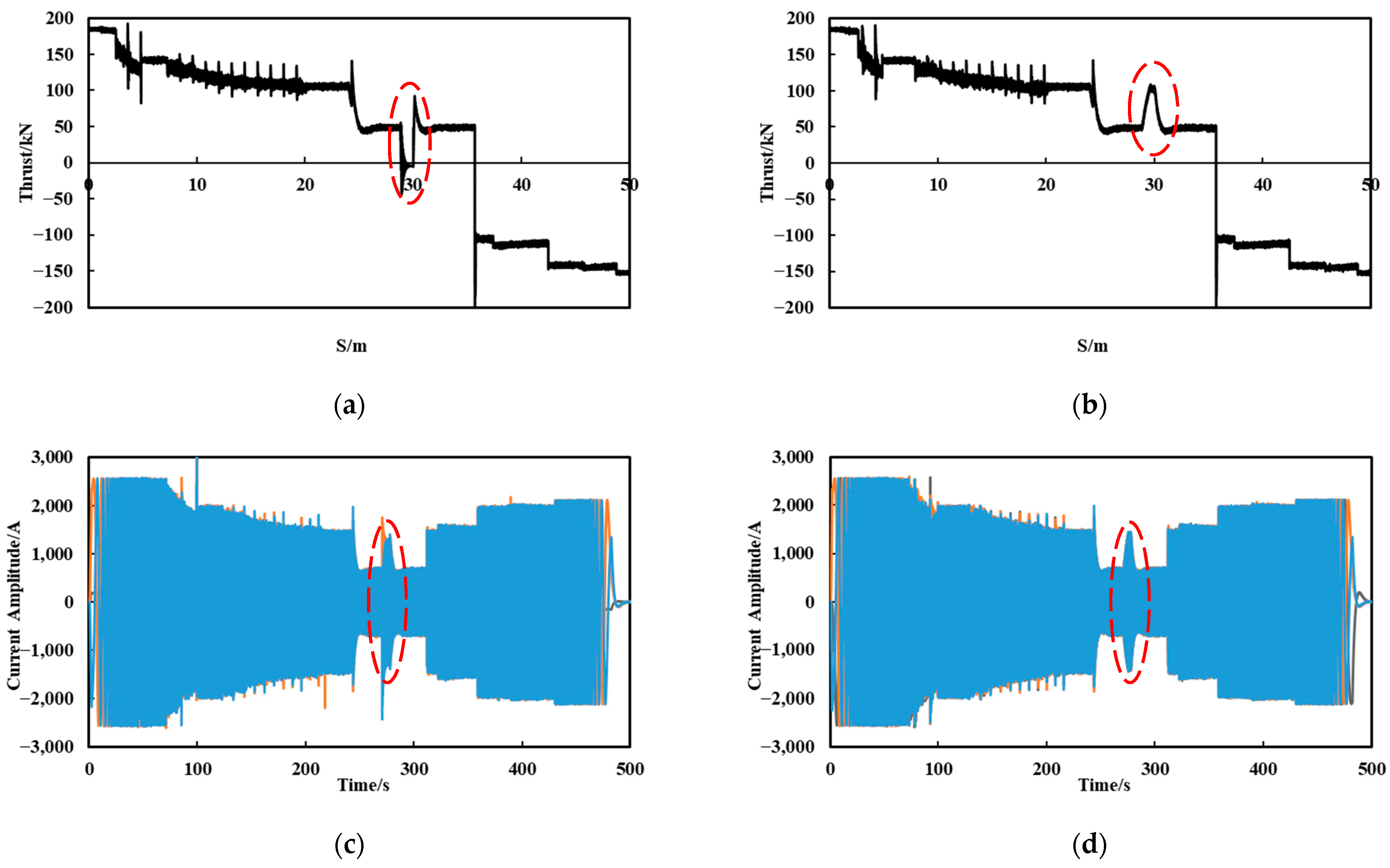
5.2. Fault during Acceleration or Deceleration Process
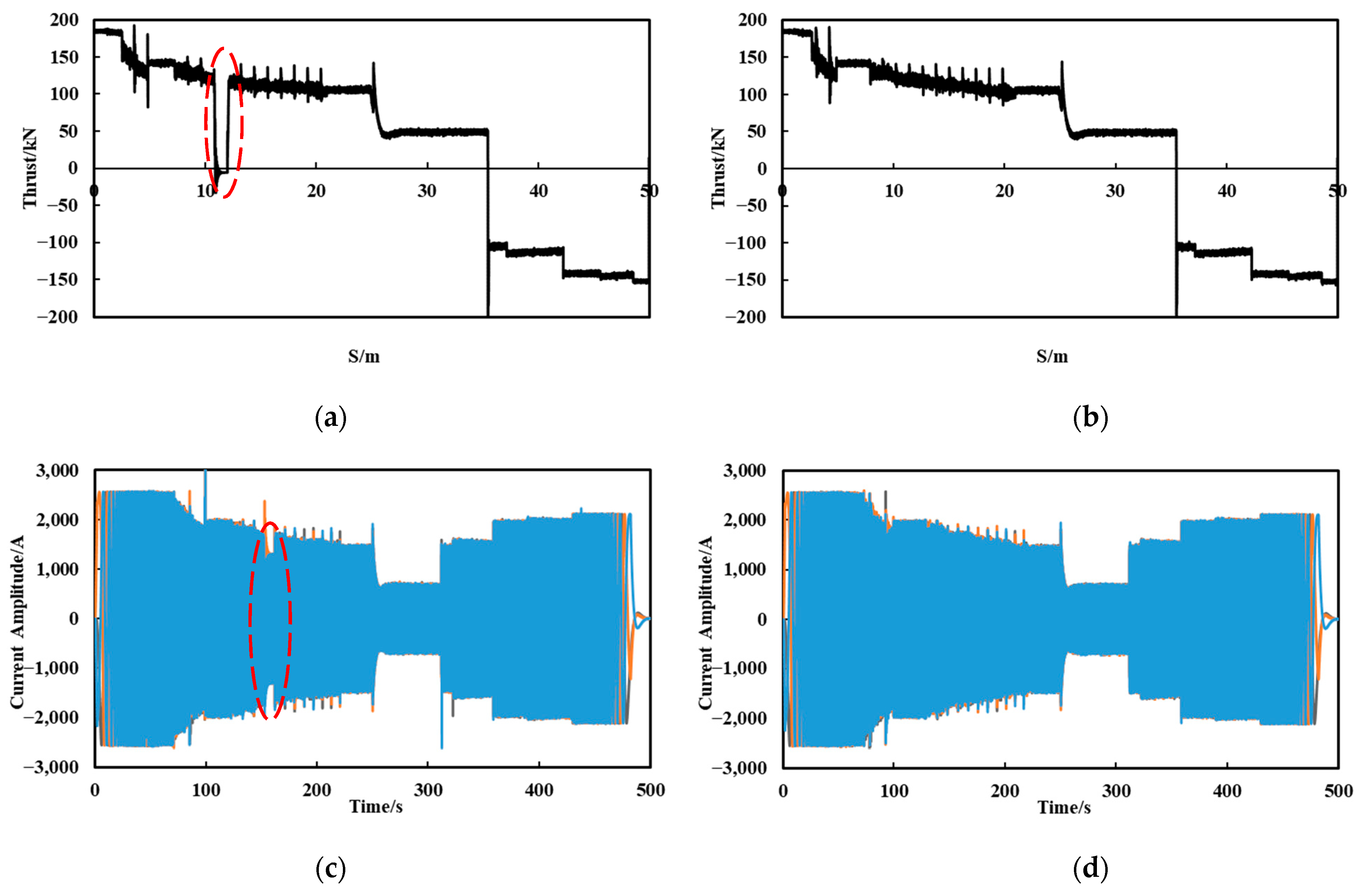
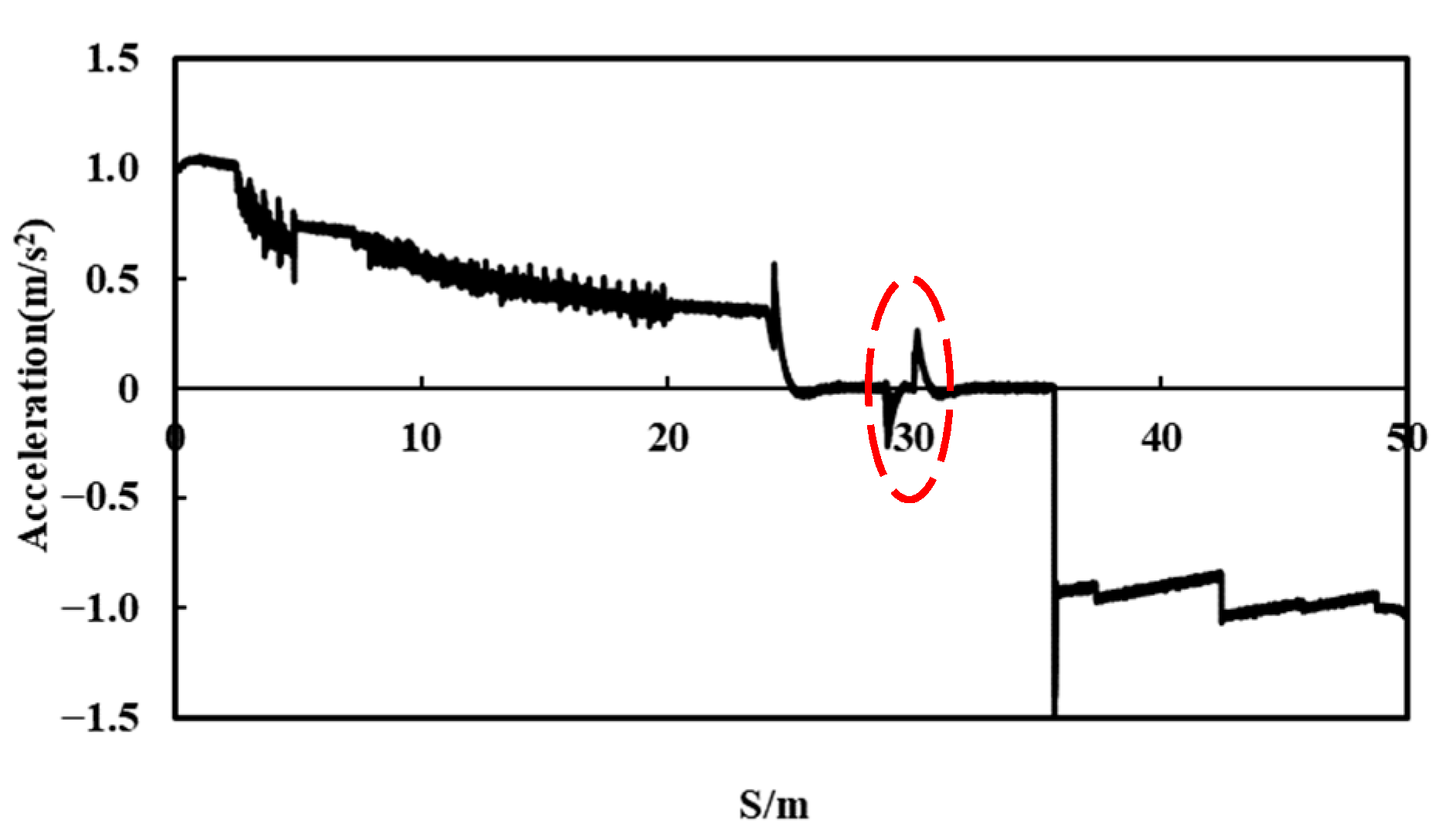
5.3. Fault during Constant Speed
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, H.-W.; Kim, K.-C.; Lee, J. Review of Maglev Train Technologies. IEEE Trans. Magn. 2006, 42, 1917–1925. [Google Scholar] [CrossRef]
- Luguang, Y. Progress of the Maglev Transportation in China. IEEE Trans. Appl. Supercond. 2006, 16, 1138–1141. [Google Scholar] [CrossRef]
- Luo, R.; Wu, J.; Wang, Z. Analysis and research on several faults of high speed maglev train long stator track. J. Railw. Sci. Eng. 2019, 16, 2658–2667. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, J.; Hong, X.; He, Y. Short-Circuit Fault Detection in Laminated Long Stators of High-Speed Maglev Track Based on Fractal Dimension. Measurement 2021, 176, 109177. [Google Scholar] [CrossRef]
- Zou, Z.; Zheng, M.; Lu, Q. Modeling and Simulation of Traction Power Supply System for High-Speed Maglev Train. WEVJ 2022, 13, 82. [Google Scholar] [CrossRef]
- Zhai, M.; Long, Z.; Li, X. Fault-Tolerant Control of Magnetic Levitation System Based on State Observer in High Speed Maglev Train. IEEE Access 2019, 7, 31624–31633. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, W.; Tian, W. Fault-Tolerant Control for Five-Leg Two-Mover Permanent-Magnet Linear Motor Traction Systems with Open-Phase Fault. In Proceedings of the 2021 13th International Symposium on Linear Drives for Industry Applications (LDIA), Wuhan, China, 1–3 July 2021; pp. 1–4. [Google Scholar]
- Lin, Y.; Wang, X.; Qin, F.; Jin, Y.; Lu, D.; Ni, F. A New Concept Structure of the Propulsion System for a Medium Speed Maglev System—Simulation and Analysis. In Proceedings of the 2019 12th International Symposium on Linear Drives for Industry Applications (LDIA), Neuchatel, Switzerland, 1–3 July 2019; pp. 1–4. [Google Scholar]
- Hao, L.; Huang, Z.; Dong, F.; Qiu, D.; Shen, B.; Jin, Z. Study on Electrodynamic Suspension System with High-Temperature Superconducting Magnets for a High-Speed Maglev Train. IEEE Trans. Appl. Supercond. 2019, 29, 3600105. [Google Scholar] [CrossRef]
- Li, L.; Zhang, J.; Lu, Q. Investigation of Electromagnetic Coupling Field of Traction and Levitation Systems in High Speed Maglev Train. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–6. [Google Scholar]
- Liu, J.; Ge, Q.; Wang, X. Traction-system research for high-speed maglev based on double-end supply. Adv. Technol. Electr. Eng. Energy 2015, 34, 16–21. [Google Scholar]
- Tseng, W.-T. Thrust Reduction of Magnetic Levitation Vehicle Driven by Long Stator Linear Synchronous Motor. Math. Probl. Eng. 2013, 2013, 850615. [Google Scholar] [CrossRef]
- Lin, Y.; Ying, L.; Qin, F.; Geng, Q.; WAng, X.; Xiaohua, W. The Simulation and Analysis for a New Concept of the Stator Power Supply Mode of a Medium Speed Maglev System. Transp. Syst. Technol. 2018, 4, 225–233. [Google Scholar] [CrossRef]
- Tan, Q.; Wei, R.; Wang, X.; Ge, Q. Traction-System Research Based on Different Proportion of Current in Double-End Supply for High-Speed Maglev. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 11–14 August 2017; pp. 1–5. [Google Scholar]
- Cui, D.; Wei, R.; Liu, J.; Ge, Q. Linear Synchronous Motor Drive System Based on Proportion Resonant Current Controller in Maglev Transportation. In Proceedings of the 2014 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014; pp. 1289–1292. [Google Scholar]
- Xu, L.; Wei, R.; Ge, Q.; Wang, X.; Li, Y. Hardware-in-Loop Simulation of Linear Synchronous Motor Based on Three-Level Converter. In Proceedings of the 2013 International Conference on Electrical Machines and Systems (ICEMS), Busan, Korea, 26–29 October 2013; pp. 1944–1947. [Google Scholar]
- Ikeda, H.; Kaga, S.; Osada, Y.; Ito, K.; Mugiya, Y.; Tutumi, K. Development of Power Supply System for Yamanashi Maglev Test Line. In Proceedings of the Power Conversion Conference—PCC ’97, Nagaoka, Japan, 6 August 1997; Volume 1, pp. 37–41. [Google Scholar]
- Lee, J.; Jo, J.; Han, Y.; Lee, C. Development of LSM Control System for Super Speed Maglev. In Proceedings of the 2013 13th International Conference on Control, Automation and Systems (ICCAS 2013), Gwangju, Korea, 20–23 October 2013; pp. 466–469. [Google Scholar]
- Liu, Y.; Fan, K.; Ouyang, Q. Intelligent Traction Control Method Based on Model Predictive Fuzzy PID Control and Online Optimization for Permanent Magnetic Maglev Trains. IEEE Access 2021, 9, 29032–29046. [Google Scholar] [CrossRef]
- Zhang, Y.; Qing, G.; Zhang, Z.; Li, J.; Chen, H. Calculation and Simulation of Propulsion Power Supply System for High-Speed Maglev Train. In Proceedings of the 2020 IEEE Vehicle Power and Propulsion Conference (VPPC), Gijon, Spain, 18 November–16 December 2020; pp. 1–5. [Google Scholar]


| Parameters | Value |
|---|---|
| Pitch Length (m) | 0.258 |
| Back EMF Coefficient (V/(km/h)/km) | 74.84 |
| One-side Motor Thrust Coefficient (kN/A/km) | 0.735 |
| Train Length (m) | 128.5 |
| Stator Segment Length (m) | 1200 |
| Train Mass (t) | 330 |
| Parameters | Value |
|---|---|
| Feeder Cable Resistance (/km) | 0.05833 |
| Feeder Cable Inductance (H/km) | 0.000071 |
| Stator Resistance () | 0.23 |
| D-axis Inductance (mH) | 3 |
| Q-axis Inductance (mH) | 2.8 |
| Converter Maximum Capacity (MVA) | 24 |
| DC Bus Voltage (V) | 4400 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Li, Y.; Lu, Q. Performance Simulation of Long-Stator Linear Synchronous Motor for High-Speed Maglev Train under Three-Phase Short-Circuit Fault. World Electr. Veh. J. 2022, 13, 216. https://doi.org/10.3390/wevj13110216
Yang H, Li Y, Lu Q. Performance Simulation of Long-Stator Linear Synchronous Motor for High-Speed Maglev Train under Three-Phase Short-Circuit Fault. World Electric Vehicle Journal. 2022; 13(11):216. https://doi.org/10.3390/wevj13110216
Chicago/Turabian StyleYang, Hongyi, Yanxin Li, and Qinfen Lu. 2022. "Performance Simulation of Long-Stator Linear Synchronous Motor for High-Speed Maglev Train under Three-Phase Short-Circuit Fault" World Electric Vehicle Journal 13, no. 11: 216. https://doi.org/10.3390/wevj13110216
APA StyleYang, H., Li, Y., & Lu, Q. (2022). Performance Simulation of Long-Stator Linear Synchronous Motor for High-Speed Maglev Train under Three-Phase Short-Circuit Fault. World Electric Vehicle Journal, 13(11), 216. https://doi.org/10.3390/wevj13110216










