Analysis and Roll Prevention Control for Distributed Drive Electric Vehicles
Abstract
1. Introduction
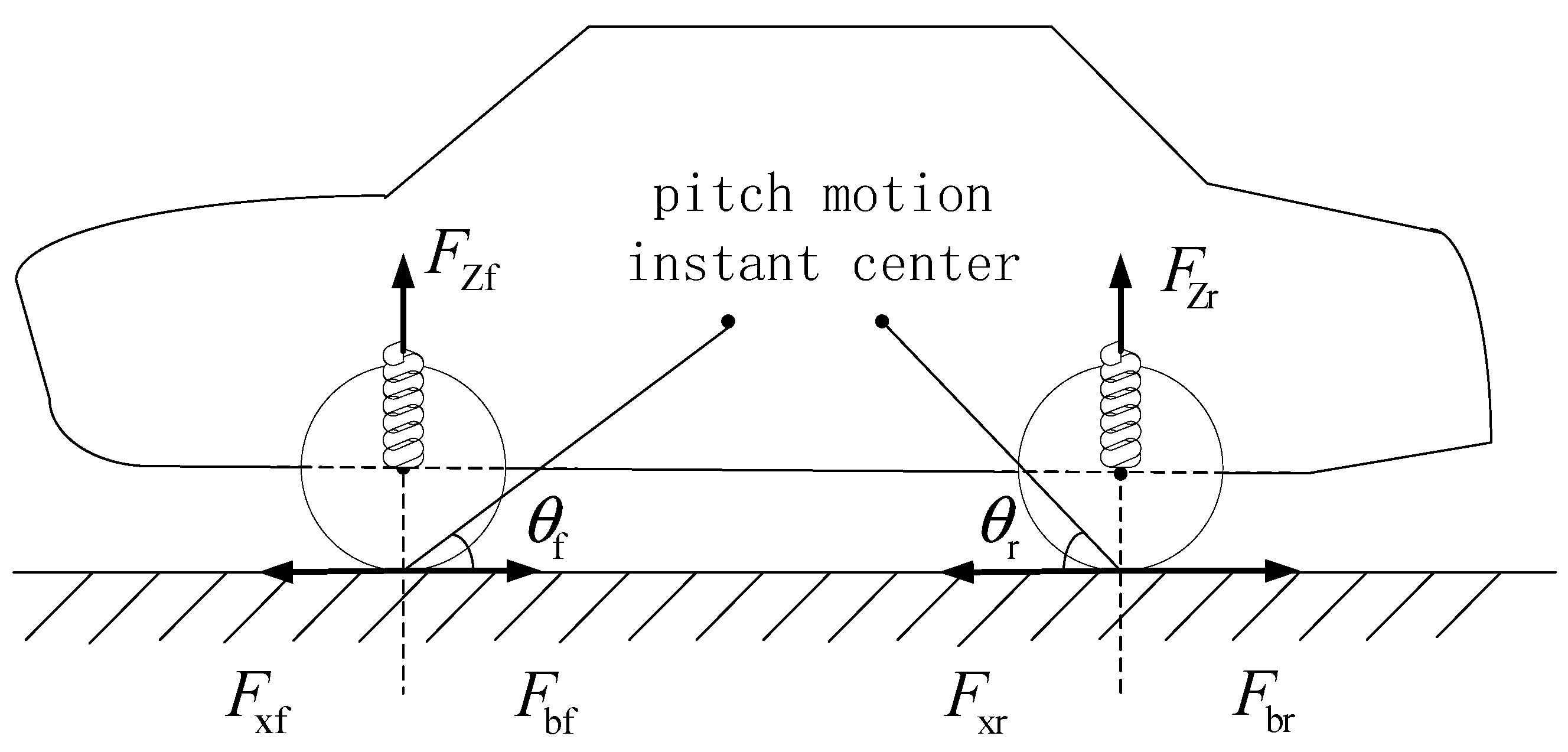
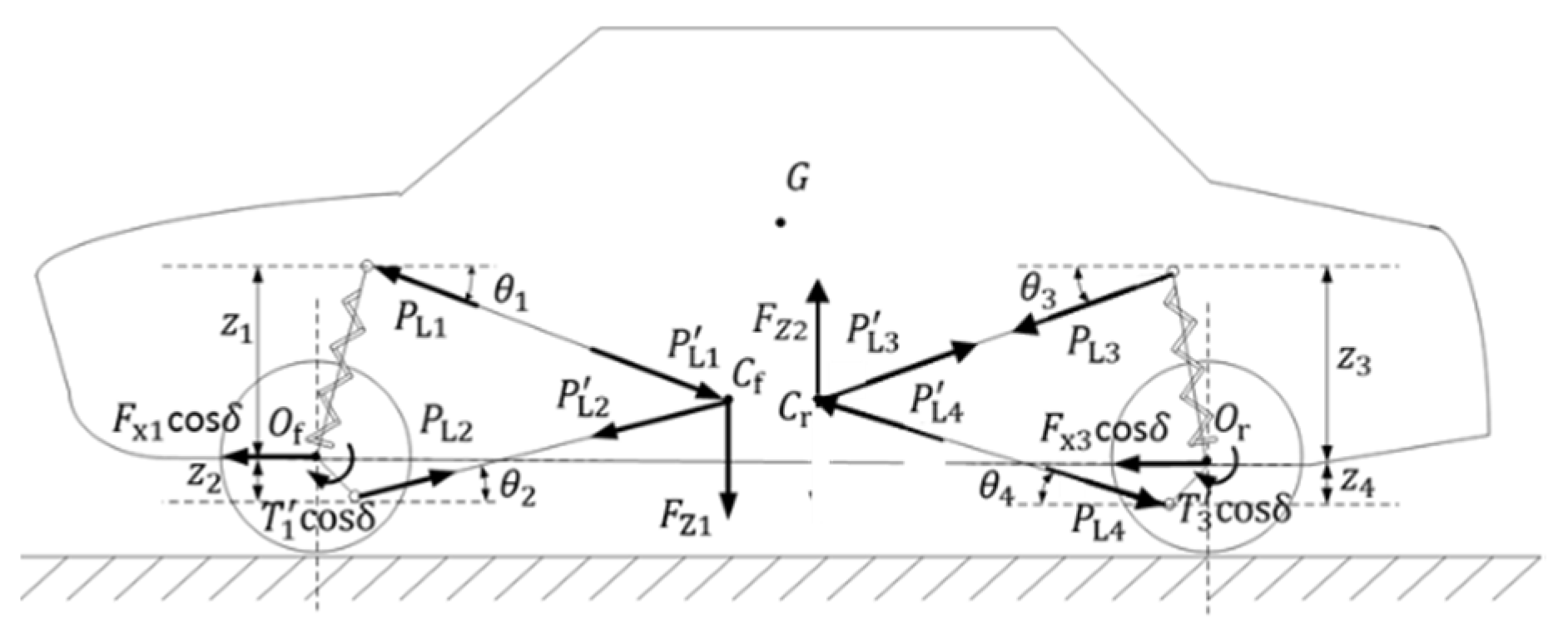
2. Generating Mechanism of the Rolling Moment of DDEV
2.1. Rolling Moment of DDEV
2.2. Analysis of the Rolling Effect for the Additional Vertical Force of DDEV
3. Roll Stability Control Algorithm
3.1. Yaw and Roll Decoupling Control Algorithm
3.1.1. Yaw Stability Control
3.1.2. Roll Stability Control
3.1.3. Torque Distribution Strategy for Decoupling Control
3.2. Anti-Rollover Control Algorithm Based on Differential Brake
3.2.1. Evaluation Index of Vehicle Rollover
3.2.2. Fuzzy Control Algorithm
3.2.3. Distribution Strategy of Yaw Moment
4. Simulation and Verification
4.1. Vehicle Model
4.2. Simulation Verification of Yaw and Roll Decoupling Control Algorithm
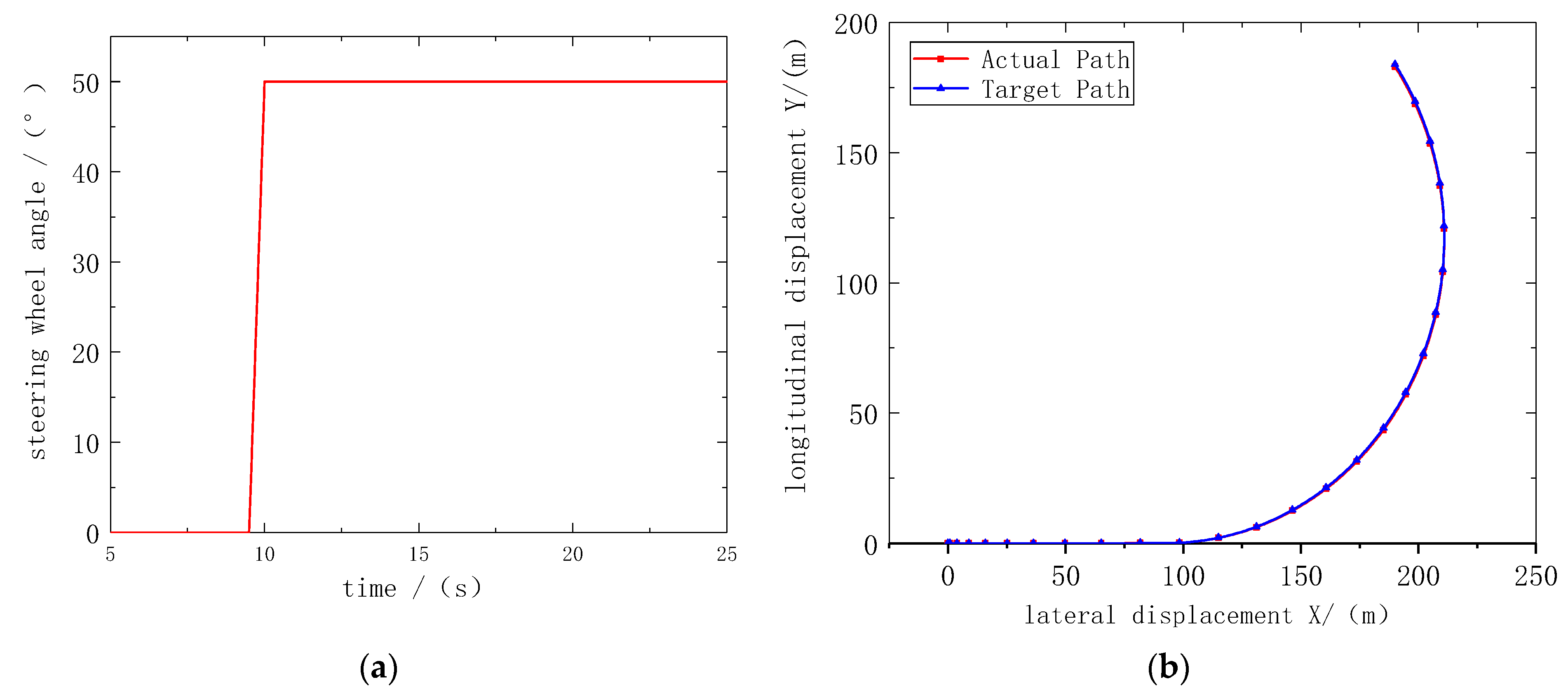
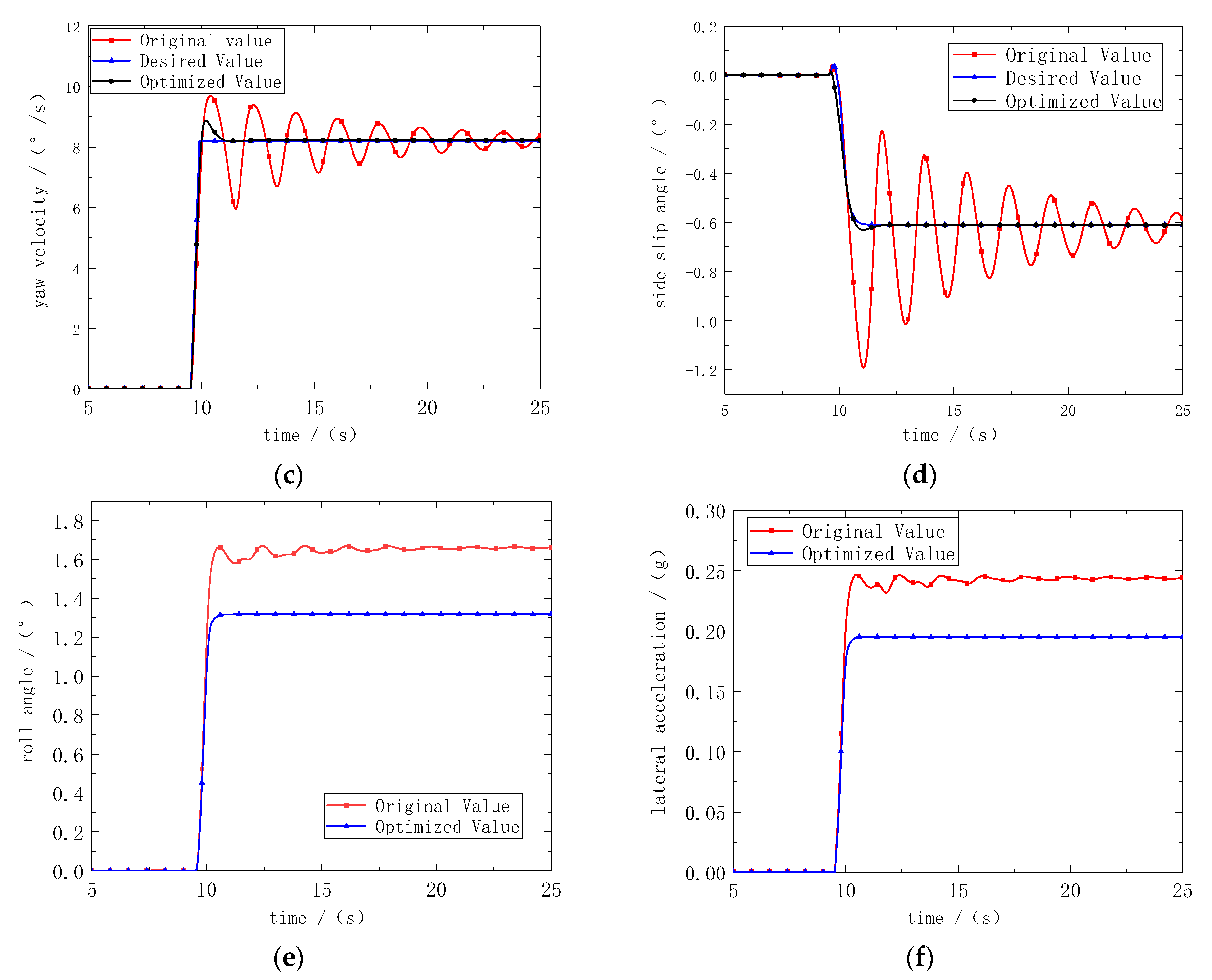
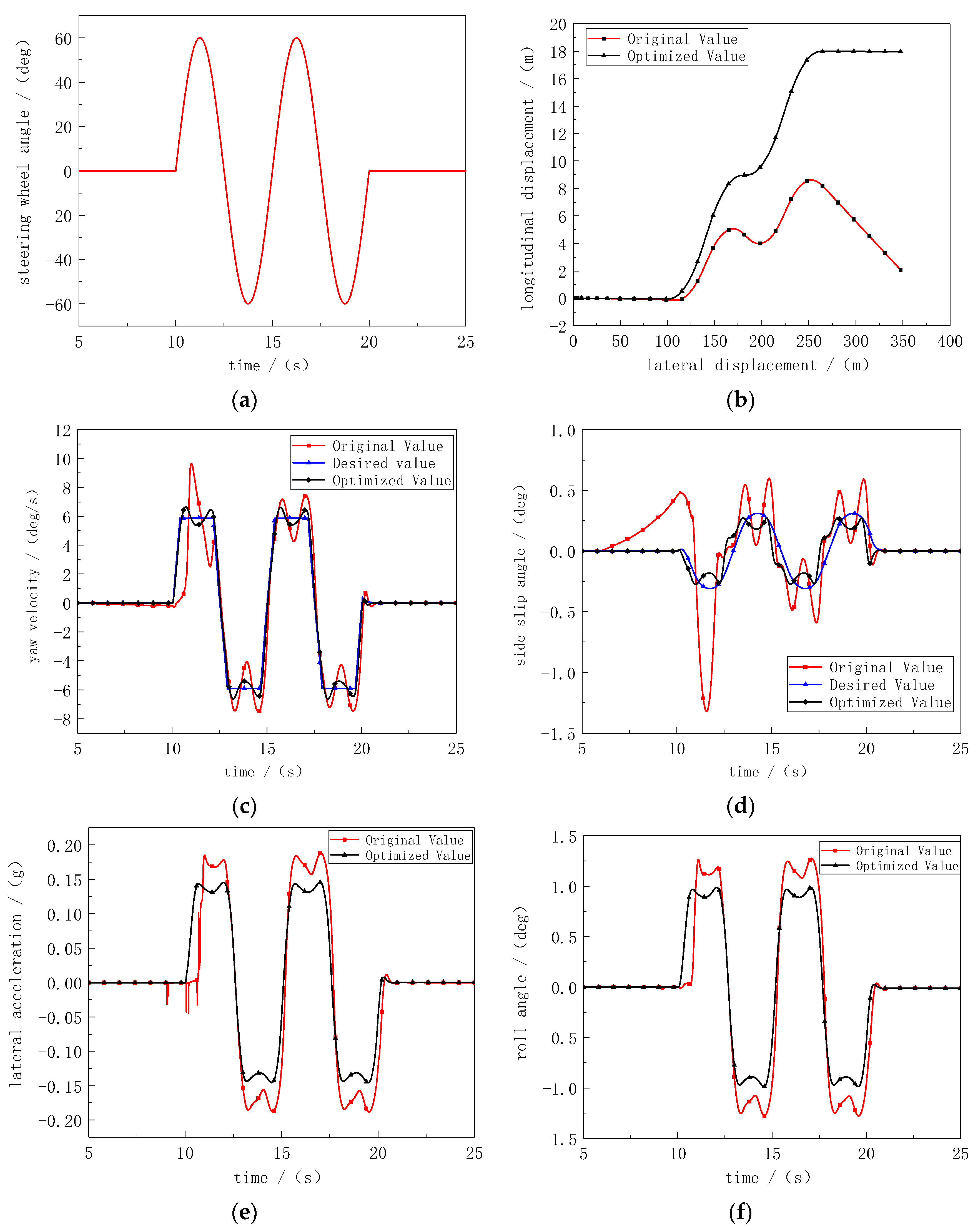
4.2.1. Angular Step Input Condition
4.2.2. Sine Input Condition
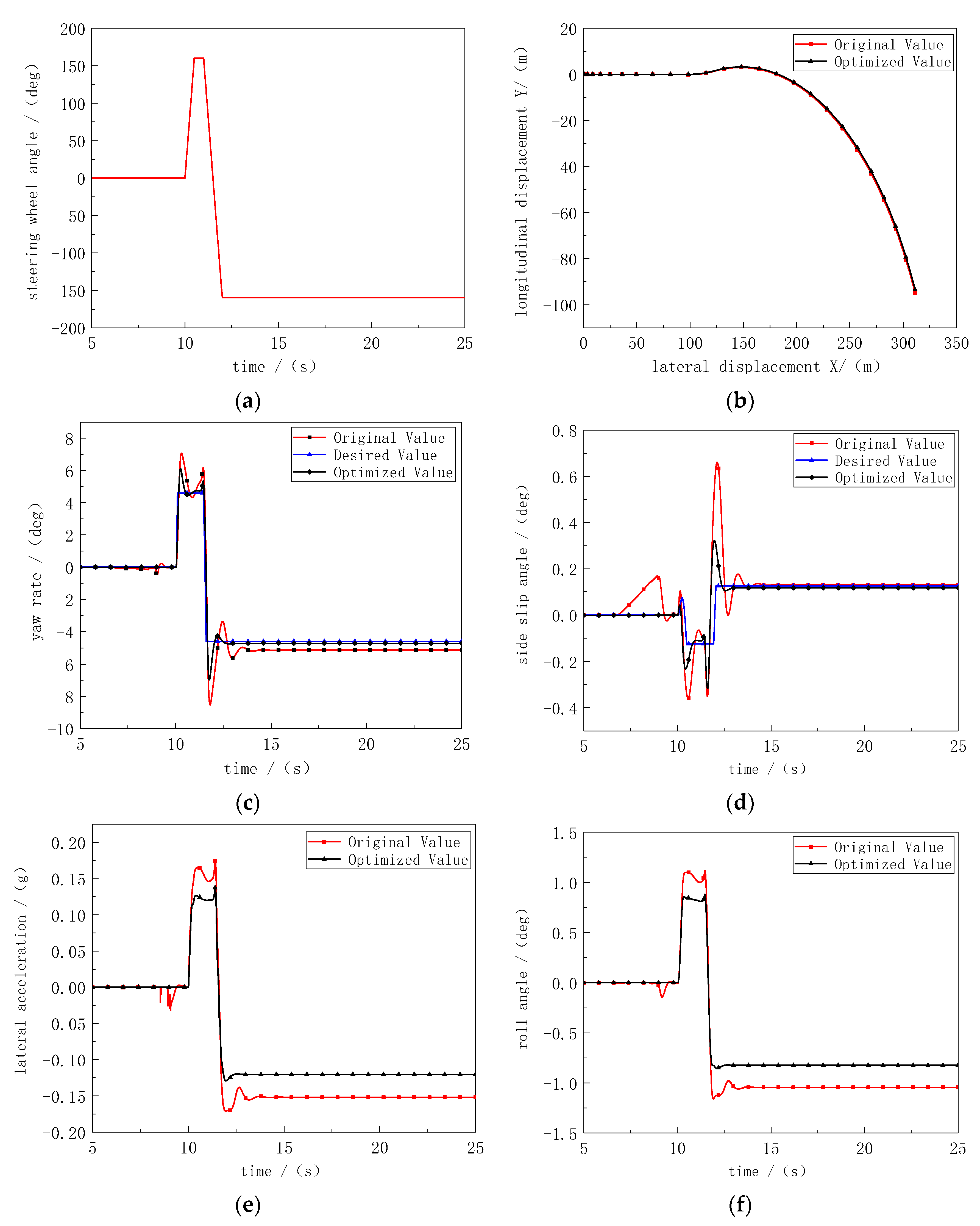
4.2.3. Fish Hook Test Condition
4.3. Simulation Verification of Anti-Rollover Control Algorithm
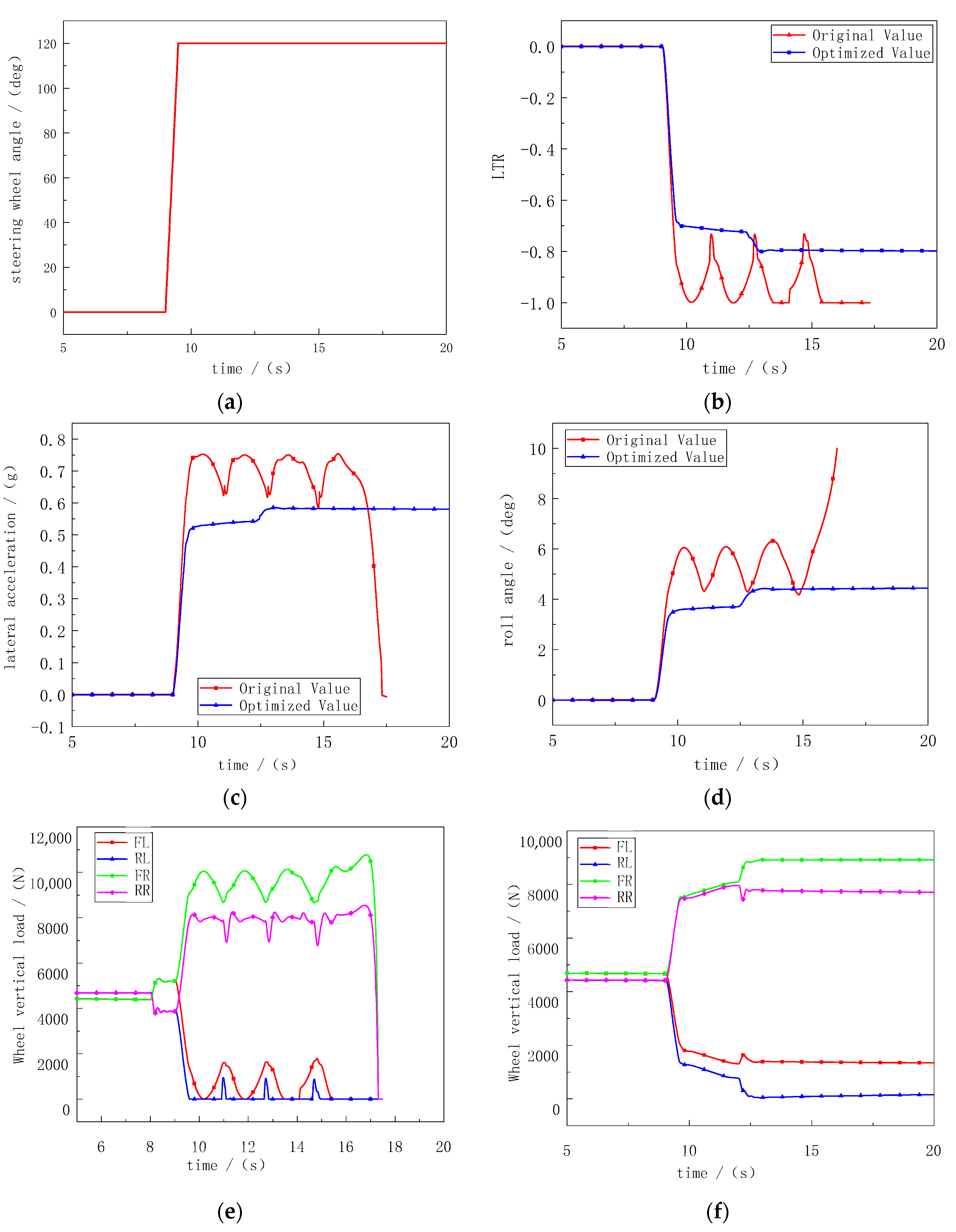
4.3.1. J-Turn Condition
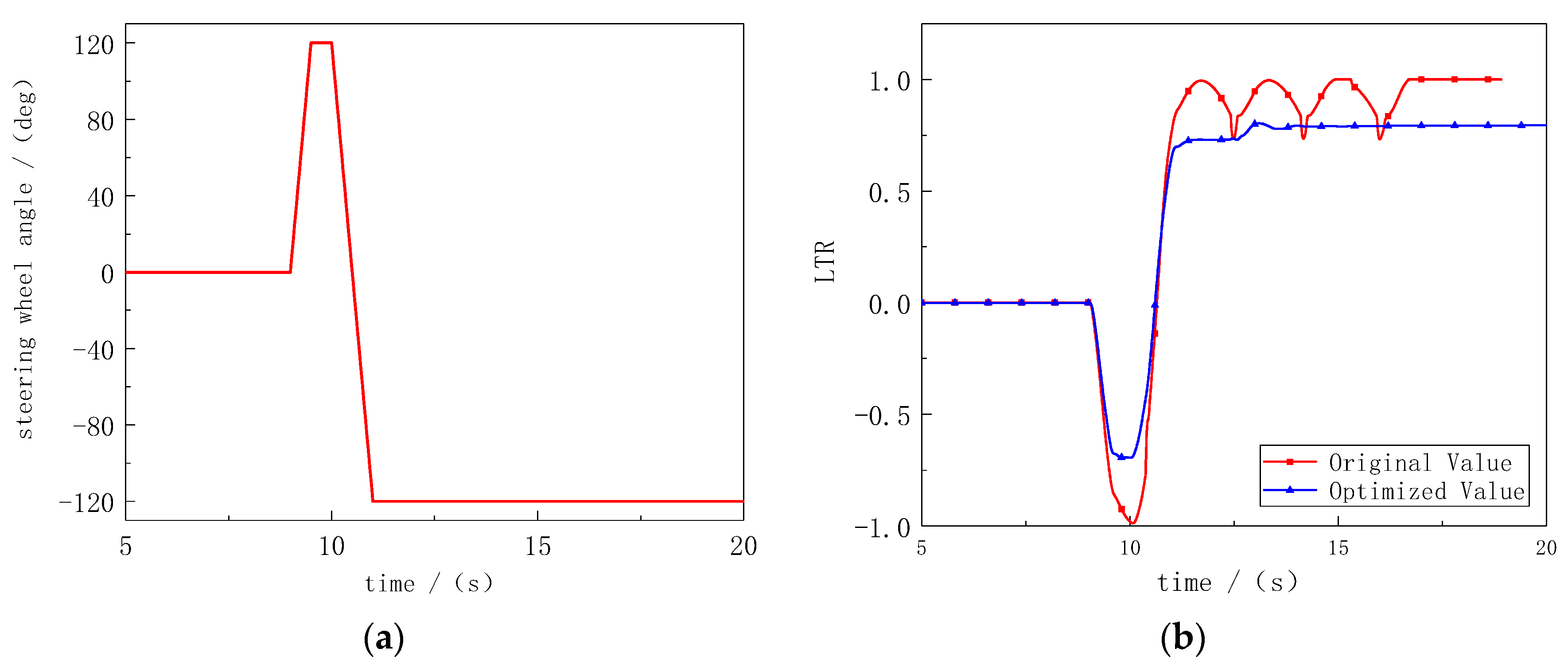
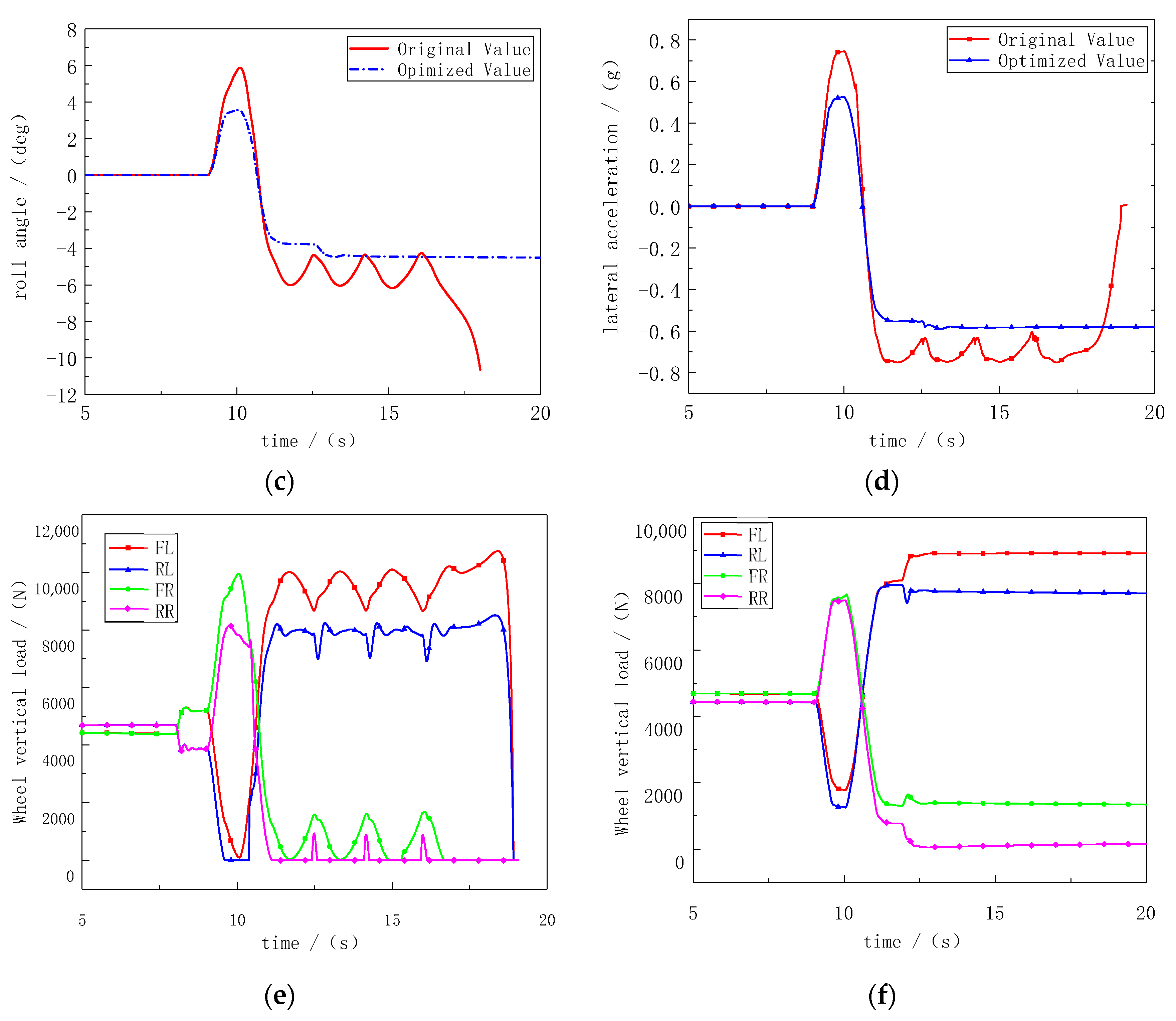
4.3.2. Fish Hook Test Condition
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | |
| Iₓ (kg·m2) (deg) | rotational inertia of the vehicle around the x axis vehicle roll angle |
| ms (kg) | vehicle sprung mass |
| hs (m) | distance from the center of the sprung mass to the roll center of the car |
| b (m) | distance from center of mass to rear axle |
| a (m) | distance from center of mass to front axle |
| m (kg) | vehicle mass |
| vy (km/h) | vehicle lateral speed |
| vx (km/h) | vehicle longitudinal speed |
| ay (m/s2) | vehicle lateral acceleration |
| ω (rad/s) | angular velocity of the wheel |
| kr, kf (N/rad) | cornering stiffness of the rear and front wheel |
| L (m) | vehicle wheelbase |
| r (m) | wheel rolling radius |
| B (m) | track width |
| (deg) | front wheel angle |
| K | stability factor |
| gy (m/s2) | gravitational acceleration |
| Fyf, Fyr (N) | side force of vehicle front and rear wheels |
| Kϕ (N/rad) | equivalent roll stiffness of the car |
| Cϕ (N/(km/h)) | equivalent roll damping of automobile |
| ΔMX (N·m) | additional roll moment. |
| Fx1 (N) | ground driving force |
| T1 (N·m) | motor torque transmitted from the front wheel to the vehicle body via the suspension |
| PLi (i = 1, 2, 3, 4) (N) | force exerted by the left body on the front suspensions |
| PLi (i = 1, 2, 3, 4) (N) | force exerted by the front suspensions on the left body |
| Pij (j = 1, 2) (N) | force exerted by the car body on the side of the front-inner suspension |
| Pij (j = 1, 2) (N) | force exerted by the front-inner suspension on the car body |
| Poi′ (j = 1, 2) (N) | force exerted by the front-outer suspension on the car body |
| Ki (i = 1, 2, 3, 4, 5, 6) | the corresponding coefficient of the roll moment |
| zi (i = 1, 2, 3, 4) (m) zij (j = 1, 2) (m) lout, lin (m) | the corresponding distance |
| θi (i = 1, 2, 3, 4) (rad) θij (j = 1, 2) (rad) θoi (i = 1, 2) (rad) | the corresponding angle |
| MXj (j = 1, 2, 3, 4) (N·m) | roll moment generated by the suspension to the vehicle body |
| MXi, MXo (N·m) | roll moment generated by the front wheel via the suspension |
| ωr (dge/s) | vehicle yaw rate |
| ωrd (dge/s) | ideal yaw rate |
| ωrmax (dge/s) | the maximum values of yaw rate |
| βd (dge) | ideal side slip angle |
| βrmax (dge) | the maximum values of side slip angle |
| weight coefficient between the roll angle and roll angular velocity | |
| e (dge) | the error of roll angle |
| switching gain | |
| road adhesion coefficient | |
| sat (s) | the saturation function |
| ΔFxi (i = 1, 2, 3, 4) (N) | increment of each driving force |
| ΔTi (i = 1, 2, 3, 4) | wheels drive torque |
| Tmax (N·m) | maximum driving moment of the motor |
| Fb (N) | braking force exerted on the front outer wheel |
| Iw (kg·m2) | rotating inertia of front outer wheel |
| Tb (N·m) | vehicle braking torque. |
| Fzi (i = 1, 2, 3, 4) (N) | wheels vertical load |
| P | braking pressure |
| S | braking efficiency coefficient. |
References
- Chakraborty, S.; Kumar, N.M.; Jayakumar, A.; Dash, S.K.; Elangovan, D. Selected Aspects of Sustainable Mobility Reveals Implementable Approaches and Conceivable Actions. Sustainability 2021, 13, 12918. [Google Scholar] [CrossRef]
- Boada, B.L.; Boada, M.J.L.; Vargas-Melendez, L. A robust observer based on H ∞ filtering with parameter uncertainties combined with neural networks for estimation of vehicle roll angle. Mech. Syst. Signal Process. 2018, 99, 611–623. [Google Scholar] [CrossRef]
- Zhou, B.; Lü, X.N.; Fan, L. Integrated control of active suspension system and active roll stabilizer. China Mech. Eng. 2014, 14, 1978–1983. [Google Scholar]
- Chen, S.; Xia, C.G.; Pan, D.Y. A study on hybrid rollover control of vehicle with active anti-roll bar. Automot. Eng. 2017, 39, 667–674. [Google Scholar]
- Parsons, K.G.R.; Pask, M.; Burdock, W. The development of ACE for discovery II. In Proceedings of the SAE 2000 World Congress, Detroit, MI, USA, 6–9 March 2000. [Google Scholar]
- Karnopp, D. Active and semi-active vibration isolation. Curr. Adv. Mech. Des. Prod. VI 1995, 117, 409–423. [Google Scholar]
- Xiao, L.J.; Wang, M.; Zhang, B.J. Vehicle roll stability control with active roll-resistant electro-hydraulic suspension. Front. Mech. Eng. 2020, 15, 43–54. [Google Scholar] [CrossRef]
- Yakub, F.; Abu, A.; Mori, Y. Enhancing the yaw stability and the manoeuvrability of a heavy vehicle in difficult scenarios by an emergency threat avoidance manoeuvre. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2017, 231, 615–637. [Google Scholar] [CrossRef]
- Lua, C.A.; Castillo-Toledo, B.; Cespi, R.; Gennaro, S.D. Nonlinear observer-based active control of ground vehicles with non negligible roll dynamics. Int. J. Control Autom. Syst. 2016, 14, 743–752. [Google Scholar] [CrossRef]
- Dal Poggetto, V.F.; Serpa, A.L. Vehicle rollover avoidance by application of gain-scheduled LQR controllers using state observers. Veh. Syst. Dyn. 2016, 54, 191–209. [Google Scholar] [CrossRef]
- Imine, H.; Fridman, L.M.; Madani, T. Steering control for rollover avoidance of heavy vehicles. IEEE Trans. Veh. Technol. 2013, 61, 3499–3509. [Google Scholar] [CrossRef]
- Chen, B.C.; Peng, H. Differential-braking-based rollover prevention for sport utility vehicles with human-in-the-loop evaluations. Veh. Syst. Dyn. 2001, 36, 359–389. [Google Scholar] [CrossRef]
- Solmaz, S.; Akar, M.; Shorten, R. Adaptive rollover prevention for automotive vehicles with differential braking. IFAC Proc. Vol. 2008, 41, 4695–4700. [Google Scholar] [CrossRef]
- Feng, F. Study on Roll Stability of Electric Wheel Drive Vehicle on Uneven Pavement. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2017. [Google Scholar]
- Li, G.; Zong, C.F.; Chen, G.Y.; Wei, H.; Lei, H. Integrated control for X-by-wire electric vehicle with 4 independently driven in-wheel motors. J. Jilin Univ. (Eng. Technol. Ed.) 2012, 42, 796–802. [Google Scholar]
- Wang, Z. The Integrated Control of Active Suspension and Drive Force Distribution Based on 4 In-Wheel Motor Driven Electric Vehicle. Master’s Thesis, Southeast University, Nanjing, China, 2016. [Google Scholar]
- Kiyotaka, K.; Toshiyuki, U.; Yoichi, H. Normal force stabilizing control using small EV powered only by Electric double layer capacitor. World Electr. Veh. J. 2008, 1, 62–67. [Google Scholar]
- Fujimoto, H.; Sato, S. Pitching control method based on quick torque response for electric vehicle. In Proceedings of the 2010 International Power Electronics Conference, Sapporo, Japan, 21–24 June 2010. [Google Scholar]
- Kawashima, K.; Uchida, T.; Hori, Y. Rolling stability control of in-wheel electric vehicle based on two-degree-of-freedom control. In Proceedings of the IEEE International Workshop on Advanced Motion Control, Trento, Italy, 26–28 March 2008. [Google Scholar]
- Kawashima, K.; Uchida, T.; Hori, Y. Rolling stability control based on electronic stability program for in-wheel-motor electric vehicle. World Electr. Veh. J. 2009, 3, 34–41. [Google Scholar] [CrossRef]
- Katsuyama, E. Decoupled 3D moment control using in-wheel motors. Veh. Syst. Dyn. 2013, 51, 18–31. [Google Scholar] [CrossRef]
- Murata, S. Innovation by in-wheel-motor drive unit. Veh. Syst. Dyn. 2012, 50, 807–830. [Google Scholar] [CrossRef]
- Yu, Z.S. Automobile Theory, 5th ed.; China Machine Press: Beijing, China, 2009. [Google Scholar]
- Liu, B.; Tang, W.S. Modern Control Theory; China Machine Press: Beijing, China, 2006. [Google Scholar]
- Zhang, X.Z.; Zheng, L. Vehicle stability control of distributed-driven electric vehicles based on optimal torque allocation. China Mech. Eng. 2018, 29, 1780–1787. [Google Scholar]
- Ren, Z.Y.; Zhao, W.Q.; Zong, C.F. Research on vehicle yaw stability control based on improved LQR method. Sci. Technol. Eng. 2017, 17, 97–102. [Google Scholar]
- Yan, S. Research on Roll Stability Control of Distributed Drive Electric Vehicle. Master’s Thesis, Shanghai University of Engineering Science, Shanghai, China, 2020. [Google Scholar]


| Steering Condition | Yaw Velocity | Additional Yaw Moment |
|---|---|---|
| left understeer | > 0 | > 0 |
| left oversteer | > 0 | < 0 |
| light understeer | < 0 | < 0 |
| light oversteer | < 0 | > 0 |
| Wheel | Compensated Roll Moment | Compensated Yaw Moment |
|---|---|---|
| front left wheel torque | ||
| rear left wheel torque | ||
| front right wheel torque | ||
| rear right wheel torque |
| ΔMZ | e | |||||||
|---|---|---|---|---|---|---|---|---|
| NB | NM | NS | ZO | PS | PM | PB | ||
| ec | PB | ZO | ZO | NW | NS | NM | NB | NB |
| PS | PM | PS | ZO | NW | NS | NB | NB | |
| ZO | PB | PM | PW | ZO | NW | NM | NB | |
| NS | PB | PB | PS | PW | ZO | NS | NM | |
| NB | PB | PB | PM | PS | PW | ZO | ZO | |
| Parameters | Value |
|---|---|
| Vehicle mass sprung mass un-sprung mass | 1380 900 480 |
| Distance from center of mass to front axle | 1.05 |
| Distance from center of mass to rear axle | 1.57 |
| front wheel tread | 1.4 |
| rear wheel tread | 1.4 |
| height of centroid | 0.6 |
| Tire diameter load radius | 0.33 |
| tire type | 255/75 R16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, X.; Zhang, H.; Yan, S.; Hu, S.; Meng, Y. Analysis and Roll Prevention Control for Distributed Drive Electric Vehicles. World Electr. Veh. J. 2022, 13, 210. https://doi.org/10.3390/wevj13110210
Chang X, Zhang H, Yan S, Hu S, Meng Y. Analysis and Roll Prevention Control for Distributed Drive Electric Vehicles. World Electric Vehicle Journal. 2022; 13(11):210. https://doi.org/10.3390/wevj13110210
Chicago/Turabian StyleChang, Xiaoyu, Huanhuan Zhang, Shuai Yan, Shengli Hu, and Youming Meng. 2022. "Analysis and Roll Prevention Control for Distributed Drive Electric Vehicles" World Electric Vehicle Journal 13, no. 11: 210. https://doi.org/10.3390/wevj13110210
APA StyleChang, X., Zhang, H., Yan, S., Hu, S., & Meng, Y. (2022). Analysis and Roll Prevention Control for Distributed Drive Electric Vehicles. World Electric Vehicle Journal, 13(11), 210. https://doi.org/10.3390/wevj13110210






