Drivability Optimization of Electric Vehicle Drivetrains for Brake Blending Maneuvers

Abstract

Electric vehicle drivetrains are considered a way to reduce greenhouse gas emissions from road traffic. The use of electric drives in automotive vehicles offers advantages, such as the potential to recover energy during braking (regenerative braking). The limitation of the maximum air gap torque of the vehicle drive machine by several factors requires a temporary standalone or simultaneous use of the conventional vehicle wheel brake. In several studies, it is shown that during braking operations, the drive machine and the vehicle wheel brake can induce torsional oscillations in the drivetrain, which have a negative influence on the driving comfort and lead to a high mechanical load. To reduce these oscillations, the simultaneous use of an active anti-jerk control is necessary. Due to the problem of oscillation excitations caused by a brake intervention, the used drivability function (integrated prefilter, anti-jerk control) is investigated and optimized with regard to brake blending maneuvers and the effectiveness for damping torsional oscillations. Therefore, the dynamics of the drivetrain are adapted to the dynamics of the braking system using the prefilter, which leads to precise fulfilment of the driver’s braking desire, even during dynamic brake blending maneuvers. All investigations are carried out with a hardware-in-the-loop test bench to create reproducible results.

1. Introduction and Motivation

Electric vehicle drivetrains are considered a way to reduce greenhouse gas emissions from road traffic and thus a contribution to solving climate problems. The use of electric drives in automotive vehicles offers advantages. Primarily, the reduction of the required mechanical components (e.g., elimination of the clutch) and the potential to regenerate energy during braking (regenerative braking) should be mentioned [1,2].

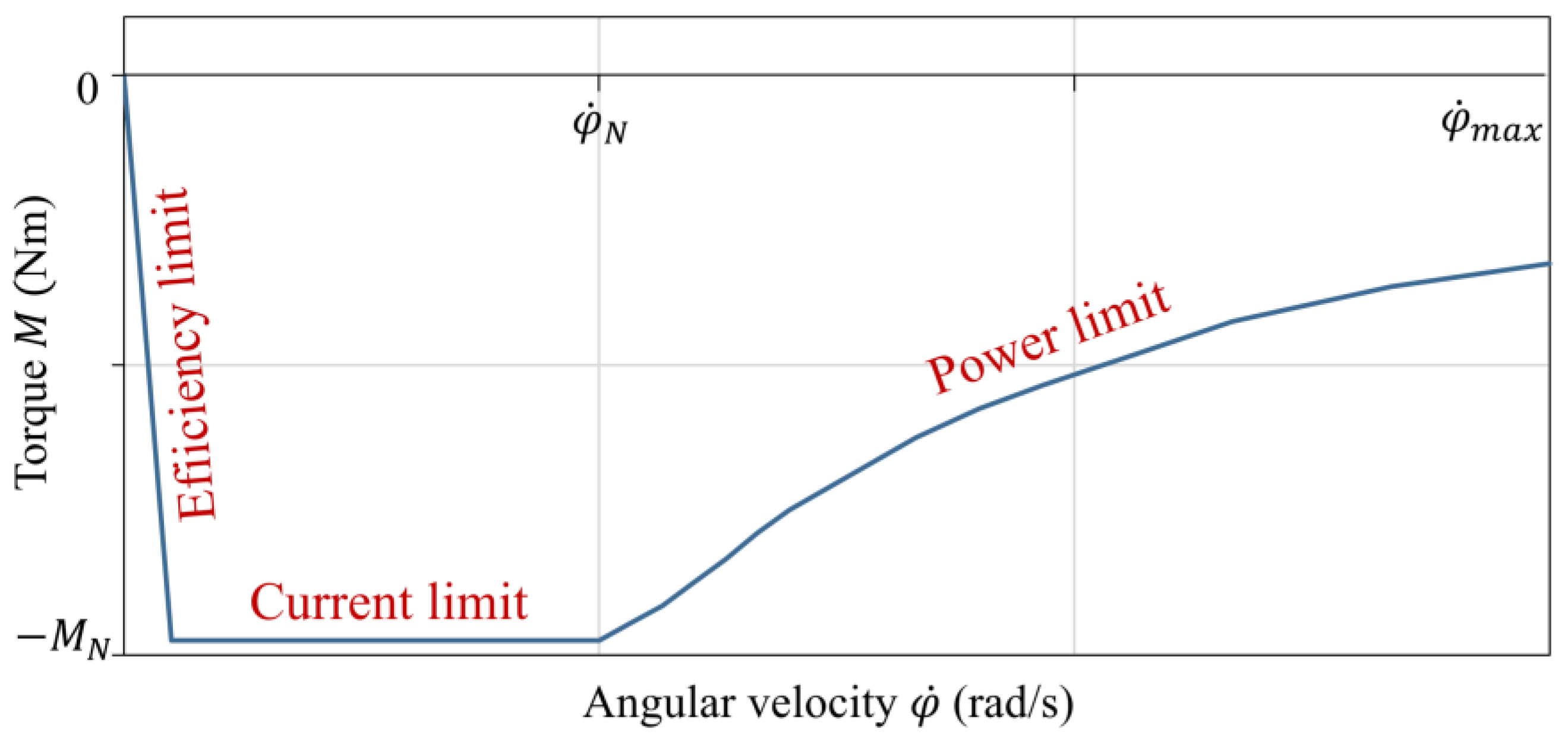
For a high proportion of regenerative energy, as many braking operations as possible should be carried out by using the regenerative operation of the vehicle drive machine [1]. However, the maximum air gap torque of the vehicle drive machine is limited by several factors [1,3,4]. Figure 1 shows an example of the torque–angular velocity characteristics of an electric machine for regenerative operations according to [5].

In [1,3,4], it is described that regenerative braking can be dispensed with due to the efficiency and performance at low speeds. At high speeds (field weakening operation), a power limit results in a reduction of the air gap torque of the vehicle’s electric machine [1,3]. Furthermore, the maximum thermal load capacity of the electric drive leads to a possible limitation of the maximum possible air gap torque [3,6]. In addition, a high state of charge (SOC) of the vehicle battery and the corresponding maximal free capacity for energy regeneration as well as a necessary limitation of the maximum charging currents of the battery limit the operation of the vehicle drive machine [4,7]. Thus, an adjustment of the distribution between the regenerative braking torque of the vehicle drive machine and the friction braking torque of the vehicle wheel brake is essential [5].

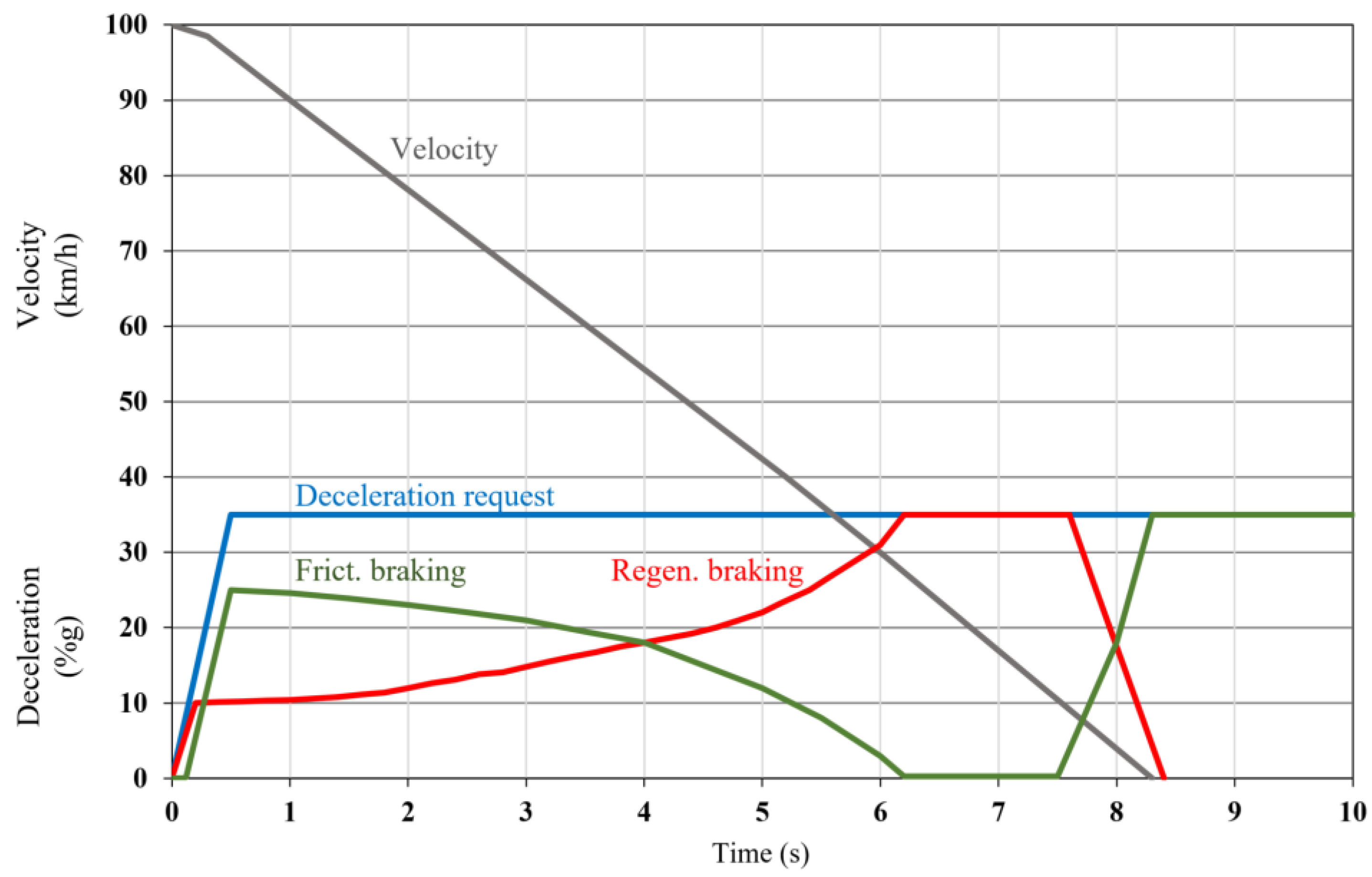
This superposition of the friction braking torque of the vehicle wheel brake with the regenerative braking torque of the vehicle drive machine is called brake blending. Various strategies for this are described in the literature [1,4,7,8,9]. Figure 2 shows an example of the sequence of a braking process with alternating percentage of the two braking systems according to the explanations in [1].

For this, the possibility of decoupling the friction braking torque of the vehicle wheel brake from the brake pedal actuation is required. Mostly, mechatronic braking systems are applied which represent the brake pedal characteristics by adding a pedal simulator [1,2,5].

The development of appropriate brake blending algorithms faces a number of challenges. These include, for a particular example, the necessary application of brake-by-wire systems and the related requirements for functional safety [1,2,10].

The advantages of regenerative braking maneuvers can be used, for example, when several vehicles travel in a convoy. The literature [11] describes a cooperative driving control strategy that takes into account the distance-dependent air drag in order to optimize energy efficiency.

Strategies for distributing torques between the individual wheels or between the drive machines and the vehicle wheel brakes are described in [12,13,14,15]. The literature [12] proposes a method for optimal torque distribution to maximize the driving efficiency while maintaining driving stability of a four-wheel independent-drive electric vehicle with in-wheel motors. The coordination of a vehicle wheel brake is not considered.

In [13], a double layer multi parameters control strategy for regenerating energy during braking is under investigation. In addition to a first layer that distributes the braking force to the front and rear axles, a fuzzy controller is used to calculate the mechanical braking force and the motor braking force on the front axle. Torsional oscillations of the drivetrain are not considered.

In the literature [14], the theory of model predictive control (MPC) is used for the braking torque distribution of the front and rear wheels and for the distribution to the torque of the vehicle wheel brake and to the torque of the drive machine of an electric vehicle with four in-wheel motors.

In [15], nonlinear model predictive control (NMPC) is used for the coordinated distribution of motor braking and friction braking. It is assumed that the driving wheels are rigidly connected to the motor via the transmission system.

In the literature mentioned above [12,13,14,15], drivetrain oscillations are not considered. Some of the studies refer to vehicles with in-wheel motors, in which the torques of the drive machine and the vehicle wheel brake act directly on the wheel, so that oscillation phenomena are of secondary importance.

In contrast, other drivetrain variants use body-mounted electric machines coupled to the wheels via vehicle side shafts with low torsional stiffness, causing torsional oscillations in the drivetrain. In addition, the drive machines and the vehicle wheel brakes also intervene in the drivetrain at different locations, leading to different dynamics in the torque build-up.

The brake blending of a corresponding drivetrain is investigated in [16] using a test bench. Due to the occurring drivetrain oscillation, the necessity of an active vibration controller is concluded.

In this research, the focus is on the optimization of drivability functions (prefilter, anti-jerk control) for regenerative braking operations of drivetrains including a vehicle side shaft with low torsional stiffness. The approach is based on using drivability functions that are already active during normal driving also in the context of brake blending maneuvers. This means that no different approaches or structural changes are required in the transitions between driving and braking. Drivetrain oscillations and torque build-up dynamics are taken into account. The setpoint for the distribution between drive machine and vehicle wheel brake can be specified dynamically. This allows different brake blending strategies. Various approaches for corresponding strategies to optimize distribution are described in [13,14,15], for example.

Further, in [2,17], it is described that there should be no further negative effects for the driver regarding pedal feel, noise, and vibrations. Among other things, the dynamic behavior of the drive machine using drivability functions should be adjusted to the dynamic behavior of the vehicle wheel brake [2,17].

Furthermore, in [17,18,19,20], it is shown that especially during strong braking operations, the vehicle wheel brake can induce high torsional oscillations in the drivetrain. In particular, anti-lock braking system (ABS) control operations are critical due their high torque build-up dynamics and cyclical interventions in terms of vibration behavior. A problem is that the typically occurring control frequencies of 5–10 Hz are close to the typical natural frequencies of electrified vehicle drivetrains [18]. This may lead to oscillation excitations of the drivetrain. Further, with the removal of the clutch, typically integrated friction dampers in the clutch are removed. Therefore, the electrified drivetrains are typically weakly damped [21]. In [17,18], various investigations were carried out for the development of an ABS control for an electric vehicle drivetrain using the vehicle wheel brake and the vehicle drive machine. The torsional oscillations of the drivetrain are taken into account in simulations and vehicle tests.

In addition, the fact that the inertial mass of the vehicle’s drive machine is not separable from the rest of the drivetrain due to the removal of a clutch is a disadvantage in the case of interventions of the vehicle’s wheel brake. On the other hand, an optimal simultaneous control of the vehicle wheel brake and the vehicle drive machine improves the overall vehicle braking behavior—even in the case of ABS control interventions. Detailed studies on this are described in [3,22,23,24], for example. The main focus in these studies is on vehicle acceleration without detailed analysis of the torsional oscillations of the vehicle drivetrain.

These occurring torsional oscillations of the drivetrain have a negative influence on the driving comfort and lead to a high mechanical load on the drivetrain [17,25,26]. To reduce these torsional oscillations, the simultaneous use of an active anti-jerk control is necessary. Corresponding algorithms are described in [17,26,27,28,29,30,31,32], for example.

The explanations in [26] show that corresponding algorithms are primarily investigated and optimized for start-up, tip-in and tip-out maneuvers. Considerations of the oscillation behavior during braking operations or additional interventions of the vehicle wheel brake are carried out less frequently.

However, simulative investigations with consideration of the torsional oscillations of the drivetrain during regenerative braking as well as during brake blending maneuvers are described in [19,20]. For the damping of these torsional oscillations, corresponding control algorithms are explained.

In this research, brake blending maneuvers are considered under close-to-reality conditions on a hardware-in-the-loop test bench (HiL test bench). Due to the problem of oscillation excitations caused by a brake intervention, the drivability function described in [27] with an integrated prefilter as well as an integrated anti-jerk control is investigated and optimized with regard to brake blending maneuvers as well as the effectiveness for damping torsional oscillations during braking operations.

As in [27,32,33], the following investigations are carried out with the HiL test bench described in Section 2. It replicates an electric single-wheel drivetrain where a vehicle drive machine is directly connected to a drive wheel by a gearbox and a side shaft. As typical for such drive systems, there is no clutch in the drivetrain. To impress a friction braking torque, the HiL test bench has a suitable wheel braking system close to the vehicle. 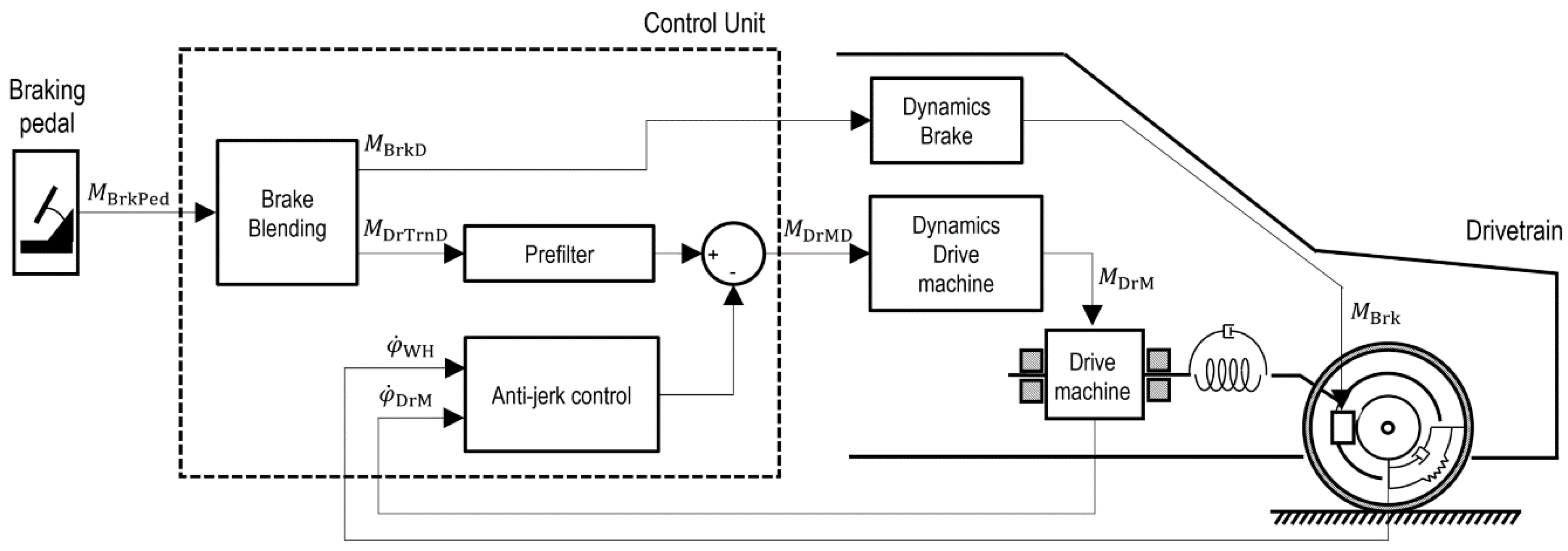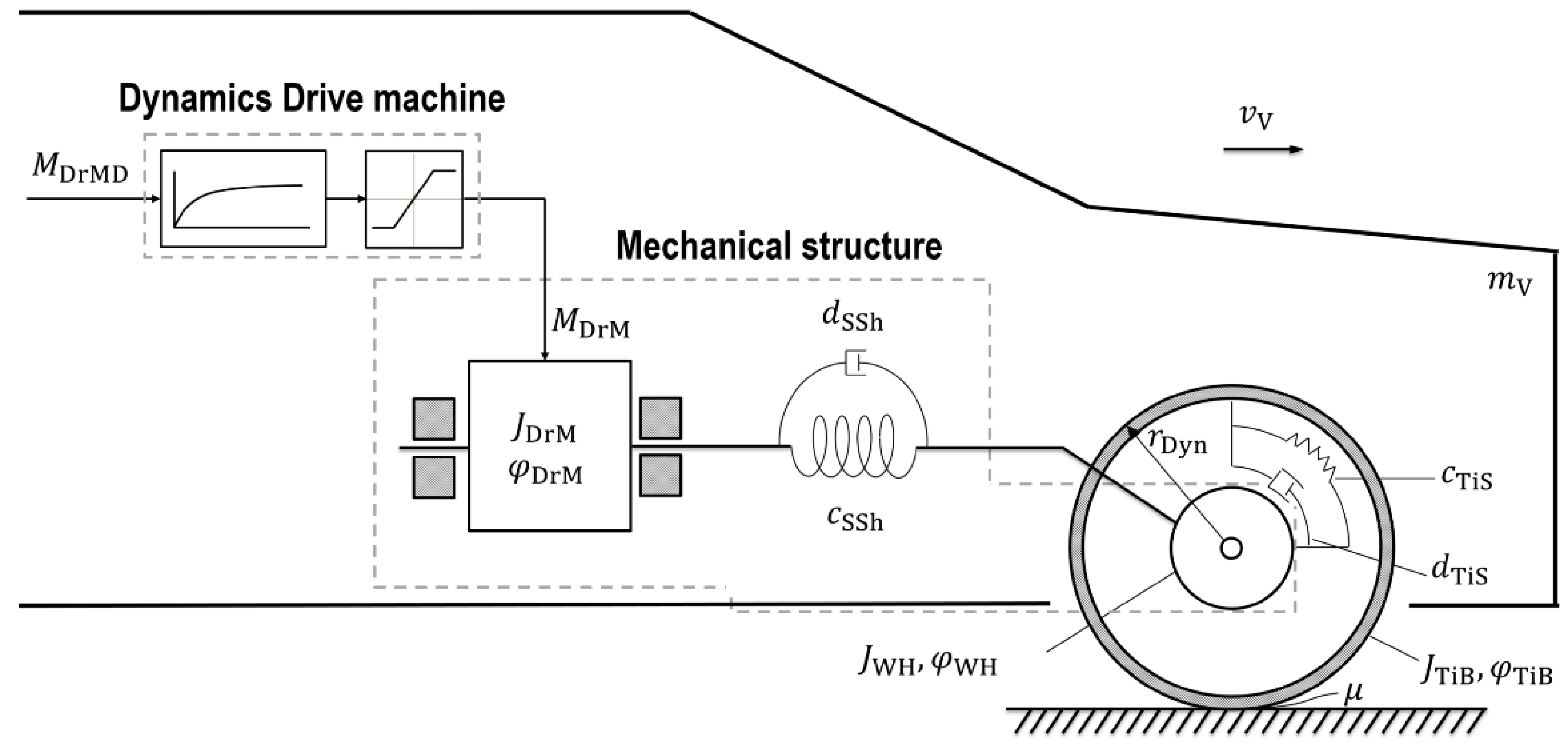Figure 3 shows the simplified system of the investigated vehicle.

In Section 3 and Section 4, the used drivability function as described in [27] and a necessary adaptation to the dynamics of the braking system is described. Following this, braking maneuvers are analyzed in which the braking torque is impressed into the drivetrain only with the vehicle drive machine (Section 5) or with the vehicle wheel brake (Section 6) as well as the final usage of both actuators (Section 7). Section 8 gives a summary of the results and a short outlook on further investigations.

2. Test Environment

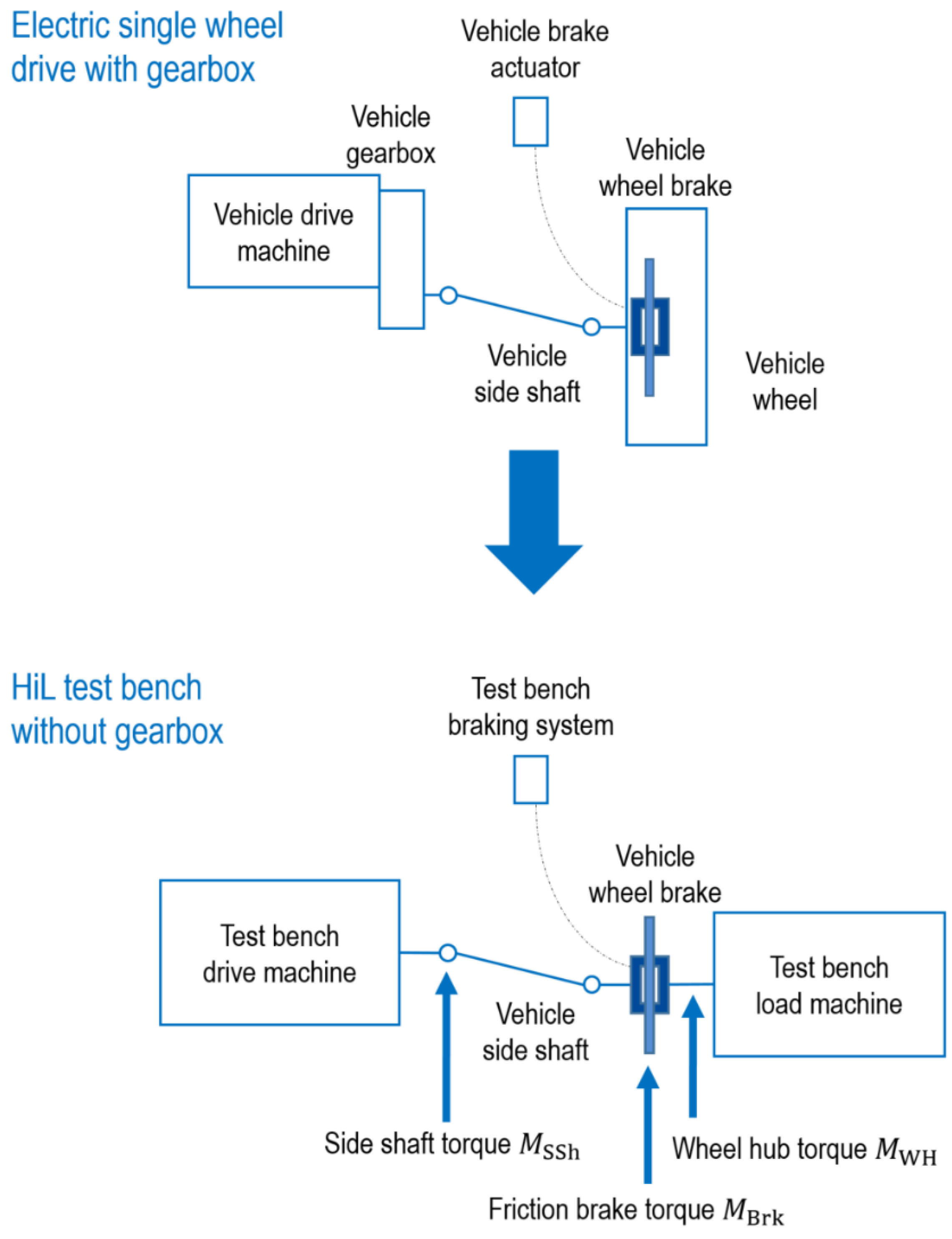
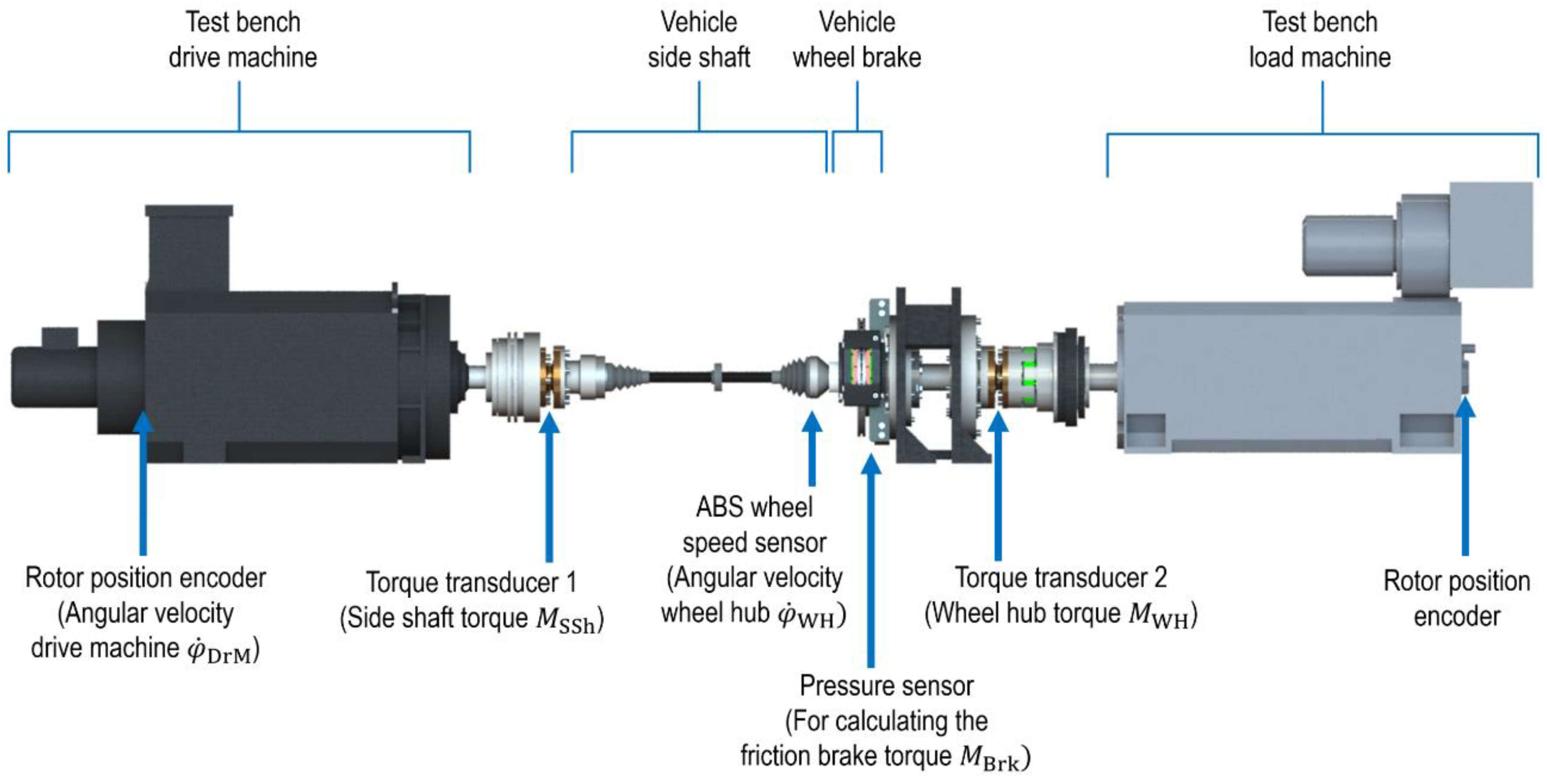
In accordance with the research in [27,32,33], the following investigations were carried out on a HiL test bench. Figure 4 shows a comparison of a real single-wheel drive to the HiL test bench.

An electric vehicle of the compact class is considered. The front axle has individual wheel drives. The electric drive machine including a gearbox (gear ratio of 7.03 according to [17]) is reproduced by a test bench drive machine. Therefore, the drive machine provides the inertia, torque, and angular velocity related to the gearbox output shaft and applies the desired drivetrain torque $M_{\mathrm{DrTrnD}}$, that is modified by the investigated drivability function. A HiL simulation of the vehicle wheel, the tire–road contact and the driving resistance forces (vehicle longitudinal dynamics) calculates the load torque and angular velocity at the vehicle wheel hub that is applied by a test bench load machine [32,33]. A vehicle wheel brake and a vehicle side shaft with low torsional stiffness are integrated in the HiL test bench [34]. By using a vehicle wheel brake, non-linear effects of the brake hydraulics are also taken into account. The HiL test bench braking system enables brake pressure modulation at typical vehicle dynamics as well as the simulation of ABS/ESP systems (Electronic Stability Program) [33,34]. Compared to the use of a real ABS/ESP hydraulic unit, such a system allows the reproduction of different braking system hardware and the optimization of the necessary algorithms.

A real-time control (cycle time 250 µs) and a network with programmable logic (FPGA, EtherCAT) enable high dynamics of the HiL test bench [33,35,36]. In addition, many high-resolution sensors are integrated into the HiL test bench for the detailed measurement of torques and angular velocities (see Figure 5). Some of the sensors are typical for automobiles, such as an ABS wheel speed sensor.

In [27,32,33,37], it is demonstrated that the natural frequency of the HiL test bench together with the HiL simulation model is approximately 8 Hz which complies with a real electrified vehicle drive system.

3. Drivability Function

For the investigations in this research, the drivability function described in [27] is used. The essential aspects of this drivability function are summarized in the following.

Figure 6 shows the simplified system of the investigated electric vehicle drive system. The vehicle braking system is initially ignored for the description of the drivability function.

The desired torque of the vehicle’s drive machine $M_{\mathrm{DrMD}}$ is modified by the drivability function (see Figure 3). The dynamics for the air gap torque of the drive machine $M_{\mathrm{DrM}}$, the moment of inertia of the drive machine $J_{\mathrm{DrM}}$ as well as the torsional stiffness $c_{\mathrm{SSh}}$ and torsional damping $d_{\mathrm{SSh}}$ of the vehicle side shaft are considered.

The desired torque of the drive machine $M_{\mathrm{DrMD}}$ is defined as the system input. In traction mode, this torque is positive and is detected from the current position of the accelerator pedal. In braking mode, the desired torque of the drive machine $M_{\mathrm{DrMD}}$ is negative and is detected from the brake pedal with the support of the brake blending functions (see Figure 3). In both cases, this torque is adjusted by the drivability function.

Following the description in [27], the vehicle wheel hub is defined as the system boundary. Through this, a necessary determination of the tire–road contact and the vehicle longitudinal dynamics is eliminated. For example, the observation and estimation of the vehicle mass $m_{\mathrm{V}}$, the vehicle speed $v_{\mathrm{V}}$, the vertical wheel contact forces, and the friction coefficient of the tire $\mu$ is not required. Moreover, the parameterization of the prefilter is minimized for different vehicle configurations. In addition, the moments of inertia of the wheel hub $J_{\mathrm{WH}}$ and the tire belt $J_{\mathrm{TiB}}$, the dynamic behavior of the rotation angle of the tire belt ${\phi }_{\mathrm{TiB}}$, the dynamic tire radius $r_{\mathrm{Dyn}}$, the torsional stiffness $c_{\mathrm{TiS}}$, and the torsional damping $d_{\mathrm{TiS}}$ of the tire sidewall are neglected.

ABS wheel speed sensors are used to measure the rotation angle ${\phi }_{\mathrm{WH}}$ or the angular velocity ${\dot{\phi }}_{\mathrm{WH}}$ of the vehicle wheel hub. Corresponding sensors detect the rotation angle ${\phi }_{\mathrm{DrM}}$ or the angular velocity ${\dot{\phi }}_{\mathrm{DrM}}$ of the drive machine.

Figure 7 shows the structure of the drivability function developed in [27] consisting of the subsystems feedforward control and anti-jerk control. Furthermore, the simplified real system is shown by means of modeling the dynamics of the drive machine and the transfer function for the vehicle side shaft torque $M_{\mathrm{SSh}}$. The dynamics of the drive machine can be approximated with a first order lag element with the time constant $T_{\mathrm{DrM}}$.

The prefilter reduces torsional oscillations of the vehicle side shaft during load changes of the drive machine. The desired drivetrain torque $M_{\mathrm{DrTrnD}}$ is used as the input variable. According to the explanations in [27], a simplified system model for the vehicle side shaft torque $M_{\mathrm{SSh}}$ can be used to derive the prefilter. The simplified transfer function results in

$$M_{\mathrm{SSh}}\left(s\right)=\frac{d_{\mathrm{SSh}}s+c_{\mathrm{SSh}}}{J_{\mathrm{DrM}}{s}^2+d_{\mathrm{SSh}}s+c_{\mathrm{SSh}}} M_{\mathrm{DrM}}\left(s\right)$$

(1)

The transfer function $F\left(s\right)$ of the prefilter compensates the poles of the stable real system [38,39]

$$F\left(s\right)=\frac{J_{\mathrm{DrM}}{s}^2+d_{\mathrm{SSh}}s+c_{\mathrm{SSh}}}{J_{\mathrm{DrM}}{s}^2+d_{\mathrm{SSh}}^{*}s+c_{\mathrm{SSh}}}$$

(2)

A pair of zeros is included in the prefilter to eliminate the underdamped poles of the real system. The real physical parameters of the drive system can be chosen as the parameters of the prefilter of Equation (2), only the damping constant $d_{\mathrm{SSh}}^{*}$ should be significantly increased [27]. This leads to a higher damping ratio of the poles inserted by the prefilter. Then, the desired transfer function remains similar to that of the simplified real system. As a result, the dynamics of the required air gap torque $M_{\mathrm{DrM}}$ are retained at a low level. The damping constant $d_{\mathrm{SSh}}^{*}$ is a design parameter for compromise between comfort level and acceleration capability [26,31,40,41].

The anti-jerk control uses the angular velocities of the vehicle drive machine ${\dot{\phi }}_{\mathrm{DrM}}$ (related to the gearbox output shaft) and the vehicle wheel hub ${\dot{\phi }}_{\mathrm{WH}}$. A comparison of both values results in a differential angular velocity $\Delta \dot{\phi }$ and is subtracted from a demand differential angular velocity $\Delta {\dot{\phi }}_{\mathrm{Dem}}$ [27]. The system model of the prefilter is used to calculate the demand differential angular velocity (Figure 7).

A damping torque $M_{\mathrm{D}}$ is determined using a positive gain factor $K_{\mathrm{D}}$:

$$M_{\mathrm{D}}=K_{\mathrm{D}} \left(\Delta {\dot{\phi }}_{\mathrm{Dem}}-\Delta \dot{\phi }\right)$$

(3)

The gain factor $K_{\mathrm{D}}$ is also a design parameter for a compromise between comfort level and acceleration capability. Furthermore, a derivative element with first order lag filter and a torque limiter are implemented. The damping torque $M_{\mathrm{D}}$ and the desired drivetrain torque $M_{\mathrm{DrTrnD}}$ modified by the prefilter generate the demand torque $M_{\mathrm{DrMD}}$ of the vehicle drive machine (see Figure 7).

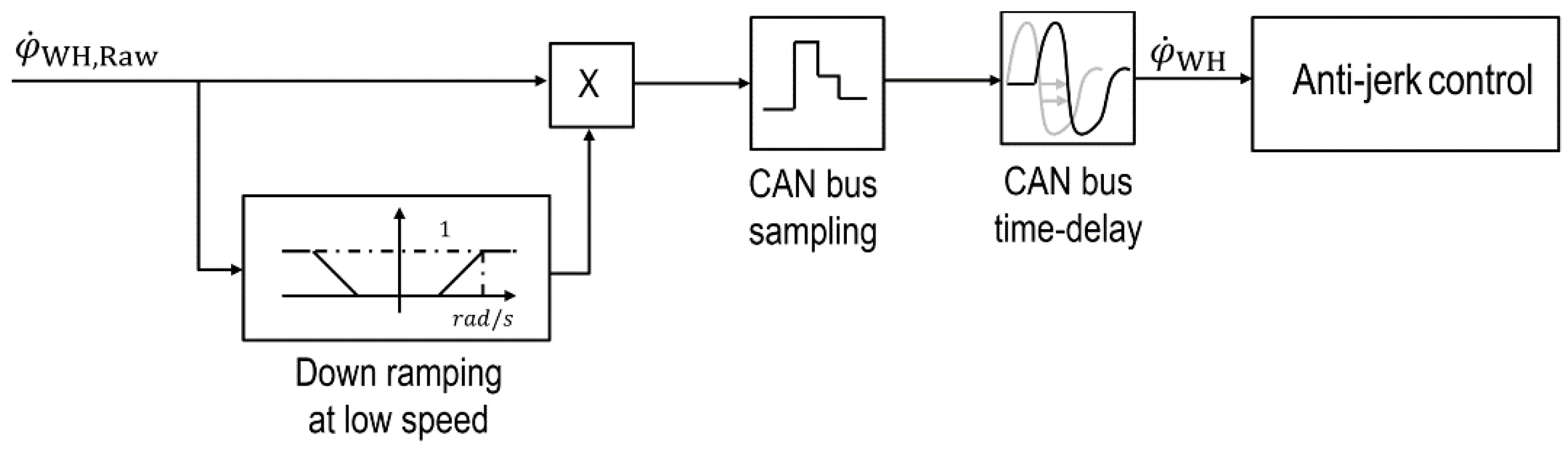
For the anti-jerk control, the angular velocity of the vehicle wheel hub ${\dot{\phi }}_{\mathrm{WH}}$ is used as an input. This angular velocity is measured by an ABS wheel speed sensor and the signal is typically transmitted via a CAN bus network in real vehicles. In the HiL test bench, a vehicle-related ABS wheel speed sensor is integrated (Figure 5) and evaluated by the FPGA. At low values, the raw value ${\dot{\phi }}_{\mathrm{WH},\mathrm{Raw}}$ of the angular velocity of the vehicle wheel hub is ramped down [42]. An emulation of the CAN bus network is realized by a sample rate of 20 ms and an additional time-delay of 20 ms (Figure 8).

In [27], it is described that the torque of the vehicle side shaft shows almost no oscillations during torque build-up while tip-in procedures. At 120 ms after a setpoint step, the driver’s desired torque is reached. The torque of the vehicle side shaft shows an overshoot within a range of approximately 5% and well-damped oscillation.

As described in Section 1, it is important to ensure that the driver’s pedal feeling and the resulting deceleration behavior of the vehicle remain the same in all operating conditions. For this purpose, the dynamic behavior of the electric vehicle drive system using the drivability functions should correspond to the dynamic behavior of the vehicle wheel brake. In Section 4, a time constant of about 50 ms is assumed for the hydraulic path of the vehicle wheel brake.

For this, the transfer function of the prefilter in Equation (2) is modified to

$$F\left(s\right)=\frac{J_{\mathrm{DrM}}{s}^2+d_{\mathrm{SSh}}s+c_{\mathrm{SSh}}}{J_{\mathrm{DrM}}^{*}{s}^2+d_{\mathrm{SSh}}^{*}s+c_{\mathrm{SSh}}}$$

(4)

The moment of inertia $J_{\mathrm{DrM}}^{*}$ is reduced compared to the moment of inertia of the real drive machine $J_{\mathrm{DrM}}$ and represents an additional design parameter. With the introduction of this additional design parameter, the dynamics of the prefilter can be increased and thus the dynamics of the complete vehicle drive system according to Figure 7. In this research, the dynamics of the vehicle drive system is adapted to the dynamics of the braking system by appropriate choice of the values of the moment of inertia $J_{\mathrm{DrM}}^{*}$ and damping constant $d_{\mathrm{SSh}}^{*}$. For this purpose, the moment of inertia $J_{\mathrm{DrM}}^{*}$ used in the prefilter is reduced by approximately 50% compared to the moment of inertia $J_{\mathrm{DrM}}$ of the real drive machine.

Additionally, it should be mentioned that the intervention of the braking system and the related impression of a braking torque in the drivetrain can be interpreted as a disturbance variable that is not detectable by the prefilter. Therefore, corresponding oscillation excitations by the braking system must be completely compensated by the anti-jerk control.

4. Dynamics of the Braking System

According to [43,44], in vehicle braking systems, the transfer function between the brake master cylinder and the brake caliper can be approximated with a first order lag behavior with a typical time constant between 50 ms and 250 ms. In a braking operation with active ABS control, the dynamics of the hydraulic path only depend on the transfer path between the inlet/outlet valve and the brake calipers. This transfer path can also be approximated with a first order lag behavior [17]. For fully opened valves, the minimum possible time constant is between 30 ms and 40 ms [45]. It is assumed that brake blending is realized with the help of the inlet/outlet valves, therefore a magnitude of 50 ms is taken as a basis for the dynamics of the vehicle braking system. This almost corresponds to the dynamics of the real by-wire friction brake described in [46].

According to [33,34], the HiL test bench used for this research contains a highly dynamic braking system with integrated vehicle wheel brake, with which ABS braking operations can be simulated. The achievable dynamics of this test bench braking system are significantly faster than the dynamics of a real vehicle braking system. To adapt the dynamic behavior, an additional first order lag filter is added to the control system of the HiL test bench.

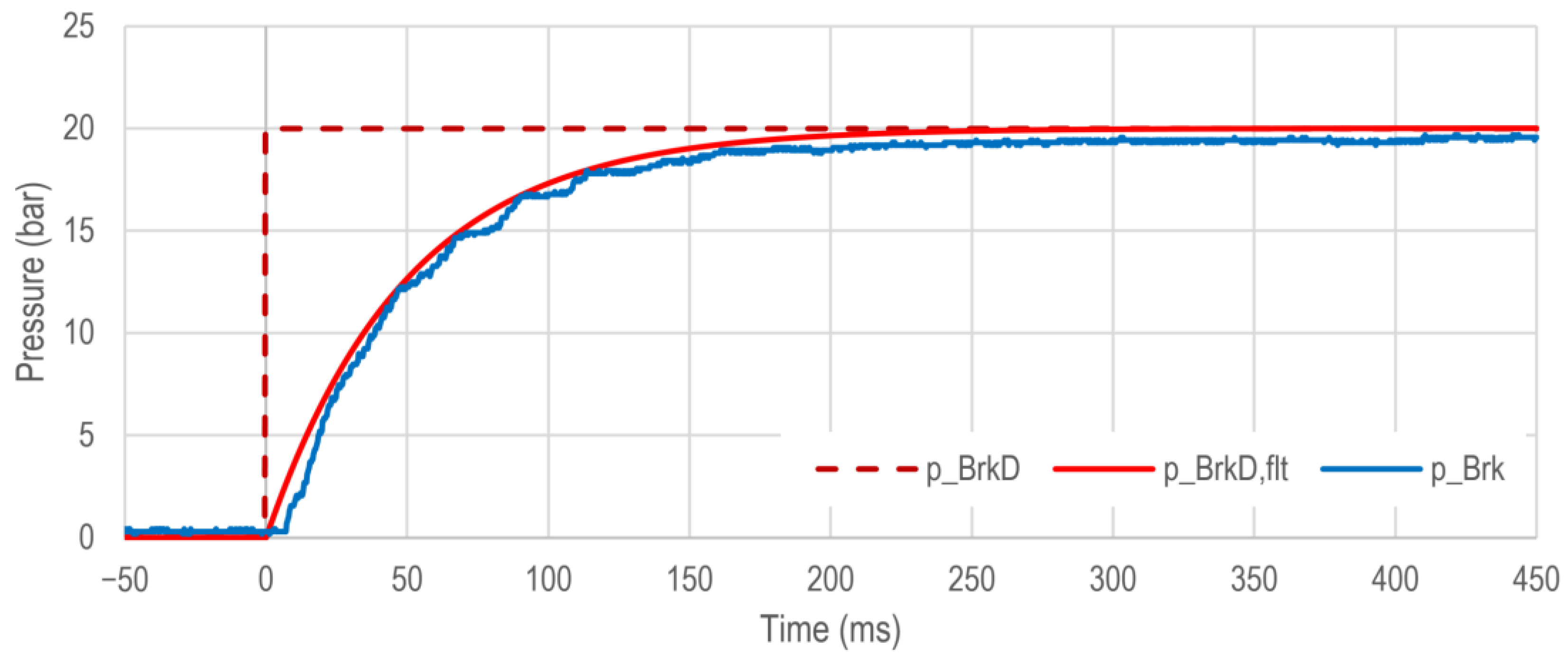
Figure 9 shows the build-up dynamics of the vehicle wheel brake pressure $p_{\mathrm{Brk}}$ in case of a step in the desired pressure $p_{\mathrm{BrkD}}$ using an additional first order lag filter with a time constant of about 50 ms. According to this, the value of 90% of the desired pressure is almost reached after approximately $t_{90}$ = 131 ms. At time t = 450 ms, a remaining deviation of approximately 0.3 bar is noticeable, which is primarily due to static friction effects of the linear actuator of the braking system [33]. Furthermore, vehicle-typical pressure oscillations are visible during the pressure build-up (compare [46,47]).

According to [1,33] the effective friction braking torque $M_{\mathrm{Brk}}$ can be derived from the pressure $p_{\mathrm{Brk}}$ in the vehicle wheel brake with the help of the physical parameters of the braking system. Moreover, the “Dynamics Brake” block shown in Figure 3 contains a corresponding transition from the desired friction braking torque $M_{\mathrm{BrkD}}$ to the desired pressure $p_{\mathrm{BrkD}}$. Thus, the “Dynamics Brake” block includes the dynamics from the desired friction braking torque $M_{\mathrm{BrkD}}$ to the actual braking torque $M_{\mathrm{Brk}}$, based on the dynamics of the pressure build-up.

As described above, by appropriate choice of the values of the moment of inertia $J_{\mathrm{DrM}}^{*}$ and damping constant $d_{\mathrm{SSh}}^{*}$, the dynamics of the complete vehicle drive system are increased compared to the investigations in [27] and are adapted to the dynamics of the braking system. A comparison is carried out by the following measurement results. For this purpose, braking operations (ideal flat road surface, no wind) are analyzed with the drive machine only, with the vehicle braking system only, as well as with simultaneous use of both systems in each case without and with activated anti-jerk control.

5. Regenerative Braking System

For the investigation of the braking operations, the simulated vehicle is initially accelerated by the drive machine on an ideal, flat, asphalted road to slightly over a vehicle speed $v_{\mathrm{V}}$ = 25 km/h and then the driver’s desired torque is set to 0 Nm. Thus, the simulated vehicle slowly rolls out. On reaching a vehicle speed of 25 km/h, a braking torque of −400 Nm is impressed into the drivetrain. In the context of the first considerations, only the drive machine impresses the full braking torque. To initiate the braking process, the desired drivetrain torque $M_{\mathrm{DrTrnD}}$ in relation to the gearbox output shaft is decreased by a step from 0 Nm to −400 Nm.

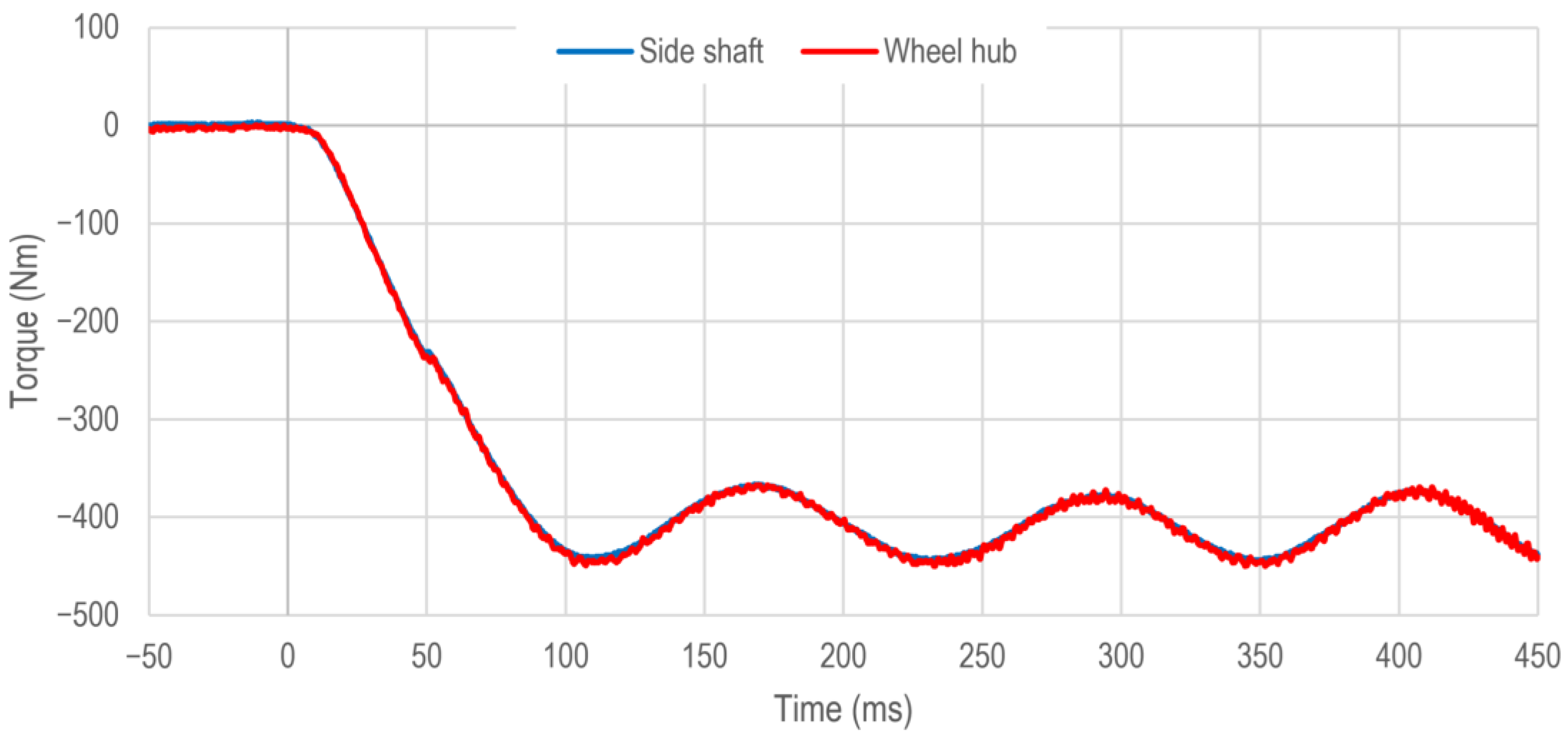
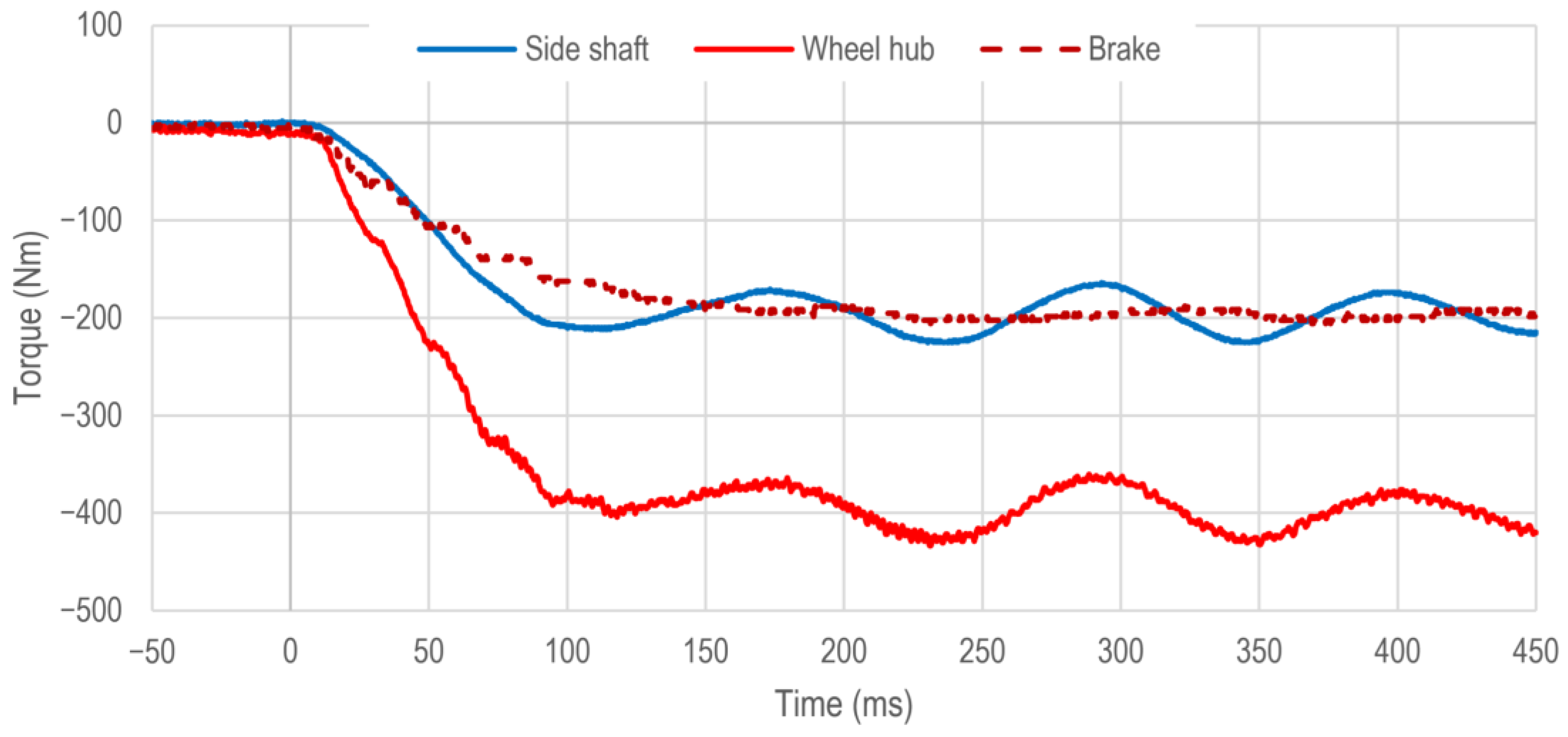
Figure 10 shows the regenerative braking operation. In this case, the prefilter shown in Section 3 is active. However, the anti-jerk control is deactivated. The time courses of the torques of the vehicle side shaft $M_{\mathrm{SSh}}$ and the vehicle wheel hub $M_{\mathrm{WH}}$ are shown. Both variables are measured using the integrated torque transducers of the HiL test bench as shown in Figure 5. The braking operation is initiated at time $t$ = 0 ms.

The time courses of the measured torques are almost synchronous during the observed period. In order to compare the dynamic behavior of the individual braking operations and actuators, the times until 63% as well as 90% of the stationary end value (desired drivetrain torque $M_{\mathrm{DrTrnD}}$) are reached are considered. In the case of regenerative braking using the drive machine with activated prefilter and deactivated anti-jerk control, these are $t_{63}$ = 54 ms for the 63% of the stationary end value and $t_{90}$ = 77 ms for the 90% of the stationary end value.

The time courses of both torques show the typical course after reaching the desired drivetrain torque $M_{\mathrm{DrTrnD}}$ in the form of a very weakly damped oscillation. Here, the amplitudes of the torque of the vehicle side shaft are approximately 40 Nm and of the vehicle wheel hub approximately 45 Nm. The oscillation frequency in both cases is approximately 8.7 Hz and lies within the typical range for electric vehicle drivetrains [17,33].

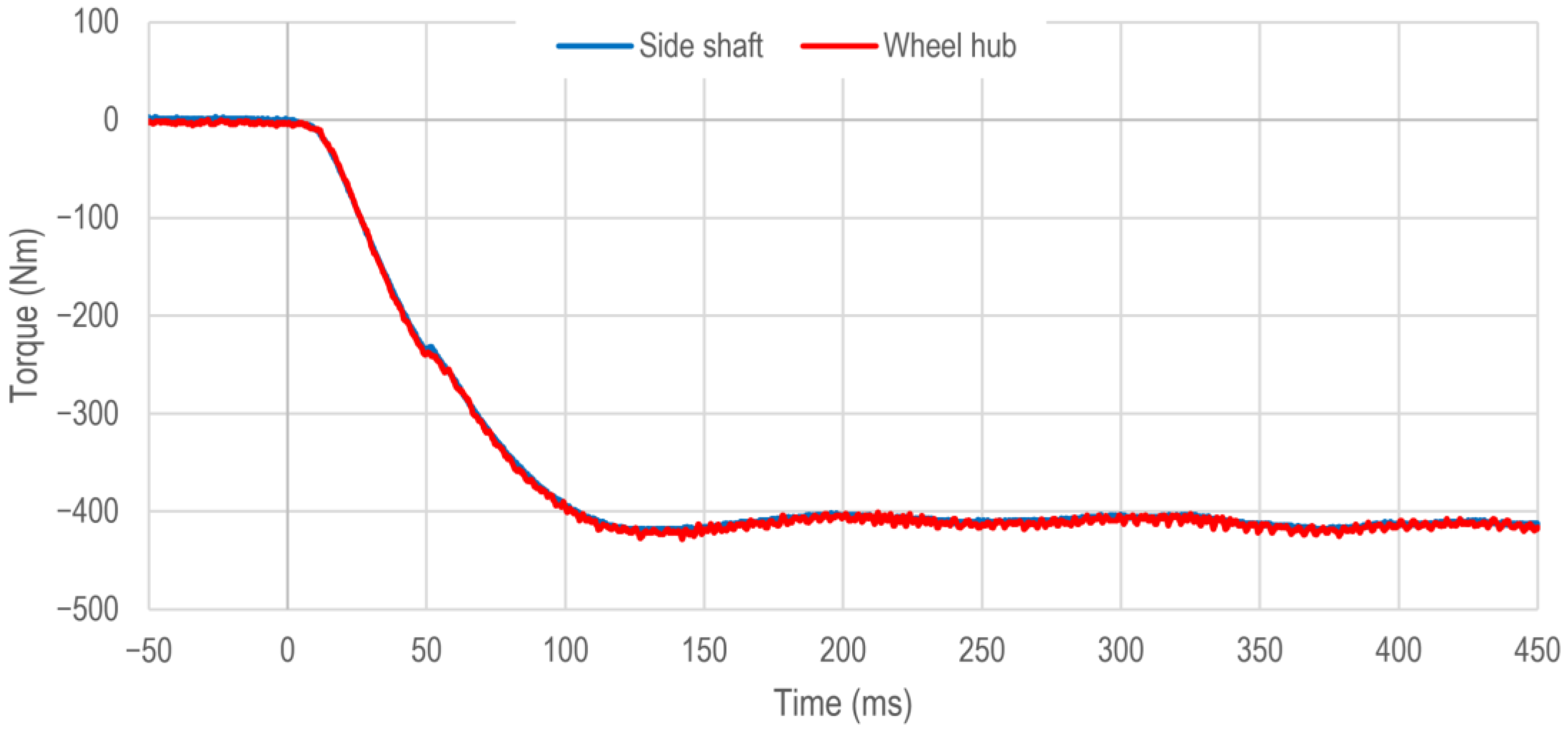
To reduce these oscillations, the anti-jerk control described in Section 3 is additionally used for the second regenerative braking operation. All other boundary conditions remain the same as compared to the previous braking operation. Figure 11 again shows the time course of the torques of the vehicle side shaft $M_{\mathrm{SSh}}$ and the vehicle wheel hub $M_{\mathrm{WH}}$.

The time courses of both torques are again almost congruent during the observed period. However, due to the anti-jerk control, the torque build-up is slightly slower. Thus, after $t_{63}$= 57 ms both torques amount to 63% of the desired drivetrain torque $M_{\mathrm{DrTrnD}}$ and after $t_{90}$ = 85 ms the value of 90% of the desired drivetrain torque is reached.

The further courses of both torques show a slight overshoot with an amplitude of approximately 17 Nm. Thus, both torques are already within the 10% limit of the step of the desired drivetrain torque. Afterwards, only slight oscillations close to the desired drivetrain torque are noticeable.

Therefore, the dynamics of the regenerative braking system with activated prefilter and anti-jerk control correspond closely to the dynamics of the investigations described in [30] for tip-in maneuvers while driving.

6. Conventional Vehicle Braking System

According to the explanations in Section 1, it is not possible to use the drive machine for all braking operations. Above all, the limitations described lead to a restriction in the possible use of the drive machine. Therefore, some braking operations have to be carried out with the vehicle’s wheel brake alone.

In contrast to the braking operations in Section 5, the full braking torque of approximately −400 Nm is now impressed into the drivetrain with the help of the vehicle wheel brake. For this purpose, the desired friction braking torque $M_{\mathrm{BrkD}}$ is decreased by a step from 0 Nm to −400 Nm. Thus, the desired pressure $p_{\mathrm{BrkD}}$ is increased abruptly from 0 bar to approximately 14.4 bar in accordance with the explanations in Section 4 and controlled by the test bench braking system. The desired drivetrain torque in this case is $M_{\mathrm{DrTrnD}}$= 0 Nm. Therefore, the prefilter has no possibility of influence. The braking operation is again initiated at time $t$ = 0 ms and at a vehicle speed of 25 km/h, as described in Section 5.

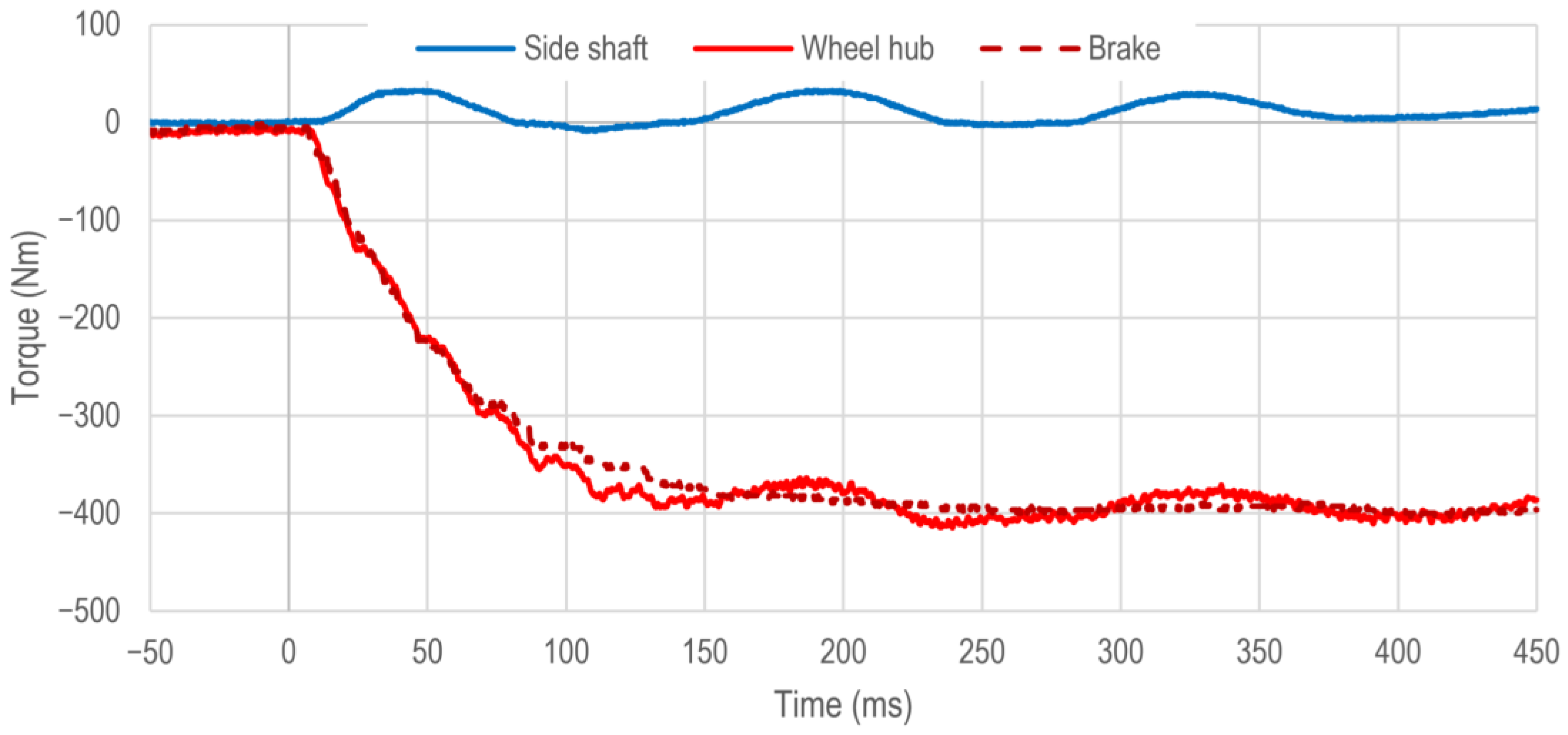
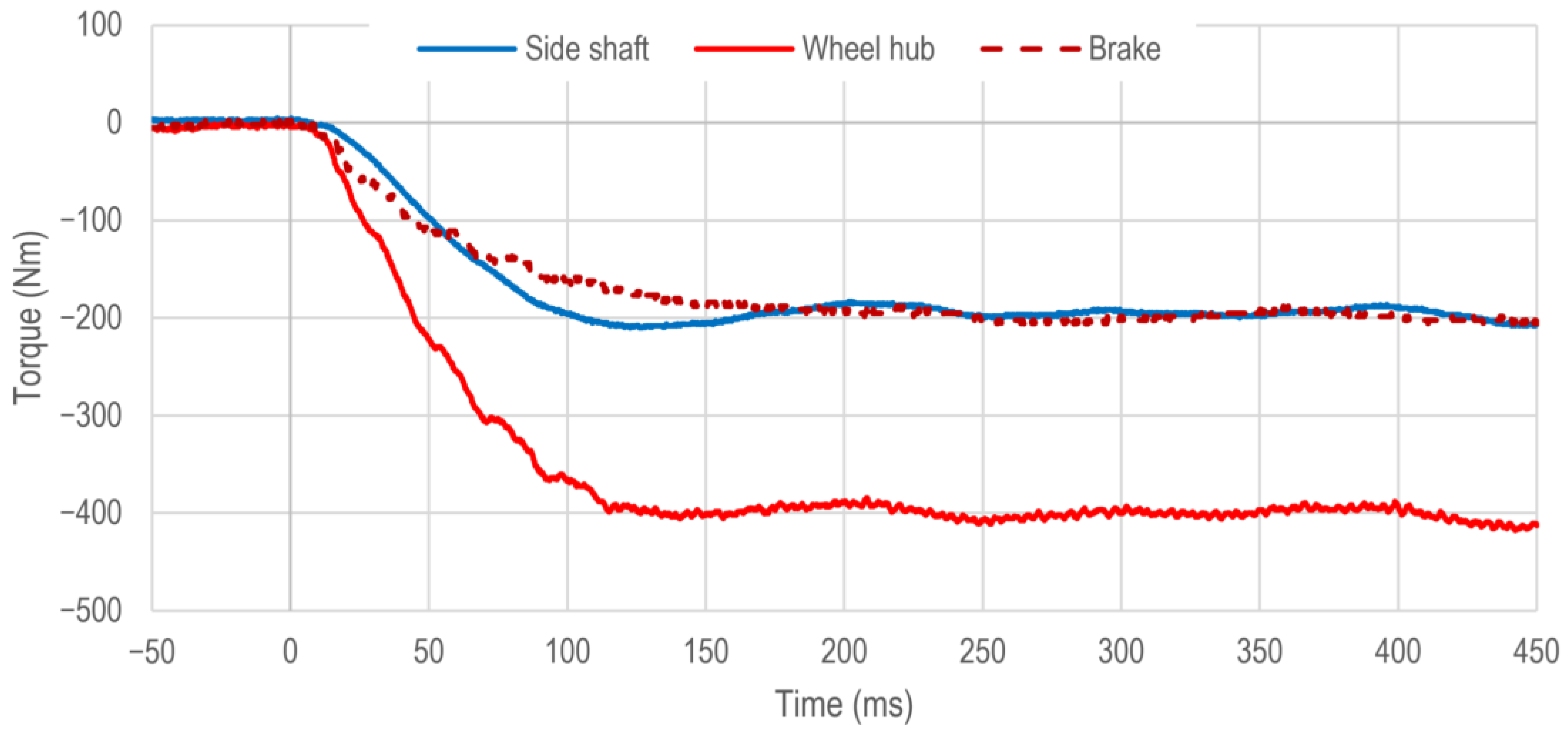
Figure 12 shows the torque courses of the vehicle side shaft $M_{\mathrm{SSh}}$ and the vehicle wheel hub $M_{\mathrm{WH}}$ as well as the friction braking torque $M_{\mathrm{Brk}}$ applied by the vehicle wheel brake without activated anti-jerk control. The friction braking torque of the vehicle wheel brake $M_{\mathrm{Brk}}$ is calculated from the measured pressure $p_{\mathrm{Brk}}$ in the vehicle brake caliper (see Figure 5).

Analogous to the explanations in Section 4, the course of the friction braking torque $M_{\mathrm{Brk}}$ shows the expected first order lag behavior. Also as described, slight oscillations due to pressure oscillations in the braking system can only be detected during the torque build-up.

The torque of the vehicle wheel hub $M_{\mathrm{WH}}$ closely follows the friction braking torque $M_{\mathrm{Brk}}$ in the torque build-up area and has almost comparable dynamics. The torque of the vehicle wheel hub $M_{\mathrm{WH}}$ reaches the value of 63% of the desired friction braking torque $M_{\mathrm{BrkD}}$ after $t_{63}$= 59 ms and the value of 90% of the desired friction braking torque $M_{\mathrm{BrkD}}$ after $t_{90}$= 105 ms. Therefore, the conventional vehicle braking operation is slightly slower than the regenerative braking operation.

Additionally, from approximately 60 ms after the initiation of the braking operation, oscillations with an amplitude of approximately 20 Nm can be detected in the torque of the vehicle wheel hub $M_{\mathrm{WH}}$. These oscillations are caused by the oscillation behavior of the vehicle side shaft.

The course of the torque of the vehicle side shaft $M_{\mathrm{SSh}}$ shows a weakly damped oscillation with an amplitude of approximately 20 Nm and a median of approximately 10 Nm. The offset of the median results from the inertial mass of the drive machine, which also has to be decelerated by the vehicle wheel brake. In addition, during the change of the direction of the effective torque in the vehicle side shaft, several plateaus caused by the backlash in the vehicle side shaft can be detected.

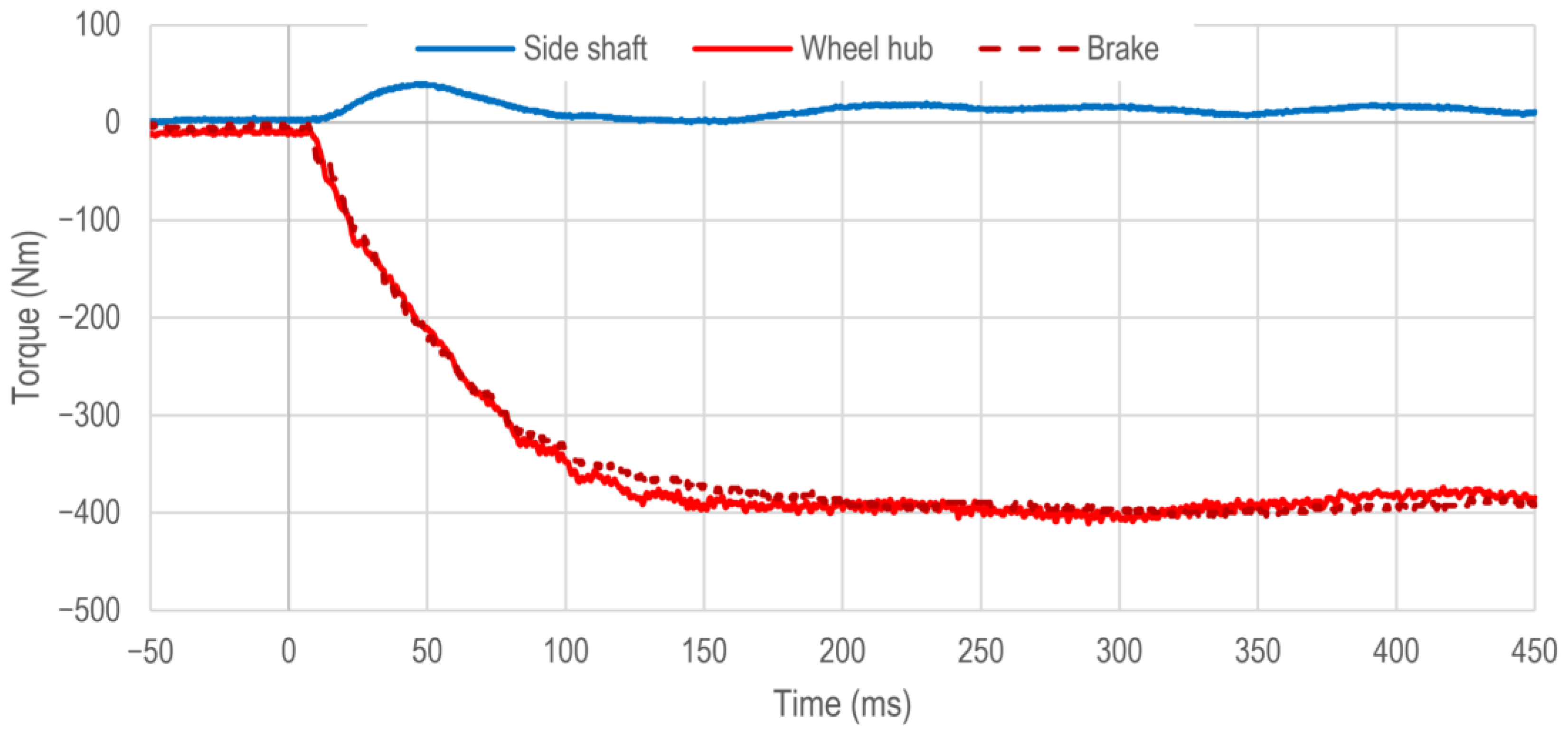
In order to reduce the oscillations in the vehicle side shaft, a braking operation with the conventional braking system and activated anti-jerk control is now considered. All other boundary conditions are retained compared to the previous braking operation. The corresponding time courses of the torques of the vehicle side shaft $M_{\mathrm{SSh}}$, the vehicle wheel hub $M_{\mathrm{WH}}$ as well as the friction braking torque $M_{\mathrm{Brk}}$ impressed by the vehicle wheel brake are shown in Figure 13.

The anti-jerk control has no influence on the build-up of braking torque by the vehicle wheel brake. The dynamic behavior of the friction braking torque $M_{\mathrm{Brk}}$ is almost the same as in the previous braking operation in Figure 12.

The oscillations in the course of the torque of the vehicle wheel hub $M_{\mathrm{WH}}$ are very well damped by the anti-jerk control. Only a slight overshoot in the time range between 75 ms and 200 ms is still detectable. The dynamic behavior thus almost corresponds to that of the vehicle wheel brake. Accordingly, the value of 63% of the desired friction braking torque $M_{\mathrm{BrkD}}$ is reached after $t_{63}$ = 60 ms. Due to the slight overshoot, the value of 90% of the desire is reached slightly faster than without activated anti-jerk control after $t_{90}$ = 102 ms.

The previously occurring oscillations in the torque of the vehicle side shaft are also well compensated by the anti-jerk control. Only one oscillation amplitude is still recognizable. In addition, there are no changes in the effective direction of this torque. The median torque of the vehicle side shaft is again approximately 10 Nm.

7. Brake Blending

In Section 1, it is shown that for a most effective energy recovery considering the limitation of the maximum air gap torque of the drive machine, a parallel use of both braking systems is to be preferred. For this purpose, the next step is to investigate braking operations with a defined split between both braking systems. This corresponds to a parallel brake blending strategy according to [4,7,48].

Correspondingly, the total desired braking torque of −400 Nm is divided equally between the vehicle wheel brake and the drive machine as an example. At the initiation of the braking operation at time $t$ = 0 ms at a vehicle speed of 25 km/h, the desired drivetrain torque $M_{\mathrm{DrTrnD}}$ is thus changed in a step from 0 Nm to −200 Nm. At the same time, the desired friction braking torque $M_{\mathrm{BrkD}}$ is also changed in a step from 0 Nm to −200 Nm. Thus, the desired brake pressure $p_{\mathrm{BrkD}}$ is increased in a step from 0 bar to 7.2 bar.

Figure 14 again shows the torque courses of the vehicle side shaft $M_{\mathrm{SSh}}$, the vehicle wheel hub $M_{\mathrm{WH}}$ and the friction braking torque $M_{\mathrm{Brk}}$ applied by the vehicle wheel brake for a braking operation with simultaneous use of both braking systems without activated anti-jerk control. The friction braking torque $M_{\mathrm{Brk}}$ of the vehicle wheel brake is again calculated from the measured pressure in the vehicle brake caliper.

The course of the torque of the vehicle wheel hub $M_{\mathrm{WH}}$ is almost comparable with the course during the regenerative braking operation without activated anti-jerk control. The value of 63% of the total desire is reached after $t_{63}$ = 56 ms and thus requires only 2 ms longer. However, the value of 90% of the total desire is only reached after $t_{90}$= 87 ms. This is 10 ms slower than with the regenerative braking system alone and 18 ms faster than with the conventional braking system alone. The reason for this is the superposition of the dynamics of the regenerative braking system (approximately second order lag behavior) and the conventional braking system (approximately first order lag behavior) (see Figure 10 and Figure 12). Afterwards, the oscillation is again weakly damped and has an amplitude of approximately 30 Nm.

The course of the torque of the vehicle side shaft $M_{\mathrm{SSh}}$ is similar to the corresponding braking operation in Section 5 (see Figure 10). Only the oscillation amplitudes are reduced due to the smaller step size in the desired drivetrain torque $M_{\mathrm{DrTrnD}}$.

In order to reduce the oscillations in the vehicle side shaft and at the vehicle wheel hub, a comparable braking operation with activated anti-jerk control is analyzed in the following. All other boundary conditions are retained compared to the previous braking operation. The corresponding torque courses over time are shown in Figure 15.

By activating the anti-jerk control, the torque build-up at the vehicle wheel hub is minimally slower, analogous to the previous braking operations. The value of 63% of the total desired braking torque is therefore reached after $t_{63}$ = 59 ms and the value of 90% of the total desire after $t_{90}$ = 91 ms. In the further course, only a minimal oscillation with an amplitude of less than 10 Nm is detectable.

The time course of the torque of the vehicle side shaft is again analogous to the braking operation in Section 5. As before, only the remaining oscillation amplitudes are slightly reduced compared to the investigations in Section 5 due to the smaller step in the desired drivetrain torque $M_{\mathrm{DrTrnD}}$.

The build-up of the friction braking torque $M_{\mathrm{Brk}}$ is not influenced by the anti-jerk control, like in Section 6. The dynamic behavior thus remains almost unchanged.

Table 1. Overview of the rise times for the different braking operations.

Braking Operation	$\mathbf{Time} {\mathit{t}}_{63} \mathbf{until} 63\% \mathbf{of} \mathbf{the} \mathbf{Total} \mathbf{Desired} \mathbf{Braking} \mathbf{Torque} \mathbf{Is} \mathbf{Reached} \left(\mathbf{ms}\right)$	$\mathbf{Time} {\mathit{t}}_{90} \mathbf{until} 90\% \mathbf{of} \mathbf{the} \mathbf{Total} \mathbf{Desired} \mathbf{Braking} \mathbf{Torque} \mathbf{Is} \mathbf{Reached} \left(\mathbf{ms}\right)$
Regenerative braking system without AJC	54	77
Regenerative braking system with AJC	57	85
Conventional braking system without AJC	59	105
Conventional braking system with AJC	60	102
Brake blending without AJC	56	87
Brake blending with AJC	59	91

summarizes the achieved dynamics of the torque of the vehicle wheel hub $M_{\mathrm{WH}}$. For this purpose, the relevant times until reaching the value of 63% of the total desired braking torque as well as the value of 90% of the total desired braking torque are listed.

The value of 63% of the total desired braking torque is reached almost at the same time in all six braking operations. Especially with activated anti-jerk control (AJC), the difference between the regenerative braking system, the conventional braking system and brake blending is only $\Delta t_{63}$= 3 ms. Thus, the dynamic behavior of the different systems is almost equal in this range.

In contrast, the times $t_{90}$ until the value of 90% of the total desired braking torque is reached show a slightly larger difference between the various braking operations. With activated anti-jerk control, the difference between the three braking operations (regenerative, conventional, brake blending) is $\Delta t_{90}$ = 17 ms. This is caused by the general dynamic torque behavior of the regenerative and the conventional braking system. For the conventional braking system, a first order lag behavior can be assumed in accordance with the explanations in Section 4. For the regenerative braking system, this is an approximately second order lag behavior even with activated anti-jerk control.

The last braking operation includes a variable split between the two braking systems. During the first 100 ms of the braking operation, the full braking torque of −400 Nm is applied by the drive machine alone. Then, while retaining the total braking torque, the percentage of the drive machine in the total braking torque is continuously reduced over a period of 500 ms and at the same time the percentage of the vehicle wheel brake is continuously increased. At the end of the braking operation, the full braking torque of −400 Nm is thus impressed into the drivetrain by the vehicle wheel brake alone. This process corresponds to a limitation of regenerative braking as a result of reaching the limits of the electric system, particularly at higher velocities or more powerful braking operations (SOC, power limits, current limits, voltage limits, etc.).

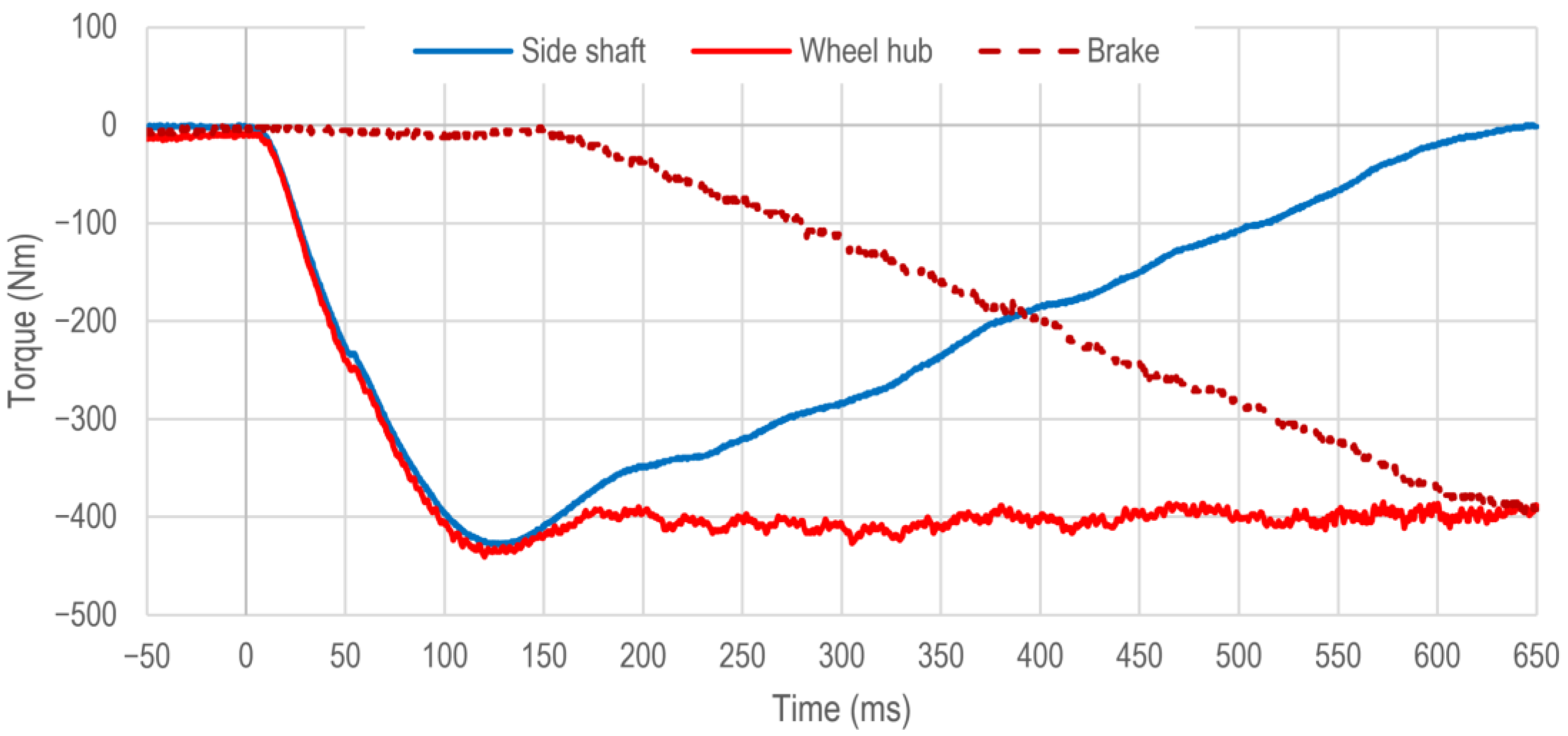
Figure 16 again shows the corresponding torque courses for the vehicle side shaft $M_{\mathrm{SSh}}$, the vehicle wheel hub $M_{\mathrm{WH}}$ and the vehicle wheel brake $M_{\mathrm{Brk}}$. In this case, both the prefilter and the anti-jerk control are activated.

The courses of the three torques show that even with a continuous modification of the percentages of the regenerative and the conventional braking system, the occurring oscillations are almost completely compensated by the anti-jerk control. Only a slight overshoot in the time range between 100 ms and 175 ms is detectable, as described in Section 5.

In [46], different torque blending strategies for a robot vehicle with four in-wheel motors (IWM) are presented. In a daisy chain method, the electric machine is used as long as possible, and the vehicle wheel brake is only applied in case of torque limitation of the electric machine. This provides a high regenerative potential. In simulation studies, the times when 90% of the total desired braking torque is reached are around 90 ms, which is comparable to Figure 16.

The other torque blending strategies described in [46], Dynamic Control Allocation (DCA) and Model Predictive Control Allocation (MPCA), use the high dynamics of the electric machine combined with the fact that it is applied directly to the wheel. This allows significantly higher dynamics, but with reduced energy efficiency.

The approach described in this research aims to avoid oscillations in a drivetrain with a vehicle side shaft with low torsional stiffness. For this purpose, the drivability functions during braking operations are analyzed and optimized. Thus, the splitting between both braking systems can be dynamically adjusted, see Figure 16. Hence, different brake blending strategies can be realized. In addition, a similar dynamic is achieved as described in [30] for pure driving.

8. Summary and Outlook

This research focuses the problem of excitation of oscillations in electric single-wheel drivetrains during braking operations. Not only the drive machine, but also the conventional vehicle wheel brake are potential sources of oscillation excitation. It should also be noted that, due to limitations of the regenerative braking system, simultaneous use of both braking systems is also necessary in the context of brake blending operations.

In order to reduce the occurring oscillations during the investigated braking operations, the drivability function presented in [27] including a prefilter and anti-jerk control is used. In order to avoid potential negative effects for the driver in terms of deceleration behavior of the vehicle and oscillations, the algorithms are optimized with regard to an adaptation of the dynamic behavior of the drive machine to the dynamic behavior of the vehicle wheel brake using the drivability functions.

The subsequent braking operations with the regenerative braking system only, the conventional braking system only and in the context of brake blending maneuvers show that the dynamic behavior during the braking operations is comparable, especially when the anti-jerk control is activated. In addition, the anti-jerk control system can almost completely compensate for the oscillations of the vehicle’s side shaft during the various braking operations. The optimized drivability function used is thus not only well qualified for acceleration operations, but also for braking operations.

In future investigations, the effects of different and varying road conditions during brake blending maneuvers will be considered in combination with the anti-jerk control system, in accordance with the descriptions in [49]. The focus will also be on investigating anti-jerk control in the case of dynamic, periodic braking operations as they occur during interventions of ABS/ESP systems.