Abstract
In the operation process of a power battery pack, the inconsistency among lithium-ion cells may seriously restrict the pack’s capacity, power capability and lifetime, which may bring hidden danger to the use of electric vehicles. Equalization management systems (EMSs) are crucial to alleviate such inter-cell inconsistency, whose performance such as accuracy and stability, mainly depends on the setting of equalization control strategies. This paper proposes an equalization strategy aimed at throughput maximization of series battery in the whole life cycle based on Model Prediction Control (MPC). In this paper, a Mean-plus-difference model (M+D) model is selected as the series battery model and the parameters are identified by Recursive Least Squares (RLS). Based on the model predictive control theory, the control model of series battery pack is established and the objective function of maximizing the throughput in the whole life cycle is derived. At the end of the paper, the simulation results show that the proposed equalization strategy can achieve greater life cycle throughput compared with the traditional SOC equalization strategy, which verifies the guiding significance of the equilibrium strategy proposed in this paper.
1. Introduction
Due to the limited power of lithium-ion battery, the power module of electric vehicle is usually composed of multiple batteries in series and parallel to meet the power requirements [1,2,3]. In the operation process of a power battery pack, the inconsistency among lithium-ion cells may seriously restrict the pack’s capacity, power capability and lifetime, which may bring hidden danger to the use of electric vehicles [4,5]. Equalization management systems (EMSs) are crucial to alleviate such inter-cell inconsistency, whose performance such as accuracy and stability, mainly depends on the setting of equalization control strategies [6,7]. To this end, the aim of this paper is to design an equalization strategy aiming at throughput maximization of series battery based on Model Prediction Control (MPC).
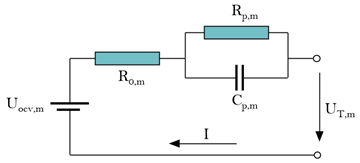
To solve the balance control problem of battery pack, the first step is to complete the modelling and parameter identification of battery pack [8,9]. According to the topological structure of the actual connection, the battery pack can be divided into four connection modes: series battery pack, parallel battery pack, series battery pack before parallel battery pack and series battery pack after parallel battery pack [10,11]. A parallel battery pack is often used to analyze the effect of inconsistency between cells on branch shunt, aging and failure of battery pack [12]. The structure of series connection before parallel connection and parallel connection before series connection can be simplified and applied to the parameter analysis of battery [13]. Based on the characteristic that the input current of cells in the same branch is identical, series batteries can be used in state estimation and equalization management. The equivalent circuit models of the series-connected battery pack consist of Big Cell Model (BCM), Multi-Cell Model (MCM), Vmin-plus-Vmax Model (VVM) and Mean-plus-difference model (M+D). BCM regards the battery pack as a single cell which deduces single cell modelling to the battery pack modelling. MCM uses the same model for each cell of the battery pack and extracts the parameters of each cell to realize the research of the cell characteristics [14]. VVM uses the maximum voltage cell in the charging process and the minimum voltage cell in the discharging process to represent the battery pack [15]; M+D model divides the battery model into a mean value and several deviation correction models to realize the overall description of the battery [16]. Compared with other models, M+D model is simpler in calculation, lower in complexity and higher in identification accuracy, so the M+D model is selected as the series battery model in this paper.
The research in the field of EMS can be divided into two aspects: equalization topology and equalization strategies. Equalization topology is based on the hardware structure and provides the circuit information to the upper strategies. Wu et al. [17] proposed an equilibrium topology based on a Cuk equalizer combined with double-layer selector switch, which led to higher efficiency of energy transfer among batteries. Crespo et al. [18] and Li et al. [19] uses module-level DC/DC power converters in different circuit structure to achieve active equalization of series or parallel battery modules. Xiong et al. [20] proposed a battery equalization circuit on the basis of a bi-directional flyback converter. To sum up, the main aim on equalization topology is to achieve higher efficiency of energy transform.
Equalization strategies can be divided into three categories: variable-based, objective-based and algorithm-based [10]. At present, equalization variables often include operating voltage, SOC, open circuit voltage (OCV), capacity and multivariate fusion [21]. The objective function selects a specific physical quantity to maximize the energy utilization rate and prolongs the service life of the battery [22]. Wang et al. [23] proposed a equalization strategies for series batteries using Fuzzy logic control aimed at shortening the time cost of the equalization process. Song et al. [24] achieved battery pack equalization based on the uniform cell charging voltage curve, and the whole capacity of the pack was improved by more than 10%. Lin et al. [25] used electrochemical-thermal coupling model to realize state of charge (SOC) estimation and achieved pack equalization based on SOC equilibrium. Appropriate equalization algorithm can avoid over equalization and repeated equalization, greatly shorten the equalization time and improve efficiency and robustness [26].
In this paper, an equilibrium strategy aiming at maximum of throughput of the series battery pack is proposed firstly. Figure 1 shows the flow chart of this paper. This work covers battery model selection, parameter identification and equilibrium strategy construction. M+D model is selected as the series battery pack model and the parameters are identified using RLS. The algorithm of this strategy is based on model predictive control. The system model corresponding to model predictive control can be any form of model describing system dynamics [27]. At last, the priority of proposed strategy is proved with a higher throughput by comparison with the traditional SOC equalization.
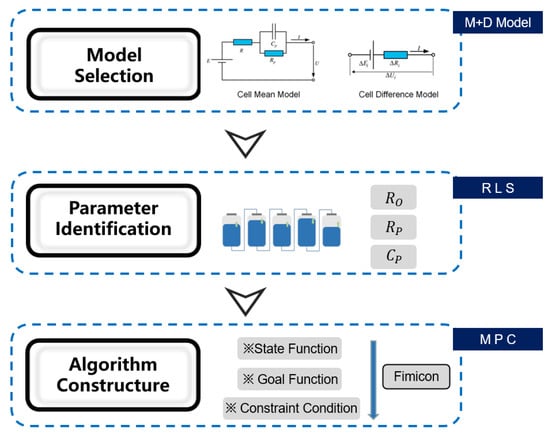
Figure 1.
Flow chart of this work.
The rest of this paper consists of the following sections: In Section 2, the parameter identification process for series battery is showed covering the model choosing and the use of algorithm. In Section 3, the equalization strategy is aimed at maximizing the throughput of the battery pack in the whole life cycle. In Section 4, the simulation results verify the superiority of the proposed strategy.
2. Parameter Identification for Series Batteries
The M+D model is selected as the model of series battery pack, which can be divided into four kinds according to the different types of difference variables. Based on the selected M+D#2 model, the RLS algorithm is used for parameter identification and the accuracy of the model is tested.
2.1. M+D Model
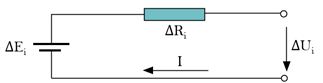
M+D model is divided into cell mean model (CMM) and cell difference model (CDM). The average model represents the overall state of the battery pack and the characteristic parameters can be identified by the average voltage and input current of all the cells of the battery pack. The deviation model describes the difference between the cell and the average value of the battery pack [28]. According to the different types of difference variables, the deviation models are divided into four categories, as shown in Figure 2. CDM#2 is selected as the deviation model for parameter identification which considers resistance and SOC as the difference variables [29]. The state equations of M+D model is shown in Table 1.
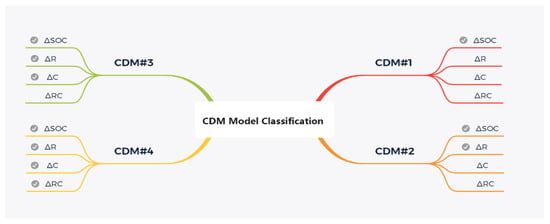
Figure 2.
CDM model classification.

Table 1.
State equations of M+D model. Adapted from ref. [28].
2.2. Parameter Identification Based on RLS
Parameters of M+D model are identified with a forgetting factor. To use the RLS algorithm, the CMM is discretized as follows [30].
where represents sampling interval, , define , state function can be rewritten as:
where , and are the parameter coefficient of the model.
The parameter can be obtained from the above formula.
In order to use RLS algorithm, the equation is written in the form of , where
Similarly, the expression of CDM#2 can be deduced. The RLS identification process is shown in Table 2.

Table 2.
M+D Model parameter identification.
2.3. Parameter Identification Results
The OCV-SOC curve of the battery is the average value of the voltage in the process of charging and discharging. The fitting coefficient is obtained by polynomial fitting of the OCV-SOC curve of CMM, of which the results are showed as follows.
Based on the experimental data of HPPC experiment, the parameters of series battery pack model are identified. The identification results are shown in Table 3.

Table 3.
The identification results.
The accuracy of the identification results is verified, as shown in the Figure 3. The fitting error is less than 1%, of which the accuracy meets the requirements.
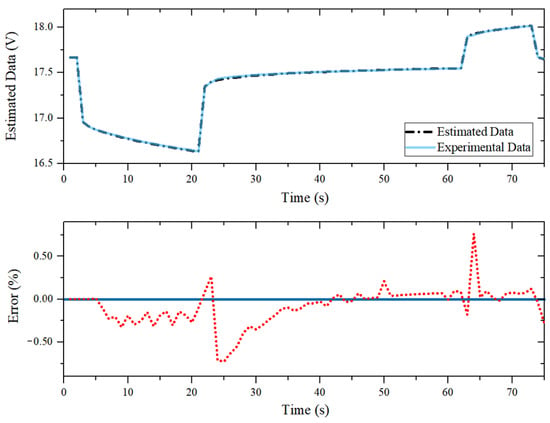
Figure 3.
Identification results.
3. Equalization Strategy Design Based on Model Predictive Control
Based on the results of parameter identification, the MPC-based equalization strategy is designed. The derivation of MPC space equation, the determination of objective function, the determination of constraint conditions and the solution of quadratic problem are completed respectively [31,32]. The result is finally obtained using the fimicon algorithm in Matlab and the simulation results are tested by comparative verification.
3.1. State Space Model of Series Batteries
In order to explain the effect of the equalization strategy and take into account the computational complexity, the number of series batteries is selected as five. Both the prediction time domain p and control time domain m are selected as six. A complete multi-input multi-output state space model is obtained by taking the first-order RC equivalent circuit model of battery as the prediction model [33,34].
Cell equivalent circuit model is:
where the state variable is: . The output variable is: .
The four coefficient matrices are:
Based on the model predictive control theory, the space equation is derived:
According to the selected parameters: number of batteries, prediction time domain and control time domain, it can be derived as follows:
where two corner markers in the lower right corner of a letter xij, indicating the state of the ith battery in the battery pack at the j moment. The matrix is a diagonal matrix formed by the coefficient matrix in the cell model, which can be written as:
3.2. Objective Function and Solution Method of Equilibrium Strategy
① The objective function of maximizing the throughput.
Define c = Cact/Cinit, where Cinit is the initial capacity of the battery, which can be regarded as a constant, define K = dc/dn as the battery aging rate, define n as the number of life cycles, define at the time that c = 0.8, the number of life cycles as the maximum number of battery cycles, Q represents the throughput of the battery life cycle [3]. Where
Combine the above equations:
It is obvious that the larger the value K is, the smaller the value N is, the smaller the battery throughput is. Conversely, the smaller the value K is, the larger the battery throughput is. Therefore, it can be concluded that there is a positive correlation between the battery life cycle throughput and the aging rate [3], the empirical formula of aging rate and aging rate was put forward through data fitting
According to the above formula, the equilibrium objective function can be written as follows:
where represents the battery aging rate of ith cell in the pack at j moment.
② The objective function of the traditional SOC equalization
In order to prove the effectiveness of the life cycle balancing strategy, the balancing strategy considering SOC consistency is used as a comparative analysis. SOC consistency is to make the SOC of each cell in the whole battery reach the average SOC, so the objective function can be obtained as follows:
where represents the SOC of the ith cell in the pack at j moment, represents the mean SOC of the whole pack.
③ Input constraints
For the model predictive control of this problem, the input constraints are as follows:
The first term of the above formulas is set to limit the SOC. The maximum aging rate of the battery is at the end of SOC 0 or 1 and the function of which is a convex function in the interval, so that the SOC is controlled in the range [0.1, 0.9]. The second term is set to limit the output voltage of the battery and the output voltage range of the battery used in this work is [2.7 V, 4.2 V]. The third equation is the limitation of the equalization current, in which the maximum equalization current is not more than 10 A. The fourth is the fluctuation limit of the equalization voltage. During the equalization process, the batteries charge and discharge each other. From the overall point of view of the battery pack, the equalization power is zero. As a result, the power balance constraint is added, which is five to eight equations of the above formulas. Based on the goal function and constraint condition, the result can be obtained using the fimicon optimization function in Matlab in time-varying condition.
Since the objective function of this paper has the compensation term of DOD causing certain nonlinearity, fmincon function is applied to solve the problem [35,36]. In this way, the optimal control sequence is obtained by invoking the fmincon function at each time and the first element of the solution is applied to the system, of which the process is repeated so as to achieve the equilibrium control under different objectives.
4. Simulation Result
This article compares the results of the two equalization strategies under static and constant current charging conditions, of which the simulation results verify that the equalization strategy proposed in this article can maximize the throughput of the battery pack throughout its life cycle. In the following analysis, the balance strategy for maximizing throughput throughout the life cycle is option 1 and the traditional SOC uniform balance strategy of the battery pack is option 2.
In the static state, two equalization strategies are used to balance the battery pack. Figure 4a,b show the results of the two equalization strategies. Figure 4c shows the comparison of the instantaneous aging rate under the two strategies. It can be seen that the sum of instantaneous aging rate of option 1 is smaller and the battery pack’s life cycle throughput is greater.
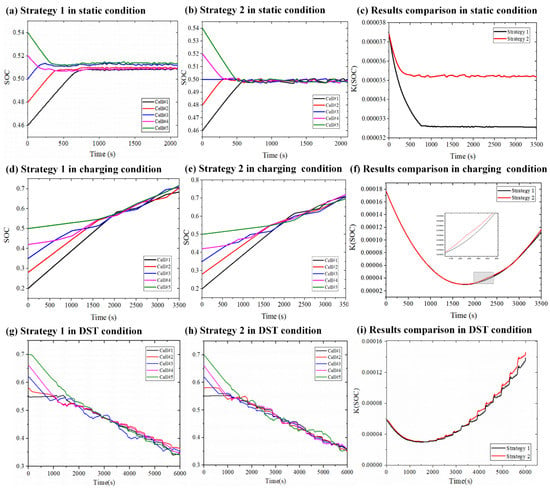
Figure 4.
Simulation results.
Figure 4d,e show the simulation results of the two strategies in the constant current charging condition. In Figure 4f, the result of the sum of instantaneous aging rate shows that option 1 can achieve a little greater life cycle throughput of the battery pack.
Figure 4g,h show the simulation results of the two strategies in the DST condition. In Figure 4i, the result of the sum of instantaneous aging rate shows that option 1 can achieve a greater life cycle throughput of the battery pack.
The comparison results prove that the equilibrium strategy proposed in this paper can achieve greater life cycle throughput of the series battery pack than the traditional SOC equilibrium strategy. This equilibrium strategy combines the battery aging state and MPC algorithm to achieve equation of battery pack in different conditions. Moreover, the proposed equilibrium strategy as an alternative of previous strategy provides a possibility to improve BMS performance to some extent.
5. Conclusions
This paper proposed an equilibrium strategy based on model predictive control aimed at maximum throughput in battery whole life cycle. This work contains battery pack model selection, parameters identification and equilibrium strategy construction, which achieved closed loop simulation. The identified model in this work can achieve an accurate description of the series battery pack considering the mean and difference value in a time-varying condition. The predictive control model is selected as the main algorithm of the equalization strategy, which can adapt to various actual conditions. The battery series used in this work consists of five cells. For further applications, this equalization strategy is adequate for series battery pack containing more cells and can realize a higher profit of throughput of the battery pack. As a result, the equalization strategy proposed in this work can be obtained in the context of real-world battery management easily. Compared to the traditional battery equalization strategy, this work, aiming at throughput maximum, considered not only voltage and SOC, but also the ageing state of the battery cell, and can achieve the internal balance of the battery pack safely and efficiently.
Author Contributions
Conceptualization, R.C. and Z.Z.; methodology, R.C.; software, R.C. and X.L.; validation, H.C., R.C. and M.W.; formal analysis, X.G.; investigation, S.Y.; resources, S.Y.; data curation, X.L.; writing—original draft preparation, R.C.; writing—review and editing, X.L. and X.Y.; visualization, Z.Z.; supervision, H.C.; project administration, M.W.; funding acquisition, S.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Xinjiang Uygur Autonomous Region Regional Collaborative Innovation Program (Science and Technology Assistance to Xinjiang Project: No.2019E0240), the National Key Research and Development Program of China (2018YFB0104400), and National Natural Science Foundation of China (No. U1864213).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The [hppc.xls] data used to support the findings of this study are available from the corresponding author upon request.
Acknowledgments
The authors would like to thank Evs34 conference group for recommendation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Feng, F.; Hu, X.; Liu, K.; Che, Y.; Lin, X.; Jin, G.; Liu, B. A practical and comprehensive evaluation method for series-connected battery pack models. IEEE Trans. Transp. Electrif. 2020, 6, 391–416. [Google Scholar] [CrossRef]
- Liu, X.; Ai, W.; Naylor, M.; Patel, Y.; Wu, B. The effect of cell-to-cell variations and thermal gradients on the performance and degradation of lithium-ion battery packs. Appl. Energy 2019, 248, 489–499. [Google Scholar] [CrossRef]
- Schmalstieg, J.; Käbitz, S.; Ecker, M.; Sauer, D.U. A holistic aging model for Li(NiMnCo)O2 based 18650 lithium-ion batteries. J. Power Sources 2014, 257, 325–334. [Google Scholar] [CrossRef]
- Yang, S.; He, R.; Zhang, Z.; Cao, Y.; Gao, X.; Liu, X. CHAIN: Cyber hierarchy and interactional network enabling digital solution for battery full-lifespan management. Matter 2020, 3, 27–41. [Google Scholar] [CrossRef]
- Weng, C.; Feng, X.; Sun, J.; Peng, H. State-of-health monitoring of lithium-ion battery modules and packs via incremental capacity peak tracking. Appl. Energy 2016, 180, 360–368. [Google Scholar] [CrossRef] [Green Version]
- Gao, X.; Liu, X.; He, R.; Wang, M.; Xie, W.; Brandon, N.P.; Wu, B.; Ling, H.; Zang, S. Designed high-performance lithium-ion battery electrodes using a novel hybrid model-data driven approach. Energy Storage Mater. 2021, 36, 435–458. [Google Scholar] [CrossRef]
- Wu, B.; Widanage, W.D.; Yang, S.; Liu, X. Battery digital twins: Perspectives on the fusion of models, data and artificial intelligence for smart battery management systems. Energy AI 2020, 1, 100016. [Google Scholar] [CrossRef]
- Che, Y.; Deng, Z.; Lin, X.; Hu, L. Learning and online model Correction. IEEE Trans. Veh. Technol. 2021, 70, 1269–1277. [Google Scholar] [CrossRef]
- Yang, S.; Gao, X.; Li, Y.; Xie, W.; Guo, B.; Zhang, L.; Liu, X. Minimum lithium plating overpotential control based charging strategy for parallel battery module prevents side reactions. J. Power Sources 2021, 494, 229772. [Google Scholar] [CrossRef]
- Feng, F.; Hu, X.; Liu, J.; Lin, X.; Liu, B. A review of equalization strategies for series battery packs: Variables, objectives, and algorithms. Renew. Sustain. Energy Rev. 2019, 116, 109464. [Google Scholar] [CrossRef]
- Li, W.; Sengupta, N.; Dechent, P.; Howey, D.; Annaswamy, A.; Sauer, D.U. Online capacity estimation of lithium-ion batteries with deep long short-term memory networks. J. Power Sources 2021, 482, 228863. [Google Scholar] [CrossRef]
- Nguyen, N.; Oruganti, S.K.; Na, K.; Bien, F. An adaptive backward control battery equalization system for serially connected lithium-ion battery packs. IEEE Trans. Veh. Technol. 2014, 63, 3651–3660. [Google Scholar] [CrossRef]
- Ugle, R.; Li, Y.; Dhingra, A. Equalization integrated online monitoring of health map and worthiness of replacement for battery pack of electric vehicles. J. Power Sources 2013, 223, 293–305. [Google Scholar] [CrossRef]
- Zheng, Y.; Ouyang, M.; Lu, L.; Li, J.; Han, X.; Xu, L. On-line equalization for lithium-ion battery packs based on charging cell voltages: Part 1. Equalization based on remaining charging capacity estimation. J. Power Sources 2014, 247, 676–686. [Google Scholar] [CrossRef]
- Zou, C.; Manzie, C.; Ne, D. Multi-time-scale observer design for state-of-charge and state-of- health of a lithium-ion battery. J. Power Sources 2016, 335, 121–130. [Google Scholar] [CrossRef]
- Dai, H.; Wei, X.; Sun, Z.; Wang, J.; Gu, W. Online cell SOC estimation of Li-ion battery packs using a dual time-scale Kalman filtering for EV applications. Appl. Energy 2012, 95, 227–237. [Google Scholar] [CrossRef]
- Wu, T.; Qi, Y.; Liao, L.; Ji, F.; Chen, H. Research on equalization strategy of lithium-ion batteries based on fuzzy logic control. J. Energy Storage 2021, 40, 102722. [Google Scholar] [CrossRef]
- Crespo, M.; Georgious, R.; Garcia, P.; Villa, G. Active equalization of series/parallel Li-ion battery modules including no-load conditions. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Detroit, MI, USA, 11–15 October 2020; pp. 4431–4437. [Google Scholar]
- Li, K.; Zong, X.; Liu, Q.; Sun, Y.; Xue, F. Design of an active battery equalization circuit with DC-DC converter. In Proceedings of the 3rd Asia Energy and Electrical Engineering Symposium, Chengdu, China, 26–29 March 2021; pp. 863–866. [Google Scholar]
- Xiong, H.; Song, D.; Shi, F.; Wei, Y.; Jinzhen, L. Novel voltage equalisation circuit of the lithium battery pack based on bidirectional flyback converter. IET Power Electron. 2020, 13, 2194–2200. [Google Scholar] [CrossRef]
- Zhang, S.; Qiang, J.; Yang, L.; Zhao, X. Prior-knowledge-independent equalization to improve battery uniformity with energy efficiency and time efficiency for lithium-ion battery. Energy 2016, 94, 1–12. [Google Scholar] [CrossRef]
- Diao, W.; Xue, N.; Bhattacharjee, V.; Jiang, J.; Karabasoglu, O. Active battery cell equalization based on residual available energy maximization. Appl. Energy 2018, 210, 690–698. [Google Scholar] [CrossRef]
- Wang, B.; Qin, F.; Zhao, X.; Ni, X.; Xuan, D. Equalization of series connected lithium-ion batteries based on back propagation neural network and fuzzy logic control. Int. J. Energy Res. 2020, 44, 4812–4826. [Google Scholar] [CrossRef]
- Song, L.; Liang, T.; Lu, L.; Ouyang, M. Lithium-ion battery pack equalization based on charging voltage curves. Int. J. Electr. Power Energy Syst. 2020, 115, 105516. [Google Scholar] [CrossRef]
- Lin, Y.; Xu, X.; Wang, F.; Xu, Q. Active equalization control strategy of Li-ion battery based on state of charge estimation of an electrochemical-thermal coupling model. Int. J. Energy Res. 2020, 44, 3778–3789. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, L.; Zhao, X.; Qiang, J. Electrical power and energy systems a GA optimization for lithium-ion battery equalization based on SOC estimation by NN and FLC. Int. J. Electr. Power Energy Syst. 2015, 73, 318–328. [Google Scholar] [CrossRef]
- Einhorn, M.; Guertlschmid, W.; Blochberger, T.; Kumpusch, R.; Permann, R.; Conte, F.V.; Kral, C.; Fleig, J. A current equalization method for serially connected battery cells using a single power converter for each cell. IEEE Trans. Veh. Technol. 2011, 60, 4227–4237. [Google Scholar] [CrossRef]
- Zheng, Y.; Ouyang, M.; Lu, L.; Li, J.; Han, X.; Xu, L.; Ma, H.; Dollmeyer, T.A.; Freyermuth, V. Cell state-of-charge inconsistency estimation for LiFePO4 battery pack in hybrid electric vehicles using mean-difference model. Appl. Energy 2013, 111, 571–580. [Google Scholar] [CrossRef]
- Hu, L.; Hu, X.; Che, Y.; Feng, F.; Lin, X.; Zhang, Z. Reliable state of charge estimation of battery packs using fuzzy adaptive federated filtering. Appl. Energy 2020, 262, 114569. [Google Scholar] [CrossRef]
- Feng, T.; Yang, L.; Zhao, X.; Zhang, H.; Qiang, J. Online identification of lithium-ion battery parameters based on an improved equivalent-circuit model and its implementation on battery state-of-power prediction. J. Power Sources 2015, 281, 192–203. [Google Scholar] [CrossRef]
- Altaf, F.; Egardt, B. Gain-scheduled control of modular battery for thermal and SOC balancing. Engineering 2016, 49, 62–69. [Google Scholar]
- Liu, J.; Chen, Y.; Fathy, H.K.; Chen, Y. Nonlinear model-predictive optimal control of an active cell-to-cell lithium-ion battery pack balancing circuit. IFAC 2017, 50, 14483–14488. [Google Scholar] [CrossRef]
- Liu, J.; Duan, Q.; Chen, H.; Sun, J.; Wang, Q. An optimal multistage charge strategy for commercial lithium ion batteries. Sustain. Energy Fuels 2018, 2, 1726–1736. [Google Scholar]
- Han, W.; Zhang, L. Battery cell reconfiguration to expedite charge equalization in series-connected battery systems. IEEE Robot. Autom. Lett. 2018, 3, 22–28. [Google Scholar] [CrossRef]
- Burgos-Mellado, C.; Orchard, M.E.; Kazerani, M.; Cárdenas, R.; Sáez, D. Particle-filtering-based estimation of maximum available power state in Lithium-Ion batteries. Appl. Energy 2016, 161, 349–363. [Google Scholar] [CrossRef]
- Birkl, C.R.; Roberts, M.R.; McTurk, E.; Bruce, P.G.; Howey, D.A. Degradation diagnostics for lithium ion cells. J. Power Sources 2017, 341, 373–386. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).