Core Loss Analysis and Modeling of a Magnetic Coupling System in WPT for EVs
Abstract
:1. Introduction
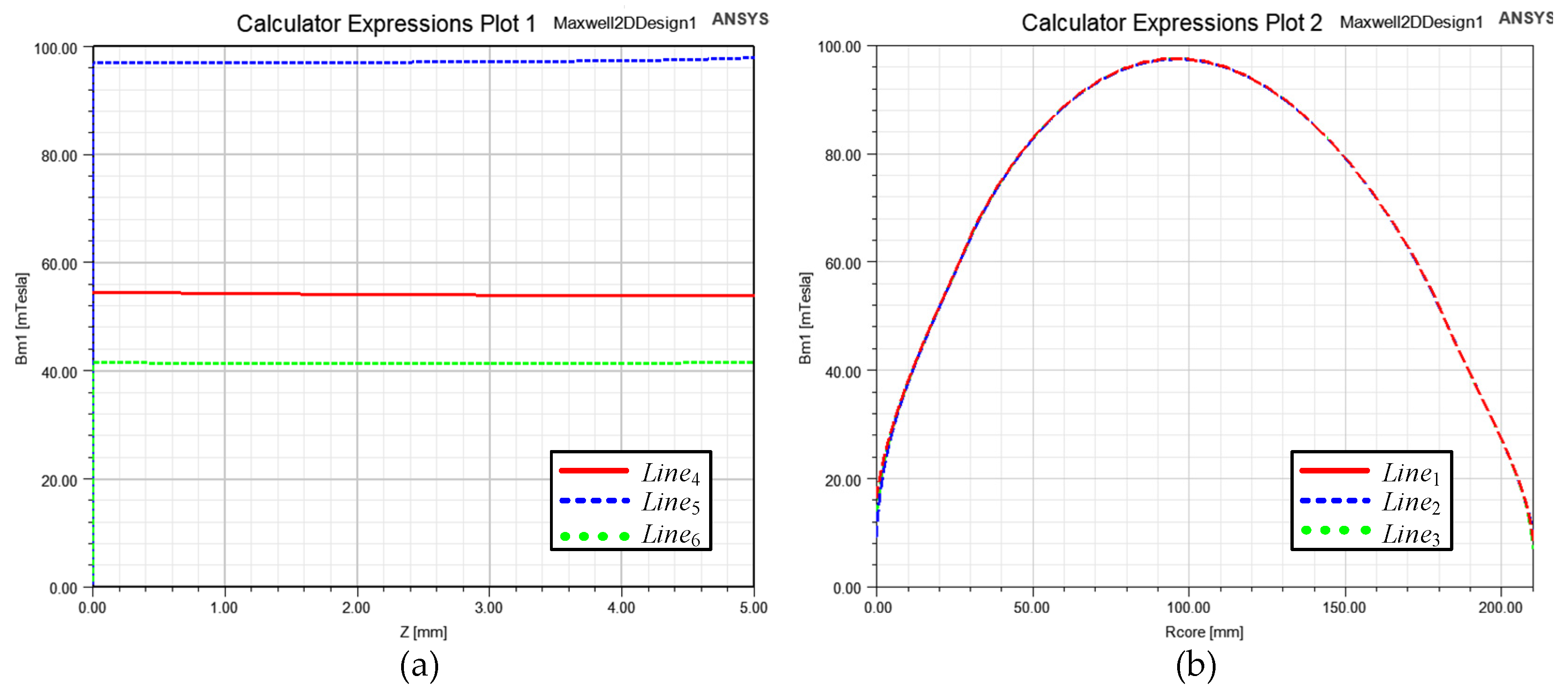
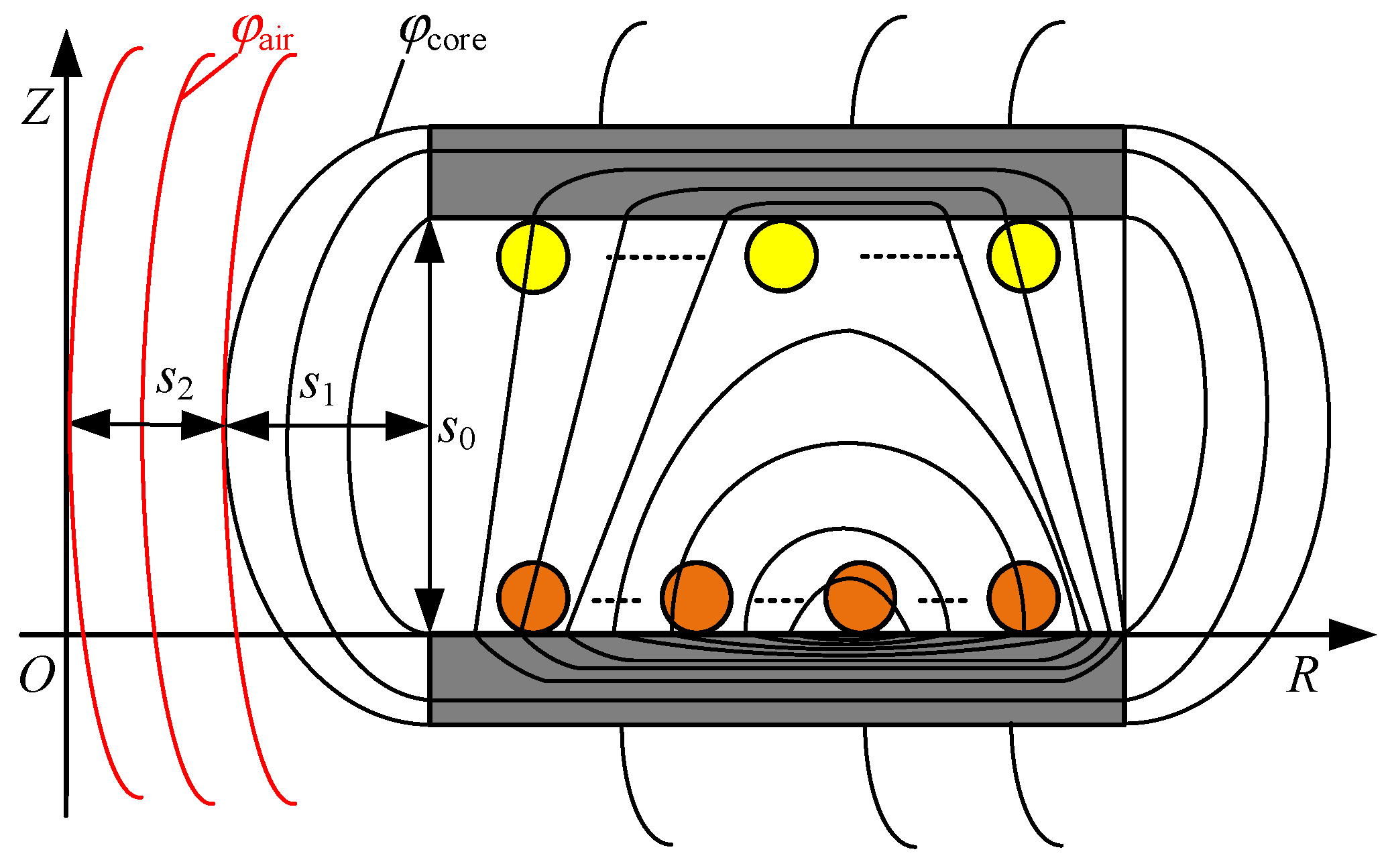
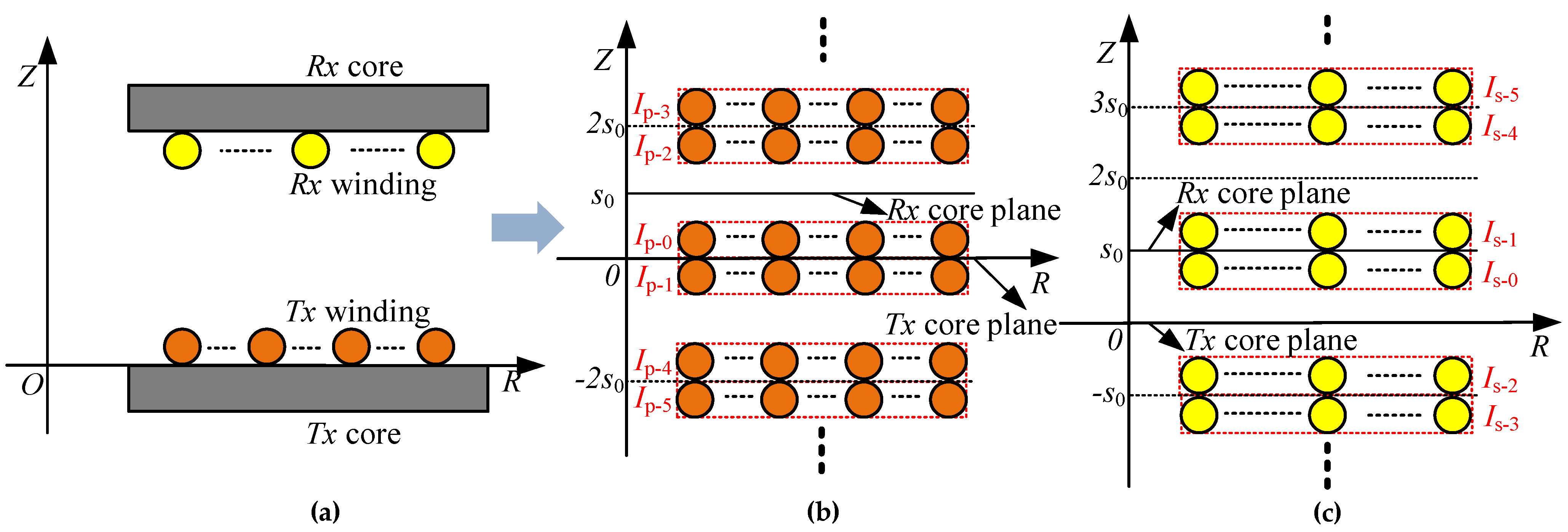
2. The Distribution of Magnetic Flux Density in the Disk Core
3. Analysis and Modeling of Core Loss
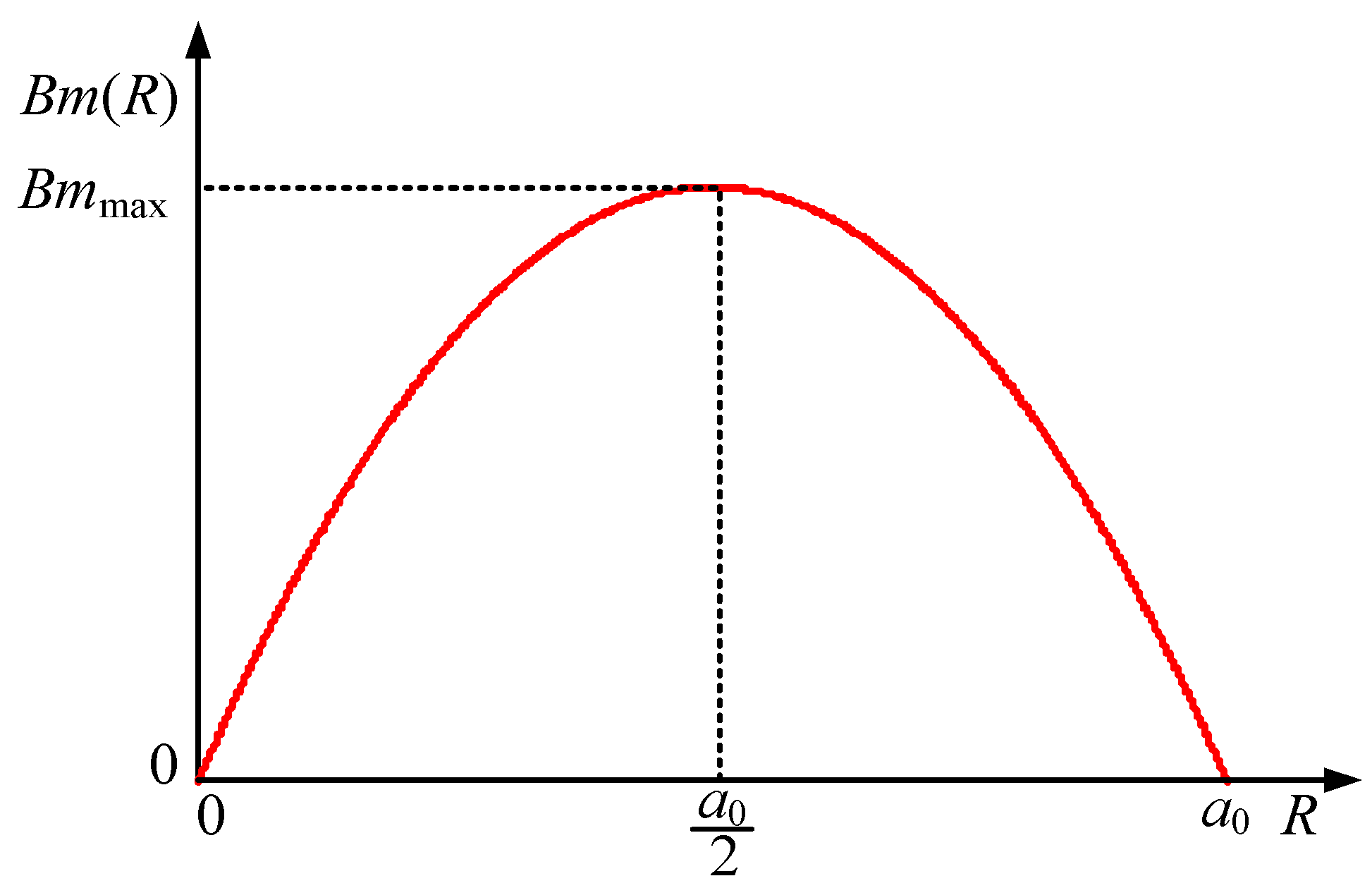
3.1. Modeling of Magnetic Flux Density Distribution
3.2. Theoretical Calculation Method of Magnetic Flux Density Model Parameters
3.3. Core Loss Modeling
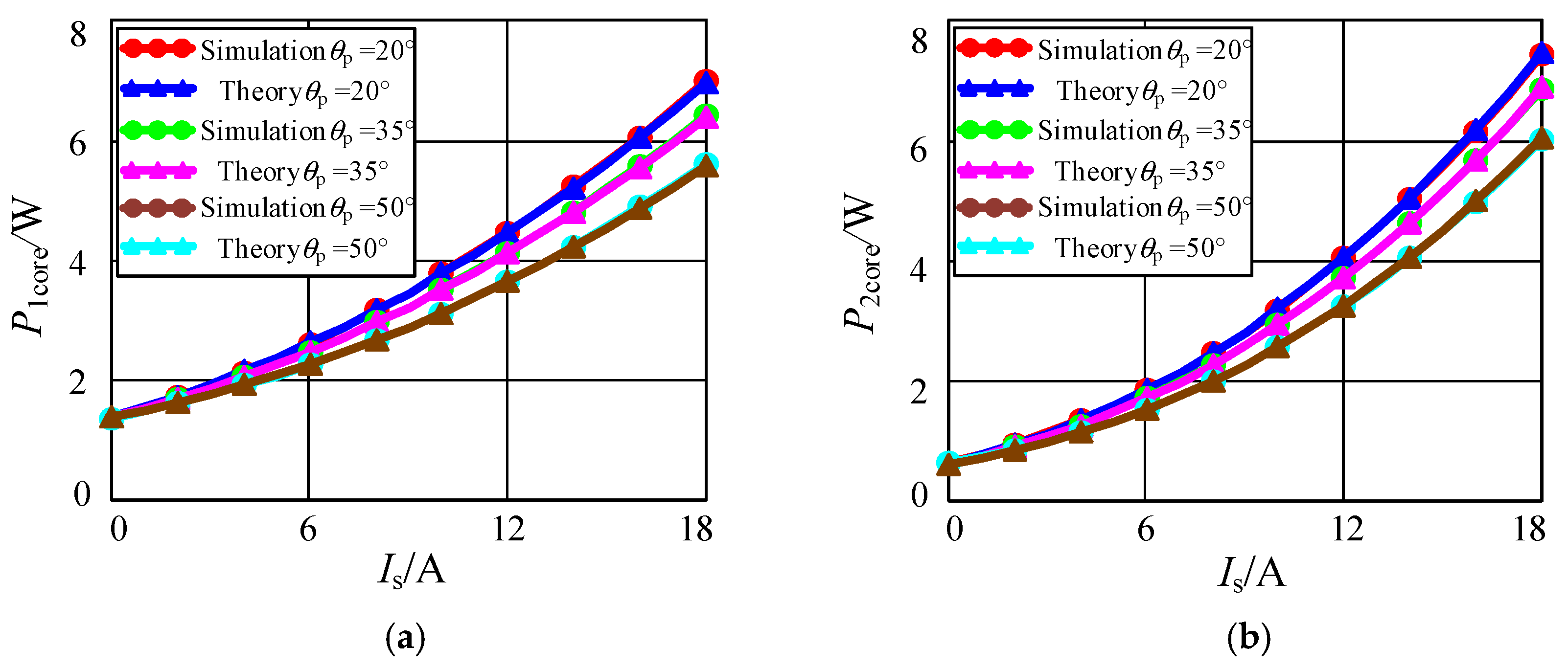
4. Simulation and Verification
5. Conclusions
- The magnetic flux density inside the disk core through each radial circle sheet core is different; consequently, the average magnetic flux density cannot be used to calculate the overall core loss because of the non-linear core loss characteristic of the magnetic core.
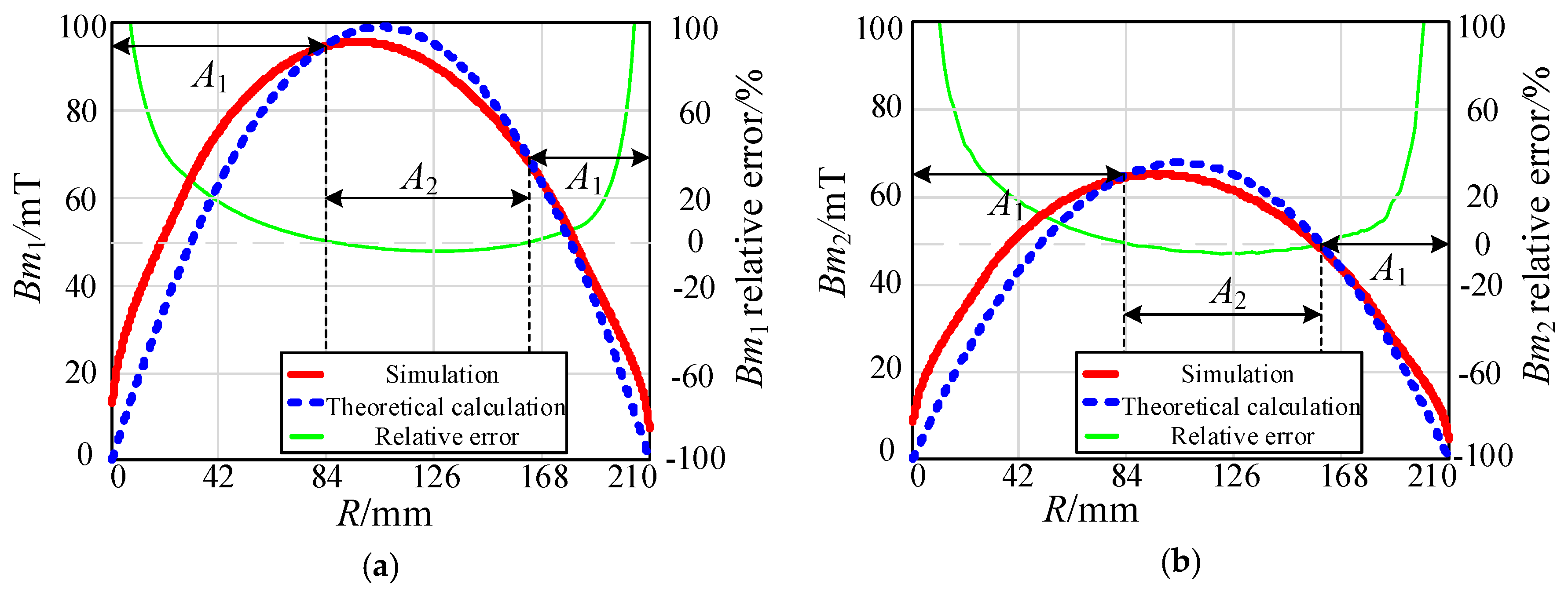
- In the core loss calculation, the distribution of the magnetic flux density in the core needs to be taken into consideration. According to FEA simulation results, the mathematical model of the distribution of magnetic flux density is established. This model can be described as a quadratic function in which the parameters are extracted from the magnetic-field distribution of the magnetic coupling system.
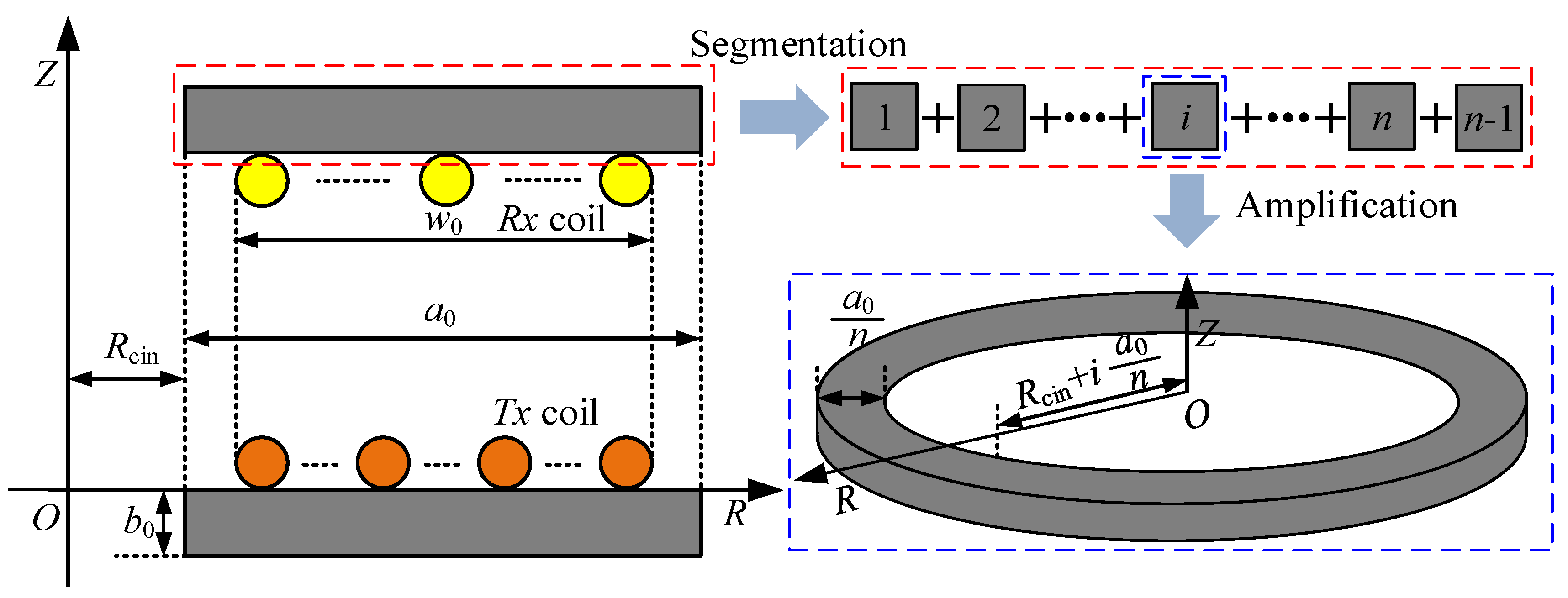
- In order to build the disk core loss model of the WPT system, the disk core is divided into several circle sheets. In each circle sheet, the magnetic flux density can be seen to be the same and the core loss can be calculated by the Steinmetz formula. Combining the model of the distribution of magnetic flux density inside the magnetic core, the disk core loss model of the WPT system is proposed.
- The FEA simulation results show that the magnetic core loss calculated by the proposed model has good accuracy. This core loss model can provide an easier way to calculate the disk core loss of the WPT system than the FEA simulation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chan, C.C.; Bouscayrol, A.; Chen, K. Electric, Hybrid, and Fuel-Cell Vehicles: Architectures and Modeling. IEEE Trans. Veh. Technol. 2010, 59, 589–598. [Google Scholar] [CrossRef]
- Griffith, P.; Bailey, J.R.; Simpson, D. Inductive Charging of Ultracapacitor Electric Bus. World Electr. Veh. J. 2008, 2, 29–37. [Google Scholar] [CrossRef]
- Zhao, Z.M.; Zhang, Y.M.; Chen, K.N. New Progress of Magnetically-Coupled Resonant Wireless Power Transfer Technology. Proc. Chin. Soc. Electr. Eng. 2013, 33, 1–13. [Google Scholar]
- Costanzo, A.; Dionigi, M.; Masotti, D.; Mongiardo, M.; Monti, G.; Tarricone, L. Electromagnetic Energy Harvesting and Wireless Power Transmission: A Unified Approach. Proc. IEEE 2014, 102, 1692–1711. [Google Scholar] [CrossRef]
- Papastergiou, K.D.; Macpherson, D.E. An airborne radar power supply with contactless transfer of energy—Part I: Rotating transformer. IEEE Trans. Ind. Electron. 2007, 54, 2874–2884. [Google Scholar] [CrossRef]
- Liu, X.; Hui, S.Y. Simulation study and experimental verification of a universal contactless battery charging platform with localized charging features. IEEE Trans. Power Electron. 2007, 22, 2202–2210. [Google Scholar]
- Kim, H.J.; Hirayama, H.; Kim, S.; Han, K.J.; Choi, J.W. Review of Near-Field Wireless Power and Communication for Biomedical Applications. IEEE Access 2017, 5, 21264–21285. [Google Scholar] [CrossRef]
- Meyers, D.; Willis, K. Sorting Through the Many Total-Energy-Cycle Pathways Possible with Early Plug-In Hybrids. World Electr. Veh. J. 2008, 2, 66–88. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Liu, F.; Chen, K. New Progress of Wireless Charging Technology for Electric Vehicles. Trans. China Electro.-Tech. Soc. 2016, 31, 30–40. [Google Scholar]
- Choi, S.Y.; Jeong, S.Y.; Gu, B.W.; Lim, G.C.; Rim, C.T. Ultraslim S-Type Power Supply Rails for Roadway-Powered Electric Vehicles Generalized Models onSelf-Decoupled Dual Pick-Up Coils for a Large Lateral Tolerance. IEEE Trans. Power Electron. 2015, 30, 6456–6468. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Wang, X.M.; Zhang, B.; Qiu, D.Y. Advances of Wireless Charging Technology in Electric Vehicle. J. Power Supply 2014, 3, 27–32. [Google Scholar]
- Meyers, D.; Willis, K. Globally Cool Vehicles: When Only Electric Will Do. World Electr. Veh. J. 2008, 2, 10–18. [Google Scholar] [CrossRef]
- Asfani, D.A. Electric Vehicle Research in Indonesia: A Road map, Road tests, and Research Challenges. IEEE Electrif. Mag. 2020, 8, 44–51. [Google Scholar] [CrossRef]
- Zhang, W.J.; Bi, L.F.; Ming, L.Y.; Song, J.C.; Jia, L.; Ren, H. Research on Misalignment Performance of Magnetic Coupling Structure in Magnetically Coupled Resonant Wireless Power Transfer System. High. Volt. Eng. 2020, 46, 4087–4095. [Google Scholar]
- Kavitha, M.; Bobba, P.B.; Prasad, D. A Study on Effect of Coil Structures and Core Configurations on Parameters of Wireless EV Charging System. In Proceedings of the 2017 IEEE Transportation Electrification Conference (ITEC), Pune, India, 13–15 December 2017; pp. 1–6. [Google Scholar]
- Xiao, C.; Chen, G.; Odendaal, W.G.H. Overview of Power Loss Measurement Techniques in Power Electronics Systems. IEEE Trans. Ind. Appl. 2007, 43, 657–664. [Google Scholar] [CrossRef]
- Tan, F.D.; Vollin, J.L. A Practical Approach for Magnetic Core-Loss Characterization. IEEE Trans. Power Electron. 1995, 33, 124–130. [Google Scholar]
- Hou, D.; Mu, M.; Lee, F.C.; Li, Q. New High-Frequency Core Loss Measurement Method with Partial Cancellation Concept. IEEE Trans. Power Electron. 2017, 32, 2987–2994. [Google Scholar] [CrossRef]
- Thottuvelil, V.J.; Wilson, T.G. High-frequency measurement techniques for magnetic cores. IEEE Trans. Power Electron. 1990, 5, 41–53. [Google Scholar] [CrossRef]
- Han, Y.; Liu, Y.F. A Practical Transformer Core Loss Measurement Scheme for High-Frequency Power Converter. IEEE Trans. Ind. Electron. 2008, 55, 941–948. [Google Scholar] [CrossRef]
- Dai, X.; Li, X.; Li, Y.; Hu, A.P. Maximum Efficiency Tracking for Wireless Power Transfer Systems with Dynamic Coupling Coefficient Estimation. IEEE Trans. Power Electron. 2018, 33, 5005–5015. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, Y.; Liu, X.; Lu, K.; Xu, D. Analysis and Design of an S/SP Compensated IPT System to Minimize Output Voltage Fluctuation Versus Coupling Coefficient and Load Variation. IEEE Trans. Veh. Technol. 2018, 67, 9262–9272. [Google Scholar] [CrossRef]
- Iero, D.; Corte, F.; Fiorentino, G. A Calorimetry-Based Measurement Apparatus for Switching Losses in High Power Electronic Devices. In Proceedings of the 2016 IEEE International Energy Conference (ENERGYCON), Leuven, Belgium, 4–8 April 2016; pp. 1–5. [Google Scholar]
- Szabados, B.; Mihalcea, A. Design and Implementation of a Calorimetric Measurement Facility for Determining Losses in Electrical Machines. IEEE Trans. Instrum. Meas. 2002, 51, 902–907. [Google Scholar] [CrossRef]
- Sun, C.; Shi, Z.; Shi, L.; Yue, C.; Yu, J. Measurement of LVDC Customer-end Inverter Efficiency by Calorimetry Method. In Proceedings of the 2019 IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 21–23 November 2019; pp. 2708–2712. [Google Scholar]
- Chen, B.; Li, L.; Zhao, Z. Magnetic Core Losses Under High-Frequency Typical Non-Sinusoidal Voltage Magnetization. Trans. China Electrotech. Soc. 2018, 33, 1696–1704. [Google Scholar]
- Yu, X.; Li, Y.; Yang, Q.; Yue, S.; Zhang, C. Loss Characteristics and Model Verification of Soft Magnetic Composites Under Non-Sinusoidal Excitation. IEEE Trans. Magn. 2019, 55, 1–4. [Google Scholar] [CrossRef]
- Jung, Y.W.; Kim, H.K. Prediction of Nonlinear Stiffness of Automotive Bushings by Artificial Neural Network Models Trained by Data from Finite Element Analysis. Int. J. Automot. Technol. 2020, 21, 1539–1551. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, Q.; Wong, S.C.; Tse, M.; Cao, L. Reluctance Circuit and Optimization of a Novel Contactless Transformer. Proc. Chin. Soc. Electr. Eng. 2010, 30, 108–116. [Google Scholar]
- Lee, W.Y. Finite-Width Magnetic Mirror Models of Mono and Dual Coils for Wireless Electric Vehicles. IEEE Trans. Power Electron. 2013, 28, 1413–1428. [Google Scholar] [CrossRef]
- Steinmetz, C.P. On the Law of Hysteresis. Trans. Am. Inst. Electr. Eng. 1892, 9, 1–64. [Google Scholar] [CrossRef]
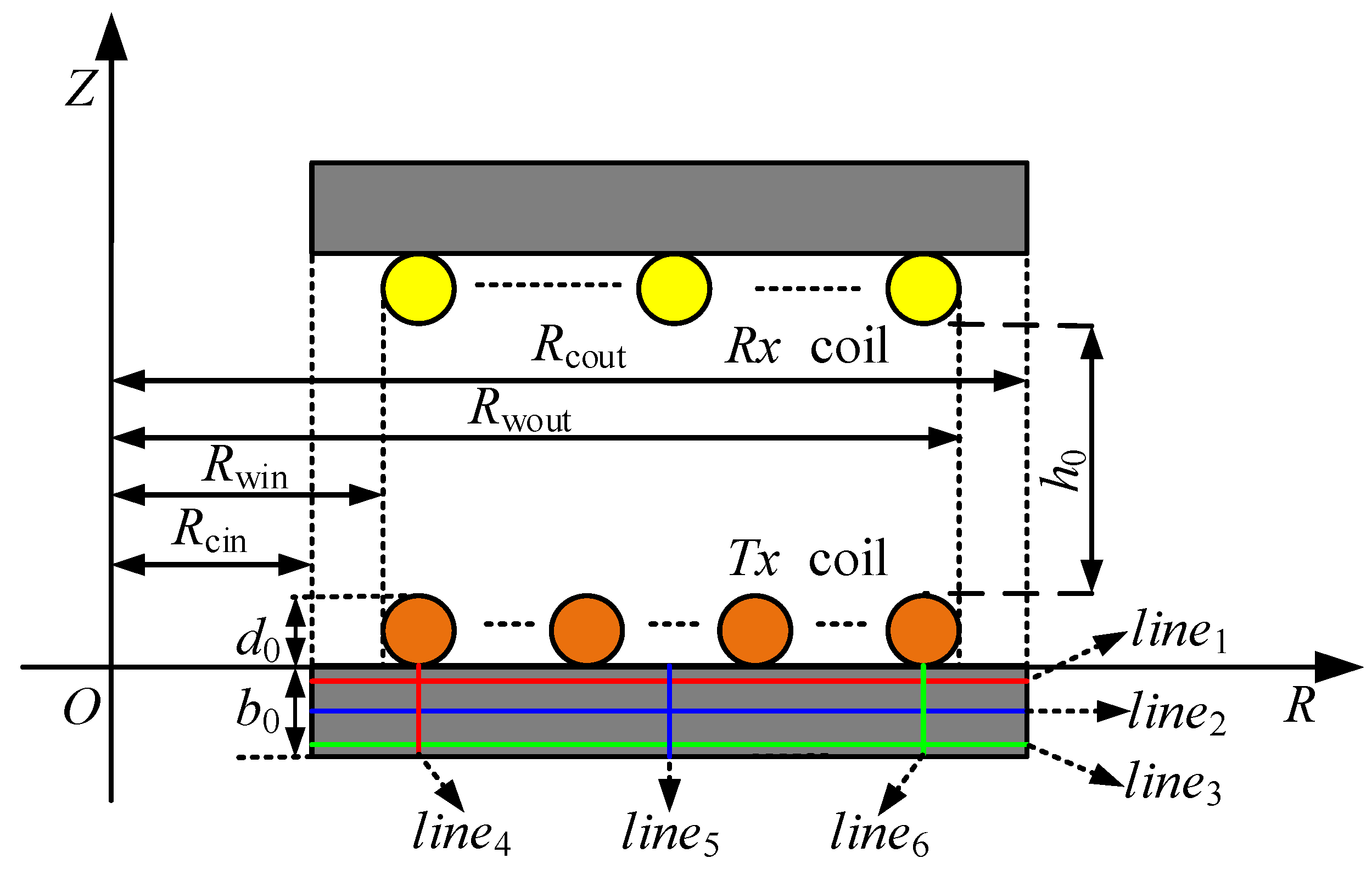


| Magnetic Coupling System Model Parameters | Parameters and Setup | |
|---|---|---|
| The inner and outer radius of the winding | Rwin = 100 mm | Rwout = 250 mm |
| The inner and outer radius of the core | Rcin = 70 mm | Rcout = 280 mm |
| Coil diameter and core thickness | d0 = 4.2 mm | b0 = 100 mm |
| Turns of transmitter winding and receiver winding | Np = 23 turns | Ns = 18 turns |
| Transmitter winding current and receiver winding current | Ip = 12 A | Is = 18 A |
| Core material | Philips-3C96 | |
| Boundary conditions | Balloon border | |
| The transmission distance between coils | h0 = 50 mm | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Fan, F.; Wang, J.; Chen, W. Core Loss Analysis and Modeling of a Magnetic Coupling System in WPT for EVs. World Electr. Veh. J. 2021, 12, 198. https://doi.org/10.3390/wevj12040198
Chen Q, Fan F, Wang J, Chen W. Core Loss Analysis and Modeling of a Magnetic Coupling System in WPT for EVs. World Electric Vehicle Journal. 2021; 12(4):198. https://doi.org/10.3390/wevj12040198
Chicago/Turabian StyleChen, Qingbin, Feng Fan, Jinshuai Wang, and Wei Chen. 2021. "Core Loss Analysis and Modeling of a Magnetic Coupling System in WPT for EVs" World Electric Vehicle Journal 12, no. 4: 198. https://doi.org/10.3390/wevj12040198
APA StyleChen, Q., Fan, F., Wang, J., & Chen, W. (2021). Core Loss Analysis and Modeling of a Magnetic Coupling System in WPT for EVs. World Electric Vehicle Journal, 12(4), 198. https://doi.org/10.3390/wevj12040198






