A Multi-Particle Physics-Based Model of a Lithium-Ion Battery for Fast-Charging Control Application
Abstract
:1. Introduction
2. Multi-Particle Battery Model
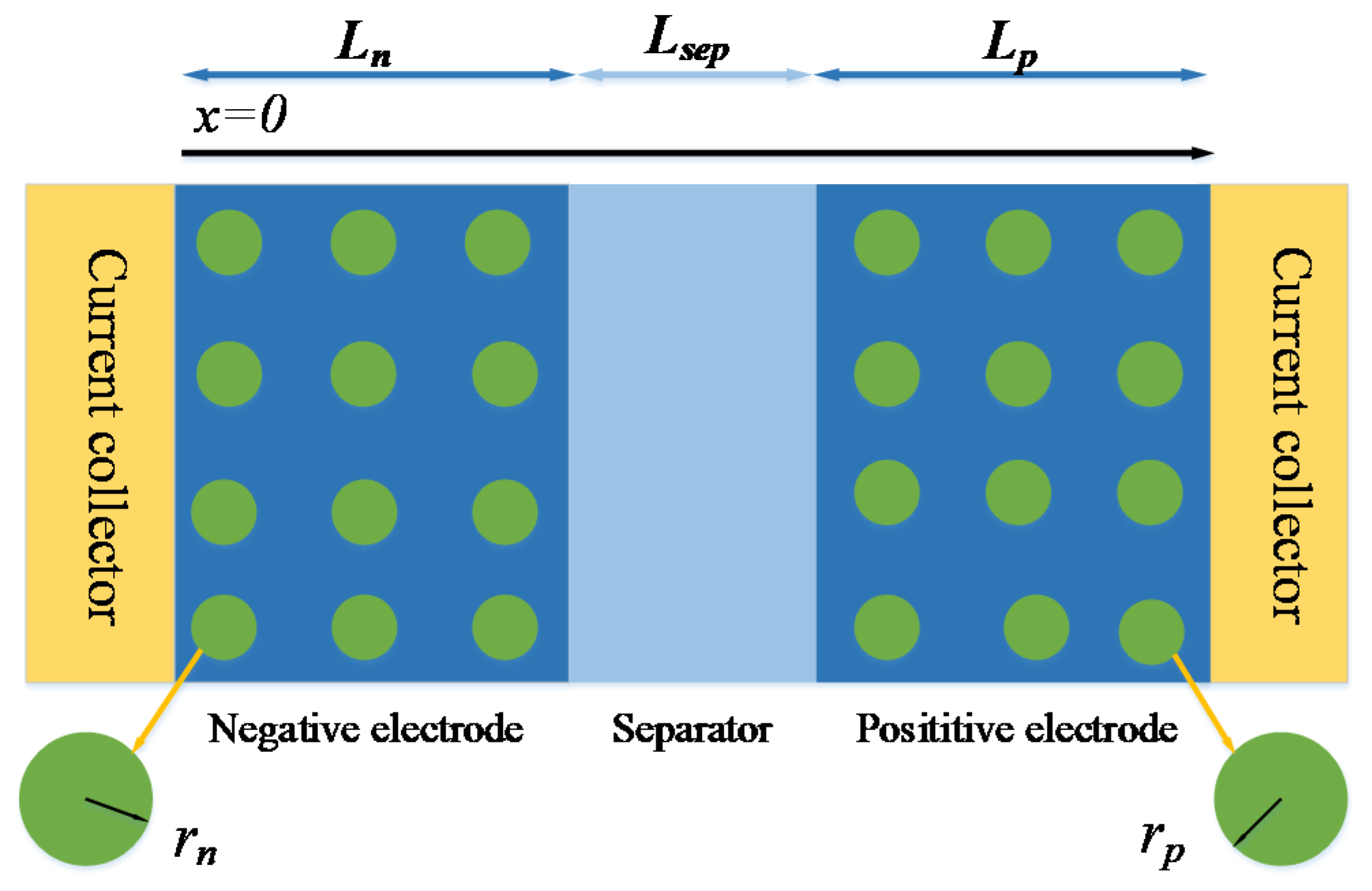
2.1. P2D Model
2.2. Battery Physical Modeling
2.3. Quasi-Linearization Approximation
3. Potential Balance Equation Calculation
3.1. Solid and Liquid Ohmic Potential
3.2. Electromotive Force and Liquid Overpotential
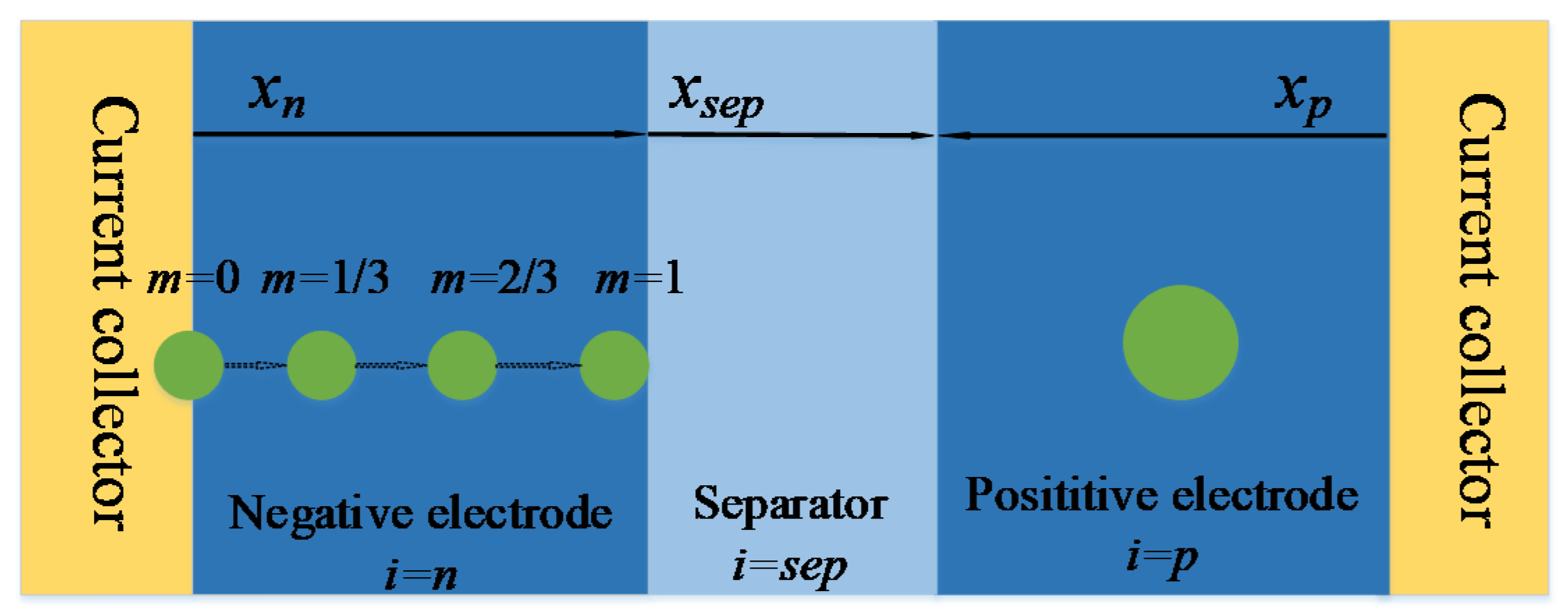
3.3. Calculation of the Heterogeneous Pore Wall Flux
4. The Update of Ion Concentration
5. Battery Terminal Voltage
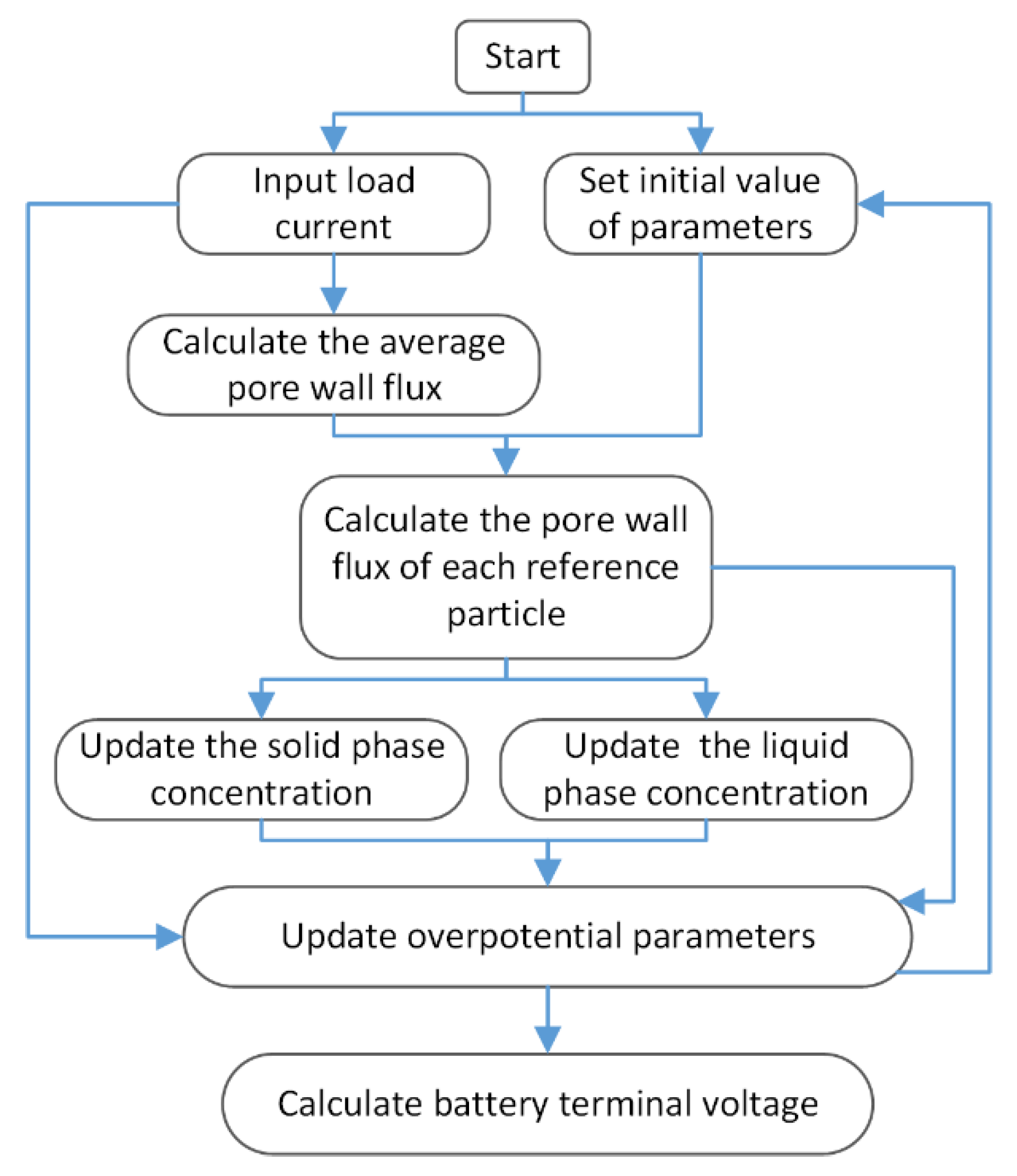
6. Model Simulation and Battery Experiment
7. Results and Discussion
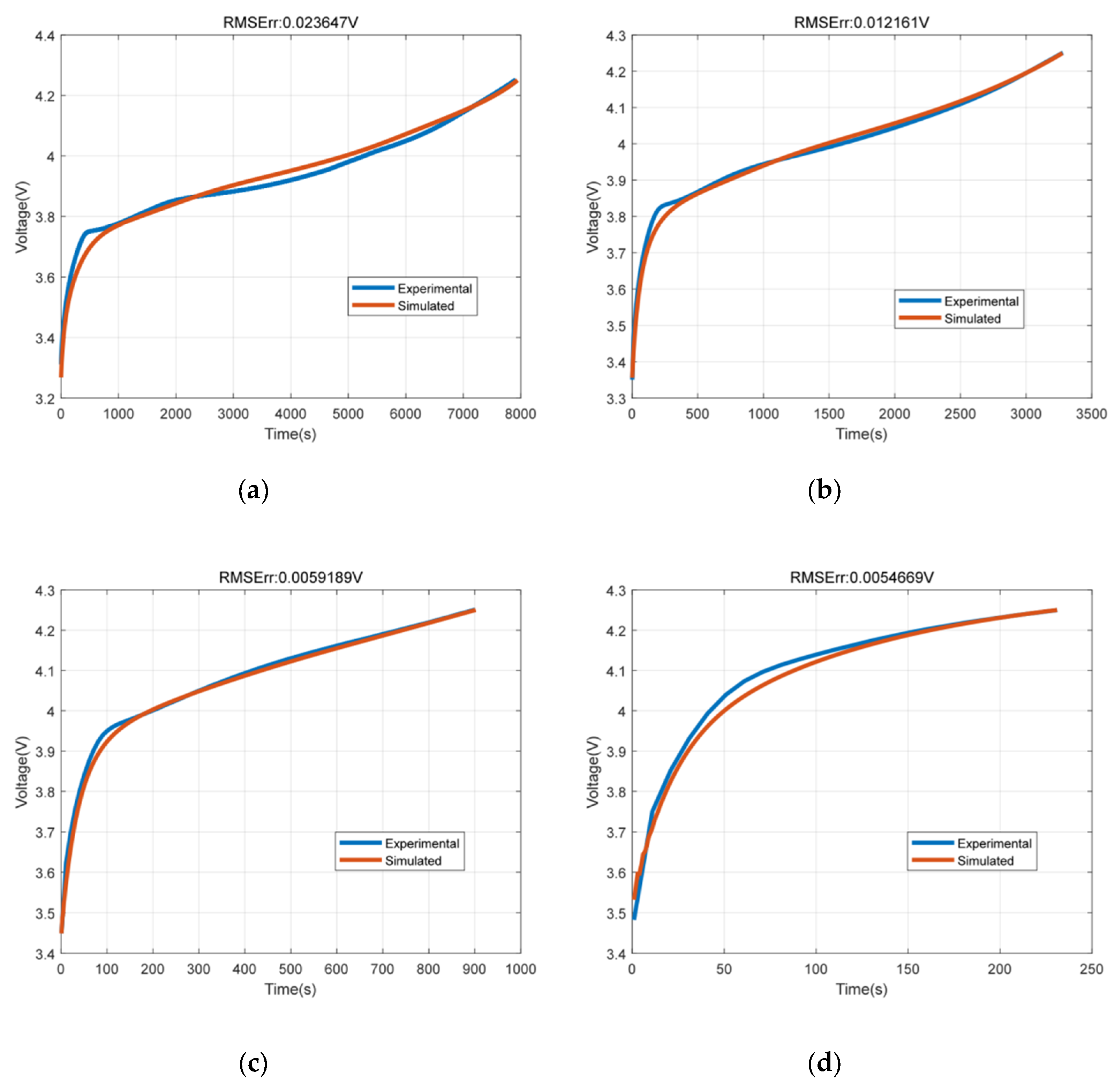
7.1. Terminal Voltage Results
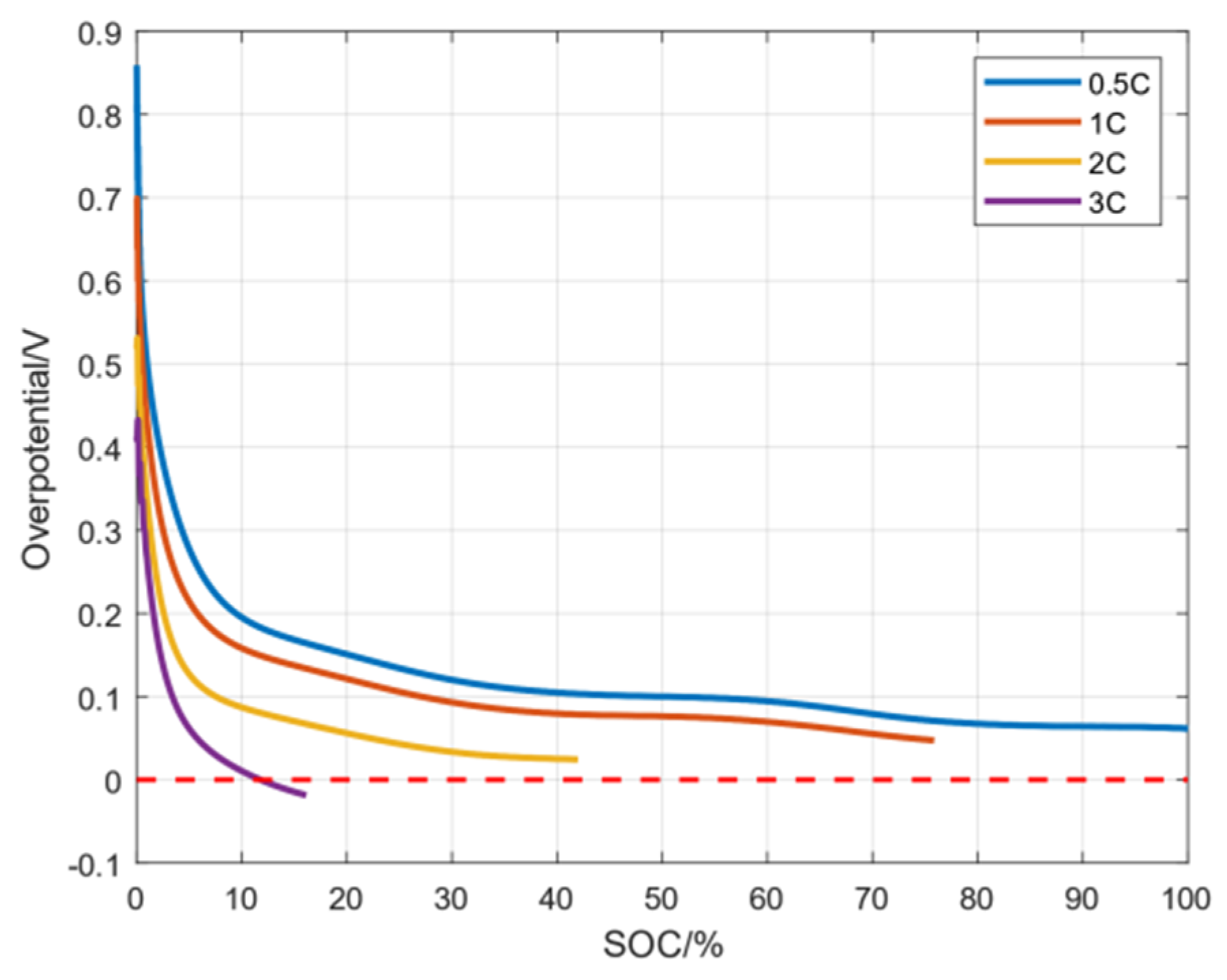
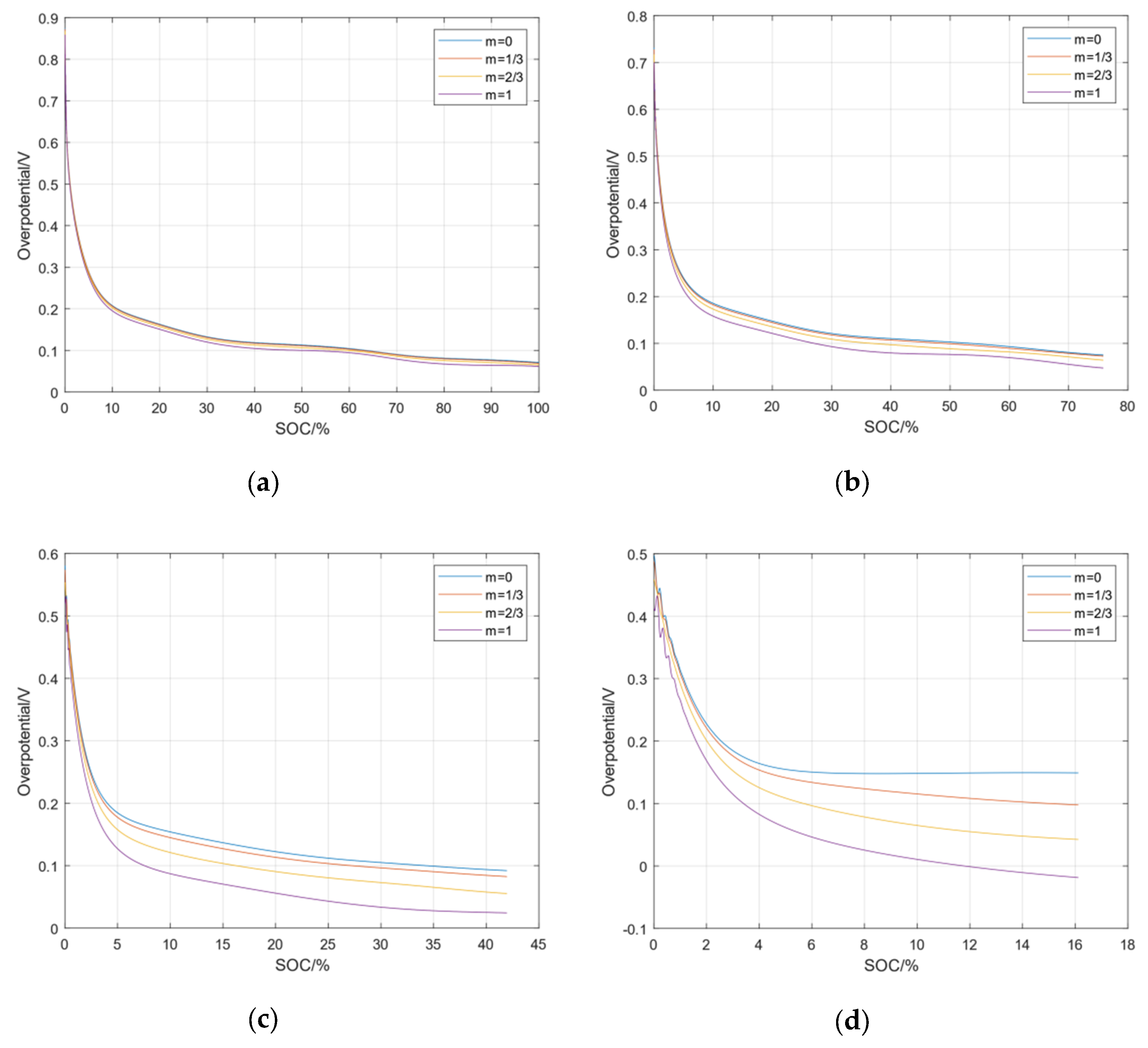
7.2. Simulation Analysis of Lithium Precipitation
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Subramanian, V.R.; Diwakar, V.D.; Tapriyal, D. Efficient macro-micro scale coupled modeling of batteries. J. Electrochem. Soc. 2005, 152, A2002–A2008. [Google Scholar] [CrossRef]
- Doyle, M. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell. J. Electrochem. Soc. 1993, 140, 1526. [Google Scholar] [CrossRef]
- Haran, B.S.; Popov, B.N.; White, R.E. Determination of the hydrogen diffusion coefficient in metal hydrides by impedance spectroscopy. J. Power Sources 1998, 75, 56–63. [Google Scholar] [CrossRef]
- Hui, P. Lithium ion battery parameter identification strategy based on extended single particle model. Acta Phys. Sin. 2018, 67, 259–269. [Google Scholar] [CrossRef]
- Majdabadi, M.M.; Farhad, S.; Farkhondeh, M.; Fraser, R.A.; Fowler, M. Simplified electrochemical multi-particle model for LiFePO4 cathodes in lithium-ion batteries. J. Power Sources 2015, 275, 633–643. [Google Scholar] [CrossRef]
- Kemper, P.; Li, S.E.; Kum, D. Simplification of pseudo two dimensional battery model using dynamic profile of lithium concentration. J. Power Sources 2015, 286, 510–525. [Google Scholar] [CrossRef]
- Jokar, A.; Rajabloo, B.; Désilets, M.; Lacroix, M. Review of simplified pseudo-two-dimensional models of lithium-ion batteries. J. Power Sources 2016, 327, 44–55. [Google Scholar] [CrossRef]
- Li, X.Y. Physical Model Simplification and Parameter Identification for State Estimation of the Retired Lithium Ion Battery; Harbin Institute of Technology: Harbin, China, 2018. [Google Scholar]
- Forman, J.C.; Bashash, S.; Stein, J.L.; Fathy, H.K. Reduction of an electrochemistry-based li-ion battery model via quasi-linearization and padé approximation. J. Electrochem. Soc. 2011, 158, A93–A101. [Google Scholar] [CrossRef]
- Han, X. Study on li-ion Battery Mechanism Model and State Estimation for Electric Vehicles; Tsinghua University: Beijing, China, 2014. [Google Scholar]
| Nomenclature | |||
|---|---|---|---|
| Electrochemical reaction overpotential (V) | Solid phase potential (V) | ||
| Gas constant (J/(mol·K)) | Liquid phase potential (V) | ||
| Temperature (K) | Liquid phase concentration | ||
| Faraday constant (C/mol) | Particle surface electromotive force (V) | ||
| Pore wall flux (mol·s−1·m−3) | SEI film potential (V) | ||
| Exchange current density (A/m3) | Liquid phase current density (V) | ||
| Average hole wall flow (mol·s−1·m−3) | Effective conductivity (S/m) | ||
| Input current (A) | Lithium intercalation rate (%) | ||
| Specific interfacial surface area (m−1) | Lithium ion concentration (mol/L) | ||
| Effective area of electrode (m2) | Activation coefficient | ||
| Electrode thickness (m) | Particle radius (s) | ||
| SEI film resistance (Ω) | Contact resistance (Ω) | ||
| Average concentration flux (mol/L) | Solid diffusion coefficient(m2/s) | ||
| Equation Name | Governing Equations |
|---|---|
| Butler–Volmer equation | |
| Potential balance equation | |
| Ohmic effect | |
| Liquid-phase diffusion equation | |
| Solid-phase diffusion equation | |
| Terminal voltage |
| Parameter | LiCoO2 Battery | ||
|---|---|---|---|
| PositiveElectrode | Separator | Negative Electrode | |
| Electrode thickness L (m) | 55 × 10−6 | 20 × 10−6 | 70 × 10−6 |
| Electrode plate area (m2) | 1.74 × 10−3 | / | 1.81 × 10−3 |
| Transference number | 0.363 | ||
| Effective conductivity in solid phase | 0.3055 | / | 40.7891 |
| Maximum Li+ concentration in solid phase | 56,000 | / | 26,390 |
| Liquid volume fraction | 0.18 | 0.55 | 0.4 |
| Specific interfacial surface area (m−1) | 144,000 | / | 165,000 |
| Particle radius Rs (m) | 15 × 10−6 | / | 10 × 10−6 |
| Initial liquid Li+ concentration (mol/L) | 1200 | 1200 | 1200 |
| Solid diffusion coefficient (m2/s) | 2.2 × 10−14 | / | 5 × 10−14 |
| Reaction rate constant(Am2.5/m1.5) | 5.8 × 10−11 | / | 8.8 × 10−11 |
| Liquid phase effective diffusion coefficient (m2/s) | 3.8184 × 10−11 | 2.0395 × 10−11 | 1.2649 × 10−11 |
| Liquid phase effective conductivity (S/m) | 0.0816 | 0.0153 | 0.0506 |
| Initial SOC | 0.85 | 0.02 | |
| Temperature (K) | 298.15 | ||
| Negative SEI film resistance (Ω) | 0.003 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Hua, W.; Tian, J.; Tian, Y. A Multi-Particle Physics-Based Model of a Lithium-Ion Battery for Fast-Charging Control Application. World Electr. Veh. J. 2021, 12, 196. https://doi.org/10.3390/wevj12040196
Li X, Hua W, Tian J, Tian Y. A Multi-Particle Physics-Based Model of a Lithium-Ion Battery for Fast-Charging Control Application. World Electric Vehicle Journal. 2021; 12(4):196. https://doi.org/10.3390/wevj12040196
Chicago/Turabian StyleLi, Xiaoyu, Wen Hua, Jindong Tian, and Yong Tian. 2021. "A Multi-Particle Physics-Based Model of a Lithium-Ion Battery for Fast-Charging Control Application" World Electric Vehicle Journal 12, no. 4: 196. https://doi.org/10.3390/wevj12040196
APA StyleLi, X., Hua, W., Tian, J., & Tian, Y. (2021). A Multi-Particle Physics-Based Model of a Lithium-Ion Battery for Fast-Charging Control Application. World Electric Vehicle Journal, 12(4), 196. https://doi.org/10.3390/wevj12040196








